1. Solución gráfica de equilibrio l´ıquido-vapor

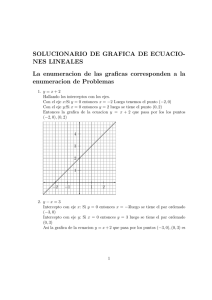
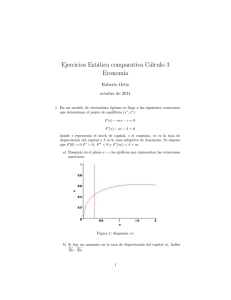
Termodinámica del equilibrio
Profesor: Alı́ Lara
Solución gráfica de equilibrio lı́quido-vapor
1.
Solución gráfica de equilibrio lı́quido-vapor
De los gráficos de fases podemos conocer la fracción de vapor
y lı́quido con respecto a la mezcla total. Para ello lo que
tenemos que hacer es un balance de masa global, si llamamos
F la cantidad de mezcla total, L la cantidad de lı́quido y V
la de vapor, entonces;
P ctte
vapor
Rocío
A
L
V
B
L+V
F =L+V ⇒1=
C
Burbuja
líquido
0
x1
L V
+
F
F
z1
y1 1
donde L/F y V /F representan la fracción de lı́quido y vapor,
respectivamente.
Si ahora hacemos un balance en el componente 1:
z1 F = x1 L + y1 V ⇒ z1 = x1
L
V
+ y1
F
F
(1)
Si combinamos esta ecuación con el balance global obtenemos que;
Si
L
L
L
L
z1 − y1
V
= 1 − ⇒ z1 = x 1 + y 1 − y 1 ⇒
=
F
F
F
F
F
x1 − y1
(2)
Si
L
V
V
V
V
z1 − x1
= 1 − ⇒ z1 = x1 − x1 + y1 ⇒
=
F
F
F
F
F
y1 − x1
(3)
donde el término V /F se conoce como Factor de Vaporización
El factor de vaporización (Ψ), es la cantidad de vapor que se
genera con respecto de la cantidad que se alimenta
Para soluciones binarias, es posible encontrar las composiciones de la fase lı́quida y vapor que
se encuentran en equilibrio a partir de una gráfica como la que se muestra a continuación. En dicha
gráfica se muestra la curva de equilibrio y la recta y = x.
La ecuación (3), puede reescribir se forma general de la siguiente manera:
(1 − Ψ)
z
x+
Ψ
Ψ
Esta lı́nea se conoce como recta de operación. Un método para obtener las composiciones x e
y para las corrientes de salida en equilibrio en función de Ψ consiste en hallar la intersección de la
lı́nea de operación con la lı́nea de equilibrio.
y=−
1
Recta de referencia y=x
yi
ψ=ψ
ψ=0
y
i
más volátil
ψ=1
x
z
xi
Como casos extremos, para Ψ = 0, la alimentación está a su temperatura de burbuja; para
Ψ = 1, la alimentación está a su temperatura de rocio.
2.
ELV entre fases ideales
El estudio del ELV cuando ambas fases de comportan idealmente es una simplificación del
comportamiento del sistema real pero que puede ser utilizado como base para medir la desviación
del comportamiento real del mismo.
En este caso, sabemos que cuando una mezcla se comporta de forma ideal, una fase gaseosa se
comporta de forma ideal f = P y que cuando el sistema está en equilibrio, se debe cumplir que:
fˆV = fˆL
(4)
i
+,V
y i fi
i
= xi fi+,L
yi P = xi Pisat → Ley de Raoult
(5)
(6)
Esta ley es el modelo más simple de ELV disponible, requiere que los componentes sean similares
quı́micamente y que cada componentes esté por debajo de su Pc .
En otras palabras, cuando ambas fases se comportan
como soluciones ideales entonces cada componente de la
T ctte.
solución ejerce una presión de parcial que es proporcional
ro
a su presión de saturación como componente puro y la
pa
P=P1+P2
PSat1
v
fracción molar en la fase lı́quida. Es decir, que para una
edPSat
2
mezcla binaria;
nó
is
Sat
y1 P = P1sat x1
(7)
P2=P 2 . x2
e
r
P
en tanto que para el componente 2;
P1=PSat1 . x1
0
x1
1
Sumando ambas ecuaciones;
y2 P = P2sat x2 = P2sat − P2sat x1
)
(
P = P1sat − P2sat x1 + P2sat
(8)
(9)
y esto es lo que da que la presión total del sistema es una recta cuya pendiente es (P1sat − P2sat ) e
intersecta en el origen en P2sat , tal como se muestra en la figura anterior.
Una vez obtenido el valor de P , la composición en la fase gaseosa del componente i será:
x1 P1sat
(10)
y1 =
(P1sat − P2sat ) x1 + P2sat
2
3.
Caso especial para hidrocarburos
Para el caso de ELV para hidrocarburos, se cuenta con una gráficas conocidas como Nomogramas de De Priester. Para el uso de estas gráficas se debe considerar:
Son válidos para hidrocarburos ligeros.
Se debe chequear los intervalos de P y T para cada uno de los nomogramas, para saber cuál
se puede usar.
Es necesario conocer P y T de nuestro sistema para obtener los Ki .
Si T y/o P de la mezcla en equilibrio se desconocen, se requiere un proceso de ensayo y error
A continuación se presenta la forma tı́pica de estos nomogramas.
P↑
Componente i
T↑
Ki
Con estas gráficas, es posible estimar las propiedades de saturación de un componente puro a
partir de la P o T del sistema y la condición Ki = 1
3