2-Teoria FUNCION CUADRATICA

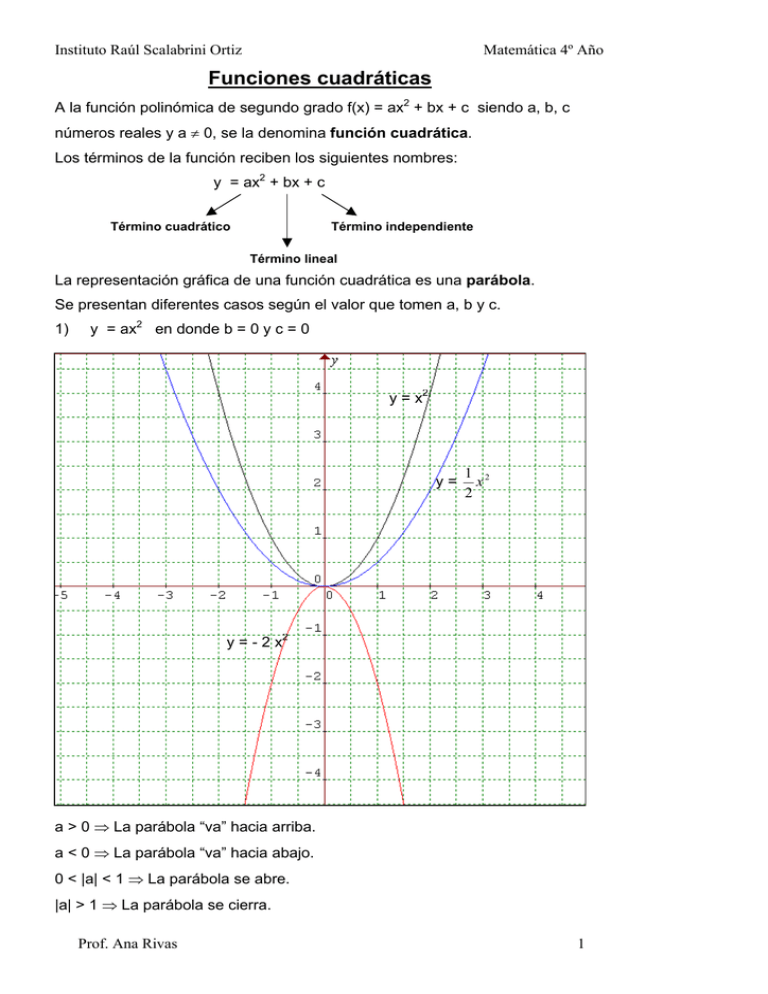
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
Funciones cuadráticas
A la función polinómica de segundo grado f(x) = ax2 + bx + c siendo a, b, c
números reales y a ≠ 0, se la denomina función cuadrática.
Los términos de la función reciben los siguientes nombres:
y = ax2 + bx + c
Término cuadrático
Término independiente
Término lineal
La representación gráfica de una función cuadrática es una parábola.
Se presentan diferentes casos según el valor que tomen a, b y c.
1)
y = ax2 en donde b = 0 y c = 0
y = x2
y=
1 2
x
2
y = - 2 x2
a > 0 ⇒ La parábola “va” hacia arriba.
a < 0 ⇒ La parábola “va” hacia abajo.
0 < |a| < 1 ⇒ La parábola se abre.
|a| > 1 ⇒ La parábola se cierra.
Prof. Ana Rivas
1
Instituto Raúl Scalabrini Ortiz
2)
Matemática 4º Año
y = x2 + c en donde a = 1 b = 0
y = x2 +2
y = x2
y = x2 - 3
c > 0 ⇒ La gráfica se desplaza hacia arriba.
c < 0 ⇒ La gráfica se desplaza hacia abajo.
3) y = a x2 + bx
en donde c = 0
Si a y b tienen el mismo
y =
1 2
x + 2x
2
signo, la gráfica se
desplaza hacia la
izquierda.
y =-
Prof. Ana Rivas
1 2
x - 2x
2
2
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
y= −
1 2
x + 2x
2
Si a y b tienen distinto
signo, la gráfica se
desplaza hacia la derecha.
y=
1 2
x − 2x
2
Resolve los ejercicios 1 y 2
Y después hace la actividad
con el graficador
Prof. Ana Rivas
3
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
Gráfica de la parábola
Para realizar el gráfico de una parábola, f(x) = ax2 + bx + c se deben
calcular los elementos de la misma y luego representarla:
1) Raíces de la parábola
2) Vértice de la parábola
3) Eje de simetría
4) Ordenada al origen
Vértice
Ordenada al origen
Punto Simétrico
Raíz
X1
Raíz
X2
Eje de Simetría
1) Raíces de la parábola:
Son los puntos de intersección de la gráfica con el eje x, vale decir que
f(x) = 0.
− b ± b2 − 4ac
x1,2 =
2a
2) Vértice de la parábola:
xv =
x1 + x2
2
Prof. Ana Rivas
o
xv =
−b
2a
4
Instituto Raúl Scalabrini Ortiz
yv = f (xv )
Matemática 4º Año
4ac − b2
yv =
4a
o
Las coordenadas del vértices son:
V = (xv ; yv )
3) Eje de Simetría:
Es la recta que tiene por ecuación:
x = xv
4) Ordenada al origen:
Es el punto de intersección de la gráfica con el eje y, vale decir que
f (0) = c
La parábola tiene un y sólo un punto de intersección con el eje Y. Las
coordenadas de ese punto son: ( 0 , c )
Ejemplo:
Dada la siguiente función f(x) = x2 + 2x – 3 calcular los elementos de la
misma:
a=1
b=2
c=-3
Raíces:
x1,2 =
− 2 ± 4 − 4.1.(−3) − 2 ± 4 + 12 − 2 ± 16 − 2 ± 4
=
=
=
2.1
2
2
2
x1 =
−2+4
=1
2
x2 =
−2−4
= −3
2
Vértice:
xv =
−2
= −1
2.1
Resolver el
ejercicio 3
yv = (- 1)2 + 2 . (- 1) – 3 = - 4
V = (- 1; - 4)
Eje de simetría:
x=-1
Ordenada al origen: ( 0; - 3)
Punto simétrico:
Prof. Ana Rivas
( - 2; - 3)
5
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
Posiciones relativas respecto del eje de las abscisas
Las raíces de una parábola, y = ax2 + bx + c se calculan mediante la
fórmula:
x1,2 =
− b ± b2 − 4ac
2a
Al radicando b2 – 4.a.c se lo llama discriminante, ya que el valor del mismo
sirve para discriminar la naturaleza de las raíces y se lo simboliza con la letra
griega ∆ ( delta)
∆ = b2 – 4.a.c
Si ∆> 0 ⇒ Raíces reales distintas
Si ∆= 0 ⇒ Raíces reales iguales
Si ∆< 0 ⇒ Raíces no reales
∆> 0
la grafica tiene dos puntos de
intersección con el eje x.
x1
x2
∆= 0
La gráfica tiene 1 punto de
intersección con el eje x
x1 ≡x2
Prof. Ana Rivas
6
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
∆< 0
La gráfica no tiene puntos de
intersección con el eje x
Ejemplo:
Calcular el discriminante e indicar cuantas raíces tiene:
a) y = x2 + 2 x – 3
∆ = 22 – 4. 1. (- 3) = 16
dos raíces distintas
b) y = x2 + 2 x + 1
∆ = 22 – 4. 1. 1 = 0
una raíz coincidente
c) y = x2 + 2 x + 2
∆ = 22 – 4. 2. 1 = - 4
no tiene raíces
Ejercicio:
Completar con > , <, o =, según corresponda:
∆ 0
∆ 0
∆ 0
Resolver los
ejercicio 4 y 5
Prof. Ana Rivas
7
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
Ecuación polinómica, canónica y factorizada
La función cuadrática puede ser expresada de distintas manera:
Se desarrolla el
cuadrado de un
binomio
Se buscan las
raíces
POLINOMICA
f(x) = ax2 + b x + c
Se busca el
vértice
Se aplica
propiedad
distributiva
CANÓNICA
f(x) = a.(x - x v)2+ yv
FACTORIZADA
f(x) = a.(x - x 1).(x – x2)
El vértice y el eje de
simetría se reconocen
con facilidad
Las raíces se identifican
en forma inmediata
Ejemplo:
1) Pasar de la forma canónica a la polinómica:
y = (x - 2)2 + 3 = x2 – 4 x + 4 + 3 = x2 – 4 x + 7
2) Pasar de la forma factorizada a la polinómica:
y = - 2(x + 1) (x + 3) = - 2( x2 + 3x + x + 3) = - 2( x2 + 4x + 3) = - 2 x2 - 8x - 6
3) Pasar de la forma polinómica a la factorizada:
y=
1 2 7
1
x - x + 5 ⇒ las raíces son x1 = 2 y x2 = 5 ⇒ y =
(x - 2) (x - 5)
2
2
2
4) Pasar de la forma polinómica a la canónica:
y=-
1 2
7
x – 3x ⇒las coordenadas del vértice son: V (3 ; 1)
2
2
⇒y=-
1
( x + 3)2 + 1
2
Resolver los
ejercicios del 6 al 8
Prof. Ana Rivas
8
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
Reconstrucción de una ecuación de segundo grado:
Dada la ecuación:
y = ax2 + bx + c
los coeficientes de su forma polinómica son: a, b y c; y las raíces son: x1, x2
Estos elementos se relacionan de la siguiente manera:
x1 + x2 = −
ax2 + bx + c = 0 ⇒
b
a
y
x1.x2 =
c
a
ax 2 bx c 0
bx c
+
+ = ⇒ x2 +
+ =0
a
a a a
a a
Ejemplo:
Reconstruir la ecuación de segundo grado cuyas raíces son
x1 = −
−
2
3
y
x2 =
3
2
2 3
b
5
b
b
5
+ =− ⇒ =− ⇒ =−
3 2
a
6
a
a
6
2 3 c
6 c
c
− . = ⇒ − = ⇒ = −1
3 2 a
6 a
a
⇒ x2 −
5
x −1 = 0
6
Resolver el
ejercicio 9
Prof. Ana Rivas
9
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
Máximos y mínimos. Crecimiento y decrecimiento
Una pelota es lanzada verticalmente hacia arriba, con una velocidad inicial
de 24 m/seg. La altura alcanzada por la pelota (h, expresada en metros) en
función del tiempo (t, expresado en segundos), está dada por la siguiente
fórmula: h(t) = - 3 t2 + 24 t.
Analizando el gráfico que describe la trayectoria de la pelota, se puede
concluir que:
•
La altura máxima alcanzada por la pelota es 48 m.
•
Alcanza la altura máxima a los 4 seg de haber sido lanzada.
•
El intervalo de tiempo en el cual la pelota asciende (desde que es
lanzada hasta el momento que alcanza la altura máxima) es (0;4) ;
intervalo de crecimiento.
•
El intervalo de tiempo en el cual la pelota desciende (desde que
alcanza la altura máxima hasta que vuelve a tocar el suelo) es (4;8) ;
intervalo de decrecimiento.
f(x) es creciente si: x2 > x1 ⇒ f(x2) > f(x1)
Una función continua es creciente en un
cierto intervalo de su dominio cuando al
aumentar los valores de la variable
independiente (x), aumentan los valores
de la variable dependiente(y).
Prof. Ana Rivas
f(x) es decreciente si: x2 > x1 ⇒ f(x2)< f(x1)
Una función continua es decreciente en
un cierto intervalo de su dominio cuando
al aumentar los valores de la variable
independiente (x), disminuyen los
valores de la variable dependiente(y)
10
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
En general, dada la función f(x) = ax2 + bx + c , se verifica que:
Si a > 0, la función:
•
Alcanza un mínimo en el vértice de
la parábola.
•
Decrece en el intervalo (- ∞; xv).
•
Crece en el intervalo (xv ;+∞).
Si a < 0, la función:
•
Alcanza un máximo en el vértice de la
parábola.
•
Crece en el intervalo (- ∞; xv).
•
Decrece en el intervalo (xv ;+∞).
Resolver los
ejercicios del
10 al 12
Prof. Ana Rivas
11
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
Intersección de parábolas, parábolas y rectas:
Resolver analíticamente un sistema de ecuaciones significa encontrar los
valores de las incógnitas que verifican simultáneamente las ecuaciones del
sistema.
Resolver gráficamente un sistema de ecuaciones significa encontrar los
puntos de intersección de ambas gráficas.
En los casos en que el sistema está formado al menos por una ecuación de
segundo grado, se puede reconocer cuantas soluciones tiene el mismo
analizando el discriminante de la ecuación cuadrática que surge al resolver
el sistema por el método de igualación o sustitución.
∆>0
∆=0
∆< 0
Dos puntos de
Un punto de
Ningún punto de
Intersección
Intersección
Intersección
La recta es secante a
La recta es tangente
la parábola
a la parábola
Sistema formado
por una recta y una
parábola
y = mx + d
y = ax2 +bx +c
La recta es exterior a
la parábola
Sistema formado
por dos parábolas
y = ax2 +bx +c
y = dx2 +ex +f
Ejemplo: a)
y=2x+1
y = – x2 – x + 5
Prof. Ana Rivas
12
Instituto Raúl Scalabrini Ortiz
Matemática 4º Año
2 x + 1 = – x2 – x + 5
– x2 – 3x + 4 = 0 ⇒ x1 = - 4 ∧ x2 = 1 ⇒ La recta es secante a
la parábola en los puntos (- 4; - 7) y (1;3).
b)
y = 3 x2 + 2x + 1
y = x2 + x - 4
3 x2 + 2x + 1 = x2 + x - 4
2 x2 + x + 5 = 0 ⇒ No tiene raíces reales.
Las parábolas no se cortan.
Resolver los ejercicios
del 13 al 15
Prof. Ana Rivas
13