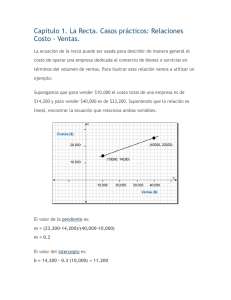
Texto Básico Geometría II

AUTOR: Dr. C. Juan Enrique García La Rosa
2008
PRÓLOGO
El presente texto básico ha sido confeccionado mediante una compilación de temas de
diferentes autores. El mismo consta de cinco capítulos en los que se aborda, en lo esencial,
los contenidos de la Estereometría como rama de la Geometría Euclideana o Geometría
Elemental y los contenidos de la Geometría Analítica del plano y del espacio.
Para mejor comprensión de los contenidos que se abordan en cada capítulo, se explican las
definiciones de los conceptos esenciales, las demostraciones de los teoremas por diferentes
vías y los procedimientos a seguir en la resolución de determinados ejercicios y problemas.
Al final de cada capítulo se proponen ejercicios y problemas para que los y las estudiantes
comprueben si han asimilado con solidez los contenidos que en este se han abordado.
1
ÍNDICE
CAPÍTULO 1: ESTEREOMETRÍA O GEOMETRÍA DEL ESPACIO.
1.1. Objeto de estudio de la Estereometría. Sistema de axiomas para su
construcción.
1.2. Algunos corolarios de los axiomas de la Estereometría.
CAPÍTULO 2: RECTAS Y PLANOS EN EL ESPACIO.
2.1. Paralelismo de rectas y planos.
2.2. Perpendicularidad de rectas y planos.
CAPÍTULO 3: ÁNGULOS EN EL ESPACIO.
3.1. Ángulos entre rectas y planos.
3.2. Ángulos diedros, triedros y poliedros.
CAPÍTULO 4: POLIEDROS Y CUERPOS DE REVOLUCIÓN: ÁREAS Y
VOLÚMENES.
4.1. Poliedros.
4.2. Cuerpos de revolución.
4.3. Volúmenes de cuerpos simples.
4.4. Volúmenes se cuerpos de revolución.
CAPÍTULO 5: GEOMETRÍA ANALÍTICA DEL PLANO Y DEL ESPACIO.
5.1. Nociones de Álgebra Vectorial.
5.2. Estudio analítico del plano.
5.3. Estudio analítico de la recta en el espacio.
5.4. Estudio analítico de las cónicas.
PÁG. 3
PÁG. 3
PÁG. 4
PÁG. 9
PÁG. 9
PÁG. 15
PÁG. 30
PÁG. 30
PÁG. 35
PÁG. 42
PÁG. 42
PÁG. 47
PAG. 50
PAG. 56
PÁG. 64
PAG. 64
PAG. 85
PAG. 92
PAG. 100
2
CAPÍTULO 1: ESTEREOMETRÍA O GEOMETRÍA DEL ESPACIO.
En el texto básico Geometría I correspondiente al básico curricular del mismo nombre, se
abordaron los contenidos de la Geometría Plana o Planimetría, los cuales comenzamos a
introducir, a partir de un sistema de axiomas convenientemente seleccionado que se
construyó sobre la base de los conceptos básicos: punto, recta y plano. De estos axiomas se
construyó la teoría de la Planimetría que estudiamos en esta carrera.
De manera análoga comenzaremos el estudio de la Estereometría o Geometría del Espacio,
con la cual culminaremos el tratamiento de los contenidos esenciales de la Geometría
Euclideana.
1.1. Objeto de estudio de la Estereometría. Sistema de axiomas para su construcción.
La Estereometría es la parte de la Geometría en la que se estudian las figuras del espacio.
En la Estereometría, igual que en la Planimetría, las propiedades de las figuras geométricas
se establecen mediante la demostración de teoremas correspondientes, partiendo de las
propiedades de las figuras elementales expresadas por los axiomas.
En el espacio los conceptos primarios o primitivos son también el punto, la recta y el plano.
La introducción de esta nueva Geometría, hace que se amplíe el sistema de axiomas ya
asumido para la Planimetría mediante la incorporación de un grupo de axiomas que,
conjuntamente con los ya existentes, expresan las propiedades fundamentales de los planos
en el espacio.
El sistema de axiomas para la Estereometría quedará conformado de la siguiente manera:
I. Axiomas de incidencia.
I1. Cualquiera que sea la recta, existen puntos que pertenecen a la recta y puntos que no
pertenecen a la recta.
I2. Cualesquiera que sean dos puntos, existe una recta y sólo una que pasa por estos
puntos.
I3. Cualquiera sea el plano existen puntos que pertenecen a este plano y puntos que
no le pertenecen.
I4. Si dos planos diferentes tienen un punto común, se cortan según una recta.
I5. Si dos rectas distintas tienen un punto común, se puede trazar por estas un plano y
sólo uno.
II. Axiomas de orden
II1. De tres puntos de una recta, uno de ellos, y sólo uno, se halla entre los otros dos.
II2. Un punto situado en una recta la divide en dos semirrectas. Los puntos de una semirrecta
no están separados por el punto de división. Los puntos de diferentes semirrectas están
separados por este punto.
II3. Toda recta divide el plano en dos semiplanos. Si los extremos de un segmento cualquiera
pertenecen a un mismo semiplano, el segmento no corta la recta. Si los extremos del
segmento pertenecen a diferentes semiplanos, el segmento corta la recta.
3
III. Axiomas de medición de segmentos y ángulos (son las propiedades fundamentales
de la medición de segmentos y ángulos).
III1. Todo segmento tiene una longitud determinada mayor que cero,
III2. Si el punto C de la recta AB se halla entre los puntos A y B, la longitud del segmento
AB es igual a la suma de las longitudes de los segmentos AC y BC .
III3. Todo ángulo tiene una amplitud en grados determinada mayor que cero. El ángulo llano
es igual a 1800.
III4. Si una semirrecta OC parte del vértice O de un ángulo AOB y pasa entre sus lados, el
ángulo AOB es igual a la suma de las amplitudes de los ángulos AOC y BOC.
IV. Axiomas de construcción de segmentos y ángulos (son las propiedades
fundamentales de la construcción de segmentos y ángulos).
IV1. Cualquiera que sea el número positivo m, en una semirrecta se puede construir a partir
de su punto de origen un segmento de longitud m (en centímetros) y sólo uno.
IV2. Cualquiera que sea el número positivo n menor que 180, se puede construir a partir de
una semirrecta dada y en el semiplano dado, un ángulo de n grados, y sólo uno.
V. Axioma del primer criterio de igualdad de triángulos.
Si dos triángulos tienen dos lados y el ángulo comprendido entre estos respectivamente
iguales, los triángulos son iguales.
VI. Axioma de las paralelas.
Por todo punto B que no se halla en la recta a se puede trazar en el plano no más de una
paralela a la recta a.
Como bien puede apreciarse al sistema de axiomas de la Planimetría se le han incorporado
tres axiomas al grupo de los de incidencia (subrayados y en negritas), quedando así
conformado el sistema de axiomas sobre la base del cual construiremos la teoría de la
Estereometría.
El axioma I4 afirma que si dos planos distintos α y β tienen un punto común C, existe una
recta c que pertenece a cada unos de estos planos. Además, todo punto C que pertenezca a
ambos planos ha de pertenecer a la recta c.
1.2. Algunos corolarios de los axiomas de la Estereometría.
Teorema 1.1: Por una recta y un punto que no le pertenece se puede trazar un plano y sólo
uno.
Demostración:
Según el axioma I1, se tiene una recta a y un punto B que no le pertenece. También por este
axioma, sea A un punto que pertenece a esa recta (figura 1.1). Por el axioma I2, por los
puntos A y B se puede trazar una recta b y sólo una. Las rectas a y b son distintas, pues el
4
punto B de la recta b no pertenece a la recta a. El punto A es común para las rectas a y b.
Por tanto, por el axioma I5 por estas rectas se puede trazar un plano α.
α/
a
a
α
A
A
Figura 1.1
B
b
Figura 1.2
Demostremos ahora que el plano α que pasa por la recta a y el punto B es único.
Supongamos que existe otro plano α / distinto de α, que pasa por la recta a y el punto B. Por
el axioma I5, los planos α y α / se cortan según una recta, pues son distintos. Por
consiguiente, cualesquiera tres puntos comunes de los planos α y α / se hallan en esta
recta. Pero, el punto B y dos puntos cualesquiera de la recta a no se encuentran
indiscutiblemente en una recta. Hemos llegado a una contradicción. Queda demostrado
completamente el teorema.
Teorema 1.2: Si dos puntos de una recta pertenecen a un mismo plano, toda la recta
pertenece a este plano.
Demostración (figura 1.2):
Sean a la recta y α el plano. Según el axioma I1, existe un punto A que no está en la recta a.
Tracemos el plano α / , que pasa por la recta a y por el punto A. Si el plano α / coincide con α,
el plano α contiene la recta a, que es lo que afirma el teorema. Si el plano α / es distinto de α,
estos planos se cortan según la recta a / que contiene los dos puntos de la recta a. En virtud
del axioma I2, las rectas a y a / coinciden y, por consiguiente, la recta a se encuentra en el
plano α. Queda demostrado el teorema.
Del teorema 1.2 se deduce que el plano y la recta que no está en él, no se cortan o se
cortan en un punto.
Teorema 2.3: Por tres puntos que no se hallan en una recta se puede trazar un plano, y sólo
uno.
Demostración (figura 1.3):
Sean A, B y C tres puntos que ni se hallan en una recta. Tracemos las rectas AB y AC.
Estas rectas son distintas ya que los puntos A, B y C no están alineados.
5
B
α
A
C
Figura 1.3
Según el axioma I5, por las rectas AB y AC se puede trazar un plano α. Este plano contiene
los puntos A, B y C.
Demostremos que el plano α es único. Efectivamente, en virtud del teorema 1.2, el plano
que pasa por los puntos A, B y C contiene las rectas AB y AC. Pero, según el axioma I5, este
plano es único. Queda demostrado el teorema.
Teorema 1.4: Todo plano divide el espacio en dos semiespacios. Si los puntos X e Y
pertenecen a un mismo semiespacio, el segmento XY no corta el plano. En cambio, si los
puntos X e Y pertenecen a distintos semiespacios, el segmento XY corta el plano.
Demostración:
Sea α un plano. Tomemos un punto A que no se halla en el plano α. Este punto existe por el
axioma I3. Dividamos todos los puntos del espacio que no pertenecen al plano α en dos
clases, a tenor con el criterio siguiente: incluiremos el punto X en la primera clase si el
segmento AX no corta el plano α; incluiremos el punto X en la segunda clase si el segmento
AX corta al plano α. Así, todo punto X del espacio que no pertenezca al plano α será incluido
en una clase. Mostremos que esta división del espacio posee las propiedades indicadas en
el teorema.
Supongamos que los puntos X e Y pertenecen a la primera clase. Tracemos por los puntos
A, X e Y el plano α / . Si el plano α / no corta al plano α, el segmento XY , que está en el
plano α / , tampoco lo corta. Supongamos que el plano α / corta al plano α (figura 1.4)
α/
a
A
X
α
Y
Figura 1.4
6
Puesto que los planos son distintos, la intersección de los mismos es una recta a. La recta a
divide al plano α / en dos semiplanos. Los puntos X e Y pertenecen a un mismo semiplano;
concretamente al que contiene el punto A. por esto, el segmento XY no corta la recta a ni,
por consiguiente, el plano α.
Si los puntos X e Y pertenecen a la segunda clase, el plano α / corta indudablemente al
plano α, ya que el segmento AX corta a α. Los puntos X e Y pertenecen a uno de los
semiplanos que en que la recta a divide al plano α. Es decir, el segmento XY no corta la
recta a ni, por consiguiente, al plano α.
Finalmente, si el punto x pertenece a una clase y el punto Y a la otra, el plano α / corta a α y
los puntos X e Y se encuentran en distintos semiplanos del plano α / respecto a la recta a.
Por eso, el segmento XY corta la recta a y, por ende, al plano α. Queda demostrado el
teorema.
Hagamos ahora una observación al axioma I1. En tanto que este axioma es un axioma de la
Estereometría, el mismo adquiere un sentido distinto del que tiene en la Planimetría. En la
Planimetría afirma la existencias de puntos fuera de la recta en el plano al que esta recta
pertenece. Precisamente en este sentido lo hemos empleado al construir la Geometría del
Plano. Ahora, este axioma afirma la existencia general de puntos que no se hallan en la
recta. Esto no implica directamente la existencia de puntos fuera de la recta en el plano al
que esta pertenece. Esto exige una demostración especial. Demos esta demostración.
Sea α un plano y sea a una recta en este plano. Demostremos la existencia en el plano α de
puntos que no se hallan en la recta a. Tomemos un punto A de la recta a y in punto B fuera
del plano α. Tracemos el plano α / por la recta a y por el punto B (figura 1.5).
C
B
β
a
α/
α
A
Figura 1.5
Tomemos un punto C fuera del plano α / y tracemos el plano β que pasa por la recta AB y
por el punto C. Los planos α y β se cortan según una recta que pasa por el punto A. los
puntos de esta recta distintos de A están en el plano α y fuera de la recta a, que es lo que se
quería demostrar.
7
EJERCICIOS DEL CAPÍTULO
1. Sean a una recta y A un punto fuera de ella. Demuéstrese que todas las rectas que
pasan por el punto A y que cortan a la recta a están en un mismo plano.
2. Sean a y b dos rectas que no se hallan en un mismo plano y C un punto que no está en
ninguna de estas rectas. Demuéstrese que por el punto C se puede trazar una recta, y
sólo una, que corta las rectas a y b.
3. Sean a1 , a 2 , a3 ,... unas rectas. Demuéstrese que si dos cualesquiera de estas rectas se
cortan, todas ellas pasan por un mismo punto o pertenecen a un mismo plano.
4. Demuéstrese que si cuatro puntos cualesquiera de una figura están en un mismo plano,
la figura plana, o sea, se encuentra en un mismo plano.
5. ¿Por qué no cojea una mesa de tres patas?
6. ¿Por qué cojea una mesa de cuatro patas con una más corta que las otras?
7. Se tienen 7 puntos entre los que hay 4 en un mismo plano. ¿Cuántos planos
determinan?
8. ¿Cuántos planos determinan 20 puntos, no hallándose nunca 4 de ellos en el mismo
plano, ni tres en línea recta? ¿Cuántos planos determinan n puntos en las mismas
condiciones?
9. Si 4 puntos no están en un plano, prueba que 3 de ellos no están alineados.
8
CAPÍTULO 2: RECTAS Y PLANOS EN EL ESPACIO.
En este capítulo estudiaremos las definiciones y propiedades relacionadas con: rectas
paralelas en el espacio; paralelismo de rectas y planos; paralelismo de planos; rectas
cruzadas o alabeadas; perpendicularidad de rectas en el espacio; perpendicularidad de
rectas y planos; perpendicular y oblicua y; perpendicularidad de planos.
2.1. Paralelismo de rectas y planos.
Definición 2.1: Dos rectas en el espacio se llaman paralelas si están en un mismo plano y
no se cortan.
Teorema 2.1: Por el punto que está fuera de una recta se puede trazar una recta paralela a
esta y sólo una.
Demostración:
Sea a una recta y sea A un punto que no se halla en esta recta (figura 2.1). Tracemos el
plano α que pasa por la recta a y por el punto A. Tracemos en el plano α la recta a1 que
pasa por el punto A y que es paralela a la recta a. Demostremos que la recta a1 , paralela a
la recta a, es única.
a1
a
A
α
Figura 2.1
Supongamos que existe otra recta a 2 que pasa por el punto A y que es paralela a la recta a.
Por las rectas a y a 2 se puede trazar el plano α 2 . Este plano pasa por la recta a y por el
punto A, o sea, según el teorema 1.1, coincide con α . Ahora, basándonos en el axioma de
las paralelas, deducimos que a1 y a 2 coinciden. Queda demostrado el teorema.
Teorema 2.2: Si la recta a es paralela a las rectas b y c, las rectas b y c son paralelas.
Demostración:
El caso en que las rectas a, b y c están en un plano ha sido considerado en la Planimetría.
Supongamos, por eso, que las rectas no se hallan en un plano. Sea β el plano en el que
están las rectas a y b y sea γ el plano en que se encuentran las rectas a y c. Los planos β
y γ son distintos (figura 2.2).
9
b1
b
β
B
γ/
a
γ
A
c
Figura 2.2
Tomemos en la recta b un punto B y tracemos el plano γ / que pasa por la recta c y el punto
B. El plano γ / corta al plano β según la recta b1 . Afirmamos que la recta b1 es paralela a la
recta a.
Supongamos que la recta b1 corta a la recta a en un punto A. el punto A pertenece al plano
γ y al plano γ / , o sea, está en la recta c según la que se cortan estos planos. Hemos
llegado a una contradicción ya que las rectas a y c son paralelas y no pueden tener el punto
A común. Por esto, la recta b1 es paralela a la recta a.
Según el axioma de las paralelas, la recta b1 , paralela a la recta a, debe coincidir con la
recta b. puesto que la recta b coincide con b1 , las rectas b y c están en un mismo plano, en
el plano γ / . No pueden cortarse ya que esto estaría en contradicción con el teorema 2.1,
pues ambas son paralelas a la recta a. Es decir, las rectas b y c se hallan en un plano, o
sea, son paralelas. Queda demostrado el teorema.
Definición 2.2: La recta y el plano se denominan paralelos si no se cortan.
Teorema 2.3: El plano α y la recta a , que no le pertenece, son paralelos si en el plano α
existe una recta a1 paralela a la recta a .
Demostración (figura 2.3):
Consideremos el plano α / que pasa por las rectas a y a1 . Es distinto del plano α ya que la
recta a no se halla en el plano α . Los planos α y α / se cortan según la recta a1 . Si la recta
a cortase al plano α , el punto de intersección pertenecería a la recta a1 . Pero esto es
imposible, pues las rectas a y a1 son paralelas. Por lo tanto, la recta a no corta al plano α .
Queda demostrado el teorema.
10
a
α/
a1
α
A
Figura 2.3
Teorema 2.4: Si una recta es paralela a cada uno de dos planos que se cortan, también es
paralela a la recta de intersección de los mismos.
Demostración:
Sean α y β dos planos secantes, c la recta según la que se cortan estos planos y c1 una
recta paralela a cada uno de los planos α y β (figura 2.4). Debemos demostrar que las
retas c y c1 son paralelas.
c
c1
γ
α
a
β
b
Figura 2.4
Tracemos el plano γ que pasa por la recta c1 y por un punto cualquiera de la recta c. El
plano γ se corta con los planos α y β según las rectas a y b paralelas a c1 . Efectivamente,
las rectas a y b (pertenecientes a los planos α y β paralelos a la recta c1 ) no pueden cortar
esta recta.
Por el axioma de las paralelas, las rectas a y b coinciden. Como quiera que la recta a se
halla en el plano α y la recta b está en el plano β , las rectas a y b deben coincidir con la
recta c, que es la intersección de los planos α y β . Es decir, la recta c es paralela a la recta
c1 . Queda demostrado el teorema.
11
Definición 2.3: Dos planos se denominan paralelos si no se cortan.
Teorema 2.5: Si un plano α es paralelo a dos rectas que se cortan y que pertenecen a un
plano β , los planos α y β son paralelos.
Demostración:
Sean b1 y b2 dos rectas que se cortan en el plano β , paralelas al plano α (figura 2.5). Los
planos α y β son distintos. Supongamos que se cortan según la recta c.
β
c
b2
α
b1
Figura 2.5
Las rectas b1 y b2 no cortan al plano α ni, por consiguiente, a la recta c de este plano. Pero
esto es imposible en virtud del axioma de las paralelas ya que las rectas b1 , b2 y c se hallan
en un mismo plano, en el plano β . Hemos llegado a una contradicción. Queda demostrado
el teorema.
Teorema 2.6: Por todo punto A exterior a un plano α pasa un plano paralelos a este, y sólo
uno.
Demostración:
Tomemos en el plano α dos rectas cualesquiera a1 y a 2 que se corten. Tracemos por el
punto A las rectas b1 y b2 paralelas a estas. Según el teorema 2.5, el plano que pasa por las
rectas b1 y b2 es paralelo al plano α .
Supongamos que por el punto A pasan dos planos distintos β 1 y β 2 , paralelos al plano α
(figura 2.6). Sea b la recta de intersección de estos planos. Tomemos en el plano β 2 un
punto B2 que no se halla en la recta b y tomemos un punto C en el plano α . Tracemos el
plano γ que pasa por los puntos A, B2 y C, el cual corta a los planos β 1 y β 2 según las
rectas b1 y b2 y al plano α según la recta c. las rectas b1 y b2 no cortan a la recta c porque
no cortan al plano γ , en el que están dichas rectas. Según el axioma de las paralelas, las
rectas b1 y b2 coinciden. Es decir, los planos β1 y β 2 pasan por dos rectas secantes b y b1
distintas, por lo tanto, coinciden según el axioma I5. Hemos llegado a una contradicción.
Queda demostrado el teorema.
12
b
B2
b2
A
γ
β2
b1
β1
c
Figura 2.6
C
α
Teorema 2.7: Si una recta corta a un plano entonces, corta a cualquier plano paralelo a
este. Si un plano corta a una recta entonces, corta a cualquier recta paralela es esta.
Demostración:
Demostremos la primera afirmación.
Sea a la recta que corta al plano α y sea el plano β , tal que β // α . Demostremos que la
recta a corta al plano β (figura 2.7).
a
α
γ
Figura 2.7
b
β
b1
Consideremos el plano γ que pasa por la recta a, que corta al plano β según la recta b1 y al
plano α según la recta b. Si la recta a no cortase al plano β , las rectas a y b serían paralelas
a la recta b1 . Pero esto es imposible por el axioma de las paralelas. Queda demostrada la
primera afirmación del teorema.
13
Demostramos la segunda afirmación de teorema. Supongamos que el plano α corta a la
recta b. Demostremos que corta a toda recta b1 paralela a b. Tracemos por las rectas b y b1
el plano β , el cual corta al plano α según la recta a (figura 2.8).
b1
b
β
Figura 2.8
α
a
Si el plano α no cortase a la recta b1 , las rectas a y b serían paralelas a la recta b1 . Pero
esto es imposible por el axioma de las paralelas. Queda demostrado completamente el
teorema.
Teorema 2.8: Los segmentos de rectas paralelas comprendidos entre planos paralelos son
iguales.
Demostración:
Sean dos planos α y β , tal que α // β (figura 2.9). Sean las rectas c1 y c 2 , c1 // c 2 , que
cortan a dichos planos.
c2
c1
A2
A1
α
Figura 2.9
B2
B1
β
14
La recta c1 corta los planos en los puntos A1 y B1 y la recta c 2 , en los puntos A2 y B2 .
Demostremos la igualdad de los segmentos A1 B1 y A2 B2 .
El cuadrilátero A1 B1 B2 A2 está en el mismo plano que las paralelas c1 y c 2 . Sus lados
opuestos A1 B1 y A2 B2 son paralelos por premisas del teorema. Los lados A1 A2 y B1 B2 son
paralelos porque α // β . Luego, el cuadrilátero A1 B1 B2 A2 es un paralelogramo, por lo tanto,
sus lados opuestos A1 B1 y A2 B2 son iguales. Queda demostrado el teorema.
Definición 2.4: Dos rectas, en el espacio, que no se encuentran en un mismo plano se
denominan cruzadas o alabeadas. Por consiguiente, las rectas que se cruzan no son
paralelas ni se cortan.
Teorema 2.9: Dos rectas cruzadas cualesquiera se hallan en planos paralelos.
Demostración:
Sean a y b dos rectas que se cruzan. Tracemos por un punto cualquiera de la recta a la
recta a1 paralela a la recta b y por un punto cualquiera de la recta b la recta b1 paralela a la
recta a (figura 2.10).
a
A
a1
α
Figura 2.10
b1
B
b
β
Tracemos por las rectas a y a1 el plano α y por las rectas b y b1 el plano β . Los planos
trazados son distintos, pues de lo contrario las rectas a y b estarían en un mismo plano. Los
planos α y β son paralelos porque las rectas a y a1 son paralelas al plano β . Queda
demostrado el teorema.
2.2. Perpendicularidad de rectas y planos.
El concepto de perpendicularidad de rectas para que el caso que se corten y, por
consiguiente, que pertenecen a un mismo plano ya fue estudiado en la Planimetría y es bien
conocido. En este epígrafe definamos el mismo para el caso de rectas que se cruzan. Para
ello, demostremos primeramente el siguiente teorema.
15
Teorema 2.10: Si dos rectas a y b que se cortan, son perpendiculares entonces, las rectas
a1 y b1 paralelas a estas también son perpendiculares.
Demostración:
Si las rectas a, b, a1 y b1 están en un mismo plano, el teorema ya es conocido de la
Planimetría. Supongamos, por eso, que las rectas no pertenecen a un mismo plano. En este
caso las rectas a y b están en un plano α y las rectas a1 y b1 están en un plano β (figura
2.11).
a C
b
A
B
α
Figura 2.11
b1
a1
C1
B1
A1
β
Según el teorema 2.3, las rectas a y b son paralelas al plano β . En virtud del teorema 2.5,
los planos α y β son paralelos.
Sea C el punto de intersección de las rectas a y b y sea C1 el punto de intersección de las
rectas a1 y b1 . Tracemos en el plano que contiene las rectas a y a1 la paralela a la recta
CC1 , que corta a las rectas a y a1 en los puntos A y A1 , respectivamente. Tracemos
análogamente en el plano que contiene las rectas b y b1 la paralela a la recta CC1 , que corta
a las rectas b y b1 en los puntos B y B1 , respectivamente.
Los cuadriláteros CAA1C1 y CBB1C1 son paralelogramos ya que sus lados opuestos son
paralelos. El cuadrilátero ABB1 A1 también es un paralelogramo, ya que sus lados AA1 y BB1
son paralelos al ser cada uno de ellos paralelo a la recta CC1 . Los lados AB y A1 B1 se
hallan en planos paralelos y, por ello, también son paralelos.
Puesto que los lados del paralelogramo son iguales, se tiene AB = A1 B1 ; AC = A1C1 y
BC = B1C1 . Los triángulos ABC y A1 B1C1 son iguales por el tercer criterio de igualdad de
triángulos. Esto significa que ∠A1C1 B1 = ∠ACB , por lo que ∠A 1C1 B1 recto, o sea, que las
rectas a1 y b1 son perpendiculares. Queda demostrado el teorema.
16
Definición 2.5: Dos rectas que se cruzan se llaman perpendiculares si son perpendiculares
a las rectas secantes paralelas a ellas.
De esta definición y del teorema 2.10 se deduce que cualesquiera que sean las rectas
perpendiculares (secantes o cruzadas) las rectas secantes paralelas a ellas son
perpendiculares.
Teorema 2.11: Si la recta a es perpendicular a la recta b, también es perpendicular a
cualquier recta b1 paralela a b.
Demostración:
Tracemos las rectas secantes a 2 y b2 paralelas, respectivamente, a las rectas a y b. Las
rectas a 2 y b2 son perpendiculares por se r perpendiculares las rectas a y b. debido a la
propiedad de las paralelas, b2 // b1 . Por consiguiente, las rectas a y b son paralelas a las
rectas secantes perpendiculares a 2 y b2 y, por eso, son ellas mismas perpendiculares.
Queda demostrado el teorema.
Definición 2.6: La recta se denomina perpendicular al plano si es perpendicular a toda recta
que se encuentra en dicho plano.
Teorema 2.12 (Criterio principal de perpendicularidad de la recta y el plano): Si una
recta es perpendicular a dos rectas secantes pertenecientes a un plano dado, dicha recta es
perpendicular a ese plano.
Demostración (figura 2.12):
A1
B
D
b
Figura 2.12
X
x
A
α
C
a
c
A2
Sean b y c dos rectas secantes pertenecientes al plano α y perpendiculares a la recta a.
Sea A el punto de intersección de las rectas b y c. Consideremos primero el caso en que la
recta a pasa por el punto A.
17
Tracemos en el plano α una recta cualquiera x por el punto A y demostremos que es
perpendicular a la recta a. Podemos aceptar que la recta x es distinta de las rectas b y c.
tomemos en la recta c dos puntos C y D a distintos lados del punto A y tomemos en la recta
b un punto B distinto de A. La recta x corta el lado CD del triángulo CDB y, por consiguiente,
corta en un punto X uno de los otros dos lados. Supongamos, para puntualizar, que se trata
del lado BC .
Tomemos en la recta a, partiendo del punto A, dos segmentos iguales AA1 y AA2 a distintos
lados de ese punto. El triángulo A1CA2 es isósceles, pues el segmento AC es altura por
premisas del teorema y mediana por construcción ( AA1 = AA2 ). Por la misma razón, es
también isósceles el triángulo A1 BA2 . Entonces, son iguales los triángulos A1 BC y A2 BC en
virtud del tercer criterio de igualdad de triángulos.
De la igualdad de los triángulos A1 BC y A2 BC se infiere la igualdad de los ángulos A1 BX y
A2 BX y, por consiguiente, la igualdad de los triángulos A1 BX y A2 BX por el primer criterio
de igualdad de triángulos. De la igualdad de los lados A1 X y A2 X de estos triángulos
deducimos que el triángulo A1 XA2 es isósceles. Por eso, su mediana XA es también altura.
Esto significa precisamente que la recta x es perpendicular a la recta a.
Como la recta a es perpendicular a toda recta que pasa por el punto A, es perpendicular a
cualquier recta x1 que se halla en el plano α . Efectivamente, para esa recta x1 se puede
indicar la recta paralela x que pasa por el punto A. la perpendicularidad de las rectas a y x
implica la perpendicularidad de las rectas a y x1 debido al teorema 2.11. O sea, queda
demostrado el teorema para el caso en que la recta a pasa por el punto A de intersección de
las rectas b y c.
Consideremos el caso general. Supongamos que la recta a no pasa por el punto A.
Tracemos por el punto A la recta a1 paralela a la recta a. La recta a1 es perpendicular a las
rectas b y c según el teorema 2.11. Por lo tanto, la recta a1 es perpendicular, como le hemos
demostrado, al plano. Esto significa que la recta a1 es perpendicular a cualquier recta del
plano α . Según el teorema 2.11, la recta a, paralela a la recta a1 , también es perpendicular
a cada una de estas rectas x. Es decir, la recta a es perpendicular al plano α . Queda
demostrado el teorema.
El teorema anterior tiene un importante corolario que lleva el nombre de teorema de las tres
perpendiculares.
Teorema 2.13 (teorema de las tres perpendiculares): Si tres puntos A, B y C no están en
una recta y dos de las tres rectas AB, BC y AC son perpendiculares a una recta a, la tercera
recta es también perpendicular a la recta a.
18
Efectivamente, por los tres puntos no alineados A, B y C se puede trazar un plano. Este
plano es perpendicular a la recta a porque la recta a es perpendicular a dos rectas secantes
que se encuentran en este plano. Por consiguiente, la recta a es perpendicular a la tercera
recta de este plano y, en particular, es perpendicular a la tercera de las rectas.
Teorema 2.14: Si una recta a y un plano α son perpendiculares, toda recta a1 paralela a la
recta a es perpendicular al plano α . Todo plano α 1 paralelo al plano α es perpendicular a la
recta a.
Demostración:
La recta a es perpendicular a toda recta x del plano α . Según el teorema 2.11, la recta a1
paralela a la recta a también es perpendicular a cada una de esas rectas x. Por
consiguiente, la recta a1 es perpendicular al plano α . Queda demostrada la primera
afirmación del teorema.
Demostremos la segunda afirmación. Tomemos una recta x1 en el plano α . Tracemos por
ella un plano que corte al plano α según la recta x. Puesto que las rectas x y x1 son
paralelas y que la recta a es perpendicular a la recta x, resulta por el teorema 2.11 que la
recta a es perpendicular a la recta x1 . Esto significa que la recta a es perpendicular al
plano α 1 . Queda demostrado completamente el teorema.
Teorema 2.15: Dos rectas perpendiculares a un mismo plano son paralelas. Dos planos
perpendiculares a una misma recta son paralelos.
Demostración:
Sean a y a1 rectas perpendiculares al plano α . Supongamos que las rectas a y a1 no son
paralelas. Tracemos por el punto de intersección de la recta a1 y del plano α la recta a 2 ,
paralela a la recta a (figura 2.13).
a2
a1
a
b
Figura
2.13
α
B
19
Según el teorema 2.14, la recta a 2 es perpendicular al plano α . Tracemos el plano que
pasa por las rectas a1 y a 2 . Estas cortan al plano α según la recta b. Puesto que las rectas
a1 y a 2 son perpendiculares al plano α , también son perpendiculares a la recta b. Pero esto
es imposible. Hemos llegado a una contradicción. Queda demostrada la primera afirmación
del teorema.
Demostremos la segunda afirmación. Sean α y α 1 dos planos perpendiculares a la recta b.
Supongamos que los planos α y α 1 no son paralelos y, por tanto, tienen un punto común A.
Tracemos por el punto A la recta b1 paralela a la recta b (figura 2.14).
b1
b
Figura 2.14
α
α1
B
A
Según el teorema 2.14, la recta b1 es perpendicular a los planos α y α 1 . Tomemos en el
plano α un punto B exterior al plano α 1 y consideremos el plano que pasa por la recta b1 y
por el punto B. Este plano corta los planos α y α 1 según dos rectas distintas,
perpendiculares a la recta b1 , que pasan por el punto A. Pero esto es imposible. Hemos
llegado a una contradicción. Queda demostrado completamente el teorema.
Teorema 2.16: Por un punto se puede trazar un plano único perpendicular a una recta dada.
Demostración:
Sean A un punto y a una recta (figura 2.15). Tracemos por la recta a dos planos distintos
β 1 y β 2 . Tomando un punto cualquiera B de la recta a, tracemos por él en los planos β 1 y β 2
las rectas b1 y b2 perpendiculares a la recta a. Tracemos el plano α por las rectas b1 y b2 .
La recta a es perpendicular al plano α porque es perpendicular a dos rectas b1 y b2 de este
plano (teorema 2.12). Tracemos el plano α 1 que pase por el punto A y sea paralelo al
plano α . El plano α 1 es perpendicular a la recta a, según el teorema 2.14.
20
a
B
Figura 2.15
b2
b1
α
β1
β2
A
α1
Demostremos la unicidad el plano α 1 que pasa por el punto A y que es perpendicular a la
recta a. Supongamos que por el punto A pasa un plano α 2 distinto de α 1 también
perpendicular a la recta a. En virtud del teorema 2.15, los planos α 1 y α 2 son paralelos. Pero
esto es imposible, pues tienen un punto común A. Hemos llegado a una contradicción.
Queda demostrado el teorema.
Teorema 2.17: Por un punto se puede trazar una recta única perpendicular al plano dado.
Demostración:
Sean A un punto y α un plano. Tomemos en el plano α dos rectas secantes distintas.
Tracemos por el punto de intersección de las mismas los planos β 1 y β 2 perpendiculares a
estas rectas (teorema 2.16). Los planos β 1 y β 2 cortan el plano α según las rectas b1 y b2 ,
las cuales se cortan según la recta a. La recta a es perpendicular a las rectas b1 y b2 , o sea,
es perpendicular al plano α . Tracemos por el punto A la recta a1 paralela a la recta a. según
el teorema 2.14, la recta a1 es perpendicular al plano α .
Demostremos la unicidad de la recta a1 que pasa por el punto A perpendicularmente al
plano α . Supongamos que por el punto A pasa una recta a 2 , distinta de a1 , también
perpendicular al plano α . Según el teorema 2.15, las rectas a1 y a 2 son paralelas. Pero esto
21
es imposible porque tienen el punto común A. Hemos llegado a una contradicción. Queda
demostrado el teorema.
a
A
β2
β1
Figura 2.16
a1
α
b2
b1
Sean α un plano, A un punto exterior al plano α y B un punto de dicho plano (figura 2.17)
A
Figura 2.17
B
α
C
Definición 2.7: El segmento AB se denomina perpendicular trazada desde el punto A al
plano α si la recta AB es perpendicular al plano α . Sea C un punto del plano α distinto de
B. El segmento AC se llama oblicua trazada desde el punto A al plano α . El segmento BC
se denomina proyección de la oblicua.
La perpendicular y la oblicua trazadas al plano poseen propiedades análogas a las que
tienen la perpendicular y la oblicua trazadas a una recta en el plano. Es decir, la longitud de
la perpendicular trazada desde el punto A al plano α es menor que la longitud de cualquier
oblicua trazada desde el mismo punto. La oblicua mayor es la que tiene mayor proyección.
Efectivamente, como el triangulo ABC es rectángulo en B, según el teorema de Pitágoras
2
2
2
tenemos AC = AB + BC . De aquí resulta, primero, que AC > AB , o sea, que la oblicua
AC es mayor que la perpendicular AB y, segundo, que cuanto mayor sea AC mayor será
BC .
22
Definición 2.8: Se llama distancia entre el punto A y el plano α , a la longitud de la
perpendicular trazada desde el punto A al plano α . La distancia entre el punto A y el plano
α es la menor de todas las distancias entre el punto A y los puntos del plano α .
Al igual que las rectas paralelas en el plano, los planos paralelos en el espacio son
equidistantes. Esto significa que siendo α y β planos paralelos, dos puntos cualesquiera
del plano α están a la misma distancia del plano β . La demostración de esta propiedad
se propone como ejercicio del capítulo.
Definición 2.9: Sean a y b dos rectas que se cruzan y sean A y B puntos de estas rectas. El
segmento AB se llama perpendicular común de las rectas a y b si la recta AB es
perpendicular a la recta a y a la recta b.
Teorema 2.18: Las rectas cruzadas tienen una y sólo una perpendicular común.
Demostración:
Sean a y b rectas que se cruzan. Según ya demostramos, existen dos planos paralelos α y
β que pasan por las rectas a y b. Tracemos desde un punto arbitrario C de la recta a la
perpendicular CD al plano β . Tracemos por el punto D, la recta paralela a la recta a (figura
2.18).
a
α
A
C
Figura 2.18
β
b
B
D
Esta última recta corta a la recta b en el punto B. Tracemos por el punto B la recta paralela a
CD, la cual corta a la recta a en el punto A. La recta AB es perpendicular a los planos α y β
y, por ello, es perpendicular a las rectas a y b. Es decir, el segmento AB representa la
perpendicular común de las rectas a y b.
Demostremos la unicidad de la perpendicular común. Supongamos que existe otra
perpendicular común A1 B1 . La recta BD es paralela a la recta a. Por eso, las rectas AB y
A1 B1 , perpendiculares a las rectas a y b, son perpendiculares al plano β y, en
consecuencia, son paralelas. Pero, entonces, las rectas AA1 y BB1 , o sea, las rectas a y b,
23
se hallan en un mismo plano, lo que es imposible puesto que ellas se cruzan. Queda, de
esta forma, demostrado el teorema.
Definición 2.10: Sean α y β dos planos que se cortan según la recta c. Tracemos un plano
γ perpendicular a la recta c (figura 2.19), que cortará los planos α y β según las rectas a y
b. Se dice que los planos α y β son perpendiculares si lo son las rectas a y b.
C
β
α
b
D
a
Figura 2.19
γ
b1
a1
γ1
El concepto de perpendicularidad de los planos α y β definido de esta forma no depende
de qué plano γ se elija. Efectivamente, tracemos otro plano γ 1 , distinto de γ , perpendicular
a la recta c, que corta a los planos α y β según las rectas a1 y b1 . Los planos γ y γ 1 son
paralelos pues son perpendiculares a la recta c. De aquí resulta que las rectas a y a1 y las
rectas b y b1 son paralelas. Pero, la perpendicularidad de las rectas a y b implica la
perpendicularidad de las rectas a1 y b1 .
Teorema 2. 19: El plano α es perpendicular al plano β , si es perpendicular a una recta del
plano β .
Demostración:
Sea c la recta por donde se cortan los planos α y β y sea b una recta que está en el plano
β y que es perpendicular al plano α (figura 2.20). Tracemos en el plano α la recta a que
pasa por el punto de intersección de las rectas b y c que es perpendicular a la recta c.
La recta b es perpendicular a las rectas a y c, pues estas pertenecen al plano α
perpendicular a la recta b. La recta a es perpendicular a la recta c por construcción. Luego,
el plano en el que se encuentran las rectas a y b es perpendicular a la recta c. puesto que
las rectas a y b son perpendiculares, los planos α y β lo son también por definición. Queda
demostrado el teorema.
24
b
β
Figura 2.20
C
a
c
α
Del teorema anterior se deduce que el plano β que pasa por la recta b perpendicular al
plano α es también perpendicular al plano α .
Teorema 2.20: Si una recta a y un plano α son perpendiculares a un plano β , la recta a
está en el plano α o es paralela al plano α .
Demostración:
Sea c la recta de intersección de los planos α y β (figura 2.21). Tracemos el plano γ
perpendicular a la recta c. Este cortará los planos α y β según las rectas perpendiculares
a1 y b1 .
a1
a
γ
α
Figura 2.21
c
β
b1
La recta a1 , perpendicular a las rectas c y b1 , es perpendicular al plano β . Por consiguiente,
la recta a1 es paralela a la recta a en virtud del teorema 2.15. Si la recta a no se encuentra
en el plano α , es paralela a este, pues es paralela a la recta a1 que se halla en este plano.
Queda demostrado el teorema.
De este teorema se deduce que la perpendicular trazada desde un punto cualquiera del
plano α al plano perpendicular β , se encuentra en el plano α .
Teorema 2.21: Sean α y β dos planos distintos que se cortan (secantes) y sea γ un plano
perpendicular a cada uno de los planos α y β . El plano γ es, entonces, perpendicular a la
recta c de intersección de los planos α y β .
25
Demostración:
Tracemos la recta c1 que es perpendicular al plano γ y que pasa por un punto exterior a los
planos α y β (figura 2.22).
c
c1
β
α
Figura 2.22
c
γ
Según el teorema 2.20, la recta c1 es paralela a los planos α y β . Por consiguiente, la recta
c1 es paralela a la recta c. Por el teorema 2.14, se infiere que la recta c es perpendicular al
plano γ . Queda demostrado el teorema.
Teorema 2. 22: Sean β un plano y b una recta no perpendicular a él. Entonces, por la recta
b se puede trazar un plano perpendicular al plano β y sólo uno.
Demostración:
Tracemos por un punto arbitrario de la recta b la recta b1 perpendicular al plano β (figura
2.23).
b1
γ
b
Figura 2.23
β
El plano γ que pasa por las rectas b y b1 es perpendicular al plano β en virtud del teorema
2.19.
26
Supongamos que por la recta b pasa otro plano γ 1 también perpendicular al plano β . Según
el teorema 2.20, la recta b1 está en el plano γ 1 . Por el axioma I5, los planos γ y γ 1 coinciden.
Hemos llegado a una contradicción. Queda demostrado el teorema.
EJERCICIOS DEL CAPÍTULO
1. Demuestre que tres planos distintos se cortan en un punto, pasan por una misma recta o
son paralelos a una recta.
2. Demuestre que todas las rectas que pasan por un mismo punto y son paralelas a un
mismo plano se encuentran en un plano.
3. Sean α , β y γ tres planos paralelos y sean a y b dos rectas que los cortan. Demuestre
que son proporcionales los segmentos correspondientes de las rectas a y b
comprendidos entre los planos α , β y γ , o sea, que si A1 , A2 y A3 son los puntos de
intersección de la recta a con los planos α , β y γ si B1 , B2 y B3 son los puntos de
intersección de la recta b con estos planos, se tiene
A1 A2
B1 B2
=
A2 A3
B2 B3
=
A3 A1
B3 B1
.
4. Sean A1 , A2 , A3 y A4 cuatro puntos que no se hallan en un mismo plano. Demuestre que
el plano paralelo a las rectas cruzadas A1 A2 y A3 A4 , corta las cuatro rectas restantes que
unen estos puntos de dos en dos en los vértices de un paralelogramo.
5. Demuestre que es un plano el lugar geométrico de los puntos medios de los segmentos
cuyos extremos están en dos rectas que se cruzan.
6. Sean A, B, C y D cuatro puntos que no están en un plano. Demuestre que se cortan en
un punto las tres rectas que unen los puntos medios de los segmentos cruzados
AB y CD, AC y BD, AD y BC .
7. Demuestre que las rectas que pasan por un mismo punto y que son perpendiculares a
una misma recta pertenecen a un mismo plano.
8. Demuestre que por un punto se puede trazar una recta única que sea perpendicular a
dos rectas no paralelas.
9. Demuestre que no existen cuatro rectas perpendiculares dos a dos.
10. Sean A, B, C y D cuatro puntos que no están en un mismo plano. Demuestre que se
cortan en un punto los seis planos perpendiculares en los puntos medios de los
segmentos que unen de dos en dos estos puntos.
11. Demuestre que el lugar geométrico de los puntos equidistantes de dos puntos A y B es el
plano que pasa por el punto medio del segmento AB y que es perpendicular a él.
27
12. Sea ABC un triángulo situado a un lado del plano α y sean a, b y c las distintas entre el
plano α y los vértices del triángulo. Demuestre que la distancia entre el centro de
a+b+c
.
gravedad o baricentro del triángulo y el plano α es igual a
3
13. Demuestre que si las rectas AB y CD no están en un mismo plano, entonces las rectas
AC y BD tampoco están en un mismo plano.
14. ¿Cuántos planos determinan tres rectas paralelas?
15. ¿Cuál es el número mayor de planos que pueden determinar tres rectas paralelas y un
punto cualquiera exterior a estas?
16. Dos rectas se cortan. Si una tercera recta cruza a una de ellas y es paralela a la otra,
¿cuántos planos distintos determinan?
17. Demuestre que si una recta de un plano, que pasa por el pie de una oblicua al plano, es
perpendicular a la proyección de la oblicua, entonces es perpendicular a la oblicua.
18. Dos puntos A y B se encuentran en semiespacios distintos con respecto a un plano α . Si
las distancias de A y B al plano son de 20 cm y 40 cm, respectivamente, y la distancia
entre sus proyecciones es de 80 cm, ¿cuál es la distancia entre A y B?
19. Los puntos M y N se encuentran situados en el mismo semiespacio en relación con el
plano α . Si sus distancias al plano se encuentran en la razón 2: 3 y la recta que ellos
determinan corta al plano en un punto P situado a 12 cm del punto M, ¿a qué distancia
de P se encuentra N?, ¿a qué distancia se hallan entre si los puntos M y N?
20. Por un punto exterior a un plano se han trazado a este una perpendicular que mide 12
cm y una oblicua que mide 16 cm. Calcula la proyección de la perpendicular sobre la
oblicua.
21. Los extremos superiores de dos columnas verticales que están a una distancia de 3,4 m
se unen por una viga. La altura de una columna es 5,8 m y la de la otra es 3,9 m. Halla la
longitud de la viga.
22. En la siguiente figura AD es la altura del triángulo ABC y PA ⊥ α .
a) Prueba que ΔPDC es rectángulo.
b) Calcula PC si PD = 4,0 cm y CD = 5,0 cm .
28
P
A
α
B
C
D
23. Por el centro O de un círculo de radio igual a 3,0 dm se ha trazado una perpendicular OB
a su plano; se ha trazado también una tangente en el punto A de la circunferencia y en
esta tangente se ha tomado, desde el punto de tangencia, un segmento AC = 2,0 dm .
Calcula la longitud de la oblicua BC , si OB = 60 cm .
24. Los lados de un triángulo miden 15 cm, 37 cm y 44 cm. Por el vértice del mayor de los
ángulos del triángulo se ha trazado una perpendicular al plano de este, igual a 16 cm.
Calcula la distancia del extremo de la perpendicular al lado mayor.
25. Un punto se encuentra a 10 cm del centro de la circunferencia circunscrita a un triángulo
equilátero de 30 cm de lado. ¿A qué distancia se encuentra este punto de cada uno de
los vértices del triángulo, si es exterior al plano del triángulo?
26. Por los extremos de un segmento AB = 26 cm , que se encuentra fuera de un plano α , se
han trazado las perpendiculares AC = 80 cm y BD = 60 cm a dicho plano. Calcula la
distancia del punto medio de AB al plano α .
27. Por los extremos de un segmento AB y su punto medio M, se han trazado rectas
paralelas que intersecan a un plano en los puntos C, D y E. Halla la longitud del
segmento ME , si AC = 50 cm, BD = 70 cm y
a) AB no interseca al plano.
b) AB interseca al plano.
28. Por un punto M, que se encuentra fuera de dos planos paralelos, se han trazado dos
rectas que cortan a dichos planos en los puntos A y B la primera, C y D la segunda.
Calcula la longitud del segmento AC , si BD = 28 cm y MA : AB = 5 : 2.
29. Dos segmentos están comprendidos entre dos planos paralelos. Las proyecciones de
estos segmentos sobre los planos son de 10 dm y 70 dm. Calcula las longitudes de estos
segmentos si su diferencia es igual a 4,0 dm.
30. Por los vértices de un triángulo ABC que está sobre uno de dos planos paralelos, se han
trazado rectas paralelas que cortan al otro plano en los puntos A1 , B1 y C1 . Demuestra
que los triángulos ABC y A1 B1C1 son iguales.
29
CAPÍTULO 3: ÁNGULOS EN EL ESPACIO.
En Planimetría estudiamos los ángulos en el plano, así como todas las definiciones y
propiedades relacionadas con estos. En este capítulo nos adentraremos en el estudio de los
ángulos en el espacio, que tienen gran aplicación en el estudio de los cuerpos geométricos,
así como en la comprensión del espacio físico que nos rodea. Para ello, estudiaremos las
definiciones de ángulos entre rectas en el espacio, ángulos entre rectas y planos y ángulos
entre planos, así como de sus propiedades fundamentales, para lo cual aplicaremos los
conocimientos aprendidos en Planimetría.
3.1. Ángulos entre rectas y planos.
Desde Planimetría se conoce que dos rectas secantes forman ángulos adyacentes y
opuestos por el vértice. Los ángulos opuestos por el vértice son iguales y las amplitudes de
los adyacentes suman 1800.
Definición 3.1: La medida angular del menor de estos ángulos la llamaremos valor
principal del ángulo entre rectas. Por consiguiente, el valor principal del ángulo entre rectas
no es mayor que 900 (
π
2
). En lo adelante entenderemos por ángulo entre rectas el valor
principal.
Definición 3.2: Llamaremos ángulo entre rectas cruzadas al ángulo entre rectas secantes
paralelas a ellas.
Teorema 3.1: La amplitud del ángulo entre rectas cruzadas no depende de las rectas
secantes, paralelas a ellas, que se tomen.
Demostración:
Sean a1 y a 2 dos rectas que se cortan en un punto A y que son paralelas a las rectas
cruzadas consideradas. Sean b1 y b2 otro par de rectas que se cortan en un punto B y que
son paralelas a las rectas cruzadas consideradas. Supongamos que las rectas a1 , a 2 , b1 y b2
no pertenecen a un mismo plano (figura 3.1).
a2
A1
A
a1
A2
Figura 3.1
b2
b1
B1
B
B2
30
En este caso, los planos α y β , que contienen a las rectas a1 y a 2 y a las rectas b1 y b2 ,
respectivamente, son paralelos. Tomemos en las rectas a1 y a 2 unos puntos A1 y A2
distintos de A y tracemos las rectas A1 B1 y A2 B2 paralelas a la recta AB. Los cuadriláteros
AA1 B1 B, AA2 B2 B y A1 A2 B2 B1 son paralelogramos.
Por consiguiente, AA1 = BB1 , AA2 = BB2 y A1 B1 = A2 B2 . En virtud del tercer criterio de
igualdad de triángulos, ΔAA1 A2 ≅ ΔBB1 B2 . De la igualdad de estos triángulos resulta la
igualdad de sus ángulos A y B y, por consiguiente, la igualdad de los ángulos entre las
rectas a1 y a 2 y las rectas b1 y b2 en el sentido del valor principal.
Si las rectas a1 , a 2 , b1 y b2 están en un mismo plano, tomemos las rectas secantes c1 y c 2
que son paralelas a estas y que no pertenecen al plano mencionado. Según lo demostrado,
los ángulos entre las rectas a1 y a 2 y las rectas b1 y b2 son iguales al ángulo entre las rectas
c1 y c 2 y, consecuentemente, son iguales entre sí. Queda demostrado el teorema.
Se han definido los conceptos de ángulos entre rectas secantes y rectas cruzadas. Ahora
completaremos esta definición aceptando que el ángulo entre rectas paralelas o
coincidentes es igual a cero. Esta acepción sobre el ángulo entre rectas paralelas o
coincidentes nos libera de la necesidad de considerar especialmente los casos peculiares de
posición de rectas al enunciar los teoremas correspondientes a los ángulos.
Teorema 3.2: Sean a1 y a 2 dos rectas y sean b1 y b2 rectas paralelas a estas. El ángulo
entre las rectas a1 y a 2 es entonces igual al ángulo entre las rectas b1 y b2 .
Demostración:
Si las rectas a1 y a 2 son paralelas o coinciden, las rectas b1 y b2 también son paralelas o
coinciden. En ambos casos los ángulos entre las rectas a1 y a 2 y entre las rectas b1 y b2
son iguales a cero y, por consiguiente, son iguales entre sí. La igualdad de los ángulos para
el caso de rectas secantes ha sido demostrada en el teorema anterior. En el caso de rectas
cruzadas, la igualdad de los ángulos se desprende de la definición del concepto de ángulo
entre tales rectas. Queda demostrado el teorema.
Definición 3.3: Sea α un plano y sea a una recta. El ángulo entre la recta a y el plano α se
define como sigue:
si la recta a es paralela al plano α o se halla en este plano, el ángulo entre la recta y el
plano se considera igual a cero;
-
si la recta a es perpendicular al plano α , el ángulo se considera igual a 900 (
π
);
2
si la recta a no es ni paralela ni perpendicular al plano α , se traza entonces por la recta
a un plano perpendicular al plano α , que corta a este según la recta a1, la cual se
denomina proyección de la recta a sobre el plano α . Se llama entonces, ángulo entre la
recta a y el plano α , al ángulo que se forma entre la recta a y su proyección a1 sobre el
plano α .
31
Teorema 3.3: El ángulo entre la recta a y el plano α es complementario con el ángulo entre
la recta a y toda perpendicular al plano.
Demostración:
Si la recta a se encuentra en el plano α o es paralela a este, el ángulo entre a y α es igual
a cero. Como el ángulo entre la recta a y toda perpendicular al plano α es igual a 900, la
afirmación del teorema es evidente. Si la recta a es perpendicular al plano α , toda
perpendicular a este coincide con a o es paralela e ella. El ángulo entre la recta a y el plano
α es de 900 y el ángulo entre la recta a y toda perpendicular al plano α es igual a cero. La
afirmación del teorema también es evidente.
Consideremos el caso general. Supongamos que la recta a corta al plano α en el punto A
(figura 3.2). Tracemos por el punto A la perpendicular n al plano α . Las rectas a, a1 y n
están en un mismo plano, o sea, en el plano que proyecta a la recta a sobre el plano α .
n
a
Figura 3.2
A
a1
α
Como quiera que el ángulo entre n y a1 es recto, los valores principales de los ángulos entre
las rectas a y n y entre las rectas a1 y a se complementan hasta 900. Queda demostrado el
teorema.
Teorema 3.4: Sean a y b dos rectas paralelas y sean α y β dos planos paralelos. El ángulo
entre la recta a y el plano α es igual, entonces, al ángulo entre la recta b y el plano β .
Demostración:
Sean a1 y b1 dos rectas perpendiculares a los planos α y β , respectivamente. Las rectas
a1 y b1 son paralelas o coincidentes. Según el teorema 3.2, los ángulos entre las rectas a y
a1 y entre las rectas b y b1 son iguales. Por eso, los ángulos que complementan estos hasta
900 también son iguales. Según el teorema 3.3, de aquí se desprende la igualdad de los
ángulos entre la recta a y el plano α y entre la recta b y el plano β . Queda demostrado el
teorema.
Definición 3.4: El ángulo entre dos planos se define como sigue:
si los planos α y β son paralelos o coinciden, consideramos el ángulo entre ellos igual
a cero.
32
-
si los planos α y β no son paralelos ni coinciden entonces, se cortan según la recta c
(figura 3.3). Tracemos un plano γ perpendicular a la recta c, el cual corta a los planos
α y β según las rectas a y b, respectivamente. El ángulo entre los planos α y β se
considera igual al ángulo entre las rectas a y b.
c
β
α
Figura 3.3
b
b1
a
γ
a1
γ1
Esta definición del ángulo entre planos no depende de qué plano secante γ se elija.
Efectivamente, sea γ 1 otro plano perpendicular a la recta c, el cual corta a los planos α y β
según las rectas a1 y b1 paralelas a las rectas a y b. Por consiguiente, las rectas a1 y b1
forman el mismo ángulo que las rectas a y b.
Teorema 3.5: El ángulo entre los planos α y β es igual al ángulo entre las perpendiculares
a y b a estos planos.
Demostración:
Realicemos, ante todo, una observación. Sean a y b dos rectas perpendiculares
pertenecientes a un mismo plano. Sea c cualquier recta de este plano que pasa por el punto
de intersección de las rectas a y b. En este caso, los ángulos que la recta c forma con las
rectas a y b son complementarios (figura 3.4).
33
a
c
Figura 3.4
b
Pasemos a la demostración del teorema.
Si los planos α y β son paralelos o coinciden, las rectas a y b, perpendiculares a ellos,
también son paralelas o coinciden. En este caso, el ángulo entre los planos y el ángulo entre
las rectas son iguales a cero. Por consiguiente, el ángulo entre los planos es igual al ángulo
entre las perpendiculares a los mismos.
Supongamos ahora que los planos α y β no coinciden ni son paralelos, o sea, que se
cortan según la recta c. Tracemos un plano γ perpendicular a la recta c (figura 3.5).
b
α
a
a1
γ
Figura 3.5
b1
C
c
β
El plano γ corta a los planos α y β según las rectas a1 y b1 y corta a la recta c en el punto
C. Tracemos por el punto C las rectas a y b perpendiculares a los planos α y β , que
pertenecen al plano γ .
Como se ha explicado, el ángulo entre las rectas a1 y b complementa hasta 900 al ángulo
entre las rectas a1 y b1 . El ángulo entre las rectas a y b complementa hasta 900 al ángulo
entre las rectas a1 y b. En resumen, el ángulo entre las rectas a1 y b1 es igual al ángulo
entre las rectas a y b. queda demostrado el teorema.
Teorema 3.6: Si un plano α es paralelo a un plano α 1 y un plano β es paralelo a un plano
β 1 , el ángulo entre los planos α y β es igual al ángulo entre los planos α 1 y β 1 .
Demostración:
Tracemos una recta a perpendicular al plano α . Esta recta es perpendicular al plano α 1 .
Análogamente, toda recta b perpendicular al plano β es perpendicular al plano β1 . Según el
34
teorema 3.5, el ángulo entre dos planos es igual al ángulo entre las perpendiculares a estos
planos. Por consiguiente, el ángulo entre los planos α y β y el ángulo entre los planos
α 1 y β 1 tienen ambos el mismo valor, el del ángulo entre las rectas a y b. Queda demostrado
el teorema.
3.2. Ángulos diedros, triedros y poliedros.
Definición 3.5: Sean α y β dos planos que se cortan según la recta c. La recta c divide
cada uno de los planos α y β en dos semiplanos. Tomemos en cada uno de estos planos
un semiplano y denotémoslos por α 1 y β 1 (figura 3.6). La figura formada por los semiplanos
α 1 y β 1 se llama ángulo diedro y los propios semiplanos α 1 y β1 se denominan caras del
ángulo diedro. La recta c recibe el nombre de arista del ángulo diedro.
S
b1
c
β1
c
a1
a
b
α1
Figura 3.6
Figura 3.7
Tracemos un plano cualquiera γ perpendicular a la recta c. Este cortará a los semiplanos
α 1 y β 1 según las semirrectas a1 y b1 , respectivamente. El ángulo que forman las
semirrectas a1 y b1 se denomina ángulo rectilíneo del ángulo diedro. La medida del ángulo
diedro se considera igual a la medida del ángulo rectilíneo correspondiente. Todos los
ángulos rectilíneos de un ángulo diedro son iguales y, por ello, la medida del ángulo diedro
no depende de qué ángulo rectilíneo se elija.
Es importante aclarar la diferencia entre el ángulo formado por los planos α y β y el ángulo
entre los semiplanos α 1 y β1 de estos planos. El ángulo entre los planos no es mayor nunca
que 900. El ángulo diedro puede tener cualquier valor comprendido entre 00 y 1800. Si el
ángulo diedro es menor o igual a 900, el ángulo entre los planos a los que pertenecen sus
caras es igual al ángulo diedro. En caso contrario, complementa hasta 1800 al ángulo diedro.
Definición 3.6: Sean a, b y c tres semirrectas que parten de un mismo punto S y que no
pertenecen a un mismo plano (figura 3.7). Las semirrectas a, b y c forman tres ángulos
∠(a, b), ∠(b, c) y ∠(a, c) . La figura constituida por estos tres ángulos se denomina ángulo
35
triedro. El punto S recibe el nombre de vértice del ángulo triedro; las semirrectas a, b y c se
denominan aristas y los propios ángulos planos se llaman caras.
Los planos de los ángulos ∠(a, b) y ∠(a, c) se cortan según la recta que contiene la
semirrecta a. Los semiplanos de estos planos que contienen las semirrectas b y c forman un
ángulo diedro. Este ángulo se denomina ángulo diedro relativo a la arista a del ángulo
triedro. También se dice que es el ángulo diedro opuesto al ángulo plano ∠(b, c) .
Teorema 3.7 (Teorema de los cosenos para el ángulo triedro): Sean α , β y γ los
ángulos planos del ángulo triedro y sea C el ángulo diedro opuesto al ángulo plano γ .
Entonces, se tiene cos γ = cos α cos β + sen α sen β cos C .
Demostración:
Sean: S, el vértice del ángulo triedro; a, b y c sus aristas; α , β y γ los ángulos planos
formados por las aristas b y c, c y a, a y b, respectivamente y; C el ángulo diedro relativo a la
arista c, es decir, el ángulo diedro opuesto al ángulo plano γ (figura 3.8).
S
B
B1
B2
A1
b
c
A
Figura 3.8
a
Tomemos en las aristas a y b los segmentos SA y SB de longitud unidad. Aplicando el
2
teorema de los cosenos para el triángulo ASB, tendremos AB = 1 + 1 − 2 cos γ .
Calculemos ahora la longitud del segmento AB por otro método. Tracemos, para ello, los
planos que pasan por los puntos A y B y que son perpendiculares a la arista c. estos planos
cortarán a esta arista o su prolongación en los puntos A1 y B1 . Sea B2 el pie de la
perpendicular trazada desde el punto B al plano que pasa por el punto A. Aplicando el
teorema de los cosenos para el triángulo AA1 B2 , tendremos
2
2
2
AB2 = AA1 + A1 B2 − 2 AA1 ⋅ A1 B2 ⋅ cos C
Pero AA1 = sen β y A1 B2 = BB1 = sen α . Por lo tanto,
2
AB2 = sen 2 α + sen 2 β − 2sen α ⋅ sen β ⋅ cos C
2
2
2
Del triángulo rectángulo ABB2 obtenemos por el teorema de Pitágoras AB = AB2 + BB2 .
36
Pero BB2 = cos β − cos α . Por eso,
2
AB = sen 2 α + sen 2 β + (cos β − cos α ) 2 − 2sen α ⋅ sen β ⋅ cos C = 2 − 2 cos α cos β − 2 sen α sen β cos C
2
Comparando las dos expresiones obtenidas para AB , encontramos:
cos γ = cos α cos β + sen α sen β cos C
Queda demostrado el teorema.
Teorema 3.8 (Teorema de los senos para el ángulo triedro): Sean α , β y γ los ángulos
planos del ángulo triedro y sean A, B y C los ángulos diedros opuestos a estos. Entonces se
sen α sen β sen γ
tiene
.
=
=
sen A sen B sen C
Demostración:
Tomemos en la arista c del ángulo triedro el segmento SC de longitud unidad (figura 3.9).
Tracemos desde el punto C la perpendicular al plano del ángulo ∠(a, b) . Sea C1 el pie de
esta perpendicular. Tracemos por el punto C los planos perpendiculares a las aristas a y b y
llamemos A y B los puntos de intersección de estos planos con las aristas a y b o con sus
prolongaciones.
c
C
β
S
Figura 3.9
A
a
α
C1
B
b
Calculemos la longitud de la perpendicular CC1 . El triángulo rectángulo SCB de ángulo recto
B da CB = 1 ⋅ sen α . Ahora, partiendo del triángulo CBC1 de ángulo recto C1 , encontramos la
longitud de la perpendicular CC1 :
CC1 = CB sen B = sen α sen B
La longitud de la perpendicular CC1 se puede determinar de otro modo, empleando los
triángulos rectángulos ACS y CAC1 . Esto da CC1 = sen β sen A.
Comparando las expresiones obtenidas para el segmento CC1 , encontramos que
sen α sen B = sen β sen A .
37
sen α sen β
sen β sen γ
. Análogamente se obtiene la proporción
. Queda
=
=
sen A sen B
sen B sen C
demostrado así el teorema.
De aquí resulta
Teorema 3.9 (Relación entre los ángulos planos del ángulo triedro): En el ángulo triedro
todo ángulo plano es menor que la suma de los otros dos ángulos planos.
Demostración:
Sean α , β y γ los ángulos planos del ángulo triedro. Mostremos que γ < α + β . Aplicando
al ángulo triedro el teorema 3.7, obtenemos cos γ = cos α cos β + sen α sen β cos C . Puesto que
y que
son positivos, tenemos la desigualdad
cos C > −1
sen α y sen β
cos γ > cos α cos β − sen α sen β . El segundo miembro de esta desigualdad no es otra cosa que
cos (α + β ) . Por consiguiente, cos γ > cos (α + β ) . Como se sabe, el coseno del ángulo
disminuye cuando el ángulo aumenta de 00 hasta 1800. de aquí resulta que γ < α + β . queda
demostrado el teorema.
Definición 3.7: Supongamos que las semirrectas a1 , a 2 , ..., a n parten de un mismo punto S de
modo que tres semirrectas consecutivas cualesquiera a1 , a 2 , a3 ; a 2 , a3 , a 4 ;…; a n , a1 , a 2 no se
hallen en un mismo plano. La figura formada por los ángulos planos
∠(a1 , a 2 ), ∠(a 2 , a3 ),..., ∠(a n , a1 ) se llama ángulo poliedro (figura 3.10). El punto S se
denomina vértice del ángulo poliedro y las semirrectas a1 , a 2 , ..., a n son sus aristas.
Definición 3.8: El ángulo poliedro se dice convexo si está a un lado de cualquiera de sus
ángulos planos.
S
S
A3
An
an
A1
A2
a4
A4
A1
a1
a2
Figura 3.10
a3
A2
A3
Figura 3.11
Teorema 3.10: La suma de los ángulos planos del ángulo poliedro convexo es menor que
3600.
Demostración:
38
Sean a1 , a 2 , ..., a n las aristas del ángulo poliedro convexo de vértice S. Tomemos en las
aristas a1 y a 2 unos puntos A1 y A2 . Tomemos ahora en la arista a3 un punto A3
suficientemente próximo al vértice S y consideremos el plano α que pasa por los puntos
A1 , A2 y A3 (figura 3.10). Si el punto A3 está suficientemente próximo al vértice S, el plano
α corta las aristas a1 , a 2 , ..., a n . Sean A1 , A2 , A3 ,..., An los puntos de intersección del plano α
y de las aristas del ángulo S. Como el ángulo poliedro S es convexo, resulta que es convexo
el polígono P de vértices A1 , A2 , A3 ,..., An (figura 3.11).
Consideremos el ángulo poliedro S y los ángulos triedros de vértices A1 , A2 , A3 ,..., An . La
suma de todos los ángulos planos de estos últimos se compone de la suma de los ángulos
del polígono P (o sea, de 1800n - 3600) y la suma de los ángulos de los triángulos
A1 A2 S , A2 A3 S ,..., An A1 S (o sea, de 1800n). Por lo tanto, la suma de todos los ángulos planos
es igual a 2 ⋅ 180 0 n − 360 0 .
En cualquiera de los ángulos triedros Ak el ángulo perteneciente al polígono P es menor que
la suma de los otros dos ángulos. Por eso, la suma que hemos encontrado de todos los
ángulos planos es mayor que 2 ⋅ (180 0 n − 360 0 ) + ϑ , donde ϑ es la suma de los ángulos
planos en el vértice S, o sea, 2 ⋅ (180 0 n − 360 0 ) + ϑ < 2 ⋅ 180 0 n − 360 0 . De aquí resulta que
ϑ < 360 0 . Queda demostrado el teorema.
EJERCICIOS DEL CAPÍTULO
1. Sean A, B y C tres puntos que no se hallan en una recta. ¿Cuánto mide el ángulo entre
las rectas CA y CB si estas rectas forman ángulos α y β con la recta AB, siendo
α + β < 90 0 ?
2. Sean α un plano, a una recta que lo corta y x una recta cualquiera del plano α .
Demuestre que el ángulo entre las rectas a y x no es menor que el ángulo entre la recta a
y el plano α .
3. Sea a una recta y sean α 1 , α 2 y α 3 los ángulos que formaron tres rectas recíprocamente
perpendiculares. Demuestre que cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1.
4. Sean α 1 , α 2 y α 3 los ángulos que forma una recta con tres planos recíprocamente
perpendiculares. Demuestre que sen 2α 1 + sen 2α 2 + sen 2α 3 = 1.
5. Tres rectas a, b y c no pertenecientes a un mismo plano se cortan en el punto O. El
punto O divide cada una de estas rectas en dos semirrectas. Tomando una semirrecta de
cada recta, se puede construir ocho ángulos triedros. Exprésense sus ángulos planos y
diedros a través de los ángulos planos y diedros de uno de ellos.
39
6. Sean, en un ángulo triedro, α , β y γ los ángulos planos y A, B y C los ángulos diedros
opuestos a ellos. Sea ϕ el ángulo entre la arista del ángulo diedro C y el plano del
ángulo γ . Demuestre que sen ϕ = sen β sen A = sen α sen B .
7. Dos ángulos planos del ángulo triedro son iguales a α y el ángulo diedro comprendido
entre ellos es igual a ϕ . Hállense los ángulos restantes.
8. Un ángulo diedro del ángulo triedro es recto y los ángulos planos contiguos son iguales a
α y β . Halle los restantes ángulos.
9. En el ángulo triedro son conocidos un ángulo plano y dos ángulos diedros contiguos a
este con la particularidad de que uno de estos ángulos diedros es recta. Halle los
restantes ángulos.
10. Halla la longitud de la proyección sobre un plano de una oblicua de 18 cm de longitud
que forma un ángulo de 60o con dicho plano.
11. Un cartabón con ángulos de 300 y 600 se coloca sobre la mesa apoyado sobre el lado
menor que mide 10 cm. Si el “lado medio” queda inclinado formando con el plano de la
mesa un ángulo de 450, ¿cuánto mide la proyección del lado mayor sobre la mesa?
12. Por el vértice M del triángulo MNP rectángulo e isósceles se traza una perpendicular MA
al plano α del triángulo. Si el lado base NP = 10 cm y AP = 11,2 cm , calcula el ángulo que
forma con el plano α la mediana AB del triángulo ANP y la distancia de A al plano.
13. Se tiene un triángulo RST contenido en un plano α . Por el vértice R se levanta una
perpendicular RM al plano α . La perpendicular trazada desde M al lado ST mide 6,0 cm
y forma un ángulo de 600 con α . Halla el área del triángulo RST si ST = 10 cm . Halla el
volumen de la pirámide MRST.
14. En la figura ABCD es un cuadrado. AB está contenido en α y AD forma un ángulo de
450 con α . Si el área de ABCD es 80 cm2, halla el área de la proyección del cuadrado
sobre el plano α .
D
A
C
B
α
15. Por el punto M exterior al plano α se trazan dos oblicuas iguales que miden 3,46 cm
cada una y que forman un ángulo de 300 con la perpendicular bajada del punto al plano.
40
Halla la distancia entre los pies de las oblicuas si sus proyecciones sobre α forman un
ángulo de 1200.
16. En el interior de un ángulo diedro recto se ha tomado un punto que está a 12 cm y 16 cm
de sus caras. Calcula la distancia de este punto a la arista,
17. La distancia de un punto M, situado en una cara de un ángulo diedro a la otra cara es
igual a 12 cm. En el punto M se traza una perpendicular a la cara sobre la cual se
encuentra este punto hasta intersecar la otra cara. Calcula la longitud de esta
perpendicular si el ángulo diedro es de 600.
41
CAPÍTULO 4: POLIEDROS Y CUERPOS DE REVOLUCIÓN: ÁREAS Y VOLÚMENES.
Los conocimientos adquiridos en los capítulos anteriores encuentran su aplicación en el
estudio de los poliedros y los cuerpos en revolución, que frecuentemente se observan en el
entorno físico que nos rodea. En este capítulo se definirán los conceptos de poliedro, cuerpo
geométrico, prisma, poliedros regulares, paralelepípedo rectangular y oblicuo, pirámide,
cilindro, cono y esfera, así como sus elementos fundamentales y las fórmulas para el cálculo
de áreas y volúmenes de los mismos.
4.1. Poliedros.
Definición 4.1: Sea G una figura plana. El punto X de la figura G se llama punto interior si
todos los puntos del plano suficientemente próximos al punto X pertenecen a la figura G.
Definición 4.2: La figura G se denomina recinto si todos sus puntos son interiores y
cualesquiera dos de sus puntos se pueden unir mediante una poligonal que pertenece
íntegramente a la figura G.
Por ejemplo, el círculo sin su circunferencia es un recinto.
Definición 4.3: Sea G un recinto plano. El punto X del plano se denomina punto frontera
del recinto G si tan cerca de X como se quiera existen puntos que pertenecen a la figura G y
puntos que no le pertenecen.
Por ejemplo, la circunferencia del círculo consta de puntos frontera.
Definición 4.4: Los puntos frontera forman la frontera del recinto G. Agregando al recinto G
sus puntos frontera obtenemos una nueva figura G , que se le llama recinto cerrado.
Por ejemplo, los puntos interiores del polígono convexo definidos en Planimetría constituyen
un recinto; agregándole el propio polígono obtenemos un recinto cerrado.
Literalmente igual que para las figuras planas, se definen los conceptos de punto interior de
una figura espacial, de recinto espacial y de su frontera, por lo que no es necesario repetir
estas definiciones.
Definición 4.5: Todo recinto espacial cerrado se denomina cuerpo.
Definición 4.6: El cuerpo cuya frontera consta de un número finito de polígonos se llama
poliedro. Los polígonos que limitan el poliedro se denominan caras del poliedro. También
el poliedro se define como todo cuerpo limitado por un número finito de planos.
Definición 4.7: El poliedro se llama convexo si se encuentra a un lado del plano de cada
una de sus caras o si está contenido en un solo lado de cualquiera de los planos que lo
limitan.
Definición 4.8: Sean α y α 1 dos planos paralelas y sea h una recta que los corta. Sea P un
polígono convexo en el plano α y sean A1 , A2 ,..., An sus vértices. Tracemos por todo punto
X del polígono P la recta paralela a la recta h; sea X 1 el punto de su intersección con el
plano α 1 (figura 4.1). Los segmentos XX 1 forman un poliedro. Este poliedro se denomina
42
prisma. Su frontera consta del polígono P, del polígono igual P1 en el plano α 1 y de los
paralelogramos A1 A2 A2/ A1/ ; A2 A3 A3/ A2/ , … Los polígonos P y P1 se llaman bases del prisma y
los paralelogramos, caras laterales. Los segmentos A1 A1/ , A2 A2/ ,… son las aristas
laterales del prisma.
α1
X1
/
n
A
A1/
A3/
A2/
Figura 4.1
h
A3
An
α
X
A1
A2
Definición 4.9: El prisma se denomina recto si sus aristas laterales son perpendiculares a
las bases. En el caso contrario, se dice que el prisma es oblicuo.
Definición 4.10: Se llama superficie lateral del prisma (más exactamente, área de la
superficie lateral) a la suma de las áreas de las caras laterales. La superficie total del
prisma consta de su superficie lateral más las áreas de as bases.
Teorema 4.1: La superficie lateral del prisma recto es igual al producto del perímetro de la
base por la altura del prisma, o sea, por la longitud de sus aristas laterales.
Demostración:
Las caras laterales del prisma recto son rectángulos. Las bases de estos rectángulos son los
lados del polígono que constituyen la base del prisma y sus alturas son iguales a la longitud
de las aristas laterales. De aquí se deduce que la superficie lateral del prisma es igual a:
A = a1l + a 2 l + ... + a n l = (a1 + a 2 + ... + a n )l = P ⋅ l , donde a1 , a 2 ,..., a n son las longitudes de los
lados del polígono de la base, P es el perímetro lateral del prisma y l es la longitud de las
aristas laterales. Queda demostrado el teorema.
Definición 4.11: El prisma se denomina paralelepípedo si tiene como base un
paralelogramo (figura 4.2). Todas las caras del paralelepípedo son paralelogramos. Se llama
diagonal del paralelepípedo todo segmento que une dos vértices no pertenecientes a una
misma cara. El paralelepípedo tiene cuatro diagonales AG, BH , CE y DF .
43
G
H
G
H
F
E
D
O
C
F
E
O
D
B
A
Figura 4.2
C
B
A
Figura 4.3
Teorema 4.2: Las diagonales del paralelepípedo se cortan en un punto que las divide por la
mitad.
Demostración:
Consideremos dos diagonales cualesquiera del paralelepípedo, digamos BH y CE (figura
4.3). Puesto que los cuadriláteros ABCD y ADHE son paralelogramos, el cuadrilátero BCHE
es también un paralelogramo. Las diagonales BH y CE del paralelepípedo son las
diagonales de este paralelogramo. Por eso, se cortan y el punto de intersección O las divide
por la mitad. Análogamente se demuestra que las diagonales AG y DF , AG y BH , así
como DF y CE se cortan y el punto de intersección las divide por la mitad. De aquí resulta
que las cuatro diagonales del paralelepípedo se cortan y que el punto de intersección las
divide por la mitad. Queda demostrado el teorema.
Las caras del paralelepípedo que no tienen vértices comunes se llaman opuestas.
Teorema 4.3: Las caras opuestas del paralelepípedo son paralelas e iguales.
Demostración:
Consideremos dos caras opuestas cualesquiera del paralelepípedo, por ejemplo, ABFE y
DCGH (figura 4.2). Como quiera que todas las caras del paralelepípedo son paralelogramos,
la recta AB es paralela a la recta CD y la recta EF es paralela a la recta GH. De aquí se
deduce que son paralelos los planos donde están las caras consideradas del
paralelepípedo. Puesto que las caras del paralelepípedo son paralelogramos, resulta que
todos los segmentos AB, CD, EF y GH son paralelos e iguales. De aquí deducimos que la
cara ABFE se superpone a la cara DCGH, por efecto de la traslación paralela según el
→
vector AD . Por lo tanto, estas caras son iguales. Análogamente, se demuestra que son
paralelas e iguales los otros pares de caras opuestas del paralelepípedo. Queda demostrado
el teorema.
Definición 4.12: El paralelepípedo recto cuya base es un rectángulo se denomina
paralelepípedo rectangular. Todas sus caras son rectángulos.
44
Las longitudes de las aristas no paralelas del paralelepípedo rectangular se llaman
dimensiones lineales del mismo. Todo paralelepípedo rectangular tiene tres dimensiones
lineales: largo (por ejemplo, AB ); profundidad o ancho (por ejemplo, BC ) y; altura (por
ejemplo, AE ).
Teorema 4.4: En el paralelepípedo rectangular el cuadrado de cualquier diagonal es igual a
la suma de los cuadrados de sus tres dimensiones lineales.
Según la figura 4.2, el teorema se puede formular de esta forma:
2
2
2
2
AG = AB + BC + CG .
La demostración de este teorema queda como ejercicio del capítulo.
Definición 4.13: Sea P un polígono convexo perteneciente al plano α y sea S un punto que
no pertenece al plano α . Unamos el punto S con cada uno de los puntos X del polígono P
mediante el segmento XS . Los segmentos XS forman un poliedro. Este poliedro se
denomina pirámide (figura 4.4).
S
A3
An
α
Figura 4.4
X
A1
A2
Si P es un polígono de n lados, se dice que la pirámide es n – angular. La pirámide triangular
también se llama tetraedro. El polígono P es la base de la pirámide y el punto S es el vértice
de la misma. Se denomina altura de la pirámide a la perpendicular bajada desde su vértice
al plano α al que pertenece su base. Sean A1 , A2 ,..., An los vértices del polígono P, base de
la pirámide. Los triángulos A1 SA2 , A2 SA3 ,… reciben, entonces, el nombre de caras laterales
de la pirámide y los segmentos A1 S , A2 S ,… reciben el nombre de aristas laterales.
Definición 4.14: Una pirámide se llama regular si su base es un polígono regular y si el pie
de la altura coincide con el centro de este.
Es evidente que las aristas laterales de la pirámide regular son iguales y que, por ende, sus
caras laterales son triángulos isósceles iguales. La altura de la cara lateral de la pirámide
regular trazada desde su vértice recibe el nombre de apotema.
45
Definición 4.15: Se denomina superficie lateral de la pirámide a la suma de las áreas de sus
caras laterales.
Teorema 4.5: La superficie lateral de la pirámide regular es igual al producto del
semiperímetro de la base por la apotema.
Demostración:
Si el lado de la base es a y el número de los lados es n, la superficie lateral de la pirámide es
al
an
P
n=
l = l , donde l es la apotema y P es el perímetro de la base. Queda demostrado
2
2
2
el teorema.
Definición 4.16: Si se traza un plano paralelo a la base de una pirámide, al cuerpo limitado
por la base y el plano trazado se le denomina pirámide truncada. Por ende, la pirámide
truncada tiene dos bases (figura 4.5).
Figura 4.5
Las bases de la pirámide truncada representan polígonos semejantes y las caras laterales
son trapecios. Si la pirámide truncada ha sido obtenida de una pirámide regular, también se
le llama regular. Las caras de la pirámide truncada regular son trapecios isósceles; las
alturas de estos se denominan apotemas.
Definición 4.17: Un poliedro convexo se llama regular si sus caras son polígonos regulares
de un mismo número de lados y si en todo vértice del poliedro converge un mismo número
de aristas.
Las caras de un poliedro regular son triángulos equiláteros, cuadrados o pentágonos
regulares. Efectivamente, a partir del hexágono regular, los ángulos internos no son
menores que 1200 y, como quiera que en todo vértice del poliedro convergen como mínimo
tres aristas, resulta que la suma de los ángulos planos del ángulo poliedro correspondiente a
cualquier vértice del poliedro regular no sería menor que 3 ⋅ 120 0 = 360 0 , lo que es imposible
pues, la suma de los ángulos planos de cualquier ángulo poliedro convexo es menor que
3600.
Si las caras del poliedro regular son triángulos regulares, o sea, equiláteros, en todo vértice
del poliedro no pueden converger más de cinco aristas. Efectivamente, si son más, la suma
de los ángulos planos relativos al vértice del poliedro no será menor que 3600, cosa
imposible. Por consiguiente, en un poliedro regular de caras triangulares el número de
46
aristas convergentes en un mismo vértice puede ser sólo tres, cuatro o cinco. Estas tres
posibilidades efectivamente tienen lugar. Los poliedros correspondientes son el tetraedro, el
octaedro y el icosaedro regulares (figura 4.6). En todo vértice del tetraedro concurren tres
aristas, del octaedro cuatro y del icosaedro cinco.
Tetraedro
Cubo
Octaedro
Figura 4.6
Icosaedro
Dodecaedro
Si las caras del poliedro regular son cuadrados, el número de aristas convergentes en todo
vértice del poliedro no es mayor que tres y, por consiguiente, es igual a tres. El poliedro
correspondiente es el cubo (figura 4.6).
Si las caras del poliedro son pentágonos regulares, en todo vértice también convergen tres
aristas solamente. El poliedro correspondiente es el dodecaedro regular (figura 4.6).
4.2. Cuerpos de revolución.
Definición 4.18: Sean α y α 1 dos planos paralelos y sea a una recta que los corta.
Tomemos un círculo cualquiera k en el plano α (figura 4.7). Tracemos la recta que pasa por
un punto X cualquiera del círculo k y que es paralela a la recta a; sea a X el segmento de
esta recta comprendido entre los planos α y α 1 . Si el punto X describe el círculo k, los
segmentos a X forman un cuerpo. Este cuerpo recibe el nombre de cilindro circular.
La frontera del cilindro circular consta del círculo k, del círculo k1 en el plano α 1 y de la
superficie lateral. La superficie lateral del cilindro es la descrita por el segmento a X cuando
el punto X recorre la circunferencia del círculo k. En este caso los segmentos a X se
denominan generatrices del cilindro. Los círculos k y k1 son las bases del cilindro.
47
Definición 4.19: El cilindro circular se llama recto si sus generatrices son generatrices son
perpendiculares a las bases. En este caso las generatrices coinciden con la altura del
cilindro circular recto.
Como podemos observar un cilindro circular recto está limitado por dos círculos iguales a los
que se denomina bases y por una superficie curva a la que se le denomina superficie lateral.
Si cortamos esta superficie a lo largo de una de sus generatrices, entonces podemos
extenderla hasta formar una superficie plana. Como resultado obtenemos una superficie
rectangular con uno de sus lados igual a la longitud de la circunferencia de la base: L = 2π r ,
y el otro es igual a la altura del cilindro (figura 4.8).
h
h
L = 2π r
Figura 4.8
Si denotamos el área lateral por AL obtenemos:
AL = 2π r h
Como d = 2 r , la formula anterior también se puede escribir: AL = π d h .
En estas fórmulas r es el radio del círculo de la base, h la altura del cilindro circular recto y
d diámetro del círculo de la base.
Por ende, queda demostrado el siguiente teorema:
Teorema 4.6: El área lateral de un cilindro circular recto es igual al producto de la longitud
de la circunferencia de la base por la altura.
48
En el caso que se quiera determinar el área total del cilindro circular recto procedemos del
mismo modo que para el prisma y la pirámide, es decir, el área total del cilindro circular recto
es igual a la suma del área lateral y las áreas de las bases. Si denotamos por AB al área de
la base y por AT el área total del cilindro circular recto, obtendremos la siguiente fórmula:
AT = 2 AB + AL = 2π r 2 + 2π r h = 2π r (r + h) .
Definición 4.20: Sean α un plano y S un punto que no le pertenece. Tomemos en el plano
α un círculo cualquiera k (figura 4.9). Unamos un punto cualquiera X del círculo con el punto
S mediante el segmento SX . Si el punto X describe el círculo k, los segmentos SX forman
un cuerpo. Este cuerpo recibe el nombre de cono circular.
La frontera del cono consta del círculo k (base del cono) y de la superficie lateral. La
superficie lateral del cono es la descrita por el segmento SX cuando el punto X se desplaza
por la circunferencia del círculo k. El punto S se llama vértice del cono. Los segmentos SX
que unen el vértice del cono con los puntos de la circunferencia de la base se denominan
generatrices del cono.
Definición 4.21: Se dice que el cono circular es recto si la proyección ortogonal o
perpendicular de su vértice en el plano de la base coincide con el centro de esta. En este
caso, la recta que pasa por el vértice del cono y que es perpendicular a la base se denomina
eje del cono, además, el segmento de este eje comprendido entre el vértice y el centro del
círculo de la base se le llama altura del cono circular recto.
Como podemos observar un cono circular recto está limitado por el círculo de la base y por
una superficie curva a la que se le denomina superficie lateral. Si cortamos esta superficie a
lo largo de una de sus generatrices, entonces podemos extenderla hasta formar una
superficie plana. Como resultado obtenemos un sector circular de radio g (generatriz del
cono) determinado por un arco cuya longitud es igual a la longitud L de la circunferencia de
la base (figura 4.10).
49
El área de esta superficie lateral del cono se halla utilizando la siguiente proporción:
AL
2π r
=
2
2π g
πg
2π r ⋅ π g 2
AL =
2π g
AL = π r g
De esta forma se obtiene el siguiente teorema:
Teorema 4.7: El área lateral de un cono circular recto es igual al producto de la mitad de
longitud de la circunferencia de la base por la longitud de la generatriz.
En el caso que se quiera determinar el área total del cono circular recto procedemos del
mismo modo que para el prisma y la pirámide, es decir, el área total del cono circular recto
es igual a la suma del área lateral y el área de la base. Si denotamos por AB al área de la
base y por AT el área total del cono circular recto, obtendremos la siguiente fórmula:
AT = AB + AL = π r 2 + π r g = π r (r + g ) .
Definición 4.22: Sea O un punto cualquiera y sea R un número positivo arbitrario. Se llama
esfera al cuerpo formado por todos aquellos puntos X del espacio, de forma tal que la
longitud de todos los segmentos OX no sea mayor que R.
El punto O es el centro de la esfera y el número R es le radio de la esfera. La frontera de la
esfera se denomina superficie esférica. Por lo tanto, los puntos de la superficie esférica son
aquellos puntos de la esfera que están respecto al centro a una distancia igual al radio. El
segmento que une el centro de la esfera con cualquier punto de la superficie esférica
también se denomina radio. El segmento que une dos puntos de la superficie esférica y que
pasa por el centro de la esfera se llama diámetro. Los extremos de todo diámetro se
denominan puntos diametralmente opuestos de la esfera.
4.3. Volúmenes de cuerpos simples.
El problema de la determinación del volumen de los cuerpos se remonta a la antigüedad.
Surgió en relación con la actividad práctica del hombre.
50
Definición 4.23: Imaginemos dos recipientes: uno cúbico y otro de forma arbitraria (figura
4.11). Supongamos que ambos han sido llenados de líquido, empleándose para el primero
m kg de líquido y n kg para el segundo.
Figura 4.11
n
veces mayor que el primero.
m
Llamaremos volumen del segundo recipiente al número que indica cuántas veces es mayor
que el primero. El primer recipiente es la unidad de medición.
Lo natural es considerar que el segundo recipiente es
De esta definición del volumen se obtienen las siguientes propiedades del mismo:
1. Puesto que para llenar todo el recipiente se necesita una cantidad determinada de
líquido, resulta que todo recipiente posee un volumen (positivo) determinado.
2. Para llenar recipientes iguales se necesita la misma cantidad de líquido y, por eso, los
recipientes iguales tienen volumen igual.
3. Si dividimos el recipiente en dos partes, la cantidad de líquido necesaria para llenar todo
el recipiente constará de las cantidades de líquido necesarias para llenar sus partes. Por
ello, el volumen de todo recipiente es igual a la suma de los volúmenes de sus
partes.
Definición 4.24: Un cuerpo se llama simple si puede ser dividido en un número finito de
tetraedros, es decir, de pirámides triangulares.
En particular, son cuerpos simples, por ejemplo, el prisma, la pirámide y, en general, el
poliedro convexo.
Volumen del paralelepípedo rectangular.
En la figura 4.12 se representa un cubo como unidad de medición y un paralelepípedo
rectangular cuyo volumen debe ser medido. Dividamos las aristas del cubo que convergen
en un mismo vértice en N partes iguales y tracemos por los puntos de división planos
perpendiculares a estas aristas. El cubo quedará dividido en N3 cubos pequeños. En la
figura, las aristas del cubo han sido divididas en 5 partes cada una. El número de cubos
pequeños es de 25 x 5 = 53.
Determinemos el volumen del cubo pequeño. Por la propiedad del volumen, el volumen del
cubo grande es igual a la suma de los volúmenes de los cubos pequeños.
51
Figura 4.12
Puesto que el volumen del cubo grande es iguala la unidad y que el número de cubos
1
pequeños es igual a N3, el volumen del cubo pequeño es igual a
. Sea q la arista del
N3
1
y, por consiguiente, el volumen del cubo pequeño es
cubo pequeño. Entonces, q =
N
1
= q3 .
3
N
Construyamos en las aristas del paralelepípedo, que convergen en un mismo vértice,
segmentos iguales a q, 2q, 3q, ... y tracemos por sus extremos planos perpendiculares a las
aristas del paralelepípedo. Obtendremos un conjunto de cubos de aristas iguales a q que
llenan el paralelepípedo. Determinemos el número de cubos que contiene el paralelepípedo
y el número de cubos en que está contenido el paralelepípedo.
Sean a, b y c las aristas del paralelepípedo. Indiquemos mediante l el entero de la división
de a por q, mediante m el entero de la división de b por q y mediante n el entero de la
división de c por q. Entonces, el número de cubos que contiene el paralelepípedo será lmn ,
mientras que el número de cubos en que está contenido el paralelepípedo no será mayor
que (l + 1)(m + 1)(n + 1) . De aquí resulta que el volumen V del paralelepípedo está
comprendido
entre
los
números
lmnq 3
y
(l + 1)(m + 1)(n + 1)q 3 ,
o
sea,
lmnq ≤ V < (l + 1)(m + 1)(n + 1)q .
3
3
Demostremos ahora que el producto abc está comprendido entre estos mismos números.
Efectivamente, se tiene lq ≤ a < (l + 1)q, mq ≤ b < (m + 1)q y nq ≤ c < (n + 1)q . Por eso,
lmnq 3 ≤ abc < (l + 1)(m + 1)(n + 1)q 3
Puesto que ambos números, V y abc , están comprendidos entre los números lmnq 3 y
(l + 1)(m + 1)(n + 1)q 3 , difieren a lo sumo en (l + 1)(m + 1)(n + 1)q 3 - lmnq 3 , o sea, en
lmq 3 + mnq 3 + l nq 3 + lq 3 + mq 3 + nq 3 + q 3 . Como quiera que lq ≤ a, mq ≤ b y nq ≤ c , de aquí se
deduce que V y abc difieren no más que en abq + bcq + acq + aq 2 + bq 2 + cq 2 + q 3 . Este
1
número es todo lo pequeño que se quiera si es suficientemente pequeño el número q = .
N
52
Resulta que la diferencia entre los números V y abc es tan pequeña como se quiera. Pero
esto puede darse sólo si son iguales.
Por consiguiente, el volumen del paralelepípedo rectangular de dimensiones lineales a,
b y c es V = abc. Aquí a, b y c se miden con la arista del cubo que se ha tomado como
unidad de medición del volumen.
Volumen del paralelepípedo oblicuo.
Determinemos el volumen del paralelepípedo oblicuo (figura 4.13). Tracemos el plano que
pasa por la arista BC y que es perpendicular a la base ABCD y agreguemos al
paralelepípedo el prisma triangular BB1 B2 CC1C 2 . Separemos del cuerpo obtenido un prisma
triangular trazando el plano que pasa por la arista AD y que es perpendicular a la base
ABCD. Obtenemos un nuevo paralelepípedo. Su volumen es igual al volumen del
paralelepípedo inicial. Efectivamente, el prisma agregado y el prisma separado son iguales
y, por consiguiente, tiene volúmenes iguales.
A1
D1
D2
A2
D
C1
C2
2
1
C
B1
A
B2
B
Figura 4.13
C
D
A
B
Figura 4.14
Al realizar con el paralelepípedo las transformaciones señaladas, el área de su base y su
altura se conservan. También se conservan los planos de dos caras laterales, mientras que
las otras dos se hacen perpendiculares a la base. Aplicando una vez más esta
transformación, obtendremos un paralelepípedo de caras laterales perpendiculares a la
base, o sea, un paralelepípedo recto. Transformémoslo análogamente en un paralelepípedo
rectangular agregándole el prisma 1 y quitándole el prisma 2 (figura 4.14). Esta
transformación conserva también el volumen, el área de la base y la altura del
paralelepípedo.
El volumen del paralelepípedo rectangular es igual al producto de sus dimensiones lineales.
El producto de dos dimensiones lineales es el área de a base y la tercera dimensión es la
altura. Por consiguiente, el volumen del paralelepípedo rectangular es igual al producto del
área de su base por la altura. Puesto que en la transformación descrita del paralelepípedo
inicial en paralelepípedo rectangular se conservan en cada una de las fases el volumen, el
área de la base y las atura, resulta que el volumen del paralelepípedo inicial es igual al
producto del área de la base por la altura. Por lo tanto, el volumen de todo paralelepípedo
es igual al producto del área de la base por la altura.
Volumen del prisma.
53
Determinemos el volumen del prisma. Consideremos el prisma triangular (figura 4.15).
Complementémoslo con otro prisma triangular igual al inicial, obteniendo así un
paralelepípedo como se indica en la figura. Es evidente que el volumen del prisma agregado
es igual al volumen del prisma inicial. Por lo tanto, el volumen del paralelepípedo construido
es igual al doble del volumen del prisma.
B1
A1
C1
aX
B
X
C
A
Figura 4.15
Δ
Figura 4.16
El volumen del paralelepípedo es igual al producto de su base por la altura. El área de la
base es igual al área duplicada del triángulo ABC y la altura es igual a la altura del prisma
inicial. De aquí podemos deducir que el volumen del prisma inicial es igual al producto del
área de su base por la altura.
Consideremos ahora un prisma cualquiera (figura 4.16). Dividamos su base en triángulos.
Sea Δ uno de ellos. Tracemos la recta que pasa por un punto cualquiera X del triángulo Δ y
que es paralela a las aristas laterales. Sea a X el segmento de esta recta perteneciente al
prisma. Si el punto X describe el triángulo Δ , los segmentos a X forman un prisma triangular.
Construyendo tal prisma para todo triángulo Δ , lograremos dividir el prisma inicial en
prismas triangulares. Todos estos prismas tienen una misma altura igual a la altura del
prisma inicial.
El volumen del prisma inicial es igual a la suma de los volúmenes de los prismas triangulares
que lo componen. Según lo demostrado, el volumen del prisma triangular es igual al
producto del área de su base por la altura. De aquí se deduce que el volumen del prisma
inicial es V = A1 H + A2 H + ... + An H = ( A1 + A2 + ... + An ) H , donde A1 , A2 , ... An son las áreas de
los triángulos Δ en que se ha sido dividida la base del prisma. Pero la suma de las áreas de
los triángulos Δ es igual al área AB de la base del prisma inicial. Por eso, V = AB H y, por
consiguiente, el volumen de todo prisma es igual al producto del área de su base por la
altura.
Volumen de la pirámide.
54
Para determinar el volumen de la pirámide seguiremos el siguiente procedimiento.
Analicemos primeramente una pirámide triangular. Dividamos la altura de esta en n partes
iguales y tracemos por los puntos de división planos paralelos a la base de la pirámide
(figura 4.17). La pirámide quedará dividida entonces en capas. Construyamos para cada una
de estas capas dos prismas: uno conteniendo la capa y otro contenido en la capa, como se
representa en la figura.
Figura 4.17
El poliedro P1 , formado por la pila de prismas que contienen las capas respectivas, contiene
también la propia pirámide y, por lo tanto, su volumen es mayor que el de la pirámide. El
poliedro P2 , formado por la pila de de prismas contenidos en las capas respectivas, está
contenido en la propia pirámide y, por eso, su volumen es menor que el de la pirámide. Sea
V el volumen de la pirámide y sean V1 y V2 los volúmenes de los poliedros P1 y P2 .
Entonces, V2 < V < V1 .
Determinemos los volúmenes de los poliedros P1 y P2 . Las secciones de la pirámide
correspondientes a los planos paralelos a la base son semejantes a esta. Por eso, el área de
2
⎛m⎞
la base del prisma m – ésimo en el poliedro P1 sera A⎜ ⎟ , donde A es el área de la base
⎝n⎠
m
de la pirámide y
es el coeficiente de semejanza. El volumen del prisma respectivo será
n
2
⎛m⎞ H
y el volumen del poliedro P1 , igual a la suma de los volúmenes de los prismas que
A⎜ ⎟
⎝n⎠ n
lo componen, será
2
2
2
H ⎧⎪⎛ 1 ⎞ ⎛ 2 ⎞
⎛ n ⎞ ⎫⎪ AH
V1 = A ⎨⎜ ⎟ + ⎜ ⎟ + ... + ⎜ ⎟ ⎬ = 3 12 + 2 2 + 3 2 + ... + n 2 .
n ⎪⎩⎝ n ⎠ ⎝ n ⎠
⎝ n ⎠ ⎪⎭ n
(
)
Análogamente determinamos el volumen V2 del poliedro P2
V1 = A
H
n
2
⎧⎪⎛ 1 ⎞ 2 ⎛ 2 ⎞ 2
⎛ n − 1 ⎞ ⎫⎪ AH 2
2
2
2
+
+
...
+
⎜
⎟
⎜
⎟
⎜
⎟
⎨
⎬ = 3 (1 + 2 + 3 + ... + (n − 1) )
n
n
n
n
⎪⎩⎝ ⎠ ⎝ ⎠
⎝
⎠ ⎪⎭
Como se conoce 1 + 2 2 + 3 2 + ... + n 2 =
1 + 2 2 + 3 2 + ... + (n − 1) 2 =
n3 n 2 n
+
+ y, por eso,
3
2 6
n3 n 2 n
−
+ . Por consiguiente,
3
2 6
55
AH
V1 = 3
n
V2 =
AH
n3
⎛ n3 n 2 n ⎞
1 ⎞
⎛1 1
⎜⎜ +
+ 2⎟ y
+ ⎟⎟ = AH ⎜ +
2 6⎠
⎝ 3 2n 6n ⎠
⎝ 3
⎛ n3 n 2 n ⎞
1 ⎞
⎛1 1
⎜⎜ −
+ 2⎟
+ ⎟⎟ = AH ⎜ −
2 6⎠
⎝ 3 2n 6 n ⎠
⎝ 3
1 ⎞
1 ⎞
⎛1 1
⎛1 1
Luego, AH ⎜ −
+ 2 ⎟.
+ 2 ⎟ < V < AH ⎜ +
⎝ 3 2n 6 n ⎠
⎝ 3 2n 6n ⎠
AH
1 ⎞
1 ⎞
⎛ 1
⎛ 1
+ 2 ⎟ <V −
< AH ⎜ + 2 ⎟ .
De aquí AH ⎜ −
3
⎝ 2n 6n ⎠
⎝ 2n 6 n ⎠
AH
AH
difieren en
. Puesto que
3
n
n es arbitrario y, por lo tanto, puede ser tomado tan grande como se quiera, los números
AH
AH
difieren todo lo poco que se quiera. Pero esto puede darse sólo sí V =
. O sea,
V y
3
3
el volumen de toda pirámide triangular es igual a un tercio del producto del área de su
base por la altura.
De esta igualdad se puede apreciar que los números V y
Consideremos una pirámide no triangular cualquiera. Dividamos su base en triángulos
Δ 1 , Δ 2 ,..., Δ n . La pirámide considerada se compone de aquellas pirámides que tienen como
bases estos triángulos y como vértice el vértice de la pirámide considerada. El volumen de
esta es igual a la suma de los volúmenes de las pirámides que la componen. Puesto que
todas ellas tienen la misma altura H que la pirámide considerada, el volumen de la última es
1
1
V = H ( A1 + A2 + ... + An ) = AH . Por consiguiente, el volumen de toda pirámide es igual a
3
3
un tercio del producto del área de su base por la altura.
4.4. Volúmenes de cuerpos de revolución.
Definición 4.24 (Definición general de volumen): Se denomina volumen del cuerpo T al
número V que posee las siguientes propiedades:
1) El número V no es mayor que el volumen de cualquier cuerpo simple en que está
contenido el cuerpo T;
2) No existe ningún número mayor que V que posee la propiedad anterior.
Por consiguiente el número V es el mayor de los números con la propiedad 1). En el caso de
un cuerpo simple, esta definición conduce al mismo resultado que antes, pues el cuerpo
considerado se encuentra entre los cuerpos simples que lo contienen.
Propiedades del volumen que se derivan directamente de la definición anterior:
• Si el cuerpo T1 está contenido en el cuerpo T2, el volumen del cuerpo T1 no es mayor
que el volumen del volumen del cuerpo T2.
• Si los cuerpos T1 y T2 son iguales, sus volúmenes también lo son.
56
•
Si el cuerpo es dividido por un plano o por una superficie cilíndrica, cónica o esférica,
el volumen del cuerpo es igual a la suma de los volúmenes de los cuerpos en los que
está dividido.
Volumen del cilindro.
Teorema 4.8: El volumen del cilindro es igual al producto del área de su base por la altura.
Demostración:
Construyamos un prisma n – angular regular inscrito en el cilindro y un prisma n – angular
circunscrito al cilindro. El prisma inscrito está contenido en el cilindro y, por consiguiente, su
volumen no es mayor que el volumen del cilindro. El prisma circunscrito contiene el cilindro
y, por tanto, su volumen no es menor que el volumen del cilindro.
Consideremos la circunferencia inscrita en la base del prisma (figura 4.18). El radio de esta
circunferencia es R1 = R cos
π
. El área de la base del prisma inscrito no es menor que el
n
área del cilindro de radio R1 contenido en aquella. Por eso, el volumen del prisma inscrito en
el cilindro no es menor que π R 2 H cos 2
π
n
, donde H es la altura del cilindro. O sea, para el
volumen del cilindro tenemos V ≥ π R 2 H cos 2
R2
π
π
n
.
R
n
O
R1
Figura 4.18
Consideremos ahora la circunferencia circunscrita a la base del prisma circunscrito. El radio
R
. La base del prisma circunscrito está contenida en el
de esta circunferencia es R2 =
π
cos
n
π R2
. Para el
círculo de radio R2 . Por eso, el área de la base del prisma no es mayor que
2 π
cos
n
2
πR H
volumen del cilindro tenemos entonces V ≤
.
2 π
cos
n
57
Las dos desigualdades obtenidas son válidas para cualquier valor de n . Para n → ∞ , se
tiene cos
π
→ 1 . Por eso, de la primera desigualdad se deduce que
V ≥ π R 2 H y de la
n
segunda que V ≤ π R 2 H . Es decir, V = π R 2 H que es lo que se quería demostrar.
Volumen del cono.
Teorema 4.9: El volumen del cono es igual a un tercio del producto del área de su base por
la altura.
Demostración:
Construyamos una pirámide n – angular regular inscrita en el cono y una pirámide n –
angular regular circunscrita al cono. La pirámide inscrita está contenida en el cono y, por
consiguiente, su volumen no es mayor que el volumen del cono. La pirámide circunscrita
contiene el cono y, por tanto, su volumen no es menor que el volumen del cono.
Consideremos la circunferencia inscrita en la base de la pirámide inscrita (figura 4.18). El
radio de esta circunferencia es R1 = R cos
π
n
. El área de la base de la pirámide inscrita no es
menor que el área del circulo de radio R1 contenido en aquella. Por eso, el volumen de la
1
π
pirámide inscrita en el cono no es menor que π R 2 H cos 2 , donde H es la altura del
3
n
1
π
cono. O sea, para el volumen del cono tenemos V ≥ π R 2 H cos 2 .
3
n
Consideremos ahora la circunferencia circunscrita a la base de la pirámide circunscrita. El
R
. La base de la pirámide circunscrita está
radio de esta circunferencia es R2 =
π
cos
n
contenida en el círculo de radio R2 . Por eso, el área de la base de la pirámide no es mayor
que
π R2
1 π R2H
. Para el volumen del cono tenemos entonces V ≤
.
3
2 π
2 π
cos
cos
n
n
Las dos desigualdades obtenidas son válidas para cualquier valor de n . Para n → ∞ , se
1
π
tiene cos → 1 . Por eso, de la primera desigualdad se deduce que V ≥ π R 2 H y de la
n
3
1
1
segunda que V ≤ π R 2 H . Es decir, V = π R 2 H que es lo que se quería demostrar.
3
3
Volumen de la esfera.
4
Teorema 4.10: El volumen de la esfera de radio R es V = π R 3 .
3
Demostración:
El plano que pasa por el centro de la esfera la divide en dos partes iguales, dos semiesferas.
Por eso, basta determinar el volumen de la semiesfera. Para mayor comodidad,
58
aceptaremos que la semiesfera ocupa la posición indicada en la figura 4.19. Tracemos el
radio perpendicular a la base de la semiesfera y dividámoslo en n partes iguales. Tracemos
por los puntos de división los planos paralelos a la base de la semiesfera. La dividirán en n
capas (figura 4.20). Construyamos para toda capa el cilindro que la contiene de radio igual al
radio de la base inferior de la capa. Sea Vm el volumen del m – ésimo cilindro contado desde
la base de la semiesfera.
Figura 4.20
Figura 4.21
El cuerpo formado por los cilindros construidos contiene la semiesfera y, por ello, su
volumen no es menor que el volumen de esta. Si hacemos descender todos los cilindros a la
R
, todos quedarán dentro de la semiesfera a excepción del primero. Por eso, el
distancia
n
volumen del cuerpo formado por todos los cilindros menos el primero no es mayor que el
volumen de la semiesfera. Indicando por V el volumen de la semiesfera, obtenemos de esta
forma la desigualdad V2 + V3 + ... + Vn ≤ V ≤ V1 + V2 + V3 + ... + Vn … (1).
Tomemos ahora el cono de radio R en la base y de altura también R . Dividámoslo en capas
de la misma forma que la semiesfera y construyamos para cada capa el cilindro que la
contiene (figura 4.21). Sea Vm/ el volumen del m - ésimo cilindro contando desde el vértice
del cono. El cuerpo formado por estos cilindros contiene el cono. Por eso, el volumen de
este cuerpo no es menor que el volumen del cono. Si elevamos los cilindros a la distancia
R
, todos ellos menos el último quedarán dentro del cono. Por eso, el volumen del cuerpo
n
formado por estos cilindros no es mayor que el volumen del cono. Si V / es el volumen del
cono, obtenemos se esta forma la desigualdad
/
/
/
/
/
/
V1 + V2 + ... + Vn −1 ≤ V / ≤ V1 + V2 + ... + Vn … (2).
Hallemos la suma de los volúmenes Vm/ + Vm+1 . Según el teorema de Pitágoras, el radio de la
2
base del (m + 1) – ésimo cilindro en el caso de la semiesfera es igual a
eso, se tiene Vm +1
⎛m ⎞
R − ⎜ R ⎟ . Por
⎝n ⎠
2
⎡ 2 ⎛ m ⎞2 ⎤ R
= π ⎢R − ⎜ R ⎟ ⎥ .
⎝ n ⎠ ⎥⎦ n
⎢⎣
En el caso del cono, el radio del m – ésimo cilindro es igual a
m
R . Por eso, se tiene
n
59
2
⎛m ⎞ R
.
V = π⎜ R⎟
⎝n ⎠ n
π R3
.
Vemos, entonces, que Vm +1 + Vm/ =
n
π R3
π R3
Observemos que V1 =
y Vn/ =
.
n
n
Sumando miembro a miembro las desigualdades (1) y (2), encontramos
/
m
n −1
n −1
n +1
π R3 ≤ V + V / ≤
π R 3 + V1 + Vn/ =
π R3 .
n
n
n
Puesto que estas desigualdades son válidas para cualquier valor de n y como
n −1
n +1
→1 y
→ 1 si n → ∞ , obtenemos π R 3 ≤ V + V ′ ≤ π R 3 . Por consiguiente,
n
n
V + V ′ = π R3 .
1
2
Ya que el volumen del cono es V ′ = π R 3 , el volumen de la semiesfera es igual a π R 3 y
3
3
4
3
el volumen de la esfera es igual a π R . Queda demostrado el teorema.
3
Área total de la esfera.
A diferencia de la superficie lateral de un cono o de un círculo, la superficie de una esfera no
se puede desarrollar en un plano. Si queremos hallar una fórmula para el área de una esfera
de radio R , imaginamos un cuerpo inscrito en la esfera y limitado por n superficies
triangulares. En este caso, el pie de la perpendicular desde el centro de la esfera a una
superficie triangular, debe estar situado en el interior de esta superficie. Si se unen los
vértices del cuerpo inscrito con el centro de la esfera, entonces se obtienen n pirámides de
bases A1 , A2 ,..., An y de alturas h1 , h2 ,..., hn (figura 4.22).
O
Figura 4.22
Si existe un número n suficiente de pirámides y si la arista mayor del cuerpo inscrito es lo
suficientemente pequeña, entonces la suma de las áreas de las bases de las pirámides se
diferencian muy poco del área total AT de la superficie esférica.
60
Además, el volumen de la esfera se diferencia muy poco del volumen del cuerpo inscrito, y
el radio R también se diferencia poco de la altura de cada pirámide.
El volumen del cuerpo inscrito está formado por el volumen de las pirámides:
1
1
1
Vn = A1 h1 + A2 h2 + ... + An hn … (1).
3
3
3
Cuando existe un número suficiente de pirámides y el área de la mayor de sus bases es lo
suficientemente pequeña, entonces la altura menor de las pirámides se diferencia muy poco
del radio R de la esfera. Por esta razón podemos transformar (1) en:
1
1
1
A1 R + A2 R + ... + An R
3
3
3
1
Vn ≈ ( A1 + A2 + ... + An ) R
3
3V
A1 + A2 + ... + An ≈ n
R
Vn ≈
La suma A1 + A2 + ... + An se diferencia, entonces, tan poco como se quiera de AT :
A1 + A2 + ... + An ≈ AT
3Vn 3 4
= ⋅ π R 3 = 4 π R 2 , de esto resulta que AT = 4 π R 2 . Queda así
R
R 3
demostrado el siguiente teorema:
Como también
Teorema 4.11: El área total AT de una esfera de radio R es AT = 4 π R 2 .
EJERCICIO DEL CAPÍTULO
1. La altura de una pirámide regular de base cuadrada mide 14 cm y el lado de la base es
de 16 cm. Halla la longitud de la arista lateral.
2. Halla la superficie total de una pirámide recta de base cuadrada de 20 cm de altura, si el
lado de la base mide 42 cm.
3. La altura de una cara de una pirámide regular de base triangular es igual a 12 cm y forma
un ángulo de 300 con el plano de la base. Halla el área lateral y el volumen de la
pirámide.
4. La base de la pirámide SABC es un triángulo rectángulo ABC. La arista SA es
perpendicular al plano de la base e igual a 18 cm. Halla el área total de la pirámide si la
hipotenusa AB de la base mide 25 cm y el cateto BC mide 7,0 cm.
5. Halla la superficie lateral de un prisma regular de base hexagonal cuya diagonal mayor
mide 13 dm y la arista lateral 5,0 dm.
61
6. En la base de un prisma hexagonal regular se ha inscrito una circunferencia de radio
igual a 10 cm. Si la distancia entre las bases del prisma es de 20 cm, calcula su volumen
y su área lateral.
7. El plano que contiene al triángulo equilátero BCE es perpendicular al que contiene la
cuadrado ABCD. Halla el volumen de la pirámide ABCDE en función del lado del
cualdrado.
8. Calcula el área lateral, área total y el volumen de un tetraedro regular si se conoce que el
radio de la circunferencia circunscrita a la base es de 40 cm.
9. La superficie total de un cubo es de 486 cm2. Calcula el área total del prisma
cuadrangular que resulta de cortar el cubo por un plano que contiene un lado de la base
y forma con esta un ángulo de 300.
10. El área total de una pirámide triangular regular es de 60 m2 y el radio del círculo inscrito
en la base mide 2,0 m. Halla la altura de la pirámide.
11. Se desea excavar un pozo cilíndrico de 1,50 m de diámetro. ¿Cuántos metros cúbicos de
tierra se tendrían que excavar si el pozo tiene una profundidad de 12 m?
12. De un tronco cilíndrico de madera, de 10 cm de largo y 6,0 cm de diámetro, se quiere
obtener una pirámide regular triangular, de forma tal que el vértice de la pirámide
coincida con el centro de una de las bases del tronco y la base de la misma quede
inscrita en la otra base de dicho tronco. ¿Cuántos metros cúbicos de madera se
desechan en la obtención de dicha pirámide?
13. Una pila de arena en forma de cono mide 2,10 m de altura y su perímetro es 24,80 m.
¿De cuántos metros cúbicos de arena es la pila y cuál es su masa si 1 m3 de arena seca
pesa 1 800 kg?
14. ¿Cuántas esferas de diámetro d = 2,1 m se pueden fabricar con un tubo de plomo de
1,80 m de longitud, 3 cm de espesor y 9 cm de diámetro interior, si al derretir el tubo de
pierde un 4 %?
15. A un cubo de madera cuya arista es a = 28 cm se le debe dar en el torno la forma de una
esfera, de modo que el desperdicio sea el mínimo posible. ¿Cuántos metros cúbicos de
madera se desperdician?
16. Calcula el diámetro, el área total y el volumen de una esfera, en la que una circunferencia
máxima tiene una longitud de 157 cm.
17. Un depósito de hierro para agua consta de un cilindro que termina, en su parte inferior,
en una semiesfera. La parte cilíndrica del depósito tiene 1,80 m de altura; la
circunferencia de su base tiene 2,00 m de diámetro (ancho interior).
a) ¿Cuántos hectolitros de agua caben en este depósito?
b) ¿Cuál es su área total?
18. El radio de la Tierra es de 6 370 km. Suponiendo que la Tierra sea una esfera, calcula:
62
a) La longitud de un meridiano de la esfera terrestre.
b) El área de su superficie total.
c) Su volumen.
19. El radio del Sol es de 695 400 km. Calcula su volumen. ¿Cuántas esferas terrestres
tienen el mismo volumen que le sol?
63
CAPÍTULO 5: GEOMETRÍA ANALÍTICA DEL PLANO Y DEL ESPACIO.
Hasta el capítulo anterior hemos demostrado las proposiciones geométricas y hemos
resuelto ejercicios y problemas geométricos utilizando la vía sintética. En este capítulo
estudiaremos otra vía, la cual se apoya en los conocimientos que del Álgebra Vectorial ya
conoces. Esta vía recibe el nombre de vía analítica y la Geometría que la utiliza se le ha
llamado Geometría Analítica. La misma nos permitirá, además de demostrar proposiciones y
resolver ejercicios y problemas geométricos que realizamos por la vía sintética, conocer
nuevos conceptos, proposiciones y procedimientos geométricos que constituyen la base del
estudio de la Geometría Analítica.
Para comenzar el estudio de la Geometría Analítica del plano y del espacio es necesario
puntualizar los conocimientos del Álgebra Vectorial que nos servirán de sustento para el
desarrollo de la teoría de esta Geometría.
5.1. Nociones de Álgebra Vectorial.
La idea básica de la Geometría Analítica consiste en sustituir problemas de índole
geométrica por otros de carácter algebraico, lo cual se logra mediante el empleo de ciertos
recursos que son los sistemas de coordenadas cartesianas. Para el estudio de estos
sistemas daremos primeramente la noción de eje, de la cual se derivarán otros conceptos,
proposiciones y procedimientos.
Definición 5.1: Sea r una recta en la que escogemos dos puntos O y U. Convendremos en
que el primero de estos puntos representará gráficamente al número real 0 (cero) y el
segundo, al número real +1. La recta orientada bajo estas condiciones recibe el nombre de
eje. Al punto O se le denomina origen del eje y al punto U, punto unidad.
Del curso de Álgebra conoces que entre el conjunto de los números reales x y el conjunto de
los puntos P de un eje queda establecida una bisección. Si el número real x es positivo, el
punto P del eje que le corresponde queda en el semieje positivo (a la derecha del punto O).
Si el número real x es negativo, el punto P del eje que le corresponde queda en el semieje
negativo (a la izquierda del punto O).
Si en un eje E se corresponden mutuamente el punto P y el número real x, entonces x se
llamará abscisa o coordenada de P. Escribiremos: P (x) y leeremos: punto P, de abscisa x.
Definición 5.2: Sean A( x A ) y B( x B ) dos puntos de un eje E. se denomina medida
algebraica del segmento de origen A y extremo B, al número real x B − x A , o sea, a la
diferencia entre la abscisa del extremo del segmento y la de su origen. Tal medida
algebraica se denota: AB , es decir, AB = x B − x A .
Obsérvese que la abscisa de un punto P es la medida algebraica del segmento de origen O
y extremo P y que AB = − BA ; de igual manera, que la distancia entre A y B viene dada por
xB − x A .
64
Definición 5.3: Sean A y B dos puntos de un eje E. Se llama punto medio del segmento
AB ( y de BA) al punto M de E tal que AM = MB .
Si conocemos las abscisas de A y B, podemos hallar de inmediato las abscisas de M.
Efectivamente, de AM = MB se tiene que x M − x A = x B − x M , de lo que se obtiene que
x + xB
.
xM = A
2
Definición 5.4: Se denomina sistema de coordenadas rectangulares en el plano a dos ejes
perpendiculares con el origen común. A este origen común se le conoce como origen del
sistema de coordenadas y a los ejes, ejes coordenados o ejes de coordenadas (figura 5.1).
Generalmente, al eje “horizontal” orientado positivamente “hacia la derecha” se le llama eje
de las abscisas (se denota por OX) y, al eje “vertical” orientado positivamente “hacia arriba”
se le llama eje de las ordenadas (se denota OY). El sistema habitualmente se denota por XY
o XOY. Usualmente, en ambos ejes de coordenadas se elige la misma longitud como
unidad, aunque en algunos casos es aconsejable escoger unidades distintas. Los ejes
dividen al plano en cuatro regiones llamadas cuadrantes.
2
1
-2
-1
1
2
3
-1
Figura 5.1
-2
Definición 5.5: Se denomina sistema de coordenadas rectangulares en el espacio a tres
ejes perpendiculares dos a dos, con el origen común. A este origen común se le conoce
como origen del sistema de coordenadas y a los ejes, ejes coordenados o ejes de
coordenadas.
Cada par de ejes determina un plano que se llama plano coordenado. Sean O el origen;
OX, OY, OZ los ejes coordenados, que suelen llamarse: de las abscisas, de las ordenadas y
de las cotas, respectivamente. Los planos coordenados se denotan:
65
XY el que determinan OX y OY.
YZ el que determinan OY y OZ.
ZX el que determinan OZ y OX.
El sistema se denota XYZ o OXYZ. Los tres planos dividen el espacio en ocho regiones
(triedros trirrectangulares), que se llaman octantes.
En el espacio cada par de ejes forma un ángulo recto. Sin embargo, un observador
solamente puede ver uno de esos ángulos como recto. Se convendrá en que dos de los ejes
del sistema están en el plano del dibujo, y que la visual es normal a este. En la figura 5.2, los
ejes OY y OZ son los que están en el plano del dibujo. Si adoptamos en cada eje
coordenado la misma longitud como unidad, entonces la longitud unidad en el eje OX se ve
menor que el segmento de longitud unidad en cada uno de los otros dos ejes (habitualmente
se toma la mitad de la unidad que se escogió para cada uno de los otros dos ejes).
z
1
O
y
1
1
Figura 5.2
x
Representación de puntos en un sistema de coordenadas rectangulares en el plano y
en el espacio.
Todo punto P en el plano tiene dos coordenadas: la de las abscisas y la de las ordenadas,
que se representa como un par ordenado, es decir, P( x P ; y P ) . Para representarlo por el
valor x P de las abscisas del punto P se traza una recta paralela al eje OY, y por el valor y P
de las ordenadas del punto P se traza una recta paralela al eje OX; en el punto de
intersección de estas rectas estará ubicado el punto P (figura 5.3).
En el espacio, todo punto P tiene tres coordenadas: la de las abscisas, la de las ordenadas y
la de las cotas, que se representa por triada ordenada, es decir, P ( x P ; y P ; z P ) . Para
representarlo por el valor x P de las abscisas del punto P se traza una recta paralela al eje
OY, y por el valor y P de las ordenadas del punto P se traza una recta paralela al eje OX; por
el punto de intersección de estas rectas se traza una recta paralela al eje OZ; por ese mismo
punto de intersección y por el origen de las coordenadas se traza una recta que queda
contenida en el plano XY. Seguidamente por el valor z P de las cotas se traza una recta
66
paralela a la trazada en el plano XY, hasta que corte a la recta que fue trazada paralela al
eje OZ. En el punto de intersección de estas dos últimas rectas quedará ubicado el punto P
(figura 5.4).
y
yP
P( x P ; y P )
O
xP
x
Figura 5.3
z
zP
P( x P ; y P ; z P )
yP
O
y
xP
x
Figura 5.4
Coordenadas del punto medio de un segmento en el plano y en el espacio.
Sean A( x A ; y A ) y B( x B ; y B ) dos puntos de un plano y M ( x M ; y M ) el punto medio del
segmento AB . Hallemos las coordenadas de M en función de las coordenadas de A y B
(figura 5.5).
67
y
B2
B
M
M2
A
A2
A1
O
M1
B1
x
Figura 5.5
Si A1 , B1 y M 1 son las proyecciones de A, B y M sobre el eje X, sabemos que de la
Geometría Elemental que M 1 es el punto medio de A1 B1 . Si A2 , B2 y M 2 son las
proyecciones de A, B y M sobre el eje X, sabemos que de la Geometría Elemental que M 2
es el punto medio de A2 B2 . Como las abscisas de A1 , B1 y M 1 y las ordenadas de
A2 , B2 y M 2 son las mismas que las de A, B y M, respectivamente, tendremos, por la
x + xB
y + yB
definición 5.3, que: x M = A
y yM = A
.
2
2
Sean ahora A( x A ; y A ; z A ) y B ( x B ; y B ; z B ) dos puntos de un plano y M ( x M ; y M ; z M ) el punto
medio del segmento AB . Hallemos las coordenadas de M en función de las coordenadas de
A y B (figura 5.5).
z
B
M
A
O
y
A1
M1
x
Figura 5.6
B1
De manera análoga a como procedimos en el plano, procedemos en el espacio. Si
designamos por A1 y B1 las proyecciones de A y B sobre XY, entonces, el punto medio, M ,
68
de AB se proyectará en M 1 , punto medio de A1 B1 . Como A1 , B1 y M 1 son puntos del plano
x + xB
y + yB
y yM = A
, que son la abscisa y
XY, las coordenadas de M 1 en XY son x M = A
2
2
y + yB
y
la ordenada de M. Análogamente, proyectando AB sobre YZ, tendremos y M = A
2
z + zB
⎛ x + xB y A + yB z A + z B ⎞
, donde z M es la cota de M. Por tanto: M ⎜ A
zM = A
;
;
⎟.
2
2
2 ⎠
⎝ 2
Fórmula de la distancia de dos puntos en el plano y en el espacio.
Sean P1 ( x1 ; y1 ) y P2 ( x 2 ; y 2 ) dos puntos distintos del plano. Consideremos primeramente el
caso en que ambos puntos tengan una de sus dos coordenadas iguales, por ejemplo y1 = y 2
(figura 5.7).
y
P1
M1
P2
M2
O
x
Figura 5.7
Entonces d ( P1 , P2 ) = d ( M 1 , M 2 ) y, como en OX, M 1 ( x1 ) y M 2 ( x 2 ) ; d ( M 1 , M 2 ) = x 2 − x1 , luego
d ( P1 , P2 ) = x 2 − x1 . Análogamente, si x1 = x 2 : d ( P1 , P2 ) = y 2 − y1 .
Supongamos que x1 ≠ x 2 y y1 ≠ y 2 (figura 5.7).
y
P2
P1
Q
M1
M2
O
x
Figura 5.8
69
Sean M 1 y M 2 las proyecciones de P1 y P2 sobre OX, y Q la proyección de P1 sobre la
recta que pasa por P2 perpendicular a OX. En las condiciones supuestas, se forma el
triángulo P1QP2 , rectángulo en Q( x 2 ; y1 ) . Aplicando el teorema de Pitágoras:
[d ( P1 , P2 ) ]2
= [d ( P1 , Q ) ] + [d ( Q , P2 ) ]
2
2
Pero, d ( P1 , Q ) = d ( M 1 , M 2 ) = x 2 − x1 y d (Q, P2 ) = y 2 − y1 .
Por tanto: d ( P1 , P2 ) = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2 , que es la fórmula buscada. Nótese que es
válida para cuando x1 = x 2 o y1 = y 2 .
Sean P1 ( x1 ; y1 ; z1 ) y P2 ( x 2 ; y 2 ; z 2 ) dos puntos distintos del espacio. Supongamos, en primer
lugar, que x1 = x 2 y y1 = y 2 . Entonces P1 y P2 están sobre un recta paralela a OZ y la
distancia entre P1 y P2 será igual a la distancia entre sus proyecciones respectivas sobre
OZ. Como estas proyecciones son, en OZ, Q1 ( z1 ) y Q2 ( z 2 ) : d ( P1 , P2 ) = z1 − z 2 .
Supongamos ahora que no coincidan las proyecciones, sobre XY de P1 y P2 (figura 5.9) y
que z1 ≠ z 2 . Sean M 1 y M 2 las proyecciones de P1 y P2 sobre el plano XY; y Q la
proyección de P1 sobre la recta que pasa por P2 , perpendicularmente al plano XY. Entonces
el triángulo P1QP2 , rectángulo en Q ( x 2 ; y 2 ; z1 ) , por lo que se cumple que:
[d ( P1 , P2 ) ]2
= [d ( P1 , Q ) ] + [d ( Q , P2 ) ]
2
2
Pero, como d ( P1 , Q ) = d ( M 1 , M 2 ) = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2 y d (Q, P2 ) = z 2 − z1 , queda:
d ( P1 , P2 ) = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2 + ( z 2 − z1 ) 2 , que es la fórmula buscada, la cual es también
valida cuando z1 = z 2 .
z
P2
P1
Q
O
y
M1
x
Figura 5.9
M2
70
Vectores.
Uno de los conceptos más importantes que utilizaremos en este capítulo es el de vector
como herramienta importante para abordar numerosos aspectos de la Geometría Analítica.
Definición 5.6: Sea E el conjunto de todos los puntos del espacio. Llamaremos vector a
todo par ordenado de elementos de E. Si A y B son dos puntos, la notación (A, B) designa
un vector. El punto A se llama origen del vector y el punto B será el extremo.
Al vector (A, B) asociaremos gráficamente el segmento “dirigido” de A hacia B. para
distinguir, en el gráfico, el extremo B del origen A, colocaremos en B la punta de una flecha
(figura 5.10).
B
A
Figura 5.10
→
Esta representación sugiere designar el vector (A, B) de la siguiente forma: AB .
En la definición no se establece que a y b sean distintos. Si A y B coinciden, entonces se
→
→
→
dice que el vector AB es nulo y se denota por 0 . Si AB no es nulo, la recta que determinan
→
A y B se denomina recta soporte del vector AB .
→
Se llama longitud o módulo del vector AB a la distancia entre el origen y el extremo del
→
vector; se denota AB .
→
→
Si dos vectores AB y CD son no nulos, se dirá que tienen la misma dirección si las rectas
soporte de ambos son paralelas o coinciden. Si dos vectores tienen la misma dirección, se
acostumbra a decir que son paralelos.
Componentes de un vector según un eje.
→
Sean: E un eje y AB un vector, no situados necesariamente en un mismo plano (figura 5.11)
B
A
O
A1
Figura 5.11
B1
E
71
Proyectemos A y B, ortogonalmente (perpendicularmente) sobre E; sean A1 y B1 sus
→
proyecciones respectivas. Llamaremos componente de AB según E, a la medida algebraica
del segmento con origen en A1 y extremo en B1 . Si O es el origen adoptado en E, entonces,
→
la componente de AB según E, viene dada por:
A1 B1 = OB1 − OA1 = x B1 − x A1 .
Nótese que la componente de un vector nulo según E, es cero. Sin embargo, la componente
de un vector sobre E puede ser cero sin que le vector sea nulo. En efecto, basta tomar un
vector no nulo cuya recta soporte sea perpendicular al eje.
Componentes de un vector en un sistema de coordenadas.
→
Sean OXYZ un sistema de coordenadas y AB el vector de origen A y extremo B. denotemos
por A1 , A2 , A3 las proyecciones de A sobre los ejes X, Y y Z, respectivamente y B1 , B2 , B3
las proyecciones de B sobre los mismos ejes (figura 5.12).
z
B3
B
A3
A
A2
O
A1
B2
y
M1
B1
x
Figura 5.12
→
→
Llamaremos componentes de AB en el sistema OXYZ a las componentes de AB según
cada uno de los ejes del sistema.
→
Si A( x1 ; y1 ; z1 ) y B( x 2 ; y 2 ; z 2 ) entonces, las componentes de AB en OXYZ, son:
A1 B1 = x 2 − x1
A2 B2 = y 2 − y1
A3 B3 = z 2 − z1
→
Escribiremos AB = x 2 − x1 ; y 2 − y1 ; z 2 − z1 ) .
Consecuencias:
• Un vector es nulo si y sólo sí sus tres componentes son nulas.
72
•
Si el origen de un vector es P1 ( x1 ; y1 ; z1 ) y su extremo es P2 ( x 2 ; y 2 ; z 2 ) entonces, la
longitud o módulo del vector que determinan es la distancia entre ambos puntos,
→
resultando que P1 P2 = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2 + ( z 2 − z1 ) 2 .
•
→
Si el vector viene dado por sus componentes, o sea, v = (a; b; c) entonces,
→
v = a2 + b2 + c2 .
→
→
Definición 5.7: Se dice que dos vectores a = (a1 ; a 2 ; a3 ) y b = (b1 ; b2 ; b3 ) son iguales si y sólo
→
→
sí a1 = b1 ; a 2 = b2 y a3 = b3 . Se denota: a = b .
Nota: Los vectores en el plano se caracterizan por dos componentes y son válidas las
mismas definiciones y propiedades que los vectores en el espacio estudiadas anteriormente.
→
→
En efecto, sean los ventores a = (a1 ; a 2 ) y b = (b1 ; b2 ) ; se dice que estos vectores son iguales
si y sólo sí a1 = b1 y a 2 = b2 .
Propiedades de la igualdad de vectores.
1. Todo vector es igual a sí mismo.
→
→
→
→
→
→
2. Si a = b , entonces b = a .
→
→
→
→
3. Si a = b y b = c , entonces: a = c .
Significado geométrico de la igualdad de vectores.
→
→
Sean AB y CD dos vectores iguales. Veremos que ambos tienen, necesariamente, la misma
longitud y dirección.
Sean A( x A ; y A ; z A ), B( x B ; y B ; z B ), C ( xC ; y C ; z C ) y D( x D ; y D ; z D ) que supondremos no alineados.
Entonces:
→
AB = ( x B − x A ; y B − y A ; z B − z A )
→
CD = ( x D − xC ; y D − y C ; z D − z C )
→
→
AB = CD ⇔ x B − x A = x D − xC ⇔ x B + xC = x A + x D ⇔
Análogamente,
y B + yC
y + yD
= A
2
2
y
z B + zC z A + z D
=
2
2
x B + xC x A + x D
=
2
2
Las igualdades anteriores prueban que los puntos medios O y O/ de AD y BC deben
coincidir, luego el cuadrilátero ABCD es un paralelogramo. Por tanto, la recta AB es paralela
a la recta CD y, además, d ( A, B) = d (C , D).
73
Solamente hay dos tipos de figuras que poseen las dos últimas propiedades, que son las
que mostramos en las figuras 5.13 y 5.14.
B
B
A
A
O/
O ≡ O/
O
D
C
C
D
Figura 5.13
Figura 5.14
Pero el modelo presentado en la figura 5.14 no es admisible pues O y O / no coincidirían. De
→
→
modo que si AB = CD con A, B, C y D no alineados, estos 4 puntos deben formar una figura
→
→
como la 5.13. Obsérvese que CD puede hacerse coincidir con AB mediante una traslación,
→
→
la que lleva en punto C al punto A. En tal caso diremos que AB y CD tienen el mismo
sentido.
Consecuencia de la igualdad de vectores.
→
Sea AB = (a; b; c) y P0 un punto cualquiera. Entonces, existe un punto único Q , tal que:
→
→
→
→
AB = P0 Q . En efecto, sea P0 ( x0 ; y 0 ; z 0 ) y pongamos Q( x; y; z ) . Entonces AB = P0 Q si y sólo
sí
(a; b; c) = ( x − x0 ; y − y 0 ; z − z 0 )
x = a + x0
y = a + y0
z = a + z0
Luego, Q existe y es único.
De aquí se infiere que para todo vector de R3, existen infinitos vectores iguales a él y todos
ellos de caracterizan por tener las mismas componentes en el mismo orden.
Adición de vectores.
→
→
Definición 5.8: Sean los vectores OA = (a1 ; a 2 ; a 3 ) y OB = (b1 ; b2 ; b3 ) . Se denomina suma de
→
→
→
los vectores OA y OB al vector OS cuyas componentes se obtienen sumando, a las
→
→
componentes del primer vector, que es OA , las del segundo, que es OB . Es decir:
→
→
→
→
→
OS = (a1 + b1 ; a 2 + b2 ; a3 + b3 ) . La suma de OA y OB se denota: OA+ OB .
74
La suma de vectores se representa gráficamente utilizando la regla del paralelogramo, la
→
→
cual consiste en: trazar por los extremos de cada uno de los vectores OA y OB dos
semirrectas, hasta que se corten en un punto S (figura 5.15). El vector resultante de origen
→
→
en O y extremo S, será la representación gráfica de la suma OA+ OB .
z
S
A
B
O
y
Figura 5.15
x
Propiedades de la adición de vectores.
Teniendo en cuenta las propiedades de la adición en R, resulta de inmediato que:
1. La adición de vectores es conmutativa, es decir, cualesquiera que sean los vectores
→
→
→
→
→
→
v1 y v 2 ; v1 + v 2 = v 2 + v1 .
2. La adición de vectores es asociativa, es decir, para cualesquiera sean los vectores
→ →
→
⎛→ →⎞ → → ⎛→ →⎞
v1 , v 2 y v3 : ⎜ v1 + v 2 ⎟ + v3 = v1 + ⎜ v 2 + v3 ⎟ .
⎝
⎠
⎝
⎠
3. En el conjunto de todos los vectores existe un elemento neutro para la adición, es
→
→
→
→
→
→
→
decir, un vector n , tal que para todo v : n + v = v + n = v . Para la adición el vector nulo
cumple esta propiedad.
→
→
→
→
→
→
→
4. Para todo v existe v / tal que v + v / = v / + v = 0 .
→
Definición 5.9: Al vector v / = (− a;−b;−c) se le denomina opuesto o simétrico al vector
→
v (a; b; c) .
La suma de un vector y su opuesto da como resultado al vector nulo.
→
→
El opuesto del vector v se denota por − v .
75
Sustracción de vectores.
→
→
→
→
Definición 5.10: Sean v1 y v 2 dos vectores. Se denomina diferencia de v1 y v 2 a un vector
→
→
→
→
→
→
→
→
→
→
d tal que: v1 = d + v 2 . El vector d , diferencia de v1 y v 2 , se denota: v1 − v 2 (se lee v1 menos
→
v 2 ).
→
→
→
→
Para hallar la diferencia de v1 y v 2 , basta sumar a v1 el opuesto de v 2 (figura 5.16), por lo
→
→
que para representarlo gráficamente, desde el origen del vector v 2 se traza su opuesto − v 2
→
que queda en la misma recta soporte que v 2 , pero en sentido contrario. De aquí se aplica la
→
→
regla del paralelogramo para la suma: v 2 +( − v 2 ).
→
v1
→
→
d
v2
Figura 5.16
→
− v2
Multiplicación de un número natural por un vector.
→
Definición 5.11: Sean: α un número real y v = (a1 ; a 2 ; a3 ) un vector. Se denomina producto
α
de
y de
→
al vector
v
(α a1 ; α a 2 ; α a3 ) , que se denota por
→
α v . Así que
→
α v = (α a1 ; α a 2 ;α a3 ) .
Teniendo en cuenta las propiedades de las operaciones con números reales, resultan de
→
→
inmediato las siguientes propiedades, cualesquiera que sean los vectores v y w y los
números reales α y β :
→
→
→
1. α ( β v ) = (αβ ) v = β (α v ) .
→
→
→
2. (α + β ) v = α v + β v .
→
→
→
→
3. α ( v + w) = α v + β w .
→
→
→
→
4. α v = 0 si y sólo sí α = 0 o v = 0 .
5.
→
→
(− 1) v = − v .
76
→
→
6. α v = α v .
→
→
→
Si c1 , c 2 ,..., c n son números reales y v1 , v 2 ,..., v n son vectores, una expresión del tipo
→
n
∑c
i =1
i
vi
se llama combinación lineal de los vectores dados; c1 , c 2 ,..., c n se llaman coeficientes de la
combinación lineal.
Ángulos directores de un vector. Cosenos directores.
→
Definición 5.12: Sea v = (a1 ; a 2 ; a3 ) un vector no nulo. Sabemos que existe A (a1 ; a 2 ; a3 ) tal
→
→
→
que OA = v . Se denominan ángulos de dirección de v en el sistema de coordenadas XYZ a
los ángulos α , β y γ que la semirrecta OA forma, respectivamente, con las semirrectas OX,
OY y OZ (figura 5.17).
z
A
→
v
γ
β
O α
y
A1
Figura 5.17
x
Definición 5.13: Los cosenos de los ángulos de dirección de un vector se llaman cosenos
directores de este.
→
Calculemos los cosenos directores de v en función de sus componentes. Sea A1 la
proyección de A sobre OX. Entonces, el triángulo OAA1 es rectángulo en A1 y ∠A1OA = α ,
luego, tenemos:
cos α =
OA1
OA
=
a1
a + a 22 + a32
2
1
De manera análoga, proyectando sobre los ejes OY y OZ, obtendremos:
cos β =
a2
a12 + a 22 + a32
; cos γ =
a3
a12 + a 22 + a32
.
Es evidente que se cumple: cos 2α + cos 2 β + cos 2 γ = 1 .
77
→
→
Nota: Si v es un vector no nulo de R2, v = (a1 ; a 2 ) y las fórmulas de los cosenos directores
se reducen a:
cos α =
a1
a +a
2
1
2
2
;
cos β =
a2
a + a 22
2
1
.
Ejemplo:
→
Sea v = (−5;3;−4) . Hallemos los ángulos directores de este vector:
→
v =5 2
cos α =
−5
y, como α ∈ [0, π [ : α = 135 0 .
2
3 2
cos β =
=
≈ 0,42426 ; β ≈ 64 0 54 / .
10
5 2
cos γ =
5 2
3
1
=−
−4
5 2
4 2
≈ −0,56568 ; γ ≈ 124 0 27 / .
10
=−
→
→
Teorema 5.1: Sean k un número real distinto de cero y v un vector no nulo. Los vectores v
→
y k v son paralelos.
Demostración:
→
→
Si v = (a1 ; a 2 ; a3 ) entonces, k v = (k a1 ; k a 2 ; k a3 ) . Sean α , β y γ los ángulos de dirección de
→
→
v y α / , β / y γ / los ángulos de dirección de k v . Tenemos, por tanto:
a
ka
cos α = →1
cos α / = →1
v
kv
cos β =
a2
→
cos β / =
v
cos γ =
a3
→
→
kv
cos γ / =
v
→
ka 2
ka3
→
kv
→
Como k v = k v , cos α / =
ka1
→
k v
. Además,
k
es igual a 1 o a -1, según sea k > 0 o k < 0.
k
78
⎧cos α = cos α /
⎪
Si k > 0, resulta 1) ⎨cos β = cos β /
⎪cos γ = cos γ /
⎩
⎧cos α = − cos α /
⎪
Si k < 0, resulta 2) ⎨cos β = − cos β /
⎪cos γ = − cos γ /
⎩
→
→
Se han obtenido así dos posibilidades y, en ambas, v y k v son paralelos. En el caso 1)
ambos vectores tienen el mismo sentido; en el 2), tienen sentidos opuestos.
Definición 5.14: Llamaremos vector unitario a todo vector cuya longitud es igual a 1.
⎛6 2 3⎞ ⎛ 3 4⎞
Por ejemplo, los vectores: ⎜ ;− ; ⎟; ⎜ − ; ⎟; (1;0 ); (0;0;1) son unitarios.
⎝7 7 7⎠ ⎝ 5 5⎠
Vectores coordenados unitarios.
Sea OXYZ un sistema de ejes rectangulares en el espacio.
→
→
→
Consideremos el conjunto de vectores: i (1;0;0) ; j (0;1;0) y; k (0;0;1) . Estos tres vectores son
unitarios. Además, tienen la misma dirección y sentido que los ejes OX, OY y OZ,
respectivamente. Por ambas razones, diremos que forman un sistema de vectores
coordenados unitarios (en la figura 5.18 se representa el sistema de vectores coordenados
unitarios adoptado).
z
→
k
→
j
O
y
→
i
Figura 5.18
x
→
→
En el caso de R2, los vectores i (1;0) ; j (0;1) forman un sistema de vectores coordenados
unitarios.
79
Veamos a continuación cómo es posible expresar cada vector de R3 como combinación
→ → →
→
lineal de los vectores coordenados unitarios i , j , k . En efecto, sea v = ( x; y; z ) . Entonces:
→
v = ( x;0;0) + (0; y;0) + (0;0; z )
= x(1;0;0) + y (0;1;0) + z (0;0;1)
→
→
→
= x i + y j+ z k
Producto escalar.
→
→
Definición 5.15: Sean v1 y v 2
dos vectores del mismo número de componentes.
→
→
Llamaremos producto escalar de v1 y v 2 a la suma de los productos de las componentes del
→
→
primer vector por las componentes respectivas del segundo. El producto escalar de v1 y v 2
→
→
→
→
3
se denota: si v1 (a1 ; a 2 ; a3 ) y v 2 (b1 ; b2 ; b3 ) , v1 ⋅ v 2 = a1b1 + a 2 b2 + a3 b3 = ∑ ai bi .
i =1
Propiedades del producto escalar:
→
→
→
→
→
→
1. Cualesquiera que sean v1 y v 2 , entonces v1 ⋅ v 2 = v 2 ⋅ v1 , o sea, el producto escalar es
conmutativo. Basta tener en cuenta la propiedad conmutativa de la multiplicación en
R.
→
→ →
→ →
2. Para todo vector v : 0⋅ v = v ⋅ 0 = 0 .
→
→
→
→
→
→
→
→
→
→
3. Cualesquiera que sean los vectores v1 , v 2 y v3 : v1 ⋅ (v 2 + v3 ) = v1 ⋅ v 2 + v1 ⋅ v3 .
4. Cualesquiera
→
→
→
que
sean
→
→
los
vectores
→
→
v1 y v 2
y
el
número
real
c:
→
(c v1 ) ⋅ v 2 = v1 ⋅ (c v 2 ) = c(v1 ⋅ v 2 ) .
→
→ →
→ →
→
→
5. Para todo vector v : v ⋅ v ≥ 0, y v ⋅ v = 0 si y sólo sí v = 0 .
→
→
6. Cualesquiera que sean los vectores v1 y v 2 ,
→
→ 2
→
→ 2
→
→
a) v1 + v 2
b) v1 − v 2
→ 2
→
→
→ 2
→ 2
→
→
→ 2
= v1 + 2 v1 ⋅ v 2 + v 2
,
= v1 − 2 v1 ⋅ v 2 + v 2 ,
→
→
c) v1 + v 2 ≤ v1 + v 2 (desigualdad triangular).
Interpretación geométrica del producto escalar.
→
→
Sean v1 y v 2 , dos vectores, de R2 o R3, ninguno nulo y que no tienen la misma dirección.
Sea θ el ángulo que forman ambos vectores.
80
A2
S
→
→
→
v1 + v 2
v2
Figura 5.19
π −θ
θ
→
O
A1
v1
Aplicando la ley de los cosenos al triángulo OA1S, tenemos:
2
2
2
OS = OA1 + A1 S − 2OA1 ⋅ A1 S ⋅ cos(π − θ ) ; luego:
→ 2
2
→
→
2
→
→
OS = OA1 + A1 S − 2 OA1 ⋅ A1 S ⋅ cos(π − θ ) , o sea,
→ 2
→
v1 + v 2
→ 2
→ 2
→ 2
→
→
= v1 + v 2 − 2 v1 ⋅ v 2 ⋅ cos(π − θ ) . Por propiedad 6 a) tendremos:
→ 2
→
→ 2
→
→ 2
→
→
v1 + v 2 + 2 v1 ⋅ v 2 = v1 + v 2 + 2 v1 ⋅ v 2 ⋅ cos θ , de donde resulta que:
→
→
→
→
v1 ⋅ v 2 = v1 ⋅ v 2 ⋅ cos θ
Veamos que la igualdad anterior también es válida para cuando los dos vectores tienen la
→
→
misma dirección. En tal caso, sabemos que existe α ∈ R ∗ tal que: v1 = α v 2 y que el ángulo
de los vectores es θ = 0 o θ = π .
Calculemos el ángulo θ partiendo de la fórmula hallada para el caso de vectores no
paralelos.
→
cos θ =
→
v1 ⋅ v 2
→
→
=
→
→
→
α v2 ⋅ v2
v1 ⋅ v 2
Luego, cos θ =
→
α (v 2 ) ⋅ v 2
→
=
→
α (v 2 ⋅ v 2 )
→
→
α v2 ⋅ v2
→
=
→
α (v 2 ⋅ v 2 )
→ 2
.
α v2
α
.
α
→
→
→
→
Si α > 0 , v1 y v 2 tienen el mismo sentido y resulta cos θ = 1 , luego θ = 0 0 , lo cual es correcto;
si α < 0 , v1 y v 2 tienen sentidos opuestos y resulta cos θ = −1 , luego θ = π , que también es
correcto.
81
→
→
Veamos qué sucede cuando los vectores v1 y v 2 son perpendiculares u ortogonales, es
π
decir, cuando θ =
. Sustituyendo en la fórmula hallada para cuando los vectores no son
2
paralelos, tendremos:
→
→
→
→
v1 ⋅ v 2 = v1 ⋅ v 2 ⋅ cos
π
2
→
→
= v1 ⋅ v 2 ⋅ 0 = 0 , por lo que podemos concluir que si dos vectores son
→
→
ortogonales, su producto escalar es igual a cero y viceversa. En efecto si v1 ⋅ v 2 = 0 , por la
→
fórmula hallada tendremos que cos θ =
→
v1 ⋅ v 2
→
→
v1 ⋅ v 2
=
0
→
→
= 0 , resultando que θ =
v1 ⋅ v 2
π
2
.
Producto vectorial de dos vectores de R3.
Seguidamente nos proponemos encontrar un vector que sea ortogonal a dos vectores dados
→
de R3, no paralelos y ninguno nulo. Es decir, dados dos vectores v1 = (a1 ; b1 ; c1 ) y
→
→
v 2 = (a 2 ; b2 ; c 2 ) no paralelos y no nulos, queremos hallar otro vector v = ( x; y; z ) que sea
→
→
→
→
→
→
→
→
→
ortogonal a v1 y v 2 . Ahora bien, v es ortogonal a v1 y a v 2 si y sólo sí v ⋅ v1 = v ⋅ v 2 = 0 , de
lo que obtenemos el sistema:
⎧a x + b1 y + c1 z = 0
S :⎨ 1
⎩a 2 x + b2 y + c 2 z = 0
El sistema S es posible e indeterminado ya que es homogéneo y consta de dos ecuaciones
a b1
b1 c1
c1 a1
con tres incógnitas y al menos uno de los determinantes: 1
es
a 2 b2
b2 c 2
c2 a2
→
→
distinto de cero por ser v1 y v 2 no paralelos y no nulos.
Una solución de este sistema es: x =
b1
c1
b2
c2
y=
c1
a1
c2
a2
z=
a1
b1
a2
b2
lo cual es fácil de
verificar.
En efecto, sustituyendo en las ecuaciones se S tenemos:
a1 b1 c1
b1 c1
c1 a1
a1 b1
a1 x + b1 y + c1 z = a1
+ b1
+ c1
= a1 b1 c1 = 0
, por tener dos filas iguales.
b2 c 2
c2 a2
a 2 b2
a 2 b2 c 2
82
a2
a 2 x + b2 y + c 2 z = a1
b2
b1
c2
c1 = 0
a2
b2
c2
→
Entonces el vector v =(
b1
b2
, por la misma razón.
c1 c1
;
c2 c2
→
→
b1
) es ortogonal a los vectores v1 y v 2 .
b2
a1 a1
;
a2 a2
→
→
Definición 5.16: Sean v1 = (a1 ; b1 ; c1 ) y v 2 = (a 2 ; b2 ; c 2 ) dos vectores cualesquiera de R3. se
→
→
denomina producto vectorial de v1 y v 2 (en ese orden) al vector:
→
v =(
b1
b2
c1 c1
;
c2 c2
→
a1 a1
;
a2 a2
→
→
→
→
b1
), que se denota v1 × v 2 y se lee v1 cruz v 2 .
b2
→
→
→
El vector v1 × v 2 puede escribirse en la forma v1 × v 2 =
b1
c1
b2
c2
→
i+
c1
a1
c2
a2
→
→
→
i
j
k
puede considerarse como el “desarrollo” del determinante: a1
b1
c1 .
a2
b2
c2
→
→
→
→
→
→
→
i
j
k
Por ejemplo si v1 = (3;−1;2) y v 2 = (4;0;−1) , v1 × v 2 = 3 − 1
4
→
→
→
j+
a1
b1
a2
b2
→
k , que
→
2 = i + 11 j + 4 k .
−1
0
Propiedades del producto escalar:
→
→
1. Cualesquiera que sean v1 y v 2 en R3,
→
→
→
v1 × v 2 es ortogonal a cada uno de los
→
vectores v1 y v 2 .
→
→
→
→
→
→
2. Cualesquiera que sean v1 y v 2 en R3, v1 × v 2 = - ( v 2 × v1 ).
→
→
→
→
3. Cualquiera que sea v en R3, v × v = 0 .
→
→
→
→
→
→
4. Cualesquiera que sean v1 y v 2 en R3 y α ∈ R; (α v1 ) × v 2 = α (v1 × v 2 ) .
→
→
→
→
→
→
→
→
5. Cualquiera que sea v en R3, 0 × v = v × 0 = 0 .
→
→
→
6. Si v1 y v 2 son paralelos, entonces: v1 × v 2 = 0 .
→
→
→
→
→
→
→
→
→
→
7. Si v1 = (a1 ; b1 ; c1 ) , v 2 = (a 2 ; b2 ; c 2 ) y v3 = (a3 ; b3 ; c3 ) , entonces: v1 × (v 2 + v3 ) = v1 × v 2 + v1 × v3
→
→
→
→
→
→
→
y (v1 + v 2 ) × v3 = v1 × v3 + v 2 × v3 .
→
→
→
→ 2
→
→
→ 2
→ 2
8. Cualesquiera que sean v1 y v 2 en R3, se cumple que: v1 × v 2 + (v1 ⋅ v 2 ) − v1 ⋅ v 2
= 0.
83
Las propiedades anteriores son fáciles de demostrar aplicando los conocimientos del
Álgebra, por lo que sugerimos al lector su demostración de forma independiente.
Interpretación geométrica del producto escalar.
→
→
Sean v1 y v 2 dos vectores de R3 no paralelos, con origen común y ninguno nulo, y que por
tanto forman un ángulo θ ∈ ]0, π [ .
→
→ 2
→
→
→ 2
→ 2
Sabemos que se cumple v1 × v2 + (v1 ⋅ v 2 ) − v1 ⋅ v2
→
→
= 0 y, además, de la interpretación
→
→
geométrica del producto escalar tenemos v1 ⋅ v 2 = v1 ⋅ v 2 ⋅ cos θ . Como consecuencia de
ambos,
→
→ 2
v1 × v 2
→ 2
→ 2
→ 2
→ 2
→ 2
→ 2
→ 2
→ 2
= v1 ⋅ v 2 − v1 ⋅ v 2 cos 2 θ
= v1 ⋅ v 2 (1 − cos 2 θ )
= v1 ⋅ v 2 sen 2θ
→
→
→
→
De donde, v1 × v 2 = v1 ⋅ v 2 sen 2θ , pues θ ∈ ]0, π [ .
→
→
Por otra parte, si completamos el paralelogramo de lados v1 y v 2 observamos que el área
→
→
→
→
del mismo es (figura 5.20): A = v1 h y, como h = v 2 senθ , resulta A = v1 v 2 senθ , de donde
podemos concluir que el área del paralelogramo es numéricamente igual a la longitud del
→
→
producto vectorial de v1 y v 2 .
S
→
v2
Figura 5.20
h
θ
O
→
v1
Una aplicación del resultado anterior es el cálculo del área de un triángulo dadas las
coordenadas de sus vértices.
Sean P1, P2, P3 tres puntos no alineados (figura 5.21).
84
z
Q
P3
O
P2
P1
y
Figura 5.20
x
Sea Q el punto tal que P1P2QP3 es un paralelogramo. Entonces el área de este viene dada
→
→
por P1 P2 × P1 P3 , que puede calcularse conociendo las coordenadas de P1, P2 y P3. Como los
triángulos P1P2P3 y P2 QP3 son iguales, resulta que: A(ΔP1 P2 P3 ) =
→
1 →
P1 P2 × P1 P3 .
2
Con esto concluimos el tratamiento de los conocimientos básicos del Álgebra Vectorial que
nos interesan para comprender las aplicaciones de estos a la Geometría Analítica del plano
y del espacio, que abordaremos en el próximo epígrafe.
5.2. Estudio analítico del plano.
En este epígrafe caracterizaremos analíticamente al plano, para lo cual aplicaremos los
conocimientos básicos del Álgebra Vectorial estudiados en el epígrafe anterior.
Ecuación vectorial de un plano.
→
Sean: P0 un punto cualquiera del espacio y N un vector no nulo de R3. Sea r una recta que
pasa por P0, tal que exista un punto M que pertenece a dicha recta, distinto de P0, de modo
→
→
que P0 M = N . Tal recta existe y es única, según conocemos de la Geometría Elemental
(figura 5.21).
También sabemos que existe un plano único, que pasa por el punto P0 y es perpendicular a
la recta r. Sea π dicho plano.
85
M
→
N
P
Figura 5.21
P0
π
Sea P un punto de π , distinto de P0. Entonces, P ∈ π si y sólo sí la recta que determinan P0
y P es perpendicular a r.
En el lenguaje vectorial, la propiedad anterior puede traducirse de la siguiente manera: P ∈ π
→
→
→
→
(P distinto de P0), si y sólo sí P0 P es ortogonal a P0 M , o bien, como P0 M = N , P ∈ π (P
→
→
distinto de P0) si y sólo sí: P0 P⋅ N = 0 … (1).
La propiedad expresada por (1) la cumplen todos los puntos P del plano π , y solamente
ellos, por lo que se considera una propiedad característica de π . Diremos, entonces que (1)
→
es una ecuación vectorial de π y que N es un vector normal a dicho plano. El empleo de
artículos indeterminados se debe a que (1) no es la única forma de caracterizar al plano π ,
→
ya que N no es el único vector normal a π , ni P0 el único de sus puntos. En efecto, todos
→
los vectores paralelos al vector N son vectores normales del plano π .
Ecuación cartesiana de un plano.
→
Sea π el plano que pasa por el punto P0 y que admite a N como vector normal. Como
sabemos una ecuación vectorial de π es:
→
→
P0 P⋅ N = 0 … (1).
Elijamos ahora un sistema de coordenadas en el espacio; en este sistema, sean
→
→
P0 ( x0 ; y 0 ; z 0 ) y N = ( A; B; C ) . Si P( x; y; z ) , entonces: P0 P = ( x − x0 ; y − y 0 ; z − z 0 ) , y (1) es
equivalente a:
A( x − x0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 . Efectuando en esta última ecuación obtenemos:
Designando
al
número
Ax + By + Cz + (− Ax0 − By 0 − Cz 0 ) = 0 .
D = − Ax0 − By 0 − Cz 0 ,
obtenemos la ecuación cartesiana del plano π : Ax + By + Cz + D = 0 … (2).
86
Por ejemplo, la ecuación del plano que pasa por el punto P0 (−1;2;5) con vector normal
→
N = (2;3;−1,5) , se determina hallando al número:
D = − Ax0 − By 0 − Cz 0 = −2.(−1) − 3.2 − (−1,5).5 = 3,5 ; luego, se sustituye en (2) y se obtiene la
misma: 2 x + 3 y − 1,5 z + 3,5 = 0 .
Casos particulares de la ecuación del plano y su representación gráfica.
Cuando la ecuación del plano presenta alguna particularidad algebraica, es de suponer que
el mismo posee alguna particularidad algebraica respecto al sistema de coordenadas
adoptado. Veamos los distintos casos:
1. caso: Un plano de ecuación Ax + By + Cz + D = 0 con A, B, C y D distintos de cero corta a
cada eje coordenado en un punto.
Por ejemplo, si el plano tiene por ecuación: 2x+3y+z-6=0, determinamos los puntos de
intersección del plano con cada eje (si queremos hallar el punto de intersección con el eje
OX, igualamos a cero las variable x e y, en el caso del ejemplo, obtendríamos: 2x-6=0; x=3,
por lo que este punto tendría coordenadas (3; 0; 0). De manera análoga se hallan los puntos
de intersección con los otros dos ejes coordenados).
Obtendríamos los puntos de intersección: (3; 0; 0), (0; 2; 0) y (0; 0; 6), los cuales
representamos en un sistema de coordenadas cartesianas, uniéndolos dos a dos. De esta
forma representamos gráficamente este plano (figura 5.22).
z
(0; 0; 6)
(0; 2; 0)
O
y
(3; 0; 0)
Figura 5.22
x
2. caso: Si en la ecuación del plano uno de los coeficientes A, B o C es igual a cero,
obtendríamos tres ecuaciones:
•
•
•
By+Cz+D=0. Este plano será paralelo al eje OX y no lo contiene.
Ax+Cz+D=0. Este plano será paralelo al eje OY y no lo contiene.
Ax+By+D=0. Este plano será paralelo al eje OZ y no lo contiene.
87
Por ejemplo, el plano de ecuación 2x+3y=6, es paralelo al eje OZ y se representa de la
siguiente forma: se determinan los puntos de intersección de este plano con los otros dos
ejes y, por estos se trazan rectas paralelas al eje OZ (figura 5.23). En este caso el punto de
intersección del plano con el eje OX es (3; 0; 0) y con el eje OY es (0; 2; 0).
3. caso: Si en la ecuación A, B y C son no nulos y D = 0, el plano pasa por el origen de
coordenadas pero, no contienen a ninguno de los ejes. Para representar estos planos se
procede de la siguiente manera:
•
•
Determinamos dos puntos, no alineados con el origen de coordenadas, en dos de los
planos ordenados: XY y XZ u XY y YZ u XZ y YZ (si por ejemplo, queremos
determinar dos puntos en los planos XY y XZ, en la ecuación dada del plano,
igualamos a cero la variable z y la variable y, respectivamente. En cada caso a la
ecuación resultante le damos un valor cualquiera, excepto cero, a una de sus
variables y determinamos la otra).
Estos puntos y el origen de coordenadas se unen dos a dos.
Por ejemplo para representar el plano 2x+3y+z=0 se determinan dos puntos en dos de los
planos coordenados. Sean estos planos XY y XZ. En el plano XY hacemos cero a z,
obteniendo la ecuación 2x+3y=0; le damos a y el valor de 2 y obtenemos x = - 3; luego el
punto tendrá las coordenadas (-3; 2; 0). En el plano XZ hacemos cero a y, obteniendo la
ecuación 2x+z=0; le damos a z el valor -2 y obtenemos x = 1; luego el punto tendrá las
coordenadas (1; 0: -2). En la figura 5.24 queda representado este plano.
4. caso: Si en la ecuación D = 0 y uno de los coeficientes A o B o C es igual a cero,
obtendríamos:
•
•
•
Si A = 0, resultaría el plano de ecuación By+Cz=0, que es paralelo al eje OX,
conteniéndolo.
Si B = 0, resultaría el plano de ecuación Ax+Cz=0, que es paralelo al eje OY,
conteniéndolo.
Si C = 0, resultaría el plano de ecuación Ax+By=0, que es paralelo al eje OZ,
conteniéndolo.
88
Este se representa gráficamente escogiendo dos puntos del eje al que es paralelo: uno de
estos por lo general es el origen de coordenadas, el otro se escoge arbitrariamente; se
busca otro punto en el plano que no contiene al eje y; se unen estos puntos dos a dos.
Por ejemplo, el plano de ecuación 2x – 3y = 0 contiene al eje OZ, por lo que escogemos dos
puntos distintos de este eje. Buscamos otro punto del plano XY, que no contiene a este eje,
por ejemplo, (3; 2; 0) (figura 5.25).
z
z
(-3; 2; 0)
O
O
y
y
(3; 2; 0)
Figura 5.24
x
Figura 5.25
x
(1; 0: -2)
5. caso: Si en la ecuación D ≠ 0 y dos de los coeficientes A, B o C son iguales a cero,
obtendríamos:
•
Si B = 0 y C = 0, la ecuación del plano resultaría Ax +D=0. Este plano es paralelo al
plano YZ.
•
Si A = 0 y C = 0, la ecuación del plano resultaría By +D=0. Este plano es paralelo al
plano XZ.
•
Si A = 0 y B = 0, la ecuación del plano resultaría Cz +D=0. Este plano es paralelo al
plano XY.
Estos planos de representan determinando el punto de intersección con el eje y trazando por
este rectas paralelas a los otros dos ejes.
Por ejemplo, el plano x – 3 = 0 es paralelo al plano YZ. Para representarlo resolvemos la
ecuación y obtenemos x = 3, obteniendo el punto de intersección del plano con el eje OX
que tiene coordenadas (3; 0; 0) (figura 5.26).
Nota: Las ecuaciones x = 0, y = 0, z = 0 representan la los planos coordenados YZ, XZ, XY,
respectivamente.
89
Observaciones necesarias:
1. Es fácil demostrar que si dos planos son paralelos, sus vectores normales son
→
→
paralelos, o sea, que si M y N son los vectores normales de dos planos paralelos,
→
→
→
→
basta demostrar que existe un número real α ∈ R ∗ , tal que M = α N o N = α M .
2. Si dos planos son perpendiculares es fácil demostrar que sus vectores normales son
perpendiculares, es decir que su producto escalar es igual a cero.
3. Para determinar la ecuación cartesiana de un plano que pasa por tres puntos A, B y
→
C, se halla un vector normal N que sea resultado del producto vectorial de los
→
→
→
→
→
→
vectores AB × BC o AB × AC o AC × BC . Con ese vector y cualquiera de los puntos A,
B o C se procede como ya fue explicado anteriormente.
Distancia de un punto a un plano.
Definición 5.16: Sea P1 un punto cualquiera y π un plano. Se llama distancia de P1 a π , a
la longitud del segmento de perpendicular trazada desde P1 al plano π .
Determinemos una fórmula para calcular la distancia de un punto a un plano cuando se
conocen la ecuación del plano y las coordenadas del punto.
Sean π
el plano de ecuación
A( x − x0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 de vector normal
→
N = ( A; B; C ) y que pasa por el punto P0 ( x0 ; y 0 ; z 0 ) . Sea P1 ( x1 ; y1 ; z1 ) un punto que no
pertenece a ese plano.
90
Sea P el pie de la perpendicular trazada de P1 al plano π (figura 5.27). La distancia de P1 al
→
→
plano π será, por definición, d = P1 P . Por ser P1 P un vector normal de π , existe t ∈ R ∗ , tal
que
→
→
→
t N = P1 P … (1). Como N es conocido, bastará hallar t .
→
→
Ya que P pertenece al plano; P0 P . N = 0 … (2).
→
→
→
Pero P0 P = P0 P1 + P1 P … (3).
Sustituyendo (3) en (2) y teniendo en cuenta (1), resultará:
→
→
→
→
→
→
→
→
( PO P1 + t N ). N = 0 . Despejamos t : PO P1 . N + (t N ). N = 0 ⇒ t = −
→
PO P1 . N
→ 2
… (4).
N
→
→
→
De (1) tenemos P1 P = t N = t . N . Sustituyendo aquí la igualdad (4) obtenemos:
→
d ( P1 , π ) =
→
P0 P1 . N
→
=
A( x1 − x0 ) + B ( y1 − y 0 ) + C ( z1 − z 0 )
N
→
N
=
Ax1 + By1 + Cz1 + D
A2 + B 2 + C 2
. Hemos obtenido
así la fórmula deseada.
→
N
P0
P
Figura 5.27
P1
91
Aunque la fórmula ha sido obtenida para cuando P1 no pertenezca al plano, también es
válida para cuando el mismo esté en el plano, ya que, en este caso, el numerador de la
fracción que aparece en el segundo miembro tomará el valor cero.
Ejemplo: La distancia del punto (1; -1; 1) al plano 3x-2y+6z+3=0 se obtiene del modo
siguiente: el primer miembro de la ecuación evaluado para el punto dado es
→
→
14
3(1)-2(-1)+6(1)+3 = 14; N = (3;−2;6); N = 7 . Luego d =
= 2.
7
Distancia entre dos planos paralelos.
Sean π y π / dos planos paralelos, de ecuaciones:
π : Ax + By + Cz + D = 0
π / : Ax + By + Cz + D / = 0
La distancia entre ambos planos es igual a la distancia de un punto de uno cualquiera de
ellos al otro.
Sea P0 un punto cualquiera de π / y d la distancia entre ambos planos. Entonces,
Ax0 + By 0 + Cz 0 + D
… (1). Como P0 pertenece a π / ,
d = d ( P0 , π ) y; sabemos que d ( P, π ) =
2
2
2
A + B +C
/
entonces, Ax0 + By 0 + Cz 0 + D = 0 , de lo que resulta que: Ax0 + By 0 + Cz 0 = − D / .
Sustituyendo este último resultado en (1) obtenemos la fórmula para calcular la distancia
D − D/
entre dos planos paralelos: d ( P, π ) =
.
A2 + B 2 + C 2
Ejemplo 1: Los planos: 2x+y-2z+11=0 y 2x+y-2z+2=0 son paralelos. La distancia entre
ambos se obtiene del modo siguiente:
→
→
N = (2;1;−2); N = 3; d =
11 − 2
3
=3
Ejemplo 2: Los planos : 2x+y-z-3=0 y 4x+2y-2z+5=0 son paralelos. Para hallar la distancia
entre ellos, la ecuación de uno de ellos debe escribirse de manera que los coeficientes de
las variables sean iguales en ambos planos. Por ejemplo 4x+2y-2z-6=0 y 4x+2y-2z+5=0.
−6−5
11
=
.
Luego, d =
24
24
5.3. Estudio analítico de la recta en el plano y en el espacio.
Ecuación vectorial de la recta en el espacio.
Sean A y B dos puntos distintos del espacio. De la Geometría elemental conocemos que
estos puntos determinan una recta única r. sea P0 un punto cualquiera, que puede
pertenecer o no a la recta r. También conocemos que existe una recta única r/, que pasa por
92
P0 y tiene la misma dirección (es paralela) que r. esto significa que si P0 no pertenece a r, r/
es paralela a r, y si pertenece a r, r/ coincide con r.
→
→
En ambos casos al vector AB = V , se llama un vector director de r. Si t es cualquier
→
→
número real y P un punto tal que P0 P = t V , necesariamente P ∈ r/. Recíprocamente, si P ∈
→
→
r/, existe un t real tal que P0 P = t V . Cuando t recorre R, el punto P describe la recta r/. Así,
→
→
pues, la ecuación P0 P = t V , con t recorriendo R es una ecuación vectorial de r/. La
variable t se llama parámetro. Decimos que la recta r/ es la recta que pasa por P0 de vector
→
→
→
director V , y se denota r/ (P0, V ). Es esencial que V sea no nulo. Si fuese nulo, cuando t
→
→
→
→
recorre R, P0 P = t V solamente se cumple cuando P0 P = 0 , o lo que es lo mismo, cuando P
coincide con P0.
→/
→
Puede probarse que si V es un vector de la misma dirección que V , y P1 es cualquier punto
→
→
de r/, entonces: P1 P = s V (donde s recorre R), es también una ecuación vectorial de r/.
→
→
La ecuación P0 P = t V , t ∈ R , puede concebirse como definiendo una aplicación de R en el
conjunto de puntos de r/. Esta aplicación es inyectiva y sobreyectica, o sea, es una
bisección.
Sistema de ecuaciones paramétricas de una recta en el espacio y en el plano.
→
→
Sea la recta r (P0, V ), donde P0 ( x0 ; y 0 ; z 0 ) y V =(a; b; c) en cierto sistema de coordenadas.
→
→
Entonces: P0 P = t V , t ∈ R es una ecuación vectorial de r. Vamos a obtener un sistema de
→
→
tres ecuaciones equivalentes a la ecuación vectorial. Poniendo P( x; y; z ) tenemos: P0 P = t V ,
t ∈ R , equivale a ( x − x0 ; y − y 0 ; z − z 0 ) = t (a; b; c) , igualdad que, a su vez, es equivalente al
sistema:
⎧ x − x0 = at
⎧ x = x0 + at
⎪
⎪
⎨ y − y 0 = bt ; t ∈ R . Por tanto: ⎨ y = y 0 + bt ; t ∈ R .
⎪ z − z = ct
⎪ z = z + ct
0
0
⎩
⎩
El sistema obtenido anteriormente se denomina sistema de ecuaciones paramétricas de
la recta r.
→
Observación importante: Si estamos trabajando en el plano, con P0 ( x0 ; y 0 ) y V =(a; b) ,
→
entonces, un sistema de ecuaciones paramétricas de r (P0, V ) se reduce a:
⎧ x = x0 + at
; t∈R.
⎨
⎩ y = y 0 + bt
93
Recta determinada por dos puntos.
Sean P0 y P1 dos puntos distintos. Designamos por r la recta que determinan. Un vector
→
→
→
director de r es P0 P1 ; una ecuación vectorial es: P0 P = P0 P1 con t ∈ R . Si P0 ( x0 ; y 0 ; z 0 ) y
P1 ( x1 ; y1 ; z1 ) , un sistema de ecuaciones paramétricas de r será:
⎧ x = x0 + ( x1 − x0 )t
⎪
⎨ y = y 0 + ( y1 − y 0 )t ; t ∈ R .
⎪ z = z + ( z − z )t
0
1
0
⎩
Por ejemplo, dados los puntos P0 (−2;3;1) y P1 (4;−2;0) obtengamos un sistema de ecuaciones
paramétricas de la recta que pasa por ambos puntos y determinemos cuál de los siguientes
puntos, A(−8;8;2), B(10;−7;0) , pertenece a la recta. Un sistema de ecuaciones paramétricas
→
de la recta r (P0, P0 P1 ) es:
⎧ x = −2 + 6t
⎪
⎨ y = 3 − 5t ;
⎪z = 1 − t
⎩
t∈R
.
El punto A pertenece a r si existe un t ∈ R , único, tal que, para dicho valor de t , los valores
de x, y y z dados por las ecuaciones del sistema, sean, respectivamente: -8, 8, 2.
Para x = - 8, la primera ecuación da t = - 1, que sustituido en las dos restantes ecuaciones,
nos da y = 8, z = 2. Luego, A pertenece a la recta.
Veamos si B pertenece a la recta. Para x = 10 la primera ecuación da t = 2, que sustituida en
la segunda se obtiene y = -7, que es la ordenada de B. Pero, en la tercera ecuación para
t = 2, resulta z = -1, que no es la cota de B; por lo tanto B no pertenece a la recta.
Ecuación simétrica de la recta en el espacio.
Del sistema de ecuaciones paramétricas de la recta r:
⎧ x − x0 = at
⎪
⎨ y − y 0 = bt ; t ∈ R
⎪ z − z = ct
0
⎩
si a ≠ 0, b ≠ 0, c ≠ 0, se obtiene, despejando t de cada una de ellas, la llamada ecuación
x − x0 y − y 0 z − z 0
, que pasa por el punto P0 ( x0 ; y 0 ; z 0 ) y vector
simétrica de la recta:
=
=
a
b
c
→
director V =(a; b; c) .
94
Planos proyectantes de una recta.
Definición 5.17: Sea r una recta definida analíticamente en un sistema XYZ. Se llaman
planos proyectantes de r a los tres planos que contienen a r y son respectivamente
perpendiculares a cada plano coordenado.
⎧ x = x0 + at
⎪
Sea : r: ⎨ y = y 0 + bt ; t ∈ R .
⎪ z = z + ct
0
⎩
Hallemos la ecuación del plano proyectante de r sobre el plano XY. Para ello, supongamos
que a y b no son nulos ambos, o sea, que la recta no es paralela al eje Z. Multipliquemos la
primera ecuación por b y la segunda por a; restando queda: bx − ay = bx0 − ay 0 .
Esta ecuación es la del un plano π XY pues los coeficientes de x y de y no son nulos ambos;
como falta el término en z, el plano es paralelo al eje OZ y, por tanto, perpendicular al plano
XY. Además, la recta r está contenida en π XY , pues, para todo t ∈ R :
b( x0 + at ) − a( y 0 + bt ) = bx0 − ay 0 .
De esta forma, π XY es el plano proyectante de r sobre XY (figura 5.28).
z
r
π XY
O
x
y
Figura 5.28
Si a y b fuesen nulos ambos, r sería paralela al eje OZ; todo plano que contenga a r es
paralelo al eje OZ y, por tanto, es un plano proyectante de r sobre el plano XY. Luego, en
este caso, hay infinitos planos proyectantes de r sobre XY; dos de ellos son x = x0 ; y = y 0
(figura 5.29).
95
Las ecuaciones de la recta serían de la forma:
⎧ x = x0
⎪
; t ∈ R , con c ≠ 0
⎨ y = y0
⎪ z = z + ct
0
⎩
La proyección de r sobre XY no es, en este caso, una recta sino el punto (x0; y0; 0).
En la figura 5.29 se han trazado tres planos proyectantes sobre el plano XY de una recta
paralela al eje OZ. Procediendo de manera análoga en el caso general, se obtienen los
planos proyectantes de cualquier recta sobre XZ y YZ. Si a = b = 0, x = x0, es el plano
proyectante de r sobre XZ y un plano proyectante de r sobre XY.
Ejemplos:
Los planos proyectantes de la recta:
⎧ x = 2 − 3t
⎪
⎨ y = −5 + 4t ; t ∈ R
⎪z = 3 + t
⎩
son: 4x + 3y +7 = 0; x + 3z -11 = 0 y; y - 4z -17 = 0.
Los planos proyectantes de la recta:
⎧x = 3
⎪
⎨ y = 2 − 5t ; t ∈ R
⎪z = 4 + t
⎩
96
son: x = 3 (sobre el plano XY); x = 3 (sobre el plano XZ) y; y + 5z – 22 = 0 (sobre el plano
XZ).
Nótese que x = 3 es, a la vez, el plano que proyecta r sobre XY y XZ, lo cual se debe a que r
está contenida en el plano de ecuación x = 3, y este es perpendicular a XY y a XZ.
Paralelismo y perpendicularidad de rectas.
→
→
Dos rectas r1 (P1, V1 ) y r1 (P2, V2 ) en el espacio o en el plano son:
→
→
•
Paralelas, si y sólo sí existe α ∈ R ∗ tal que: V1 = α V2 .
•
Perpendiculares, si y sólo sí V1 ⋅ V2 = 0 .
→
→
La ecuación cartesiana de la recta en el plano.
Sea la recta:
⎧ x = x0 + at
r: ⎨
; t∈R.
⎩ y = y 0 + bt
Si eliminamos t en este sistema, llegamos a la ecuación bx − ay = bx0 − ay 0 . Denotando
b = A; − a = B; y bx0 − ay 0 = −C , se obtiene la ecuación de la forma: Ax + By + C = 0 , que se
conoce por forma general de la ecuación cartesiana de la recta r en el plano. En esta
→
fórmula A y B son ambos no nulos, además, un vector normal a ella es N = ( A; B ) y un
→
vector director es V = ( B;− A) .
Casos particulares de la ecuación de la recta en el plano:
1. caso: Una recta Ax + By + C = 0 pasa por el origen de coordenadas, si y sólo sí las
coordenadas de este punto satisfacen la ecuación, o sea, si y sólo sí C = 0.
2. caso: Veamos ahora una condición necesaria y suficiente para que la recta r:
Ax + By + C = 0 sea paralela al eje OX. Un vector director de este eje es el que tiene
→
origen en (0; 0) y extremo en (1; 0), o sea, i = (1; 0) . Un vector director de r es
→
V = ( B;− A) . Por tanto, r es paralela al eje OX si y sólo sí A = 0. Entonces, toda recta
paralela al eje OX tiene una ecuación de la forma By + C = 0 , con B ≠ 0 , o bien y = k,
donde k es constante. La ecuación del eje OX, es, por tanto, y = 0.
3. caso: De manera análoga se llega a la conclusión de que r es paralela al eje OY si y
sólo sí B = 0, o sea, si y sólo sí su ecuación es de la forma Ax + C = 0 , o bien x = h,
donde h es constante. La ecuación del eje OY, es, por tanto, x = 0.
Representación de rectas en R2:
Consideraremos primeramente que la recta viene dada por un sistema de ecuaciones
paramétricas:
⎧ x = x0 + at
; t∈R.
r: ⎨
⎩ y = y 0 + bt
97
Para representarla, bastará situar dos de sus puntos: uno de ellos es el (x0 ; y0); otro, distinto
de este, puede obtenerse dándole a t un valor distinto de cero. Por ejemplo, para t =1
hallamos (x0 + a; y0 + b).
Si la recta viene dada por su ecuación cartesiana, se procede de manera análoga (si no es
paralela a ningún eje coordenado). En caso de que sea paralela a uno de los ejes, se
determina y sitúa el punto donde corta al otro; entonces, la recta quedará perfectamente
determinada conociendo su dirección y uno de sus puntos.
Distancia de un punto a una recta en R2.
Sean P0 ( x0 ; y 0 ) y r: Ax + By + C = 0 . Queremos deducir una fórmula que nos permita calcular
la distancia de un punto P0 a la recta r. Sea r/ la recta que pasa por P0 y es perpendicular a r
(figura 5.30). Si P1 es el punto de intersección de r y r/, la distancia de P0 a P1 es igual a la
distancia buscada. Hallemos las coordenadas de P1 .
→
Como N = ( A; B ) es normal a r, un sistema de ecuaciones paramétricas a r/ será:
⎧ x = x0 + At
; t∈R.
⎨
⎩ y = y 0 + Bt
y
r/
P1
r
PO
O
x
Figura 5.30
Hallemos el valor de t correspondiente a P1
A( x0 + At ) + B( y 0 + Bt ) + C = 0
( Ax0 + By 0 + C ) + ( A 2 + B 2 ) = 0
98
Como A 2 + B 2 ≠ 0 , tendremos: t = −
Ax 0 + By 0 + C
, el cual sustituido en las ecuaciones de r/,
A2 + B 2
resulta:
( Ax0 + By 0 + C ) A
A2 + B 2
( Ax0 + By 0 + C ) B
y1 = y 0 t = −
A2 + B 2
x1 = x0 −
d ( P0 , r ) = d ( P0 , P1 ) = ( x1 − x0 ) 2 + ( y1 − y 0 ) 2
Entonces, =
=
( Ax0 + By 0 + C ) 2 A 2 ( Ax0 + By 0 + C ) 2 B 2
+
=
( A2 + B 2 ) 2
( A2 + B 2 ) 2
( Ax0 + By 0 + C ) 2
( A2 + B 2 )
Ax0 + By 0 + C
A2 + B 2
Queda así deducida la formula de la distancia de un punto a una recta en R2.
Nótese que esta fórmula es enteramente análoga a la de la distancia de un punto a un
plano. Por otra parte, la distancia entre las rectas paralelas siguientes: Ax + By + C = 0 y
Ax + By + C = 0 , viene dada por:
/
C −C/
A2 + B 2
.
Vector director de la recta de intersección de dos planos.
Sean los planos:
π 1 : A1 x + B1 y + C1 z + D1 = 0
π 2 : A2 x + B2 y + C 2 z + D2 = 0
no paralelos; por tanto, su intersección es
una recta r.
Es importante notar que si una recta está contenida en un plano, todo vector director de la
recta debe ser ortogonal a todo vector normal al plano. Como r está contenida a la vez en
→
ambos planos, todo vector director de r será, a la vez, ortogonal a N 1 = ( A1 ; B1 ; C1 ) y a
→
→
N 2 = ( A2 ; B2 ; C 2 ) . Un vector con esta propiedad es N
⎛ B1
⎜
⎜B
⎝ 2
C1
C1
A1
C2 C2
A2
;
;
A1
A2
1
×
→
N
2
, o sea,
B1 ⎞
⎟
B2 ⎟⎠
→
→
Este vector no es nulo ya que si lo fuese N 1 y N 2 tendrían que ser proporcionales y, por
tanto, los planos serían paralelos, contrario a lo supuesto.
99
5.4. Estudio analítico de las cónicas.
En el curso de Geometría Elemental estudiamos varios lugares geométricos como fueron:
dos rectas paralelas, la mediatriz de un segmento, la bisectriz de un ángulo, la
circunferencia, entre otros. Si analizamos detenidamente cada una de las definiciones de
estos lugares geométricos podemos definir de manera general ¿qué se denomina lugar
geométrico?
Definición 5.18: Se denomina lugar geométrico al conjunto de todos aquellos puntos que
satisfacen determinadas condiciones.
Es bueno destacar que solamente los puntos de un lugar geométrico satisfacen las
condiciones exigidas para que sea ese lugar geométrico y no otro. Por ejemplo, sólo los
puntos de la mediatriz de un segmento cumplen la condición de equidistar de los vértices de
dicho segmento. Si al menos un punto del conjunto de puntos no satisface las condiciones
exigidas, entonces no existiría ese lugar geométrico.
Las cónicas o las secciones cónicas que estudiaremos en este epígrafe son, por excelencia,
lugares geométricos. El estudio más completo de las secciones cónicas se realizó en la
antigua Grecia por Apolonio de Perga, quien enseñó en Alejandría y en Pérgamo en la
segunda mitad del siglo III antes de Cristo y es considerado el segundo gran matemático de
la antigüedad, después de Arquímedes. Este estudio fue tan completo que sólo ha sido
superado en los tiempos modernos.
Es importante señalar que las cónicas constituyen el modelo matemático para describir el
movimiento de los planetas de acuerdo a las leyes descubiertas por Johann Kepler (1571 –
1630), utilizadas y ampliadas después por Isaac Newton.
En Geometría Elemental estudiamos a la circunferencia desde el punto de vista sintético. En
este epígrafe la estudiaremos desde el punto de vista analítico.
Estudio analítico de la circunferencia.
Definición 5.19: Sean π un plano, C un punto fijo en π , y r un número real mayor que
cero. Se llama circunferencia al lugar geométrico de todos los punto de π cuya distancia a C
es igual a r.
Ecuación de la circunferencia.
Sea Γ la circunferencia de centro C y radio r situada en el plano π . En este plano
adoptemos un sistema de coordenadas rectangulares en el cual C tiene abscisa h y
ordenada k. Sea P(x; y) un punto del plano (figura 5.31).
→
→ 2
Entonces, P ∈ Γ si y sólo sí CP = r , o sea, CP = r 2 , que equivale, a su vez, a
( x − h) 2 + ( y − k ) 2 = r 2 …(1), que es la ecuación de Γ . Esto significa que, si un punto P(x; y)
pertenece a Γ sus coordenadas deben satisfacer dicha ecuación y recíprocamente, es decir,
que si las coordenadas de un punto satisfacen la ecuación, tal punto está en la
circunferencia.
100
y
Γ
P(x; y)
r
C
O
Figura 5.31
x
Forma general de la ecuación de la circunferencia.
La
ecuación
de
la
circunferencia
( x − h) 2 + ( y − k ) 2 = r 2 es
equivalente
a
x + y − 2hx − 2ky + h + k − r = 0 , la cual es de la forma x + y + 2 Dx + 2 Ey + F = 0 .. (2).
Por tanto, a toda circunferencia le corresponde una ecuación de la forma (2), que se conoce
como la forma general de la ecuación de la circunferencia.
2
2
2
2
2
2
2
Es importante señalar que el recíproco no es cierto, o sea, que no toda ecuación de la forma
(2) define una circunferencia. En efecto, partiendo de esta ecuación, completando cuadrados
y trasponiendo, se obtiene la ecuación equivalente: ( x + D) 2 + ( y + E ) 2 = D 2 + E 2 − F … (3).
Se presentan tres casos:
1. caso: D 2 + E 2 − F > 0, la ecuación define la circunferencia de centro C (- D; - E) y radio
r = D2 + E 2 − F .
2. caso: D 2 + E 2 − F = 0. En este caso, dada equivale a ( x + D) 2 + ( y + E ) 2 = 0 que admite
solamente una solución: el punto (- D; - E). Por lo tanto, cuando esto ocurre la
ecuación general no define una circunferencia.
3. caso: D 2 + E 2 − F < 0. La solución es ahora vacía, pues el primer miembro de (3) es,
para todo (x; y) mayor o igual que cero.
Resumiendo, podemos afirmar que la ecuación x 2 + y 2 + 2 Dx + 2 Ey + F = 0 define una
circunferencia (no reducida a un punto) si y sólo sí D 2 + E 2 − F > 0. El centro de la
circunferencia es el punto C (- D; - E) y el radio r = D 2 + E 2 − F .
Por ejemplo, dadas las siguientes ecuaciones, determinar cuál define a una circunferencia:
a) x 2 + y 2 − 6 x + 2 y − 6 = 0
b) x 2 + y 2 − 6 x + 2 y + 10 = 0
c) x 2 + y 2 − 6 x + 2 y + 11 = 0
a) D 2 + E 2 − F = 9 + 1 + 6 = 16 >0; por tanto define una circunferencia de centro C (3; -1) y radio
r = 4.
101
b) D 2 + E 2 − F = 9 + 1 − 10 = 0 ; por tanto no define una circunferencia.
c) D 2 + E 2 − F = 9 + 1 − 11 = −1 ; por tanto no define una circunferencia.
Estudio analítico de la elipse.
Definición 5.20: Sean F1 y F2 dos puntos distintos y π un plano que los contiene. Se llama
elipse de focos F1 y F2 a todo lugar geométrico de puntos de π tales que la suma de sus
distancias a F1 y F2 es una constante, mayor que la distancia entre F1 y F2.
Designaremos por 2c la distancia de F1 a F2, que llamaremos distancia focal, y por 2a la
suma de las distancias de todo punto de la elipse a sus focos.
Trazado de la elipse.
Conocidos a y c podemos obtener fácilmente un punto de la curva. Sean F1 y F2 dos puntos
situados a una distancia 2c; O el punto medio del segmento F1 F2 ; A1 un punto de la recta
F1F2 situado a una distancia a de O, y A2 el simétrico de A1 respecto a O (figura 5.32).
→
Entonces, A1 A2 = 2a.
P
A1
F1
O
M
F2
A2
Figura 5.32
→
→
Elijamos un punto arbitrario M en el segmento A1 A2 . Observemos que A1 M + MA2 = 2a .
→
→
Haciendo centro en F1 con radio A1 M y centro en F2 con radio A2 M las circunferencias
correspondientes se cortan en dos puntos P y P/ que pertenecen a la elipse. Variando la
posición del punto M se obtienen tantas parejas de puntos como se desee, todos
pertenecientes a la elipse. La curva buscada pasará por todos ellos y, además, por A1 y A2.
En la figura 5.33 se ha trazado una elipse de focos F1 y F2.
Ecuación canónica de la elipse.
Obtengamos a continuación la ecuación cartesiana más simple de la elipse, a la cual
llamaremos ecuación canónica de esta. Para ello, ubiquemos el sistema de coordenadas
cartesiana con origen en el punto O (punto medio de F1 F2 ) como en la figura 5.33 y el eje
OX como se ve en esta. En tales condiciones, las coordenadas de F1 son –c y 0 y las de F2,
c y 0. Sea P (x; y) un punto del plano. Este punto pertenece a la elipse si y sólo sí:
d ( F1 , P) + d ( F2 , P ) = 2a , o sea,
( x + c) 2 + y 2 + ( x − c) 2 + y 2 = 2a … (1).
102
Aunque esta es la ecuación de la elipse en el sistema adoptado, su utilización resulta poco
práctica, por lo cual buscaremos una ecuación equivalente desprovista de radicales.
Trasponiendo uno de estos obtenemos una ecuación equivalente a (1):
( x + c) 2 + y 2 = 2a − ( x − c) 2 + y 2 … (2).
Elevando al cuadrado y simplificando se llega a:
a ( x − c) 2 + y 2 = a 2 − cx … (3)
Es conocido que al elevar al cuadrado pueden aparecer soluciones extrañas, es decir,
puntos que satisfagan (3), pero que no pertenecen a la elipse. Lo que sí podemos afirmar es
que todo punto de la elipse satisface (3) y, por tanto, a toda ecuación obtenida a partir de
esta. Elevando al cuadrado ambos miembros de (3), simplificando y agrupando
convenientemente, obtendremos:
(a 2 − c 2 ) x 2 + a 2 y 2 = a 2 (a 2 − c 2 ) … (4)
Como a > c> 0, a 2 − c 2 > 0. Haciendo b = a 2 − c 2 y dividiendo por a 2 b 2 resulta que todo
punto de la elipse satisface la ecuación:
x2 y2
+
= 1 … (5).
a2 b2
Dicho de otro modo (1) ⇒ (5).
Demostremos ahora que (5) ⇒ (1) y que, por tanto, (1) ⇒ (5), es decir, que (5) es la
ecuación del lugar geométrico. Al partir de (5) y realizando los pasos en sentido opuesto,
cada elevación al cuadrado da lugar a una extracción de raíz cuadrada, con la consiguiente
aparición
del
doble
signo.
Como
esto
sucede
dos
veces,
llegaremos
a: ± ( x + c) 2 + y 2 ± ( x − c) 2 + y 2 = 2a , donde hay cuatro posibilidades, que son:
a) + +
b) + c) - +
103
d) -
-
Las tres últimas son inadmisibles. En efecto, la b) y la c) contradicen la desigualdad
triangular. En cuanto a la d) hay que desecharla pues, el primer miembro sería menor que
cero, mientras que el segundo sería mayor que cero. Por tanto, (5) ⇒ (1), luego (5) es la
ecuación buscada que se llama la ecuación canónica o reducida de la curva.
Partiendo de la ecuación canónica de la elipse se pueden deducir varias propiedades
importantes, por ejemplo, la simetría respecto a los ejes coordenados y al origen.
En efecto, la simetría con respecto al eje OX se deduce del hecho de que si la elipse pasa
por el punto (x; y), también pasa por su simétrico respecto al eje OX, que es (x; -y). De
manera análoga se garantiza la simetría respecto al eje OY y al origen. De esta forma se
puede concluir que los ejes coordenados son ejes de simetría y el origen es el centro de
simetría de la curva.
Otra propiedad importante de la elipse que se deduce de su ecuación, es que esta curva es
acotada. En efecto, para todo punto (x; y) de la elipse:
x2
≤1
a2
y
y2
≤ 1 , o sea, − a ≤ x ≤ a
b2
y
−b ≤ y ≤ b.
Esto significa que la elipse está situada dentro de un rectángulo cuyos vértices son; (-a; -b);
(a; -b); (a; b) y (-a; b) (figura 5.34), lo que prueba que es acotada.
Los puntos A (-a; 0), B (0; b), A/ (a; 0) y B/ (0; -b), donde la curva corta a sus ejes de
simetría, se llaman vértices de la elipse. La máxima distancia entre todos los pares de
puntos de la curva, que es 2ª, se llama longitud de su eje mayor; los únicos puntos de la
curva situados a esta distancia son A y A/. La distancia de B a B/, que es 2b, se llama
longitud del eje menor.
104
c
se llama excentricidad de la elipse y se denota por e. Como 0 < c < 0, resulta
a
que 0 < e < 1. Si e es próximo a 1, la elipse es “redondeada”; si es próximo a 0, es
“alargada”.
Otra forma sencilla de la ecuación de la elipse es cuando adoptamos el sistema de
coordenadas de modo que los focos sean F1 (0; -c) y F2 (0; c) (o sea, cuando los focos están
x2 y2
situados en el eje OY), obtendremos como ecuación de la elipse: 2 + 2 = 1 .
b
a
El cociente
Entre a, b y c se establece una relación importante que es útil para la determinación de
cualquiera de estos tres elementos cuando dos de ellos son conocidos. Esta relación es:
a 2 = b 2 + c 2 . La misma es equivalente a la relación b = a 2 − c 2 , que utilizamos para
obtener la ecuación canónica de la elipse.
Estudio analítico de la hipérbola.
Definición 5.21: Sean F1 y F2 dos puntos distintos y π un plano que contiene a estos. Se
denomina hipérbola de focos F1 y F2 a todo lugar geométrico de puntos de π tales que el
valor absoluto de la diferencia de sus distancias a F1 y F2 es una constante, menor que la
distancia entre F1 y F2.
Nótese que de acuerdo con la desigualdad triangular, esta constante no puede ser mayor
que d ( F1 , F2 ) . Si fuese igual a d ( F1 , F2 ) el lugar geométrico estaría formado por todos los
puntos de la recta F1 F2 , excepto aquellos que son interiores al segmento F1 F2 .
Designemos por 2c la distancia entre los focos y por 2a la constante que se menciona en la
definición. Entonces, un punto P de π pertenece a la hipérbola, si y sólo sí:
d ( P, F1 ) − d ( P, F2 ) = 2a
Trazado de la hipérbola.
Conocidos a y c podemos obtener fácilmente un punto de la curva (una vez elegidos los
focos).
Sean F1 y F2 dos puntos situados a la distancia 2c; O el punto medio del segmento F1 F2 ; A1
un punto de la recta F1 F2 situado a la distancia a de O, y A2 el simétrico de A1 respecto a O
(figura 5.35).
P
F1 A1
O
A2 F2
M
Figura 5.35
105
Elijamos un punto arbitrario M, sobre la recta determinada por los puntos F1 y F2, pero
→
→
exterior al segmento F1 F2 . Tomando como centros F1 y F2 y con radios A1 M y A2 M se
trazan dos circunferencias que se cortan en dos puntos P y P/, ambos pertenecientes a la
hipérbola. Variando la posición del punto M, se obtienen tantas parejas de puntos como se
desee, todos pertenecientes a la curva, la cual pasará por todos ellos y, además, por A1 y
A2. En la figura 5.36 se ha trazado la hipérbola de focos F1 y F2.
Ecuación canónica de la hipérbola.
Para obtener la ecuación canónica de la hipérbola ubiquemos el origen de coordenadas en
el punto O (punto medio de F1 F2 ) y el eje X pasando por F1 y F2 como en la figura 5.36.
En estas condiciones las coordenadas de F1 son –c y 0 y las de F2 son c y 0. Sea P (x; y) un
punto del plano. Este punto pertenece a la hipérbola si y sólo sí:
d ( P, F1 ) − d ( P, F2 ) = 2a , o sea,
( x + c) 2 + y 2 − ( x − c) 2 + y 2 = 2a … (1)
Busquemos una ecuación equivalente. En primer lugar, (1) equivale a:
( x + c) 2 + y 2 − ( x − c) 2 + y 2 = ± 2a … (2).
Siguiendo un proceso análogo al empleado en el caso de la elipse para racionalizar, se
llegará a la ecuación:
(c 2 − a 2 ) x 2 − a 2 y 2 = a 2 (c 2 − a 2 ) … (3)
Como c > a > 0, c 2 − a 2 > 0. Poniendo b = c 2 − a 2 , la última ecuación puede escribirse:
x2 y2
b 2 x 2 − a 2 y 2 = a 2 b 2 . Dividiendo por a 2 b 2 , resulta: 2 − 2 = 1 …(4).
a
b
106
Los cálculos efectuados permiten afirmar que las coordenadas de todo punto de la hipérbola
satisfacen (4). Es decir, (1) ⇒ (4). Para poder afirmar que (4) es la ecuación de la hipérbola,
es preciso probar ahora que (4) ⇒ (1).
A partir de (4) realizando los pasos en sentido opuesto, cada elevación al cuadrado exige
una extracción de raíz cuadrada, con la consiguiente aparición del doble signo, se llega a:
± ( x + c ) 2 + y 2 − ( x − c ) 2 + y 2 = ± 2a
El signo menos del primer radical es inamisible, pues llegaremos a una contradicción tanto si
tomamos el signo positivo como el negativo del segundo miembro. En efecto, la elección -; -;
+ es contradictoria, pues el primer miembro sería negativo mientras que el segundo es
positivo. La otra alternativa, o sea, -; -; -; equivale a +; +; +; contradice la desigualdad
triangular. En efecto, quedaría d ( P, F1 ) + d ( P, F2 ) = 2a . Pero, d ( P, F1 ) + d ( P, F2 ) > 2c > 2a .
Eliminando estas dos posibilidades, queda
Queda así establecido que:
( x + c) 2 + y 2 − ( x − c) 2 + y 2 = ± 2a , o sea (1).
x2 y2
−
= 1 es la ecuación de la hipérbola en el sistema de
a2 b2
coordenadas adoptado.
Algunas propiedades algebraicas de esta ecuación pueden traducirse de inmediato en
propiedades de la hipérbola que define. Así, por ejemplo, si el par (x; y) satisface la
ecuación, también la satisfacen los pares (x; -y) y (-x; y), propiedades que significan que la
curva es simétrica respecto a los ejes OX y OY, respectivamente. Como consecuencia,
también hay simetría respecto al origen.
También se concluye, a partir de la ecuación (4) que la curva no corta al eje OY; al eje OX lo
corta en los puntos (-a; 0) y (a; 0) que se llaman sus vértices. Si despejamos y obtenemos:
b
y=±
x 2 − a 2 que nos dice que solamente existen puntos de la curva para − a ≤ x o
a
x ≥ a . Consecuencia de esto es que la hipérbola no es una curva acotada y que consta de
dos partes disjuntas que se llaman ramas, situadas una en el semiplano x ≤ −a y la otra en
el semiplano x ≥ a . De la ecuación (4) puede obtenerse, asimismo, que para todo punto (x;
b
b
y) de la curva se cumple: − x < y < x .
a
a
Un análisis de esta relación, permitirá establecer que para x ≥ a la curva está situada por
b
b
debajo de la recta y = x , y por encima de y = − x . Por otra parte, cuando x “tiende a
a
a
b
b
infinito”, la distancia de un punto de la curva a alguna de las rectas y = x ; y = − x , “tiende
a
a
a cero”.
107
En efecto, tomemos, por
b
analíticamente por y =
a
b
resultará igual a:
b2 + a2
infinito”.
ejemplo, la parte superior de la rama derecha, caracterizada
b
x 2 − a 2 ; x ≥ a . La distancia de uno de sus puntos a y = x
a
2
a
; expresión que “tiende a cero” cuando x “tiende a
⋅
x + x2 − a2
Consideraciones de simetría permiten afirmar que un hecho análogo se repite en los
restantes cuadrantes.
Por todo lo anterior se dice que la hipérbola tiende asintóticamente a las rectas
consideradas, que se llaman: las asíntotas de la hipérbola. La posición de la hipérbola
x2 y2
−
= 1 con respecto a sus asíntotas, y la región del plano donde está ubicada puede
a2 b2
apreciarse en la figura 5.37.
x2 y2
−
= 1 define la hipérbola cuyos vértices son los puntos
a2 b2
b
b
(-a; 0) y (a; 0) y sus asíntotas son las rectas: y = x ; y = − x , siendo 2a la distancia entre
a
a
y2 x2
los dos vértices. De manera análoga puede establecerse que la ecuación: 2 − 2 = 1 … (5)
a
b
corresponde a la hipérbola cuyos vértices están en (0; -a) y (0; a) y cuyas asíntotas son las
a
a
rectas: y = x ; y = − x .
b
b
Nótese que las ecuaciones (4) y (5) definen la misma curva pero en posiciones distintas.
Hemos visto que la ecuación
Excentricidad en la hipérbola.
Se llama excentricidad de una hipérbola a la relación entre la distancia focal y la distancia
entre los dos vértices; se denota por e.
108
Así, para la hipérbola cuya ecuación es (4): e =
m la pendiente de la asíntota y =
c
. Como c > a > 0, e >1. Si designamos por
a
a
x , y tenemos en cuenta que: c 2 = a 2 + b 2 , resulta que
b
e = 1 + m 2 , que nos dice que cuando e aumenta la asíntota se “aleja” del eje OX, y la
hipérbola se “abre”, y recíprocamente.
Estudio analítico de la hipérbola.
Definición 5.22: Sean: D una recta y F un punto que no pertenece a D. Sea π el plano que
determinan D y F. Se llama parábola de directriz D y foco F al lugar geométrico de los
puntos de π equidistantes de D y F.
Trazado de la parábola.
Una vez ubicados D y F podemos obtener fácilmente un punto de la curva. Sean r la recta
que pasa por F y es perpendicular a D; I es el punto de intersección de r y D; y V el punto
medio del segmento FI . Tomemos ahora un punto cualquiera M en la semirrecta de origen
V que contiene a F. Tracemos por M la recta r/, paralela a D. Con el compás, tomamos la
distancia de I a M; haciendo centro en F con un radio igual a esta distancia, cortamos a r/ en
los puntos P y P/, que, por construcción, pertenecen a la parábola (figura 5.38).
r/
D
P
r
I
V
Figura 5.38
F
M
P/
Variando la posición de M, se obtendrán tantos pares de puntos como se desee, todos
pertenecientes a la parábola. La curva buscada pasará por todos los puntos y, además, por
V, al cual se denomina vértice. En la figura 5.39 se ha trazado un arco de la parábola de
foco F y directriz D.
109
Ecuación canónica de la parábola.
Nos proponemos, a continuación, obtener la ecuación más simple de la parábola, a la cual
llamaremos ecuación canónica o reducida de esta. Para ello, ubiquemos el sistema de
coordenadas con origen en el punto V, y el eje OX pasando por F como en la figura 5.39.
Designemos por 2p la distancia de F a D. Entonces, las coordenadas de F son (p; 0), y la
ecuación de la directriz: x + p = 0. Sea P (x; y) un punto del plano. Este punto pertenece a la
parábola si y sólo sí: d ( P, F ) = d ( p, D) , o sea,
( x − p) 2 + y 2 = x + p … (1).
Busquemos una ecuación equivalente desprovista de radicales. Elevando al cuadrado
ambos miembros de (1), efectuando el cuadrado indicado y simplificando, llegaremos a:
y 2 = 4 px … (2), equivalente a (1). Por tanto (2) es la ecuación buscada.
Partiendo de esta ecuación se pueden deducir varias propiedades importantes de la curva.
Si p > 0, la parábola está situada en el semiplano derecho cuyo borde es el eje OY; si p < 0,
en el semiplano izquierdo. Si la curva pasa por el punto (x; y), pasará necesariamente por (x;
-y) y, por tanto, es simétrica con respecto al eje OX.
A diferencia de la elipse, la parábola no es una curva acotada. En efecto, si p > 0, para toda
x arbitrariamente grande, existen puntos de la curva, de modo que no es posible encerrar
esta en ningún círculo.
Si ahora, adoptamos el sistema de coordenadas de modo que F (0; p), y la ecuación de la
directriz sea y + p = 0, entonces la ecuación de la parábola será: x 2 = 4 py . Si p > 0, la curva
se encuentra en el semiplano superior cuto borde es el eje OX; si p < 0, en el semiplano
inferior. En cualquiera de los casos, es simétrica respecto al eje OY.
Cónicas desplazadas.
Las ecuaciones canónicas de la elipse, la hipérbola han sido obtenidas a partir de la
ubicación del origen del sistema de coordenadas en el punto medio del segmento
determinado por los focos, de forma tal que sus ejes coincidan con los ejes de estas
cónicas. En el caso de la parábola la ecuación canónica fue obtenida haciendo coincidir el
origen del sistema de coordenadas con el vértice de esta y el eje OX u OY con la recta que
contiene al foco. Obtengamos ahora las ecuaciones canónicas de estas cónicas cuando, en
110
el caso de la elipse y la hipérbola, sus ejes son paralelos no coincidentes a los ejes
coordenados, y, en el caso de la parábola, cuando la recta que contiene a su vértice y foco
es paralela no coincidente a los OX u OY.
Para la obtención de estas ecuaciones estudiaremos la traslación de ejes coordenados en el
plano.
Sean XOY y X/O/Y/ dos sistemas se coordenadas en el plano. Se dirá que el sistema X/O/Y/
se ha obtenido por una traslación del sistema XOY si O/X/ es paralelo y del mismo sentido
que OX y O/Y/ es también paralelo y del mismo sentido que OY (figura 5.40).
Determinemos la relación entre las coordenadas (x; y) de un punto P en el sistema XOY y
las coordenadas (x/; y/) de ese mismo punto en el sistema X/O/Y/; para ello, supongamos que
→
→
(h; k) son las coordenadas del punto O/ en el sistema XOY y que i y j son los vectores
→
→
→
coordenados unitarios en ambos sistemas. Entonces, como OP = OO / + O / P , tendremos:
/
→
→
→
→
→
→
⎪⎧ x = x + h
/
/
i x + j y = i h + j k + ( i x + j y ) , lo cual equivale a: ⎨
que se llaman: las
⎪⎩ y = y / + k
coordenadas de traslación del sistema XOY al sistema X/O/Y/.
y/
y
P
O/
x/
Figura 5.40
O
x
Si las ecuaciones de la elipse, la hipérbola y la parábola la hubiésemos obtenido en el
sistema de coordenadas X/O/Y/, las mismas tendrían las siguientes formas:
x/2 y/2
+ 2 =1
o
a2
b
x/2 y/2
HIPÉRBOLA: 2 − 2 = 1
a
b
x/2 y/2
+ 2 = 1.
b2
a
y/2 x/2
o
− 2 = 1.
a2
b
ELIPSE :
2
PARÁBOLA: y / = 4 px /
o
2
x / = 4 py / .
111
Sustituyendo las ecuaciones de traslación del sistema XOY al sistema X/O/Y/, obtendremos
las ecuaciones de las cónicas desplazadas que queríamos:
( x − h) 2 ( y − k ) 2
+
=1
o
a2
b2
( x − h) 2 ( y − k ) 2
HIPÉRBOLA:
−
=1
a2
b2
PARÁBOLA: ( y − k ) 2 = 4 p( x − h)
ELIPSE :
( x − h) 2 ( y − k ) 2
+
= 1.
b2
a2
( y − k ) 2 ( x − h) 2
o
−
= 1.
a2
b2
o
( x − h) 2 = 4 p ( y − k ) .
En el caso de la parábola, las ecuaciones dadas es para cuando la parábola abre hacia la
derecha o hacia arriba, respectivamente. Pero, además, existen las ecuaciones
( y − k ) 2 = −4 p( x − h) o ( x − h) 2 = −4 p( y − k ) , para cuando la parábola abre hacia la
izquierda o hacia abajo, respectivamente.
A partir de estas ecuaciones hay que ubicar las coordenadas de los demás puntos de estas
cónicas. Veamos para mejor comprensión los siguientes ejemplos.
Ejemplo:
1. Dada la ecuación de la elipse 9 x 2 + 16 y 2 = 144 , determina centro, distancia de los
semiejes, vértices, focos y excentricidad.
Solución:
1
x2 y2
, obtenemos
+
= 1 , de la que se deduce
144
16 9
que a = 4 y b = 3 , que son la distancia de los semiejes mayor y menor, respectivamente de
la elipse. Por el tipo de ecuación obtenida resulta que el centro de la elipse tiene
coordenadas (0; 0), o sea, coincide con el origen de coordenadas. Los vértices de la elipse
en el eje mayor tienen coordenadas (-4; 0) y (4; 0) y, en el eje menor: (0; 3) y (0; -3). Como
Si en la ecuación dada multiplicamos por
es conocido a 2 = b 2 + c 2 , por lo que c = a 2 − b 2 = 16 − 9 = 7 ; por tanto, las coordenadas
de los vértices son: (- 7 ; 0) y ( 7 ; 0), y la excentricidad e =
7
.
4
( x − 3) 2 ( y + 1) 2
+
= 1 , determina centro, distancia de los semiejes,
16
9
vértices, focos y excentricidad.
2. Dada la ecuación
Solución:
En este ejemplo las distancias de los semiejes de la elipse a y b, la semidistancia focal c y la
excentricidad e, se hallan de manera análoga y obtenemos los mismos resultados. La
diferencia con el ejemplo anterior está dada en las coordenadas del centro, de los vértices y
de los focos. En este caso, el centro tendrá coordenadas (h; k), es decir, (4; -1); por lo tanto,
las coordenadas de los vértices en el eje mayor son (-a+h; k) y (a+h; k), o sea: (0; -1) y (8; -
112
1); las de los vértices en el eje menor son: (h; -b+k) y (h; b+k), o sea, (4; -4) y (4; 2) y; las
coordenadas de los focos serán (-c+h; 0) y (c+h; 0), o sea, (- 7 +4; 0) y ( 7 +4; 0).
Estos dos ejemplos son representados en la figura 5.41. Los vértices de la elipse del
ejemplo 1 son: A1 y A2 en el eje mayor; B1 y B2 en el eje menor y sus focos son: F1 y F2. Los
vértices de la elipse del ejemplo 2 son: A1/ y A2/ en el eje mayor; B1/ y B2/ en el eje menor y
sus focos son: F1/ y F2/.
3
B1
B1/
2
1
A1
-4
F1
-3
A2
F2
-2
-1
O
-1
1
A1/
2
3
4
5
F1/
6
7
F2/
8
9
A2/
-2
Figura 5.41
-3
-4
B2
B2/
3. Determinar centro, distancia del semieje, vértices, focos y excentricidad de la siguiente
hipérbola: 25 x 2 − 4 y 2 + 150 x + 325 = 0 .
Solución:
En primer lugar tenemos que transformar la ecuación dada en su equivalente de la forma
x2 y2
y2 x2
−
=
1
o
−
= 1 . Para ellos agrupamos los términos que tienen la variable
a2 b2
a2 b2
x y los que tienen la variable y; luego realizamos para cada agrupamiento los
113
completamientos cuadráticos respectivos (en el caso que lo requiera) y hacemos las
operaciones pertinentes. Veamos esto en el caso que nos ocupa.
25 x 2 − 4 y 2 + 150 x + 325 = 0
(25 x 2 + 150 x) − 4 y 2 + 325 = 0
25( x 2 + 6 x) − 4 y 2 + 325 = 0
25( x 2 + 6 x + 9) − 25.9 − 4 y 2 + 325 = 0
25( x + 3) 2 − 4 y 2 − 225 + 325 = 0
25( x + 3) 2 − 4 y 2 + 100 = 0
4 y 2 − 25( x + 3) 2 = 100
y 2 ( x + 3) 2
−
=1
25
4
( y − k ) 2 ( x − h) 2
−
= 1.
De esta forma hemos obtenido la ecuación de la hipérbola de la forma
a2
b2
De acuerdo con la ecuación obtenida el eje de la hipérbola es paralelos al eje de las
ordenadas, o sea, OY. El centro de la hipérbola tendrá coordenadas (h; k), o sea, (-3; 0). La
distancia del semieje será a = 5, por lo que sus vértices tendrán coordenadas (h; k-a) y
(h; k+a), o sea, (-3; -5) y (-3; 5). Como b = 2, la semidistancia focal c se calcula por la
fórmula c 2 = a 2 + b 2 ; luego, c = 25 + 4 = 29 . Las coordenadas de los focos serán (h; k-c) y
(h; k+c), o sea, (-3; - 29 ) y (-3;
29 ). La excentricidad e =
c
29
=
.
a
5
Todos los resultados de los ejemplos 1, 2 y 3 se pueden comprobar realizando el trazado de
estas cónicas. Le sugerimos al lector realizarlo.
4. Halla el vértice, el foco y la ecuación de la directriz de la parábola 2 x 2 − 12 x + 3 y − 9 = 0 .
Solución:
Transformemos la ecuación dada a la forma:
( y − k ) 2 = 4 p ( x − h)
o
( x − h) 2 = 4 p ( y − k )
2 x 2 − 12 x + 3 y − 9 = 0
2( x 2 − 6 x ) + 3 y − 9 = 0
2( x 2 − 6 x + 9) − 18 + 3 y − 9 = 0
2( x − 3) 2 + 3( y − 9) = 0
3
( x − 3) 2 = − ( y − 9)
2
114
3
3
, de donde p = y V (3;9) . El eje de la parábola es paralelo al eje OY y esta
2
8
3⎞
⎛ 69 ⎞
⎛
abre hacia abajo. Por tanto F ⎜ 3; 9 − ⎟; F ⎜ 3;
⎟ . La ecuación de la directriz será
8⎠
⎝ 8 ⎠
⎝
3
y = k + p ⇒ y = 9 + ⇒ 8 y − 75 = 0 .
8
Luego 4 p =
Algunos ejemplos de las aplicaciones de la Geometría Analítica a la resolución de
ejercicios y problemas.
Ejemplo 1: Demostración de la propiedad de la mediatriz de un segmento.
Para ello, ubicamos de manera conveniente el segmento en un sistema de coordenadas, de
forma tal que sea fácil determinar las coordenadas de los extremos del segmento. Demos
dos posibilidades de esto en la siguiente figura.
y
y
a
C( ; c)
2
C(0; c)
A(-a; 0)
B(a; 0)
Primera posibilidad
x
A(0; 0)
B(a; 0)
x
Segunda posibilidad
En la primera posibilidad se ha ubicado el segmento AB sobre el eje OX, de forma tal que el
punto medio del mismo coincida con el origen de coordenadas y la mediatriz coincida con el
eje OY. En la segunda posibilidad se ha ubicado el segmento AB sobre el eje OX, de forma
tal que uno de sus extremos coincida con el origen de coordenadas; en este caso las
coordenadas del otro extremo se pueden fácilmente determinar al quedar ubicado sobre el
eje OX.
Se selecciona el punto C de la mediatriz. En la primera posibilidad este punto estará sobre el
eje OY, por lo que es fácil determinar sus coordenadas. En la segunda posibilidad la abscisa
del punto coincide con la abscisa del punto medio del segmento AB ; la ordenada se elige de
forma arbitraria.
115
Para ambas posibilidades hay que demostrar que d (C , A) = d (C , B) . Esta demostración
aparece reflejada en el siguiente cuadro para ambas posibilidades:
Primera posibilidad
d (C , A) = (0 − (−a)) + (c − 0) = a + c
2
2
2
2
d (C , B ) = (0 − a) 2 + (c − 0) 2 = a 2 + c 2
Queda demostrado que d (C , A) = d (C , B) .
Segunda posibilidad
a
a
d (C , A) = ( − 0) 2 + (c − 0) 2 = ( ) 2 + c 2
2
2
a
a
d (C , B) = ( − a) 2 + (c − 0) 2 = (− ) 2 + c 2
2
2
a
= ( )2 + c2
2
Queda demostrado que d (C , A) = d (C , B ) .
Ejemplo 2: Demostración de la propiedad de la paralela media de un triángulo.
La figura siguiente muestra una de las posibilidades de ubicación del triángulo en el sistema
de coordenadas cartesianas.
y
C(b; c)
M
A(0; 0)
N
B(a; 0)
x
Escribamos las ecuación de la recta que contienen a los puntos A y B y de la que contiene a
los puntos M y N, donde M y N son los puntos medios de los lados AC y BC ,
→
⎛b c⎞
⎛b+a c⎞
respectivamente. M ⎜ ; ⎟ ; N ⎜
; ⎟ . Un vector director de la recta AB es AB = (a; 0) ; un
⎝2 2⎠
⎝ 2 2⎠
→
→
⎛a ⎞
vector director de la recta MN es MN = ⎜ ;0 ⎟ . Analizando el vector MN , resulta que:
⎝2 ⎠
→
→
1
1
MN = (a;0) = AB , lo que demuestra que las rectas AB y MN son paralelas. Además.
2
2
116
2
→
a
1
⎛a⎞
MN = ⎜ ⎟ = , lo que demuestra que el MN = AB . Queda así
2
2
⎝2⎠
demostrada la propiedad de la paralela media de un triángulo.
→
AB = a 2 = a ;
Ejemplo 3: Muestra que el triángulo cuyos vértices son los puntos A (2; -3), B (5; -2) y
C (4; 1) es rectángulo. Halla la longitud de la altura relativa a la hipotenusa.
De gran ayuda para resolver este ejercicio sirve su representación en un sistema de
coordenadas cartesianas, como se muestra en la siguiente figura:
3
2
C (4; 1)
1
3
-2
-1
1
2
3
4
5
-1
-2
B (5; -2)
-3
A (2; -3)
→
→
Por la representación gráfica probemos que los vectores AB = (3;1) y BC = (−1; 3) son
→
→
perpendiculares. Para ello, calculemos el producto escalar AB⋅ BC = 3 ⋅ (−1) + 1 ⋅ 3 = −3 + 3 = 0 ;
de esto resulta que el triángulo es rectángulo en B.
Para hallar la altura relativa a la hipotenusa tenemos que hallar la distancia del punto B a la
recta AC. Para ello, hallemos la ecuación de la recta AC. Se conoce que la recta AC tiene
como ecuación cartesiana: ax + by + c = 0 . También conocemos que para hallar esta
→
ecuación tenemos que hallar el vector director (en nuestro caso, un vector director es AC ),
que tiene como componentes (p; q); luego se determina un vector normal de componentes
(q; - p); haciendo a = p y b = - q obtenemos parte de dicha ecuación. En efecto, un vector
→
→
director es AC = (2; 4) y, por tanto, un vector normal es N = (4; − 2) . Haciendo a = 4 y b = - 2,
resulta la ecuación: 4 x − 2 y + c = 0 . Sustituyendo en dicha ecuación las coordenadas de uno
de los puntos A o C, hallamos c. En efecto, al sustituir A en la ecuación resulta
4 ⋅ 2 − 2 ⋅ (−3) + c = 0 y despejando c obtenemos c = −14 . De esta forma la ecuación de la
recta AC es 4 x − 2 y − 14 = 0 . Hallemos la altura relativa a la hipotenusa del triángulo:
117
h AC = d ( B, AC ) =
4 ⋅ 5 − 2 ⋅ (−2) − 14
=
16 + 4
10
20
=
10
2 5
= 5 ≈ 2,24.
EJERCICIOS DEL CAPÍTULO
1. En un sistema de coordenadas rectangulares del plano se dan los puntos: A (1; -2),
B (3: 2) y C (-1; 0).
a) Representar el triángulo ABC.
b) Determinar analíticamente que este triángulo es isósceles.
c) Determinar si ABC es equilátero.
d) Determinar si ABC es rectángulo.
2. Los puntos medios de los lados de un triángulo son (3; -6), (-2; -1) y (8; 4) están situados
en una recta.
3. Demostrar analíticamente que en todo triángulo rectángulo, el punto medio de la
hipotenusa equidista de los vértices.
4. Demostrar analíticamente que las rectas que unen los puntos medios de los lados
opuestos de un cuadrilátero plano convexo, se bisecan mutuamente.
5. Demostrar analíticamente que en todo paralelogramo las diagonales se cortan en su punto
medio.
6. Demostrar analíticamente el recíproco de la propiedad anterior, es decir: “si en
cuadrilátero plano convexo las diagonales se cortan en su punto medio, el cuadrilátero es
un paralelogramo”.
7. Los vértices de un triángulo son: A (0; -2,6), B (4,8; -4) y C (-2; 0). Calcular la longitud de
la mediana correspondiente al lado mayor.
8. En un sistema de coordenadas rectangulares del espacio se dan los puntos: (3; 2; 5),
(1; 1; -4), C (-3; -2; 2) y D (5; 0; 1).
a) Situar los cuatro puntos en un sistema de coordenadas cartesianas y representar los
→
→
vectores BA y CD .
b) Hallar las componentes de estos dos vectores y sus longitudes.
→
→
→
→
c) Calcular BA ⋅ CD y BA × CD .
→
9. Dado el vector V = ( 2 ;1;−1) , determinar sus ángulos e dirección respecto a los ejes
coordenados.
10. Sea O el origen de un sistema de coordenadas en le espacio. Calcular las coordenadas
→
del punto M sabiendo que OM forma ángulos iguales con los ejes del sistema y que
→
OM = 3 .
118
11. Dados los puntos A (2; -1: 3), B (5; 2; 6), C (-1; 4; 2). Determinar las coordenadas del
punto D, de tal modo que, junto a los tres dados, como vértices, se forme un
paralelogramo.
→
→
12. Sean A (1; 0; -3), B (4; 5; -1), C (-1; -6; 3) y D (5; 4; 7). Probar que AB y DC son
paralelos y de distinto sentido.
13. Determinar los ángulos formados por las siguientes parejas de vectores:
→
→
a) V1 = (1;5); V2 = (−2;3) .
→
→
b) V1 = (3;0;−1); V2 = (−2;0;−1)
→
→
c) V1 = (1;−4;−1); V2 = (0;1;−1)
14. Dados los puntos A (2; 1; -1), B (-3; 0; 2); C (1; 4; -1). Calcular el área del triángulo cuyos
vértices son los puntos dados.
15. En cada uno de los casos siguientes escribir la ecuación cartesiana del plano que:
→
a) pasa por el punto P0 (−1;3;2) y admite como vector normal a N = (5;4;−3) .
→
b) pasa por el punto P0 (6;−4;7) y admite como vector normal a N = (2;−1;0) .
→
c) pasa por el punto P0 (0;2;−1) y admite como vector normal a N = (0;5;0) .
→
d) Pasa por el origen y admite como vector normal a N = (4;−5;7) .
16. Hallar la ecuación cartesiana de un plano sabiendo que el pie de la perpendicular trazada
del origen al plano es (2; 4; -1).
17. Determine la ecuación del plano que pasa por el punto (3; -1; -2) y es paralelo al plano
2x + y – 4z +5 = 0.
18. Hallar la ecuación del plano perpendicular al plano x – y – z = 3 y que pasa por los
puntos (1; 1; 3) y (3; -3; -1).
19. Hallar la ecuación del plano que pasa por los puntos (1; 0; 2), (-1; -3; 2) y (0; 0; 5).
20. Hallar la distancia entre el plano 2x – 2y + z -5 = 0 y el plano paralelo a él que pasa por el
punto (3; -1: 6).
21. El plano 2x + 6y + 3z = 6 2 forma un tetraedro con los planos coordenados. Calcular el
área total y el volumen del tetraedro.
22. Representar una parte significativa de cada uno de los planos cuyas ecuaciones son:
a) 2x - 3y - 6z + 12 = 0.
119
b)
c)
d)
e)
f)
g)
5x + 2y – z = 0.
3x + y - 4z – 5 = 0.
x + 3z – 6 = 0.
2y + 3z = 0.
y + 3 = 0.
2z – 3 = 0.
23. Determinar los puntos del eje OX cuya distancia al plano 2x – y + 2z + 2 = 0 es de 4
unidades.
24. Determinar las ecuaciones de los planos paralelos a: 2x – y + 2z + 1 = 0, que distan de
este 7 unidades.
25. Hallar un sistema de ecuaciones paramétricas de cada una de las rectas siguientes:
a) Pasa por (2; -3; 0) de vector directos (-1; 3; 4).
b) Pasa por (1; 1; -3) de vector director (0; 0; 4).
c) Pasa por (-2; 4; 5) y (7; -1; 2).
26. Hallar los puntos de intersección, con los planos coordenados, de la recta que pasa por
(9; -6; -2) y (-6; 3; 4).
27. Hallar las ecuaciones de los planos proyectantes, sobre los planos coordenados, de la
recta que pasa por los puntos (1; -2; 3) y (4; -1; 1).
28. Hallar las ecuaciones cartesianas de cada una de las rectas siguientes:
a) La que pasa por (3; -4) de vector director (1; -5).
b) La que pasa por (5; 0) de vector normal (-2; 3).
c) La que pasa por (7; -1) paralela a la recta 2x – y + 5 = 0.
d) La que pasa por (0; 0) perpendicular a la recta x + 4y = 0.
e) La que pasa por los puntos (-2; 1) y (3; 7).
29. Hallar las ecuaciones cartesianas de las rectas que pasan por (7; 1), a 5 unidades de
distancia del origen.
30. Las ecuaciones de los lados de un paralelogramo son: 2x + 3y – 7 = 0; x – 3y + 4 = 0. Un
vértice está en el punto (5; 5). Hallar las ecuaciones de los otros dos lados.
31. Sean A (1; -1), B (-2; 1) y C (3; 5) los vértices de un triángulo. Hallar la ecuación
cartesiana de la recta que pasa por A y es perpendicular a la mediana trazada desde el
vértice B.
32. Determinar el área y el perímetro del triángulo formado por la recta 12x + 5y = 60 con los
ejes coordenados.
33. Hallar un sistema de ecuaciones paramétricas de la recta que pasa por (2; -1; 6) y es
paralela a la recta de intersección de los planos: 3x – 2y + z + 5 = 0 y 4x -3y – 4z = 0.
34. Determinar las ecuaciones de las siguientes circunferencias:
a) La que tiene su centro en (3; -5) y su radio es de 6 unidades.
120
b) La que tiene so centro en (2; -1) y pasa por (4; 0).
c) La que tiene como diámetro el segmento que une los puntos (5; -3) y (-1; -7).
d) La que tiene su centro en (1; 0) y es tangente a la recta: 4x – y + 2 = 0.
35. Determinar cuáles de las siguientes ecuaciones definen circunferencias. En caso
afirmativo, halle las coordenadas del centro y la longitud del radio, y represéntalas.
a) x 2 + y 2 − 4 x − 6 y + 12 = 0 .
b) x 2 + y 2 + 10 x − y + 29 = 0 .
c) x 2 + y 2 + 8 x + 2 y + 17 = 0 .
d) 2 x 2 + 2 y 2 + 2 x + 10 y − 33 = 0 .
e) 5 x 2 + 5 y 2 − 6 x − 2 y + 17 = 0 .
36. Hallar las ecuaciones de las circunferencias que tienen su centro en la recta
4x -5y + 1 = 0 y son tangentes a las dos rectas: 2x – 3y – 8 = 0; 3x – 2y + 8 = 0.
37. Escribe la ecuación de una parábola si:
a) Las coordenadas del vértice son (-1; 2) y las del foco, (3; 2).
b) Las coordenadas del vértice son (0; 3) y la ecuación de su directriz es: y = 5.
c) Las coordenadas del foco son (3; 0) y la ecuación de la directriz es: x + 3 = 0.
d) Las coordenadas del vértice son (-4; -1), su eje está sobre la recta x – 4 = 0 y pasa
por el punto (3; -3).
38. Dadas las siguientes ecuaciones, investiga si representan una parábola y, en caso
positivo, determina las coordenadas de su vértice y foco y la ecuación de su directriz.
a) y 2 − 20 x = 0 .
b) x 2 + 3x = 0 .
c) y 2 − 8 x − 6 y + 9 = 0.
d) x 2 − 6 x + 4 y − 3 = 0.
e) 3 x 2 + 18 x − 4 y + 27 = 0.
f) y 2 − 8 x + 32 = 0.
g) x 2 + y 2 + 4 y = 0.
h) x 2 − 5 x − 3 y − 8 = 0.
39. Escribe la ecuación de la parábola que pasa por el origen de coordenadas y es simétrica
respecto al eje de ordenadas, si las coordenadas del foco son (0; -3).
40. Una parábola contiene a los puntos de intersección de la recta y = x y la circunferencia
x2 + y2 – 10y = 0 y es simétrica respecto al eje de ordenadas. Escribe la ecuación de la
parábola y de su directriz.
41. Escribe la ecuación de la elipse:
a) Con eje mayor paralelo al eje OX, a = 5, b = 2 y centro (3; 1).
12
y centro (5; 0).
b) Con eje mayor paralelo al eje OY, 2c = 12, e =
13
121
2
y centro (-1; 2).
5
d) Los focos tienen coordenadas (-3; 0) y (3; 0) y a = 4.
e) Con centro (5; 3), uno de los vértices del eje menor tiene coordenadas (5; 0) y uno de
los vértices del eje mayor tiene coordenadas (-1; 3).
f) Donde los vértices de su eje menor tienen coordenadas (6; 8) y (6; -2) y uno de los
vértices de su eje mayor tiene coordenadas (0; 3).
g) Donde los vértices de su eje mayor tienen coordenadas (5; 4) y (5; -3) y su
2
excentricidad es e = .
3
42. Determina distancia de los semiejes, coordenadas de los vértices y focos y la
excentricidad de las siguientes elipses.
a) x 2 + 4 y 2 = 25.
b) 4 x 2 + 9 y 2 + 8 x − 18 y − 23 = 0.
c) x 2 + 4 y 2 + 4 x − 36 = 0.
d) 10 x 2 + 20 y 2 + 60 x − 20 y − 105 = 0.
e) 3 x 2 + y 2 + 2 y − 11 = 0.
f) 18 x 2 + 8 y 2 + 72 x + 16 y − 64 = 0.
g) x 2 + 4 y 2 − 24 y + 48 = 0.
h) 2 x 2 + 3 y 2 − 16 x + 6 y + 29 = 0.
c) Con eje mayor paralelo al eje OY, b =
3, e =
43. Calcula el área del cuadrilátero que tiene dos vértices en los focos de la elipse
b 2 x 2 + a 2 y 2 = a 2 b 2 y los otros dos coinciden con los vértices del eje menor.
44. Escribe la ecuación de la hipérbola:
a) Con el eje principal paralelos al eje OX, a = 3, b = 2 y centro O (1; 3).
6
b) Con el eje principal paralelo al eje OY, 2c = 12, e = y centro O (3; 0).
5
c) Con el eje principal paralelo al eje OY, 2b = 6 , e = 2 y centro O (-5: 1).
d) Con centro O ((0; 0), foco F1 (0; 5) y vértice A1 (0; 3).
e) Con focos F1 (4; -2) y F2 (4; -8) y 2a = 4.
f) Con vértices A1 (-6; 3), A2 (1; 3) y foco F1 (-8; 3).
45. Determina distancia la distancia del semieje, las coordenadas de los vértices y focos y la
excentricidad de las siguientes hipérbolas.
a) x 2 − 9 y 2 = 25.
b) 4 y 2 − 9 y 2 = 36.
c) 4 x 2 − 9 y 2 + 32 x + 36 y − 8 = 0.
d) 4 x 2 − 9 y 2 − 24 x − 36 y − 36 = 0
e) 4 x 2 − y 2 + 2 y − 2 = 0.
f) 16 x 2 − 20 y 2 − 20 y − 75 = 0 .
g) 3 x 2 − y 2 + 30 x + 78 = 0.
122
h) 4 x 2 − 20 y 2 − 8 x − 80 y − 79 = 0 .
46. Escribe la ecuación de una hipérbola de centro en el origen y focos sobre el eje OX, si se
16 ⎞
⎛
sabe que pasa por el punto N ⎜ − 5; ⎟ y su distancia focal es igual a 10 unidades.
3⎠
⎝
47. Halla la ecuación de la hipérbola de centro en el origen, eje principal sobre el de las
ordenadas y que pasa por los puntos (4; 6) y (1; -3).
48. El centro de la circunferencia x 2 + y 2 − 4 x + 2 y − 5 = 0 es el vértice de una parábola cuyo
eje tiene por ecuación y + 1 = 0. Si la parábola pasa por el punto A (4; 3), halla su
ecuación y la de la directriz.
49. Halla la ecuación de la elipse que tiene focos en los focos de las parábolas
( y + 2) 2 = 8( x − 1) , ( y + 2) 2 = −16( x − 6) y cuyo semieje mayor a = c + p, donde p es el
menor de los semiparámetros de las parábolas dadas.
50. Demuestra que el producto de las distancias de cualquier punto de la hipérbola
a 2b 2
b 2 x 2 − a 2 y 2 = a 2 b 2 a sus dos asíntotas es una cantidad constante e igual a 2
.
a + b2
123
Bibliografía
- BALDOR, A. (1992) Geometría plana y del espacio. Editorial Cultural Venezolana S. A.
Caracas.
- BALLESTER, C. (1995) Geometría. Fondo Editorial. CNAMEC. Caracas.
- HEMMERLING, E. (1991) Geometría Elemental. Editorial Limusa. México.
- KINDLE, J. (1976) Teoría y problemas de Geometría Analítica. Editorial Pueblo y
Educación. La Habana. Cuba.
- MOISE, E. y DOWNS, J. (1972) Serie Matemática Moderna (Geometría). Fondo
Educativo Interamericano. Colombia.
- MOISE, E. (1998) Elementos de Geometría Superior. Centro Regional de ayuda técnica.
México
- POGORELOV, A. (1984) Geometría Elemental. Editorial Pueblo y Educación. La
Habana. Cuba.
- REGUERA, R. y SOLANO, M. (1989) Geometría Analítica. Editorial Pueblo y Educación.
La Habana. Cuba.
- WEXLER, CH. (1962) Analytic Geometry: A vector approach. Editorial Addison – Wesley.
Datos del autor:
Juan Enrique García La Rosa.
Licenciado en Matemática y Física.
Doctor en Ciencias Pedagógicas.
Profesor Auxiliar.
Instituto Superior Pedagógico “Frank País García”, Santiago de Cuba, Cuba.
e-mail: [email protected]
124