Apunte MATLAB 2009 Archivo

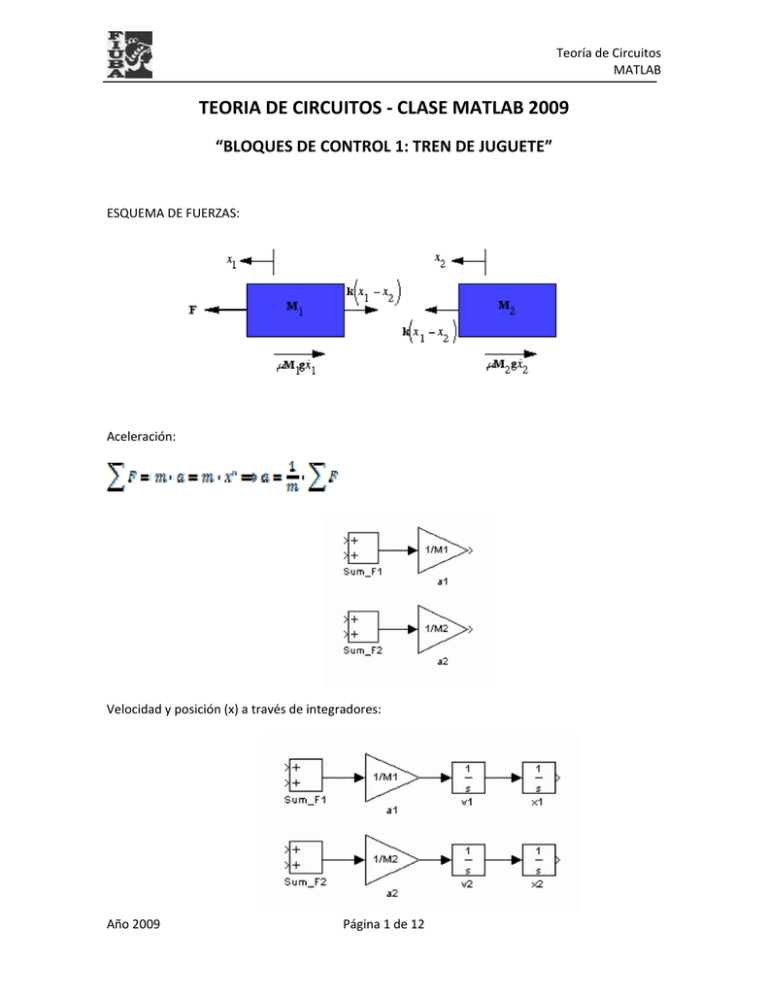
Teoría de Circuitos MATLAB TEORIA DE CIRCUITOS ‐ CLASE MATLAB 2009 “BLOQUES DE CONTROL 1: TREN DE JUGUETE” ESQUEMA DE FUERZAS: Aceleración: Velocidad y posición (x) a través de integradores: Año 2009 Página 1 de 12 Teoría de Circuitos MATLAB Fuerzas: Masa 1: F Masa 2: Sumador y Ganancia: Integrador: Osciloscopio: Fuente: Solver: ODE23s Simulink / Math Operations Simulink / Continuous Simulink / Sinks Simulink / Sources Constantes: desde MATLAB: file/new/M‐File: Genero archivo: “xxx.M” M1=1; M2=0.5; k=1; F=1; mu=0.002; g=9.8; Luego: debug / run Respuesta “v1” ante una forma de onda cuadrada (F = ”square”) Para obtener datos del osciloscopio: Parameters / Data History / Save Data to Workspace: Le doy un nombre y elijo Format: “Array”; luego corro y en el workspace obtengo el vector con los datos (puedo copiar y llevar a Excel). Año 2009 Página 2 de 12 Teoría de Circuitos MATLAB “BLOQUES DE CONTROL 2: PROCESO DE NIVEL” Considérese el proceso de nivel indicado en la figura: Proceso de nivel con dos recipientes. Donde: qi: caudal de entrada h1: nivel del recipiente Nº1 qp: caudal de perturbación h2: nivel del recipiente Nº2 En la siguiente tabla se indican los parámetros asignados al proceso de nivel: Parámetro Valor Unidad Capacitancia del recipiente Nº1 Capacitancia del recipiente Nº2 Resistencia de la válvula 1 Resistencia de la válvula 2 C1 3 m2 C2 4 m2 R1 1.5 seg/m2 R2 2 seg/m2 Si se considera que las variables de entrada son: u1 = qi u2 = qp Las variables de salida son: y1 = h1 y2 = h2 Y designando como variables de estado aquellas que definen la energía, se tiene: x1 = h1 x2 = h2 Así definidas las entradas, las salidas y variables de estado, el modelo matemático del proceso de nivel es: 1
⎤
⎡ dx1 ⎤ ⎡− 1
1 ⎤
⎥ ⎡x ⎤ ⎡ 1
R1C1
⎢ dt ⎥ ⎢ R1C1
1
⎥ ⋅ ⎡ u1 ⎤ ⎢
⎥
⎢
⋅
+
=
C
C
⎢ dx ⎥
⎢
⎥
2
⎛ 1
1
1 ⎞⎥ ⎣ x2 ⎦ ⎢ 1
⎥ ⎢⎣u 2 ⎥⎦
⎢ 2⎥ ⎢
⎜⎜
⎟⎟
−
+
0
0
⎦
⎣
⎥
⎣ dt ⎦ ⎢⎣ R1C2
⎝ R1C2 R2C2 ⎠⎦
y
x
1
0
⎡ 1⎤ ⎡
⎤ ⎡ 1 ⎤ ⎡0 0⎤ ⎡ u1 ⎤
⎢ y ⎥ = ⎢0 1⎥ ⋅ ⎢ x ⎥ + ⎢0 0⎥ ⋅ ⎢u ⎥ ⎦ ⎣ 2⎦ ⎣
⎦ ⎣ 2⎦
⎣ 2⎦ ⎣
Año 2009 Página 3 de 12 Teoría de Circuitos MATLAB Reemplazando por los valores numéricos de los parámetros, las ecuaciones de estados se convierten en: ⎡ dx1 ⎤
⎢ dt ⎥ ⎡− 0.222 0.222 ⎤ ⎡ x1 ⎤ ⎡0.333 0.333⎤ ⎡ u1 ⎤ ⋅
⎢ dx ⎥ = ⎢
⎥⋅⎢ ⎥+ ⎢
0 ⎥⎦ ⎢⎣u 2 ⎥⎦
⎢ 2 ⎥ ⎣ 0.167 − 0.292⎦ ⎣ x2 ⎦ ⎣ 0
⎣ dt ⎦
⎡ y1 ⎤ ⎡1 0⎤ ⎡ x1 ⎤ ⎡0 0⎤ ⎡ u1 ⎤ ⎢ y ⎥ = ⎢0 1⎥ ⋅ ⎢ x ⎥ + ⎢0 0⎥ ⋅ ⎢u ⎥
⎦ ⎣ 2⎦
⎦ ⎣ 2⎦ ⎣
⎣ 2⎦ ⎣
A) Simulación mediante el diagrama de estados (diagrama de simulación). Sobre la base de estas ecuaciones se construye el diagrama de simulación indicado en la siguiente figura: Sumador y Ganancia: Integrador: Osciloscopio: Fuente: Manual Switch: Solver: ODE45 Simulink / Math Operations Simulink / Continuous Simulink / Sinks Simulink / Sources Simulink / Signal Routing A.1) La primera simulación se realiza considerando: ‐ Tanques vacíos [h1(0)=0 y h2(0)=0], es decir condiciones iniciales nulas en los integradores. ‐ Caudal de perturbación qp(t)=u2(t)=0. El “Manual Switch 1” está en constante igual a cero. ‐ Caudal de entrada u1(t) = escalón unitario [1 m3/seg], aplicado en t=1seg. y1 = h1 Año 2009 Página 4 de 12 y2 = h2 Teoría de Circuitos MATLAB A.2) La segunda simulación del modelo se realiza de tal manera que, estando el sistema en régimen estacionario con h1=3.5m y h2=2m, se aplica un caudal de perturbación u2(t) con forma de escalón de amplitud 0.2 m3/seg y en el instante t=80seg. Esto último se selecciona con el generador escalón “step 1”. y1 = h1 y2 = h2 A.3) La tercera simulación se realiza sobre la base de: ‐ u1(t) escalón unitario aplicado en t=1seg. ‐ u2(t) perturbación nula. ‐ Condiciones iniciales; h1(0)=1.5m y h2(0)=1m (se especifican en los integradores). y1 = h1 y2 = h2 Detalle de los primeros segundos (se observa el descenso del nivel): y1 = h1 y2 = h2 Año 2009 Página 5 de 12 Teoría de Circuitos MATLAB B) Simulación del proceso de nivel mediante el uso del icono “State‐Space”. Conociendo las matrices A, B, C y D, las condiciones iniciales y las entradas se puede construir un modelo de simulación empleando el ícono “State‐Space” localizado dentro del menú “Continuous”: Haciendo doble “Click” sobre el bloque “State‐Space” se cargan las matrices A, B, C, D y las condiciones iniciales. De la misma manera el generador de la señal escalón debe generar la entrada u1 y u2, es decir un vector, haciendo doble “Click” en el bloque “Step”. A modo de ejemplo se muestran los datos necesarios para obtener la simulación nro. 2 (con escalón de perturbación): Resultado de la simulación: Año 2009 Página 6 de 12 Teoría de Circuitos MATLAB “RESOLUCION DE CIRCUITOS” Régimen permanente (CC o CA): R, L,C: SimPowerSystem / Elements Fuente: SimPowerSystem / Electrical Soruces Tierra, Conector “T”: SimPowerSystem / Connectors Multímetro: SimPowerSystem / Measurements PowerGui: SimPowerSystem Deben estar el multímetro (agregarle las mediciones necesarias) y el bloque “Powergui”. Después de realizar la corrida entro al bloque PowerGui y entro a “Steady‐State Voltages and Currents” Solver: ODE15s Régimen transitorio (continua o alterna): Se debe modelar el “Ideal Switch” (porque el “Breaker” no interrumpe corriente) con un temporizador. La R interna debe ser muy pequeña y el circuito “Snubber” infinito. Ideal Switch: SimPowerSystem / Power Electronics Timer: SimPowerSystem / Extra Library / Control Blocks Solver: ODE15s Año 2009 Página 7 de 12 Teoría de Circuitos MATLAB En el multímetro debo seleccionar “Plot selected measurements”, luego corro la simulación y obtengo las curvas de los transitorios. El graficador del multímetro me permite copiar las curvas y pegarlas en otro gráfico. Por ejemplo puedo realizar varias simulaciones alterando algún parámetro como el tiempo de apertura de un interruptor o el valor de alguna resistencia, luego copio las curvas y las superpongo en un mismo gráfico. Además me permite cambiarle los colores, cambiar las escalas, salvar y restaurar, escribir leyendas, copiarlo al clipboard de Windows, etc . Ib: L1
80
t=0
t=T/4
t=T/2
t=3T/4
t=T
60
40
20
0
-20
-40
-60
-80
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
Diagrama de Bode: Se debe estar midiendo la variable de salida de la transferencia (x ej. UR4 si quiero UR4/U) ‐
‐
‐
‐
‐
‐
Entrar a PowerGUI Use LTI Viewer Elijo entrada y salida Open new LTI viewer Edit / Plot Configurations. Elijo “Bode” Año 2009 Página 8 de 12 Teoría de Circuitos MATLAB Barridos en CC y CA: Valor en régimen permanente de alguna corriente o tensión en función de algún parámetro del circuito (por ejemplo una R, L o C). Amperímetro o Voltímetro: Valor Eficaz (RMS): Osciloscopio / Display: Terminal de salida (Out): SimPowerSystem / Measurements SimPowerSystem / Extra Library / Measurements Simulink / Sinks Simulink / Sinks Mediante Programación en MATLAB (genero un archivo “*.M” con el siguiente código): SAL=[1:1:10] {Genero vector de resultados de 1 a 10 con incremento de 1} RES=[0.3:0.3:3] {Genero vector de resistencias de 0.3 a 3 con incremento de 0.3} for n=1:10 {Inicio ciclo “for” con “n” variando de 1 a 10} R4=RES(n) {Le doy valor a R4 de 0.3 a 3 ohm, (La resistencia en Simulink debe tener como valor “R4”)} [t,x,y]=sim('tpg307_g') {Ejecuto el modelo de Simulink con nombre “tpg307_g”; se guardará en el vector “t” la escala de tiempo, en “x” las variables de estado y en “y” las salidas seleccionadas en el modelo Simulink (terminales OUT), p.ej. una corriente} SAL(n)=y(100) {Asigno al vector de resultados la salida de la simulación. Si es alterna y quiero el valor RMS debo tomarlo en el tiempo necesario para que se estabilice el valor} end {cierro el ciclo “for”} plot(RES,SAL) {Grafico SAL en función de RES} Año 2009 Página 9 de 12 Teoría de Circuitos MATLAB Luego: debug / run, corre las 10 simulaciones y obtengo el gráfico de la corriente en R1/L1 en función del valor de la resistencia R4. En el vector “SAL” (Workspace del MatLab) obtengo los resultados de las “n” simulaciones. Se puede copiar y graficar también en un Excel. 45
40
Corriente [A]
35
30
25
20
0
0.5
1
1.5
Resistencia [Ohm]
2
2.5
3
Fuentes no sinusoidales: Controlled Voltage Source: SimPowerSystem / Electrical Sources Sumador: Simulink / Math Operators Simulink / Sources Ramp / Step/ Signal Builder: Se debe utilizar el bloque “Controlled Voltage Source” que convierte una señal cualquiera en una tensión. La señal de entrada puede lograrse como suma de varias rampas, escalones, etc. o utilizando el “Signal Builder” (ubicado en “Simulink/Sources”). Año 2009 Página 10 de 12 Teoría de Circuitos MATLAB Nota: para agregarle puntos de quiebre a la señal, se presiona shift sobre la curva en el lugar deseado. Para lograr una excitación que responda a una función aritmética, debo utilizar el bloque “Fcn”, ubicado en “Simulink / User ‐Defined Functions” donde voy a ingresarle como dato la expresión matemática de la función y conectarle a la entrada el bloque “Clock” (ubicado en “Simulink/Sources”). Año 2009 Página 11 de 12 Teoría de Circuitos MATLAB Análisis de Fourier: Para realizar un análisis de Fourier de una señal: ‐ Primero modelamos nuestro circuito teniendo en cuenta que debe estar presente el ícono “Powergui” en el modo “Discretize electrical model”. ‐ La señal a la que queremos analizar por Fourier debe estar dirigida a un osciloscopio y el mismo debe dirigir la salida al Workspace. ‐ Luego corremos la simulación y entramos a “FFT Analysis”, dentro Del ícono “powergui”. Año 2009 Página 12 de 12