984729350.TP 03 - Variables Aleatorias -2011-

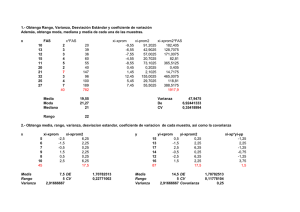
ESTADÍSTICA I
Práctico: Unidad 3 – Variables Aleatorias
D.E.A. Lanza Mariano
1. Si se lanza un dado balanceado dos veces y llamamos X a la cantidad cuatros que
pueden obtenerse en dicho experimento. Obtener para la variable aleatoria X:
A) El espacio muestral.
B) La distribución de probabilidades.
C) La función de distribución
D) La esperanza matemática
E) La varianza
2. Dada la siguiente distribución de probabilidades:
X:
P(X):
2
0,14
5
0,30
8
0,2
11
0,36
A) Calcular la media.
B) Calcular el desvío.
3. Si se lanzan 2 tetraedros (dado de 4 caras que contienen los números 1, 2, 3 y 4).
Suponga que consideramos las variables aleatorias X e Y, donde:
X= nº que se obtendrá en el primer dado
Y= nº que se obtendrá en el segundo dado
A) Obtenga los resultados posibles de Z y R, donde:
Z= X+Y
R= 3X-2Y
B) Desarrolle el cuadro de la función de distribución para las variables Z y R
C) Represente la “distribución de probabilidades” y la “función de distribución” de las
variables Z y R.
D) Calcular la media y la varianza de las variables Z y R.
4. Si X e Y son variables aleatorias independientes, demostrar que:
A) V(X-Y)= V(X) + V(Y), donde V() significa varianza
B) V(X+Y)= V(X) + V(Y), donde V() significa varianza
5. Sea la variable aleatoria continua X, cuya función de densidad está definida por:
1 / 2 − (1 / 8) x
f ( x) 
0
0< x < 4
∀otro
x
A) Graficar la función de densidad
B) Obtener la esperanza matemática de X.
C) Obtener la Varianza de X
D) Comprobar la ley de cierre de la función de distribución.
Calcular las siguientes probabilidades:
E) P (1< x < 2)
F) P (0< x < 1)
G) P (0< x < 3)
H) P(3<X<4)
-1-
6. Un concesionario de autos clasifica los vehículos por su color y por su tamaño de la
siguiente forma:
El 50% de los autos son rojos, el 30% son blancos y el resto azules. El 55% de los autos
son medianos, el 25% chicos y el resto grandes. El 40% de los autos chicos son blancos.
De los autos chicos, el 40% son blancos, el 20% azules y el resto rojos. De los autos
grandes, el 25% son blancos, el 25% azules y el resto rojos. Determinar:
A) El espacio muestral de cada variable
B) El espacio muestral de la variable bidimensional
C) La función de probabilidad marginal para cada variable
D) La probabilidad de que un auto sea blanco
7. En una empresta productora de bienes de precisión desea analizar las probabilidades de
encontrar bienes fallados en su producción diaria. Se denomina X a la cantidad de
bienes defectuosos por no corresponder con el largo correspondiente y a Y a la cantidad
de bienes fallados por no presentar el ancho especificado. Suponga que la función de
probabilidad conjunta de X e Y ( de producción diaria) está dada por la siguiente tabla:
X
0
1
2
0
0,4
0,15
0,10
Y
1
0,12
0,08
0,03
2
0,08
0,03
0,01
Determinar:
A) P(X= 0 y Y = 2)
B) P(X > 0 y Y ≤ 1)
C) P(X ≤ 1)
D) P(Y> 0)
E) La probabilidad de que todos los pernos de la muestra satisfagan la especificación
de la longitud.
F) La probabilidad de que todos los pernos de la muestra satisfagan la especificación
del diámetro.
G) La probabilidad de que los pernos cumplan con las especificaciones de largo y
ancho.
H) Calcular la E(X) yE(Y).
I) Calcular la V(X) y V(Y).
J) Calcular la Cov(XY) y el coeficiente de correlación entre X e Y.
K) Representar en una tabla la función de probabilidad marginal de X
L) Representar en una tabla la función de probabilidad marginal de Y
x
, para 0< x <2. Averiguar si es función de densidad y, en caso afirmativo,
2
graficar la función de distribución, calcular la media y la varianza.
8. Sea f(x) =
9. La duración en horas de la producción de un bien particular responde a la siguiente
función de densidad:
−t
1 ( 200 )
f (t ) =
e
∀t ≥ 0 .
200
A) Encontrar la forma funcional de F(t).
B) Calcular la probabilidad de que la producción de un bien dure menos de 150 hs.
C) Calcular la probabilidad de que la producción de un bien dure entre 100 y 150 horas.
-2-
D) Si se sabe que la producción de un bien fue mayor a 100 horas ¿cual es la
probabilidad de que se haya demorado menos de 150 horas?
10. Sea:
X:
P(X):
0
1/30
2
3/30
5
12/30
6
8/30
10
6/30
Si Z= 2X-20.
A) Representar la función de distribución de Z.
B) Calcular la media y la varianza de X y Z.
11. Dada la V.A: X y su distribución de probabilidades. Calcular E(Y) y Var(Y), sabiendo
que Y = 1000X.
X:
P(X):
-5
0,4
-4
0,2
-3
0,1
-2
0,25
-1
0,05
12. Sea
f (t ) = 0,2e −0, 2t ; ∀t ≥ 0 la función de densidad correspondiente a la duración (en
minutos) de una llamada telefónica. Si se efectuaron tres llamadas telefónicas, calcular
la probabilidad de que todas las llamadas tengan una duración menor a 15 minutos
(considerar que la duración de cada llamada es independiente de las demás).
13. En un juego que consiste en arrojar una moneda y un dado. Se gana 200$ si se obtiene
cara y 300$ por cada punto del dado. ¿Cuál es el valor esperado de ganancia del juego?
b) suponga ahora que para poder ingresar al juego debe pagarse un importe de 1000$,
¿Cuál sería ahora el valor esperado de la ganancia del juego?
c) Suponga ahora que el juego consiste en arrojar tres veces una moneda y una vez un
dado. Se gana 200$ por la cantidad de caras obtenida y 300$ por cada punto del dado
(no hay que pagar para ingresar al juego). ¿Cuál es el valor esperado de ganancia del
juego?
14. Sea X el número de llantas defectuosas en un lote de cuatro moldeadas al mismo
tiempo. La distribución de probabilidades de X es:
X:
P(X):
0
0,8
1
0,1
2
0,05
3
0,03
4
0,02
a) Hallar el valor esperado de X
b) Hallar el desvío estándar de X
c) Suponga que una llanta defectuosa representa una pérdida de $20. y sea Y=20$X .
Calcular el valor esperado y la varianza de Y
15. Un inversor posee sus recursos en 3 tipos de activos diferentes: el 40% en plazos fijos
(X), el 30% en bonos del tesoro nacional (Y) y el restante 30% en acciones de una
empresa que cotiza en bolsa (Z). Se sabe que los rendimientos de estos activos
financieros son variables aleatorias con las siguientes características:
-3-
X- media 0,04 y varianza 0,001
Y- media 0,08 y varianza 0,05
Z- media 0,10 y varianza 0,25
A) calcular el rendimiento esperado por dicho inversor
B) calcular la varianza del rendimiento de sus activos
C) Si el rendimiento total del inversor está dado por R= 0,4*X + 0,3*Y + 0,3*Z.
Respuestas:
1.
a) X= {0, 1, 2}
b y c)
X:
P(X):
F(X):
0
25/36
25/36
1
10/36
35/36
2
1/36
1
d) 0,3333
e) 0,2799
2.
a) 7,34
b) 3,2472
3.
a) Z= {2,3,4,5,6,7,8} R={-5, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 10}
b)
Z
P(Z)
2
1/16
3
2/16
4
3/16
5
4/16
6
3/16
7
2/16
8
1/16
R
-5
-3
-2
-1
0
1
2
3
4
5
6
7
8
10
1/16
1/16
1/16
1/16
1/16
2/16
1/16
1/16
2/16
1/16
1/16
1/16
1/16
1/16
P(R)
c) E(Z)= 5
V(Z)= 2,5
E(R)= 2,5
V(R)= 16,25
4.
Demostración.
5.
a) Gráfico.
b) 4/3
e) 0,3125
6.
c) 8/9
f) 7/16
d) Demostración.
g) 15/16
h) 1/16
a) X = {chicos, medianos, grandes}
X = {Rojos, blancos, azules}
b) (XY) =
(Chicos; R)
(Med; R)
(Grandes; R)
(Chicos; B)
(Med; B)
(Grandes; B)
(Chicos; Az)
(Med; Az)
(Grandes; Az)
-4-
X
Chicos
Medianos
Grandes
P(Y)
c)
X: Chicos
P(X):
0,25
Y:
P(Y):
Y
Blancos
0,1
0,15
0,05
0,3
Rojos
0,1
0,3
0,10
0,5
Medianos
0,55
Rojo
0,5
Azules
0,05
0,1
0,05
0,2
P(X)
0,25
0,55
0,2
Grandes
0,2
Blanco
0,3
Azul
0,2
d) 0,3
7.
a) 0,08
b) 0,36
c) 0,86
d) 0,35
e) 0,6
f)0,65
g) 0,40
h) E(X)= 0,54; E(Y)= 0,47 i) V(X)= 0,5284; V(Y)= 0,4891
j) Cov(XY)= -0,0138 ; Coef Correl (XY)= -0,0271
k)
X:
0
1
2
P(X):
0,6
0,26 0,14
l)
Y:
0
1
2
P(Y):
0,65 0,23 0,12
8.
a) Es función de densidad. b) Gráfico. c) E(x)=8/6; V(x)= 0,22222.
9.
a)
 0 ∀t < 0
−t
F (t )
(
)
1 − e 200
∀t ≥ 0
b) 0,527633
c) 0,134164
10.
a)
Z:
P(Z):
11.
0,221210
-20
1/30
-16
3/30
-10
12/30
b) E(X)=5,8 E(Z)=-8,4
V(X)= 6,36
V(Z)= 25,44
-8
8/30
0
6/30
E(X) = -3,65 y V(X)= 1,8275
E(Y) = -3650 y V(Y)= 1.827.500
12.
13.
0,857951
a) 1150$
14.
a) 0,37 b) 0,86781 c) E(Y)=7,4 V(Y)=301,24
15.
a) 0,07
b) 150$
c) 1350$
b) 0,02716
-5-