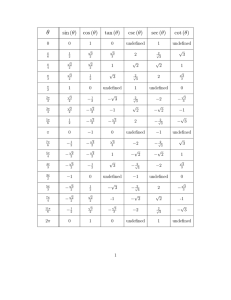
Trigonometric Identity Dependency csc t = sin t = sec t = cos t = cot t

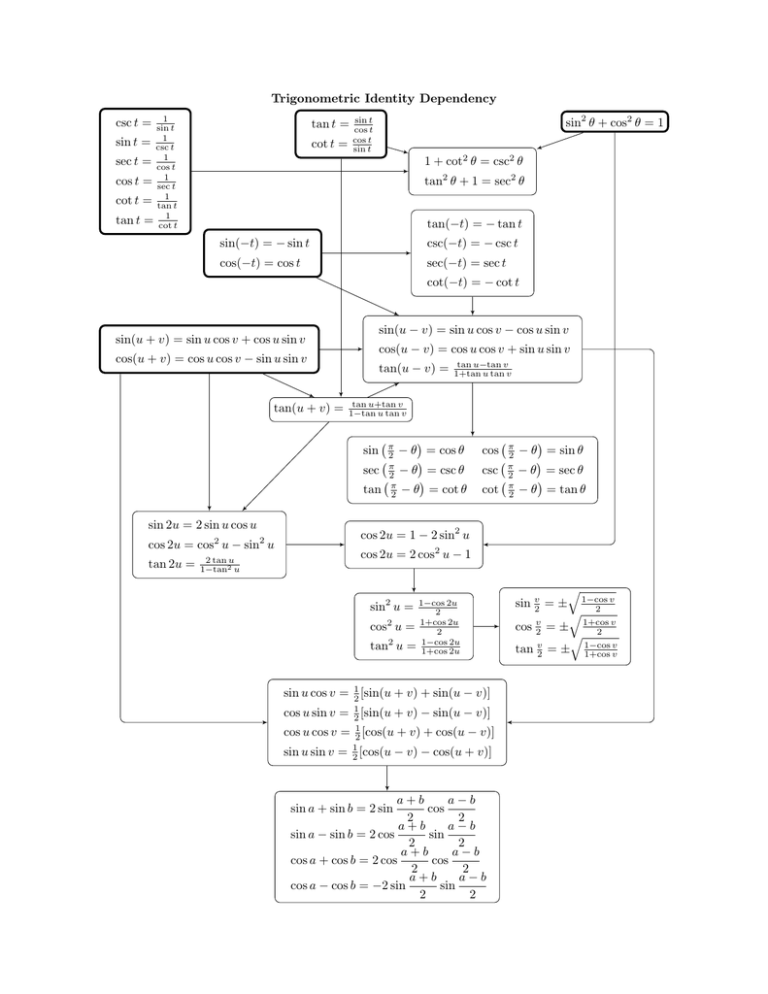
Trigonometric Identity Dependency
1
sin t
sin t = csc1 t
1
sec t = cos
t
cos t = sec1 t
1
cot t = tan
t
1
tan t = cot
t
csc t =
tan t =
cot t =
sin2 θ + cos2 θ = 1
sin t
cos t
cos t
sin t
1 + cot2 θ = csc2 θ
tan2 θ + 1 = sec2 θ
tan(−t) = − tan t
sin(−t) = − sin t
csc(−t) = − csc t
cos(−t) = cos t
sec(−t) = sec t
cot(−t) = − cot t
sin(u − v) = sin u cos v − cos u sin v
sin(u + v) = sin u cos v + cos u sin v
cos(u − v) = cos u cos v + sin u sin v
cos(u + v) = cos u cos v − sin u sin v
tan(u + v) =
tan(u − v) =
tan u+tan v
1−tan u tan v
sin
sec
tan
sin 2u = 2 sin u cos u
cos 2u = cos2 u − sin2 u
tan 2u =
2 tan u
1−tan2 u
tan u−tan v
1+tan u tan v
π
2 − θ = cos θ
π
2 − θ = csc θ
π
2 − θ = cot θ
cos
csc
cot
π
2
π
2
π
2
− θ = sin θ
− θ = sec θ
− θ = tan θ
cos 2u = 1 − 2 sin2 u
cos 2u = 2 cos2 u − 1
sin2 u =
1−cos 2u
2
2u
cos2 u = 1+cos
2
2u
tan2 u = 1−cos
1+cos 2u
sin u cos v = 21 [sin(u + v) + sin(u − v)]
cos u sin v = 12 [sin(u + v) − sin(u − v)]
cos u cos v = 12 [cos(u + v) + cos(u − v)]
sin u sin v = 12 [cos(u − v) − cos(u + v)]
a+b
a−b
cos
2
2
a+b
a−b
sin a − sin b = 2 cos
sin
2
2
a+b
a−b
cos a + cos b = 2 cos
cos
2
2
a+b
a−b
cos a − cos b = −2 sin
sin
2
2
sin a + sin b = 2 sin
q
v
sin v2 = ± 1−cos
q 2
v
cos v2 = ± 1+cos
q 2
v
tan v2 = ± 1−cos
1+cos v