Tracción-Compresión 2

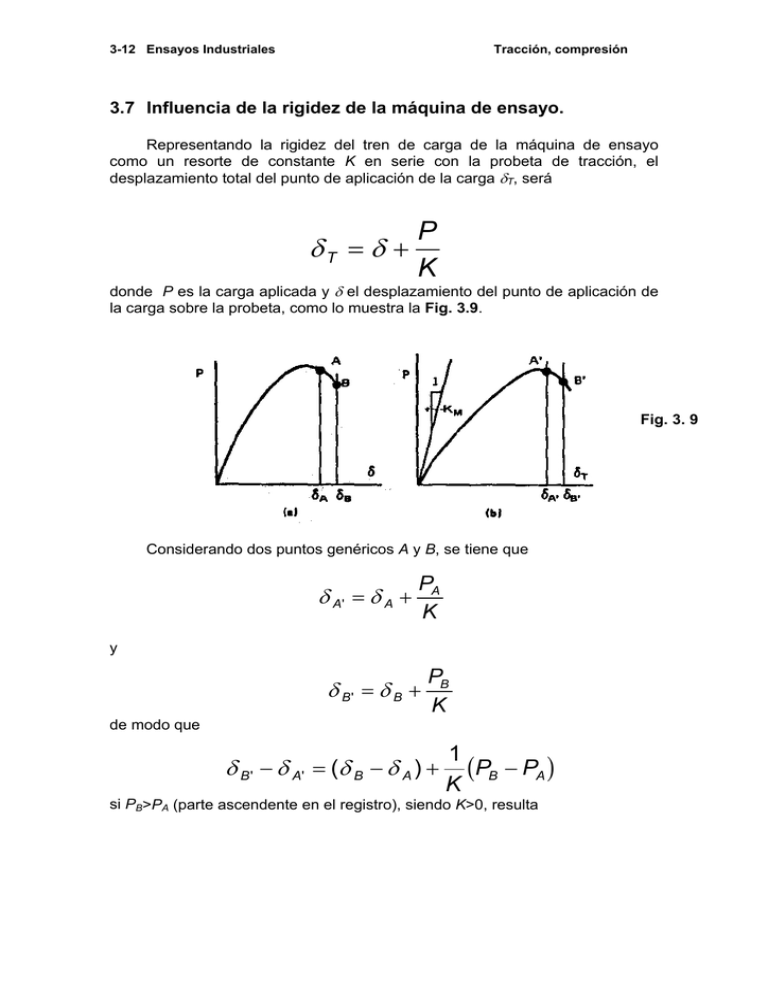
3-12 Ensayos Industriales
Tracción, compresión
3.7 Influencia de la rigidez de la máquina de ensayo.
Representando la rigidez del tren de carga de la máquina de ensayo
como un resorte de constante K en serie con la probeta de tracción, el
desplazamiento total del punto de aplicación de la carga δT, será
P
δT = δ +
K
donde P es la carga aplicada y δ el desplazamiento del punto de aplicación de
la carga sobre la probeta, como lo muestra la Fig. 3.9.
Fig. 3. 9
Considerando dos puntos genéricos A y B, se tiene que
δ A' = δ A +
PA
K
y
δ B' = δ B +
PB
K
de modo que
δ B ' − δ A' = (δ B − δ A ) +
b
1
PB − PA
K
si PB>PA (parte ascendente en el registro), siendo K>0, resulta
g
Ensayos Industriales
bδ
Tracción, compresión 3-13
g b
− δ A' > δ A − δ B
B'
g
dado que PB – PA es positivo.
En cambio, si PB<PA (parte descendente del registro), es
bδ
B'
g b
− δ A' < δ A − δ B
g
En el límite
bδ
g b
g K1 bP − P g = 0
B ' − δ A' = δ A − δ B +
B
A
(3. 17)
ya que la diferencia (δB’ - δA’) puede hacerse tan pequeña como se desee con
tal de adoptar un valor de K lo suficientemente grande pero no puede ser
negativa por las condiciones de contorno del sistema.
De la (3.17) surge que
K=−
bP − P g = − ∆P
bδ − δ g ∆δ
B
A
B
A
y considerando los puntos A y B como infinitamente próximos
K=−
dP
dδ
(3. 18)
Ahora bien, la anulación de la diferencia (δB’ - δA’) representa físicamente
una caída vertical de la carga, es decir la inestabilización del sistema y la rotura
súbita de la probeta, que según (3.18) se alcanza cuando a menos del signo, la
pendiente de la curva P - δ iguala el valor de K.
De manera que la condición que lleva a la rotura más prematura posible
de la probeta, está dada por K = 0, lo que físicamente representa una condición
de carga constante o “peso muerto”.
3.8 Deformación de polímeros y elastómeros.
Hasta aquí hemos hecho en general referencia a las propiedades de
tracción de materiales metálicos. Si bien la mayoría de los conceptos que
hemos introducido son aplicables a la deformación por tracción de polímeros, el
3-14 Ensayos Industriales
Tracción, compresión
comportamiento de estos difiere en algunos aspectos importantes del de los
metales. A continuación vemos la curva de tracción ingenieril típica de un
polímero termoplástico parcialmente cristalino como por ejemplo el polietileno
de alta densidad.
Fig. 3. 10
Puede verse en la Fig. 3.10 que una vez superado el período elástico se
alcanza rápidamente la carga máxima y a continuación se produce una
disminución de la tensión como consecuencia del desarrollo de la estricción. La
deformación continúa sin un aumento significativo de la carga aplicada debido
a que esta deformación obedece a la rotura de los enlaces débiles entre
moléculas. Esta deformación produce una orientación de las moléculas en la
dirección del esfuerzo como se muestra en la figura. Una vez alcanzada esta
condición, una ulterior deformación requiere un incremento de la carga aplicada
ya que ahora son los enlaces primarios o fuertes los que se oponen a la
deformación, alcanzándose eventualmente la rotura.
Fig. 3. 11
Los elastómeros son polímeros que se distinguen por su capacidad para
alcanzar deformaciones de 100% a 200% ó más. Esta deformación es casi
totalmente recuperable cuando se remueve la carga. La Fig. 3.11 muestra
algunas curvas típicas de tracción ingenieril para estos materiales. Obsérvese
la influencia del vulcanizado que es un proceso mediante el cual, a través de la
adición de azufre y por la acción de presión y temperatura, se aumenta la
interconexión entre las moléculas del elastómero.
Ensayos Industriales
Tracción, compresión 3-15
3.9 Materiales compuestos.
a)
Análisis por isodeformación
Consideremos a título de ejemplo un material compuesto por una matriz
polimérica reforzado por fibras largas, es decir que se extienden a toda la
longitud de la matriz y que se encuentra sometido a un esfuerzo en la dirección
paralela a las fibras. Es evidente que en tal situación la deformación que
experimentará el compuesto es la misma que experimentará la matriz y similar
a la de la fibra.
De manera que llamando εc a la deformación unitaria del compuesto, εm a
la de la matriz y εf a la de la fibra, podemos escribir
εc = εm = εf
(3. 19)
Por otra parte, llamando σc a la tensión media actuante sobre el
compuesto, σm a la tensión actuante sobre la matriz y σf a la de la fibra, es
σ c Ac = σ m Am + σ f Af
(3. 20)
donde Ac, Am y Af son las secciones transversales del compuesto, la matriz y la
fibra respectivamente.
Introduciendo ahora la fracción volumétrica de matriz Vm y la fracción
volumétrica de fibra Vf y aceptando que las mismas pueden ser aproximadas
por los cocientes:
Am
≅ Vm ,
Ac
Af
≅ Vf
Ac
(3. 21)
reemplazando en (3.20) teniendo en cuenta (3.21), resulta
b
g
σ c = σ m Am + σ f Af = σ m 1 − Vf + σ fVf
donde hemos utilizado la relación Vm + Vf = 1
Por otra parte, teniendo en cuenta la ley de Hooke, es
(3. 22)
3-16 Ensayos Industriales
Tracción, compresión
σ c = Em ε mVm + Ef ε fVf = Ec ε c
de manera que teniendo en cuenta la (3.19), simplificando resulta
b
g
Ec = EmVm + EfVf = Em 1 − Vf + EfVf
(3. 23)
Las (3.22) y (3.23) son muy importantes porque nos permiten estimar la
resistencia y el módulo de elasticidad del compuesto respectivamente. Sin
embargo es necesario tener en cuenta que en general la deformación de
fractura de la fibra puede ser inferior a la de la matriz, de modo que la
contribución de ésta a la resistencia del compuesto será σ’m(1-Vf), donde σ’m es
la tensión de la matriz a la deformación de rotura de la fibra. De manera que la
resistencia del compuesto estará dada por
b
g
σ c = σ 'm Am + σ f Af = σ 'm 1 − Vf + σ fVf
(3. 24)
Si Vf es menor a un valor crítico, la resistencia del compuesto es inferior
que la de la matriz actuando sola como se muestra en la Fig. 3.12. Esto se
debe a que por debajo de tal valor crítico la matriz es capaz de transmitir una
carga superior a la de las fibras si aquella presenta un endurecimiento por
deformación apreciable. Por lo tanto la (3.24) es valida si se cumple que σc >
σu(1-Vf), donde σu es la resistencia última de la matriz. Introduciendo esta
condición en la (3.24), obtenemos que Vc =1/[1+σf(σu - σ’m)].
Fig. 3. 12
Hasta aquí hemos considerado el caso en que las fibras se extienden en
toda la longitud del compuesto. Sin embargo, muchas veces las fibras son
cortas y por lo tanto discontinuas. Cuando las fibras son discontinuas, la
resistencia teórica del compuesto es inferior a la resistencia ideal dada por las
(3.23) ó (3.24) para un compuesto con fibras largas.
Ensayos Industriales
Tracción, compresión 3-17
Analizaremos las tensiones actuantes en una fibra corta (de longitud
inferior a la de la matriz). El estudio de la distribución de tensiones en el
compuesto muestra que la carga aplicada es transferida a la fibra a través de
tensiones tangenciales que actúan a lo largo de la interfase matriz-fibra en la
vecindad de los extremos de la fibra.
Para el caso de una fibra cilíndrica de radio r, estas tensiones
tangenciales producen una tensión normal axial a lo largo de la fibra, dada por
σ zzπ r 2 = τ rz 2π rl t
donde σzz es la tensión normal que actúa longitudinalmente en la fibra, τrz es la
tensión tangencial actuando en la interfase matriz-fibra y lt es la longitud de
transferencia de esta tensión tangencial medida a partir de ambos extremos de
la fibra. De modo que resulta
σ zz =
2τ rz l t
r
Obsérvese que en los extremos de la fibra es σzz ya que allí es lt = 0, y
aumenta hacia el centro de la fibra. Cuando σzz se hace igual a la resistencia
de la fibra σf la misma se romperá o se deformará plásticamente. Cuando se
alcanza esta condición se cumple
σf =
2τ rz l tc
r
(3. 25)
donde ltc es la longitud de transferencia crítica y lc es la longitud crítica de fibra
para la cual se alcanza en el punto medio de su longitud la tensión de rotura o
de fluencia de la fibra. De manera que
lc
l tc =
2
(3. 26)
Para calcular la contribución de la fibra a la resistencia del compuesto,
consideremos la distribución de la tensión normal en la fibra indicada en la Fig.
3.13. La Fig. 3.13 (a) muestra el caso de una fibra de longitud crítica, mientras
que la Fig. 3.13 (b) corresponde al caso de una fibra de longitud mayor a la
crítica y donde se asume deformación plástica de la fibra en su porción central.
3-18 Ensayos Industriales
Tracción, compresión
Fig. 3. 13
En el primer caso, podemos definir una tensión media equivalente de
fibra, como
σf =
σf
FG l IJ
H 2K = σ
c
lc
f
(3. 27)
2
En el segundo caso, la tensión equivalente de fibra será
σf =
σfl −σf
l
lc
2 = σ 1 − lc
f
2l
FG
H
IJ
K
(3. 28)
de modo que la resistencia del compuesto para este último caso, es
FG
H
σ c = σ f 1−
IJ
K
b
lc
Vf + σ 'm 1 − Vf
2l
g
(3. 29)
donde nuevamente σ’m es la tensión en la matriz a la deformación de fractura
de la fibra y lc/2 se obtiene de las (3.25) y (3.26), como
Ensayos Industriales
Tracción, compresión 3-19
σfr
lc =
2τ rz
(3. 30)
Obsérvese que cuando l >> lc recuperamos la expresión (3.24) que
corresponde a la resistencia de un compuesto con fibras continuas. La tensión
de corte τrz es la resistencia al corte de la interfase o de la matriz según la que
sea menor. Dado que τrz transfiere el esfuerzo de la matriz a la fibra, depende
de las condiciones de adherencia en la interfase matriz/fibra, por lo que la
resistencia del compuesto depende críticamente de la integridad de esta
interfase.
b)
Análisis por isotensión
En el caso de que las fibras del compuesto se encuentren orientadas
perpendicularmente a la dirección del esfuerzo, la carga transmitida por la
matriz y la fibra son idénticas, de modo que
Pc = Pm = Pf
(3. 30)
σc = σm = σf
(3. 31)
Por lo tanto
Aceptando que se cumple aproximadamente que la deformación
específica del compuesto está dada por
b
g
ε c = Vm ε m + Vf ε f = 1 − Vf ε m + Vf ε f
resulta, teniendo en cuenta la ley de Hooke
b
g
V E σ + 1 − Vf Ef σ m
σc
σ
σ
= 1 − Vf m + Vf f = f m f
Ec
Em
Ef
Em Ef
b
g
De manera que
Ec =
Em Ef
Vf Em + 1 − Vf Ef
b
g
(3. 33)
(3. 32)
3-20 Ensayos Industriales
Tracción, compresión
siendo la (3.33) la expresión del módulo de elasticidad del compuesto en el
caso de isotensión.
3.10 Influencia de la orientación de las fibras.
Consideraremos ahora los modos de falla del compuesto en función de la
orientación de las fibras con relación a la dirección en que se encuentra
aplicado el esfuerzo.
Para ello analicemos el caso genérico que se ilustra en la Fig. 3.14 en
que la orientación de las fibras y la dirección del esfuerzo forman un ángulo φ.
Fig. 3. 14
Resulta entonces
Aφ =
Ao
Cosφ
y
Pf = PoCosφ
De manea que la tensión normal que actúa en el compuesto en la
dirección de las fibras, es
σc =
Pf
P Cosφ
= o
= σ oCos 2φ
Aφ Ao / Cosφ
(3. 34)
Ensayos Industriales
Tracción, compresión 3-21
donde
σo =
Po
Ao
La sección sujeta a esfuerzos de corte en la dirección paralela a las fibras,
es
As =
Ao
Senφ
siendo la correspondiente tensión de corte
τm =
Pf
P Cosφ
= o
= σ oSenφ Cosφ
As Ao / Senφ
(3. 35)
La tensión normal que actúa en la dirección perpendicular a las fibras, es
σN =
PN
P Senφ
= o
= σ oSen 2φ
As Ao / Senφ
(3. 36)
Eliminando σo entre (3.34) y (3.35), obtenemos
tgφ =
τm
σc
de donde
τ m = σ c tgφ
Ahora bien, el modo de rotura del compuesto dependerá de la orientación
relativa de la dirección de las fibras y del esfuerzo con que se lo solicita. Si la
resistencia del compuesto a la rotura longitudinal es σc, la resistencia a la rotura
por corte en la dirección de las fibras es τm y la resistencia a la fractura normal
a las fibras es σN, la resistencia σoRot. y el modo de rotura del compuesto
dependerá de la orientación relativa de las fibras y el esfuerzo en la forma en
que se muestra en la Fig. 3.15.
3-22 Ensayos Industriales
Tracción, compresión
Fig. 3. 15