¿Cuánto sé de vectores?

¿Cuánto sé de vectores?
Dino E. Risso
11 de agosto de 2007
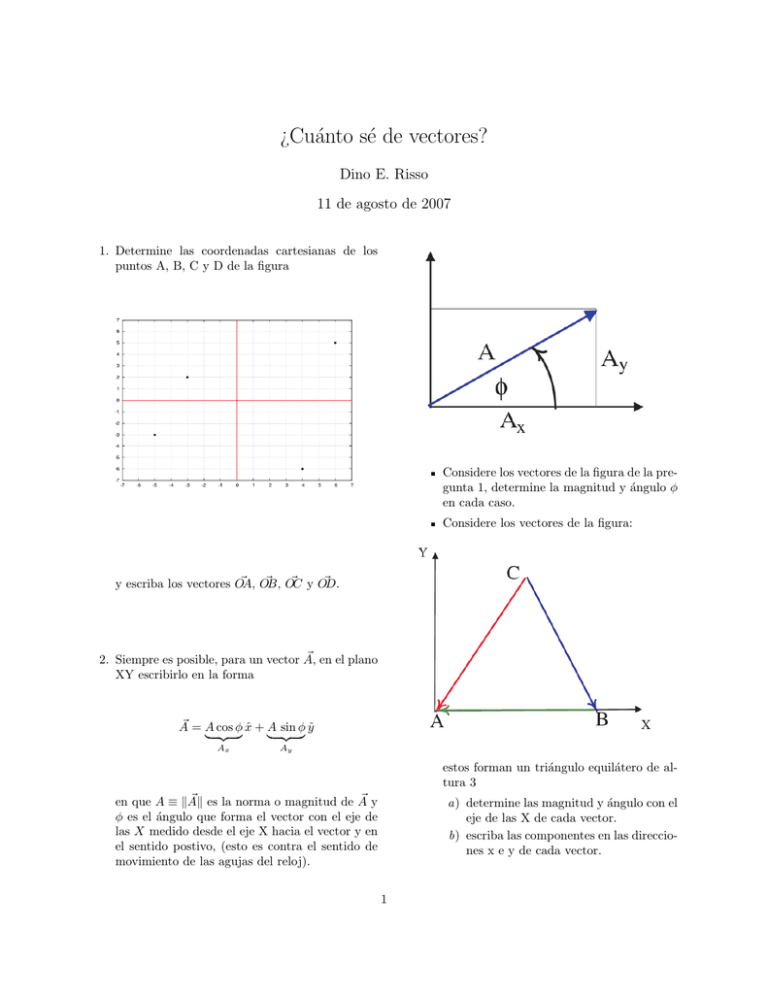
1. Determine las coordenadas cartesianas de los
puntos A, B, C y D de la figura
Considere los vectores de la figura de la pregunta 1, determine la magnitud y ángulo φ
en cada caso.
Considere los vectores de la figura:
~ OB,
~ OC
~ y OD.
~
y escriba los vectores OA,
~ en el plano
2. Siempre es posible, para un vector A,
XY escribirlo en la forma
~ = A cos φ x̂ + A sin φ ŷ
A
| {z }
| {z }
Ax
Ay
estos forman un triángulo equilátero de altura 3
~ es la norma o magnitud de A
~y
en que A ≡ kAk
φ es el ángulo que forma el vector con el eje de
las X medido desde el eje X hacia el vector y en
el sentido postivo, (esto es contra el sentido de
movimiento de las agujas del reloj).
a) determine las magnitud y ángulo con el
eje de las X de cada vector.
b) escriba las componentes en las direcciones x e y de cada vector.
1
~ ·B
~
10. Es posible demostra que el producto punto A
aparte de valer Ax Bx + Ay By + Az Bz simultaneamente vale AB cos(φAB ) donde A y B son
~ B.
~ Esto es A
~·B
~ =
el módulo o norma de A,
Ax Bx + Ay By + Az Bz = AB cos(φAB ).
~ = 3x̂ + 4ŷ y B
~ = 5x̂ + 13ŷ,
Dados los vectores A
~
~
~
~
determine: kAk, kBk y A · B. Use esto para determinar cos(φAB ).
3. Para los vectores de la pregunta 2, determine
gráfica y analı́ticamente la sumas
~ + B,
~ B
~ +C
~
A
y las restas
~ − B,
~ C
~ − A,
~B
~ − C.
~
A
4. Para los vectores de la pregunta 2 determine
gráficamente los vectores
~ C
~ − 1/2A,
~ A
~ + 1/2B.
~
−1/2A,
11. Para los vectores de la pregunta anterior calcule
~ = A
~+B
~ y use esto para calcular el ángulo
C
~
~ También calcule el ángulo entre C
~
entre C y A.
~
y B.
~ (o sea use letras
5. Considere un vactor abritrario A
no números). Determine el valor de los productos
puntos siguientes:
(Ax x̂ + Ay ŷ + Az ẑ) · (Bx x̂ + By ŷ + Bz ẑ)
12. Note que el producto punto de un vector consigo
~ 2 = A2 . Esto
~ ·A
~ = A2x + A2y + A2z = kAk
mismo A
es. si A es la magnitud de un vector y B es la
~ 2=A
~ · A.
~
magnitud de otro, entonces A2 = kAk
(Ax x̂ + Ay ŷ) · (Bx x̂ + By ŷ + Bz ẑ)
(Ax x̂) · (Bx x̂ + By ŷ + Bz ẑ)
(x̂) · (Bx x̂ + By ŷ + Bz ẑ)
~ B)·(
~ A+
~ B)
~ = A·
~ A+2
~ A·
~ B
~ +B
~·
Muestre que (A+
~
~
~
~
~
B. Aplique esto a (A−B)·(A−B) para demostrar
el teorema del coseno: C 2 = A2 −2AB cos φ+B 2 ,
~ =A
~ + B.
~
vı́a C
6. Para los vectores de la pregunta 2 determine el
valor (numérico) de los productos punto:
~ · B,
~ B
~ · C,
~ (1/2A
~ + B)
~ · A.
~
A
13. ¿Como se determina un vector unitario  a par~
tir de un vector A?.
7. Si para un vector descrito en coordenadas cartesianas en vez de escribir el vector con la notacion
Calcule, para los vectores del triángulo equilatero de la pregunta 2, los vectores unitarios Â, B̂ y
Ĉ correspondientes.
~ = Ax x̂ + Ay ŷ + Az ẑ
A
14. Como Ud. aprendió en el apunte de vectores al
~ y un
hacer el producto punto entre un vector A
vector unitario û se está calculando la proyección del vector en la dirección de û. Calcule, para los vectores de la pregunta 2 las proyecciones
~ · B̂ (proyeccionde A sobre la direcsiguientes: A
~ sobre la direccion
cion de B), la proyeccion de B
~ − 1/2B
~ sobre la dirección
ĉ, la proyeccion de A
~
de C.
lo describimos con la notación
~ = {Ax , Ay , Az }
A
entonces ¿cuales de las siguientes cantidades
correpsonderian al vector ŷ?:
I {0,0,1}
II {1,0,1}
III {0,1,0}
IV {0,2,0}
V {2,0,2}
8. Escriba los vectores unitarios x̂ y ẑ en la notacion
{Ax , Ay , Az }.
9. ¿Cuánto valen los productos punto siguientes?:
x̂ · ŷ, x̂ · x̂, x̂ · (−x̂), (x̂ − ŷ) · ẑ, (x̂ + ŷ + ẑ) · x̂,
(x̂ + ŷ) · (x̂ − ŷ − ẑ).
Tambien evalúe cuanto valen los productos punto
siguientes:
x̂ · (Ax x̂ + Ay ŷ + Az ẑ), ŷ · (Ax x̂ + Ay ŷ + Az ẑ) y
ẑ · (Ax x̂ + Ay ŷ).
2