Guía de Matemáticas - FICA

UNIVERSIDAD NACIONAL DE SAN LUIS
INGRESO 2013
MAYORES DE 25 AÑOS
GUIA DE TRABAJOS PRACTICOS
Y
RESOLUCION DE PROBLEMAS
DE
MATEMATICA
2012
1
NUMEROS ENTEROS
1. Asocien un número entero a cada enunciado, como en el ejemplo

Tengo $ 20 en el bolsillo

La temperatura subió 4º

Debo $ 15 a un amigo

La temperatura bajó 2º

El garaje está en 3º subsuelo

Gané $ 10

Yo vivo en el 4º piso de un edificio

Perdí $ 25

Hace calor, el termómetro marca 32º


El hecho ocurrió en el año 75 a. C.

+ 20
Deposité un cheque de $ 30 en mi
cuenta
Hace frío, el termómetro marca 5
grados bajo cero
2. Ubiquen en la recta numérica los siguientes números enteros: 5; -8; -2; 7; 3; -5; -7
3. Ordena de menor a mayor los siguientes números enteros: -4; -2; 5; -11; -14; 8; -8; 0
4. Escribe el anterior y el consecutivo de cada uno de estos números enteros:
........ -7 .......... ; ........ 0 ......... ; ........-89........ ; ;........ - 1 ....... ; ........- 30........
5. Completa el cuadro
Numero entero
+ 12
+9
-6
........
0
Su opuesto
-12
..........
...........
15
......
6. Completa con un signo de < , > ó = según corresponda
a) -10
-20
b) 0
-15
c) -120
-119
d) 21
-21
e) -3
-42
f) 57
-34
7. Resuelve las siguientes sumas
8.

7 + (-10) =

30 + (-22) + (-8) =

-12 + (-3) =

-6 + (-3) + 7 =

-20 + (-50) =

-2 + (-3) + 4 =

-15 + 20 =

-5 + 6 + (-2) =

-10 + (-20) + 10 =
Expresa cada uno de los siguientes enunciados mediante una suma
a) Mi tío me regaló $ 15, pagué los $ 7 que debía en kiosco, encontré un billete de $ 10 en la
vereda y le devolví $ 3 a mi hermana.
b) Durante un experimento, la temperatura de un compuesto químico subió 6º C en la
primera hora, subió 2º C más en la segunda hora y bajó 10ºC en la tercera hora.
9.
Calcula

12 - 20 =

-75 - 4 =

100 - (-50) =

22 - 20 - 20 =

- 30 - (-10) =

16 - (-12) =

- 25 - (-25) =

-1 - 2 – 9 + 15 - 3 =

-7 + 12 + 19 - 9 + 6 =

-4 - 18 + 20 - 1 + 3 =

-2 - 3 - 10 =

9 + 7 - 24 - 30 + 5 - 8 =
10. Suprime paréntesis y resuelve
11.
a) (+ 10) - (+9) + (+3) - (-7) =
b) (-3) - 5 + (-4) + (-1) - (-10) =
c) 12 - (-15) + 15 + (-22) - 13 =
d) (-18) + (-5) - (-30) - 27 - (-12) =
e) 4 + (-3) - (-1) - 8 - 2 + (-6) =
f) 15 - (10 +8 - 2) - (5 - 3 +1) =
Para pensar un poco
 Una cuenta corriente que tiene un saldo deudor (negativo) de $ 6000. Luego recibe tres
depósitos de $ 2500 c/u y dos depósitos de $ 1200 c/u. Luego se extraen tres veces $ 2300 y
una vez $ 1800 ¿Cuál es el saldo actual?
 De una cuenta bancaria que tiene un saldo inicial de $ 5000 se hacen tres retiros de $320 c/u.
Luego se deposita una suma igual al doble de c/u de los retiros realizados, y finalmente se
extrae la mitad del dinero que quedó depositado hasta ese momento.
¿Cuál es el saldo actual?
 En una carrera de coches hay 32 participantes. Por diversas razones se retiran sucesivamente
5 corredores en la primera vuelta, 7 en la vuelta Nº 13 y uno en la vuelta Nº 25. Exprese
mediante números enteros cuántos participantes acabaron la carrera.
12. Calcula
a) 6 . (-2) =
b) 6 : (-2) =
c) (-2) . (-3) . (-4) =
d) 7 . (-1) =
e) (-5) . 3 =
f) (-9) : (-9) =
g) (12) : (-2) : (-3) =
h) 12 : 6 =
i) (-8) . (-1) =
j) (-10) : 10 =
k) 5 . (-6) : 10 =
l) 3 . (-4) : (-4) =
13. Resuelve
a) -8 + 10 – 3 – 7 + 2 – 1 =
g) (-8) . (2 – 6) – 3.[-1 – (-5)]=
b) -15 + 28 – 140 + 10 – 25 =
h) 4.[4 – 2 + (-10) – (-7)] + (-4) . 3
c) -3.3 + (-4).5 + 2(-2) =
i) -4.(-3)(-2) + [12 : (-6)](-2) =
d) -3.(-2) + (-12):3 - 4.0 =
j) 9 - (4 - 7) + 3[2(3-5) + 8:2] =
e) -10:(-5) - 2.(-1) + (-2).3 =
k) 10 - [2 - (4-2).(2+8)] =
f) 7 + 8 : (-2) - (-3):(-1) =
l) 9 + 3(7-8) – 4 : (-4) - [(9+12) : (-3)] =
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
m) (-9-7) : (-8) + (-2)(-3) =
o) -{7 – 2 + [-(3-4) + 7] - (7 - 15)} =
n) 16 - ( -8 - 2) + [-(4 + 8) + 3 - 7] =
p) {(15) - [4 - (-6) + 2]} - (-3) =
14. Resuelve
a)
 42 . 

- 52 . - 5 
36 : 4 .  3 
 
 8. 1  27 12 . 
5
b) 102 .109 
0
c)
 81  16 .- 5
d)
 2  5 .1  6 . 4  3  
7
2
64  36  100 . 4 
4 7
2
e) 2 . - 3  3  8 . 2 
0
25 



49  5  32 . 40   2
 1
2 3
29
.
f) 50 . (52)3 : 55 =
g) 82 . 83 . 8 : 84 =
15. .- Realizar las siguientes operaciones con números enteros
a) (-5)2 + 62 – (-8) ÷ 2 – 32 =
b) 72 – (53)2 ÷ 25 =
c) (-5) + 2 – (-4) + (-8) – (+7) =
d) (-1 +3)2 – (-3)2 + ( 123 + 345)0 =
PROBLEMAS
Problema 1. ¿Que diferencia de altura hay desde la cima del Everest, que se tiene 8.862 metros
y el fondo de la fosa marina de las islas Marianas que esta a 10.915 m de la superficie?
Problema 2. Cierto día de tiempo variable, el termómetro señalaba -8 C, a las siete de la
mañana. A lo largo de esta, la temperatura subió 13 C y, durante la tarde descendió el doble de
lo que había subido. ¿Que temperatura marcaba el termómetro al atardecer?
Problema 3. La temperatura registrada a las 7:00 horas en la ciudad de Neuquén ha sido de 5º
C bajo cero y a las 13:00 horas, 7º C. ¿Cuál ha sido el incremento de la temperatura en ese
tiempo?
Problema 4. Se compraron 9 balones a 12 pesos, cada balón y 13 pares de zapatillas deportivas
a 35 pesos cada par. ¿Cuánto dinero pagaron?
Problema 5. ¿Qué peso lleva un camión que transporta 95 bolsas de trigo de 68 Kg. cada una y
67 bolsas de cebada de 64 Kg. cada una?
Problema 6. ¿A cuanto asciende la factura por la reparación de un vehículo en la que la mano
de obra supone $384, las piezas cambiadas, $ 852 y el IVA $16?
Problema 7. Dar un ejemplo de un número entero que al multiplicarlo por 2 resulte un número
más pequeño. ¿Como son los números que cumplen esa condición?
Problema 8. ¿Por que numero hay que multiplicar a dos números enteros cualquiera para que
los resultados coincidan?
Problema 9. En la antigua Mesopotámica, sobre el año 539 a.C., se produjo la invasión persa y
en 1792 a.C. era gobernante Hammurabi.
a) ¿Cuál de los dos eventos es más antiguo?
b) ¿Cuánto tiempo transcurrió entre ambas fechas?
c) ¿Cuántos años han transcurrido entre cada uno de los eventos y la fecha de inicio de
clases, del ciclo 2007, en el Colegio Maria Auxiliadora?
Problema 10. Una empresa de transporte tiene servicio a tres localidades de la zona. Al Volcán
sale cada tres horas, al Trapiche cada cinco horas y a Villa Mercedes cada diez horas. Hoy a las
6:00 salieron los tres colectivos a sus destinos, ¿dentro de cuantas horas saldrán nuevamente
juntos?
Problema 11. Tres señoras se encontraron hoy en la peluquería. Una de ellas visita la peluquería
cada 6 días, la otra señora visita la peluquería cada 8 días y la restante cada 4 días. ¿Dentro de
cuantos días se vuelven a juntar las tres señoras?
Problema 12. El planeta Júpiter tiene cuatro satélites. El primero tarda 54 horas en dar una
vuelta alrededor del planeta, el segundo tarda 85 horas en efectuar ese mismo recorrido, el
tercero tarda 172 horas y el cuarto 400. Considerando como posición inicial de todos los satélites
la actual. ¿Cuánto tiempo habrá de transcurrir para que los cuatro satélites vuelvan a coincidir?
¿Cuántas vueltas darán cada satélite en ese tiempo?
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
Actividades de refuerzo
Problema 1. Si efectuamos la siguiente operación
99 - 97 + 95 - 93
¿Que resultado obtenemos?
(a) 48
(b) 64
+
91
–
89
+
(c) 32
87
–
85+........+7
(d) 50
–
5
+3
-
1
=
(e) 0
Problema 2. Una sala de cine tiene 26 filas con 24 asientos cada una. El total de los asientos se
numera de izquierda a derecha, comenzando por la primera fila y hacia atrás. ¿En qué número de
fila está el asiento número 375?
(a) 12
(b) 13
(c) 14
(d) 15
(e) 16
Problema 3. Si efectuamos el producto de todos los números impares comprendidos entre 1 y
1994, ¿cuál es la cifra de las unidades del número así obtenido?
(a) 1
(b) 3
(c) 5
(d) 7
(e) 9
Problema 4. A las 9 a.m. el termómetro marca + 12° y de esta hora a las 8 p.m. ha bajado 15°.
Expresar la temperatura a las 8 p.m.
Respuesta: A las 8 p.m., la temperatura es de -3°.
Problema 5. A las 6 a.m. el termómetro marca -3°. A las 10 a.m. la temperatura es 8° más alta
y desde esta hora hasta las 9 p.m. ha bajado 6°. Expresar la temperatura a las 9 p.m.
Respuesta: A las 9 p.m. la temperatura es de -1°.
Problema 6. A la 1 p.m. el termómetro marca +15° y a las 10 p.m. marca -3°. ¿Cuántos grados
ha bajado la temperatura?
Respuesta: la temperatura ha bajado un total de 18°.
Problema 7. A las 3 a.m. el termómetro marca -8° y al mediodía +5°. ¿Cuántos grados ha
subido la temperatura?
Respuesta: la temperatura ha subido un total de 13°.
Problema 8. A las 8 a.m. el termómetro marca -4°; a las 9 a.m. ha subido 7°; a las 4 p.m. ha
subido 2° más y a las 11 p.m. ha bajado 11°. Expresar la temperatura a las 11 p.m.
Respuesta: A las 11 p.m. la temperatura es de -6°.
Problema 9. A las 6 a.m. el termómetro marca -8°. De las 6 a.m. a las 11 a.m. sube a razón de
4° por hora. Expresar la temperatura a las 7 a.m., a las 8 a.m. y a las 11 a.m.
Respuesta: la temperatura a las 7 a.m. es de -4°, a las 8 a.m. de 0° y a las 11 a.m. de 12°.
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
NUMEROS RACIONALES
Problema 1. Utilizando el símbolo ‘>’ o ‘<’ enuncia la relación de orden para cada uno de los
siguientes pares de números.
a) 6 , -3
4
3
23 23
4 9
h)
9 4
4
-3
23 23
1
3
i)
,
2
4
c)
b) -2 , -5
e) 4
d)
5 -3
7 3
g)
3
2
8 5
Problema 2. Ordena los siguientes numero racionales de menor a mayor.
f)
 37
61
4
5
3
2
5
4
7
2
j)
5
-3
2
11
3
,
2
14
14
5
Problema 3. Decidir cuáles de los siguientes pares de números racionales son iguales.
3
2
5
25
1
25
1)
2)
3)
y
y
y
6
4
2
4
6
400
4) 2 y
8
4
5)
9
24
y
6
18
6)
6
4
y
3
2
Problema 4. Escribir la forma irreducible de cada número racional.
1)
6
8
2)
32
20
3)
22
121
4)
200
25
5)
24
36
6)
37
1250
Problema 5. Transformar los siguientes números racionales de la forma de fracción a la forma
decimal
1.
6121
150
2.
37
9
3.
29
15
4.
200
25
5.
7. Calcula las siguientes sumas
a) 37,429 + 8,093 + 12,456 =
b) 123 + 0,39 + 27,2 + 3,004 =
c) 4,85 + 0,56 + 63,4 =
d) 0,0073 + 6,56 + 79,0258 =
8. Calcula las siguientes restas:
a) 245,379 - 156,093 =
b) 0,39 - 0,0023 =
c) 7,85 - 0,56 =
d) 6 - 3,0258 =
9. Expresa en forma de fracción las siguientes expresiones periódicas:
a) 0,103103103….. =
b) 0,11111111…….. =
c) 7,85858585….... =
d) 3,0258258258….. =
4
3
6.
3
8
10. Operar
a)
3 1
 
2 4
b)
2 1
 
3 6
c)
3 1
 1 
2 4
d) 2 
e)
3 1 2
  
5 3 15
f)
1 1 7
  
2 4 8
g)
2 13 4
  
7 7 7
h)
3 1
i) 1     
2 4
j)
2 3
 2
5 4
k) 1 
1

4
3 1
 
2 4
1 2 3
  
6 5 2
l) 3 
3

2
11. Operar
a)
3 1
 
2 4
b)
2 1
 
3 6
c)
3 1
 1 
2 4
d) 2 
e)
3 1 2
  
5 3 15
f)
1 1 7
  
2 4 8
g)
2 13 4
  
7 7 7
h)
3 1
i) 1     
2 4
2 3
j)     2 
5 4
 1
k) 3  1    1 
 4
3 1
 
2 4
1 2 3
   
6 5 2
 3 2
l) 4  3     3 
 2 3
12. Operar
2
 1
b) 4   
 2
 1
d)  1  
 2
 3
e)  1   
 5
2
g)
  3
c) 
 
 5 
2
3
1

a)   2  
2

3
1 1
 
3 3
h) 1 
8
1
 ( 3 )2  
9
2
f)
1
3 1 
5
i)
1 3
 2
  27     
16
 3
13. Calcular el valor de:
1  1
 1 7  
 1 1  1
i)    2       1   2       
4  3
 3 12   
 6 3  2
 1  1 3 2 
ii)      
 2  3 4  
1

1
iii)
 1
3
 1 3  3
  3   1       
5
 4 8  4
 3
 2   1   1 
3 
v)   1        2   
4 
 3   2   4 
2
4 2 7 1
1
vii)      .   5   
7 5 4 9
6
2
2

1 
2 2
iv)  3      2    
3 
3  

3 5 5
vi)      
2 4 6
3 
6
 : 3   
7 
5
2
 2  3  1   4  2 7  3
viii) 5 :    .     : 
 2    3  9  5

INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
14. Utilizando el símbolo ‘>’ o ‘<’ enuncia la relación de orden para cada uno de los siguientes pares
de números.
a) 3,52
3,57
b) 2,01
2,1
c) 1,2
1,3
e) 0,17
0,17
f) 0.17
0,176
g) 2,48
d) 0,167
3,48
h) 0.23
0,168
0,231
15. Expresa cada número como fracción, resuelva y halle la expresión decimal de la fracción
obtenida
a)
3
 0,5 
2
b)
2
2
1
c)    1,2  
3
2
5 1
  0,6 
4 3
d) 0,3 
1 3
  0,5 
3 3
16. Para cada fracción, halla su expresión decimal y resuelva.
a)
8
 2  0,1 
10
d) 0,24  5 
1
 4  0,8 
2
b)
1
9 
25
e) 0,25  25 
c) 0,6 
7
 70 
10
f) 0,3 :
1
 0,03  10 
5
1 5
  0,5 
3 3
17. Complete la tabla
Fracción
Expresión decimal
Porcentaje
3
4
0,32
60%
1,28
18. Expresar en forma de fracción las siguientes potencias de exponente entero
 13
 32
2 1
 33
 12
2 4
19. Expresar en forma radical las siguientes potencias de exponente racional.
 3 13
5
1
2
2
1
2
 32 3
7
3
5
5
3
4
20. Calcular las siguientes potencias de base racional:
  1
 
 2 
2
 1 
 
 2 
2
1
 1 2
 
4
4
 
9
1
2
21. Aplicando las propiedades de la potencia, simplifica las siguientes expresiones
a) 3 .5  2  3 
2
3
4
 1   3  1  5   1   2
b)         
 2   2    2 
c)
 22 . 23

 2 4
PROBLEMAS
Problema 1. En un concurso de radio se reparten $18.000 entre dos concursantes que han
acertado 32 y 28 preguntas respectivamente. ¿Cómo se debe repartir el dinero?
Problema 2. Las piezas que se utilizan en la fabricación de un determinado tipo de coche están
formadas por una aleación que contiene 24/29 de cobre, 4/29 de estaño y 1/29 de cinc.
¿Cuántos kg de cada metal entrarán en 846 kilogramos de aleación?
Problema 3. Un delineante está dibujando el plano de una casa a escala 1:175, es decir,
cualquier longitud en la realidad, el delineante la divide entre 175 y ésta es la longitud que tendrá
en el plano. Si la planta de una casa es un rectángulo de 28,45 metros de largo por 14,354 m. de
ancho. ¿Qué dimensiones tendrá en el plano la planta de la casa?
Problema 4. En una tira de papel rectangular se dibujan líneas verticales que la dividen en 4
partes iguales. También se dibujan líneas verticales que la dividen en 3 partes iguales.
Finalmente, se corta la tira siguiendo las líneas dibujadas. ¿Cuántos pedazos de diferente
longitud se tienen?
Problema 5. ¿Cuál es el volumen de aire que hay en mi habitación que mide 3,52 x 2,47 x 2,5
metros? Calcula también la superficie de las paredes, del suelo y del techo. (Nota: Las
dimensiones se indican: largo x ancho x alto).
Problema 6. De un campo se vendieron las 2/3 parte de su superficie y después las 2/3 de lo
que quedaba. El Municipio expropió los 3.200 m2 restantes para un parque público. ¿Cuál era la
superficie del campo?
Problema 7. Un año-luz es la distancia que recorre la luz en un año. Sabiendo que la luz se
desplaza en el vacío con una velocidad de 3 x 105 km/sg., calcula a cuántos km. corresponde un
año-luz.
Problema 8. Se desea cubrir con baldosas cuadradas el suelo de una habitación que mide 330
cm. de ancho por 390 cm. de largo. Se quiere realizar el trabajo utilizando baldosas lo más
grandes que sea posible y sin cortar ninguna. ¿Cuál debe ser el tamaño de las baldosas?
Problema 9. En una cierta ciudad, la mitad de la población está entre los 20 y los 50 años, y
por cada tres habitantes mayores de 50 años, hay cinco menores de 20.
a) ¿Cuál es el porcentaje de personas de cada grupo?
b) Se desea representar esta proporción en un diagrama de sectores. ¿Qué ángulo central
corresponde a cada sector?
Problema 10. Un chico sale de marcha y gasta primero los 2/5 de su dinero y luego 1/6 de lo que
le quedaba. Si regresa con $39.¿Con cuánto dinero salió?
Problema 11. Una agencia propone un viaje de fin de curso a los alumnos de 6º año de San Luís.
Inicialmente interesa el viaje a una octava parte de los estudiantes. Cuando se concreta el precio
se retiran 3/5 de los que pensaban ir. Por causas diversas, una semana antes se retiran 1/21 de los
que quedaban. Si al final van 80 personas. ¿Cuántos alumnos de 6º año hay en San Luís?
Problema 12. Un viajero se dirige desde San Luís a Córdoba. El 34% de este trayecto lo recorre
en tren y las dos terceras partes de lo queda en auto. El resto en moto. ¿Qué tanto por ciento
recorre en moto? Si la distancia total son 360 Km. ¿Cuánto recorrió en moto?
INGRESO 2013
U.N.S.L.
Mayores de 25 años
MATEMÁTICA
Problema 13. Calcula el número aproximado de glóbulos rojos que tiene una persona, sabiendo
que tiene unos 4.500.000 por milímetro cúbico de sangre, y que su cantidad de sangre es de 5
litros. Exprésalo en notación científica.
Problema 14. Calcula la longitud que ocuparían esos glóbulos rojos puestos en fila, si su
diámetro es 0,008 milímetros por término medio.
Problema 15. Tres toneles, cuyas capacidades son 250, 306 y 504 litros están llenos de
diferentes clases de vino. Se quieren envasar, sin mezclar, en botellas iguales. Halla la capacidad
máxima que pueden tener estas botellas, y el número de botellas necesarias para proceder al
envasado.
Problema 16. ¿Cuántos músicos, como mínimo, hay en una banda de música que cuando desfila
de dos en dos sobra uno, y también sobra uno si desfilan de tres en tres, de cuatro en cuatro y de
cinco en cinco?
Actividades de refuerzo
Problema 1. Andrea compró una docena de huevos en un almacén. Al llegar a su casa se cayó y
sólo quedaron 5 huevos enteros. ¿Qué fracción de los huevos no se quebró?
Problema 2. Un ciclista da diariamente 30 vueltas a una pista. Ayer, mientras hacía su rutina,
comenzó una gran lluvia y sólo alcanzó a pedalear 13 vueltas. ¿Qué fracción de lo que
Normalmente recorre alcanzó a hacer?
Problema 3. Una micro realiza el mismo recorrido 7 veces al día. Debido a la congestión vehicular
hoy sólo recorrió 5 veces su ruta. ¿Qué fracción de su recorrido habitual logró hacer?
Problema 4. Si el numerador de una fracción es el triple del denominador, ¿qué racional
tenemos?
4
Problema 5. En un cine hay 56 personas, de las que
son chicas. ¿Cuántos chicos y cuántas
7
chicas hay?
2
1
de agua,
de edulcorante y el resto
5
5
por una composición de distintos elementos. ¿Qué cantidad de cada elemento hay en 10 gramos
de dicho compuesto químico?
Problema 6. Un compuesto químico está formado por
Problema 7. Durante un viaje, un viajante consume
1
de la gasolina que lleva en el depósito
8
2
de lo que le quedaba. Sabe que le quedan en el
3
depósito 20 litros. ¿Cuántos litros puede llevar en el depósito?
de su vehículo. En un segundo viaje consume
Problema 8. En una competencia Juan ganó 15 bolitas. Si regaló 3 de ellas a su hermano menor,
¿qué fracción de las bolitas que había regalado ganó?
Problema 9. En un almacén tenían 100 agendas para vender. Si vendieron sólo 78 agendas, ¿qué
fracción del total vendieron?
Problema 10. Francisca tomó una bebida de medio litro y María tomó dos bebidas de un cuarto de
litro cada una. ¿Tomaron ambas la misma cantidad de líquido?
Problema 11. Dos ciclistas deben recorrer un circuito. Si el primero ha recorrido dos tercios de
éste y el segundo cuatro sextos del mismo, ¿han recorrido hasta ahora la misma distancia?
Problema 12. En la especialidad de alimentación se preparan tortas para una recepción, Susana
preparó 2 tortas de igual tamaño, una de piña y otra de manjar. La de piña la dividió en 24 trozos
iguales y la otra en 12 trozos iguales. y don Juan comió 3 pedazos de torta de piña y dos de manjar,
¿comió lo mismo de ambas?
1. Desafio: Escribe en forma de fracción la parte sombreada de las siguientes figuras
a)
3 2  1 2
    
5 5  6 3
1
3
4
4

  2  5
7



1 4 
  3
10  3 
1

2 
1

3
 1
  
 5
c) 
2
7
e)
2
3
3
4
g)
 1 1 13   3  2 1 
      :    
 3 2 6   5  5 4 
2
 2 1  5   1 
  1      
 3 2  4   12  
b)
3
1
2
6
1
:3 
2 3
d) 5
4 5 1
: 
3 6 4
3 1 5 1
   :
4 5 6 3 
f)
9 3 1 1
 : 
5 2 3 5
2
h)
3
3 2  3

   :   1
 2 7   17 
1

INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
RESOLUCION DE ECUACIONES DE PRIMER GRADO
EJERCICIO 1
Resolver las siguientes ecuaciones y verificar la solución hallada.
1. 3 + 2 - 5 + x = 2 + 1 – 3
2. -2 + 6 -12 = x + 5 – 1
3. 2 + 6 - 1 = x + 6 - 4
4. -5 - 6 + x = 5 - 8 + 3
5. 6 - 9 + x + 9 = 2 – 6
6. 6 - 9 - 3 = 4 + x +3 - 5
7. 2 + 5 – 9 = 2 + x - 6 – 8
8. 2 + 9 + 6 - 9 = x + 3 – 5
9. 9 - 5 + 6 +x = -5 -9 +3
EJERCICIO 2
Resolver las siguientes ecuaciones y verificar la solución hallada.
1. 2x = -4
2. x : (-3) = 6
3. -3.x = 18
4. x : (-5) = 4
5. 3x = 9
6. x :(-4) = (-6)
EJERCICIO 3
Resolver las siguientes ecuaciones y verificar la solución hallada:
1. 4x - 2 = 10
2. 6x – 3 = x + 17
3. 2x + 5 = 3
4. 7x = 4x + 6
5. 2x = 9 + x
6. 6x = 24 - 2x
7. 10 = 15 - 5x
8. x – 8 = 4 - x
11. 2-3x-5 = 5-8x+x
12. x + 2 =3 - 2x + 8
9. 3x – 10 = 18 - x 10. 7x – 8 = 3x + 4
EJERCICIO 4
Resolver las siguientes ecuaciones con coeficientes enteros y raíces enteras
y verificar la solución hallada.
1) 3x – 10x = 8x – 30
2) -4x – 5x = 3x – 12
3) 12 – 4x = x – 8
4) -6x + 2x = -5x + 5
5) -5x – 4x = 3x + 24
6) 10x + 4x = -2x – 16
7) x – 1 = 3x = 21
8) 4x +4 = -6x – 16
9) -2x – 3 = -30 + 4x +27
EJERCICIO 5
Resolver las siguientes ecuaciones con coeficientes fraccionarios y raíces
enteras y verificar la solución hallada.
3x 5 x 7


4
2 2
x  3 x 1 x  2


3
4)
2
2
3
1)
7)
10  5 x 8  2 x 11

 0
2
2
2
x x
 7
3 4
2x  1 x 9
 
5)
4
2 4
8)
4 x  2 3x x
35

 
2
2 6
6
2)
x x
  2  13
2 3
2 x 3x
37

4
6)
3
2
6
3)
9) 
x x x x 15
   
2 3 6 4 4
Actividades de refuerzo
Ecuaciones con operaciones indicadas y raíces entera o fraccionarias.
1) 24  x   4 x  22
R: x = 5
2) 5 x  1  3 x  3
R: x = 4
3) 2 x  3 x  4  24 x  5  3
R: x = 1
1 x  2 
4

4) 4 x   
 3 x  
3
2
9


R: x =
5) 5 x  1  25  x   4  2100  x   206
R: x = -5
6)  8a  10  6
R: a  
7) 120 y  1  2 y  51
R: y 
8) 2 x  1  x   x  2  4 x  1 
4
7
2
 x  2  4  x  1  2 1  x 
5
3
3
3
12
7
10)  x  6  x   0
5
5
5
9)
EJERCICIO 6
2
3
1
2
1
2
4
R: x 
7
7
R: x 
6
5
R: x 
3
Resuelve las siguientes ecuaciones:
2 x  3 3x  2
x 1

 x
4
8
4
x  2 x 1
x 5

 x4
b)
3
9
9
2  x  70  x  30  6  2 x x  7
c) 



5  80 
40
5
5
a)
Colección de problemas
Problema 1. Hallar tres números enteros consecutivos, tales que el doble del menor más el
triple del mediano, más el cuádruple del mayor equivalgan a 740.
Problema 2. ¿Qué número se debe restar de 22 para obtener 5?
Problema 3. El doble de un número aumentado en 12 es igual a su triple disminuido en 5.
¿Cuál es el número?
Problema 4. Tres números impares consecutivos suman 81. ¿Cuáles son los números?
Problema 5. El doble de un número más el triple de su sucesor, más el doble del sucesor de
éste es 147. Hallar el número.
INGRESO 2013
U.N.S.L.
Mayores de 25 años
MATEMÁTICA
Problema 6. Si el lado de un cuadrado es aumentado en 8 unidades, su perímetro se triplica.
¿Cuánto mide el lado?
Problema 7. Un padre tiene 20 años más que su hijo. Dentro de 12 años, el padre tendrá el
doble de la edad del hijo. ¿Cuántos años tiene cada uno actualmente?
Problema 8. Las edades de un matrimonio suman 62 años. Si se casaron hace 10 años y la edad
de la novia era
3
de la edad de la novia. ¿Qué edad tienen actualmente?
4
Problema 9. La edad de Pedro excede a la de su amigo Santiago en 4 años y a la de su amigo
Juan en 2 años. Hace 6 años la razón entre sus edades era 2:3:4. ¿Qué edad tienen
actualmente?
Problema 10. La edad de María es el triple de la de Ester y excede en 5 años a la edad de Isabel.
Si las edades de Ester e Isabel suman 23 años. Hallar la edad de cada una.
Problema 11. Guiso tiene la cuarta parte de la edad de su padre Andrés y el triple de la edad de
su hermano David. ¿Qué edad tiene cada uno, si sus edades suman 48 años?
Problema 12. Hace 6 años un padre tenía el cuádruplo de la edad de su hijo. En 10 años más
tendrá sólo el doble. Hallar la edad actual del padre e hijo.
Problema 13. Un padre tiene 52 años y su hijo 16. ¿Hace cuántos años el hijo tenía la séptima
parte de la edad del padre?
Problema 14. Se compran 25 lápices, 32 cuadernos y 24 gomas de borrar y se paga por ello la
suma de $ 16.900. Si cada cuaderno cuesta el triple de cada goma, más $ 20 y cada lápiz
cuesta el doble de cada goma, más $ 8. ¿Cuánto cuesta cada material?
Problema 15. Hernán tiene el doble de dinero que Gladis y el triple que María. Si Hernán
regalara $ 14 a Gladys y $ 35 a María, los tres quedarían con igual cantidad. ¿Cuánto dinero
tiene cada uno?
Problema 16. Una persona puede pintar una muralla en 5 horas, otra lo hace en 6 horas y una
tercera persona tarda 12 horas en pintar la misma muralla. ¿Cuánto tardarían si la pintaran
entre las tres?
Problema 17. La cabeza de un pez corresponde al tercio de su peso total, la cola a un cuarto del
peso y el resto del cuerpo pesa 4 kg. 600 gramos. ¿Cuánto pesa el pez?
Problema 18. Un trozo de alambre de 28 cm. de largo se ha doblado en forma de ángulo recto.
Determina la distancia entre ambos extremos del alambre, si uno de los lados del ángulo
formado mide 12 cm.
Problema 19. Al preguntársele a Pitágoras por el número de sus alumnos, dio la siguiente
respuesta: “La mitad de mis alumnos estudia Matemática, la cuarta parte estudia Física, la
séptima parte aprende Filosofía y aparte de éstos hay tres niños muy chicos” ¿Puedes deducir
cuántos alumnos tenía el famoso matemático griego?
Problema 20. Al comprar 3 Kg. de tomates y 4 Kg. de papas, una dueña de casa pagó $ 119.
¿Cuánto vale el kilo de tomates, sabiendo que es $ 14 más caro que el kilo de papas?
Problema 21. La entrada para una función de teatro al aire libre vale $ 60, adultos, y $ 25, niños.
La recaudación arrojó un resultado de 280 asistentes y fue de $ 14.000. ¿Cuántos niños
asistieron a la función?
Cuestiones de Geometría
Problema 22. Un rectángulo tiene un perímetro de 392 metros. Calcula sus dimensiones
sabiendo que mide 52 metros más de largo que de ancho.
Problema 23. El perímetro de un rectángulo mide 36 metros. Si se aumenta en 2 metros su base
y se disminuye en 3 metros su altura el área no cambia. Calcula las dimensiones del
rectángulo.
Problema 24. Uno de los ángulos agudos de un triángulo rectángulo es 18º mayor que el otro.
¿Cuánto mide cada ángulo del triángulo?
Problema 25. La altura de un trapecio isósceles mide 4 cm, la suma de las bases es de 14 cm, y
los lados oblicuos miden 5 cm. Averigua las bases del trapecio.
Problema 26. El perímetro de un triángulo rectángulo mide 30 m y el área 30 m2. Calcula los
catetos.
Problema 27. La diferencia de las diagonales de un rombo es de 2 m. Si a las dos las
aumentamos en 2 m el área aumenta en 16 m2. Calcula las longitudes de las diagonales, el
perímetro y el área de dicho rombo.
Obreros
Problema 28. Un obrero ha trabajado durante 30 días para dos patrones ganando $2.070. El
primero le pagaba $65 diarios y al segundo $80. ¿Cuantos días trabajó para cada patrón?
Problema 29. Dos obreros trabajan 8 horas diarias en la misma empresa. El primero gana $500
diarias menos que el segundo; pero ha trabajado durante 30 jornadas mientras que el primero
sólo 24. Si el primero ha ganado $33.000 más que el segundo calcula el salario diario de cada
obrero.
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
SI.ME.L.A.
Creado por Ley Nacional Nº 19511
Ejercicio 1
Reducir a g
a) 0,06003 kg
Ejercicio 2
c) 7452 mg
d) 5,21 cg
b) 2,7 dl
c) 2851 dal
d) 34,121 cl
Reducir a cl
a) 2,03008 Kl
Ejercicio 3
b) 2,7 dag
Expresar en dal
a) 23,8 l + 256 cl + 0,58 hl =
Ejercicio 4
b) 153,21 dl + 1,650 l + 365 cl =
Expresar en dam2
a) 72,04 hm2 + 2006 dm2 + 7,3 m2 =
Ejercicio 5
Expresa en metros
a) 6,3 Km. + 0,1 dam + 5,004 hm =
Ejercicio 6
b) 7,8 cm + 564 mm + 0,15 dam =
Completa el siguiente cuadro.
Volumen
Ejercicio 7
b) 1,05 km2 – 23,17 hm2 =
3
Capacidad
1
24 dm
_______ hl
2
_______ cm3
406 dl
3
0,002 m3
_______ kl
4
_______ cm3
0,54 l
5
0,0024 dm3
_______ hl
Completa el siguiente cuadro.
Peso
Volumen
1
_______ hg
37 dm3
2
1,002 dag
_______ cm3
3
_______ g
0,032 m3
4
7,002 dg
_______ mm3
5
_______ cg
0,036 cm3
Problemas de aplicación
Problema 1. ¿Cuántos hl se necesitan para llenar un depósito de 20m de largo, 5m de ancho y
2m de alto?
Problema 1. ¿Cuántos litros de agua hacen falta para llenar totalmente una piscina de 26,7m de
largo, 6m de ancho y 4,50m de profundidad ?
Problema 2. Un trabajador cobró $1,25 por pintar cada metro cuadrado de un edificio de 15m
de largo por 22m de altura. ¿Cuánto cobrará para pintar las cuatro paredes de 14 edificios
iguales al primero ?
Problema 3. Si 2 cl de un aceite especial cuestan $11,35. ¿Cuánto costarán 8 hectolitros ?
Problema 4. ¿Cuántos metros de alambre harán falta para cercar un terreno de 180m de largo y
150m de ancho ?
Problema 5. ¿Cuántos hg le faltan a 26,35 hg para hacer 35,75kg ?
Problema 6. ¿Qué longitud debe tener un alambre para que rodee 4 veces un terreno cuadrado
de 56,30m de lado? Expree el resultado en km, dam y mm.
Problema 7. Una pecera de 100cm de largo y 7,6 dm de ancho está llena hasta una altura de
90cm. ¿Cuántos litros de agua contiene hasta esa altura?
Problema 8. ¿Cuánto costará alfombrar un salón de 7,50m de ancho y 8,70m de largo si el dm2
sale a razón de $0,45 ?
Problema 9. Se siembran a ambos lados de una avenida de 3,75km de largo árboles
ornamentales a 2,50m uno de otro. ¿Cuál fue el precio de cada árbol si en total costaron
$10500?
Problema 10. Si un depósito contiene 7230hl de vino. ¿Cuántos barriles de 10 litros se podrían
llenar ?
Problema 11. ¿Cuál será el área de un complejo deportivo que tiene 0,18km de largo y 120m de
ancho ?
Problema 12. Si una caja mide 18cm de largo, 15cm de ancho y 10 cm de alto, ¿cuál es su
volumen ?
Problema 13. ¿Cuál será el volumen de una masa de agua destilada en el vacío y a una
temperatura de 4ºC que pesa 6870kg?
Problema 14. ¿Cuánto costará un terreno que mide 2,3 km de largo por 13 dam de ancho, si el
m2 vale $4,20?
Problema 15. Con un rollo de tela de 80m de largo por 1,10m de ancho se quiere confeccionar
camisas. Si cada una de ellas requiere 2m2, ¿cuántas camisas se pueden hacer?
Problema 16. Se quiere almacenar la mayor cantidad posible de cajas de 60 cm de largo, 40 cm
de ancho y 25 cm de alto conteniendo determinado producto. Si el almacén tiene 30 m de
largo, 10 m de ancho y 4 m de alto calcule, ¿cuántas cajas podrían guardarse en el?
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
Problema 17. Un artista cobra, por decorar la pared central del lobby de un hotel, $17,50 por
cada m2. Si la pared mide 4,70 m de alto por 15m de largo, ¿cuánto cobraría el artista por
pintar 5 paredes iguales.
Problema 18. Para abonar un terreno se necesita 10cm3 de abono por dam2. Si el terreno mide
450m de largo por 350m de ancho. ¿Cuántos cm3 harían falta ?
Problema 19. Un comerciante vende 4 toneles de vino, el primero de 45 hl, el segundo de 25
dal, el tercero de 320 dl y el cuarto de 28 litros. ¿A cuánto ascendió la venta si el precio en
que se vendió cada litro fue de $0,35 ?
Problema 20. ¿Cuántas hojas de 15cm de largo por 7cm de ancho puede sacarse de un rollo de
papel de 1,75m de largo por 1,2 m de ancho ?
Problema 21. Se necesita limpiar un terreno que mide 314 m de largo por 220 m de ancho y para
ello se contrata un jornalero pagándole $0,20 por m2. ¿Cuánto ganó el jornalero?
Problema 22. Un estanque de 3,50m de largo, 2,25m de ancho y 1,5m de profundidad contiene
11300 litros de agua. ¿Cuántos litros de agua le faltan para llenarse totalmente ?
Problema 23. Una plancha de cierto metal tiene 5,50m de largo, 60cm de ancho y 20mm de
espesor. Si cada dm3 cuesta $15,50, calcule su valor.
Actividades de refuerzo
Pasar a metros
543 mm
54,23 dm
125 mm
45,25 cm
0,02 km
45,15 dam
7841 cm
1,052 hm
0,025 km
12 mm
15,1 dm
1200 km
12,5 m
4,525 cm
200 km
0,4515 dam
78,41 cm
10,52 hm
2,5 km
12 m
1,51 dm
12,006 km
522 ml
450,25 cl
0,07 kl
145,15 dal
1458 cl
10,52 hl
0,0425 kl
1,2 ml
18,1 dl
12,003 kl
Pasar a mm
5,43 m
0,5423 dm
Pasar a l
345 ml
518,23 dl
Completar el cuadro
km
hm
0,001
dam
m
dm
cm
mm
520
1,55
1280
0,8
Completar el cuadro
kg
hg
10
dag
g
dg
cg
5,89
15,5
12,80
800
mg
PERIMETRO Y AREA
Problema 1. Hallar el perímetro y el área de las siguientes figuras:
Cuadrado
Rectángulo
Trapecio rectángulo
Problema 2. Hallar el perímetro y el área de:
Triangulo equilátero
Trapecio Isósceles
Indique la opción correcta
1. Si un rectángulo tiene base 15cm y área 105cm2 ¿Cuánto mide su altura?
A) 90 cm
B) 10 cm
C) 7 cm
D) 15 cm
2. En un triángulo escaleno sus lados son números enteros consecutivos (por ejemplo 6, 7 y 8).
Encuentra la medida del lado menor si su perímetro es de 87 cm
A) 30 cm
B) 13 cm
C) 28 cm
D) 21 cm
3. Si el área de un cuadrado es 144 cm2. ¿Cuánto miden sus lados?
A) 14 cm
B) 36 cm
C) 12 cm
D) 17 cm
4. Se quiere empastar un terreno rectangular que es 10 metros más largo que ancho y su
perímetro es de 100 metros. ¿Cuántos metros cuadrados de pasto necesitan comprar para
empastarlo?
A) 875 m2
B) 900 m2
C) 600 m2
D) 120 m2
5. El perímetro de un triángulo equilátero es 60 cm más grande que la medida de sus lados.
¿Cuánto miden los lados de dicho triángulo?
A) 15 cm
B) 20 cm
C) 30 cm
D) 12,5 cm
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
6. Si el perímetro de un cuadrado es 36 cm más grande que uno de sus lados. ¿Cuánto mide su
área?
A) 121 cm2
B) 81 cm2
C) 36 cm2
D) 144 cm2
7. Si el área de un triángulo es de 112 cm2 y su base es de 14cm ¿cuánto mide su altura?
A) 20 cm
B) 8 cm
C) 7 cm
D) 16 cm
8. Si el perímetro de un rombo es de 48 cm ¿cuánto miden sus lados? Nota: No olvides escribir
la respuesta con sus unidades, es decir, dejando un espacio y poniendo: cm
9. Si el perímetro de un cuadrado mide 20 cm. ¿Cuánto mide su área?
A) 16 cm2
B) 5 cm2
C) 25 cm2
D) 400 cm2
Qué área es mayor?
4cm
2cm
3cm
3cm
8cm
Figura 1
Figura 2
Figura 3
Que triangulo tiene área mas grande?
4cm
4cm
3cm
6cm
2cm
5cm
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
TRABAJO PRÁCTICO Nº 7
FUNCIONES
BOLSAS DE AZÚCAR
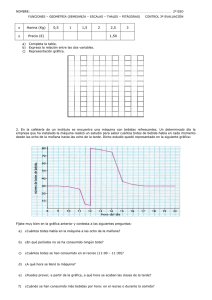
Ej. 1. Cada punto de este gráfico
representa una bolsa de azúcar.
A. ¿Qué bolsa es la más
pesada?
B. ¿Qué bolsa es la más
barata?
C. ¿Qué bolsas tienen el
mismo peso?
D. ¿Qué bolsas tienen el
mismo precio?
E. ¿Qué bolsa sale mejor de precio: F ó C? ¿Por qué?
LA FAMILIA
Ej. 2. En el gráfico de abajo tenemos una fotografía de la familia López: Juan es
el abuelo, los hijos de Bella y José son Pablo que va a la guardería, Pepe está estudiando 3º año
del Secundario, Alicia que estudia medicina y Luís.
a) ¿Quién está representado por cada uno de los puntos del diagrama de la derecha?
b) ¿Es apropiada la escala utilizada? Razona la respuesta. (Realiza las hipótesis que consideres
oportunas)
c) Realiza una representación de toda la familia donde representes en el eje horizontal la edad y
el eje vertical la altura de cada uno de ellos.
TEMPERATURAS
Ej. 3. En una ciudad se han tomado distintas mediciones de la temperatura a lo largo de un día
de julio. Éstas vienen reflejadas en la gráfica:
9
6
3
0
-3
2
4
6
8
10
12
14
16
18
20
22
24
-6
-9
Comenta su significado y completa la siguiente tabla:
Hora del día
2
4
6
8
10
12
14
16
18
20
22
24
Temperatura (ºC)
BOLAS
Ej. 4. Si A y B representan bolas de distinto material y tamaño, mirando los gráficos, indica si
son ciertas o falsas las afirmaciones siguientes:
Nota: Elige el grafico adecuado según las magnitudes que vayas a comparar en cada caso.
a) La que tiene más volumen, tiene más peso.
b) La que tiene menos peso, tiene más volumen.
c) La que tiene más peso, cae más rápidamente
d) La que tiene más volumen cae más
rápidamente
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
LATAS DE REFRESCOS
Ej. 5. El número de latas de refrescos vendidos a través de una máquina en una EG3 cercana
está indicado por la tabla siguiente:
Hora del día
Latas vendidas
7
8
9
10
13
15
10
18
11
12
12
20
13
25
14
16
15
12
16
8
A. Haz una representación gráfica.
B. ¿Cuál es la hora de mayor consumo?
C. ¿Cuántos se han consumido hasta las 11 h.?
D. Si la capacidad de la máquina es de 100 botes, ¿a qué hora se ha rellenado?
E. ¿Puede representar una situación real esa tabla? ¿Por qué?
PASEO DE DOS AMIGOS
Ej. 6. Rafa y Alicia son compañeros de clase, quedan un día para salir. Rafa sale de su casa y
recoge a Alicia, que tarda un poco en bajar. Después dan un paseo y se sientan en una cafetería a
tomar un refresco. Al regreso se acercan a casa de unos compañeros a recoger unos apuntes y allí
se entretienen un tiempo. Después regresan a casa. La gráfica del paseo viene aquí representada.
RESPONDE:
1. ¿Qué variables se relacionan?
6. ¿A qué hora salieron de la cafetería?
2. ¿Cuál es la variable dependiente y la
variable independiente?
7. ¿A qué casa regresaron?
8. ¿Cuánto tiempo pasearon los dos
juntos?
3. ¿Cuánto dista la casa de Alicia de la
de Rafa?
9. ¿Cuándo pasearon más deprisa: de la
cafetería a casa de sus amigos o de
ésta al final del paseo? ¿Por qué?
4. ¿Cuánto tiempo esperó Rafa a que
bajara Alicia?
5. ¿Cuánto tiempo tardaron en llegar a
la cafetería?
E
s
p
a
c
i
o
(metros)
2.000
1.500
1.000
500
10
11
12
HORA
13
14
LA EXCURSIÓN
Ej. 7. Se alquila un microbús de 12 plazas para realizar una excursión, por un total de 36.000
pesos:
A. Haz una tabla del precio de la excursión por persona, en función de las plazas cubiertas.
B. Representa los datos de la tabla en un diagrama (número de pasajeros-precio).
C. ¿Puedes establecer alguna relación entre las dos variables?
D. ¿La variable independiente es discreta o continua?
E. ¿Tiene sentido unir mediante una línea los puntos de la gráfica? ¿Por qué?
SALARIO
Ej. 8. Un oficial gana $1.500 a la hora y su ayudante $1.000 a la hora. Un día, el ayudante
empieza a trabajar a las 8 de la mañana y el oficial a las 10.
A. ¿Cuánto dinero lleva ganado cada uno a las 10 y las 11 de la mañana?
B. El oficial y, su ayudante siguen trabajando hasta la hora 15. Construye una tabla en la que
reflejes hora a hora el dinero que va ganando cada uno de ellos.
C. Representa gráficamente los valores de la tabla. ¿A qué hora han ganado la misma
cantidad?
D. ¿Puedes deducir la expresión algebraica o fórmula que determina lo que gana el oficial
según las horas trabajadas? ¿Y de su ayudante?
FUNCION LINEAL
1.
Clasifica las siguientes fórmulas como funciones constantes, lineales y dibuja su gráfica:
a) y = 4
b) y  x
2
c) y  3  x
d) y  2 x  3
2.
María, al pasear, camina a razón de 5 km/h. Expresa el espacio recorrido en función del
tiempo empleado y represéntalo en una gráfica.
3.
La rueda de una bicicleta mide 26 cm de radio.
a) ¿Qué espacio recorrerá al dar 5 vueltas?
c) Representa gráficamente los valores.
b) Haz una tabla de valores.
d) Halla la expresión algebraica de la función.
e) ¿Cuántas vueltas tendrá que dar la rueda para hacer un trayecto de 1,5 km?
4.
De una fuente mana un volumen de agua de 120 litros por cada 5 minutos. Elabora una
tabla de valores y representa gráficamente cómo varía el volumen en función del tiempo.
5.
Dada la función que calcula el perímetro de un triángulo equilátero en función de la
medida de su lado:
INGRESO 2013
Mayores de 25 años
U.N.S.L.
MATEMÁTICA
a) Haz la tabla de valores:
Lado
1
2
3
4
Perímetro
b) Represéntala gráficamente
c) Escribe la fórmula y =
d) ¿Qué tipo de función es?
e) Halla la pendiente
6.
Al abrir las compuertas de un estanque para regar una huerta, el nivel del agua en el
estanque desciende a razón de 6 cm./minuto.
a) Haz la tabla de valores:
Tiempo (min)
1
2
3
4
Nivel de descenso (cm.)
b) Represéntala gráficamente.
d) ¿Qué tipo de función es?
c) Escribe su fórmula y =
e) Halla la pendiente
7.
Dada la función: f ( x ) 
2 x
calcula:
3
c) La imagen de –4/3
b) f (1 3)
a) f (3)
d) f (4)
8.
Representa gráficamente las funciones siguientes en un mismo sistema de ejes
coordenados. ¿Qué observas?
f ( x)  2 x
g ( x)  2 x
h( x)  3x
i( x)  3x
9.
Representa gráficamente las funciones siguientes en un mismo sistema de ejes
coordenados. ¿Qué observas?
yx
10.
y  3  x
Representa gráficamente estas funciones y diga cuál es su pendiente y su ordenada.
a) y  2 x  1
11.
y  x2
y  x 1
b) y  1 3x
c) f ( x ) 
2
x4
3
d) g ( x) 
7 3
 x
3 4
¿En qué puntos cortan a los ejes de coordenadas a las gráficas de estas funciones?
a) y = -4x
b) y = -3x + 5
c) y=2 – 4x
d) y = 4
12.
Indica cuál es la pendiente y la ordenada en el origen de las siguientes funciones y
represéntalas.
a) y = -2x + 1
b) y = 3x – 2
c) y - 3x= – 2
1
y que pase por el punto:
2
d) y + 2= 3x
1 1
 , .
2 2
13.
Calcula la recta paralela a y  4 x 
14.
Halla el punto de intersección de la recta 3x – 2y = 0 y la recta y = 6x – 2.
15.
¿Cuál es el punto de intersección de las rectas y = 3 con y = -2x + 3?
16.
Halla la ecuación de la recta que pasa por los puntos (-2, -4) y (2, 4).
17.
Escribe la ecuación de la recta que pasa por el punto (5,6) y tiene pendiente 4
FUNCION CUADRATICA
18.
Representar gráficamente las siguientes funciones.
a) y  x 2  2
d) f ( x)  2x 2  1
19.
b) y  3x 2
c) y  2 x 2  7
e) y  2 x  1  1
2
f) f ( x)  3x x  1
Representar gráficamente las siguientes funciones.
f ( x)  3x 2  10 x  3
g ( x)  2 x 2  3 x  1
1

y  2 x  1 x  
3

FUNCION VALOR ABSOLUTO
20.
Representar Gráficamente las funciones f ( x)  x  3 ; g ( x)  x 2  2 e y  x  2
OTRAS FUNCIONES
21.
Mediante una tabla obtenga los puntos para representa el grafico de:
a) y  x 3  1
c) y 
b) y  x
d) f ( x)  2 x  1  1
e) y   x  1  2
g) f ( x)  1  3
1
h) f ( x)   
 2
2
x
2
1
x
f) f ( x)  2 x
x
i) f ( x) 
1
x 1