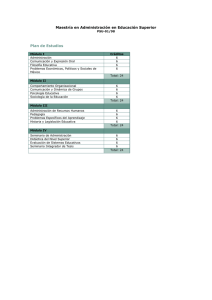
Memorias XVIII Encuentro de Profesores de Matemáticas III

Universidad Michoacana de San Nicolás de Hidalgo
Facultad de Ciencias Físico Matemáticas
Área de Matemática Educativa
Memorias
XVIII Encuentro de Profesores de Matemáticas
III Seminario Nacional sobre resolución de problemas
y el aprendizaje de las matemáticas
11, 12 y 13 de Agosto de 2010, Ciudad Universitaria. Morelia, Michoacán
Comité Editorial
Armando Sepúlveda López
Jesús Roberto García Pérez
Luz Manuel Santos Trigo
Fernando Barrera Mora
Aarón Sánchez Reyes
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Cítese como:
Sepúlveda, L. A., García, P. R., Santos, T. L. M., Barrera, M. F., Sánchez, R. A. (Eds.).
(2010). Memorias. XVIII Encuentro de Profesores de Matemáticas, III Seminario Nacional
sobre Resolución de Problemas y el Aprendizaje de las Matemáticas, Morelia: UMSNH.
Editores:
Armando Sepúlveda López
Jesús Roberto García Pérez
Luz Manuel santos Trigo
Fernando Barrera Mora
Aarón Sánchez Reyes
Área de Matemática Educativa de la Facultad de Ciencias Físico
Matemáticas de la Universidad Michoacana de San Nicolás de Hidalgo.
Francisco J. Mújica s/n, Edificio D, planta baja, Ciudad Universitaria,
Morelia, Michoacán, México.
Fax: (443) 3262146 Ext. 130
Copyright © Todos los derechos reservados
Certificado en el Registro Público del Derecho de Autor: 03-2006-082215233400-01
ISBN: 970-95130-0-5
Impreso en el Área de Matemática Educativa, UMSNH. Morelia, Michoacán
XVIII Encuentro de Profesores de Matemáticas
Página 2
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
CONTENIDO
Página
I.
Presentación
4
II
Conferencias y Reportes de investigación
6
1.
Reconstruyendo un marco conceptual en la resolución de problemas que
incorpore el uso de herramientas computacionales. Manuel Santos Trigo.
7
Herramientas virtuales: medios poderosos para favorecer el entendimiento
de ideas matemáticas y competencias en resolución de problemas. Juan
Estrada, Enrique Arenas.
17
La relación entre conocimiento conceptual y la habilidad para usarlo en la
resolución de problemas: experiencias con profesores de nivel medio
superior. César Cristóbal Escalente, Verónica Vargas.
27
Introducción al Cálculo integral mediante el cálculo del área de regiones
planas. Héctor Suárez Alfaro.
48
El papel del profesor en el desarrollo de competencias matemáticas mediante
resolución de problemas. Verónica Vargas, César Cristobal Escalante.
54
2.
3.
4.
5.
III Mesas de discusión
63
1.
El posgrado de Matemática Educativa en la UAEM. Enrique Vega Villanueva.
64
2.
La formación de profesores de matemáticas: el caso del nivel medio superior.
César Cristóbal Escalente.
68
3.
Formación de profesores y uso de tecnología. Aarón Reyes Rodríguez.
71
4.
Formación de profesores y uso de tecnología en la Educación Matemática.
Marcos Campos Nava.
73
Acerca de la existencia de programas de formación de profesores de
matemáticas de bachillerato. Ignacio Morales González.
74
5.
IV Talleres (Cursos cortos)
1.
78
Algunas características de actividades de aprendizaje con tecnología.
Fernando Barrera Mora, Aarón Reyes Rodríguez.
79
La enseñanza del Álgebra en el bachillerato con Geogebra. Armando
Sepúlveda, Diana I. Sepúlveda, Roberto García.
99
La enseñanza de la Geometría euclideana en el bachillerato con Cabri.
Armando Sepúlveda López.
112
4.
Curso de Cálculo infinitesimal para el bachillerato. Ismael Arcos Quezada.
127
5.
Geometría dinámica para el bachillerato: un enfoque de ambientes de
con Cabri. Eugenio Díaz Barriga
131
Reflexiones en torno a la tarea, la técnica y la teoría en un ambiente de
resolución de problemas algebraicos. José Guzmán Hernández.
136
Resolución de problemas de olimpiada. María Luisa Pérez Segui.
138
2.
3.
6.
7.
XVIII Encuentro de Profesores de Matemáticas
Página 3
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
I. Presentación
XVIII Encuentro de Profesores de Matemáticas
Página 4
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Presentación
Un propósito fundamental de la celebración de este evento conjunto III Seminario Nacional
sobre Resolución de Problemas y el Aprendizaje de las Matemáticas y XVIII Encuentro de
Profesores de Matemáticas es disminuir la distancia existente entre el trabajo que realizan los
investigadores en educación matemática y el trabajo cotidiano que hacen los profesores de
matemáticas en el salón de clases. Si bien es cierto que la investigación es el motor que
genera, básicamente, el avance y desarrollo de toda disciplina, también es cierto que la
investigación adquiere sentido cuando aparece relacionada con situaciones que, en ese
momento, enfrenta el profesor en el aula.
Los esfuerzos del Área de Matemática Educativa de la Facultad de Ciencias Físico
Matemáticas, de la Universidad Michoacana de San Nicolás de Hidalgo, hacen posible llegar
a este XVIII Encuentro de Profesores Matemáticas que, en esta ocasión, da cobijo al
Seminario Nacional con la idea de contribuir al mejoramiento de la enseñanza y el
aprendizaje de las matemáticas, preferentemente, en el nivel medio superior mediante la
actualización e intercambio de experiencias de los profesores de matemáticas, a través de tres
conferencias, cuatro reportes de investigación, dos mesas de discusión, una mesa redonda; así
como la impartición de ocho talleres o cursos cortos impartidos por especialistas.
El tema que se tendrá presente durante el desarrollo de las actividades, será el de la formación
de profesores, como continuación de los dos primeros Seminarios Nacionales que se han
llevado a cabo hasta la fecha, algunas de cuyas interrogantes que se tomaron en cuenta para la
elaboración de las agendas respectivas son: ¿qué es la resolución de problemas como
propuesta de aprendizaje de las matemáticas?, ¿cuál es el papel del empleo de herramientas
computacionales en el desarrollo del conocimiento matemático de los estudiantes?, ¿cuál es el
papel del profesor cuando se diseñan actividades de aprendizaje en el marco de la resolución
de problemas?, ¿qué tipo de competencias matemáticas requiere un profesor para matematizar
el aprendizaje de los estudiantes?
Finalmente, dos de las preguntas relacionadas con las anteriores y que aún están vigentes son:
¿quiénes deben participar en la formación y actualización de los profesores de matemáticas?,
¿cómo deben incorporar los profesores de matemáticas las herramientas tecnológicas de
manera que se considere la resolución de problemas como el aspecto primordial para lograr el
aprendizaje?
Esperamos que el desarrollo de las actividades de este evento conjunto y el contenido de estas
Memorias sean de utilidad para los profesores de matemáticas, y siembren la inquietud por
incorporar algunas de las propuestas y reflexiones planteadas.
Armando Sepúlveda López
XVIII Encuentro de Profesores de Matemáticas
Página 5
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
II. Conferencias,
Reportes de
Investigación
XVIII Encuentro de Profesores de Matemáticas
Página 6
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Reconstruyendo un Marco Conceptual en la Resolución de Problemas que
Incorpore el Uso de Herramientas Computacionales
Dr. Manuel Santos Trigo
[email protected]
CINVESTAV – IPN
Resumen
¿Qué se distingue en los acercamientos de resolución de problemas que incorporan
sistemáticamente el empleo de diversas herramientas computacionales en el desarrollo del
pensamiento matemático de los estudiantes? En este artículo, se esbozan elementos de un
marco conceptual que caracteriza fases que sustentan el uso de las herramientas en la
resolución de problemas. Se aborda la solución de un problema de variación para esbozar el
marco. Entre los componentes de destacan el acercamiento visual y empírico, la
representación funcional, la búsqueda de diversos caminos para la construcción de un modelo
algebraico incluyendo métodos analíticos y geométricos y la relevancia de contrastar los
procesos y estrategias utilizadas en los diversos acercamientos.
Summary
What are the common mathematical features that distinguish a problem solving approach that
fosters the use of computational tools in students‟ development of mathematical knowledge?
In this paper, I sketch a conceptual framework that characterizes phases or episodes that
support the use of computational tools in problem solving approaches. A task is used to
identify elements of the framework that include visual and empirical approaches to explore a
functional relation; the construction of an algebraic model by focusing on analytic and
geometric approaches; and the relevance of contrasting the use of different processes,
resources, and strategies exhibited in all the approaches to the problem. This framework could
be used by teachers to structure their problem solving activities.
Introducción
Existen diversas tradiciones o escuelas de pensamiento que permiten sustentar y orientar el
desarrollo de proyectos o programas académicos en educación matemática. Hoyles y
Lagrange (2010) reportan que varios programas de investigación han analizado y discutido el
papel que desempeña el empleo de diversas herramientas digitales en el aprendizaje de los
estudiantes. Se observa además, que en todos los marcos de investigación se reconoce que los
problemas o tareas matemáticas desempeñan un papel fundamental en la construcción del
conocimiento matemático de los estudiantes. Así, los problemas y las formas en que se
utilizan en los escenarios de instrucción no son solamente un ingrediente esencial que
estructura y guía el desarrollo de las actividades de aprendizaje; sino que también el proceso
de resolver problemas influye en el tipo de pensamiento matemático que desarrolla el
estudiante al interactuar con los problemas o tareas (Santos-Trigo, 2009b). El Consejo
Nacional de Profesores de Matemáticas (NCTM, por sus siglas en inglés) (2009) reconoce
que para que los estudiantes desarrollen un pensamiento matemático robusto, estos se deben
involucrar en actividades de resolución de problemas donde tengan la oportunidad de
desarrollar distintas maneras de comprender y razonar acerca de un problema o situación. De
manera similar, Schoenfeld (2010) afirma que el currículum puede hacerse más atractivo e
XVIII Encuentro de Profesores de Matemáticas
Página 7
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
interesante si este incluye problemas relevantes, que promuevan más la búsqueda de
soluciones con sentido y consideren un acercamiento coherente hacia la construcción de
habilidades de resolución de problemas, no como algo adicional, sino como una parte
fundamental de la actividad matemática. Así, se plantea la necesidad de exhibir diversas
formas de encontrar el sentido de las ideas matemáticas, enunciados de los problemas y
soluciones. Cai (2010) establece que “sólo [la discusión de] los problemas que valen la pena
le dan la oportunidad a los estudiantes de solidificar y extender lo que ya conocen y los
estimula en sus experiencias de aprendizaje” (p. 252). Además, en la resolución de problemas
se destaca que la construcción del conocimiento matemático de los estudiantes es un proceso
gradual que demanda de los estudiantes un acercamiento inquisitivo hacia los problemas y
estudio de los contenidos. En esta dirección resulta importante reflexionar acerca de las
formas de razonamiento que los estudiantes construyen en actividades de resolución de
problemas que promueven el empleo sistemático de herramientas computacionales (SantosTrigo, 2007b). Así, el propósito de este artículo es caracterizar las fases y dimensiones
relevantes que aparecen en los procesos de resolución de problemas que se abordan y discuten
con el uso de la tecnología. Es decir, se intenta identificar y esbozar los elementos de un
marco conceptual ( Santos-Trigo & Camacho-Machín, 2009)que oriente a los estudiantes en
el empleo de las herramientas que los conduzca a una reflexión matemática en las distintas
fases asociadas con la resolución de problemas. Este marco surge al analizar las formas de
solución que muestran estudiantes al trabajar series de problemas con el uso de herramientas
como el software dinámico. La esencia del marco se asocia con la construcción de
representaciones dinámicas de los problemas u objetos matemáticos; sin embargo, las
representaciones numéricas de relaciones que se ordenan en una tabla con el uso de una hoja
de cálculo también se pueden explicar con el uso del marco.
Antecedentes
Kaput (1992) en una revisión del impacto del uso de la tecnología en la construcción del
conocimiento matemático afirmó que “las limitaciones mayores del uso de la computadora en
las siguientes décadas serían probablemente menos debidas a las limitaciones tecnológicas y
más a las limitaciones de la imaginación humana y a las restricciones [producidas por] de los
viejos hábitos y estructuras sociales” (p. 515). A casi dos décadas, la predicción de Kaput se
confirma ya que el desarrollo tecnológico ha generado herramientas poderosas y fáciles de
utilizar; sin embargo, las reformas recientes de las propuestas curriculares y las formas de
instrucción no han incorporado de manera sustantiva los cambios necesarios que reclaman el
empleo sistemático de las herramientas computacionales. Se observa por ejemplo que las
evaluaciones internacionales del aprovechamiento matemático de los estudiantes no incluyen,
en general, evaluar los métodos y estrategias que aparecen al resolver problemas con el
empleo de la tecnología (PISA, 2006). El uso de las herramientas implica investigar las
formas de razonamiento matemático que se producen durante la comprensión de los
conceptos matemáticos y en la resolución de problemas. La existencia de una variedad de
herramientas tecnológicas con distintos potenciales para ser utilizadas en la instrucción
matemática plantea un reto no sólo a los profesores (Santos-Trigo, 2010) sino también a los
investigadores en educación matemática en términos de ofrecer información sustentada acerca
de cómo utilizar esas herramientas en el desarrollo del pensamiento matemático de los
estudiantes. Es decir, resulta importante conocer el potencial o ventajas reales que puede
XVIII Encuentro de Profesores de Matemáticas
Página 8
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
ofrecer el uso de determinada herramienta en la construcción del conocimiento matemático de
los estudiantes. Zbiek, Heid, Blume & Dick (2007) distinguen dos tipos de actividad
matemática donde el empleo de herramientas computacionales juega un papel importante: las
actividades técnicas y conceptuales. Las técnicas se refieren a las acciones sobre los objetos
matemáticos o sobre sus representaciones como realizar una construcción geométrica, una
medición, un cálculo numérico, una manipulación algebraica, resolver una ecuación, recoger
datos, ordenarlos, etc. Mientras que una actividad conceptual se refiere a aspectos
relacionados con formas de comprender ideas y resolver problemas matemáticos. En ese
proceso, es necesario que los estudiantes desarrollen recursos que les permita comunicar y
buscar conexiones, estructuras y relaciones matemáticas. Algunos ejemplos incluyen
encontrar y describir patrones, conjeturar, generalizar, abstraer, conectar representaciones,
predecir, probar y refutar. Las dos actividades se complementan ya que ambas demandan una
actitud inquisitiva por parte de los estudiantes que los conduzca a lograr una articulación y
una justificación de resultados. Es decir, las actividades técnicas que se realizan con el empleo
de la tecnología pueden involucrar una combinación de acciones rutinarias orientadas o
justificadas a partir de un razonamiento conceptual.
Es evidente también que la sola existencia de distintos artefactos no se transforma
automáticamente en los medios que requieren los estudiantes para utilizarlos de manera
eficiente en la resolución de problemas. Trouche (2004) establece que un instrumento puede y
debe ser considerado como una extensión del organismo humano, un órgano funcional
constituido de un componente “artefacto” (un artefacto, o la parte de un artefacto movilizado
en la actividad de resolución de problemas) y un componente psicológica. Es decir, las
características del artefacto (su ergonomía y limitaciones) y el esquema desarrollado por los
estudiantes durante las actividades son elementos cruciales para que los estudiantes
transformen el artefacto en un instrumento para resolver problemas o comprender conceptos
matemáticos. En este contexto, se describen elementos de un marco conceptual que distingue
fases relevantes en el empleo de herramientas computacionales en la resolución de problemas.
Los componentes del marco emergen y se sustentan en el análisis de los procesos de solución
que muestran los estudiantes en actividades de resolución de problemas que promueven y
demandan el empleo de las herramientas. La presentación del marco se estructura alrededor
de la solución de un problema que involucra examinar un fenómeno de variación. Este tipo de
problemas es representativo de un conjunto de problemas o tareas que se han utilizado en
diversos estudios que forman parte de un programa de investigación sobre la resolución de
problemas y el empleo de herramientas computacionales. Otros ejemplos de este tipo de
actividades se encuentra en la página: http://www.matedu.cinvestav.mx/~santos/atat/
El problema: Dado un triángulo cualquiera ABC, inscribir un paralelogramo tomando
un punto P sobre uno de los lados (AB) del triángulo. Desde el punto P trace una recta
paralela a uno de los lados del triángulo (AC). Esta recta interseca el lado BC en Q.
Desde Q trace ahora una paralela al lado AB y esta recta interseca el lado AC en R.
Así el paralelogramo inscrito en el triángulo tiene como vértices los puntos APQR
(Figura 1). ¿Qué es lo que le ocurre al área del paralelogramo APQR cuando el punto
P se mueve a lo largo del segmento AB? Existe alguna posición para el punto P donde
el área del paralelogramo sea máxima?
XVIII Encuentro de Profesores de Matemáticas
Página 9
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
C
R
A
Q
P
B
Figura 1: Inscribir un paralelogramo en un triángulo dado.
Elementos del Marco Conceptual
Problematizar: Comprensión, sentido y representación del problema. Polya (1945)
reconoce la importancia de que los estudiantes comprendan y discutan el sentido del
enunciado del problema o idea matemática. Es decir, comprender un enunciado o concepto
significa examinar y analizar la información del problema, identificar los conceptos relevantes
y pensar acerca de las formas de representar y explorar el enunciado del problema
matemáticamente. Con el uso de las herramientas esta fase demanda del estudiante una
problematización de la actividad. Es decir, que formule una serie de preguntas que lo
conduzcan no solo hacia la comprensión y a la búsqueda del sentido de la situación o
problema; sino también hacia una construcción de una representación dinámica del problema.
Por ejemplo, algunas preguntas que pueden guiar al proceso de comprensión y representación
del problema incluyen: ¿Qué significa que se dé un triángulo cualquiera? ¿Qué información es
necesaria para construir un triángulo? ¿Existen diferentes maneras de inscribir un
paralelogramo en un triángulo? En la figura 1, si desde el punto P ahora se traza una paralela
al lado BC (en lugar de AC) , esta paralela corta al lado AC en R y desde ese punto de
intersección se traza una paralela al lado AB la cual interseca al lado BC en Q. Así los puntos
R, Q, P y B forman ahora el paralelogramo inscrito, ¿cómo es este último paralelogramo
comparado con el de la figura 1? ¿Tienen la misma área? ¿cómo se puede saber y explicar que
para diferentes posiciones del punto P sobre el segmento AB, el área del paralelogramo
inscrito cambia?
Una Exploración Visual y Empírica. En esta etapa se resalta la construcción de un modelo
dinámico del problema que permite visualizar y cuantificar el comportamiento de los
parámetros asociados en el problema (Santos Trigo, 2007). Con el empleo de un software
dinámico (Cabri-Geometry o Geogebra) se puede construir un triángulo seleccionando tres
puntos (A, B, C) que no estén alineados. Este triángulo ABC en realidad genera una familia
de triángulos al cambiar la posición en el plano de alguno de sus vértices. Ahora, sobre lado
AB del triángulo se identifica el punto P y a partir de este punto se trazan las paralelas
correspondientes que llevan a la construcción del paralelogramos PQRA inscrito. Con la
ayuda de la herramienta se puede calcular directamente el área de ese paralelogramo. Además,
XVIII Encuentro de Profesores de Matemáticas
Página 10
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
se puede observar que al variar la posición del punto P el valor del área asociado al
paralelogramo correspondiente cambia. Por lo tanto tiene sentido investigar para que posición
del punto P el paralelogramo alcanza el área máxima. El uso de la herramienta también
permite construir gráficamente una representación funcional del problema sin explicitar el
modelo algebraico. Esto es, la Figura 2 muestra una relación entre la distancia del punto P y
el valor del área correspondiente del paralelogramo inscrito. Es decir, para cada posición del
punto P sobre el segmento AB, se le asocia el valor del área del paralelogramo
correspondiente. Además, esta relación se puede representar gráficamente. Aquí, la distancia
del segmento AP se traslada al eje x y el valor correspondiente se traslada al eje y. Las
coordenadas del punto S son entonces la longitud del segmento AP y el valor del área del
paralelogramo correspondiente. Con la ayuda del software se puede generar el lugar
geométrico del punto S cuando el punto P se mueve a los largo del segmento AB (Figura 2).
Se observa que el dominio de la función A(x) es el conjunto de valores que toma la longitud
AP cuando P se mueve a lo largo de AB, mientras que el rango de la función es el conjunto
de valores de las áreas correspondientes de los paralelogramos generados al mover el punto P.
Resulta relevante mencionar que la representación gráfica de la función se construye sin
conocer de manera explícita el 
modelo algebraico que da cuenta de la variación del área.
y
S
C
Ar ea of APQR =
8.58 cm
2
Q
R
B
P
A
d( A, B) =
d( A, P) =
6.60 cm
3.30 cm
1
1
x
Figure 2: Representation and visual exploration of the problem.
La representación gráfica genera una solución empírica del problema ya que al mover el
punto P sobre el segmento AB se visualiza que el valor máximo del área se alcanza cuando el
punto P se encuentra a determinada posición sobre el segmento AB. Al realizar las
mediciones correspondientes con la herramienta, se observa que en este caso cuando la
longitud del lado AB es 5.60 cm, entonces el valor del área máxima de los paralelogramos
generados (8.56 cm2) se alcanza cuando P se ubica a 2.30 cm del punto A (Figura 2). A partir
de esta información se puede plantear una conjetura:
Cuando el punto P es el punto medio del segmento AB, entonces el paralelogramo
correspondiente alcanzará el máximo valor del área.
Gráficamente se observa que el comportamiento de las rectas tangentes a la curva para en
distintos puntos de la gráfica, lo que permite observar que la ordenada (valor del área)
XVIII Encuentro de Profesores de Matemáticas
Página 11
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
máxima se obtiene cuando la recta tangente a la curva es paralela al eje x. Es decir cuando su
pendiente es cero (Figura 3).
y
S
C
Area o f APQR = 8.58 c m
2
Q
R
A
B
P
d(A, B ) = 6.60 c m
d(A, P ) = 3.30 c m
1
1
x
Figura 3: Trazado de rectas tangentes a la curva.
Búsqueda de Múltiples Métodos de solución. La búsqueda y discusión de diversas formas
de resolver un problema representa un aspecto fundamental en el proceso de construir una
comprensión conceptual de las ideas matemáticas y en el desarrollo de competencias en la
resolución de problemas. En este contexto, el acercamiento visual y empírico son el punto de
partida para utilizar diferentes recursos y conceptos que permitan representar y explorar el
problema desde perspectivas distintas. Así, un objetivo en el tratamiento del problema será la
construcción de un modelo algebraico que permita representar y explorar el problema en
términos de propiedades algebraicas. En esta perspectiva, dos acercamientos guían la
construcción del modelo: Uno que se basa en el uso del sistema cartesiano para representar y
operar los objetos asociados con el problema, el otro se construye a partir del uso de
propiedades geométricas (triángulos semejantes) que permiten representar las relaciones entre
los objetos.
A. Acercamiento Analítico. En este método la meta inicial es representar y examinar el
problema directamente en términos algebraicos. Aquí el uso del sistema cartesiano es esencial
para representar los objetos de manera simbólica. Por ejemplo, sin pérdida de generalidad, se
puede situar el sistema cartesiano de tal manera que uno de los lados del triángulo coincida
con el eje-x y el otro lado se ubique sobre la recta y  m1x (Figura 4). El punto D se
identifica sobre el lado BC y sus coordenadas son D(x1 ,0).El punto C( x2 ,0) es el vértice C
del triángulo dado (Figura 4). A partir de esta información se tiene que:

XVIII Encuentro de Profesores de Matemáticas
Página 12
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 4: Uso del sistema cartesiano para construir el modelo algebraico del problema
1. La ecuación de la recta AC es y  m1 x ; la ecuación de la recta PQ es y  m1 (x  x1 ). Esto es
porque la recta AC y PQ tienen la misma pendiente (son paralelas). La ecuación de la recta
BC es y  m 3 (x  x 2 ) .
2. Para obtener las coordenadas
del punto Q, se resuelve el sistema
de ecuaciones asociado con


las rectas PQ y BC. Esto es,



m1 x1  m 3 x 2
, entonces para obtener el
m1  m 3
valor de la ordenada y del punto Q se sustituye este valor de x en y  m1 (x  x1 ). Es decir,
m m x  x 2 
y este valor representa la altura del paralelogramo APQR. Por lo tanto,
y  1 3 1
m1  m 3

m1 m 3
x12  x 2 x1 

para encontrar su área, si AP  x1 , entonces A(x1 ) 
.
m1  m 3
m1 (x  x1 )  m 3 (x  x 2 ) , de donde se tiene que x 
3. Para determinar el valor máximo de la función área se tiene que:
m1 m
x
3 (2x1  x 2 )
, ahora, cuando A'(x1 )  0 , se tiene que x1  2 , por lo tanto la

m1  m 3
2
x
función A(x1 ) tiene un máximo cuando x1  2 .
2

Para el caso particular que se muestra en la Figura 4, se 
puede utilizar una calculadora para
A'(x1 ) 

determinar la derivada de la función área y el punto donde se evalúa la función para obtener el
 área máxima (Figura 5).

XVIII Encuentro de Profesores de Matemáticas
Página 13
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Uso de la calculadora para obtener el valor máximo del caso que se muestra en la figura 4.
La Figura 6 muestra la gráfica de la función área:
Figura 6: Representación gráfica de la función área.
B. Un Acercamiento Geométrico. En este acercamiento interesa construir el modelo
algebraico a partir del empleo de propiedades geométricas asociadas con los objetos que
aparecen en la representación del problema. Por ejemplo, en la figura 7 se observa que:
1.
2.
3.
El triángulo ABC es semejante al triángulo PBQ , esto es porque el ángulo QPB es
congruente al ángulo CAB (son ángulos correspondientes) y el ángulo ABC es el mismo
que PBQ (criterio AA). Por lo tanto se cumple que:
PB QN
a  x h1

, esto es si AP  x y AB  a , entonces
 . Con base en esta última
AB CM
a
h
h( a  x )
igualdad, se tiene que, h1 
.
a
El área del paralelogramo APQR se puede expresar como A  xh1 , esto implica que,
hx
 h(a  x) 
. Esta expresión representa
A( x)  x
 . De aquí se tiene que: A( x)  xh 
a
a


una parábola.
2
XVIII Encuentro de Profesores de Matemáticas
Página 14
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
4.
2h x
, ahora si A'  h  2ah x  0 , entonces x  a / 2 . Se observa que A' '  0
a
para cualquier punto definido en el dominio de A(x) , por lo tanto, cuando x toma ese
valor, la función alcanza un máximo relativo.
A ' ( x)  h 
C
h
R
R R
h1
AP = x
A
x
Q
P
N
M
B
a-x
AB = a
Figura 7: Uso de propiedades geométricas en la construcción del modelo algebraico.
Episodio de Reflexión. Conviene reflexionar acerca de los procesos matemáticos que se
exhiben durante las fases de resolución del problema. En la fase inicial resulta relevante
formular y discutir abiertamiente una serie de preguntas que ayuden a comprender y encontrar
el sentido asociado con el enunciado del problema (Santos-Trigo, 2008). Esta etapa que se
denomina problematizar se caracteriza por la presencia de un método inquisitivo que
conduzca al estudiante a identificar la información relevante del problema y los conceptos
relevantes asociados con los objetos matemáticos que aparecen en la representación. Esta fase
proporciona las bases para comenzar a construir un modelo dinámico del problema con el uso
de un software dinámico. Este modelo se convierte en un medio interesante para explorar el
comportamiento de objetos matemáticos (rectas, segmentos, figuras) y atributos (áreas,
longitudes, etc.) de manera visual y empírica. De hecho, este acercamiento visual resulta
esencial para la construcción de una relación funcional del problema que permite visualizar
gráficamente el comportamiento del área de la familia de paralelogramos inscritos. Este
proceso permite formular una conjetura acerca de la solución del problema. Posteriormente,
con la ayuda de la herramienta se identifican los elementos necesarios para construir un
modelo algebraico del problema a partir de identificar las ecuaciones de algunos objetos del
problema. Un aspecto importante en este acercamiento es el empleo del sistema cartesiano.
Después el mismo modelo algebraico que caracteriza la variación del area de los
paralelogramos inscritos se obtiene a partir de utilizar propiedades geométricas de objetos del
problema. Es evidente, que en cada una de las fases que integran este marco de resolución de
problemas se plantean acercamientos al problema que demandan no sólo el empleo de
diversos conceptos y recursos; sino también diferentes formas de operararlos. Por ejemplo, en
el modelo visual, la relación funcional no requiere de una representación simbólica explícita;
XVIII Encuentro de Profesores de Matemáticas
Página 15
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
sin embargo, el estudiante inmediatamente puede examinar el comportamiento de la
representación gráfica de la variación. En los modelos algebraicos el objetivo es construir un
modelo simbólico del problema que permita asociar la posición del punto P con el valor del
área. Los caminos para construir ese modelo algebraico se basan en utilizar conceptos y
recursos distintos: Uno involucra el empleo del sistema cartesiano que permite determinar las
ecuaciones y elementos relevantes del problema con recursos de geometría analítica; mientras
que el segundo acercamiento se sustentan a partir del uso de propiedades de semejaza de
triángulo. Los dos acercamientos ofrecen a los estudiantes la oportunidad de conectar los
contenidos que aveces estudian de manera separada y que aquí convergen en la búsqueda del
modelo algebraico del problema.
Referencias
Hoyles, C. & Lagrange, J-B. (2010) (Eds). Mathematics education and technology-Rethinking
the terrain. The 17th ICMI Study. International Commission on Mathematical
Instruction. NY: Springer.
Kaput, J. (1992). Technology and mathematics education. In D. Grouws (Ed.), Handbook of
research on mathematics teaching and learning, pp. 515-556. NY: Macmillan.
PISA (Programme for International Student Assessment) 2006. Assessing Scientific, Reading
and Mathematical Literacy. A Framework for PISA 2006. Paris: Organization for
Economic Co operation and Development.
Polya, G. (1945). How to solve it. Princeton: Princeton University Press.
Santos-Trigo, M. (2007). La resolución de problemas matemáticos: fundamentos cognitivos.
México: Trillas.
Santos-Trigo, M. (2007b). Mathematical problem solving: An evolving research and practice
domain. ZDM - The International Journal on Mathematics Education, pp. 523-536.
Santos-Trigo, M. (2008). An inquiry approach to construct instructional trajectories based on
the use of digital technology. Eurasia Journal of Mathematics, Science & Technology
Education, 4(4), pp. 347-357.
Santos-Trigo, M. & Camacho-Machín M. (2009). Towards the construction of a framework to
deal with routine problems to foster mathematical inquiry. PRIMUS Journal, 19(3),
260-279.
Santos-Trigo, M. (2010). A mathematical problem-solving approach to identify and
explore instructional routes based on the use of computational tools. In J.
Yamamoto, J. Kush, R. Lombard, & J. Hertzog, (Eds.), Technology implementation
and teacher education: Reflective models, pp 208-313. IGI Global: Hershey PA.
Schoenfeld, A. H. (2010). Reflections of an accidental theorist. Journal for Research in
Mathematics Education, 41(2), pp. 104-116.
Trouche, L. (2004). Managing the complexity of human/machine interactions in computerized
learning environments: Guiding students‟ command process through instrumental
orchestrations. International Journal of computers for Mathematical Learning 9(3):
281-307.
Zbiek, R. M., Heid, M.K., & Blume, G. W. (2007). Research on technology in mathematics
education. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics
teaching and learning (pp. 1169-1207). NCTM, Charlotte, NC: Information Age
Publishing.
XVIII Encuentro de Profesores de Matemáticas
Página 16
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Herramientas virtuales: medios poderosos para favorecer el entendimiento
de ideas matemáticas y competencias en resolución de problemas
Dr. Juan Estrada
M. C. Enrique Arenas
[email protected]
[email protected]
Universidad Nacional Autónoma de México
Resumen
Se documenta el proceso mostrado por dos estudiantes de ingeniería cuando acometían dos
problemas geométricos usando las herramientas disponibles de un software (Geogebra)El
objetivo de la presente investigación se centró en la cuestión: ¿Hasta qué punto la
interacción de los alumnos en este escenario ayudó al entendimiento de las ideas
matemáticas involucradas en los problemas, identificar propiedades relevantes de los objetos
matemáticos, establecer conexiones entre ellas, y sobre todo, resolver las tareas?
Introducción
¿Hasta qué punto los escenarios virtuales son fundamentales para el entendimiento de objetos
matemáticos y promover competencias en resolución de problemas?, ¿La manipulación de
estos objetos en tales ambientes ayuda a los alumnos a identificar sus propiedades relevantes?,
También, ¿Estas acciones sobre los objetos les permite establecer relaciones entre estas
propiedades, que son esenciales para la resolución de los problemas? Las dificultades
manifestadas por los alumnos cuando tratan de entender y/o resolver un problema, ¿Son
superadas debido a los atributos inherentes de estos escenarios comparados con las
características de un medio estático (papel y lápiz)? Finalmente, ¿Cuál es el papel de un
instructor en estos ambientes? Estas interrogantes fueron abordadas en el presente estudio.
La lista de investigadores que han examinado estas cuestiones es amplia, por ejemplo,
Schoenfeld (1985, 1992, 1988, y 1998) y Santos (2002, 2003, 2006 y 2007), por mencionar
algunos. Ambos autores ha hecho contribuciones importantes en el campo. Santos ha
estudiado el potencial de las herramientas tecnológicas en el proceso de resolución de
problemas, línea de investigación que sigue el presente trabajo.
Objetivo
Documentar el proceso mostrado por una pareja de estudiantes de ingeniería cuando
acometían dos problemas geométricos, usando las herramientas de un software (Geogebra).
Preguntas de investigación
1. ¿Hasta qué punto la posibilidad de manipular objetos matemáticos en un medio virtual
ayudan a los estudiantes a entender ideas matemáticas, identificar propiedades relevantes
de objetos matemáticos, establecer conexiones entre ellas que permiten resolver los
problemas propuestos?
2. ¿La interacción en este tipo de escenarios coadyuvó a que los alumnos desplegaran los
conocimientos que son necesarios para resolver los problemas?
3. ¿Los pupilos fueron capaces de superar las dificultades que surgieron en el proceso de
resolución de los problemas por la posibilidad de manipular los objetos matemáticos que
ofrece este tipo de ambientes?
XVIII Encuentro de Profesores de Matemáticas
Página 17
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Marco conceptual
Schoenfeld (1985, 2008) señala que una vez que un individuo se compromete a resolver un
problema, empieza a desplegar conocimientos y a generar estrategias, las cuales piensa que
serán útiles para resolver el problema. Durante el proceso, podría adoptar otras estrategias que
sustituirían las iniciales y también otro nuevo conocimiento puede ser accesado, hasta que
resuelve el problema o el individuo decide abandonar el problema. Esta conceptualización
resumida de un proceso complejo, sirvió como marco para analizar el proceso de la pareja de
estudiantes que participaron en el estudio cuando se les pidió resolver dos problemas. Por otro
lado, Schoenfeld (1992) recomienda que cuando se realiza una investigación en resolución de
problemas, es importante clarificar el punto de vista utilizado sobre este tema en el estudio.
Así, el presente trabajo se basa en el concepto de Frensch y Funke (1995) denominado
Complex Problem Solving (CPS): “CPS se presenta para superar barreras entre un estado dado
y un deseado estado meta a través de diversas actividades conductuales y/o cognitivas. El
estado dado, estado meta y las barreras que se interponen entre ellos son complejos, cambian
dinámicamente durante la resolución de problemas, y no son transparentes. Al inicio, las
propiedades precisas del estado dado, estado meta y barreras son desconocidas a quien trata
de resolver el problema. CPS implica una interacción eficiente entre el individuo y las
circunstancias de la tarea, y los aspectos cognitivos, emocionales, personales, sociales y
conocimientos que influyen en quien resuelve el problema” (Citado en Santos, 2008, p. 525).
Las nociones que aparecen en la cita anterior: estado dado, estado meta, barreras y
propiedades. En el contexto de nuestro estudio, se interpretan como el problema dado,
encontrar la solución del problema, y dificultades que se presentan en el camino de quien trata
de resolver el problema, respectivamente. Las propiedades, son los atributos y las relaciones
matemáticas involucradas en la situación. Sin embargo, como señala la definición CPS, estos
aspectos no son transparentes a quien trata de resolver el problema al comienzo.
Metodología
El estudio se ubica en una perspectiva cualitativa y de carácter exploratorio. Los participantes
fueron dos estudiantes de ingeniería de 18 años de edad que habían cursado el primer
semestre en una Universidad Pública. Los pupilos trabajaron en pareja y antes de acometer los
problemas fueron expuestos a un periodo de familiarización con el uso de las herramientas de
Geogebra con tareas que involucraban los conocimientos básicos relacionados con los
problemas que abordarían en la experimentación. Para recolectar información, se colocaron
dos cámaras de video. Una se situó al frente de la pareja y la otra enfocó la pantalla de la
computadora que registró la construcción de las figuras usadas para resolver los problemas.
Estas dos vistas permitieron analizar el proceso de manera global y en detalle de los
comportamientos de la pareja. La experimentación fue llevada a cabo en una sola sesión de
dos horas. Los investigadores intervinieron en las situaciones en las que los alumnos se
atoraban mediante la formulación de preguntas, para ayudarlos a salir del atasco.
Problemas usados en el estudio
1. Considere una parábola y encuentre una construcción geométrica que localice el vértice de
la curva
2. Considere una circunferencia C con centro en O y un punto P en ella, y una línea recta L
que no interseca a la circunferencia dada. Construir una circunferencia C’ que sea tangente
a la circunferencia C en el punto P y a la recta L (Tomado de Santos, 2007, p. 214)
XVIII Encuentro de Profesores de Matemáticas
Página 18
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Discusión y resultados
Conocimiento previo: el diámetro de una cónica. La parábola fue dada en la pantalla de la
computadora en una posición “vertical” desprovista de un sistema coordenado. Para resolver
el problema del vértice de la parábola, es necesario conocer la noción de diámetro de una
sección cónica, la cual dice que es una línea recta que pasa por los puntos medios de cualquier
familia de rectas paralelas a una recta dada que interseca a la cónica en dos puntos, dicho
conjunto de paralelas también interseca la curva en dos puntos. La propiedad importante de
estos diámetros de cualquier familia de paralelas a una recta dada cualquiera que interseca la
cónica en dos puntos es que pasan por el centro de la cónica. En el caso particular de la
parábola, el centro está en el punto al infinito, por tanto, los diámetros son paralelos. Uno de
estos diámetros cruza el vértice de dicha curva que constituye el eje de simetría de la curva.
Sin embargo, a los alumnos no se le dio esta definición, se deseaba observar si los alumnos
podrían „descubrir‟ esta propiedad usando las herramientas de Geogebra . A continuación se
describe como la pareja identificó esta propiedad.
La sesión se inició pidiendo a los estudiantes localizar dos puntos A y B en la curva y unirlos
mediante una línea recta. Es importante comentar que la línea antes trazada y los puntos de
intersección A y B con la parábola en el ambiente de Geogebra no son objetos estáticos, por
ejemplo, si se selecciona el punto A ó B y se mueve sobre la curva, la línea AB también se
mueve, en contraste cuando se hace este trazo en medio estático. Una vez que los pupilos
hicieron esta construcción, se les solicitó construir tres paralelas al segmento AB que
intersecaran a la curva. Luego se les pidió encontrar los puntos medios de estos segmentos
paralelos incluyendo el segmento AB usando las herramientas de Geogebra (Figura 1).
Figura 1.
Aquí un instructor, pregunta: ¿Qué observan? La Alumna A responde: “Los puntos medios
siempre van en la misma dirección vertical, van hacia el centro de la parábola, como si
estuvieran alineados…” Instructor: ¿Cómo pueden verificar o mostrar? Alumno B:
“Escogemos dos cualquiera y trazamos una línea que pase por estos puntos, la línea pasará
por los otros puntos” [Lo verifican usando Geogebra]. Posteriormente se les pidió mover toda
la configuración y comentar lo que notaban.
Como ilustración de las figuras que se generaron se presentan las siguientes (Figura 2 y 3).
XVIII Encuentro de Profesores de Matemáticas
Página 19
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 2.
Figura 3.
¿Qué propiedades vieron los alumnos al mover la configuración?
Algunos comentarios de los alumnos fueron:
Alumna A: “Si movemos el punto A todas las rectas siguen siendo paralelas”
Alumno B: “Los puntos medios se mueven y la distancia entre ellos se agranda pero siempre
en la misma dirección. No importa como movamos los puntos, las líneas serán paralelas al
segmento AB”.
Hasta este momento, al parecer la pareja no ha notado que el diámetro se mueve paralelo a sí
mismo, no obstante, que esta propiedad se vea en el monitor. Debido a esto, un instructor
pregunta: ¿Qué otras propiedades pueden observar? Los alumnos no aportan nada nuevo a lo
ya dicho (“Las direcciones van hacia arriba o abajo, etc.,”) [La pareja está moviendo la figura
la cual oscila como si fuera un péndulo que pasa por la forma simétrica] Advirtiendo que la
pareja no muestra un avance, un instructor pregunta: ¿Qué sucede con la línea que pasa a
través de los puntos medios? Alumna A: “Esta línea se mueve así…es como un balanceo”
[Ella usa un lápiz para mostrar el movimiento de vaivén que realiza el diámetro] (Figura 4).
Es importante comentar que el movimiento mencionado si provoca esta percepción, sin
embargo, no „abstraen‟ la propiedad matemática de paralelismo. Bajo la presión del instructor,
la alumna se da cuenta de esta propiedad. “Esta línea [el diámetro] siempre se mueve
paralelamente a sí misma, ah! era tan fácil”.
Figura 4.
XVIII Encuentro de Profesores de Matemáticas
Página 20
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Tarea: Determinar el vértice de la parábola.
Dada la parábola a la pareja se le pidió encontrar un procedimiento para localizar su vértice.
Es importante puntualizar que a los alumnos no se les dijo que utilizaran la noción de
diámetro recién „descubierta‟. En el proceso de resolución de la pareja se identificaron dos
acercamientos.
El primero fue construir un “segmento horizontal” el cual intersecaría la parábola en dos
puntos opuestos [simétricos]. Si lograban esta construcción, el siguiente paso sería obtener el
punto medio de este segmento y luego trazar una perpendicular a dicho segmento por este
punto medio. Conjeturaban que esta perpendicular intersecaría la parábola precisamente en el
vértice. Sin embargo, esta no podía prosperar ya que para construirla necesitan precisamente
un diámetro. No se intuye que sea posible hacer esta construcción sin usarlo, además esta
„horizontalidad‟ requiere un referente y no se tiene, excepto si se introduce un sistema
coordenado rectangular, pero el problema demanda una construcción geométrica no analítica.
El segundo acercamiento involucró trazar un diámetro, esto les permitió resolver el problema.
Enseguida se describen dichos acercamientos.
Primer acercamiento: Construir un „segmento horizontal‟.
La alumna A dice: “Necesitamos una línea que sea horizontal” [Usa el lápiz como un
„segmento‟ y lo coloca en una posición horizontal] (Figura 5).
Alumno B: “Primero necesitamos trazar dos puntos”
Alumna A: “Pero estos dos puntos debe ser una línea con pendiente cero… ¿Cómo saber que
los puntos están a la misma distancia? [Con respecto al punto medio del segmento horizontal].
La pareja hizo intentos para construir dicho segmento, pero no funcionó (Figura 5). Los
siguientes comentarios indican este dilema: “Los puntos A y B deben estar en un segmento
que no esté inclinado sino que sea horizontal… Si conseguimos esto podemos encontrar el
punto medio y construir una perpendicular por este punto, luego conseguimos el vértice de la
parábola”. Ante esta dificultad, el alumno B sugiere otras construcciones: “¿Por qué no
trazamos un cuadrado o un círculo?” Estos intentos tampoco funcionaron.
Segundo acercamiento: Construir un diámetro
El alumno B sugiere introducir un sistema coordenado. Esta inclusión provocó que la alumna
A evocara la noción de diámetro que la permitió intuir la idea de la solución, pero expresada
no muy claramente: “Ajá, ¿sabemos lo que vamos hacer? Esta línea [señala el eje y] era la
que obteníamos cuando sacábamos diferentes puntos medios, teniendo esta línea [el
diámetro] ya podemos trazar una perpendicular a esta línea [al diámetro], y esta siempre va
ser perpendicular; y ya podemos trazar el punto medio, ¿si me entiendes?” El alumno dice
que „si‟, pero no muy convencido. A continuación se explica como la pareja llegó a la
solución. La pareja trazó dos rectas paralelas AB y CD que intersecan la parábola y sus puntos
medios y una línea que pasa por dichos puntos medios [el diámetro], luego trazaron una
perpendicular a este diámetro, la cual pasa por el punto de intersección entre el diámetro y el
segmento AB. Sin embargo, cuando movieron uno de los puntos libres A ó B, toda la
configuración se les movió (Figura 6), excepto que la perpendicularidad entre el diámetro y la
línea perpendicular antes trazada a dicho diámetro se mantiene. Notando esto, la alumna A
XVIII Encuentro de Profesores de Matemáticas
Página 21
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
dice: “Aunque los puntos estén en diagonal [Puntos A y B] estas líneas siempre son
perpendiculares”. Es decir, el diámetro se mueve. Por tanto, se enfrentan con el problema de
construir un diámetro que esté fijo e interseque la parábola en el vértice. Esta dificultad la
expresa la alumna A: “Esta línea [diámetro] debe permanecer fija, pero si movemos este
punto todo se va a mover, bueno al menos sabemos que estas líneas siempre son
perpendiculares. Para que permanezca fija, estas distancias tienen que ser la misma” [los
puntos opuestos de intersección entre la perpendicular y la curva respecto al diámetro].
Debido a este escollo, los alumnos intentan otro camino que los aleja momentáneamente de la
estrategia anterior. Este consistió en tratar de construir una tangente „horizontal‟, pero no
funcionó, ya que asumen que dicha tangente pasa por el vértice de la curva, que es
precisamente la cuestión por resolver. Ante este fracaso, la pareja regresa a la situación
anterior (“aquí íbamos”) (Figura 6). Empiezan a mover de nuevo la configuración.
Figura 5.
Figura 6.
En este contexto, los alumnos se percataron de que los puntos de intersección entre la
perpendicular que trazaron al diámetro y la parábola, son puntos extremos de un segmento
que siempre permanece „horizontal‟, independientemente del movimiento de la configuración.
Observando esta propiedad, se ilumina en la alumna A la solución del problema: “¡Ya está!
Tenemos que encontrar el punto medio de este segmento, y luego trazar una perpendicular
que pase por este punto que pasará por el vértice” [Usan las herramientas de Geogebra y
comprueban que la idea funciona] (Figura 7).
Figura 7.
XVIII Encuentro de Profesores de Matemáticas
Página 22
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
La tarea: Construir una circunferencia tangente a una circunferencia dada en punto P y
a una línea recta que no interseca a la circunferencia dada.
Los conocimientos requeridos para resolver este problema son: perpendicularidad,
propiedades de la tangencia entre dos circunferencias, las tangentes trazadas desde un punto
exterior a una circunferencia tienen la misma longitud y la bisectriz de un ángulo. Estas
nociones fueron vistas en el periodo de familiarización con las herramientas de Geogebra,
excepto que no se explicitó una propiedad que fue relevante en la resolución del problema, a
saber, que la línea que une los centros de dos circunferencias tangentes pasa por dicho punto
de tangencia, quizás por suponer que era una intuición obvia que debían tener los alumnos.
Sin embargo, esto no fue así, la alumna A, reveló que no tenía esta intuición. Esta deficiencia
ocasionó dificultades en la solución del problema, pero fueron superadas por la interacción
con las herramientas y las intervenciones de los instructores. Procedemos a describir los
acercamientos de la pareja.
Primer acercamiento: El centro se localiza en la prolongación del radio.
La pareja intuyó que el centro de la circunferencia buscada podría encontrarse en la
prolongación de la línea OP (radio) , lo cual es cierto, pero veamos lo que sucedió. La pareja
prolongó dicha línea hasta intersecar la recta L denotada por S (Figura 8).
Figura 8.
Luego obtuvieron el punto medio (M) de PS y trazaron una circunferencia con centro en M y
radio igual a MP, sin embargo, la circunferencia cortó la línea L en dos puntos. Debido a este
fracaso, la pareja descartó la posibilidad de que el centro se localizaba en la prolongación de
OP (“Esta línea no nos sirve”, alumna A) Así, desechó esta línea como parte de la solución.
Enseguida se explican otros acercamientos
Segundo Acercamiento: El centro se encuentra en una región del plano limitada por la
circunferencia y la recta L.
La alumna A dice: “tiene que estar en esta parte”. Trazan una paralela a la recta L que pase
por P y bajan una perpendicular PH desde este punto a la recta L (H es el pie de la
perpendicular). Para situar el centro dentro de esta región, trazan otra paralela a la recta L que
pasa por el punto medio del segmento PH. Luego toman un punto móvil sobre la paralela, el
XVIII Encuentro de Profesores de Matemáticas
Página 23
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
cual se supone es un centro de la circunferencia buscada, pero al trazar una circunferencia que
pasa por P, esta corta a la recta L en dos puntos (“si haces esto, tocará a L en dos puntos”,
alumna A). Después de otros intentos que tampoco funcionan, interviene un instructor: ¿Qué
significa que la circunferencia que andan buscando sea tangente a la circunferencia dada en el
punto P? [Esta pregunta intenta que la pareja regrese a considerar que el centro debe estar
situado en la prolongación de OP]. Como la pareja no se orienta en esta dirección, el
instructor insiste: ¿Cómo es la tangente en el punto P respecto al radio OP? La alumna A,
responde: “es perpendicular al radio”, sin embargo, tiene dudas que esta propiedad sea cierta
también para la circunferencia buscada (“Tiene que ser perpendicular al otro radio, ¿crees?”).
Tercer acercamiento: El regreso a la prolongación de la línea OP
Observando la configuración (Figura 9), la alumna A dice: “Esta línea [la tangente en P] es
perpendicular a OP, tiene que ser perpendicular al otro radio, aunque no esté [el punto P]
exactamente sobre la línea OP” [subrayado nuestro].
Aquí se nota que la alumna no ve que el punto P de tangencia de las dos circunferencias y el
centro de tales circunferencias están en una misma línea recta.
Figura 9.
No obstante, acepta que la tangente en P es perpendicular a ambos radios, resulta
contradictorio que no acepte que dicho punto pertenezca a la línea que une los centros. Esta
misconception también se manifiesta en los episodios: “El otro radio también tiene que ser
perpendicular a esta línea [la tangente en P], pero en esta [la circunferencia buscada] el centro
lo necesitamos por aquí, aunque no esté exactamente sobre el segmento OP” [subrayado
nuestro].
Este „error‟ tiene una explicación: La pareja anteriormente había rechazado la posibilidad de
que el centro se localizaba sobre la línea OP debido a que no les funcionó. Por tanto, esta idea
estaba descartada. Por ello, dice: “Cómo le hacemos, el punto medio no sirve”. Ante este
dilema, un instructor pregunta: “Entonces dónde debería estar el centro? El alumno B
basándose en la figura anterior, comenta: “Sobre esta línea [La prolongación de OP] Sin
embargo, la alumna A está en desacuerdo por lo explicado anteriormente: “Sobre esta línea
[prolongación de OP] no puede estar”. Aquí el instructor aprovecha esta afirmación para
interrogar a la alumna: “¿Por qué el centro no debería estar sobre esta línea?” La alumna
intenta dar una explicación de porqué no puede estar pero muestra dificultades para hacerlo y
no termina su explicación: “Porque si está sobre esta línea…” En este momento recapacita y
XVIII Encuentro de Profesores de Matemáticas
Página 24
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
expresa: “¡Ah!, Puede que si esté sobre esta línea” y la misconception es superada: “De hecho
este radio [el buscado] tiene que estar sobre esta línea OP”.
Una vez que se dieron cuenta que el centro debe estar sobre la línea OP (“El centro si tiene
que estar sobre esta línea, pero el punto medio entre P y la recta L, no sirve, ahora lo que
necesitamos es saber a qué distancia”) Explorando con las herramientas de Geogebra toman
un punto cualquiera sobre la prolongación de OP y generan un circunferencia que visualmente
satisface las condiciones del problema (Figura 10).
Figura 10.
Basados en esto, el procedimiento emerge: Con las herramientas de Geogebra trazan un
segmento GH sobre la línea L que tiene la misma longitud que la tangente PG (P es el punto
sobre la circunferencia dada y G es la intersección con la recta L). Unen los puntos P y H,
después obtienen su punto medio. Luego trazan la línea que va desde el punto G a este punto
medio. La prolongación de esta línea interseca la prolongación de OP- el cual es
precisamente el centro buscado-Tomando como centro este punto de intersección y radio PH,
la circunferencia toca a la recta L en el punto H. La idea esencial de esta construcción, fue el
trazo de un triángulo isósceles cuyos lados iguales son el PG y GH, el otro lado PH les sirvió
para obtener el punto medio. Así, trazando la línea desde G y que pasa por este punto
interseca la prolongación de OP en centro de la circunferencia. Observe que la solución
encontrada, no se menciona explícitamente que la línea que interseca la prolongación de OP
en el centro buscado es la bisectriz del ángulo PGH. Notando esto, un instructor les pregunta:
Esa línea que interseca la prolongación de OP, ¿Cómo se llama? Pero, no la reconocieron.
Conclusiones
Las evidencias obtenidas en este estudio muestran que la interacción de los alumnos con las
herramientas de Geogebra ayudó a entender las ideas matemáticas y promover competencias
en la resolución de los problemas. Por ejemplo, las propiedades y relaciones involucradas las
cuales son relevantes para la solución, que al inicio no eran transparentes, la manipulación
con los objetos matemáticos permitió que dichas propiedades y relaciones se hicieran
evidentes. Así, los alumnos fueron capaces de alcanzar el „estado meta‟. También, lograron
superar sus misconceptions y dificultades. Sin embargo, debemos señalar que la formulación
de preguntas y la presión de los instructores jugaron un papel importante en el avance y la
salida de los atascos de los alumnos. Basándonos en estos resultados, creemos que los
ambientes virtuales tienen potencial para favorecer las capacidades de los pupilos en
XVIII Encuentro de Profesores de Matemáticas
Página 25
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
resolución de problemas, no obstante, no debe verse como contrapuestos con el de papel y
lápiz, sino combinarlos para potenciar el entendimiento de las matemáticas.
Referencias
Santos-Trigo, M. (2007) Mathematical problem solving: an evolving research and practice
domain. In ZDM-The International Journal on Mathematics Education. (pp. 523-536).
Springer Berlin/Heidelberg.
Santos-Trigo, M., H. Espinoza and A. Reyes. (2006) constructing a parabola‟s world using
dynamic software to explore properties an meaning. International Journal for
Technology in Mathematics Education,vol. 12.
Santos-Trigo, M. et al (2003) Student‟s use of technology in mathematical problem solving:
Transforming technological artifacts into mathematical tools, in N.A. Pteman, B. J.
Doughherty and J. Zilliox (eds.). Proceedings of the 2003 Joint meeting of PME and
PMENA,Vol. 4. Honolulu, Hawaii.
Santos-Trigo, M. & Espinosa-Pérez, H. (2002) Searching and exploring properties of
geometric configurations via the use of dynamic software. International Journal of
Mathematical Education in Science and Technology, 33(1), 37-50.
Schoenfeld, A. H. (1985). Mathematical Problem Solving. New York: Academic Press.
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition
and sense making in mathematics. In: D. A. Grows (Ed.) Handbook of research on
mathematics teaching and learning (pp. 334-370). NY: Macmillan.
Schoenfeld, A. H. (1998). Reflections on a course in mathematical problem solving. In: A. H.
Schoenfeld, J. Kaput, & E. Dubinsky (Eds.), Research in Collegiate Mathematics
Education III (pp.81-113). Washington, D. C: American Mathematical Society.
XVIII Encuentro de Profesores de Matemáticas
Página 26
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
La relación entre conocimiento conceptual y la habilidad para usarlo en la
resolución de problemas: experiencias con profesores
de nivel medio superior
Dr. César Cristóbal Escalante
Dra. Verónica Vargas Alejo,
[email protected]
[email protected]
Universidad de Quintana Roo
Resumen
Las actividades de instrucción para desarrollar competencia matemática requieren de
ambientes y dinámicas de trabajo que involucren activamente a los estudiantes y al profesor, y
al uso variado de recursos y formas de comunicar y representar las ideas. ¿Qué experiencias y
competencias deben adquirir los profesores para seleccionar, organizar y administrar las
secuencias de instrucción que deben seguir los estudiantes para desarrollar los conocimientos
y habilidades que integran esas competencias? ¿Cómo deben ser capacitados los profesores y
como deben ser formados los futuros profesores de matemáticas para participar en el
desarrollo e implementación de la nueva currícula? Se describen aspectos sobre la relación
que guarda el desarrollo del conocimiento conceptual y el de la habilidad para resolver
problemas que exhiben profesores del nivel medio superior.
Introducción
La Reforma Integral de la Educación Media Superior (RIEMS) se plantea mejorar la
formación que adquieren los egresados y estudiantes de este ciclo. Los documentos de la
RIEMS (SEP, 2009) señalan como ejes de la reforma el Marco Curricular Común basado en
Competencias (que son la integración de habilidades, conocimientos y actitudes en un
contexto específico), los Mecanismos de Gestión (que involucra la formación y el perfil de
los profesores, y el tipo de organización e instalaciones, que se requieren para llevarla a cabo),
y la Certificación complementaria del SNB (que señala la posible evaluación de los egresados
para constatar la adquisición del perfil básico).
La RIEMS ha establecido once Competencias: Genéricas (comunes a cualquier egresado del
NMS, que son transversales y útiles para desarrollar otras), y Disciplinares Básicas
(obligatorias para toda la EMS).
Las Competencias Disciplinares para Matemáticas (SEP, 2009. Acuerdo 444. DOF) son las
siguientes:
1. Construye e interpreta modelos matemáticos mediante la aplicación de
procedimientos aritméticos, algebraicos, geométricos y variacionales, para la
comprensión y análisis de situaciones reales, hipotéticas o formales.
2 Formula y resuelve problemas matemáticos, aplicando diferentes enfoques.
3. Explica e interpreta los resultados obtenidos mediante procedimientos matemáticos
y los contrasta con modelos establecidos o situaciones reales.
4. Argumenta la solución obtenida de un problema, con métodos numéricos, gráficos,
analíticos o variacionales, mediante el lenguaje verbal, matemático y el uso de las
tecnologías de la información y la comunicación.
XVIII Encuentro de Profesores de Matemáticas
Página 27
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
5. Analiza las relaciones entre dos o más variables de un proceso social o natural
para determinar o estimar su comportamiento.
6. Cuantifica, representa y contrasta experimental o matemáticamente las magnitudes
del espacio y las propiedades físicas de los objetos que lo rodean.
7. Elige un enfoque determinista o uno aleatorio para el estudio de un proceso o
fenómeno, y argumenta su pertinencia.
8. Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y
científicos.
¿Cómo se reflejan estas competencias en las actividades docentes? ¿Qué tipo de actividades
de aprendizaje deben realizar los estudiantes para desarrollarlas? ¿Qué criterios deben utilizar
los profesores para seleccionar las actividades de aprendizaje? ¿Qué experiencias y
competencias deben adquirir los profesores para seleccionar, organizar y administrar las
secuencias de instrucción que deben seguir los estudiantes para desarrollar los conocimientos
y habilidades que integran esas competencias? ¿Cómo deben ser capacitados los profesores y
como deben ser formados los futuros profesores de matemáticas para participar en el
desarrollo e implementación de la nueva currícula? Son el tipo de preguntas que deben ser
respondidas en aras de llevar por buen camino esta reforma.
Esta investigación explora aspectos relacionados con las experiencias y competencias
matemáticas que deben adquirir los profesores para realizar sus funciones docentes. Estamos
interesados en caracterizar la relación que existe entre el desarrollo de conocimiento de
conceptos y el desarrollo de las habilidades para utilizarlos en el análisis de situaciones
semejantes a las reales. Llegar a tener una comprensión amplia y profunda del conocimiento
matemático que requieren los profesores para enseñar, y de cómo pueden desarrollarlo de
manera que les sea útil, requiere de una investigación sistemática y disciplinada. En este
sentido son pertinentes plantearnos preguntas del tipo: ¿Cómo las diferentes experiencias
matemáticas que tiene un profesor inciden en lo que conocen y pueden utilizar en el aula?
¿Cómo su comprensión de las matemáticas afecta su desempeño como profesor? ¿Qué tipos
de problemas matemáticos debe poder resolver con la formación adquirida? Presentamos aquí
algunos avances realizados, mismos que han servido para ir afinando la metodología y los
criterios de análisis.
Marco Teórico
En general se está de acuerdo en que aprender matemáticas va más allá de memorizar
definiciones, propiedades de conceptos y de realizar procedimientos de cálculo. Aprender
matemáticas implica desarrollar competencia matemática, que significa mostrar comprensión
conceptual, manejo fluido de procedimientos, competencia estratégica, capacidad de
razonamiento flexible, disposición productiva (Kilpatrick, 2002). En otras palabras, y de
acuerdo con Lesh y Doerr (2000), significa tener capacidad para desarrollar modelos o
sistemas conceptuales inmersos en una variedad de sistemas de representación, que les
permitan comprender y explicar los fenómenos y procesos de la vida cotidiana. Schoenfeld
(2006) considera que una persona con competencia matemática se caracteriza por ser hábil
para resolver problemas en contextos nuevos, diferentes a los contextos en los que aprendió,
es decir, es una persona capaz de transferir los conocimientos adquiridos. Es una persona
competente en matemáticas porque dispone de un sólido conocimiento base, dispone de
estrategias productivas para solucionar problemas, utiliza adecuadamente esas estrategias y el
XVIII Encuentro de Profesores de Matemáticas
Página 28
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
conocimiento de que dispone, posee un conjunto de valores y creencias positivas sobre sí
mismo y sobre la actividad matemática.
Se reconoce que las actividades de resolución de problemas son importantes para que los
estudiantes desarrollen o construyan su conocimiento matemático, pues propician que ellos
practiquen y valoren procesos que involucran la formulación de preguntas, la búsqueda de
relaciones matemáticas, el uso de diferentes formas de representación, la utilización de varios
argumentos para apoyar conjeturas y la comunicación de resultados (Schoenfeld 1985),
propiciando la transformación del aula en una comunidad de aprendizaje. Desarrollar en los
estudiantes la habilidad para resolver problemas es, y ha sido, uno de los objetivos de la
instrucción matemática.
Los conocimientos, habilidades, valores y actitudes que tiene los profesores sobre las
matemáticas inciden en la selección, en la organización, en el desarrollo y en la
instrumentación de las actividades de instrucción y sobre el desempeño de los estudiantes
(Hill, Rowan, Ball, 2005).
¿Qué debe aprender primero una persona? ¿Los conceptos? ¿Las habilidades? ¿Pueden
aprenderse los conceptos y las habilidades para resolver problemas, en forma paralela?
Muchos de los profesores que participan en la reforma han adquirido sus conocimientos
matemáticos en programas elaborados sobre la base de desarrollar primero conocimiento
sobre los conceptos, los procesos y las estrategias para resolver problemas, y posteriormente
generar las habilidades para enfrentar los problemas y obtener la solución.
Lesh y Doerr (2003) señalan que el proceso de aprendizaje de conceptos se realiza
considerando varias dimensiones tales como de lo particular a lo general, de lo abstracto a lo
concreto, situado a lo descontextualizado, de lo intuitivo a lo analítico y a lo axiomático, de lo
burdo a lo refinado, y que este proceso involucra fases de diferenciación, de integración y de
refinamiento de los conceptos y de sus relaciones con otros conceptos, en el marco de
desarrollar sistemas conceptuales para describir y explicar situaciones. En este sentido, para
ellos el conocimiento de los conceptos no sigue un proceso lineal, más bien un proceso que
sigue varias direcciones y discontinuidades, con retrocesos en algunas direcciones y avances
en otros, sujeto a las experiencias que tenga la persona y que le lleven a considerar los
sistemas conceptuales previamente desarrollados.
Método
Los casos que se presentan han sido recopilados en el contexto de cursos de matemáticas para
actualización y para formación de profesores de matemáticas del nivel medio superior, que he
impartido desde 2006 a la fecha. Estos cursos tenían como propósito mejorar la comprensión
y la habilidad matemática de los participantes. La instrucción se basó en la resolución de
problemas, la mayoría de los cuales no tenía solución única. Los contextos en los problemas
fueron situaciones sobre poblaciones, créditos, concentraciones, desplazamiento, cálculo de
volúmenes y estudio de mezclas. Al resolverlos los estudiantes podían usar computadoras,
calculadoras, o cualquier otro recurso. Cada problema se trabajó en tres fases: manera
individual, en parejas, y con exposiciones de las parejas ante el grupo completo. Los
estudiantes realizaban sus aproximaciones en la computadora o en sus cuadernos, y
elaboraban reportes individuales en cada fase, estos productos fueron recopilados. Al final del
curso entregaban un reporte individual, semejante a un “portafolio de trabajo”. Esto permitió
contrastar las aproximaciones que cada participante realizó al problema, y observar la forma
XVIII Encuentro de Profesores de Matemáticas
Página 29
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
en que evolucionó su comprensión del problema, los conceptos matemáticos utilizados y su
comprensión y la forma en que los relaciona con la situación.
Análisis de casos
Cisterna
Un granjero desea construir una cisterna para almacenar agua. Ha estimado que una
cisterna de N metros cúbicos de volumen, es más que suficiente para cubrir sus necesidades
durante un largo período. Decidió que el depósito no tendrá tapa, que la base y las paredes
serán de concreto y tendrán un grosor de g cms. Debe seleccionar la forma de la base:
circular o cuadrada. ¿Qué opción debe tomar el granjero si desea minimizar la cantidad de
concreto utilizada en la construcción de la cisterna? ¿Qué dimensiones debe tener la
cisterna?
Esta actividad tuvo como propósito que los estudiantes utilizaran conceptos y procedimientos
matemáticos relacionados con las funciones, a la vez de estrategias y procesos
experimentados en las actividades anteriores.
El problema base de la actividad demanda del alumno la identificación espacial de cuerpos
tridimensionales (las paredes de las cisternas), de sus dimensiones, de las relaciones
necesarias para determinar su volumen y de percibir la dependencia funcional del volumen de
este cuerpo en cada caso, de dimensiones variables y del uso de procesos y criterios para
determinar las dimensiones donde el volumen de estos cuerpos sean el menor posible,
manteniendo la condición de encerrar un volumen dado.
En cada caso, deben establecer el volumen de las paredes del depósito partiendo de las
dimensiones del cuerpo y de la condición inicial de que el volumen del depósito debe ser
igual a N unidades cúbicas.
Desarrollo de la actividad
Las primeras aproximaciones al problema, muestran acciones exploratorias asociadas al
proceso de comprensión del problema.
XVIII Encuentro de Profesores de Matemáticas
Página 30
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Sitación
Problema
Identificación de relaciones entre los
datos y la geometría del problema
Exploración de casos numéricos
particulares (volumen interior y
grosor dados) para cada situación
Determinación del volumen de la pared
como función de las dimensiones y del
volumen interno de cada cisterna
Determinación de las dimensiones
de la cisterna cuyas paredes
tienen el menor volumen y
encierran el volumen interior
dado para cada caso con datos
numéricos particulares
Determinación de las dimensiones de la
cisterna cuyas paredes tienen el menor
volumen, pero con el volumen interior
dado
Comparación de los volúmenes
de las paredes obtenidos en
cada caso
Elección de
conveniente
Comparación de las expresiones para el
menor volumen de las paredes obtenidas en
cada caso
la
opción
más
Algunos elaboraron dibujos para explorar la situación (fig. 1, 2, 3, 4), otros no lo hacen. En
algunos casos resaltan en el dibujo el grosor de las paredes (Figura 3 y 4) y escriben las
fórmulas para determinar el área del cuadrado y el círculo, el volumen de un cubo y de un
cilindro. Julia considera valores particulares para el lado y altura del prisma de base cuadrada
y del cilindro. Sin determinar o expresar la cantidad de concreto necesaria en la construcción
de las paredes de la cisterna (Figuras 1 y 2).
XVIII Encuentro de Profesores de Matemáticas
Página 31
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 1. Fragmento del reporte de G después del trabajo individual.
Figura 2. Fragmento del reporte de J después del trabajo individual.
D, mediante el dibujo de la cisterna cuadrada y de su base, expresó el área de la base de las
paredes de concreto, como la diferencia entre el área externa (que denomina área total) y la
interna. No obtiene el volumen de las paredes multiplicando esta área de la base de las
paredes por la altura, sino lo hace considerando los dos prismas separadamente (el externo y
el interno), restando del volumen exterior (que denomina total) el volumen interno de la
cisterna (Figura 3). Hace esto para ambas formas. Este procedimiento lleva a expresar el
XVIII Encuentro de Profesores de Matemáticas
Página 32
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
volumen de las paredes de la cisterna como una función del lado de la base y de la altura, en
forma directa.
Figura 3. Fragmento del reporte de D después del trabajo individual.
F (Figura 4) utilizó el área de las paredes internas de las cisternas como elemento de
comparación para decidir cuál es la que usa menor material. Expresó estas áreas como función
del lado y la altura en un caso, y del radio y la altura en el otro. Identificó este problema
como determinar los extremos de una función de dos variables sujeta a una restricción. En la
representación algebraica de esta situación, exhibe elementos que llevan a suponer utilizará el
método de los multiplicadores de Lagrange (ver los últimos renglones de la Figura 4). No va
más allá en esta fase de trabajo.
XVIII Encuentro de Profesores de Matemáticas
Página 33
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 4. Fragmento del reporte de F después del trabajo individual.
B (Figura 5) realizó algo semejante a F, sólo que utilizó el hecho de que el volumen interno
de la cisterna es conocido, para despejar una de las dos variables y la sustituye en la función
del área, transformándola así en una función de una sola variable. Esto lo hace para cada tipo
de cisterna. A continuación empleó la derivada para determinar el valor de la variable para el
cual la función área toma el menor valor. No va más allá en esta fase.
Ambas aproximaciones usaron el área de la superficie interna de las paredes en lugar de
considerar su volumen.
XVIII Encuentro de Profesores de Matemáticas
Página 34
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 5. Fragmento del reporte de B después del trabajo individual.
En la fase de trabajo individual, sólo tres estudiantes (B, F e I) mostraron un nivel de
compresión del problema que los lleva a identificar que para obtener la solución deben
determinar las dimensiones de cada cisterna, de manera que tengan el volumen establecido,
pero en la cual se utilice la menor cantidad de volumen de concreto en cada caso, si es de base
cuadrada o circular. Muestran que deben obtener esa información como parte esencial para
alcanzar la respuesta a la pregunta del problema.
B y D trabajan juntos el problema y continúan con lo realizado por B (Figura 6), quien utilizó
el área interior de cada cisterna y la expresó como una función del lado de la base, en un caso,
y del radio de la base, en el otro.
XVIII Encuentro de Profesores de Matemáticas
Página 35
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Para poder comparar las dos opciones, minimizaremos la superficie que contiene
cada cisterna o tinaco.
Para el caso en que tenga la base cuadrada, el volumen viene dado por la expresión
x2y = N, donde x es el lado del cuadrado de la base, y y es la altura. La superficie del
tinaco es x2 + 4xy; entonces si despejamos y de la fórmula del volumen nos queda
y=N/x2 y si sustituimos en la expresión de la superficie nos queda:
S = x2 + 4·N/x.
Para minimizar la superficie sacamos la derivada de S y la igualamos a cero.
Entonces:
S‟ = 2x -4N/x2; haciendo el quebrado nos da: (2x3 -4N)/x2. Si igualamos a cero y
despejamos nos queda: x = (2N)1/3, el cual es nuestro punto crítico. Si sacamos la
segunda derivada nos queda (x2(6x2)- 2x(2x3 -4N))/x4 , que reduciéndola nos da :
(6x4 – 4x4 +8xN)/x4 que es igual a 2 + 8N/x3 si sustituimos el valor de x en este
resultado nos queda: 2+ 8N/2N = 6 > 0, por lo tanto es un mínimo. Si sustituimos x
en la ecuación de la superficie nos da (2N)2/3 + 4N/(2N)1/3
Para el caso del tinaco de base circular, el volumen está dado por ∏r2·h =N y su
superficie viene dada por la expresión ∏r2 +2r∏·h. Si despejamos h de la fórmula del
volumen, nos queda h= N/∏r2, y si sustituimos esta expresión en la fórmula de la
superficie nos queda: S = ∏r2 +2r∏· N/∏r2 =∏r2 + 2N/r. Si derivamos e igualamos a
cero nos da:
S‟ = 2∏r -2N/r2 que si hacemos el quebrado nos da (2∏r3 -2N)/r2 ; si igualamos a
cero y despejamos r nos da (N/∏)1/3
Si sacamos la segunda derivada obtenemos:
S”= 2∏ +4N/r3 si sustituimos el valor de r, observamos que es mayor que cero, por lo
que es un mínimo. Sustituyendo r en la expresión para superficie nos da:
S = ∏(N/∏)2/3 + 2N/( N/∏)1/3, la cual si la simplificamos nos da S = 3∏1/3N2/3
Si simplificamos la expresión de superficie para el tinaco de base cuadrada, nos
queda: 3·41/3N2/3. si comparamos esta expresión con la del tinaco de base
circular, nos queda que 41/3 > ∏1/3, por lo que se gasta más en el material que
forra al tinaco si se usa el de base cuadrada.
Por lo tanto, conviene el tinaco cilíndrico, que al multiplicarlo por los g cms., del
espesor de la pared de concreto, se convertiría en volumen, que de todas maneras es
menor que el de base cuadrada.
Figura 6. Reporte de la pareja formada por los estudiantes B y D.
En esta fase, complementaron lo realizado por B utilizando el criterio de la segunda derivada
para determinar los valores de cada variable (lado o radio) en los que la función que expresa
el área interior de cada cisterna tiene un extremo. Identificaron un solo valor y que el extremo
de la función es un mínimo. Determinaron el valor que toma cada función para los valores
críticos de la variable independiente y los compararon, concluyendo que la opción que usa
menor material es la cisterna de base circular (Figura 6). La forma en que D pretendía
determinar el volumen de las paredes de la cisterna durante la fase de trabajo individual
XVIII Encuentro de Profesores de Matemáticas
Página 36
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
(basada en considerar las diferencias entre el volumen total y el interno) no fue utilizada por
ellos. Predominó la aproximación de B.
Figura 7. Fragmento del reporte de la pareja F e I.
Durante la exposición ante el grupo de la pareja que utilizó Multiplicadores de Lagrange, C
pidió le explicaran el método utilizado por ellos. Durante este intercambio, I mostró que su
conocimiento del método le permitía utilizarlo, pero no logró hacer una explicación
convincente del mismo. Esto se muestra en el segmento de la transcripción de la exposición
en el grupo en esta actividad, que se muestra a continuación (Figura 8):
XVIII Encuentro de Profesores de Matemáticas
Página 37
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Celia: ¿De dónde sacaste L … ?
Inés: ¿L?
Celia: L.
Inés: L así se define, este es el método que se llama eh… multiplicadores de
Lagrange. Yo ya no me acuerdo la verdad este, …. tengo la idea de cómo se
sustenta en el cálculo, en el calculo diferencial de varias variables. Pero aquí se
puede… que hay que dar la… (no se entiende). La verdad no, yo me acuerdo que los
chavos en estadística, para minimizar o maximizar funciones, sujetas a una
restricción que era también una función y además minimizar funciones de varias
variables que es interesante,
Fidel: Y no lineales ¿te acuerdas?
Inés: Y no necesariamente lineales.
Celia: O sea, L ya venia, ya viene dada.
Inés: L así se define.
Celia: ¿Así se define?
Fidel: Así se define.
Inés: Yo creo que si … sanalizamos un poco… este… este asunto de qué son las
derivadas en superficie, entonces veríamos porque la cuestión es así. Pero así
ahorita, te digo, no me acuerdo.
I: … ¿qué significaría obtener un extremo por ejemplo de una función en una
variable sujeta a restricciones? ¿Cuáles podrían ser las restricciones? O sea,
simplemente cuando tú te preguntas sobre cuál es el mayor valor que toma una
función donde tú acotas algo ¿no? o sea.
Inés: Por
función y
casa, esta
telarañas.
posible.
ejemplo en dos variables, perdón en una variable, que tuviéramos esta
esta función representa por ejemplo estén…pues el gasto, el gasto de mi
es la función gasto ¿no? … Gasto y pues ya tenemos dudas y u… unas
… Bueno, pues a mi me gustaría pues gastar lo más posible o lo menos
Celia: Lo menos ¿no?
Inés: O que sé yo… pero tengo restricciones ¿no? y pues este a lo mejor só lo mi
sueldo, pues este, entonces ¿cuál es el máximo que puedo gastar? No más hasta
aquí. Este, aunque teóricamente si hago la derivada pues el máximo del gasto.
Tengo una restricción, pues ya no resulta. Y acá por cierto la restricción es un
plano.
Celia: No dice nada tampoco.
I: Si está en dos variables ¿a qué, a qué se estaría refiriendo?
Inés: Sería, bueno es que yo me imagino que es como una, una superficie así y
tienes otra, porque esta es otra superficie, que esta pues por ahí la intercepta o algo
y tienes que encontrar el máximo o el mínimo que no se salga de él, aquí de hecho
es que tengo a Lupita ahí.
Figura 8. Segmento de la explicación dada por I a C. Transcripción del audio de
exposición en el grupo.
En la exposición ante el grupo se discutió en torno a la forma de obtener la cantidad de
concreto. Durante la presentación de I (Figura 9a), el instructor pide que piensen en extender
la pared del cilindro y señalen las dimensiones del mismo, para determinar su volumen. B
observa que las longitudes correspondientes a las bases son diferentes. Por lo que el volumen
no se obtiene multiplicando el área interior por el grosor. En un momento posterior, D, quien
había considerado una forma de obtener el volumen de las paredes, lo manifestó ante el grupo
(Figura 9b).
XVIII Encuentro de Profesores de Matemáticas
Página 38
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Inés: Entonces, lo que tienen que hacer es encontrar la expresión de la superficie lateral
de cada tinaco y ver para el que la dimensión es mínima, del que tiene la superficie
lateral mínima, pues la menor de todas de ellas. Y ese va a ser el que contenga el
volumen… el mismo volumen ¿si? Y va con el supuesto de que si tiene una superficie
lateral mínima, entonces, con el grosor va ser el mismo. El volumen de este elemento
que se requiera va ser también mínimo. Bueno.
Instructor. Entonces ¿el volumen de las paredes de las cisternas se obtiene
multiplicando el área lateral por el grosor?
Inés: Si, …, si.
Instructor. ¿Qué sucede si cortan la pared verticalmente? Así. Y luego lo estiran.
¿Cuánto miden estos lados?
Bruno: Una es mayor porque el radio es mayor. … no nos da el volumen.
Inés: Pero no importa, Pues aquí ya no hicimos la pregunta que preguntábamos. O sea,
¿cuál es el que te conviene? o sea, ¿conviene el…?
Figura 9 a. Segmento de la transcripción del audio de la exposición ante el
grupo.
Dora: Yo había propuesto de manera individual pues no había visto el área del concreto,
que el había… del área total, área interior y lo mismo hice con el volumen.
Celia: ¿El área total menos el área interior?
Dora: O sea ya, digamos el contenedor menos el tinaco. …Contemplo dos alturas. …
Entonces, para ver el área, como yo lo había empezado a plantear por medio del
concreto, porque era lo que queríamos…
Inés: O sea, consideraste los radios y las alturas y capacidades …
Dora: Y todo eso. Que bueno no, no realmente, no terminé pero no…
Figura 9b. Segmento de la transcripción del audio de la exposición ante el grupo.
Aunque los estudiantes identificaron que el volumen de las paredes no era igual al producto
de la superficie interior por el grosor, observaron que considerar la superficie interior lleva
también a obtener la respuesta al problema (Figura 9a).
El estudiante B (Figura 10) resolvió el problema usando las dos aproximaciones y encontró
que ambas llevan a los mismos resultados, aunque hace la observación que el hecho de no
considerar el grosor en el procedimiento basado en el área, puede llevar a resultados
incorrectos.
XVIII Encuentro de Profesores de Matemáticas
Página 39
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Si simplificamos la expresión de superficie para el tinaco de base cuadrada, nos queda:
3·41/3N2/3. si comparamos esta expresión con la del tinaco de base circular, nos queda
que 41/3 > ∏1/3, por lo que se gasta más en el material que forra al tinaco si se usa el de
base cuadrada.
Por lo tanto, conviene el tinaco cilíndrico, que al multiplicarlo por los g cms., del
espesor de la pared de concreto, se convertiría en volumen, que de todas maneras es
menor que el de base cuadrada.
………
podemos observar, que si comparamos término a término cada expresión, vemos que:
3·41/3gN2/3 >3g 1/3N2/3 ya que 4>
3·42/3g2N1/3 > 3g2N1/3 2/3 ya que 4>
4g3 > g3 ya que 4>, por lo tanto la superficie del tinaco en forma de cilindro, es
menor que la del prisma.
Cuando resolví el problema, sólo había considerado la superficie como S = x 2 + 4·N/x
en donde al minimizar nos quedaba x = (2N)1/3 que al sustituir en la fórmula de
superficie, nos da (2N)2/3 + 4N/(2N)1/3, que simplificando nos da 3·41/3N2/3
Para el caso del tinaco de base circular, teníamos r = (N/∏)1/3 , que al sustituir en la
fórmula de la superficie nos daba:
S = (N/)2/3 + 2N/( N/)1/3 , la cual si la simplificamos nos da
S = 3 1/3N2/3
Como vemos, el valor de x y el de r mínimos son iguales, pero al no considerar el ancho
g del concreto, podría resultar que la superficie del tinaco de base cuadrada fuera más
pequeña que la circular.
Con este último método, consideramos tanto el volumen exterior como el interior, y con
toda certeza podemos concluir que siempre conviene el tinaco de base circular, para ese
volumen N.
Figura 10. Dos fragmentos del reporte final de B. El segundo fragmento se
refiere a la resolución usando el volumen de las paredes de la cisterna, en el que
aparece su grosor g.
Es de resaltar el hecho de que B fue el único que no incluyó dibujo alguno en sus reportes
sobre este problema. Las representaciones utilizadas por él al comunicar sus resultados fueron
el lenguaje natural y expresiones algebraicas. Usando secuencias de expresiones algebraicas y
el lenguaje natural para expresar lo que procedió para obtener la siguiente expresión
algebraica, como se observa en la figura 10.
XVIII Encuentro de Profesores de Matemáticas
Página 40
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 11. Fragmento del reporte final de F sobre el problema de la cisterna.
F desarrolló sus primeras aproximaciones mediante funciones de dos variables y los
multiplicadores de Lagrange. En su reporte final dio más énfasis al método de la derivada
para determinar los extremos de las funciones. También en sus reportes iníciales había
empleado la función que proporcionaba el área de las paredes de las cisternas. En su reporte
final utilizó las funciones que proporcionan el volumen de las paredes como función del lado
y la altura, quizá como resultado de la discusión de la situación en el grupo.
XVIII Encuentro de Profesores de Matemáticas
Página 41
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 12. Fragmentos del reporte final de F sobre el problema de la cisterna.
Así mismo, analiza el caso para valores particulares del volumen de la cisterna y grosor de la
pared. Usa Derive para obtener las derivadas de las funciones, y determinar los valores
críticos. Recurre a Derive para resolver las ecuaciones polinomiales de cuarto grado que
aparecen en el proceso, también lo empleó para obtener las gráficas de las funciones, en las
que identificó visualmente donde se encuentra el valor mínimo de la función (Figuras 11 y
12) y decidir cuál de las raíces debe considerar. En este sentido aprovecha las herramientas
de Derive para verificar los resultados que va obteniendo.
Debo comentar que el reporte final de F, exhibe, por iniciativa propia, el empleo de Derive
para analizar y dar respuesta a este problema; motivado, quizá, por la discusión en el grupo de
los acercamientos utililizados por sus compañeros. Aunque el uso de Derive para obtener
derivadas de funciones, soluciones de ecuaciones, y gráficas de funciones, no fue utilizado
previamente por alguno de sus compañeros.
Reflexión.
En el desarrollo de esta actividad se presentan como momento crítico del proceso para obtener
la solución del problema, la identificación de la relación del volumen de las paredes de cada
cisterna con el área interior de sus paredes y con el volumen interior de ella. Esto permitió
aplicar sus conocimientos sobre funciones en una y dos variables, y los métodos para
determinar los valores extremos de ellas. Con base en las preguntas planteadas en el
enunciado del problema y los reportes individuales de los estudiantes, se observa que
identificaron, desde un inicio, la necesidad de comparar el volumen de las paredes en ambos
casos, aunque durante el trabajo individual, no lo hicieron directamente sino por medio del
área de la superficie interior, con excepción de D. El uso de la superficie interior de las
XVIII Encuentro de Profesores de Matemáticas
Página 42
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
cisternas para resolver el problema, se basa en la consideración de la forma de obtener el
volumen de un prisma: “área de la base por la altura”, y en que: “a menor área menor
volumen” (Figura 7). La intervención del instructor llevó a observar que el volumen de la
pared no se obtenía multiplicando la superficie interior por el grosor, y propició la reflexión
en torno a lo que están realizando y obteniendo. En este contexto, D expuso la forma en que
ella determinó el volumen de las paredes, considerando la diferencia entre el volumen exterior
y el interior de cada cisterna.
Al considerar los recursos utilizados en los dos acercamientos para resolver el problema:
funciones de una variable y el criterio de las derivadas, y el uso de funciones de dos variables
y el método de los multiplicadores de Lagrange, y el hecho de obtener resultados similares. El
instructor planteó preguntas respecto a la relación entre ambas formas, pero el tiempo no
permitió la discusión sobre ello.
Concentración de sal en un estanque
Un acuario contiene n unidades de agua. Cada semana se evapora una unidad de agua y
debe ser reemplazada con agua fresca. El agua fresca contiene de manera uniforme cierta
cantidad de sal, existiendo la posibilidad de que la concentración de sal en el acuario llegue
a ser peligrosa para los peces. Para evitar este riesgo, al final de la semana, cuando el
acuario tiene n – 1 unidades de agua, se saca una unidad más (dejando n-2 unidades de
agua) y se adicionan 2 nuevas unidades de agua fresca. Esto no resuelve el problema, ya que
sigue presentándose un incremento en la concentración de sal, pero menos que la que habría
si no se removiera una unidad adicional. Describa la concentración de sal en el acuario de
acuerdo con el tiempo. ¿En qué momento hay el doble de la concentración inicial?
Las primeras aproximaciones individuales se caracterizan porque los estudiantes analizan
casos particulares, asignando valores numéricos al volumen de agua y a la concentración (o a
la cantidad) de sal en el estanque, y por utilizar procedimientos recursivos en Excel, para
determinar la concentración de sal al final de cada semana (fig. 13). En esta fase solo la
estudiante I uso una aproximación algebraica. La comprensión del problema implica para los
estudiantes responder preguntas relacionadas con la concentración de sal, con entender los
factores y procesos que la modifican. El procedimiento recursivo es dado implícitamente en
Excel, como el realizado por el estudiante G (fig. 13) que le permite obtener la cantidad de sal
al final de una semana en términos de la cantidad de sal existente al final de la semana
anterior, C7, del volumen de agua en el estanque B7, y de la concentración de sal inicial D6.
Se obtiene la concentración de sal al final de la semana, considerando el cociente entre la
cantidad de sal y el volumen de agua, al final de la semana. Obteniendo la concentración de
sal al final de las siguientes semanas, repitiendo el procedimiento.
XVIII Encuentro de Profesores de Matemáticas
Página 43
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 13. Fragmento del reporte del estudiante G después del trabajo individual, en el
que supone un V de 400 m3 y una concentración de 1kg/m3.
El trabajo en parejas, permitió superar algunas dificultades, y mejorar la representación del
proceso en Excel y de la algebraica. Los estudiantes hicieran explícitas los cambios en las
variables volumen de agua, cantidad y concentración de sal, en las diferentes etapas del
proceso, al inicio y al final de cada semana. Se observa que trabajar en parejas, implica
explicar y clarificar el proceso de solución desarrollado en forma individual (figuras 14 y 15).
Figura 14. Fragmento del reporte elaborado por los estudiantes C y G, mostrando la
tabla en Excel modificada, respecto a la elaborada antes por G, incluyendo valores al
inicio y al final de la semana (Concentración de sal).
Se observa el cuidado puesto en identificar los pasos o eventos que se presentan cada semana
en el estanque y que tienen que ver con la concentración de sal (pasos 1, 2 y 3), así como la
naturaleza recursiva del proceso. No identifican las etapas inicial y final en cada fase. Esto los
lleva a tener imprecisiones, como al señalar en el segundo párrafo la concentración y la
cantidad de sal en la segunda semana, y luego pasar a la tercera, cuando se estarían refiriendo
al inicio de la segunda semana, considerar el proceso y establecer cuál sería la cantidad de sal
y la concentración al finalizar la segunda semana y al inicio de la tercer semana (que son las
mismas).
La exposición de los estudiantes ante el grupo propició la evaluación de lo realizado en
parejas, en términos de responder a las preguntas y dudas de los otros participantes. Después
de la presentación de las aproximaciones en Excel (dos parejas), se expuso la aproximación
XVIII Encuentro de Profesores de Matemáticas
Página 44
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
algebraica. Esta atrajo la atención hacia los aspectos estructurales del procedimiento y a
considerar criterios para evaluar la relación entre los datos y los resultados obtenidos.
Presentándose algunos problemas con la representación utilizada pues no les permitía
identificar las fases del proceso. Así se incorporaron a esta aproximación elementos utilizados
en el desarrollo del procedimiento en Excel, como son la identificación de estados inicial y
final de las variables en el proceso semanal y la representación de la concentración de sal
como una función del tiempo.
Para resolver el problema, primero identifiquemos nuestras variables:
x es la cantidad de sal en el agua, V es el volumen de agua inicialmente.
Paso 1. En la primera semana tenemos que la concentración de sal es
Paso 2. Al final de la primera semana la concentración cambia a
x
V
Para analizar que pasa en la tercera semana, sustituyamos
x(V 2  2)
por x
V (V  1)
y efectuemos los pasos 1,2,3 y 4 descritos anteriormente, la expresión de la
concentración a la que debemos llegar es:
x
ya que se
V 1
evapora una unidad de agua.
Paso 3. Cuando se saca una unidad más de agua de la pecera la concentración
x
x
V
1 .
es
V 2
Paso 4. Al reponer las 2 unidades de agua al acuario nos queda la
x 2x
x 
V
1 V
concentración:
V
………..
Por lo tanto la concentración de sal en el agua en la segunda semana es:
x(V 2  2)
x(V 2  2)
, y la cantidad de sal en la segunda semana es
V (V  1)
V 2 (V  1)
x(V 2  2)
…(1),
V 2 (V  1)
si sustituimos la cantidad de sal, la concentración a la tercera semana nos
queda:
x(V 2  2) V 2  2
x(V 2  2) 2

x(V 2  2) 2
V (V  1)
1
V (V  1)


V 2 (V  1)
V 2 (V  1)
V 3 (V  1) 2
1
La cantidad de sal en este caso es
x(V 2  2) 2
V 2 (V  1) 2
Si sustituimos esta cantidad de sal en la expresión (1), la concentración de sal
en el agua para la cuarta semana es:
x(V 2  2) 2 V 2  2
x(V 2  2) 3

1
x(V 2  2) 3
V 2 (V  1) 2
V 2 (V  1) 2


V 2 (V  1)
V 2 (V  1)
V 4 (V  1) 3
1
Si observamos las concentraciones de sal en las semanas 2,3 y 4 podemos
proponer la siguiente expresión para la concentración de sal.
Cn 
x(V 2  2) n 1
V n (V  1) n 1
Figura 15. Fragmentos del reporte del trabajo en parejas realizado por los estudiantes F e I.
Las aportaciones expuestas en el grupo se analizaron en forma individual y se elaboró un
nuevo reporte en forma individual, que se discutió con su pareja y se elaboró y realizó una
nueva presentación al grupo. En ésta, todos los estudiantes aceptaron la expresión y los
argumentos alcanzados por una de las parejas, quienes resaltaron la naturaleza recursiva del
proceso, y utilizando este hecho, aunque en forma incorrecta, obtiene en forma simple una
expresión algebraica, que los lleva a establecer que el proceso en la semana 2 se repite salvo
por que la cantidad inicial de sal es X1, y que así sucede con las siguientes semanas (Figura
16).
XVIII Encuentro de Profesores de Matemáticas
Página 45
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Ya que al iniciar la primera semana hay X0 = nc cantidad de sal en el acuario.
Al final de cada una de las siguientes semanas habrá:
X0
X0
n2
(n 2  2)
 2c  (
)X 0  2
 X0
n 1
n 1
n
n ( n  1)
si consideramos que al inicio de la semana 2 hay X 1 de sal :
X1  X 0 
X 2  X1
( n 2  2)
( n 2  2) 2
 X0
n(n  1)
n 2 ( n  1) 2
Xk  X0
, ... y tambien
la concentración en la semana k es : C ( k )  X 0
( n 2  2) k
n k ( n  1) k
( n 2  2) k
n k 1 ( n  1) k
Figura 16. Segmento del reporte del estudiante G que muestra la identificación de un
proceso recursivo incorrecto.
Continuando con el proceso de responder las preguntas del problema, usan esta expresión
para determinar el tiempo en el que la concentración alcanzaría un valor igual al doble de la
2
k
concentración inicial, resolviendo la ecuación 2 X 0  X k0(1n  2)k usando un procedimiento
n
n
(n  1)
numérico en Excel, que les proporciona k=15 como resultado.
En la discusión en grupo nadie puso en duda los resultados obtenidos, y no consideraron el
procedimiento desarrollado en Excel durante la primera y segunda fase de trabajo en el que se
observa un crecimiento lento de la concentración de sal. El instructor intervino para propiciar
la identificación de esta discrepancia por los estudiantes y llevarlos a reflexionar sobre lo
realizado, los conceptos de modelo y las representaciones de una situación o fenómeno.
Planteó preguntas del tipo: ¿Cuál de los dos procedimientos proporciona la respuesta
correcta? ¿Cuál de ellos proporciona una descripción adecuada del proceso? ¿Cómo lo
podemos saber? ¿Qué criterio podemos utilizar para evaluar cada procedimiento?
Esto llevó a los estudiantes a considerar que las dos aproximaciones deberían proporcionar los
mismos resultados, o muy parecidos, y el mismo comportamiento en lo general. Algunos
revisaron el procedimiento en Excel y volvieron a considerar el carácter recursivo del mismo,
lo cual utilizaron para obtener una nueva expresión algebraica, pero no detectaron el error
cometido al deducir las expresiones algebraicas anteriores. Solo el estudiante G elaboró por
escrito un nuevo reporte donde verificó la nueva expresión algebraica para la concentración
de sal mediante un procedimiento en Excel para evaluarla.
Esto actividad muestra que los estudiantes no han integrado los conocimientos de que
disponen y los que van construyendo. Ven cada aproximación al problema como
representaciones diferentes de cosas diferentes, no de una misma situación.
Reflexiones.
En estos ejemplos los alumnos usaron procedimientos numéricos para explorar la situación
general por medio de casos particulares y con base en su comprensión de cada situación. Las
exploraciones fueron utilizadas para obtener expresiones algebraicas funcionales que
describieran la situación. Expusieron y discutieron las propuestas, y llegaron a obtener una
expresión y una respuesta a las preguntas planteadas en los enunciados. Se observa que no
recurren a los resultados obtenidos en sus primeras aproximaciones, particularmente cuando
son de tipo numérico. Tienen mayor confianza en el uso de las expresiones algebraicas (caso
de la concentración de sal). Los estudiantes que utilizan los Multiplicadores de Lagrange,
XVIII Encuentro de Profesores de Matemáticas
Página 46
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
obtuvieron de inmediato una representación algebraica funcional de la situación e
identificaron una situación y una restricción, que los llevó a plantear de inmediato esta
estrategia. Pero no fueron capaces de identificar la relación de este método con el método de
determinación de los extremos mediante la derivada de la función en una variable.
En este sentido, se observa que el conocimiento conceptual y de procedimientos está asociado
con la capacidad para la comprensión de las relaciones en la situación y para representarlas.
La utilización de conceptos y procedimientos de cálculo por los estudiantes en la resolución
de algunos problemas, mostró que tenían cierto dominio de las técnicas y de las condiciones
para utilizarlas. Por ejemplo, la determinación de los extremos de funciones en una y en varias
variables, la derivación de funciones, de funciones implícitas y derivación parcial, así como la
resolución de ecuaciones diferenciales.
Si bien los resultados anteriores muestran relación entre el desarrollo de la comprensión
conceptual y el de la habilidad para resolver problemas, es necesario contar con más
evidencia, particularmente, tratando de identificar la posibilidad de establecer niveles de
desempeño. ¿Cómo identificar niveles en el desarrollo del conocimiento conceptual? ¿Cómo
identificar niveles en el desarrollo de las habilidades para resolver problemas?
Referencias
Hill, H., Rowan, B., Ball, D.L. (2005). Teachers' mathematics knowledge for teaching on
student achievement. American Educational Research Journal, 42(2), p. 371- 406
Kilpatrick, J. ( 2002). Understanding Mathematical Literacy: The contribution of research.
Educational Studies in Mathematics 47, 101 – 116.
Lesh, R., & Doerr, H. (2000). Symbolizing, communicating, and mathematizing: Key
components of models and modeling. In P. Cobb, E. Yackel, and K. McClain (Eds.),
(2000). Symbolizing, communicating, and mathematizing. Mahwah, NJ: Lawrence
Erlbaum
Associates.
Tomado
el
10.05.05
de
http://tcct.soe.purdue.edu/books_and_journals/models_and_modeling/appendices/reso
urces/ch05_1998.pdf
Lesh, R., English, L., & Fennnewald, T. (2007). Methodologies for investigating
relathionships between concept development and the development of problem solving
abilities. TSG19: Problem Solving in Mathematics Education. ICME 11. Monterrey.
México.
Tomado el 20.01.2010 de http://tsg.icme11.org/tsg/show/20
Schoenfeld, A. H. (1985). Metacognitive and epistemological issues in mathematical
understanding. In: Edward A. Silver (Ed.).Teaching and learning mathematical
problem solving: Multiple research perspectives. Lawrence Erlbaum Associates,
Publishers. Hillsdale, NJ.
Schoenfeld, A. H. (2006). Mathematics teaching and learning. In P. A. Alexander & P. H.
Wiinne (Eds.), Handbook of Educational Psychology (2nd edition) (pp. XX-XX).
Mahwah, NJ: Erlbaum.
SEP (2009). Acuerdo 444 de la Secretaría de Educación Pública. Diario Oficial de la
Federación, 23 de junio de 2009, México.
XVIII Encuentro de Profesores de Matemáticas
Página 47
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Introducción al Cálculo integral mediante el cálculo del área de regiones
planas
Ing. Héctor Suárez Alfaro
[email protected]
Universidad Michoacana de san Nicolás de Hidalgo
Resumen
Se presenta una propuesta alternativa para el inicio del Cálculo integral, con la característica
de que no es necesario se tengan antecedentes como el Cálculo diferencial, las técnicas de
integración indefinida o las herramientas teóricas que comúnmente se presentan como
requisitos para las aplicaciones del Cálculo integral.
Introducción
La cuantificación de áreas para las figuras planas es un problema que puede plantearse de
manera general en el contexto de un plano cartesiano, en términos de dos funciones de la
variable x : ¿Cuál es la medida de la superficie de la región del plano cartesiano comprendida
entre las gráficas de f  x  y g  x  , desde una abscisa x  a , hasta otra x  b ?
Tradicionalmente, se ha considerado un tema que deba tratarse dentro del Cálculo integral
como una aplicación de la integral definida, lo cual significa que deba tener como requisito a
las técnicas de la integración indefinida y el Teorema fundamental del Cálculo; sin embargo,
en el nivel del Bachillerato, las regiones que se proponen para ejemplificar el uso de esas
herramientas son, en la mayoría de los casos tan simples, que bastan algunas reglas sencillas
para cuantificar áreas de regiones básicas, que usadas convenientemente permiten calcular
áreas de regiones hasta de cierto grado de complejidad. Al mismo tiempo, la justificación de
esas reglas puede considerarse como una alternativa para introducir el Cálculo integral. A
continuación, se propone una alternativa al cálculo de áreas, que se basa esencialmente en
establecer una secuencia de expresiones correspondientes a una serie de regiones elementales
construidas a partir de otra interpretación de las figuras planas sencillas como el rectángulo y
el triángulo.
XVIII Encuentro de Profesores de Matemáticas
Página 48
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Regiones elementales
Según la Enciclopedia libre Wikipedia, un rectángulo es un paralelogramo cuyos cuatro lados
forman ángulos rectos entre sí. Los lados opuestos tienen la misma longitud.
La superficie de un Rectángulo se cuantifica de acuerdo con la muy conocida regla de
multiplicar sus dos dimensiones.
Aceptemos como una región elemental al rectángulo y la proposición asociada básica de la
cuantificación de su superficie, la regla del producto "base por altura", pero interpretemos de
forma diferente su definición de manera tal que nos permita considerar otras regiones
elementales como la región triangular, el segmento parabólico, el segmento parabólico
cúbico, etc. Con el fin de establecer una regla general para la obtención del área de cada una
de estas regiones.
Un Rectángulo es una región del plano en la cual las alturas respecto de cualquier punto de
una base, son iguales. Su área es el producto de la altura común por la base.
Una región triangular elemental es la región del plano en la cual la altura respecto de un punto
de la base es proporcional a la distancia desde ese punto a uno de los extremos de la base. El
área es el producto de la altura máxima, por la base, dividido por dos.
Un segmento parabólico elemental es la región plana en la que la altura respecto de un punto
de la base es proporcional al cuadrado de la distancia desde ese punto a un extremo de la base.
El área se obtiene multiplicando la altura máxima por la base y dividiendo por tres. Etc.
Lo anterior se justifica al considerar los dos primeros casos, relacionándolos con la secuencia
1 1
de fracciones , .
1 2
Es claro que si se establecen condiciones similares para generar las regiones, la secuencia
deba extenderse aumentando en uno los divisores, es decir, se tiene de manera natural la
1 1 1 1
secuencia , , , , …, en la siguiente figura, se ilustra gráficamente este hecho:
1 2 3 4
En general, una región elemental se genera por medio de las alturas proporcionales a una
potencia entera de la distancia a uno de los extremos de un segmento base. El área se obtiene
como el producto de la altura máxima por la base, dividido por el exponente de la potencia
aumentado en uno.
La regla anterior puede aplicarse para calcular el área de un buen número de regiones
propuestas en la mayoría de los textos usados en el nivel del Bachillerato, en los cuales,
abundan los ejercicios que involucran rectas y parábolas. En cualquiera de estos casos, el área
de una región determinada se obtiene por medio de una suma algebraica de áreas
correspondientes a las regiones elementales obtenidas por medio de una teselación que
incluya la región de interés.
XVIII Encuentro de Profesores de Matemáticas
Página 49
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
A continuación, se aplica la regla en algunos ejemplos:
Un caso sencillo, muy común en la mayoría de los textos. El área de la región limitada por
y  x , y  x2
A
11  11  1
2
3
6
La combinación de dos parábolas, el área de la región limitada por y  2 x  x 2 , y  x 2
A  11  2
Área de la región determinada por y  x , y 
11  1
3
3
x
2
A   4  2  
 4  2    4  2   4
3
2
3
O
A
 4  2    4  2   4
2
3
3
La región definida por y  x  1 , y 2  2 x  6
A   8  6  
8 4    2  2    6  6   18
3
3
2
Obviamente, el proceso tiene limitaciones como se puede observar en regiones determinadas
por funciones polinomiales de grado 3 o superior, por ejemplo, la región limitada por
XVIII Encuentro de Profesores de Matemáticas
Página 50
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
y  1  x 2 , y  x 4  x 2 ; o la región definida por x  y 3  y , x  1  y 4 . Sin embargo, es
posible plantear un método mas general basándose en las propiedades de las regiones
elementales, mismo que puede aplicarse de forma simbólica:
Sea dada la función y  cx n , para expresar el área entre su gráfica y el eje x, desde el orígen a
cualquier abscisa x , se aplica la regla para las regiones elementales, obteniendo A 
cx n 1
,
n 1
como se ilustra en la figura:
Se está ahora en posibilidades de abordar el problema original, para algunas funciones
algebraicas f  x  y g  x  ; la región comprendida entre sus gráficas es equivalente a la región
comprendida entre el eje x y la gráfica de la función s  x   f ( x)  g  x  ,
Para cuantificar el área de esta región, aceptamos el hecho que, como antes, dado que las
áreas son expresadas en números reales, se pueden operar bajo la suma y la diferencia y que,
entonces, para una expresión dada como una suma algebraica de términos expresados en
forma general como cx n , el área correspondiente es la suma algebraica de las áreas
individuales, cada una referida al origen de coordenadas. Esto permite establecer un proceso
simbólico que conduce a obtener el número que cuantifica el área de la región propuesta
originalmente.
XVIII Encuentro de Profesores de Matemáticas
Página 51
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Considérese en primer lugar el caso en que la región definida por la función s  x  , inicia en
x  0 y termina en cualquier abscisa x  0 entonces a cada término cxn de la función le
cx n 1
corresponde una región elemental que contribuye con el área
, llamemos a la suma de
n 1
estas expresiones, una función generadora de área A  x  .
Una vez obtenida A  x  , el área de la región se calcula por medio de la diferencia
Ab  A a 
Para ilustrar el proceso simbólico, consideremos la región del primer ejemplo, se tiene
s  x   f ( x)  g  x   x  x2 .
Entonces
x 2 x3
A x 

2 3
Y el área se obtiene sustituyendo los extremos de la región, 0 y 1:
1
1 1
A  A 1  A  0        0  
6
 2 3
Área de la región limitada por y  2 x  x 2 , y  x 2
s  x   2x  2x2 , A  x   x2 
2 x3
1
 2
, A  A 1  A  0   1     0  
3
3
 3
x
, representamos las
2
ecuaciones de las curvas con y como variable independiente: x  y 2 , x  2 y , con lo que
resulta:
Para calcular el área de la región determinada por y  x , y 
y3
4
 8
s  y   2 y  y , A( y)  y  , A  A  2   A  0    4     0  
3
3
3

2
2
XVIII Encuentro de Profesores de Matemáticas
Página 52
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Para la región definida por y  x  1 , y 2  2 x  6 , expresamos de manera equivalente las
ecuaciones como x  y  1, x 
s  y  4  y 
y2
 3 , así que
2
y2
y 2 y3
32  
4

, A  y   4 y   , A  A  4   A  2   16  8     8  2    18
2
2 6
3 
3

Se tiene ahora, un método para calcular el área de cada una de las regiones antes
mencionadas: y  1  x 2 , y  x 4  x 2 así como la región definida por x  y 3  y , x  1  y 4
Conclusiones
Una introducción al Cálculo integral puede darse temprano en el Bachillerato, puesto que no
necesita de muchos requisitos mas allá de un dominio aceptable de la manipulación algebraica
y de la graficación de funciones.
No se requiere de herramientas teóricas muy elaboradas, dejando para cursos posteriores un
tratamiento mas riguroso de la integral, muy probablemente en otro contexto.
Desde el punto de vista de los alumnos, el concepto de área se ubica dentro de una perspectiva
visual y les resulta mas natural la manipulación gráfica como un antecedente al tratamiento
simbólico.
Referencias
Spivak, M. (1992). Calculus, Cálculo Infinitesimal. Editorial Reverté, S.A., España.
Swokowski, E. W. (1982). Cálculo con geometría Analítica. Editorial Iberoamérica, Belmont,
Cal., USA.
XVIII Encuentro de Profesores de Matemáticas
Página 53
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
El papel del profesor en el desarrollo de competencias matemáticas
mediante resolución de problemas
Dra. Verónica Vargas Alejo
[email protected]
Dr. César Cristóbal Escalante
[email protected]
Universidad de Quintana Roo
Resumen
En este artículo se reporta un análisis de procedimientos emprendidos por estudiantes de nivel
superior al abordar un problema algebraico. Se destaca el papel del profesor y sus
intervenciones en el proceso de resolución del problema. El problema reportado forma parte
de una serie de problemas resueltos en el curso de álgebra lineal, los cuales fueron
implementados en el aula en un ambiente de lápiz y papel. Los resultados encontrados
muestran la importancia de la intervención del profesor en el trabajo del aula para lograr el
análisis, discusión y búsqueda de estrategias en la resolución de problemas, de manera
simultánea al desarrollo de conocimiento matemático, aspectos centrales de lo que se
considera como competencia matemática.
Introducción
De acuerdo con las actuales políticas educativas, en esta era de conocimiento científico y
tecnológico, donde la constante es el cambio, se manifiesta como una necesidad contribuir a
la sociedad con la formación de ciudadanos, que no solo estén más informados sino mejores
educados; que posean la capacidad de afrontar con éxito desde la toma de decisiones en su
vida cotidiana hasta la expresión de ideas en torno a políticas públicas que se apoyen en la
ciencia y la tecnología. En este sentido se requiere (así se manifiesta en diversos documentos)
de una educación que busque el desarrollo de competencias en los estudiantes.
La reflexión anterior no es nueva, históricamente la sociedad creó a las instituciones
educativas con el fin de educar a sus ciudadanos para que pudieran participar en sus diversas
actividades de subsistencia, control y al mismo tiempo de desarrollo. La pregunta es entonces,
para nosotros, los educadores en matemáticas: ¿Cómo se ha estado participando desde la
educación matemática? Y ¿cómo se puede seguir participando en la educación de los
ciudadanos con el fin de desarrollar competencias?
Varias discusiones han emergido en este sentido ¿qué significa desarrollar competencias
matemáticas? ¿Qué competencias matemáticas deben desarrollarse en los estudiantes? ¿Cómo
deben ser los procesos de aprendizaje que deben propiciarse para generar en los estudiantes la
adquisición de competencias matemáticas? ¿Cuál es el papel del profesor en el desarrollo de
competencias?
En este artículo se reporta, mediante los registros de un par de estudiantes, el tipo de
procedimientos emprendidos por estudiantes de nivel superior al abordar problemas
algebraicos. El problema formó parte de una serie de problemas resueltos en el curso de
álgebra lineal de la carrera de Sistemas Comerciales. Los problemas fueron implementados en
el aula en un ambiente de lápiz y papel y resolución de problemas, con el propósito de
desarrollar competencias matemáticas, en particular de desarrollar conocimiento matemático
de manera simultánea al análisis, discusión y búsqueda de estrategias de resolución. Las
preguntas que se pretenden responder en este documento son: ¿qué competencias matemáticas
XVIII Encuentro de Profesores de Matemáticas
Página 54
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
exhiben los estudiantes del nivel superior al resolver problemas algebraicos? ¿Qué tipo de
intervenciones del profesor pueden apoyar los procesos de resolución de problemas y
propiciar el desarrollo de competencias matemáticas? Para ello se analiza en forma detallada
tanto los procedimientos de los estudiantes como el papel del profesor en el proceso de
resolución. La discusión en torno a las competencias matemáticas en la cual se basa este
documento es la establecida por De Corte (2007).
Revisión de la literatura
Adquirir una competencia matemática de acuerdo con De Corte (2007) implica adquirir una
disposición matemática, la cual es caracterizada por cinco aspectos (De corte, 2007, p. 20-21):
una base de conocimientos accesible, auto organizado y flexible, métodos heurísticos, metaconocimiento, creencias positivas relacionadas con la disciplina y habilidades autoregulatorias. Implica, además, que el estudiante sea capaz de transferir habilidades y
conocimiento a nuevas tareas y contextos de aprendizaje. En varios de estos aspectos
coinciden diferentes investigadores cuando discuten el tipo de educación matemática que se
requiere para los estudiantes (NCTM, 2000/2003) y, por lo tanto, el tipo de competencias
matemáticas a desarrollar en ellos. La discusión se transforma entonces en ¿cómo lograr el
desarrollo de estas competencias matemáticas? ¿Cómo se desarrollan las competencias en los
diferentes niveles educativos? ¿Hay niveles de desarrollo de las competencias? ¿Se deben
desarrollar unas competencias antes que otras? ¿Cuáles?
Definitivamente no será con cursos tradicionales de matemáticas, donde el interés central es el
aprendizaje memorístico de conceptos y la manipulación simbólica sin comprensión, como se
desarrollarán competencias. Se requiere, de acuerdo con De Corte (2007) de la creación de un
proceso de aprendizaje activo/constructivo, autoregulado, situado y colaborativo, donde se
considere que es el estudiante quien construye significados y conocimientos matemáticos.
Una de las tendencias en la enseñanza de las matemáticas que contempla discusiones como
las precedentes es la Resolución de Problemas. No solo discute muchos de los temas
mencionados sino que aporta metodologías de trabajo en el aula, donde se caracteriza el tipo
de escenarios y discusiones que deben fomentarse en el aula para promover el desarrollo de
conocimientos y habilidades del pensamiento matemático.
Centrar la enseñanza de las matemáticas en la Resolución de problemas implica despojarse de
la idea de introducir los problemas en la currícula con la única finalidad de practicar
algoritmos de cálculos o reforzar aplicaciones específicas en las operaciones, lo cual es
importante en la enseñanza y aprendizaje de las matemáticas pero no es central. Esta
propuesta señala que aprender matemáticas va más allá de memorizar un conjunto de
definiciones, algoritmos y técnicas para resolver actividades rutinarias (Schoenfeld, 1985). Se
debe propiciar en el aula un ambiente en el cual los estudiantes puedan comunicar sus ideas,
hacer preguntas, usar múltiples representaciones, construir conjeturas y formular
contraejemplos (Santos, 1997).
En la Resolución de problemas el papel del profesor es fundamental, pues influye de manera
determinante en el aula para fomentar la creación del espacio de aprendizaje (Grouws, 2004).
El profesor puede favorecer ambientes en el aula donde se promuevan aspectos como: el
desarrollo de una solución significativa personal por parte del estudiante, la justificación y
explicación del pensamiento entre estos, con sus parejas o equipos y con el profesor, la toma
de sentido de las explicaciones y justificaciones de otros; el cuestionamiento y desafío a los
XVIII Encuentro de Profesores de Matemáticas
Página 55
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
compañeros si no hubo comprensión o hay desacuerdo. Las interacciones sociales en el aula
son factores fundamentales para el desarrollo del razonamiento de los alumnos y los procesos
de adquisición de significados (Rasmussen, Yackel & King, 2004). El profesor puede
apoyarse de configuraciones en el aula para favorecer esta interacción en el grupo, así como
de la tecnología.
Los problemas pueden diseñarse teniendo como objetivo que al implementarse en el aula
posibiliten discusiones en torno a conceptos matemáticos pero, además, permitan desarrollar
estrategias de solución, representaciones, análisis de información y viabilidad de la solución o
soluciones (NCTM 2000/2003). Es decir, los problemas pueden diseñarse e implementarse
con el objetivo de que el alumno adquiera una actitud reflexiva al fomentar la estructuración
de inferencias, construcción de argumentos, lecturas críticas, escritura y comunicación eficaz,
toma de decisiones, entre otros aspectos, los cuales son considerados como características de
un alumno competente en la disciplina. Generar ambientes de Resolución de Problemas en el
aula, por lo tanto, posibilita desarrollar competencias matemáticas en los estudiantes; es decir,
permite adquirir una disposición matemática (De Corte, 2007).
Metodología
En este artículo se discuten los procedimientos emprendidos por equipos de estudiantes para
resolver el Problema 1.
Problema 1. Una fotocopiadora cuesta $20 000.00 y elabora 1000 fotocopias por
hora, con un costo de producción por cada copia de $0.1. Otra tiene un costo de $40
000.00 y elabora 1500 fotocopias por hora, con un costo de producción de cada
copia igual a $0.05. ¿Cuántas horas debe usarse la fotocopiadora más cara para que
esta resulte costeable?
El sistema de ecuaciones lineales (SEL) que representa este problema es el siguiente:
100 x  y  20000
75 x  y  40000
Donde x corresponde al número de fotocopias y y al costo de producción total, considerando
el costo de las fotocopiadoras. 100x y 75x provienen de los costos de producción de las
fotocopiadoras 1 y 2, sin considerar el costo inicial de las fotocopiadoras: 1000*0.1 x y
1500*.75x . La solución del SEL es: x  800, y  100000
El Problema 1 fue implementado en una Universidad Pública del Estado de Quintana Roo. El
grupo estuvo constituido por 12 estudiantes de la carrera de Sistemas Comerciales, quienes
estaban estudiando una materia que comprende tópicos de álgebra lineal, cálculo diferencial e
integral en el semestre par del primer año de sus estudios universitarios. El contenido del
curso incluye resolver sistemas de ecuaciones lineales usando la Regla de Cramer, Matriz
Inversa y el Método de Gauss Jordan.
Los conocimientos básicos del grupo corresponden a sus cursos de bachillerato y, en algunos
casos, a un curso de matemáticas generales que reciben en primer semestre. El Problema 1
formó parte de una serie de cuatro problemas implementados en el aula, este fue el cuarto
problema implementado. Todos los problemas previos también podían resolverse mediante un
sistema de ecuaciones lineales.
XVIII Encuentro de Profesores de Matemáticas
Página 56
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
En una sesión de trabajo en el aula de dos horas se entregó el Problema 1 al grupo en estudio,
el cual estaba conformado por equipos de tres estudiantes. El problema fue abordado en un
tiempo aproximado de hora y media; durante este tiempo los estudiantes trabajaron en equipo
y discutieron en diferentes momentos el problema en forma grupal con apoyo del profesor. Al
final se les pidió redactar reportes individuales.
Resultados
Características iniciales del grupo y aspectos considerados en cuenta durante el curso. Es
importante destacar algunas dificultades identificadas al inicio del curso en los estudiantes del
grupo en cuanto a sus competencias matemáticas. La mitad del grupo de estudiantes no
recordaba los procedimientos para resolver sistemas de ecuaciones lineales, por ejemplo, los
métodos de sustitución e igualación. Los estudiantes no tenían claro que un SEL pudiera tener
una solución única, un conjunto infinito de soluciones o no tuviera solución. Aunque tenían
antecedentes de cómo graficar un SEL, y de que existían métodos de solución, no habían
tenido la experiencia de integrar estos procedimientos y utilizarlos para resolver un problema.
Resolver un problema algebraico, significaba para ellos únicamente representarlo mediante
un SEL y resolverlo mediante algún método. Sin embargo, mostraban bastante dificultad en la
traducción del lenguaje verbal al lenguaje simbólico, no era claro a partir del enunciado del
problema determinar las incógnitas y ecuaciones. Cuando resolvían un SEL asociado a un
problema, no explicitaban en su reporte cuál era la solución del problema (lo cual falta en el
reporte del problema aquí presentado), es decir, no revisaban el enunciado del problema para
evaluar si el resultado obtenido era correcto. Solo subrayaban la solución encontrada para el
SEL, sin explicitar en su reporte cuál era la relación entre esta solución y la pregunta del
problema.
Mostraron renuencia al trabajo en equipo, estaban acostumbrados al trabajo individual y
exposición del profesor. Tampoco les fue agradable saber que ellos debían validar sus propios
avances en los procesos de solución. En varias ocasiones manifestaron inconformidad por no
escuchar por parte de la profesora la validación de sus ideas y avances, sino preguntas de
reflexión.
Durante el desarrollo del curso se observaron y consideraron los elementos mencionados
anteriormente; con base en ello, el trabajo en el aula se orientó hacia el desarrollo de las
competencias matemáticas siguientes. En cuanto a la base de conocimientos accesible, auto
organizado y flexible (De Corte, 2007) se trató de profundizar en conceptos matemáticos
como incógnita, variable, ecuaciones y el aprendizaje de diferentes métodos para dar solución
a un SEL. En cuanto a métodos heurísticos (De Corte, 2007) se promovió el manejo de
distintos registros de representación. En cuanto a las habilidades autoregulatorias (De Corte,
2007) se trabajó en el proceso de argumentación de ideas, discusión y presentación de las
mismas y se insistió en buscar la validación de los propios procedimientos. Se enfatizó en el
regreso al problema continuamente, recordando cuál era la pregunta planteada. Lo anterior fue
trabajado en el aula mediante la implementación de problemas; la siguiente discusión es una
muestra de ello.
Procedimientos para resolver el Problema 1. En una primera aproximación los equipos de
estudiantes trataron de comprender el Problema 1 a partir del enunciado. Relacionaron las
cantidades involucradas, aunque no consideraron todas. Un ejemplo de la forma de proceder
se observa en la Figura 1.
XVIII Encuentro de Profesores de Matemáticas
Página 57
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 1. Procedimiento para resolver el Problema 1. Se observa cómo los estudiantes
calcularon el costo de producción por hora de cada fotocopiadora sin considerar el costo
total. Las cantidades de 20000 y 40000 se utilizaron solo como etiquetas para distinguir las
fotocopiadoras.
Con avances como estos, los equipos de estudiantes intentaron escribir un sistema de
ecuaciones, pero ninguno logró establecer de manera correcta las ecuaciones, pues no les fue
claro cómo relacionar todas las cantidades involucradas en el problema (Figura 2).
Figura 2. Proceso de simbolización de las relaciones identificadas entre los datos del
problema. La simbolización surge del procedimiento mostrado en la Figura 1.
Los equipos de estudiantes se estancaron y no pudieron continuar. Había confusión en el
proceso de resolución implementado. Las dudas que explicitaban, en general en el grupo, en
ese momento a la profesora eran: ¿Cómo usar x y y? ¿Cómo escribir las ecuaciones? ¿Cuántas
literales usar? ¿Cuántas ecuaciones debían surgir?
El papel de la profesora, al observar los avances de los equipos de estudiantes, fue orientar el
trabajo de los equipos hacia la relectura y comprensión del Problema 1 con preguntas como:
¿Qué dice el problema? ¿De qué trata? ¿Qué nos pide encontrar o calcular? Exprésalo con tus
propias palabras sin leerlo. Sin embargo, la actividad de los equipos de estudiantes una y otra
vez se reducía a releer el problema textualmente, pues como estaban casi convencidos de su
forma de proceder no se veían interesados en revisar de nuevo el enunciado del Problema 1,
aunque denotaban confusión cuando se les preguntaba si ya tenían una posible respuesta para
la interrogante del problema: ¿Cuántas horas debe usarse la fotocopiadora más cara para que
esta resulte costeable?
La profesora reorientó su intervención ante los equipos de estudiantes y contextualizó el
Problema 1 con el objetivo de propiciar un nuevo análisis del problema. El Problema 1 se
expresó de manera diferente: Supongamos que vamos a organizar un congreso para
estudiantes; como ustedes saben en estos eventos a veces se tienen que comprar
fotocopiadoras para el proceso de inscripción. Debido a que estas fotocopiadoras las usan
diferentes personas, terminan casi siempre descompuestas al terminar el congreso. Es decir, la
vida de las fotocopiadoras puede ser sólo de algunas horas. Ahora bien, tenemos dos
XVIII Encuentro de Profesores de Matemáticas
Página 58
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
opciones: comprar una fotocopiadora de 40000.00 o una de 20000 ¿Cuál conviene comprar si
la fotocopiadora que cuesta $20 000.00 elabora 1000 fotocopias por hora, con un costo de
producción por cada copia de $0.1 mientras que la fotocopiadora que tiene un costo de $40
000.00 elabora 1500 fotocopias por hora, con un costo de producción de cada copia igual a
$0.05? ¿Conviene comprar la de 40000 o la de 20000? ¿De qué depende?
Es más, supongamos que ustedes son vendedores de una empresa que se dedica a vender
fotocopiadoras y tienen un cliente, quien desea comprar una de las dos fotocopiadoras. ¿Qué
le recomendarían comprar? ¿Cómo sustentarían la opción de compra de cada una de las
fotocopiadoras? ¿Qué tiene que ver las horas de uso de la fotocopiadora para elegir la más
apropiada? ¿Qué pasa con el costo de producción si elijo la de 40000.00 o la de 20000? ¿Cuál
de las dos me conviene si solo las voy a utilizar un determinado tiempo, por ejemplo 12
horas?
Esta nueva contextualización dio la pauta para que la discusión de los equipos se orientara
hacia un análisis aritmético del Problema 1. Pero los estudiantes empezaron a escribir sin
orden sus operaciones. Nuevamente la profesora intervino para solicitar que ordenaran sus
operaciones de tal manera que el orden permitiera visualizar a los equipos de estudiantes las
relaciones involucradas entre las cantidades inmersas en el Problema 1 (Figura 3), comparar
lo que ocurría con los costos de producción en una y otra fotocopiadora y detectar las
cantidades que estaban variando y las que permanecían constantes.
Figura 3. Procedimiento para resolver de forma aritmética el Problema 1. Al final se ilustra
la simbolización de las relaciones identificadas en el problema mediante literales.
El análisis que emprendieron los equipos de estudiantes consistió en comparar el costo de
producción total de ambas fotocopiadoras) si se pusieran a funcionar solo un número
determinado de horas como: 1 hora, 2 horas, 5 horas y 10 horas.
Con estos cálculos (Figura 3) los equipos de estudiantes observaron que había cierta
estructura que se conservaba en las operaciones llevadas a cabo, pero también había
cantidades que estaban variando. Las preguntas que ahora la profesora planteó fueron ¿Cómo
están variando las cantidades? ¿Hay cantidades que permanecen constantes? ¿Cómo puedo
generalizar estos casos particulares? ¿Puedo escribir con ecuaciones los cálculos llevados a
XVIII Encuentro de Profesores de Matemáticas
Página 59
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
cabo? ¿Qué podemos decir de la variación del costo de producción de la fotocopiadora 1 con
respecto a la fotocopiadora 2? ¿Cuántas horas debe usarse la fotocopiadora más cara para que
esta resulte costeable?
A partir de las preguntas planteadas a los equipos de estudiantes, y el análisis aritmético del
Problema 1, los estudiantes rápidamente detectaron las ecuaciones y escribieron el SEL
(último renglón de la Figura 3). A las cantidades que variaban les llamaron x y y. Pero, de
nuevo hubo dificultades para llevar a forma matricial el SEL y resolverlo. La profesora tuvo
que intervenir para que con base en ejercicios anteriores de clase revisaran cuál debía ser la
forma adecuada de escribir el SEL en forma matricial (Figura 4). Los equipos de estudiantes
usaron el método de Gauss Jordan debido a que era el que se estaba trabajando en clase.
Figura 4. Solución del SEL, que representa al Problema 1, mediante el método de Gauss
Jordán.
Los equipos de estudiantes encontraron que al cabo de 800 horas, las fotocopiadoras
igualaban su costo de producción; entonces, hicieron algunos cálculos aritméticos para
determinar qué ocurría después de las 800 horas.
Posteriormente, se les recordó la importancia de graficar las ecuaciones del SEL, para no solo
identificar la solución de éste (Figura 5), sino para tener una mejor comprensión del Problema
1. Con base en la gráfica la profesora les pidió que argumentaran en cuanto al problema. Esto
condujo a los equipos de estudiantes a interpretar la gráfica y la intercepción de las rectas.
No todos los equipos de estudiantes graficaron de manera correcta. La Figura 5 es una
muestra de ello, donde se observan dificultades para graficar e identificar las líneas rectas que
representan al Problema 1. En este trabajo, en particular, tampoco se respondió en forma
escrita y explícita la solución del problema. En cambio, en otros trabajos se graficó de mejor
manera e incluso se agregó la respuesta a la pregunta del Problema 1.
XVIII Encuentro de Profesores de Matemáticas
Página 60
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 5. Gráfica obtenida a partir del SEL que representa al Problema 1.
Discusión de Resultados y Conclusiones
Los resultados muestran que hubo dificultades en los equipos de estudiantes para comprender,
en la primera aproximación, el problema en su totalidad. No lograron relacionar todos los
datos del Problema 1 y no tenían claro cómo responder la pregunta planteada en éste. Es
decir, no tenían claro cuál era la incógnita del problema. El apoyo de la profesora para
contextualizar el Problema 1 llevándolo hacia una situación cercana a los estudiantes indujo a
una nueva revisión del problema, el cual ya se consideraba casi resuelto.
La conversión del Problema 1 a un problema aritmético (Figura 3) como primera estrategia
heurística de solución fue la primera orientación que la profesora promovió como
procedimiento de solución y sirvió para que los equipos de estudiantes tuvieran una primera
comprensión del problema. Además, la orientación hacia la organización de las operaciones,
permitió la identificación del SEL que representaba al problema, apoyó el proceso de escritura
simbólica de las ecuaciones (es decir, la identificación de incógnitas, datos y relaciones entre
estos) y, en consecuencia, el desarrollo de procesos de generalización con base en la
observación de patrones, lo cual es importante como razonamiento algebraico y, por lo tanto,
como competencia matemática.
Durante todo el proceso de solución los equipos de estudiantes estuvieron interactuando con
los conceptos de incógnita, variable y ecuación, desde el análisis en forma aritmética (Figura
3), donde los equipos de estudiantes reconocieron patrones, hasta la obtención de la gráfica
(Figura 5). Haber integrado el proceso de graficación, como proceso de solución del SEL,
permitió a los estudiantes tener una mejor comprensión del problema y responder las
preguntas planteadas tanto por el problema como por la profesora.
El Problema 1 fue realmente un problema para los equipos de estudiantes, quienes tuvieron
dificultad para abordarlo. El papel de la profesora fue esencial para replantear, contextualizar,
propiciar discusiones y análisis del problema y, por lo tanto, para apoyar el proceso de
solución a partir de cuestionamientos dirigidos a los equipos de estudiantes. Las preguntas
que planteó permitieron reflexionar a los estudiantes respecto a los conceptos de incógnita,
variable, ecuación y solución de un SEL. El monitoreo constante de los procedimientos de los
equipos fue importante para evaluar el conocimiento matemático de los estudiantes, el nivel
XVIII Encuentro de Profesores de Matemáticas
Página 61
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
de comprensión del problema, y por lo tanto, el planteamiento de preguntas que propiciaran
discusión en los equipos. La observación constante permitió plantear preguntas pertinentes en
momentos claves del proceso de resolución. Los procedimientos que emprendieron los
estudiantes dieron acceso a la profesora respecto al nivel de desarrollo de contenidos
matemáticos así como del nivel de comprensión del problema.
Referencias
De Corte, E. (2007). Learning from instruction: the case of mathematics. En Learning Inquire,
1, 19-30.
Grouws, D. A. (2004). The Teacher‟s Role in Teaching Mathematics through Problem
Solving. En H. L. Shoen (Ed.), Teaching Mathematics through Problem Solving.
Grades 6-12 (pp. 129-141). USA: NCTM.
National Council of Teachers of Mathematics. (2003). Principios para la Educación
Matemática. (M. Fernández, Trad.). España: Sociedad Andaluza de Educación
Matemática Thales. (Trabajo original publicado en 2000).
Rasmussen, C., Yackel, E. & King, K. (2004). Social and Sociomathematical Norms in the
Mathematics Classroom. En H. L. Shoen (Ed.), Teaching Mathematics through
Problem Solving. Grades 6-12 (pp. 143-154). USA: NCTM.
Santos, L. M. (1997). Principios y métodos de la resolución de problemas en el aprendizaje
de las matemáticas. México: Grupo Editorial Iberoamérica.
Schoenfeld, A. H. (1985). Mathematical problem solving. USA: Academic Press, Inc.
XVIII Encuentro de Profesores de Matemáticas
Página 62
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
III. Mesas de discusión
XVIII Encuentro de Profesores de Matemáticas
Página 63
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
El posgrado de Matemática Educativa en la UAEM
Dr. Enrique Vega Villanueva
[email protected]
Universidad Autónoma del Estado de Morelos
Los inicios
Desde que se creó, en 1990, la Unidad de Matemática Educativa (UME) estuvo funcionando
con el apoyo académico de profesores-investigadores del CINVESTAV-IPN. El convenio que
se tuvo fue de manera tangencial con esa institución pues se firmaron, primero con el
Programa Nacional de Formación y Actualización de Profesores de Matemáticas (PNFAPM)
y posteriormente con la Sociedad Mexicana de Matemática Educativa (SMME). Al frente se
encontraba el Dr. Eugenio Filloy Yagüe.
Evaluación del CIEES
El Comité Interinstitucional de Evaluación de la Educación Superior realiza en 1997 una
evaluación a la UME en la cual resulta con serias deficiencias, sobre todo porque no tiene
asignados Tiempos Completos ni independencia académica respecto del SMME.
Reestructuración
En el 2003 se termina el convenio con la SMME. En el 2004 se inicia un proceso de
reestructuración de su programa de posgrado, para lo cual se nombra al Dr. Mario Flores
como responsable de la comisión y como integrantes al M.C. Antonio Arana Pineda, director
del ICE, y al Dr. Enrique Vega Villanueva, recién nombrado coordinador académico de la
UME. En el 2004 se presentó al Rector una primera propuesta de reestructuración, la cual
quedó pendiente.
Programas: Matemática Educativa y Enseñanza de las Ciencias
La UME contó con dos programas de posgrado, el primero de especialidad, maestría y
doctorado en Matemática Educativa, y el otro de especialidad y maestría en Enseñanza de las
Ciencias. La idea central de la reestructuración fue tener un único programa de posgrado hasta
doctorado, centrado en la idea de ofrecer a los docentes de todos los niveles educativos, la
posibilidad de una actualización disciplinar, de una preparación en los aspectos pedagógicos
de su actividad, y de una formación como investigadores en el campo de los problemas de
enseñanza y aprendizaje que se presentan al interior de las aulas.
Resultados
La UME hasta el 2003 tuvo 11 generaciones y diez convenios que suscribió la UAEM con
diversas instituciones del país donde el PNFAPM o la SMME eran los encargados de la
operación de los pro-gramas académicos, dando la UAEM el grado (ver anexo).
XVIII Encuentro de Profesores de Matemáticas
Página 64
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Última etapa
Del 2004 al 2009 todas las actividades fueron llevadas a cabo con la restricción de ser
estrictamente auto-financiables. Se tuvieron en la UME dos generaciones de maestría, tres
convenios con dos instituciones, tres grupos de titulación extemporánea y un grupo de
doctorado. Se llevó a cabo la regularización de la maestría en Enseñanza de las Ciencias de la
cual se iniciaron dos grupos uno en la UME y otro en convenio con la UJED (Ver anexo).
Condiciones en los últimos convenios
A partir del 2004 los convenios que se firmaron fueron con la modalidad de que los alumnos
inscritos pagaran una colegiatura trimestral a la UAEM, haciéndose responsable la UME-ICE
de aportar un profesor y otro la otra institución de los dos que se requieren en cada período.
Los gastos de operación corren también a cargo de la otra institución.
Planta docente
Los docentes que participaron en la última etapa de la UME-ICE, de finales del 2003 al 2009,
fueron once de la UAEM; doce Invitados; y 20 de convenios. El programa en las generaciones
de la UME-ICE funcionaron, fundamentalmente, con profesores de la UAEM adscritos a
diferentes unidades académicas. Regularmente se invitaron a algunos investigadores del
CINVESTAV y de la UNAM, a impartir algunos seminarios y dirigir tesis.
Los profesores de la UME-ICE que han participado en los distintos proyectos son:
1.
Dr. José Rubén Rosas Salgado. Preparatoria de Cuautla.
2.
Dr. Valentín de Mata Arce. Facultad de Psicología; ICE.
3.
Dr. Jorge Armando Peralta Sámano. TC de la ETLB.
4.
Dr. Ignacio Delgado Escobar. Facultad de Agropecuarias.
5.
Dr. Enrique Vega Villanueva. Preparatoria 1 Diurna.
6.
Mtro. Guillermo Tinoco Ojeda. Preparatoria de Cuautla.
7.
Mtro. Miguel Ángel Ibarra Robles. Preparatoria de Jojutla.
8.
Mtro. Jesús Martínez Rogel. Preparatoria 2 Diurna.
9.
Mtra. Areli Canales Sánchez. Preparatoria de Cuautla.
10.
Mtro. Javier Bahena. Preparatoria 1 Diurna.
11.
Dr. Vicente Hernández Sánchez. SEP y colaborador de la UME desde 1995.
12.
Dr. José Guzmán Hernández. CINVESTAV.
13.
Dr. Marco Antonio Santillán. UNAM.
14.
Dr. Rodrigo Cambray Núñez. UNAM.
15.
Dr. Celerino. UAG.
16.
Mtro. Luis Arau Roffiell. ITZ y alumno de doctorado de la UME-ICE.
XVIII Encuentro de Profesores de Matemáticas
Página 65
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
17.
Mtra. Dana Matosic. Marymount de Cuernavaca y alumno de doctorado de la UMEICE.
18.
Mtro. Valois Nájera. SEP y alumno de doctorado de la UME-ICE.
19.
Mtro. Raúl Muñoz Astudillo. SEP y alumno de doctorado de la UME-ICE.
20.
Mtro. Humberto Velázquez Solorio. UPN y alumno de doctorado de la UME-ICE.
Generaciones
Generación
Ume 01
Ume 02
Ume 03
Ume 04
Ume 05
Ume 06
Ume 07
Ume 08
Ume 09
Ume 10
Ume 11
Ume 12
Ume 13
Instituto Tecnológico de Zacatepec
Benemérita Universidad Autónoma de Puebla
Universidad de Baja California
Tecnológico del Estado de Chihuahua
Colegio de Bachilleres del Estado de Michoacán
Universidad Autónoma de Ciudad del Carmen
Secretaría de Educación Pública del Estado de
Chiapas
Tecnológico del Estado de Aguascalientes
Colegio de Bachilleres del Distrito Federal
Universidad Michoacana de San Nicolás de
Hidalgo (3)
Universidad Modelo de Yucatán
Universidad Juárez del Estado de Durango MEM
Universidad Juárez del Estado de Durango MEC
Smme-Doctorado
Ume-Doctorado
XVIII Encuentro de Profesores de Matemáticas
Inscritos
42
21
13
15
25
16
27
15
17
8
17
25
25
22
22
6
14
10
15
Egresados
33
13
12
13
18
11
16
10
11
7
8
19
20
20
15
6
10
8
12
Titulados
20
5
6
5
7
6
10
5
3
3
0
En proceso
En proceso
8
2
2
0
4
8
11
15
11
8
12
8
7
10
3
33
16
23
31
25
30
22
15
22
25
20
26
15
9
En proceso
En proceso
Página 66
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Actividades 2003-2009
Actividad
Fecha
U-Modelo
UME-Extemporáneo-1
UME-12ª
UME-Doctorado
UJED-Matemáticas
UME-Extemporáneo-2
UME-Ciencias
UJED- Ciencias
UME-13ª
UME-Extemporáneo-3
2003
2004
2004
2004
2004
2005
2005
2006
2006
2006
Alumnos
Total
16
40
23
26
23
34
11
31
31
17
XVIII Encuentro de Profesores de Matemáticas
Uaem
X
11
4
15
X
4
11
X
8
0
Profesores
Uaem Convenio
8
8
7
1
16
x
6
3
8
8
6
5
6
x
8
16
16
x
5
2
Página 67
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
La formación de profesores de matemáticas:
el caso del nivel medio superior
Dr. César Cristóbal Escalante
[email protected]
Universidad de Quintana Roo
El profesorado de matemáticas en el nivel medio superior, está conformado por personas que
han realizado estudios de licenciatura en matemáticas y/o física, ingeniería, ciencias naturales,
o economía, principalmente (ver por ejemplo Anuario Estadístico, SEQ, 2006). La mayor
parte de ellos no tiene formación docente, aunque algunas de las instituciones de NMS donde
laboran, les ofrecen alternativas para superar esta deficiencia mediante cursos de educación
continua principalmente en el ámbito de la disciplina o de didáctica general.
En los diferentes sistemas de educación media superior, el número de profesores de tiempo
completo es bajo, la mayoría de los docentes son profesores de asignatura, por lo que existe
mucha movilidad y por ello el impacto de los cursos de actualización de los profesores en el
desempeño de los estudiantes puede ser pobre y difícil de evaluar.
La formación matemática de los profesores de la disciplina en este nivel se basa en los cursos
de matemáticas que constituyen la currícula de las diferentes carreras de la licenciatura
estudiada. Esta formación matemática en la licenciatura pretende dotar al profesionista de
conocimientos matemáticos útiles para enfrentar los problemas en su ejercicio profesional,
pero no para la docencia. Puede incluir conocimientos sobre álgebra (resolución de
ecuaciones lineales y sistemas de ecuaciones lineales, elementos del álgebra lineal), geometría
analítica, cálculo diferencial e integral en una y dos variables, ecuaciones diferenciales,
métodos numéricos, estadística y probabilidad.
La currícula matemática del NMS, se puede caracterizar por dos aspectos del mismo: el
carácter propedéutico y el formativo. Propedéutico en el sentido de preparar al estudiante para
realizar estudios superiores, y formativo por dar la formación general, esto es, por desarrollar
en el estudiante los conocimientos que le permita incorporarse a la vida productiva de la
sociedad. Por ello la currícula matemática del NMS tiene el propósito de dar una formación
integral en matemáticas de manera que el estudiante tenga una visión de ellas como parte del
conocimiento humano, y que desarrolle conocimientos, habilidades, valores y actitudes
matemáticas para usarlas en su vida cotidiana, en sus actividades productivas y /o al realizar
estudios superiores.
También, y derivado del desempeño de los egresados del NMS en los cursos de licenciatura,
se han identificado algunas características de los conocimientos matemático adquiridos por
ellos. Se ha observado que el conocimiento desarrollado en el NMS por los estudiantes es
más algorítmico y memorístico, esto es, los egresados recuerdan definiciones de conceptos y
descripciones de procedimientos y reglas, y las pueden aplicar en situaciones muy semejantes
a las abordadas en el aula, pero no pueden transferirlas a situaciones que se les presentan en
su casa, taller, oficina, o al realizar estudios posteriores. Dado que la currícula de matemáticas
del NMS tiene dentro de sus objetivos el desarrollo de conocimientos, habilidades, valores y
actitudes en esta dirección, este objetivo no es alcanzado plenamente.
XVIII Encuentro de Profesores de Matemáticas
Página 68
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
En muchos sistemas educativos, en particular en el NMS en México, al tratar de mejorar los
conocimientos matemáticos que adquieren los estudiantes se tiende a realizar modificaciones
en el ámbito de la currícula, sin considerar otros factores que inciden en el proceso de
aprendizaje, y sin ver la naturaleza sistémica de los procesos educativos. Un proceso de
evaluación del proceso educativo en el nms debería incorporar un análisis de los diferentes
factores que inciden el aprendizaje: entre ellos, el papel de los profesores.
Todas estas actividades para mejorar los resultados en el aprendizaje de las matemáticas
requieren de personal académico capacitado, con conocimientos matemáticos amplios que le
den una visión general de las matemáticas como una área del conocimiento desarrollada por la
humanidad, usando la reflexión y la sistematización de experiencias, que utiliza diversas
formas de representación para comunicar sus ideas y resultados; con un conocimiento del
sistema y procesos educativos y de aprendizaje, que les permita reconocer la función de las
instituciones educativas en la sociedad y el papel del estudiante en el proceso de aprendizaje.
¿Qué conocimientos deben desarrollar los profesores de matemáticas sobre la disciplina,
sobre su enseñanza y sobre su aprendizaje para que los estudiantes aprendan los
conocimientos establecidos en los objetivos curriculares?
Shulman (1986) propuso que el conocimiento profesional para enseñar debe estar integrado
por siete elementos base, a saber: (i) Conocimiento del contenido, tanto “sustantivo” como
“sintáctico” (Por conocimiento sustantivo se entiende el conocimiento de hechos y conceptos
de la disciplina, y las formas en que están organizados. Por conocimiento sintáctico se
entiende el conocimiento sobre la naturaleza de la indagación en ese campo, como se genera y
acepta nuevo conocimiento en esa comunidad, e incluye conocimiento sobre demostraciones
y reglas de estructuras); (ii) Conocimiento pedagógico general: principios genéricos de
manejo del aula; (iii) Conocimiento curricular: materiales y programas; (iv) Conocimiento de
contenido pedagógico: para un área dada, e incluye formas de representación de conceptos,
analogías útiles, ejemplos y demostraciones; (v) Conocimiento de los estudiantes; (vi)
Conocimiento de los contextos, comunidades y culturas educativas; (vii) Conocimiento de los
propósitos y valores educativos. Señala que la integración del conocimiento de la disciplina
con el conocimiento sobre la enseñanza y el aprendizaje es un aspecto importante para que la
enseñanza sea exitosa.
Un análisis de las funciones y tareas que debe realizar un profesor de matemáticas, permitirá
ubicar la pertinencia de lo señalado por Shulman.
Las tareas docentes que realiza un profesor de matemáticas en el NMS son: Seleccionar,
diseñar, elaborar, administrar las actividades de instrucción, guiar y coordinar las actividades
de los estudiantes en el aula, y evaluar los conocimientos aprendidos, de acuerdo con los
programas oficiales vigentes, fundamentalmente. Participa en comisiones de revisión
curricular o envía opiniones sobre la aplicación de los cursos y el desempeño de los
estudiantes en los mismos.
Para realizar estas actividades, el profesor debe tener un conocimiento “suficiente” de: los
temas matemáticos incluidos en los programas de los cursos, de los problemas de aprendizaje
asociados con los conceptos y métodos matemáticos involucrados, de las prácticas de
instrucción que propician el desarrollo de habilidades, valores y actitudes positivas hacia el
conocimiento y el conocimiento matemático en particular, de cómo aplicar esos
conocimientos matemáticos y conceptos a situaciones no matemáticas, y analizarlas usando
XVIII Encuentro de Profesores de Matemáticas
Página 69
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
los conceptos y teorías matemáticas. Debe tener conocimientos sobre lo que significa evaluar
y sobre los criterios adecuados para tomar decisiones respecto a los conocimientos
desarrollados por los estudiantes.
Para poder enfrentar futuros cambios en la currícula, debe tener los conocimientos y
habilidades que lo capaciten para poder acceder a nuevos conocimientos por él mismo. Esto
es debe desarrollar sus habilidades para aprender a aprender.
Si bien se está de acuerdo en que los profesores deben tener conocimientos de los aspectos
arriba mencionados, hay discrepancias acerca de la profundidad y de la amplitud de esos
conocimientos. Es de notar que la cantidad de conocimiento en torno a los aspectos señalados
es muy amplia, toda ella susceptible de ser estudiada y aprendida por los profesores. Esta debe
ser elegida en función de criterios ligados con el perfil de profesor que se desea formar.
El proceso de aprendizaje de un individuo se da en un contexto de su interacción con otros
individuos para enfrentar conjuntamente una situación, y en la cual juegan un papel
importante sus conocimientos, habilidades y valores previamente desarrollados, los cuales
sirven de base para el desarrollo de nuevos conocimientos, de nuevas habilidades, actitudes y
valores hacia las matemáticas y hacia su aprendizaje (Lesh y Doerr, 2003).
El tiempo de los programas de formación es finito, por lo general de dos años en el nivel de
maestría. Esto tiene implicaciones sobre las actividades que deben desarrollar el profesor y el
tiempo que les debe dedicar para desarrollar los conocimientos, habilidades, actitudes y
valores que caracterizan al egresado del programa.
Deben ser considerados diferentes tipos de programas, (por lo menos para México): (a).
Programas de formación complementaria para la docencia en el nms. Esto es la capacitación
para los actuales profesores y para los que desean obtener capacitación para la docencia en
matemáticas, y que no han tenido ninguna formación docente. (b) Programas de formación
docente en matemáticas. Que son licenciaturas y posgrados dirigidos a la formación de
profesores de matemáticas.
Referencias
Lesh, R. and Doerr, H. M. (Eds.) (2003). Beyond Constructivism. Models and modeling
perspectives on mathematics problem solving, learning, and teaching. Lawrence
Erlbaum Associates, Publishers. Mahwah, NJ.
Secretaría de Educación (2006). Anuario Estadístico. Secretaría de Educación del Estado de
Quintana Roo.
Shulman, L. S. (1986). Those who understand: knowledge growth in teaching. Educational
Researcher, 15(2), 4- 14.
XVIII Encuentro de Profesores de Matemáticas
Página 70
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Formación de Profesores y Uso de Tecnología
Dr. Aarón Reyes Rodríguez
[email protected]
Universidad Autónoma del Estado de Hidalgo
¿Cuáles son los objetivos de la formación docente? ¿Qué características debe tener un
programa de formación de profesores? ¿Quiénes deben participar en esos programas de
formación? ¿Cuál es el papel del uso de las tecnologías digitales en la formación de los
profesores de matemáticas?
El objetivo principal de los programas de formación docente, es brindar a los profesores
oportunidades que les permitan adquirir conocimientos, para llevar a cabo acciones que
apoyen a los estudiantes en la adquisición de una forma matemática de pensar y un
entendimiento conceptual de diversas ideas matemáticas, lo cual significa poseer fluidez
procedimental; capacidad mental para conectar hechos, procedimientos e ideas de una misma
área, con los de otras áreas de las matemáticas o de otras disciplinas (Hiebert y Grouws,
2007), así como una actitud creativa.
Los programas de formación deben proporcionar oportunidades para que los profesores
desarrollen conocimientos, habilidades y la disposición que se requiere para enseñar
matemáticas. Los profesores requieren conocer a profundidad los contenidos que enseñan;
entender cómo aprenden matemáticas los estudiantes y saber cuáles son los principios que
orientan esas formas de aprendizaje, lo cual lleva consigo la adopción de una postura en
relación con la naturaleza de las matemáticas y del conocimiento matemático; también es
importante que los profesores comprendan a profundidad la didáctica del contenido
matemático, que adquieran habilidades para enseñar, acordes con la naturaleza del
conocimiento matemático (Harel, 1994; Harel y Lim, 2004). Idealmente, este conocimiento
permitirá a los profesores elegir actividades apropiadas para favorecer la compresión
matemática de sus estudiantes (Sowder, 1997).
Se argumenta que los programas de formación de profesores de matemáticas, deben ser
diseñados y puestos en práctica por las universidades públicas, además de que los mismos
deben contar con la participación coordinada de: (1) profesores en servicio, quienes cuentan
con los conocimientos de la complejidad diaria que se vive en el aula; (2) de los matemáticos,
ya que son ellos los generadores de nuevos conocimientos en la disciplina y (3) de los
educadores matemáticos, quienes tratan de entender la problemática del aprendizaje. Estas
consideraciones se basan en evidencias tomadas de algunos programas de formación de países
como Estados Unidos, Canada y España, entre otros; en los que por un lado se ofrecen cursos
de matemáticas y por otro, cursos de “metodología” los cuales no están estructurados
apropiadamente (Harel, 1994).
El uso de las herramientas computacionales en el aula es una práctica cada vez mayor, por
esta razón, el entendimiento de los principios que regulan el aprendizaje de los estudiantes
mediado por el uso de las tecnologías digitales debe ser parte del conocimiento básico del
profesor. En este contexto, el uso de las tecnologías digitales en los programas de formación
docente resulta fundamental, así como la discusión de ideas tales como el principio de
mediación instrumental, el cual señala que toda acción cognitiva está mediada por el uso de
XVIII Encuentro de Profesores de Matemáticas
Página 71
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
instrumentos (Wertsch, 1993); la función de las tecnologías como reorganizadores cognitivos
o el papel de las representaciones ejecutables en la construcción del conocimiento matemático
(Moreno-Armella y Sriraman, 2005; Moreno-Armella, Hegedus y Kaput, 2008). Los
profesores deben experimentar los fenómenos mencionados, con el objetivo de que a través de
una reflexión sobre su propio proceso de aprendizaje, puedan comprender la forma en cómo
los estudiantes aprenden y los ayuden a construir una forma matemática de pensar.
Referencias
Harel, G., & Lim, K. H. (2004). Mathematics teachers‟ knowledge base: preliminary results.
En M. J. Hoines & A. B. Fuglestad (Eds.), Proceedings of the 28th Conference of the
International Group for the Psychology of Mathematics Education. Bergen, Norway:
PME.
Harel, G. (1994). On teacher education programmes in mathematics. International Journal of
Mathematical Education in Science and Technology, 25(1), 113-119.
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on
students‟ learning. En F. K. Lester Jr. (Ed.), Second Handbook of Research on
Mathematics Teaching and Learning (pp.371-404). Charlotte, NC: Information Age
Publishing.
Moreno-Armella, L., & Sriraman, B. (2005). The articulation of symbols and mediation in
mathematics education. ZDM, 36(6), 476-486.
Moreno-Armella, L., Hegedus, S. J., & Kaput, J. J. (2008). From static to dynamic
mathematics: historical and representational perspectives. Educational Studies in
Mathematics, 68, 99-111.
Sowder, J. T. (2007). The mathematical education and development of teachers. En F. K.
Lester Jr. (Ed.), Second Handbook of Research on Mathematics Teaching and
Learning (pp.157-224). Charlotte, NC: Information Age Publishing.
Wertsch, J. V. (1993). Voices of the Mind: a sociocultural approach to mediated action.
Cambridge, Massachusetts: Harvard University Press.
XVIII Encuentro de Profesores de Matemáticas
Página 72
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Formación de profesores y uso de tecnología en la Educación Matemática
Ing. Marcos Campos Nava
Universidad Autónoma del Estado de Hidalgo
Se sabe que existe resistencia entre algunos profesores, incluidos los de matemáticas, para
incorporar a su práctica docente a las nuevas tecnologías, como es el caso de calculadorasgraficadoras o computadoras con software especializado, esto puede ocurrir en parte por la
instrucción matemática que recibió el profesor en su etapa como estudiante, la cual está ligado
con la forma en que concibe a las matemáticas y el cómo las enseña.
Esta resistencia al cambio es incomprensible, pues en la vida cotidiana, los profesores de
matemáticas hacen uso de todo tipo de tecnologías que no estaban a su alcance hace algunos
años, por ejemplo el uso de cajeros automáticos, o enviar mensajes de texto por medio del
teléfono celular, lo cual implicó que modificaran sus concepciones y prácticas acerca del
manejo de sus finanzas o de la forma de comunicarse con sus semejantes, en este sentido,
debería existir una actitud de aceptación por parte del profesor para incorporar nuevas
tecnologías a su actividad.
¿Qué implicaciones tiene para el profesor de matemáticas adoptar el uso de la tecnología en
su práctica profesional? De inicio un cambio de actitud, de igual forma que se necesitó para
aceptar el hecho de que utilizar el cajero automático o el teléfono celular puede hacer más
eficiente algún tipo de transacción o necesidad de comunicación.
No dudamos que exista un gran número de profesores de matemáticas en funciones, sobre
todo aquellos que acumulan varios años de servicio, que puedan considerar que la tecnología
necesaria para dar una buena clase de matemáticas es a lo más una pizarra, una tiza o plumín,
y un libro de texto, lo cual no sería discutible, si la enseñanza tradicional de las matemáticas
hubiera probado ser efectiva para un mayor número de estudiantes.
El cambio de actitud debería ser precedido por un cambio de concepción respecto la
matemática en sí misma, que le permitiera concebirla como una ciencia experimental, la cual
está lejos de ser solamente una serie de reglas que se deben memorizar para aplicarlas
automáticamente ante la necesidad de resolver un problema, es decir, el profesor se debería
convencer de que hay que disminuir las prácticas algorítmicas y rutinarias y favorecer más el
pensar matemáticamente; lo anterior implicaría también cambios o modificaciones al
currículum de matemáticas .
Para que el profesor de matemáticas conozca la tecnología de que puede disponer y el uso que
le puede dar, es necesario que participe en programas de formación y actualización
permanentes, en los que además de profesores se deberán incluir a profesionales en educación
matemática y en términos generales fomentarse la creación de una comunidad de práctica en
el uso de la tecnología para el aprendizaje de las matemáticas.
XVIII Encuentro de Profesores de Matemáticas
Página 73
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Acerca de la existencia de programas de formación de profesores de
matemáticas de bachillerato
M. C. Ignacio Morales González
[email protected]
Universidad Michoacana de San Nicolás de Hidalgo
Introducción
Existen programas de educación y formación de profesores de kínder, primaria y secundaria;
los profesores que atienden estos niveles de estudios, egresan de algún programa en el que se
estudian contenidos relacionados con la educación. Sin embargo, a nivel bachillerato y
licenciatura, en general, no existen tales programas. La mayoría de profesores del bachillerato
somos egresados de distintas carreras de nivel licenciatura que no contemplan la formación de
profesores dentro su programa curricular, ni se estudian contenidos relacionados con la
educación; en el nivel superior los profesores son egresados de licenciaturas afines a las que
trabajan.
En los programas de formación se enseñan conocimientos de pedagogía y psicología que
tienen que ver con la enseñanza y el aprendizaje de las matemáticas; en consecuencia, los
profesores que trabajamos en el bachillerato no tenemos tales conocimientos, sobre todo
cuando nos iniciamos en el trabajo docente. En nuestra carrera adquirimos conocimientos que
nos servirán para desenvolvernos en nuestra vida profesional, pero no somos preparados para
llevar a cabo el proceso de la enseñanza y aprendizaje de las matemáticas, en el cual estamos
inmersos cada día.
Existe la creencia de que dado que “poseemos el conocimiento de los contenidos”,
matemáticos en nuestro caso, podemos enseñarlo y divulgar a los demás pero, surge la
pregunta: ¿cómo debemos impartir el conocimiento para que sea accesible a nuestros
estudiantes?, pregunta nada fácil de responder.
En nuestras escuelas, frecuentemente escuchamos decir a los estudiantes que ciertos
profesores no sabemos enseñar matemáticas y que como consecuencia de esto se tiene un alto
índice de reprobación en matemáticas; las autoridades y padres de familia no pierden
oportunidad para señalarnos como los culpables de tal situación, lo cual refleja una visión
simplista del complejo problema que representa el proceso de enseñanza aprendizaje. Quizás
por la presión y por falta de preparación, nosotros como profesores nos preocupamos por
hacer algo para disminuir el índice de reprobación, y damos oportunidades haciendo más
exámenes a los alumnos, dando cursos extras o dejando trabajos; a final de cuentas
terminamos aprobando a la mayoría de los estudiantes los estudiantes que es una de las
principales angustias de las autoridades educativas y, de esta manera aunque sea
artificialmente, se “resolvió el problema de los altos índices de de reprobación”.
Estas situaciones hacen la necesidad de que existan programas de formación en educación
matemática para profesores de bachillerato y licenciatura, si bien el problema se acentúa en el
bachillerato no podemos descartar que tal situación se presenta también en la licenciatura.
Surge la necesidad de que existan programas de formación y actualización en educación
matemática: programas de maestría y doctorado, foros de actualización y formación,
diplomados y encuentros de profesores de matemáticas.
XVIII Encuentro de Profesores de Matemáticas
Página 74
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Estos programas nos permiten recibir y prepararnos acerca de los conocimientos de pedagogía
y psicología que nos permitan comprender porque los conocimientos se dificultan a los
estudiantes, pero también debemos ser preparados y actualizados en los objetos matemáticos
que tenemos que enseñar, “no divulgar” y que no basta que los adquirimos cuando estudiamos
la licenciatura, es claro que los adquirimos con un fin; pero no fue el de impartirlos para
enseñar.
Los encuentros de profesores de matemáticas nos permiten enterarnos de lo que cada profesor
está haciendo en su trabajo, en la docencia o en la investigación, o de qué manera aborda los
objetos matemáticos para que le sean más accesibles a los estudiantes.
Los profesores de bachillerato y licenciatura nos formamos en el camino de nuestro trabajo
cotidiano; cuando nos iniciamos como docentes la mayoría de nosotros no sabemos como
empezar y lo primero que hacemos es imitar al profesor que mejor sentimos nos enseñó o fue
nuestro mejor maestro, y esta situación es un modelo de profesor que se repite cada que nos
iniciamos como docentes, estudiamos los temas que vamos a impartir, buscamos estrategias
de cómo enseñar ciertos objetos matemáticos y seguimos las formas tradicionales de
evaluación y creemos que estamos en el camino correcto. Probamos estos métodos cada
semestre o cada año según sea el ciclo escolar, lo hacemos de una manera empírica, pero no
científica y creemos que así debe ser y que lo podemos generalizar hacia los demás
estudiantes y que esa es la forma correcta de enseñar como profesor y de aprender de los
estudiantes. Sin embargo, no podemos darnos cuenta que esto no puede ser lo más indicado
que debe hacerse en el proceso de enseñanza y aprendizaje de las matemáticas, lo
generalizamos sin tener bases científicas o conocimientos probados científicamente por
investigadores.
Esta situación hace la necesidad de que surjan programas de formación y actualización de
profesores en educación matemática, que nos permitan prepararnos y estar actos para que
nuestro trabajo empírico que hacemos lo podamos hacer mejor y extensivo y generalizarlo
cuando sea necesario, programas que nos den la pauta de buscar alternativas de cómo hacer
más accesibles los conocimientos de los objetos matemáticos que enseñamos, que nos
permitan buscar formas de evaluar el aprendizaje de los objetos matemáticos y dejemos las
formas tradicionales con las que fuimos evaluados durante nuestra formación.
Si bien es cierto, a estas alturas las formas de evaluar siguen siendo las mismas con las que
nos evaluaron, todavía existimos profesores que seguimos el viejo modelo de evaluación de
aquellos profesores duros rígidos que decían: el diez es para el libro, el nueve para el profesor
y del ocho para abajo para los alumnos, modelo que no permite al profesor que es lo que va a
evaluar ni como lo va a evaluar.
La forma tradicional de evaluar solo con exámenes parciales o finales, con tareas y en
ocasiones algún trabajo. Los exámenes no nos permiten ver si el estudiante comprende los
conocimientos que impartimos día a día, solo al final del periodo de evaluación nos daremos
cuenta si los comprendió o no si es que estudia y ahí está el me hoyo del asunto, la mayoría de
los alumnos no tienen la costumbre de estudiar para el día del examen y como consecuencia
reprueban, pero sabemos que todo conocimiento aprendido se olvida con el tiempo o se pierde
de manera parcial y aquel estudiante que aprendió durante la clase y que no nos dimos cuenta
que lo aprendió reprueba, y no nos dimos cuenta porque nuestra forma de evaluar no nos lo
XVIII Encuentro de Profesores de Matemáticas
Página 75
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
permitió, ese estudiante al final del semestre engruesa las filas de los reprobados haciendo que
aumente el índice de reprobación.
Actualmente, ya existen varios programas de formación y actualización de profesores en
educación matemática, pero los hay solo en ciertos lugares y que además no son accesibles a
la mayoría de profesores de matemáticas, se requiere de más programas que cuenten con
recursos para que el profesor pueda acceder a ellos, tales recursos deben ser: descargas
académicas a los profesores interesados, apoyos económicos, tales como becas y cualquier
otro apoyo que haga que los profesores se interesen en los programas y en esa medida creo
que nuestros índices de reprobación van a disminuir, claro que siempre tendremos alumnos
reprobados, alumnos que tendrán otro tipo de problemas o que simplemente no estudian y que
van a la escuela porque los mandan sus papas, pero este índice de reprobación siempre será
muy inferior al actual.
Yo por mi parte puedo decirles que el haber hecho una maestría en educación matemática me
ha puesto en el primer escalón de la escalera de mi trabajo como docente y que veo que son
muchos más los escalones que tengo que subir y que siento ahora que es más fácil subir que
bajar al piso donde estaba, con haber estudiado esta maestría me he dado cuenta que hay
mucho que hacer en mi trabajo de docente y que me he dado cuenta de cómo conducir este
trabajo que he venido haciendo de manera empírica. Siempre estoy en la búsqueda de
modelos o recursos que me permitan hacer más accesible los objetos matemáticos a los
estudiantes y no el de quitar el grado de dificultad que los objetos matemáticos presentan,
pues eso será difícil, o quizás imposible, la enseñanza de los objetos matemáticos radica en
cómo hacerlos más accesibles a los alumnos, aún con su grado de dificultad, buscando
modelos de enseñanza o recursos didácticos, de tal manera que los alumnos puedan acceder a
los conocimientos y no como algunos pensábamos que se pueden enseñar como un arte o que
existe una forma única de enseñar y tengamos que buscarla o aprendamos la receta de cómo
enseñar, creo que en la medida que estemos más preparados y dominemos los objetos
matemáticos que pretendemos enseñar, es taremos en el camino correcto de la educación
matemática.
Propuesta para la factorización algebraica
A continuación presento un modelo geométrico que me ha funcionado para impartir el tema
de factorización, el cual fue parte de mi trabajo de tesis de maestría.
Este modelo geométrico funciona para factorizar polinomios cuyas raíces sean racionales y
que se facilita a los estudiantes cuando son enteras. El algoritmo del modelo consiste en
formar un cuadrado o rectángulo con los términos del polinomio, que a su vez representan
también cuadrados o rectángulos que comparten la altura o la base entre ellos y por medio de
la compensación de áreas, que consiste en agregar rectángulos de áreas positivas o negativas
hasta formar el cuadrado o rectángulo deseado, en caso de que este no sea posible formarse
agotando todas las formas posibles, se concluye que el polinomio no es factorizable en los
racionales. En las siguientes imágenes se presenta la factorización de los polinomios:
x5 – 32;
y
2x4 + 3x3 – 12x2 – 7x + 6
XVIII Encuentro de Profesores de Matemáticas
Página 76
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 1. Factorización usando álgebra geométrica.
XVIII Encuentro de Profesores de Matemáticas
Página 77
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
IV. Talleres
XVIII Encuentro de Profesores de Matemáticas
Página 78
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Algunas características de actividades de aprendizaje con tecnología
Dr. Fernando Barrera Mora
Dr. Aarón Reyes Rodríguez
[email protected]
[email protected]
Universidad Autónoma del Estado de Hidalgo
Introducción
Algunos medios escritos nacionales han señalado que existen serias deficiencias en la
educación matemática de los estudiantes en el nivel bachillerato; por ejemplo, durante el año
2009 La Jornada publicó algunas notas en las que se indica que alrededor de 81% por ciento
de los estudiantes del nivel medio superior poseen un nivel ínfimo en matemáticas (Avilés,
2009; Fernández-Vega, 2009; Poy, 2009). Asimismo, también se menciona que 40 por ciento
de los profesores de bachillerato no tienen un título que avale sus conocimientos (Avilés,
2009; Olivares-Alonso, 2009).
Al considerar estos datos, necesariamente surgen preguntas relacionadas con la correlación
que existe entre los niveles de aprovechamiento de los estudiantes y los conocimientos
disciplinares y pedagógicos de los profesores. En este sentido, algunos investigadores
consideran que la clave para el mejoramiento de los conocimientos matemáticos de los
estudiantes consiste en colocar en cada salón de clases a profesores altamente preparados
(Sowder, 2007). Pero, ¿qué significa preparar a los profesores?, y ¿cuál es el papel que deben
jugar las instituciones nacionales de educación superior, principalmente las universidades
públicas, en la formación y actualización de los profesores de los diferentes niveles? En países
como Estados Unidos, Canadá y España, la formación de los docentes de bachillerato está a
cargo de las universidades; sin embargo en muchos casos es una formación que no se
encuentra estructurada, ya que por un lado, los futuros profesores cursan algunas materias de
matemáticas en las facultades de ciencias y algunos cursos de didáctica en las facultades de
educación.
No se discute que las instituciones públicas de educación superior deben adoptar un papel
como rectoras en la formación y actualización de profesores en el nivel bachillerato, dada la
inexistencia de programas específicos para tal fin (Barrera, 2009a). Sin embargo, los
programas que se ofrezcan deben estructurar y unificar los contenidos matemáticos,
pedagógicos y didácticos necesarios para la actividad docente y contar con la participación
coordinada de matemáticos y educadores matemáticos.
La formación y actualización docente en el nivel medio superior es relevante, pues profesores
bien preparados estarán en mejores condiciones de apoyar y guiar el desarrollo cognitivo de
los estudiantes de ese nivel. Se requiere de manera particular, que los profesores de
matemáticas estén capacitados para ofrecer una enseñanza de la disciplina en la que se
destaquen posibles aplicaciones, tanto en la vida cotidiana como en los estudios que
posteriormente emprenderán.
En esta dirección, algunos investigadores han argumentado que los programas de formación y
actualización de los profesores de matemáticas debe girar en torno a tres componentes del
conocimiento: (i) matemáticas, (ii) epistemología y (iii) didáctica (Harel, 1994; Harel y Lim,
2004; Shulman, 1987). Adicionalmente a esto, se sugiere que estos programas estén
estructurados de forma que permita a los profesores participar en comunidades profesionales
XVIII Encuentro de Profesores de Matemáticas
Página 79
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
en donde tengan la oportunidad de reflexionar e intercambiar ideas que sustenten y amplíen
sus conocimientos matemáticos y didácticos (Santos-Trigo, 2008). En la constitución de estas
comunidades se resalta la importancia de la participación de los propios profesores, así como
de matemáticos y educadores matemáticos.
El conocimiento de los contenidos matemáticos se refiere a la habilidad para entender un
amplio rango de temas, pero de manera más importante, a la profundidad con la que se
conocen y dominan tales temas. Esta característica del conocimiento matemático de los
profesores es crucial en su actividad en el aula, pues influye de manera directa en lo que
enseñan y en cómo lo enseñan, así como en el tipo de tareas y rutas de instrucción que
proponen para orientar el aprendizaje de los estudiantes. Los profesores deben ser capaces de
transformar el salón de clase en un lugar de práctica matemática, en el cual la colaboración,
para construir conocimiento a partir de tareas matemáticas sustantivas, sea un elemento para
que los estudiantes desarrollen un pensamiento matemático.
Los maestros deben conocer la materia que enseñan. Ciertamente no puede haber algo
más fundamental para la competencia del profesor. La razón es simple: los profesores
quienes no dominan bien un tema muy probablemente no tendrán el conocimiento
necesario para ayudar a los estudiantes a aprender ese tema. (Ball, Thames y Phelps,
2008, p. 404)
El conocimiento de la epistemología incluye el entendimiento de principios sicológicos
básicos que se refieren a cómo aprenden los estudiantes; los profesores deben entender que
los estudiantes construyen su conocimiento al darle significado a los conceptos a partir de sus
conocimientos previos, así como de su relación con los objetos del mundo que les rodea. Los
aspectos didácticos del conocimiento de los profesores se refieren a la forma en que
implementan algunos principios sicológicos para enseñar de acuerdo con la concepción
particular que sostengan sobre la naturaleza de las matemáticas y del aprendizaje (Harel,
1994).
Esta distinción de las tres componentes de conocimientos que debe incluir la formación de un
profesor de matemáticas es únicamente con fines de exposición, pues de hecho, los contenidos
matemáticos en el contexto escolar no pueden separarse de la epistemología y la didáctica;
por el contrario, los tres elementos señalados se encuentran estrechamente estructurados para
ayudar a entender la forma en que los procesos de generación de las ideas matemáticas se
llevan a cabo en el aula; para comprender y abordar las dificultades a las que los estudiantes
se enfrentan durante el aprendizaje de alguna idea matemática y la forma en que los
estudiantes construyen su conocimiento matemático a través de la ejecución de tareas de
instrucción.
Tareas de Aprendizaje y Formación Docente
¿Cuál es la importancia del diseño de actividades o tareas de instrucción? ¿Cuál es la relación
de las tareas con el proceso de aprendizaje? ¿Cuál es la relevancia del diseño de tareas de
instrucción en la formación y actualización profesional de los profesores de matemáticas? En
una perspectiva de resolución de problemas en el aprendizaje de las matemáticas, el
conocimiento se construye a través de la acción que los estudiantes ejercen sobre los objetos
del conocimiento durante el proceso de resolver problemas. En este contexto, las actividades
de instrucción son el vehículo para que los estudiantes aprendan matemáticas. Por lo anterior,
XVIII Encuentro de Profesores de Matemáticas
Página 80
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
las actividades que se implementen en el salón de clase deben diseñarse de forma que den
lugar a procesos inquisitivos de discusión y reflexión matemática que a su vez apoyen la
construcción de un aprendizaje con entendimiento (Hiebert et al., 1997), de un aprendizaje en
el que se de sentido a las ideas o conceptos matemáticos.
De acuerdo con Hiebert “entendemos algo si podemos ver cómo este algo se relaciona con
otras cosas que conocemos” (op. cit., p. 4). Así, el objetivo de las tareas de aprendizaje es
ayudar a que los estudiantes estructuren redes conceptuales robustas a través de las cuales
puedan establecer conexiones entre diversos conceptos de una o diversas áreas de las
matemáticas o entre conceptos matemáticos y de otras áreas del conocimiento.
[Una red o estructura conceptual robusta] se manifiesta mediante la exhibición de
diversas conexiones entre contenidos al abordar una situación problemática. Por
ejemplo, discutir las soluciones enteras de la ecuación x 2  2 y 2 puede llevar a
concluir que 2 es irracional; por otro lado, modificando ligeramente esta ecuación
se obtiene x 2  2 y 2  1 , cuyas soluciones llevan a una forma de aproximar 2 . A la
vez, esta ecuación se puede generalizar para estudiar la irracionalidad de la raíz
cuadrada de cualquier número primo, p. La discusión de las soluciones de la ecuación
x 2  py 2  1 , con p un primo, también puede llevar a establecer una relación con la
teoría de fracciones continuadas, herramienta fundamental en diversas áreas de las
matemáticas, tanto puras como aplicadas. (Barrera y Reyes, 2010, pp. 4-5)
Características de las Tareas de Aprendizaje
Con base en lo expresado con anterioridad, el diseño de tareas de instrucción constituye un
elemento clave en la formación docente, ya que estas tareas son el medio para favorecer el
proceso de construcción de conocimiento con entendimiento de los estudiantes. ¿Qué es una
tarea de aprendizaje matemático? ¿Cuáles son las características de estas tareas? ¿Cómo
diseñar tareas de aprendizaje matemático en las que el uso de la tecnología apoye el
aprendizaje de las matemáticas? ¿Qué tipo de preguntas o dilemas pueden formular los
estudiantes como resultado de utilizar sistemáticamente las herramientas tecnológicas en la
ejecución de las tareas? ¿En qué medida las tecnologías digitales funcionan como una
herramienta útil para que los estudiantes visualicen, exploren y construyan relaciones
matemáticas durante sus experiencias de aprendizaje? ¿Qué competencias deben mostrar los
diseñadores de tareas de aprendizaje matemático? ¿Cuáles principios teóricos pueden
sustentar el diseño de las tareas de aprendizaje?
Para los fines que se persiguen en la presente discusión, una tarea de aprendizaje matemático
debe considerar el conocimiento previo del estudiante y proveerle de elementos para el
desarrollo de nuevos conceptos que se articulen con los ya existentes en su red conceptual. De
forma más específica, una tarea de aprendizaje matemático tendrá los siguientes elementos: (i)
un objetivo de aprendizaje, (ii) elementos matemáticos estructurados en torno al objetivo de
aprendizaje, (iii) escenarios para ejecutar la tarea y, (iv) un proceso inquisitivo para
desarrollarla (Barrera, 2009b).
El objetivo de aprendizaje. Es un enunciado en el que se establecen los elementos
conceptuales a ser desarrollados y articulados durante la ejecución de la tarea.
XVIII Encuentro de Profesores de Matemáticas
Página 81
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Los elementos matemáticos estructurados por el objetivo de aprendizaje. En esta parte se
identifican dos clases de elementos. Los externos a la actividad, también llamados recursos
matemáticos, así como aquellos específicamente relacionados con el enunciado del problema.
Los escenarios para desarrollar la tarea. Por un escenario para desarrollar la tarea
entenderemos un lugar físico provisto de los elementos apropiados para realizarla, así como
una comunidad (compañeros, profesor) que permita al estudiante interactuar con sus
miembros, con la finalidad de fomentar un proceso inquisitivo y de esta forma desarrollar los
elementos que le ayuden a expresar o comunicar ideas matemáticas.
Para que los estudiantes vean a la matemática como una actividad con sentido,
necesitan aprenderlas en un salón de clase que sea un microcosmos de la cultura
matemática es decir, clases donde los valores de las matemáticas como una disciplina
se reflejen en la práctica cotidiana. (Schoenfeld, 1988; citado en Santos-Trigo, 1997,
p. 3)
El proceso inquisitivo. Una componente importante al ejecutar una tarea de aprendizaje
matemático consiste en formular preguntas o dilemas tendientes a articular los elementos
matemáticos iniciales con aquellos que conduzcan a la consecución de lo planteado en el
objetivo de aprendizaje y posibles extensiones. Durante el proceso inquisitivo, el tipo de
preguntas o dilemas que se formulen darán lugar al surgimiento de diferentes trayectorias
hipotéticas de aprendizaje (Simon y Tzur, 2004). Es importante mencionar que el proceso
inquisitivo se ve ampliado significativamente con la incorporación de herramientas
computacionales, como se ilustra en las tareas matemáticas que se proponen en este
documento.
El diseño y puesta en práctica de las tareas de aprendizaje matemático suponen del profesor
dos componentes esenciales. Por un lado, poseer conocimientos matemáticos que le permitan
satisfacer sus necesidades instruccionales, es decir, que sus conocimientos sean apropiados
para dar sentido a los procesos matemáticos involucrados en una tarea; que sea capaz de
identificar relaciones matemáticas y apreciar conexiones e interpretaciones así como el uso de
varios tipos de argumentos para validar y sustentar dichas relaciones (Davis y Simmt, 2006).
Y por otro, conocer y reflexionar acerca de los procesos que tienen lugar durante el
aprendizaje de las matemáticas.
¿De qué manera puede un profesor de matemáticas adquirir las competencias necesarias que
le permitan diseñar tareas de aprendizaje matemático? ¿Quiénes deben participar en la
formación y actualización de profesores de matemáticas? ¿En qué tipo de programas
educativos deben participar los profesores de matemáticas en servicio para revisar y extender
sus conocimientos matemáticos e incorporar los resultados de investigación a su práctica
docente? ¿Qué experiencias de aprendizaje deben incluir esos programas educativos? Estas
son algunas de las preguntas que deben ser consideradas al diseñar programas de formación y
actualización de profesores de matemáticas tendientes a desarrollar las competencias
requeridas para diseñar y poner en práctica tareas de instrucción. Sin lugar a dudas, los
educadores matemáticos y los matemáticos debieran jugar un papel central en la formación y
actualización de los docentes.
La función del profesor durante el desarrollo de las tareas. Su función consiste en guiar al
estudiante: (a) en la ejecución de la tarea desde el punto de vista puramente matemático,
ayudándole a formular preguntas que lo orienten en una ruta de aprendizaje y, (b) a
XVIII Encuentro de Profesores de Matemáticas
Página 82
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
conceptualizar las matemáticas como un modo de pensar crítico en el proceso de resolver
problemas. La formulación de preguntas que orienten las rutas de aprendizaje tiene el objetivo
de aportar elementos que lleven al desarrollo de un proceso inquisitivo, entendiéndose por
esto, a la formulación sistemática de preguntas encaminadas a entender y proponer soluciones
a una tarea; así como extender o generalizar el problema original para continuar con un nuevo
ciclo de resolución de problemas (Santos-Trigo, 2007). Como señalan Ball y Bass (2003),
“enseñar matemáticas involucra establecer conexiones a través de diferentes dominios
matemáticos, ayudar a los estudiantes a construir ligas y coherencia en su conocimiento” (p.
12).
Tareas de Instrucción que Promueven el Uso Sistemático de Tecnologías Digitales
Las actividades que se presentan tienen un doble objetivo; por un lado, que los profesores
identifiquen aquellos elementos que constituyen a una tarea de aprendizaje matemático, y de
este modo caractericen algunos principios teóricos y prácticos que pueden apoyarlos en el
diseño de sus propias tareas de instrucción; y por otro, que al abordar las tareas desarrollen
una forma matemática de pensar, que les permita “desempacar” ideas matemáticas,
procedimientos y principios (Ball y Bass, 2003). Es decir, las tareas se enfocan en la
“promoción o construcción de formas particulares de pensamiento, más que en la adquisición
de conceptos o habilidades específicas” (Harel, 1997, p. 117).
A través del desarrollo de cada una de las actividades se resalta la importancia del uso de las
tecnologías digitales durante el proceso de formulación de conjeturas y de procedimientos
para resolver problemas; así como la importancia de elaborar justificaciones deductivas de las
conjeturas u observaciones.
División de áreas de polígonos convexos
El objetivo de esta actividad consiste en fortalecer el pensamiento geométrico de los
profesores, entendiendo por éste a la capacidad para visualizar, describir y analizar, a través
de técnicas inductivas y deductivas, una diversidad de formas y relaciones entre los atributos
de configuraciones geométricas.
Dado un triángulo ABC, encontrar un punto P en su interior, de tal forma que el área de cada
uno de los triángulos ABP, BCP y CAP sea la misma (Figura 1).
Figura 1: Entendimiento del problema.
Considerar casos particulares. Una estrategia para abordar el problema general consiste en
considerar casos particulares que puedan ser más fáciles de resolver y que a la vez aporten
elementos que permitan identificar estrategias generales. Por ejemplo considerar un triángulo
equilátero, un triángulo isósceles o un triángulo rectángulo.
XVIII Encuentro de Profesores de Matemáticas
Página 83
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Triángulo equilátero. Se puede conjeturar que el circuncentro del triángulo es el punto P que
satisface los requerimientos del problema. Se puede obtener evidencia de esta conjetura al
utilizar la herramienta para medir áreas del software y verificar que los tres triángulos (ABP,
BCP y CAP) tienen la misma área (Figura 2).
Figura 2: Explorando un triángulo equilátero.
En este caso se observa que el punto buscado se encuentra sobre una de las alturas del
triángulo. ¿Puede ser de utilidad esta observación para abordar algún otro caso particular?
Considérese ahora un triángulo isósceles ABC; se traza la altura que pasa por el vértice A, al
que concurren los lados iguales, y sea D el pie de ésta.
Considérese ahora el triángulo CBP, con P un punto sobre el segmento AD. ¿Existe algún
punto P, sobre AD, tal que el área del triángulo CBP sea igual a un tercio del área del
triángulo ABC? Con el uso de un software dinámico se puede obtener evidencia de que ese
punto existe (Figura 3). Además, se puede justificar la existencia de tal punto mediante un
argumento de continuidad, pues cuando P=D, el área es cero, mientras que cuando P=A, las
áreas coinciden.
Ahora hay que determinar la posición exacta del punto P de tal forma que sastisfaga las
condiciones que se requieren.
Figura 3: Caso particular de un triángulo isósceles.
XVIII Encuentro de Profesores de Matemáticas
Página 84
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
El área del triángulo ABC (Figura 3) se puede calcular usando la fórmula, Área 
BC  DA
;
2
BC  DP
. Por lo tanto, para que el área del
2
triángulo BCP sea un tercio del área del triángulo ABC se requiere
 que la altura DP sea un
tercio de la altura CA. Con el uso del software se puede obtener evidencia de que los tres
triángulos ABP, BCP y CAP tienen la misma área (Figura 4).
asimismo, el área del triángulo BCP es çrea 
Figura 4: Evidencia numérica de la igualdad de áreas.
¿Es posible proporcionar una prueba formal de que el punto P satisface la condición requerida
sobre los triángulos ABP, BCP y CAP en cuanto a tener la misma área? Por construcción, el
área del triángulo BCP es igual a un tercio del área del triángulo ABC. Además, la recta AD es
eje de simetría del triángulo ABC, entonces los triángulos ABD y ACD son congruentes, así
mismo los triángulos BDP y CPD también lo son. Además, cada uno de los triángulos BDP y
CPD tiene área igual a un sexto del área del triángulo ABC. Por lo tanto los triángulos ABP y
1
1
CAP tienen la misma área y es igual a A( ABC)  A( ABC) , la cual es un tercio del área
2
6
del triángulo ABC.
¿Puede generalizarse el procedimiento empleado con un triángulo isósceles a cualquier tipo
de triángulo? Considérese un triángulo rectángulo, y trácese la altura que pasa por el vértice
en donde el ángulo es recto (ya que en otro caso las alturas son los catetos y el punto P sería
un punto en la frontera del triángulo y no en su interior). Localícese un punto P‟ tal que la
distancia DP‟ sea igual a un tercio de la distancia DA. Este punto satisface que el área del
triángulo BCP‟ es un tercio del área del triángulo ABC. Con el uso del software dinámico se
puede obtener evidencia de que P‟ no es solución del problema (Figura 5).
XVIII Encuentro de Profesores de Matemáticas
Página 85
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 5: Uso del software para refutar una conjetura.
¿Es posible modificar el procedimiento anterior para encontrar un punto P que resuelva el
problema? En la Figura 5, por construcción, se tiene que el área del triángulo BCP’ es igual a
un tercio del área del triángulo ABC. ¿Es posible variar la posición del punto P‟ de tal forma
que el área del triángulo BCP‟ no cambie? Esto es posible siempre que el punto P‟ se mueva
sobre una recta paralela al lado BC del triángulo (Figura 6), por lo que de existir un punto que
sea solución del problema, debe encontrarse sobre esta recta paralela a BC
Figura 6: Trazo de triángulos de igual área.
El procedimiento empleado para construir el triángulo BCP’ podría emplearse de forma
análoga con algún otro de los lados del triángulo, es decir, trazar una recta paralela al lado CA
de forma que la distancia entre este lado y la paralela sea igual a un tercio de la altura del
triángulo ABC que pasa por el vértice B. El punto P, intersección de las paralelas a los lados
BC y CA es solución al problema ya que si cada uno de los triángulos BCP y CAP, por
construcción, tiene área igual a un tercio del área del triángulo ABC, entonces necesariamente
el triángulo ABP tendrá también área igual a un tercio del área del triángulo ABC (Figura 7).
El lector puede comprobar que el mismo procedimiento funciona para cualquier tipo de
triángulo.
XVIII Encuentro de Profesores de Matemáticas
Página 86
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 7: Justificando que el baricentro es solución del problema.
Otra forma de abordar el problema puede consistir en verificar si alguno de los puntos
notables del triángulo (circuncentro, baricentro, ortocentro, incentro) satisface las condiciones
de la solución del problema. Con el uso del software dinámico es posible trazar un triángulo
cualquiera, encontrar los puntos notables y con el uso de las herramientas de medida del
software obtener evidencia o refutar la conjetura en la que se establece que alguno de esos
puntos es una solución del problema.
En el caso del ortocentro, al arrastrar los vértices del triángulo se puede notar que para
algunos triángulos este punto queda fuera de éste, por lo que no es una opción válida para ser
solución del problema general; lo mismo ocurre con el circuncentro. Veamos ahora que
sucede con el incentro y el baricentro del triángulo.
(a)
(b)
Figura 8: Área de los triángulos ABP, BCP y CAP, tales que P es: (a) el incentro del triángulo
ABC y (b) el baricentro del triángulo ABC.
Por definición, el incentro es la intersección de las bisectrices de los ángulos del triángulo; las
perpendiculares trazadas desde el incentro a cada uno de los lados son las alturas de los
triángulos APC, APB y BPC; son todas iguales al radio de la circunferencia incrita en el
triángulo ABC, de ahí que tienen la misma área si y solo si los lados son iguales, es decir, el
único caso en que el punto P, igual al incentro, es solución, es cuando el triángulo es
equilátero.
XVIII Encuentro de Profesores de Matemáticas
Página 87
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
A
E
G
P
B
F
C
Figura 9: El incentro resuelve en el caso de triángulos equiláteros.
Con base en el uso de las herramientas de medida del software dinámico, se puede conjeturar
que el baricentro del triángulo ABC es solución del problema. Sin embargo, es necesario
presentar una demostración de la conjetura.
Una prueba geométrica se puede construir al considerar que la distancia del baricentro a un
vértice del triángulo es el doble de la distancia al punto medio del lado opuesto
correspondiente. Se traza una paralela, por ejemplo, al lado BC por P. Con base en el teorema
de Tales se justifica que la altura del triángulo BCP que pasa por el vértice P es igual a un
tercio de la altura del triángulo ABC que pasa por el vértice A y de ahí se concluye que el área
del triángulo BCP es igual a un tercio del área del triángulo ABC (Figura 10). Aplique un
procedimiento análogo a los triángulos ABP y CAP para concluir que los triángulos ABP,
BCP y CAP tienen la misma área.
A
E
P
G
B
H
F
C
Figura 10: Aplicación del Teorema de Tales a los segmentos AH y AF.
Para elaborar una prueba algebraica del mismo resultado se puede utilizar el hecho de que una
mediana del triángulo ABC divide a éste en dos triángulos de igual área. En la Figura 11, P es
el baricentro del triángulo ABC y M1, M2 y M3 son puntos medios de los lados AB, BC y CA,
respectivamente, de ahí que el área del triángulo BCM1 es igual a la del triángulo CAM1- Con
esta notación, el triángulo ABC queda dividido en seis regiones cuyas áreas las denotamos
por: a1, a2, a3, a4 , a5, a6 . Con base en lo observado antes, se tiene a 2  a3  a 4  a5  a 6  a1 .
Al considerar las otras dos medianas se pueden obtener ecuaciones análogas. Además hay que

XVIII Encuentro de Profesores de Matemáticas
Página 88
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
notar que a1  a 2 ya que los triángulos a los que corresponden dichas áreas tienen bases y
alturas de la misma longitud, por lo tanto sus áreas son iguales, lo mismo se deduce para a 3 y
a 4 así como para a 5 y a 6 . Al operar las ecuaciones anteriores, se puede concluir que
a1  a 2   a 6 .
Figura 11: Las áreas a1, a2, a3, a4 , a5, a6 son iguales.
Un aspecto importante en el desarrollo del pensamiento matemático consiste en extender o
generalizar un problema. En este caso las siguientes preguntas tienen por finalidad estudiar el
caso de un cuadrilátero. Dado un
 cuadrilátero ABCD, ¿existe un punto P en su interior tal que
a partir de este se formen los triángulos ABP, BCP, CDP y DAP, con la misma área? ¿Qué es
el baricentro de un cuadrilátero ABCD? ¿Cómo se construye el baricentro de un cuadrilátero
ABCD? ¿El baricentro del cuadrilátero ABCD es el punto que soluciona el problema, como en
el caso del triángulo? Si el baricentro resuelve el problema del cuadrilátero ¿cuál es la razón?,
si no lo resuelve cabe preguntarse si el problema puede resolverse en general o sólo es posible
encontrar una solución para cuadriláteros particulares.
A
D
B
P
C
Figura 12: Buscando un punto P que divida al cuadrilátero en cuatro triángulos de igual área.
Criterios de divisibilidad
El objetivo fundamental de esta actividad consiste en aportar elementos que ayuden a los
profesores a fortalecer el sentido numérico, entendiendo este como la habilidad para
identificar propiedades de divisibilidad entre números enteros, usar propiedades de los
números primos para resolver preguntas aritméticas, usar relaciones entre las operaciones en
XVIII Encuentro de Profesores de Matemáticas
Página 89
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
los enteros para resolver problemas, entender y usar la representación en base 10 de los
enteros para contestar preguntas de tipo aritmético, estimar, dar sentido a los números y
reconocer sus magnitudes relativas y absolutas, esto último de acuerdo con Sowder (1992;
citado en NCTM, 2000, p. 31).
En el espíritu del estándar, números y operaciones (NCTM, 2000), los estudiantes de nivel
medio superior deben desarrollar un entendimiento profundo de los números y sus
operaciones, así como contrastar las propiedades de los números y los sistemas numéricos. En
esta misma línea de ideas, Silverman (2006) argumenta: “Los años 1990 vieron una oleada
con la reforma del cálculo, cuyo propósito es enseñar a los estudiantes a pensar por ellos
mismos y a resolver problemas sustanciales, en lugar de solamente memorizar fórmulas y
aplicar manipulaciones algebraicas… nuestro tema elegido, Teoría de Números, es
particularmente apropiado para lograr esos propósitos” (Ibíd., p. v).
Tomando como punto de partida los elementos mencionados, hemos elegido hacer una
discusión de algunos criterios de divisibilidad, con la finalidad de aportar elementos que
ayuden a los profesores a construir una estructura conceptual robusta, que les permita diseñar
actividades de aprendizaje a través de las cuales los estudiantes puedan desarrollar un
entendimiento profundo de los números y sus operaciones.
Una de las preguntas más importantes y a la vez de difícil respuesta en teoría de números, es:
dado un número entero n  2 , ¿se puede decidir si es primo o compuesto? Por ejemplo, ¿es
primo el número n = 101010101010101010101? Claramente n no es divisible entre dos, pues
el dígito de las unidades es impar. ¿Cómo saber si n es divisible entre tres o en general entre
algún otro primo
 menor que n?
Posiblemente se conoce el criterio de divisibilidad entre tres, el cual establece: un número es
divisible entre tres, si y sólo si la suma de sus dígitos es divisible entre tres. Usando este
criterio se concluye de manera directa que n no es divisible entre 3.
Un elemento fundamental del pensamiento matemático consiste en proporcionar argumentos
en la discusión de un problema; en esta línea de ideas surge la pregunta. ¿Cuál es la
justificación de este criterio de divisibilidad? Si el número tiene solamente tres dígitos,
digamos n  abc , se debe justificar la razón por la cual, si tres divide a a  b  c , entonces 3
divide a n. En base 10, la representación del número n  abc significa que
n  abc  a  10 2  b  10  c . Esta representación se puede escribir en la forma:
n  abc : a  10 2  b  10  c  a  99 a  b  9b  c  a b  c  99 a  9b .

Se tiene que 99a  9b  9(11a  b) y claramente este número es divisible entre 3; ahora, si
a  b  c es divisible entre 3, entonces a  b  c  99 a  9b también es divisible entre 3,
probando con esto que si 3 divide a la suma de los dígitos de n, entonces 3 lo divide.
Recíprocamente, si 3 divide a n  abc , entonces 3 divide a n  99a  9b  a  b  c , con lo

cual queda justificado el criterio de divisibilidad por tres, para números de tres dígitos. Si el
número n tiene k dígitos, digamos:


n 
 ak1ak2
a0  ak110k1  ak2
10k2 
 a110  a0 ,
entonces n se puede representar en la forma:
n  (ak 1  ak 2 

a1  a0 )  ak 1 10k 1  1 ak 2 10k 2  1
XVIII Encuentro de Profesores de Matemáticas
 a1 10  1.
Página 90
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Notamos que el factor de ai es 10i 1 y que este factor es divisible entre 3 para todo i  0 .
Por ejemplo, para i  1, 2 , el correspondiente factor es 9 y 99, respectivamente, los cuales son
divisibles entre 3, de hecho entre 9. La explicación de esto se tiene al factorizar a 10i 1 en la
i 1, entonces
10 i 1  10 i  2   1. Dado que 9 divide a cada factor 10
forma 10 i  1  10  1

9 divide a ak 1 10k 1  1  ak 2 10k 2  1   a1 10  1. Otra forma de justificar lo anterior
 garantiza que es
es notar que los dígitos de 10i 1 son todos iguales a 9, y esto claramente
 a1  a 0 ) , entonces
divisible entre 3. Recíprocamente, si 3 divide al número (a k 1  a k 
2 
3 divide a la suma de este con otro que sea divisible entre 3; como 3 divide a cada sumando
de la forma ai 10i 
1 , entonces divide a






 a1  a0 )  ak 1 10k 1  1 ak 2 10k 2  1
 a1 10  1.
Recíprocamente, si 3 divide a

n  (ak 1  ak 2  a1  a0 )  ak 1 10k 1  1  ak 2 10k 2  1 
 a1 10  1,
n  (ak 1  ak 2 


entonces divide a n  ak 1 10k 1  1  ak 2

10
k 2

 1


 a1 10  1  ak 1 
 a0 .
El criterio de divisibilidad entre 9 es similar al criterio de divisibilidad entre 3: un número es
divisible entre nueve, si y sólo si la suma de sus dígitos es divisible entre nueve. La prueba del
resultado es análoga a la desarrollada para divisibilidad entre 3 y se deja como ejercicio para
el lector.
La representación de un entero en base 10 ha sido de utilidad para justificar el criterio de
divisibilidad entre 3, esta misma idea puede ayudar ha contestar si
n=101010101010101010101 es primo o compuesto. Haciendo uso de la representación en
1022 1
base 10 se tiene: 101010101010101010101 1 102  104   1020  2
. Por otro lado,
10 1
el numerador de esta última fracción se puede factorizar en la forma
10 22 1
10 22  1  10 11  110 11  1; de esto concluimos que el cociente
tiene al menos dos
2
10
1

factores mayores que 1, por lo que 101010101010101010101 no es primo.
Usando la representación de un número en base 10 se puede intentar obtener otros criterios de
divisibilidad. Una pequeña modificación en la discusiónanterior proporciona un criterio para
divisibilidad entre 11. Para esto notemos que si un entero se representa en la forma
n  ak1ak2
a0  ak110k1  ak210k2 
 a110  a0
entonces se puede escribir como

n  ak110k1  ak210k2 
 a0  a1  a2 
 a110  a0
 1 ak1  11a1  99a2 
k1
Notemos que en la representación anterior, el segundo bloque de sumandos consiste de
aquellos de la forma ai 10i  1 , de manera más precisa, el signo + aparece exactamente

cuando i es impar
y parece que cada uno de ellos es divisible entre 11. ¿Cómo justificar esta
observación? Notemos que el factor 10i 1 puede ser considerado como suma o diferencia




XVIII Encuentro de Profesores de Matemáticas

Página 91
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas


de k-ésimas potencias. ¿Cómo se factoriza ak  bk ? Procederemos al análisis dividiendo
en casos: si k es impar, y si k es par.
¿Cuál es el resultado de factorizar la expresión a k  b k para k un entero positivo impar? Con
el uso de un CAS (Computer Algebra
 System) se pueden considerar varios casos particulares
y tratar de identificar algún patrón.
Figura 13: Uso de un CAS en la búsqueda de patrones.
Con base en la información de la Figura 13, es posible conjeturar que para k impar, la
expresión a k  b k se puede factorizar como:
a
k
 bk  (a  b)(ak1  ak2b  ak3b2 
 (1)ki akibi1 
 bk1) ,
Esta igualdad se puede verificar desarrollando el producto de la derecha.
De esto se tiene, haciendo a  10 y b  1, que 10 k  1  10 k  1k se puede factorizar como:

10k 1  (10 1)(10k1 10k2   (1)ki10ki  1) ,


que claramente esdivisible
 entre 11 para k impar.

Si k es par, podemos factorizarlo en la forma k  2e m , para algún entero e 1 y m entero
positivo impar. Mostraremos que a  b divide a ak bk . Usando la representación de k

e 1
e 1

e 1
e 1

a k  bk  a 2 m  b2 m  a 2 m  b2 m a 2 m  b2 m .


m
m
Si e  1, el factor de la 
izquierda se reduce
a
;
como
m
es impar, por lo demostrado
a

b

antes, a  b es uno de sus factores y de esto se tiene que a  b es factor de ak bk . Si e  1, el
e 1
e 1
proceso se repite en el factor a 2 m  b 2 m hasta que el exponente de 2 sea uno y

nuevamente se invoca el caso m impar.
 Nuevamente, haciendo a  10 y b  1 se concluye que

 11 divide a 10k 1 para k par.


e
e


De esta discusión hemos demostrado que 11 divide al segundo bloque de sumandos en



XVIII Encuentro de Profesores de Matemáticas
Página 92
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
n  ak110k1  ak210k2 
 a0  a1  a2 
 a110  a0
 1 ak1  11a1  99a2 
k1
Por lo que 11 divide a n si y solo si, 11 divide a a0  a1  a2 
 1 ak1 .
k1
Ejemplo. Decidir si 11 divide a n=1 358 016. Aplicando el criterio, calculamos 6-1+0-8+5
3+1 que es cero, concluyendo que 11 si lo divide.

El resultado que hemos probado proporciona
más información; en caso de que 11 no divida a
n, el residuo que deja la división es igual al residuo que se obtiene al dividir
k1
a0  a1  a2   1 ak1 entre 11.
Los criterios de divisibilidad entre 2 y 5 son de los más fáciles de aplicar, lo cual se debe a
que, al representar un entero n en base 10, digamos

n  ak1ak2
a0  ak110k1  ak210k2 
 a110  a0 ,
todos los sumandos, excepto el de las unidades, tienen de factor al 2 y al 5, por lo cual, n es
divisible entre 2 o 5 si y solo si el dígito de las unidades es divisible entre 2 o 5.
Tomando esta observación en cuenta, las hipótesis que siguen sobre un entero m, son
naturales.
Teorema 1. Sea m>1 un entero que no tiene de factores al 2 y al 5, entonces existe un entero
positivo k mínimo, tal que m divide a 10k 1.



Demostración. Como m y 10 son primos relativos, entonces para todo n entero positivo, al
dividir 10n entre m deja residuo diferente de cero. Los residuos de la división por m son
0, 1, 2, , m 1, entonces
 existen n y l enteros positivos diferentes tales que
n
l
10  qm  r y 10  q1m  r , para algunos enteros q y q1. De estas ecuaciones se obtiene
n
l
 10  qm  10  q1m . Como n y l son diferentes, entonces uno es mayor que el otro;
supongamos por ejemplo que n>l, entonces de la ecuación anterior se llega a


10 l 10 n l  1  m q  q1 . Como m y 10 son
 primos relativos, entonces necesariamente m
nl
divide a 10 1. Tome el menor exponente de 10 que cumple la condición.
Teorema 2. Sean m y k como en el teorema anterior. Pongamos r 10k y representemos a un
l
entero N en base r, es decir, sea N   ai r i , 0  ai  r para todo i desde 1 hasta l.

i 0
Entonces m divide a N si y solo si m divide a (al  al1   a1  a0 ) .
La demostración del Teorema 2 sigue
 las mismas líneas que la demostración del criterio de

divisibilidad entre 9 y usa el hecho de que m divide a 10k 1 y éste divide a ri 1.

En lo que sigue presentamos otro criterio
de divisibilidad que sigue líneas diferentes. Este
criterio lo justificamos cuando un estudiante mencionó conocer un procedimiento para
establecer la divisibilidad entre 7, pero no sabía
 porqué funcionaba.
Deseamos determinar si 8
642 046 es divisible entre 7; para responder usamos el criterio siguiente:
La cifra de las unidades del número, en este caso el 6, se multiplica por dos y el resultado se
resta del número que se obtiene del original “suprimiendo” las unidades (el resultado que se
XVIII Encuentro de Profesores de Matemáticas
Página 93
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
obtiene al suprimir 6 es 864 204). Traducido a símbolos se tiene 864204 - 2(6)= 864 192.
Ahora el mismo procedimiento se aplica al nuevo número (864 192). Este proceso se repite
hasta obtener un número en el que sea “fácil” saber si es divisible o no entre 7 (ver Figura 14).
El último resultado que se ha obtenido es cero, el cual es divisible entre 7. Notemos que el
proceso pudo haberse detenido cuando se obtuvo el 84, que es divisible entre 7.
8
6
8
6
8
6
8
6
8
6
(-2)
8 4
(-8)
0
4
2
0 4
-(1 2)
4 1 9 2
(-4)
4 1 5
(-1 0)
3 1
(-2)
1
6
Figura 14: Aplicación del criterio para divisibilidad entre 7.
La fundamentación de este criterio se aplica a cualquier primo diferente de 2 y 5. En la
justificación del criterio será necesario el siguiente resultado.
Lema. Sea p un primo diferente de 2 y 5, entonces existen enteros positivos l y k tales que
10l 1 kp.


Demostración. Aplicando el algoritmo de la división a p y 10 se tiene que existen enteros q y
r tales que p 10q  r , con 0  r  10 . Como p es primo, los posibles valores de r son 1, 3, 7
y 9. Si r=1, tomamos l=q y k=1; si r=3, entonces p 10q  3. Multiplicando esta ecuación por
7 y agrupando se tiene 7p 10(7q  2) 1; tomamos l  7q  2 y k=7. Si r=7, entonces

por 3 esta ecuación y agrupando se tiene 3 p  10 3q  2 1 .
p10q  7 , multiplicando
Tomamos l  3q  2 y k=3. Si r=9, entonces
p 10q  9; multiplicando por 9 y agrupando se

tiene 9 p  10 9q 8 1 . Tomamos l  9q  8 
y k=9. Con esto se ha terminado la prueba del
lema.
Dado
en la aplicación del criterio de divisibilidad, y

 que el valor de l es muy importante
depende de p, lo escribimosen la siguiente forma.
 p 1
 10 si p  1 mod 10
7 p 1
si p  3 mod 10


lp   10
 3p -1 si p  7 mod 10
 10
 9 p -1 si p  9 mod 10

 10

XVIII Encuentro de Profesores de Matemáticas
(*)
Página 94
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Teorema. Sea n un entero positivo representado en la forma n 10rn  un , con 0  un 10 y p
un primo diferente de 2 y 5. Entonces existe un l tal que: (a) el primo p divide a 10l  1; (b) p
divide a n sí y solo sí p divide a rn  lun .

Demostración. El inciso (a) es justamente el lema
anterior; para

 probar la parte (b),

declaramos m  rn  lun , entonces despejando rn y sustituyendo en la ecuación
que expresa a
n, obtenemos n  10 m
 lu n  u n  10 m  10 l  1u n . Por el inciso (a) sabemos que p divide
a 10l  1, entonces p divide a n si y solo si p divide a 10 m , como p y 10 son primos relativos,
p divide a n si y solo si p divide a m  rn  lun .


Ejemplos. En la aplicación del criterio, se debe determinar el valor de l de acuerdo con la

7 (13)  1 90
ecuación (*). Por ejemplo, si p 13, el valor de l13 es: l13 

 9 . Si p  23,
10
10

7 23 1 161  1
entonces l 23 

 16 .
10
10



1. Decidir si 23 divide a 287 476 123.
En primer término se calcula l 23 , el cual es igual a 16 por lo mencionado en el párrafo previo.
La cifra de las unidades del número, en este caso el 3, se multiplica por 16 y el resultado se
resta del número que se obtiene del original “suprimiendo” las unidades (el resultado que se
obtiene al suprimir 3 es 28 747 612). Traducido a símbolos se tiene 28747612- 16(3)= 28 747
564. Ahora el mismo procedimiento se aplica al nuevo número (28 747 564). Este proceso se
repite hasta obtener un número en el que sea “fácil” decidir si es divisible o no entre 23 (ver
Figura 15). El último resultado que se ha obtenido es 172, el cual no es divisible entre 23. Por
lo tanto, el número original tampoco es divisible entre 23.
2
8
7
4
7
6
2
8
7
4
7
2
8
7
4
2
8
2
8
2
-(1
1
8
1
7
7
-(1
6
-(1
4
2)
2
4
1
3
6)
7
6
-(3
3
2)
1
5
-(6
9
2)
7
1
-(4
6
4)
2
2
8)
4
3
Figura 15: Aplicación del criterio para divisibilidad entre 23.
2. Decidir si 602 468 38 037 es divisible entre 11
11  1 10

 1 . La cifra de las unidades del número, en este
10
10
caso el 7, se multiplica por uno y el resultado se resta del número que se obtiene del original
“suprimiendo” las unidades (el resultado que se obtiene al suprimir 7 es 6024683803).
Traducido a símbolos se tiene 6024683803 - 1(7)= 6 024 683 796. Ahora el mismo
procedimiento se aplica al nuevo número (6 024 683 796). Este proceso se repite hasta
obtener un número en el que sea “fácil” saber si es divisible o no por 11 (ver Figura 16). El
En primer lugar calculamos l11 
XVIII Encuentro de Profesores de Matemáticas
Página 95
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
último resultado que se ha obtenido es 1, el cual no es divisible entre 11. Notemos que el
proceso pudo haberse detenido cuando se obtuvo el 54, que no es divisible entre 11.
6
0
2
4
6
8
3
8
0
6
0
2
4
6
8
3
7
6
0
2
4
6
8
3
6
0
2
4
6
8
6
0
2
4
6
6
0
2
4
6
0
2
6
0
5
9
-5
4
1
-6
5
3
-7
6
5
-8
7
7
-9
8
3
-4
9
7
-3
4
9
-6
3
5
-4
1
3
-7
6
7
Figura 16: Aplicación del criterio de divisibilidad entre 11.
Los criterios para divisibilidad entre 9 y 11 son muy fáciles de recordar y de aplicar, además
de tener algunas propiedades interesantes, por ejemplo, al aplicar el criterio de divisibilidad
entre 9, a un número n, y posteriormente a la suma de sus dígitos hasta obtener una cifra, ésta
última es igual al residuo que resulta de dividir n entre 9. Por ejemplo, apliquemos el criterio
de divisibilidad entre 9 al número 47 893 425, la suma de sus dígitos es 42, al sumar 4+2
47893425
obtenemos el número 6 que es el residuo de la división
.
9
Otro ejemplo, la suma de los dígitos del número 5 673 412 856 es 47, al sumar 4+7
obtenemos el número 11, y nuevamente al sumar 1+1 obtenemos el número 2, que es el
5673412856
residuo que resulta del cociente
.
9
Algo similar ocurre al aplicar el criterio de divisibilidad entre 11. Por ejemplo, considérese el
número 3 475 468 923, al sumar los dígitos, iniciando por las unidades con signos alternados
se tiene como resultado 3  2  9  8  6  4  5  7  4  3  3 , el cual es el residuo de la
3475468923
división
.
11
Agradecimientos
El primer autor Agradece al CONACYT el apoyo recibido, a través del proyecto de
investigación con número de referencia 61996, para la realización de este material.
Referencias
Avilés, K. (2009, Septiembre 8). En los dos niveles más bajos de matemáticas, 81.2% de los
alumnos de Bachillerato. La Jornada, p. 41.
XVIII Encuentro de Profesores de Matemáticas
Página 96
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Ball, D. L, Thames, M. H. & Phelps, G. (2008). Content knowledge for teaching: What makes
it special? Journal of Teacher Education, 59, 389-407.
Ball, D. L., & Bass, H. (2003). Toward a practice-based theory of mathematical knowledge
for teaching. In B. Davis & E. Simmt (Eds.), Proceedings of the 2002 Annual Meeting
of the Canadian Mathematics Education Study Group (pp. 3-14). Edmonton, AB:
CMESG/GCEDM.
Barrera, F. (2009a, Diciembre 9). El aprovechamiento de los estudiantes y su relación con los
conocimientos de los profesores. El Independiente de Hidalgo.
Barrera, F. (2009b). Reporte de la segunda fase del proyecto “Bases teóricas y conceptuales
en la construcción del conocimiento matemático y el empleo de herramientas
digitales”. Informe del proyecto financiado por Conacyt con número de referencia
61996. Pachuca, Hidalgo.
Barrera, F. y Reyes, A. (2010). Curso: Pensamiento Matemático, Resolución de Problemas y
Formación Docente. Pachuca, Hidalgo: Centro Universitario de Formación (UAEH).
Davis, B. & Simmt, E. (2006). Mathematics-for-teaching: An ongoing investigation of the
mathematics that teachers (need to) know. Educational Studies in Mathematics, 61,
293-319.
Fernández-Vega, C. (2009, Agosto 26). México SA. La Jornada. Recuperado de
http://www.jornada.unam.mx/2009/08/26/index.php?section=opinion&article=028o1eco, el
18 de Junio de 2010.
Harel, G. & Lim, H. K. (2004). Mathematics teachers‟ knowledge base: Preliminary results.
En M. J. Hoines & A. B. Fuglestad (Eds.), Proceedings of the 28th Conference of the
International Group for the Psychology of Mathematics Education (Vol. 3, pp. 25-32).
Bergen, Norway: PME.
Harel, G. (1994). On teacher education programmes in mathematics. International Journal of
Mathematical Education in Science and Technology, 25(1), 113-119.
Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K. C., Wearne, D., Murray, H., Olivier, A.,
& Human, P. (1997). Making sense: teaching and learning mathematics with
understanding. Portsmouth: NH: Heinemann.
NCTM (2000). Principles and Standards for School Mathematics. Reston, Virginia: National
Council of Teachers of Mathematics.
Olivares-Alonso, E. (2009, Enero 28). Sin título, 40% de maestros de bachillerato público;
emprenderá la SEP programas de formación docente. La Jornada. Recuperado de
http://www.jornada.unam.mx/2009/01/28/index.php?section=sociedad&article=045n1so, el 18
de junio de 2010.
Poy, L. (2009, Diciembre 30). Creará UAM centro especializado ante bajos resultados de
matemáticas. La Jornada, p. 25.
Santos-Trigo, M. (2007). Mathematical problem solving: an evolving research and practice
domain. ZDM, 39, 523-536.
Santos-Trigo, M. (2008). Sobre la construcción de una comunidad de práctica en la resolución
de problemas. En F. Barrera, et al. (Eds.), Memorias del Segundo Seminario Nacional
sobre Resolución de Problemas y el Aprendizaje de las Matemáticas (pp. 133-144).
Pachuca, Hidalgo.
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard
Educational Review, 57(1), 1-22.
Silverman, J. H. (2006). A friendly introduction to number theory. Pearson Prentice Hall, third
edition.
XVIII Encuentro de Profesores de Matemáticas
Página 97
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Simon, M. A. & Tzur, R. (2004). Explicating the role of mathematical tasks in conceptual
learning: An elaboration of the hypothetical learning trajectory. Mathematical
Thinking and Learning, 6(2), 91-104.
Sowder J. T. (2007). The mathematical education and development of teachers. In F. K.
Lester, Jr. (Ed.), Second Handbook of Research on Mathematics Teaching and
Learning (pp. 167-224). Charlotte, NC: Information Age Publishing.
XVIII Encuentro de Profesores de Matemáticas
Página 98
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
La enseñanza del álgebra en el bachillerato con Geogebra
Dr. Armando Sepúlveda
F. M. Diana Itzel Sepúlveda
Dr. Roberto García
[email protected]
[email protected]
[email protected]
Universidad Michoacana de San Nicolás de Hidalgo
Introducción
Entre las materias escolares que mayor importancia tienen para la formación matemática de
cualquier ciudadano, se encuentra el álgebra que, sin duda, ocupa la mayor parte del
currículum escolar. Efectivamente, varios contenidos relacionados con ella aparecen incluso
desde la educación primaria como las fórmulas para calcular áreas y volúmenes de figuras
geométricas; a partir de la educación secundaria aparecen cursos con su nombre propio, pero
en casi todas los demás cursos de matemáticas y de otras ciencias como Física y Química se
estudian sus contenidos con cierta relevancia. Además, varias de las ideas algebraicas tienen
sus orígenes en conceptos y procedimientos propios de la aritmética y de la geometría; con el
tiempo, en la medida que se fueron desarrollando otras ramas de las matemáticas, se han ido
incorporando otras nociones y conceptos de manera que, en la actualidad, la concepción
moderna del álgebra (NCTM, 2000) se identifica con ideas de: sucesiones, patrones, razones,
proporciones, variación, generalización, relaciones y funciones.
Esta importancia no corresponde a los resultados regularmente obtenidos en el aprendizaje
por parte de los estudiantes, convirtiéndose el álgebra en un obstáculo insuperable para
muchos en el sentido de adquirir una competencia aceptable; al grado de que frecuentemente
esta materia es señalada como la causante de haber elegido una carrera en la que “no se
estudien muchas matemáticas” o de “haber abandonado los estudios”.
Ahora bien, existe el reconocimiento de que los resultados en el aprendizaje de las
matemáticas en los diferentes niveles escolares de nuestro sistema educativo, históricamente,
no han sido satisfactorios, de acuerdo a las expectativas planteadas en la mayoría de los
proyectos curriculares; pues distintas evaluaciones nacionales e internacionales muestran que
el nivel de conocimientos adquiridos por los estudiantes mexicanos no es bueno (TIMSS,
1999; CENEVAL, 2006; PISA, 2000), a pesar de la existencia de políticas que tienden a
presionar a los profesores para promover a los estudiantes a toda costa.
Por un lado, las cifras oficiales relacionadas con: la escolaridad de la población; los índices de
deserción y reprobación escolar; la eficiencia terminal en los distintos niveles educativos; el
número de estudiantes que ingresan al bachillerato y a la licenciatura (INEGI, 2002), indican
que en el proceso educativo se presentan serias dificultades, de diversa naturaleza, por lograr
los objetivos curriculares. Dicha problemática ha sido motivo de preocupación de los
investigadores de la educación en general y de los educadores matemáticos en particular.
Por otro lado, se debe considerar que un factor determinante en la complejidad del sistema
educativo nacional es la diversidad en la formación matemática de los profesores del nivel
medio superior; y si a esto agregamos la existencia de distintos planes y programas de estudio,
se originan diferentes perfiles de egreso de los estudiantes en cuanto a sus niveles de
competencia y a la adquisición de habilidades matemáticas. Es decir, podemos tener alumnos
del mismo bachillerato que estudiaron cursos distintos de matemáticas con el mismo nombre,
XVIII Encuentro de Profesores de Matemáticas
Página 99
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
incluso impartidos en la misma escuela y, en consecuencia, ellos egresan con desiguales
niveles de exigencia y con diferentes resultados en el aprendizaje.
Además, las características propias de las matemáticas como su nivel de abstracción, su
carácter epistemológico, el hecho de que cuente con un lenguaje propio en el que la lógica
interviene, y su gran aplicabilidad en las demás ciencias y en distintos ámbitos de la vida
cotidiana, representan serias dificultades de aprendizaje para la mayoría de los estudiantes.
Todo ello permite apreciar lo irresponsable que resulta que algunos sectores de la sociedad
culpen a los profesores por los resultados obtenidos en el aprendizaje de las matemáticas.
Para atender algunas de estas dificultades, varias instituciones han implementado acciones
con el propósito de enfrentarlas en mejores condiciones. Por ejemplo, se promueve la
incorporación de medios tecnológicos en la enseñanza y el estudio de las matemáticas, se ha
conformado equipos de trabajo para realizar investigaciones y producir materiales que
mejoren la calidad de la educación de los estudiantes (NCTM, 1980, 2000; Alarcón, 1994;
Verdugo et al., 2001; Sepúlveda y Santos, 2004); entre otros.
Con ello se intenta influir en el currículum para que los estudiantes se involucren en el
desarrollo de procesos matemáticos y puedan particularizar, generalizar, descubrir patrones y
relaciones, plantear conjeturas y justificar resultados (Mason, Burton, Stacey, 1987; Steen,
1990; Schoenfeld, 1992); es decir, estos investigadores plantean la necesidad de involucrar a
los estudiantes en las acciones típicas que caracterizan el quehacer matemático, para lograr un
aprendizaje matemático profundo, que vaya más allá del aprendizaje rutinario. Pero lograr que
los estudiantes lleven a cabo estas acciones implica enfrentar retos en la enseñanza y el
aprendizaje de las matemáticas. En esta dirección, el currículum, los materiales, las
herramientas y las condiciones en que se desarrolla el aprendizaje son ingredientes
importantes que inciden en el desarrollo de competencias matemáticas1 de los estudiantes.
Así, es necesario que los profesores cuenten con espacios de formación y actualización que
les permita estudiar y profundizar sobre los contenidos matemáticos, así como estar al día de
las innovaciones y propuestas metodológicas sobre la problemática de la enseñanza y el
aprendizaje de las matemáticas.
En este curso presentamos una revisión histórica del surgimiento de algunas de las ideas
algebraicas, haciendo notar que éstas están presentes en diferentes temas aritméticos y
geométricos. Enseguida, se expone una visión moderna de la enseñanza del álgebra que,
básicamente, está fundamentada en el proyecto curricular del Consejo Nacional de Profesores
de Matemáticas (NCTM -por sus siglas en inglés-, 2000); finalmente, entre las sesiones en las
que se cubrirán los temas, se tendrán tres sesiones de uso del Geogebra, el cual es un
software dinámico de carácter geométrico-algebraico que permite la construcción y
manipulación de ciertos “objetos” matemáticos. Su sencillez, versatilidad y potencia de sus
herramientas lo hacen atractivo para ser incorporado en el trabajo cotidiano del profesor, ya
sea para preparar sus clases o, por qué no, para estudiar matemáticas.
1
Se usa el término competencias matemáticas para designar lo que los estudiantes saben
hacer por sí solos; implica la manera en que usan los recursos matemáticos, las formas de
representación que utilizan y las maneras de comunicar sus resultados (Sepúlveda 2004).
XVIII Encuentro de Profesores de Matemáticas
Página 100
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
La propuesta curricular del NCTM
Los Principios y Estándares para las Matemáticas Escolares es un proyecto curricular del
Consejo Nacional de Profesores Matemáticas (NCTM, 2000) según el cual se pretenden
lograr los fines de la educación -que en la mayoría de currículum escolares en matemáticas es:
formar ciudadanos educados con una identidad cultural y conocimientos matemáticos sólidos
que le permitan interactuar y desenvolverse en su medio social-, a través de una serie
principios y estándares donde se flexibiliza la visión del orden tradicional en que deben
cubrirse los contenidos matemáticos, desde el primer año escolar hasta el bachillerato y,
además, se logre un aprendizaje diferente, que vaya más allá del tradicional.
La obra contiene seis principios que establecen la filosofía de la educación a la que se aspira
con ese proyecto educativo y diez estándares; criterios de calidad previamente establecidos
que contienen instrucciones sobre contenidos a cubrir y procesos de pensamiento que se
pretende promover para conseguir las metas de aprendizaje significativo de los estudiantes.
Cinco de los estándares se refieren a líneas de contenido y los otros cinco a procesos de
pensamiento que se espera desarrollar a lo largo de los 12 grados escolares. También se
contempla, con una visión amplia y flexible, la forma en que se entrelazan las líneas de
contenido y los procesos de pensamiento a lo largo de los 12 grados escolares.
Uno de los estándares es el de resolución de problemas y en él se plantea la utilización de
problemas adecuados para promover el aprendizaje de las matemáticas. En este proceso, los
maestros juegan un papel importante en la educación matemática, pues ellos seleccionan los
problemas que tengan ciertas cualidades que permitan alcanzar los objetivos y metas
planteadas, ayudan a los estudiantes a plantear o explorar conjeturas basadas en evidencia;
además en este nivel de desarrollo, los estudiantes, son manipulables y demasiado
influenciables por la dirección de sus maestros.
Además, vivimos tiempos con grandes cambios, avances en la tecnología, nuevos
conocimientos, nuevas herramientas, mejor comunicación, entre otras muchas cosas. Las
calculadoras y computadoras que en los ochentas eran costosas y escasas, ahora son comunes
y baratas; y pueden propiciar un aprendizaje más completo.
La necesidad de comprender y saber usar las matemáticas es cada vez más grande, ya que: son
importantes para la vida; forman parte de la herencia cultural; son importantes en el trabajo; y
son importantes para la comunidad científica y tecnológica.
En general, las matemáticas nos ayudan a organizar y ordenar nuestros pensamientos; nos
hace competentes tanto para el desarrollo de diversas actividades intelectuales como hacia los
demás. Sin embargo, a pesar de estos puntos destacables, la mayoría de las personas tienen
dificultades y muestran deficiencias en el aprendizaje de las matemáticas. Algunas de las
posibles razones son: los alumnos no tienen la oportunidad de entender la importancia de lo
que significa aprender matemáticas; el currículum que se ofrece es demasiado rígido; y los
estudiantes y profesores no están comprometidos con el aprendizaje de las matemáticas.
Los seis principios del proyecto curricular del NCTM (2000) son:
1) Principio de la equidad. La excelencia en la educación matemática requiere de equidad.
Todos los estudiantes deben tener las mismas oportunidades y facilidades para adquirir las
herramientas y conceptos que requieren para un mejor aprendizaje de las matemáticas, sin
importar color, raza o posición social.
XVIII Encuentro de Profesores de Matemáticas
Página 101
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
2) Principio del currículum. El currículum es más que una colección de actividades; éstas
deben ser coherentes, centradas en matemáticas importantes y bien articuladas a través de los
grados escolares. El desarrollo del pensamiento matemático y el razonamiento de técnicas
específicas, incluyendo el planteamiento de conjeturas y la generación de argumentos fuertes,
son importantes porque sirven como base para el surgimiento de nuevas ideas que motiven al
estudiante a consolidar lo aprendido y a seguir estudiando. Este principio es importante
porque un currículum bien articulado sirve como guía para que los maestros de cada nivel,
sepan qué matemáticas deben ser estudiadas en cada uno de ellos.
3) Principio de la enseñanza. Una enseñanza efectiva de las matemáticas requiere de la
comprensión de lo que los estudiantes necesitan saber para aprender mejor. No existe un
“camino recto” para aprender; elaborar y escoger procedimientos de instrucción para aplicarse
en un salón de clase, es una tarea difícil, continuamente hay que buscar su mejoramiento.
4) Principio del aprendizaje. Los estudiantes deben aprender matemáticas con comprensión,
construyendo nuevos conocimientos a partir de sus experiencias y conocimientos previos. La
comprensión conceptual es una componente importante de una competencia. Cuando los
estudiantes alcanzan este tipo de aprendizaje, obtienen una capacitación resolver diversos
problemas que se les presenten en el futuro.
5) Principio de la evaluación. La evaluación debe promover y respaldar el aprendizaje de
matemáticas importantes, así como proporcionar información útil a maestros y estudiantes.
Una sola evaluación no permite obtener suficientes argumentos para calificar el conocimiento
de un estudiante, es necesario llevar a cabo varias evaluaciones para considerar cuáles son los
factores que influyen y son reflejados en sus resultados. El ambiente de aprendizaje es un
factor importante que debe ser considerado en la evaluación.
6) Principio de la tecnología. La tecnología es esencial en la enseñanza y el aprendizaje de las
matemáticas, influye en las matemáticas que se enseñan en la actualidad y aumenta las
posibilidades de aprendizaje de los estudiantes. Este principio es importante, ya que brinda la
oportunidad de que los estudiantes estén actualizados en los avances tecnológicos que se
producen en el mundo, independientemente del país donde se encuentren.
Los diez estándares están divididos de la siguiente forma: los primeros cinco describen los
contenidos que los estudiantes deben aprender; y los siguientes cinco, corresponden a
procesos de pensamiento que ayudan a desarrollar habilidades y estrategias para aprender
matemáticas.
Los principios y estándares se aplican a lo largo de los 12 grados escolares básicos (de la
Primaria al Bachillerato), durante los cuales los estudiantes alcanzan cierta profundidad en la
comprensión de los conceptos y adquieren un nivel de dominio de los procedimientos
descritos en los puntos en el currículum.
Primero. Números y operaciones. Si se alcanza una buena comprensión de los números, los
sistemas de numeración, así como sus relaciones y operaciones, se tiene un gran avance en el
currículum, pues eso permitirá la comprensión de las demás áreas de matemáticas con mayor
facilidad, ya que todas tienen como base a los números.
Segundo. Álgebra. Todo estudiante debe aprender álgebra. Las ideas incluidas en éste
estándar constituyen la mayor componente del currículum escolar de matemáticas. El álgebra
XVIII Encuentro de Profesores de Matemáticas
Página 102
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
es más que una colección y manipulación de signos y símbolos; implica la comprensión de
modelos, relaciones y funciones. En este estándar se maneja la representación y el análisis de
situaciones y estructuras matemáticas usando símbolos algebraicos. Los estudiantes de
secundaria y bachillerato deben ser capaces de desarrollar técnicas para encontrar expresiones
matemáticas equivalentes y resolver sistemas de ecuaciones lineales y/o cuadráticas; algunas
incluso mentalmente, otras con papel y lápiz, y cuando amerite el caso, con auxilio de la
tecnología.
Tercero. Geometría. Las ideas geométricas son de gran utilidad en la representación y
resolución de problemas. Los estudiantes deben tener experiencias usando una variedad de
representaciones visuales a través de figuras, con o sin coordenadas, para analizar un
problema. Asimismo, deben practicar un razonamiento espacial y modelado geométrico.
Cuarto. Medición. Es necesario que los estudiantes alcancen a comprender los atributos de la
medición de objetos: unidades, sistemas y procesos de medición. Con este estándar se
pretende que el estudiante aprenda a elegir una unidad apropiada para su problema (algunos
aspectos relacionados con las estimaciones y redondeos quedan incluidos); cuando esto
ocurre, se da el mayor avance en la comprensión de la medición.
Quinto. Probabilidad y análisis de datos. Con este estándar se pretende que los estudiantes
aprendan a analizar datos de libros, periódicos u algún otro documento. El propósito es que
aprendan a manejar datos, reunirlos, organizarlos, y mostrar los datos relevantes que les son
útiles para responder ciertas preguntas. Deben saber seleccionar y usar apropiados métodos
estadísticos para analizar los datos. También deben saber obtener los datos de la observación
de estudios y experimentos, así como hacer predicciones basadas en los datos. Además, los
estudiantes deben conocer y aplicar conceptos básicos de probabilidad para analizar los datos.
Sexto. Resolución de problemas. Cuando los estudiantes aprenden a resolver problemas,
desarrollan procesos de pensamiento ordenados que, poco a poco, se van convirtiendo en una
habilidad para encontrar estrategias adecuadas para determinado tipo de problemas, lo cual
permite el desarrollo de nuevas comprensiones matemáticas. Los estudiantes deben ser
animados e involucrados en procesos de resolución de problemas, se debe propiciar el espíritu
de aferrarse a encontrar y formular una solución cuando intenta resolver un problema
complejo.
Para aprender a resolver problemas en matemáticas, los estudiantes deben adquirir formas de
pensamiento, hábitos de persistencia, curiosidad y confianza en sus acciones para explorar
situaciones desconocidas. Esto contribuye a un dominio de situaciones similares y a la
adquisición de la capacidad de exteriorizar ideas matemáticas. Hoy en día, se considera que la
resolución de problemas puede ser una guía importante para lograr grandes avances.
La resolución de problemas no es una parte aislada de la educación matemática y de los
programas de las materias, es una parte fundamental para todo aprendizaje matemático. La
resolución de problemas debe estar inmersa en los cinco primeros estándares.
El contexto de los problemas puede variar de experiencias que son familiares a los
estudiantes, hasta aplicaciones involucradas con las ciencias. La idea es que en los problemas
estén involucrados los conceptos matemáticos importantes del currículum; y si se hace una
buena elección respecto al nivel y familiaridad con los estudiantes, se puede lograr un gran
avance en el aprendizaje matemático que, posteriormente, será el soporte para atacar y
resolver problemas más complejos.
XVIII Encuentro de Profesores de Matemáticas
Página 103
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Los profesores juegan un papel muy importante al elegir los problemas que valen la pena,
pues la resolución de problemas debe ser útil para ayudar a los estudiantes a desarrollar
dominios de contenidos con técnicas específicas.
Un problema muy bien resuelto, ayuda al estudiante a enfrentar problemas en situaciones de
su vida cotidiana. Inicialmente consideran casos simples y familiares y luego van aumentando
la complejidad de los problemas y del análisis involucrado. Los estudiantes deben aprender a
aplicar y adoptar una variedad de estrategias apropiadas para resolver problemas. Algunas de
las mejores sugerencias para aprender a resolver problemas las podemos encontrar en Polya
(1945); Santos (2007).
Séptimo. Razonamiento y prueba. El razonamiento y prueba es un aspecto fundamental en
matemáticas. El objetivo de este estándar es que el estudiante aprenda a planear e investigar
conjeturas matemáticas; así se abre camino al descubrimiento. También es importante que los
estudiantes descubran y evalúen matemáticamente los argumentos y las pruebas.
Octavo. Comunicación. La comunicación es una parte esencial en la educación matemática y
de las matemáticas mismas. Los estudiantes deben aprender a comunicar sus pensamientos
matemáticos en forma clara y coherente a sus compañeros, profesores y otros miembros de su
comunidad. Los profesores deben proporcionar un ambiente de confianza que permita la
comunicación entre los estudiantes, motivar dicha acción y evitar la imposición de un
lenguaje matemático formal.
Noveno. Conexiones. El establecimiento de conexiones entre diferentes conocimientos
matemáticos es uno de los procesos de pensamiento más poderosos y, a su vez, de los más
sofisticados de lograrse en la educación matemática de los estudiantes. Implica el
reconocimiento de situaciones en las que es posible establecer conexiones entre ideas
matemáticas. Este estándar es una facultad que caracteriza a los matemáticos talentosos y
frecuentemente está asociado al proceso de resolución de problemas.
Décimo. Representaciones. Con el estándar de representaciones se espera desarrollar en los
estudiantes la capacidad de representar de diferentes maneras una situación determinada, lo
cual contribuye significativamente en el aprendizaje de las matemáticas; el libre tránsito entre
diferentes representaciones de una noción conceptual o una situación problemática, es una
muestra de un entendimiento profundo de técnicas y conocimientos matemáticos. Puede estar
asociado al estándar de comunicación.
Con estos principios y estándares se espera que los estudiantes logren un aprendizaje con
entendimiento (Hiebert y Carpenter, 1992); un tipo de aprendizaje donde los estudiantes le
ven sentido a lo que están estudiando y que, posteriormente, puede llevarlos a un profundo
entendimiento de los conceptos e ideas matemáticas. Estos y otros investigadores han acuñado
esta expresión para referirse a un aprendizaje que es interpretado a través de representaciones
externas e internas que maneja el sujeto; estas representaciones necesariamente están ligadas e
interconectadas. El manejo o generación de representaciones externas (comunicar una idea en
forma oral o escrita, elaborar un esquema o dibujo, etc.) conlleva a la elaboración o
reacomodo de representaciones internas que el sujeto tiene en su mente; y que, a su vez, estas
representaciones internas hacen posible la generación de las representaciones externas.
XVIII Encuentro de Profesores de Matemáticas
Página 104
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Así, el aprendizaje con entendimiento se da cuando se generan redes de representaciones
internas en la mente del sujeto, con nodos y articulaciones fuertemente conectadas, que hacen
posible la emisión de representaciones externas; el libre tránsito entre representaciones
externas e internas es señal inequívoca de que se está generando un aprendizaje con
entendimiento.
La observación de los principios debe mantenerse durante esta etapa del proceso educativo y
los estándares de líneas de contenido y de pensamiento se van a ir entrelazando en el
desarrollo del curso, algunos de estos se promoverán con mayor ahínco en un momento dado,
dependiendo del tema o curso que se esté impartiendo. Sin embargo, en la actualidad especial
atención merecen el Principio de la tecnología y el Estándar de resolución de problemas; por
un lado, los avances en el desarrollo tecnológico implica exigencias en la enseñanza de las
matemáticas, las cuales son inherentes a la propia evolución de la sociedad y, por otro lado,
además de que la resolución de problemas es la actividad que mayor progreso ha proveído a la
matemática, en el ámbito educativo es el proceso de pensamiento que involucra y aglutina a
los demás estándares.
Así, aunque este curso se enfoca fundamentalmente en el estándar de algebra, se mantienen
presentes la resolución de problemas y el uso de tecnología en la enseñanza.
Resolución de problemas
Si bien es cierto que, en buena medida, el desarrollo en el conocimiento matemático se debe a
la resolución de los problemas que matemáticos y otros investigadores se han planteado, es
hasta los trabajos de George Polya, en 1945, que esta actividad empieza a ser importante en el
ámbito educativo.
Polya (1945) establece que la resolución de problemas en una característica esencial que
distingue a la naturaleza humana y cataloga al hombre como “el animal que resuelve
problemas”. Ante el acostumbrado fracaso de sus estudiantes en los cursos de matemáticas
que impartía, Polya se propuso diseñar un método que pudiera ayudarles a resolver problemas
y así, superaran sus dificultades de aprendizaje. Fue entonces cuando diseñó su famoso
método de los cuatro pasos: i) Entender el problema; ii) Diseñar un plan de solución; iii)
Ejecutar el plan; y iv) Realizar una revisión retrospectiva de lo realizado, los cuales van
acompañados de preguntas y reflexiones con la intensión de esclarecer lo que debe realizar el
estudiante y así, quizás pueda resolver el problema.
Lo que intentó hacer Polya es, como matemático productivo que era, exteriorizar el diálogo
interior que realizaba consigo mismo cuando estaba inmerso en el proceso de resolución de
problemas. En este proceso intervienen la utilización de heurísticas; que son acciones
típicamente útiles que ayudan a descubrir pistas para resolver los problemas, y la reflexión.
Polya creía que la práctica de este proceso permitiría a los estudiantes interiorizar estas
acciones y, posteriormente, realizarlas por sí mismos. Una heurística es toda acción física o
mental que facilita, da pistas sobre o permite visualizar el camino de solución de un problema.
Las heurísticas planteadas por Polya corresponden a las estrategias más usuales, sin que ello
quiera decir que son las únicas; cada quien, de acuerdo a su experiencia y capacidad
desarrollada en el estudio y comprensión de las matemáticas podrá incorporar estrategias
heurísticas propias, con un tinte de aplicación personal. Las heurísticas dadas por Polya son:
XVIII Encuentro de Profesores de Matemáticas
Página 105
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Tomar casos particulares; Usar analogías; Establecer submetas; Simplificar un problema;
Hacer un dibujo, un trazo; Regresar a las definiciones; Establecer una simetría; Realizar una
rotación.
La interpretación del aprendizaje en resolución de problemas, idealmente se ubica en la teoría
cognoscitiva de Jean Piaget que fundamenta la teoría actual denominada como
Constructivismo. Es decir, la resolución de problemas nos ubica el umbral de esta teoría del
aprendizaje que asegura la no existencia de un mundo exterior independiente de nuestras vías
de conocimiento (Simon, 1995); más bien, el mundo exterior existe en la medida en que el
sujeto interactúa con él y va adaptando sus nuevas experiencias con las anteriores. El sujeto
aprende en la medida en que interactúa con los objetos y va adaptando sus experiencias a
través de los procesos básicos de Piaget, asimilación y acomodación, modificando las
estructuras mentales con que cuenta.
Actividades con Geogebra
A continuación se da una introducción general al uso del software dinámico llamado
Geogebra, a través de actividades o problemas, cuyo manual de uso se encuentra disponible
en Internet, a través de casi cualquier buscador. Algunas de estas actividades coinciden con
los problemas que se enlistan a continuación, en el punto cinco.
i)
Visión de la geometría dinámica que ofrece Geogebra; manipulación de conceptos de
geometría como mediatriz y circuncentro, mediana y baricentro, bisectriz e incentro,
altura y ortocentro.
ii)
Estudio de las funciones con Geogebra.
a)
Dada una función, algebraica o trascendente, analizar su estructura algebraica y
geométrica al realizar traslaciones o reflexiones.
Dadas dos funciones cualesquiera, observar sus transformaciones al realizar operaciones
entre ellas como suma, producto, cociente, composición.
b)
iii)
Analizar la solución de un sistema de ecuaciones utilizando Geogebra.
iv)
Solución dinámica del problema: ¿Para qué valores de a el sistema de ecuaciones
x 2  y 2  0 & ( x  a) 2  y 2  1 ; tiene 0, 1, 2, 3, 4, ó 5 soluciones? (Schoenfeld, 1999)
v)
Solución dinámica del problema: Sombras. (Balanced Assessment Package for the
Mathematics Curriculum, 1999)
vi) Problema: Al agua patos. (Carmona, 2004)
vii) Sean P( x)  ax 2  bx  c; y Q( x)  cx 2  bx  a; ¿cuál es la relación entre las raíces de
P(x) y Q(x)?
viii) Explorando polinomios -actividad para los estudiantes.
ix) Uso de Geogebra para comprobar el teorema de Pitágoras.
x)
Uso de Geogebra para comprobar el teorema de la suma de los ángulos internos de un
triángulo.
xi) Problema de Optimización. De una pieza cuadrada de hojalata de lado a, se desea
construir una caja, abierta por arriba, del mayor volumen posible, cortando de las
esquinas cuadrados iguales y doblando hacia arriba la hojalata para formar las caras
laterales. Cuál debe ser la longitud del lado de los cuadrados cortados.
XVIII Encuentro de Profesores de Matemáticas
Página 106
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Problemas
A continuación presentamos una serie de problemas y situaciones que, esperamos,
desencadenen el proceso descrito por Polya y que el profesor sea consciente de ello; es decir,
que identifique tanto los pasos del método como las heurísticas utilizadas. En la medida en
que esto se hace consiente por parte del aprendiz, se está en el sendero de un aprendizaje de
las matemáticas diferente, con sentido y significado.
1.
Encontrar un entero positivo a tal que la suma a + 2a + 3a + 4a + 5a + 6a + 7a + 8a + 9a,
resulta ser un número con todas sus cifras iguales. (Pérez 1997)
2.
Si m y n son enteros positivos que satisfacen m n  m n1  m n 2  39 , ¿cuánto vale n m ?
3.
Si el área sombreada es de 256 cm2, ¿cuál es el valor de x?
x
x
4 cm.
4.
Si x 2  8 x  2  0 , ¿cuánto vale x 4  8x 3  16x  10 ?
5.
Encontrar dos números a y b tales que la suma, producto y cociente de los dos números,
sean iguales.
6.
Sean P( x)  ax 2  bx  c; y Q( x)  cx 2  bx  a; ¿cuál es la relación entre las raíces de
P(x) y Q(x)? Extensión: ¿Qué ocurre si se trata de polinomios de grado tres
P ( x)  a 3 x 3  a 2 x 2  a1 x  a 0 ; y Q( x)  a 0 x 3  a1 x 2  a 2 x  a 0 ?; ¿si el grado fuera n?
7.
¿Cuánto vale la suma de los coeficientes de  x  1 ?
8.
¿Para qué valores de a el sistema de ecuaciones x 2  y 2  0 & ( x  a) 2  y 2  1 ; tiene
0, 1, 2, 3, 4, ó 5 soluciones? (Schoenfeld, 1999)
9.
Las diagonales de un cuadrilátero lo dividen en cuatro
triángulos, cuyas áreas de tres de ellos se conocen. Hallar
el área del otro triángulo.
31
x
12
30
20
10. Se aumentó en la misma proporción la longitud de los lados de un cuadrado y su área
aumentó 69%, ¿en qué proporción aumentaron sus lados?
11. Se tienen dos jarras con capacidad de dos litros. En una de ellas hay un litro de agua y en
la otra hay un litro de jugo de limón. Se toma un cuarto de litro de la jarra con agua y se
pasa a la jarra que tiene jugo de limón; se revuelve y se toma un cuarto de litro de la
mezcla para pasarlo a la jarra que tiene agua. ¿Qué cantidad de jugo de limón hay en la
jarra que contenía sólo agua al principio?
XVIII Encuentro de Profesores de Matemáticas
Página 107
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
12. Dos barriles se llenaron con jerez de dos clases diferentes. El barril A contiene una
mezcla de jerez en la razón 2:7, mientras que la mezcla en el barril B la razón es 1:5.
¿Qué cantidad de jerez debe tomarse de cada uno de los barriles para formar una mezcla
que contenga 6 litros de una clase y 27 litros de la otra?
13. Dos trenes viajan a 50 Km./h en sentidos opuestos sobre una vía rectilínea. Cuando hay
una distancia de 100 Km. entre ellos, un pájaro vuela de uno al otro a una velocidad de
100 Km./h, luego regresa a la misma velocidad, en línea, del segundo al primero; y
vuelve a regresar del primero al segundo; y así sucesivamente hasta que los trenes
chocan. ¿Qué distancia recorrió el pájaro hasta el choque?
14. El consumo de carbón de una locomotora varía proporcionalmente al cuadrado de la
velocidad; cuando la velocidad es de 24 Km./h el consumo de carbón es de dos toneladas
por hora. Si el precio del carbón es de cuatro dólares por tonelada y los demás gastos de
la máquina son de cinco dólares por hora. Hallar el costo mínimo de un viaje de 100
kilómetros.
15. Problema: Al agua patos (Carmona, 2004).
…AYÚDANOS, Evaristo Colunga vive en la ciudad de Morelia, Michoacán. Acaba de
heredar un balneario que ofrece servicio de hotel. El Sr. Colunga se dedica al negocio de
la construcción, por lo cual no tiene ninguna experiencia en la administración de
balnearios ni hoteles. Por esta razón ha decidido cerrar el lugar. Al enterarse las
comunidades cercanas al balneario de esta decisión, se presentaron ante el Sr. Colunga
para pedirle que no cerrara el parque, puesto que atrae mucho turismo que representa
importantes ingresos para la comunidad así como un buen número de empleos para las
personas que viven en ella. Así, le propusieron que si decidía no cerrar el lugar, la
comunidad lo asesoraría en los diversos aspectos que conlleva la administración y manejo
del parque. Afortunadamente, el Sr. Colunga aceptó gustoso.
Actualmente, el hotel del Sr. Colunga cuenta con 40 habitaciones. Se sabe que si cobra
$250 por habitación por noche, se tendrá cupo lleno (es decir, se ocupará el total de las
habitaciones). Sin embargo, también se sabe que por cada $10 que se aumente al precio,
una habitación quedará desocupada. Además, el Sr. Colunga debe pagar $50 por noche,
por cada habitación ocupada, por el costo de limpieza y mantenimiento. El Sr. Colunga
quisiera saber qué tarifa debe cobrar por cada habitación para poder obtener la máxima
ganancia posible, aún cuando esto signifique tener una o varias habitaciones desocupadas.
Ayuda al Sr. Colunga escribiendo una carta donde expliques, con la información que se
tiene, cuánto debería cobrar por cada habitación por noche para obtener las mayores
ganancias posibles. Explica bien e método que utilizaste para realizar estos cálculos, para
que el Sr. Colunga pueda calcular la tarifa en el futuro y siempre obtenga las mayores
ganancias posibles. Con tu ayuda, el Sr. Colunga obtendrá buenas ganancias y sobre todo,
la comunidad del lugar seguirá con sus ingresos y con sus empleos.
16. Problema: Sombras (Balanced Assessment Package for the Mathematics Curriculum,
1999)
I.
Alicia mide 1.5 m. de estatura y se encuentra de pie a 3 m. de la base de un poste con
lámpara. La lámpara está a 4.5 m. de altura. ¿Cuánto mide la sombra de Alicia?
XVIII Encuentro de Profesores de Matemáticas
Página 108
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Longitud
de la
sombra
Distancia a la base del poeste
II. ¿Cómo variará la longitud de la sombre de Alicia cuando camina alrededor del poste, ya
sea acercándose o alejándose. Traza la gráfica que corresponda en los ejes de la derecha;
¿puedes encontrar una fórmula conveniente para esta gráfica.
III. Simón mide 2 m. de estatura. Supongamos que se aplica a Simón la pregunta 2. ¿Cómo
será su gráfica comparada con la trazada para Alicia? Expresa tus ideas mediante dibujos,
cálculos y explica tu razonamiento.
17. Problema: Azulejos en la cocina (Balanced Assessment Package for the Mathematics
Curriculum, 1999).
Federico decide cubrir el piso de su cocina con azulejos de diferentes modelos. Comienza con
una fila de cuatro azulejos del mismo tipo; enseguida, rodea esos cuatro azulejos con borde de
diferente modelo… El diseño continúa como se muestra en la figura. Federico hace una tabla
con el número de azulejos que necesita para cada borde:
Número de borde
1
2
3
No. azulejos en el
borde
10
14
18
XVIII Encuentro de Profesores de Matemáticas
Página 109
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
I.
Escribe una fórmula que le permita a Federico encontrar el número de azulejos a partir
del número de borde.
II. Emma quiere comenzar con cinco mosaicos en una fila y supone lo siguiente:
Si Federico comenzó con 4 azulejos y su fórmula fue
A=4b+6; entonces si yo comienzo con cinco azulejos
la fórmula será … A=5b+6.
Verifica la fórmula de Emma y muestra que no es correcta.
III. Encuentra la fórmula correcta para el inicio con cinco azulejos.
IV. Se puede obtener una extensión de este problema: considera como variables el número de
borde y el número inicial de azulejos; ¿cuál es la fórmula?
18. Evaluar un dibujo (Balanced Assessment Package for the Mathematics Curriculum,
2000; Sepúlveda, 2004).
La figura muestra un cuadrado de 60.96 cm. de lado, más el borde negro. Es el dibujo de un
vitral hecho de diminutos vidrios rectangulares coloreados.
Para la sección roja se usan 288 vidrios.
Para la sección azul se usan 144 vidrios.
Para la sección ámbar se usan 144 vidrios.
El dibujo corresponde al plafón para cubrir el claro
de un edificio que será enmarcado con el borde
negro. El borde completo contiene 40 vidrios negros
y su ancho consiste de un vidrio de lado.
El constructor se plantea las siguientes preguntas.
Ayúdale a responder cada una, anotando todo lo que
consideres necesario (no borres).
I.
Dibujo dado
azul
roja
60.96 cm.
ámbar
¿Cuántos vidrios de cada color se necesitan para
cubrir un claro de un edificio de 121.92 cm. x
121.92 cm.? (no olvidar que el borde es negro).
II. Escribe un enunciado que explique cómo puede
obtenerse el número de vidrios necesarios de
cada color, para cubrir un dibujo similar de
cualquier tamaño.
60.96 cm.
III. Supongamos que se tienen únicamente 6000 vidrios rojos y que de los otros colores hay
de sobra. ¿Cuál es el tamaño del mayor dibujo, como el de la figura, que puede hacerse?
XVIII Encuentro de Profesores de Matemáticas
Página 110
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Referencias
Alarcón, B. J. (1994). Libro para el Maestro. Matemáticas. Secundaria. Secretaría de
Educación Pública. México.
Balanced Assessment Package for the Mathematics Curriculum. High School Assessment
Package 1. (1999). White Plains, N. Y.: Dale Seymours Publications.
Balanced Assessment Package for the Mathematics Curriculum. High School Assessment
Package 2. (2000). White Plains, N. Y.: Dale Seymours Publications.
Hiebert, J., Carpenter, T. P. (1992). Learning and Teaching with Understanding. En D. A.
Grouwns (Ed.), Handbook of Research in Mathematics Teaching and Learning (pp.
65-97). New York: Macmillan Publishing Co.
Instituto Nacional de Estadística, Geografía e Informática (2002). PR. Segundo Informe de
Gobierno, 2002. Dirección General de Estadística. Dirección de Estudios
Demográficos y Sociales. http://www.inegi.gob.mx
Mason, J., Burton, L., Stacey, K. (1987). Thinking Mathematically. New York.: Adison
Wesley.
National Council of Teachers of Mathematics. (1980). An Agenda for Action:
Recommendations for School Mathematics for the 1980s. Reston Va.: National
Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (2000). Principles and Standards in School
Mathematics. Reston Va.: National Council of Teachers of Mathematics.
Polya, G. (1945). How to solve it. Princeton: Princeton University Press.
Santos, T., L. M. (2007). La resolución de problemas matemáticos. Fundamentos cognitivos.
Editorial Trillas. México.
Schoenfeld, A. (1992). Learning to think mathematically: Problem Solving, Metacognition,
and sense making in mathematics. En D. A. Grouwns (Ed.), Handbook of Research in
Mathematics Teaching and Learning (pp. 334-370). New York: Macmillan Publishing
Co.
Sepúlveda, A. (2004). Tesis de doctorado no publicada, presentada en el Centro de
Investigación y de Estudios Avanzados del IPN. Impresa en los talleres del
CINVESTAV, DF, México.
Verdugo, Santos, Rivera, Palmas, Briceño, Barrera. (2001). Un Estudio sobre los Propósitos y
Contenidos de los Cursos de Matemáticas del nivel Medio Superior. “El curriculum
de matemáticas en el nivel medio superior en México”. Proyecto de la Sociedad
Matemática Mexicana, financiado por CONACYT. México.
XVIII Encuentro de Profesores de Matemáticas
Página 111
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
La enseñanza de la geometría euclideana en el bachillerato
con Cabri
Dr. Armando Sepúlveda López
[email protected]
Facultad de Ciencias Físico Matemáticas, UMSNH
Introducción
Cuatro elementos trascendentes se consideran en el desarrollo de este curso. Primero: la
importancia del estudio de la geometría en la formación de los individuos y la existencia de
niveles de razonamiento geométrico; Segundo: la aceptación de la relevancia que representa
el enfoque de resolución de problemas en el estudio de las matemáticas; Tercero: el estudio de
los contenidos básicos de la geometría euclideana, a un nivel que permita al profesor de
matemáticas transmitir, con seriedad, los conocimientos de geometría; y Cuarto: la
conveniencia y necesidad de incorporar el uso de los medios tecnológicos en la enseñanza y el
aprendizaje de las matemáticas; en particular, el uso del software dinámico para estudiar
geometría.
Sin duda, entre las distintas materias que se estudian en la escuela, la geometría es una de las
ramas de las matemáticas básicas en la que se observa un mayor descuido en el currículum
escolar del nivel medio básico y medio superior de nuestro sistema educativo; mientras que
en el nivel superior, prácticamente, no se contempla en la gran mayoría de los planes de
estudio. Efectivamente, en secundaria los temas de geometría se abordan superficialmente y
en el bachillerato se destina muy poco tiempo o, simplemente, se omite su estudio
privilegiando contenidos algebraicos y de trigonometría; lo cual tiene sus efectos y
consecuencias en la formación matemática de los estudiantes en el nivel superior.
Marco teórico
Importancia del estudio de la geometría. La función formativa de la geometría ha sido
esencial en el desarrollo personal de profesores, profesionales de la educación matemática,
estudiantes y, en general, de toda persona educada, pues presenta valores insustituibles que
Thom (1973) resume en tres puntos: 1) La geometría proporciona distintas formas de ver en
todas las áreas de las matemáticas y otras ciencias. 2) Las interpretaciones geométricas
proporcionan visiones directoras del entendimiento intuitivo y permiten avanzar en la mayoría
de las áreas de las matemáticas. 3) Las técnicas geométricas proporcionan herramientas
eficaces para resolver problemas en casi todas las áreas de las matemáticas.
Por su parte, Hiele (1984) establece que el razonamiento geométrico de los estudiantes puede
evolucionar desde las nociones más intuitivas a otros niveles. Su modelo consta de cinco
niveles: En el Nivel 1 el estudiante percibe los objetos como unidades, describe semejanzas y
diferencias globales, pero no reconoce sus componentes y propiedades. En el Nivel 2 percibe
los objetos con sus partes y propiedades aunque no identifica las relaciones entre ellas;
describe los objetos de manera informal pero no es capaz de hacer clasificaciones lógicas;
hace deducciones informales a partir de la experimentación. En el Nivel 3 realiza
clasificaciones lógicas de los objetos, describe las figuras de manera formal, comprende los
pasos individuales de un razonamiento lógico, pero no es capaz de formalizar estos pasos, no
comprende la estructura axiomática de las Matemáticas. En el Nivel 4 el estudiante es capaz
XVIII Encuentro de Profesores de Matemáticas
Página 112
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
de realizar razonamientos lógicos formales, comprende la estructura axiomática de las
matemáticas y acepta la posibilidad de llegar a un mismo resultado desde distintas premisas.
Según los autores, existe un Nivel 5 al que muy pocas personas llegan a acceder y tiene que
ver con la generación de nuevos modelos y teorías geométricas.
La resolución de problemas en la educación matemática.
En este contexto, existe el reconocimiento de que la formación matemática de los estudiantes
y la evolución de su razonamiento geométrico, se robustecen cada vez que éstos se involucran
en procesos de resolución de problemas (Polya, 1945; NCTM, 2000; Santos, 2007). La
resolución de problemas es la línea de desarrollo que mayor progreso ha procurado a la
educación matemática; está presente en casi todas las áreas o especialidades que conforman
esta disciplina y, si bien es cierto que el desarrollo del conocimiento matemático se debe, en
buena medida, a la resolución de los problemas que matemáticos y otros científicos se han
planteado a lo largo de la historia, es hasta los trabajos de George Polya, en 1945, que esta
actividad comienza a considerarse importante en la educación matemática.
Con la idea inicial de ayudar a sus estudiantes a superar sus dificultades de aprendizaje, Polya
(1945) propuso un método que consta de las ya conocidas cuatro fases: Entender el problema;
Diseñar un plan de solución; Ejecutar el plan; y Revisar el trabajo realizado. Los argumentos
esgrimidos en este método se convirtieron en un paradigma que trajo consecuencias
importantes para la educación matemática. Aunque esto se planteó en 1945, fue hasta la
década de 1970 que empezó a reconocerse ampliamente el trabajo de Polya, quien argumenta
que en la resolución de problemas es necesaria la incorporación de los procesos heurísticos,
así como el monitoreo y control que se desarrolla como consecuencia de la reflexión y el uso
de recursos matemáticos. Es decir, en el proceso de resolución de problemas interviene
fuertemente la heurística, la reflexión y el uso de recursos matemáticos.
Las acciones físicas o mentales que contribuyen a encontrar pistas o ideas que ayudan a
resolver los problemas, fueron identificadas por Polya (Ibíd.) como heurísticas; algunas veces
son trazos, toma de valores extremos, aplicación de resultados conocidos, comparaciones,
visualizaciones, descarte de posibilidades, etc., los cuales necesariamente se combinan con los
procesos de reflexión.
El NCTM (2000) destaca la importancia de considerar a la resolución de problemas como el
eje central de las matemáticas escolares y se promueve el desarrollo de estudios e
investigaciones relacionados con la enseñanza y el aprendizaje de las matemáticas. Se
propone la resolución de problemas como una actividad fundamental que los estudiantes
deben realizar en forma individual y colectiva, pues propicia un ambiente para lograr un
aprendizaje significativo que implica la intervención de otros procesos de pensamiento como
son: la búsqueda de conexiones, el empleo de distintas representaciones, la necesidad de
justificar los pasos dados en la solución de un problema y comunicar los resultados obtenidos.
Para Schoenfeld (1998), aprender matemáticas es un proceso continuo que se ve favorecido
en un ambiente de resolución de problemas, donde los estudiantes tienen oportunidad de
desarrollar formas de pensar que son consistentes con el quehacer de la disciplina. De esta
manera, los estudiantes pueden conceptualizar a la disciplina en términos de preguntas que
necesitan examinar, explorar y resolver a través del uso de distintas estrategias y recursos
matemáticos. Previamente, Schoenfeld (1992) ya había identificado las características propias
del pensamiento matemático con las acciones típicas que realiza un matemático cuando se
XVIII Encuentro de Profesores de Matemáticas
Página 113
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
encuentra en el proceso de resolver un problema, las cuales son: tomar casos particulares;
descubrir patrones y relaciones; plantear conjeturas; hacer generalizaciones; y justificar
resultados.
Así, el reto en la instrucción matemática es generar condiciones de aprendizaje para los
estudiantes donde se reflejen valores propios relacionados con el desarrollo de la disciplina.
En particular, el salón de clase debe promover actividades y hábitos consistentes con la
práctica real de la disciplina (Schoenfeld, 1992, p. 345).
…Para desarrollar los hábitos apropiados y la disposición de interpretación y de
encontrar sentido a las ideas matemáticas y el desarrollo de modelos apropiados de
pensamiento matemático –la comunidad de práctica en donde los estudiantes aprenden
matemáticas debe soportar y desarrollar las formas de pensar de la práctica
matemática. Esto es, el salón de clase deben ser comunidades en la cual el encontrar
sentido a las ideas debe ser lo que se espera que los estudiantes practiquen.
Ahora bien, el NCTM (2000) plantea como aspiración central que los estudiantes desarrollen
los distintos tipos de razonamiento matemático a lo largo del currículum escolar; en particular
el razonamiento geométrico. La geometría está inmersa en el mundo físico, el sujeto empieza
a aprenderla, incluso, antes de la educación escolar, sus nociones se desarrollan inicialmente a
través de los sentidos (el tacto, la vista) que le permiten distinguir formas, hacer
clasificaciones y, posteriormente, con la aparición del lenguaje, hacer descripciones y
deducciones de objetos y proposiciones matemáticas, aspectos que forman parte de los
elementos básicos del razonamiento geométrico. La geometría es “el lugar” del currículo
donde los estudiantes pueden aprender e iniciarse en la estructura axiomática de las
matemáticas.
Uso de medios tecnológicos en el estudio de las matemáticas.
El uso de la tecnología resulta cada vez más relevante en la enseñanza y el aprendizaje de las
matemáticas en general; en particular de problemas de variación. La incorporación de la
computadora con software dinámico (Cabri géomètre, por ejemplo) como herramienta de
estudio, permite que la atención del estudiante se centre en los procesos de razonamiento, de
reflexión y de resolución de problemas; donde pueden aflorar ciertas formas de pensar que de
otra manera sería difícil observar (Santos, 2007). Regularmente, los problemas de variación
presentan dificultades para ser entendidos por los estudiantes, quizás esto se debe a la
naturaleza misma de la noción de variación; en la actualidad, se considera que el uso
adecuado de la tecnología puede ayudar a entender problemas de variación y de las
denominadas matemáticas del cambio.
El empleo de la tecnología es un aspecto importante en la instrucción matemática (NCTM,
2000). En este contexto propone:
La tecnología es esencial en la enseñanza y el aprendizaje de las matemáticas. Influye
en la matemática que se enseña y ayuda al aprendizaje de los estudiantes. (NCTM,
2000, p. 30).
El uso de Cabri es un software dinámico que puede denominarse "procesador de ideas
matemáticas" (Goldenberg, 2000), también puede clasificarse dentro del grupo de software
abierto, en el sentido en que los estudiantes producen ideas, las expresan, desarrollan y editan.
En este tipo de ambientes computacionales, el maestro y el alumno deciden qué hacer con la
XVIII Encuentro de Profesores de Matemáticas
Página 114
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
herramienta, en lugar de que el propio programa de cómputo guíe de manera directa el trabajo
del usuario, como ocurre con los llamados tutoriales. Cabri permite manipular los objetos
geométricos que aparecen en la pantalla. Esto hace posible que el estudiante trace y deforme
figuras, un seguimiento de los cambios que se producen en esta transformación puede
conducir a la construcción de propiedades invariantes de las figuras.
Goldenberg y Cuoco (1997) hacen una descripción del software de geometría dinámica en los
siguientes términos:
Un nuevo tipo de software conocido como geometría dinámica, está generando tal
interés y entusiasmo que, también, está incursionando rápidamente en las escuelas. El
software proporciona ciertos objetos primitivos (puntos, líneas, círculos),
herramientas básicas (por ejemplo, perpendicular a una línea L a través del punto P);
agrupando todo esto en los objetos compuestos, y varias posibles transformaciones,
incluyendo, por ejemplo, la reflexión a través de un punto o una línea. También le
permite al usuario medir ciertas partes del dibujo, y examinar la traza que dejan los
puntos, segmentos, o círculos cuando se aplica una transformación dinámica.
Este tipo de software le permite al usuario la transformación de las figuras en tiempo real.
Esta característica notable permite que los estudiantes, después de que hagan una
construcción, muevan libremente ciertos elementos de un dibujo y que observen cómo se van
transformando otros elementos. Mientras que los elementos libres se mueven en el dominio en
el cual existen, el software mantiene todas las relaciones que fueron especificadas como
atributos esenciales de la construcción original.
Algunas características importantes que tiene el uso del Cabri en el estudio de la geometría
son:
a. El software dinámico permite estudiar la deformación continua de una construcción
geométrica, o el lugar geométrico de un cierto objeto mientras que otros se transforman
de una manera continua.
b. El software puede ayudar a los estudiantes a explorar y construir conjeturas.
c. Permite hacer simulaciones de los problemas matemáticos para ayudar a encontrar
relaciones.
d. Posibilita un acercamiento gráfico a la solución de problemas de variación.
e. Permite el empleo de diferentes registros de representación (gráficos, tabulares y
algebraicos).
El desarrollo de la visualización en matemáticas.
Finalmente, un aspecto central en el estudio y aprendizaje de las matemáticas es el desarrollo
de la visualización, proceso asociado a la “formación” de imágenes y a su uso para el
entendimiento y descubrimiento matemático (Zimmerman y Cunningham, 1995, p. 5). Esta
formación de imágenes puede ser producida por un acto mental (imaginarla), o mediante uso
de lápiz y papel o con tecnología. En este sentido, Presmeg (2006) realiza investigaciones
sobre la visualización e imaginación espacial y aborda el papel de la mediación de los
procesos visuales en matemáticas de la escuela secundaria; hace una revisión histórica sobre
el uso y evolución de este tema y sugiere que la construcción imágenes mentales en los
estudiantes puede tomar más tiempo que el requerido en los aspectos analíticos.
XVIII Encuentro de Profesores de Matemáticas
Página 115
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Estudio de los contenidos de geometría y uso del Cabri
A continuación se presentan algunos de teoremas y problemas de Geometría euclideana del
material elaborado por Armando Sepúlveda y, al mismo tiempo, se darán instrucciones para
usar el software dinámico Cabri II Plus.
Durante el desarrollo del curso se destacan los siguientes aspectos:
a.
El patrón axiomático sugerido por Euclides;
b.
Las características de las demostraciones directas e indirectas;
c.
La relevancia de la aplicación de estrategias heurísticas en la demostración de los
teoremas o solución de los problemas geométricos;
d.
La importancia de las posibilidades de visualización y de exploración que suministra el
software dinámico; y
e.
Si bien es cierto que el uso de los medios tecnológicos puede influir, de diferentes
maneras, en el aprendizaje de los estudiantes, esto no sustituye la argumentación
necesaria para constituir una demostración propiamente dicha.
Entre los temas que se estudiarán en el curso, con su argumentación geométrica y con el uso
del software, se cubrirán, en lo posible, lo siguiente:
1.
Problemas introductorios: a) Dado un arco, construir la circunferencia que lo contiene; b)
construir un cuadrado a partir de una de sus diagonales; c) partición de un segmento en
una razón dada.
2.
Teorema del ángulo externo y teorema de la desigualdad del triángulo.
3.
Teoremas de los lugares geométricos: mediatriz y bisectriz.
4.
Teoremas de concurrencia de la mediatrices y de las bisectrices.
5.
Cuadriláteros y sus propiedades (teoremas relacionados); teorema del segmento que une
puntos medios de dos lados de un triángulo.
6.
Teorema de concurrencia de las medianas.
7.
Áreas de polígonos; teoremas sobre el cálculo de áreas de: triángulo, trapecio, razón de
áreas de triángulos con igual base o altura.
8.
Teorema de Pitágoras.
9.
Teorema fundamental de proporcionalidad y teoremas de semejanza.
10. Teorema del ángulo central y teorema de la potencia de un punto.
11. Teorema de la concurrencia de las alturas.
Esquema de un teorema y formas de demostración
Un teorema es una proposición verdadera que puede demostrarse (deducirse) a partir de la
utilización de argumentaciones verdaderas, que pueden ser: definiciones, axiomas, postulados
o resultados de otros teoremas. La palabra entonces relaciona la parte del enunciado de una
XVIII Encuentro de Profesores de Matemáticas
Página 116
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
proposición que nos proporciona la información verdadera (hipótesis) que es necesaria para
iniciar el discurso de la prueba; y la parte de dicho enunciado en la que se afirma algo, lo que
debe demostrarse (tesis) a través, en este caso, del razonamiento deductivo; eslabonamiento
de argumentos simples y verdaderos. Así, esquemáticamente, podemos representar a un
teorema de la siguiente manera:
p  q
Donde p es la hipótesis, q la tesis y el símbolo  , es la implicación lógica. Cuando en un
teorema se intercambian p y q se obtiene el teorema recíproco, cuya forma esquemática es
q  p.
Demostración directa. Si el eslabonamiento de los argumentos utilizados en la deducción,
parte de p y son dirigidos hacia q, se dice que la demostración es directa.
Este tipo de demostración es utilizado por Euclides en la mayoría de las proposiciones de Los
elementos; sin embargo, muy pronto se dio cuenta que en algunas ocasiones es conveniente no
seguir este camino (Proposición 6 del Libro I), sino utilizar una forma indirecta de
demostración.
Demostración indirecta. Una demostración indirecta parte de p y de la negación de q, para que
mediante el eslabonamiento de argumentos simples y verdaderos, se llegue a un resultado que
es absurdo lógicamente o que contradice una afirmación verdadera (puede ser la hipótesis, un
postulado o algún resultado de otro teorema; en este caso se dice que hay una contradicción).
Ejemplo de una demostración directa. El siguiente es uno de los teoremas indispensables
para poder demostrar el primero de nuestros teoremas, que llamaremos Teoremas
fundamentales de la Geometría Euclideana. Los teoremas que son utilizados en la
demostración de otro teorema, se llaman lemas.
Lema. Teorema del ángulo externo. Si se considera cualquiera de los ángulos exteriores de un
triángulo ABC, entonces su medida es mayor que la medida de cualquiera de los ángulos
interiores no adyacentes a él.
Aquí la hipótesis p es: El
es un ángulo exterior del triángulo ABC; y la tesis q:
medida
es mayor que
y medida
es mayor que
.
Demostraremos la primera desigualdad.
Demostración. Consideremos el ángulo exterior DCA del
y sea M el punto medio del
lado AC; trazamos la mediana BM y la prolongamos hasta el punto N tal que
(Figura 1); finalmente, tracemos CN.
XVIII Encuentro de Profesores de Matemáticas
Página 117
5,85 cm
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
A
N
M
B
C
D
Figura 1. Trazo necesario para demostrar el Teorema del ángulo externo.
Analicemos la correspondencia AMB y CMN de los triángulos
:
por definición de punto medio;
por ser ángulos opuestos por el vértice; y
por construcción (así lo trazamos)
entonces
por el Postulado de congruencia LAL.
Por lo tanto,
Entonces
. Pero el ángulo NCM es una parte del ángulo DCA; de ahí que
, que es precisamente lo que queríamos de mostrar.
Para demostrar la otra desigualdad basta con localizar L, el punto medio de BC, trazar la
mediana AL y seguir el razonamiento de manera similar.
Ejemplo de una demostración indirecta. [Aquí, necesariamente, recurriremos a dos lemas:
Teorema del triangulo isósceles y Teorema del ángulo externo].
Teorema (“recíproco del Teorema del triángulo isósceles”): Si un triángulo tiene dos ángulos
iguales entonces los lados opuestos a estos ángulos también son iguales.
Aquí p es: dos ángulos del ABC son iguales; q es: los lados opuestos a estos ángulos son
iguales.
Demostración: Consideremos el ABC con ABC  ACB .
Supongamos que los lados opuestos no son iguales; esto es, que AB  AC , por lo tanto uno
es mayor que el otro. Sea AB  AC .
XVIII Encuentro de Profesores de Matemáticas
Página 118
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
A
B
C
D
Figura 2. Triángulo isósceles y trazo para su prueba.
[Comentario: Euclides diría: “si así no fuera (es decir, que los lados opuestos son iguales)
habría uno mayor que el otro; sea AB el mayor …”. Nótese que aquí se está recurriendo a la
Ley de tricotomía de los números reales].
Entonces, en la prolongación de AC existe D tal que AB  AD , trazamos BD para formar el
BCD (Figura 2).
Aplicando el teorema del triángulo isósceles al
ACB es ángulo externo al BCD , por lo tanto
ABD , tenemos ABD  ADB . Pero
ACB  ADB
y como ABD ABC  ACB  ABC , lo cual contradice la hipótesis.
Así que no debemos suponer que AB  AC . De la misma manera se llega a una contradicción
si AB  AC . Por lo tanto, utilizando la propiedad de tricotomía de los reales: AB  AC , lo
cual se quería probar.
El eslabonamiento lógico de argumentos nos llevó a hacer evidente que para los lados AB y
AC no hay otra alternativa más que ser iguales. Obsérvese que en esta demostración se usaron,
en forma relevante, dos resultados establecidos por el Teorema del triángulo isósceles y el
Teorema del ángulo externo; los Teoremas que son necesarios en la demostración de otro
Teorema, se llaman Lemas.
[Comentario: En varias ocasiones, puede no existir un camino único en la demostración de un
Teorema; por ejemplo, la demostración que se da en Los Elementos de este teorema, en los
puntos suspensivos del comentario anterior Euclides dice: “entonces existe un punto D entre A
y B para el cual BD  AC …”; y usando congruencia de triángulos (criterio LAL) concluye
“resulta que el menor es igual al mayor, lo cual es absurdo”].
Concluimos esta parte refiriéndonos al trazo permisible: Euclides eligió esta forma axiomática
de hacer deducciones, razonamiento que va de lo general a lo particular, en el que se
XVIII Encuentro de Profesores de Matemáticas
Página 119
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
requieren figuras y trazos que deben ser elaboradas siguiendo normas, bien establecidas, para
el uso de la regla y el compás:
La regla es no graduada; se usa sólo para trazar rectas, segmentos y rayos. Esto lo permiten
los Postulados 1 y 2 del Libro I de Los Elementos.
El compás euclideano contiene un resorte que impide mantenerlo fijo; una vez que hemos
trazado un arco o una circunferencia, en un punto como centro y una distancia como radio,
éste se cierra. Esta es la restricción que impone el Postulado 3.
El Postulado 4 indica que la perpendicularidad será utilizada como uno de los elementos
básicos para armar el discurso; el ángulo recto será el punto de referencia. El Postulado 5,
conocido como “Postulado de la paralelas” o “Quinto postulado”, es la proposición que
caracteriza a la Geometría Euclideana, alrededor de la cual se ha generado el desarrollo de la
matemática producto de amplias discusiones e intentos infructuosas por demostrar que dicha
proposición es teorema.
Así, las deducciones en el método axiomático, además de la secuencia lógica que debe
seguirse, los recursos de trazos y figuras auxiliares se sujetan a las normas de uso de la regla y
el compás.
Teorema de la desigualdad del triángulo. Si ABC es un triángulo entonces la suma
de las longitudes de cualesquiera dos de sus lados es mayor que la longitud del tercer
lado (Proposición 20-I).
Es un teorema de extrema importancia; establece la posibilidad de construir la figura plana
convexa con el menor número de lados. Prácticamente el desarrollo de toda la geometría
depende, en mayor o menor parte, de él. Juega un papel fundamental en diferentes ramas de
las matemáticas como variable compleja, análisis matemático, álgebra superior, cálculo, entre
otras; y también está presente en otras ciencias; Física, Química, Ingeniería.
Demostración: Sea ABC el triángulo dado (esto es p; la hipótesis) y representémoslo
gráficamente. Debemos probar que
AB  BC  CA ; o BC  CA  AB ; o CA  AB  BC .
Probemos la primera desigualdad. Para ello usaremos un trazo auxiliar (permisible con regla y
compás) y los lemas: “En todo triángulo, a ángulo mayor se opone lado mayor” y Teorema
del triángulo isósceles.
Trazo: Con centro en B dibujemos la circunferencia de radio BA
prolongación de CB en P y trazamos PA. Así, se ha formado el APB.
XVIII Encuentro de Profesores de Matemáticas
que interseca a la
Página 120
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Figura 3. Trazo asociado al Teorema de la desigualdad del triángulo.
Como el BPA es isósceles con BP  BA , entonces APB  BAP por el Teorema del
triángulo isósceles.
Pero el BAP es una parte del CAP , entonces CAP  BAP ; de ahí que
CAP  APB  APC (aquí de está utilizando el axioma: “el todo es mayor que la parte”);
y como a ángulo mayor se opone lado mayor, tenemos que en el APC se cumple PC  CA ;
pero
PC  PB  BC  AB  BC , luego entonces:
AB  BC  CA ,
que es lo que queríamos probar.
Obsérvese un encadenamiento de argumentos verdaderos que van directamente de p a q: un
“trazo permisible”; definiciones de triángulo y triángulo isósceles; el axioma “el todo es
mayor que la parte”; Teoremas del triángulo isósceles y el de “ángulo mayor se opone lado
mayor”. Así, la argumentación condujo a evidenciar que, efectivamente, la suma de cuales
quiera dos lados de un triángulo es mayor que el tercer lado.
Con este teorema y otros que hemos enlistado, se pueden probar los Teoremas de congruencia
LAA y el llamado hipotenusa-cateto; así como el Teorema de la charnela y su recíproco, entre
otros. Cabe mencionar que este último es el único teorema que permite aplicar transitividad,
en triángulos distintos, entre la desigualdad de lados o ángulos a partir de la desigualdad de
ángulos o lados.
En relación a la congruencia de triángulos hemos citado tres postulados (LAL, ALA, LLL) y
un teorema LAA. Las reproducciones a escala son muestra de que a partir de la
correspondencia del tipo AAA, entre los vértices de dos triángulos, no se puede concluir una
relación de congruencia. En general, esto también ocurre con la correspondencia LLA; salvo
cuando el ángulo es recto, lo que origina el Teorema de congruencia hipotenusa cateto. Esto
se ilustra en la Figura 4: i) en la de la derecha, el B es recto y se puede demostrar que si
CA  AD y DBA  ABD  90 , entonces ABC  ABD; ii) en cambio, la figura de la
izquierda muestra que los triángulos BAC y BAD cumplen con tener dos lados congruentes,
XVIII Encuentro de Profesores de Matemáticas
Página 121
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
AB es común, AC  AD y B es común; sin embargo, los triángulos ABC y ABD no
son congruentes.
Figura 4. Teorema de congruencia hipotenusa cateto.
Una consecuencia (corolario) importante, en extremo, del Teorema de la desigualdad del
triángulo es la definición de la distancia de un punto a una recta, que se ilustra en la Figura 5.
Si l es una recta y P un punto que pertenece a ella, la distancia de P a l necesariamente es la
longitud del segmento PQ ( PQ  l ), así se define, ya que con cualquier otro punto R sobre l
se forma el PQR en el que el ángulo RQP es recto; y por lo tanto PR es mayor que PQ
(¿por qué).
Figura 5. Ilustración base para la definición de la distancia de un punto a una recta.
Una vez enunciados los teoremas relativos al paralelismo, se definen y clasifican los
cuadriláteros, adquiriendo especial atención los paralelogramos. Un paralelogramo es un
cuadrilátero que tiene pares de lados opuestos paralelos. Luego se da una lista grande de
teoremas; sus demostraciones dependen de los teoremas sobre paralelas:
i.
Cada diagonal descompone a un paralelogramo en dos triángulos congruentes.
ii.
En un paralelogramo dos lados opuestos cualesquiera son congruentes.
iii.
Si dos rectas son paralelas, entonces todos los puntos de cada recta equidistan de la otra.
iv.
En un paralelogramo, dos ángulos opuestos cualesquiera son congruentes.
v.
En un paralelogramo, dos ángulos consecutivos cualesquiera son suplementarios.
vi.
Las diagonales de un paralelogramo se bisecan.
XVIII Encuentro de Profesores de Matemáticas
Página 122
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
vii. Si ambos pares de lados de un cuadrilátero son congruentes, entonces el cuadrilátero es
un paralelogramo.
viii. Si dos lados de un cuadrilátero son paralelos y congruentes, entonces el cuadrilátero es
un paralelogramo.
ix.
Si las diagonales de un cuadrilátero se bisecan, entonces el cuadrilátero es un
paralelogramo.
x.
Si un paralelogramo tiene un ángulo recto, entonces tiene cuatro ángulos rectos y se
trata de un rectángulo.
xi.
En un rombo, las diagonales son perpendiculares entre sí.
xii. Si las diagonales de un cuadrilátero se bisecan y son perpendiculares, entonces el
cuadrilátero es un rombo.
Ahora estamos preparados para estudiar una proposición que más usos y aplicaciones tiene
para demostrar otros teoremas o resolver una variedad de problemas; en particular, nos servirá
para probar que las medianas concurren. Nos referimos al siguiente:
Lema. Teorema del segmento que une los puntos medios de dos lados de un triángulo. En un
triángulo dado, si trazamos el segmento que une los puntos medios de dos de sus lados,
entonces el segmento es paralelo al tercer lado y mide la mitad de este.
Demostración. Sea ABC el triángulo dado, N y M los puntos medios de AB y AC,
1
respectivamente; si trazamos NM, queremos probar que NM || BC y NM  BC .
2
Como en la Figura 6, prolongamos NM por N hasta D, de modo que NM  MD y trazamos
CD. Analicemos la correspondencia ANM  CDM : AM  MC pues M es punto medio;
AMN  CMD por ser opuestos por el vértice; NM  MD por trazo. La correspondencia
es tipo LAL, por lo tanto ANM  CDM . Entonces AN  CD y MNA  MDC , estos
ángulos son alternos internos, por lo tanto AN || CD y como N es punto medio de AB, se
sigue que NB  CD .
Figura 6. Teorema del segmento que une punto medios de dos lados.
Entonces tenemos un cuadrilátero NBCD con un par de lados opuestos paralelos y
congruentes; por lo tanto, el cuadrilátero es un paralelogramo. De ahí que, por definición,
1
NM || BC y además MD  2NM  BC ; por tanto NM  BC , como lo queríamos probar.
2
XVIII Encuentro de Profesores de Matemáticas
Página 123
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Pasemos ahora a enunciar y demostrar el siguiente teorema fundamental, cuya utilización es
sustancial en diversas aplicaciones físicas y de ingeniería:
Teorema de la concurrencia de las medianas de los lados de un triángulo. Si se
trazan las medianas de los lados de un triángulo, entonces concurren en un punto
interior llamado Centro de gravedad (centroide o baricentro del triángulo).
Demostración. Sea el triángulo PQR con L, M y N los puntos medios de los lados QR, RP y
PQ, respectivamente. Si dibujamos las medianas PL y RN, estas se cruzan en un punto G
(Figura 7). Ahora localicemos los puntos medios de PG y RG, sean estos D y F. Tracemos el
cuadrilátero LNDF.
Aplicando el lema anterior al PQR :
NL || PR y NL 
1
PR .
2
Pero al aplicarlo también al triángulo PGR
DF || PR y DF 
1
PR ;
2
es decir LNDF es un cuadrilátero con un par de lados opuestos paralelos y congruentes,
entonces el cuadrilátero es un paralelogramo. Y como en un paralelogramo las diagonales se
bisecan, entonces DG  GL y FG  GN . Como que D y F son puntos medios de PG y RG,
resulta que G es un punto común a las dos medianas, tal que
PG RG

2
GL GN
(i).
Figura 7. Localización del Centro de gravedad.
Ahora trabajemos con las medianas PL y QM (Figura 7). Si llamáramos G’ al punto en que
éstas se cruzan, D’ al punto medio de PG’ y E’ el punto medio de QG’; trazamos D’MLE’, y
XVIII Encuentro de Profesores de Matemáticas
Página 124
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
de manera similar al anterior, llegaremos a: LM || PQ || D' E ' y LM  D' E ' 
1
PQ ; es decir,
2
DMLE es un paralelogramo en el que las diagonales se bisecan.
Por lo tanto, D' G'  G' L  PD' y EG'  G' M  QE' ; de donde, también se tiene que G’ es un
punto común a las medianas PL y QM, tal que
PG' QG'

2
G' L G' M
(ii).
Observemos que PL participa en las relaciones (i) y (ii) y sabemos que dado un segmento PL,
existe un único punto que “está entre” y que lo divide en una razón dada; así que G’ y G es el
mismo punto para las tres medianas. Por lo tanto las tres medianas concurren en G.
De aquí sale la regla práctica para la localización del Centro de gravedad en un triángulo
dado, la cual consiste en trazar una mediana y “localizar el punto tal que la divide en la razón
2 a 1, o 1 a 2, o que la triseca (es decir que la divide de manera que una de sus partes es la
tercera parte del total).
El lema anterior también es esencial en otras aplicaciones; por ejemplo, para responder o
resolver el problema involucrado en la pregunta siguiente: ¿Qué tipo de cuadrilátero se forma
cuando se unen, mediante segmentos, los puntos medios de los lados consecutivos de
cualquier cuadrilátero?
Concluimos este documento con otro de los teoremas fundamentales de la Geometría
euclideana en el ámbito escolar. Para mí, este es el penúltimo de los teoremas fundamentales,
respetando el orden axiomático deductivo.
Teorema de la concurrencia de las alturas. Si se trazan las alturas correspondientes
a los tres lados de un triángulo, entonces éstas concurren en un punto (interior o
exterior) llamado ortocentro.
Demostración. Dado el ABC , consideremos las alturas AL y BM que se cruzan en O.
Tracemos CO que interseca a AB en N; vamos a demostrar que CN es altura, probando que
CNA es recto (Figura 8).
Figura 8. Concurrencia de las alturas.
XVIII Encuentro de Profesores de Matemáticas
Página 125
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Si trazamos la circunferencia de diámetro AB, ésta pasara por L y M, ya que son ángulos
rectos (inscritos en una semicircunferencia). De igual manera, la circunferencia de diámetro
CO pasa por L y M.
Trazando ML, observamos que BAL  BML, por ser ángulos inscritos que subtienden el
mismo arco (BL). Además, en la otra circunferencia también tenemos que OML  OCL;
entonces, por transitividad NAO  OCL . Como AON  LOC entonces los terceros
ángulos de ambos triángulos deben ser iguales y como uno de ellos es recto, el otro también;
es decir,
CNA  ALC  90 .
Esto demuestra que CN también es altura, la cual pasa por el punto O.
Referencias
Goldenberg, E. & Cuoco, A. (1997). Habits of Mind: an Organizing Principle for the
Curricula. Journal of Mathematical Behavior. 15, (pp.375-402).
Goldenberg, P. (2000). Thinking (and talking) about technology in math classrooms.
Education Development Center, Inc.
Hiele-Geldof, D. (1984). The didactics of geometry in the lower class of secondary school (de
didaktiek van de meetkunde in de eerste klas van het V.H.M.O.). En Fuys; Geddes,
Tischler. Selected writings of Dina Van Hiele-Geldof and Pierre M. Van Hiele,
Brooklyn College, C.U.N.Y., Nueva York.
National Council of Mathematics Teachers. (2000). Principles and Standars for School
Mathematics. NCTM, Reston Va. USA.
Presmeg, N. (2006). Handbook of Research on the Psychology of Mathematics Education.
Research on Visualization in Learning and Teaching Mathematics (pp. 205-235).
ISBN 90-77874-19-4
Polya, G. (1945). How to solve it. Princeton: Princeton University Press, USA.
Santos, M. (2007). La resolución de Problemas Matemáticos. Fundamentos Cognitivos,
México: Biblioteca de la ANPM, Trillas, México.
Schoenfeld, A. (1992). Learning to think mathematically: Problem Solving, Metacognition,
and sense making in mathematics. En D. A. Grouwns (Ed.), Handbook of Research in
Mathematics Teaching and Learning (pp. 334-370). New York: Macmillan Publishing
Co.
Schoenfeld, A. H. (1998). Reflections on a course in mathematical problem solving. Research
in Collegiate Mathematics Education III., pp. 81-113.
Thom, R. (1973). Matemáticas de hoy y matemáticas de siempre. En J. Hernández (Ed.) La
enseñanza de la matemática moderna. Madrid: Alianza Editorial, España.
Zimmerman, W., Cunningham, S. (1995). Visualización Matemática, en Memorias del
CIEAEM 01.95; Disco flexible, 10/02/95.
XVIII Encuentro de Profesores de Matemáticas
Página 126
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Curso de Cálculo Infinitesimal para el Bachillerato
Dr. José Ismael Arcos Quezada
[email protected]
Universidad Autónoma del Estado de México
Resumen
Desde sus orígenes, el cálculo infinitesimal leibniziano mostró sus ventajas para el modelado
de fenómenos naturales y en la comprensión de los conceptos básicos, lo que no ocurre con la
presentación usual en las escuelas. Aquí se presenta una propuesta en la que se intenta
recuperar esas cualidades.
Introducción
La manera en la que se imparte el curso de cálculo que se ofrece en el Nivel Medio Superior
generalmente se orienta al desarrollo de habilidades operativas en el alumno.
Así, la tradición nos ha llevado a considerar como medida del aprendizaje del cálculo a la
habilidad algorítmica del alumno para el cálculo de límites, derivadas e integrales, para lo
cual se invierte casi todo el tiempo del curso, soslayando aspectos más de carácter conceptual
o de resolución de problemas.
Para remediar tal situación, es necesario implementar nuevas metodologías de enseñanza, así
como diseñar e instrumentar actividades de aprendizaje para el desarrollo de competencias
como la resolución de problemas. Sin embargo, el análisis de la pertinencia de los contenidos,
así como su influencia en los niveles de aprendizaje alcanzados por los alumnos, es un asunto
que no ha sido, creo yo, suficientemente atendido en la investigación en matemática
educativa.
En el presente trabajo se parte de la convicción de que la temática que compone
tradicionalmente el curso escolar de cálculo, es un factor importante en el bajo aprendizaje de
la materia en el nivel medio superior.
Justificación de la propuesta
Los cursos de cálculo que tradicionalmente se ofrecen en el Nivel Medio Superior están
basados en el concepto de límite, el cual, la experiencia nos indica, es incomprensible para la
mayoría de los estudiantes, sobre todo si se pretende abordar con todo el rigor que le
caracteriza.
Por otra parte, y debido entre otras cosas a que las calculadoras graficadoras y el software
especializado es cada vez más accesible, el nivel de rigor ha venido disminuyendo,
sustituyéndose por el recurso de la visualización, que no era bien visto en las aulas hasta antes
de los 80.
Sin embargo, el enfoque basado en el concepto de límite ha seguido utilizándose, y ello
supone que, antes de abordar la problemática propia del cálculo diferencial e integral, se
busque capacitar a los alumnos en el uso de toda la herramienta conceptual y algorítmica
requerida para ello. Así, se consume una buena cantidad de tiempo en las aulas en cuestiones
tales como el conjunto de los números reales, las funciones reales o la solución de
desigualdades.
XVIII Encuentro de Profesores de Matemáticas
Página 127
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Si se busca desarrollar competencias matemáticas tales como la representación gráfica de
relaciones y funciones, la resolución de problemas, o el modelado, debemos de diseñar el
curso de cálculo de manera que favorecer dicho desarrollo, “robándole” tiempo a esos temas
que, en este contexto, ya no resultan tan importantes. Esa es la intención de este trabajo.
Un poco de historia
En sus orígenes, el cálculo infinitesimal estuvo claramente asociado con la solución de
problemas y se presentaba generalmente en un contexto geométrico, aunque desde los
primeros escritos de Leibniz se manifestaba ya la potencialidad de la nueva herramienta para
abordar y resolver problemas de la Física y otras ciencias.
Así por ejemplo, el libro de L‟Hôpital, que se reconoce como el primer libro de texto de
cálculo, desde el mismo título expresaba su propósito principal: Análisis de los infinitamente
pequeños para el estudio de las líneas curvas. En esta obra se dedicaba sólo la primera
sección para exponer las reglas para obtener las diferenciales, mientras que las nueve restantes
se dedicaban a la solución de determinados problemas relativos a la geometría de las curvas,
tales como la recta tangente, los puntos de inflexión y la curvatura.
Medio siglo más tarde, Bezout, utilizando también el cálculo leibniziano, y por lo tanto,
basándose en las cantidades infinitamente pequeñas o infinitesimales, escribió su Cálculo
infinitesimal con el propósito de que sus alumnos entendieran y resolvieran problemas de
mecánica.
En cambio, en el Análisis de Cauchy, en lugar de cantidades infinitamente pequeñas, vemos
“límites y convergencia”, términos que subsisten hasta ahora. Por otra parte, como lo indica
Jean Dhombres, con la propuesta de Cauchy se adoptó un Cálculo totalmente
descontextualizado:
En el Análisis algebraico Cauchy no hace ninguna referencia a la física matemática,
a pesar de que él mismo la cultivó con mucho talento, y no parece interesarse en el
conocimiento del mundo sensible ni en las aplicaciones de la ciencia matemática
(…) Si bien no es el primer texto de matemáticas puras, la obra de Cauchy es tal
vez la primera, en análisis, que por sus objetivos, no intenta ninguna justificación
ajena a las relaciones intrínsecamente matemáticas. Muy sintomática es también la
diferencia con manuales como los de Bezout, sus cursos de matemáticas para el uso
de la artillería o para el uso de los guardias de la marina, redactados cincuenta años
antes, pero editados en la época de Cauchy y en los cuales muchas páginas evocan
las aplicaciones, libros en los cuales el cálculo diferencial mismo no se presenta
sino como preliminar a la mecánica y sólo para su utilización práctica.
Así pues, Cauchy no mostraba ningún interés en aplicación alguna. Podría decirse incluso que
consiguió “liberar” al cálculo de sus aplicaciones y, por lo tanto, de una problemática por
resolver.
Considerando lo anterior, se busca una propuesta para la enseñanza del cálculo, que recupere
el valor didáctico del cálculo infinitesimal leibniziano.
El Taller
La propuesta se ha estado explorando en las aulas de la Facultad de Ingeniería de la
Universidad Autónoma del Estado de México, en donde la mayoría de los profesores la utiliza
XVIII Encuentro de Profesores de Matemáticas
Página 128
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
en el primer curso de cálculo. A partir de esas experiencias se escribió un texto para ser
utilizado en el bachillerato.
Se han elegido algunas partes del texto para ser abordadas en el Taller, las cuales se describen
a continuación:
1.
Aritmética y geometría infinitesimalistas.
Partiendo de la pregunta de cuánto varía la masa de la Tierra si le cae un meteorito, o incluso,
si se considera la masa de toda la gente de la Tierra, con la condición de hacer las operaciones
con calculadora, y con otras actividades con calculadora, se obtienen las reglas para operar
con cantidades infinitamente pequeñas, finitas e infinitamente grandes.
Por otra parte, y con base en la concepción leibniziana de las curvas, es decir, de considerarlas
como poligonales con una infinidad de lados, cada uno de ellos uniendo dos puntos
infinitamente próximos entre sí, se motiva la idea de utilizar el arco, la cuerda o la tangente,
indistintamente, cuando los puntos del arco están infinitamente próximos. Esa idea es
fundamental para obtener importantes resultados, como el de que “el seno de un ángulo
infinitamente pequeño (medido en radianes) es igual al ángulo mismo”.
2.
Serie geométrica y serie binomial
A partir del “problema de los granos de arroz en el tablero de ajedrez”, se genera la definición
de la progresión geométrica y puede obtenerse la expresión para la suma parcial. Luego puede
recurrirse a la paradoja de Zenón (de Aquiles y la tortuga) y las características de la gráfica de
la función exponencial para llegar a la expresión correspondiente a la serie binomial.
La idea de “suma de una infinidad de términos” nos permite introducirnos en el importante
concepto de convergencia.
Por otra parte, partiendo de la idea newtoniana para la generación de los coeficientes de la
potencia de un binomio, se obtiene la expresión para la serie binomial, es decir, de la potencia
de un binomio cuando el exponente no es un número natural.
Al seguir explorando con la calculadora la idea de convergencia, se puede hablar del
problema de “cómo evaluar una función trascendente”.
Con el estudio de estas cuatro secciones pueden ahora abordarse los problemas
fundamentales: el cálculo diferencial y el cálculo integral.
3.
Incremento, diferencial, recta tangente y función derivada
Considerando una ecuación en dos variables como la representación simbólica de la relación
entre dos cantidades variables, y una curva en el plano como su representación gráfica, se
generan los importantes conceptos de incremento y razón promedio de cambio. Para ello
simplemente hay que considerar dos puntos cualesquiera de la curva.
Si uno de estos se supone fijo, mientras que el otro se mueve sobre la curva acercándose al
fijo, en el momento en que los puntos estén infinitamente próximos se obtienen las
definiciones de diferencial y razón (instantánea) de cambio. Después, al considerar variable la
abscisa del punto fijo, se obtiene la definición de función derivada.
Por otra parte, al reconocer la coincidencia entre el arco, la cuerda y la recta tangente cuando
los puntos de la curva están infinitamente próximos, se reconoce la relación entre la derivada
y la pendiente de la recta tangente.
XVIII Encuentro de Profesores de Matemáticas
Página 129
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
4.
Graficación y optimización
Apoyándose en la relación entre derivada y recta tangente, y estudiando la relación entre la
concavidad y la segunda derivada, se proponen los elementos para la el trazo de la gráfica de
una función, con ayuda del cálculo diferencial. Particularmente se proponen los dos criterios
básicos para la determinación de los valores extremos de la función.
Enseguida se estudia cómo utilizar los criterios mencionados para la solución de problemas de
optimización.
5.
Proceso de integración, área bajo la curva y longitud de un arco
El cálculo integral se puede introducir con la simple idea de considerar la operación inversa a
la diferenciación.
Luego, es importante reconocer el proceso de integración como le que se requiere para
“recuperar” el valor de una cantidad completa (íntegra) a partir del conocimiento de una parte
infinitamente pequeña (elemento) de la misma.
El contexto geométrico brinda buenas oportunidades para realizar el proceso de integración en
diversas situaciones, en particular para el cálculo del área de una región plana y el cálculo de
un arco de una curva.
En cada sección se puede partir de una o varias situaciones problemáticas, y la naturaleza de
los contenidos resulta idónea para recurrir a la tecnología, desde la calculadora básica hasta la
computadora y paquetes de software especializado, preferentemente uno libre, como el
GeoGebra, e internet.
Comentario final
Conociendo los bajos niveles de aprendizaje de los conceptos del cálculo, cuando se basa en
el concepto de límite, y conociendo, por otro lado, que en la modelación de los fenómenos
propios de las ciencias básicas, generalmente se recurre a un cálculo más próximo a la
presentación leibniziana, valdría la pena el explorar una presentación infinitesimalista en las
aulas del nivel medio superior.
Referencias
Arcos, I. (2010), Cálculo infinitesimal para bachillerato, editorial Kali, Toluca, México.
Bezout, E. (1770 ?), Cálculo infinitesimal, Limusa-IPN, México, 1999. Traducción de la
edición original en francés.
Cauchy, A. L. (1823), Curso de análisis, colección MATHEMA, UNAM, México, 1994.
Versión en español basada en los trabajos originales en francés: cours d’analyse
(1821) y Résume des leçons sur le calcul ininitésimal (1823). Selección, traducción
directa del francés y notas de Carlos Álvarez e introducción de Jean Dhombres.
L‟Hôpital, Marqués de (1696), Análisis de los infinitamente pequeños para el estudio de las
líneas curvas, colección MATHEMA, UNAM, México, 1998. Traducción al español
del original en francés: Analyse des infiniment petits pour l’intelligence des lignes
courbes, de 1696. Traducción e introducción de Rodrigo Cambray.
XVIII Encuentro de Profesores de Matemáticas
Página 130
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Geometría Dinámica para el Bachillerato:
un enfoque de Ambientes de Aprendizaje con Cabri
Dr. Eugenio Díaz Barriga Arceo
[email protected]
Universidad Autónoma del Estado de México
Resumen
Se presentarán diversas actividades realizadas con Geometría Dinámica con Cabri II plus y
Cabri 3D enfocadas a la obtención de competencias disciplinares en matemáticas y ciencias
experimentales a nivel bachillerato. Un aspecto importante que ellas enfatizan es el diseño del
ambiente virtual de aprendizaje en el que se involucra al estudiante. Entre las actividades a
desarrollar en el taller se encuentran: geometría de regla y compás, rectas notables en el
triángulo, coordenadas y regiones en el plano, lugares geométricos, cuerpos en el espacio,
entre otras. Para Cabri II plus se enfatizará la noción de macro.
Actividad 1. Triángulos rectángulos
Una forma de trazar un triángulo rectángulo es comenzar por trazar el ángulo de 90º, tomar al
vértice de tal ángulo como uno de los vértices del triángulo y un punto en cada lado del
ángulo como los vértices restantes. Esta construcción es muy útil y conocida; dibújala en el
entorno Cabri.
Los triángulos rectángulos pueden surgir de otra forma también: traza un segmento AB
cualquiera y dibuja el punto medio del segmento; llamémosle M. Trace la circunferencia de
radio AM que tiene su centro en M. Dibuje un punto C arbitrario de la circunferencia. ¿Qué
observa en el triángulo ABC?
Una variación de la idea anterior: dibuja dos puntos A y M cualesquiera, en seguida al punto
simétrico de A con respecto a M y llámale B. Después se traza de nuevo la circunferencia de
radio AM con centro en M y ya se sigue la construcción como antes.
¿Tienes otra forma de construir triángulos rectángulos? Trázala en el entorno Cabri y verifica
que se mantiene rectángulo haciéndole la prueba del arrastre.
Para que Cabri almacene este conocimiento en su entorno, puedes definir una macro para cada
uno de los métodos de construcción que se han tratado. Recuerda que es necesario identificar
de manera precisa el o los objetos iniciales de los cuales se ha partido; en todos los casos, el
objeto final será el triángulo rectángulo.
XVIII Encuentro de Profesores de Matemáticas
Página 131
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Si deseas mantener diferenciadas las macros que aquí has trabajado, te sugerimos que para los
nombres de las macros utilices algo que describa al método que usaste (por ejemplo
“triángulo rectángulo método 1”, o mejor aún “triángulo rectángulo inicia 90º”).
Actividad 2. Cuadrados construidos sobre los lados de un triángulo
El objetivo de esta actividad es trazar cuadrados sobre los lados de un triángulo rectángulo y
explorar las relaciones entre ellos. Los cuadrados tendrán como lado los catetos e hipotenusa
del triángulo rectángulo y serán externos al triángulo.
Primero construya un triángulo rectángulo por el método que se describió en la actividad
anterior. En seguida, defina una macro cuadrado que construya cuadrados dado un segmento
como lado y aplíquela sobre los lados del triángulo rectángulo (o mejor aún, sus vértices),
cuidando que los cuadrados permanezcan externos al triángulo rectángulo. La figura que se
obtiene es la llamada “silla de la novia”.
Utilice el comando de medición de áreas y mida las que corresponden a los cuadrados que ha
construido. Manipule los vértices del triángulo rectángulo, ¿qué relación existe entre las
áreas? Recuerde: cuando se busca un invariante geométrico, en su forma más básica,
alteramos una figura (o sus elementos) azarosamente en primer lugar, y observamos si
podemos encontrar alguna regularidad.
Problema 1
Realice una construcción para resolver el siguiente problema: dos círculos congruentes se
cortarán de una tarjeta rectangular de 9 por 12. ¿Cuál es el radio máximo posible de estos
círculos? ¿Qué porcentaje representa este corte del área del rectángulo?
XVIII Encuentro de Profesores de Matemáticas
Página 132
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Sugerencia: construyamos un rectángulo ABCD cuyas medidas de los lados sea puedan
ajustar de tal manera que m(AB) = 12 y m(BC) = 9.
Problema 2. Cacería de triángulos
Traza un segmento AB fijo. ¿Cuál es el conjunto de puntos C tales que el triángulo ABC que
se forma sea oblicuángulo? ¿Y acutángulo?
Actividad 3. Antiprismas en el espacio
En la interfase de Cabri 3D existen varios conjuntos de sólidos que pueden ser construidos por
defecto (poliedros platónicos, tetraedros, cajas xyz, prismas y pirámides). Uno de los
conjuntos que no ha sido incluido es el de los llamados antiprismas, poliedros convexos cuyas
bases en planos paralelos son polígonos regulares como en los prismas, pero que se
encuentran una girada respecto a la otra (el ángulo de giro resulta ser la mitad del ángulo
central del polígono base, lo que deriva en que las caras laterales sean triángulos en lugar de
los rectángulos que aparecen en los prismas. El objetivo de esta actividad es la construcción
de dicho sólidos.
Actividad 4. Comparando volúmenes
Si contruyéramos un prisma y antiprisma pentagonales con la misma base, atrapados entre los
mismos planos paralelos, ¿tendrían o no el mismo volumen? La interfase Cabri 3D permite
obtener el volumen de los poliedros convexo que hayamos creado y de los cuerpos que tiene
por defecto, aproveche esto para dar respuesta a la pregunta que hemos planteado.
XVIII Encuentro de Profesores de Matemáticas
Página 133
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Problema 3. Policubos
Un policubo es un poliedro que se forma uniendo cubos (cuya arista imaginaremos unitaria)
haciendo coincidir cara a cara. Dependiendo del número de cubos empleados se habla del
orden del policubo.
Para formar un policubo podemos emplear dos tipos distintos de tiras de papel, aquella que
contiene sólo cuadrados y aquella que contiene triángulos rectángulos isósceles. En el primer
caso, un cuadrado del poliedro quedará rígido cuando dos tiras de papel lo atraviesen en
direcciones mutuamente perpendiculares. Abordaremos ahora con cierto detenimiento el
método de plegar policubos con tiras que contienen triángulos rectángulos isósceles.
Cuando la tira rectangular contiene triángulos rectángulos isósceles y estos se doblan hacia
uno u otro sentidos, los cuerpos poliédricos que pueden tejerse son los policubos, que son
ensambles de cubos unitarios; las uniones se realizan haciendo coincidir caras cuadradas de
cubos unitarios. Para que una cara cuadrada quede rígida, cuatro triángulos rectángulos
deberán recubrirla; los lados iguales en los triángulos formaran el contorno cuadrado, las
hipotenusas formarán las diagonales. En el tejido de una cara, cada triángulo tiene una mitad
que se sitúa en el exterior del cuerpo y la otra mitad queda en el interior.
Policubo de orden 1. Cubo
El policubo más simple que se puede construir es el policubo de orden uno, es decir, el cubo
mismo. Una ilustración antigua de cómo puede efectuarse el plegado del cubo bajo estas
condiciones es la siguiente:
La siguiente secuencia de fotografías muestra un ejemplo de cómo se va tejiendo un policubo
de orden 4, llamado T, en donde la primera tira rectangular recubre solo algunas de las caras
cuadradas con que cuenta; la última tira de papel permite cerrar el tejido, dando firmeza a la
construcción.
XVIII Encuentro de Profesores de Matemáticas
Página 134
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
(a)
(b)
(d)
(c)
(e)
(f)
Por defecto el ambiente Cabri 3D proporciona la construcción del cubo o hexaedro. Al tejer el
poliedro con la técnica de plegado, frecuentemente es necesario resolver en la construcción
distintos requerimientos, tales como: observar la parte del cubo que recubre una tira aislada de
papel; el cubo mismo debe tener cierta transparencia para observar caras internas y externas
desde distintos ángulos; la pieza debe ser manejable como un todo para observar su
orientación en el cubo.
Una vez construido el cubo, mediante triángulos rectángulos sobre el mismo y bajo
translación de un vector externo al cuerpo, la tira de papel exhibe la forma en que se ensambla
con el cubo, mostrando los vértices y las aristas por donde pasa, así como las regiones del
cubo que son recubiertas con ella.
Bibliografía
Coxeter, H.S.M. (1973). Regular Polytopes. Dover publications.
Davis, Ch., Grünbaum, B. , Sherk, F. A. (1981). The Geometric Vein. The Coxeter
Festschrift. Springer –Verlag.
Díaz Barriga, E. (2009). Geometría dinámica con Cabri-Géomètre. Editorial Kali. 3a Edición.
Díaz Barriga, E. (2010). Descubriendo Dn con Cabri 3D. Editorial Kali.
Eves, H. (1969). Estudio de las Geometrías, Vols. 1, 2. UTEHA.
Polya, G. (1954). Mathematics and Plausible Reasoning. Princeton University Press.
XVIII Encuentro de Profesores de Matemáticas
Página 135
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
Reflexiones en torno a la tarea, la técnica y la teoría en un ambiente de
resolución de problemas algebraicos
Dr. José Guzmán Hernández
[email protected]
Centro de Investigación y de Estudios Avanzados del IPN
Problemas a utilizar en la primera parte del taller:
Resuelve los siguientes problemas. En cada uno de ellos, hay teoría (Tecnología desde el
punto de vista de Chevallard, 1999) que justifica la Técnica que utilices para resolverlos. En
tus procesos de solución especifica, claramente, qué teoría (Tecnología) justifica la Técnica
utilizada. Puedes resolver los problemas con ayuda de alguno de tus compañeros, o bien de
manera individual.
1.
Prueba que
1
1
74 3 
74 3 2
2
2
2.
Encuentra la raíz real de la ecuación
(1  i ) x 3  (1  2i ) x 2  (1  i ) x  1  2i  0
3.
Resuelve la ecuación
x8  1  0
4.
Una raíz de la ecuación cúbica x3  (2a  1) x 2  a(a  2) x  a(a  1)  0 es a  1 , ¿cuáles
son las demás raíces de esta ecuación?
5.
Resuelve la ecuación x 4  x3  x 2  x  1  0 , usando radicales cuadráticos. Sugerencia:
divide a cada uno de los sumandos de la ecuación entre x 2 y busca un cambio de variable
pertinente.
6.
Factoriza la expresión x n  1 donde n es cualquier entero positivo.
7.
Demuestra que x  1 es factor de x n  1 , si n es par.
8.
La ecuación x8  x7  8x6  6 x5  21x 4  9 x3  22x 2  4 x  8  0 tiene raíces múltiples,
¿cuáles son?
9.
Una cantidad de dinero fue repartida en cantidades iguales entre cierto número de
personas. Si hubiera habido dos personas más, cada una de ellas hubiera recibido $1
XVIII Encuentro de Profesores de Matemáticas
Página 136
III Seminario Nacional sobre Resolución de Problemas y el Aprendizaje de las Matemáticas
menos; si hubiera habido dos personas menos, cada una hubiera recibido $2 más. ¿Cuál
es el número de personas y qué cantidad de dinero recibió cada una de ellas?
10. Si el ancho de un terreno rectangular es aumentado en 10 metros y su longitud es
disminuida en 10 metros, entonces el área aumenta 100 m2 , pero si el ancho disminuye 5
metros y la longitud aumenta 10 metros, entonces el área disminuye 50 m2 . ¿Cuáles son
las dimensiones del terreno?
11. Se sabe que la ecuación de una recta en el plano está dada por la igualdad: y  mx  b .
Determina la ecuación de la recta que pasa por los puntos (1, 2) y (2, 1).
12. Se sabe que la ecuación de un plano está dada por la igualdad: ax  by  cz  d  0 .
Determina la ecuación del plano que contiene los puntos: (1,  1, 1), (1, 1, 1), (1, 1,  1) .
13. Bosqueja la gráfica de la función:
y
x2  1
.
x 1
XVIII Encuentro de Profesores de Matemáticas
Página 137
Resoluión de problemas de Olimpiada
por María Luisa Pérez Seguí
agosto 2010
El presente trabajo ontiene problemas de matemátias que han formaron parte de exámenes de
promoión de las matemátias del Canguro Matemátio Mexiano 2010 y de seleión estatal para
la Olimpiada Mexiana de Matemátias 2009 y 2010.
Los problemas inluyen las áreas de
Lógia y Combinatoria, Geometría, Aritmétia y Álgebra
En
ada una de las áreas se presentan problemas de distintos niveles:
Benjamín. Para estudiantes de 10 a 14 aáos.
Olímpio. Para estudiantes que se interesan en partiipar en la Olimpiada de Matemátias.
Estudiante. Para estudiantes de último año de bahillerato o profesional.
Seminal. Segunda ronda para seleionar alumnos que representarán al Estado en la Olimpiada
de Matemátias.
Final.
Última ronda para seleionar alumnos que representarán al Estado en la Olimpiada de
Matemátias.
Selección del Examen Benjamín del Canguro Matemático Mexicano 2010.
1. El número 4 está junto a dos espejos así que se refleja
como se muestra en la figura. ¿Cuándo el 5 se refleja en los
dos espejos, qué figura se obtiene?
(a)
(b)
(c)
(d)
2. En la figura se tiene que llegar del círculo A al círculo B siguiendo las
flechas. En cada camino se calcula la suma de los números por los
cuales se pasó. ¿Cuántas sumas diferentes se pueden obtener?
(a) 2
(b) 3
(c) 4
(d) 5
(e) 6
3. Ana conectó todos los puntos de arriba en la figura con los
de abajo. ¿Cuántas líneas dibujó?
(a) 20
(b) 25
(c) 30
(d) 35
(e) 40
4. Usando la siguiente figura podemos observar que 1357=4×4.
Determinar el valor de 1357911131517.
(a) 9×9
(b) 14×14
(c) 4×4×4
(d) 16×16
(e) 4×9
5. Los números 1, 4, 7, 10 y 13 se tienen que escribir en los cuadros de la
figura de manera que la suma de los números en la columna sea la misma
que la suma de los números en el renglón. ¿Cuál es la mayor suma posible?
(a) 18
(b) 20
(c) 21
(d) 22
(e) 24
(e)
Selección del Examen Cadete del Canguro Matemático Mexicano 2010.
1. El dibujo de abajo a la izquierda representa un tablero. Todos los triángulos deben llenarse usando los
números 1, 2, 3 y 4 de tal manera que cada vez que una ficha de la forma dibujada a la derecha se ponga
encima de cuatro triángulos la ficha tape 4 números distintos. (La ficha puede girarse, así que puede
ponerse en cualquier posición.) Algunos de los números ya se escribieron. ¿Qué número debe ir en lugar
de *?
(a) sólo 1
(b) sólo 2
(c) sólo 3
(d) sólo 4
(e) cualquiera de 1, 2 o 3
2. ¿Cuántos enteros positivos de tres cifras tienen la propiedad de que su cifra central es el promedio de
las otras dos?
(a) 9
(b) 12
(c) 16
(d) 25
(e) 45
3. Las longitudes de los lados de un triángulo son los enteros 13, x y y. Encontrar el perímetro si se
sabe que xy=105.
(a) 35
(b) 39
(c) 51
(d) 69
(e) 119
4. Los números enteros x y y satisfacen 2x=5y. Sólo uno de los siguientes puede ser x y.
¿Cuál es?
(a) 2009
(b) 2010
(c) 2011
(d) 2012
5. En la figura, el ángulo α mide 7o y los segmentos OA1, A1 A2 , A2 A3 , ... son
todos de la misma longitud. En un primer paso se dibuja A1 A2 , en un segundo
paso se dibuja A2 A3 , y así sucesivamente. ¿Cuál es el mayor número de
segmentos que pueden dibujarse de esta manera?
(a) 10
(b) 11
(c) 12
(d) 13
(e) infinidad
(e) 2013
Selección del Examen Estudiante del Canguro Matemático Mexicano 2010.
1. En el cuadrilátero ABCD se tiene que AD =BC , y los ángulos
DAC ,
DCA y ACB miden lo que se indica en la figura. ¿Cuánto mide
ABC
el ángulo
?
(a) 55o
(b) 60o
(d) 70o
(c) 65o
(e) 75o
2. Doce personas participaron en una carrera. No hubo empates. A cada una se le preguntó en qué lugar
había llegado. Algunas mintieron pero todas las respuestas fueron números del 1 al 12 y la suma total de
las respuestas fue 36. ¿Cuál es el menor número posible de respuestas falsas?
(a) 4
(b) 5
(c) 6
(d) 7
(e) 8
3. En cada círculo de la figura debe escribirse un número entero.
Algunos de los números ya están escritos. Si la suma de cualesquiera tres
números alineados es la misma, ¿cuál es la suma de todos los números
que faltan?
(a) 19
(b) 22
(c) 25
(d) 29
(e) 32
4. Los tres números  7 , 3 7 y 6 7 son términos consecutivos en una progresión geométrica con razón
r , es decir cada uno se obtiene del anterior multiplicando por la constante r. El siguiente término de
la progresión es:
(a)
5 7
(b)
9 7
(c)
10
7
(d)
12
7
5. En la figura los dos círculos tienen el mismo centro y la cuerda AB
del círculo mayor es tangente al menor. Si AB mide 16, ¿cuál es el área
de la región sombreada?
(a) 32π
(b) 63π
(c) 64π
(d) 32π 2
(e) falta información
(e) 1
Seleión del Examen Seminal Estatal de la
Olimpiada Mexiana de Matemátias, 2010
1. Enontrar 5 enteros positivos diferentes tales que el produto de ualesquiera dos de ellos
sea múltiplo de ada uno de los demás.
2. En la gura las retas son tangentes a las irunferenias en los puntos indiados. Calular
|CD| si se sabe que |AB| = 10. (¾Es importante el tamaño de los írulos?)
C
A
............................................................................................ D
...... • ..........
....... .............
. ...
..•
.......
.............•
....
...
.
... ...
..
.......
.....
... ... ...
..
...
....
.. ...
...
....
...
...
.. ...
...
...
....
...
... ....
......
...
...
.
.
.
.
... ..
...
..
..
.
.
.
... ..
..
....
..
.
.
.
.
.
.
......
......
...............................
...
.
.
....
........... ..
..
...
............
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...........
...
..
.
...
...
....................................... .........
..
....................
... ..........
....
........................
.....
... ......
....... ..................................
...........
.
.
......
....
....
......
...
...
...
...
...
....
...
...
..
..
..
....
..
...
...
...
..
.
...
.
.
.
...
...
...
..
...
...
...
....
....
.
.
.
.....
.
......
....
........
......
.............. .....................
........
•
•
•
B•
•
•
•
3. En una la hay 6 has. Cada ha tiene una ara negra, N , y la otra blana, B . Al
prinipio se enuentran en la posiión: N BN BN B . Lulú puede haer lo siguiente tantas vees
omo quiera: Esoge dos has y las voltea (por ejemplo, si se esoge la primera y la uarta,
las has quedan en la posiión BBN N N B ; si luego esoge la primera y la sexta, entones la
nueva posiión es N BN N N N ). Haiendo esto, ¾uántas posiiones distintas puede lograr?
Seleión del Examen Final Estatal de la
Olimpiada Mexiana de Matemátias, 2009
1. En un tablero uadriulado de 6 × 10 se juega un juego entre dos personas que alternan
turnos. El jugador que iniia el juego pone una ha en ualquiera de los uadros; a partir
del segundo turno debe ponerse ada vez una ha en algún uadro vaío que esté en el mismo
renglón o la misma olumna que la ha que se puso en el turno anterior. Pierde el primer
jugador que no puede jugar (es deir, que enuentra llenos todos los uadros que están en el
renglón y la olumna de la ha que se puso en el tablero en el turno anterior). Determinar uál
de los jugadores puede asegurar su triunfo y ómo debe jugar para lograrlo.
2. Enontrar todos los enteros positivos n menores que 100 tales que los siguientes números
son todos primos: n + 2, n + 4, n + 8 y n + 16.