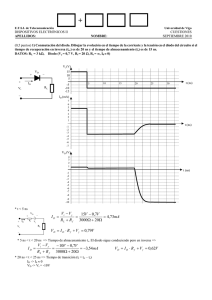
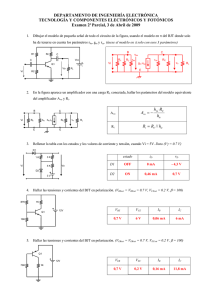
PROBLEMA 1 (2 puntos) Dado el circuito de la figura, calcular los

PROBLEMA 1 (2 puntos)
Dado el circuito de la figura, calcular los siguientes valores:
a) La ganancia de tensión, ganancia de corriente, resistencia de entrada y resistencia de salida a frecuencias
medias. (1 punto)
b) La frecuencia de corte superior si las capacidades internas del transistor son despreciables (C -> 0).
(1 punto)
C2 = 120 pF
Datos: C1 = 47 µF
RS = 500 Ω RB = 5 kΩ R1 = 200 kΩ RC = 10 kΩ RL = 1 kΩ
hfe = 50 hie = 1 kΩ
Solución apartado a)
VCC
RC
io
C2
R1
AV
AI
Ri
Ro
-7,54
-45,22
5,995 kΩ
10 kΩ
Solución apartado b)
+
ii
fH
RS +
C1
RB
vo
33,912 kHz
RL
vi
vS
_
_
a) Circuito equivalente de pequeña señal a frecuencias medias (C1 es un cortocircuito y C2 es un circuito abierto):
RS
ii
ib
RB
io
+
+
vi
vS
R1
hie
hfe⋅ib
RL
RC
-
vo
-
0
AV =
vo
;
vi
vo = −h fe ⋅ ib ⋅ (RC // RL );
RC // R L =
10 K ⋅ 1K
= 0,90909 K
10 K + 1K
200 K ⋅ 1K
= 0,995 K
200 K + 1K
R + hie
R + hie
R1
ib ⋅ (R B + (R1 // hie ))
⇒ ii = 1
ib ⇒ v i = 1
ib = ii
R1
R1
R1 + hie
vi = ii ⋅ (R B + (R1 // hie ));
R1 // hie =
− h fe ⋅ ib ⋅ (RC // RL )
h fe ⋅ (RC // RL )
vo
50 ⋅ 0,90909 K
=
=−
=−
= −7,54
R1 + hie
R1 + hie
200 K + 1K
vi
K
K
⋅
5
+
1
ib ⋅ (R B + (R1 // hie ))
⋅ RB + hie
200 K
R1
R1
RC
RC
h fe ⋅ ib ⋅
h fe ⋅
i
RC
R + hie
RC + RL
RC + R L
AI = o ;
io = −h fe ⋅ ib ⋅
ii = 1
;
ib ⇒ AI = −
=−
R1 + hie
R1 + hie
ii
RC + R L
R1
ib
R1
R1
AV =
10 K
10 K + 1K = −45,22
AI = −
200 K + 1K
200 K
vi
Ri = = R B + R1 // hie = 5 K + 0,995 K = 5,995kΩ
ii
50 ⋅
Ro = RC = 10kΩ
b) La frecuencia de corte superior la establece el condensador C2. El circuito equivalente de pequeña señal a altas frecuencias es el
siguiente (hay que considerar C2 y C1 es un cortocircuito):
C2
ii
RS
ib
RB
io
+
+
vi
vS
R1
hie V1
V2
hfe⋅ib
RL
RC
vo
-
-
0
Se aplica el teorema de Miller y se obtiene el siguiente circuito:
RS
ii
ib
RB
io
+
+
vS
vi
R1
hie
C21
hfe⋅ib
C22
RC
-
RL
vo
-
0
C 21 = C 2 ⋅ (1 − K ) , K =
v 2 v0
=
=
v1 v1
v0
R + (R1 // hie )
5K + 0,995 K
= AV B
= −7,54
= −45,42
R1 // hie
R1 // hie
0,995 K
vi
R B + (R1 // hie )
C 21 = 120 pF ⋅ (1 + 45,42 ) = 5,5704nF
1⎞
⎛
C 22 = C 2 ⋅ ⎜1 − ⎟ ≈ C 22 = 120 pF
⎝ K⎠
El condensador C21 provoca un polo en:
R21 = (R1 // hie ) // (RS + R B ) =
f p1 =
1
;
2 ⋅ π ⋅ R21 ⋅ C 21
f p1 =
1
= 33,912kHz
2 ⋅ π ⋅ 0,8425 K ⋅ 5,5704nF
(R1 // hie ) ⋅ (RS + RB ) 0,995K ⋅ 5,5K
=
(R1 // hie ) + (RS + RB ) 0,995K + 5,5K
= 0,8425 K
El condensador C22 provoca un polo en:
f p2 =
1
;
2 ⋅ π ⋅ R22 ⋅ C 22
R22 = (RC // RL ) = 0,90909 K ⇒ f p 2 =
Por lo tanto, la frecuencia de corte superior va a ser fH = 33,912 kHz
1
= 1,458MHz
2 ⋅ π ⋅ 0,90909 K ⋅ 120 pF