Trabajo Practico 2

ILSE-2º Año-
MATEMÁTICA: TRABAJO PRÁCTICO 2
Funciones
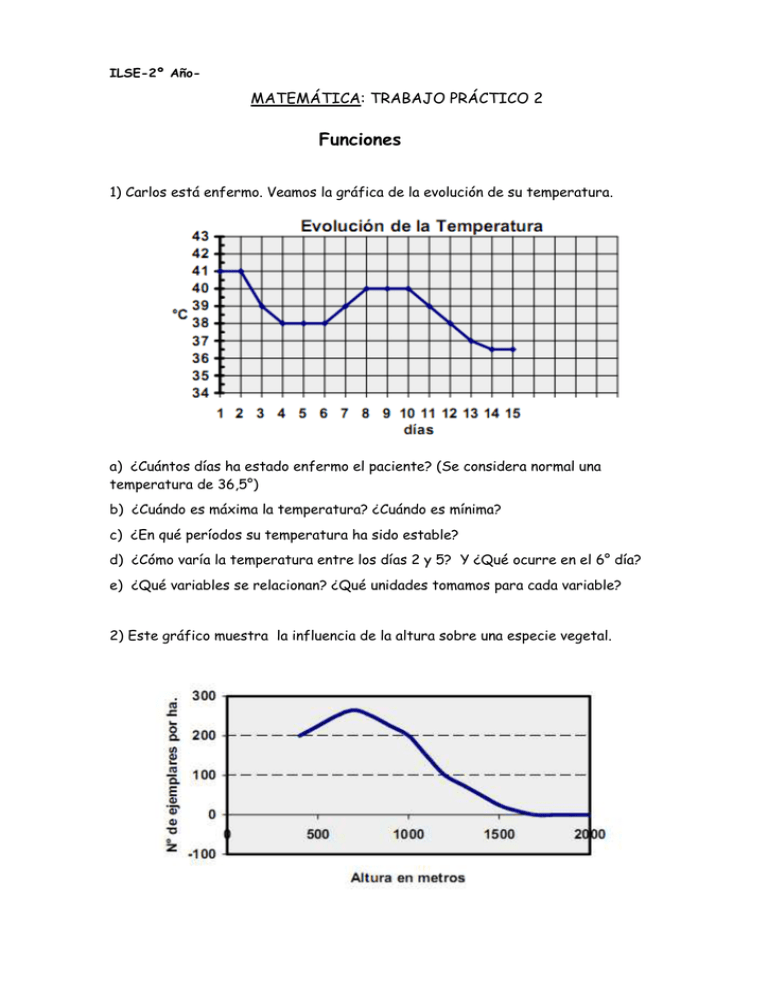
1) Carlos está enfermo. Veamos la gráfica de la evolución de su temperatura.
a) ¿Cuántos días ha estado enfermo el paciente? (Se considera normal una
temperatura de 36,5°)
b) ¿Cuándo es máxima la temperatura? ¿Cuándo es mínima?
c) ¿En qué períodos su temperatura ha sido estable?
d) ¿Cómo varía la temperatura entre los días 2 y 5? Y ¿Qué ocurre en el 6° día?
e) ¿Qué variables se relacionan? ¿Qué unidades tomamos para cada variable?
2) Este gráfico muestra la influencia de la altura sobre una especie vegetal.
a) ¿Plantarías a 2000 metros de altura?
b) ¿A qué altura hay aproximadamente 200 ejemplares por hectárea?
c) ¿A qué altura plantarías para obtener mayor cantidad de vegetales?
d) ¿La cantidad de ejemplares depende de la altura o la altura depende del número de
ejemplares?
3) A un paciente internado en un hospital le controlan la presión arterial máxima de
manera continua. El siguiente gráfico muestra la evolución de dicha presión a partir
del momento en que fue internado. Se considera normal una presión arterial máxima
entre 11 y 13.
a) ¿Durante cuánto tiempo se tomaron los datos de la presión arterial del paciente?
b) ¿En qué momento la presión fue descendiendo? ¿Y ascendiendo?
c) ¿En qué momento la presión fue máxima? ¿Y mínima?
d) ¿En qué momento le dieron el alta?
e) ¿Qué otras preguntas se te ocurren, que puedas contestar con los datos que te
proporciona el gráfico?
4) En el gráfico de abajo tenemos una fotografía de la familia López: Juan es el abuelo,
los hijos de Bella y José son Pablo que va a la guardería, Pepe está estudiando, Alicia
que estudia medicina y Luis.
¿Quién está representado por cada uno
de los puntos del diagrama de la
derecha?
5) El gasoil que hay en un depósito de un autobús viene representado por la siguiente
gráfica:
a) ¿Cuántos litros tenía el depósito al salir?
b) ¿Cuántos litros tenía a su llegada?
c) ¿Cuándo puso el conductor por primera vez gasoil? ¿Cuántos litros tenía el
depósito?
d) ¿Cuántos litros consumió durante el viaje?
e) ¿Qué ocurrió cuando recorrió 250 Km.?
f) ¿En que parte del recorrido se observa mayor consumo? ¿Y menor?
6) En el diario de un barrio de la Capital Federal se publicaron los valores de
temperatura, en distintos momentos del día 25 de abril:
a) ¿Cuál es la temperatura a las 10hs? ¿Y a
las 21?
b) En un cierto momento del día la
temperatura era de 9°.
¿Se puede saber a partir de la tabla qué hora
era?
c) ¿En qué momentos de día la temperatura
se mantuvo estable?
d) ¿En qué momentos de día la temperatura
subió y en cuáles bajó?
e) ¿Cuál habrá sido la temperatura máxima
de ese día? ¿A qué hora?
f) ¿Cuál de los siguientes gráficos
corresponde a esta situación? ¿Por qué?
7) El siguiente gráfico muestra la cantidad de espectadores que concurrieron al cine
en una semana.
a) ¿Cuántos espectadores concurrieron al cine el día lunes?
b) ¿Qué día concurrió mayor cantidad de gente?
c) ¿Qué días hubo igual cantidad de espectadores?
d) ¿Qué día concurrieron 200 espectadores?
8) Álvaro va cada tarde al instituto, pasa primero por la panadería, luego se detiene en
la siguiente esquina a esperar a un compañero. Por fin, después de las clases,
vuelve a casa. El siguiente gráfico muestra la situación.
a) ¿Qué distancia hay de la casa al instituto? ¿Y a la panadería?
b) ¿Cuánto demora en la panadería?
c) ¿Tiene que esperar mucho a su compañero?
d) ¿Cuánto duran las clases?
e) Si las clases comienzan a las 4 de la tarde, ¿dónde estaba a las 3 h. 32
minutos, 3 h. 36 minutos y a las 3 h. 54 minutos?
f) ¿Durante cuánto tiempo estuvo a 500 metros de su casa? ¿ Y a 600 metros?
9) La gráfica muestra la velocidad que alcanza un carrusel de una feria a lo largo de
diferentes viajes que realiza.
a)
b)
c)
d)
e)
f)
¿Cuánto dura cada parada?
¿A qué velocidad va el carrusel?
¿Cuánto dura cada viaje?
¿En qué espacios de tiempo acelera? ¿En cuáles frena?
¿Cada cuánto tiempo se repite el movimiento del carrusel?
¿Qué hará el carrusel a las dos horas de ponerlo en marcha?
10) A continuación se muestran, el perfil de una pista de ciclismo y el gráfico del
espacio recorrido en función del tiempo.
a) ¿Cuál es la longitud de la etapa? ¿Cuánto tiempo tarda en recorrerla?
b) ¿En qué tramo adquiere mayor velocidad y en cuál menos? ¿Cuándo pasa por
la cima más alta?
c) ¿Qué distancia hay de C a D? ¿Cuánto tiempo tarda en recorrerla? ¿Qué
velocidad lleva?
11) Los seis recipientes tienen la misma altura 80 cm y la misma capacidad de 100
litros.
Se llenan sucesivamente utilizando un grifo que vierte 1/3 de litro por segundo.
Las gráficas representan, para cada uno de los recipientes, la altura de la
columna de agua en el recipiente en función del tiempo empleado en su llenado.
Encontrar la curva correspondiente a cada recipiente.
12) Aquí se muestra una jeringa sin marcas:
a) Calcular el volumen en función de la altura h.
b) Confeccionar una tabla que relacione el volumen con la altura y dibuja su
gráfica.
c) Colocar las marcas en la jeringa de: 5 cm3 y de 1.000 cm3.
13) ¿Cuáles de las siguientes gráficas corresponden a una función de ℝ 
→ℝ ?
14) Una piedra se lanza verticalmente hacia arriba desde la ventana de una habitación
con una velocidad inicial de 10 metros por segundo.
Se sabe que h(t) = –5 t2 + 10t + 15, es la fórmula que permite calcular la altura a la cual
se encuentra la piedra, medida desde el suelo, t segundos después de que fue lanzada.
a) ¿A qué altura se encuentra la piedra 0,5 segundos después de que fue lanzada?
b) ¿A qué altura se encuentra la ventana?
15) Supongamos que en el mismo instante en que se lanza la piedra del problema
anterior, simultáneamente, desde el suelo, se lanza otra piedra con una velocidad de 20
m/s.
Se sabe que en este caso j(t) = –5 t2 + 20t es la fórmula que permite calcular la altura
a la cual se encuentra esta piedra, medida desde el suelo, t segundos después de que
fue lanzada.
a) ¿En qué momento esta piedra vuelve a tocar el suelo?
b) ¿En algún momento las piedras alcanzan la misma altura? ¿A qué altura sucede esto?
16) Escribir la fórmula que hace corresponder a la variable independiente “x” e indicar
en cada caso un dominio adecuado y su correspondiente conjunto imagen:
a) su tercera parte.
b) su cuadrado.
c) su doble aumentado en una unidad.
d) el doble de su siguiente.
e) el número 5.
17) Cada una de las tablas que se dan a continuación establece una relación entre la
variable independiente “x” y la variable dependiente “y”:
Tabla II
Tabla I
x
-3
-2
-1
0
1
x
-2 -1
0
1
2
y
7
5
3
1
-1
y
-8
-1
0
1
8 para cada tabla, “y” en función de “x”.
a) Representar
gráficamente,
Encontrar, en cada caso, la fórmula que permite relacionar la variable dependiente
“y” con la variable independiente “x”.
18) El lado de un cuadrado mide 6 cm. Se aumenta el lado en x cm tal como lo muestra
la figura.
a) Expresar mediante una fórmula, el perímetro de la figura sombreada en función
de x.
b) Representar gráficamente la relación entre el perímetro de la zona sombreada y
“x” suponiéndola definida de R+0 → R
x
c) Ídem para el área de la región sombreada.
6
x
19) Expresar en cada caso el área de la parte coloreada en función de x:
20) Considerar el conjunto de todos los rectángulos de perímetro 20 cm. Se pide:
a) Expresar mediante una fórmula la base de los mismos en función de la altura.
Indicar cuál debe ser el dominio más amplio.
b) Representar gráficamente la fórmula determinada en a).
c) Expresar la fórmula que te permita calcular el área de dichos rectángulos en
función de la altura,
21) Un cubo tiene diagonal x. Expresar, en función de la diagonal:
a) La diagonal de la cara del cubo.
b) La arista del cubo.
c) El área total del cubo.
d) El volumen del cubo.
22) Un rombo tiene la diagonal mayor igual al doble de la menor. Expresar:
a) El lado del rombo en función de la diagonal menor.
b) El perímetro del rombo en función de la diagonal menor.
c) El área del rombo en función de la diagonal menor.
23) Dibujar el gráfico de una función que cumpla simultáneamente las siguientes
condiciones:
C 0 = {−2;1; 4}
C + = (−2;1) ∪ (4; +∞)
C − = (−∞; −2) ∪ (1; 4)
C ↑ = (−∞;0) ∪ (3; +∞)
C ↓ = (0;3)
Intersección con el eje y: (0;3)
24) Se da información sobre una función f:
Dom = ℝ, C + = (−3; −1), C ↑ = (−4; −2) ∪ (1;3), Im = ( −∞;5]
El gráfico de f tiene 3 raíces
y se pide:
a) Dibujar el gráfico de una función que cumpla simultáneamente con la información
dada.
b) ¿Es posible, conocer la ordenada de 3?
c) ¿Es posible, conocer la ordenada de 1?
d) ¿Es posible, conocer la ordenada de -2?