Solución: Tarea 3.

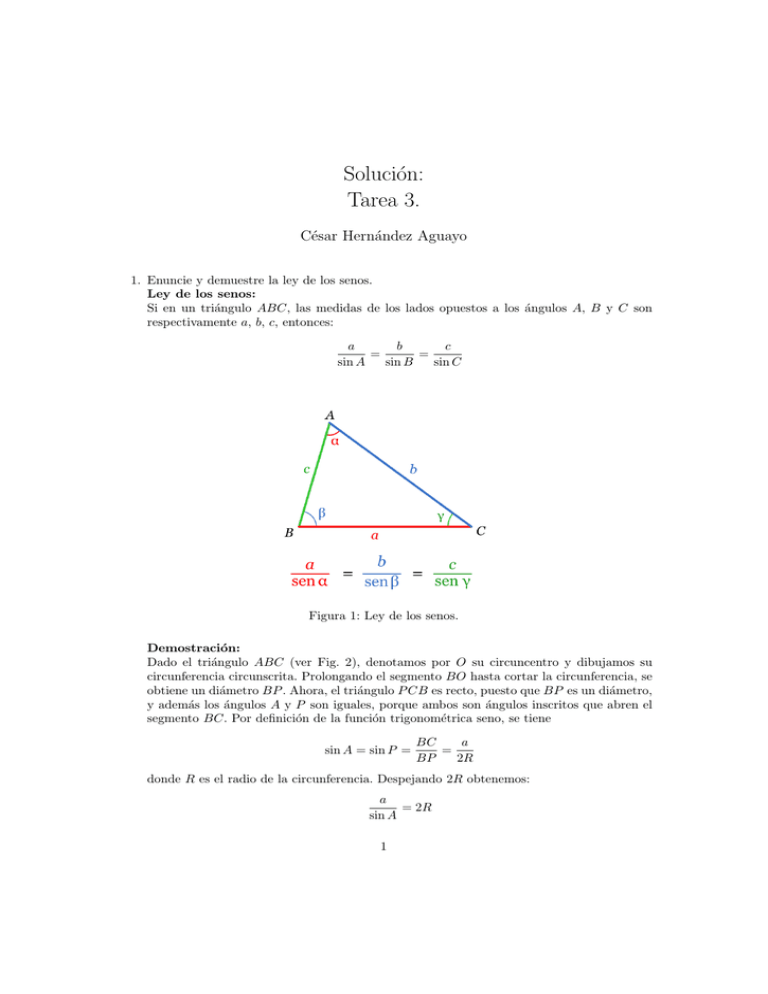
Solución:
Tarea 3.
César Hernández Aguayo
1. Enuncie y demuestre la ley de los senos.
Ley de los senos:
Si en un triángulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son
respectivamente a, b, c, entonces:
a
b
c
=
=
sin A
sin B
sin C
Figura 1: Ley de los senos.
Demostración:
Dado el triángulo ABC (ver Fig. 2), denotamos por O su circuncentro y dibujamos su
circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se
obtiene un diámetro BP . Ahora, el triángulo P CB es recto, puesto que BP es un diámetro,
y además los ángulos A y P son iguales, porque ambos son ángulos inscritos que abren el
segmento BC. Por definición de la función trigonométrica seno, se tiene
sin A = sin P =
BC
a
=
BP
2R
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
a
= 2R
sin A
1
2
Figura 2: El teorema de los senos establece que a/ sin(A) es constante.
Repitiendo el procedimiento con un diámetro que pase por A y otro que pase por C, se
llega a que las tres fracciones tienen el mismo valor 2R y por tanto son iguales.
La conclusión que se obtiene suele llamarse teorema de los senos generalizado y establece:
Para un triángulo ABC donde a, b, c son los lados opuestos a los ángulos A, B, C respectivamente, si R denota el radio de la circunferencia circunscrita, entonces:
a
b
c
=
=
= 2R .
sin A
sin B
sin C
3
2. Pruebe las siguientes identidades trigonométricas.
sec2 θ = tan2 θ + 1 .
Teniendo en cuenta que sec θ = 1/ cos θ y tan θ = sin θ/ cos θ, pasamos a desarrollar
el lado derecho de la ecuación:
tan2 θ + 1
sin2 θ
+1
cos2 θ
sin2 + cos2 θ
cos2 θ
=
=
Ahora usamos la identidad sin2 θ + cos2 θ = 1 y la sustituimos en la expresión anterior
tan2 θ + 1
=
=
1
cos2 θ
sec2 θ .
csc2 θ = cot2 θ + 1 .
Sabemos que csc θ = 1/ sin θ y cot θ = cos θ/ sin /θ, y sustituyendo la definición de
cot θ en el lado derecho de la ecuación
cot2 θ + 1
=
=
cos2 θ
+1
sin2 θ
cos2 θ + sin2 θ
sin2 θ
Usando la identidad sin2 θ + cos2 θ = 1.
cot2 θ + 1
=
=
1
sin2 θ
csc2 θ .
sec x
tan x+cot x
= sin x .
Pasando a senos y cosenos, todas las funciones del lado izquierdo
sec x
tan x + cot x
=
=
1
cos x
sin x
cos x
cos x + sin x
1
cos x
sin2 x+cos2 x
sin x cos x
Ahora usamos la identidad sin2 x + cos2 x = 1
sec x
=
tan x + cot x
1
cos x
1
sin x cos x
Finalmente aplicamos la regla de la herradura de las fracciones y simplificamos
sec x
tan x + cot x
=
=
sin x cos x
cos x
sin x .
4
(1 − sin2 x)(1 + tan2 x) = 1 .
Desarrollando el lado izquierdo de la ecuación
(1 − sin2 x)(1 + tan2 x)
=
1 + tan2 x − sin2 x − sin2 x tan2 x
pasando la función tangente a senos y cosenos y desarrollando
(1 − sin2 x)(1 + tan2 x)
=
=
2
sin2 x
2
2 sin x
−
sin
x
−
sin
x
cos2 x
cos2 x
2
2
2
sin x − sin x cos x
sin4 x
1+
−
2
cos x
cos2 x
1+
Usando la identidad cos2 x = 1 − sin2 x y sustituyendo
(1 − sin2 x)(1 + tan2 x)
sin4 x
sin2 x − sin2 x(1 − sin2 x)
−
cos2 x
cos2 x
sin2 x − sin2 x + sin4 x
sin4 x
= 1+
−
cos2 x
cos2 x
4
4
sin x
sin x
= 1+
−
cos2 x cos2 x
= 1.
=
1+
cot2 x
csc x−1
= csc x + sin2 x + cos2 x .
Pasando a senos y cosenos todas las funciones del lado izquierdo y desarrollando
cot2 x
csc x − 1
=
=
cos2 x
sin2 x
1
sin x −
cos2 x
sin2 x
1−sin x
sin x
1
Usando la regla de la herradura y continuando con el desarrollo
cot2 x
csc x − 1
=
=
sin x cos2 x
sin2 x(1 − sin x)
cos2 x
sin x(1 − sin x)
Aplicando cos2 x = 1 − sin2 x = (1 + sin x)(1 − sin x), obtenemos
cot2 x
csc x − 1
=
=
=
(1 + sin x)(1 − sin x)
sin x(1 − sin x)
1 + sin x
sin x
1
+1
sin x
Finalmente con csc x = 1/ sin x y 1 = sin2 x + cos2 x
cot2 x
= csc x + sin2 x + cos2 x .
csc x − 1
5
cot2 x + sin2 x = csc2 x − cos2 x .
Vamos a desarrollar el lado derecho al pasar la csc x a 1/ sin x:
2
2
csc x − cos x =
=
1
sin x
2
− cos2 x
1 − cos2 x sin2 x
sin2 x
Como 1 = sin2 x + cos2 x, y cos2 x = 1 − sin2 x, obtenemos
csc2 x − cos2 x
=
=
=
=
=
sin2 + cos2 −(1 − sin2 x) sin2 x
sin2 x
2
2
sin x + cos x − sin2 x + sin4 x
sin2 x
cos2 x + sin4 x
sin2 x
2
cos x sin4 x
+
sin2 x
sin2 x
2
cot x + sin2 x .
En el último paso se usó: cot x = cos x/ sin x.
6
3. Grafique:
f (x) = 3x sin 2x .
Figura 3: Gráfica de la función f (x) = 3x sin 2x.
7
f (x) = esin x .
Figura 4: Gráfica de la función f (x) = esin x .