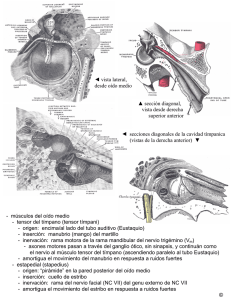
Elementos de Física de los Medios Continuos

Elementos de Física de los
Medios Continuos
Martín Rivas
e-mail:[email protected]
Departamento de Física Teórica
http://tp.lc.ehu.es/martin.htm
UPV/EHU
Leioa, Febrero 2006
En la imagen de la portada, vemos un avión volando a muy alta velocidad.
Se aprecia la onda de choque, provocada al cruzar la barrera del sonido.
Aparece una onda de alta presión que comprime una masa de aire
lo que produce la condensación del vapor de agua
con la forma de la onda de choque.
http://www.milair.simplenet.com
c
°
Martín Rivas, Bilbao.
2
Índice general
1. Cinemática
1.1. Medios continuos y discretos . . . . . . . . . . . . . . . . . . . . . . . .
1.1.1. Notación indicial . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.2. Componentes de un vector y de un operador lineal . . . . . . .
1.1.3. Componentes covariantes y contravariantes de un vector . . . .
1.1.4. Descomposición polar de una matriz no singular . . . . . . . .
1.1.5. Transformación de un tensor . . . . . . . . . . . . . . . . . . .
1.2. Conguraciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1. Líneas de corriente, líneas de emisión y trayectorias . . . . . . .
1.2.2. Campo de velocidad . . . . . . . . . . . . . . . . . . . . . . . .
1.3. Tensor de deformaciones . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.1. Diagonalización del tensor de deformaciones . . . . . . . . . . .
1.3.2. Tensor de deformaciones linearizado . . . . . . . . . . . . . . .
1.3.3. Tensor de deformación esférico y tensor desviador . . . . . . . .
1.3.4. Estados de deformación planos . . . . . . . . . . . . . . . . . .
1.3.5. Condiciones de compatibilidad en deformaciones lineales . . . .
1.4. Tensor de velocidad de deformación . . . . . . . . . . . . . . . . . . . .
1.5. Sólido rígido . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.6. Derivada material . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.6.1. Campo de aceleración . . . . . . . . . . . . . . . . . . . . . . .
1.6.2. Variación temporal del elemento de línea, supercie y volumen
1.6.3. Transformación del elemento de línea, supercie y volumen . .
1.6.4. Derivada material de integrales curvilíneas . . . . . . . . . . . .
1.6.5. Derivada material de integrales de supercie . . . . . . . . . . .
1.6.6. Derivada material de integrales de volumen . . . . . . . . . . .
1.7. Teoremas integrales . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.7.1. Teorema de Stokes . . . . . . . . . . . . . . . . . . . . . . . . .
1.7.2. Teorema de Gauss . . . . . . . . . . . . . . . . . . . . . . . . .
2. Tensiones
2.1.
2.2.
2.3.
2.4.
Campo de densidad . . . . . . . . . . . . . . . . . . .
Campo de tensiones . . . . . . . . . . . . . . . . . .
Tracción, compresión y cortadura . . . . . . . . . . .
Equilibrio estático. Simetría del tensor de tensiones .
2.4.1. Valor medio del tensor de tensiones . . . . . .
2.4.2. Direcciones principales. Tensiones principales
2.4.3. Círculos de Mohr de las tensiones . . . . . . .
2.4.4. Estados de tensión planos . . . . . . . . . . .
2.4.5. Tensor de tensión esférico y tensor desviador
2.4.6. Círculos de Mohr de las deformaciones . . . .
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
3
3
4
4
5
5
6
8
9
10
11
11
13
13
14
15
16
18
18
19
20
21
22
22
22
23
23
29
29
29
30
31
33
33
34
37
38
38
4
ÍNDICE GENERAL
2.5. Tensor de tensiones del campo electromagnético . . . . . . . . . . . . . . . . . .
3. Dinámica
Leyes fundamentales
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
45
Ecuación de continuidad . . . . . . . . . . . . . . . . . . . . . . . .
Ecuación de continuidad de la masa . . . . . . . . . . . . . . . . .
Segunda ley de Newton . . . . . . . . . . . . . . . . . . . . . . . .
Momento de la cantidad de movimiento. Simetría de σij . . . . . .
Conservación de la energía. Primer principio de la Termodinámica
Segundo Principio de la Termodinámica . . . . . . . . . . . . . . .
Ecuaciones constitutivas . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5.1. Fluidos Newtonianos . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2. Fluidos Stokesianos . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3. Ecuaciones de Navier-Stokes . . . . . . . . . . . . . . . . . . . . . .
5.3.1. Ecuación de Euler . . . . . . . . . . . . . . . . . . . . . . .
5.3.2. Flujo estacionario. Hidrostática . . . . . . . . . . . . . . . .
5.3.3. Ecuación de Bernoulli . . . . . . . . . . . . . . . . . . . . .
5.3.4. Teorema de Kelvin . . . . . . . . . . . . . . . . . . . . . . .
5.3.5. Densidad de impulso . . . . . . . . . . . . . . . . . . . . . .
5.4. Ecuaciones de Helmholtz . . . . . . . . . . . . . . . . . . . . . . . .
5.4.1. Número de Reynolds . . . . . . . . . . . . . . . . . . . . . .
5.5. Problemas bidimensionales . . . . . . . . . . . . . . . . . . . . . . .
5.5.1. Fuerza y Momento sobre un obstáculo. Fórmulas de Blasius
5.5.2. Ejemplos de problemas bidimensionales irrotacionales . . .
5.5.3. Teorema de la aplicación de Riemann . . . . . . . . . . . .
5.5.4. Transformación de Joukowski . . . . . . . . . . . . . . . . .
5.6. Capa límite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.6.1. Turbulencia . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4. Elasticidad
4.1. Ley de Hooke generalizada . . . . . . . . .
4.2. Tensor elástico. Constantes elásticas . . .
4.2.1. Ley de Hooke de medios isótropos
4.2.2. Consideraciones termodinámicas .
4.2.3. Ecuaciones de Navier . . . . . . . .
4.2.4. Estados de tensión planos . . . . .
4.3. Deformación de una viga (línea elástica) .
4.3.1. Pandeo . . . . . . . . . . . . . . .
4.3.2. Torsión . . . . . . . . . . . . . . .
4.3.3. Ondas de tensión . . . . . . . . . .
39
45
45
46
47
47
49
49
53
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5. Fluidos
53
54
56
57
57
59
59
62
64
65
69
6. Ondas en medios continuos
6.1. Ondas elásticas libres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2. Propagación en un medio elástico. Onda longitudinal y onda transversal . . . .
6.3. Ondas en uidos perfectos. Ondas sonoras . . . . . . . . . . . . . . . . . . . . .
69
69
70
70
71
71
71
72
72
73
73
73
75
77
78
81
84
89
89
90
90
ÍNDICE GENERAL
7. Análisis dimensional y semejanza física
7.1. Semejanza geométrica, cinemática y dinámica . . . . .
7.1.1. El sistema natural de unidades . . . . . . . . .
7.1.2. Algunas expresiones o números adimensionales
7.2. Teorema Π de Buckingham . . . . . . . . . . . . . . .
A. Rotaciones
5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A.0.1. Parametrización normal o canónica del grupo SO(3) . . . . . . . . . . .
A.0.2. Ley de composición de las rotaciones . . . . . . . . . . . . . . . . . . . .
B. Operadores diferenciales
93
93
93
94
95
97
99
101
105
6
ÍNDICE GENERAL
Introducción
Hoy en día sabemos que la materia está formada por sistemas ligados de partículas elementales, que según el modelo estándar se reducen a las partículas cargadas eléctricamente y de
espín 1/2, quarks y leptones. Tres quarks dan lugar a la formación de los protones y neutrones y
de los leptones el único estable y cargado resulta ser el electrón. Los átomos son estados ligados
de protones y neutrones formando el núcleo y un conjunto de electrones a su alrededor, en igual
número que el de protones del núcleo. Existen del orden de unos 100 átomos diferentes, en
cuanto a su constitución electrónica, con pequeñas variaciones en el número de neutrones de sus
núcleos. Estos diferentes átomos pueden formar entre sí estados ligados que los denominamos
moléculas. El número de moléculas diferentes conocidas es enorme. Solamente las moléculas
de tipo orgánico, que involucran átomos de C, H, O y N, pueden suponer del orden de 108
moléculas diferentes.
Salvo la fuerza fuerte que liga a los quarks y por lo tanto a los protones y neutrones para
formar los núcleos, el resto de las estructuras ligadas, es decir átomos y moléculas, se forman
mediante fuerzas exclusivamente electromagnéticas.
Las partículas elementales parecen no tener tamaño, o en su caso, sus dimensiones oscilan
alrededor de valores del orden de 10−19 m para un electrón o de 10−15 m para el protón. El
tamaño aparente de un átomo es del orden de 10−10 a 10−11 m, lo que da a entender que la
estructura de un átomo es un conjunto de pequeñas entidades sumergidas en una región en
la que casi todo es vacío. La materia es discreta, existiendo zonas muy localizadas donde se
concentran las partículas, moviéndose en el vacío.
Sin embargo, es posible analizar sistemas extensos de materia, como si ésta estuviera constituida por un todo continuo, sin espacios vacíos. Una roca, un recipiente con agua, el aire que nos
rodea, son sistemas materiales, que si pretendemos hacer de ellos una descripción macroscópica
sin reparar en el detalle a la escala atómica, aparecen como un medio continuo.
El objeto de la Física de los Medios Continuos es el estudio de los sistemas materiales cuya
apariencia a escala macroscópica es la de un todo continuo. El análisis y desarrollo teórico de la
física de los medios continuos fue el objeto de estudio de la Física del siglo XIX. Termodinámica,
Mecánica Estadística, Teoría de la Elasticidad, Mecánica de uidos, Electromagnetismo, son
algunos de los grandes campos de aplicación de la Física de los Medios Continuos.
Para su análisis vamos a proceder como en el análisis de cualquier otro sistema material. Comenzaremos por la Cinemática, entendiendo por tal de forma general la descripción
geométrica de las variables y observables que vamos a utilizar, así como el tipo de objetos
matemáticos con que los vamos a representar y sus relaciones operativas. Veremos que entre las
propiedades de los sistemas materiales existen algunas que llamaremos escalares, vectores y más
generalmente, tensores. El distinguir el tipo de objeto geométrico asociado a una propiedad física
es una de las características más importantes de su denición. La temperatura es una propiedad
escalar, que no es de tipo global, pues distintas partes de un sistema extenso pueden tener distintas temperaturas. Es una propiedad local, que en sentido estricto está denida en cada punto
del sistema. La masa del sistema es otra propiedad escalar, pero esta es de tipo global. Sin
embargo, distinguiremos la masa global de la masa de pequeñas porciones innitesimales de
1
2
ÍNDICE GENERAL
materia, lo que nos llevará al concepto de densidad. La densidad de un medio material será, por
lo tanto una propiedad escalar local, denida en cada punto del medio continuo. El desplazamiento de un punto, su velocidad, son magnitudes vectoriales, puesto que además de tener una
magnitud, involucran una dirección en el espacio. Todas estas propiedades dependen del punto y
del instante en que las estamos midiendo. Se dice que estas magnitudes denen un campo. Así,
hablaremos del campo de temperatura, campo de densidad, de velocidad, de desplazamiento,
etc. El que el medio en el que están denidas es un medio continuo, se reeja en la propiedad
matemática de que todas estas magnitudes vienen caracterizadas por funciones continuas (y
derivables) del espacio y del tiempo.
La descripción de las fuerzas que se hacen los sistemas materiales, así como la fuerza que
una parte del sistema hace sobre otra, la analizaremos en el capítulo dedicado a las tensiones.
Aunque las fuerzas entre dos partículas son vectores, cuando lo que tenemos son innitos puntos
que hacen fuerza sobre otros innitos puntos, la forma de caracterizar esto es mediante un objeto
geométrico que se va a denominar un tensor. Viene caracterizado por tener varias componentes,
algunas más que en el caso de un vector que es una magnitud geométrica de tres componentes.
Cuando a un sistema material le sometemos a fuerzas externas, esto produce modicaciones
tanto en la forma como en la evolución del sistema. Estudiaremos por lo tanto, las deformaciones
que se producen en los sistemas continuos y su forma de describirlo, así como las leyes generales
que nos permiten determinar la evolución temporal del sistema y de sus partes, que se conoce
genéricamente con el nombre de dinámica.
En esos capítulos va a quedar descrito de forma general el formalismo que se va a utilizar
para tratar cualquier sistema material que consideremos como un medio continuo. Su utilidad la
veremos en el estudio de dos tipos diferentes de medios continuos: los medios materiales sólidos
y los medios uidos. No existen medios materiales estrictamente rígidos. En general todos los
sistemas materiales se deforman en mayor o menor grado. De una forma general podríamos
decir que un sólido es un medio material que se resiste a ser deformado. Un uido, en cambio,
es un medio material que parece que se puede adaptar a la forma de cualquier recipiente y,
por lo tanto, su característica principal no es que no se deforme, sino que en general ofrecerá
resistencia a los posibles cambios en su estado de deformación.
De los medios materiales sólidos vamos a estudiar aquellos sistemas materiales en los que va
a existir una relación lineal entre los esfuerzos realizados sobre el sistema y las deformaciones
producidas. Es lo que se denomina teoría de la elasticidad lineal. El objeto de estudio de
los sistemas materiales líquidos, es lo que constituye el cuerpo de la mecánica de uidos.
Entre los uidos examinaremos los uidos ideales y los uidos reales o viscosos. Veremos que la
viscosidad juega un papel fundamental. Si el aire no fuera viscoso los aviones no volarían.
Cada vez que perturbamos el estado de equilibrio de un sistema material extenso, la perturbación no viaja de forma instantánea a toda la masa del sistema. Se produce lo que se conoce
como una onda. El análisis de las ondas en medios materiales, será el objeto de estudio de
un capítulo, en el que analizaremos este fenómeno de propagación, tanto en sólidos como en
líquidos, poniendo de maniesto sus diferencias.
Finalizaremos con un capítulo general dedicado al análisis dimensional. Las variables
físicas poseen dimensiones, pero redeniendo adecuadamente nuevas variables, podemos hacer
que una expresión o ley física aparezca en términos de variables adimensionales y de algún o
algunos parámetros numéricos, también adimensionales. La resolución de dichas ecuaciones o
leyes dependerá de su estructura matemática, la cual es independiente de la naturaleza física
de las variables utilizadas, ya que éstas se han hecho adimensionales. Dos problemas físicos
diferentes, cuyas ecuaciones fundamentales sean exactamente las mismas, una vez reducidos los
dos problemas a variables adimensionales, tendrán el mismo tipo de solución, la cual dependerá
solamente de los valores numéricos de las constantes que aparezcan.
Capítulo 1
Cinemática
1.1. Medios continuos y discretos
Se trata de aproximar los sistemas extensos mediante la hipótesis de que un sistema material de muchas partículas puede ser considerado como un continuo. Son situaciones en las que
el comportamiento macroscópico del sistema material se explica sin tener presente su estructura molecular. Contrasta esto con la consideración atomística según la cual la materia está
discretizada. Todas las propiedades del sistema como densidad, presión, velocidades y aceleraciones, viscosidad, estado de tensiones, etc., serán funciones continuas de punto y del tiempo.
Estas propiedades o magnitudes físicas, las conocemos con el nombre genérico de campos. Cada
una de estas magnitudes es función f (r, t), donde r ∈ R3 toma valores en una cierta región del
espacio físico tridimensional R y durante un intervalo de tiempo t ∈ (t1 , t2 ) arbitrario. Además,
el carácter geométrico de estas magnitudes hará que hablemos de campos escalares, vectoriales,
tensoriales, etc.
1.1.1. Notación indicial
Como las distintas magnitudes escalares φ, vectoriales vi , tensoriales Tij , etc, que serán en
general funciones de punto y del tiempo, se van realizar con ellas las operaciones normales
del cálculo y se van a derivar respecto de las variables espaciales y del tiempo, adoptamos los
siguientes convenios y notaciones:
Convenio de suma Cada vez que en una expresión aparezcan multiplicadas dos o más magnitudes con índices repetidos, se sobreentenderá que existe suma sobre ese índice. Por ejemplo
vi Tij ≡
i=3
X
vi Tij = v1 T1j + v2 T2j + v3 T3j = wj
i=1
Las diferentes derivadas parciales se escriben como
∂φ
≡ ∂i φ = φ,i
∂xi
∂vj
≡ ∂i vj = vj,i
∂xi
∂Tjk
≡ ∂i Tjk = Tjk,i
∂xi
div v = ∇ · v = ∂i vi = vi,i ,
rot v = ∇ × v,
∇=
i=3
X
i=1
ei
∂
∂
= ei
= ei ∂i
∂xi
∂xi
(∇ × v)i = ²ijk ∂j vk .
El tensor antisimétrico ²ijk vale +1 si sus índices ijk son una permutación par de 123, −1 si es
una permutación impar y 0 si hay dos índices repetidos y satisface
¯
¯
¯ δiq δjq δkq ¯
¯
¯
²ijk ²qrs = ¯¯ δir δjr δkr ¯¯ y al sumarlo sobre un índice ²ijk ²rsk = δir δjs − δis δjr ,
¯ δis δjs δks ¯
siendo δij = δji un tensor simétrico que vale 1 si i = j , y 0 si i 6= j .
3
4
1.1.2.
CAPÍTULO 1. CINEMÁTICA
Componentes de un vector y de un operador lineal
En un espacio vectorial tenemos una base formada por tres vectores linealmente independientes ei , i = 1, 2, 3, no necesariamente ortogonales ni de norma unidad. Si damos un vector
arbitrario v , denominamos componentes covariantes de v y las designamos por vi a los valores
reales vi = ei · v .
Un operador lineal sobre un espacio vectorial A es un objeto que transforma vectores en
vectores pero de forma lineal, esto es, A(av + bw) = aAv + bAw. Basta por lo tanto conocer
cómo actúa A sobre los vectores de la base ei para saber cómo actúa sobre cualquier otro
vector. Por lo tanto nos interesa conocer las componentes de los vectores transformados Aei .
A estas componentes les denominamos componentes matriciales del operador A en la base ei y
las representamos por
Aji = ej · Aei ≡< ej |A|ei >,
y en general Aij 6= Aji .
Sea f k , k = 1, 2, 3 otra base del espacio vectorial. Se podrá expresar una en términos de la
otra mediante unos coecientes Bkl o bien Ckl :
f k = Bkl el ,
ek = Ckl f l .
⇒
f k = Bks Csl f l ,
Bks Csl = δkl .
También Ckl Bls = δks . Como matrices, B y C son inversas la una de la otra.
Si la base primera fuera ortonormal, es decir que los vectores de la base fueran ortogonales
y de norma unidad, ei · ej = δij , los coecientes Bkl son precisamente
f k · el = Bkr er · el = Bkr δrl = Bkl .
Veamos cómo se expresan las componentes covariantes de los vectores y de las matrices en
una y otra base.
vk0 = f k · v = Bkl el · v = Bkl vl .
vj = ej · v = Cjl f l · v = Cjl vl0 .
A0kr = f k · Af r = Bkl el · A Brs es = Bkl Brs el · Aes = Bkl Brs Als .
0
Aij = ei · Aej = Cir f r · ACjk f k = Cir Cjk f r · Af k = Cir Cjk Ark
.
1.1.3.
Componentes covariantes y contravariantes de un vector
Anteriormente hemos denido como componentes covariantes de un vector v en una base
formada por los vectores ei a las magnitudes vi = ei · v . Sin embargo, la expresión del vector
como combinación lineal de los vectores básicos se escribe v = v i ei , en términos de otros
números reales v i , en los que hemos puesto el índice en la parte superior (o superíndice). Las
componentes covariantes vi son en general distintas de las v i . Salvo que la base esté formada
por vectores ortonormales, esto es ei · ej = δij , en cuyo caso valen lo mismo. En efecto,
vi = ei · v = ei · v j ej = v j ei · ej = v j δij = v i .
A las componentes v i las denominamos componentes contravariantes del vector. La distinción
entre ambos tipos de componentes se basa en que bajo los cambios de base transforman de
manera diferente. Así, si f k = Bkl el es un cambio de vectores básicos, hemos visto que las
componentes covariantes vk0 = f k · v transformaban vk0 = Bkl vl con los mismos coecientes de
paso que los dados entre los vectores básicos. Sin embargo
k
v = v 0 f k = v j ej = v j Cjk f k ,
⇒
k
v 0 = Cjk v j ,
transforman con los coecientes de cambio contrario, de la base f k a la ei , y además sumando
sobre el primer índice, el j , de Cjk .
1.1. MEDIOS CONTINUOS Y DISCRETOS
5
1.1.4. Descomposición polar de una matriz no singular
Dada una matriz no singular A, siempre es posible descomponerla en un producto de dos
matrices no singulares de las que una de ellas es una matriz de rotación R y otra es una matriz
no singular simétrica S o T
A = RS = T R.
En ambos casos la matriz de rotación es la misma pero la matriz simétrica T no tiene por qué
√ ser
la misma que la S . Como det R = 1
,
se
tiene
que
det
A
=
det
S
=
det
T
.
La
matriz
S
=
AT A
√
y R = AS −1 . En el otro caso T = AAT que coincidirá con S si A conmuta con AT .
Efectivamente, si A es no singular AT A es una matriz simétrica denida positiva pues
det(AT A) = (det A)2 > 0. Sus valores propios son números positivos y sus vectores propios
son ortogonales. Por lo tanto existe una matriz de rotación que la diagonaliza. Sea S esa
2
matriz de rotación. Entonces D2 = S T AT AS , con D una matriz diagonal
√ y D una matriz
2 T
T
T
T
diagonal de números positivos. Entonces SD S = A A y SDS = A A = S , simétrica
pero no necesariamente diagonal. Si ahora hacemos
AT A = SRT RS = S 2 ,
⇒
RT R = I
y R es una matriz de rotación. El nombre de descomposición polar hace referencia a que
S o T representa al módulo de A y la matriz R es el argumento o fase.
1.1.5. Transformación de un tensor
Lo que caracteriza a una magnitud tensorial no es el hecho de que sea un objeto geométrico
con un conjunto de índices, sino la forma de transformar bajo los cambios de los sistemas de
referencia. Aquí nos vamos a ceñir a cambios de sistemas de referencia cartesianos en los que
ejes ortonormales son transformados en ejes ortonormales, pero la denición de tensor se puede
extender a cualquier cambio de coordenadas, no necesariamente cartesianas ni ortogonales. Bajo
un cambio de coordenadas, las componentes del vector de posición transforman
x0i = Rij xj ,
xj = R−1 ji x0i = Rij x0i
donde la matriz de paso Rij es una matriz de rotación y la matriz de paso inversa es su
transpuesta. Las componentes del vector velocidad transforman de la misma manera que las del
vector de posición
vi0 = Rij vj ,
por eso decimos que la velocidad es una magnitud vectorial. El gradiente de una función φ,
denotado por las tres magnitudes φ,i es también una magnitud vectorial pues:
φ0,i (x0 ) =
∂φ(x(x0 )) ∂xj
∂φ
0
0
≡
∂
φ(x
)
=
= Rij φ(x(x0 )),j
i
∂x0i
∂xj
∂x0i
transforma como las componentes del vector de posición.
Un tensor de dos índices Tij es una magnitud que transforma de esa manera para cada uno
de sus índices, es decir
Tij0 = Rik Rjs Tks ,
de la misma forma que las componentes de una matriz 2 × 2, y se puede extender esto mismo
para un tensor de más índices.
Las ecuaciones de transformación de un tensor de dos índices pueden tener una escritura
matricial, si consideramos que el primer índice es el índice de la y el segundo el de columna,
con lo que si T representa la matriz de componentes Tij y R la matriz de rotación, la anterior
expresión se escribe
T 0 = RT RT ,
6
CAPÍTULO 1. CINEMÁTICA
siendo RT la matriz de rotación transpuesta.
Si el cambio de coordenadas no es ortogonal, esto es, pasamos de las coordenadas xi a las
coordenadas x0j , que no es necesario que sean ni siquiera cartesianas, dado por las ecuaciones
de transformación x0j = fj (xi ), quien juega el papel de la matriz de rotación Rij es la matriz
Jacobiana de la transfomación Fij = ∂x0i /∂xj . De esta forma un pequeño vector, el elemento de
arco, transforma:
∂x0j
dx0j =
dxi = Fji dxi .
∂xi
En el caso particular de un cambio de ejes ortogonales esta matriz Jacobiana es precisamente
la matriz de rotación Rij . De esta manera, la transformación de un tensor es
Tij0 (x0 ) = Fik Fjs Tks (x(x0 )).
Conviene observar que, además de utilizar los coecientes de transformación Fij (x), hay que
reescribir todo en términos de las nuevas variables x0i , por lo que tanto las componentes Tij (x(x0 ))
como las Fij (x(x0 )) deben ser nalmente expresadas en términos de estas últimas.
Ahora, quien juega el papel de la matriz de paso Bij es la Fji = ∂x0j /∂xi y de la matriz de
paso inversa Ckl , la Gkl = ∂xk /∂x0l , es decir, la matriz Jacobiana inversa.
Un tensor se dice simétrico si sus componentes Tij = Tji , cualesquiera que sean i y j . Un
tensor se dice antisimétrico si sus componentes Tij = −Tji , cualesquiera que sean i y j . En
este caso, cada una de las componentes diagonales Tjj = 0 (ahora no consideramos el criterio
de suma). Los dos tensores ²ijk y δij son invariantes bajo los cambios de coordenadas, y el
carácter simétrico o antisimétrico de un tensor es también una propiedad invariante. En el caso
de tensores de dos índices, su traza Tii , (sumado en i), es otra propiedad invariante.
Los tensores simétricos de dos índices tienen la propiedad de que poseen valores propios
reales y que además los vectores propios correspondientes son ortogonales, por lo que escogiendo
como sistema de referencia unos ejes coordenados en las tres direcciones propias del tensor, éste
aparecerá en este sistema de referencia como un tensor cuyas únicas componentes no nulas son
las de su diagonal Tii (sin suma sobre i), que serán precisamente los correspondientes valores
propios del tensor.
1.2.
Conguraciones
Sea un medio material continuo que en el instante t = 0 ocupa una región R(0) del espacio
físico tridimensional y la región R(t) en el instante t. Sea X un punto de R(0) de coordenadas
(X1 , X2 , X3 ) y que en el instante t se halla en el punto (x1 , x2 , x3 ) de R(t). A las (X1 , X2 , X3 )
se les denomina coordenadas Lagrangianas del punto material y a las (x1 , x2 , x3 ) se les da el
nombre de coordenadas Eulerianas del mismo punto material, estando todas ellas referidas
a un mismo sistema cartesiano de referencia con origen en O.
Ambas coordenadas de acuerdo con la dinámica del sistema se pueden expresar en términos
unas de otras:
xi = fi (X, t),
Xi = gi (x, t),
i = 1, 2, 3 y que también Xi = fi (X, 0),
y como el punto x al que llega el punto X en el instante t es único y está determinado, resulta
que las funciones fi y gi son invertibles y dependen explícitamente del tiempo transcurrido t. La
condición necesaria y suciente para que dichas funciones sean invertibles es que el determinante
Jacobiano
¯
¯
¯ ∂xi ¯
¯
¯ 6= 0
J =¯
∂Xj ¯
1.2. CONFIGURACIONES
7
Figura 1.1: Conguración inicial R(0) y en el instante t, R(t), de un medio material.
Se pueden distinguir tres tipos diferentes de curvas: trayectorias de las partículas,
líneas de corriente y líneas de emisión. El vector desplazamiento u es el que une el
punto inicial X con su desplazado x en el instante t.
Las matrices (o tensores) obtenidas por estas ecuaciones de transformación
Fij =
∂fi
,
∂Xj
Gij =
∂gi
,
∂xj
verican
J = det F ,
F G = GF = I,
det G = 1/J,
donde usamos el convenio de que si las expresamos por componentes el primer índice representa
la la y el segundo la columna F ≡ Fij y F G ≡ Fik Gkj , habiendo utilizado el convenio de
sumación sobre índices repetidos.
A veces lo interesante es expresar las diferentes magnitudes en términos de los puntos materiales reales del sistema por lo que se utilizará la descripción Lagrangiana en la que cada punto
material posee unas coordenadas jas Xi que son su posición en el instante inicial. Otras veces,
cuando no es posible distinguir los diferentes puntos materiales del sistema, lo que se hace es
asignar las magnitudes físicas a los diferentes puntos de la región de observación, aún cuando
en éstos la materia que los ocupa sea diferente en cada instante. Estamos en este caso en una
descripción Euleriana de la evolución.
1.1 Sea un medio continuo de forma esférica de radio R con centro en el origen
de coordenadas. Su deformación entre el instante t = 0 y un cierto tiempo t viene dada por
las ecuaciones de transformación, (que son la solución general de las ecuaciones dinámicas)
Ejemplo
x1 = (1 + t)X1 ,
x2 = (1 + 2t)X2 ,
x3 = (1 − t/2)X3 .
Lo que nos dan son las tres funciones fi (X, t). Las funciones gi (x, t) son las que denen la
transformación inversa
X1 = x1 /(1 + t),
X2 = x2 /(1 + 2t),
X3 = x3 /((1 − t/2).
8
CAPÍTULO 1. CINEMÁTICA
El origen queda donde estaba y lo que se produce es un aumento en el eje e1 otro aumento
en la dirección e2 y se comprime el sistema en la dirección e3 . El gradiente de deformación
es


(1 + t)
0
0
∂fi
 , det F = (1 + t)(1 + 2t)(1 − t/2).
F ≡ Fij =
= 0
(1 + 2t)
0
∂Xj
0
0
(1 − t/2)
Este determinante es distinto de cero simpre que t 6= 2. Por lo tanto, salvo para ese instante,
las ecuaciones de transformación son invertibles. Esto implica, que desde el punto de vista
físico, las ecuaciones de la dinámica solamente son válidas para los instantes 0 ≤ t <
2. Analicemos a partir de ahora el sistema en el instante t = 1. Entonces, det F = 3,
independiente del punto, por lo que todo elemento innitesimal de volumen del material ha
aumentado su volumen 3 veces después de la deformación en ese momento, puesto que F
además de gradiente de la deformación es la matriz jacobiana y los elementos de volumen
cambian con el valor absoluto del Jacobiano, como veremos más adelante.
La supercie exterior viene dada por la ecuación de la esfera X12 + X22 + X32 = R2 , que
después de la deformación y en el instante t = 1, resulta ser
x21
x2
+ 2 + 4x23 = R2 ,
4
9
x21
x22
x23
+
+
= 1,
(2R)2
(3R)2
(R/2)2
es decir un elipsoide cuyos ejes principales son los ejes coordenados, pero de semiejes de
valores (2R, 3R, R/2). El interior de la esfera al deformarse, da lugar al interior del elipsoide.
Los puntos que permanecen invariantes bajo la deformación son los que satisfacen el sistema
de ecuaciones
X1 = 2X1 ,
X2 = 3X2 ,
X3 =
1
X3 ,
2
⇒
X1 = X2 = X3 = 0,
por lo que el origen es el único punto que no se desplaza.
La esfera poseía un volumen V = 4πR3 /3, en tanto que el elipsoide tiene por volumen en
el instante t = 1
4
4
V 0 = πabc = π(2R)(3R)(R/2) = 3V.
3
3
El sistema como un todo triplica su volumen.
1.2.1.
Líneas de corriente, líneas de emisión y trayectorias
Existen tres familias de curvas diferentes:
Trayectoria de un punto material es la curva que describe dicho punto material a lo largo del
tiempo. La trayectoria de un punto X se expresa en coordenadas Lagrangianas mediante las
funciones
xi (t) = fi (X, t),
(1.1)
con los valores Xi jos. Parte del punto inicial X y llega en el instante t al punto actual x. La
expresión (1.1) es la solución general del sistema dinámico.
Línea de emisión de un punto dado P es la curva formada uniendo todos los puntos materiales
de la conguración inicial, que en algún instante pasarán por P . Su expresión es la
Xi (t) = gi (x, t),
curva parametrizada por el tiempo t, pero con las coordenadas xi del punto P , jas. Su gráca
geométrica queda connada en la región inicial R(0).
Línea de corriente es cada una de las curvas que en el instante t su vector tangente en cada
punto tiene la dirección del vector velocidad de ese punto. Estas curvas se deben calcular en
cada instante t, en la correspondiente conguración R(t).
1.2. CONFIGURACIONES
9
1.2.2. Campo de velocidad
Es un campo vectorial. Si el punto X se encuentra actualmente en el x dado por (1.1) dicho
punto se mueve en el instante t con la velocidad
V (X, t) =
dx
∂f
=
(X, t)
dt
∂t
y se dice que esta función V (X, t) constituye una descripción Lagrangiana del campo de velocidad. La función
v(x, t) = V (g(x, t), t),
representa el campo de velocidad en la descripción Euleriana y se expresa en términos de puntos
del espacio x.
Supuesto conocido el campo de velocidad en la descripción Euleriana, cada punto se mueve
con una velocidad tal que las líneas de corriente del sistema son las curvas tridimensionales
cuyas tangentes son precisamente los vectores velocidad del medio:
dx
dy
dz
=
=
,
vx (x, y, z, t)
vy (x, y, z, t)
vz (x, y, z, t)
o bien
dr = vdt,
cuya solución general en cada instante t nos producirá la descripción geométrica de las líneas
de corriente del sistema. Esta denominación es genérica y es independiente de que el sistema
material sea o no un uido.
En general se dice que la evolución dinámica del sistema material es estacionaria si las
diferentes magnitudes físicas del sistema no son funciones explícitas del tiempo y por lo tanto
las líneas de corriente del sistema son siempre las mismas. En particular el campo de velocidad
no es función de t y las trayectorias son unas curvas jas en el espacio. En este caso trayectorias,
líneas de corriente y de emisión coinciden.
Un caso particular de evolución estacionaria es aquél en el que el sistema material está quieto
y en este caso se dice que haremos un análisis estático del mismo.
Ejemplo
1.2 Continuando con el ejemplo anterior, el campo de velocidad resulta ser:
v1 =
∂x1
= X1 ,
∂t
v1 =
∂x2
= 2X2 ,
∂t
v3 =
∂x3
= −X3 /2,
∂t
expresado en coordenadas Lagrangianas. En realidad el vector v está en realidad localizado
en el punto x, por lo que es preciso expresarlo en coordenadas Eulerianas, es decir:
v1 =
x1
,
1+t
v2 =
2x2
,
1 + 2t
v3 =
x3
.
t−2
En este instante t, las líneas de corriente se obtendrán de integrar las ecuaciones
dx2
dx3
dx1
=
=
,
v1
v2
v3
dx1
dx2
dx3
=
=
,
x1 /(1 + t)
2x2 /(1 + 2t)
x3 /(t − 2)
cuya solución general es
µ
¶
1 + 2t
(1 + t) ln x1 =
ln x2 + ln a,
2
(1+t)
x1
(t+1/2)
= ax2
,
(1 + t) ln x1 = (t − 2) ln x3 + ln b,
(1+t)
x1
= bxt−2
3 ,
a, b ∈ R.
10
1.3.
CAPÍTULO 1. CINEMÁTICA
Tensor de deformaciones
Los sistemas materiales en general sufren desplazamientos. Deberemos distinguir por lo
tanto entre un desplazamiento sin deformación de otro en el que además se pueda producir una
alteración del sistema, que denominaremos deformación. Se dice que un medio continuo sufre
deformaciones si las distancias relativas entre sus puntos cambian.
Si consideramos un punto del sistema que en el instante t = 0 se encuentra en el punto de
coordenadas (X1 , X2 , X3 ) y que en el instante t se halla en (x1 , x2 , x3 ) que de acuerdo con la
dinámica del sistema se puede expresar en términos del punto anterior mediante xi = fi (X, t),
entonces un punto que distaba dXi del X distará dxi del x dado por
dxi =
∂fi
(X, t)dXj
∂Xj
y a la matriz Fij = ∂fi /∂Xj se le da el nombre de gradiente de la deformación en el punto
X y en el instante t. Análogamente, si tenemos otro punto próximo al X que dista δXi entonces
distará del x en el instante t un valor δxi dado por
δxi = Fij (X, t)δXj .
Para determinar la deformación no basta con medir las diferencias entre las componentes dXi
y dxi pues en general una rotación las modica. Una posibilidad es comparar los módulos |dX|
y |dx|. Si estos cambian es evidente que hay una deformación, pero esto hay que medirlo en
cualquier dirección y en todos los puntos. Supongamos ahora que los módulos de dos vectores
δX y dX no cambian. Podríamos decir que no ha habido deformación, pero si sucede que el
ángulo que forman esos vectores cambia, entonces sí que ha habido deformación. Uno ha rotado
relativo al otro. Por eso se dene la deformación estudiando la variación del producto escalar
entre dos elementos arbitrarios
dx · δx − dX · δX = dxi δxi − dXk δXk = Fij dXj Fil δXl − dXk δXk
pero los últimos elementos los podemos poner
dXk = δkj dXj ,
δXk = δkl δXl ,
dXk δXk = δkj dXj δkl δXl = δjl dXj δXl
con lo que podemos agrupar lo anterior en
(Fij Fil − δjl ) dXj δXl = 2Rjl (X, t) dXj δXl .
En esta expresión tenemos dos partes: Una, las componentes de dos vectores arbitrarios dXj
y δXl con origen en X , y otra 2Rjl (X, t), que solamente es función del punto analizado. Si
esta parte es cero, entonces el resultado nulo resulta ser independiente de los dos vectores que
escojamos.
Al tensor Cij = Fki Fkj se le denomina tensor de las dilataciones, ya que establece en
cada punto cómo se expresa dx · δx en términos de dX · δX . El tensor Rij = (Cij − δij )/2 recibe
el nombre de tensor de deformaciones. Está denido en cada punto del medio material y
sirve para calcular alrededor de cada punto cómo han variado los diferentes productos escalares
entre pares de vectores con origen en ese punto. Si todas sus componentes Rij (X, t) son nulas
en un punto, es que no ha habido deformación alrededor de ese punto. Si alguna componente
es diferente de cero, es posible encontrar direcciones en las que el resultado anterior arroja
diferencias entre los vectores iniciales y los actuales.
Teorema La condición necesaria y suciente para que no exista deformación en
el punto X desde el instante inicial t = 0 hasta el tiempo t, con respecto a la
conguración inicial es que el tensor de deformaciones Rij (X, t) = 0, en el punto X .
1.3. TENSOR DE DEFORMACIONES
11
1.3.1. Diagonalización del tensor de deformaciones
El tensor de dilataciones Cij = Cji es simétrico y denido positivo por lo que sus valores
propios son reales positivos.
El tensor de deformaciones Rij = Rji es simétrico y posee los mismos vectores propios que el
Cij y sus valores propios RJ están ligados con los de éste CJ mediante RJ = (CJ −1)/2 > −1/2.
Los valores propios RJ , en el caso de ser pequeños comparados con la unidad, representan la
deformación relativa de los correspondientes elementos de longitud, pues a lo largo√de la correspondiente dirección principal se tiene dx2 − dX 2 = 2RJ dX 2 , con lo que dx/dX = 1 + 2RJ ≈
1 + RJ + O(RJ2 ), y así dx ≈ dX + RJ dX . Si inicialmente tenemos un elemento de volumen de
lados dX , dY y dZ , y después de la evolución se transforma en el elemento de lados dx, dy y
dz , el volumen del sistema vale
dV 0 = dxdydz = (1+R1 )(1+R2 )(1+R3 )dXdY dZ ≈ (1+R1 +R2 +R3 )dXdY dZ = (1+Rii )dV,
a primer orden en las deformaciones, ya que la traza de un tensor es invariante bajo los cambios
de coordenadas. Despejando la traza Rii
Rii =
dV 0 − dV
,
dV
(1.2)
La traza del tensor de deformaciones nos mide la variación relativa del volumen del sistema en
cada punto. Por eso un tensor de deformaciones de traza nula corresponde a una deformación
sin cambio local de volumen.
Si un valor propio RI < 0, entonces en la correspondiente dirección principal
p
dx = 1 + 2RI dX < dX
y por lo tanto existe una contracción, en tanto que existe una dilatación si RI > 0. Si el valor
propio es nulo, entonces no existe modicación del elemento de arco que tiene esa dirección.
En cualquier otra dirección, la deformación de cada elemento no tiene por qué tener su
misma dirección, en cuyo caso decimos que existe deformación normal (contracción o dilatación)
y deformación tangencial o de deslizamiento.
Si n es un vector unidad, la magnitud
p
dxN = 2ni Rij nj dX
nos mide la deformación normal del elemento de arco dX = ndX , de esa dirección.
En los ejemplos 1.1 y 1.2

Rij
(1 + t)2 − 1
1
0
=
2
0
0
(1 + 2t)2 − 1
0

0
.
0
2
(1 − t/2) − 1
1.3.2. Tensor de deformaciones linearizado
Si llamamos u = x − X al desplazamiento sufrido por el punto X , resulta que
xi = Xi + ui (X, t)
y de aquí Fij = δij + ∂ui /∂Xj , con lo que
µ
¶
∂uj
1 ∂uk ∂uk
1 ∂ui
+
+
Rij =
2 ∂Xj
∂Xi
2 ∂Xi ∂Xj
(1.3)
12
CAPÍTULO 1. CINEMÁTICA
que contiene una parte lineal en el desplazamiento y otra cuadrática. Si las variaciones de los
desplazamientos |∂uj /∂Xi | ¿ 1 son muy pequeñas entonces es buena la aproximación del tensor
de deformaciones por el tensor de deformaciones linearizado en la formulación Lagrangiana
µ
¶
∂uj
1 ∂ui
+
Lij =
2 ∂Xj
∂Xi
o en su formulación Euleriana
1
Eij =
2
µ
∂uj
∂ui
+
∂xj
∂xi
¶
En general es el tensor Euleriano el que consideraremos como tensor de deformaciones en el
caso de cuerpos sólidos cuando el gradiente de los desplazamientos sea despreciable.
En este caso de pequeños desplazamientos, si u(x, t) es lo que se ha desplazado el punto
x, entonces dui = ∂ui /∂xj dxj = Uij dxj . Al tensor Uij le denominamos tensor gradiente
de los desplazamientos. Si esta modicación que es lineal en los dxi se puede poner como
dui = ²ikj ωk (x, t)dxj , la modicación en el punto x de la variación du = ω × dx, corresponde
a una rotación local. En este caso Uij = −Uji . El tensor de deformaciones linearizado es,
precisamente, la parte simétrica del tensor Uij ,
1
(Uij + Uji ) ,
2
en tanto que la parte antisimétrica de Uij contiene información local de cómo ha rotado el medio
alrededor del punto. Por eso, si el gradiente de desplazamientos Uij es un tensor antisimétrico
entonces Eij = 0.
Eij =
Ejemplo 1.3 Sea la deformación de un medio continuo en el instante t = 1 del ejemplo
anterior, dada por
1
x1 = 2X1 , x2 = 3X2 , x3 = X3 ,
2
X1 = x1 /2, X2 = x2 /3, X3 = 2x3 ,
El gradiente de deformación es


2 0 0
F =  0 3 0  , det F = 3,
0 0 1/2

1/2
G= 0
0

0 0
1/3 0  ,
0 2
El tensor de dilataciones y de deformación son:



3/2 0
4 0 0
1
C = F T F =  0 9 0  , R = (C − I) =  0 4
2
0 0
0 0 1/4
det G = 1/3.

0
0 .
−3/8
1.3. TENSOR DE DEFORMACIONES
13
En este caso los tensores de deformación linearizados son



1 0
0
1/2
1
1
L = (F + F T ) − I =  0 2
0  , E = I − (G + GT ) =  0
2
2
0 0 −1/2
0
0
2/3
0

0
0 .
−1
Conviene observar que en este ejemplo el gradiente del desplazamiento no es despreciable
pues en la descripción Lagrangiana los desplazamientos
u1 = x1 − X1 = X1 ,
u2 = x2 − X2 = 2X2 ,
u3 = x3 − X3 = −X3 /2,
y en la Euleriana
u1 = x1 − x1 /2 = x1 /2,
u2 = x2 − x2 /3 = 2x2 /3,
u3 = x3 − 2x3 = −x3 ,
y |∂ui /∂Xj | no son mucho más pequeñas que 1, de ahí que la aproximación lineal del tensor
de deformaciones discrepe de su valor real, pues la parte que se desprecia en la descripción
Lagrangiana vale




1 0
0
1/2 0 0
∂ui
1 T
UL =
≡ 0 2
0 ,
U UL =  0 2 0 
∂Xj
2 L
0 0 1/8
0 0 −1/2
Estamos ante un sistema que se ha deformado mucho y por lo tanto la aproximación lineal
no es útil. En este caso, para calcular deformaciones hay que usar el tensor de deformaciones
completo 2R.
1.3.3. Tensor de deformación esférico y tensor desviador
Toda matriz n×n y simétrica A, se puede descomponer en la suma de dos matrices simétricas,
una de ellas de traza nula y la otra diagonal y cuya traza sea la de la matriz original, y cuyos
elementos de la diagonal principal son todos iguales y de valor TrA/n.
Esta idea se puede extender al tensor simétrico de deformación R o a su aproximación lineal
E . Éstos se pueden desdoblar en un tensor diagonal denominado esférico y en otro de traza
nula llamado desviador, denotados Re y E e y Rd y E d , respectivamente, dados por
1
1
R = Rd + Re = Rd + (TrR) I, o bien E = E d + E e = E d + (TrE) I.
3
3
De esta manera el tensor de deformaciones que es simétrico aparece como la suma de dos tensores
simétricos que los asociamos a dos tipos distintos de deformaciones. Los tensores desviadores,
que son de traza nula, están asociados con la deformación cortante o tangencial, en tanto que
los esféricos lo están con la dilatación o contracción isótropa, ya que en el caso de pequeñas
deformaciones hemos visto que la traza (1.2) representa la variación relativa de volumen, por
lo que la deformación debida al desviador no modica los elementos de volumen, cuyo cambio
está contenido en la parte esférica del tensor.
1.3.4. Estados de deformación planos
Otra de las características de la matrices n × n simétricas es que sus valores propios son
reales y los correspondientes vectores propios son vectores ortogonales. Si escogemos como base
del espacio vectorial estos vectores propios, entonces en esta base la matriz queda representada
como una matriz diagonal en la que los elementos de la diagonal son precisamente sus valores
propios. Esto mismo es válido para los tensores simétricos.
Cuando uno de los valores propios del tensor de deformación en un punto es nulo, entonces se
dice que en ese punto el estado de deformaciones es plano y el tensor adopta la forma matricial


R11 R12 0
Rij =  R12 R22 0  .
0
0
0
14
CAPÍTULO 1. CINEMÁTICA
El estado de deformación se puede caracterizar de forma gráca mediante los círculos de Mohr,
que los estudiaremos al analizar las tensiones en el interior de los sistemas continuos.
1.3.5.
Condiciones de compatibilidad en deformaciones lineales
En el caso de pequeñas deformaciones (estamos, por ejemplo, pensando en sistemas sólidos), de tal forma que podamos despreciar los términos cuadráticos de (1.3), y el tensor de
deformaciones lo caracterizamos mediante el tensor de la descripción Euleriana
¶
µ
∂uj
1 ∂ui
+
, i, j = 1, 2, 3.
eij (x, t) = eji (x, t) =
2 ∂xj
∂xi
Estas ecuaciones las podemos considerar como un sistema de 6 ecuaciones diferenciales en
derivadas parciales, de las que conocemos los primeros miembros eij (x, t) y en las que las
incógnitas son las 3 funciones ui (x, t). El sistema anterior será integrable no para cualquier
tipo de funciones eij (x, t) escogidas de forma aleatoria, sino si cumplen ciertas condiciones.
Estos condiciones recogen la idea de que debido a la continuidad de las funciones ui y de sus
derivadas, debe exitir igualdad entre las derivadas cruzadas de distintos órdenes, como por
ejemplo
∂ 2 ui
∂ 2 ui
∂ 3 ui
∂ 3 ui
=
,
=
, ∀i, j, k, l, etc.
∂xj ∂xk
∂xk ∂xj
∂xj ∂xk ∂xl
∂xl ∂xj ∂xk
Esto impone ciertas restricciones a las funciones eij (x, t) del primer miembro. Se denominan
condiciones de compatibilidad a las condiciones de integrabilidad de este sistema de ecuaciones
diferenciales. Demostraremos más adelante que éstas se reducen a condiciones que involucran
solamente a las derivadas segundas de las eij (x, t) y son:
²ipr ²jqs
∂ 2 epq
= 0,
∂xr ∂xs
i, j = 1, 2, 3.
(1.4)
Parece que son 9 pero solamente son 6 independientes que se reducen a
∂ 2 e11 ∂ 2 e22
∂ 2 e12
+
=
2
,
∂x1 ∂x2
∂x22
∂x21
∂ 2 e22 ∂ 2 e33
∂ 2 e23
+
=2
,
2
2
∂x2 ∂x3
∂x3
∂x2
∂ 2 e33 ∂ 2 e11
∂ 2 e31
+
=
2
,
∂x3 ∂x1
∂x21
∂x23
µ
¶
∂e23 ∂e31 ∂e12
∂ 2 e11
∂
−
+
+
=
,
∂x1
∂x1
∂x2
∂x3
∂x2 ∂x3
µ
¶
∂
∂e23 ∂e31 ∂e12
∂ 2 e22
−
+
=
,
∂x2 ∂x1
∂x2
∂x3
∂x3 ∂x1
µ
¶
∂
∂e23 ∂e31 ∂e12
∂ 2 e33
+
−
=
.
∂x3 ∂x1
∂x2
∂x3
∂x1 ∂x2
En el caso particular de deformaciones planas las distintas funciones no dependen de la variable
x3 que indica la dirección en que no existe deformación y las componentes ei3 = e3i = 0, en ese
caso las condiciones de compatibilidad se reducen solamente a la primera de estas ecuaciones.
1.4. TENSOR DE VELOCIDAD DE DEFORMACIÓN
15
1.4. Tensor de velocidad de deformación
Hasta el momento hemos representado la deformación global sufrida en cada punto de un
medio desde el instante inicial t = 0 hasta el instante nito t. Ahora lo que vamos a expresar
es cómo se deforma un medio por unidad de tiempo. Esto es especialmente interesante en el
caso de medios materiales uidos, en los que los cambios de posición de un punto material
pueden ser importantes, pero lo que interesa medir es con qué velocidad cambian estos cambios
de posición. Esto contrasta con el análisis de la deformación de un sólido que prácticamente
permanece estático, del cual interesa medir su deformación global. En cambio un uido, por el
hecho de desplazarse está continuamente deformándose. Si consideramos como anteriormente la
variación del producto escalar dx · δx − dX · δX de dos elementos innitesimales ahora lo que
queremos es determinar cómo cambian por unidad de tiempo, esto es la d(dx·δx−dX ·δX)/dt =
d(dx · δx)/dt, ya que tanto dX como δX no son funciones de t. Entonces
µ
¶
µ
¶
∂
d(dxi )
∂ ∂fi (X, t)
∂fi (X, t)
∂vi (X, t)
∂vi (x, t)
=
dXj =
dXj =
dXj =
dxk , (1.5)
dt
∂t
∂Xj
∂Xj
∂t
∂Xj
∂xk
pues
∂vi ∂xk
∂vi
∂vi
dXj =
dXj =
dxk .
∂Xj
∂xk ∂Xj
∂xk
Si ahora calculamos
d(dx · δx)
∂vi (x, t)
∂vk (x, t)
=
dxk δxi + dxk
δxi =
dt
∂xk
∂xi
µ
∂vi
∂vk
+
∂xk
∂xi
¶
dxk δxi = 2Dik dxk δxi .
El gradiente espacial del campo de velocidad instantáneo dene un tensor que lo llamamos
tensor gradiente de velocidad Yij ≡ ∂vi /∂xj , el cual puede descomponerse en sus partes
simétricas y antisimétricas Dij y Vij , respectivamente. Y = D + V . Al tensor simétrico
µ
¶
∂vj
dRij
1 ∂vi
+
= Dji =
.
Dij =
2 ∂xj
∂xi
dt
donde vi (x, t) es el campo de velocidad en el punto x en el instante t, se le denomina tensor
de velocidad de deformación y está descrito en términos de las variables Eulerianas, y
como acabamos de ver contiene la información que da cuenta de la velocidad de deformación (o
deformación por unidad de tiempo)de dx · δx, para cada par de elementos dx y δx alrededor
de cualquier punto.
Al tensor antisimétrico
µ
¶
∂vj
1 ∂vi
Vij =
−
= −Vji
2 ∂xj
∂xi
se le denomina tensor de vorticidad o giro y representará, como veremos en el caso de un
sólido, la velocidad angular de giro del medio alrededor de cada punto. En el caso de un uido,
nos dene la existencia de torbellinos alrededor de cada punto.
Teorema La condición necesaria y suciente para que no exista deformación de una
cierta región R entre los instantes t1 y t2 es que el tensor de velocidad de deformación
D(x, t) = 0, en todo punto x ∈ R de la región y para todo t ∈ (t1 , t2 ).
En este caso de medio sin deformación la estructura del campo de velocidad es de la forma
v(x, t) = A(t) + B(t) × x,
con A(t) y B(t) dos funciones vectoriales arbitrarias del tiempo, jugando B(t) el papel de
una velocidad instantánea de rotación como veremos a continuación. De esta manera, aunque
16
CAPÍTULO 1. CINEMÁTICA
exista movimiento no existe deformación y el movimiento se reduce a una traslación y rotación
sin deformación. El conjunto de trayectorias de todos los puntos del medio constituyen una
congruencia rígida.
Si Dij (t) = 0 a partir de un cierto t1 , entonces dRij /dt = 0 a partir de ese momento, lo
cual implica que el tensor de deformaciones Rij va a mantenerse constante en el tiempo. Esto
no quiere decir que el sistema no se haya deformado desde el comienzo, sino que a partir de
ese instante t1 el sistema no se deforma más, quedando con la deformación que había adquirido
hasta ese momento.
Ejemplo
1.4 Sea la deformación plana dada por las ecuaciones dependientes del tiempo
x1 = X1 + X2 (et − 1),
x2 = X1 (e−t − 1) + X2 ,
x3 = X3 ,
con transformación inversa
−x1 + x2 (et − 1)
x1 (et − 1) − x2
, X2 =
, X3 = x3 .
t
−t
1−e −e
1 − et − e−t


1
et − 1 0
1
0  , det(Fij ) = et + e−t − 1 = 2 cosh t − 1.
Fij =  e−t − 1
0
0
1
X1 =
La deformación es continua y el medio incrementa su volumen a medida que crece t. El
campo de velocidad es
V1 = X 2 e t ,
V2 = −X1 e−t ,
V3 = 0.
o en la descripción Euleriana
v1 =
x1 (et − 1) − x2 t
e,
1 − et − e−t
v2 =
x1 − x2 (et − 1) −t
e ,
1 − et − e−t
v3 = 0.
El gradiente de velocidad y los tensores de velocidad de deformación Dij y vorticidad Vij
 t

 t
(e − 1)et
−et
0
(e − 1)et
− sinh t
1
1
−t
t
−t

 − sinh t (et − 1)e−t
e
(e − 1)e
0  , Dij =
Yij =
1 − 2 cosh t
1 − 2 cosh t
0
0
0
0
0


0
− cosh t 0
1
 cosh t
0
0.
Vij =
1 − 2 cosh t
0
0
0
Esto corresponde a una vorticidad que tiene la dirección del eje OZ y que incrementa con
el tiempo. Las líneas de corriente provienen de integrar
dx1
dx2
dx3
=
=
,
v1
v2
v3
1.5.
dx1
dx2
=
,
(x1 (et − 1) − x2 )et
(x1 − x2 (et − 1))e−t
dx3 = 0.
Sólido rígido
La evolución de un sólido rígido con un punto jo es una rotación. Un punto cualquiera
referido a un sistema de coordenadas que tiene su origen en el punto jo tiene una posición
inicial X y en el instante t se encuentra en x = R(α(t))X ≡ R(t)X , siendo R(α(t)) la
rotación global sufrida por el sólido desde el instante inicial.
El movimiento más general de un sólido rígido es
xi = R(t)ij Xj + si (t),

0
0,
0
1.5. SÓLIDO RÍGIDO
17
y se compone de una rotación arbitraria y de un desplazamiento arbitrario, funciones continuas
del tiempo.
El gradiente de la deformación es por lo tanto
Fij =
∂xi
= R(t)ij ,
∂Xj
por lo que el tensor de deformación es
R(x, t)ij =
1
1
1
(Fki Fkj − δij ) = (R(t)ki R(t)kj − δij ) = (δij − δij ) = 0,
2
2
2
e independientemente del punto inicial X que estemos considerando (No confundir aquí el tensor
de deformación R(x, t)ij con la matriz de la rotación Rij ). Un cuerpo al rotar y trasladarse no
sufre una deformación en ninguno de sus puntos y por lo tanto tampoco sufre una deformación
global. Como el determinante de la matriz Jacobiana es 1, ya que se trata de una matriz
ortogonal, entonces no experimenta cambio de volumen. Podemos verlo también sabiendo que
si Rij = 0, también su traza Rii es nula y por lo tanto la modicación relativa de los elementos
de volumen es cero.
Supongamos que la traslación si (t) = 0. La velocidad del punto arbitrario
v=
dx
T
˙
˙
≡ ẋ = R(α(t))X
= R(α(t))R(α(t))
x,
dt
que es una función explícita de x. Como toda matriz que representa una rotación es una matriz
ortogonal, satisface RRT = I, también lo hacen las R(α(t)), con lo que derivando se tiene
ṘRT + RṘT = 0 = Ω + ΩT . La matriz Ω = ṘRT es antisimétrica y sus tres componentes
esenciales denen la velocidad angular del sólido ω(t), con lo que también podemos poner
v = ω × x,
vi (xj , t) = ²ijk ωj (t)xk = Ωik xk ,
con lo que la relación entre la velocidad angular y la matriz antisimétrica Ω es


0
−ω3 ω2
1
Ωik = ²ijk ωj , ωj = − ²jkl Ωkl Ω =  ω3
0
−ω1  .
2
−ω2 ω1
0
La divergencia y el rotacional de este campo de velocidad son
div v = ∇ · v = 0,
rot v = ∇ × v = 2ω,
por lo que no posee fuentes, sus líneas de campo son curvas cerradas y está producido por su
rotacional que es un campo vectorial uniforme ω(t), pero función de t en general, en todo punto
del cuerpo. El tensor de velocidad de deformación resulta ser:
D(x, t)ij =
1
1
(²ikj ωk + ²jki ωk ) = (−²ijk ωk + ²ijk ωk ) = 0,
2
2
independientemente del punto x y del instante t. Un sólido rígido en rotación no sufre ninguna
deformación en ningún instante de su evolución.
En el caso de que además haya traslación, el campo de velocidad en la descripción Euleriana
resulta ser:
vi = ẋi = Ṙ(t)ij Xj + ṡi (t),
y como
Xj = RT (t)jk (xk − sk ),
18
CAPÍTULO 1. CINEMÁTICA
se escribe
vi (x, t) = Ω(t)ij xj + wi (t),
donde wi (t) = ṡi (t) − Ω(t)ik sk (t),
por lo que el tensor de velocidad de deformación tiene la misma estructura que en el caso
anterior.
La traza del tensor de velocidad de deformación
µ
¶
1 ∂vi
∂vi
Dii =
+
= ∇ · v,
2 ∂xi ∂xi
que en el caso del campo de velocidad del sólido rígido se anula.
Las componentes esenciales del tensor de vorticidad son la mitad del rotacional del campo
de velocidad con lo que en el caso del sólido nos conduce a que Vij = −²ijk ωk = Ωij .
Como las ecuaciones que denen todo campo vectorial son las que nos precisan cuanto valen
en cada punto y en cada instante su divergencia y su rotacional, junto con las condiciones de
contorno en un instante dado, para un campo de velocidad general tendremos:
div v = ∇ · v = Dii (x, t) = Yii ,
(rot v)i = ²ijk Ykj = ²ijk (Dkj + Vkj ) = ²ijk Vkj .
Al ser Dij simétrico, una vez diagonalizado es en la diagonal, y por lo tanto en su traza, donde
se encuentran las fuentes del campo. Las fuentes del campo están relacionadas con la traza, y
por lo tanto con la parte simétrica, del tensor gradiente de velocidad. Los torbellinos del campo
lo están donde la vorticidad sea distinta de cero, esto es, en la parte antisimétrica del mismo
tensor gradiente de velocidad Yij .
1.1 Compárense las ecuaciones del campo de velocidad de un sólido rígido con
las ecuaciones de Maxwell del electromagnetismo en el caso estático
Ejercicio
div E = ρ/²0 ,
rot E = 0,
div B = 0,
rot B = µ0 j.
¾Qué magnitud física juega el papel de la ω ?
1.6.
Derivada material
Una magnitud física B en un punto r de un medio continuo y en el instante t puede cambiar
con el tiempo y en el instante t + dt tomar un valor distinto. Esto puede ser debido a dos
motivos: Uno es que simplemente la propiedad en dicho punto cambia de valor con el tiempo, y
otro que el punto r en el que está denida se mueve y por lo tanto lo que llamamos punto jo
r con respecto a un sistema de referencia prejado está ocupado en el instante t + dt por otra
partícula del sistema físico. De esta manera
dB
∂B(x, y, z, t) ∂B(x, y, z, t) dx ∂B(x, y, z, t) dy ∂B(x, y, z, t) dz
∂B
=
+
+
+
=
+ v · ∇B.
dt
∂t
∂x
dt
∂y
dt
∂z
dt
∂t
(1.6)
a la primera parte se le conoce como el cambio temporal de la magnitud y a la segunda el
cambio convectivo debido a la convección, es decir al desplazamiento material del sistema.
La anterior relación (1.6) se dice que es la derivada material con respecto al tiempo de la
magnitud B , ya que se ha tenido en cuenta el cambio material del punto.
1.6.1.
Campo de aceleración
En particular, el campo de aceleración en cada punto X se denirá como el campo vectorial
A(X, t) =
d2 x
∂2f
= 2 (X, t)
2
dt
∂t
1.6. DERIVADA MATERIAL
19
en la descripción Lagrangiana en tanto que en la descripción Euleriana
a(x, t) ≡
dv
∂v
=
(x, t) + (v · ∇) v.
dt
∂t
Los campos de aceleración son interesantes puesto que ligados a ellos tendremos las fuerzas
que se realizan entre las diferentes partes del sistema, y las leyes de la dinámica Newtoniana
lo que establecen es la relación entre las fuerzas externas y las aceleraciones de cada elemento
innitesimal de materia. Como vemos se componen de dos partes, una lineal en la velocidad
del medio y otra cuadrática, y por lo tanto también lineal y cuadrática en los desplazamientos,
respectivamente. Es esta segunda parte la que va a hacer que las ecuaciones de evolución de
un medio continuo no sean lineales en los desplazamientos y por lo tanto con esta parte están
ligados los fenómenos dinámicos del caos determinista.
1.6.2. Variación temporal del elemento de línea, supercie y volumen
Un elemento de línea dxi es una magnitud vectorial. En sentido estricto es una magnitud
vectorial covariante, también llamada 1-forma, cuyo cambio temporal viene dado por (1.5)
∂vi
d(dxi )
=
dxj .
dt
∂xj
(1.7)
Un elemento de supercie es una magnitud bivectorial orientada que en el sentido tensorial es
una 2-forma lineal antisimétrica. Existen 3 elementos de supercie diferentes
dS12 = dx1 dx2 ,
dS23 = dx2 dx3 ,
dS31 = dx3 dx1 ,
que en rigor matemático habría que representar mediante la notación
dS12 = dx1 ∧ dx2 = −dS21 ,
dS23 = dx2 ∧ dx3 = −dS32 ,
dS31 = dx3 ∧ dx1 = −dS13 ,
es decir
dSij = dxi ∧ dxj = −dSji ,
para recalcar que necesariamente i 6= j . El símbolo ∧, que a veces se utiliza para designar el
producto vectorial, representa el símbolo del producto exterior de dos magnitudes vectoriales,
que es cero cuando éstas son colineales. De esta forma la variación temporal de un elemento de
supercie será:
∂vj
d(dSij )
∂vi
=
dxl ∧ dxj + dxi ∧
dxr .
dt
∂xl
∂xr
donde necesariamente en el primer término l 6= j y en el segundo i 6= r. En la práctica se
dene un elemento de supercie orientada como si fuera un vector de tamaño dS y orientado
mediante el vector unidad ni , perpendicular a la misma, dSi = dS ni . Este elemento `vectorial'
de supercie está denido en términos de dSij mediante:
²ijk dSk = dSij ,
1
dSi = ²ijk dSjk ,
2
dS1 ≡ dS23 ,
dS2 ≡ dS31 ,
dS3 ≡ dS12 .
Por eso el ujo de una magnitud vectorial ki (x, t) es en realidad
Z
Z
1
²ijk ki (x, t)dSjk
ki dSi =
2 Σ
Σ
De esta forma, por ejemplo
d(dS12 )
∂v1
∂v1
∂v2
∂v2
=
dx1 ∧ dx2 +
dx3 ∧ dx2 + dx1 ∧
dx2 + dx1 ∧
dx3 ,
dt
∂x1
∂x3
∂x2
∂x3
20
CAPÍTULO 1. CINEMÁTICA
es decir
d(dS12 )
∂v1
∂v1
∂v2
∂v2
=
dS12 −
dS23 +
dS12 −
dS31 .
dt
∂x1
∂x3
∂x2
∂x3
que en términos del elemento dS3 ≡ dS12 , resulta:
∂v1
∂v1
∂v2
∂v2
d(dS3 )
=
dS3 −
dS1 +
dS3 −
dS2 .
dt
∂x1
∂x3
∂x2
∂x3
Si a esta expresión le sumamos y restamos la magnitud
±
∂v3
dS3 ,
∂x3
la anterior expresión la podemos poner:
d(dS3 )
= vi,i dS3 − vi,3 dSi ,
dt
y en general
d(dSk )
= vi,i dSk − vi,k dSi .
(1.8)
dt
El elemento de volumen es un trivector o bien la 3-forma completamente antisimétrica
dV123 = dx1 ∧ dx2 ∧ dx3 ≡ dV , que por abuso de lenguaje solemos representar por dx1 dx2 dx3 ,
sobreentendiéndose que los diferentes dxi no son colineales. Por eso su derivada temporal
∂v1
∂v2
∂v3
d(dV )
=
dx1 ∧ dx2 ∧ dx3 + dx1 ∧
dx2 ∧ dx3 + dx1 ∧ dx2 ∧
dx3 = vi,i dV.
dt
∂x1
∂x2
∂x3
(1.9)
Resumiendo
d(dxi )
= vi,j dxj ,
dt
1.6.3.
d(dSk )
= vi,i dSk − vi,k dSi ,
dt
d(dV )
= vi,i dV.
dt
Transformación del elemento de línea, supercie y volumen
Bajo un cambio de coordenadas x0i = fi (xj ), el elemento de línea (también llamado elemento
de arco) transforma de acuerdo con
dx0i =
∂x0i
dxj = Fij dxj ,
∂xj
siendo Fij la matriz Jacobiana de la transformación. Por lo tanto el elemento de volumen
dV 0 = dx01 ∧ dx02 ∧ dx03 transformará
dV 0 =
∂x01
∂x0
∂x0
dxi ∧ 2 dxj ∧ 3 dxk ,
∂xi
∂xj
∂xj
pero en el segundo miembro debido al símbolo ∧, solamente los términos con los tres i, j, k
diferentes sobreviven. Si lo desarrollamos resulta:
dV 0 =
∂x01
∂x0
∂x0
∂x0
∂x0
∂x0
∂x0
∂x0
∂x0
dx1 ∧ 2 dx2 ∧ 3 dx3 + 1 dx1 ∧ 2 dx3 ∧ 3 dx2 + 1 dx2 ∧ 2 dx1 ∧ 3 dx3 +
∂x1
∂x2
∂x3
∂x1
∂x3
∂x2
∂x2
∂x1
∂x3
∂x0
∂x0
∂x0
∂x0
∂x0
∂x0
∂x0
∂x0
∂x01
dx2 ∧ 2 dx3 ∧ 3 dx1 + 1 dx3 ∧ 2 dx1 ∧ 2 dx2 + 1 dx3 ∧ 2 dx2 ∧ 2 dx1 =
∂x2
∂x3
∂x1
∂x3
∂x1
∂x2
∂x3
∂x2
∂x1
1.6. DERIVADA MATERIAL
21
= (det F )dx1 ∧ dx2 ∧ dx3 = (det F )dV ≡ J dV,
debido a que dx1 ∧ dx3 ∧ dx2 = −dx1 ∧ dx2 ∧ dx3 , y lo mismo para los demás términos, que
permutando sus elementos y teniendo presente el correspondiente cambio de signo se llevan a
la forma dx1 ∧ dx2 ∧ dx3 . El elemento de volumen transforma con un factor global que es el
determinante de la matriz Jacobiana. Si nos restringimos a rotaciones como det Rij = 1, el
elemento de volumen no cambia. Si existieran inversiones, entonces habría un cambio de signo
dV 0 = −dV .
Para el elemento de supercie sucede lo siguiente:
0
dS12
= dx01 ∧ dx02 =
∂x01
∂x0
∂x0
∂x0
∂x0
∂x0
dx1 ∧ 2 dx2 + 1 dx1 ∧ 2 dx3 + 1 dx2 ∧ 2 dx1 +
∂x1
∂x2
∂x1
∂x3
∂x2
∂x1
∂x01
∂x0
∂x0
∂x0
∂x0
∂x0
dx2 ∧ 2 dx3 + 1 dx3 ∧ 2 dx1 + 1 dx3 ∧ 2 dx2 =
∂x2
∂x3
∂x
∂x1
∂x3
∂x
µ 0
¶
µ 0 3 0
¶
µ 20
¶
0
0
0
0
0
∂x1 ∂x2 ∂x1 ∂x2
∂x1 ∂x2 ∂x1 ∂x2
∂x1 ∂x02 ∂x01 ∂x02
−
dx2 ∧dx3 +
−
dx3 ∧dx1 +
−
dx1 ∧dx2
∂x2 ∂x3 ∂x3 ∂x2
∂x3 ∂x1 ∂x1 ∂x3
∂x1 ∂x2 ∂x2 ∂x1
que resulta ser una combinación lineal de dS23 , dS31 y dS12 y donde los coecientes son menores
de la matriz Jacobiana, y que responde a la ley general de transformación de un tensor covariante
de dos índices
∂x0j ∂x0k
0
dSpq .
dSjk
=
∂xp ∂xq
En términos del elemento `vectorial' de supercie dSi esta ley de transformación es
dSi0 = [J]ij dSj ,
siendo [J]ij el correspondiente adjunto del elemento Fij de la matriz Jacobiana.
Resumiendo:
dx0i =
∂x0i
dxj ,
∂xj
dSi0 = [J]ij dSj ,
0
dSjk
=
∂x0j ∂x0k
dSpq ,
∂xp ∂xq
dV 0 = JdV,
0
dV123
=
∂x01 ∂x02 ∂x03
dVijk .
∂xi ∂xj ∂xk
1.6.4. Derivada material de integrales curvilíneas
Hemos visto cómo se deriva una magnitud asociada a un punto del sistema cuando este
punto se mueve. Si lo que tenemos son propiedades físicas de tipo global, asociadas al sistema
como un todo o bien a una parte del mismo, que en general las podremos representar como
integrales de ciertas densidades extendidas a regiones volúmicas, superciales o lineales, vamos
a ver cómo cambian con el tiempo dichas magnitudes globales. Sea K(t) esa propiedad global
que se expresa como una integral a lo largo de una curva C(t)
Z
K(t) =
ki (x, t) dxi
C(t)
En este caso el elemento de línea dxi (o bien la curva respecto de la que se integra C(t)) es
también función del tiempo y su derivada temporal viene dada de acuerdo con (1.5)
d(dxi )
∂vi
=
dxj ,
dt
∂xj
con lo que si tenemos la magnitud expresada como una integral de línea a lo largo de la curva
su derivada temporal queda
µ
¶
Z
∂kj (x, t) ∂kj (x, t)
dK(t)
∂vi
=
+
vk + ki (x, t)
dxj .
dt
∂t
∂xk
∂xj
C(t)
22
CAPÍTULO 1. CINEMÁTICA
1.6.5.
Derivada material de integrales de supercie
Si Σ(t) es una región supercial del sistema material y la magnitud global K(t) viene expresada como una integral de supercie
Z
Z
K(t) =
k(x, t) · ndS =
ki (x, t)dSi ,
Σ(t)
Σ(t)
entonces, teniendo presente (1.8), ya que el elemento de supercie cambia con el tiempo
dK(t)
=
dt
µ
Z
Σ(t)
∂vj
∂vi
∂ki (x, t)
∂ki
v j + ki
− kj
+
∂t
∂xj
∂xj
∂xj
¶
dSi
que se puede condensar en
dK(t)
=
dt
1.6.6.
µ
Z
Σ(t)
∂ki (x, t) ∂(ki vj )
∂vi
− kj
+
∂t
∂xj
∂xj
¶
dSi .
Derivada material de integrales de volumen
Sea K(t) esa propiedad global que se expresa en forma de una densidad volúmica
Z
K(t) =
k(x, t) dV
R(t)
donde R(t) representa una cierta región volúmica del sistema en el instante t y dV ≡ dx1 dx2 dx3
es el elemento de volumen. Es claro que K(t) puede cambiar en el tiempo porque su densidad
k(x, t) cambie con el tiempo y además porque la región de integración R(t) puede cambiar con
el tiempo. Esto se traduce que en la integral anterior, el elemento de volumen se sobreentiende
que cambia con el tiempo. El resultado, teniendo presente que la derivada temporal del elemento
de volumen viene dada por (1.9), es
dK(t)
=
dt
Z
R(t)
µ
∂k(x, t) ∂[k(x, t)vi (x, t)]
+
∂t
∂xi
¶
dV
o bien, usando el teorema de Gauss
dK(t)
=
dt
Z
R(t)
∂k(x, t)
dV +
∂t
Z
k(x, t)v · n dS
∂R(t)
siendo ∂R la supercie (o borde) exterior de la región R, n un vector unidad normal a la
supercie y dirigido hacia el exterior y dS el valor del elemento de supercie.
1.7.
Teoremas integrales
Cuando tenemos una integral extendida a un circuito cerrado C , el cual es el contorno de
una supercie, o bien tenemos una integral de supercie extendida a una supercie cerrada S
que engloba a un cierto volumen, la correspondiente integral se puede convertir en otra de un
orden superior. Lo que se hace es tomar la diferencial (exterior) del integrando y luego volverla
a integrar. Estos teoremas integrales son conocidos como el teorema de Stokes y el teorema de
Gauss, respectivamente.
1.7. TEOREMAS INTEGRALES
23
1.7.1. Teorema de Stokes
Si tenemos una integral curvilínea en R3 a lo largo de una curva cerrada C , de un cierto
campo vectorial v(r),
I
I
v · dr ≡
vx dx + vy dy + vz dz,
C
C
por una parte procedemos a hacer la diferencial del integrando y luego integramos esa diferencial,
es decir
¶
µ
¶
Z Z µ
∂vy
∂vy
∂vy
∂vx
∂vx
∂vx
dx +
dy +
dz ∧ dx +
dx +
dy +
dz ∧ dy+
∂x
∂y
∂z
∂x
∂y
∂z
µ
¶
∂vz
∂vz
∂vz
dx +
dy +
dz ∧ dz,
∂x
∂y
∂z
donde hemos intercalado el signo ∧ para indicar que lo que hacemos es el producto `exterior' de
la diferencial con la diferencial de arco. Por lo tanto, el resultado, teniendo en cuenta el carácter
antisimétrico dx ∧ dy = −dy ∧ dx, etc., nos queda
¶
µ
¶
µ
¶
µ
Z Z
Z Z
∂vy
∂vy
∂vx ∂vz
∂vx
∂vz
−
dy∧dz+
−
dz∧dx+
−
dx∧dy =
rotv·dS
∂y
∂z
∂z
∂x
∂x
∂y
S(C)
S(C)
La circulación de un campo vectorial a lo largo de una curva cerrada C , es igual al ujo de su
rotacional a través de la supercie cuyo contorno es C .
1.7.2. Teorema de Gauss
Si lo que tenemos es el ujo de un campo vectorial a través de una supercie cerrada S ,
podemos hacer lo mismo:
I
I
v · dS =
vx dy ∧ dz + vy dz ∧ dx + vz dx ∧ dy.
S
S
Al tomar la diferencial, resulta
µ
¶
µ
¶
Z
∂vy
∂vy
∂vy
∂vx
∂vx
∂vx
dx +
dy +
dz ∧ dy ∧ dz +
dx +
dy +
dz ∧ dz ∧ dx+
∂x
∂y
∂z
∂x
∂y
∂z
V (S)
µ
∂vz
∂vz
∂vz
dx +
dy +
dz
∂x
∂y
∂z
¶
∧ dx ∧ dy
que nos produce
Z
V (S)
µ
∂vx ∂vy
∂vz
+
+
∂x
∂y
∂z
¶
Z
dx ∧ dy ∧ dz =
∇ · vdV
V (S)
El ujo saliente de un campo vectorial a través de una supercie cerrada S , es igual a la integral
de volumen de su divergencia, extendida al volumen encerrado por S .
24
CAPÍTULO 1. CINEMÁTICA
Problemas
1.1 Demostrar que el tensor antisimétrico ²ijk satisface la identidad
²ipq ²jrs
¯
¯ δij
¯
= ¯¯ δir
¯ δis
δpj
δpr
δps
¯
δqj ¯¯
δqr ¯¯
δqs ¯
¾A qué se reduce si los índices i = j ?
1.2 Vericar, usando las propiedades del tensor ²ijk , que el producto vectorial
a × (b × c) = b(a · c) − c(a · b).
1.3 Vericar que los tensores δij y ²ijk son invariantes bajo los cambios de coordenadas.
1.4 Si tenemos una matriz simétrica Dij , demostrar que su ecuación característica (la que dene
sus valores propios) se puede escribir como
λ3 − ID λ2 + IID λ − IIID = 0,
donde los tres coecientes ID , IID y IIID son propiedades invariantes de la matriz y por lo
tanto son independientes de la base en que está representada la matriz. Determinar la expresión
general de estos tres invariantes en términos de las componentes matriciales Dij , en cualquier
base.¾Qué podemos decir si Dij no es simétrica?
1.5 ¾Cómo son los invariantes de una matriz de rotación?
1.6 La descripción Lagrangiana de una deformación está dada por
x1 = X1 + X3 (a2 − 1),
x2 = X2 + X3 (a2 − a−2 ),
x3 = a2 X3 ,
donde a es una constante. Probar que el Jacobiano de la transformación J no se anula y
permite invertir la transformación, lo que da lugar a las ecuaciones Eulerianas que describen
esta deformación.
1.7 Sea el campo de desplazamientos u = X1 X32 e1 + X12 X2 e2 + X22 X3 e3 . Hallar independientemente el gradiente de deformación material F y el gradiente de desplazamiento material U .
¾Cómo es el tensor de deformaciones?
1.8 Un medio continuo sufre un desplazamiento dado por u = (3X2 − 4X3 )e1 + (2X1 −
X3 )e2 + (4X2 − X1 )e3 . Hallar en la posición desplazada el vector que unía los puntos A(1, 0, 3)
y B(3, 6, 6). Hallar el vector de posición desplazada del punto C(2, 6, 3).
1.9 Una deformación se dice que es homogénea si el campo de desplazamientos es lineal en
las coordenadas, ui = Aij Xj , donde las Aij son constantes o a lo sumo solamente funciones de
t pero no de las Xk . Probar que en este tipo de deformaciones las secciones planas del material
permanecen planas y que las rectas permanecen rectas.
1.10 Un medio continuo extenso y en régimen bidimensional evoluciona de tal manera que el
campo de velocidad en un punto de coordenadas (x, y) viene dado por:
v(x, y, t) = −ωye1 + (a0 t + ωx)e2 ,
1.7. TEOREMAS INTEGRALES
25
con a0 y ω constantes. Se pide:
(a) ¾Puede dicho sistema ser considerado como un uido en régimen incompresible?
(b) ¾Es el régimen estacionario?
(c) ¾Es el régimen irrotacional?
(d) Encontrar las líneas de corriente.
(e) Determinar la trayectoria de un punto de coordenadas iniciales (X, Y, 0).[Examen Junio
2005]
1.11 Para el desplazamiento de un medio continuo dado por
x1 = X1 ,
x2 = X2 ,
√
x3 = X3 + 2X2 / 3
se pide:
(a) ¾Es un desplazamiento cortante?
(b) Calcular la dirección del elemento de línea en el plano X2 X3 para el cual la deformación
normal es nula.
(c) ¾Cuánto vale la deformación tangencial en esas direcciones?
(d) Hallar la ecuación de la elipse en la que se deforma el círculo X22 + X32 = 1.
1.12 Si un cuerpo sufre un desplazamiento rígido, esto es
xi = Rij (t)Xj + si (t),
donde Rij (t) es una rotación arbitraria función del tiempo y si (t) un desplazamiento arbitrario
solamente función del tiempo, demostrar que el tensor de deformaciones y el tensor de velocidad
de deformación son nulos. Al conjunto de trayectorias seguidas por los puntos materiales se le
da el nombre de congruencia rígida.
1.13 Dado el campo de desplazamientos
x1 = X1 + 2X3 ,
x2 = X2 − 2X3 ,
x3 = X3 − 2X1 + 2X2 ,
hallar los tensores de deformaciones nitas Lagrangiano y Euleriano L y E . Encontrar la forma
principal y direcciones principales de los dos tensores anteriores. ¾Qué tipo de deformaciones se
dan en las direcciones principales?
1.14 El tensor de deformaciones de un punto está dado por
√ 
1
−3
√2

Eij = √
−3
1
− 2.
√
2 − 2
4

√
Hallar la deformación normal en la√dirección ν = e1 /2−e2 /2+e3 / 2 y la deformación cortante
∗ , teniendo en cuenta
entre ν y µ = −e1 /2 + e2 /2 + e3 / 2. Hallar la forma principal de Eij , Eij
que tanto ν como µ son direcciones principales. Calcular los tres invariantes de deformación
∗ . Calcular el tensor desviador E
usando tanto Eij como Eij
d ij y sus valores principales.
1.15 Demostrar que la derivada temporal del Jacobiano se reduce a
dJ
= J ∇ · v.
dt
1.16 Un campo de velocidad está dado por v = x21 te1 + x2 t2 e2 + x1 x3 te3 . Determinar la
velocidad y aceleración de una partícula que se encuentra en el punto P (1, 3, 2) en el instante
t = 1. Determinar las líneas de corriente en el instante t = 1, las líneas de emisión y las
trayectorias de los puntos de este sistema. ¾Las líneas de corriente son las mismas en el instante
t = 2? Expresar el campo de velocidad en la descripción Lagrangiana.
26
CAPÍTULO 1. CINEMÁTICA
1.17 Determinar las líneas de corriente producidas en un campo de velocidad dado por
v = −Ωye1 + Ωxe2 + w0 e3 ,
con Ω y w0 constantes.
1.18 En un régimen bidimensional de un uido, la evolución de un punto de coordenadas
iniciales (X, Y ) es
x(t) = Xekt ,
y(t) = Y e−kt .
Determinar la trayectoria de una partícula del uido. Encontrar las componentes de su velocidad
y las líneas de corriente.
1.19 Probar que el campo de aceleración a se puede escribir como
∂v
1
+ q × v + ∇v 2 ,
∂t
2
el vector torbellino (el rotacional del campo de velocidad).
a=
siendo qi = ²ijk Vkj
1.20 Calcular que el rotacional del campo de aceleración se puede poner como
∇×a=
dq
+ q(∇ · v) − (q · ∇)v,
dt
en términos del vector torbellino q .
1.21 Un campo de velocidad está dado por v = x1 /(1 + t)e1 + 2x2 /(1 + t)e2 + 3x3 /(1 +
t)e3 . Calcular el campo de aceleración de este sistema material. Integrar las ecuaciones de
velocidad para obtener las ecuaciones de desplazamiento xi (X, t) y a partir de éstas estimar las
componentes de la aceleración en la formulación Lagrangiana. Determinar las líneas de corriente,
de emisión y las trayectorias de los puntos de este sistema.
1.22 Un cierto ujo está dado por v = a(x1 x2 − x23 )e−bt e2 + a(x22 − x1 x3 )e−bt e3 donde a y b
son constantes. Estimar el gradiente de velocidad ∂vi /∂xj en este movimiento y de él calcular el
tensor de velocidad de deformación D y el tensor de giro o vorticidad V para el punto P (1, 0, 3)
cuando t = 0.
1.23 Probar que para el campo de velocidad v = (ax3 − bx2 )e1 + (bx1 − cx3 )e2 + (cx2 − ax1 )e3
las líneas de vorticidad o torbellino son líneas rectas. Determinar sus ecuaciones. Demostrar que
el campo representa la rotación de un medio rígido, probando que D = 0.
1.24 Dado el campo de velocidad estacionario
v1 = x21 x2 + x32 ,
v2 = −x31 − x1 x22 ,
v3 = 0,
hallar los valores principales del tensor de velocidad de deformación Dij y de la vorticidad Vij ,
en cualquier punto.
1.25 Encontrar que el tensor de deformaciones linearizado eij se escribe en coordenadas polares
esféricas en la forma:
∂ur
1 ∂uθ
ur
1 ∂uφ uθ
ur
err =
, eθθ =
+ , eφφ =
+
cot θ + ,
∂r
r ∂θ
r
r sin θ ∂φ
r
r
µ
¶
1 ∂uθ
∂uθ
uθ
1 ∂ur
1 ∂uφ
− uφ cot θ +
, 2erθ =
−
+
2eθφ =
r ∂θ
r sin θ ∂φ
∂r
r
r ∂θ
∂uφ uφ
1 ∂ur
+
−
.
2eφr =
r sin θ ∂φ
∂r
r
¾Cómo se escribe en coordenadas cilíndricas?
1.7. TEOREMAS INTEGRALES
27
1.26 Un campo de velocidad estacionario está dado por v = 2x3 e1 + 2x3 e2 . Hallar los valores
y las direcciones principales (velocidades de extensión) del tensor de velocidad de deformación
para este movimiento.
1.27 Un campo de velocidad en una descripción Lagrangiana está dado por v = −X2 e−t e1 −
X3 e2 + 2te3 . Hallar las trayectorias, las líneas de emisión y las componentes de la aceleración
en la descripción Euleriana.
1.28 Sea R(α(t)) la rotación activa que en el instante t nos rota los ejes del laboratorio y
nos los lleva a coincidencia con los ejes principales de un sólido rígido. De esta manera, la
cinemática del sólido rígido queda descrita por el conocimiento de la función del tiempo α(t).
Por lo tanto, un punto cualquiera del sólido, que en el instante inicial se encuentra en r(0),
en el instante t se encontrará en r(t) = R(α(t))r(0). Encontrar que la velocidad de dicho
punto viene dada por ṙ(t) = ω(t) × r(t) y expresar el vector velocidad angular instantánea
en términos de los parámetros α(t) y de sus primeras derivadas. ¾Cómo es la expresión de la
velocidad angular si utilizamos la parametrización ρ = u tan(α/2)? ¾Cuál es la expresión, en
ambas parametrizaciones, de la velocidad angular referida al sistema de referencia del sólido
rígido? [Sugerencia: R(α(t + dt)) = R(ω(t)dt)R(α(t)).]
1.29 Se ha encontrado en el ejercicio anterior la forma explícita en que la velocidad angular
depende de las variables que caracterizan a la orientación y de sus primeras derivadas. Si en
un sistema Lagrangiano la dependencia de la Lagrangiana de la orientación del cuerpo lo es
solamente a través de su dependencia de la velocidad angular, L(. . . , ω, . . .), encontrar la forma
general de las ecuaciones dinámicas que se obtienen aplicando el principio variacional a las
variables de orientación. Hacer los cálculos en términos de varias parametrizaciones del grupo
de rotaciones. Y si la lagrangiana la expresamos en términos de la velocidad angular w medida
en el sistema de referencia ligado al cuerpo? [Sol. Si llamamos Si = ∂L/∂ωi , Ṡ = ω × S . Si
hacemos Wi = ∂L/∂wi , Ẇ = W × w.]
28
CAPÍTULO 1. CINEMÁTICA
Capítulo 2
Tensiones
2.1. Campo de densidad
Es un campo escalar. Si consideramos un cierto elemento de volumen dV = dxdydz alrededor
de un punto r y en el instante t, el campo de densidad ρ(r, t) es aquella función continua de r
y de t tal que en cada punto ρ(r, t)dV = dm representa el valor de la masa del sistema en ese
elemento de volumen.
2.2. Campo de tensiones
Un material sólido o líquido, un medio continuo en general, en el que los distintos componentes interaccionan entre sí deberemos conocer cuál es la fuerza que una parte del sistema hace
sobre otra en los distintos puntos del mismo. Para ello es necesario denir cuál es el sistema
sobre el cual vamos a considerar la fuerza que hace el resto del material, que se considera como
el exterior al sistema.
Pueden existir dos tipos de fuerza: Una fuerza de tipo volúmico que actúa sobre cada elemento de volumen que también recibe el nombre de fuerza másica (como la gravitatoria y
electromagnética) y otro tipo de fuerza que actúa sobre cada elemento de supercie, bien sobre
la supercie exterior de la frontera del medio continuo, bien sobre cada elemento de supercie
de una parte del sistema por parte de otra como fuerza de contacto.
Supongamos pues una pequeña porción del medio continuo y jémonos en su supercie
exterior. Cada elemento de supercie de valor dS tiene una orientación caracterizada por un
vector unidad n perpendicular al plano tangente en ese punto. A veces solemos representar dicho
elemento de supercie por el vector dS = ndS . Queda claro lo que se entiende por exterior al
elemento de supercie ya que la orientación n la interpretamos siempre en la dirección normal
hacia el exterior. La fuerza de contacto que la materia exterior hace sobre este elemento de
supercie dependerá tanto de la extensión dS como de la orientación n. El Principio de tensión
de Cauchy establece que en el límite cuando dS → 0 en un punto r , existe una fuerza resultante
denida por unidad de área en dicho punto que solamente depende del punto y de la orientación,
y que el momento de las fuerzas sobre el elemento dS respecto del punto es cero, en ese límite.
Debemos por lo tanto denir en cada punto r de un medio continuo (y en cada instante t
en el caso de una evolución dinámica), una fuerza por unidad de área f (r, n) para cada posible
valor de la orientación n. De esa manera, sobre cada elemento de supercie de valor dS y
orientación n se ejercerá por parte de la materia exterior una fuerza de valor dF = f (r, n)dS .
Aunque la expresión general de f (r, n) pudiera parecer muy complicada, pues cada una de
sus tres componentes depende de seis variables xi y nj , i, j = 1, 2, 3, sin embargo la dependencia
29
30
CAPÍTULO 2. TENSIONES
de la orientación es simple: es una dependencia lineal.
fi (r, n) = σij (r)nj .
(2.1)
La razón es que si la fuerza supercial total sobre un elemento de volumen se reduce a Fi dV , el
valor de su integral extendido a cualquier volumen se reducirá a una integral sobre la supercie
exterior de este volumen debido al Principio de acción y reacción, y por el teorema de Gauss, esa
integral de volumen será la de la divergencia de un campo Fi (r) = ∂σij /∂xj , con lo que
Z
Z
Z
Z
∂σij
Fi dV =
dV =
σij dSj =
σij nj dS,
V
V ∂xj
S(V )
S(V )
y sobre cada elemento de supercie la fuerza por unidad de área es fi = σij (r)nj (r).
A las 9 funciones (luego veremos que solo 6 son independendientes) σij (r) se les conoce con el
nombre de componentes del tensor de tensiones σ en el punto r . El conocimiento de esas
9 funciones en cada punto, junto con (2.1), nos sirve para calcular en cada punto de un medio
continuo la fuerza que una parte del sistema ejerce sobre otra. Tenemos así denido sobre el
sistema material el campo tensorial de tensiones.
La expresión (2.1) también admite la representación matricial
  
 
f1
σ11 σ12 σ13
n1
 f2  =  σ21 σ22 σ23   n2 
f3
σ31 σ32 σ33
n3
Si denominamos por ei al vector unidad en la dirección xi y por σ queremos representar
el tensor de tensiones en forma matricial, resulta que las componentes del tensor se pueden
calcular, mediante
σji = eTj · σ · ei .
Esto nos servirá para calcular las componentes del tensor de tensiones en cualquier otro sistema
de referencia ortogonal, como es el caso de usar coordenadas esféricas o cilíndricas. En efecto,
si hacemos un cambio de base, e0i = Rij ej , siendo Rij la matriz de rotación de cambio de base,
entonces
0
0
σji
= ejT · σ · e0i = Rjk eTk · σ · Ril el = Rjk Ril σkl ,
que es la forma de transformar de un tensor.
2.3.
Tracción, compresión y cortadura
Hemos visto que la fuerza por unidad de área f es un vector, que con respecto a la orientación
n del elemento de supercie dS puede tener una componente en la dirección de n o componente
normal y otra perpendicular a n o componente tangencial al elemento de supercie. Si la
componente normal está dirigida en el sentido del vector n entonces se dice que el exterior
estira al material hacia fuera. Se dice que en ese punto y respecto de esa orientación el material
está sometido a tracción. Si la orientación es la contraria entonces el exterior empuja y se
dice que está sometido a compresión. Respecto a la componente tangencial, el exterior está
tratando de deslizar tangencialmente al material, como cortándolo en el sentido de su supercie.
A esa componente se le denomina fuerza de cortadura o cizalladura.
Ejemplo
el tensor
2.1 Supongamos que el estado de tensiones en un punto lo caracterizamos por

2
σ = 1
0

1 0
−1 0 
0 0
2.4. EQUILIBRIO ESTÁTICO. SIMETRÍA DEL TENSOR DE TENSIONES
31
Si queremos saber qué fuerza se ejerce en ese punto sobre un elemento de supercie de valor
dS , deberemos conocer primero cómo está orientado ese elemento de supercie. Supongamos
que el elemento de supercie está orientado perpendicularmente al eje OX . Entonces ese
elemento de supercie viene caracterizado por el vector dS = dSex . La fuerza que se hace
sobre ese elemento es

 
 
2 1 0
1
2
df = σdS =  1 −1 0   0  dS =  1  dS,
0 0 0
0
0
que vemos tiene una componente de intensidad 2 a lo largo de OX , que la denominamos
componente normal y otra en la dirección perpendicular OY y de intensidad 1 que recibe
el nombre de componente tangencial o de cortadura. La componente normal es positiva, lo
que nos indica, con nuestro convenio de signos, que es una fuerza de tracción, es decir, se
está estirando de la supercie.
Si, por otra parte consideramos que el elemento de supercie está orientado perpendicularmente al eje OY , entonces:

 


2 1 0
0
1
df = σdS =  1 −1 0   1  dS =  −1  dS.
0 0 0
0
0
Existe una fuerza normal de valor −1, en la dirección de OY , que resulta ser de compresión,
por tener sentido contrario al eje ey , y una fuerza de cortadura, hacia la dirección positiva
del eje OX , de valor 1.
En el caso de que dS estuviera orientada perpendicularmente a OZ , la fuerza sobre este
elemento sería nula.
2.4. Equilibrio estático. Simetría del tensor de tensiones
Si cada elemento de volumen dV está en equilibrio, las ecuaciones fundamentales de la
dinámica establecen que la suma de las fuerzas exteriores y los momentos de la fuerzas exteriores
respecto de un punto cualquiera deben ser cero.
Sea V un volumen arbitrario. La suma de fuerzas externas sobre él es
Z
Z
ρkdV +
f dS.
V
S(V)
siendo k la fuerza externa por unidad de masa (si se trata únicamente del campo gravitatorio
como en muchos ejemplos, tomaremos k = g ). Como fi dS = σij nj dS , la última integral extendida a la supercie cerrada S(V) es en realidad el ujo exterior del campo σij , por lo que
el teorema de Gauss nos permite transformarla en una integral extendida al volumen V , de la
divergencia del campo. Así, la componente i de la fuerza total que actúa sobre el volumen V se
escribe:
¶
Z µ
∂σij
ρki +
dV = 0.
∂xj
V
Como el volumen de integración es arbitrario, ya que la condición anterior se verica para todo
V , entonces, en cada punto de un medio continuo se debe satisfacer
ρki +
∂σij
= 0.
∂xj
(2.2)
Son las ecuaciones de equilibrio que satisfacen el tensor de tensiones σ , el campo de densidad
ρ y el campo exterior másico k. Cuando el sistema no sea estático, y exista por lo tanto una
evolución, el segundo miembro de la ecuación (2.2) ya no será cero, sino que dependerá de la
32
CAPÍTULO 2. TENSIONES
masa por unidad de volumen y de la aceleración del medio, de acuerdo con la segunda ley de
Newton.
Los momentos de las fuerzas externas respecto del origen de coordenadas son
Z
Z
ρr × kdV +
r × f dS.
V
S(V)
Si usamos (2.2)
∂σlk
∂xk
La componente i de la segunda integral, como ²ijk xj fk = ²ijk xj σkl nl , se expresa como un ujo
y usando el teorema de Gauss nos lleva a
Z
Z
∂σlk
∂
−²ijl xj
dV +
(²ijk xj σkl ) dV = 0.
∂xk
V
V ∂xl
ρ(r × k)i = ρ²ijl xj kl = −²ijl xj
Nos resulta
Z
V
²ilk σkl dV = 0,
que como el volumen es arbitrario, se tiene ²ilk σkl = 0, es decir σkl = σlk y el tensor σ es
necesariamente simétrico.
Ejemplo 2.2 Consideremos un sólido con un estado de tensiones plano, en el que no hay
dependencia de la variable z . Analicemos un elemento de volumen de lados dx y dy y altura
unidad como el de la gura. Sobre la cara situada en x + dx la componente normal de la
fuerza por unidad de área es σ11 (x + dx) y la componente tangencial es la σ12 (x + dx)
dirigida hacia arriba. Si no existen fuerzas por unidad de volumen en la dirección x, kx = 0,
entonces, el balance de fuerzas en esa dirección implica que
σ11 (x + dx)dy − σ11 (x)dy − σ21 (y)dx + σ21 (y + dy)dx = 0,
σ11 (x + dx) = σ11 (x) +
El balance nos lleva a
pero por la simetría del tensor
por lo que se satisface (2.2).
µ
∂σ11
dx,
∂x
∂σ11
∂σ21
+
∂x
∂y
σ21 (y + dy) = σ21 (y) +
¶
dxdy = 0,
∂σ21
∂σ12
=
∂y
∂y
∂σ21
dy.
∂y
2.4. EQUILIBRIO ESTÁTICO. SIMETRÍA DEL TENSOR DE TENSIONES
33
2.4.1. Valor medio del tensor de tensiones
Supongamos un medio deformable que posee una supercie exterior S(V). Si en un punto
de la supercie exterior actúa una fuerza externa de valor F dS , la condición de equilibrio del
correspondiente elemento de supercie es que σij nj dS = Fi dS , en ese punto y en todos y cada
uno de los puntos en que existan fuerzas externas. Supongamos que no existen fuerzas másicas,
es decir ki = 0, por lo que multiplicando (2.2) por xk e integrando a todo el volumen del cuerpo
Z
Z
Z
∂(σij xk )
∂σij
∂xk
xk dV =
dV −
σij
dV = 0,
∂xj
∂xj
V
V
V ∂xj
es decir que como ∂xk /∂xj = δkj , y hay que sumar sobre el índice k , resulta
Z
Z
Z
∂(σij xk )
dV =
σij xk dSnj =
Fi xk dS,
σik V =
∂xj
V
S(V)
S(V)
siendo σik el valor medio de la correspondiente componente del tensor de tensiones en el interior
del volumen V . Como σij = σji , podemos poner el valor medio del tensor de tensiones σ̄
Z
1
σ̄ij =
(Fi xj + Fj xi ) dS
2V S(V)
como una integral extendida a la supercie exterior del cuerpo de la anterior expresión en la
que aparecen solamente las densidades superciales de las fuerzas exteriores que actúan sobre
la supercie.
2.4.2. Direcciones principales. Tensiones principales
El tensor de tensiones σ , considerado como matriz es una matriz real simétrica. Por lo tanto
posee tres valores propios reales y sus vectores propios correspondientes son ortogonales. A las
tres direcciones de sus vectores propios se les da el nombre de direcciones principales y a los
correspondientes valores propios el nombre de tensiones principales. Si tomamos como ejes
coordenados tres ejes paralelos a las direcciones principales en un punto, entonces en ese punto
el tensor de tensiones se escribe en la forma diagonal


σ(1)
0
0
σ= 0
σ(2)
0 ,
0
0
σ(3)
siendo σ(i) , i = 1, 2, 3 las tres tensiones principales. En esas direcciones el estado de tensión del
material en ese punto es solamente de tracción o compresión (según que la correspondiente σ(i)
sea positiva o negativa) ya que la fuerza por unidad de área tiene la misma dirección que el
correspondiente vector propio n(i) .
Vemos pues que para calcular el estado de tensiones en un punto de un medio continuo,
hay que medir solamente tres fuerzas en tres direcciones perpendiculares. Si los vectores unidad
de los ejes coordenados son e1 , e2 y e3 , entonces midiendo las fuerzas por unidad de área que
se ejercen sobre cada sección transversal a las direcciones dadas por los vectores anteriores, y
llamamos f 1 , f 2 y f 3 a las correspondientes fuerzas por unidad de área, el tensor de tensiones
se construye escribiendo por las (o por columnas, debido a la simetría del tensor) sus nueve
componentes:

 

f1 1 f2 1 f3 1
f1 1 f1 2 f1 3
σ =  f2 1 f2 2 f2 3  =  f1 2 f2 2 f3 2 
f1 3 f2 3 f3 3
f3 1 f3 2 f3 3
De alguna manera el tensor de tensiones σ es equivalente a la medida de tres vectores según
tres direcciones ortogonales, con la restricción de que fi j = fj i .
34
CAPÍTULO 2. TENSIONES
Ejemplo
2.3 Tensor de tensiones de una barra sometida a tracción
Sea una barra de sección transversal A y longitud l, como la de la gura, y en sus extremos
ejercemos sendas fuerzas F , que las suponemos uniformemente aplicadas sobre la sección.
Si consideramos ahora un elemento de ese material de sección ∆S , sobre él se ejercerá una
fuerza (F/A)∆S sobre cada extremo. Analicemos el estado de tensiones en el punto P . Si
cortamos este elemento por ese punto, mediante una sección perpendicular al eje OX , que
consideramos que es el eje de la barra, la fuerza que hace la barra suprimida es (F/A)∆S
y dirigida según OX . Si la proyectamos en las direcciones OY y OZ nos dará cero. Por
lo tanto la tensión en ese punto y según la sección considerada nos dene el vector de
componentes (F/A, 0, 0), y el tensor de tensiones en ese punto vale de momento


F/A 0 0
σij =  ∗
∗ ∗,
∗
∗ ∗
donde los ∗ representan entradas todavía sin evaluar. Para evaluarlas tendremos que colocar
en P dos elementos de supercie perpendiculares al eje OY y al OZ y medir las fuerzas que
se hacen en esa sección. Después, proyectarlas sobre los tres ejes, como en el caso anterior.
El resultado, si la única fuerza que actúa es F , es


F/A 0 0
σij =  0
0 0.
0
0 0
2.4.3.
Círculos de Mohr de las tensiones
Si las direcciones principales de cada punto son las únicas direcciones en las que el estado
de tensión es solamente de tracción o compresión pura, esto signica que en cualquier otra
dirección distinta de estas tres existen tensiones de cortadura.
Si en un punto de un medio continuo denimos un elemento de supercie jando su dirección
normal n, calculamos la fuerza por unidad de supercie mediante fi = σij nj . Denominamos
tensión normal al elemento de área, y lo representamos por σN , a la proyección de esta fuerza
por unidad de área en la dirección normal: σN = f · n = σij nj ni . Como |f |2 = (σij nj )(σik nk )
es el valor absoluto al cuadrado de la tensión en ese punto, entonces la componente tangencial
de la tensión, es decir la tensión de cortadura σT , se obtiene de
2
2
σT2 = |f |2 − σN
= (σij nj )(σik nk ) − σN
.
2.4. EQUILIBRIO ESTÁTICO. SIMETRÍA DEL TENSOR DE TENSIONES
35
Si el tensor de tensiones está referido a sus direcciones principales la expresión anterior toma la
forma:
2
2
2
σT2 = σ(1)
n21 + σ(2)
n22 + σ(3)
n23 − (σ(1) n21 + σ(2) n22 + σ(3) n23 )2 ≥ 0,
por lo que σT es en cada punto una función de las variables ni sometidas a la ligadura ni ni = 1.
Las direcciones en las que la cortadura es máxima o mínima se obtendrán de maximizar o
minimizar la función F = σT2 − λ(ni ni − 1), donde λ es un multiplicador de Lagrange. Haciendo
∂F/∂ni = 0 y ∂F/∂λ = 0, se obtienen las condiciones extremales de la σT .
Estas ecuaciones son:
¡ 2
¢
n1 σ(1)
− 2σ(1) (σ(1) n21 + σ(2) n22 + σ(3) n23 ) − λ = 0,
¢
¡ 2
n2 σ(2)
− 2σ(2) (σ(1) n21 + σ(2) n22 + σ(3) n23 ) − λ = 0,
¢
¡ 2
n3 σ(3) − 2σ(3) (σ(1) n21 + σ(2) n22 + σ(3) n23 ) − λ = 0,
n21 + n22 + n23 − 1 = 0.
Las tres ni no pueden ser nulas simultáneamente, ya que no se satisface la última ecuación. Un
conjunto de soluciones, en las que dos de las ni = 0 y la tercera es ±1, son las que corresponden
a las tres direcciones principales, y hacen mínima a σT , ya que en esas direcciones la σT = 0. Las
demás soluciones corresponderán a máximos de σT2 , ya que se trata de una función positiva. Si una
de las ni es nula y las otras dos no, por ejemplo n1 = 0 y n2 6= 0 y n3 6= 0, eliminando λ entre la
segunda y tercera de las ecuaciones se llega a:
2n22 σ(2) + 2n23 σ(3) = σ(3) − σ(2) ,
2n22 (σ(2) − σ(3) ) = σ(2) − σ(3) ,
→
n23 = 1 − n22 ,
n22 = 1/2,
n23 = 1/2.
Si las tres ni 6= 0 se llega a una contradicción ya que llamando A = σ(1) n21 + σ(2) n22 + σ(3) n23 y
eliminando λ entre la tres ecuaciones llegamos a σ(1) + σ(2) = σ(1) + σ(3) = σ(2) + σ(3) , es decir
σ(1) = σ(2) = σ(3) , que no es cierto en general y por lo tanto no hay solución.
Las direcciones y valores de los máximos de σT son:


0√
1
nI =  ±1/√2  , σTI = |σ(2) − σ(3) |,
2
±1/ 2
√ 

±1/ 2
1
nII =  0√  , σTII = |σ(3) − σ(1) |,
2
±1/ 2
√


±1/√2
1
nIII =  ±1/ 2  , σTIII = |σ(1) − σ(2) |.
2
0
Estas direcciones corresponden a los bisectores de cada par de direcciones principales. Si dos
tensiones principales son iguales entonces en el plano constituido por esas direcciones principales
no existe cortadura. Si las tres tensiones principales son iguales entonces no existe cortadura en
niguna dirección. Un ejemplo de esto es el de un uido sin viscosidad y en reposo, en el que el
tensor de tensiones σ = −pI siendo p la presión del uido en ese punto, como corresponde a un
medio continuo sometido a compresión en todos sus puntos.
Supongamos que ordenamos las tensiones principales σ(1) ≥ σ(2) ≥ σ(3) . En general, en una
dirección cualquiera n tenemos:
σN = σ(1) n12 + σ(2) n22 + σ(3) n23 ,
2
2
2
2
σN
+ σT2 = σ(1)
n21 + σ(2)
n22 + σ(3)
n23 ,
que juntamente con n21 + n22 + n23 = 1, nos permite despejar las n2i en la forma:
(n1 )2 =
(σN − σ(2) )(σN − σ(3) ) + σT2
(σ(1) − σ(2) )(σ(1) − σ(3) )
(2.3)
36
CAPÍTULO 2. TENSIONES
(σN − σ(3) )(σN − σ(1) ) + σT2
(σ(2) − σ(3) )(σ(2) − σ(1) )
(2.4)
(σN − σ(1) )(σN − σ(2) ) + σT2
(n3 ) =
(σ(3) − σ(1) )(σ(3) − σ(2) )
(2.5)
(n2 )2 =
2
Conviene observar que el sistema de ecuaciones cuyas incógnitas son las n2i es un sistema lineal
que además tiene simetría frente a las permutaciones cíclicas de (123), esto es, conocida una
solución las permutaciones cíclicas de los índices producen el resto de las soluciones.
Figura 2.1: Círculos de Mohr donde se sitúan las tensiones normal y tangencial en un punto
de un medio material
Como (n1 )2 ≥ 0 y el denominador de la primera ecuación (2.3) es positivo, resulta que las
tensiones normal y tangencial satisfacen
σT2 + (σN − σ(2) )(σN − σ(3) ) ≥ 0.
Esta expresión equivale a que los valores admisibles de σN y σT son los que están fuera del
círculo C1 de ecuación
(σT )2 + ((σN − (σ(2) + σ(3) )/2)2 = ((σ(2) − σ(3) )/2)2 ,
es decir un círculo de centro en el eje de la σN , ((σ(2) + σ(3) )/2, 0), en el punto medio de las dos
tensiones σ(2) y σ(3) y de radio (σ(2) − σ(3) )/2.
La segunda condición (2.4) implica
(σN − σ(3) )(σN − σ(1) ) + σT2 ≤ 0
es decir dentro del círculo C2 y la tercera
(σN − σ(1) )(σN − σ(2) ) + σT2 ≥ 0
en el exterior de C3 . En realidad la tensión de cortadura está tomada en valor absoluto, por
lo que de los círculos de Mohr basta con considerar la región en que σT ≥ 0. Es la región
rayada comprendida entre los tres círculos de la gura (2.1) la que nos determina los posibles
2.4. EQUILIBRIO ESTÁTICO. SIMETRÍA DEL TENSOR DE TENSIONES
37
valores de σN y σT para las diferentes secciones. Las direcciones en la cuales el material está
caracterizado por las tensiones normal y de cortadura representada por un punto como el P
de la gura se obtendrán de resolver las ecuaciones (2.3-2.5). El valor máximo de la tensión de
cortadura es el (σ(1) − σ(3) )/2 y se encuentra en una dirección en la que n2 = 0, es decir en el
plano XOZ , de acuerdo con (2.4). Como sobre los tres círculos se anulan en cada uno de ellos
alguna de las componentes ni , entonces representan el estado de tensiones en el correspondiente
plano coordenado subtendido por los ejes nj , nk que no se anulan, una vez determinadas las
direcciones principales.
2.4.4. Estados de tensión planos
Son aquellos en los que una de las tensiones principales es nula. Supongamos que la tomamos
como σ(3) = 0 en la dirección del tercer eje. De esta manera el tensor de tensiones se escribe


σ11 σ12 0
σij =  σ12 σ22 0  .
0
0 0
En este caso basta con dibujar el círculo de Mohr entre σ(1) y σ(2) , ya que sus puntos nos van
a describir el estado de tensiones del plano x1 x2 . Los valores principales del tensor se obtienen
2 = 0, cuya solución general es
de resolver la ecuación característica (σ11 − λ)(σ22 − λ) − σ12
p
2
σ11 + σ22 ± (σ11 − σ22 )2 + 4σ12
σ(1,2) =
2
Como el centro del círculo está en el punto
σ(1) + σ(2)
σ11 + σ22
=
,
2
2
y de radio
σ(1) − σ(2)
R=
=
2
sµ
σ11 − σ22
2
¶2
2
+ σ12
entonces sin necesidad de calcular las tensiones principales y con el solo conocimiento de los σij
podemos dibujarlo de acuerdo con la gura 2.2.
Es importante observar que la fuerza sobre la cara perpendicular al eje e1 vale f 1 ≡
(σ11 , σ12 , 0) en tanto que la fuerza sobre la cara perpendicular al eje e2 es f 2 ≡ (σ12 , σ22 , 0).
El punto A de la gura cuya tensión normal es σ11 y de cortadura σ12 representa el estado de
tensiones de la primera cara, en tanto que el B es el estado de tensiones de la segunda.
Si queremos medir el estado de tensiones en una sección cuyo vector normal forma un ángulo
θ con el eje e1 en el plano x1 x2 , entonces n(θ) ≡ (cos θ, sin θ, 0). La tensión normal vale
σN (θ) = (σ11 cos θ+σ12 sin θ) cos θ+(σ12 cos θ+σ22 sin θ) sin θ = σ11 cos2 θ+σ22 sin2 θ+σ12 sin 2θ.
Por otra parte, el punto C de la gura, desplazado del punto A un ángulo −2θ, viene caracterizado por una tensión normal
σN (C) =
σ11 + σ22
+ R cos(α − 2θ),
2
siendo α el ángulo que forma OA con el eje horizontal. Por otra parte
cos α =
σ11 − σ22
,
2R
sin α =
σ12
.
R
Sustituyendo estos valores se llega a que precisamente este punto representa el estado de tensiones en la sección considerada.
38
CAPÍTULO 2. TENSIONES
Figura 2.2: Círculo de Mohr de la tensión en el plano x1 x2 . Los puntos A y B corresponden
a los estados de tensión de las caras perpendiculares a los dos ejes coordenados. El punto
C , desplazado un ángulo 2θ desde A, es el estado de tensiones según una dirección que
forma en el plano x1 x2 un ángulo θ con el eje x1 .
De acuerdo con la gura, como el segmento OA forma un ángulo α con el eje de la σN , entonces
la dirección principal correspondiente al valor propio σ(1) se obtendrá de girar los ejes coordenados
un ángulo α/2 alrededor de OZ . Por lo tanto, como
r
r
1
1
cos(α/2) =
(1 + cos α), sin(α/2) =
(1 − cos α),
2
2
la matriz de rotación pasiva (rotación de los ejes) es la


cos(α/2)
sin(α/2) 0
R(α/2, OZ) =  − sin(α/2) cos(α/2) 0  ,
0
0
1
por lo que en los nuevos ejes coordenados



σ11 σ12 0
σ(1)
T
R  σ12 σ22 0  R =  0
0
0
0
0
0
σ(2)
0

0
0.
0
Ahora el nuevo eje OX 0 es la dirección principal de valor propio σ(1) .
2.4.5.
Tensor de tensión esférico y tensor desviador
Como la Traza de un tensor σ(1) + σ(2) + σ(3) = 3σM es un invariante, a veces es conveniente
expresar σ = σM I + d, donde σM I representa un estado de tensiones de naturaleza esférica,
siendo σM la tracción o compresión de cada punto y el tensor d de traza nula que lo que produce
es una deformación en promedio nula y que se conoce como tensor desviador.
2.4.6.
Círculos de Mohr de las deformaciones
Como tanto el tensor de deformaciones eij como el de velocidad de deformación Dij son
tensores simétricos, podemos aplicar lo aquí desarrollado para el tensor de tensiones a estos
otros tensores simétricos. Por lo tanto hablaremos de las deformaciones principales e(1) , e(2)
y e(3) , de las deformaciones normal eN y tangencial eT y una vez clasicadas por orden estas
2.5. TENSOR DE TENSIONES DEL CAMPO ELECTROMAGNÉTICO
39
deformaciones principales, e(1) ≥ e(2) ≥ e(3) , construir los círculos de Mohr en el plano (eN , eT ),
en el que se obtendrá el análisis para cualquier dirección del estado de deformación. También
aquí las bisectrices de las direcciones principales corresponden a las direcciones en las que
la deformación tangencial es máxima. En principio, el tensor de tensiones σij y el tensor de
deformaciones eij son tensores distintos, por lo que sus direcciones principales no tienen por
qué ser las mismas.
Como en el caso de pequeñas deformaciones los valores propios nos miden las deformaciones
relativas normales, en las direcciones principales se tiene:
dxi
≈ 1 + e(i) ,
dXi
dxi − dXi
≈ e(i) .
dXi
En el resto de las direcciones existirá deformación normal y tangencial.
2.5. Tensor de tensiones del campo electromagnético
Si en un medio material establecemos un campo electromagnético, estamos realizando unas
fuerzas que se superponen a las fuerzas electromagnéticas de cohesión de la propia estructura
molecular del sistema. El tensor de tensiones asociado al campo electromagnético en el vacío,
en el sistema internacional de unidades, viene dado por
¶
µ
1
αβ
2
α
σµν = ²0 c −Fµα Fν + gµν Fαβ F
4
donde de las componentes con subíndices 0 llamados subíndices temporales, h = σ00 representa
la densidad de energía del campo y gi ≡ σ 0i /c = σ i0 /c la densidad de momento lineal y las
componentes σij , i, j = 1, 2, 3 son propiamente las componentes del tensor de tensiones de
Maxwell.
El tensor campo electromagnético viene dado por:
Fαβ =
∂Aβ
∂Aα
−
,
∂xα
∂xβ
Aα ≡ (φ/c, −A)
siendo φ el potencial escalar y A el potencial vector. Con el índice 0 la variable x0 = ct. En
forma matricial y en términos del campo eléctrico y magnético, resulta:




0
Ex /c Ey /c Ez /c
0
−Ex /c −Ey /c −Ez /c
 −Ex /c

0
−Bz
By 
0
−Bz
By 
 , F αβ ≡  Ex /c

Fαβ ≡ 
 −Ey /c Bz
 Ey /c
0
−Bx 
Bz
0
−Bx 
−Ez /c −By
Bx
0
Ez /c −By
Bx
0
²0 2
(E + c2 B 2 ), gi = σ 0i /c = ²0 (E × B)i ,
2
µ
¶
1
2
2
2 2
σij = −²0 Ei Ej + c Bi Bj − δij (E + c B ) .
2
h = σ00 =
Ejemplo 2.4 Supongamos dos placas planas conductoras y cargadas entre las que introducimos un material dieléctrico de permitividad ². Se establece un campo eléctrico uniforme
de valor E en el interior de este material. La dirección del campo eléctrico la escogemos como
la dirección OX . La densidad de energía electromagnética en este material vale h = ²E 2 /2.
La densidad de momento lineal es nula. El tensor de tensiones de Maxwell tiene todas las
componentes σij nulas, salvo la componente σ11 = −²E 2 /2. Es una componente negativa,
lo que indica que cada elemento de supercie del interior del material, cuya normal tiene la
dirección del eje OX , está sometida a una compresión de ese valor.
40
CAPÍTULO 2. TENSIONES
Que la tensión en el interior de este material es de compresión se aprecia claramente debido a que las dos placas se atraen comprimiendo el material entre ellas. En efecto, si es F
la fuerza de atracción entre las placas, cuya supercie es S , la fuerza de compresión será
F/S . Pero la fuerza entre dos placas cargadas de valor Q es QE0 , siendo E0 el campo que
cada una crea sobre la otra. Pero en el caso de un conductor plano, el campo creado en el
exterior vale Q/2²S . Este campo es la mitad del campo E que existe en el interior entre las
dos placas. Por lo tanto
µ 2 ¶
F
QE0
Q2
1
Q
1
=
=
= ² 2 2 = ²E 2 .
S
S
2²S 2
2
² S
2
El signo menos se lo adjuntaremos debido a que el estado de tensiones es de compresión.
2.5. TENSOR DE TENSIONES DEL CAMPO ELECTROMAGNÉTICO
41
Problemas
2.1 Si el tensor de tensiones en un punto P de un medio material es

7 0 −2
σij =  0 5 0  ,
−2 0 4

determinar la fuerza por unidad de supercie que se hace en ese punto sobre un plano cuya
normal unitaria es el vector n = 2/3e1 − 2/3e2 + 1/3e3 . Determinar el esfuerzo normal y el
tangencial o de cortadura (Observar que estamos denominando `esfuerzo' a una tensión). ¾Cómo
son las tensiones y direcciones principales?
2.2 Construir el círculo de Mohr del estado de deformación plana dado por

0 0 √0
Eij =  0 √5
3,
0
3 3

y hallar la deformación cortante máxima. Comprobar el resultado gráca y analíticamente.
2.3 El estado de tensiones de un punto está dado por

2 √
−2
0
2
0 .
σij =  −2
√
0
0 − 2

Si cambiamos los ejes coordenados mediante la matriz
√

0√
1/ 2
A =  1/ √2
1/2
−1/ 2 1/2
ortogonal
√ 
1/ 2
−1/2  ,
−1/2
¾cómo se expresa el tensor en el nuevo sistema de coordenadas?
2.4 El tensor de tensiones de un punto está dado por


5
0
0
σij =  0 −6 −12  .
0 −12
1
Determinar el valor máximo de la tensión de cortadura y en qué plano tiene lugar. Dibujar los
círculos de Mohr del estado de tensiones de este punto. ¾Cómo es el vector de tensión según un
plano cuyo vector unitario normal es el n = 2/3e1 + 1/3e2 + 2/3e3 ? Comprobar estos resultados
mediante los diagramas de Mohr.
2.5 Construir los círculos de Mohr del estado de tensiones plano dado por

0
σij =  τ
0
τ
0
0

0
0
0
Considérese un prisma recto de lados a, b y c. ¾Cómo se puede lograr que esté sometido a un
estado de tensiones como el indicado?
42
CAPÍTULO 2. TENSIONES
2.6 En el punto P de un medio continuo el estado de tensiones es tal que las tensiones principales
cumplen 2σII = σI +σIII . Determinar el vector normal unitario al plano según el cual la tensión
normal σN = σII y la tangencial o de cortadura σT = (σI − σIII )/4. Aplicarlo al caso del tensor


4 0 0
σij =  0 5 0  .
0 0 6
2.7 Representar los círculos de Mohr y determinar la cortadura máxima en los siguientes estados
de tensión:




τ τ 0
τ
0
0
σij =  τ τ 0  , σij =  0 −τ
0 .
0 0 0
0 0 −2τ
2.8 El estado de tensión de un medio continuo está dado por

σ

σij = aσ
bσ
aσ
σ
cσ

bσ
cσ  .
σ
donde a, b, c son constantes. Determinar estas constantes
que √
la tensión sea nula
√ de tal manera
√
según el plano cuyo vector unitario normal es el n = 1/ 3e1 + 1/ 3e2 + 1/ 3e3 . ¾Cómo es la
tensión normal y la de cortadura según los tres planos coordenados? Determinar las tensiones
y direcciones principales y los correspondientes círculos de Mohr.
2.9 Probar que σij σjk σki es un invariante de tensión bajo los cambios de sistemas de referencia.
Vericarlo en los ejemplos anteriores.
2.10 Probar, usando el método de los multiplicadores de Lagrange que las tensiones normales
máxima y mínima corresponden a los valores principales.
2.11 En un medio material elástico, homogéneo e isótropo, el tensor de tensiones en un punto
viene dado por


3/2 0 −5/2
σij ≡  0
2
0 
−5/2 0 3/2
Determinar:
(a) Las tensiones y direcciones principales.
(b) ¾Cuál es la máxima tensión de cortadura?
(c) Dibujar los círculos de Mohr del punto.
(d) ¾En qué direcciones está sometido el punto a compresión pura?
(e) ¾En qué direcciones está sometido el punto a tracción pura?
2.12 Una columna de longitud l, sección circular de radio R, densidad ρ, módulo elástico Y , y
coeciente de Poisson σ = 0, se encuentra verticalmente apoyada sobre una supercie horizontal.
Determinar:
(a) Su acortamiento debido a la acción de la gravedad.
(b) Si en el extremo superior soporta una fuerza de valor F , uniformemente repartida, determinar
el estado de tensiones en un punto a una altura z sobre el suelo.
(c) En el caso de estar sometida a esta nueva carga, ¾que acortamiento adicional sufrirá?
(d) Dibujar el círculo de Mohr en el centro de gravedad de la barra.
(e) ¾En qué dirección, alrededor de este punto, se produce la fuerza de cortadura máxima? ¾De
qué valor? [Examen Junio 2005]
2.5. TENSOR DE TENSIONES DEL CAMPO ELECTROMAGNÉTICO
43
2.13 El estado de tensión de un medio continuo viene dado por el campo:

0

σij = Cx3
0
Cx3
0
−Cx1

0
−Cx1 
0
donde C es una constante. Se pide:
a) Probar que corresponde al estado de tensión de un medio en equilibrio estático y en ausencia
de fuerzas volúmicas por unidad de masa.
b) Calcular la tensión en el punto P = (4, −4, 7) según el plano 2x1 + 2x2 − x3 = −7, determinando la tensión normal y la tangencial.
c) Determinar las tensiones y direcciones principales en P .
d) Determinar el estado de tensiones sobre los puntos de la esfera x21 + x22 + x23 = 92 . En qué
punto de la esfera es la tensión normal máxima?
44
CAPÍTULO 2. TENSIONES
Capítulo 3
Dinámica
Leyes fundamentales
3.1. Ecuación de continuidad
Como la masa de un sistema cuya densidad es ρ0 (X, 0) en el instante inicial y ocupa un
volumen V0 y que al cabo del tiempo t tiene una densidad ρ(x, t) y ocupa un volumen V , resulta
Z
Z
Z
ρ0 (X, 0)dV0 =
ρ(x, t)dV =
ρ(X, t)J(t)dV0 ,
(3.1)
V0
V
V0
donde la segunda integral se ha hecho un cambio de variables en el instante t a las variables en
el instante 0. Al ser V0 arbitrario implica ρ0 (X) = ρ(X, t)J(t), con lo que la conservación de la
masa implica d(ρ(X, t)J(t))/dt = 0.
De otra manera, esta ecuación lo que establece es que la materia no se crea ni se destruye
y que por lo tanto la diferencia de materia entre la que entra y la que sale de un cierta región
innitesimal debe ser igual a la que se ha quedado dentro. Estableceremos ecuaciones de continuidad para la masa y carga de un sistema y para aquellas otras propiedades en las que este
principio general se aplique.
3.2. Ecuación de continuidad de la masa
Supuesto un volumen arbitrario V , rodeado por una supercie S la diferencia entre la masa
que entra y la que sale de ese volumen es
¶
Z
Z µ
Z
∂ρ
∂ρ
dV +
ρv · ndS =
+ ∇(ρv) dV = 0,
∂t
S
V
V ∂t
donde n es un vector unidad ortogonal a la supercie y dirigido hacia el exterior de la misma.
La segunda integral es la aplicación del teorema de Gauss a la primera. Esta ecuación se debe
vericar cualesquiera que sea el volumen V . En particular si se verica para todo elemento
innitesimal de volumen se vericará para cualquier volumen. Por lo tanto, la forma innitesimal
de esta ecuación es
∂ρ
+ ∇(ρv) = 0.
(3.2)
∂t
Como ∇(ρv) = v · ∇ρ + ρ∇ · v , la anterior ecuación se puede poner
dρ
+ ρ∇ · v = 0.
dt
45
46
CAPÍTULO 3. DINÁMICA
LEYES FUNDAMENTALES
La ecuación (3.2) no es ni más ni menos que la derivada material de la ecuación (3.1), y
restringida a un volumen innitesimal arbitrario. En efecto, la derivada material de (3.1) es
d
dt
Z µ
Z
ρ(x, t)dV =
V
V
Z µ
=
V
¶
Z
∂ρ(x, t)
d
+ ∇ρ(x, t) · v dV +
ρ(x, t) (dV )
∂t
dt
V
¶
∂ρ(x, t)
+ ∇ρ(x, t) · v + ρ(x, t)∇v dV
∂t
Si ahora consideramos un volumen V , arbitario e innitesimal, obtenemos (3.2).
La evolución del sistema se dice que es incompresible si cada partícula material (cada
elemento innitesimal) de volumen no cambia su densidad, es decir dρ/dt = 0, por lo que en
este caso de sistema incompresible la ecuación de continuidad de la masa queda ρ∇ · v = 0, y
como la densidad, aunque sea función de punto, es en general denida positiva resulta ∇ · v = 0:
el campo de velocidad es necesariamente de divergencia nula y se dice que es solenoidal. Las
líneas del campo de velocidad o bien se cierran sobre ellas mismas o su origen y nal tiene lugar
sobre la supercie de contorno del medio continuo.
Si la evolución es estacionaria, ρ no es función explícita de t y la ecuación de continuidad
se escribe:
∇(ρv) = 0,
en la que la evolución no es necesariamente solenoidal, puesto que en general la densidad no
tiene por qué ser independiente del punto.
3.3.
Segunda ley de Newton
Es la segunda Ley de Newton la que establece que si las fuerzas internas de un sistema
material obedecen a la tercera Ley de Newton (Principio de acción y reacción) entonces la
variación por unidad de tiempo del momento lineal del sistema (cantidad de movimiento) es
igual a la suma de las fuerzas externas que actúan sobre el sistema.
Como por sistema material podemos considerar cualquier parte de nuestro medio continuo.
Consideremos la materia que está dentro del volumen V de frontera o supercie exterior S(V),
que está en contacto con el medio continuo que le rodea. Supongamos que el exterior hace sobre
el medio material una fuerza másica por unidad de volumen k, entonces la segunda Ley de
Newton nos lleva a
Z
Z
Z
d
ρvdV =
ρkdV +
f dS,
dt V
V
S(V)
donde la última integral está extendida a la supercie exterior de nuestro volumen S(V), y
representa la fuerza de contacto fi = σij nj que el resto del material hace sobre nuestro sistema.
Usando el teorema de Gauss para convertir la integral de supercie en una de volumen, y como
lo anterior se verica para cualquier V del medio material, esto implica que en cada punto de
nuestro medio continuo se satisface
∂σij
dvi
+ ρki = ρ
,
∂xj
dt
(3.3)
y donde para obtener le segundo miembro se ha hecho uso de la ecuación de continuidad (3.2).
Si el material estuviera eléctricamente cargado, por ejemplo un plasma y tuviera una densidad
volúmica de carga ρe , si se aplica un campo eléctrico externo E , además de la fuerza másica k,
en el miembro de la izquierda de (3.3) existirá otro término de la forma ρe E .
3.4. MOMENTO DE LA CANTIDAD DE MOVIMIENTO. SIMETRÍA DE σIJ
47
3.4. Momento de la cantidad de movimiento. Simetría de σij
Si cada par de fuerzas internas que satisfacen el principio de acción y reacción están aplicadas
en el mismo punto, entonces sus momentos respecto de un punto arbitrario son nulos y nos lleva
a que la variación por unidad de tiempo del momento angular de un sistema respecto de un
punto jo es igual al momento, respecto de ese punto jo, de todas las fuerzas externas.
Si consideramos como en el apartado anterior el mismo volumen del medio continuo y
consideramos como punto jo el origen del sistema de coordenadas se llega a:
Z
Z
Z
d
ρr × vdV =
ρr × kdV +
r × f dS,
dt V
V
S(V)
Esta ecuación no suministra ninguna ecuación diferencial adicional, pero nos lleva a que σij = σji
y el tensor de tensiones del medio material es necesariamente simétrico.
En efecto, si la integral de supercie la transformamos en una integral de volumen, y de todo
lo anterior analizamos una de sus componentes, resulta:
¶
Z
Z µ
dρ
drj
dvk
d
(ρr × v)i dV =
²ijk rj vk + ρ²ijk
vk + ρ²ijk rj
+ ρ²ijk rj vk vl,l dV
dt V
dt
dt
dt
V
Ahora bien, el primero y el cuarto término dan lugar a
µ
¶
dρ
²ijk rj vk
+ ρvl,l = 0,
dt
debido a la ecuación de continuidad de la masa. El segundo es también cero pues drj /dt = vj y
²ijk vj vk = 0. El término que sobrevive es el
Z
dvk
ρ²ijk rj
dV
dt
V
En el segundo miembro, la componente i resulta ser
¶
Z µ
∂
ρ²ijl rj kl +
(²ijk rj σkl ) dV = .
∂rl
V
pero
∂
∂σkl
(²ijk rj σkl ) = ²ijk δjl σkl + ²ijk rj
,
∂rl
∂rl
con lo que
²ijk rj ρ
dvk
∂σkl
= ²ijl rj ρkl + ²ijk rj
+ ²ilk σkl
dt
∂rl
que si utilizamos la ecuación de la dinámica (3.3) el único término que sobrevive es el ²ilk σkl = 0.
Esto no sería así si por ejemplo el exterior hiciera momentos pero no fuerzas, como es el
caso de un material ferromagnético en un campo magnético exterior uniforme. Además de los
momentos de las fuerzas externas, habría Rque haber incluido en el segundo miembro de la
ecuación anterior un término de la forma µ × BdV , donde µ es la densidad volúmica de
momento magnético del material y B el campo magnético exterior aplicado.
3.5. Conservación de la energía. Primer principio de la Termodinámica
Si la única interacción es de tipo mecánico y no hay aporte energético en forma de calor sobre
el sistema, entonces a partir de las ecuaciones de la dinámica (3.3), multiplicando escalarmente
por el desplazamiento dr de cada punto (o bien por el vector velocidad de cada punto si lo
que queremos es determinar el trabajo por unidad de tiempo) se dene el trabajo por unidad
48
CAPÍTULO 3. DINÁMICA
LEYES FUNDAMENTALES
de volumen (o por unidad de volumen y de tiempo) como el trabajo de las fuerzas volúmicas
externas y las fuerzas de tensión
vi
∂σij
dvi
1 dv 2
+ ρvi ki = ρ
vi = ρ
∂xj
dt
2 dt
que se iguala a la variación por unidad de tiempo de la energía cinética por unidad de volumen.
La ecuación local anterior la integramos a todo el medio continuo, y llamando
Z
Z
ρv 2
dK
1 dv 2
K=
dV,
=
dV
ρ
dt
V 2
V 2 dt
a la variación de la energía cinética del sistema, y como vi σij,j = (vi σij ),j − vi,j σij y por otra
parte vi,j = Yij = Dij + Vij , resulta vi,j σij = Dij σij , ya que la vorticidad Vij = −Vji . Al hacer
la integral de volumen de la divergencia (vi σij ),j se nos transforma en una integral de supercie
extendida a la supercie exterior del medio, del ujo del campo vectorial vi σij . Separando
términos obtenemos
Z
Z
Z
dK
+
Dij σij dV =
vi σij nj dS +
ρvi ki dV,
dt
V
S(V)
V
que lo podemos resumir diciendo que en el miembro de la derecha tenemos el trabajo por unidad
de tiempo de las fuerzas externas que actúan sobre la supercie del medio continuo S(V) y el
trabajo de las fuerzas volúmicas, que es igual a los términos del primer miembro que representan
la variación por unidad de tiempo de la energía cinética del sistema y la variación por unidad
de tiempo del trabajo de las fuerzas internas, que se suele llamar energía mecánica interna U .
dU
dK
+
= Trabajo de las fuerzas externas.
dt
dt
Llamemos u a la función que nos dene la energía interna por unidad de masa, de tal manera
que
Z
U=
ρudV.
V
Si hubiera un aporte de energía térmica por unidad de tiempo y unidad de volumen mediante
una generación interna de calor q y a su vez un aporte de un ujo externo de calor a través de
la supercie exterior mediante un campo j entonces
Z
Z
δQ
=
qdV −
j · ndS,
δt
V
S(V)
donde la segunda integral se extiende a la supercie del medio siendo n el vector unidad perpendicular a la supercie y dirigido hacia el exterior con lo que el signo menos indica que calculamos
el ujo de calor que `entra'. Por ejemplo, el ujo de calor j en un medio homogéneo e isótropo
está relacionado con la temperatura mediante j = −κ∇T , siendo κ la conductividad del medio.
La ecuación de conservación de la energía (por unidad de tiempo) o primer principio de la
Termodinámica se expresa de forma global:
dK
dU
δW
δQ
+
=
+
.
dt
dt
δt
δt
A las magnitudes W y Q los términos de la forma δW /δt no quieren representar derivadas
temporales, ya que las funciones W y Q no son campos o propiedades globales que se puedan
derivar como es el caso de K y de U o de sus campos locales ρv 2 (x, t)/2 y ρu(x, t).
3.6. SEGUNDO PRINCIPIO DE LA TERMODINÁMICA
49
Si las integrales de supercie las ponemos como integrales de volumen podemos recuperar
la forma local de la ley de conservación de la energía:
µ
¶
d v2
+ u = (vi σij ),j + ρvi ki + q − ∇ · j,
ρ
dt 2
y utilizando (3.3) se llega a
du
1
= (σij Dij + q − ∇ · j) ,
dt
ρ
(3.4)
que la podemos enunciar como: La variación de la energía especíca interna por unidad de
tiempo es igual al trabajo por unidad de volumen y de tiempo de las fuerzas internas de tensión
más el aporte de calor por unidad de tiempo.
3.6. Segundo Principio de la Termodinámica
Si admitimos que además de energía mecánica se intercambia calor con el exterior, deberemos
tener presente el Segundo Principio de la Termodinámica. Puesto que la evolución no pasa
necesariamente por estados de equilibrio termodinámico entonces la variación de la entropía del
sistema debe ser mayor o a lo sumo igual a la entropía que entra en el sistema por su supercie
exterior más la entropía que se genera en su interior. Así:
Z
Z
Z
d
j·n
dS +
ρedV,
ρsdV ≥ −
dt V
V
∂V T
siendo s la entropía especíca y e la producción interna de entropía por unidad de masa y unidad
de tiempo que estará expresada en términos del aporte volúmico de calor q y de la temperatura
del medio. Si la última integral la transformamos en una integral de volumen, obtenemos la
desigualdad local conocida como desigualdad de Clausius-Duhem:
µ ¶
1 ji
ds
−e+
≥ 0.
(3.5)
dt
ρ T ,i
3.7. Ecuaciones constitutivas
Las ecuaciones dinámicas de un medio continuo son las 5 ecuaciones (3.2-3.4):
Ecuación de continuidad
∂ρ
+ (ρvj ),j = 0,
∂t
Ecuación del movimiento
σij,j + ρki = ρv̇i ,
i = 1, 2, 3
Primer principio de la Termodinámica
du
1
= (σij Dij + q − ∇ · j) .
dt
ρ
Si suponemos conocidas las fuerzas volúmicas externas ki y los aportes de calor q , las incógnitas
son las 14 variables o campos ρ, vi , σij , ji y u. Como además se ha de cumplir el
Segundo principio de la Termodinámica
ds
1
−e+
dt
ρ
µ ¶
ji
≥0
T ,i
50
CAPÍTULO 3. DINÁMICA
LEYES FUNDAMENTALES
tenemos una desigualdad que añade dos variables más s y T . Como hay un total de 16 variables
o campos y 5 ecuaciones más una desigualdad, es necesario suministrar once condiciones o
ecuaciones adicionales que dependan de la estructura del medio continuo. Tres serán del tipo
ji = −κij T,j que nos relacionan el ujo de calor con la temperatura y con unos parámetros
físicos, la conductividad térmica κij del medio. Dos serán las ecuaciones termodinámicas de
estado del medio continuo que nos ligarán la densidad ρ, el estado de tensiones σij (la presión
p en el caso de un gas), la energía interna y la entropía con la temperatura T . En el caso
de gases perfectos éstas serían, por ejemplo p/ρ = kT , y la denición de la energía interna
u = cv T , o bien la de la entropía s = cp T siendo cv y cp , los calores especícos a volumen
constante y presión constante, respectivamente. Las otras seis restantes que reciben el nombre
de ecuaciones constitutivas, reejarán la estructura y propiedades físicas del medio continuo.
Un ejemplo de ecuaciones constitutivas es la relación lineal σij = Kijkl Dkl entre el tensión de tensiones y el tensor de velocidad de deformación, en términos de un conjunto de
constantes Kijkl , características del medio material. La elasticidad lineal y la mecánica de uidos Newtonianos establecen unas ecuaciones constitutivas de tipo lineal σij = Cijkl ekl o bien
σij = (−p + λDkk )δij + 2µDij .
3.7. ECUACIONES CONSTITUTIVAS
51
Problemas
3.1 Probar que la ecuación de continuidad en su forma diferencial Lagrangiana se escribe
d(ρJ)/dt = 0, donde ρ es la densidad y J el Jacobiano de la evolución.
3.2 Utilizando la ley de continuidad demostrar que
d
dt
Z
Z
V
ρvi dV =
ρ
V
dvi
dV,
dt
d
dt
Z
Z
V
ρvi vi dV =
ρ
V
dvi vi
dV.
dt
3.3 Probar que el campo de velocidad vi = Axi /r3 , con A una constante y r2 = xi xi satisface
la ecuación de continuidad de un uido incompresible.
3.4 En un punto de un medio continuo los tensores de velocidad de deformación Dij y de
tensión σij son




1 6 4
4
0 −1
Dij =  6 3 2  , σij =  0 −2 7  .
4 2 5
−1 7
8
Determinar en ese punto el trabajo por unidad de tiempo y de volumen realizado por las fuerzas
de tensión en ese punto.
3.5 Si en un medio continuo (por ejemplo un uido ideal sin viscosidad) de densidad ρ, el tensor
de tensiones es σij = −pδij , probar que el trabajo por unidad de volumen y unidad de tiempo
debido a las tensiones del medio se puede expresar por la ecuación Dij σij = (p/ρ)dρ/dt, siendo
Dij el tensor de velocidad de deformación.
3.6 Comprobar que el ujo representado por el campo de velocidad:
v1 = −
2x1 x2 x3
,
r4
v2 =
(x21 − x22 )x3
,
r4
v3 =
x2
,
r2
r2 = x21 + x22 ,
satisface la ecuación de continuidad de un ujo incompresible. ¾Es irrotacional?
3.7 Probar que para el campo de velocidad vi = xi /(1 + t) se cumple ρx1 x2 x3 = ρ0 X1 X2 X3 .
En el supuesto de que se tratara de un uido perfecto, determinar el trabajo de las fuerzas de
tensión internas.
3.8 Un ujo incompresible bidimensional está dado por v1 = A(x21 − x22 )/r4 , v2 = A(2x1 x2 )/r4 ,
v3 = 0, con A una constante y r2 = x21 + x22 . Probar que la ecuación de continuidad se satisface.
¾Es este ujo laminar irrotacional?
3.9 En un ujo bidimensional incompresible y estacionario está dado por v1 = −Ax2 /r2 , con A
una constante y r2 = x21 + x22 . Determinar la componente v2 , con la condición de que v2 (0, x2 ) =
0. Demostrar que el movimiento es irrotacional y encontrar las líneas de corriente.
3.10 Probar que si q es el vector torbellino, es decir qi = −²ijk Vjk donde Vjk es la vorticidad,
entonces se satisface la ecuación:
d
dt
µ ¶
q
1
= (∇ × a + (q · ∇)v)
ρ
ρ
donde a es el campo de aceleración.
52
CAPÍTULO 3. DINÁMICA
LEYES FUNDAMENTALES
3.11 Demostrar que en el caso de ausencia de fuerzas volúmicas y en situación estática el campo
tensorial plano más general

σ11
σij (x) =  σ21
0
σ12
σ22
0

0
0,
0
tiene la forma
σ11 =
∂ 2 φ(x1 , x2 )
,
∂x22
σ12 = −
∂ 2 φ(x1 , x2 )
,
∂x1 ∂x2
σ22 =
∂ 2 φ(x1 , x2 )
,
∂x21
donde φ(x1 , x2 ) es una función arbitraria, denominada función de Airy, a determinar.
Capítulo 4
Elasticidad
Supongamos una barra uniforme de longitud l y sección A que la sometemos a tracción.
Debido a esto, la deformación de la barra tiene dos partes: se estirará en la dirección de la
fuerza y por otra parte se contraerá en las direcciones transversales. Se pueden denir, asociadas
a estas deformaciones, dos características de la barra:
Módulo de Young (Y ): En un medio material elástico de longitud l si lo sometemos a una
fuerza por unidad de área o tensión F/A, se deformará en la dirección de aplicación de la fuerza
una longitud ∆l tal que
∆l
F
=Y
.
A
l
Coeciente de Poisson (σ): Generalmente, en las direcciones perpendiculares a la de la
fuerza aplicada, sufrirá una deformación de sentido contrario (contracción o extensión), tal que
la deformación ∆h en una dirección transversal de longitud original h
∆l
∆h
= −σ .
h
l
El signo menos hace referencia a la deformación en sentido contrario. Los dos parámetros Y y
σ dependen de la naturaleza del material y no de sus dimensiones o forma. Y tiene dimensiones
de fuerza por unidad de área en tanto que σ es adimensional. Generalmente 0 ≤ σ ≤ 1/2.
Estamos acostumbrados al estudiar sistemas elásticos, que la fuerza necesaria que hay que
aplicar es proporcional a la deformación producida F = k∆l. Visto lo anterior, esa constante de
proporcionalidad no es otra que k = Y A/l. Y además, resulta, que también existe una relación
lineal entre las deformaciones transversales y las tensiones longitudinales. Como el estado de
tensiones de un medio viene caracterizado por el tensor σij y el estado de deformación por el
tensor eij , lo anterior está sugiriendo una relación entre ambos campos tensoriales.
4.1. Ley de Hooke generalizada
En el caso de pequeñas deformaciones, si representamos por eij el tensor de deformaciones
linearizado en la descripción Euleriana, la Ley de Hooke generalizada establece que existe una
relación lineal entre el tensor de tensiones y el tensor de deformaciones 1 . La expresión general
de esta relación es
µ
¶
∂uj
1 ∂ui
σij = Cijkl ekl , eij =
+
2 ∂xj
∂xi
1
Augustin Louis Cauchy. Las ecuaciones fundamentales de la teoría de la elasticidad fueron
desarrolladas por Cauchy y Poisson hacia el año 1820.
53
54
4.2.
CAPÍTULO 4. ELASTICIDAD
Tensor elástico. Constantes elásticas
Al tensor Cijkl se le denomina tensor elástico. En principio tiene 34 = 81 componentes,
pero debido a que σ y e por ser simétricos solamente tienen 6 componentes independientes cada
uno, se reduce a un conjunto de 36 componentes independientes.
Si es posible expresar la densidad de energía de deformación, por unidad de volumen
1
1
u∗ = ρu = Cijkl eij ekl = CKL eK eL ,
2
2
K, L = 1, . . . , 6,
CKL = CLK .
entonces el tensor elástico tiene 21 componentes independientes.
Teorema: La condición necesaria y suciente para que exista una función de energía
de deformación u es que los coecientes del tensor elástico satisfagan las condiciones
Cijkl = Cklij ,
en cuyo caso
u=
1
Cijkl eij ekl ,
2ρ
σij = ρ
∂u
,
∂eij
Cijkl = ρ
∂2u
.
∂eij ∂ekl
Si los efectos térmicos no juegan un papel importante y los procesos que analizamos los podemos
considerar como adiabáticos, entonces el primer principio de la termodinámica nos lleva a que si
la energía interna es una función del estado de deformación del medio, y por lo tanto una función
del tensor de deformaciones eij , se tiene de (3.4)
du
1
1
deij
= σij Dij = σij
,
dt
ρ
ρ
dt
con lo que
σij = ρ
∂u
,
∂eij
⇒
ρ
du
∂u deij
=
,
dt
∂eij dt
∂u
= Cijkl ekl ,
∂eij
u=
1
Cijkl eij ekl .
2ρ
En el caso de medios isótropos de las 36 componentes solamente 2 son independientes, por lo que
las características elásticas de un material dependen solamente de dos constantes: El módulo
de Young Y (o módulo elástico) y el coeciente de Poisson σ .
Si la energía interna del medio elástico viene expresada por la relación
u=
¢
1 ¡
1
Cijkl eij ekl =
Cxxxx e2xx + Cxxxy exx exy + · · ·
2ρ
2ρ
y el sistema tiene simetría de reexión en la dirección OY , entonces una deformación en esa
dirección, seguida de una inversión espacial, produce un valor de e0xy = −exy , por lo que como
la energía de interna debe ser invariante, resulta que los coecientes Cxxxy = Czzzy = 0 y en
general aquellos que contengan un número impar de y 0 s y lo mismo para el resto de las variables.
Si el medio material posee simetría cúbica, además de las tres reexiones según los tres ejes,
también posee simetría en las permutaciones x → y → z de forma cíclica, por lo que los únicos
coecientes distintos de cero serán: Cxxxx = Cyyyy = Czzzz , Cxxyy = Cxxzz = Cyyxx = . . .,
Cxyxy = Cxzxz = Czyzy = . . ., con lo que la energía por unidad de volumen y de masa tendrá la
forma
u=
ª
1 ©
Cxxxx (e2xx + e2yy + e2zz ) + 2Cxxyy (exx eyy + exx ezz + ezz eyy ) + 4Cxyxy (e2xy + e2xz + e2yz )
2ρ
4.2. TENSOR ELÁSTICO. CONSTANTES ELÁSTICAS
55
Si enumeramos las componentes del tensor de tensiones y de deformaciones de acuerdo con los seis
índices σ1 = σ11 , σ2 = σ22 , σ3 = σ33 , σ4 = σ23 , σ5 = σ31 y σ6 = σ12 , y lo mismo para eij la
relación más general en el caso de simetría cúbica será de la forma σI = CIJ eJ , I, J = 1, . . . , 6.
σ  C
C
C
0
0
0 e 
xxxx
xxyy
xxyy
 σ2   Cxxyy
  
 σ3   Cxxyy
 =
 σ4   0
  
0
σ5
0
σ6
Cxxxx
Cxxyy
0
0
0
Cxxyy
Cxxxx
0
0
0
1
1
0
0
2Cxyxy
0
0
  e2 
 
  e3 
 
  e4 
 
e5
e6
2Cxyxy
0
0
0
0
0
0
0
2Cxyxy
0
La última parte diagonal proviene de que el último sumando debe escribirse en la notación indicial
como
4Cxyxy (e2xy + e2xz + e2yz ) = 2Cxyxy (e2xy + e2yx + e2xz + e2zx + e2yz + e2zy ).
En el caso isótropo, como la traza es una propiedad invariante, resulta que
Tr(σij ) = σ11 + σ22 + σ33 = (Cxxxx + 2Cxxyy )Tr(eij ),
con lo que esta suma dene un único coeciente físico, y el otro independiente tiene que ser el
Cxyxy . Por lo tanto existirá una relación f (Cxxxx , Cxxyy , Cxyxy ) = 0. El tensor elástico tiene los
tres coecientes el Cxxxx = λ + 2µ, Cxxyy = λ y el Cxyxy = µ, que no son independientes pues
Cxxxx = Cxxyy + 2Cxyxy , por lo que solamente dos de ellos son independientes.
σ 
1
 λ + 2µ
 σ2  
  
 σ3  
 =
 σ4  
  
σ5
σ6
λ
λ
0
0
0
λ
λ + 2µ
λ
0
0
0
λ
λ
λ + 2µ
0
0
0
0
0
0
2µ
0
0
0
0
0
0
2µ
0
0   e1 
0   e2 
 
0   e3 
 
0   e4 
 
e5
0
e6
2µ
Se suelen tomar como componentes independientes las componentes Cxxyy = λ y Cxyxy = µ de
tal manera que λ y µ se conocen como coecientes de Lamé del medio isótropo. La relación
entre estos coecientes e Y y σ , es
µ
¶
σ
Y
Y
, Cxyxy = µ =
.
Cxxyy = λ =
1 + σ 1 − 2σ
2(1 + σ)
Cuando sometemos un cuerpo a cortadura pura, veremos que la relación entre la tensión de
cortadura τ y la deformación angular del material θ, viene dada por τ = µθ, y al coeciente
de proporcionalidad µ se le llama módulo de torsión (o módulo de rigidez) y es precisamente el
coeciente µ de Lamé.
Y
acero
aluminio
cobre
vidrio
madera
hormigón (compr.)
N/cm2
1,96 × 107
6,86 × 106
1,07 × 107
6,8 × 106
9,8 × 106
2,74 × 106
µ
N/cm2
8 × 106
2,4 × 106
4 × 106
En medios anisótropos pero con simetría cristalina, la simetría de la red hace que no todos
los coecientes del tensor elástico sean diferentes. Por ejemplo, en el caso de una red con simetría
cúbica, los átomos próximos están separados una misma distancia a y los únicos coecientes
diferentes son los Cxxxx , Cxxyy y Cxyxy , y donde estos dos últimos son aproximadamente iguales.
En el caso isótropo, la invariancia por rotación establece que Cxxxx = Cxxyy + 2Cxyxy , como
puede vericarse y reduce a dos constantes la caracterización del tensor elástico.
En general, el número de coecientes independientes para monocristales de los diferentes
sistemas cristalinos, es:
56
CAPÍTULO 4. ELASTICIDAD
Cúbico
Hexagonal
Rómbico
Tetragonal
3
5
6
7
Ortorrómbico
Monoclínico
Triclínico
9
13
21
Si el material no es un monocristal sino una aglomeración de pequeños monocristales orientados
al azar, entonces es equivalente a un medio isótropo con solamente dos coecientes elásticos
independientes.
4.2.1.
Ley de Hooke de medios isótropos
Otra forma de ver que en los medios isótropos solamente dos coecientes son sucientes se
basa en que la relación entre σij y eij debe ser lineal e independiente de la orientación. Una
posibilidad es que σij = Keij , pero como la traza del tensor eij , es también una función lineal
e invariante del tensor, la posibilidad es que σij = Keij + L(ekk )δij . Los otros invariantes bajo
rotaciones del tensor eij no son lineales en las componentes eij .
En los medios isótropos, los coecientes Ciijj = λ, i 6= j , Ciiii = λ + 2µ, y los Cijij = µ,
i 6= j , de tal manera que los que no son de esta forma, son nulos.
σij = λδij ekk + 2µeij .
Esta ecuación se puede invertir para obtener el tensor de deformaciones linearizado en términos
del tensor de tensiones
eij =
−λ
1
δij σkk +
σij ,
2µ(3λ + 2µ)
2µ
eij =
1+σ
σ
σij − δij σkk .
Y
Y
Si las deformaciones producidas en un medio isótropo no modican su volumen, entonces como
hemos visto esto trae consigo que la traza ekk = 0, el coeciente λ no juega ningún papel pues
σij = 2µeij , y esto traerá consigo que la velocidad de propagación de las perturbaciones dependa
solamente de µ.
Resumiendo, en un medio homogéneo e isótropo el tensor elástico tiene la forma:
Cijkl = λδij δkl + µ(δik δjl + δil δjk ),
y la energía de deformación queda
u=
¢
1 ¡
λ(ekk )2 + 2µ(e2 )kk .
2ρ
La forma explícita de las distintas componentes del tensor de tensiones y del tensor de
deformaciones son:
σxx =
Y
[(1 − σ)exx + σ(eyy + ezz )] ,
(1 + σ)(1 − 2σ)
σyy =
Y
[(1 − σ)eyy + σ(exx + ezz )] ,
(1 + σ)(1 − 2σ)
σzz =
Y
[(1 − σ)ezz + σ(exx + eyy )] ,
(1 + σ)(1 − 2σ)
σxy =
Y
exy ,
1+σ
σyz =
Y
eyz ,
1+σ
σxz =
Y
exz .
1+σ
y recíprocamente
exx =
1
[σxx − σ(σyy + σzz )] ,
Y
eyy =
1
[σyy − σ(σxx + σzz )] ,
Y
ezz =
1
[σzz − σ(σxx + σyy )] ,
Y
4.2. TENSOR ELÁSTICO. CONSTANTES ELÁSTICAS
57
1+σ
1+σ
1+σ
σxy , eyz =
σyz , exz =
σxz .
Y
Y
Y
Si quisiéramos establecer esta relación en coordenadas esféricas o cilíndricas, entonces
exy =
σαβ = λ(eγγ )δαβ + 2µeαβ ,
α, β, γ = r, θ, φ,
o bien α, β, γ = r, φ, z.
Por ejemplo, en coordenadas cilíndricas
σrr = λ(err + eφφ + ezz ) + 2µerr ,
σrθ = 2µerθ
4.2.2. Consideraciones termodinámicas
La variación de la energía interna de un medio continuo se expresa como
dU = T dS + σij eij ,
como la variación debida al cambio de entropía y el cambio debido a la deformación, supuesta
ésta pequeña.
En el caso de un uido, σij = −pδij y la traza del tensor de deformaciones eii = dV /V , por
lo que por unidad de volumen
dU = T dS − pdV.
Si denimos la energía libre de Helmholtz de un medio material mediante F = U − T S ,
resulta que la variación de la energía libre
dF = −SdT + σij eij .
En términos de las deformaciones la energía libre de Helmholtz se expresa:
1
1
1
F = F0 + λ(eii )2 + µ(eij eij ) = F0 + µ(eij − δij ekk )2 + Ke2kk ,
2
3
2
donde F0 es la energía libre en ausencia de deformación y K = Y /3(1 − 2σ), el módulo elástico
volúmico.
4.2.3. Ecuaciones de Navier
En estados de equilibrio, y para medios homogéneos e isótropos, las ecuaciones de la dinámica
(3.3) se reducen a las ecuaciones de equilibrio para el tensor de deformaciones eij ,
µ
¶
∂eij
∂uj
1 ∂ui
∂ekk
+ 2µ
+ ρki = 0, eij =
+
,
λ
∂xi
∂xj
2 ∂xj
∂xi
y por lo tanto también para el vector de desplazamiento u,
(λ + µ)
∂
(∇ · u) + µ∇2 ui + ρki = 0,
∂xi
que como ∇ × (∇ × u) = ∇(∇ · u) − ∇2 u, se puede poner como
(λ + 2µ)∇(∇ · u) − µ∇ × (∇ × u) + ρk = 0.
(4.1)
En términos de las otras constantes aparece como:
Y (1 − σ)
Y
∇(∇ · u) −
∇ × (∇ × u) + ρk = 0.
(1 + σ)(1 − 2σ)
2(1 + σ)
(4.2)
58
CAPÍTULO 4. ELASTICIDAD
Ejemplo 4.1 Determinar la deformación de un cilindro sólido de radio R que rota con
velocidad angular Ω alrededor de su eje.
El problema tiene simetría radial, supuesto el cilindro muy largo. No existirán componentes
del vector desplazamiento uz ni uθ y solo existirá deformación en la dirección radial, ur ,
que es únicamente función de r. Por lo tanto, los términos de la ecuación de Navier (4.1),
en coordenadas cilíndricas son:
µ
¶
d 1 d(rur )
∇(∇ · u) =
er , ∇ × (∇ × u) = 0.
dr r dr
En nuestro caso, aunque la situación es estacionaria, no es una situación estática y el segundo
miembro de (4.1) no es nulo sino que es ρdvr /dt = −ρΩ2 r. Si suponemos la acción volúmica
exterior ρk nula, se tiene:
µ
¶
d 1 d(rur )
(λ + 2µ)
= −ρΩ2 r,
dr r dr
µ
¶
d 1 d(rur )
ρΩ2
= −Kr, K =
,
dr r dr
(λ + 2µ)
que se integra, con las condiciones de que ur (0) sea nita (y como comprobaremos es nula)
1 d(rur )
= −Kr2 /2 + B,
r dr
rur = −Kr4 /8 + Br2 /2 + C,
C = 0.
y que la tensión radial en la supercie, expresada en coordenadas cilíndricas, se anule
σrr (R) = λ(err +eφφ +ezz )+2µerr = 0,
sabiendo que err =
resulta
µ
¶
µ
¶
1
3KR2
B
2
λ − KR + B + 2µ −
+
= 0,
2
8
2
B=
dur
,
dr
eφφ =
ur
,
r
ezz = 0,
KR2 (2λ + 3µ)
KR2
= (3 − 2σ)
4(λ + µ)
4
¢
K ¡
r (3 − 2σ)R2 − r2 .
8
Así, un punto de la supercie del cilindro, se ha desplazado radialmente una distancia
ur (r) =
ur (R) =
ρσΩ2 R3
.
4λ
Teorema: Para que las ecuaciones de Navier tengan solución, es necesario y suciente que el campo tensorial de deformaciones eij (x), satisfaga las condiciones de
compatibilidad siguientes
²ipq ²jrs
∂ 2 epr
= 0,
∂xq ∂xs
i, j = 1, 2, 3
En el caso de deformación plana en el plano XOY se reducen a una sola:
∂ 2 e11 ∂ 2 e22
∂ 2 e12
+
=
2
.
∂x1 ∂x2
∂x22
∂x21
Si tenemos el sistema de ecuaciones
∂Φ
= Ei (x),
∂xi
(4.3)
i = 1, 2, 3
donde se dan las funciones arbitrarias Ei (x) y la incógnita es la función Φ(x), para que el sistema
tenga solución es necesario que las Ei no sean totalmente arbitrarias, sino que debido a la continuidad de la solución ∂ 2 Φ/∂xi ∂xj = ∂ 2 Φ/∂xj ∂xi , lo que implica ∂Ei /∂xj = ∂Ej /∂xi , esto es
²kij Ei,j = 0. De la denición del tensor de deformaciones, si lo derivamos respecto de xk , se tiene
eij,k = (ui,jk + uj,ik )/2,
²pjk eij,k = ²pjk uj,ik /2 = ωp,i ,
pues
²pjk ui,jk = 0,
4.3. DEFORMACIÓN DE UNA VIGA (LÍNEA ELÁSTICA)
59
siendo ωp = ²pjk uj,k /2. Llamando Ei(p) = ωp,i , estamos en el caso de la compatibilidad de la
ecuación anterior y por lo tanto
²ipq ²jrs
∂ 2 epr
= 0,
∂xq ∂xs
i, j = 1, 2, 3
Ecuaciones de Beltrami: En estados de equilibrio, y para medios homogéneos e isótropos,
una vez utilizadas las condiciones de compatibilidad, resulta que el tensor elástico satisface las
ecuaciones:
∇2 σij +
1 ∂ 2 σkk
∂ρki ∂ρkj
σ ∂ρkl
+
+
+
δij = 0,
1 + σ ∂xi ∂xj
∂xj
∂xi
1 − σ ∂xl
1, j = 1, 2, 3.
que son independientes del módulo de Young.
4.2.4. Estados de tensión planos
En estados de tensión planos, es decir σ3i = 0, i = 1, 2, 3, entonces las únicas componentes
no nulas del tensor de tensiones son las σij (x1 , x2 ), i, j = 1, 2 que solamente son funciones de
x1 y de x2 . Si además suponemos que estamos en una situación estática y sin fuerzas másicas
externas, resulta que la ecuación dinámica se nos transforma en la ∂σij /∂xj = 0 lo que da lugar
a que las componentes no nulas del tensor se pueden construir a partir de una función de esas
dos variables φ(x1 , x2 ), que recibe el nombre de función de Airy tal que
σ11 =
∂2φ
,
∂x22
σ12 = −
∂2φ
,
∂x1 ∂x2
σ22 =
∂2φ
.
∂x21
Las condiciones de compatibilidad (4.3) para el tensor eij se reducen en este caso para el tensor
de tensiones y para las funciones de Airy a
∂ 2 σ12
∂ 2 σ11 ∂ 2 σ22
+
=
2
,
∂x1 ∂x2
∂x22
∂x21
φ,1111 + φ,2222 + 2φ,1122 = 0.
4.3. Deformación de una viga (línea elástica)
Supongamos una viga horizontal de longitud l y sección transversal A sometida a esfuerzos.
Debido a éstos, dejará de ser horizontal y adoptará una cierta forma curvada. Analicemos lo que
60
CAPÍTULO 4. ELASTICIDAD
ocurre en un elemento de la viga de pequeño tamaño a. Adoptará la forma de la gura donde
la línea intermedia BC corresponde a una longitud del mismo valor a que la viga sin deformar.
La parte superior a la línea BC se estira y la inferior se contrae por efecto de las tensiones
existentes en la sección, esto es, la parte superior estará sometida a tracción y la parte inferior
a compresión. La bra que pasa por el punto D, que dista una distancia y de la bra neutra
BC (que permanece de la misma longitud), tendrá por longitud a + ∆a. Como a = Rθ, resulta
a + ∆a = (R + y)θ, con lo que la tensión a esa altura y vale
∆a
y
= ,
a
R
σxx = Y
∆a
Y
= y.
a
R
La componente σxx es positiva para y > 0 y negativa en el caso contrario, por lo que vericamos
que, en efecto, la mitad superior está sometida a tracción y la mitad inferior a compresión. El
momento que estas fuerzas de tensión producen con respecto al punto C será
Z
Z
Y b/2 2
Y
MC = yσxx dA =
y dA = I,
R −b/2
R
siendo I = ab3 /12 el momento de inercia de la sección con respecto a un eje que pasa por su
centro de gravedad.
Figura 4.1: Sección transversal de la viga de dimensiones a × b.
Conviene observar que R es el radio de curvatura de la curva que dibuja la bra intermedia
que no se deforma. La curvatura se dene como el cambio, por unidad de longitud, de la
pendiente de la tangente a una curva. Como la pendiente de una tangente vale tan α = dy/dx =
y 0 (x), la curvatura será
dα
dα dx
y 00
1
y 00
p
=
=
=
,
ds
dx ds
1 + y02 1 + y02
(1 + y 0 2 )3/2
p
p
pues ds = dx2 + dy 2 = dx 1 + y 0 2 . Si la curva que forma la bra intermedia es prácticamente
horizontal y 0 ' 0, por lo que la curvatura
1
dα
=
≈ y 00 (x).
ds
R
Esto nos da pie para, conocido el valor del momento ector M (x) en cada sección transversal
de la viga, poder integrar la ecuación
M (x) = Y Iy 00 (x),
(4.4)
4.3. DEFORMACIÓN DE UNA VIGA (LÍNEA ELÁSTICA)
61
y obtener la forma que adopta la bra intermedia de la viga y(x), que recibe el nombre de línea
elástica.
Ejemplo 4.2 Supongamos una viga de sección transversal rectangular de dimensiones a
y b y longitud l, simplemente apoyada en sus extremos. Sobre ella actúa en su centro una
fuerza vertical F . l problema estático es simple y por lo tanto sobre la viga actúan sendas
Figura 4.2: E
fuerzas verticales de valor F/2 en cada uno de sus extremos y dirigidas hacia arriba. Si
tomamos un sistema de referencia con origen en el extremo izquierdo y en el centro de la
viga y el eje OX en el sentido de la viga, en una sección cualquiera a una distancia x,
x < l/2, existirán fuerzas sobre esa sección que darán lugar a una resultante total de valor
F/2, pero también un momento total de valor M (x) = F x/2, en la dirección positiva del eje
OZ . Esto quiere decir que además de la fuerza vertizal total hacia abajo de valor F/2 que
actúa en la sección, deben existir fuerzas horizontales, de resultante nula, que den lugar a
ese momento ector M (x) en la sección. Por lo visto anteriormente, esas fuerzas horizontales
darán lugar a las tensiones que se dibujan en la parte derecha. La componente horizontal
de la tensión, σ11 (x, y) = −A(x)y como hemos visto varía linealmente con la coordenada
y con respecto a la bra neutra. El signo menos hace referencia a que para y negativos, la
fuerza es hacia la derecha, con una función A(x) > 0. La parte A(x) se determinará con la
condición de que el momento con respecto a O de esas fuerzas, nos produzca el momento
total en la sección M (x) = F x/2.
Z
Z
b/2
b/2
(−y)σ11 ady = aA(x)
−b/2
y 2 dy = aA(x)b3 /12 = F x/2,
A(x) =
−b/2
6F x
ab3
Como σ11 es conocido, y suponiendo la viga sin masa y por lo tanto despreciable la acción
gravitatoria, el tensor de tensiones satisface ∂σij /∂xj = 0, resulta
σ11 (x, y) = −
6F xy
,
ab3
∂σ11
∂σ12
+
= 0,
∂x
∂y
σ12 (x, y) =
3F y 2
+ g(x)
ab3
Esta función arbitraria g(x) se determina con la condición de que la suma de las fuerzas
verticales en la sección tiene que ser F/2 hacia abajo.
Z
µ
b/2
σ12 ady =
−b/2
¶¯b/2
¯
F 3
¯
y
+
ag(x)y
= −F/2,
¯
3
b
−b/2
g(x) = −
3F
,
4ab
σ12 =
3F
ab
µ
y2
1
−
b2
4
¶
.
62
CAPÍTULO 4. ELASTICIDAD
Esta tensión es la de cortadura según la sección dada, está dirigida hacia abajo, es nula
en las supercies superior e inferior, y = ±b/2, y alcanza su valor máximo en el centro,
y = 0, σ12 (x, 0) = −3F/4ab, como se ve en la parte derecha de la gura. Vemos que en
el centro la tensión normal vale cero y la tangencial es máxima. Lo mismo ocurre en los
puntos extremos, pero en sentido contrario, en los que la tensión normal es máxima y la
tangencial es nula. Podríamos, por lo tanto, determinar en qué punto de la viga la tensión
principal es máxima.
Por otra parte σ12 = σ21 , con lo que σ21,1 + σ22,2 = 0, es decir σ22,2 = 0 y σ22 (x) = K(x).
Resulta ser independiente de y y por lo tanto sobre la supercie superior y = b/2, no existe
esfuerzo normal, cualesquiera que sea x, luego σ22 (x, y) = 0. Como es un ejemplo de un
campo de tensiones bidimensional y en ausencia de fuerzas volúmicas, la función de Airy
que resuelve este problema es la
φ(x, y) = −
F xy 3
3F xy
.
+
3
ab
4ab
En la hipótesis de haber supuesto la viga con masa, la segunda de las ecuaciones del campo
de tensiones sería
−ρg +
∂σ21
∂σ22
+
= 0,
∂x
∂y
σ22 (x, y) = ρgy + h(x).
Como para y = b/2 la tensión es cero, ρgb/2 + h(x) = 0, y σ22 (x, y) = ρg(y − b/2) < 0, que
es una fuerza de compresión. En este caso no hay función de Airy que resuelve el problema.
Para el cálculo de la elástica, resulta que si es I = ab3 /12 el momento de inercia de la
sección con respecto al centro, se tiene que
y 00 (x) =
M (x)
F
=
x,
YI
2Y I
y 0 (x) =
F 2
x + B,
4Y I
y(x) =
F
x3 + Bx + C.
12Y I
Esta expresión es válida hasta x = l/2. Las condiciones de contorno que debemos imponer
son que y(0) = 0 (que implica C = 0) y por otra parte en el punto medio de la viga la
tangente es horizontal, es decir y 0 (l/2) = 0. Esto nos lleva a que la ecuación de la elástica
es la curva
µ 2
¶
F
x
l2
y(x) =
x
−
, x ∈ (0, l/2).
4Y I
3
4
Se llama echa de la viga a la máxima deformación que ocurre en el centro y que vale
c = y(l/2) = −
F l3
48Y I
El tensor de deformaciones en cada punto (x, y), resulta ser
e11 =
1
σ11 ,
Y
e22 = e33 = −
σ
σ11 ,
Y
e12 =
1+σ
σ12 .
Y
por lo que vemos que también existe deformación transversal según el eje OZ .
4.3.1.
Pandeo
Si tenemos una barra y la sometemos en sus extremos a compresión pura, desde el punto de
vista estático el sistema permanece estacionario. Sin embargo, dependiendo de la relación entre
4.3. DEFORMACIÓN DE UNA VIGA (LÍNEA ELÁSTICA)
63
su longitud y sus dimensiones transversales, existe una tensión de compresión mínima tal que
para valores superiores a ésta, la viga se exa como en la gura.
Si a una distancia x del extremo izquierdo, la viga se ha deformado una altura y , el momento
ector en esa sección vale M (x) = −F y . Como se deduce de (4.4), resulta
à r
!
F
00
−F y = Y Iy , y(x) = K sin x
+ B , y(0) = y(l) = 0,
YI
lo que nos da B = 0 y
r
l
F
= π,
YI
⇒
F = π2
YI
,
l2
independiente de la deformación K que se produzca en su centro. Si sometemos a la viga a una
fuerza de compresión inferior a este valor, el equilibrio estático se mantiene. Sin embargo, para
fuerzas superiores al valor anterior, la viga se exa y se dice que sufre pandeo. A esta fuerza
mínima, capaz de producir pandeo, se le conoce como fuerza de Euler.
Si en vez de una viga se trata de una columna de un edicio, la carga que soporta es conocida,
y en función de su esbeltez, es decir de la relación l2 /I , cuanto más esbelta sea, menor es la
fuerza límite que puede producir pandeo, de ahí que sea necesario modicar este factor para
que la carga que soporte cualquier columna, en las peores circunstancias, sea siempre inferior
a este valor crítico. Leonardo da Vinci y Galileo estudiaron el problema del pandeo de forma
experimental. En particular, Galileo llegó a la conclusión de que los huesos de los pájaros eran
huecos porque con igualdad de masa ósea, se conseguía un mayor momento de inercia de la
sección, y por lo tanto mayor resistencia a la exión, y al pandeo.
Si la viga no es de sección cuadrada y son I1 e I2 los dos momentos de inercia de la sección
con respecto a los dos ejes principales, perpendiculares, que se cruzan en su centro de masa, el
valor que debemos usar para la estimación de la fuerza crítica de Euler, es el menor de ellos.
Una columna pandea según la bra del menor momento de inercia.
Ejemplo
4.3 Material trabajando a cortadura
Supongamos un cubo de lado a sometido a un estado de cortadura pura τ según sus
64
CAPÍTULO 4. ELASTICIDAD
caras. Esto equivale a que el material estuviera sometido a tracción τ según una diagonal
y a compresión −τ , según la otra, pero con la misma tensión que la de cortadura, como
puede verse del analísis del correspondiente círculo de Mohr. La modicación unitaria de
la diagonal es por una parte el alargamiento longitudinal debido a la tracción y por otra el
alargamiento debido al acortamiento transversal, teniendo presente el coeciente de Poisson:
∆D
τ
τ
(1 + σ)τ
=
+σ =
.
D
Y
Y
Y
Por otra parte el cuadrado se deforma lateralmente y se transforma en un rombo, uno de
cuyos lados ha girado un ángulo θ respecto de su posición primitiva en el cuadrado. El
desplazamiento lateral equivale a
∆a
= θ,
a
∆a =
de donde
θ=
√
2∆D,
√
a = D/ 2,
2(1 + σ)τ
τ
= ,
Y
µ
∆a
∆D
=2
,
a
D
τ = µθ.
ya que el coeciente de Lamé µ = Y /2(1 + σ).
4.3.2.
Torsión
Supongamos una barra de sección circular de radio R y longitud l, de tal manera que
sometemos a sus extremos a un par de fuerzas que producen un momento en la dirección del
eje. La barra sufrirá una deformación angular.
Figura 4.3: Torsión de una barra de sección circular. Supondremos que la barra está formada
por un conjunto de tubos concéntricos de espesor ∆r. En cada tubo, un elemento de forma
rectangular (inicialmente de la forma rayada) está trabajando a cortadura y se deforma
adquiriendo la forma romboidal de la gura de la derecha. (Dibujo sacado del libro de Feynman,
The Feynman lectures on Physics, vol 2, cap. 38)
Supongamos la barra circular de radio a y longitud L, de tal manera que bajo la acción de
un par de fuerzas en sus extremos la deformamos haciéndola girar un ángulo φ alrededor de su
eje. Podemos considerar que la barra es una yuxtaposición de cilindros concéntricos, embebidos
unos en otros, y de radios crecientes. Analicemos uno de esos tubos cilíndricos de radio r y
espesor ∆r.
El desplazamiento del borde del tubo vale rφ = Lθ, siendo θ el ángulo que la arista del
cilindro forma con su dirección original. Si es ∆F la fuerza que actua sobre la cara lateral del
elemento indicado en la gura, esta fuerza produce un par con respecto al eje de valor r∆F .
Como ∆F = τ ∆r∆l, siendo τ la tensión tangencial de cortadura, por lo visto en el ejemplo
anterior τ = µθ = µrφ/L, siendo µ el coeciente de Lamé. Si lo sumamos para toda la sección
del tubo, este momento será dM = ∆r2πrµr2 φ/L = 2πr3 µφ∆r/L. El momento de torsión
debido a todos los tubos
Z a
2πr3 µφ
πa4
M=
dr = µ
φ.
L
2L
0
4.3. DEFORMACIÓN DE UNA VIGA (LÍNEA ELÁSTICA)
65
Este es el momento de torsión aplicado al cilindro para su deformación. El momento de torsión
varía linealmente con el ángulo girado, lo que se suele utilizar para la construcción de péndulos
de torsión y su uso para medidas experimentales.
4.3.3. Ondas de tensión
Si un medio está trabajando a cortadura pura, por ejemplo la barra anterior sometida a
torsión, entonces la deformación angular de una sección depende de su posición y del tiempo.
Para medios longitudinales, si la deformación angular φ(z, t) no es uniforme y depende de la
distancia al extremo, hay que sustituir en la expresión del momento anterior, φ/L ≡ ∂φ/∂z ,
por lo que en una sección arbitraria el momento de torsión es
M (z) =
µπa4 ∂φ
,
2 ∂z
Una rodaja de cilindro de altura ∆z experimenta entre sus extremos una diferencia de momento
M (z +∆z)−M (z), que no es en general nula y que se invierte en modicar su momento angular.
El momento angular de una rodaja vale Iω , siendo I = ma2 /2 = ρπa2 ∆za2 /2 el momento de
inercia con respecto al eje y ω = ∂φ(z, t)/∂t, la velocidad angular. Por lo tanto
d
∂M (z)
∆z = Iω,
∂z
dt
µπa4 ∂ 2 φ
ρπa4 ∆z ∂ 2 φ(z, t)
∆z
=
.
2 ∂z 2
2
∂t2
La deformación angular de una rodaja de cilindro, situada a una distancia z de su extremo,
satisface la ecuación de ondas
∂2φ ρ ∂2φ
−
= 0,
∂z 2
µ ∂t2
lo que da lugar a que esa perturbación viaja a lo largo del cilindro con la velocidad de propagación
r
µ
ctrans =
ρ
es decir una ecuación de ondas transversales que se propaga con la velocidad ctrans .
Si lo que producimos es un estado de tensiones normales, entonces el vector desplazamiento en la dirección de la barra u(z, t), satisface la ecuación de ondas para las deformaciones
longitudinales:
s
∂2u
ρ ∂2u
Y
−
= 0, clong =
> ctrans .
2
2
∂z
Y ∂t
ρ
4.4 Consideremos Un prisma recto homogéneo e isótropo de longitud l y dimensiones transversales a y b, que está sometido a sendas fuerzas de tracción según las tres
direcciones, de tal manera que queda estirado en la dirección longitudinal pero no en las
direcciones transversales en las que permanece sin deformarse.
Si llamamos lx = l, ly = a, lz = b en este caso, la deformación en la dirección 0X
Ejemplo
1 Fx
σ Fy
σ Fz
∆lx
=
−
−
,
lx
Y Ax
Y Ay
Y Az
y
∆ly
1 Fy
σ Fx
σ Fz
=
−
−
= 0,
ly
Y Ay
Y Ax
Y Az
1 Fz
σ Fx
σ Fy
∆lz
=
−
−
= 0,
lz
Y Az
Y Ax
Y Ay
lo que hace que
Fy
Fz
σ Fx
=
=
,
Ay
Az
1 − σ Ax
66
CAPÍTULO 4. ELASTICIDAD
que sustituido en la primera nos da
1
∆lx
=
lx
Y
µ
1 − σ − 2σ 2
1−σ
¶
Fx
Ax
por lo que la relación entre la tensión aplicada en la cara transversal y el correspondiente
alargamiento longitudinal es
F
1−σ
∆l
=
Y
.
ab
(1 + σ)(1 − 2σ)
l
El coeciente delante de Y es mayor que 1 lo que implica que es necesario aplicar una
tensión mayor para deformar longitudinalmente un cuerpo cuyos lados se mantienen rmes.
Diríamos que es más rígido cuando se le sujeta lateralmente.
Si el medio en el que se propaga la onda longitudinal no sufre deformación transversal, entonces
en vez del módulo elástico Y deberemos usar el coeciente
Y0 =
Y (1 − σ)
.
(1 + σ)(1 − 2σ)
en vez del Y para determinar la velocidad de propagación de las ondas longitudinales.
4.3. DEFORMACIÓN DE UNA VIGA (LÍNEA ELÁSTICA)
67
Problemas
4.1 Si el medio es isótropo con una deformación lineal isótropa, demostrar que el estado de
tensiones más general del medio es de la forma


σ τ τ
σij =  τ σ τ  .
τ τ σ
4.2 Sea una barra de longitud l y sección transversal S sometida a una fuerza de tracción en
sus extremos de valor F . Determinar el tensor de tensiones y el tensor de deformaciones en el
supuesto de que se trate de un material elástico homogéneo e isótropo.
4.3 Determinar la relación entre las constantes de Lamé λ y µ y las constantes Y y σ . Ex-
presar en términos de estos nuevos parámetros la relación entre el tensor de tensiones y el de
deformaciones
4.4 Probar que φ =
3F
3
2
2
4ac [xy +(l −x)y /3c ]+P y /4ac es una función de tensión de Airy y hallar
tensor σij . Vericar que son las tensiones de una viga en voladizo (incrustada
las componentes del
por un extremo), de dimensión transversal a y 2c, sometida a una fuerza perpendicular F en el
otro extremo y a una fuerza P longitudinal.
4.5 Hallar la relación entre las constantes A y B para que la función φ = Ax21 x32 + Bx52 sea una
función de tensión de Airy. ¾Qué tipo de estado de tensiones representa?
4.6 Determinar la función de Airy y el estado de tensiones de una viga de sección rectangular
de dimensiones transversales a y b y longitud l, simplemente apoyada en sus extremos y que
soporta una carga vertical de valor F aplicada en el centro. Suponer la viga sin masa para
despreciar la fuerza gravitatoria.
4.7 Determinar la función de Airy y el estado de tensiones de una viga de sección rectangular
de dimensiones transversales a y b y longitud l, simplemente apoyada en sus extremos y que
soporta una carga vertical de valor F repartida uniformemente a lo largo de la misma. Suponer
la viga sin masa para despreciar la fuerza gravitatoria.
4.8 Determinar en los estados de tensión planos de medios isótropos, el tensor de deformaciones.
Determinar asímismo, en los estados de deformación planos, el tensor de tensiones.
4.9 Si suponemos un medio continuo homogéneo e isótropo sometido a compresión pura en
todas sus direcciones de valor p, determinar la relación entre esta presión externa y la variación
unitaria de volumen ∆V /V . Al coeciente de proporcionalidad se le llama módulo elástico
volúmico. Como al comprimir el cuerpo su volumen disminuirá, establecer una cota superior
para el coeciente de Poisson.
4.10 Un paralelepípedo homogéneo e isótropo de longitud l y dimensiones transversales a y b,
está sometido a un campo de deformaciones de cizalladura tal que el campo de desplazamientos
es u1 = kx3 , u2 = u3 = 0. Encontrar el tensor de tensiones y el tensor de deformaciones, en
ausencia de fuerzas volúmicas.
4.11 Comprobar que la función de tensión de Airy φ = 2x41 + 12x21 x22 − 6x42 satisface las
condiciones exigidas y determinar las componentes del tensor de tensiones en el supuesto de un
estado de tensiones plano (lo que no quiere decir un estado de deformaciones plano). Determinar
el tensor de deformaciones y vericar que se satisfacen las ecuaciones de compatibilidad para
deformaciones lineales.
68
CAPÍTULO 4. ELASTICIDAD
4.12 Si tenemos una barra de longitud l y sección circular de radio R, demostrar que si a
un extremo le aplicamos un momento externo de valor +M y al otro de −M , entonces la
deformación angular que se produce entre las dos caras extremas es φ que viene dado por la
relación φ = 2lM/πR4 µ.
4.13 Sea una barra de longitud l y sección transversal de momento de inercia respecto de su
centro de gravedad I . Determinar la fuerza mínima de compresión que es necesario aplicar entre
sus extremos, para que la barra sufra pandeo (Fuerza de Euler).
4.14 Sea una barra de longitud l y sección transversal de momento de inercia respecto de su
centro de gravedad I . Determinar la fuerza mínima de compresión que es necesario aplicar entre
sus extremos, para que la barra sufra pandeo como en el problema anterior pero ahora cuando
uno o los dos extremos se encuentran empotrados [El momento ector es distinto de cero en el
caso de empotramiento].
4.15 Obtener las ecuaciones de Navier de un medio homogéneo e isótropo en equilibrio.
4.16 Obtener las ecuaciones de Beltrami de un medio homogéneo e isótropo en equilibrio.
4.17 Determinar la deformación y el estado de tensiones de una barra larga de longitud l
mantenida de forma vertical en un campo gravitatorio.
4.18 Determinar la forma de una viga horizontal, apoyada en sus extremos y sometida a su
propio peso.
4.19 Determinar la forma de una barra de longitud l sometida exclusivamente a su propio
peso, pero con diferentes tipos de apoyos en los extremos: (a) Ambos extremos empotrados.
(b) Ambos extremos apoyados. (c) Un extremo apoyado y el otro empotrado. (d) Un extremo
empotrado y el otro libre. Determinar asímismo las echas máximas.
4.20 Determinar la relación entre el módulo de Young y el coeciente de Poisson y los coecientes elásticos de un cristal cúbico a lo largo de uno de sus ejes
Capítulo 5
Fluidos
Un sólido es en general un medio continuo que experimenta resistencia a la deformación,
en tanto que un uido (líquido o gas) es un medio continuo que experimenta resistencia a la
modicación de su velocidad de deformación y que posee la característica de ser isótropo.
Entonces, como en un sólido el tensor de tensiones depende de la deformación del medio,
un uido es un medio material isótropo en el que el tensor de tensiones es función del tensor de
velocidad de deformación.
El tensor de tensiones admite la forma general
σij = −pδij + τij ,
donde p es la presión hidrostática y τij es el tensor de tensión viscoso, que es nulo en el caso de
uidos ideales, sin viscosidad, y que en general será una función del tensor Dij .
5.1. Fluidos Newtonianos
Se denominan Newtonianos a aquellos uidos en los que existe una relación lineal entre el
tensor τij y el tensor de velocidad de deformación Dij
τij = Kijpq Dpq ,
1
Dij =
2
µ
∂vj
∂vi
+
∂xj
∂xi
¶
.
A los coecientes Kijpq se les denomina coecientes de viscosidad, que debido a la isotropia de
un uido solo dos de ellos son independientes, ya que una función lineal e isótropa de Dij es de
la forma αTrDδij + βDij .
5.2. Fluidos Stokesianos
Son aquellos uidos en los que no existe una relación lineal entre el tensor τij y el tensor de
de velocidad de deformación Dij , pero la isotropía lleva al siguiente
Teorema: Toda función isótropa de Dij es de la forma
τij = f0 δij + f1 Dij + f2 Dik Dkj ,
donde los fi , i = 0, 1, 2 son funciones de los tres invariantes del tensor simétrico Dij , que se
reducen a su traza I = Dii , II = (Dii Djj − Dij Dji )/2, III = det D.
69
70
5.3.
CAPÍTULO 5. FLUIDOS
Ecuaciones de Navier-Stokes
En el caso de un uido homogéneo e isótropo y Newtoniano, los coecientes de viscosidad se
reducen simplemente a dos de ellos independientes de tal manera que las ecuaciones constitutivas
del medio se reducen a
σij = −pδij + τij = −pδij + λδij Dkk + 2µDij ,
donde la viscosidad del medio continuo viene caracterizada por los dos coecientes λ y µ.
Las ecuaciones de la dinámica de los medios continuos para un tensor de tensiones de la
forma dada, reciben el nombre de ecuaciones de Navier-Stokes, que resultan ser:
ρ
∂vi
∂vi
∂p
∂(∇ · v)
dvi
=ρ
+ ρvj
= ρki −
+ (λ + µ)
+ µ∇2 vi .
dt
∂t
∂xj
∂xi
∂xi
(5.1)
Si ∇ · v = 0, nos quedan las ecuaciones de Navier-Stokes para uidos incompresibles
ρ
∂vi
∂vi
∂p
+ ρvj
= ρki −
+ µ∇2 vi .
∂t
∂xj
∂xi
(5.2)
Estas tres ecuaciones junto con la ecuación de continuidad forman un conjunto completo de 4
ecuaciones con 4 incógnitas: la presión p(x, t) y el campo de velocidad v(x, t), supuesta conocida
la fuerza másica externa k y el campo de densidad ρ(r, t). Para uidos perfectos basta con tomar
λ = µ = 0 en las anteriores ecuaciones. En general para líquidos la incompresibilidad se suele
simplicar y suponer que ρ es constante en todo instante y en todo punto del uido. En el caso
de los gases ρ no es constante en toda la masa uida e incluso en el régimen incompresible es
necesaria la ecuación de estado F (ρ, p, v(T )) = 0 para tener un número suciente de ecuaciones
para resolver las 5 incógnitas p, ρ, v . Si el régimen no es incompresible entonces hay que utilizar
las ecuaciones de Navier-Stokes en la forma (5.1).
La dicultad de resolución matemática de las ecuaciones anteriores, estriba en el término no
lineal en las variables de velocidad vj ∂vi /∂xj , que existe incluso en el caso de uidos perfectos
(µ = 0). Esta no linealidad hace que no se verique el principio de superposición, esto es
que suma de soluciones del campo de velocidad no tiene por qué ser una nueva solución. Al
coeciente ν = µ/ρ se le denomina coeciente de viscosidad cinemático, y para algunos uidos
toman los valores:
aire
agua
alcohol
glicerina
mercurio
5.3.1.
µ g/s cm
1,8 × 10−4
0.010
0.018
8.5
0.0156
ν cm2 /s
0.150
0.010
0.022
6.8
0.0012
Ecuación de Euler
Para uidos perfectos (µ = 0) la ecuación de Navier-Stokes en un campo gravitatorio se
reduce a
∂vi
∂vi
∂p
ρ
+ ρvj
= ρgi −
,
(5.3)
∂t
∂xj
∂xi
que se conoce como ecuación de Euler.
5.3. ECUACIONES DE NAVIER-STOKES
71
5.3.2. Flujo estacionario. Hidrostática
Si tanto p como v no son funciones explícitas del tiempo t estamos en la situación de ujo
estacionario. Entonces, las ecuaciones de Euler toman la forma
ρvj
∂vi
∂p
= ρgi −
.
∂xj
∂xi
Un caso particular de ujo estacionario es aquel en el que toda la masa uida permanece en
reposo en todo instante, por lo que la solución para el campo de velocidad es v = 0, por doquier.
Estamos en el caso que se denomina hidrostática, y la única variable a determinar es la presión
del uido en todos sus puntos.
5.3.3. Ecuación de Bernoulli
Supongamos que
R p la densidad ρ se puede expresar como una función de la presión ρ(p).
Llamemos P (p) = p0 dp/ρ(p). Además supongamos que las fuerzas externas se pueden derivar
de una función potencial Φ, gi = −∂Φ/∂xi , la ecuación dinámica queda:
dvi
∂(Φ + P (p))
=−
.
dt
∂xi
En el caso de un campo gravitatorio uniforme g en la dirección vertical z , Φ = gz . Si se integra
la ecuación de Euler (5.3) a lo largo de una línea de corriente resulta
v2
Φ + P (p) +
+
2
Z
∂vi
dxi = C(t),
∂t
(5.4)
con C(t) = constante a lo largo de cada línea de corriente. En el caso de ujo irrotacional
rotv = 0, podemos obtener v = ∇V , siendo V el potencial de velocidad, con lo que
Φ + P (p) +
v 2 ∂V
+
= C(t).
2
∂t
En el caso de ujo estacionario (ρ = cte.) se nos convierte en la ecuación de Bernoulli
Φ+
p v2
+
= cte.
ρ
2
5.3.4. Teorema de Kelvin
Para uidos ideales, en presencia de un campo exterior conservativo que deriva de un potencial Φ, si llamamos Γ(t) a la circulación en el instante t, del vector velocidad alrededor de
cualquier curva cerrada C(t) formada por puntos del uido, entonces
I
Γ(t) =
v · dr = cte.
C(t)
es decir dΓ/dt = 0.
La derivada material de la circulación Γ vale:
¶
¶
I µ
I
I µ
dΓ
d
∂vi
∂vj
p
1
∂vi
2
=
+
vk + vj
dxi =
−d(Φ + ) + d(v ) = 0,
vi dxi =
dt
dt
∂t
∂xk
∂xi
ρ
2
por tratarse de la integral de una diferencial exacta a lo largo de un circuito cerrado. Se han
reemplazado los dos primeros términos por el segundo miembro de la ecuación de Euler (5.3).
72
CAPÍTULO 5. FLUIDOS
5.3.5.
Densidad de impulso
Supongamos un uido no sometido a fuerzas volúmicas externas. El momento lineal por
unidad de volumen de un cierto elemento de corriente es ρv . Si pretendemos determinar lo
que cambia en cada punto por unidad de tiempo deberemos calcular ∂(ρv)/∂t. Si utilizamos la
ecuación de continuidad y la ecuación de Euler en el caso de uido perfecto se llega a
∂Πij
∂(ρvi )
=−
,
∂t
∂xj
Πij = pδij + ρvi vj ,
y al tensor simétrico Πij se le da el signicado de densidad de impulso por unidad de tiempo,
de tal manera que su ujo a través de una supercie nos suministra el momento lineal que por
unidad de tiempo atraviesa esa supercie. Para uidos viscosos y Newtonianos toma la forma
Πij = pδij + ρvi vj − τij = −σij + ρvi vj ,
5.4.
σij = −pδij + λδij Dll + 2µDij .
Ecuaciones de Helmholtz
Para un uido incompresible, en un campo de fuerzas conservativo ki = −∂i Φ, es posible
obtener una ecuación dinámica que involucre solamente al campo de velocidad. Como
dv
∂v
1
=
+ (v · ∇)v,
(v · ∇)v = (∇ × v) × v + ∇(v · v),
dt
∂t
2
si denimos el vector ω = ∇ × v , resulta ser un vector cuyas componentes son las componentes
esenciales del tensor vorticidad, ωi = ²ijk Vjk . Sustituyendo esto en las ecuaciones de NavierStokes, y tomando su rotacional, se llega a las ecuaciones de Helmholtz para el campo de
velocidad y de vorticidad:
∇ · v = 0,
(ecuación de continuidad)
∇ × v = ω, (denición de ω)
µ
∂ω
+ ∇ × (ω × v) = ∇2 ω (rotacional de la Ec. de Navier-Stokes)
∂t
ρ
Para uidos ideales (µ = 0), si inicialmente en todos los puntos de una región ω(r, 0) = 0, y
v(r, 0) es uniforme, entonces ω(r, t) = 0 para todo t posterior. En un uido ideal, si asociado a
una cierta masa de uido no existe inicialmente vorticidad, ésta no aparece posteriormente. En
un uido real, que inicialmente no tiene vorticidad, la posible vorticidad que aparezca se deberá
a la presencia del término de viscosidad.
En efecto, si µ = 0, el cálculo de
ω(r, ∆t) = ω(r, 0) +
¯
∂ω ¯¯
∆t + · · · ,
∂t ¯t=0
y las sucesivas derivadas temporales de este desarrollo, se calculan a partir de la ecuación de la
dinámica, que se reduce a
∂ω
= ω(∇ · v) − v(∇ · ω) + (v · ∇)ω − (ω · ∇)v = 0.
∂t
Como ∇ · ω = 0, las líneas de vorticidad o bien son cerradas o terminan sobre la supercie
de contorno del medio uido. Helmholtz enuncia la evolución de las líneas de vorticidad en la
forma:
1. Las líneas de vorticidad son convectadas por el ujo.
2. El valor de ω aumenta con el estiramiento de las líneas de vorticidad.
3. El producto ωS se mantiene constante siendo S la sección transversal de un tubo de
vorticidad.
Tanto 1 como 3 se deducen de forma simple a partir del teorema de Kelvin.
5.5. PROBLEMAS BIDIMENSIONALES
73
5.4.1. Número de Reynolds
Si en las ecuaciones de Helmholtz expresamos todas las magnitudes en función de variables adimensionales, tomando por ejemplo como referencia de longitudes una dimensión L del
sistema, como velocidad tipo la velocidad v0 del uido en una zona límite, como unidad de
tiempo L/v0 , entonces si denimos x = Lx0 , y = Ly 0 , z = Lz 0 , vx = v0 vx0 , etc. ∇ = ∇0 /L, ∂/∂t =
∂/∂t0 L/v0 , ω = ω 0 v0 /L, la ecuación de Helmholtz se escribe en las magnitudes adimensionales:
µ
∂ω 0
1 0
0
+ ∇0 × (ω 0 × v 0 ) =
∇ 2ω0 = ∇ 2ω0,
0
∂t
ρv0 L
R
donde la magnitud adimensional R = ρv0 L/µ es el número de Reynolds que caracteriza al
sistema físico. Es el único parámetro relevante que caracteriza a toda la dinámica de los uidos
incompresibles.
5.5. Problemas bidimensionales
En aquellos sistemas uidos bidimensionales, incompresibles y estacionarios, en los que dada
la simetría del problema la velocidad solamente tiene dos componentes vx (x, y) y vy (x, y) la
ecuación de continuidad se escribe ∂vx /∂x + ∂vy /∂y = 0. Supongamos que queremos analizar
movimientos irrotacionales, es decir que en toda la masa uida rotv = 0 y por lo tanto podemos
derivar el campo de velocidad de una función potencial v = ∇Ψ. Si existe una función Ψ(x, y)
tal que vx = ∂Ψ/∂x, vy = ∂Ψ/∂y , la ecuación de continuidad equivale a la búsqueda de una
función potencial de la velocidad Ψ que satisface la ecuación de Laplace en dos dimensiones
∇2 Ψ = 0.
Como tanto la parte real como la imaginaria de cualquier función analítica satisfacen esta
condición, resulta que la solución de estos problemas bidimensionales equivale a la búsqueda de
ciertas funciones analíticas cuya geometría se adapte al problema físico estudiado. Si tenemos
un perl sumergido en el uido, el contorno del perl debe ser una línea de corriente, ya que
sobre él, el vector velocidad del uido debe ser necesariamente tangente.
Como toda función analítica se escribe f (z) = U (x, y) + iV (x, y), siendo U su parte real y
V su parte imaginaria, estas funciones satisfacen ∇2 U = ∇2 V = 0. Se dice que son funciones
armónicas conjugadas, pues además satisfacen ∂U/∂x = ∂V /∂y , ∂U/∂y = −∂V /∂x. Las curvas
U (x, y) =cte son ortogonales a las curvas V (x, y) =cte. Si consideramos que la parte real U
es el potencial de velocidad del correspondiente problema bidimensional, entonces las curvas
V (x, y) =cte son precisamente las líneas de corriente del ujo, y una de estas líneas de corriente
debe ser el perl dado. Como
f 0 (z) =
∂V
∂U
∂U
∂U
+i
=
−i
= vx (x, y) − ivy (x, y) ≡ w
∂x
∂x
∂x
∂y
y las componentes real e imaginaria de f 0 (z) nos dan las componentes vx y −vy del correspondiente problema. Como además la ecuación de Laplace es lineal, podemos sumar soluciones para
dar nuevas soluciones.
5.5.1. Fuerza y Momento sobre un obstáculo. Fórmulas de Blasius
Si un uido toma contacto con un obstáculo de forma cualquiera, le realizará una fuerza y
un momento. En el caso bidimensional como tenemos el potencial de velocidad que nos produce
la función compleja w = vx − ivy , podemos utilizar su expresión para calcular las componentes
cartesianas de la fuerza externa sobre el obstáculo y el momento de estas fuerzas con respecto al
74
CAPÍTULO 5. FLUIDOS
origen de coordenadas. Si la región que dene al obstáculo tiene por contorno la curva cerrada
C , entonces Blasius da las siguientes expresiones para la fuerza y el momento:
I
I
iρ
ρ
2
Fx − iFy =
w dz, M = Re
w2 zdz.
2 C
2
C
De esta forma si la función w es analítica en el interior y sobre el contorno de integración C del
obstáculo, las anteriores integrales son nulas. Para obtener algún tipo de empuje es necesario
que w posea alguna singularidad en el interior de C .
Si no existe viscosidad la fuerza es debida solamente a la presión. Sobre el obstáculo, si es θ el
ángulo que forma el elemento de arco dr con el eje OX
I
I
I
I
I
I
Fx = −
p cos(n, x)ds = −
p sin θds = −
pdy, Fy = −
p cos(n, y)ds =
p cos θds =
pdx.
C
C
C
C
C
C
p0 −ρ(vx2 +vy2 )/2
El teorema de Bernoulli, supuesta una velocidad nula en el innito, nos lleva a p =
donde la velocidad v está evaluada sobre el perl. Como vx2 + vy2 = (vx − ivy )(vx + ivy ) = ww̄, de
tal manera que
I
I
I
iρ
−ß pdz̄ = −i p(dx − idy) = Fx − iFy =
ww̄dz̄,
2 C
pero sobre el contorno w̄dz̄ = wdz , lo que brinda el resultado. En efecto
µ
¶
µ
¶
∂U
∂U
∂U
∂U
∂V
∂V
w̄dz̄ =
+i
(dx − idy) =
dx +
dy − i
dx +
dy = dU − idV = dU = wdz,
∂x
∂y
∂x
∂y
∂x
∂y
ya que el contorno es una línea V =cte.
Para el cálculo del momento hay que tener presente que
I
I
I
I
ρ
ρ
M=
pds(−x cos θ −y sin θ) = −
p(xdx+ydy) =
(vx2 +vy2 )(xdx+ydy) = Re
ww̄zdz̄,
2 C
2
C
C
C
y con el mismo razonamiento que antes se obtiene el resultado.
Si en general lo que estudiamos es un obstáculo moviéndose en el seno de un uido en
reposo, entonces la velocidad será diferente de cero en el entorno del obstáculo, pero se anulará
a distancias lejanas del objeto. La velocidad compleja debe anularse en el innito, por lo que
será de la forma
B
A
w = + 2 + ···
z
z
conteniendo solamente potencias negativas de z . Si lo que consideramos es un obstáculo en
reposo con respecto al observador y en una masa uida moviéndose uniformemente, entonces
su comportamiento en el innito tiende a un régimen constante v0 , por lo que w será
w = v0 +
De aquí
A
B
+ 2 + ···,
z
z
⇒
f (z) = v0 z + A ln z −
B
+ ···
z
(5.5)
µ
¶2
A
B
A
w = v0 + + 2 + · · · = v02 + 2v0 + O(1/z)2 ,
z
z
z
2
que al integrarlo en un circuito cerrado solamente el término en 1/z puede dar una contribución
no nula siempre que el punto z0 = 0 esté dentro del circuito de integración. Como en este caso
I
dz
= 2πi
z
resulta que el empuje vale
Fx − iFy =
iρ
2v0 A2πi = −2πvo Aρ,
2
5.5. PROBLEMAS BIDIMENSIONALES
75
y dependiendo de que A sea real o imaginario tendremos fuerza de arrastre Fx 6= 0 o fuerza
de sustentación Fy 6= 0. En cualquier caso el coeciente A es el residuo en el punto z0 = 0
de la función w = f 0 (z), y por lo tanto es proporcional a la circulación del campo de velocidad
complejo alrededor del obstáculo. En ausencia de viscosidad tendremos fuerza si el campo de
velocidad poseee una circulación no nula. Si la circulación es nula, como en el caso de un
régimen simétrico, con simetría de reexión, entonces no existirá ninguna fuerza (paradoja de
D'Alembert).
5.5.2. Ejemplos de problemas bidimensionales irrotacionales
Dada la expresión general (5.5) de la función analítica f (z) que resuelve el problema dinámico
estacionario de uidos ideales incompresibles en régimen irrotacional, vamos a analizar distintos
ejemplos, según los diferentes términos que consideremos en su desarrollo.
1.
f (z) = v0 z = v0 x + iv0 y
Corresponde a un ujo laminar bidimensional con velocidad constante v0 .
vx = v0 ,
vy = 0.
2.
f (z) = v0 ze−iα = v0 (x cos α + y sin α) + iv0 (y cos α − x sin α)
Corresponde a un ujo laminar bidimensional con velocidad constante v0 , pero inclinada
un ángulo α respecto del eje OX .
vx = v0 cos α,
vy = v0 sin α.
3.
Q
ln(z − z0 )
2π
Representa a un manantial (Q > 0) o sumidero (Q < 0), situado en el punto z0 , de caudal
Q. Las líneas de corriente son rectas radiales que salen (o llegan) al punto z0 .
f (z) =
f 0 (z) =
Q1
Q x − iy
=
,
2π z
2π x2 + y 2
f (z) = v0 z +
vx =
Q
x
,
2
2π x + y 2
vy =
Q
ln z
2π
4. Superposición de una corriente uniforme y un manantial.
Simula a un cuerpo con borde romo si sustituimos alguna líneas de corriente por un obstáculo. Sobre el perl
simétrico y romo la circulación de la velocidad es nula,
aunque f 0 (z) ' Q/z .
vx = v0 +
Q
x
,
2
2π x + y 2
vy =
Q
y
.
2
2π x + y 2
Q
y
.
2
2π x + y 2
76
CAPÍTULO 5. FLUIDOS
5.
m
,
z
f (z) =
Flujo correspondiente a un dipolo de intensidad m, como
límite de un manantial y un sumidero cuya separación
tiende a cero.
vx =
m(x2 − y 2 )
,
(x2 − y 2 )2 + 4x2 y 2
vy =
(x2
2mxy
.
− y 2 )2 + 4x2 y 2
6.
f (z) = Cz n ,
n 6= 1
Flujo cuyo contorno son dos paredes que forman un ángulo π/n. La constante C representa
la intensidad del ujo por unidad de longitud. Aquí la velocidad crece cuando nos alejamos.
f 0 (z) = nCz n−1 ,
n = 4,
n = 2,
vx = 2Cx,
vx = 4C(x3 − 3xy 2 ),
vy = −2Cy.
vy = 4C(y 3 − 3x2 y).
7.
iΓ
ln(z − z0 )
2π
Corresponde a un punto singular z0 en el que existe un torbellino tal que la circulación del
campo de velocidad a lo largo de un circuito que rodee a z0 vale Γ. Las líneas de corriente
son circunferencias con centro en el punto z0 . Si una de las circuferencias se sustituye por
un perl cilíndrico del mismo radio, entonces se nos describe el régimen irrotacional en el
exterior de un cilindro con circulación no nula Γ del campo de velocidad. Existirá por lo
tanto una fuerza de sustentación sobre dicho cilindro, siempre que la velocidad del uido
en el innito v0 6= 0. Para ello basta considerar esta f (z) con el término adicional v0 z .
f (z) =
f 0 (z) = v0 +
Γ ix + y
,
2π x2 + y 2
vx = v0 +
Γ
y
,
2
2π x + y 2
vy =
Γ −x
,
2π x2 + y 2
F = v0 Γρ.
5.5. PROBLEMAS BIDIMENSIONALES
µ
¶
R2
f (z) = v0 z +
,
z
8.
µ
¶
R2
−iα
f (z) = v0 ze
+ −iα
ze
Representa al ujo alrededor de un cilindro de radio R
centrado en el origen, y tal que en el innito tiende a
un ujo uniforme de velocidad v0 . El segundo caso es el
mismo, salvo que el campo de velocidad está girado un
ángulo α. Como f 0 (z) no posee términos en 1/z , el empuje
sobre el cilindro es nulo.
f (z) =
9.
77
Q
ln(z 2 − a2 )
2π
Fuente en las proximidades de una pared innita. Es la
superposición de dos manatiales en los puntos a y −a.
donde la imagen corresponde a la mitad derecha del ujo.
µ
¶
R2
Γ
z
f (z) = v0 z +
+ i ln
z
2π R
10. Flujo alrededor de un cilindro circular de radio R con
circulación Γ, y por lo tanto con empuje, por unidad de
longitud, de valor ρv0 Γ. En la gura se ha tomado k =
Γ/2π = 1.
5.5.3. Teorema de la aplicación de Riemann
Sea C una curva simplemente conexa que es el contorno de una región R. Sea C 0 la circunferencia unidad centrada en el origen, que es el contorno de la región R0 , llamada disco unidad.
Entonces existe una aplicación analítica 1 a 1 en R, w = f (z) que aplica R en R0 y C en C 0 .
Esta función depende de tres constantes arbitrarias y aunque Riemann demuestra su existencia no suministra ningún método para encontrarla.
Ejemplo
5.1 Sea H(x, y) una función armónica en el plano, ∂ 2 H/∂x2 + ∂ 2 H/∂y 2 = 0.
Sea z = x + iy = f (w) ≡ f (u + iv) una función analítica, que dene la transfomación
del plano R2 dada por las correspondientes funciones x = x(u, v), y = y(u, v). Entonces la
función F (u, v) = H(x(u, v), y(u, v)) es una función armónica en el plano, en términos de
las variables u y v . En efecto
∂H ∂x ∂H ∂y
∂F
=
+
,
∂u
∂x ∂u
∂y ∂u
∂2F
∂2H
=
∂u2
∂x2
µ
∂x
∂u
¶2
∂F
∂H ∂x ∂H ∂y
=
+
.
∂v
∂x ∂v
∂y ∂v
∂H ∂ 2 x ∂ 2 H
∂ 2 H ∂x ∂y
+
+
+2
∂x∂y ∂u ∂u
∂x ∂u2
∂y 2
µ
∂y
∂u
¶2
+
∂H ∂ 2 y
.
∂y ∂u2
78
CAPÍTULO 5. FLUIDOS
∂2H
∂2F
=
∂v 2
∂x2
µ
∂x
∂v
¶2
+2
∂ 2 H ∂x ∂y ∂H ∂ 2 x ∂ 2 H
+
+
∂x∂y ∂v ∂v
∂x ∂v 2
∂y 2
µ
∂y
∂v
¶2
+
∂H ∂ 2 y
.
∂y ∂v 2
Como la transformación es analítica, las funciones x e y satisfacen las condiciones de CauchyRiemann
∂x
∂y
∂x
∂y
=
,
=− ,
∂u
∂v
∂v
∂u
y sumando las dos expresiones anteriores, teniendo en cuenta estas condiciones y que tanto
x como y son funciones armónicas, resulta que F es también una función armónica.
De esta forma si la función armónica H es la función potencial de velocidad de un régimen
irrotacional alrededor de un obstáculo circular, y z = f (u + iv) es la función analítica que
nos transforma el círculo en un perl cualquiera C , entonces la función transformada F será
el potencial de velocidad del régimen irrotacional alrededor de un obstáculo de la forma C ,
siempre y cuando se sigan cumpliendo las condiciones asintóticas del problema físico.
5.5.4.
Transformación de Joukowski
Como caso particular del teorema anterior, consideremos la transformación propuesta por
Joukowski. Se dene mediante la aplicación
w=z+
a2
,
z
y es una aplicación conforme del plano que transforma el círculo de radio a, centrado en el
origen, en el segmento del eje OX comprendido entre [−2, 2]. Los puntos z = ±a tienen la
peculiaridad que en ellos w0 = 0 y por lo tanto en ellos la transformación no es conforme. Sin
embargo como la transformación es analítica en el exterior de la circunferencia, resulta que la
transformación de un campo vectorial que satisface la ecuación de Laplace, lo transforma en
otro campo vectorial que satisface la ecuación de Laplace, pero que se adapta al perl de una
placa sin espesor, contenida en el eje OX y de tamaño 4a.
El semicírculo superior se transforma en el segmento [−2a, 2a] y el inferior en el [2a, −2a], que
al no ser la transformación conforme en los puntos de encuentro, en los que los dos semicírculos
se encuentran bajo un ángulo de 180◦ , como la derivada segunda w00 = 2a2 /z 3 6= 0 no se anula
en esos puntos entonces las imágenes se encuentran formando un ángulo de 360◦ . Supongamos
el régimen alrededor del cilindro circular dado por el ejemplo bidimensional 10.
La transformación que hay que realizar es la
µ
¶
µ
¶
1
1
u=x 1+ 2
, v =y 1− 2
x + y2
x + y2
5.5. PROBLEMAS BIDIMENSIONALES
79
80
CAPÍTULO 5. FLUIDOS
y una vez obtenida la trayectoria en el plano (x, y) (guras de la izquierda) la transformamos
en la correspondiente trayectoria en el plano (u, v) (guras de la derecha).
Si el círculo lo hacemos excéntrico de tal manera que pase siempre por el punto (1, 0) y de
radio R2 = (1 − x0 )2 + y02 , la transformación de Jukowski nos transforma este círculo en un
perl de ala cuyo borde de salida es el punto (2, 0) en el que la transformación no es conforme
y al analizar el ujo irrotacional en este caso nos sale el régimen de la gura:
Ejemplo 5.2 Una bola de radio R se desplaza en el seno de un uido perfecto e incompresible. Determinar las características del régimen potencial alrededor de la bola. Suponer
nalmente, que la velocidad de la bola no es necesariamente constante.
La solución relativa es la misma que una bola en reposo y un uido que se mueve desde el innito con una velocidad uniforme −u. Consideremos primero un uido en reposo
y situemos el origen del sistema de referencia en el centro de la esfera que se mueve con
velocidad u.
Si hacemos v = ∇V , la ecuación de continuidad implica ∇2 V = 0. Debemos buscar soluciones de la ecuación de Laplace que se anulen en el innito. Éstas son de la forma 1/r
y sus derivadas. V debe ser una función escalar, lineal en la velocidad de la bola u, ya
que la ecuación de Laplace es lineal, luego debe ser proporcional a u · ∇(1/r), es decir
V = −C(u · n)/r2 = −C(u · r)/r3 siendo n el vector unitario en la dirección radial. El
valor de C se determina por la condición de que la componente de la velocidad del uido
normal a la supercie de la esfera sea la misma que la correspondiente componente de la
velocidad de la esfera, ya que supuesto el uido ideal puede tener una componente tangencial no necesariamente nula. De esta forma V = −R3 (u · n)/2r2 , pues ∇(u · r) = u,
∇(1/r3 ) = −3/r4 n. De aquí resulta que el campo de velocidad del uido, con respecto a un
5.6. CAPA LÍMITE
81
observador situado en cada instante en el centro de la esfera y que ve moverse a ésta con
velocidad u, es
R3
v = 3 (3n(u · n) − u) .
2r
Es un campo de velocidad que tiende a cero en el innito. Si lo calculamos con respecto a
un observador jo en la esfera que está en reposo en el origen, entonces deberemos imprimir
una velocidad −u a tod el sistema, luego
v=
R3
(3n(u · n) − u) − u.
2r3
(5.6)
Podemos vericar que rotv = 0 y que divv = 0. Si aplicamos el teorema de Bernouilli a lo
largo de una línea de corriente, tenemos que en el innito la presión vale p0 , la velocidad es
u, resulta entonces que en otro punto de la línea de corriente
1
1
∂V
,
p0 + ρu2 = p + ρv 2 + ρ
2
2
∂t
pero
∂V
∂V du
R3
du
=
·
= − 2n ·
,
∂t
∂u dt
2r
dt
ya que la posible dependencia temporal del potencial V con el tiempo lo es a través de una
posible dependencia de u con t. Si el punto nito está sobre la supercie de la esfera y
llamamos θ al ángulo que forma el vector normal a la supercie de la esfera con la dirección
de u,
¯
¯
¢ u2 1 ¡
¢ 9u2
∂V du ¯¯
v 2 ¯¯
R du
u2 ¡
·
n·
,
3 cos2 θ + 1 + − 3(u · n)2 − u2 =
(1−cos2 θ),
=
−
=
¯
¯
∂u dt R
2
dt
2 R
8
2 2
8
de donde sobre un punto de la esfera
p(R, θ) = p0 +
ρR
du
ρu2
(9 cos2 θ − 5) +
n·
.
8
2
dt
Si con este campo de presiones calculamos la fuerza que el uido hace sobre la esfera resulta
F = −(M/2)du/dt, siendo M la masa de la esfera. Si ésta no está acelerada, entonces la
fuerza es nula.
5.6. Capa límite
La teoría de la capa límite fue desarrollada por Prandtl. Establece que cuando una masa
uida se encuentra con un obstáculo, los fenómenos viscosos que dan lugar a pérdidas por
fricción tienen lugar solamente en una capa alrededor del obstáculo, que se denomina capa
límite, en tanto que en el resto de la masa uida su comportamiento se puede tomar como
carente de viscosidad. En general el espesor de la capa límite depende del número de Reynolds.
Para números de Reynolds altos toda la capa
√ límite es gobernada por los fenómenos viscosos y el
régimen es laminar. El espesor es δ/L ' 1/ R. Existe por lo tanto un problema exterior (como
uido perfecto, sin viscosidad) y un problema interior (dentro de la capa límite). El problema
exterior se resuelve con la condición de que la velocidad es tangencial al obstáculo (en el caso
bidimensional el perl del obstáculo corresponde a posibles líneas de corriente). El problema
interior se resuelve con la condición de que la velocidad del uido es nula sobre la supercie del
obstáculo y va variando continuamente hasta llegar en el borde de la capa límite a empalmar
con la solución exterior de uido perfecto.
En el caso de problemas bidimensionales, laminares, incompresibles, estacionarios y de
número de Reynolds grande, la solución exterior al obstáculo se resuelve aplicando la ecuación
de Bernoulli y se obtiene la solución para el campo de velocidad y de presión pe + ρve2 /2 = cte.
a lo largo de las líneas de corriente. Para la solución interior, si llamamos pi (x, y) al campo de
presión y v i ≡ (u(x, y), v(x, y)) al campo bidimensional de velocidad, las ecuaciones de continuidad y de Navier-Stokes nos llevan a que el campo de presión no es función de la variable
82
CAPÍTULO 5. FLUIDOS
Figura 5.1: Coordenadas adaptadas al análisis bidimensional de la capa límite, cuyo espesor
δ varía a lo largo del contorno del cuerpo. La línea de puntos delimita lo que denominamos
la región interior, en la que existen fenómenos de viscosidad, de la región exterior en la
que la solución es la de uido perfecto. La velocidad del uido en contacto con la pared es
nula.
transversal al obstáculo y , y por lo tanto pi (x) = pe (x) y para las demás a
∂u ∂v
+
= 0,
∂x ∂y
u
∂u
∂u
1 dpe µ ∂ 2 u
+v
=−
+
∂x
∂y
ρ dx
ρ ∂y 2
ecuaciones que fueron ya establecidas por Prandtl en 1904. Las condiciones de contorno son
u(x, 0) = v(x, 0) = 0,
(u(x, δ), v(x, δ)) = v e (x, δ),
con lo que se consigue el empalme de las soluciones en el borde de la capa límite. En la expresión
anterior hemos supuesto que la variación de v a lo largo de la distancia longitudinal x, es muy
pequeña, ∂v/∂x ≈ 0, lo que da, a partir de la ecuación de continuidad, que ∂ 2 u/∂x2 ≈ 0. Como
estamos suponiendo que ∂v/∂x ≈ 0, pero ∂u/∂y 6= 0, entonces el rot v i 6= 0 en los puntos del
interior de la capa límite, por lo que en general el ujo laminar es rotacional.
La ecuacion de Navier-Stokes para la segunda componente queda:
µ
¶
∂v
∂v
1 dpe
µ ∂2v
∂2v
u
+v
=−
+
+
,
∂x
∂y
ρ dy
ρ ∂x2
∂y 2
y las aproximaciones que estamos suponiendo para la componente v y la presión pe nos llevan a que
v∂v/∂y ≈ 0 por ser cuadrática en v y ∂ 2 v/∂y 2 ≈ 0, con lo que esta ecuación suministra información
adicional de que ∂pi ∂y = 0, pi (x) = pe (x).
Como la presión a lo largo de la capa límite coincide con la presión de la solución irrotacional,
resulta:
1 dpe
∂ue
= −ue
,
ρ dx
∂x
siendo ue la velocidad del uido exterior a lo largo de una línea de corriente.
Si U0 es la velocidad lejos del obstáculo, L es una dimensión longitudinal del mismo y R el
número de Reynolds del problema en cuestión, mediante el cambio
√
√
x = Lx0 , y = Ly 0 / R, u = U0 u0 , v = U0 v 0 / R, R = U0 Lρ/µ,
las ecuaciones de Prandtl quedan (una vez suprimidas las primas) en términos de las variables
adimensionales:
∂u ∂v
∂u
∂u ∂ 2 u
due
+
= 0,
u
+v
− 2 = ue
,
∂x ∂y
∂x
∂y
∂y
dx
que son independientes del número de Reynolds y por lo tanto sometidas a la invariancia por
semejanza. Se llega al resultado de que cuando el número de Reynolds varía, el movimiento del
5.6. CAPA LÍMITE
83
uido dentro de la capa límite es tal que dejando invariantes las dimensiones y velocidades longitudinales, las distancias y velocidades transversales varían en razón inversa de la raiz√cuadrada
de R, de ahí que se estime que el espesor de la capa límite varía como δ/L ' 1/ R. Si
√ las
0
0
velocidades adimensionales u y v son del orden de la unidad, entonces u ' U0 y v ' U0 / R.
Ejemplo 5.3 Perl de velocidad de la capa límite de una placa innita. El uido
exterior se mueve con velocidad U0 a lo largo del eje OX . Es un problema bidimensional,
por lo que las ecuaciones de la capa límite quedan con v ≡ (u, v)
∂u ∂v
+
= 0,
∂x ∂y
u
∂u
∂u
1 ∂pe
∂2u
+v
=−
+ν 2,
∂x
∂y
ρ ∂x
∂y
∂pe
= 0,
∂y
que al ser el régimen laminar, en la parte superior de la placa las líneas de corriente siguen
siendo rectas y =cte., por lo que al aplicar el teorema de Bernouilli al uido exterior nos
lleva a ∂pe /∂x = 0. Las condiciones de contorno son que u(x, 0) = v(x, 0) = 0, x > 0, y
que lı́my→∞ u(x, y) = U0 . Blasius (1908) propone un cambio de variables, sabiendo que el
√
espesor de la capa límite varía con x/ R de la forma
r
U0
∂
∂
∂ ∂η
∂η
η
ξ = x, η = y
,
=
+
,
=− ,
2νx
∂x
∂ξ ∂η ∂x
∂x
2x
∂
∂
=
∂y
∂η
r
U0
,
2νx
∂2
∂ 2 U0
=
.
∂y 2
∂η 2 2νx
Si denimos la función de corriente V tal que v =rot(0, 0, V ), se nos garantiza que se cumple
la ecuación de continuidad divv = 0.
r
r
p
∂V
∂V
U0
∂V
νU0
0
V = 2νxU0 f (η), u =
=
= U0 f (η), v = −
=
(ηf 0 − f ) .
∂y
∂η 2νx
∂x
2x
Se debe observar que f 0 = u/U0 . Si introducimos estos cambios resulta
!r
µ
¶ Ãr
p
∂η 00
∂η 0
νU0
U0
U0 000
0
U0 f U0 f
−
f + 2νxU0 f
U0 f 00 = νU0
f .
∂x
2x
∂x
2νx
2νx
Esto se simplica y da
f 000 + f f 00 = 0. f (0) = f 0 (0) = 0,
f 0 (∞) = 1.
Esta ecuación es independiente del número de Reynolds, por lo que nos da una solución
de semejanza para este problema. Su solución nos brinda un perl de velocidad que es
independiente de la posición x, de tal manera que si representamos grácamente la función
f 0 (η) = u/U0 , obtenemos la curva de la gura.
84
5.6.1.
CAPÍTULO 5. FLUIDOS
Turbulencia
La no linealidad de las ecuaciones de Navier-Stokes produce el efecto de que para números
de Reynolds grandes el ujo deja de ser estable. Los ujos reales, aparentemente estacionarios,
en realidad no lo son sino que están sometidos a perturbaciones de tipo local que en general
se amortiguan rápidamente de tal manera que las perturbaciones no modican sustancialmente
el aparente ujo estacionario. En otras situaciones, los ujos aparentemente estacionarios son
perturbados por pequeñas modicaciones y dejan de comportarse de forma laminar. La estabilidad de un ujo se mide en relación a su comportamiento frente a pequeñas perturbaciones
con respecto a un ujo laminar estacionario. Sea v 0 (r) y p0 (r) la solución de un ujo laminar
estacionario. Satisface, en ausencia de fuerzas volúmicas externas, las ecuaciones
(v 0 · ∇)v 0 = −
∇p0
+ ν∇2 v 0 ,
ρ
ν = µ/ρ.
Si p = p0 + p1 (r, t), v = v 0 + v 1 (r, t) donde v 1 y p1 son perturbaciones dependientes del tiempo,
entonces a primer orden en éstas, deben satisfacer las ecuaciones lineales
∂v 1
∇p1
+ (v 0 · ∇)v 1 + (v 1 · ∇)v 0 = −
+ ν∇2 v 1 ,
∂t
ρ
∇ · v1 = 0
que son lineales y homogéneas en p1 y v 1 y donde los coecientes no son funciones de t. Por
lo tanto la solución general se podrá expresar como una combinación lineal de soluciones particulares y, al ser de primer orden en la derivada temporal, la dependencia en el tiempo es de
la forma e−iωt , v 1 (r, t) = e−iωt u(r), p1 (r, t) = e−iωt q(r), donde u(r) y q(r) son en general
funciones complejas, para que v 1 y p1 sean reales. Las frecuencias ω están sujetas a las condiciones que resulten de aplicar las anteriores ecuaciones. Si las ω son reales eso produce una
perturbación oscilante, pero si posee una parte imaginaria ω = ω1 + iγ1 , eso conduce a que
la solución e−iω1 t eγ1 t se estabilice si (γ1 = Im ω < 0) o que su comportamiento sea caótico o
turbulento cuando (γ1 = Im ω > 0) en cuyo caso la perturbación crece de forma exponencial
con el tiempo. En este caso se dice que hemos entrado en el régimen turbulento. Dos partículas
próximas que en su régimen laminar describen trayectorias que mantienen un comportamiento
similar, al entrar en el régimen turbulento sus distancias relativas crecen de forma exponencial
con el tiempo.
No cabe duda que, como el único parámetro físico que caracteriza a las ecuaciones de NavierStokes es el número de Reynolds, la parte imaginaria de las frecuencias será función de él. Su
dependencia a primer orden del número de Reynolds es de la forma
γ1 ' C(R − Rcr ),
donde el número de Reynolds crítico Rcr , se dene como aquél que γ1 (Rcr ) = 0. Para R < Rcr
el coeciente γ1 < 0 y la perturbación se amortigua.
Como el comportamiento laminar de la capa límite se ha analizado para números de Reynolds
grandes, resulta que en estos caso puede ocurrir que estemos próximos al valor crítico, por lo
que la capa límite se puede hacer turbulenta. El resultado es que la capa límite se despega del
cuerpo. El perl de la velocidad de la capa límite cambia y en el punto en el que ∂vx /∂y = 0,
deja de existir fuerza de cortadura sobre la pared del obstáculo. Es el punto de despegue. A
veces, en puntos posteriores al de despegue, el perl de velocidad se invierte y la fuerza de
cortadura que el uido ejerce sobre el perl cambia de sentido. En este caso la turbulencia
`ayuda' al movimiento del cuerpo en el seno del uido con una fuerza de sentido contrario, por
lo que la sensación es que al entrar en el régimen turbulento disminuye el rozamiento.
En la parte (a) tenemos el perl normal en la paca límite; en (b) resulta que el gradiente
∂vx /∂y = 0 sobre el obstáculo y comienza el desprendimiento de la capa límite, ya que no
5.6. CAPA LÍMITE
85
hay fuerza de rozamiento con el uido, y nalmente para números de Reynolds más altos, la
vorticidad hace que este gradiente ∂vx /∂y < 0 sea negativo por lo que la fuerza de fricción entre
el uido y el obstáculo tiene sentido contrario (el obstáculo está a `rebufo' de la turbulencia).
Al desprenderse del cuerpo la capa límite, genera en la parte posterior una región de turbulencia en la que existe vorticidad por doquier. Es la estela del objeto, que no existiría en el
caso de un uido perfecto. Esto es lo que da lugar a la denominada crisis de resistencia, de tal
manera que al aumentar el número de Reynolds, y por lo tanto la velocidad relativa del uido,
disminuye la resistencia del uido.
La fuerza de resistencia de un obstáculo en un uido viscoso se puede siempre escribir como
F = C(R)ρA
v2
,
2
donde A es la sección transversal del objeto, ρ la densidad del uido y v su velocidad, siendo
C(R) una constante adimensional, llamada coeciente de resistencia, que es función de la
geometría del objeto y del número de Reynolds. En el caso de una esfera y para números de
Reynolds bajos C = 24/R. Cuando el número de Reynolds crece, esta ley deja de aplicarse.
Siguiendo con el caso de una esfera, y para números de Reynolds altos, obtenemos la descripción de las guras, en la que la segunda gura corresponde a un número de Reynolds más
alto y en la que el desprendimiento de la capa límite se hace a un ángulo inferior al del primer
caso. De cualquier manera es notable la estela de turbulencia que se genera, que es provocada
por la creación de vorticidad en la capa límite, debida a los fenómenos de viscosidad. En el
primer caso, (R = 2 × 105 y coeciente de resistencia Cx = 0,4) la capa límite se desprende a
un ángulo de 95◦ en tanto que para un número de Reynolds doble de 4 × 105 y coeciente de
arrastre la mitad Cx = 0,2 pasa a desprenderse a un ángulo de 60◦ .
86
CAPÍTULO 5. FLUIDOS
Problemas
5.1 Determinar la forma de la supercie de un líquido viscoso, incompresible, en un campo gravitatorio uniforme, en un recipiente cilíndrico y sometido a un movimiento de rotación uniforme
alrededor de su eje, con velocidad angular constante Ω.
5.2 Una presa cierra el paso a una masa uida, de forma que la pared de contención en contacto
con el uido forma un ángulo de 60◦ con la horizontal. Si la altura de la masa uida es h,
determinar el esfuerzo a que está sometida cada unidad de área de la presa. Si la longitud de la
presa es l, determinar la fuerza total debida al empuje del agua.
5.3 Demostrar la fórmula 5.4.
5.4 Establecer la expresión de las componentes del tensor de tensiones de un uido viscoso
incompresible, en coordenadas polares esféricas. Lo mismo en coordenadas cilíndricas.
5.5 Analizar los ejemplos bidimensionales de la sección 5.5.2. Establecer las ecuaciones que nos
dan las líneas de corriente y en aquellos casos en que sea posible, determinar el empuje del uido
sobre el obstáculo.
5.6 Un cilindro innito de radio R se desplaza en el seno de un uido perfecto e incompresi-
ble. Determinar las características del régimen potencial alrededor del cilindro. Suponer que la
velocidad del cilindro no es necesariamente constante.
5.7 Una bola de radio R se desplaza en el seno de un uido viscoso e incompresible con velocidad
constante. Determinar las características del régimen estacionario alrededor de la bola bajo la
hipótesis de un régimen con número de Reynolds bajo. Despreciar la acción gravitatoria.[Stokes
1851]
5.8 Una esfera de masa m y radio R se lanza verticalmente hacia abajo con una velocidad v0 ,
en un uido de densidad ρ y viscosidad µ situado en la supercie de la Tierra. Determinar:
(a) ¾Qué velocidad máxima alcanzará la esfera?
(b) ¾ Al cabo de cuanto tiempo adquirirá esta velocidad límite?
(c) ¾En qué instante se alcanza una velocidad que resulte ser la velocidad media entre la velocidad inicial y la velocidad límite nal?
(d) ¾Qué diferencia existe en los casos anteriores si en vez de lanzarla la dejamos caer?
(La fuerza de fricción para una esfera y números de Reynolds bajos es F = 6πµRv .)[Examen
Junio 2005]
5.9 Se denomina ujo de Couette al ujo laminar unidireccional de un uido viscoso entre
dos placas planas paralelas separadas una distancia h, moviéndose con velocidad relativa V y
en el supuesto de que el gradiente longitudinal de presión es nulo (No hay pérdida de carga).
Determinar el campo de velocidad, las fuerzas de fricción y el caudal del ujo.
5.10 Se denomina ujo de Poiseuille al ujo laminar unidireccional de un uido viscoso entre
dos placas planas paralelas y en reposo, separadas una distancia h, y en el supuesto de que
el gradiente longitudinal de presión es constante (Hay una pérdida de carga a lo largo del
conducto). Determinar el campo de velocidad, las fuerzas de fricción y el caudal del ujo.
5.11 Suele también denominarse ujo de Poiseuille al ujo laminar estacionario en un tubo de
sección circular. Determinar el campo de velocidad, de presión y el caudal.
5.12 Determinar el ujo laminar estacionario entre dos tubos concéntricos de radios R1 y R2 .
5.6. CAPA LÍMITE
87
5.13 Determinar el ujo laminar estacionario de un uido viscoso entre dos tubos concéntricos
de radios R1 y R2 que giran con velocidades angulares Ω1 y Ω2 , respectivamente. Determinar
el par de fuerzas, por unidad de longitud de tubo, necesario para mantener este movimiento
5.14 Se denomina problema de Rayleigh al ujo laminar unidireccional no estacionario de un
uido viscoso junto a una placa plana en reposo, que súbitamente se pone en movimiento a una
velocidad V . Determinar el campo de velocidad en todo punto y para todo t.
5.15 Analizar la difusión de la vorticidad en el caso de un torbellino innito a lo largo de un
eje.
5.16 Vericar que la transformación de Joukowski del plano complejo w = z +R2 /z , transforma
una circunferencia centrada en el origen de radio R, en el segmento del eje real comprendido
entre −2R y 2R. Si la circunferencia tiene radio r 6= R entonces es transformada en una elipse
centrada en el origen. Determinar sus semiejes. ¾Y si la circunferencia no está centrada en el
origen? ¾Qué ocurre si su centro se desplaza al punto (x0 , y0 ) y modicamos su radio de tal
manera que siga pasando por el punto (R, 0)? [Considerar el caso R = 1]
88
CAPÍTULO 5. FLUIDOS
Capítulo 6
Ondas en medios continuos
Vamos a analizar la diferencia que existe entre un medio continuo sólido y un uido en
cuanto a los comportamientos no estacionarios. Se va a producir una perturbación local, la cual
se va a propagar por el medio. Esta propagación va a depender del tipo de medio, sólido o uido,
pero los fenómenos ondulatorios van a ser una consecuencia de las propias leyes dinámicas y del
hecho de que el fenómeno analizado es no estacionario.
6.1. Ondas elásticas libres
Las ecuaciones dinámicas de un medio continuo vienen dadas en (3.3) por
∂σij
dvi
+ ρki = ρ
.
∂xj
dt
En el caso de medios materiales sólidos, homogéneos e isótropos
σij = λδij ²kk + 2µ²ij ,
1
²ij =
2
∂σij
∂²ij
∂²kk
=λ
+ 2µ
,
∂xj
∂xi
∂xj
vi =
µ
∂uj
∂ui
+
∂xj
∂xi
¶
∂ui
+ (v · ∇)ui ,
∂t
y que en términos del vector desplazamiento ui , se pone como:
µ∇2 ui + (λ + µ)
∂ 2 ul
∂ 2 ui
+ ρki = ρ 2 .
∂xi ∂xl
∂t
En esta ecuación hemos supuesto que el medio material sólido no tiene un desplazamiento global,
por lo que en la derivada del segundo miembro la parte de la derivada convectiva es nula.
Lo que obtenemos es una ecuación de ondas para los desplazamientos relativos ui , pues es
un sistema de ecuaciones diferenciales en derivadas parciales que involucra derivadas segundas
respecto al tiempo y respecto de las variables espaciales. De esta manera, en ausencia de fuerzas
volúmicas, la ecuación anterior se puede poner como
ρü = µ∇2 u + (λ + µ)∇(∇ · u) =
Y
Y
∇2 u +
∇(∇ · u).
2(1 + σ)
2(1 + σ)(1 − 2σ)
89
90
6.2.
CAPÍTULO 6. ONDAS EN MEDIOS CONTINUOS
Propagación en un medio elástico. Onda longitudinal y onda
transversal
Supongamos un medio elástico alargado, tal que la deformación u(x, t) sea solo función de
una variable espacial x y del tiempo t. La ecuación para la componente x queda:
ρ
∂ 2 ux
∂ 2 ux
Y (1 − σ)
∂ 2 ux
=
(λ
+
2µ)
=
,
∂t2
∂x2
(1 + σ)(1 − 2σ) ∂x2
para la componente y
ρ
∂ 2 uy
∂ 2 uy
∂ 2 uy
Y
=µ 2 =
,
2
∂t
∂x
2(1 + σ) ∂x2
y una ecuación idéntica a ésta para uz . Si las escribimos en la forma
1 ∂2f
∂2f
=
,
c2 ∂t2
∂x2
el parámetro c juega el papel de velocidad de propagación del fenómeno en el medio.
La solución general de este tipo de ecuaciones depende de dos funciones arbitrarias F1 y F2
de las variables x − ct y x + ct, respectivamente
f (x, t) = F1 (x − ct) + F2 (x + ct),
donde F1 (x − ct) representa un fenómeno que se desplaza sin amortiguarse a lo largo del eje OX
en el sentido positivo, en tanto que F2 (x + ct), se desplaza en el sentido negativo. Los valores
especícos de las funciones F1 y F2 deberán quedar jados por las condiciones de contorno, por
ejemplo en t = 0. En nuestro ejemplo, representaría la deformación ui súbita producida en el
instante t = 0 una cierta región. Si la onda solamente viaja hacia la derecha, esto nos determina
el perl de la función F1 (x), en t = 0.
Del análisis anterior resulta que la componente longitudinal del desplazamiento ux se desplaza con una velocidad cL y las componentes transversales uy y uz con distinta velocidad
cT :
s
s
s
r
λ + 2µ
Y (1 − σ)
µ
Y
cL =
=
, cT =
=
, cL > cT .
ρ
ρ(1 + σ)(1 − 2σ)
ρ
2ρ(1 + σ)
Las ondas sísmicas contienen ambas componentes que se detectan con una diferencia en el
tiempo de llegada después de ocurrido un terremoto.
Como las componentes del tensor de deformaciones dependen de las derivadas de todas las
componentes ui , resulta que además de la propagación de las deformaciones tenemos una propagación del tensor de deformaciones, y por lo tanto del tensor de tensiones con una superposición
de los dos movimientos.
6.3.
Ondas en uidos perfectos. Ondas sonoras
Supongamos un uido compresible perfecto (µ = 0). Se va a analizar su comportamiento en
el caso de que la velocidad v sea pequeña comparada con la velocidad del sonido en el medio
c, hipótesis que vericaremos a posteriori. De esta manera, si provocamos alguna perturbación,
resulta que las diferentes magnitudes físicas van a uctuar con respecto a unos valores medios
constantes. Así, supondremos que
p(r, t) = p0 + p0 (r, t),
ρ(r, t) = ρ0 + ρ0 (r, t).
6.3. ONDAS EN FLUIDOS PERFECTOS. ONDAS SONORAS
91
La ecuación de continuidad aparece:
∂ρ0
∂ρ
+ ∇ · (ρv) =
+ ρ0 ∇ · v = 0,
∂t
∂t
(6.1)
pues ρ0 v es muy pequeño comparado con el otro término. La ecuación de Euler (Navier-Stokes
sin viscosidad)
µ
¶
∂v
+ (v · ∇)v = −∇p − ρ∇Φ
ρ
∂t
en términos dominantes a primer orden, y en ausencia de campo gravitatorio, queda
∂v
1
+ ∇p0 = 0,
∂t
ρ0
(6.2)
donde las incógnitas a resolver son las cinco variables v , p0 y ρ0 y solamente tenemos las cuatro
ecuaciones (6.1) y (6.2). Se necesita una quinta condición que se puede obtener de la ecuación
de estado del uido compresible. En general los fenómenos de vibración mecánica de un uido
son adiabáticos, en los que la presión se puede estimar que es una función de la densidad
p(ρ) = p(ρ0 + ρ0 ), lo que nos permite desarrollar
µ
¶
∂p
p = p0 + p0 = p(ρ0 ) +
ρ0 ,
∂ρ0 S
es decir
µ
0
p =
∂p
∂ρ0
¶
ρ0 ,
(6.3)
S
donde la derivada está tomada a entropía constante S , por ser el proceso adiabático. Esa derivada
parcial la calcularemos explícitamente con la ecuación de estado, es solamente función de ρ0 y
de T , supuestas constantes, y por lo tanto toma valores constantes. Podemos pues eliminar la
ρ0 en la ecuación anterior (6.3), sustituir en (6.1) y obtener
µ
¶
∂p
∂p0
+ ρ0
∇ · v = 0,
(6.4)
∂t
∂ρ0 S
que juntamente con (6.2) completamente describen el fenómeno. Si estamos en un régimen
irrotacional, podemos denir el potencial de velocidad, v = ∇Ψ, con lo que
∂(∇Ψ)
1
+ ∇p0 = 0,
∂t
ρ0
⇒
p0 = −ρ0
∂Ψ
,
∂t
(6.5)
donde la constante de integración es cero pues el valor medio de p0 también es cero. Sustituido
en (6.4) nos da para el potencial de la velocidad
sµ
¶
1 ∂2Ψ
∂p
2
− ∇ Ψ = 0, c =
(6.6)
c2 ∂t2
∂ρ0 S
que es una ecuación de ondas para Ψ. Pero si tomamos el gradiente de esta expresión, resulta
que cada componente de su gradiente, es decir cada componente de la velocidad, satisface una
ecuación de ondas con el mismo coeciente de velocidad c. Si la derivamos parcialmente respecto
de t, resulta de (6.5) que la uctuación de la presión p0 , satisface la misma ecuación de ondas
con la misma c, lo mismo que la uctuación de la densidad ρ0 , a partir de (6.3), y resulta
que p0 = c2 ρ0 . Toda perturbación de un medio uido que se mueve despacio, se propaga con la
velocidad c en todo el espacio, siendo esta propagación una alteración local tanto de la velocidad
del medio como de los valores medios de la presión y densidad.
92
CAPÍTULO 6. ONDAS EN MEDIOS CONTINUOS
Supongamos que el fenómeno se propaga a lo largo de OX , con lo que Ψ = f (x − ct).
v = f 0 (x − ct) y p0 = ρ0 cf 0 (x − ct) = c2 ρ0 , con lo que se llega a que
v=
cρ0
.
ρ0
Si la uctuación ρ0 ¿ ρ0 , esto nos lleva a que la velocidad del uido v ¿ c, hipótesis que
habíamos planteado de partida.
En el uido existirán uctuaciones locales de la temperatura que estarán ligadas con las
uctuaciones de presión mediante
µ
¶
∂T
0
T =
p0 ,
∂p S
y que viajan con la misma velocidad c, pero de la ley
µ
µ
¶
¶
∂T
T ∂V
=
,
∂p S
cp ∂T p
con lo que la uctuación de la temperatura depende de la velocidad del medio
µ
¶
cβT M
1 ∂V
T0 =
v, M = ρ0 V, β =
,
cp
V ∂T p
siendo M la masa del sistema, β el coeciente de dilatación térmica a presión constante. Como
por otra parte
µ ¶
µ ¶
cp ∂p
∂p
ρV
RT ρ
2
c =
=
, pV = nRT, n =
⇒ p=
,
∂ρ S
cv ∂ρ T
m
m
siendo R la constante de los gases y m el peso molecular, resulta nalmente que la velocidad
de propagación del sonido en un gas perfecto es1
c2 = γ
γRT
p
=
,
ρ
m
γ = cp /cv .
Problemas
6.1 Determinar las frecuencias propias de las oscilaciones sonoras de un uido perfecto contenido en un recipiente en forma de paralelepípedo.
1
Fue Newton en 1687 quien propuso que la velocidad del sonido en un gas es de c2 ' p/ρ. Fue Laplace quien
corrigió esto añadiendo el factor γ = cp /cv .
Capítulo 7
Análisis dimensional y semejanza física
7.1. Semejanza geométrica, cinemática y dinámica
Dos objetos materiales tienen semejanza geométrica cuando existe una relación constante
entre sus dimensiones espaciales. La diferencia geométrica entre un sistema y su modelo es un
factor global de escala de las longitudes.
Dos sistemas materiales poseen semejanza cinemática si las trayectorias de partículas homólogas son geométricamente semejantes y la relación entre las velocidades de partículas homólogas
son las mismas. La estructura de las líneas de corriente se diferencia en un factor de escala y
además la velocidad está reescalada. Además del reescalamiento geométrico, es decir las trayectorias deben ser geométricamente semejantes, es necesario una adecuación puntual de la escala
de tiempos, para dar lugar a velocidades semejantes. Las trayectorias semejantes deben ser
recorridas a ritmos semejantes. Deberá existir un factor de escala temporal.
La semejanza es dinámica cuando establecidas las ecuaciones de la dinámica del sistema y
de su modelo y una vez reducidas las variables a magnitudes adimensionales, los parámetros
adimensionales que controlan las ecuaciones son los mismos. Las ecuaciones dinámicas lo que
establecen es la relación entre las fuerzas y la cinemática del sistema.
Podríamos decir que las tres clases de semejanza anteriores establecen que deben existir tres
tipos de magnitudes básicas o fundamentales asociadas a ellas, de ahí que se suelen considerar
como tales magnitudes fundamentales la Longitud [L], el Tiempo [T ] y la Fuerza [F ]. En el
sistema internacional de unidades se sustituye esta última por la magnitud Masa [M ]. El resto
de las magnitudes mecánicas de cualquier sistema, tendrán dimensiones que se expresarán en
función de éstas.
7.1.1. El sistema natural de unidades
Planck propuso un sistema de unidades tales que las constantes fundamentales de la física
valieran 1 en este sistema. Se le denomina el sistema natural de unidades, y las constantes
físicas son: el valor de la velocidad de la luz en el vacío, c, La constante de la Gravitación universal
G, la constante de Planck reescalada ~ = h/2π , la constante de Boltzmann k y nalmente la
constante de proporcionalidad que nos da la fuerza de Coulomb 1/4π²0 . Todas estas constantes,
en el sistema internacional de unidades, se pueden expresar en términos de 5 dimensiones, en
principio independientes, que son longitud [L], masa [M ], tiempo [T ], carga eléctrica [C], o bien
intensidad y nalmente temperatura [K].
En términos de esas constantes físicas, las unidades anteriores quedarían denidas como:
Longitud de Planck
r
lP =
~G
= 1,61624 × 10−35 m
c3
93
94
CAPÍTULO 7. ANÁLISIS DIMENSIONAL Y SEMEJANZA FÍSICA
Masa de Planck
r
mP =
Tiempo de Planck
Carga de Planck
~c
= 2,17645 × 10−8 kg
G
r
lP
~G
tP =
=−
= 5,39121 × 10−44 s
c
c5
qP =
p
4π²0 ~c = 1,8755459 × 10−18 C
Temperatura de Planck
mp c2
TP =
=
k
7.1.2.
r
~c5
= 1,41679 × 1032 K
Gk 2
Algunas expresiones o números adimensionales
Si las fuerzas presentes son de tipo viscoso entonces si L es una dimensión longitudinal de
un sistema, sumergido en un uido con una densidad media ρ, una velocidad media V y µ su
coeciente de viscosidad, resulta que la dinámica depende de un solo parámetro,
R=
ρV L
,
µ
el número de Reynolds. Un modelo a escala L0 , en otro uido de velocidad media V 0 , densidad
ρ0 y viscosidad µ0 , tal que R0 = R, posee el mismo comportamiento dinámico, y las líneas de
corriente son geométrica y cinemáticamente semejantes.
Por ejemplo, un modelo a escala de la corteza terrestre, hecho en plastilina, sometido a
esfuerzos y moviéndose con velocidad vp , puede reproducir la tectónica de placas moviéndose
con velocidad vT , siempre que se realice la prueba con el modelo de tal manera que ρT vT LT /µT =
ρp vp Lp /µp , siendo el subíndice p para las propiedades de la plastilina y T para la tierra. Como
ρp ' ρT , µp ' µT , implica que vp = vT (LT /Lp )(ρT /ρp )(µp /µT ), por lo que la experiencia se
debe realizar a una velocidad muy superior a la que se realiza realmente, siendo el factor de
reescalamiento de la velocidad del orden de la escala de longitudes. Sin embargo, las líneas de
corriente serán semejantes, y por lo tanto los desplazamientos relativos de materiales, fallas y
otros accidentes que surjan en el modelo, servirán para predecir el comportamiento dinámico
de la Tierra, pero hecho a una velocidad menor, es decir a una escala de tiempos más grande.
Si las fuerzas son elásticas, el parámetro característico es el número de Cauchy
C=
ρV 2
,
Y
p
cuya raíz cuadrada es M = V / Y /ρ, que es el número de Mach que relaciona la velocidad
del sistema con la velocidad del sonido (o de las ondas elásticas) en dicho material.
Para fuerzas gravitatorias, se dene el número de Froude
V
F=√ ,
Lg
aunque hay veces que se toma como tal a su cuadrado.
Si lo que existen son fuerzas debidas a la presión y por otra parte fuerzas de inercia, se dene
el número de Euler
ρv 2
E=
.
p
7.2. TEOREMA Π DE BUCKINGHAM
95
7.2. Teorema Π de Buckingham
Todas las magnitudes físicas poseen dimensiones y las expresiones de los diferentes observables contienen términos que deben ser de la misma dimensión. En mecánica existen unas
dimensiones fundamentales que en el sistema internacional de unidades las tomamos como masa
M , longitud L y tiempo T , de tal manera que cualquier otro observable mecánico posee dimensiones que se pueden expresar en términos de medidas de estas 3 magnitudes. Así, la velocidad
posee dimensión de longitud dividida por tiempo, lo cual lo expresamos como: [V ] = LT −1 ,
fuerza como [F ] = M LT −2 , etc. En electrodinámica es necesario añadir otra unidad fundamental más, que tenga en cuenta la naturaleza de los fenómenos electromagnéticos. Se suele tomar
como unidad fundamental la carga eléctrica [Q] o bien, en el sistema internacional, la intensidad
de la corriente [I].
El teorema conocido como teorema Π de Buckingham establece que si la expresión más
general de cualquier ecuación física completa es de la forma
f (x1 , x2 , . . . , xn ) = 0,
se puede reducir a la forma
F (π1 , π2 , . . . , πk ) = 0,
donde los πi son monomios adimensionales independientes que pueden formarse con las n magnitudes consideradas. El número de monomios independientes es k = n − m, siendo m el número
de unidades fundamentales necesarias para medir las n magnitudes.
En realidad no se trata de un teorema sino de una proposición o hipótesis según la cual las
expresiones que controlan los diferentes procesos físicos involucran a variables que se pueden
agrupar en forma de monomios adimensionales.
Problemas
7.1 Determinar la expresión que da el alcance d de un proyectil de masa m, que se lanza con
velocidad v , inclinada un ángulo θ con respecto a la horizontal, en el campo gravitatorio g .
7.2 Determinar el espacio recorrido d, al cabo de un tiempo T , por un cuerpo de peso P , bajo
la acción del campo gravitatorio g y partiendo del reposo.
7.3 El número de Reynolds es una función de la densidad, viscosidad, velocidad así como de
una longitud característica. Establecer la expresión del número de Reynolds mediante el análisis
dimensional.
7.4 En el caso de un uido ideal por una conducción, el caudal Q es función de la densidad
del líquido, el diámetro de la conducción y de la diferencia de presiones entre los extremos.
Establecer su relación funcional.
7.5 Determinar la expresión de la fuerza de arrastre de un objeto de dimensión transversal L,
en un uido de densidad ρ, viscosidad µ que se mueve con velocidad u.
7.6 Determinar la expresión de la pérdida de carga (diferencia de presiones entre sus extremos)
en una tubería de longitud L, diámetro D, por la que circula un uido de densidad ρ, viscosidad
µ y con una velocidad media u.
7.7 Un modelo de avión a escala 1 : 80 es ensayado en un túnel de viento con aire a 20◦ C y a
una velocidad de 45m/s. ¾A qué velocidad habrá que arrastrarse el modelo si está totalmente
sumergido en agua a 27◦ C? ¾Qué arrastre sobre el prototipo en el aire corresponderá a una resistencia en el modelo en el agua de 0,55Kg? [Viscosidad cinemática del aire a 20◦ C, µaire /ρaire =
0,864 × 10−6 m2 /s, viscosidad cinemática del agua a 27◦ C, µagua /ρagua = 1,49 × 10−5 m2 /s.]
96
CAPÍTULO 7. ANÁLISIS DIMENSIONAL Y SEMEJANZA FÍSICA
Apéndice A
Rotaciones
Vamos a describir geométricamente una rotación de valor α alrededor de un eje arbitrario,
descrito por el vector unitario u. Interpretamos que para α > 0 el giro se realiza en el sentido
horario cuando miramos en la dirección del vector unitario u. Si α < 0, el sentido de giro es el
antihorario. Por lo tanto, según la gura A.1, un punto cualquiera caracterizado por el vector
r , pasará a la posición dada por el vector r 0 ,
Figura A.1: Rotación activa de valor α alrededor del eje OA
Vectorialmente, r 0 = OA + AD + DC , siendo DC perpendicular al vector AB .
OA = (r · u)u
AD = AB cos α = (r − (r · u)u) cos α
DC = |AC| sin α n
siendo n un vector unitario perpendicular a u y r y por lo tanto
n=
u×r
|u × r|
pero |u × r| = |AC| = |AB| con lo que
DC = u × r sin α
97
98
APÉNDICE A. ROTACIONES
De esta manera el vector r 0 se expresa como:
r 0 = r cos α + (r · u)u(1 − cos α) + u × r sin α,
(A.1)
que expresado por componentes:
x0 i = xi cos α + (xj uj )ui (1 − cos α) + εijk uj xk sin α =
= (δik cos α + ui uk (1 − cos α) + εijk uj sin α)xk = R(α, u)ik xk .
Si denimos el vector α = αu, entonces toda rotación queda parametrizada por un vector de
R3 ,
αj
αi αk
R(α)ik = δik cos α + 2 (1 − cos α) + εijk sin α
(A.2)
α
α
donde el índice superior i es un índice de la y el inferior k de columna de la matriz que
caracteriza a esta rotación. Si jamos el vector u, entonces una rotación en el sentido positivo
alrededor de un eje de valor α produce el mismo efecto que una rotación de valor 2π − α
tomada en sentido contrario. Entonces, a la hora de singularizar cada rotación por un vector
α, la variedad que caracteriza al grupo se reduce al conjunto de puntos contenidos dentro y
sobre la supercie de una esfera de radio π , (ver gura A.2) pero donde los puntos opuestos
de la supercie de la esfera, que representan rotaciones de valor π , corresponden a una misma
rotación y por lo tanto están identicados.
Figura A.2: Variedad doblemente conexa del grupo SO(3)
Esta particularidad hace que si tratamos de unir dos puntos de la variedad mediante una
curva de puntos de la variedad, hay dos tipos de curvas que nos unen dichos puntos. Estos
tipos de curvas no pueden reducirse, por deformación, el uno al otro, ya que o pasan por la
supercie de la esfera y saltan a su punto opuesto, o bien unen directamente ambos puntos.
La variedad es un conjunto cerrado y acotado, es decir compacto. El grupo de rotaciones es un
grupo compacto doblemente conexo. El det(R(α)) = 1, con lo que el grupo de rotaciones se
identica con SO(3).
Otras parametrizaciones alternativas se obtienen deniendo el vector φ = sin(α/2)u y la
matriz de rotación se representa por:
p
R(φ)ik = (1 − 2φ2 ) δik + 2φi φk + 2 1 − φ2 εijk φj
(A.3)
99
y la variedad es una esfera de radio unidad con identicación de puntos opuestos sobre la
supercie.
Si denimos el vector ρ = tan(α/2)u en esta parametrización una rotación se expresa
mediante:
1
R(ρ)ik =
[(1 − ρ2 ) δik + 2ρi ρk + 2εijk ρj ]
(A.4)
1 + ρ2
y la variedad es el espacio R3 compacto, donde la compacticación se ha obtenido añadiendo
los puntos del innito en cada dirección, y que además cada par de puntos opuestos se han
identicado. Denotaremos esta variedad por R3c .
Ejercicio
A.1 Dada la matriz ortogonal siguiente:

0 1 0
 0 0 1
−1 0 0

determinar qué tipo de transformación de coordenadas genera.
A.2 Calcular, utilizando dos parametrizaciones distintas del grupo de rotaciones, la matriz que representa una rotación, en el sentido pasivo, de valor α = 30◦ alrededor de un eje cuyos cosenos directores son proporcionales a los números (−1, 2, 2).
Ejercicio
A.0.1. Parametrización normal o canónica del grupo SO(3)
A partir de la relación RT R = 1, obtenemos nueve ecuaciones entre las nueve componentes
de la matriz de rotación R. Sin embargo sólo son en realidad seis ecuaciones independientes, ya
que considerada cada matriz como tres vectores la o columna, dichas relaciones lo que establecen es que dichos vectores son ortogonales dos a dos y de norma unidad. El que el determinante
sea +1 representa que tomados consecutivamente, dichos vectores forman un triedro ortonormal
directo(antihorario), siendo un triedro inverso(horario) en el caso de que el determinante valga
−1. Quedan por lo tanto tres parámetros libres de ahí que la variedad que caracteriza al grupo
sea de dimensión 3. La parte conectada continuamente con la unidad SO(3) como grupo de Lie,
tendrá un álgebra de Lie de dimensión 3. Sea R = I + ²M una rotación próxima a la unidad, con
² innitesimal y M una matriz a determinar. Como RT = R−1 = I + ²M T = I − ²M , resulta
que M T = −M por lo que M es una matriz antisimétrica arbitraria 3 × 3, que se denomina
generador de la rotación.
El álgebra de Lie de los generadores de SO(3), que se suele representar por so(3), es el
espacio vectorial real de las matrices reales antisimétricas 3 × 3. Una base de dicho espacio viene
dada por las tres matrices linealmente independientes:






0 −1 0
0 0 1
0 0 0
J3 =  1 0 0  ,
J2 =  0 0 0  ,
J1 =  0 0 −1  ,
0 0 0
−1 0 0
0 1 0
con lo que comprobamos que generan un espacio vectorial de dimensión 3. Un álgebra de Lie,
además de ser espacio vectorial posee una ley de composición interna, que es distributiva respecto de la suma vectorial, pero que no es en general conmutativa ni asociativa. Basta para
caracterizarla, el conocer dicha ley para los vectores de la base. Para matrices la ley [ , ] se
reduce a su conmutador. Los tres Ji cumplen las reglas de conmutación:
[Ji , Jk ] = εikl Jl ,
i, k, l = 1, 2, 3,
(A.5)
100
APÉNDICE A. ROTACIONES
es decir la tabla que dene la operación [ ., .] del álgebra de Lie so(3) es la
so(3) J1
J2
J3
J1
0
J3 −J2
J2
−J3
0
J1
J3
J2 −J1
0
P
Sea M =
αi Ji una combinación lineal arbitraria de los elementos de la base
P Ji , con tres
números reales arbitrarios αi . Esa suma la vamos a escribir formalmente como
αi Ji = αu · J ,
siendo αi = αui en términos de las tres componentes de un vector unidad u yP
donde mediante
el `producto escalar' u · J ≡ U lo que queremos expresar es el sumatorio
ui Ji en forma
compacta. Calculemos la matriz
 

µ
¶n
0
−u3 u2 

M
≡ exp(αU ) = exp α  u3
0
−u1  =
exp(M ) ≡ lı́m I +
n→∞


n
−u2 u1
0






1 0 0
0
−u3 u2
−(u22 + u23 )
u1 u2
u1 u3
2
α 
 0 1 0  + α  u3
+
0
−u1  +
u1 u2
−(u21 + u23 )
u2 u3
1!
2!
2
2
0 0 1
−u2 u1
0
u1 u3
u2 u3
−(u1 + u2 )


0
u3 −u2
α3
0
u1  + · · ·
+  −u3
3!
u2 −u1
0
de tal manera que habiendo llamado


0
−u3 u2
U = u · J =  u3
0
−u1  ,
−u2 u1
0


−(u22 + u23 )
u1 u2
u1 u3
,
U2 = 
u1 u2
−(u21 + u23 )
u2 u3
2
2
u1 u3
u2 u3
−(u1 + u2 )
entonces U verica U 3 = −U , U 4 = −U 2 y así sucesivamente para todas sus potencias, con lo
que el desarrollo anterior se expresa en términos únicamente de las matrices I, U y U 2 , en la
forma
µ
¶
µ 2
¶
α
α3
α4
2 α
exp(αU ) ≡ exp(α · J ) = I + U
−
+ ··· + U
−
+ ··· ,
1!
3!
2!
4!
es decir la expresión obtenida anteriormente (A.2).
Si consideramos que dos de los parámetros αi son nulos y analizamos el subgrupo uniparamétrico que genera el parámetro no nulo, por ejemplo α1 , entonces
exp(αJ1 ) exp(βJ1 ) = (I + sin αJ1 + (1 − cos α)J12 )(I + sin βJ1 + (1 − cos β)J12 ) =
I + sin(α + β)J1 + (1 − cos(α + β))J12 = exp((α + β)J1 ),
con lo que en esta parametrización la ley de composición de cada subgrupo uniparamétrico es la
suma de los parámetros de los elementos del grupo que intervienen en la operación. Al parámetro
que dene la aplicación exponencial se le denomina parámetro normal o canónico.
La parametrización normal del grupo de rotaciones, corresponde por lo tanto a aquella en
la que la variedad es la esfera de radio π , con lo que en la parametrización normal una rotación
se representa por:
R(α)ik = (exp(α · J ))i k = δik cos α +
que es la expresión (A.2).
αj
αi αk
(1 − cos α) + εijk sin α,
2
α
α
101
De forma desarrollada R(α) resulta ser:


cos α + u21 (1 − cos α)
−u3 sin α + u1 u2 (1 − cos α) u2 sin α + u1 u3 (1 − cos α)
 u3 sin α + u2 u1 (1 − cos α)
cos α + u22 (1 − cos α)
−u1 sin α + u2 u3 (1 − cos α) 
−u2 sin α + u3 u1 (1 − cos α) u1 sin α + u3 u2 (1 − cos α)
cos α + u23 (1 − cos α)
Podemos ver que R(α)−1 = RT (α) = R(−α) y que la suma de los elementos diagonales
vale 1 + 2 cos α, en tanto que los cosenos directores del vector unitario u que dene el eje de giro
son proporcionales a los números (R32 − R23 , R13 − R31 , R21 − R12 ), salvo en el caso de que
la rotación sea de valor α = π , que al ser R simétrica, se obtendrán a partir de los elementos
diagonales que valen, respectivamente −1+2u21 , −1+2u22 y −1+2u23 y las dos posibles soluciones
para cada ui deben ser compatibles con el resto de los elementos Rij .
1 + 2 cos α = Rii ,
ui =
1
²ijk Rkj ,
2 sin α
α 6= 0, π.
Si α = 0, los Rkj , k 6= j son nulos y la anterior relación es indeterminada, como corresponde al
eje de una rotación nula.
Si calculamos los valores propios de toda matriz ortogonal que representa una rotación,
vemos que se reducen al valor real 1 con vectores propios en el subespacio vectorial de R3 de
dimensión 1 en la dirección del eje de giro, y otros dos valores propios en general complejos
conjugados, de la forma eiα y e−iα , sin vectores propios reales, que en el caso particular α = π
se reducen a −1 que es doble y los correspondientes vectores propios constituyen el espacio
vectorial bidimensional ortogonal al eje de giro.
Ejercicio
A.3 Las dos matrices siguientes representan sendas rotaciones. Determinarlas.


A=
√
2
√2
10
√5
10
10
√
− 10
5√
1+2 2
√5
2−2
5
√
− 10
√10
2−2
5√
8+ 2
10


,

B=
1
6
 √3−4

√6
− 3+1
3
√
− 4+6
3
1
6√
1− 3
3
√
3−1
√3
3+1
3
−1
3



El tratamiento que hemos hecho de las rotaciones se denomina representación activa, en el
sentido de que expresamos cómo cambian las coordenadas de un punto sometido a una rotación,
respecto de unos ejes coordenados que permanecen jos en el espacio. La interpretación pasiva
consiste en representar las coordenadas de un mismo punto del espacio referido a dos sistemas
de coordenadas, uno de los cuales ha sido girado respecto del otro. Pero al girar un sistema de
coordenadas mediante α las nuevas coordenadas del punto corresponde a una rotación activa en
la que hubiéramos girado al punto con la rotación inversa −α. De ahí que basta sustituir α por
−α para obtener la expresión de un cambio de coordenadas cuando cambiamos de sistema de
referencia. En este caso, las reglas de conmutación aparecen en la interpretación pasiva como:
[Ji , Jk ] = −εikl Jl ,
i, k, l = 1, 2, 3
A.0.2. Ley de composición de las rotaciones
Si cada rotación viene dada por un vector α ∈ SO(3) entonces es posible obtener el vector resultante de la composición de dos rotaciones arbitrarias. Sea R(γ) = R(α)R(β). Si los
vectores α = αu, β = βv y γ = γw, entonces haciendo el producto matricial e identicando
término a término obtenemos:
w tan
γ
u tan α/2 + v tan β/2 + tan α/2 tan β/2(u × v)
=
2
1 − tan α/2 tan β/2(u · v)
(A.6)
102
APÉNDICE A. ROTACIONES
Si en vez de utilizar la parametrización normal denimos los vectores
ρ = tan
α
u,
2
µ = tan
β
v,
2
γ
ν = tan w
2
entonces R(ν) = R(ρ)R(µ) resulta:
ν=
ρ+µ+ρ×µ
1−ρ·µ
(A.7)
Podemos ver de la anterior relación, que si α = β = π , tan(α/2) = tan(β/2) = ∞ y por lo
tanto en este límite:
γ
v×u
w tan =
2
u·v
con lo que la rotación resultante es alrededor de un eje ortogonal a los dos anteriores en el sentido
del producto vectorial del segundo al primero, que si están separados un ángulo φ se tiene que
tan(γ/2) = sin φ/ cos φ = tan φ, y el valor del ángulo es γ = 2φ, doble del que forman u y v .
Recíprocamente, toda rotación puede por lo tanto escribirse como producto de dos rotaciones
de valor π , alrededor de dos ejes ortogonales al primero y separados por un ángulo de valor
mitad al de la rotación a efectuar.
Figura A.3: Composición de rotaciones mediante giros de valor π
Esto nos da pie para representar geométricamente la composición de dos rotaciones 1 a
base de descomponer cada una de ellas en dos de valor π . Sean en la gura A.3, u y v los dos
vectores unitarios alrededor de los cuales vamos a girar sendos ángulos α y β . Si por O trazamos
los planos perpendiculares a ambos vectores, éstos se cortan según la recta caracterizada por
el vector unitario n. En el plano perpendicular a u, y en el sentido antihorario, colocamos el
vector unitario n1 , separado del n un ángulo α/2. Asímismo, en el plano perpendicular a v ,
y en sentido contrario al anterior, denimos el vector unitario n2 separado β/2 del n. Por lo
tanto:
R(α, u)R(β, v) = R(π, n1 )R(π, n)R(π, n)R(π, n2 ) = R(π, n1 )R(π, n2 ),
(A.8)
por lo que la rotación compuesta lo es alrededor de un eje perpendicular a n1 y n2 en el sentido
n2 × n1 y de valor un ángulo igual al doble del que forman estos vectores.
1
J.M. Aguirregabiria, A. Hernández, M. Rivas, Eur. J. Phys., 13, 139-141 (1992).
103
El análisis anterior se presta a otra interpretación gráca de la ley de composición de dos
rotaciones. Supongamos que tenemos dada una esfera de radio unidad. Como una rotación viene
caracterizada por el ángulo α y el vector unitario u que dene el eje de rotación, vamos a tratar
de representar ambos elementos sobre esta esfera. El vector u lo podemos denir por un punto
sobre ella que representa a su extremo o bien mediante un plano, ortogonal a u que pasando
por el centro corta a la esfera según un círculo máximo. Adoptaremos este segundo punto de
vista. En cuanto al ángulo α, asociado a este eje, deniremos sobre el círculo máximo anterior
un segmento orientado de longitud α/2.
Figura A.4: Composición de rotaciones sobre la esfera unidad
La ley de composición esquematizada en la gura anterior nos lleva en la gura A.4, a
denir dos círculos máximos asociados respectivamente a u y v que se cortan en el punto A, el
cual representaría el extremo del vector unitario n. Llevando sobre ellos en el sentido indicado
sendos segmentos circulares de valores α/2 y β/2 respectivamente se nos denen los puntos B y
C que se corresponden con los extremos de los dos vectores unitarios n2 y n1 . Como la rotación
resultante es ortogonal a éstos, entonces su eje queda denido por el círculo máximo que pasa
por B y C . Como la rotación compuesta lo es de valor doble a la separación angular entre n1
y n2 , entonces el segmento circular BC resulta ser de valor γ/2 y por lo tanto caracteriza a la
rotación compuesta.
Como la separación angular entre ambos planos es π − φ, siendo φ el ángulo que forman u
y v , sabemos por trigonometría esférica que en el triángulo esférico ABC se cumple:
cos γ/2 = cos α/2 cos β/2 + sin α/2 sin β/2 cos(π − φ) =
= cos α/2 cos β/2 − sin α/2 sin β/2 cos φ
relación que podemos obtener directamente a partir de la composición de las dos matrices que
representan dichas rotaciones.
Ejemplo
A.1 El cambio de coordenadas dado por la matriz
√
√

1/ √2 1/√2 0
A =  −1/ 2 1/ 2 0 
0
0
1

104
APÉNDICE A. ROTACIONES
corresponde desde el punto de vista activo a una rotación alrededor del eje OZ de valor
−π/4. Sin embargo, desde el punto de vista pasivo, como cambio de sistema de referencia,
corresponde a una rotación de valor π/4 de los ejes coordenados
de OZ . En
√ alrededor
√
efecto, √
el punto
P
=
(1,
0,
0)
pasa
a
tener
por
coordenadas
(1/
2,
−1/
2,
0)
y
el (0, 0, 1)
√
las (1/ 2, 1/ 2, 0), como vemos en la gura.
La matriz ortogonal
√
√

1/√2 1/ √2 0
B =  1/ 2 −1/ 2 0  ,
0
0
1

det B = −1
por ser de determinante −1 contiene una inversión espacial,
−y, z 0 = z , por lo que se puede escribir como
√
√


1/ √2 1/√2
1 0 0
B =  0 −1 0   −1/ 2 1/ 2
0 0 1
0
0
por ejemplo la x0 = x, y 0 =

0
0,
1
como la rotación A seguida de la inversión del eje e2 , por lo que e01 permanecería el mismo y
el e02 pasaría en la gura a ser el eje e002 . Los vectores unidad del nuevo sistema de referencia
forman ahora un triedro inverso, en el que los productos vectoriales ei × ej = −²ijk ek .
Apéndice B
Operadores diferenciales
Coordenadas esféricas
Algunos operadores diferenciales en coordenadas esféricas r, θ, φ: Elemento de arco
dr ≡ dxex + dyey + dzez = drer + rdθeθ + r sin θdφeφ
Elemento de supercie y de volumen
dS ≡ dydzex + dxdzey + dxdyez = r2 sin θdθdφer + r2 sin θdrdφeθ + rdrdθeφ
dV ≡ dxdydz = r2 sin θdrdθdφ

 
sin θ cos φ sin θ sin φ cos θ
er
ex
 eθ  =  cos θ cos φ cos θ sin φ − sin θ   ey 
eφ
− sin φ
cos φ
0
ez


grad V = ∇V =
∂V
∂V
∂V
ex +
ey +
ez = (∇V )r er + (∇V )θ eθ + (∇V )φ eφ ,
∂x
∂y
∂z
(∇V )r =
µ
rot v = ∇ × v =
∂V
,
∂r
1 ∂V
,
r ∂θ
(∇V )θ =
∂vy
∂vz
−
∂y
∂z
¶
µ
ex +
(∇V )φ =
∂vx ∂vz
−
∂z
∂z
1 ∂V
.
r sin θ ∂φ
¶
µ
ey +
∂vy
∂vx
−
∂x
∂y
¶
ez =
(∇ × v)r er + (∇ × v)θ eθ + (∇ × v)φ eφ ,
µ
¶
∂(sin θvφ ) ∂vθ
1
1 ∂vr
1 ∂(rvφ )
(∇ × v)r =
−
, (∇ × v)θ =
−
,
r sin θ
∂θ
∂φ
r sin θ ∂φ
r ∂r
µ
¶
1 ∂(rvθ ) ∂vr
(∇ × v)φ =
−
r
∂r
∂θ
∂vx ∂vy
∂vz
1 ∂(r2 vr )
1
div v = ∇ · v =
+
+
= 2
+
∂x
∂y
∂z
r
∂r
r sin θ
µ
∂(sin θvθ ) ∂vφ
+
∂θ
∂φ
∂2V
∂2V
∂2V
∇ · (∇V ) = ∇2 V =
+
+
=
2
2
∂x
∂y
∂z 2
µ
¶
µ
¶
∂2V
1 ∂
1
∂
∂V
1
2 ∂V
r
+
sin
θ
+
.
r2 ∂r
∂r
r2 sin θ ∂θ
∂θ
r2 sin2 θ ∂φ2
105
¶
.
106
APÉNDICE B. OPERADORES DIFERENCIALES
Coordenadas cilíndricas
Algunos operadores diferenciales en coordenadas cilíndricas r, φ, z :
Elemento de arco
dr ≡ dxex + dyey + dzez = drer + rdφeφ + dzez
Elemento de supercie
dS ≡ dydzex + dxdzey + dxdyez = rdφdzer + drdzeφ + rdrdφez
Elemento de volumen
dV ≡ dxdydz = rdrdφdz.
  
 
 
cos φ − sin φ 0
er
cos φ sin φ 0
ex
er
ex
 eφ  =  − sin φ cos φ 0   ey  ,  ey  =  sin φ cos φ 0   eφ 
ez
0
0
1
ez
ez
0
0
1
ez



grad V = ∇V =
∂V
∂V
∂V
ex +
ey +
ez = (∇V )r er + (∇V )φ eφ + (∇V )z ez +,
∂x
∂y
∂z
(∇V )r =
µ
rot v = ∇ × v =
µ
(∇ × v)r =
∂V
,
∂r
∂vy
∂vz
−
∂y
∂z
(∇V )φ =
¶
µ
ex +
1 ∂V
r ∂φ
(∇V )z =
∂vx ∂vz
−
∂z
∂z
¶
∂V
.
∂z
µ
ey +
∂vy
∂vx
−
∂x
∂y
¶
ez =
(∇ × v)r er + (∇ × v)φ eφ + (∇ × v)z ez ,
¶
µ
¶
µ
¶
∂vφ
1 ∂vz
∂vr
∂vz
1 ∂(rvφ ) ∂vr
−
, (∇ × v)φ =
−
, (∇ × v)z =
−
r ∂φ
∂z
∂z
∂r
r
∂r
∂φ
div v = ∇ · v =
∇ · (∇V ) = ∇2 V =
∂vx ∂vy
∂vz
1 ∂(rvr ) 1 ∂vφ ∂vz
+
+
=
+
+
.
∂x
∂y
∂z
r ∂r
r ∂φ
∂z
∂2V
∂2V
∂2V
1 ∂
+
+
=
2
2
∂x
∂y
∂z 2
r ∂r
µ
¶
∂V
1 ∂2V
∂2V
r
+ 2
+
.
2
∂r
r ∂φ
∂z 2
Algunas relaciones diferenciales
∇(ab) = a∇b + b∇a,
∇ · (av) = v · ∇a + b∇ · v,
∇ × (av) = b∇ × v − v × ∇a,
∇ · (v × w) = w · (∇ × v) − v · (∇ × w),
∇ × (v × w) = v(∇ · w) − w(∇ · v) + (w · ∇)v − (v · ∇)w,
∇(v · w) = v × (∇ × w) + w × (∇ × v) + (w · ∇)v + (v · ∇)w,
∇2 φ = ∇ · ∇φ,
∇ × ∇φ = 0,
∇ · r = 3,
∇2 v = ∇(∇ · v) − ∇ × (∇ × v),
∇ · (∇ × v) = 0,
∇ × r = 0,
∇r = r/r,
∇ · (r/r3 ) = −∇2 (1/r) = 4πδ (3) (r).
∇(1/r) = −r/r3 ,