EC 2272 Análisis de Circuitos Eléctricos II Solución del Segundo

EC 2272
Análisis de Circuitos Eléctricos II
Solución del Segundo Parcial
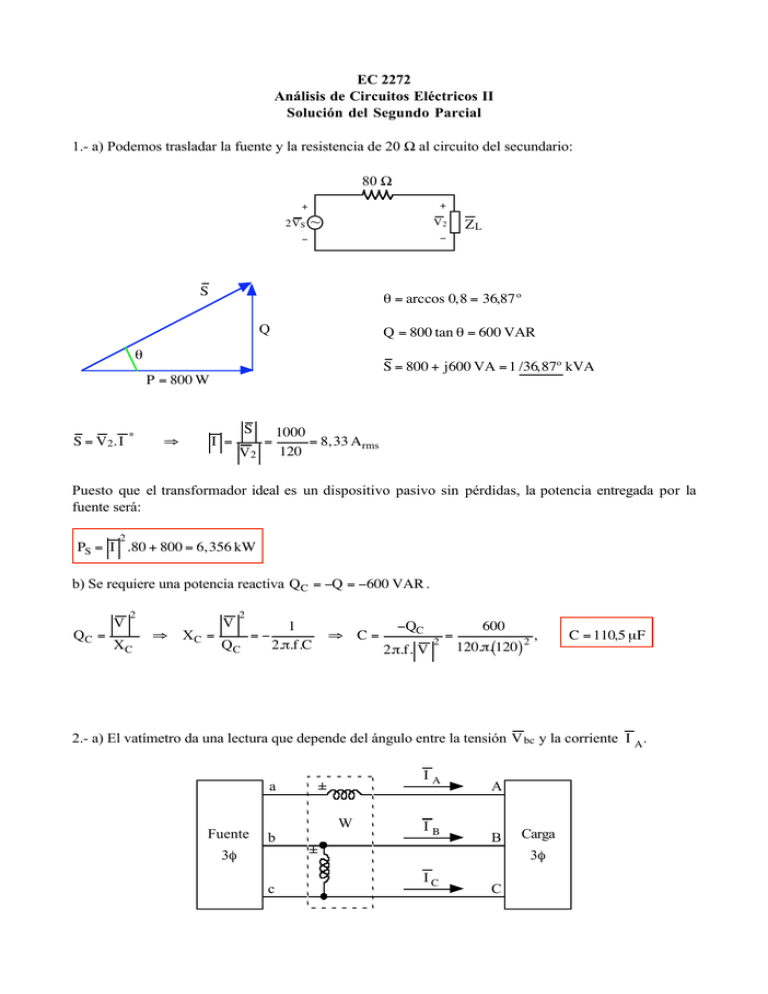
1.- a) Podemos trasladar la fuente y la resistencia de 20 Ω al circuito del secundario:
80 Ω
+
2V S
+
~
V2
€
θ = arccos 0,8 = 36,87º
€
€
S
ZL
−
−
Q
Q = 800 tan θ = 600 VAR
€
θ
€
P = 800 W
S = 800 + j600 VA = 1 /36,87º kVA
€
€
S€
= V2 .I
€
*
⇒
1000 €
I =
=
= 8,33 Arms
120
V2
S
Puesto
€ que el transformador ideal es un dispositivo pasivo sin pérdidas, la potencia entregada por la
fuente será:
€
2
PS = I .80 + 800 = 6,356 kW
b) Se requiere una potencia reactiva QC = −Q = −600 VAR .
€
QC =
V
2
XC
2
⇒
V
1
XC = € = −
QC
2.π.f.C
€
€
⇒ C=
−QC
2.π.f. V
2
=
600
120.π.(120) 2
€
€
,
C = 110,5 µF
€
€
2.- a) El vatímetro da una lectura que depende del ángulo entre la tensión V bc y la corriente I A .
a
Fuente
b
3φ
c
IA
±
€
W
±
€
IB
A
B
€
Carga
3φ
€
€
IC
C
Construímos el diagrama fasorial, tomando, por ejemplo, V an como referencia de fase:
I
C
€
V cn
€
V ab
V ca
€
30º
€
€
θ
I
€
B
V an
I
€
A
V bn
€
€
€
V bc
€ con las relaciones de fase ya conocidas para la secuencia
Las tensiones de línea y fase se dibujan
abc. Podemos suponer una conexión en estrella. Así, dado que la carga es inductiva, las corrientes de
linea deben estar atrasadas respecto a los voltajes de fase en un ángulo igual al de la impedancia
Del diagrama, el ángulo entre V bc e I aA es 90 − θ, luego:
V ab . I aA .cos(90 − θ) = Vab . I aA .sen(θ) = 2250 W
⇒
 2250 
θ = arc sen
 = 34,94º .
 220.20 
€
€
220
La potencia aparente sobre una fase €
de la carga es SF = VF .I L =
.20 = 2540,3 VA , y la
3
€
potencia compleja total será:
€
€
S3φ = 3.SF /θ = 7,621 /34,94 º kVA = (6,247 + j4,365
) kVA
€
P3φ = Re{S3φ } = 6,247 kW ,
Q 3φ = Im{S3φ } = 4,365 kVAR
€
Se llega al mismo resultado suponiendo una conexión en delta de la carga.
€
€
b) La impedancia en la conexión en estrella es:
 220 

 /0º
Van 
3
ZY =
=
,
I aA 20 / − 34,94º
€
ZY =
€
11 3
/34,94º = 6,35 /34,94º Ω = (5,2 + j3,64) Ω
3
3.- Con un f.p en atraso, la carga es inductiva. La lectura del vatímetro depende del ángulo entre VCA e
I B (corriente en la linea bB).
0,05 + j
A
a
€
€
W
0,05 + j
±
b
±
Carga
B
3φ
0,05 + j
C
c
Construímos el diagrama fasorial con las relaciones usuales para voltajes de linea y fase. Tomando V AN
como referencia de fase resulta:
I
€
C
€
VCN
V AB
VCA
€
30º
€
€
V AN
θ
I
B
I
€
€
A
V BN
€
€
€
V BC
Suponiendo una conexión estrella en la carga, las corrientes de linea deben estar atrasadas respecto a los
€
voltajes de fase en un ángulo igual al de la impedancia. Luego, el ángulo entre VCA e I B es 90º −θ, y la
expresión para la potencia leída en el vatímetro será:
W = VCA . I B .cos(90º −θ) = VL .IL .sen(θ)
€
€
€
Conocemos la potencia aparente en la carga,
V
S3φ = 3.VF .IF = 3. L .IL = 3.VL .IL
3
Comparando (1) y (2):
S3φ
W=
.sen(θ)
⇒
3
€
€
(1)
€
(2)
 3.W 
 11 3 
 = arc sen
θ = arc sen
 = 30º
 22 3 
 S3φ 
€
€
P3φ = S3φ .cos(30º) = 33 kW
Ppérdidas = (0,0454).P3φ = 1,5 kW
€
€
f.p.= cos( 30º) =
3
= 0,866 en atraso
2
Además,
€
Ppérdidas = IL 2 .3.R linea
De (1):
€
⇒
Ppérdidas
3.R linea
=
1500
3.(0,05)
€
€
€
W
11000
VL =
=
IL .sen(30º) 100.0,5
€
€
IL =
⇒
€
VL = 220 Vrms
⇒
€
I L = 100 Arms