P.útil 16,33 ∗ 100 = 18%

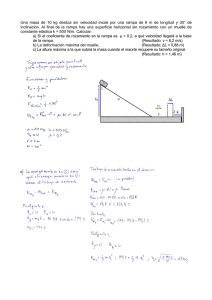
1. Área de acceso a la atracción
En ella los pasajeros accederán a la vagoneta con la que se desplazarán por la
montaña rusa. Es un área completamente horizontal, situada a nivel del suelo (que
tomaremos como referencia 0 m) y tiene una longitud de 100 m hasta comenzar el
área de subida. La vagoneta tiene un peso en vacío de 1500 kg y tiene una
capacidad máxima de 10 personas.

Si no existe rozamiento, calcula el trabajo realizado por una fuerza de 1000
N al desplazar la vagoneta a lo largo de la longitud total del área de acceso.
W = F * Δr = F*Δr*cos α
W =?
F = 1000 N
Δr = 100-0 = 100m
W = 1000*100
W = 100.000 J

La velocidad estimada para recorrer esta área en vacío (sin pasajeros) es de
12 m/s. ¿Qué potencia desarrollará el motor al ejercer la fuerza de 1000 N?
P=F*V
P =?
F = 1000 N
V = 12 m/s
P = 1000 * 12
P = 12000 W

Los motores no presentan un rendimiento del 100%. En este caso, es del
78%. ¿Qué potencia mínima en CV tendrá que tener el motor anterior para
que sea capaz de alcanzar esta velocidad?
12000 W / 735 W = 16,33 CV
P. útil
∗ 100 = 18%
16,33
P. util = 12,74
2. Rampa de subida
Tras finalizar el área de acceso, comienza la rampa de subida, en la cual pasan del
nivel del suelo hasta la altura máxima de la atracción, en este caso 60 m, a partir
de la cual se comienza el descenso. La rampa tiene una inclinación constante del
45º, la fuerza realizada por el motor, paralela a la rampa es de 30000 N y el
coeficiente dinámico de rozamiento entre la vagoneta y los raíles tiene un valor µdi
= 0.3. A partir de ahora, en los cálculos supón que en la vagoneta viajan ya 10
pasajeros, de 70 kg cada uno de ellos.

Dibuja el diagrama de fuerzas correspondiente a esta situación. ¿Cuál es la
longitud de la rampa? (¡recuerda tus conocimientos de trigonometría!)
WA y B = 0
3000N
P = 2200*9,8 = 21560 N
Fr = 0,3*21560 = 6468 N
WFr = 6468*84,85*cos 180º = -54809,8 J
Wc = 3000*84,85 = 2545500 J

Calcula el trabajo realizado por cada una de las fuerzas que has dibujado.
W = F*Δr*cos α
W = (2200*9,8) *84,85*0 = 1.829.366 J
P=
P=
R=
𝐖
𝚫𝐭
1829360
15
𝐏.ú𝐭𝐢𝐥
𝐏.𝐭𝐞ó𝐫𝐢𝐜𝐚
80% =
= 121.957,33 W = 165,93 CV
*100
𝟏𝟔𝟓,𝟗𝟑
𝐏.𝐭𝐞ó𝐫𝐢𝐜𝐚
*100
Teórica = 207,41 CV


Si se tarda 15 s en ascender la rampa y el rendimiento del sistema de
elevación es del 80%, calcula la potencia en CV que deberá tener el mismo.
Si la velocidad inicial con la que accede a la rampa es de 0.5 m/s, ¿con qué
velocidad llegará al final de la misma?
3. Recorrido en la montaña rusa
Una vez llegado al final de la rampa, la vagoneta con sus pasajeros se frena hasta
tal punto que puede tomarse su velocidad como 0 m/s, momento en el que
comienza a caer, moviéndose libremente sin rozamientos, describiendo el circuito
que observas en la figura:

Bajo estas condiciones ¿se conservará la energía mecánica? ¿Cuál será su
valor?
Em = Ec + Ep
Ec = ½*m*v2
Ep = m*g*h
EC = 0
Ep = 2200*9.8*60; Ep = 1.293.300
Em = 0 * 1.293.300 = 1.293.300 J
Toda energía mecánica se conservará si no existe rozamiento.

Calcula los valores de la energía cinética y potencial en el punto (2). ¿Con
qué velocidad pasará la vagoneta por lo alto del rizo?
1.293.600 = ½*2200*v2+2200*9,8*40
2(1293600−862400)
2.200
= v2
√392 = v
v = 19,80 m/s
Ep = 862.400 J
Ec = 1.293.600 – 862.400
Ec = 431.200 J
Energía cinética: 431.200 J
Energía potencial: 862.400 J

¿En qué punto del viaje se alcanzará la máxima velocidad? ¿Cuál será su
valor?
En el punto en que la energía cinética sea mayor, o sea, cuando la energía
potencial sea 0, y como lo único que puede variar es la altura. La velocidad
será la máxima cuando el vagón valla lo más cerca al suelo.
1.293.600 =
1
. 2200 . v 2
2
𝐯 = 𝟑𝟒, 𝟐𝟗 𝐦/𝐬

Si en el punto (4) la vagoneta pasa con una velocidad de 28 m/s, ¿a qué
altura se encuentra?
Em = 1.293.600
Ec = ½ * 2200*282
Ec = 862.400 J
Ep = Em – Ec
Ep =1293600 – 862400
Ep = 431.200 J
431.200 = 2200*9.8*h
h=
431.200
2200∗9.8
h = 20 m

Al final del trayecto, se vuelve al área de acceso, momento en el cual actúa
un resorte elástico (muelle) que frena completamente a la vagoneta. Si la
constante elástica de dicho resorte es de 30000 N/m, ¿qué energía potencial
elástica habrá almacenado? ¿Qué longitud se habrá deformado en el
proceso?

Supongamos ahora que, como sucede en la vida real, existe rozamiento
durante el movimiento de la vagoneta. ¿Cuál debería ser el trabajo realizado
por las fuerzas no conservativas para que la vagoneta no pudiera describir el
rizo?

Si el coeficiente de rozamiento fuera µdi = 0.3, y la vagoneta se encontrará
moviéndose a 100 km/h, calcula la velocidad a la que se movería al finalizar
el área de acceso (100 m) si no actuase ninguna otra fuerza.