potencial electrico

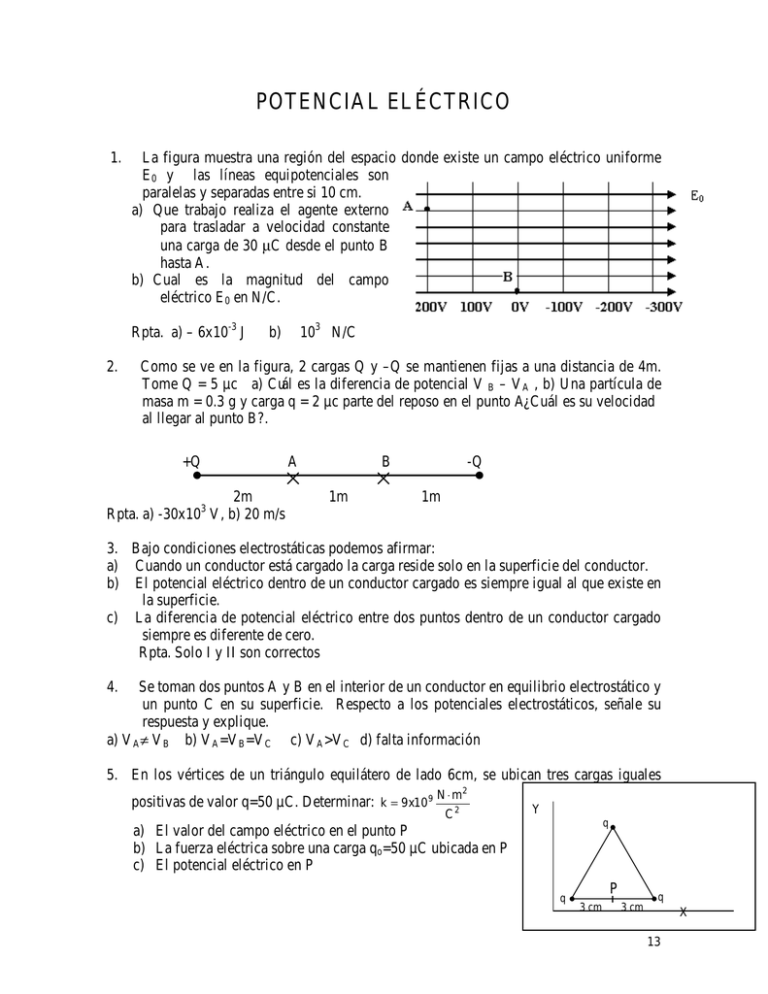
POTENCIAL ELÉCTRICO
1.
La figura muestra una región del espacio donde existe un campo eléctrico uniforme
E0 y las líneas equipotenciales son
paralelas y separadas entre si 10 cm.
a) Que trabajo realiza el agente externo
para trasladar a velocidad constante
una carga de 30 µC desde el punto B
hasta A.
b) Cual es la magnitud del campo
eléctrico E0 en N/C.
Rpta. a) – 6x10-3 J
2.
103 N/C
b)
Como se ve en la figura, 2 cargas Q y –Q se mantienen fijas a una distancia de 4m.
Tome Q = 5 µc a) Cuál es la diferencia de potencial V B – VA , b) Una partícula de
masa m = 0.3 g y carga q = 2 µc parte del reposo en el punto A¿Cuál es su velocidad
al llegar al punto B?.
+Q
2m
Rpta. a) -30x10 V, b) 20 m/s
A
B
1m
-Q
1m
3
3. Bajo condiciones electrostáticas podemos afirmar:
a) Cuando un conductor está cargado la carga reside solo en la superficie del conductor.
b) El potencial eléctrico dentro de un conductor cargado es siempre igual al que existe en
la superficie.
c) La diferencia de potencial eléctrico entre dos puntos dentro de un conductor cargado
siempre es diferente de cero.
Rpta. Solo I y II son correctos
4.
Se toman dos puntos A y B en el interior de un conductor en equilibrio electrostático y
un punto C en su superficie. Respecto a los potenciales electrostáticos, señale su
respuesta y explique.
a) VA≠ VB b) VA=VB=VC c) VA>VC d) falta información
5. En los vértices de un triángulo equilátero de lado 6cm, se ubican tres cargas iguales
positivas de valor q=50 µC. Determinar: k = 9x109
N ⋅ m2
C2
Y
q
a) El valor del campo eléctrico en el punto P
b) La fuerza eléctrica sobre una carga qo=50 µC ubicada en P
c) El potencial eléctrico en P
q
P
3 cm
3 cm
q
X
13
Rpta. (a) –16,6x107jN/C (b) –0,83x104jN (c) 38,6x106V
6. Se tiene cuatro cargas puntuales entrantes q1=q2=q3=q4=+10mC. Las cargas están
colocadas en los vértices de un cuadrado de 10cm de lado. Hallar:
a) La fuerza eléctrica resultante sobre cualquiera de las cargas
b) El potencial eléctrico en el centro del cuadrado
c) La energía potencial electrostática del sistema de las cuatro cargas
7. Considere una pirámide de altura h = 4cm y base hexagonal de lado a = 3cm, la cual
descansa en el plano XY, en cuyos vértices de la base se
encuentran cargas puntuales, de magnitudes: +q, +q, +q, -q, q y -q; como se muestra en la figura.
a) Determine el vector CE en el vértice cúspide de la
pirámide.
b) Escoja cualquiera de las cargas y llévela al infinito.
¿Qué trabajo ha tenido que hacer para tal transporte?
Rptas: a) 480 Kq î + 831,3 Kq • (N/C)
En la figura las cargas Q1= 3 µc, Q2= - 2 µc y Q3= 5
µc, están fijas.
a) Cuál es el trabajo externo necesario para mover una
carga q = - 4 µc con rapidez Constante desde el punto
A en el Centro del cuadrado hasta el punto B en la
esquina.
b) Cuál es el significado del signo de la respuesta.
Y
8.
Q1
10cm
A
Q2
10cm
Q3
X
9.
Considere una pirámide de altura h = 4 cm y base hexagonal de lado a = 3 cm, la cual
descansa en el plano XY, en cuyos vértices de la base se
encuentran cargas puntuales, de magnitudes: +q, +q, +q, -q, +q
+q
q y –q; como se muestra en la figura.
-q
+q
a) Determine el vector Campo Eléctrico en el vértice cúspide
de la pirámide.
b) Escoja cualquiera de las cargas y llévela al infinito.¿Qué
-q
-q
trabajo ha tenido que hacer para tal transporte?
RESPUESTAS: a ) 480 Kq î + 831,3 Kg ĵ ( NC)
10.
Tres cargas puntuales de 5×10−9 C están situados en los vértices A, B Y C del
rectángulo cuyos lados son 0.6 m y 0.4 m. Determinar: (INF-ExParc-2003-1)
El trabajo para llevar una carga de –1×10−6 C desde
0.6 m
B
el infinito, hasta el centro del lado CD, siempre en A
equilibrio.
0.4 m
El vector fuerza eléctrica sobre la carga de –1×10−6
C ubicada en el centro del lado CD.
a)
b)
C
D
14
11.
a)
b)
Una carga Q es colocada en cada uno de los vértices opuestos de un cuadrado.
Otra carga q es colocada en cada uno de los otros dos vértices del cuadrado. ( k =
¼ πεo=9.0×109 N.m2/C2 ). (INF-ExSust-2003-1)
Si la fuerza resultante sobre Q es cero, ¿ Cuál es la relación (Q/q), entre las cargas
Q y q ?.
Calcular el potencial eléctrico en cada uno de los puntos medios de los lados del
cuadrado. Considerar que el lado del cuadrado es 10 cm y Q = +20 µC.
12.
La figura muestra una varilla muy delgada uniformemente cargada densidad lineal
‘−λ’ y una carga puntual ‘+q’. Hallar:
a) el vector campo eléctrico debido a la carga puntual en el punto
y
(d,0).
_P
b) el potencial eléctrico debido a la carga puntual en el punto (d,0).
c) el potencial eléctrico debido a la varilla en el punto P (0, yo).
d) el trabajo que realizarían las fuerzas eléctricas para llevar una carga
d
positiva unitaria del punto O al punto P.
+q O
e) la fuerza que actuaría sobre una carga puntual +2q si estuviera en
d
el punto O.
Rptas. (a) (kq/d2)i. (b) kq/2d, (c) kλLn((yo+d)/(L+yo+d))
(d) kλLn((yo+d)(L+d)/(L+yo+d)d)
(e) (2kq2/d2)i + (2kqλL/d(L+d))j
L
−λ
13.
Un arco de circunferencia esta cargado uniformemente en
cada cuarto de circunferencia como se muestra en la
figura. Determinar:
a) La carga total del arco
b) El potencial eléctrico en el punto 0
c) La energía potencial eléctrica que tendría una carga puntual
+q ubicada en el punto 0.
Rptas: a) -πRλ/2 ; b) -2λ/π , -2λq/π
14.
Dos placas paralelas conductoras grandes tienen cargas
iguales y con signos opuestos y están separadas 5 cm. Una carga puntual de 8 µc
se coloca entre los dos y experimenta una fuerza de 2.4 x 10-2 i N. Encuentre la
diferencia de potencial entre las placas. RESPUESTA :
2K Qx
2K Q
a
a. 2
b.
c. x = ±
2
2 32
x
2
(x + a )
15.
En los vértices de un triángulo equilátero de lado 6 cm, se ubican cargas iguales

N . m2 

positivas de valor q = 50 µc. Determinar :  k = 9 x 10 9
C 2 

15
x
a) El valor del campo eléctrico en el punto P.
b) La fuerza eléctrica sobre una carga q0 = 50 µc ubicada en P.
c) El potencial eléctrico en P.
RESPUESTA:
a)
-16,6 x 107 j N/C
b)
-0,83 x 104 jN
c)
38,6 x 106V
P
La figura muestra una varilla muy delgada uniformemente cargada de densidad
lineal ‘-λ ’ y una carga puntual ‘+q’. Hallar :
a) El vector campo eléctrico debido a la carga puntual en el punto (d, 0).
b) El potencial eléctrico debido a la carga puntual en el punto (d, 0).
c) El potencial eléctrico debido a la varilla en el punto P (0, y0)
d) El trabajo que realizarían las fuerzas eléctricas para llevar una carga positiva unitaria
del punto O al punto P.
e) La fuerza que actuaría sobre una carga puntual +2q si estuviera en el punto O.
16.
RESPUESTAS:
K q iˆ
a.
d2
d.
Y
Kq
b.
2d
Kλ l n ( y 0 + d ) ( L + d )
L + y0 + d
K λ l n ( y0 + d )
c.
L + y0 + d
e.
P
d
+q
x
O
2K q
2 Kq λ L ˆj
ˆ
i
+
d ( d + L)
d2
L
-•
17.
La figura muestra dos planos infinitos de carga de densidades superficiales
uniformes –3 µC/m2 y 6 µC/m2. Encontrar:
a) El vector campo eléctrico en los puntos A, B y C
correspondiente a cada una de las regiones.
b) El valor del potencial eléctrico en cada uno de los puntos A, B
y C. Considere V = 0 y x = 0 en la lamina negativa.
c) El trabajo que realiza un agente externo al trasladar entre los
pts A y C a una carga puntual de 2µC.
Rptas: a) EA = -3,38 x 105 N/C ,..., b) VC = 20340 V , c) 0,06 J
Y
q
18. Tenemos un plano de cargas, de densidad
superficial σ =-30µC/m2, colocado en el plano XZ.
q
16
3cm
3cm
q
X
Además existe una carga puntual, q=16
µC y masa m=2x10 -6g, colocada en el
punto (0,20,0)cm
Dibuje aproximadamente las líneas de campo eléctrico y las curvas
equipotenciales
Calcule el vector campo eléctrico E resultante en el punto (0,20,20)cm
Si dejamos en liberta la carga q, calcule el tiempo que demora en chocar con el
plano de cargas
a)
b)
c)
19.
La figura muestra un plano infinito con carga superficial uniformemente
distribuida ( σ = 17,7x10-10 C/m2), ubicada en el plano
XY.
a) Aplicando la ley de Gauss, determine el vector campo
eléctrico en el punto P (0,0,a).
b) Determine la diferencia de potencial entre los puntos P
(0,0,a) y Q (0,0,2a ) siendo a = 0,2m
Rptas: a) 100 k̂ N/C; b) 20 V
20.
Un cascaron esférico conductor neutro tiene un radio interior de 10cm y un radio
exterior de 20cm. Una carga puntual de 5µC es localizada en el centro de la
cavidad. Determinar:
a) El campo eléctrico a 5cm, 15cm y 25cm de la carga puntual
b) Las densidades superficiales de carga σ (C/m2) en la superficie interior y
exterior del cascaron
c) La diferencia de potencial entre un punto de la superficie interior y otro de la
superficie exterior del cascaron
Rpta. (a) 1,8x107N/C, 0, 7,2x105N/C (b) 3,97x10-5C/m2, 9,94x10-6C/m2 (c) 0
21.
Se tiene una esfera conductora de 2 cm de radio cargada. A una distancia de 40 cm
del centro de la esfera el voltaje medido es de 3x104 voltios. Cual es
aproximadamente el valor del voltaje en voltios medido en la superficie de la
esfera conductora.
Rpta. 6x105 voltios
22.
Se tienen dos esferas conductoras concéntricas. La esfera interna de radio 30 cm y
carga total –12 µC y la externa de radio interior 60 cm y exterior 90 cm con carga
total 3 µC.
a) Hallar el campo eléctrico en cada una de las regiones.
b) Hallar el potencial eléctrico en la esfera externa y en la esfera interna.
c) Cuanto vale la diferencia de potencial entre la esfera externa y la interna.
Rptas: Eint = -108000/r2 ; b) Vint = -3,3 x 105 V ; c)2,4 x 105 V
17
23.
Una esfera uniformemente cargada tiene un potencial de 450 voltios en su
superficie. A una distancia radial de 20 cm de esta superficie, el potencial es 150
voltios. Calcule la carga y el radio de dicha esfera.
Rptas: 9,33 µC ; 6,6 cm
En una región del espacio el potencial eléctrico esta dado por : V = 2xy2 – yz2,
hallar el campo eléctrico en el punto P(1,1,1)m
Rpta. E= (-2i-3j+2k)V/m
24.
25.
a)
b)
c)
d)
Se tiene un anillo muy delgado de radio a = 40 cm con carga Q=20πεo C,
uniformemente distribuida en todo el perímetro del anillo. Si el anillo se ubica en
el plano XY, centrado en el origen, halle: (CIV-ExParc-2003-1)
la densidad lineal de carga(responda en término de εo),
el potencial eléctrico en un punto P de coordenadas (0, 0, z),
el campo eléctrico en el punto P(0, 0, z),
el trabajo realizado por las fuerzas eléctricas para llevar una carga puntual ‘q’, desde
el punto A(0,0, a 3 ) hasta el punto B (0,0, a 15 ) , a: radio del anillo.
En cada punto P(x,y,z) del espacio
se conoce el potencial eléctrico,
según :
V(x,y,z) = 3x + 2y2 + 5z V ;
x,y,z, en m (CIV-ExParc-2003-1)
a) Determine las tres componentes
cartesianas del campo eléctrico,
asociado a este potencial.
b) En el prisma en forma de cuña,
halle el flujo de este campo a través
de cada una de las superficies 1 , 2 ,
3 , 4 y 5 , respectivamente.
c) Determine la carga encerrada en la
cuña.
z (m)
26.
27.
3
10
4
x (m)
Una bolita de masa m = 5 mg (1 mg
= 10-3g) y carga q = 16 µC es
sostenida por un hilo de seda, el
cual se desvía 53º respecto a uno de
los dos planos verticales, infinitos y
uniformemente
cargados
con
densidades σ1 constante(σ1>0) y σ2
18
y (m)
constante(σ2<0). Si el campo eléctrico resultante de los 2 planos infinitos en el
punto P vale cero, hallar : (CIV-ExParc-2003-1)
la fuerza de tensión en el hilo,
el campo eléctrico resultante en los puntos S y T, respectivamente.
las densidades σ1 y σ2, de cada plano, y
la diferencia de potencial entre los planos.
a)
b)
c)
d)
28. En un sistema de coordenadas XY se tiene un cuadrado de lado b = 0,2m, en sus
correspondientes vértices están fijadas sus respectivas cargas eléctricas, de la siguiente
manera, Q1 en (0,0), Q2 en (0,b), Q3 en (b,b) y Q4 en (b,0).Los valores de las cargas
son Q1 = 12x10-2 µC, Q2 = -24x10-2µC, Q3 = 36x10-2µC, y Q4 = -24x10-2µC, calcule:
b) El campo eléctrico resultante en el punto P(2b,2b), donde b = 0,2m.
c) El potencial eléctrico en el mismo punto P.
29. En la figura se muestra dos cascarones metálicos concéntricos
y muy delgados de radios R1 = 0,2m y R2 = 0,3m. La carga
del cascarón de R1 es Q1 = Q y el de R2 es Q2 = - Q, donde Q
= 3,27µC.
b) De acuerdo a la ley de Gauss, determine el campo eléctrico
en la región R1 < r < R2
c) Calcule la diferencia de potencial Δ V (en voltios) entre
dichos cascarones.
30.
Considere dos cascarones esféricos delgados, conductores y concéntricos. El cascaron
interno tiene radio de 20cm y una carga de 10nC. El cascarón exterior tiene un radio
de 30cm y una carga de –15nC. Hallar el campo eléctrico y potencial eléctrico en:
a) El centro
b) La superficie de cada cascarón.
31.
Una línea de cargas de longitud infinita se encuentra sobre el eje X. Si la línea de
cargas tiene densidad lineal de carga igual a -5mC/m. Halle:
a) La intensidad del campo eléctrico en el punto (0,10,10)cm. en N/C. (2p)
b) La diferencia de potencial eléctrico entre los puntos (0, 20, 20)cm y (0,10,10)cm.
(3p)
32.
Se tiene una esfera conductora de 10cm de radio. Si la esfera conductora es cargada con
-10mC Hallar:
a) La densidad superficial de carga. (1p)
b) El valor del campo eléctrico a 5cm del centro de la esfera. (1p).
19
c)
El valor del potencial eléctrico en el centro de la esfera. (2p).
33.
Cuatro cargas del mismo valor q = 6µC , están ubicadas en
un cuadrado de lado L = 20 cm, como muestra la figura.
Halle: (5P)
a) La fuerza sobre la carga del vértice 1
b) El campo eléctrico en el punto P, que se encuentra
a la mitad de un lado
c) La energía potencial electrostática del sistema
los vértices de
34.
Una carga q1 = 25 nC se encuentra en el origen de
coordenadas. Halle: (5P)
a) El vector campo Eléctrico y el potencial eléctrico en el punto A(4,3,0) m
b) El vector fuerza eléctrica que ejerce una carga q2 = - 20 nC que se encuentra en el
punto A, sobre la carga q1
c) El trabajo necesario para traer una tercera carga q3 = 13 nC desde muy lejos y
colocarla en el punto B(0,0,12) m , en presencia de las cargas q1 y q2
d) El flujo eléctrico que atraviesa una esfera de radio R = 6 m centrada en el origen,
para el sistema de las tres cargas.
Rpta.a) (7,2i + 5,4j) N/C, b) (-144i -108j) x10-9 N/C, c) 6,38x10-8 J, d) 564 Nm2/C
35.
a) Suponga que una superficie gaussiana encierra una
carga puntual negativa que tiene quince líneas de
campo entrando y una carga puntual positiva con una
magnitud de carga doble que la negativa. ¿Cuál es el
número neto de líneas de campo que pasan por la
superficie gaussiana?
b) En una región del espacio el potencial eléctrico está
dado por V = 3xy2 -2yz2, calcule el campo E en el
punto (-1, 2,1). Las unidades están en SI.
c) Una esfera uniformemente cargada se encuentra a un potencial de 2,0kV. A una
distancia de 25,0cm de su superficie, el potencial es 800V.
Cuál es la carga de dicha esfera?
d) Dos grandes placas metálicas paralelas están separadas
3,0cm y conectadas a una batería de 12V. Desde un punto
M de la placa negativa parte del reposo un electrón
moviéndose hacia la otra placa. A una distancia de 2,0cm
correspondiente a un punto N (nueva posición del
electrón), calcule el valor del potencial que alcanza
electrón en dicho punto.
36.
Dos cargas puntuales q1 = -Q y q2 = Q, donde Q = 50,0µC, están fijos entre dos
puntos separados por una distancia de 40,0cm. En la línea que une a ambas cargas se
tienen dos puntos A y B, el punto A está a una distancia de 20,0cm de q1 y B está a
una distancia de 10,0cm de A y 10,0cm de la carga q2.
a) Calcule la diferencia de potencial Δ V (en voltios) entre A y B
20
b) Una carga qo = -1,6x10-10 C tiene una masa mo = 9,1x10-13 kg, parte del reposo en el
punto A y pasa por el punto B. Calcule la velocidad de esta carga en el punto B.
a. Tres cargas puntuales +q , +q y –q (q = 2 µC) se disponen en los vértices
de un triángulo equilátero de 1,5 m de lado. Se pide:
a)
b)
Trazar un sistema coordenado y determinar el vector campo eléctrico en el centro del
triángulo.
La diferencia de potencial entre el centro del triángulo y la mitad del lado que une las
dos cargas positivas +q; así como también el trabajo necesario para mover una carga
puntual de 3 µC entre estos dos puntos
37.
Se tiene un Condensador de placas esféricas (cascarones esféricos delgados,
conductores y concéntricos). El cascaron interno tiene radio de a=20cm y una carga de
+10mC. El cascarón exterior tiene un radio de b=30cm y una carga de –10mC. Hallar:
a) La expresión para el campo eléctrico E(r) dentro del cascaron (a<r<b), y calcule el
campo a 25cm del centro de las esferas.
b) El potencial eléctrico V(r) dentro del cascarón y la diferencia de potencial entre los
cascarones esféricos.
c) En un sistema coordenado, grafique E vs r y V vs. r.
d) La energía electrostática almacenada en el condensador.
38.
En la figura las cargas Q1= 10 µc, Q2= - 2 µc y Q3= 5 µc, est
án ubicadas en las
posiciones mostradas. Halle:
la energía potencial electrostática del sistema
El trabajo necesario para trasladar una carga q = - 4 µc con rapidez constante
desde el punto M en el centro del rectángulo hasta el punto N en la esquina
a)
b)
39. Se tiene tres cargas puntuales, q1 = Q está ubicada en el punto P1(5,0,5)cm, q2 = Q está
en P2(0,5,5)cm y q3 = (-2Q) está en P3(0,0,10)cm. Si Q = 100µC, calcule, el campo
eléctrico total E y el potencial V en el punto P5(10,10,0)cm. Los vectores de posición
están dados en cm. Sus respuestas dar en unidades SI.
40.
a)
b)
c)
Se tiene un anillo de radio 1,5m cargado uniformemente con densidad lineal de carga
12 mC/m. Se encuentra ubicado en el plano XZ
con centro en el origen. Se pide:
R
P
Hallar la expresión del potencial eléctrico V y del Q
campo eléctrico E sobre el eje, en función de Y.
Y
Haga una grafica cualitativa de V vs. Y y de E
vs Y.
Calcule el valor máximo del potencial eléctrico sobre el eje Y
41. Se tiene una esfera conductora de 2m de radio la cual esta cargada con 20µC.
Se
pide:
a) Utilizando la Ley de Gauss halle la expresión del campo eléctrico E en función de la
distancia al centro de la esfera ( r ). (Para r < R y r > R)
21
b)
A partir de la expresión del campo hallado en (a), encuentre una expresión para el
potencial eléctrico en función de r.
( para r < R y r > R )
c) Calcule el potencial eléctrico a 1m de distancia del centro de la esfera.
Rpta. a) r>R, 180x103/r2 V/m, r<R, E=0. b) r>R, 80x103/r V, r<R, 90x103 V. c)
90x103 V
42.
a)
b)
c)
43.
44.
45.
a)
b)
c)
La figura muestra tres cargas q1= Q , q2 = 2Q y q3 = - Q , ubicadas en los vértices de
un triangulo equilátero de lado L = 30,0 cm. Si Q = 5 µC y K
= 9 x109 N-m2/c2. Halle:
La fuerza (vector) que ejercen las cargas q2 y q3 sobre la
carga q1.
El campo (vector) en el punto P, punto medio del lado BC
La energía potencial electrostática del sistema
Una partícula de masa M = 2g , con carga eléctrica q = + 50 µC lleva una
velocidad horizontal v = 40 m/s en el
instante en que entra por el punto medio a dos
placas cargadas, las placas son paralelas y
suficientemente extensas, separadas una
distancia d = 10 cm, la
placa superior es
positiva y están sometidas a una diferencia de
potencial V = 500v. Halle:
a) El campo entre las placas,
b) Las coordenadas del punto donde impacta la partícula con la placa inferior
En la figura se muestran tres cargas Q1 = 100 µC, Q2 = -100 µC
ubicados en los vértices de un triangulo equilátero
de lado b = 20,0 cm. Calcule: ( k = 9x109 N-m2/c2)
a) El Vector campo eléctrico en el punto M (Punto
medio de la base)
b) El trabajo necesario para llevar una carga Q4 =
20 µC del punto M al punto N (centro del
triangulo)
y Q3 = -200 µC
La figura muestra un sistema de cargas puntuales y a partir de este se desea formar un
triangulo equilátero de lado a. Si Q = 6µC y a = 4
cm. Encuentre:
La energía potencial del sistema inicial
La energía potencial del sistema final
El trabajo que se hace para llevar del sistema
inicial al sistema final
22
46.
Cinco cargas iguales +Q están igualmente
espaciadas en un semicírculo de radio R como
indica la figura. Si Q = 9,0 µC y q = 4,0 µC y
R = 0,20m, determine:
a) La fuerza eléctrica total que ejercen sobre otra
carga q localizada en el centro del
semicírculo.
b) El trabajo que se realizo para traer la carga q desde x ~ ∞ hasta el origen de
coordenadas.
k = 9 x 109 N. m2/C2, ε0 = 8,85 x 10-12 C2/ N. m2
47.
Una esfera de 10cm de radio contiene una densidad de carga uniforme ρ = 5,0 x 10-7
C/m3. Se pide:
a) Calcular la carga total de la esfera.
b) Hallar el campo eléctrico en r = 5,0 cm y en r = 20cm.
c) Obtener el potencial eléctrico en r = 5,0 cm.
48. Una esfera uniformemente cargada tiene un potencial de 450V en su superficie. A una
distancia radial de 20 cm de esta superficie, el potencial es 150V.
Calcular:
a) La carga y el radio de dicha esfera.
b) La diferencia de potencial entre dos puntos A y B que se
encuentran a una distancia de 1,2 m y 1,5 m del centro de la
esfera, respectivamente.
c) El trabajo (en J) necesario para llevar una carga qo = 5mC desde el
punto A al punto B.
49.
En la Figura mostrada, q = 3,0 µC y a = 2,50 cm.
Hallar:
a) El vector campo eléctrico E en el punto P
b) El potencial eléctrico en el punto P.
c) El trabajo necesario para trasladar la carga +2q
desde el origen de coordenadas al punto P
50.
y
En los vértices de un triangulo equilátero de lado
5 cm, se ubican tres cargas iguales y positivas de
valor q=5µC, como se muestra en la figura. Los
puntos M y N son puntos medios de los lados 0P
y PQ. Determinar:
Q
•
0
•
M
N
P
x
23
a)
b)
c)
51.
a)
b)
c)
d)
52.
El campo eléctrico en el punto M.
Los potenciales eléctricos en los puntos M y N.
El trabajo necesario para trasladar la carga q0=2µC desde el punto M hasta el punto N.
Dos cargas q1 = 25 nC y q2 = - 20 nC se ubican en el plano xy , en el origen de
coordenadas y en el punto A(4,3)m respectivamente .
Hallar:
El vector fuerza eléctrica que ejerce la carga q1 sobre la
carga q2. (1p)
El potencial eléctrico en el punto B( 0,-6)m. (1p)
El trabajo necesario para traer una tercera q3 = 13 nC desde
muy lejos y colocarla en el punto B, en presencia de las
carga q1 y q2. (2p)
El flujo eléctrico que atraviesa una esfera de radio R = 5,5
m centrada en el origen para el sistema de las tres cargas.
(1p)
Se tiene una varilla muy delgada con densidad lineal de carga λ ( y ) = A y donde
A es una constante positiva e “ y “ es la coordenada de un
punto de la varilla. Hallar a.-) El potencial eléctrico en el
punto P ( a; 0) ( 3 puntos ) b.-) Utilizando el resultado anterior
encontrar la diferencia de potencial entre los puntos A ( 2 a ; 0 )
y B ( 3 a ; 0 ) ( 1 punto ) c.-) El trabajo para llevar la carga de
prueba q0 del punto A al punto B . Ver figura
53. Use el diagrama mostrado para hallar: (05 P.)
a) El campo eléctrico en el origen
b) El potencial eléctrico en el origen
c) El trabajo para trasladar una carga
de 4 µ C del infinito al punto O.
d) La fuerza eléctrica sobre la carga de
4 µ C una vez en O.
54.
Un anillo circular delgado de radio R y carga
uniforme con densidad lineal λ ,se dispone como
se muestra en la figura adjunta. Hallar en el punto
P(x,o,o): (05 P)
a) El potencial eléctrico
b) El campo eléctrico derivando el potencial.
24
55.
a)
b)
c)
d)
56.
a)
b)
c)
d)
En los vértices de un cuadrado, centrado en el origen de
un sistema de coordenadas x-y, se ubican cuatro
cargas como se indica a continuación : +q en (-a ,
+a) ; 2q en (a , a) ; -2q en (a , -a) y 6q en (-a ,-a)
. Calcular :
El vector campo eléctrico en el origen . (2p)
El potencial en el origen. (2p)
El trabajo para llevar una carga qo = 5nC del origen
de coordenadas al infinito, manteniendo fijas las
otras cargas .(1p)
Considerar : a = 5 2 cm ; q = 2uC y 1uC =
10-6C ; 1nC = 10-9 C
Tres cargas puntuales de igual magnitud: Q= 9x10-9C y de
signos diferentes, están ubicados como se muestra en la
figura. Determinar :
La expresión vectorial del campo debido a cada
una de las cargas en el punto P(3, 0) cm. (2 p)
El potencial total en el punto P(3, 0) cm (2 p)
El trabajo para llevar una carga qo= 2x10-gC del punto P al
infinito (1p)
y
-Q
(0, 9) cm
(9,0) cm
O
+Q
x
-Q
57.
En el punto x=3 m hay una carga puntual de -3 µC y en x=-2 m una carga de
2 µC .Calcular: (05 P)
a) El campo eléctrico en el punto
A situado en x=5 m.
b) La diferencia de potencial entre los puntos A y O.
c) La fuerza sobre una carga de 7 µC colocada en A.
d) El trabajo para trasladar la carga de 7 µC de A hasta O a velocidad constante.
62.
El plano x=0 tiene una carga eléctrica uniforme con densidad 8,8 µC /m2 mientras
que el plano x=6 m lleva carga uniforme con densidad 4,4 µC /m2. Calcule: (05 P)
El campo eléctrico en la región O ≤ x ≤ 6m .
La diferencia de potencial entre ambos planos
Se coloca una partícula cargada de 2 µC y 1 gr. en x=3 m. Hacia que lugar se dirige
la partícula y en que tiempo llega a la placa.
a)
b)
c)
59. Dos laminas metálicas muy grandes y paralelas se encuentran en x=0 y
x=8m. La diferencia de potencial entre ellas es 10V, estando la placa
en x=8 m a mayor potencial.(05P)
a)
Halle el vector campo eléctrico entre las láminas.
25
b)
c)
Hallar la fuerza eléctrica sobre una carga puntual de +2 µ C colocada en
x=4m.
Si la masa de dicha carga es 0,2 g hallar el tiempo para que llegue a una de las
placas.
60. Se coloca una carga puntual q en el centro O
cascarón conductor grueso de radios a y b descargado. Hallar: (05P)
a)
El campo eléctrico en las regiones 1.2 y 3
b)
El potencial del conductor
c)
Las cargas inducidas en el conductor.
de un
61. En el punto x=3 m hay una carga puntual de -3 µC y en x=-2 m una
carga de 2 µC .Calcular: (05 P)
e) El campo eléctrico en el punto A
situado en x=5 m.
f) La diferencia de potencial entre los puntos A y O.
g) La fuerza sobre una carga de 7 µC colocada en A.
h) El trabajo para trasladar la carga de 7 µC de A hasta O a velocidad constante.
62.
a)
b)
c)
El plano x=0 tiene una carga eléctrica uniforme con densidad 8,8 µC /m2 mientras
que el plano x=6 m lleva carga uniforme con densidad 4,4 µC /m2. Calcule: (05 P)
El campo eléctrico en la región O ≤ x ≤ 6m .
La diferencia de potencial entre ambos planos
Se coloca una partícula cargada de 2 µC y 1 gr. en x=3 m. Hacia que lugar se dirige
la partícula y en que tiempo llega a la placa.
63. Dos laminas metálicas muy grandes y paralelas se
encuentran en x=0 y x=8m. La diferencia de potencial
entre ellas es 10V, estando la placa en x=8 m a mayor
potencial.(05P)
a) Halle el vector campo eléctrico entre las láminas.
b) Hallar la fuerza eléctrica sobre una carga puntual de +2 µ C
colocada en x=4m.
c) Si la masa de dicha carga es 0,2 g hallar el tiempo para que
llegue a una de las placas.
64.
a)
b)
c)
Se coloca una carga puntual q en el centro O de un cascarón conductor grueso de
radios a y b descargado. Hallar: (05P)
El campo eléctrico en las regiones 1.2 y 3
El potencial del conductor
Las cargas inducidas en el conductor.
26
65.
a)
b)
c)
Se tienen tres cargas puntuales, q1 = 100 µC , ubicada en el punto M(-3, 0) m ,q2
= - 50 µC ubicada en el punto N(3,0) m y q3 = 100 µC, ubicada en el punto P(0,2) m
.Encontrar: (5P)
El potencial eléctrico en el origen de coordenadas, debido a todas las cargas
El trabajo necesario para traer una carga q = - 100 µC desde el infinito hasta el origen
de coordenadas
La energía potencial que tiene la carga q que ha sido desplazada del infinito hasta el
origen
66. Cuatro cargas del mismo valor q = 6µC, están ubicadas en
los vértices de un cuadrado de lado L = 30 cm, como muestra la
figura. Halle: (5P)
a) El vector campo eléctrico en el punto P, que se encuentra a la mitad
de un lado
b) El vector fuerza sobre una carga q1 = 10µC, que se encuentra en el
punto P
c) La energía potencial electrostática del sistema
67.
Un arco de circulo de radio R, con centro en P, subtiende
un ángulo de π /6 y tiene una carga λ por unidad de
•
longitud. Encontrar:
a) El campo eléctrico del arco en el punto P. (3p)
b) El potencial eléctrico del arco en el punto P. (2p)
R
π /6
P
68.
69.
-9
Cuatro cargas de igual magnitud Q = 2x10 c y de
signos diferentes se ubican en las esquinas de un
cuadrado de lado a = 10cm, como se muestra en la
figura. Calcular:
a) El campo eléctrico en el centro del cuadrado. (1p)
b) El potencial eléctrico en el centro del cuadrado C y en
el punto medio A del lado inferior. (1p)
c) El trabajo del campo eléctrico cuando una carga qo=
5x10-12c se desplaza del punto C al punto A. (1p)
d) La energía potencial electrostática del sistema. (2p)
-Q
a
+Q
.C
+Q
A
+Q
K =9x109N.m2/c2
En los vértices de un cuadrado de lado a = 10cm, se ubican las cargas :
q1 = 1 x 10-9C, q2 = - 4x10-9C , q3= - 4 x 10-9C y q4 = 2x10-9C como se muestra en
la figura, determinar :
a
q1
q2
a) El vector campo eléctrico en el centro del cuadrado
(punto O). 2p
b) El potencial eléctrico en el punto O. 2p
a
c) El trabajo para llevar una carga qo =
5x10-12C del punto O al infinito. 1p
q3
K = 9x109N. m2/C2
q4
a
27