analisis de componentes principales

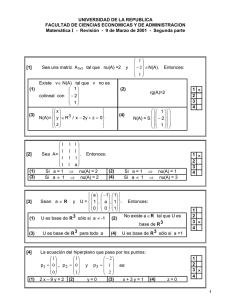
1
X2
F2
F1
e2
v2
v1
e1
X1
ANALISIS DE COMPONENTES
PRINCIPALES
José Luis Vicente Villardón
Departamento de Estadística
2
1.- EJEMPLO INICIAL..............................................................................................................................3
2.- DEFINICIONES BASICAS ................................................................................................................13
3.- OBTENCION DE LA COMPONENTES PRINCIPALES..............................................................15
3.1.3.2.3.2.1.3.2.2.3.3.-
OBTENCIÓN DE LAS CP MEDIANTE LA MAXIMIZACIÓN DE LA VARIABILIDAD. .....................15
OBTENCIÓN A PARTIR DEL SUBESPACIO DE MEJOR AJUSTE ...................................................20
Ajuste por un subespacio vectorial en Rp. ......................................................................21
Cálculo del máximo. .......................................................................................................23
COORDENADAS PRINCIPALES.....................................................................................25
4.- MEDIDAS DE LA BONDAD DEL AJUSTE ....................................................................................26
5.- PROPIEDADES ...................................................................................................................................27
6.- NÚMERO DE EJES A RETENER ....................................................................................................27
7.- ESCALAS DE MEDIDA .....................................................................................................................28
8.- INTERPRETACIÓN DE RESULTADOS.........................................................................................28
9.- CORRELACIONES DE LAS COMPONENTES Y LAS VARIABLES........................................29
10.- EJEMPLO...........................................................................................................................................30
10.1.10.2.10.3.-
DATOS................................................................................................................................30
REPRESENTACIÓN DE LOS INDIVIDUOS SOBRE EL PRIMER PLANO PRINCIPAL ........................31
SALIDA TIPICA DE ORDENADOR ................................................................................32
3
1.- EJEMPLO INICIAL
Supongamos que deseamos conocer cuales son los factores relacionados con el
riesgo de enfermedad coronaria. Del conoocimiento previo sabemos que el
riesgo la presión arterial, la edad, la obesidad, el tiempo que se ha sido
hipertenso, el pulso, y el stress.
Para la investigación seleccionamos al azar 20 pacientes hipertensos en los que
medimos las siguientes variables:
X1: Presión arterial media (mm Hg)
X2: Edad (años)
X4: Superficie corporal (m2)
X3: Peso (Kg).
X5: Duración de la Hipertensión (años)
X6: Pulso (pussaciones/minuto)
X7: Medida del stress.
Tratamos de estudiar la situación del grupo de pecientes en relación a los
factores de riesgo y las posibles interrelacions entre las distintas variables.
Iniicialmente
queremos
describir
el
conjunto
de
pacientes
utilizando
simultáneamente todas las variables
Los datos obtenidos se muestran en la tabla siguiente:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
X1
X2
X3
X4
X5
X6
X7
105
115
116
117
112
121
121
110
110
114
114
115
114
106
125
114
106
113
110
122
47
49
49
50
51
48
49
47
49
48
47
49
50
45
52
46
46
46
48
56
85,4
94,2
95,3
94,7
89,4
99,5
99,8
90,9
89,2
92,7
94,4
94,1
91,6
87,1
101,3
94,5
87,0
94,5
90,5
95,7
1,75
2,10
1,98
2,01
1,89
2,25
2,25
1,90
1,83
2,07
2,07
1,98
2,05
1,92
2,19
1,98
1,87
1,90
1,88
2,09
5,1
3,8
8,2
5,8
7,0
9,3
2,5
6,2
7,1
5,6
5,3
5,6
10,2
5,6
10,0
7,4
3,6
4,3
9,0
7,0
63
70
72
73
72
71
69
66
69
64
74
71
68
67
76
69
62
70
71
75
33
14
10
99
95
10
42
8
62
35
90
21
47
80
98
95
18
12
99
99
La dimensión inicial es 7, pero ¿Será posible describir el conjunto de datos
utilizando un número menor de dimnsiones, aprovechando las interrelaciones
4
entre las variables?
¿Es posible definir un índice general que cuantifique la situación de riesgo?
Si consideramos solamente dos variables, los resultados se pueden presentar
mediante un diagrama de dispersión como el que aparece en la figura siguiente.
Sobre el diagrama se han incluidos los números de orden de cada uno de los
pacientes.
edad By presion
57,5
20
55,0
52,5
15
edad
5
13
50,0
9
47,5
1
10
8
11
7
6
18
16
14
45,0
42,5
100
23
12
19
17
4
105
110
115
presion
120
125
130
Sobre la figura es posible interpretar la posible relación entre las variables, pero
también las similitudes entre los individuos. Dos individuos próximos en el
gráfico tendrán características similares, mientras que dos individuos alejados
tendrán características diferentes. Se pueden buscar también grupos de puntos
cercanos con características similares.
5
Si consideramos las tres primras variables, aun es posible representarlas en tres
dimensiones sobre el papel como se muestra en la figura siguiente. Las
representaciones tridimensionales sobre el papel son difíciles de interpretar ya
que no se tiene una referencia visual clara. La interpretación puede realizarse
mediante un programa de ordenador que permita el movimiento de la figura
para ver las posiciones relativas de los puntos.
Components
X presion
Y edad
y
20
Z peso
5
9
1
17
14
19
8
13
15
4
23
12
10
11 z
18
16
x
7
6
Representación tridimensional de las variables presión, edad y peso.
Si movemos la figura resultante, observaremos que los puntos están
prácticamente sobre un plano. Esto se pone de manifiesto en la figura siguiente
en la que se ha conseguido un punto de vista desde el que los puntos parecen
estar sobre una línea recta.
Este hecho pone de manifiesto que no son necesarias tres dimensiones para
describir el conjunto de datos, sino solamente dos.
6
y
20
5
13
15
94
z
2
12
1
19
3
10
8
717
11
6
14
x
18
16
Rotación de la representación tridimensional que muestra que los puntos se
encuentran aproximadamente en un plano.
Tenemos entonces que buscar un sistema de referencia para el plano
(subespacio) más cercano a la nube de puntos de forma que, al proyectarlos
todos sobre dicho plano, la pérdida de información sea mínima. La pérdida de
información puede entenderse en términos de variabilidad del conjunto de
puntos o en términos de la similitud entre las interdistancias entre los puntos,
calculadas en el espacio original y las calculadas en la proyección del
subespacio.
El subespacio quedará definido mediante un sistema de referencia para el
mismo, es decir, mediante dos vectores perpendiculares dentro del subespacio.
El primero lo situaremos en la dirección en la que más varían los datos, el
7
segundo, perpendicular al primero recogiendo la mayor parte de la variabilidad
restante y así sucesivamente.
Los vectores del sistema de referencia definen nuevas variables, que son
combinaciones lineales de las variables de partida y se denominan componentes
principales. De esta forma, podemos reducir la dimensión seleccionando
solamente las primeras componentes. La reducción de la dimensión se deriva
del hecho de que las variables están relacionadas entre si y, por tanto, tienen
información común, de alguna manera, la información común a todas ellas se
extrae en las componentes principales.
La representación de las dos primeras componentes, para los datos anteriores y
con sólo tres variables aparece en la figura siguiente. Las dos primeras
componentes absorben el 99% de la variabilidad de los datos.
2,5
20
2,0
5
1,5
Prin Comp 2
1,0
9
1
13
0,5
19
4
17
12
2
0,0
8
14
10
15
3
-0,5
11
-1,0
7
18
16
-1,5
-2,0
6
-1,5
-1,0
-0,5
0,0
0,5
Prin Comp 1
1,0
1,5
2,0
2,5
Espacio de las componentes con las tres primeras variables
Sobre el diagrama de dispersión es posible interpretar las distancias entre los
puntos en términos de similitud, buscar conjuntos de individuos similares, etc,
con la garantía de que la pérdida de información es mínima y de que hemos
recogido las fuentes de variabilidad más importantes en el conjunto de datos.
8
Cuando el número de variables es mayor, ya no es posible la representación
directa de las variables en más de tres dimensiones, pero aun sigue siendo
posible la reducción de la dimensión, teniendo en cuenta las iterrelaciones entre
las variables.
La figura siguiente muestra las dos primeras componentes principales para el
conjunto de las 7 variables. Las componentes se denotan con x e y. Se han
superpuesto sobre el gráfico vectores que representan a las variables originales
y que interpretaremos más tarde. También se han suprimido las escalas ya que,
en este contexto son menos importantes.
y
19
stress
5
duracio
9
14
16
1
13
17
edad
pulso
4
11
z
3
8
20
12
x
presion
peso
superfi
1810
2
6
7
Espacio de las componentes con todas las variables.
En este caso, las dos primeras componentes recogen aproximadamente el 77%
de la variabilidad, más aun recogen las fuentes de variabilidad más importantes
de los datos.
9
Si prescindimos, por el momento, de los vectores que representan a las
variables, podemos interpretar las distancias entre puntos y buscar grupos, tal y
como hacíamos en el diagrama de dispersión inicial.
Como las componentes son variables compuestas calculadas a partir de las
originales, solamente queda por determinar cual es la información que han
recogido las componentes, es decir, que variables explican la similitud de los
individuos en el subespacio de representación final. La interpretación se hace a
partir de las correlaciones entre las variables observadas y las componentes.
Dichas correlaciones se muestran en la tabla siguiente. (las componentes se
denominan factores en la tabla).
Unrotated Factors
Factor 1 Factor 2
presion
,965
-,230
edad
,723
,304
peso
,884
-,403
supcorp
,804
-,473
Durac.
,434
,525
pulso
,844
,284
stress
,355
,764
Correlaciones entre las componentes principales y las variables observadas
Observamos como la primera componente está altamente correlacionada con
todas las variables salvo Duración y Stress, es decir, la primera componente
muestra, fundamentalmente aspectos relacionados con el aumento de la presión
arterial y de las variables determinantes del riesgo de enfermedad coronaria,
por tanto la primera componente sería un índice del riesgo de enfermedad de
forma que, los individuos que se sitúen a la derecha en la proyección sobre el
eje del gráfico serán los que tienen riesgo más alto de enfermedad y los que se
sitúan a la izquierda, riesgo más bajo.
La segunda componente está más correlacionada con el stress y algo menos con
la duración, por lo que mostrará las diferencias en el índice de stress.
Sobre el gráfico habíamos superpuesto también vectores que representaban a
cada una de las variables originales. Los vectores representan la dirección de
mejor ajuste para cada una de las variables, en el sentido de que, si proyectamos
los puntos que representan a los individuos sobre uno de los vectores, las
puntuaciones obtenidas estarían más correlacionadas con la variable original
10
que las proyecciones en cualquier otra dirección. El coseno del ángulo que
forma cada vector con el eje, mide aproximadamente la correlación con el
mismo y los cosenos de los ángulos entre dos vectores aproximan la correlación
entre las variables a las que representan, es decir, a menor ángulo menor
correlación.
La representación con las variables añadidas se denomina representación
biplot.
A las correlaciones al cuadrado entre la variable y el eje se le denomina tambien
contribución relativa del factor al elemento, y mide la parte de la variabilidad
de la variable que explica cada uno de los ejes. Las variables con contribuciones
altas en uno de los ejes y bajas en los demás son las que han de interpretarse
para cada eje ya que son características exclusivas del mismo.
Como las componentes son incorreladas, tienen información independiente por
lo que la suma de las correlaciones al cuadrado es 1. La parte explicada por un
plano, se calcula simplemente sumando la parte explicada (contribución) por
los ejes que lo componen, a esta cantidad se la denomina también “calidad de la
representación”.
La calidad de representación puede interpretarse tambien como la correlación
al cuadrado entre los valores de la variable original y las proyecciones de los
puntos sobre la dirección que representa a la variable.
De la misma manera que hemos hecho para las variables es posible definir
calidades de representación para los individuos. Veamos una interpretación
diferente de la misma más adecuada para el estudio de los individuos.
La figura siguiente muestra la proyección de uno de los puntos de la nube en
un espacio bidimensional. Supongamos que se trata de la proyección de uno de
los vectores que representa a una variable.
11
Vector real en el
espacio
tridimensional
Vector
proyección en
el espacio
bidimensional
Si observamos el espacio tridimensional que aparece en la figura, la variable
representada y el eje horizontal forman un ángulo de casi 90° por lo que pueden
considerarse independientes; sin embargo en la proyección sobre el espacio
bidimensional, el ángulo es muy pequeño, hecho que se podría traducir en una
fuerte relación. Esto es debido a que la calidad de la representación del vector
sobre el plano es baja.
La figura siguiente muestra la situación esquematizada. El coseno al cuadrado
del ángulo se puede tomar como medida de la relación entre la variable y el eje.
i
ángulo
C
proy(i, 1)
eje 1
cos 2 (θ) = || C , proy(i, 1) || / ||C, i||
A esta medida la denominaremos CALIDAD DE LA REPRESENTACION del
punto i sobre el eje factorial. (CLRil ).
Esta cantidad puede calcularse tambien a partir del producto escalar entre el
12
vector i y un vector cualquiera en la dirección del eje.
La calidad de la representación es una medida relativa, ya que la suma de las
calidades de la representación de cada elemento sobre todos los ejes factoriales
es 1.
El gráfico siguiente muestra una representación sobre tres ejes factoriales,
donde se especifican los cosenos de los ángulos con los tres ejes que, como es
sabido, su suma de cuadrados es la unidad.
eje 3
θ3
θ2
eje 2
θ1 θ
eje 1
cos2 θ + cos2θ + cos2 θ = 1
1
2
3
cos2θ = cos2 θ + cos2 θ
1
2
La calidad de la representación con respecto a un plano se mide de la misma
manera, es decir, como el coseno al cuadrado del ángulo que forman el vector y
el plano. Este coseno al cuadrado es la suma de los cosenos al cuadrado de los
ángulos con los ejes que forman el plano.
cos2 (θlk) = cos2 (θl) + cos2 (θk)
Por tanto, la calidad de la representación del elemento es una medida aditiva
que puede calcularse para la proyección en cualquier plano factorial, sin más
que sumar las calidades de representación con respecto a los ejes factoriales que
lo forman.
13
2.- DEFINICIONES BASICAS
DATOS
Disponemos de una matriz Xnxp que contiene las medidas de p variables
tomadas sobre n individuos. Para simplificar el resto de la exposición
supondremos, sin pérdida de generalidad, que las columnas de X tienen media
cero, es decir que se le ha restado la media.
Todas las variables tienen el mismo papel, es decir, el conjunto no se divide en
variables dependientes e independientes como en el caso de la regresión.
DEFINICION
El Análisis de Componentes principales consiste en encontrar transformaciones
ortogonales de las variables originales para conseguir un nuevo conjunto de
variables incorreladas, denominadas Componentes Principales, que se obtienen
en orden decreciente de importancia.
Las componentes son combinaciones lineales de las variables originales y se
espera que, solo unas pocas (las primeras) recojan la mayor parte de la
variabilidad de los datos, obteniéndose una reducción de la dimensión en los
mismos. Luego el propósito fundamental de la técnica consiste en la reducción
de la dimensión de los datos con el fin de simplificar el problema en estudio.
Se trata de una técnica orientada a las variables, suponemos que las p columnas
de X generan un espacio p dimensional, de forma que los n individuos pueden
representarse en dicho espacio en lo que llamaremos una hipernube. La
transformación es, de hecho, una rotación en el espacio p-dimensional. El
espacio generado por las primeras q componentes es entonces, un subespacio
vectorial q-dimensional del espacio p-dimensonal original.
14
Cuando el valor de q es pequeño, por ejemplo 2, es posible una representación
gráfica directa de los individuos que nos ayudará ainterpretar las similitudes
entre los mismos.
El ACP puede entenderse también como la búsqueda del subespacio de mejor
ajuste.
Una de las diferencias fundamentales con el Análisis Factorial es que el ACP
explica variabilidad en lugar de correlaciones, aunque para obtener una
reducción efectiva de la dimensión es necesario que las variables estén
correlacionadas.
En
otras
palabras,
si
las
variables
están
altamente
correlacionadas, tienen información común y la dimensión real de los datos es
menor que p.
En muchas ocasiones es difícil encontrar el significado de las componentes,
como variables compuestas, por lo que el uso principal de la técnica es la
reducción de la dimensión como paso previo a la aplicación de otros análisis
posteriores, por ejemplo, un diagrama de dispersión de las primeras
componentes con el objeto de encontrar “clusters” en los datos o con el objeto
de contrastar similitudes o diferencias entre los individuos.
El ACP es una técnica que no necesita que se especifique un modelos concreto
para explicar el “error”, en particular, no se hace ninguna suposición sobre la
distribución de probabilidad de las variables originales, aunque si se supone
que es normal multivariante es posible obtener algunos resultados inferenciales
adicionales.
En algunos textos se hacen diferencias entre las CP poblacionales y muestrales,
aquí entenderemos la técnica como un método descriptivo, libre de
distribución, y trabajaremos directamente con los datos muestrales.
15
3.- OBTENCION
DE
LA
COMPONENTES
PRINCIPALES
La obtención de las CP puede realizarse por varios métodos alternativos:
1.- Buscando aquella combinación lineal de las variables que maximiza la
variabilidad. (Hottelling).
2.- Buscando el subespacio de mejor ajuste por el método de los mínimos
cuadrados. (Minimizando la suma de cuadrados de las distancias de cada punto
al subespacio). (Pearson).
3.- Minimizando la discrepancia entre las distancias euclídeas entre los puntos
calculadas en el espacio original y en el subespacio de baja dimensión.
(Coordenadas principales, Gower).
4.- Mediante regresiones alternadas (métodos Biplot)
3.1.- OBTENCIÓN DE LAS CP MEDIANTE LA MAXIMIZACIÓN
DE LA VARIABILIDAD.
Denotaremos con X1, … , Xp las variables originales y con Y1, … , Yp las
componentes. En principio, podemos obtener tantas componentes como
variables originales. X denotará el vector de variables originales e Y el de
componentes.
X es la matriz de datos originales, que supondremos centrada por columnas, y S
es la matriz de covarianzas entre las variables.
S=
1
X′ X
n−1
16
Buscamos combinaciones lineales de las variables observadas que sean
incorreladas y con varianzas progresivamente decrecientes
Yj = v1j X1 + K + v pj X p
Yj = Xv j
y j = Xv j
Y = XV
Donde Y es la matriz que contiene las puntuaciones de cada uno de los
individuos sobre las componentes y V es la matriz que contiene los coeficientes
de las combinaciones lineales en columnas.
Y1 será aquella componente que explique la mayor parte de la variabilidad, Y2
será ortogonal a Y1 y explicará la mayor parte de la variabilidad restante y así
sucesivamente.
En las ecuaciones tenemos un factor de escala arbitraria por lo que imponemos
la restricción
P
∑ vkj2 = 1
k =1
v ′j v j = 1
V ′V = I
Buscamos Y1 que haga máxima la varianza
Var(Y1 ) = Var(Xv 1 ) = v ′1Sv 1
Utilizando el método de los multiplicadores de Lagrange para tener en cuenta
la restricción, podemos escribir
L(v1 ) = v′1Sv 1 − λ( v ′1v 1 − 1)
Derivando e igualando a cero
L(v1 )
= 2Sv 1 − 2λv 1
∂v 1
17
es decir
Sv 1 = λv 1
lo que quiere decir que v1 debe ser un vector propio de S de valor propio λ,
pero S tiene p valores propios
λ1, … λp que supondremos distintos y ordenados en orden decreciente λ1 ≥ …
≥ λp ≥ 0.
Teniendo en cuenta que
Var(Xv1 ) = v′1Sv 1 = v′1 λ v1 = λ
λ debe ser λ1 el primer valor propio y v1 el vector propio asociado.
La segunda componente principal Y2= Xv2, se obtiene con un procedimiento
análogo pero añadiendo la restricción adicional de que Y1 e Y2 son incorreladas.
cov(Y1 , Y2 ) = v ′2 Sv1 = 0
o una condición equivalente más simple
v ′2 v 1 = 0 ya que Sv 1 = λv 1
Utilizando de nuevo el método de los multiplicadores de Lagrange, podemos
escribir
L(v 2 ) = v ′2Sv 2 − λ( v ′2 v 2 − 1) − δv ′2 v 1
Derivando e igualando a cero se obtiene
L(v 2 )
= 2Sv 2 − 2λv 2 − δv 1 = 0
∂v 2
premultiplicando por v’1,
18
2 v 1′ Sv2 − 2λv′1 v2 − δv ′1v 1 = 0
2 v1′Sv 2 − δ = 0
como v ′1Sv2 = 0 , entonces δ = 0 en el punto estacionario, de forma que ,
Sv 2 = λv 2
con lo que λ es el segundo valor propio λ2 y v2 es el segundo vector propio.
Siguiendo con el mismo argumento, podemos obtener las sucesivas componentes
principales a partir de los correspondientes valores y vectores propios.
Entonces, si
 Λ = diag(λ1 ,K, λ p )
S = V′ΛV 
V ′V = I
es la descomposición espectral de la matriz de covarianzas S, los coeficientes de
las combinaciones lineales que definen las componentes principales son las
columnas de V, es decir los vectores propios de la matriz de covarianzas.
Seleccionando q componentes, las puntuaciones de los individuos en las componentes
están dadas por
Yq = XVq
donde Vq está formada por las q primeras columnas de V, y suponiendo X
centrada.
Ahora
p
p
j=1
j=1
∑ Var(Yj ) = ∑ λ j = traza(Λ)
y
19
traza( Λ) = traza(V ′SV) = traza(SV ′V) =
p
traza(S) = ∑ Var(X j )
j=1
Este resultado nos permite calcular la proporción de varianza absorbida por
cada componente como
λj
p
∑ λi
i=1
o acumulada para un subespacio de dimensión q
q
∑λ j
j=1
p
∑ λi
i=1
- Nota: las componentes principales pueden calcularse también a partir de X'X
con X centrada ya que
S=
1
X ′X
n−1
se obtienen los mismos vectores propios aunque los correspondientes valores
propios aparecieran multiplicados por n-1, lo cual no influye en la variabilidad
absorbida.
20
Obtención a partir del subespacio de mejor ajuste
Una aproximación diferente que produce los mismos resultados es la que trata
de minimizar la suma de cuadrados de las distancias de cada punto a la
componente, entendiendo que buscamos el subespacio, en dimensión reducida,
que mejor se ajusta a la nube de puntos.
El procedimiento de ajuste se basa en el método de los mínimos cuadrados.
Sea X una matriz rectangular de datos con n filas y p columnas y con término
general xij. Abordaremos el siguiente problema:
¿es posible reconstruir los np valores xij, y por tanto las interdistancias entre
individuos, a partir de un número mas pequeño de valores numéricos?
Trataremos ahora la solución relacionada con los métodos factoriales.
Supongamos que existe un vector columna y de n componentes y un vector
1
t
1
columna v1 de p componentes de modo que X = y v .
1
Se habrán reconstruido los np valores de X con n + p valores únicamente (en
este caso la matriz es de rango 1).
En general no es posible obtener una descomposición tan simple. Buscaremos
una aproximación de rango q para X, es decir
t
1
t
2
X = y v + y v + ............ + y v
1
2
q
t
+E
q
E es una matriz residual con términos muy pequeños para que la
reconstrucción sea satisfactoria. Reconstruimos X entonces, con q(n+p) valores
t
i
de los vectores u v .
i
Resolveremos el problema mediante representaciones geométricas vinculadas
a los métodos factoriales. X dará lugar a dos representaciones; las n filas pueden
p
considerarse como n puntos en un espacio de p dimensiones R ; y las p
columnas pueden representar las coordenadas de p puntos en un espacio de n
n
dimensiones R
21
p
Ajuste por un subespacio vectorial en R .
Si la nube de n puntos que representan a las filas de la matriz X está contenida
en un subespacio de dimensión q < p será posible reconstruir las posiciones de
los n puntos a partir de las coordenadas de q nuevos ejes y de las componentes
de estos nuevos ejes.
Por lo tanto vamos a intentar ajustar la nube de n puntos por un subespacio
p
vectorial de R dotado de la distancia euclídea ordinaria. Buscaremos la recta Fl
que pasa por el origen y se ajusta lo mejor posible a nube. Sea v un vector
t
unitario de esa recta, es decir, v v = 1 Como cada fila de X representa un punto
p
de R ,las n filas de vector Xv son las n longitudes de las proyecciones de los
puntos de la nube sobre F1.
Para cada punto, el cuadrado de la distancia a origen se descompone en el
cuadrado de su proyección sobre F1 y el cuadrado de su distancia a F1. Como
las distancias al origen están fijadas, minimizar la suma de cuadrados de las
distancias a F1 es equivalente a maximizar la suma de cuadrados de las
proyecciones.
P
d
d1
F1
p
d2 = p2 + d2
1
22
X2
F2
F1
e2
v2
v1
e1
X1
Buscamos v que haga máxima la cantidad
t
t t
(Xv) Xv = v X X v
t
con la restricción v v = 1. El subespacio resultante se designará por v .
1
El subespacio vectorial de dos dimensiones que mejor se ajusta a la nube de
puntos contendrá a v . Se hallará buscando el vector unitario v ortogonal
1
2
respecto a v que haga máxima la forma cuadrática
1
t t
t
t
v2 X X v2 con las restricciones v2 v1 = 0; v2 v2 = 1.
Así sucesivamente buscamos el subespacio engendrado por q vectores
v2, ... , vq (ortogonales dos a dos) que mejor se ajustan a la nube de puntos.
v1,
23
Cálculo del máximo.
Sea λ un multiplicador de Lagrange.
t t
t
Derivamos la cantidad v X X v - λ (v v - 1) con respecto a las componentes de
v y obtenemos
t
2X Xv-2λv =0
es decir,
t
X Xv=λv
t
de valor propio λ.
Entonces, vl es un vector propio de la matiz X X
Concretamente el mayor valor propio.
t
Puede verse que, v1, v2, ... , vq son vectores propios de X X asociados a valores
propios λ1, λ2, ... , λq respectivamente y que λ1 ≥ λ2 ≥ ... ≥ λq.
t
La matriz X X es semidefinida positiva por lo que todos los valores propios
son mayores que cero
Es posible otra interpretación en términos de la variablidad. Como es bien
t
sabido, si los datos están centrados, la matriz X X es, salvo un factor de escala
dependiente del tamaño muestral, coincide con la matriz de varianzascovarianzas entre las variables.
t
S = (1/n) X X
p
Dado un vector v en R , la varianza de las proyecciones sobre Xv dicho vector,
t
es v S v.
Si buscamos el vector v unitario en aquella dirección con máxima varianza se
t
t
trata de hacer máxima la cantidad v S v con la restricción v v = 1.
El subespacio resultante se designará por v .
1
Sea µ un multiplicador de Lagrange.
24
t
t
Derivamos la cantidad v S v - µ (v v - 1) con respecto a las componentes de u
y obtenemos
2Sv-2µv =0
es decir,
Sv=µv
t
Entonces, vl es un vector propio de la matiz X X de valor propio µ = λ /n.
Luego la dirección buscada es la que maximiza la varianza y es, por tanto, la
dirección en la que pueden examinarse las diferencias entre los individuo con
pérdida de información mínima.
Los vectores directores de los q nuevos ejes se obtienen a partir de la
t
descomposición en valores y vectores propios de S (o X X) en la forma
t
S=VDV
y se corresponden con las q primeras columnas de la matriz de vectores propios
V.
Las coordenadas de los individuos en el espacio generado por las q primeras
componentes principales, es decir, las proyecciones de los puntos en el espacio
original sobre el subespacio de las componentes principales, son
Y = X V(q)
donde el subíndice (q) significa "las q primeras columnas".
Las componentes principales son nuevas variables, combinación lineal de las
variables originales, con varianza progresivamente decreciente.
25
3.2.- COORDENADAS PRINCIPALES
El tercer procedimiento de obtención se basa en hacer minima la discrepancia
entre las distancias observadas en el espacio original y las distancias estimadas
en el espacio de la aproximación.
Pj
δij
Pi
ˆ
δij
P'j
L
P'i
Min∑ij (δ ij − δˆij ) 2
δ ij =
δˆij =
p
2
∑ (xik − x jk )
k=1
q
2
∑ (yik − y jk )
k=1
(Coordenadas principales)
26
4.- MEDIDAS DE LA BONDAD DEL AJUSTE
Como se trata de una aproximación en dimensión reducida es necesario decidir
si la aproximación es satisfactoria.
- Las coordenadas de las proyecciones sobre el subespacio de las componentes
en el sistema de referencia original son
t
t
X* = Y V (q) = X V(q) V (q)
La discrepancia con los valores originales en X con los valores esperados en el
subespacio se puede medir como la suma de cuadrados de (X - X*), es decir,
como
t
traza[(X - X*) (X - X*)]
o en forma relativa
t
t
traza[(X - X*) (X - X*)] / traza[X X]
luego, una medida de la bondad del ajuste puede ser
t
t
(1 - (traza[(X - X*) (X - X*)] / traza[X X])) x 100
que puede interpretarse como el porcentaje de la variabilidad de los datos
explicado por las componentes principales.
Teniendo en cuenta las propiedades de la traza, la bondad del ajuste puede
escribirse también como
q
∑ λi
i=1
q
∑ λi
i=1
x100
27
5.- PROPIEDADES
p
- La matriz de vectores propios V define un cambio de base del espacio R en el
que se ha representado la matriz de datos originales.
p
- Las q primeras columnas de V definen la proyección de los puntos en R sobre
el subespacio q-dimensional de mejor ajuste.
- Los elementos de V son los cosenos de los ángulos que forman las variables
originales y las componentes principales.
- Las coordenadas de los individuos en el nuevo sistema de referencia son de la
forma
Y = X V.
- Las coordenadas las primeras componentes principales permiten interpretar
las similaridades entre individuos con pérdida de información mínima.
- El ACP utiliza la información redundante, a través de las correlaciones entre
las variables, para reducir la dimensión.
- La matriz de covarianzas entre las componentes es D (Λ).
- Las componentes principales son variables incorreladas y, por tanto con
información independiente.
- La varianza de las componentes principales es λi.
- Si se trabaja con datos brutos, la primera componente principal suele mostrar
la traslación de la nube de puntos con respecto al origen.
-
Si las variables están centradas, las componentes se calculan a partir de la
matriz de covarianzas y las componentes estarán dominadas por las
variables con escala de medida mayores.
-
Si se trabaja con datos estandarizados, las componentes principales se
obtienen de la diagonalización de la matriz de correlaciones. Se utilizarán
datos estandarizados cuando las escalas de medida de las variables sean
muy diferentes.
6.- NÚMERO DE EJES A RETENER
- Prueba de Anderson: Si los datos son normales, es posible realizar un test para
contrastar si las últimas (p-q) raíces son iguales a cero.
28
 p 
 ∑ λi 
p
I=q+1
2

χ = −(n − 1) ∑ ln(λ i ) + (n − 1)(p − q)ln 
 p−q
I=q+1




sigue una ji-cuadrado con (1/2) (p-q) (p-q+1) - 1 grados de libertad.
-Scree Plot: Gráfico de los valores propios. Se seleccionan ejes hasta que se vea
un decrecimiento brusco en la magnitud de los valores propios.
- Seleccionar las componentes necesarias para explicar un determinado
porcentaje de la varianza.
7.- ESCALAS DE MEDIDA
Si las escalas de medida de las variables son muy diferentes, la variabilidad
estaría dominada por las variables con magnitudes mayores de forma que las
primeras componentes pueden mostrar simplemente las diferencias en la
escala. En este caso conviene tomar la matriz x estandarizada por columnas y
centrando y dividiendo por la desviación típica. En este caso las componentes
estarían colocadas sobre la matriz de correlaciones.
8.- INTERPRETACIÓN DE RESULTADOS
-
Diagramas de dispersión que representan los valores de los individuos en
las primeras componentes principales.
-
Interpretación de distancias en términos de similitud.
-
Búsqueda de clusters (grupos) y patrones.
-
Interpretación de las componentes utilizando las correlaciones con las
variables originales. Las posiciones de los individuos se interpretan después
en relación a la interpretación dada a las componentes.
29
9.- CORRELACIONES DE LAS COMPONENTES
Y LAS VARIABLES
A los vectores escalados de la forma:
v *j = λ1/2
j vj
C = VΛ1/2
se les denomina factores de carga (C)
Cuando las componentes principales se calculan usando la matriz de
correlaciones, la matriz C contiene las correlaciones entre las variables
originales y las componentes.
Para las componentes calculadas a partir de la matriz de covarianzas, los
factores de carga dependen de la escala de medida de las variables por lo que
son difíciles de interpretar.
Los factores de carga suelen representarse en un gráfico que permite la
interpretación visual de las relaciones.
En cualquiera de los casos podemos calcular también la correlación al cuadrado
entre las componentes y las variables y las componentes. A dichas correlaciones
al cuadrado se las denomina contribuciones relativas del factor al elemento y
miden la proporción de la variabilidad de las variables explicadas por cada
componente. Esta cantidad puede utilizarse para interpretar las componentes.
30
10.- EJEMPLO
10.1.- DATOS
La tabla de datos siguiente muestra los porcentajes de personas empleadas en 9
sectores distintos para 26 países europeos (antes de los últimos cambios
políticos). En este caso, el Análisis Multivariante puede ser útil para aislar
grupos de países con distribuciones de empleo similares y en general para
intentar comprender mejor las relaciones existentes entre los países y las
variables.
SECTORES:
AGR: Agricultura,
CON: Construcción,
MIN: Minería,
MAN: Manufacturas,
SER: Industrias de servicios,
ENER: Energía,
FIN: finanzas,
SSP:
Servicios sociales y personales, TC: Transportes y comunicaciones.
PAISES
BÉLGICA
DINAMARCA
FRANCIA
RFA
IRLANDA
ITALIA
LUXEMBURGO
HOLANDA
U.K.
AUSTRIA
FINLANDIA
GRECIA
NORUEGA
PORTUGAL
ESPAÑA
SUECIA
SUIZA
TURQUÍA
BULGARIA
CHECOSLOVAQUIA
RDA
HUNGRÍA
POLONIA
RUMANIA
URSS
YUGOSLAVIA
AGR
3.3
9.2
10.8
6.7
23.2
15.9
7.7
6.3
2.7
12.7
13.0
41.4
9.0
27.8
22.9
6.1
7.7
66.8
23.6
16.5
4.2
21.7
31.1
34.7
23.7
48.7
MIN
0.9
0.1
0.8
1.3
1.0
0.6
3.1
0.1
1.4
1.1
0.4
0.6
0.5
0.3
0.8
0.4
0.2
0.7
1.9
2.9
2.9
3.1
2.5
2.1
1.4
1.5
MAN
27.6
21.8
27.5
35.8
20.7
27.6
30.8
22.5
30.2
30.2
25.9
17.6
22.4
24.5
28.5
25.9
37.8
7.9
32.3
35.5
41.2
29.6
25.7
30.1
25.8
16.8
ENER
0.9
0.6
0.9
0.9
1.3
0.5
0.8
1.0
1.4
1.4
1.3
0.6
0.8
0.6
0.7
0.8
0.8
0.1
0.6
1.2
1.3
1.9
0.9
0.6
0.6
1.1
CON
8.2
8.3
8.9
7.3
7.5
10.0
9.2
9.9
6.9
9.0
7.4
8.1
8.6
8.4
11.5
7.2
9.5
2.8
7.9
8.7
7.6
8.2
8.4
8.7
9.2
4.9
SER
19.1
14.6
16.8
14.4
16.8
18.1
18.5
18.0
16.9
16.8
14.7
11.5
16.9
13.3
9.7
14.4
17.5
5.2
8.0
9.2
11.2
9.4
7.5
5.9
6.1
6.4
FIN
6.2
6.5
6.0
5.0
2.8
1.6
4.6
6.8
5.7
4.9
5.5
2.4
4.7
2.7
8.5
6.0
5.3
1.1
0.7
0.9
1.2
0.9
0.9
1.3
0.5
11.3
SSP
26.6
32.2
22.6
22.3
20.8
20.1
19.2
28.5
28.3
16.8
24.3
11.0
27.6
16.7
11.8
32.4
15.4
11.9
18.2
17.9
22.1
17.2
16.1
11.7
23.6
5.3
TC
7.2
7.1
5.7
6.1
6.1
5.7
6.2
6.8
6.4
7.0
7.6
6.7
9.4
5.7
5.5
6.8
5.7
3.2
6.7
7.0
8.4
8.0
6.9
5.0
9.3
4.0
31
10.2.- REPRESENTACIÓN DE LOS INDIVIDUOS SOBRE EL
PRIMER PLANO PRINCIPAL
HUN
2
RDA
CHE
POL
RUM
1
BUL
URS
LUX
AUS
0
GRE
YUG
IRL
ITA
POR
TUR
ESP
FRA
-1
RFA
UK
SUI
FIN
NOR
BEL
SUE
HOL
DIN
-2
-4
-3
-2
1.0
-1
0
MINERIA
MANUF
0.5
ENERG
TRANSP
AGRIC
0.0
CONSTR
SERVSOC
-0.5
SERVICIO
FINANZAS
-1.0
-1.0
-0.5
0.0
0.5
1.0
Representación gráfica de los factores de carga.
1
32
10.3.- SALIDA TIPICA DE ORDENADOR
LATENT ROOTS (EIGENVALUES)
1
3.487
2
2.130
3
1.099
4
0.994
6
0.383
7
0.226
8
0.137
9
0.000
1
-0.978
-0.002
0.649
0.478
0.607
0.708
0.139
0.723
0.685
2
0.078
0.902
0.518
0.381
0.075
-0.511
-0.662
-0.323
0.296
5
0.543
COMPONENT LOADINGS
AGRIC
MINERIA
MANUF
ENERG
CONSTR
SERVICIO
FINANZAS
SERVSOC
TRANSP
VARIANCE EXPLAINED BY COMPONENTS
1
3.487
2
2.130
PERCENT OF TOTAL VARIANCE EXPLAINED
1
2
38.746
23.669
FACTOR SCREE PLOT
EIGENVALUES
-+-----------+-----------+-----------+-----------+-----------+4 +
+
|
|
|
A
|
|
|
3 +
+
|
|
|
|
|
A
|
2 +
+
|
|
|
|
|
A
|
1 +
A
+
|
A
|
|
A
|
|
A
A
A
|
0 +
+
-+-----------+-----------+-----------+-----------+-----------+0
2
4
6
8
10