contenido módulo de reología unidad 1. conceptos

CONTENIDO MÓDULO DE REOLOGÍA
UNIDAD 1. CONCEPTOS GENERALES EN REOLOGÍA
CAPÍTULO 1. CONCEPTOS BÁSICOS
LECCIÓN 1. COMPORTAMIENTO DE CUERPO SÓLIDO
LECCIÓN 2. CLASIFICACIÓN DEL COMPORTAMIENTO DE LOS FLUIDOS
EN
FLUJO ESTACIONARIO. FLUIDOS
NEWTONIANOS
Y NO
NEWTONIANOS
LECCIÓN
3.
MODELOS
MATEMÁTICOS
UTILIZADOS
EN
LA
CARACTERIZACIÓN
LECCIÓN 4. MÉTODOS EMPÍRICOS UTILIZADOS EN LA INDUSTRIA DE
ALIMENTOS
LECCIÓN 5. EJEMPLOS DE APLICACIÓN
CAPÍTULO 2. MÉTODOS PARA LA REALIZACIÓN DE DETERMINACIONES
REOLÓGICAS 1
LECCIÓN 6. VISCOSIMETRÍA DE TUBOS
LECCIÓN 7. ECUACIÓN DE REBINOVICH MOONEY
LECCIÓN 8. PERFILES DE VELOCIDAD EN FLUJO LAMINAR Y
TURBULENTO
LECCIÓN 9. ELEMENTOS A CONSIDERAR PARA LA REALIZACIÓN DE LAS
DETERMINACIONES
LECCIÓN 10. VISCOSÍMETROS CAPILARES
CAPÍTULO 3. MÉTODOS PARA LA REALIZACIÓN DE DETERMINACIONES
REOLÓGICAS 2
LECCIÓN 11. VISCOSÍMETROS DE CONDUCTO
LECCIÓN 12. EJEMPLOS DE APLICACIÓN
LECCIÓN 13. VISCOSÍMETRO ROTACIONAL
LECCIÓN 14. VISCOSÍMETROS DE CILINDROS CONCÉNTRICOS
LECCIÓN 15. DERIVACIÓN DE LAS ECUACIONES BÁSICAS. CÁLCULO DE
GRADIENTES DE VELOCIDAD
UNIDAD 2.MÉTODOS Y APLICACIONES EN REOLOGÍA
CAPÍTULO 4. MÉTODOS PARA LA REALIZACIÓN DE DETERMINACIONES
REOLÓGICAS 3
LECCIÓN 16. VISCOSÍMETRO DE CONO Y PLATO
LECCIÓN 17. VISCOSÍMETROS DE MEZCLA
LECCIÓN 18. EJEMPLOS DE APLICACIÓN
LECCIÓN 19. VISCOSÍMETROS DE CONO Y PLATO
LECCIÓN 20 VISCOSÍMETROS DE MEZCLA
CAPÍTULO 5. VISCOELASTICIDAD
LECCIÓN 21. CONCEPTOS BÁSICOS
LECCIÓN 22. MODELOS VISCOELÁSTICOS
LECCIÓN 23. DETERMINACIONES DE VISCOELASTICIDAD
LECCIÓN 24. EJEMPLOS DE APLICACIÓN
LECCIÓN 25. ACLARACIÓN DE LA IMPORTANCIA DE PARÁMETROS
REOLÓGICOS EN FENÓMENOS DE TRANSPORTE E INTRODUCCIÓN
CAPÍTULO 6. PARÁMETROS REOLOÓGICOS EN FENÓMENOS DE
TRANSPORTE
LECCIÓN 26. FLUJO ISOTÉRMICO EN TUBERÍAS CIRCULARES
LECCIÓN 27. CÁLCULO DE PÉRDIDAS POR FRICCIÓN
LECCIÓN 28. CAÍDA DE PRESIÓN EN VÁLVULAS
LECCIÓN 29. EFECTO EN LA TRANSFERENCIA DE CALOR
LECCIÓN 30. EFECTO EN LA TRANSFERENCIA DE MASA
UNIDAD 1. CONCEPTOS GENERALES EN REOLOGÍA
CAPÍTULO 1. CONCEPTOS BÁSICOS
Cuando un alimento se intenta deformar, exhibe, además de sus propiedades
como el olor, el color y el sabor, un comportamiento mecánico característico, de
modo que comprobaremos cómo unos fluyen con facilidad, otros son gomosos o
se quiebran. Para identificar este comportamiento se usan, o métodos sensoriales,
estudiados en una ciencia particular llamada Haptaestesis, para la cual el personal
deberá estar entrenado de modo de, a través de los sentidos, evaluar los
productos, o se utilizan métodos físicos, con un equipamiento de medición
adecuado y que le resta subjetividad a la caracterización. De este estudio físico se
ocupa la Reología. La combinación de ambos métodos es estudiada por la
Sicorreología, que se dedica a las relaciones existentes entre las evaluaciones
sensoriales y las mediciones reológicas.
Definiciones de Reología pueden ser: Ciencia que se dedica al estudio del flujo y la
deformación de materiales. Ciencia que se dedica a estudiar las deformaciones de
un cuerpo sometido a esfuerzos producidos por fuerzas externas. Ciencia que se
dedica al estudio de las propiedades que rigen las relaciones entre tensiones y
deformaciones.
Los estudios reológicos se justifican por cuatro causas fundamentales:
• Contribuir al conocimiento de la estructura.
• Realizar el control del proceso
• Utilizar parámetros para el diseño de máquinas y sistemas de movimiento
• Lograr niveles de aceptación adecuados de un producto.
Para realizar la clasificación reológica de un producto aparecen dos dificultades
principales: la infinita diversidad de productos y la posibilidad de que un mismo
producto exhiba propiedades diferentes en dependencia de las condiciones en que
se efectúa la observación.
Para orientar al investigador en este campo, y como ha sido realizado en otros
campos de la ciencia (ejemplo el gas ideal como modelo del comportamiento de
los gases, el ciclo termodinámico de Carnot como modelo ideal de un ciclo de
producción de energía, etc), se han asumido comportamientos patrones: el sólido
ideal o sólido de Hooke y el líquido ideal o líquido newtoniano. Ambos son
patrones ideales, isotrópicos (con iguales propiedades en todas direcciones) y que
siguen exactamente las leyes que los definen y que veremos más adelante.
Realice ahora el estudio de las páginas 1 a 7 del texto básico (Rheological
Methods in Food Process Engineering, de J. Steffe).
Al concluir este estudio Ud habrá conocido:
• Los tipos principales de equipos para la determinación de viscosidad, siendo
los más comunes los viscosímetros del tipo rotacional y los del tipo de
conducto. Ambos serán objeto de estudio en el tema 2.
Que existen ventajas y desventajas asociadas a cada instrumento. Se le
sugiere que prepare un cuadro en el que Ud vaya resumiendo a medida
que avance en el estudio, el tipo de viscosímetro, su aplicabilidad y sus
desventajas.
• Los conceptos de esfuerzo y deformación (en el texto, stress el primero y
strain el segundo) siendo el esfuerzo la fuerza por unidad de área y la
deformación la medida del cambio de forma y/o volumen en un material
resultante de la modificación de las distancias relativas entre los puntos del
mismo, respecto a una dirección de referencia (longitud, área, volumen).
• La posibilidad de caracterizar las deformaciones según: deformación de
Cauchy, deformación de Hencky, cizallamiento.
• La representación del esfuerzo como una magnitud tensorial de 9
componentes en coordenadas cartesianas, siendo la matriz del esfuerzo
simétrica, de donde las 9 componentes se reducen a 6. Las componentes s
ii son las normales y las componentes s ij las de cizallamiento.
LECCIÓN 1. COMPORTAMIENTO DE CUERPO SÓLIDO
Comportamiento de cuerpo sólido
El sólido de Hooke es un sólido ideal en el que la deformación es proporcional a la
fuerza que la produce. Al cesar la fuerza aplicada, se recupera completa e
inmediatamente la deformación. Este es el comportamiento característico de la
elasticidad ideal. En un sólido de Hooke, el diagrama deformación- tiempo será
una línea recta paralela al eje del tiempo. Mecánicamente se representa el
comportamiento como un muelle estirado por una fuerza.
Estudie las páginas 8 a la 13 del texto básico. Al concluir, Ud deberá saber que:
• Módulo es una relación entre un componente del tensor esfuerzo y un
componente del tensor deformación.
• Módulo de cizallamiento o de rigidez (G) es la relación entre el esfuerzo de
cizallamiento y la correspondente deformación elástica.
• Los cuerpos de Hooke no fluyen y son linealmente elásticos s12 = G g
• Módulo de Young (E) es el cociente entre el esfuerzo de tracción y la
correspondiente deformación de un material elástico, medido en extensión
uniaxial.
• Relación o coeficiente de Poisson (n) es la razón entre la deformación
transversal y la deformación axial en tracción o en compresión. Esto sucede
comúnmente cuando al comprimir un cilindro, por ejemplo el diámetro
aumenta. Su valor se encuentra entre 0, para materiales con alto contenido
de aire como el corcho, y 0.5 para aquellos en que la deformación ocurre
sin cambio de volumen, como por ejemplo la goma.
• Módulo de compresión volumétrica (K) es la razón entre la presión aplicada
sobre el material y su deformación elástica. Recuerde por ejemplo cómo las
burbujas de aire exhaladas por un buzo aumentan su tamaño a medida que
ascienden a la superficie. Este módulo mide la compresibilidad y de hecho
es la constante elástica que también poseen gases y líquidos.
En los cuerpos isótropos, conocidas dos de las constantes elásticas es
posible calcular las restantes usando las ecuaciones que aparecen en el
texto básico en la página 11.
• Hay materiales en que la relacion de s 12vs g no es lineal, aunque recuperen
la forma original al remover la deformación.
Las determinaciones de las constantes elásticas pueden realizarse de la siguiente
manera:
• Por determinaciones estáticas
• Por determinaciones dinámicas
Determinaciones estáticas del Módulo de Young: Se han realizado en barras de
spaghettis, manzanas y papas doblando o estirando la muestra. En los ensayos de
alargamiento se pinza una muesra por la parte superior, se cuelga un peso por la
inferior y se mide el alargamiento de un trozo de la muesra delimitado entre dos
señales.
Determinaciones estáticas del Módulo de rigidez: Se realiza colocando una varilla
verticalmente con uno de sus extremos fijos y el otro libre, el que se somete a
torsión.
Determinaciones estáticas del Módulo de compresibilidad: Se realiza sumergiendo
la muestra en agua, en el interior de una cámara metálica herméticamente cerrada,
ejerciendo una fuerza, por medio de aire comprimido, midiendo el cambio de
volumen con ayuda de un tubo graduado transparente.Este es el principio típico
usado con frutas y tubérculos.
Determinaciones dinámicas: El carácter de la deformación es el mismo pero los
ciclos de aplicación y supresión de la fuerza son extremadamente rápidos.
Finalmente es conveniente precisar que en un cuerpo sólido real la distribución de
fuerzas no es uniforme y los enlaces interatómicos se distorcionan bajo la acción
de la fuerza, produciéndose una deformación pregresiva y no totalmente
recuperable; la incidencia de su componente viscosa no es despreciable y deberá
tenerse en cuenta la aplicación de la teoría de la viscoelasticidad, la que será
estudiada en el capítulo 3.
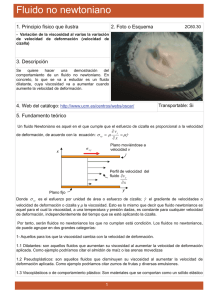
LECCIÓN 2. CLASIFICACIÓN DEL COMPORTAMIENTO DE LOS FLUIDOS
EN
FLUJO ESTACIONARIO. FLUIDOS NEWTONIANOS Y NO NEWTONIANOS
Viscosidad es la medida de la resistencia interna que ofrece un fluido a su
deformación. En el caso de un líquido verdadero, la fuerza aplicada de modo
continuo durante un período de tiempo produce un flujo continuo.
Cuantitativamente es el cociente entre el esfuerzo de cizallamiento y la velocidad
de cizallamiento (o gradiente de velocidad) en flujo estacionario.
El flujo en régimen laminar implica el deslizamiento como entidades
independientes de láminas de fluido infinitamente delgadas, realizándose este
desplazamiento de las capas paralelamente. El flujo newtoniano sólo se da en
régimen laminar.
El líquido newtoniano es aquél para el que la viscosidad es una constante. La
representación de la tensión de cizalladura contra la velocidad de deformación es
una línea recta y la constante de proporcionalidad es el coeficiente de viscosidad s
= m g. El modelo mecánico es un recipiente lleno de líquido en el que se mueve un
émbolo en sentido ascendente y descendente. El líquido newtoniano es ideal, no
tiene propiedades elásticas, es incompresible e isotrópico.
La viscosidad disminuye con el aumento de la temperatura.
La clasificación de los fluidos no newtonianos atendiendo a la caracterización
reológica es:
• Fluidos dependientes del tiempo
Tixotrópicos
Reopécticos
• Fuidos independientes del tiempo
Sin esfuerzo de fluencia
Seudoplásticos (shear thinning)
Dilatantes (shear thickening)
Con esfuerzo de fluencia o esfuerzo umbral
Plásticos
• Fluidos viscoelásticos
De igual forma deberá conocer que:
• El flujo viscosimétrico (flujo en similares condiciones a las del cizallamiento
simple en régimen laminar y estado estacionario) se describe
completamente por tres constantes del material como máximo: la función de
viscosidad y dos funciones de esfuerzos normales.
h = f (g) = s12 / g donde en este caso g = dg / dt o sea es una velocidad de
deformación. En el texto la velocidad de deformación se simboliza con un
punto sobre la variable deformación. Aquí la deformación ha sido resaltada
en negrita y la velocidad de deformación no.
2
y1 = ( s 11 - s 22) / g = N1 / g
elástica de la deformación.
2
y2= ( s 22 - s 33) / g = N2 / g
2
Esta es una medida de la recuperación
2
Considerar que N2 = 0 es en general válido.
• Este flujo viscosimétrico incluye el flujo axial en un conducto, el flujo rotacional
entre cilindros concéntricos, el flujo rotacional entre un cono y un plato y el
flujo torsional entre platos paralelos.
• Cuando un flujo es newtoniano, h es una constante, la viscosidad newtoniana
que se representa como m y N1 y N2 son 0.
• Cuando los fluidos son no newtonianos se define la viscosidad aparente para
relacionar el esfuerzo de cizallamiento puntual y la velocidad de
cizallamiento correspondiente. Los valores dependen de la velocidad de
cizallamiento.
hap = f (g) = s / g
• Muchas de las ecuaciones que se utilizan como modelos matemáticos para
describir el comportamiento de un fluido no newtoniano, usan como variable
la viscosidad aparente. Por ejemplo las de Carreau, Cross, Van Wager,
Powell- Eyring, Reiner-Philippoff. En otros casos se presentan relaciones de
s vs g como las ecuaciones de la ley de potencia, de Casson, de Casson
modificada, de Herschel-Bulkley, etc. (Ver la página 24 del texto básico)
• Para el caso de la viscosidad de soluciones es conveniente relacionar la
viscosidad de éstas con la del solvente utilizando las definiciones de:
viscosidad relativa = h rel = h solución / h solvente
viscosidad específica = h sp = h rel - 1
viscosidad reducida = h red = h sp / C
viscosidad inherente = h inh = ln h rel / C
viscosidad intrínseca = h int = (h ap / C) C= 0
En estas relaciones C es la concentración másica en g/dl o g/ 100 ml.
• Para un fluido no newtoniano un único valor de viscosidad tiene que llevar
explícitamente el valor del gradiente de cizallamiento al que fue
determinado, de lo contrario la información carece de significado. Para
homologar las percepciones sensoriales de espesor de un alimento se usa
-1
un valor de viscosidad aparente evaluado a 60 s .
• Cuando tenemos fluidos inelásticos dependientes del tiempo la respuesta de
la sustancia de trabajo es inmediata y la dependencia con el tiempo es
debida a cambios en la estructura del material. Cuando hablamos de
viscoelasticidad la respuesta del esfuerzo a la deformación aplicada no es
instantánea y no está asociada a cambios estructurales.
• Se define tixotropía como la disminución de viscosidad aparente por la acción
de un esfiuerzo a una velocidad de cizallamiento constante, seguido de una
recuperación gradual cuando se retira el estímuo. El efecto es función del
tiempo. Cuando la recuperación no se produce, o sea el fenómeno es
irreversible, se llama reodestrucción o reomalaxia, que se presenta en
algunos productos alimentarios. Al efecto del aumento de viscosidad
aparente por la acción del esfuerzo a una velocidad de cizallamiento
constante, seguida de una recuperación gradual cuando se retira el
estímulo se le llama reopexia. (También se le conoce como tixotropía
negativa)
• Los modelos matemáticos para describir el efecto de la tixotropía llevan
incluidos el parámetro tiempo y se define un parámetro estructural función
del tiempo para seguir estas transformaciones. (Ver las páginas 30 - 32 del
texto básico)
• El efecto de la variación de viscosidad con la temperatura es seguido con
modelos del tipo Arrehnius. (Ver las páginas 33-34 del texto básico)
Los fluidos no newtonianos han sido objeto de estudios para interpretar el
comportamiento que siguen en relación con su estructura. Para los fluidos
seudoplásticos, que en general están formados por partículas de forma irregular,
moléculas de largas cadenas ramificadas o entrecruzadas o que forman agregados
moleculares, se ha brindado la siguiente explicación a su comportamiento. Las
partícuylas componentes presentan en estado de reposo un movimiento
desordenado, siendo alta la resistencia a fluir; al aplicar una velocidad de
deformación creciente, éstas se orientan en la dirección del flujo, pudiendo llegar a
deslizarse mejor unas respecto a otras, lo que se traduce en una disminución de
viscosidad. Al cesar la acción, debido al movimiento browniano se recupera el
estado original. De igual forma sucede cuando se estiran las estructuras o se
destruyen los agregados.
Para los plásticos, el examen de la estructura permite apreciar tres características:
• Un sistema bifásico con una fase líquida continua y una fase "sólida" dispersa
la cual no tiene que estar conformada por un auténtico sólido, sino sólo
operar como tal (por ejemplo una gota de líquido o una burbuja de aire)
• El
"sólido" tiene que estar finamente disperso en la fase líquida,
manteniéndose este conjunto estable por efectos de cohesión interna.
• Ofrecer una relación correcta fase "sólida"/ fase líquida, ya que si la fase
"sólida" es excesiva el sistema se torna quebradizo y si hay mucho líquido
no exhibe deformación plástica. Esta relación varía de un producto a otro,
por ejemplo el puré de papas contiene 90% de agua y el chocolate fundido
35% de grasa líquida y ambos son plásticos.
Es común considerar a los líquidos plásticos como sólidos y como líquidos. En su
mayoría son dispersiones que en estado de reposo forman una red intermolecular
de fuerzas de cohesión (enlaces polares, fuerzas de Van der Waals), que evitan el
cambio de posición de los elementos de volumen e imprimen a la sustancia un
caráter de cuerpo sólido, con viscosidad infinita. Si las fuerzas externas son
menores que las que forman la red sólo se deforma elásticamente el cuerpo.
Cuando las fuerzas externas sobrepasan las fuerzas de unión de la red, la
estructura se desbarata y los elementos de volumen cambian de posición, es decir
fluyen.
De igual forma en el caso de los productos tixotrópicos se explica el
comportamiento asociado a cambios de estructura. Una dispersión en estado de
reposo forma una estructura tridimensional debida a las fuerzas de unión que a
menudo se denomina gel. Estas fuerzas se debilitan fácilmente cuando se somete
la dispersión a la cizalladura durante un tiempo. Cuando se desmorona la
estructura de gel, la viscosidad disminuye hasta que se alcanza un mínimo para un
gradiente de velocidad constante. Este valor mínimo describe el estado de sol. La
sustancia tixotrópica recupera el estado de gel tras un tiempo de reposo típico para
cada sustancia (tiempo de regeneración). En general, el 50% de la estructura se
gel se regenera en minutos.
Estudie el epígrafe 1.7 del texto básico hasta la página 43.
Se define la viscosidad elongacional o de Trouton como el cociente entre el
esfuerzo de tracción y la deformación (alargamiento). El flujo elongacional no
involucra cizallamiento por lo que también se le conoce como flujo libre de
cizallamiento. El efecto que provoca este flujo sobre el comportamiento del
material puede explicarse al conocerse la orientación de largas moléculas de alta
masa molar. (Ver página 39 del texto básico)
Cuando haya finalizado el estudio de las páginas orientadas, revise la Figura 1.25
de la página 50 del texto básico y compruebe que puede identificar cada uno de
los recuadros que aparecen en el esquema (con excepción de la clasificación de
viscoelasticidad).
LECCIÓN
3.
MODELOS
CARACTERIZACIÓN
MATEMÁTICOS
UTILIZADOS
EN
LA
Lea el material titulado Reología, capítulo 5 de la monografía Propiedades Físicas
de Alimentos páginas 89 a 93 y posteriormente estudie del libro de texto básico las
páginas 13 a 39.
LECCIÓN 4. MÉTODOS EMPÍRICOS UTILIZADOS EN LA INDUSTRIA DE
ALIMENTOS
Lea el epígrafe 1.13 del texto básico páginas 63 a 77. El objetivo de esta lectura es
que Ud conozca los múltiples instrumentos que se usan en la industria de
alimentos para seguir el comportamiento de un material. Estos no pueden usarse
para determinar propiedades reológicas fundamentales, sino que se utilizan para el
control de calidad, para identificar productos y cada día se trabaja por sustituir
estos equipos por otros que posibiliten verdaderas determinaciones reológicas que
son las que permiten la realización de objetivos de ingeniería.
Por consiguiente este epígrafe busca como objetivo sólo su familiarización con el
tema, así como la identificación de que con estos indicadores Ud no puede realizar
mediciones reológicas.
Aparecen incluidos algunos instrumentos que se aclara que sí hay actualmente
métodos que permiten encontrar correlaciones de torque y velocidad angular con
esfuerzo de cizallamiento y velocidad de cizallamiento, lo que posibilita la
realización de determinaciones reológicas.
LECCIÓN 5. EJEMPLOS DE APLICACIÓN
1. Sólidos
Spaghettis. Los spaghettis se preparan a partir de una masa elaborada con
semolina de trigo durum y agua, extruyéndola a través de un orificio para obtener
barras cilíndricas largas y uniformes que se deshidratan luego. Antes de las
determinaciones se mantienen a HR = 65% y T = 25ºC durante 48 horas.
El módulo de Young se determina poniendo en posición horizontal una pieza de
spaghetti entre dos soportes horizontales y aplicando la acción de una fuerza. Se
obtiene 0.27 .* 10
10
10
2
N / m El módulo de rigidez obtenido según el epígrafe 1.2
2
arroja 0.11 * 10 N/m . Se puede comprobar que no es isotrópico al calcular cómo
se hincha el spaghetti en agua. Se aprecia que a los 240 minutos se ha hinchado
al 35% en su diámetro, mientras que en la longitud, el mayor valor que se alcanza
es del 10% de hinchamiento.
Cáscara de huevo. La relación entre la carga que resiste la cáscara y la
deformación es prácticamente lineal (sólido de Hooke).
2. Líquidos newtonianos
Ejemplos típicos son las bebidas carbonatadas, las bebidas alcohólicas, la leche,
el agua, algunos aceites ligeros de cocina, as soluciones azucaradas.
Soluciones azucaradas
En el intervalo hasta 75% en peso, las soluciones azucaradas presentan un
comportamiento newtoniano. Valores de viscosidad de soluciones de sacarosa en
agua a 20ºC reportados por Bates, son:
% en peso
20
30
40
_ (Pa s)
0.0020
0.0032
0.0062
50
60
70
0.0155
0.0589
0.4850
Si se representan los valores de h vs concentración (% en peso) se comprueba
que el comportamiento es exponencial y que puede ajustarse por el modelo m =
1.5626 *10
-8
e
(0.2507 * % sólidos)
con un coeficiente de correlación de 0.9965
3. Líquidos no newtonianos
Estudie el problema 1.14.1 de la página 77 del texto básico, para el que se ajusta
la ley de potencia a un conjunto de resultados experimentales de s vs g medidos a
25ºC.
Se le sugiere que realice Ud los ajustes que se presentan y verifique los
resultados. Puede probar a ajustar otros modelos para su ejercitación.
Observe cómo:
• La relación s vs g no es una recta sino una curva típica de un fluido
seudoplástico. Fíjese cómo la curva pasa por el origen 0,0 de donde no hay
esfuerzo de fluencia.
• La curva h vs g no es constante sino que la viscosidad aparente disminuye a
medida que aumenta el gradiente de velocidad ( o de cizallamiento).
Estudie el problema 1.14.2 de la página 79 del texto básico en el que se trabaja un
almidón de maíz al 53% en peso a 25ºC ajustando el modelo de la ley de potencia.
• Este comportamiento es frecuente encontrarlo y el investigador debe estar
alerta. El comportamiento a bajos gradientes de cizallamiento es el de un
fluido seudoplástico, disminuyendo h al aumentar g dado el efecto
lubricante del agua para el flujo de partículas. Mientras, a altos gradientes
de cizallamiento este efecto es menor y la viscosidad aparente aumenta al
aumentar el gradiente de cizallamiento, como en un comportamiento de
dilatancia.
• Por consiguiente se deberán reportar dos modelos, uno para bajos gradientes
que tendrá un exponente menor que la unidad y otro para altos gradientes
que tendrá un valor de exponente mayor que la unidad y es el que se
presenta como respuesta del problema.
Estudie el ejemplo 1.14.3 que presenta datos reológicos para la leche con
chocolate a 40ºC.
Observe cómo:
• De la figura 1.45 se aprecia que la curva s vs g no pasa por el origen 0,0 de
donde hay esfuerzo de fluencia.
La influencia de la zona de gradientes con que se trabaja en el valor de los
parámetros reológicos del modelo.
• En la tabla 1.8 la ecuación del plástico de Bingham tiene un exponente n del
que no aparece su valor. Para el plástico de Bingham el exponente es 1.
• Actualmente hay programas de ajuste de datos muy potentes que se pueden
utilizar para la realización del problema (Ejemplo Curvexpert).
Estudie el problema 1.14.5 qe evalúa un jugo de naranja concentrado a diferentes
temperaturas y en el que se busca ajustar un modelo que incluya el efecto de la
temperatura.
Observe cómo:
n
• Al ajustar el modelo de la ley de potencia s = K g si se aplica logaritmo ln s =
ln K + n ln g , de donde al representar en papel logarítmico s vs g se
obtendrá la línea recta de intercepto K y de pendiente n.
• Los valores de n no cambian prácticamente con la temperatura de donde
puede calcularse un índice de flujo promedio.
• Los valores de K sí varían con la temperatura, aumentando al disminuir ésta.
• La relación de K = f (1/T) se obtiene de un modelo del tipo Arrehnius.
Revise del material titulado Reología Capítulo 5, de la monografía Propiedades
físicas de alimentos, lo correspondiente a las aplicaciones para la industria
alimentaria, páginas 100 a 105.
Preguntas y problemas a solucionar por el alumno.
1. Enuncie las definiciones de los siguientes términos y establezca las relaciones
entre ellos.
• Deformación de Cauchy o deformación ingenieril
• Deformación de Hencky o deformación natural o logarítmica
• Cizallamiento
• Módulo de cizallamiento
• Módulo de Young
• Relación de Poisson
• Módulo de compresión
2. Justifique la siguiente afirmación: A tensión constante, cuanto menor sea el
módulo de Young más fácil se producirá la deformación elástica del material.
3. ¿A qué atribuiría Ud que un tejido de papas tenga un coeficiente de Poisson
mayor que un tejido de manzana? Use los datos del apéndice del libro de texto
básico.
4. Seleccione entre plátanos y peras el material que Ud utilizaría para preparar un
producto del que se requiera que mantenga al máximo su forma. Utilice los datos
del apéndice del libro de texto básico.
5. Para un sirope de maíz a 38ºC se obtuvieron los siguientes resultados
experimentales.
.
-1
_ (s )
2.16
4.66
14.58
48.6
97.2
145.8
65% en peso
_ (mPa)
393.12
848.12
2650.6
8850.0
17690.4
26535.6
35% en peso
_ (mPa)
9.76
21.06
66.01
218.7
440.5
659.0
262.44
291.6
47700.2
53075.1
1190.2
1320.0
a)Caracterice el comportamiento reológico de este fluido
b)¿Cómo influye la concentración del sirope en la viscosidad?
6. Una miel de caña de azúcar de las siguientes características % sólidos totales=
81.2, % de sacarosa =54.2, T = 40ºC se estudió con un viscosímetro rotacional con
los siguientes resultados.
-1
_ (mPa)
4.333
5.881
6.933
9.595
15.599
21.356
41.164
95.480
163.240
266.110
497.730
(s )
1.2
1.8
2.16
3.6
6.48
9.72
19.44
48.60
87.48
145.8
291.6
a) Caracterice el comportamiento reológico de este fluido
b) Ajuste el modelo de la ley de potencia
c)¿Qué valor toma la viscosidad aparente para un gradiente de cizallamiento de 50
-1
-1
s y de 100 s ?
7. Para el sirope de maíz de 65% de sólidos, encuentre la dependencia de la
viscosidad con la temperatura
. ºC
15
27
38
49
60
71
82
_ (mPas)
1060.0
398.0
182.0
108.0
67.9
43.2
29.0
8. Se estudia un puré de melocotón a 26.6ºC encontrando los siguientes
resultados.
% sólidos
totales
23.4
.
-1
_ (s )
1.2
1.62
_ (Pa)
11.9
13.3
-1
_ (s )
6.48
9.72
_ (Pa)
21.5
24.8
.
.
.
.
44.3
.
.
.
.
.
55.2
.
.
.
.
.
59.3
.
.
.
.
.
1.944
2.16
3.24
4.66
1.2
1.62
1.944
2.16
3.24
4.66
1.2
1.62
1.944
2.16
3.24
4.66
1.2
1.62
1.944
2.16
3.24
4.66
14.1
14.7
16.9
18.8
59.9
67.0
71.6
82.5
86.5
99.0
161.7
179.1
190.6
197.5
226.7
256.5
318.0
350.1
371.0
383.8
437.0
490.9
19.44
29.16
48.8
87.48
6.48
9.72
19.44
29.16
48.8
87.48
6.48
9.72
19.44
29.16
48.8
87.48
6.48
9.72
19.44
29.16
48.8
87.48
31.7
36.0
43.7
53.2
111.8
129.9
167.9
195.0
236.0
292.9
282.5
329.5
416.8
478.6
570.0
695.2
537.3
621.0
775.4
883.0
1040.9
1254.7
a) Caracterice el comportamiento reológico del material.
b) Encuentre el modelo que se ajusta mejor a estos resultados.
-1
c) Encuentre para g = 50 s la dependencia de la viscosidad contra el % de sólidos
totales.
CAPÍTULO 2. MÉTODOS PARA LA REALIZACIÓN DE DETERMINACIONES
REOLÓGICAS 1
LECCIÓN 6. VISCOSIMETRÍA DE TUBOS
Estudie el epígrafe 2.1 páginas 94 - 97 del texto básico.
Al concluir Ud conocerá que:
• Existen 3 categorías de viscosímetros de tubos: viscosímetros en U,
viscosímetros capilares de alta presión y viscosímetros de conducto.
• En todos el flujo se logra por una diferencia de presión.
• La diferencia entre un capilar y un conducto es en el diámetro.
• Los datos medidos en un viscosímetro de tubos son la caída de presión y el
flujo volumétrico.
LECCIÓN 7. ECUACIÓN DE REBINOVICH MOONEY
Estudie el epígrafe 2.2, páginas 97 - 103, del libro de texto básico.
Al concluir el estudio Ud deberá saber:
• Las consideraciones realizadas para deducir la ecuación de R-M: flujo laminar
y estacionario, efectos terminales despreciables, fluido incompresible,
propiedades independientes de la presión y el tiempo, temperatura
constante, no existencia de deslizamiento en la pared del conducto, lo cual
significa que la velocidad del fluido es 0 en la interfase fluido - pared y las
componentes de velocidad radial y tangencial son 0, o sea sólo existe
componente de velocidad longitudinal.
• La ecuación de R - M relaciona la velocidad de deformación en la pared como
una función del esfuerzo en la pared, expresada en términos de flujo
volumétrico y radio (ecuación 2.20).
• Que se puede definir un gradiente de velocidad de cizallamiento aparente en
3
la pared G= 4 Q / p R , siendo
gw = (( 3n' + 1)/ 4 n') G donde n' = (d ln s w )/ (d ln G)
• Cuando se trabaja con fluidos newtonianos se obtiene la ecuación de Hagen -
Poiseuille
4
Q = p DP R / 8 L m
gN = 4 Q / p R
3
De aquí se aprecia la alta influencia del radio del conducto en el caudal de
flujo.
• Si el fluido cumple con la ley de potencia
Q = p ( DP/2LK)
1/n
( n/(3n+1)) R
(3n+1)/n
3
gw = ((3n+1)/4n) (4Q/p R
• Si el fluido es de Bingham se cumple la ecuación de Buckingham - Reinier
f(s) = 0 para 0< s < so en la región central
f(s) = (s - so) / mpl si so < s < sw
4
4
Q = {p R DP/8 mpl L }{ 1 - (4 so / 3 sw ) + (1/3) ( so / sw ) }
• Si el fluido es del tipo Herschel - Bulkley
3
1/n
Q =( pR /256) (4n/3n+1) (sw/K)
{1+(2n/(n+1))(so/sw) (1+nso/sw)}]
(1-so/sw)
1/n
[1-(so/sw)/(2n+1)
Estudie los ejemplos 2.12.1, 2.12.2 , 2.12.3 y 2.12.4 desarrollados en el epígrafe
2.12 páginas 141 a 150 del texto básico.
En el epígrafe 2.12.1 se presenta el resultado de la aplicación de la ecuación de
conservación de la cantidad de movimiento, encontrando que s = (- D P) r / 2 L.
En el apígrafe 2.12.2 se determinan las propiedades reológicas a partir de datos de
3
Q / p R y caída de presión. Observe cómo se corrigen los valores de caída de
presión por presencia de efectos de entrada a partir de medidas de DP vs L/D para
G constante, realizando la extrapolación a L/D = 0. La diferencia entre la caída de
presión medida y la caída de presión por efectos de entrada será la DP corregida
que permitirá encontrar sw. El valor de sw se calcula como DP / 4 L/D = DP R / 2L.
En este problema las pérdidas por efectos de entrada son muy elevadas, del orden
del 80% del valor de la caída de presión medida.
En el epígrafe 2.12.3 para una solución de carboximetilcelulosa sódica se obtuvo la
regresión de la recta ln sw vs ln G obteniendo n'= 0.414. Al comprobar que el
gráfico de s vs Gw es independiente del diámetro del tubo se concluye que no hay
efectos de entrada. Observe cómo se obtuvo el ajuste de un modelo del tipo de la
-0.414
ley de potencia con K= 8.14 a s
y n= 0.414 o sea el comportamiento de un
fluido seudoplástico. No realice ahora el análisis del cálculo del N Re con el que
termina el problema.
En el epígrafe 2.12.4 se desarrolla un ejemplo en el que el fluido satisface el
modelo de Casson. Se deduce la ecuación que relaciona el flujo volumétrico con el
esfuerzo de cizallamiento en la pared, de donde se puede encontrar la relación
entre el flujo volumétrico y la caída de presión.
LECCIÓN 8. PERFILES DE VELOCIDAD EN FLUJO LAMINAR
TURBULENTO
Para flujo laminar
Estudie los epígrafes 2.3 y 2.4 del texto básico, páginas 103 - 110.
Al concluir el estudio deberá conocer que:
Y
• Los viscosímetros de tubo operan en régimen laminar, de donde para la
caracterización reológica éstos son los perfiles de velocidad de interés.
• A partir de las relaciones para calcular el esfuerzo de cizallamiento, las
correlaciones que caracterizan el tipo de fluido y el gradiente de
cizallamiento se obtiene la ecuación que expresa el perfil de velocidad.
• A medida que el fluido tenga un comportamiento más seudoplástico, el perfil
de velocidad se hace más plano. Observe la figura 2.5 página 104 en la que
se muestra este comportamiento.
• El valor máximo de velocidad para un fluido sin esfuerzo de fluencia se
localiza en la línea central del tubo o sea para el radio=0 y se encuentra que
la relación u max/u media = (3n+1)/(n+1) donde u media es la velocidad
media volumétrica. De aquí se aprecia la influencia del índice de flujo en el
perfil de velocidad.
• Cuando existe esfuerzo de fluencia (plástico de Bingham) el parámetro que
identifica la familia de curvas es c= so /sw = Ro/R. Se aprecia cómo el
aumento de so aplana el perfil de velocidad y reduce la relación u/u media.
• Como criterio de aceptación del flujo laminar se considera NRe < 2100 donde
NRe = r D u media/m para fluidos newtonianos.
• Para sistemas que cumplen otro comportamiento (por ejemplo de la ley de
potencia) se obtiene una familia de curvas en la que se aprecia cómo a
medida que el índice de flujo aumenta desde 0 a 1, el NRe crítico es menor.
(Ver figura 2.7 del texto básico, página 108).
Para flujo turbulento
Estudie el epígrafe 2.11 del texto básico páginas 138 - 141.
Al concluir el estudio deberá conocer que:
• La predicción de perfiles de velocidad en flujo turbulento, de forma precisa, es
difícil.
• Para fluidos newtonianos este estudio se ha realizado y se definen tres zonas
en el conducto: la subcapa laminar, la zona de transición en la que se
generan las fluctuaciones turbulentas y la zona turbulenta desarrollada,
reportándose las ecuaciones que permiten calcular el perfil de velocidad en
cada una.
• En la tabla 2.7 del texto básico, página 139, se presentan valores de u media
/u max para fluidos newtonianos en función del NRe, observando cómo a
medida que el NRe aumenta, la velocidad media se aproxima a la máxima.
• En la misma tabla se puede apreciar cómo para fluidos que cumplan la ley de
potencia en flujo turbulento, para iguales valores de índice de flujo, a
medida que aumenta el NRe la velocidad media se aproxima a la máxima y
que mientras mayor sea el índice de flujo, aunque el comportamiento se
mantiene, el valor de la velocidad media es inferior a la correspondiente
para igual NRe a menor índice de flujo.
Retome el análisis de ejemplo 2.12.3 y observe cómo el valor del NRe se mantiene
inferior al NRe crítico calculado para un fluido que cumpla la ley de potencia y en
función del valor del índice de flujo, de donde se verifica la condición de régimen
laminar.
LECCIÓN 9. ELEMENTOS A CONSIDERAR PARA LA REALIZACIÓN DE LAS
DETERMINACIONES
El flujo de líquidos provocado por esfuerzos de cizalla puede presentarse en cuatro
formas básicas:
• Flujo entre placas planas paralelas en el que se origina una corriente laminar
en capas en el líquido entre las placas y las capas se desplazan una
respecto a otra.
• Flujo a través de capilares, toberas de anchas ranuras, tubos, ocasionado por
la diferencia de presión entre la entrada y la salida de un tubo lleno de
líquido en forma telescópica.
• Flujo en la ranura anular entre dos cilindros coaxiales, uno considerado
estacionario y el otro que gira. El flujo de líquido puede interpretarse como
el desplazamiento de láminas concéntricas.
• Flujo entre placas circulares que rotan.
Algunos de estos tipos de deformaciones son los que se utilizan cuando se desea
determinar experimentalmente la viscosidad en líquidos. El segundo de ellos, en
particular, es el que se utiliza para la determinación con viscosímetros de tubos.
Es fundamental precisar que si la viscosidad es función de la temperatura, la
presión, el tiempo, la naturaleza de la sustancia y el gradiente de cizallamiento,
cuando se desea determinar la viscosidad en función de un parámetro, los
restantes han de permancer constantes durante la realización del experimento.
Para obtener valores absolutos de viscosidad se requiere que las mediciones se
basen en determinaciones de unidades básicas de fuerza, longitud y tiempo, así
como de que el perfil de flujo en el sistema de medición pueda ser calculado
matemáticamente.
Para facilitar la solución de las ecuaciones básicas de fenómenos de transporte, se
requiere fijar determinadas condiciones de contorno como:
• Flujo laminar entre las capas, ya que la corriente turbulenta consume más
energía que la laminar y se obtendrían errores hasta del 50% al
superponerse remolinos y turbulencias en una corriente inicialmente
laminar.
• Corriente estacionaria, o sea el esfuerzo aplicado, proporcional al gradiente
de cizallamiento sólo es suficiente para mantener un flujo a velocidad
constante.
• Adherencia a las paredes por la capa externa del líquido, ya que si no se
adhiere ésta a la pared se produce desplazamiento de la placa en
movimiento sobre una capa de líquido en reposo, lo cual no es el concepto.
• Homogeneidad de la muestra, o sea cada elemento de volumen de muestra
tiene que tener la misma proporción de componentes.
• Ausencia de variaciones físicas o químicas del material durante el ensayo.
• Las muestras deben presentar sólo propiedades viscosas.
Existen numerosos errores de medición que se presentan en las determinaciones.
Un resumen de éstos puede encontrarlo en la tabla 2.1, página 111 del texto
básico.
Observe cómo muchos de estos errores están asociados a violaciones de las
condiciones de contorno necesarias, expuestas anteriormente.
Estudie los epígrafes 2.5 y 2.6, páginas 110-121 del texto básico y conozca las
causas y consecuencias de cada uno de estos problemas experimentales. Así
conocerá que:
• Se presentan pérdidas de presión debidas a la aceleración del fluido al
alcanzar la zona capilar.Estas pérdidas son función de la variación de
energía cinética y de un factor de corrección para el flujo laminar en
conductos que depende del tipo de comportamiento del fluido y que en la
tabla 2.4 se presenta para fluidos newtonianos que cumplan la ley de
potencia, que sean plásticos de Bingham y que cumplan el modelo de
Herschel-Bulkley.
• Se presentan efectos terminales, en particular pérdida de energía a la entrada
del conducto, al producirse una convergencia en este extremo del capilar.
El efecto al diverger al final del conducto puede ser despreciado. Este
efecto va unido a la pérdida de energía cinética.
• Encontrar estas pérdidas se realiza evaluando la caída de presión contra el
flujo para tubos de diferentes relaciones longitud/diámetro. A cada flujo, el
valor de DP para L/D=0 arroja el efecto de entrada.
• Se presentan errores asociados a la longitud de entrada, viendo que con
tubos largos, esta corrección puede despreciarse. Existe un valor de
longitud de entrada (XE) para el que se puede considerar flujo totalmente
desarrollado y que es función del Número de Reynolds (ecuación 2.64,
página 114 del texto básico) para fluidos newtonianos. Para fluidos
seudoplásticos depende además del índice de flujo, aumentando XE a
medida que aumenta el índice de flujo (ecuación 2.67, página 114 del texto
básico). Para fluidos plásticos, depende de la relación s0/sw, disminuyendo
XE a medida que s0 aumenta (ecuación 2.68, página 115 del texto básico).
Si XE =90D el efecto de longitud de entrada puede despreciarse en los
estudios de alimentos.
• Se presentan efectos de pared o correcciones por deslizamiento por formarse
una capa de fluido en la pared de tubo, con menor viscosidad que la del
seno del fluido. Esto ocasiona que el flujo volumétrico real sea algo mayor
que el flujo volumétrico si no existiera deslizamiento. Usando tubos de tres
3
diferentes radios se determina Qm/(pR sw) vs sw para cada R, donde Qm
3
2
es el flujo volumétrico medido. Del gráfico Qm/(pR sw) vs 1/R a sw
constante, se puede determinar el coeficiente de deslizamiento corregido
para cada sw ( Qm). Conocido éste se calcula el flujo volumétrico sin
deslizamiento de Qsd = Qm - Qm pRsw
• Se puede presentar calentamiento viscoso dada la disipación de calor al ser
cizallado el fluido. Esto se favorece para muy altas viscosidades o muy
altos gradientes de cizallamiento siendo DT= DP/rCp.
• En la figura 2.13, página 121, se presenta la secuencia de pasos para el
análisis de un conjunto de datos obtenidos con viscosímetros de tubo para
fluidos independientes del tiempo.
• El s0 de un fluido plástico puede determinarse con un viscosimetro de tubo
horizontal, determinado la DP mínima para provocar el flujo s0= DPmin
R/2L.
Revise nuevamente el ejemplo 2.12.2, una vez conocidas las fundamentaciones
para la realización de correcciones a las deteminaciones experimentales.
LECCIÓN 10. VISCOSÍMETROS CAPILARES
Estudie el epígrafe 2.9, página 125 del texto básico y conocerá:
• Las características fundamentales de los viscosímetros capilares de vidrio
(Ostwald, Cannon - Fenske).
• Que la fuerza directora de ellos es la carga hidrostática, la que varía durante
la descarga y esta DP provoca una variación en la velocidad de
cizallamiento durante la prueba, de donde no se aconseja el uso para
fluidos no newtonianos.
• Si se dispone de una precisa descripción de la geometría del capilar, se
4
puede calcular la constante del viscosímetro de k=g h pR /8LV. Lo común y
aconsejable es no hacerlo así, sino seguir el procedimiento explicado en la
página 126 del texto básico determinando las propiedades de un fluido
desconocido a partir de las propiedades de un fluido de referencia. Así: m1 /
r1 t1 = m2 / r2 t2 = k donde t es el tiempo de descarga de un volumen de
fluido desde el capilar.
CAPÍTULO 3. MÉTODOS PARA LA REALIZACIÓN DE DETERMINACIONES
REOLÓGICAS 2
LECCIÓN 11. VISCOSÍMETROS DE CONDUCTO
Observe la figura 2.3 de la página 96 del libro de texto básico y conozca que:
• El diámetro del conducto es entre 7 y 32 mm en general.
• Precise como para la determinación de DP se usan transductores.
• El flujo volumétrico puede determinarse a partir del flujo másico usando un
medidor de flujo o por pesada.
Lea las páginas 94 y 95 del capítulo 5 de la Monografía Propiedades físicas de
alimentos que resume el contenido.
LECCIÓN 12. EJEMPLOS DE APLICACIÓN
Estudie el ejemplo 2.12.4 que encuentra la relación entre la caída de presión y el
flujo volumétrico para un fluido que cumpla con el modelo de Casson. Observe el
procedimiento aplicado que le permitirá encontrar la relación para otro fluido, sólo
variando el modelo reológico seleccionado.
Estudie el ejemplo que se desarrolla a continuación. (Reportado en H. Muller,
Introducciòn a la reologìa de alimentos, Ed Acribia, España, 1992).
Soltoft estudió el comportamiento reológico de grasas utilizando un viscosímetro
capilar y aire comprimido para empujar el producto. Las grasas estudiadas fueron
aceite de maní con diversas proporciones de aceites hidrogenados y no
hidrogenados. A 16°C estos productos eran sólidos. Para poder comparar los
resultados, ya que tuvo que utilizar diferentes tubos, representó el esfuerzo de
cizalla en la pared del tubo DP R/2L en función del gradiente de velocidad de
3
cizallamiento aparente 4Q/pR . Para mezclas de más de 20% de aceite
hidrogenado se obtienen curvas que presentan esfuerzo de fluencia y un
comportamiento similar al seudoplástico. Por debajo de este valor presenta un
comportamiento casi newtoniano.
Estudie el siguiente ejemplo preparado a partir de los datos de J.N.Ness (XVIII
Congress of ISSCT, Cuba, p 699- 721,1983).
Para estudiar el comportamiento reológico de suspensiones de cristales de
sacarosa en miel (masas cocidas), se utilizaron viscosímetros de conducto,
variando las longitudes y diámetros de los tubos. Los datos primarios a obtener
son de caída de presión y de flujo volumétrico (que puede ser transformado en
2
velocidad promedio del flujo ya que V= Q/p R ), siendo Q el flujo volumétrico, R el
radio del tubo y V la velocidad promedio del flujo. Los valores de esfuerzo cortante
en la pared para un flujo totalmente desarrollado se calculan como sw=DP D/4L y
los gradientes de velocidad aparente en la pared como ga = 8V/D siendo D el
diámetro del tubo y L la longitud del tubo. La caída de presión medida incluirá la
carga del fluido más los efectos de entrada y salida. El valor de V será mayor del
teórico si existe efecto de deslizamiento en la pared. En este ejemplo se extraen
conclusiones acerca de estos efectos.
Se procedió a graficar los valors de sw vs ga y a ajustar el modelo de la ley de
potencia. Los resultados obtenidos fueron:
Muestra 1
Tubo
D mm
L mm
n
n
K (Pas )
Intervalo
de
gradiente
de
velocidad
-1
1L
1M
1S
2L
3L
3M
3S
10.15
10.14
10.18
12.55
17.04
17.05
17.07
405
300
204
400
401
300
204
0.89
0.89
0.88
0.87
0.88
0.85
0.90
(s )
0.07 - 4.9
0.07 - 6.9
0.06 - 8.9
0.09 - 6.5
0.09 - 6.2
0.10 - 8.6
0.14 - 12.0
440
460
530
460
540
570
580
Muestra 2
Tubo
D mm
L mm
n
n
K (Pas )
Intervalo
de
gradiente
de
velocidad
-1
1L
10.15
405
0.77
1700
(s )
0.08 - 0.76
1M
1S
2L
3L
3M
3S
10.14
10.18
12.55
17.04
17.05
17.07
300
204
400
401
300
204
0.82
0.79
0.84
0.74
0.73
0.74
1790
1900
2070
2180
2500
2880
0.08 - 1.00
0.12 - 1.40
0.11 - 0.81
0.13 - 1.20
0.12 - 1.17
0.17 - 1.60
Los datos muestran que a medida que la longitud del tubo es menor el valor de K
aumenta. Esto se corresponde con la influencia de los efectos terminales en los
resultados, donde una pérdida de presión adicional debida a la entrada del tubo, a
la salida del tubo y a la salida de la energía cinética que acompaña a la corriente
de salida se torna relativamente superior para tubos cortos. Los resultados también
muestran que a medida que el diámetro del tubo aumenta K también aumenta.
Esto se corresponde con el efecto de deslizamiento en la pared, ya que debido a la
migración de partículas alejándose de la pared del tubo, se obtiene un flujo mayor
que el que se obtendría si no existiera deslizamiento. El efecto es más
pronunciado con pequeños diámetros de tubo. Por consiguiente se debe trabajar
con tubos largos y de mayor diámetro para reducir ambos efectos. El valor de
índice de flujo no parece estar sistemáticamente influido por las dimensiones del
tubo.
LECCIÓN 13. VISCOSÍMETRO ROTACIONAL
Se pueden encontrar cuatro tipos fundamentales de viscosímetros rotacionales:
• de cilindros concéntricos
• de cono y plato
• de platos paralelos
• de mezcla
Pueden operar a velocidad angular constante o en modo oscilatorio (dinámico). En
general, la función a controlar es el gradiente de cizallamiento, pero hay algunos
en que la variable a controlar es el esfuerzo de cizalladura.
LECCIÓN 14. VISCOSÍMETROS DE CILINDROS CONCÉNTRICOS
Observe la figura 1.1 del texto básico y aprecie los esquemas de representación
mostrados en ésta. Como puede observar un viscosímetro de cilindros
concéntricos consta de dos componentes, el elemento que gira y el elemento que
está fijo.
En el caso de los viscosímetros tipo Searle, el cilindro interior (bob) es el que rota,
mientras que el exterior (cup) está fijo. En los viscosímetros tipo Couette, el interior
(bob) está fijo y el elemento que rota es el cilindro exterior (cup). La mayoría de los
viscosímetros comerciales son de tipo Searle.
Cuando el cilindro interior rota a velocidad constante, el instrumento de medición
leerá una lectura a que es proporcional al torque M requerido para mantener la
velocidad del cilindro interior constante. Esta velocidad de rotación es proporcional
al gradiente de cizallamiento.
LECCIÓN 15. DERIVACIÓN DE LAS ECUACIONES BÁSICAS. CÁLCULO DE
GRADIENTES DE VELOCIDAD
Estudie el epígrafe 3.2.1 del texto básico. Al concluir conocerá que:
• Las
condiciones de contorno requeridas para el desarrollo de las
determinaciones, utilizando este tipo de viscosímetro son: flujo laminar y
estacionario, efectos finales despreciables, fluido incomprescible,
propiedades independientes de la presión, temperatura constante, efecto de
deslizamiento en la pared despreciable y componentes de velocidad axial y
radial iguales a cero.
• Aplicando las ecuaciones básicas de fenómenos de transporte se encuentra
que sb = M / 2p h Rb donde el subíndice b se refiere al cilindro interior. Esta
ecuación relaciona el torque M con el esfuerzo de cizalla s.
• Existe una relación general entre la velocidad angular y el esfuerzo de cizalla
(ecuación 3.16 del texto básico). Esta ecuación proporciona un punto de
partida general para encontrar las relaciones matemáticas para tipos
específicos de fluidos.
• Si el fluido es newtoniano, el torque es proporcional a la velocidad con la que
-2
-2
el cilindro interior rota. W= (M/4pm h) ( Rb - Rc )
• Si el fluido cumple la ley de potencia, el torque no es directamente
proporcional a la velocidad de rotación y depende del índice de flujo. W=
1/n
(n/2K
2 1/n
) (M/2p h Rb )
2/n
[1 - (Rb / Rc) ]
• Si el fluido presenta esfuerzo de fluencia, la ecuación que relaciona la
-2
velocidad de rotación y el esfuerzo de cizalla es W= (M/4pmpl h) ( Rb - Rc
-2
) - so/mpl ln (Rc/Rb). Esta ecuación es válida si el esfuerzo de fluencia se
ha sobrepasado en todos los puntos, o sea que el esfuerzo de cizalla es
2
mayor que so. s min = M min / 2p h Rc >so donde M min es el torque
mínimo para vencer el esfuerzo de fluencia.
Para encontrar la mínima velocidad de rotación a que debe girar el cilindro para
que se produzca el efecto de cizallamiento en todo el intervalo, estudie el
problema 3.8.1. de la página 210 del texto básico.
Deberá precisar que:
• El fluido es un plástico de Bingham que responde a la ecuación s = 13 + 1.7 g
• Se utilizó un viscosímetro de cilindros concéntricos en el que rota el cilindro
interior y se varió el espacio anular para la solución del problema según a =
1.1,1.3,1.5.
• Se calculó para cada caso cuál es la velocidad de rotación para que el efecto
de transmisión de la cantidad de movimiento provoque el flujo desde las
capas de fluido inmediatas al rotor hasta las inmediatas al cilindro exterior.
Esto es que haya flujo por efecto de cizallamiento en todo el ánulo.
• El valor mínimo de velocidad de rotación se obtiene para cuando s = so.
• Se obtiene una ecuación para W min que es función de a= Rext/Rint (o Rc/Rb
en el libro, donde c=cup y b = bob).
• Se analiza que a medida que a aumenta, la velocidad de rotación mínima
necesaria es mayor para mantener el flujo del plástico de Bingham en el
ánulo. De aquí que se prefieran los ánulos estrechos para el desarrollo de
la experimentación.
Además de relacionar el torque (M) con la velocidad de rotación (W) se requiere
relacionar la velocidad de rotación con el gradiente de cizallamiento (g) para el
sistema de cilindros concéntricos.
En la página 96 del capítulo 5 de la monografía Propiedades físicas de alimentos
aparecen diversas ecuaciones que permiten relacionar W y g en dependencia de
las consideraciones realizadas, que dependerán de las relaciones entre los radios
de los cilindros exterior e interior, del comportamiento reológico del fluido
(newtoniano o no newtoniano que siga la ley de potencia, etc). Dadas las
simplificaciones a que estas consideraciones conducen, se recomienda que se
usen valores de Rext / Rint menores que 1.4, prefiriéndose como límite 1.1.
Estudie las páginas 164 - 169 del texto básico en las que se determinan las
expresiones que relacionan g vs W. A medida que avance en el estudio, analice
los problemas a los que remite cada epígrafe.
Al estudiar el problema del epígrafe 3.8.2 en el que se comparan los resultados
entre utilizar la aproximación de cizallamiento simple (desprecia la curvatura de la
pared del cilindro) y la aproximación de fluido que cumple con la ley de potencia
(ecuación 3.33) se concluye que:
• El % de error depende del valor de a = Rext / Rint y del valor del índice de
flujo n.
• El error menor se obtiene, dado un valor de índice de flujo n, para pequeños
espacios anulares (bajos a).
• El error menor se obtiene, para un mismo valor de a, a medida que n es
mayor.
• De la figura 3.22, página 213 del texto básico se podrá apreciar que si n = 0.4
y 1.0 < a < 1.02, el error será menor que 6%, mientras que si n = 0.2 para a
> 1.02, el error será mayor del 10%. Valores menores que 2% se obtienen
para fluidos de n cercanos a 1 y de a menores que 1.01.
La ecuación para relacionar g vs W para un fluido newtoniano conduce al problema
del epígrafe 3.8.3 página 213 del texto básico en el que se deduce la expresión
general que relaciona g = f ( W, a, radio). La aplicación de la ecuación para el radio
del cilindro interior y del cilindro exterior, conduce a la ecuación presentada como
3.32, para el valor de gradiente de cizallamiento en el cilindro interior y a la 3.157
para el cilindro exterior.
La ecuación para relacionar g vs W para un fluido que cumpla la ley de potencia
(ecuación 3.33) se deduce en el ejemplo 3.8.5, páginas 216 - 218 del texto básico,
siguiendo el mismo procedimiento que en el ejemplo 3.8.3 pero incluyendo la
n
ecuación de la ley de potencia s = Kg .
Así se concluye que:
• El valor del gradiente de cizallamiento es función de W, n y a.
• La ecuación 3. 169 permite encontrar el perfil de velocidad en el ánulo,
alcanzando valores de W para la capa de fluido junto al cilindro interior que
rota (ubicado en Rb) y de 0 para la capa de fluido junto al cilindro exterior
fijo (ubicado en Rc)
• Otra forma de relacionar g y W es mediante la aproximación de Krieger que
aparece explicada a partir de la página 165 del texto básico, la cual busca
la solución de la ecuación 3.42 a partir de la evaluación de series infinitas,
truncadas a partir del primer término de la serie, lo que da lugar a la
ecuación 3.43. Esta deducción muestra cómo la aproximación por la ley de
potencia es una excelente solución mucho más sencilla.
Estudie el epígrafe 3.2.3 (hasta la ecuación 3.50) en que se presenta una
configuración utilizada por varios fabricantes de viscosímetros: un cilindro que rota
dentro de un vaso de precipitado. Esta configuración puede aproximarse a un
cilindro interior finito que rota dentro de un cilindro exterior de radio infinito, al ser
Rext >> R int ( o Rc >>Rb)
Analice los problemas 3.8.7 y 3.8.8, páginas 221 - 223 del texto básico.
En el problema 3.8.7 se utiliza un cilindro que rota en un recipiente de gran radio.
Hacen referencias al problema anterior que aún no ha sido orientado, pero del que
sólo deben conocer que el fluido tiene un comportamiento seudoplástico, que sigue
0.307
0.307
la ley de potencia con un modelo s = 15.73 g
Pa, o sea K = 15.73 Pa s
. Se
demuestra cómo a partir de la ecuación 3.33, si a >>1, la ecuación se reduce a gb
-1.
= 2W/n = 2 ( 2p. rpm)/ 60 n = 0.6822 rpm s
La viscosidad aparente se define como s/g, de donde aplicada al cilindro interior
0.307-1
-0.693
será h ap = s/g = 15.73 gb
= 15.73 gb
Pa.s. Dando valores a gb,
encontraremos el valor de viscosidad aparente correspondiente.
El problema 3.8.8 demuestra el error que se comete al utilizar este tipo de
viscosímetro para un fluido no newtoniano que cumpla la ley de potencia. Se
puede comprobar cómo a medida que el índice de flujo n aumenta, se requieren
recipientes mucho mayores de modo que Rext/Rint ( o Rc/Rb) sea mayor. Observe
de la figura 3.24 cómo para obtener errores menores que 5% se requiere una
relación Rc/Rb =5, para un fluido newtoniano.
Por consiguiente el error en la determinación es función de la geometría del
sistema de medición (a) y de la naturaleza del fluido (n).
Estudie el epígrafe 3.5, páginas 174 a 182 del texto básico. Conocerá que en la
viscosimetría rotacional se pueden introducir errores al igual que sucedía en la
viscosimetría de tubos y que éstos pueden minimizarse o corregirse. Estos efectos
son:
• efectos terminales
• calentamiento viscoso
• deslizamiento en la pared
• flujo secundario
• cavitación
Al concluir el estudio del epígrafe deberá conocer que:
• Los efectos terminales incluyen la influencia en el torque del fondo del cilindro
que rota , ya que es ésta una superficie en contacto con el fluido que no ha
sido tomada en cuenta en el balance de fuerzas inicial. El diseño de los
rotores actuales reduce este efecto al no presentar el fondo plano.
• En caso de tener que hacer corrección por efecto terminal, el torque se mide a
una velocidad de rotación fija, llenando el ánulo al menos hasta 3 alturas
diferentes (h). Del gráfico de M vs h (altura del fluido en contacto con la
parte del rotor sumergida en el fluido) se determina ho (figura 3.6, página
175) y este valor es adicionado a la altura del cilindro reportada por el
fabricante, constituyendo la altura efectiva del rotor
• Si ocurre un incremento de temperatura durante el ensayo reológico producto
de la generación de calor por efecto viscoso, se afectará la determinación.
Se demuestra que para ánulos pequeños este efecto puede despreciarse.
• La separación en fases debida a efectos de pared puede afectar las
determinacones al igual que sucedía con los viscosímetros de tubos. Se
produce un deslizamiento que requiere ser corregido o que de ser
pronunciado obliga al uso de otro tipo de viscosímetro, el de mezcla.
• Cuando un cilindro interior rota, el fluido cercano a la superficie interior puede
tender a moverse hacia afuera debido a la fuerza centrífuga. Esto altera el
patrón laminar y se conoce como vórtice de Taylor. La ecuación 3.90
permite evaluar si se presentará o no vórtice de Taylor.
• A altos gradientes de cizallamiento la diferencia de presión en la dirección
radial a través del ánulo puede ocasionar vaporización parcial de la
muestra. Si u es la velocidad lineal, ocurrirá cavitación cuando u > (2(Patm 1/2
Pvap ) / r ) . Esto no es un problema en la reología de alimentos si se
mantiene la condición de flujo laminar.
Estudie los problemas 3.8.14, 3.8.16 y 3.8.17, páginas 231-233 y 235-237 del
libro de texto básico.
En el problema 3.8.14 aprenderá a calcular el valor de altura efectiva del
viscosímetro rotacional de cilindros concéntricos para una combinación Rb = 1.95
cm, Rc =2.00 cm o sea a = 1.026. Se estudiaron diferentes alturas para cada
velocidad angular utilizada ( 600 rpm, 900 rpm y 1100 rpm).
De los resultados del ajuste por regresión lineal de M vs h se obtuvo que la
corrección ho es mayor a medida que aumenta la velocidad de rotación. No
obstante se recomienda considerar un valor promedio.
El problema 3.8.16 usa los datos del ketchup del problema 3.8.6 para evaluar el
2
2
calentamiento viscoso. Conociendo que Tmax = To + (m g s ) / 2 k (ecuación
3.80) donde k es la conductividad térmica, puede calcularse la máxima diferencia
de temperatura ( Tmax - To) que podrá existir en la superficie del cilindro interior
sustituyendo como s la dimensión del ánulo (Rext - R int) y m del fluido newtoniano
como la h aparente al máximo gradiente de cizallamiento. Observe el pequeño
valor de DT obtenido en el problema.
El problema 3.8.17 calcula la velocidad del rotor para producir cavitación en un
sistema de cilindros concéntricos con agua a 40°C. Se obtiene un alto valor de
velocidad lineal equivalente a 6738 rpm (recuerde que u= 2pR rpm en m/s) para
que se produzca cavitación a esa temperatura. En general antes de alcanzar ese
valor de velocidad de rotación, el flujo laminar ya no existirá.
UNIDAD 2.MÉTODOS Y APLICACIONES EN REOLOGÍA
CAPÍTULO 4. MÉTODOS PARA LA REALIZACIÓN DE DETERMINACIONES
REOLÓGICAS 3
LECCIÓN 16. VISCOSÍMETRO DE CONO Y PLATO
Estudie los epígrafes 3.3 y 3.6,páginas 169-172 y 182-185 del texto básico. Al
concluir éstos conocerá que:
• Este viscosímetro, cuya forma se presenta en la parte izquierda de la figura
3.3, alcanza gradientes de cizallamiento moderados.
• Cuando el ángulo q es menor de 5° y la velocidad de rotación es baja, g = W /
tan q, o sea constante a través del espacio en que el fluido se coloca y s =
3
3M/ 2pR , donde R es el radio del cono.
n
3
• Si el fluido cumple la ley de potencia s = K g se cumple que 3M/2pR =
n
(W/tanq)
• Las fuentes de error son: el calentamiento viscoso, el flujo secundario, el
gradiente de cizallamiento no uniforme debido a ángulos grandes, los
efectos finales y la geometría no ideal (excentricidad o ángulos incorrectos,
conos truncados)
Estudie el ejempo 3.8.11, páginas 226-227 del texto básico. Observe cómo:
• El ángulo del cono es sólo 3° (0.0524 radianes)
• Conocido el intervalo de g que se quiere estudiar se puede calcular el
intervalo de velocidad a aplicar de: W = g tan q
• Para un fluido que cumpla la ley de potencia s = 15.73 g
0.307
Pa, se puede
calcular el valor del torque que el instrumento deberá ser capaz de cubrir
3
n
de: M = 2pR K g / 3.
LECCIÓN 17. VISCOSÍMETROS DE MEZCLA
Cuando se trabaja con fluidos que exhiben tendencia a sedimentar o el tamaño de
partículas es grande, comparable al tamaño de un ánulo del sistema de cilindros
concéntricos, la viscosimetría de cilindros concéntricos no es recomendable y se
sustituye el dispositivo por un viscosímetro de mezcla.
Estudie el epígrafe 3.7 páginas 185 a 190 del texto básico. Al concluir el epígrafe
deberá conocer que:
• El efecto de la agitación mecánica induce el flujo del material.
• Los tipos de impelente usados dependen de las características de los fluidos.
Si son de baja viscosidad se usan impelentes de los tipos turbinas y
propelas. Si son de alta viscosidad se usan anclas, cintas helicoidales y
tornillos helicoidales.
• Los impelentes para baja viscosidad se dividen en: de flujo radial y de flujo
axial. En los de flujo radial (turbinas de hojas planas y curvas) las hojas se
montan paralelas al eje vertical del eje de rotación. En las de flujo axial
(propelas y turbinas de hojas inclinadas) se logra el movimiento fondo tope, colocando las hojas a ángulos menores de 90° con el ángulo de
rotación.
• Para el mezclado de fluidos el análisis dimensional muestra que el número de
potencia NPo es función de NPo = f(NRe, NFr, NWe, NWi, números
adimensionales geométricos).
Precise en las páginas 188 y 189 la interpretación física de cada uno de los
números adimensionales involucrados.
2
NRe = Número de Reynolds = rWd /m = fuerzas de inercia / fuerzas viscosas
2
NFr = Número de Froude = W d/g = fuerzas de inercia / fuerzas gravitacionales
2 3
NWe = Número de Weber = W d r/ sst = fuerzas de inercia/ fuerzas de tensión
superficial
NWi = Número de Weissenberg = Y1W/h
3 5
3 5
2 5
NPo = Número de Potencia = P /rW d = MW / r W d = M / rW d donde P es la
Potencia.
Cuando los efectos de tensión superficial, elásticos y de vórtice pueden
3 5
2
B
despreciarse, sólo NPo depende de NRe y en general P /rW d = A (rWd /m)
dependiendo A y B de la geometría y del régimen de flujo.
Para flujo laminar B=-1 y para flujo turbulento B = 0. En la región intermedia A y B
dependen del sistema de mezclado.Por consiguiente P = A / NRe para flujo
laminar.
Estudie el epígrafe 3.7.1, páginas 196-197( hasta mediados de página) del texto
básico.
En este epígrafe se utilizan viscosímetros de mezcla para la evaluación de fluidos
que cumplan con la ley de potencia y sólo dependan del NRe.
5
3
n-1
2
Si se utiliza hap en lugar de m se obtiene: P/d W r = A K gav /d Wr donde gav
es el gradiente de cizallamiento promedio que se define por k'W.
5
3
n-1
n-1
2
n-1
n-2
2
P/d W r = A K k' W /d Wr= A K k' W / d r
Para determinar k' se usan dos técnicas: el método de la pendiente y el de la
comparación de viscosidades, los que aparecen descritos en las páginas 191-194
del libro de texto básico.
3
El método de la pendiente se basa en graficar log (P/ d W
3
n+1
n+1
K ) vs 1-n, ya que se
cumple que log (P/ d W
K ) = log A - (1-n) log k'. Observe que se requiere
conocer el valor de K y de n para otros fluidos evaluados en un viscosímetro
convencional.
El método de la comparación de viscosidades se basa en comparar las curvas de
potencia para fluidos newtonianos y no newtonianos según el esquema presentado
en la figura 3.12, página 193 del texto básico.
• Se evalúa A de la pendiente de la recta NPo vs NRe encontrada en el
viscosímetro de mezcla para un fluido newtoniano de viscosidad concocida.
• Se calcula K y n para un fluido no newtoniano en un viscosímetro de cilindros
concéntricos.
• Se coloca el fluido no newtoniano en el viscosímetro de mezcla y a velocidad
angular constante se evalúa NPo.
• Se calcula NRe del fluido newtoniano que correspondería a dicho NPo.
• Se evalúa una viscosidad promedio para dicho NPo y un comportamiento
2
newtoniano, o sea se evalúa m = d W r NPo / A.
• Se iguala m a hap.
• Como hap = K ga
n-1
y se conoce para el fluido no newtoniano los valores de K
y n, se evalúa ga = (h/K)
2
1/ (n-1).
• O sea quedaría ga= [d Wr NPo/KA]
• k' se evalúa de ga/W.
1/(n-1).
El método de la pendiente es más sencillo pero la precisión en el cálculo de la
pendiente puede afectar los resultados, por lo que se prefiere el de comparación
de viscosidades a pesar de lo laborioso.
Conocido k' se puede utilizar el viscosímetro de mezcla para evaluar parámetros
reológicos de fluidos que cumplan con la ley de potencia, utilizando la ecuación
3.121, página 196 del texto básico. De la pendiente de la recta log M vs log W se
calcula n y del intercepto, si se conoce A, puede depejarse K. Cuando A no se
conoce puede aplicarse la ecuación 3.125.
Estudie el ejemplo 3.8.18.parte a, páginas 237-239 del texto básico, en el que se
ejercita el cálculo de k' por el método de la pendiente. Observe cómo se requiere
conocer los valores de K y n para estos fluidos determinados con un viscosímetro
de cilindros concéntricos.
El procedimiento para calcular la Potencia P sería:
• a = Rb /R impelente
2/n
• g= (2W/n) [a
2/n
/ (a - 1)
n
• s = Kg
2
• M= 2ph Rb s
•P=MW
3
Observe que (P/d W
n+1
K) = A k'
3
Aplicando logaritmos: log (P/d W
3
n+1
n-1
.
n+1
K) = log A - (1-n) log k'
Graficando log (P/d W K) vs 1-n, de la pendiente se obtiene - log k' y por tanto
k'.
En la página 239, 2do renglón dice log10 = 0.803 y debe decir log10 A = 0.803.
-1
Conocido k' para el equipo se puede evaluar ga = 4.47 W s
Continúe con la parte b del ejemplo 3.8.18, página 289. Del gráfico log M vs log W
se obtiene n= 0.378.
El valor de ny =0.588 para 1% de hidroxipropilmetilcelulosa es el valor promedio de
los cuatro reportados, así como My es el valor promedio de los cuatro valores de
P/W.
Se obtiene el valor de K del fluido desconocido a partir de la ecuación 3.125
utilizando datos de M, K y n de otro fluido de referencia.
Calcular K a partir del intercepto del gráfico log M vs log W, conocido A, no da el
mismo valor que por la ecuación 3.125, pero la diferencia entre ellos es aceptable.
Para fluidos con comportamiento de plásticos de Bingham las investigaciones han
sido menores. El procedimiento es similar al ya estudiado pero la ecuación a
utilizar para sustituir el modelo reológico sería la del plástico de Bingham. Estudie
el epígrafe 3.7.2 páginas 199-200. Observe cómo se reporta que k' puede ser una
función del esfuerzo de fluencia (so).
LECCIÓN 18. EJEMPLOS DE APLICACIÓN
Viscosímetros de cilindros concéntricos.
Estudie el ejemplo 3.8.6, páginas 218-221 del texto básico, que presenta el
resultado de la caracterización reológica de una salsa de tomate (ketchup). Al
concluir el estudio deberá conocer que:
• Se utilizó un viscosímetro rotacional de cilindros concéntricos de a = 1.048,
con el que se obtuvieron valores de rpm vs torque para el ketchup a 25°C.
• Los datos de rpm se expresan en rad/s para que sean consistentes con el
sistema de unidades. Para ello, recuerde que W (rad/s) = 2 p rpm / 60.
2.
• Conocido el torque se calcula sb =M/2phRb
• Del ajuste por regresión lineal de ln M vs ln W se obtiene n=0.307.
• Aplicando la ecuación 3.33 se calcula el gradiente de cizallamiento (gb)
• Así quedan explicadas las columnas de la tabla 3.32.
• La ecuación que describe el comportamiento del ketchup a 25°C es s =15.73
0.307
g
Pa, teniendo un comportamiento de fluido seudoplástico.
• Se demuestra cómo al aplicar la consideración de fluido newtoniano o asumir
gradiente simple, sólo nos da idea del orden de magnitud del
gradiente de cizallamiento, pues para la mayor rpm se obtiene un 10 y 16 % de
error respectivamente.
• Para conocer si existe vórtice de Taylor que afecte la determinación, se aplica
la ecuación 3.90, y si se cumple la desigualdad, se presentará vórtice de
Taylor y por tanto flujo secundario.
Estudie el ejemplo 3.8.9 páginas 224-225 del texto básico que analiza los datos
obtenidos para una salsa.
• La relación entre el radio exterior y el radio interior es 3.64, de donde se
asume la condición de radio exterior infinito.
• Los datos primarios obtenidos de W y M se transforman en datos de gb y sb
respectivamente según las ecuaciones:
2
sb= M/2phRb
gb=2W d(lnW) / d (lnsb)
• Al graficar ln W vs ln sb se obtiene una línea recta de pendiente 2.73, de
donde sb = 2W (2.73).
• Al graficar sb vs gb a 22°C se obtiene la curva de flujo de la figura 3.26, tíipica
de un fluido seudoplástico que puede ajustarse a la ley de potencia sb=Kgb
n
• Si se aplica regresión lineal para ln sb vs ln gb se obtiene n=0.37, K= 4.43 Pa
s
n
• Compruebe que 1/n = dln W / d ln sb
Estudie el ejemplo que se presenta a continuación para un chocolate fundido. El
chocolate es una dispersión, en manteca de cacao, de azúcar finamente molida y
extracto seco de cacao. Cuando una barra de chocolate se calienta a 80°C sobre
una bandeja, el chocolate se ablanda pero mantiene su forma. Si se golpea
bruscamente la bandeja, el chocolate comienza a fluir por haberse sobrepasado el
esfuerzo de fluencia. Los primeros experimentos fueron realizados en un
viscosímetro capilar, no resultando adecuados. Luego de 1950 se utilizan
viscosímetros de cilindros concéntricos, observándose una relación
aproximadamente lineal entre s y g pero que no pasa por el origen. Lo anterior
hace suponer un modelo de plástico de Bingham. Mejores resultados se obtienen
1/2
con un modelo de Casson y si se grafica s
1/2
1/2
1/2
vs g
se obtiene de la pendiente el
valor de hpl y del intercepto so La adición de 0.3 - 0.6 % de lecitina disminuye
la viscosidad plástica, pero el esfuerzo de fluencia pasa por un valor mínimo en
0.5% de lecitina para aumentar posteriormente. Este efecto no ha sido explicado
totalmente, pero es aprovechado tecnológicamente.También con datos obtenidos
en un viscosímetro de cilindros concéntricos se reporta el ajuste del modelo de
n
Herschel Bulkley con los parámetros (a T=46.1°C): n=0.574, K= 0.57 Pa s ,so =
1.16 Pa.
Estudie el ejemplo que se presenta a continuación para la caracterización
reológica de sistemas que contienen sustitutos de azúcares y agentes gelificantes.
(Datos reportados por M. Ozdemir y H. Sadikoglu en International Journal of Food
Science and Technology Vol 33 p 439- 444, 1998.) El ejemplo se desarrolla por la
necesidad de mantener el mismo comportamiento reológico cuando la sacarosa se
sustituye por otros productos edulcorantes, buscando obtener alimentos de bajo
contenido calórico así como con el uso de agentes gelificantes apropiados para los
bajos contenidos de azúcares (pectina metil oxidada o carrageenan) Las
determinaciones fueron realizadas a 25°C con un viscosímetro Brookfield modelo
LVT (basado en el principio de radio infinito) utilizando un beaker de 600 ml como
cilindro exterior.
Se realizaron determinaciones a gradientes de velocidad ascendentes 0-60 rpm en
10 minutos y luego descendentes comprobando que no existe comportamiento
tixotrópico al coincidir los resultados. Las determinaciones se realizaron a 6,12 30
y 60 rpm. Los valores de esfuerzo de cizalla s se calculan de: s =lectura en el dial *
2
Constante del equipo/ 2p R L, siendo L, R y la constante del equipo, ofrecidas por
el fabricante. Los valores de radio se encuentran entre 0.1588 y 0.9421 cm.
Compárelos con el radio de un beaker de 600 ml.
Los resultados encontrados para el ajuste del modelo de Herschel - Bulkley para
diferentes azúcares a 40% en peso y diferentes % en peso de pectina metil
oxidada (PMO)son:
Sacarosa
n
K
_o
Isomaltosa
n
K
_o
Polidextrosa
n
K
_o
0.1% PMO
.
0.8
0.2
0
.
0.69
0.24
0
.
0.47
1.02
0
0.5% PMO
.
0.58
1.23
0
.
0.55
4.70
0.15
.
0.44
8.39
1.05
1.0% PMO
.
0.46
2.35
0.53
.
0.45
9.22
4.09
.
0.35
18.36
4.26
n
K : Pas ; so: Pa.
Los valores de n y K se calcularon del ajuste de ln (s - so) vs lng, siendo los
coeficientes de correlación mayores que 0.989. Como se aprecia, la adición de
pectina metil oxidada aleja al fluido del comportamiento newtoniano, disminuyendo
n a medida que aumenta la concentración. Este efecto es más marcado en las
soluciones de sacarosa. Esto puede explicarse por el incremento en los enlaces
hidrógeno que aumentan la interacción entre la sacarosa y le pectina metil
oxidada.
El incremento de K con la concentración de pectina metil oxidada se aprecia para
todos los casos pero en especial para la polidextrosa, lo cual puede deberse a la
mayor masa molar de la polidextrosa.
El esfuerzo de fluencia se presenta en dependencia de la naturaleza de la
sacarosa o su sustituto y de la concentración de pectina metil oxidada. Para 0.1%
ningún sistema presenta este comportamiento. La presencia de esfuerzo de
fluencia puede atribuirse a la formación de complejos entre la pectina metil oxidada
y el co-soluto o al fortalecimiento de la estructura mediante entrecruzamientos,
puentes de enlace, etc.
A medida que aumenta el gradiente de cizallamiento (o gradientede velocidad) la
viscosidad aparente disminuirá como sucede con un fluido de naturaleza
seudoplástica, dada la ruptura de las estructuras enredadas de las moléculas de
pectina metil oxidada para altos valores de gradientes de velocidad.
Los autores reportan que el movimiento de la lengua durante la masticación de
estos productos puede considerarse como un gradiente de cizallamiento de 20 - 50
rpm en un viscosímetro rotacional, ya que la lengua se mueve unas 30 veces por
minuto. De aquí que pueda calcularse la viscosidad aparente para un gradiente de
velocidad de 30 rpm y así comprobar si al paladar se sentiría una sensación
parecida o no a la del producto con sacarosa. Realice el cálculo y con él, el gráfico
de viscosidad aparente para 30 rpm vs concenración de PMO para los tres
productos y compruebe que para lograrlo, la cantidad máxima de pectina metil
oxidada a utilizar es aproximadamente 0.2%.
Estudie el ejemplo que se presenta a continuación para analizar la influencia de las
concentraciones de aceite y emulsionantes en las propiedades reológicas de
emulsiones de aceite en agua del tipo salsa fina. (Datos publicados por J. Franco,
A. Guerrero, C. Gallegos en Grasas y aceites Vol 46, Fasc 2, p108-114, 1995).
Las emulsiones alimentarias aceite en agua como la mayonesa y salsas para
ensaladas, son sistemas multicomponentes complejos cuya estabilidad se
favorece incluyendo un emulsionante en la formulación. La yema de huevo se ha
usado como estabilizante, pero actualmente hay una tendencia a su reducción
para disminuir el colesterol. El empleo de un emulsionante de baja masa molar
permitiría producir emulsiones de bajo contenido de aceite sin usar estabilizantes
(hidrocoloides). Las propiedades reológicas están relacionadas con ciertos
parámetros estructurales de la emulsión como el tamaño de la gota y la
polidispersidad. Se prepararon en el experimento varias formulaciones variando el
contenido de aceite de girasol y de estearato de sacarosa de alto balance entre
grupos hidrófilos y lipófilos (HLB=15) utilizado como emulsionante.Las
determinaciones de flujo estacionario se realizaron en un reómetro rotatorio
Rotovisco RV20/CV100 de Haake con Rext/Rint = 1.037. Las curvas de flujo se
-1
obtuvieron para un intervalo de gradientes de cizalla entre 0.5 y 300 s . Todas las
-1
muestras se precizallaron durante 10 minutos a 300 s . Las mediciones se
realizaron a 25°C. A continuación se presenta la tabla de composiciones de las
formulaciones, todas en % peso.
Aceite de
45
girasol
Agua
35.6
Yema de
6
huevo
50
50
50
50
55
32.6
30.6
28.6
25.6
25.6
6
6
6
6
6
Estearato
de
sacarosa
Vinagre
Azúcar
Sal
5
3
5
7
10
5
4
4
0.4
4
4
0.4
4
4
0.4
4
4
0.4
4
4
0.4
4
4
0.4
El comportamiento de las curvas de flujo muestra el de un fluido seudoplástico,
observándose tres zonas bien diferenciada. En la primera, a bajas velocidades de
cizalla, se aprecia una tendencia de viscosidad constante ho. A velocidades de
cizalla intermedias se aprecia una curva que se ajusta a la ley de potencia. A altas
velocidades de cizalla se aprecia de nuevo una tendencia a viscosidad constante
hinf. Se encuentra que el modelo de Carreau describe la variación de la viscosidad
aparente con el gradiente de cizallamiento. Este modelo es:
2 s
(h - h inf) / (ho - h inf) = 1 /[1 + (g/gc) ] . En esta expresión gc es el gradiente de
cizallamiento cuando comienza la caída de viscosidad y s es un parámetro
relacionado con la pendiente de la región intermedia.
A continuación se presentan los parámetros del modelo para las emulsiones con
5% de estearato para diferentes concentraciones de aceite.
%aceite
55
50
45
_o Pas
3.67
2.36
2.08
-1
_c s
7.80
7.00
5.00
s
0.35
0.36
0.36
_ inf Pas
0.15
0.14
0.14
r
0.999
0.999
0.999
Un aumentode concentración de aceite provoca un aumento significativo de ho y
de gc.
La siguiente tabla muestra los parámetros del modelo para 50% de aceite y
diferentes concentraciones de estearato.
% estearato
3
5
7
10
_o Pas
1.42
2.36
3.04
3.28
-1
_c s
11.80
7.00
5.50
7.50
s
0.38
0.36
0.40
0.41
_ inf Pas
0.06
0.14
0.20
0.25
r
0.996
0.999
0.999
0.999
Una mayor concentración provoca un aumento de hinf y de ho.
La variación de viscosidad con el gradiente de cizallamiento es el resultado del
proceso de refloculación tras la cizalla. Un alto valor de ho está relacionado con un
menor tamaño y mejor distribución de gotas (demostrado en el trabajo y no
presentado aquí). Un aumento de gc implica una mayor resistencia del entramado
de gotas refloculadas y un aumento de s, una mayor velocidad de destrucción de
dichos entramados. El aumento de viscosidad estacionaria con el contenido de
aceite puede explicarse por el doble efecto que provoca el descenso del tamaño
medio y la mejor distribución de tamaño de las gotas y a un aumento de las
interacciones entre partículas. Además este aumento favorece la reformación de
estructuras tridimensionales progresivamente más resistentes a la cizalla, lo que
explica el aumento de gc con el porcentaje de aceite. El posible desplazamiento de
las proteínas de la interfase por el incremento en la concentración de estearato
debe modificar la estructura y aumentar la viscosidad del medio continuo. Esto,
junto al aumento de concentración de la fase dispersa por la mayor concentración
de emulsionante, repercute en un aumento de viscosidad del sistema.
Se recomienda que al estudiar se construyan las curvas de viscosidad de los
sistemas haciendo uso de los valores de los parámetros del modelo de Carreau.
En el tema 3 estudiarán cómo este sistema posee también propiedades
viscoelásticas.
LECCIÓN 19. VISCOSÍMETROS DE CONO Y PLATO
Estudie el ejemplo 3.8.12, páginas 227-229 del texto básico que evalúa el
comportamiento reológico del fluido del ejemplo3.8.9 pero con un viscosímetro de
cono y plato.
• A partir de los datos de W y M se calcula g y s.
g = W / tan q
3
s = 3M /2p R
• Observe cómo el intervalo de W y M es inferior al del ejemplo 3.8.9.pero el
orden de magnitud de g y s es el mismo.
• Se construye un gráfico s vs g y se aplica regresión lineal a ln s vs ln g
n
obteniendo n = 0.303 y K = 7.64 Pa s .
• Estos resultados difieren de los del ejemplo 3.8.9 y las diferencias pueden
deberse a la consideración de radio infinito en la solución analítica y a que
el intervalo de gradiente de cizallamiento no es el mismo. En estos
productos manufacturados una posibilidad siempre presente es la variación
(aunque sea muy pequeña) en la formulación de la receta.
LECCIÓN 20 VISCOSÍMETROS DE MEZCLA
Una de las aplicaciones del viscosímetro de mezcla es la determinación del
esfuerzo de fluencia de un material plástico.
Estudie el epígrafe 3.7.3, páginas 200-207 del texto básico, en el que se describe
el procedimiento para la evaluación de so, según el "vane method". Este utliza un
impelente formado por 4,6 u 8 hojas el que rota en un recipiente. La figura 3.14
muestra un esquema del impelente tipo "vane".
En las páginas 203-207 se presentan las maneras de conducir los experimentos,
una en que la variable a controlar es la velocidad y otra en que la variable es el
esfuerzo.
Estudie los problemas 3.8.19 y 3.8.20 en los que se ejercita el procedimiento con
el impelente "tipo vane" por el modo de operación a velocidad controlada.
Al concluir el estudio del problema 3.8.19 habrá conocido que:
• La velocidad a controlar debe ser lo más baja posible (< 1rpm)
• Cómo un viscosímetro no es universal, sino que en función del intervalo de
esfuerzos a determinar, varía la serie o modelo que es posible usar.
• El cambio de la dimensión del impelente puede solucionar el problema sin
cambiar el viscosímetro pues esto redundaría en disminuir el valor de la
constante que relaciona M y so.
• Dada la deducción de la ecuación, el impelente debe estar totalmente
sumergido y guardando proporciones de alturas de líquido por encima y por
debajo de las hojas del impelente (z1 y z2), de donde el volumen de fluido
no es arbitrario, sino que depende de las dimensiones del impelente.
En el problema 3.8.20 se calcula el esfuerzo de fluencia estático y dinámico para el
ketchup. Se utilizan dos métodos para el cálculo de so. En el primero se usa la
ecuación 3.141 para m=0. Observe que Mo se calcula como: torque % * 0.00575 y
cómo h/d = altura en la 4ta columna de la tabla / 2.5 cm, dadas las dimensiones
del dispositivo. Por el método de la pendiente se usa la ecuación 3.137, graficando
Mo vs h y de la pendiente se calcula el valor del esfuerzo de fluencia. Note cómo el
valor del esfuerzo de fluencia para los experimentos estáticos son superiores a los
de los experimentos dinámicos dado que al producirse el cizallamiento previo en el
segundo caso, la estructura del material ya ha sido afectada. Compruebe en la
tabla 3.10 la validez de ambos procedimientos.
Cuando se trabaja a esfuerzo controlado, se parte de que los productos son
independientes del tiempo para que no exista influencia del tiempo de operación
en el resultado. Observe en la figura 3.16 cómo a medida que se aumenta el valor
del esfuerzo aplicado (torque M) se obtienen deformaciones mayores que van
creciendo en escalón. Para M5 cambia el comportamiento aumentando la
deformación con el esfuerzo aplicado. Entre el valor M4 y el valor M5 se encuentra
el esfuerzo de fluencia en el que el fluido cambia de su compotamiento como
sólido a su comportamiento como líquido. La figura 3.17 muestra el resultado
cuando se aplica un programa de incremento continuo de esfuerzos.
Otra aplicación del viscosímetro de mezcla es para la determinación de la
reomalaxia que consiste en la ruptura irreversible de la estructura de un material.
Estudie el epígrafe 3.7.4, páginas 208 - 210 del texto básico. La determinación
descrita se resume en:
• Medir valores de M vs tiempo a diferentes velocidades de rotación ( al menos
tres) evaluando el torque inical y el valor de equilibrio para cada una. Es
importante que cada experimento se realice con muestra nueva.
• Graficar los valores de torque inicial y de torque en equilibrio vs velocidad de
rotación, quedando un área entre las dos curvas. La determinación de esta
área es un índice del grado de reomalaxia del material.
• Cuando el material no es dependiente del tiempo no se presenta esta área.
Estudie el ejemplo 3.8.22 en el que se ejemplifica este procedimiento. Al concluir el
estudio conocerá que:
• Los datos primarios obtenidos son de torque vs tiempo para cinco velocidades
de rotación diferentes.
• A medida que el tiempo transcurre, los valores de torque tienden a un valor
constante que resulta el de equilibrio.
• Se consideró como valor inicial el de la menor velocidad y como valor final el
de la última velocidad, dado que ya se apreciaba la tendencia al valor
constante.
• Se puede ajustar un modelo de M vs W, para los valores de torque inicial y de
torque en el equilibrio, lo que permite el cálculo del área representativa de
la reomalaxia como la solución de una integral definida. El uso de
programas de ajuste de curvas como el Curvexpert, permiten calular el área
bajo cada curva y por diferencia el área encerrada.
En este ejemplo se ejercita también el cálculo de la energía mecánica entregada al
fluido ya que la potencia es: P= MW y la energía mecánica será la integral de Pdt.
Por consiguiente, en el problema se encontró para una W, la dependencia de P vs
tiempo. El exponente que afecta al tiempo será una medida del comportamiento
tixotrópico del material y mientras más negativo sea éste mayor será el
comportamiento tixotrópico o sea más rápidamente se romperá una estructura.
Cuando el material no es tixotrópico, la energía requerida es mayor y constante.
Estudie el ejemplo que se presenta a continuación. (Tomado de la tesis de
doctorado de la autora de esta guía).
A partir del análisis de la bibliografía se identifica como un problema, la
heterogeneidad en los resultados obtenidos por los diferentes investigadores
durante la caracterización reológica de las suspensiones, asociadas al
equipamiento utilizado. Atendiendo a que el uso de viscosímetros de mezcla
parecía ser el más apropiado, se procedió al diseño de un equipo que perteneciera
a esta clasificación.
El sistema de medición desarrollado pertenece a la categoría de viscosímetro de
mezcla con impelente de tornillo helicoidal con tubo de descarga. Este sistema se
construye de modo que su extremo superior pueda ser acoplado a un viscosímetro
rotacional convencional Rheotest 2.1, en calidad de elemento que rota, mientras
que la tapa del sistema se acopla al equipo, de la misma forma que lo hace el
cilindro exterior del sistema de medición convencional. La cuba cilíndrica posee
una camisa para permitir el control de temperatura en el sistema al conectarse a
un baño termostático.
Del estudio de las fuentes bibliográficas se puede presentar el conjunto de
características generales siguientes para este tipo de impelente:
• El espacio anular entre el tubo de descarga o tubo chimenea y la punta de la
hélice debe ser pequeño.
• El cambio en el sentido de rotación del agitador no afecta el consumo de
potencia del agitador ni los resultados experimentales encontrados en
estudios de circulación y mezclado.
• Resultan eficientes para el mezclado de fluidos viscosos newtonianos y no
newtonianos.
• En régimen laminar el tiempo adimensional de mezclado (tiempo de mezclado
* velocidad de rotación del agitador) es constante, tanto para fluidos
newtonianos como no newtonianos inelásticos. El intervalo para el cual se
considera flujo laminar varía según los autores, siendo el más frecuente Re
< 10 - 20. Para los fluidos no newtonianos este intervalo se amplía
reportándose valores hasta Re < 100.
3
• La potencia consumida por el agitador se puede calcular a partir de P = A d
2
W m donde A depende del tipo de agitador y de las relaciones geométricas
de éste.
• Es posible despreciar el efecto de h/d en el cálculo de A y por tanto en el
requerimiento de potencia.
• El mayor consumo de potencia es debido al flujo cortante en la pared del tubo
chimenea (70 %).
• En experiencias para estudiar los efectos de transferencia de calor se
comprueba cómo se estabiliza la temperatura en tiempos muy pequeños
-1
encontrando valores de 100 s a velocidades de rotación de 0,17 s
menores a medida que la velocidad de rotación aumenta.
y
• La aplicación de técnicas de estímulo respuesta con trazadores permite
afirmar que existe un comportamiento de mezcla perfecta, no presentando
espacio muerto.
Evaluación del equipo como viscosímetro
Con el objetivo de verificar el comportamiento del elemento diseñado, se realizaron
experiencias con fluidos homogéneos newtonianos y no newtonianos,
determinando los parámetros reológicos mediante un sistema de cilindros
concéntricos.
Como fluidos newtonianos se estudiaron soluciones de sacarosa 70,0 % en peso a
313 K, 72,1 % en peso a 308 K y 75,0 % en peso a 313 K. Como fluidos no
newtonianos se estudiaron una solución de carboximetilcelulosa ( baja viscosidad )
3 % en peso a 308 K, y mieles de caña de azúcar de 64,1, 71,8, 75,6, 76,6 78,2 y
81,2 % en peso, a 313 K.
Las determinaciones se realizaron utilizando los cilindros S-S1, S-S2 o S-S3 de un
Rheotest 2.1, obteniendo valores de esfuerzo de corte para cada gradiente de
velocidad impuesto. Los resultados se presentan en la tabla 1. En la misma se
muestra el valor medio de viscosidad para el caso de los fluidos newtonianos y el
valor de los parámetros del modelo de la ley de potencia (K y n) para los fluidos no
newtonianos. Así mismo, los sistemas homogéneos anteriores se evaluaron en el
Rheotest 2.1 pero utilizando el impelente de tornillo helicoidal con tubo de
descarga descrito anteriormente, obteniendo valores de torque para cada
velocidad de rotación impuesta, a temperatura constante.
Tabla 1 Resultados obtenidos con el viscosímetro rotacional convencional
n
Sistema
T(K)
m (Pas)
n
Pureza %
K (Pas )
Sacarosa
313
0.1141
70%
Sacarosa
308
0.2622
72.1%
Sacarosa
313
0.3900
75%
CMC 3%
308
0.8751
0.2864
Miel 64.1% 313
0.9800
0.0870
81.2
Miel 71.8% 313
0.9721
0.0900
65.8
Miel 75.6% 313
0.9607
0.2498
66.2
Miel 76.6% 313
0.8553
2.0514
41.6
Miel 78.2% 313
0.9400
0.4305
49.3
Miel 81.2%
313
0.9400
2.1982
66.7
Como quiera que para la geometría diseñada no se poseían las constantes de
calibración del instrumento ni una relación geométrica sencilla que permitiera su
evaluación, se procedió a desarrollar un modelo matemático que describiera el
comportamiento reológico del sistema a partir de los datos experimentales
obtenidos. Este modelo será presentado en el capítulo 4 del material por
corresponder a Fenómenos de Transporte.
Para el cálculo del gradiente de velocidad local se utilizó una expresión que
considera la contribución de las dos componentes de velocidad características del
flujo helicoidal, una axial y otra tangencial.
Para la solución del modelo matemático se introduce el concepto del radio
equivalente, definido como el radio de un cilindro interior en un sistema de cilindros
coaxiales que cumple la condición de que el gradiente de deformación en la
superficie del cilindro interior equivalente es igual al gradiente de deformación
promedio dentro del tubo de descarga.
El radio equivalente se determinó comparando los valores de la velocidad angular
-1
2
W (s ) y el torque por unidad de longitud M1 (Pa m ), evaluados para los fluidos
newtonianos utilizando el impelente de tornillo helicoidal, con los valores
calculados al ensayar los fluidos con el Rheotest 2.1 utilizando los cilindros
concéntricos convencionales.
El valor del flujo volumétrico en el impelente de tornillo helicoidal con tubo de
descarga para los ensayos con fluidos newtonianos puede determinarse a partir de
la ecuación deducida por Fredrickson y Bird (1958) para fluidos newtonianos en un
ánulo:
4
4
2 2
Q = p R DP / 8 m { ( 1 - k ) - ( 1 - k ) / ln ( 1/k) } donde k = radio del cilindro
interior/radio del cilindro exterior
El ajuste realizado para 64 juegos de valores W, M1, Q correspondientes a los
fluidos newtonianos estudiados (sacarosa 70, 72 y 75 % en peso) arrojó el valor de
radio equivalente re = 0,02998 m, con intervalo de confianza (95 %) : 0,02995 0.0300 m y error medio 0,3%.
Comprobación de la fiabilidad del modelo planteado con fluidos no newtonianos.
Utilizando el valor del radio equivalente encontrado se procedió a aplicar el modelo
teórico para el cálculo de los parámetros reológicos de cada fluido ( K y n ), así
como el valor de la distancia radial adimensional para la cual srz = 0. En la tabla 2
se presentan los resultados obtenidos para los fluidos homogéneos no
newtonianos .
Tabla 2 Resultados obtenidos con el torniollo helicoidal y el modelo teórico para
fluidos homogéneos no newtonianos
Sistema
CMC 3%
Miel 64.1%
Miel 71.8%
Miel 75.6%
Miel 76.6%
Miel 78.2%
Miel 81.2%
T(K)
308
313
313
313
313
313
313
n
0.8793
0.9837
0.9719
0.9452
0.8523
0.9867
0.9303
n
K (Pa s )
0.2853
0.0849
0.0937
0.2316
2.1165
0.3778
2.3340
_
0.8489
0.8492
0.8492
0.8491
0.8488
0.8492
0.8491
-1
_ (s )
8-154
15-154
15-154
8-154
4-154
2-154
1-154
La comparación de las tablas 1y 2 para los fluidos homogéneos no newtonianos
muestra una buena correspondencia entre los resultados alcanzados con los
cilindros concéntricos convencionales y el impelente de tornillo helicoidal con tubo
de descarga . A partir de los mismos se puede demostrar la fiabilidad del modelo
matemático planteado en la descripción del fenómeno reológico que se presenta
en el equipo desarrollado en esta investigación.
De los resultados se encontró que el flujo volumétrico disminuye a medida que el
valor del índice de consistencia aumenta, siendo éste el parámetro que ejerce una
mayor influencia sobre el valor del caudal. Por otra parte se observa que l puede
ser considerado constante, correspondiendo esto con la presencia de un máximo
de velocidad en la corona externa con independencia de los parámetros del fluido,
al menos en el intervalo estudiado. La posición del máximo se encontró a 0,0416 m
del centro del eje del tornillo helicoidal.
Conclusiones parciales
De los resultados anteriores se puede concluir que:
1. El modelo teórico desarrollado para la determinación de las propiedades
reológicas de los fluidos a partir de datos de velocidad angular y de torque
por unidad de longitud describe el comportamiento del sistema de impelente
helicoidal con tubo de descarga, obteniendo valores de K y n que se
corresponden con los obtenidos con cilindros concéntricos convencionales
para sistemas homogéneos.
2. Es posible considerar en la modelación la existencia de un cilindro de radio
equivalente tal que el gradiente de deformación en la superficie del cilindro
equivalente sea igual al gradiente de deformación promedio dentro del tubo
de descarga. El valor de diámetro equivalente para el equipo diseñado es
0,06 m.
3. En la corona externa existe un máximo de velocidad, independiente de los
parámetros del fluido, encontrando éste a 0,0416 m , del centro del eje del
tornillo helicoidal.
4. A partir de los resultados obtenidos con fluidos homogéneos se considera
adecuado extender la aplicación del modelo matemático para la evaluación
del comportamiento reológico de los fluidos heterogéneos.
Aplicación del modelo teórico a los sistema heterogéneos
El estudio de los sistemas heterogéneos fue realizado preparando suspensiones a
partir de mieles de diferentes contenidos de sólidos totales disueltos (64,1 - 81,2 %
en peso) y cristales de sacarosa (20 - 50 % en peso). Los sistemas se prepararon
gravimétricamente utilizando una balanza digital Sartorius de precisión 0,1 g
-3
adicionando cristales de sacarosa ( r = 1,59 g cm ) a las mieles. La caracterización
reológica de los sistemas se realizaba al día siguiente de la preparación, con el
objetivo de permitir la expulsión del aire que se pudiera haber incorporado. En la
tabla 3 se presentan los sistemas preparados para el estudio. En ella se muestran
los parámetros reológicos del modelo de la ley de potencia K y n, y la coordenada
radial adimensional.
Tabla 3 Resultados obtenidos con el tornillo helicoidal y el modelo teórico para
suspensiones (T 313K).
Sistema
Miel 64.1%,
cristales 26%
Miel 71.8%,
cristales 26%
Miel 75.6%,
cristales 26%
Miel 76.6%,
cristales 20%
Miel 76.6%,
cristales 30%
Miel 76.6%,
cristales 40%
Miel 76.6%,
cristales 50%
Miel 78.2%
cristales 26%
n
-1
n
K (Pa s )
_
_ (s )
0.9371
0.2499
0.8491
9-154
0.9539
0.2288
0.8491
9-154
0.9661
0.6031
0.8492
4-154
0.8835
4.540
0.8489
0.3-51
0.9050
5.380
0.8490
0.3-51
0.8434
13.60
0.8488
0.3-17
0.8146
32.47
0.8487
0.1-10
0.9839
1.0378
0.8492
1-154
Miel 81.2%,
cristales 20%
Miel 81.2%,
cristales 30%
Miel 81.2%,
cristales 40%
Miel 81.2%,
cristales 50%
0.8733
6.4684
0.8489
4-50
0.8428
8.1760
0.8488
4-50
0.8598
14.24
0.8488
0.3-17
0.8298
37.86
0.8487
0.1-10
Como es de esperar a medida que el Brix y el contenido de cristales aumenta, el
índice de consistencia aumenta, mientras que el índice de flujo disminuye. Por otra
parte, en correspondencia con lo encontrado para los sistemas homogéneos, l no
depende de la naturaleza del fluido, y su valor medio coincide con el obtenido
anteriormente.
Desarrollo de una metodología de calibración del sistema de tornillo helicoidal con
tubo de descarga
Por la complejidad del modelo teórico, para el desarrollo del trabajo experimental
utilizando el impelente de tornillo helicoidal con tubo de descarga, se requiere del
procesamiento de los datos por computadora, lo cual puede dificultar la extensión
de un elemento de medición del tipo propuesto. Por consiguiente, se procedió a
encontrar una metodología de calibración del equipo que permitiera trabajar con
éste de una manera sencilla, tal como se realiza para la transformación de lecturas
experimentales en un viscosímetro convencional.
Para la calibración del equipo con impelente helicoidal se siguió la metodología
propuesta por Kemblowski y colaboradores ( 1986), dirigida a encontrar las
constantes de calibración del instrumento k¢ y Z, de modo que las lecturas
realizadas en la escala de medición ( V ) y la velocidad de rotación ( w ) se puedan
transformar en valores de s y g según:
s=ZV
g = k¢ w
Nota: Se utiliza w por estar expresada en rps, mientras W es en rad/s.
La metodología para la calibración se fundamenta en la consideración de que en
régimen laminar, el número de potencia (NPo) es proporcional al número de
Reynolds (NRe) según: NPo = C /N Re donde C es una constante .
Conociendo que:
3
NPo = P / r w d
5
2
NRe = r w d / m
P = 2 p w M donde P es el consumo de potencia, r es la densidad del fluido, w es
la velocidad de rotación del impelente, d es el diámetro del impelente y M es el
torque, se obtiene:
3
m=2pM/Cwd
Para fluidos newtonianos m es una constante, mientras que para fluidos no
newtonianos depende del gradiente de velocidad, utilizándose en la ecuación
anterior el valor de viscosidad aparente definida como la relación entre el esfuerzo
cortante s y el gradiente de velocidad g, para un valor de gradiente de velocidad
dado.
La introducción de la ecuación de Metzner y Otto g = k¢ w permite obtener que:
3
s = 2 p k¢ M / C d
La determinación de los valores de g y t para un sistema de medición de una
geometría dada a diferentes valores de velocidad de rotación dependerá de la
evaluación de las constantes C y k¢ así como del valor del torque M. El cálculo del
torque se realiza conociendo que éste es proporcional a la indicación del
instrumento en la escala de medición (V), esto es:
M = a V donde a es una constante para cada instrumento. Por consiguiente:
3
s = 2 p k¢ a V / C d = ZV
3
siendo Z = 2 p k¢ a / C d
Evaluación de las constantes k¢ y Z
Para realizar la determinación de las constantes k¢ y Z se siguió un procedimiento
experimental que implica, trabajando a temperatura constante, realizar la
evaluación de:
• Las características reológicas de dos fluidos, uno newtoniano y otro no
newtoniano, en un viscosímetro de cilindros concéntricos, determinando así
la viscosidad del fluido newtoniano y las constantes de la ley de potencia K
y n del fluido no newtoniano.
• Los mismos dos fluidos pero utilizando el impelente de tornillo helicoidal con
tubo de descarga, determinando la lectura en la escala de medición ( V )
para cada velocidad de rotación impuesta (w).
Como fluido newtoniano se estudió una solución de sacarosa 72,1 Brix a 308 K, de
-3
densidad 1,3524 g cm . La determinación de viscosidad se realizó con un
viscosímetro Rheotest 2.1, utilizando el juego de cilindros S - S3 de relación de
radios a = 1,24, obteniendo un valor promedio de viscosidad m = 0,2622 Pa s.
Por otra parte se aplicó el criterio de Whorlow (1980) para verificar la inexistencia
0.5
de vórtice de Taylor: W Rint ( Rext - Rint ) r / m > 41,3 (Rext / Rext-Rint)
encontrando que el miembro de la izquierda era igual a 16,58 mientras el de la
derecha era 131,26 por lo que no existe vórtice ni aún a la mayor velocidad de
rotación.
Adicionalmente se comparó el resultado de viscosidad obtenido con el reportado
por Bates (1948) de 263,0 mPa s para soluciones de 72,1 Brix a 308 K, de donde
se aprecia la buena correspondencia entre el valor experimental y el de la
literatura.
Conocida la viscosidad y la densidad del fluido se procedió a ensayar éste
utilizando el impelente de tornillo helicoidal con tubo de descarga, determinando
las lecturas en la escala de medición para cada valor de velocidad de rotación
impuesta, con el objetivo de calcular NPo y NRe a partir de:
5
2
NPo = 2 p a V / r d w
2
NRe = r w d / m
De las expresiones anteriores se observa que se requiere conocer el parámetro a,
constante que permite transformar las indicaciones del instrumento en la escala de
medición V en valores de torque. ( M = a V ). Esta constante es propia de cada
instrumento y no depende del sistema de medición utilizado, por lo que se calculó
a partir de la información brindada por el fabricante del Rheotest 2.1 para el juego
3
de cilindros S - S3. Este valor resultó ser: a= 1,19 E-04 Pa m
Para el impelente de tornillo helicoidal con tubo de descarga diseñado, las
ecuaciones de NPo y NRe resultaron ser:
2
NPo = 4,398 V / w
NRe = 22,468 w
En flujo laminar y para fluidos newtonianos se cumple que NPo = C/ NRe, por lo
que al hacer el gráfico de NPo vs 1/NRe se obtiene el valor de C. Así C = 451,
6193.
La calibración se continúa caracterizando un fluido no newtoniano estudiándose
una solución de carboximetilcelulosa (CMC) de baja viscosidad, al 3% en peso a
308 K. Los parámetros reológicos se determinaron con el viscosímetro de cilindros
concéntricos, utilizando el juego de cilindros S-S3. El resultado de las
determinaciones experimentales arrojó un valor de índice de flujo n = 0,8751 y un
valor de intercepto -1,2254.
El trabajo con el juego de cilindros S-S3 de a = 1,24, introduce la necesidad de
corregir el valor del índice de consistencia K, al no poder ser considerados iguales
los gradientes de velocidad para los fluidos newtonianos y los no newtonianos
siendo:
Intercepto = ln K - n ln c = -1,2254
2/n
2
2
donde: c = [( 1 - a ) / ( 1 - a ) ] * a / a
2/n
n
Para a = 1,24 y n= 0,8751 se obtiene: c = 0,9720 de donde K = 0,2864 Pa s .
El fluido no newtoniano fue también ensayado utilizando el impelente de tornillo
helicoidal con tubo de descarga realizando determinaciones del torque M = a V
para cada velocidad de rotación impuesta.
n-1
Para un fluido que cumpla la ley de potencia h = K g . Al sustituir la aproximación
de Metzner y Otto g =k¢ w se obtiene: h = K ( k¢ w)
3
p k¢ M / C d se encuentra:
3
n-1
M = ( C K d / 2 p ) k¢
n
n
n
n-1
= ( s / g ) g dado Como s = 2
3
w = A1 w siendo A1 = ( C K d / 2 p ) k¢
3
n-1
n
Al relacionar M vs w se obtiene el valor de A1 = 3,78 E-03 Pa m s .
Una vez conocido el valor de A1 se puede evaluar k¢ obteniendo: k¢ = 38,0396.
3
Como Z = 2 p k¢ a / C d , se encuentra Z = 0,2182.
Por consiguiente es posible concluir que las expresiones que permiten transformar
los resultados experimentales en valores de esfuerzo cortante y de gradiente de
velocidad para el impelente de tornillo helicoidal con tubo de descarga son:
s= 0,2182 V (Pa)
-1
g = 38,0396 w (s )
Comprobación de la fiabilidad de la calibración realizada utilizando fluidos no
newtonianos
Conocidas las constantes de calibración del instrumento se procedió a transformar
los valores de V y w para los fluidos no newtonianos carboximetilcelulosa y 6
mieles de diferentes Brix. En la tabla 4 se presentan los resultados obtenidos para
los valores de las constantes de la ley de potencia (K y n) al realizar el ajuste por
un procedimiento de regresión lineal según la ecuación:
ln s = ln K + n ln g
Tabla 4 Resultados obtenidos con la metodología de calibración para fluidos
homogéneos
Sistema
CMC 3%
Miel 64.1%
Miel 71.8%
Miel 75.6%
Miel 76.6%
Miel 78.2%
Miel 81.2%
T(K)
308
313
313
313
313
313
313
n
0.868
0.973
0.964
0.960
0.866
0.949
0.929
n
K (Pa s )
0.294
0.090
0.097
0.219
1.981
0.446
2.345
La comparación para fluidos homogéneos no newtonianos muestra una buena
correspondencia entre los resultados alcanzados con los cilindros concéntricos
convencionales y el impelente de tornillo helicoidal con tubo de descarga. A partir
de esta comparación se puede demostrar la validez del procedimiento de
calibración planteado en la determinación de los parámetros reológicos para los
fluidos no - newtonianos.
Determinación de los parámetros reológicos de los sistemas heterogéneos
Comprobada la validez del procedimiento planteado para los fluidos homogéneos,
se procedió a verificar los resultados con los fluidos heterogéneos. Con los valores
de V y w obtenidos para cada suspensión , consistentes en sistemas miel cristales, se procedió a calcular los valores de s y g, utilizando las constantes de
calibración. Con posterioridad se aplicó un procedimiento de regresión lineal para
encontrar los parámetros reológicos (K y n) de estos sistemas. En la tabla 5 se
presentan los resultados obtenidos para los fluidos heterogéneos.
Tabla 5 Resultados obtenidos con la metodología de calibración para sistemas
heterogéneos
Sistema
Miel 64.1%,
26%
Miel 71.8%,
26%
Miel 75.6%,
26%
Miel 76.6%,
20%
Miel 76.6%,
30%
Miel 76.6%,
40%
Miel 76.6%,
50%
Miel 78.2%
26%
Miel 81.2%,
20%
Miel 81.2%,
30%
Miel 81.2%,
40%
Miel 81.2%,
50%
cristales
cristales
cristales
cristales
cristales
cristales
cristales
cristales
cristales
cristales
cristales
cristales
n
n
K (Pa s )
0.940
0.239
0.951
0.273
0.959
0.623
0.816
5.540
0.821
6.908
0.853
13.19
0.820
31.80
0.944
1.231
0.862
6.664
0.849
7.977
0.856
14.26
0.833
37.42
El análisis de la tabla permite afirmar que existe un incremento del índice de
consistencia al incrementar el contenido de cristales en el sistema , mientras que
para el valor del índice de flujo los intervalos de confianza se solapan (no están
mostrados en la tabla), aunque existe una tendencia poco marcada a la
disminución de éste al aumentar el contenido de cristales en la suspensión. Al
comparar los resultados obtenidos en el presente trabajo con los del modelo
teórico se verifica la buena correspondencia de éstos.
Conclusiones parciales
Del trabajo realizado se puede concluir que:
1. Es posible utilizar un sencillo procedimiento para encontrar las constantes de
calibración que permitan la determinación de los parámetros reológicos de
fluidos homogéneos y heterogéneos que cumplan la ley de potencia
mediante un impelente de tornillo helicoidal con tubo de descarga.
2. La experimentación requiere de la determinación del torque para cada valor
de velocidad de rotación impuesta una vez que se dispone de las
constantes de calibración.
3. Para la determinación de éstas se requiere evaluar el comportamiento
reológico de un fluido newtoniano y de uno no newtoniano utilizando un
sistema de cilindros concéntricos convencional y el sistema de tornillo
helicoidal con tubo de descarga.
4. Al comparar los resultados de los parámetros reológicos obtenidos con este
procedimiento para los sistemas no newtonianos homogéneos y
heterogéneos con los obtenidos aplicando la solución del modelo teórico se
obtiene una buena correspondencia entre éstos, lo cual posibilita la
aplicación del impelente de tornillo helicoidal sin requerimientos de
computación.
5. Dada la facilidad de este procedimiento, las caracterizaciones reológicas de
los restantes sistemas estudiados se realizó utilizando los valores de las
constantes de calibración del sistema de tornillo helicoidal con tubo de
descarga diseñado.
Sistemas modélicos heterogéneos
Procedimiento experimental
Para estudiar el efecto del contenido de cristales así como la influencia del tamaño
del cristal en el comportamiento reológico de los sistemas heterogéneos, se
prepararon soluciones modélicas sacarosa - agua - cristales, las que fueron
estudiadas a 313 K .Para la preparación de las suspensiones se partió de una
solución saturada de sacarosa en agua, a las que se añadió sacarosa de modo
que la cantidad añadida estuviera en el intervalo 0 - 50 % en peso de cristales.
Adicionalmente, para estudiar la influencia del tamaño del cristal, se tamizó el
azúcar refino utilizada, recogiendo dos fracciones, una con cristales de tamaño
comprendido entre 90 - 315 mm y otra con cristales de tamaño comprendido entre
500 - 710 mm.
Conociendo el papel protagónico de la dextrana en el incremento de viscosidad, se
estudiaron sistemas modélicos heterogéneos sacarosa - agua - dextrana 4
cristales, utilizando 1 % en peso de dextrana (MM = 7. 10 ) en la formulación.
Para preparar estos sistemas se sustituyó 1 % de sacarosa requerida para saturar
por el correspondiente 1 % de dextrana, de modo tal que el contenido de sólidos
totales disueltos no se alterara. En este proceder, se supone que la presencia de
la impureza no afecta el Brix de saturación, lo cual no es estrictamente cierto,
aunque por el bajo contenido de dextrana utilizado puede ser considerado así.
Las determinaciones reológicas fueron realizadas utilizando el impelente helicoidal,
dadas las limitaciones que presentan los cilindros concéntricos para estos
sistemas. Los resultados se presentan el las tablas 6 y 7, la primera para las
suspensiones sin dextrana y la segunda para aquellos sistemas que contienen
dextrana. En las tablas se reporta la media aritmética de las determinaciones
realizadas para los diferentes gradientes de velocidad, después de comprobar que
el comportamiento podía ser considerado newtoniano. Sólo para los sistemas con
50 % en peso de cristales, resulta más adecuado reportar un comportamiento
seudoplástico siguiendo la ley de potencia, con índice de flujo 0,983 e índice de
n
consistencia 0,316 Pa s , con un coeficiente de correlación 0.9981. No obstante la
consideración de fluido newtoniano es posible con un mayor error típico que en los
restantes casos.
Tabla 6 Viscosidad de suspensiones modélicas sin dextrana T= 313K
Contenido de cristales %
0.0
20.0
30.0
35.0
40.0
45.0
50.0
0.0
20.0
30.0
35.0
40.0
45.0
50.0
_ Pas para 90-315 mm
0.1187
0.1719
0.3066
0.4734
0.7086
1.2647
2.4572
0.1134
0.1749
0.2922
0.4796
0.7145
1.2984
2.4326
_ Pas para 500-710 mm
0.1187
0.1701
0.3090
0.4721
0.7285
1.2864
2.4885
0.1134
0.1780
0.2919
0.4801
0.7315
1.2800
2.4795
Tabla 7 Viscosidad de suspensiones modélicas con dextrana T = 313 K
Contenido de cristales %
0.0
20.0
30.0
35.0
40.0
45.0
50.0
0.0
20.0
30.0
35.0
40.0
45.0
50.0
_ Pas para 90-315 mm
0.1354
0.2038
0.3476
0.5704
0.8757
1.5479
2.9060
0.1421
0.2156
0.3593
0.5976
0.8931
1.5775
3.1653
_ Pas para 500-710 mm
0.1354
0.2063
0.3547
0.5821
0.9068
1.5924
3.0446
0.1421
0.2058
0.3586
0.5900
0.8864
1.6183
3.1275
Discusión de los resultados
Los resultados obtenidos para las soluciones saturadas puras a 313 K, 118,7 mPa
s y 113,4 mPa s, se corresponden con los obtenidos por Pour y Bates de 109,2
mPa s y 114,7 mPa s respectivamente, para soluciones saturadas a igual
temperatura, presentando como máximo un error relativo de 8,7 % y 3,5 %. (Pour,
1982; Bates, 1942).
Para las soluciones saturadas que contenían dextrana, se encontraron valores de
135,4 mPa s y 142,1 mPa s, inferiores al 157,4 mPa s reportado por Pour. El
máximo error relativo del 14 % puede explicarse al apreciar que en el trabajo del
investigador, a una solución de 70 Brix, correspondiente a la condición de
saturación a 313 K, se le adicionaba 1 % de dextrana, con lo que el contenido de
sólidos totales era mayor.
Para verificar la correspondencia de las determinaciones realizadas con las
reportadas por Pour, y considerando que este investigador había trabajado en un
Rheotest 2 de cilindros concéntricos, utilizando el sistema de medición S - S2, se
hicieron determinaciones en el Rheotest 2.1, usando también el sistema de
medición S - S2. Los resultados encontrados se presentan en la tabla 8. En ésta
también se presenta la comparación hecha para suspensiones utilizando los
cilindros concéntricos y el impelente helicoidal.
De la tabla es posible observar cómo el valor de viscosidad obtenido para las
soluciones saturadas haciendo uso del impelente helicoidal no difiere
significativamente del alcanzado al utilizar cilindros convencionales, tanto para las
soluciones puras como para las impuras.
Para las suspensiones de 50 % en peso de cristales se comprueba cómo el valor
de viscosidad obtenido al utilizar cilindros concéntricos se aleja más del 840 % del
encontrado al usar el impelente helicoidal, coincidiendo aproximadamente el valor
de viscosidad obtenido con el sistema de medición S - S2, con el alcanzado para el
impelente helicoidal al 30 % en peso de cristales. Adicionalmente , la inspección
ocular del cilindro permitió observar la deposición de cristales en el fondo del
cilindro exterior al terminar el experimento, de donde se comprobó que había
existido sedimentación de los cristales en suspensión que explican la gran
diferencia entre los valores de viscosidad encontrados.
Tabla 8 Comparación entre sistemas de medición.
cristales
% en peso _ Pas según _ Pas con
desviación
de cristales
literatura
cilindro S-S2
0.0
50.0
0.1092
-
0.1141
0.2595
0.0020
0.0380
Sistema sacarosa-agua_ Pas con
desviación
impelente
helicoidal
0.1187
0.0060
2.4326
0.1232
Sistema sacarosa-agua-dextrana
en peso de _ Pas según _ Pas con
desviación
cristales
literatura
cilindro S-S2
0.0
0.1578
0.1363
0.0027
_ Pas con
impelente
desviación
helicoidal
0.1354
0.0129
De lo anterior se comprueba que con el cilindro convencional no se logra mantener
en suspensión el contenido de cristales y por consiguiente la determinación
realizada no es válida.
La dependencia de la viscosidad con el tamaño de los cristales fue analizada
realizando pruebas de hipótesis para medias para los sistemas de iguales
contenidos de sólidos y temperatura y diferentes tamaños de cristales, esto es, los
comprendidos entre 90 - 315 mm y 500 - 710 mm. No se encontraron diferencias
significativas entre los valores medios de viscosidad para cada par de valores
comparados (para p = 0,05). Al no existir diferencias significativas se procedió a
realizar el ajuste estadístico de los juegos de datos obtenidos, considerados como
pertenecientes a la misma población.
El gráfico de valores de viscosidad contra % en peso de cristales presenta un
comportamiento exponencial.
Procesamiento de los resultados experimentales
Los resultados experimentales presentados en las tablas 6 y 7 se procesaron para
encontrar relaciones matemáticas entre la viscosidad y el contenido de cristales
(Q)obteniéndose las siguientes ecuaciones, utilizando el programa de regresión
lineal múltiple del sistema Statgraphics. En ellas hr representa la relación entre la
viscosidad en presencia de cristales y la viscosidad cuando no hay cristales
presentes, ambas a la misma temperatura, o sea mr =m con cristales / m sin
cristales.
Para el sistema sacarosa - agua - cristales:
2
2
ln h= -2,2336 + 0,00123 Q ln hr = -0,0796 + 0,00123 Q
Para el sistema sacarosa - agua - dextrana - cristales:
2
ln h = -2,0607 + 0,00124 Q
2
ln hr = -0,0831 + 0,00124 Q
Es de señalar cómo la presencia de dextrana aumenta el valor de viscosidad para
un contenido de cristales dado pero prácticamente no modifica la pendiente de la
2
recta ln h o ln hr vs Q .
Conclusiones parciales
Del resultado de los experimentos se concluye que:
1. La presencia de cristales de sacarosa aumenta la viscosidad en
comparación con la de las soluciones saturadas a igual temperatura, tanto
para soluciones puras como en presencia de dextrana.
2. La dependencia de la viscosidad y de la viscosidad relativa con el contenido
de cristales es explicada mediante modelos estadísticos del tipo: h = a exp (
2
2
b Q ) o hr= a exp ( b Q ) siendo a y b constantes.
3. El tamaño del cristal de sacarosa no influye en la viscosidad de los sistemas
estudiados, al menos hasta 710 mm.
4. El uso de cilindros concéntricos convencionales no es adecuado para la
determinación de la viscosidad de suspensiones en las que la tendencia a
la sedimentación se presenta.
5. Con el uso del impelente helicoidal se reproducen los valores obtenidos para
las soluciones saturadas al utilizar cilindros concéntricos, recomendándose
su uso frente a éstos para la determinación de la viscosidad en sistemas
heterogéneos.
Orientaciones para la realización del laboratorio.
El objetivo de la práctica es:
1. Determinar el comportamiento reológico de un fluido empleando un
viscosímetro rotacional.
2. Estudiar la dependencia de los parámetros reológicos con la temperatura.
Para la realización de la determinación Ud seleccionará un producto que
presuponga tenga un comportamiento no newtoniano. Puede auxiliarse de los
datos reportados en el apéndice del libro de texto básico para realizar la selección.
Colocará la muestra a evaluar en el sistema de medición que se adecue a su
producto. Para esto utilice las recomendaciones que el fabricante brinda en
relación con los intervalos de esfuerzos de corte para cada juego de cilindros de
medición. En caso de no tener idea deberá tantear cuál es el juego de cilindros
que mejores resultados le ofrece (esto es aquél con el que barre la escala
completa de lecturas) y recordar que entre varios que se puedan utilizar el que
mejor resultado brindará será el de menor espacio anular.
Utilice el control de temnperatura ya que como se le pide que estudie la
dependencia de los parámetros reológicos con la temperatura, deberá realizar el
estudio al menos a tres temperaturas diferentes.
Realice la medición de lectura en la escala para cada valor de velocidad de
rotación, en el sentido de incrementos sucesivos de velocidades de rotación y
luego en el sentido inverso. Con esto comprobará si su fluido presenta tixotropía.
En caso de presentarla, cambie el fluido para la determinación a una nueva
temperatura.
Para convertir los datos de lectura y velocidad de rotación en valores de esfuerzo
de corte y gradiente de velocidad, utilice la información que brinda el fabricante
acerca de la constante por la que debe afectar cada una. En función del espacio
anular seleccionado, analice si vale la pena realizar corrección para el valor de
gradiente de velocidad y haga este cálculo.
Ajuste un modelo matemático para los datos de esfuerzo de corte y gradiente de
velocidad que obtuvo y así encuentre los parámetros del modelo seleccionado a
cada temperatura.
Realice el ajuste de modelos para encontrar la dependencia de los parámetros
reológicos con la temperatura.
Calcule la viscosidad aparente y prepare un gráfico de viscosidad aparente vs
gradiente de velocidad a cada temperatura.
Extraiga sus conclusiones acerca del trabajo realizado.
Preguntas y problemas a solucionar por el alumno.
1. ¿Qué diferencia existe entre el perfil de velocidad en el interior de un
viscosímetro de tubo cuando se trabaja con un fluido newtoniano y cuando se
trabaja con un plástico de Bingham?
2. Para un viscosímetro rotacional de cilindros concéntricos, ¿cómo varía el
gradiente de cizallamiento en el cilindro interior y en el cilindro exterior al cambiar
la velocidad de rotación y el espacio anular? (Se sugiere la preparación de una
tabla con los resultados numéricos de gb y gc)
3. Compare la dependencia del gradiente de cizallamiento referido al cilindro
interior que rota con la velocidad de rotación y el espacio anular, para un fluido
seudoplástico y uno dilatante.
4. Construya el perfil de velocidad que se establece en un viscosímetro de cilindros
concéntricos para el que el cilindro interior rota y el exterior está fijo. Prepare este
perfil para diferentes a y n. ( Se sugiere el uso de la ecuación 3.169)
5. Estudiando el comportamiento reológico de una sopa de mazada con 7% de
cebada en la que luego de tres horas de cocción se alcanza un producto espeso
de consistencia cremosa en el que permanecen intactos granos de cebada de 4-5
mm de diámetro y 7-9 mm de longitud, se utilizó un viscosímetro de cilindros
concéntricos de espacio anular 1-2 mm. Los resultados obtenidos fueron (T cte)
rpm
lectura para gradientes en lectura para gradientes en
ascenso
descenso
3
6
18
54
162
486
6.8
7.9
9.5
11.8
14.9
19.6
5.3
6.9
8.8
11.2
14.3
-
Extraiga conclusiones acerca de este experimento y discútalos.
7. En una prueba para evaluar una mayonesa modificada a 30ºC, se realizaron
determinaciones con un viscosímetro rotacional Rotovisko Haake modelo RV3,
utilizando como cilindro y vaso el SV1. El fabricante reporta que la constante a
utilizar para transformar las lecturas en esfuerzo cortante es Z=11.28
2
dinas/cm .(Recuerde que s = Z * lectura)
-1
s
0.089
0.178
0.356
0.712
0.890
1.25
1.78
2.51
3.56
5.03
7.12
10.05
14.24
20.11
28.48
40.22
56.96
80.54
113
Lectura para gradientes Lectura para gradientes
en ascenso
en descenso
18.5
.
20.0
.
24.0
.
28.5
.
29.0
17.5
31.0
19.0
33.5
20.0
36.0
22.0
38.0
24.5
41.0
27.0
45.5
30.0
46.5
33.5
51.0
37.0
56.0
43.5
62.0
49.5
68.5
57.0
77.5
67.0
86.0
79.0
97.5
.
Caracterice el fluido y encuentre los parámetros reológicos. (Se le sugiere
represente los valores de s vs g para empezar la solución del problema).
• En caso de resultar el fluido tixotrópico reporte el % de tixotropía.
• Compare los resultados con los de una mayonesa patrón que sigue el modelo
n.
de Herschel-Bulkley con parámetros so = 83.2 Pa , n = 0.37, K= 39.0 Pa s
8. Se prepararon emulsiones de aceite de maíz en agua destilada (40%
volumen de aceite) utilizando como estabilizantes proteína de soya (0.5, 1,
2% p/p) y carboximetilcelulosa. Las determinaciones se realizaron en un
viscosímetro de cono y plato modelo Brookfield LVT usando dos conos :
cp41 (diámetro 4.8 cm y ángulo 3°) y cp52 (diámetro 2.4 cm y ángulo 3°)
(Los datos originales están reportados por B. Elizalde, A. Pilosof, G.
Bartholomai de la Facultad de Ciencias Exactas de la Universidad de
Buenos Aires y fueron utilizados para la preparación de este problema)
-1)
_ (s
0.031
0.063
0.126
0.314
0.629
1.258
3.144
6.288
0.5%
_ (Pa)
0.737
0.988
1.39
2.315
3.517
5.441
9.870
15.62
1%
_ (Pa)
0.953
1.254
1.743
2.888
4.399
6.852
12.591
20.161
2%
_ (Pa)
3.503
4.222
5.210
7.108
9.180
12.030
17.503
23.480
Determine:
• Comportamiento del fluido
• Modelo de ajuste con p<0.1
-1
• Viscosidad aparente a 12 s
8. Para precisar el comportamiento encontrado en el problema anterior los autores
determinaron el comportamiento reológico de las dispersiones de proteína de soya
de 0.5, 1 y 2% (p/p) utilizando el viscosímetro de cono y plato pero con el cono
cp40 (diámetro 4.8cm, ángulo 0.8°). Los datos primarios encontrados se presentan
en la tabla.
-1)
_ (s
0.012
0.031
0.063
0.126
0.314
0.629
1.258
6
3)
M*10 (Pa m
0.666
1.158
1.852
2.895
5.240
8.251
12.970
6
3)
M*10 (Pa m
2.779
4.661
6.977
10.335
17.399
25.881
38.416
6
M*10 (Pa m
6.021
9.727
14.156
20.439
33.137
47.912
69.190
3)
Determine:
• Comportamiento reológico
• Modelo de ajuste con p<0.1
• Compare con los resultados del problema anterior.
9. En el estudio de caldos de fermentación de Micromonospora purpurea se utilizó
un viscosímetro de mezcla con impelente tipo "vane" con las siguientes
-3
características: k'= 8.7,. dvane=0.0375 m Cvane= 5.7496* 10 Nm, donde ésta es
la constante que permite transformar la lectura en valor de torque, según M =
lectura*Cvane/100 Nm, y g = k' W.
Los datos obtenidos fueron:
-1
Lectura
9.0
9.5
9.8
11.3
11.8
13.4
16.7
19.1
_s
0.0083
0.0167
0.0417
0.0833
0.1667
0.3333
0.8333
1.6667
-3
Sabiendo que para fluidos que cumplen la ley de potencia s = 2p k' M / c dvane
(Kemblowski y Kristiansen, Biotechnology and Bioengineering, Vol 28, p 14741483, 1986) donde c es una constante que depende de la geometría del sistema y
que toma el valor de 224 para este dispositivo, calcule los parámetros reológicos
del cultivo.
9. Para estudiar la reología de las masas cocidas (suspensión de cristales de
sacarosa en miel) obtenidas en el proceso de fabricación de azúcar, J N
Ness utilizó un viscosímetro de conducto. Los datos primarios obtenidos
son de DP y de V (velocidad del flujo). Las dimensiones del conducto
son:17.04 mm de diámetro y 401 mm de longitud. Se utilizaron dos masas
cocidas de las siguientes composiciones:
Muestra
A
B
%
reductores
7.56
7.75
% sacarosa
63.9
63.8
Muestra A:
_P (Pa)
377.08
V (m/s)
2.392*10
818.88
6.090*10
1146.42
9.135*10
1879.57
1.410*10
2355.47
2.175*10
-3
-3
-3
-3
-3
Muestra B
_P (Pa)
324.58
V (m/s)
1.087*10
644.51
2.392*10
1452.92
6.090*10
2067.42
9.135*10
3354.66
1.414*10
-3
-3
-3
-3
-3
%
sólidos
% pureza
secos
91.1
70.1
92.2
69.1
% en peso
de cristales
34
38
Determine:
• Los parámetros reológicos según la ley de potencia.
• Comente los resultados.
CAPÍTULO 5. VISCOELASTICIDAD
LECCIÓN 21. CONCEPTOS BÁSICOS
Analicemos el siguiente experimento que nos conducirá a conocer el
comportamiento viscoelástico. Al mezclar harina de trigo y agua en proporciones
adecuadas, se obtendrá una masa de la que se puede preparar una tira cortándola
con tijeras. Si se estira la tira por sus extremos, se alargará y parecerá que fluye.
Al dejar libre los extremos se contraerá, aunque sin recuperar la longitud inicial. O
sea, ha exhibido también el carácter de elasticidad de un sólido. La masa es
viscoelástica. En los productos viscoelásticos, las propiedades elásticas y viscosas
se manifiestan simultáneamente a diferencia de lo que pasa con un fluido plástico,
en el que a tensiones bajas el comportamiento es elástico y a altas tensiones,
viscoso, al vencerse el so.
Las características de los productos viscoelásticos varían desde las de líquidos
viscosos con propiedades elásticas a las de sólidos con propiedades viscosas. La
elasticidad de los alimentos viscoelásticos se debe a la deformación elástica de las
macromoléculas. Estas características elásticas se favorecen si los materiales
están constituidos por moléculas de cadena larga cuyos enlaces puedan rotar
libremente, si ofrecen fuerzas intermoleculares débiles, y si poseen en unos
cuantos puntos de la cadena molecular, fuertes enlaces cruzados intermoleculares.
Con esto el resultado es una red tridimensional. Es frecuente en los alimentos que
la recuperación luego de una deformación, sea sólo parcial al desintegrarse la red
tridimensionl elástica por efecto de la tensión. Mientras más completa y resistente
sea esta red mayor la viscoelasticidad. Cuanto más fácilmente se desintegre la
red, mayor el comportamiento viscoso.
En flujo estacionario el fluido viscoelástico presenta esfuerzos normales que
caracterizan la elasticidad. Las medidas para estado no estacionario proporcionan
métodos dinámicos para evaluar la viscoelasticidad y pueden realizarse en modo
transiente y oscilatorio.
Estudie las páginas 16-19 del texto básico. En ellas encontrará 4 de los principales
comportamientos característicos de los cuerpos viscoelásticos: el efecto
Weissenberg, el efecto de hinchamiento a la salida, el efecto sifón y el efecto de
retroceso. En las figuras 1.10 y 1.11 se comparan algunos de estos efectos para
los fluidos newtonianos y viscoelásticos.
Estudie el epígrafe 1.8, páginas 47 - 49 del texto básico. Conocerá que:
• En una prueba de fluencia (creep test) el material se somete a esfuerzo
cortante y se mide la deformación en el tiempo g=f(t). Se grafica la
capacitancia de fluencia por cizalla (shear creep compliance) J = f(t) = g /s ,
contra el tiempo.
• En una prueba de relajación del esfuerzo (relaxation stress) se aplica una
deformación y se mide el esfuerzo en el tiempo s(t). Se presentan los datos
como el módulo de relajación del esfuerzo de cizalla G = f(t) = s/g contra el
tiempo.
• Se aclara que ambas pruebas pueden realizarse en cizalla, compresión o
tensión, por lo que se especifica cómo se hicieron.
• Las pruebas oscilatorias (en general sinusoidales) se aplican también. La
magnitud y el tiempo de retraso para la transmisión dependen de la
naturaleza de la sustancia. El desfase es mayor para sustancias altamente
viscosas y pequeño en materias muy elásticos.
Estudie el epígrafe 5.1, páginas 294 - 297 del texto básico y al concluir conocerá
que:
• Los experimentos de deformación en la categoría de transiente pueden ser de
cinco tipos y aparecen resumidos en la tabla 5.1.
• Los experimentos utilizando técnicas oscilatorias permiten determinar los
parámetros fundamentales que caracterizan estos productos y que
aparecen reflejados en la tabla 5.2.
• El comportamiento viscoelástico puede ser lineal o no lineal. En la zona lineal,
las funciones que se recogen en la tabla 5.2 no dependen de la magnitud
del esfuerzo, de la deformación o de la velocidad de aplicación de la
deformación. La zona no lineal, asociada a grandes deformaciones, no es
muy importante en los estudios de alimentos.
A continuación, para facilitar el estudio, aparecen algunas definiciones de términos
que serán de uso común en este tema. Han sido tomadas del Glosario de términos
reológicos para alimentos, publicado por CYTED en 1996.
Amortiguador (dashpot): Elemento analógico que representa al flujo viscoso ideal.
Consiste en un émbolo que se mueve en un cilindro lleno de un líquido
newtoniano.
Angulo de pérdida o de desfase(loss or phase angle): La diferencia de fase entre
las variables dependiente e independiente de un sistema oscilatorio. Por ejemplo
entre el esfuerzo y la deformación.
Capacitancia (compliance): Cociente entre la deformación y su correspondiente
esfuerzo. Es el inverso del módulo de elasticidad.
Capacitancia compleja (compex compliance): Expresión matemática de una
capacitancia considerada como la suma de un parte real y una imaginaria.
Capacitancia de almacenamiento (storage compliance): Cociente entre la parte de
la deformación en fase con el esfuerzo y el esfuerzo, en condiciones sinusoidales.
Parte real de la capacitancia compleja.
Capacitancia de pérdida (loss compliance) Cociente entre la parte de la
deformación en desfase con el esfuerzo y el esfuerzo, en condiciones sinusoidales.
Parte imaginaria de la capacitancia compleja.
Deformación (strain): Medida de la deformación respecto a la dimensión de
referencia (longitud, área o volumen).
Efecto de Barus (die swell, hinchamiento a la salida): Aumento de volumen de un
material viscoelástico que se produce a la salida de un orificio.
Efecto de Weissenberg (Weissenberg effect): Efecto que se manifiesta durante el
flujo de fluidos viscoelásticos como subida de un fluido por una varilla que está
girando dentro de él.
Fluencia (creep):Deformación de un material viscoelástico medida en función del
tiempo a esfuerzo constante.
Función de relajación (relaxation function): Función que caracteriza la variación del
esfuerzo con el tiempo en un sistema sometido previamente a una deformación
constante.
Modelo de Kelvin (Kelvin model): Representación del comportamiento viscoelástico
por medio de un resorte y de un amortiguador en paralelo.
Modelo de Maxwell (Maxwell model): Representación del comportamiento
viscoelástico por medio de un resorte y de un amortiguador en serie.
Módulo (modulus): Razón entre un componente del tensor esfuerzo y un
componente del tensor deformación.
Módulo complejo o dinámico(complex modulus): En reología oscilatoria es la
representación matemática de un módulo considerado como la suma de la parte
real y la imaginaria.
Módulo de almacenamiento (storage modulus): Parte real del módulo
complejo.Está relacionada con la energía almacenada por un material.
Módulo de cizallamento ( shear modulus) Cociente entre el esfuerzo de cizalla y la
deformación elástica correspondiente.
Módulo de elasticidad ( modulus of elasticity): Cociente entre el esfuerzo y la
deformación elástica. Es el recíproco de la capacitancia.
Módulo de pérdida (loss modulus): Parte imaginaria del módulo complejo. Está
relacionada con la energía disipada.
Punto de fluencia (yield point): Punto en la curva esfuerzo vs deformación o
esfuerzo vs velocidad de deformación, que corresponde a la transición desde la
deformación elástica a la plástica. Se le denomina también punto de fluencia
superior.
Punto de fluencia inferior (lower yield point): Punto en que la curva de esfuerzos de
cizalla frente a velocidad de deformación se cruza con el eje de esfuerzos.
Recuperación (recovery): Regreso a una condición reológica previa, observable al
retirar el estímulo aplicado.
Relajación del esfuerzo (stress relaxation): Disminución del esfuerzo con el tiempo
en un material deformado.
Resilencia (resilience) Energía almacenada elásticamente por unidad de volumen.
Sobreesfuerzo (overshoot) Crecimiento transitorio del esfuerzo por encima de su
valor de equilibrio a velocidad de deformación constante.
Tiempo de relajación (relaxation time): Tiempo necesario para que en un modelo
de Maxwell, el esfuerzo disminuya a 1/e de su valor inicial bajo deformación
constante.
Tiempo de retardo ( ratardation time): Tiempo necesario para que en un modelo de
Kelvin, la deformación disminuya a 1/e de su valor original después de retirar el
esfuerzo.
Viscoelasticidad lineal (linear viscoelasticity): Viscoelasticidad caracterizada por
una relación lineal del esfuerzo con la deformación y su derivada respecto al
tiempo.
Viscosidad compleja (complex viscosity): En ensayos oscilatorios es la expresión
matemática de la viscosidad como la suma de una parte real y una imaginaria. La
parte real es la viscosidad dinámica y la parte imaginara está relacionada con la
parte real del módulo complejo.
LECCIÓN 22. MODELOS VISCOELÁSTICOS
Estudie el epígrafe 5.2.1, página 298 del texto básico en el que se describen las
analogías de Maxwell y Kelvin.
A continuación amplíe lo estudiado leyendo lo siguiente:
El modelo viscoelástico más simple puede representarse por un muelle y un
recipiente lleno de un líquido newtoniano, con un émbolo que se mueve en sentido
ascendente y descendente y que se pueden acoplar en serie o en paralelo.
Acoplados en serie representan esencialmente al líquido viscoelástico ideal y se
llama Modelo de Maxwell; acoplados en paralelo, representan esencialmente al
sólido y se denomiuna Modelo de Kelvin. Si ambos modelos se acoplan en serie se
origina el Modelo de Burgers.
Modelo de Maxwell
• Al estar constituido por un muelle y un amortiguador en serie, al aplicar una
fuerza, el muelle se deformará de inmediato y el amortiguador lo hará
lentamente. Al retirar la fuerza el muelle se contrae pero el líquido
permanece inalterable.
• El líquido en el amortiguador tiene un coeficiente de viscosidad y el muelle
tiene tres módulos G, E y K (revisar el capítulo 1). Si se puede considerar el
modelo incompresible, K=0 y si es isotrópico G=1/3 E.
• A tensión constante, el muelle se alargará de inmediato hasta alcanzar la
deformación correspondiente a ese esfuerzo. Luego la deformación
dependerá de la viscosidad m.
• Los dos elementos soportan la misma tensión y el alargamiento total es la
suma de los alargamientos de cada elemento.
Modelo de Kelvin
• Al estar constituido por un muelle y un amortiguador en paralelo, el
alargamiento límite, tras un tiempo largo, depende de la magnitud de la
fuerza aplicada y se recupera totalmente cuando la carga cesa.
• Al aplicar la carga, se produce una deformación creciente tanto por el muelle
como por el amortiguador. Cuando la fuerza cesa, el muelle acorta
lentamente al líquido en el amortiguador, lo que da origen al fenómeno de
elasticidad retardada. O sea se asemeja a la recuparación retardada de una
deformación elástica. Teóricamente la recuperación total tardaría un tiempo
infinito.
• Ambos elementos experimentan igual deformación relativa y la tensión total es
la suma de las tensiones de cada elemento, el muelle y el amortiguador.
• El comportamiento límite, tras haber transcurrido un tiempo largo, es el sólido
de Hooke.
Modelo de Burgers
• Al modelo de Kelvin se le adiciona en serie el de Maxwell. Si representamos al
modelo de Kelvin por H1 (Hooke) y N1 (newtoniano) y al de Maxwell por H2
y N2, al aplicar la fuerza el muelle H2 se deformará instantáneamente y
ésta es la elasticidad instantánea. A H1 le corresponderá la elasticidad
retardada.
• Transcurrido un período de tiempo largo, la deformación se deberá sólo a N2.
• Al retirar la carga, H2 determina la recuperación instantánea y el modelo de
Kelvin será el responsable de la recuperación retardada.
• La elasticidad total es la suma de la recuperación instantánea y la retardada.
LECCIÓN 23. DETERMINACIONES DE VISCOELASTICIDAD
En flujo estacionario, los fluidos viscoelásticos exhiben esfuerzos normales. Las
diferencias entre los esfuerzos normales se calculan por las ecuaciones:
2
2
2
2
Y1 = s 11 - s 22 / g = N1 / g
Y2 = s 22 - s 33 / g = N2 / g ; recordando que se puede considerar que N2 = 0.
Del tema 1 recordemos cómo N1/s12 se conoce como deformación elástica
recuperable.
Las diferencias entre los esfuerzos se pueden medir en un reómetro rotacional que
fabrican algunas compañías y que evalúan la fuerza axial. Revise las páginas 171
y 172, en particular la ecuación 3.57 que permite el cálculo de N1 a partir de la
fuerza axial medida en un viscosímetro de cono y plato, demostrando cómo N1
aumenta con el gradiente de cizallamiento g para el fluido viscoelástico.
A continuación se describen los cuatro métodos de determinación más utilizados
en los estudios de viscoelasticidad, aunque posteriormente deberán estudiar éstos
por el texto básico.
Determinación oscilatoria.
Imaginemos un líquido de Maxwell fluyendo a lo largo de un viscosímetro de tubo
capilar. Si las condiciones de flujo son constantes, las capas de líquido adquieren
una deformación constante debido a la compomente elástica y el flujo se debe sólo
al comportamiento viscoso. Al aplicar repetidamente efectos alternos de tensiones
o deformaciones, como por ejemplo colocar un líquido entre el cono y el plato de
un viscosímetro y en lugar de ponerlo a rotar, poner a oscilar el cono, se obtiene
una onda sinusoidal de entrada al representar la amplitud del movimiento del cono
contra el tiempo. Si se representa la oscilación del plato como variable de salida,
se observa una respuesta similar pero desfasada o retardada y además
amortiguada en relación con la onda de la entrada. Basándose en estos dos
efectos, se pueden determinar las propiedades viscosas y elásticas. Observe que
estas mediciones son en condiciones dinámicas, y son características de una
determinada frecuencia de oscilación.
Experimentos de carga - descarga.
Es el principio utilizado para la determinación viscoelástica de las masas de harina
de trigo en el extensómetro. Se estira la muestra mediante la aplicación de un peso
y se mide el incremento de longitud. Al cabo del tiempo el hilo a través del que se
aplicó la carga se quema, quedando libre la masa, la que se contrae. La gráfica de
deformación contra tiempo presentará un incremento de la deformación a medida
que la carga se aplica y luego una recuperación de la longitud inicial, también en
función del tiempo pero disminuyendo la deformación, cuando la carga cesó. La
variable más común a representar en la ordenada es la capacitancia, o sea la
deformación relativa entre la tensión en cualquier momento del experimento.
Cuando se obtienen gráficas de deformación en función del tiempo a diferentes
tensiones y se encuentran linealmente relacionadas, se dice que el
comportamiento es lineal. (La ecuación que relaciona la deformación y la tensión y
sus derivadas aparecen sólo a la potencia 1). Los modelos de Maxwell y Kelvin
son lineales.
Método de la relajación bajo tensión.
Se ha demostrado que la tensión interna se relaja, si se deforma y mantiene a
deformación relativa constante, un modelo de Maxwell. En un experimento de este
tipo, se deforma bruscamente la muestra y se registra cómo va disminuyendo la
tensión en el tiempo. Se pueden usar viscosímetros de cilindros concéntricos o
diferentes extensómetros. El valor más importante a determinar es el tiempo de
relajación (h / G) . Si se representa el logaritmo de la tensión contra el tiempo y se
obtiene una recta, el comportamiento es maxweliano y el tiempo de relajación es la
pendiente de la recta. Si no es recta, aparecerá un espectro de tiempos de
relajación y se determina un tiempode relajación medio.
Componente normal de la tensión.
Si se hace girar una varilla dentro de un líquido newtoniano, el movimiento circular
origina un torbellino alrededor de la varilla. En un líquido viscoelástico esto no
sucede, sino que el líquido "trepa" por la varilla. Este es el efecto Weissenberg
observado en la leche condensada almacenada por largo tiempo, en el extracto de
malta y en la masa de harina de trigo. Queda definido este efecto como una fuerza
centrípeta que se produce durante la deformación rotacional. Se mide por un
reogoniómetro, que es en esencia un viscosímetro de cono y plato en el que se
mide la fuerza ejercida hacia arriba sobre el cono, pudiéndose medir las fuerzas
torsionales y verticales y con ello caracterizar el producto.
Estudie el epígrafe 5.2, páginas 297 - 312, en el que se describen con profundidad
los experimentos para la determinación de viscoelasticidad en condiciones
transientes. En estos experimentos se opera con valores de deformación
pequeños y todos los explicados han sido aplicados en alimentos.
Estudie el epígrafe 5.2.2 en el que se describe el experimento de relajación del
esfuerzo. Una deformación se aplica y se sigue el esfuerzo necesario para
mantener la deformación en el tiempo. Observe la figura 5.2 en que se muestran
las curvas que se obtendrían si el experimento se hiciera con un material elástico
ideal, un sólido viscoelástico, un líquido viscoelástico y un material viscoso ideal.
Deberá precisar que:
• Los materiales viscoelásticos presentan una relajación gradual y el punto final
dependerá de la naturaleza de la sustancia, alcanzándose un valor de
equilibrio no 0 para sólidos viscoelásticos
• Los datos se presentan en función del módulo de relajación G = f(t)= s / g
constante.
• El modelo de Maxwell ha sido utilizado para interpretar los datos de estos
experimentos para líquidos viscoelásticos, llegando a la ecuación : s + lrel (
ds /dt) = m g. En esta ecuación lrel = m / G.
• El tiempo de relajación se puede interpretar como el que toma a una
macromolécula estirarse cuando es deformada.
• En la tabla 5.4 se aprecia que los valores del tiempo de relajación cambian
mucho en dependencia del material.
• La ecuación 5.10 permite representar la relajación del esfuerzo luego de
aplicada una deformación por cizalla go para un modelo de Maxwell. De
ella se puede determinar el tiempo de relajación. s = so exp (-t/lrel).
• Un modelo más general presenta la combinación en paralelo de un modelo de
Maxwell y un resorte. La condición de equilibrio (se = go Go) será
representada por el resorte libre en paralelo, quedando s =se + (so - se)
exp (-t / l rel).
• También se pueden representar los resultados normalizados según: so t / (so
- s) = k1 + k2 t. La tabla 5.5 muestras valores determinados para las
constantes de ajuste del modelo lineal k1 y k2.
Estudie los problemas 5.8.1 y 5.8.2, páginas 341 - 343 del texto básico.
El primero aplica la ecuación 5.11 y el segundo la 5.14 para determinar el tiempo
de relajación. Para ambos problemas los datos primarios son de tiempo contra
esfuerzo (en este caso de compresión) a temperatura constante.
Estudie el epígrafe 5.2.3, páginas 304 -310 del texto básico. Al concluir conocerá
que:
• En el ensayo de fluencia se aplica un esfuerzo instantáneo y se sigue el
cambio de la deformación en el tiempo.
• La figura 5.5 presenta lo que sucedería si el fluido fuera un material elástico
ideal (no flujo, recuperación total al cesar el esfuerzo), un líquido ideal (flujo
estacionario, no recuperación) y un viscoelástico (flujo y recuperación
parcial al cesar el esfuerzo). Esa recuperación es lo que se conoce como
efecto de retroceso (recoil).
• Los datos pueden reportarse en términos de capacitancia J = f(t) = g/ sconst.
-1
• Se repesenta por un modelo de Kelvin para el que: G
(dg/dt).
(ds/dt) = g + lret
• La relación de g vs t es: g = (so/G) [1 - exp (-t/ lret)], donde so es el esfuerzo
constante aplicado. Esta ecuación predice una deformación que se
aproxima asintóticamente a so/G, siendo el tiempo de retardación el
necesario para que se alcance el 63% del valor final.
• Cuando el ajuste no es bueno con este modelo, se utiliza el de Burgers.
Según éste, expresado en términos de capacitancia de fluencia J = J0 + J1
[ 1 - exp (-t/ l ret)] + t/ mo.
Estudie el ejemplo 5.8.3, páginas 343 - 348 del texto básico, en el que se estiman
los parámetros del modelo de Burgers.
• Los datos primarios son de tiempo vs capacitancia de fluencia.
• Se grafica ( J - J0) vs t. De los últimos puntos se determinan, por la pendiente
y el intercepto, los valores de mo y J1.
• De los primeros puntos se calcula el tiempo de retardación al graficar ln [1- (J-
J0)/J1] vs t.
Estudie el epígrafe 5.2.4, páginas 310 - 312 del texto básico. En él se presentan
los ensayos de sobreesfuerzo (stress overshoot). Conocerá que:
• Se impone un gradiente de cizallamiento a un fluido viscoelástico previamente
en reposo. La respuesta es de un sobreesfuerzo antes de alcanzar el valor
de esfuerzo en estado estacionario.
• El comportamiento se ha modelado por la ecuación empírica de Bird-Leider en
función del tiempo y del gradiente de cizallamiento aplicado. El modelo
predice el pico inicial de esfuerzo. correspondiente a la respuesta elástica, y
a altos tiempos, el comportamiento viscoso, por la ley de potencia.
Estudie los epígrafes 5.3 y 5.4, páginas 312 - 332, en el que se presentan los
ensayos oscilatorios, los más comunes métodos dinámicos para estudiar
viscoelasticidad
• Pueden ser desarrollados en cizalla, tensión o compresión. Los instrumentos
comerciales típicos operan en cizalla. Pueden encontrarse aquellos en que
la deformación se fija y se mide el esfuerzo, y aquellos en que la amplitud
del esfuerzo se fija y se mide la deformación. La función oscilatoria es en
general la sinusoidal.
• Si se aplica una función sinusoidal de deformación g= go sen (wt), se
obtendrá un valor de gradiente de cizallamiento g= go w cos (wt), y una
repuesta de esfuerzo, s =so sen (wt + d), donde d es el ángulo de desfase.
• La respuesta del esfuerzo a una deformación sinusoidal puede representarse
por una ecuación como: s =G'g+(G''/w)g en la que G' es el módulo de
almacenamiento y G'' es el módulo de pérdida .
• G' = (s0 /g0) cos d. De aquí que: G'g0 pueda interpretarse como la
componente del esfuerzo en fase con la deformación.
• G'' = (s0/g0) sin d. De aquí que: G''g0 puede interptrtarse como la
componente del esfuerzo desfasada 90° de la deformación.
• Las ecuaciones 5.38 a 5. 44 definen otras relaciones entre módulos,
capacitancias, viscosidades que deben ser interpretadas.
• Una excelente ecuación para representar el comportamiento de estos
materiales viscoelásticos es s = G' g + h' g, donde el primer sumando es la
componente elástica y el segundo la viscosa.
• La tangente del ángulo de desfase (o tangente de delta) = G''/G' se relaciona
directamente con la energía perdida por ciclo dividida entre la energía
almacenada por ciclo.
• Cuando el material es un sólido de Hooke el esfuerzo y la deformación están
en fase y d es 0, no existiendo G'' ni h', por no haber disipación viscosa. G'
es constante e igual al módulo de cizallamiento G.
• Cuando el material es un líquido newtoniano, el esfuerzo y la deformación se
desfasan 90° y G' y h'' son 0 y el material no almacena energía. h' será
constante e igual a m. Para un líquido newtoniano el valor de d es 1.573
rad. (p/2).
• Los instrumentos comerciales operan de varias maneras. Se puede lograr
barrer los valores de esfuerzo o de deformación cambiando la amplitud de
la señal de entrada a frecuencia constante. Otra manera es cambiar las
frecuencias manteniendo la amplitud de la señal constante. En general los
materiales exhiben mayores características de sólidos a altas frecuencias.
• Para someter líquidos y semisólidos a ensayos oscilatorios se utilizan
dispositivos de platos paralelos, de cono y plato y de cilindros rotatorios.
• Las determinaciones pueden reportarse a una única frecuencia graficando la
variable medida en el tiempo, obteniendo así la respuesta sinusoidal de
salida, o reportarse los valores para el barrido de frecuencias. (figura 5.14)
• En la figura 5.8 y la tabla 5.7, página 325, puede apreciar la diferencia de
comportamiento entre una solución diluida (con comportamiento
newtoniano), un gel (comportamiento elástico) y una solución concentrada
(comportamiento viscoelástico). Compare los valores de d y vea cómo los
bajos valores son indicativos de elasticidad. De igual forma, si la frecuencia
y la amplitud de deformación son iguales, g, G', G", h' y h " son menores
para la solución diluida (newtoniana) y mayores para el gel (elástico).
• Las figuras 5.21, 5.22 y 5.23 representan la variación con la frecuencia de los
módulos de almacenamiento y de pérdidas para los tres materiales
anteriores.Para comportamiento de fluido viscoso, G'' > G', pero se
aproximan a medida que la frecuencia aumenta. Para comportamiento
elástico G' > G'' en todo el intervalo de frecuencias. Los valores de ambos
módulos en función de la frecuencia pueden representarse por una ley de
potencia. Observe cómo para la solución concentrada, a bajas frecuencias
el valor de d es alto, similar al de la solución diluida, tendiendo a un
comportamiento parecido a un líquido y a medida que aumenta la
frecuencia, se acerca al valor presentado por el gel, tendiendo al
comportamiento de un sólido.
Analice los datos para un polímero de silicona presentados en la figura 5.25.
De ellos verá que:
• Si el material se considera un fluido de Maxwell, para calcular el tiempo de
relajación se pueden utilizar los valores del gráfico h' o G vs w. El valor de h
se determina leyendo el valor de h' de la extrapolación para w = 0. El valor
de G se determina leyendo el valor de G' de la extrapolación para w
tendiendo a infinito. Así lrel = h/G.
• Además, para un frecuencia dada, leyendo los valores de G' y h' para esa
frecuencia, se cumplirá que: s = G'g + h'g .
Estudie el epígrafe 5.7, página 338 - 340. En él se presentan relaciones entre las
funciones viscosas y las de la viscoelasticidad lineal, a partir de la realización de
ensayos oscilatorios.
• Cuando la frecuencia y el gradiente de cizallamiento son iguales, la viscosidad
compleja es igual a la viscosidad en estado estacionario. Esta es la regla de
Cox-Merz
• Una extensión de esta regla plantea que al graficar la viscosidad compleja
contra gow el gráfico es equivalente a graficar la viscosidad aparente contra
el gradiente de cizallamiento. gow se define como gradiente de
cizallamiento efectivo. La equivalencia entre viscosidades complejas y
estacionarias se ha encontrado en un amplio intervalo, para suspensiones
concentradas con esfuerzo de fluencia.
LECCIÓN 24. EJEMPLOS DE APLICACIÓN
De manera general, la sangre coagulada y la nata se aproximan al modelo de
Maxwell, mientras que los geles de gelatina se aproximan al de Kelvin. Los
helados, fideos cocidos, la masa de harina de trigo, el queso, las espumas de
proteínas, se aproximan al modelo de Burgers.
Lea el experimento de Michaud que se describe a continuación. (Tomado de H
Muller: Introducción a la reología de los alimentos, Ed Acribia 1992).
Se conectan dos matraces a través de un capilar fino y se llenan con una
disolución diluida de agar. Un día después, la solución líquida en los matraces está
equilibrada y es idéntica la altura en ambos matraces. Se introduce en uno de los
matraces una varilla de vidrio que desplaza una pequeña cantidad de líquido y
hace subir el nivel en ese matraz. Si el líquido fuera newtoniano se establecería de
inmediato un flujo de líquido de uno a otro para restablecer la igualdad de nivel. La
disolución de agar ofrece resistencia al flujo y para que el flujo ocurra se requiere
la aplicación de una fuerza finita aunque sea muy pequeña. En esto sigue un
comportamiento similar al modelo de Kelvin. Si la disolución se calienta por encima
de la temperatura a la que funde el agar concentrado este efecto de resistencia a
fluir no se produce.
En el caso de los geles de gelatina (coloides hidrófilos que poseen una red
tridimensional de moléculas) se puede lograr en experimentos cortos, que se
comporten como sólidos elásticos, pudiendo determinarse su módulo de rigidez o
de cizalladura por el siguiente método (Método de Saunders y Ward): Se coloca el
producto en un recipiente en forma de tubo a temperatura controlada y se deja que
el producto gelifique. El tubo termina en un capilar en U lleno de mercurio. Se
aplica por el otro extremo abierto del sistema una presión de aire y se mide la
deformación en volumen causada por la presión, basándose en el ascenso del
4
2
mercurio en el capilar. Así G = DP r1 / 8 L r2 h, donde r1 es el radio del
recipiente, r2 el radio del capilar, L la altura del gel y h el desplazamiento del
mercurio en el capilar. Los geles de gelatina son casi hookianos. En experimentos
prolongados se acentúa el comportamiento viscoso.
Las masas de harina de trigo son unos de los productos alimenticios con
comportamiento reológico más complejo.
Muchas de las determinaciones que se realizan con ellas son aún empíricas. Entre
ellos está el sistema Brabender, que utiliza un amasador registrador, el farinógrafo.
Se coloca en el plato de mezcla la harina y se le añade agua con una bureta y se
va amasando a 30°C, al tiempo que se registra automáticamente la consistencia
de la masa. Cuando se alcanza el valor de 500 unidades empíricas se detiene el
mezclador. El agua descargada de la bureta es la que incorporó la harina. Se
repite el ensayo pero añadiendo de una vez el agua antes medida, obteniendo la
gráfica de amasado, característica para cada harina.
El sistema Brabender utiliza también un extensógrafo. Este aparato forma un
cilindro de masa conteniendo un poco de sal y el agua determinada en el
farinógrafo y tras 45 minutos de reposo a 30°C estira la masa hasta romperla. Se
obtiene una gráfica de carga-alargamiento típica de la harina utilizada.
Con las masas se han utilizados técnicas fundamentales, no empíricas, como las
oscilatorias, de carga y descarga y de relajación del esfuerzo, con buenos
resultados para el trabajo de investigación. Para uso industrial no resultan
satisfactorias por lo laboriosas, prefiriéndose los métodos empíricos, ya que
aunque no se sepa qué es lo que se mide, permite la comparación y por tanto, la
realización del control de calidad.
A continuación se presentan datos tomados en experimentos con masa de harina
de trigo reportando la deformación como deformación relativa [DL / (L+DL)].
(Tomados de H. Muller: Introducción a la reología de los alimentos, Ed Acribia,
1992). Se le sugiere que confeccione el gráfico de deformación relativa contra
tiempo a esfuerzo constante.
2
N/m
1140
t (min)
0
2
4
5.5
6
8
10
DL / (L+DL)
0.15
0.45
0.56
0.58
0.55
0.54
0.54
s N/m
570
2
t (min)
0
2
4
5.5
6
8
10
DL / (L+DL)
0.06
0.15
0.20
0.22
0.20
0.18
0.18
Al representar los datos anteriores se puede plantear que la masa se adecua al
modelo de Burgers, (aunque realmente requiere de otros elementos modificadores,
hasta el número de 12, para un mejor ajuste).
El gluten ha sido utilizado como mejorador de la harina de trigo. (Tomado de A
Saiz y colaboradores Revista Alimentaria, No 280, marzo, 1997, pag 83-87). Las
principales proteínas componentes del gluten son las gluteninas y las gliadinas.
Las primeras se relacionan con la elasticidad y producen una masa compacta y
elástica por deshidratación. Las segundas se relacionan con la extensibilidad y dan
origen a una masa fluida y viscosa por deshidratación, extensible y poco elástica, y
responsable del volumen del pan. Estas propiedades dependen de la formación de
puentes disulfuros. Durante el amasado, las partículas de harina se entrecruzan
formando una fase continua y cohesionada. A mayor contenido de grupos -SH y SS, mayor consistencia de la masa.
Para evaluar el comportamiento se utilizó un farinógrafo de Brabender en el que se
coloca una masa fija de muestra a la que se agrega agua para obtener
consistencia de 500 unidades y determinar la capacidad de absorción de agua.
Durante el amasado posterior se midió la elasticidad y las modificaciones de
consistencia.
Los resultados se muestran a continuación:
Absorción
de agua ml
Consistenci
a unidades
Brabender
Tiempo de
desarrollo
min
Elasticidad
0%gluten
2% gluten
10% gluten
20% gluten
30% gluten
63
63.8
66.8
73
79
500
532
653
900
1140
1.9
2
2.5
4
5.5
80
70
80
100
105
La consistencia y la elasticidad de la harina aumentan con la adición de gluten. La
elasticidad aumenta hasta aproximadamente el 15% de gluten agregado,
permaneciendo luego casi constante. No obstante estos resultados, los aspectos
organolépticos limitan la adición al 6% de gluten (migas oscuras, tamaño de
alveólos grandes, distribución no homogénea, resultando gomoso y no agradable).
Estudie el ejemplo 5.8.4, página 348 -349 del texto básico. En este ejemplo se
realizan diversos gráficos para pruebas oscilatorias.
• A partir de los datos de la figura 5.22 se ajusta la ley de potencia para G' y G''
en función de w.
• Conocidas éstas se puede encontrar h', h'', tan d, G* y h*.
• Observe cómo en el gráfico log-log, todas son rectas excepto la relación de G*
y h* con la frecuencia.
Lea el ejemplo que se desarrolla a continuación preparado a partir de los
experimentos realizados por J. Franco, A. Guerrero y C. Gallegos (Grasas y
aceites, Vol 46 Fasc 2, 1995, p 108-114) para describir la viscoelasticidad de
emulsiones de aceite en agua del tipo salsa fina. Las emulsiones se prepararon
utilizando un estearato de sacarosa (HLB =15) como emulsionante y aceite de
girasol y contenían además yema de huevo como emulsionante. Las
concentraciones fueron de 3 -10 % para el estearato de sacarosa y de 45 - 55 %
para el aceite y la temperatura 25°C. Las mediciones de cizalla oscilatoria se
realizaron en un reómetro Bohlin CS-50, utilizando el sistema sensor cono-plato
(4°, 40 mm).
Los valores de los módulos de almacenamiento y de pérdidas se presentan en
función de la frecuencia, para diferentes valores de % de aceite y de % de
estearato de sacarosa.
Para 45% aceite y 5% estearato de sacarosa
-1
ws
0.01
G' (Pa)
G''(Pa)
2
4.8 *10
3.0 * 102
0.1
1.2 *10
6.0 * 10
1
2.0 *10
8.2 * 10
10
3.0 *10
9.0 * 10
100
4.0 *10
1.3 * 10
3
3
3
3
2
2
2
3
Para 55% aceite y 5% estearato de sacarosa
-1
ws
0.01
G' (Pa)
G''(Pa)
2
9.0 *10
4.8 * 102
0.1
1.5 *10
9.0 * 10
1
3.2 *10
1.2 * 10
10
5.0 *10
1.2 * 10
3
3
3
2
3
3
100
3
6.0 *10
3
2.0 * 10
Para 50% de aceite y 3% de estearato de sacarosa
-1
ws
0.01
G' (Pa)
G''(Pa)
2
2.0 *10
1.5 * 102
0.1
3.5 *10
2.0 * 10
1
7.0 *10
3.0 * 10
10
1.0 *10
4.0 * 10
100
1.7 *10
7.0 * 10
2
2
3
3
2
2
2
2
Se sugiere que realicen la representación de los valores anteriores. En todos los
casos se observa una variación similar de los módulos con la frecuencia,
destacándose una zona de prácticamente pendiente 0 para el módulo de pérdida.
Se observa cómo:
• A igual concentración de aceite una mayor concentración de estearato de
sacarosa produce un aumento en ambos módulos, aunque el incremento es
cada vez menor conforme aumenta la concentración.
• A igual concentración de estearato de sacarosa, una mayor concentración de
aceite produce un aumento en ambos módulos, o sea un aumento en las
funciones viscoelásticas, de donde la variación en el contenido de aceite no
parece afectar la formación del entramado tridimensional.
• La componente elástica es mayor que la viscosa.
• Se presenta una zona prácticamente constante en G'' para concentraciones
de estearato de sacarosa mayores que 3%. La aparición de una zona
prácticamente constante en G'' ha sido relacionada en la reología de
polímeros con la existencia de entrelazamientos entre cadenas poliméricas,
por lo que para las emulsiones se puede asociar con la existencia de
entrelazamiento entre gotas, lo que conduce a una floculación extensiva.
• El aumento cada vez menor de las funciones G' y G'' con la concentración de
emulsionante puede explicarse por la saturación de la interfase por la
presencia cada vez mayor del emulsionante. Dada la baja solubilidad del
estearato en agua, éste tenderá a situarse en la interfase aceite/agua,
provocando un desplazamiento de las proteínas hacia el medio continuo.
Las proteínas del medio continuo pueden favorecer los entrelazamientos
entre los flóculos creando una estructura más resistente, aumentando el
intervalo de viscoelasticidad lineal.
Preguntas y problemas a solucionar por el alumno
1. Justifique la siguiente afirmación: " En pruebas oscilatorias un pequeño
desfasaje se corresponde con un material elástico".
2. Interprete la figura 5.2 a la luz de la estructura del material.
3.¿Cuál de los dos fluidos tendrá mayor carácter elástico a 40°C: la pasta de
tomate o el relleno de pastel de fresa? (Utilice los datos del apéndice 6 del libro de
texto básico).
4. Basándose en la ecuación 5.47, demuestre que para un fluido viscoso ideal la
curva log G' vs log w tendrá pendiente 2 mientras que para uno elástico ideal la
pendiente tenderá a 0.
6. Se obtuvieron los siguientes datos en ensayos a esfuerzo constante para una
salsa para ensaladas. Las experiencias se realizaron a un valor de so= 2.28 Pa, y
3°C.
-1
t (s)
t (s)
0
0.1
0.2
0.4
0.6
2
3
4
0.000164
0.000200
0.000236
0.000307
0.000376
0.000837
0.001145
0.001443
J (Pa ) para la t (s)
salsa regular
20
0.005927
30
0.008705
40
0.01148
50
0.01426
60
0.01703
90
0.02537
180
0.05037
240
0.06704
5
0.001734
300
0.08370
10
0.003146
400
0.11148
Determine los parámetros del modelo de Burgers.
6. A partir de los datos oscilatorios para la mantequilla reportados por Rohm y
Weidinger se presenta el siguiente problema:
w rad/s
0.001
0.005
0.01
0.05
0.1
0.5
1
5
10
50
T= 5°C
1.073E9
2.147E8
1.070E8
2.149E7
1.075E7
2.144E6
1.073E6
2.148E5
1.070E5
2.145E4
T=10°C
3.501E8
7.002E7
3.500E7
7.000E6
3.505E6
7.008E5
3.503E5
7.006E4
3.509E4
7.002E3
T=20°C
3.505E7
7.008E6
3.501E6
7.002E5
3.506E5
7.009E4
3.499E4
7.001E3
3.495E3
7.009E2
T=5°C
1.268E6
1.694E6
1.919E6
2.564E6
2.904E6
3.880E6
4.396E6
5.873E6
6.653E6
8.889E6
T=10°C
4.425E5
5.738E5
6.411E5
8.294E5
9.267E5
1.199E6
1.339E6
1.733E6
1.936E6
2.505E6
T=20°C
4.688E4
6.163E4
6.340E4
9.116E4
1.025E5
1.348E5
1.517E5
1.994E5
2.244E5
2.950E5
Encuentre los parámetros de ajuste de la relación entre viscosidad dinámica y frecuencia y
entre módulo de almacenamiento y frecuencia para cada temperatura.
• Encuentre un modelo que relacione la dependencia de la viscosidad dinámica y
del módulo de almacenamiento con la temperatura.
• Calcule el valor de frecuencia para la que tan d =1.
• Evalúe la viscosidad compleja y el módulo complejo para la frecuencia de 30
rad/s
7. En estudios con gliadina (agua añadida hasta alcanzar un 25% de humedad), H.
Madeka y J. Kokini (Journal of Food Eng.Vol 22, 1994; p. 241-252) utilizaron un
reómetro de platos paralelos (diámetro de plato 20 mm, distancia 2 mm) para la
realización de ensayos oscilatorios de pequeña amplitud para determinar G' y
G'' en el intervalo de temperatura 50 - 160°C. La deformación aplicada fue 0.5 1.0 % y la frecuencia seleccionada 6.28 rad/s.
Viscosidad dinámica (Pa s)....Módulo de almacenamiento (Pa)
T °C
G' (Pa)
G'' (Pa)
50
2.5 E4
2.5 E4
60
1.5 E4
1.5 E4
70
1.1 E4
1.1 E4
80
2.8 E4
2.3 E4
90
7.0 E4
3.8 E4
100
1.4 E5
4.2 E4
115
4.0 E5
3.8 E4
125
3.9 E5
7.0 E4
135
2.8 E5
1.1 E5
150
1.1 E5
3.8 E4
Interprete la dependencia de G' y G'' con T en términos estructurales.
• Calcule la viscosidad compleja a w=6.28 rad/s ; T = 115°C y T = 135°C .
Compare los resultados.
8. En ensayos para determinar G' y G'' en función de la frecuencia, H. Madeka y J.
Kokini (Journal of Food Eng.Vol 22, 1994; p. 241-252) obtuvieron los siguientes
resultados para gliadina al 25%:
w (rad/s)
0.1
1
T = 50°C
G' (Pa)
4000
10000
T = 50°C
G'' (Pa)
3000
10000
T = 100°C
G' (Pa)
400000
600000
T = 100 °C
G'' (Pa)
100000
60000
a. Construya la curva de viscosidad compleja vs frecuencia.
b. Determine la pendiente de la curva log G' vs log w y defina a qué temperatura
hay un mayor comportamiento elástico.
LECCIÓN 25. ACLARACIÓN DE LA IMPORTANCIA DE PARÁMETROS
REOLÓGICOS EN FENÓMENOS DE TRANSPORTE E INTRODUCCIÓN
Aclaración general
El Capítulo 4 utiliza en toda su extensión, los conocimientos de Fenómenos de
Transporte, estudiados con anterioridad. Para el estudio de este tema deberá
hacer uso del contenido de este material y cuando presente alguna duda en el
planteamiento de las ecuaciones básicas, deberá repasar los contenidos de la
asignatura Fenómenos de Transporte, utilizando para ello el texto de dicha
asignatura. No obstante, la consulta del clásico de la materia, Transport
Phenomena de Bird, Stewart y Lightfoot, será de gran utilidad.
Introducción
En el procesamiento de alimentos son comunes las operaciones unitarias de flujo
de fluidos, transferencia de masa, transferencia de calor, así como operaciones
particulares de separación. En estas operaciones juegan un papel importante las
propiedades reológicas y para el diseño y operación de los equipos del proceso, se
necesita del conocimiento de esfuerzos, tensiones, gradientes de velocidad, etc.
Datos seguros para sistemas muy bien caracterizados han sido utilizados, junto a
los fundamentos teóricos, para desarrollar modelos predictivos de propiedades de
estas sustancias, y a partir de ellos de otras sustancias puras y de sus mezclas.
El transporte de masa, energía y momentum a través de un fluido es consecuencia
del movimiento molecular y de las interacciones moleculares. A niveles
macroscópicos, asociado con el transporte de cada uno hay un coeficiente de
transporte X de modo que el flux J de cada variable es proporcional al gradiente de
una variable de estado Y. O sea J = - X ÑY.
Los tres coeficientes de transporte principales son : viscosidad, conductividad
térmica y coeficiente de difusión másico.
En este tema se estudiarán cinco casos típicos: el flujo isotérmico en tuberías
circulares, el cálculo de pérdidas por fricción, la caída de presión en válvulas, el
efecto de la viscosidad en la transferencia de calor y el efecto de la viscosidad en
la transferencia de masa.
CAPÍTULO 6. PARÁMETROS REOLOÓGICOS EN FENÓMENOS DE
TRANSPORTE
LECCIÓN 26. FLUJO ISOTÉRMICO EN TUBERÍAS CIRCULARES
En la industria de alimentos, es frecuente encontrar fluidos de viscosidad media y
alta, de donde el trabajo en flujo laminar no es extraño.
Perfiles de velocidad y flujo volumétrico para el flujo en un conducto circular.
Analicemos cómo evaluar el perfil de velocidad y el flujo volumétrico en un
conducto circular como el mostrado en la figura 2.4, página 98 del texto básico.
Tendremos una coordenada radial, representada por r y una axial representada
por z.
Ecuaciones que describen perfiles de velocidad pueden utilizarse para analizar la
influencia de diversos modelos reológicos en la distribución de velocidades y para
determinar la distribución de tiempos de residencia de las partículas.
Para el flujo de un fluido en una tubería circular de radio R, el perfil de velocidad se
establece de:
uz= ò (-duz/dr) dr
3
3
2
El flujo volumétrico Q = (p R / sw ) ò srz (-du/dr) d srz
siendo s rz =sw r/R = - (r/2) (dP/dz)
En la expresión para el cálculo de Q se puede sustituir (-duz/dr) por expresiones
de diferentes modelos reológicos, encontrando la relación de Q y DP, siendo DP la
caída de presión.
Por ejemplo para un fluido que cumpla la ley de Newton:
2
2
uz= ( DP/4mL) [R - r ]
La ecuación que expresa la velocidad en el eje z permite comprobar que el perfil
de velocidad es parabólico para un flujo laminar, incompresible.
2
La velocidad máxima se encuentra para r = 0 siendo: uzmax= (DPR /4mL)
Puede definirse una velocidad promedio calculada a partir de la suma de todas las
velocidades en una sección transversal entre el área de la sección transversal
2
siendo: <uz>= (DPR /8mL). Observe cómo <uz> = uzmax/2
El valor del flujo volumétrico se calcula de:
3
Q = (p R / 4) ( sw/m)
Aquí sw es el esfuerzo en la pared, y sustituyendo su valor DPR/2L
4
Q = (p R DP /8m L) Ecuación de Hagen - Poiseuille.
Observe cómo por estar elevado el radio a la cuarta potencia, su influencia en el
valor de Q será grande.
Por otra parte, observe cómo si se grafica srz vs r se obtendrá una línea recta
siendo:
srz = 0 para r=0 ; srz = sw para r=R .
Si el fluido cumple la ley de potencia se llega a:
uz = [n/(n+1)] ( DP/2KL)
1/n
[R
uzmax= [n/(n+1)] ( DP/2KL)
(n+1)/n
<uz> = R
(n+1)/n
1/n
[R
-r
(n+1)/n
(n+1)/n
[n / (3n+1)] ( DP /2LK)
]
]
1/n
De aquí se aprecia cómo a medida que n sea menor el perfil de velocidad será
más plano y menores las diferencias entre las partículas de fluido más lentas y
más rápidas.
Al calcular la relación uzmax / <uz> = (3n+1) / (n+1), de donde se aprecia el efecto
de n en el perfil obtenido. (Figura 2.5, página 104 del texto básico).
La ecuación para evaluar el flujo volumétrico es:
3
Q = p R [n / (3n+1)] ( sw/K)
1/n
Como sw es el esfuerzo en la pared, se obtiene:
(3n+1)/n
Q=pR
[n / (3n+1)] ( DP /2LK)
1/n
Para un fluido que cumpla el modelo de Bingham: Desde el centro del cilindro,
hasta un valor de Ro = 2 so L / DP, obtendremos un perfil de velocidad constante,
cuya velocidad será la máxima.
2
2
uzmax = DP R /4 hpl L [ (1 - Ro /R ) ]
Fuera de dicha zona, o sea para R0 < r < R
2
2
uz = 1/hpl { (DP/4L) [R - r ] - s0 (R-r)}
2
4
<uz> = ( DP R / 8L hpl) [1 - 1.75 so/sw + 1/3 (so/sw) ]
Si se calcula la relación uzmax / <uz>se obtiene: (figura 2.6, página 106 del texto
básico)
2
4
uzmax / <uz>= [2(1-2c+2cr/R- (r/R) )] /[1-1.75c+c /3]
De aquí se aprecia que a medida que el esfuerzo de fluencia aumenta, el radio de
la zona de velocidad constante aumenta y el perfil de velocidad es más plano.
El cálculo del flujo volumétrico arroja:
3
4
Q = (p R sw/ 4 hpl) [1 - 1.75 so/sw + 1/3 (so/sw) ]
4
4
Q = (p DP R / 8L hpl) [1 - 1.75 so/sw + 1/3 (so/sw) ] Ecuación de BuckinghamReinier
Aquí hpl es la viscosidad plástica, sw es el esfuerzo en la pared y so es el esfuerzo
de fluencia.
Cuando se desea calcular la caída de presión con un fluido plástico, la solución de
la ecuación de Buckingham - Reinier no es directa. El error por omitir el término
elevado a la cuarta potencia es del 6% cuando so/sw = 0.5 y del 1.8% cuando
so/sw= 0.4.
De las ecuaciones hasta aquí estudiadas se aprecia que:
• Existe una relación entre el flujo volumétrico Q y el radio del conducto R. A
mayor radio del conducto el flujo volumétrico será mayor.
• Para un fluido seudoplástico, la caída de presión por unidad de longitud DP / L
se relaciona con el flujo volumétrico y el radio del conducto según: DP/L a Q
n
/R
3n + 1
.
• Si se incrementa el radio R, en el fluido seudoplástico la modificación del
gradiente de presión será menor que en un fluido newtoniano, para igual
valor de Q. Observe que para un fluido seudoplástico de n = 0.2 se cumplirá
que DP/L a Q
4
0.2
/R
1.6
, mientras que para un fluido newtoniano DP/L a Q /R
.
Ejemplos.
Estudie el ejemplo 2.12.1 páginas 141 - 143 del texto básico analizando la
aplicación de las ecuaciones básicas de transferencia de momentum para el flujo
de fluidos por un conducto circular.
Estudie el siguiente ejercicio:
Por un conducto circular horizontal de 0.3 m de longitud y 0.025 m de diámetro
interior fluye glicerina a 26°C. ¿Qué caída de presión se producirá para un flujo
3
volumétrico de 0.019 m /s?. Se conoce que la glicerina se comporta como un fluido
3
newtoniano de viscosidad 490 mPas y que su densidad es 1261 kg/ m .
Solución:
4)
3
4
DP = (8QLm)/(pR = (8 * 0.019m /s* 0.3m* 0.490Pas) / (3.14* (0.0127m) )=
273537 Pa =0.27MPa
Puede comprobarse el carácter laminar calculando:
2
3
3
NRe= ruzD/m= rQD/(mpR ) = 1261kg/ m * 0.019m /s* 0.0254m/( 490Pas* 3.1416*
2
(0.0127m) ) = 2.45.
Perfiles de velocidad y flujo volumétrico para el flujo a través del espacio
anular entre dos cilindros concéntricos.
Si un fluido incompresible newtoniano fluye en estado estacionario en régimen
laminar por la región anular de dos cilindros concéntricos de radios aR (cilindro
exterior) y R(cilindro interior) y de longitud L, se cumplirá que:
2
srz = (DP R /2L) { (r/R)- [(1-a )/(2 ln (1/a))] R/r}
2
2
2
uz = (DP R /4 mL) {[1- (r/R) + [(1-a )/( ln (1/a))] ln (r/R)}
La velocidad máxima ocurrirá para un valor de radio entre R y aR que llamaremos
lR, de donde:
2
2
2
uzmax = (DP R /4 mL) {1- [(1-a )/(2 ln (1/a))][ 1 - ln (1-a )/(2 ln (1/a))]}
La velocidad promedio será:
2
4
2
2
<uz>= (DP R /8mL) { (1-a )/(1-a ) - (1-a )/( ln (1/a))}
Observe que si a = 0 el problema se reduce al flujo en tuberías circulares.
Por otra parte el flujo volumétrico se calcula como:
2
2
4
4
2 2
Q = p R (1-a ) <uz> = (pDP R /8mL) { (1-a ) - (1-a ) /( ln (1/a))}
Si representa los perfiles en función del radio encontrará que:
• El perfil de velocidad presenta un máximo en la región anular a una distancia
lR del centro del conducto.
• El perfil de esfuerzos toma el valor 0 en lR. En este caso el perfil no es una
línea recta, sino una curva con valores negativos y positivos, pasando por el
valor 0 en el centro del sistema de cilindros concéntricos.
Cuando el fluido es no newtoniano se han realizado múltiples trabajos con el fin de
solucionar las ecuaciones a que se llega a partir de las ecuaciones de
conservación de momentum. Para la solución se realizan simplificaciones, dada la
complejidad matemática de las mismas. Trabajos como los de Fredrickson y Bird,
Vaughn y colaboradores, constituyen clásicos del tema y más recientemente, los
realizados por Filip y colaboradores y Tuoc y Mc Given, continúan en la búsqueda
de soluciones más completas.
Fredrickson y Bird parten de las ecuaciones de continuidad y movimiento: dr/dt
+(Ñ.ru) = 0
r [du/dt + ( u.Ñ)u] = -ÑP - ( Ñ.s) + rg
La expresión de las ecuaciones anteriores en coordenadas cilíndricas y la
aplicación de las restricciones (flujo incompresible, laminar, estacionario, efectos
terminales despreciables) conduce a:
2
srz = DP( r - (lR) /r)/2 siendo l una constante que brinda la posición radial
(r=lR)para la que srz=0. Esta ecuación constituye el punto de partida de los
autores para encontrar la solución para los modelos de Bingham y la ley de
potencia.
Si el fluido cumple el modelo de Bingham se reportan tres perfiles de velocidad:
En esta deducción los autores llaman :
• R : radio del cilindro exterior
• kR: radio del cilindro interior
• T= 2srz /DPR; To =2s0 /DPR
2
• f = (2 hpl / DPR ) uz
• y = r/R
2
2
2
f- = - To(y - k) -0.5 (y -k ) + l ln y/k ; k< y< lfo= f- = f+ ; l-<l<l+
2
2
f+ = - To(1 - y) -0.5 (1- y ) + l ln y ; l+< y< 1
Para calcular el valor de l se igualan las velocidades antes y después de l, o sea:
2
2l+ (l+ - To) ln (( l+ - To)/(l+k)) - 1 + (To + k ) + 2To (1 - l+) =0
La solución de esta ecuación es presentada de forma gráfica por los autores.
(Industrial and Engineering Chemistry Vol. 50 No. 3 1958).
El flujo volumétrico se calcula de:
4
4
2
3
3
Q= (p DP R / 8 hpl) [(1-k ) - 2l+(l+ - To) (1-k )-1.75 (1+k ) To + 1/3 (2l+-To) To]
Esta expresión es válida para To < (1 - k) y no existirá flujo si To > (1-k). Los
4
resultados se presentan en forma gráfica en el artículo expresando W=Q/(p DP R /
8 hpl) vs k y To.
2
2
Para calcular la velocidad promedio <uz> = Q /pR (1-k )
Para altos Q, la ecuación se simplifica y se cumple que: (ecuación modificada del
original siguiendo una fe de erratas posterior.)
4
4
2 2
3
2
3/2
Q= (p DP R / 8 hpl) [(1-k ) - ((1-k ) /ln(1/k))-1.75 (1+k ) To + 8/3 ((1-k )/2ln(1/k))
To]
Cuando estamos en presencia de un ánulo muy estrecho (k cercano a1)
4
3
3
Q= (p DP R / 6 hpl) (1-k) [1- 3/2 To/(1-k) + 0.5 (To/(1-k)) ]
Algunos datos típicos del modelo son: (Precisar de las definiciones que To:
esfuerzo de fluencia adimensional; fo: velocidad máxima adimensional; W: flujo
volumétrico adimensional)
0.1
0.4
To=0.
1
l
0.507
0.724
To=0.
1
fo
0.182
0.064
To=0.
1
W
0.483
0.154
0.7
0.895
0.010
0.016
k
To=0.
1
W/To
4.825
1.541
0.160
0
To=0.
3
l
0.607
0.827
To
=0.3
fo
0.105
0.023
To
=0.3
W
0.307
0.065
To=0.
3
W/To
1.023
0.215
1.000
0
0
0
De aquí se aprecia cómo el tamaño del espacio anular afecta los valores del perfil
de esfuerzos, modificando el valor de radio para el que el esfuerzo de corte es 0.
También resultan afectados los valores de velocidad y de flujo volumétrico.
Ejemplo:
Analice el siguiente ejemplo resuelto.
3
Un material de densidad 1690 kg/m fluye a 1.52m/s de velocidad promedio a
través del ánulo formado entre una tubería de 0.021m de diámetro y otra de 0.0526
m de diámetro. Las constantes del modelo de Bingham son so= 25.17 Pa y
hpl=0.0279 Pas. Calcule la caída de presión por unidad de longitud requerida.
Solución:
Dimensiones del ánulo k= 0.021/0.0526=0.40; R=0.0263m
2
2
2
-3
3
Flujo volumétrico Q = pR (1-k )<uz>= 3.14*(0.0263) (1-0.16) 1.52=2.77* 10 m /s
3
La cantidad W/To = 4 hpl Q / p R
3
3
-
so = 4 *0.0279 * 2.77* 10
/3.14*(0.0263) *25.17= 0. 215
De la tabla anterior se lee que para k=0.4 el valor de W/To=0.215 corresponde a
una To = 0.3.
Por lo anterior DP/L= 2* so / (To*R)= 2*25.17/(0.3*0.0263) = 6380 Pa/m
Paa fluidos que cumplan la ley de potencia la solución de la ecuación que permite
calcular el flujo volumétrico a que arriban Fredickson y Bird es:
3
s
Q = p R (DPR/2K) W(s,k) en la que s = 1/n y la función W(s,k) se presenta en
forma de tabla.
Para que se pueda apreciar la dependencia de los parámetros con s y k se
presentan valores calculados.
umax/<u>
k=0.1
1.567
1.419
1.280
1.140
s
1
2
4
10
k=0.4
1.514
1.350
1.217
1.106
k=0.7
1.504
1.337
1.205
1.000
k=0.1
0.464
0.419
0.379
0.344
k=0.4
0.677
0.666
0.654
0.643
k=0.7
0.846
0.843
0.841
0.839
Observe cómo el valor de umax/<u> tiende a un valor constante a medida que k
aumenta, o sea cómo el valor máximo y el promedio se aproximan.
Para el caso de ánulos muy estrechos, la ecuación toma la forma de:
3
s
s+2
Q = (p R /(s+2)) (DPR/2K) (1-k)
Vaughn y Bergman (IEC Process design and development Vol 5 No 1, 1966)
presentan un método para el que usan una función esfuerzo en la pared del
2
cilindro exterir swo = (DP R / 4L) (1-l ) y la grafican contra una función modificada
3
2
del flujo 32Q/ (pR (1-k )) utilizando en la solución el valor de l de Fredrickson y
Bird.
Tuoc y Mc Given (Trans I Chem E Vol 72 Part A Set 1994) propusieron una
ecuación válida para 0.417<k<0.83 que no requiere de un modelo reológico
particular y es una aproximación de la ecuación de Rabinowitsch-Mooney.
David y Filip(Fluid Dynamic Research, Vol 14 , 1994) propusieron, a partir del
trabajo de Fredrickson y Bird, un método que elimina el cálculo del parámetro l o
sea la posición del máximo de velocidad. El método se basa en una solución de
cuasisimilaridad que permite transformar la solución individual para cada k de la
relación DP vs Q en una ecuación cuasigeneral a partir de la relación entre la
solución para una condición dada y la condición para n tendiendo a infinito. Con
posterioridad (Journal of Petroleum Science and Engineering, Vol 16, 1996)
presentaron la solución que se presenta en el siguiente ejemplo.
Ejemplo:
Estudie el siguiente ejemplo en que se utiliza el método de Davis y Filip.
Para el flujo de un fluido por un ánulo se conoce que:
0.22
R= 0.2032m; k = 0.405; n=0.22; DP/L = 97 Pa/m; K = 3.1 Pa s . Calcule el flujo
volumétrico.
Solución:
Como se aprecia de los datos el fluido cumple el modelo de la ley de potencia y es
un fluido seudoplástico.
El método consiste en:
1. Aplicación de los parámetros geométricos. Calcular un flujo volumétrico
normalizado:
2
2
Q norm (k,1)= [(1+k)/(1-k)] [ (1+k )/(1-k ) + 1/ lnk] válido para n tendiendo a 1.
0.9k3/8
Q norm (k,0)= 1/2 [ 1 + (3 Qnorm(k,1) - 2)
] válida para n=0
Así Q norm (k,1)=0.6755 y Q norm (k,0)= 0.5487.
2. Aplicación de los parámetros reológicos. Calcular un flujo volumétrico
normalizado:
Q norm (k,n)= [1/ (1+2n)] [(1-n) Q norm (k,0) +3nQ norm (k,1)]
Así Q norm (k,n)= 0.6068
3. Aplicación de parámetros cinemáticos y reológicos. Calcular el flujo volumétrico
por el ánulo:
3
Q = [(pR n)/(1+3n)] (1-k)
2+1/n
3
1/n
(1+k) Q norm (k,n) (DPR/2KL)
Q= 0.01911 m /s
Perfiles de velocidad y flujo volumétrico para el flujo en un impelente de
tornillo helicoidal con tubo de descarga. (Desarrollado en la tesis doctoral de
la autora de esta guía )
Un caso interesante se presenta cuando tenemos un sistema formado por: un
impelente helicoidal que rota dentro de un cilindro de radio rt, el cual está rodeado
de otro cilindro de radio R . El movimiento ascendente del fluido en el espacio
entre el eje del impelente y el cilindro de radio rt tiene dos componentes, una axial
y una radial. Cuando el fluido llega a la parte superior pasa hacia el espacio anular
comprendido entre rt y R con un flujo axial descendente.
Desarrollo del modelo teórico
Las ecuaciones que describen el flujo de un fluido incompresible e isotérmico son
la de continuidad y la de cantidad de movimiento:
( Ñ. u ) = 0 ......................................................................................(1)
r {d u / d t + ( u . Ñ ) u } = -Ñ p - (Ñ . s) + r g ..................................(2)
En coordenadas cilíndricas el campo de velocidades puede expresarse como:
( u r , u q , u z ) = ( 0, r w (r) , v (r) ) .................................................(3)
Cuando el sistema se encuentra en estado estacionario y el flujo es laminar, las
componentes de velocidad axial y tangencial pueden expresarse como:
m v¢( r) = a r + b / r .......................................................................(4)
2
m r w ¢( r ) = - M1 / 2 p r ..............................................................(5)
siendo m la viscosidad y M1 el momento por unidad de longitud ejercido en el
cilindro interior de radio r, v¢( r)=dv/dr y w ¢( r )= dw /dr.
Como quiera que la viscosidad del fluido depende en general del gradiente de
velocidad y que éste presenta dos componentes, una axial y otra tangencial, se
puede suponer que :
2
2
0.5
g = ( ( r w¢) )+ v¢ ) ................................................................ (6)
donde g es el gradiente de velocidad local.
Si el fluido cumple la ley de potencia:
n-1
m = K ( g ) .................................................................................(7)
Combinando las ecuaciones (4) y (5) se obtiene:
2
2
v¢ = - 2 p ( a r + b ) r w¢/ M1 ......................................................(8)
Combinando las ecuaciones (4), (5), (6) , (7) y (8) se obtiene que:
w¢= - ( M1/ 2 p K )
1/n
r
-(1+2/n)
f
1-(1/n)
2 2
(r,a,b ) ........................(9)
2
2
2 -0.5
donde: f( r, a , b ) = ( 1 +( 4 p r / M1 ) ( a r + b) ) ....... (10)
Puesto que para una geometría compleja como la que presenta el tornillo helicoidal
la solución matemática es difícil, se necesita introducir el concepto de radio
equivalente, definido como el radio de un cilindro interior en un sistema de cilindros
concéntricos que cumpla la condición de que el gradiente de deformación en la
superficie del cilindro interior equivalente sea igual al gradiente de deformación
promedio dentro del tubo de descarga. Este radio, denominado re, permite la
evaluación de los parámetros a y b a partir de las condiciones de contorno.
Si se considera que no existe efecto de deslizamiento, las condiciones de contorno
entre el cilindro de radio equivalente y el tubo central son:
v(re) = 0; v(rt) = 0 ...........................................................................(11)
w(re) = W; w(rt) = 0........................................................................ (12)
donde W es la velocidad angular a la cual rota el tornillo helicoidal, mientras el tubo
central permanece fijo.
Al integrar (9) bajo las condiciones de contorno declaradas en (11) y (12) se
obtiene:
1/n
-(1+2/n)
(1-1/n)
W = ( M1 / 2 p K ) ò r
f
(r,a,b) dr ....................(13)
La ecuación anterior permite relacionar la velocidad de rotación con el torque por
unidad de longitud, conocidos a y b, realizando la integración de forma definida
entre re y rt.
La evaluación de los parámetros a y b puede realizarse conociendo el flujo axial. Al
ser el sistema estacionario, el caudal por la corona externa, esto es, entre el tubo
de descarga y la cuba cilíndrica, es igual al caudal en el espacio comprendido
entre el eje del tornillo y el tubo de descarga.
Como quiera que la corona externa es un ánulo entre dos cilindros concéntricos
por el cual circula un fluido no newtoniano, su evaluación puede realizarse a partir
de las ecuaciones presentadas por Fredrickon y Bird para un fluido no newtoniano
que cumpla la ley de potencia.
1/n
v(r) = R (P R / 2 K)
2
ò (l / q - q )
2
1/n
dq ; k < q < l .....................(14)
1/n
v(r) = R ( P R/ 2 K)1/n ò( q - l / q ) dq; l < q < 1 .......................(15)
donde: q = r/R es la distancia radial adimensional ;l es la distancia radial
adimensional para la cual, en el ánulo, srz = 0 ; k = rt / R ; P= (po - pL) / L + r gz
Las condiciones de contorno que permiten integrar las ecuaciones (14) y (15) son:
v(rt) = 0 y v(R) = 0 equivalente a v = 0 para los valores de q= k y q = 1.
Las ecuaciones (14) y (15) deben arrojar idénticos valores de velocidad axial para
q= l por lo que se ha de cumplir que:
2
ò( l / q - q )
1/n
2
1/n
dq = ò (q- l / q ) .................................................(16)
La ecuación anterior permite evaluar l en función de la geometría del sistema y del
índice de flujo n al integrar de forma definida, en el lado izquierdo de la igualdad
entre k y l y en el lado derecho entre l y 1.
Al sustituir las ecuaciones (14) y (15) en la definición del flujo volumétrico se
obtiene:
2
Q = 2 p R òv(r) q dq
3
1/n
2
2 1/n+1
-1/n
Q = p R ( P R / 2 K ) ò |l - q |
q
dq .........................(17)
la cual puede integrarse entre k y 1, una vez conocida l a partir de la ecuación (16).
Si se combinan las ecuaciones (5), (6), (7),(8) y (9) e integrando de acuerdo a (11)
se obtiene, integrando definidamente entre re y rt:
(1-2/n)
òr
2
(a r + b ) f
(1-1/n)
(r, a, b )dr = 0 ......................................(18)
2
mientras que la condición de flujo axial p ò r v'(r) dr + Q = 0 se convierte en:
(3 - 2/n)
2
(1-1/n)
1/n
2
òr
(ar +b)f
(r, a, b) dr + (2 p K / M1) M Q / 2 p ......(19)
El par de ecuaciones no lineales (18) y (19), integradas entre re y rt, determinan
los valores de a y b que serán utilizados para resolver la ecuación (13) y encontrar
la dependencia de W y M1.
Para la determinación de los parámetros reológicos Ky n, los datos experimentales
obtenidos ( W y M1) para cada fluido se ajustan, utilizando un método de regresión
no lineal basado en el algoritmo de Marquardt en el que la función a minimizar es:
2
2
c = S [ W exp - W ec13 ] i ................................................................. (20)
La estrategia de solución se resume en que a partir de un juego de valores
aproximados de K y n se evalúa l ( ecuación 16) utilizando el método de Newton y
la regla de Simpson. Con ello puede evaluarse el flujo volumétrico Q (ecuación 17).
Seguidamente se evalúan los parámetros a y b ( ecuaciones 18 y 19) utilizando
una modificación del algoritmo de Marquardt. Finalmente se calcula W (ecuación
13) y se compara con el valor obtenido experimentalmente, repitiendo el
procedimiento iterativo hasta que se alcance la convergencia, encontrando los
valores de K y n del fluido en cuestión.
Cálculo generalizado de la caída de presión.
Para fuidos independientes del tiempo en flujo laminar se desarrolló la siguiente
ecuación generalizada.
3 n'
DP R /2L = K' (4Q /pR )
3
donde n' = d (ln sw) / d ln G ; G= (4Q /pR )
Los valores de K' y n' se determinan del gráfico de los resultados experimentales
de sw vs G en coordenadas logarítmicas. En la mayoría de los casos sus valores
no son constantes, sino que varían con G.
n'
Se define un NRe generalizado = D <u>
2-n'
n'-1
r / K' 8
n'-1
n'
n'+1
La caída de presión será DP= 32 K' 8 L <u> / D
Esta ecuación puede
considerarse como una generalización de la ecuación de Hagen Poiseuille. Se
comprueba con esta ecuación que para fluidos de n' bajos los cambios de DP se
afectan poco con los cambios de radio o velocidad. De esta forma se puede
incrementar la capacidad de un conducto variando la velocidad de la bomba sin
que se afecte prácticamente la caída de presión.
n
Para fluidos que cumplan la ley de potencia: n=n'; K' = K ((3n+1) / 4n)
4
Para fluidos que cumplan el modelo de Bingham: n'= [1-1.75 so/sw+ 1/3 (so/sw) ]/
4
(1- (so/sw) ).
4
Si (so/sw) <<1: n'= 1-1.75 so/sw
4
n'
K' = sw {h pl / [ sw ( 1-1.75 so/sw+ 1/3 (so/sw) )]} .
LECCIÓN 27. CÁLCULO DE PÉRDIDAS POR FRICCIÓN
Estudie el epígrafe 2.10, página 128 - 138 del texto básico.
Al estudiar el balance de energía mecánica, precise que:
• En la ecuación 2.105 hay un término debido a la variación de energía
cinética, uno debido a la variación de energía potencial y uno debido a la
carga presión. Los otros términos que aparecen en la ecuación son la
sumatoria de pérdidas por fricción y el trabajo mecánico.
• En el término pérdidas por fricción se incluyen las debidas a los cambios
de diámetro de las tuberías y a la contribución realizada por los
aditamentos que se coloquen en éstas, válvulas, codos, etc.
• El trabajo mecánico con signo negativo implica trabajo realizado sobre el
sistema, por ejemplo el realizado por una bomba o un compresor.
Para calcular las pérdidas por fricción se utiliza el factor de fricción de Fanning
(f) que se define como la relación entre el esfuerzo cortante en la pared y la
2
energía cinética por unidad de volumen, de donde: f = DPD/(r 2L <u> )
2
Esta definición permite calcular DP/r = f 2L <u> / D .
2
Para flujo laminar newtoniano <u> = DPD /( 32 L m), lo que conduce a que
f = 16 / NRe que se utiliza para calcular factores de fricción para NRe< 2100
Para un fluido que cumpla la ley de potencia: f = 16 / NRe, PL
n
Para los fluidos que cumplen la ley de potencia: NRe, PL=(D <u>
n
2-n
r / (8
n-1
K)
) ( 4n/(3n+1))
Para un fluido que cumpla con el modelo de Bingham: f = 16(6 NRe,B + NHe) /
2
6NRe,B . Es de señalar que esta es la ecuación calculada eliminando el
término de la cuarta potencia de la ecuación de Buckingham Reinier lo cual
4
sucede si (so/sw) <<1. La ecuación exacta es :
-1
2
4
3
8
NRe,B = f/16 - 1/6 (NHe/ NRe,B ) +1/3 (NHe / f NRe,B )
2
En esta ecuación NHe es el número de Hedstrom = soD r/hpl
2.
Para los fluidos de Bingham: NRe,B = r <u> D / hpl
A medida que el NRe,B es mayor, f decrece, mientras que aumenta con el
aumento de NHe.
Para flujo turbulento las ecuaciones no son válidas y se utilizan fórmulas
empíricas obtenidas a partir de datos experimentales y presentadas en la tabla
2.3, página 131 del texto básico. De la figura 2.16 se aprecia cómo para flujo
turbulento de fluidos que cumplen la ley de potencia, a medida que el NRe, PL
aumenta, el factor de fricción de fanning disminuye, para un mismo valor de n.
Este comportamiento el válido para toda n. Por otra parte para un mismo NRe,
PL, mientras mayor sea n mayor será el factor de fricción de fanning.
La evaluación del término variación de energía cinética en la ecuación del
balance de energía mecánica es en general pequeña y el término puede ser
despreciado para la mayor parte de las aplicaciones. Cuando se necesita
2
calcular, se utiliza un factor de corrección a de modo que D KE = <u> / a. En
flujo turbulento este factor toma el valor de 2 para cualquier fluido. Para flujo
laminar, la tabla 2.4, página 133 presenta cómo evaluar el factor de corrección.
Este factor de corrección depende del tipo de fluido. El comportamiento general
es que el factor de corrección aumenta a medida que el valor de n disminuye.
Cálculo de pérdidas por fricción.
Estudie el epígrafe 2.10, página 128 - 138 del texto básico.
Al estudiar el balance de energía mecánica, precise que:
• En la ecuación 2.105 hay un término debido a la variación de energía
cinética, uno debido a la variación de energía potencial y uno debido a la
carga presión. Los otros términos que aparecen en la ecuación son la
sumatoria de pérdidas por fricción y el trabajo mecánico.
• En el término pérdidas por fricción se incluyen las debidas a los cambios
de diámetro de las tuberías y a la contribución realizada por los
aditamentos que se coloquen en éstas, válvulas, codos, etc.
• El trabajo mecánico con signo negativo implica trabajo realizado sobre el
sistema, por ejemplo el realizado por una bomba o un compresor.
Para calcular las pérdidas por fricción se utiliza el factor de fricción de Fanning
(f) que se define como la relación entre el esfuerzo cortante en la pared y la
2
energía cinética por unidad de volumen, de donde: f = DPD/(r 2L <u> )
2
Esta definición permite calcular DP/r = f 2L <u> / D .
2
Para flujo laminar newtoniano <u> = DPD /( 32 L m), lo que conduce a que
f = 16 / NRe que se utiliza para calcular factores de fricción para NRe< 2100
Para un fluido que cumpla la ley de potencia: f = 16 / NRe, PL
n
Para los fluidos que cumplen la ley de potencia: NRe, PL=(D <u>
n
2-n
r / (8
n-1
K)
) ( 4n/(3n+1))
Para un fluido que cumpla con el modelo de Bingham: f = 16(6 NRe,B + NHe) /
2
6NRe,B . Es de señalar que esta es la ecuación calculada eliminando el
término de la cuarta potencia de la ecuación de Buckingham Reinier lo cual
4
sucede si (so/sw) <<1. La ecuación exacta es :
-1
2
4
3
8
NRe,B = f/16 - 1/6 (NHe/ NRe,B ) +1/3 (NHe / f NRe,B )
2
En esta ecuación NHe es el número de Hedstrom = soD r/hpl
2.
Cálculo de pérdidas por fricción.
Estudie el epígrafe 2.10, página 128 - 138 del texto básico.
Al estudiar el balance de energía mecánica, precise que:
• En la ecuación 2.105 hay un término debido a la variación de energía cinética,
uno debido a la variación de energía potencial y uno debido a la carga
presión. Los otros términos que aparecen en la ecuación son la sumatoria
de pérdidas por fricción y el trabajo mecánico.
• En el término pérdidas por fricción se incluyen las debidas a los cambios de
diámetro de las tuberías y a la contribución realizada por los aditamentos
que se coloquen en éstas, válvulas, codos, etc.
• El trabajo mecánico con signo negativo implica trabajo realizado sobre el
sistema, por ejemplo el realizado por una bomba o un compresor.
Para calcular las pérdidas por fricción se utiliza el factor de fricción de Fanning (f)
que se define como la relación entre el esfuerzo cortante en la pared y la energía
2
cinética por unidad de volumen, de donde: f = DPD/(r 2L <u> )
2
Esta definición permite calcular DP/r = f 2L <u> / D .
2
Para flujo laminar newtoniano <u> = DPD /( 32 L m), lo que conduce a que
f = 16 / NRe que se utiliza para calcular factores de fricción para NRe< 2100
Para un fluido que cumpla la ley de potencia: f = 16 / NRe, PL
n
Para los fluidos que cumplen la ley de potencia: NRe, PL=(D <u>
n
2-n
r / (8
n-1
K) ) (
4n/(3n+1))
Para un fluido que cumpla con el modelo de Bingham: f = 16(6 NRe,B + NHe) /
2
6NRe,B . Es de señalar que esta es la ecuación calculada eliminando el término
de la cuarta potencia de la ecuación de Buckingham Reinier lo cual sucede si
4
(so/sw) <<1. La ecuación exacta es :
-1
2
4
3
8
NRe,B = f/16 - 1/6 (NHe/ NRe,B ) +1/3 (NHe / f NRe,B )
2
2.
En esta ecuación NHe es el número de Hedstrom = soD r/hpl
Para los fluidos de Bingham: NRe,B = r <u> D / hpl
A medida que el NRe,B es mayor, f decrece, mientras que aumenta con el
aumento de NHe.
Para flujo turbulento las ecuaciones no son válidas y se utilizan fórmulas empíricas
obtenidas a partir de datos experimentales y presentadas en la tabla 2.3, página
131 del texto básico. De la figura 2.16 se aprecia cómo para flujo turbulento de
fluidos que cumplen la ley de potencia, a medida que el NRe, PL aumenta, el factor
de fricción de fanning disminuye, para un mismo valor de n. Este comportamiento
el válido para toda n. Por otra parte para un mismo NRe, PL, mientras mayor sea n
mayor será el factor de fricción de fanning.
La evaluación del término variación de energía cinética en la ecuación del
balance de energía mecánica es en general pequeña y el término puede ser
despreciado para la mayor parte de las aplicaciones. Cuando se necesita
2
calcular, se utiliza un factor de corrección a de modo que D KE = <u> / a. En
flujo turbulento este factor toma el valor de 2 para cualquier fluido. Para flujo
laminar, la tabla 2.4, página 133 presenta cómo evaluar el factor de corrección.
Este factor de corrección depende del tipo de fluido. El comportamiento general
es que el factor de corrección aumenta a medida que el valor de n disminuye.
Para los fluidos de Bingham: NRe,B = r <u> D / hpl
A medida que el NRe,B es mayor, f decrece, mientras que aumenta con el
aumento de NHe.
Para flujo turbulento las ecuaciones no son válidas y se utilizan fórmulas
empíricas obtenidas a partir de datos experimentales y presentadas en la tabla
2.3, página 131 del texto básico. De la figura 2.16 se aprecia cómo para flujo
turbulento de fluidos que cumplen la ley de potencia, a medida que el NRe, PL
aumenta, el factor de fricción de fanning disminuye, para un mismo valor de n.
Este comportamiento el válido para toda n. Por otra parte para un mismo NRe,
PL, mientras mayor sea n mayor será el factor de fricción de fanning.
La evaluación del término variación de energía cinética en la ecuación del
balance de energía mecánica es en general pequeña y el término puede ser
despreciado para la mayor parte de las aplicaciones. Cuando se necesita
2
calcular, se utiliza un factor de corrección a de modo que D KE = <u> / a. En
flujo turbulento este factor toma el valor de 2 para cualquier fluido. Para flujo
laminar, la tabla 2.4, página 133 presenta cómo evaluar el factor de corrección.
Este factor de corrección depende del tipo de fluido. El comportamiento general
es que el factor de corrección aumenta a medida que el valor de n disminuye.
LECCIÓN 28. CAÍDA DE PRESIÓN EN VÁLVULAS
Los datos reportados en la literatura que permitan evaluar la caída de presión a
través de válvulas y otros elementos son escasos. La caída de presión en válvulas
y otros aditamentos se expresa en términos de coeficientes de fricción kf según:
2
DP /r = kf <u> /2.
Existe un conjunto de "reglas" a seguir para utilizar los coeficientes de fricción:
• El comportamiento de los coeficientes de fricción para fluidos newtonianos y
no newtonianos es similar.
• A medida que aumenta el diámetro de la tubería el valor del coeficiente de
fricción disminuye.
• El coeficiente de fricción aumenta abruptamente con la dismunición del
Número de Reynolds en la región laminar y permanece constante en la
región de flujo turbulento.
• Las pérdidas de presión por efecto de entrada en la región laminar para un
fluido que cumpla la ley de potencia disminuye con la disminución del índice
de flujo n.
• Las pérdidas por efecto de entrada para fluidos que cumplan con el modelo de
Bingham disminuyen a medida que so aumenta, cuando el esfuerzo
cortante en la pared es constante.
• La resistencia al flujo de fluidos no newtonianos en la región de flujo laminar
es 133 % mayor que la observada para un fluido newtoniano que pase a
través de una válvula similar.
En las tablas 2.5 y 2.6, páginas135 y 136 del texto básico se reportan valores
de kf. En la tabla 2.5 para flujo laminar y en la 2.6 para flujo turbulento.
Observe cómo en dependencia del tipo de válvula, las pérdidas serán
diferentes.
Investigadores han realizado trabajos con diferentes elementos. Por ejemplo Steffe
reporta para fluidos seudoplásticos las siguientes correlaciones:
kf = 30.3 NRe, PL - 0.492 Válvula de 3 vías
kf = 29.4 NRe, PL - 0.504 Punto en T
kf = 191.0NRe, PL - 0.896 Codo 90°
Adicionalmente se aconsejan las siguientes "reglas" :
• Para fluidos newtonianos usar los datos de las tablas 2.5 y 2.6.
• Para fluidos no newtonianos para valores de número de Reynolds mayores
que 500, usar los datos de la tabla 2.6.
• Para fluidos no newtonianos en el intervalo de número de Reynolds entre 20 y
500 usar las ecuaciones kf = A/ NRePL; kf = A /NReB ; mientras que el
valor de A = kf turbulento (500) .
Ejemplo:
Estudie el ejemplo 2.12.6, página 152 - 155 del texto básico. En el ejemplo se
calculan las pérdidas por fricción durante el bombeo de dos fluidos que cumplen la
ley de potencia y tienen igual n pero diferentes K. Al concluir podrá apreciar que:
• Las pérdidas por fricción incluyen la caída de presión en los tramos de
tuberías recta,una válvula de disco, 3 codos, 1 efecto de cambio de
diámetro y un filtro.
• Los valores de los coeficientes de fricción se calculan a partir de los
reportados para flujo turbulento afectados por el parámetro A, para el caso
1 en que el NRe es 323.9, o sea laminar.
• Los valores de los coeficientes de fricción para el caso 2, se calculan a partir
de los valores para flujo turbulento, ya que en este caso el flujo es
turbulento.
• En la ecuación 2.115 se considera que el término D pequeño / D grande es 0.
• En el término de la contribución de las pérdidas por los tramos rectos de
tuberías, se suman las longitudes de cada tramo y esa suma es la que se
considera L.
• Cómo a menor K, para un mismo n, el NRe aumenta.
Estudie el siguiente problema resuelto:
3
3
3
40 m /h de aceite mineral(r 15°C = 960 kg/m ; r 50°C = 890 kg/m ; m 15°C = 3.43
Pas; m 50°C = 0.187 Pas) se bombean por una tubería de 100 mm de diámetro
hacia un recipiente instalado a 20m de altura. La longitud de tubería recta
horizontal es de 430 m. En el tramo hay instalados 3 codos a 90° y 1 válvula de
compuerta. El recipiente de almacenamiento y el de recepción están abiertos a la
atmósfera. Calcular la potencia del motor(con eficiencia total = 0.5) de la bomba si
la impulsión se realiza a 15°C y a 50°C.
Solución:
2
2
<u> = Q/área= Q/0.7854 D = 40/0.7854* 0.1 * 3600 = 1.415 m/s
A 15°C
NRe = <u> D r/m= 1.415* 0.1*960/3.43= 39.6 Régimen laminar
f= 16/NRe = 16/39.6= 0.404
De la ecuación del balance de energía mecánica:
DEk + DEp+DP/r + SF + W = 0
2
2
SF= S(2f<u> L/D) + S(kf <u> /2) Ecuación 2.106 página128 del texto básico
Elemento
Entrada a tubería
Codo
Válvula compuerta
S = 32.9
kf
0.5
7.5
9.9
Número
1
3
1
2
Total
0.5
22.5
9.9
2
SF= 2*0.404*1.415 *450/0.1 + 32.9* 1.415 /2 = 7280.09 + 32.93 =7313.02 J/kg
2
2
DEk= <u> */2 =1.415 * /2 = 1.001 J/kg (Fluido en la succión con velocidad 0)
DEp = gh = 9.8* 20 = 196 J/kg
El término relativo a la diferencia de presión entre un recipiente y otro es 0 dado
que ambos están abiertos a la atmósfera.
Observe cómo de acuerdo a los valores relativos, los términos de las pérdidas por
resistencia locales (kf) y la variación de energía cinética pueden despreciarse.
-W = DEp+DEk+SF= 196 +1.001 + 7313 = 7510 J/kg
3
La potencia necesaria será : -W*Q*r / eficiencia del motor = 7510 J/kg * 40 m /h *
3
960 kg/m / 3600 s/h / 0.5 = 80106/ 0.5 J/s = 160.2 kW.
A 50°C
NRe = <u> D r/m= 1.415* 0.1*890/0.187= 673 Régimen laminar pero de mayor
NRe
f= 16/NRe = 16/673= 0.024 El valor de f es menor.
De la ecuación de balance de energía mecánica:
DEk + DEp+DP/r + SF + W = 0
2
2
SF= S(2f<u> L/D) + S(kf <u> /2) Ecuación 2.106 página128 del texto básico
Cálculo de kf: (Tabla 2.5 página 135 del texto básico)
Elemento
Entrada a tubería
Codo
Válvula compuerta
kf
0.5
1.0
1.7
Número
1
3
1
Total
0.5
3.0
1.7
S = 5.2
Observe que los valores de kf son menores al ser el NRe mayor.
2
2
SF= 2*0.024*1.415 *450/0.1 + 5.2* 1.415 /2 = 432.5 + 5.21= 437.71 J/kg
2
2
DEk= <u> */2 =1.415 * /2 = 1.001 J/kg (Fluido en la succión con velocidad 0)
DEp = gh = 9.8* 20 = 196 J/kg
El término relativo a la diferencia de presión entre un recipiente y otro es 0 dado
que ambos están abiertos a la atmósfera.
Observe cómo de acuerdo a los valores relativos, los términos de las pérdidas por
resistencia locales (kf) y la variación de energía cinética pueden despreciarse.
-W = DEp+DEk+SF= 196 +1.001 + 437.71= 634.7J/kg
3
La potencia necesaria será : -W*Q*r / eficiencia del motor = 634.7 J/kg * 40 m /h *
3
890kg/m / 3600 s/h / 0.5 = 6276.5/ 0.5 J/s = 12.6 kW.
Observe cómo para bombear aceite frío se necesita una potencia mucho mayor.
Ejemplo:
Analice el siguiente ejemplo en el que se presenta cómo vincular la determinación
de datos experimentales con la modelación matemática de resultados.
MODELOS MATEMATICOS PARA CALCULAR LA VISCOSIDAD EFECTIVA Y SU
APLICACIÓN EN EL DISEÑO Y EVALUACION DE REDES DE TUBERIAS
(Tomado de G. Riera y O. Méndez. Facultad de Ingeniería Química. ISPJAE)
Cada día más, para el estudio, evaluación y diseño de procesos, se emplea la
simulación; para esto es indispensable contar con modelos matemáticos que
representen lo mejor posible el fenómeno en cuestión o sus propiedades
fundamentales y que su respuesta no difiera de la realidad.
En los procesos industriales es muy común el transporte de fluidos. Diferentes
autores han desarrollado métodos para evaluar, diseñar y seleccionar equipos de
impulsión. En el caso específico de los fluidos no-newtonianos de la Industria
Alimentaria se tiene el trabajo de Steffe (Steffe, J.; Morgan, R. Pipeline Design and
Pump Selection for Non-Newtonian Fluids Foods. Food Technology 40 (12) 7885.1986) donde se describe un método para el diseño de sistemas de tuberías y
selección de bombas para fluidos no-newtonianos empleando el balance de
energía mecánica y haciendo uso de la viscosidad efectiva (µe) ,determinada a
partir del modelo reológico de Herschel-Bulkley. Méndez (Méndez, O. Metodología
para el diseño de sistemas tuberías- bomba en la Tecnología de Alimentos.
Memorias CICTA-4. Ciudad Habana.1994), también presentó una metodología
similar presentando otras opciones para la determinación de la viscosidad efectiva.
Ambos trabajos se quedan en la definición de la metodología. En esta misma línea
Méndez y Riera (Méndez, O.; Riera, G. Programa de computación para diseño de
sistemas bomba-tuberías de la Industria Alimentaria. Memorias I Taller
Internacional de Propiedades Físicas de Alimentos. RIPFADI, IIIA, C. Habana.1995
) desarrollaron un software que permite realizar el diseño y evaluación de sistemas
de redes de tuberías en primera versión para fluidos newtonianos y posteriormente
para no-newtonianos (SIDESTUB); en este último caso se parte de información
obtenida en un viscosímetro rotacional o en un viscosímetro capilar y así con ella
determinar los parámetros reológicos del fluido y su viscosidad efectiva. La
aplicación de este programa ha dado buenos resultados pero es frecuente
encontrar que en la industria no existe el equipamiento
requerido para realizar las mediciones necesarias o se precisan los resultados con
mayor rapidez. Basado en estas experiencias se valoró la importancia de contar
con modelos matemáticos que sean capaces de predecir la viscosidad efectiva en
función de parámetros de operación como son: temperatura, concentración de
sólidos y gradiente de velocidad en tuberías (8u/D).
El trabajo fue realizado con pulpas de frutas y hortalizas y de las mieles finales de
la industria azucarera, utilizando la información reportada por varios autores.de
Hombre y col (De Hombre, R.; Casals, C.; Zumalacárregui, L. (1993). Propiedades
reológicas de alimentos elaborados en Cuba. RIPFADI. CYTED), Koralov y Garcell
(Kolarov, K.; Garcell, L. Comportamiento reológico de mieles finales de la provincia
de Oriente. CubaAzúcar /Julio/Septiembre/; p. 22-34.1974). Los productos
resultaron tener un comportamiento no elástico, independiente del tiempo y
seudoplástico en las mayoría de los casos.
Esta información presenta la viscosidad aparente con su correspondiente gradiente
de velocidad (du/dy) y valores de índice de flujo e índice de comportamiento para
un intervalo de gradientes de velocidad (du/dy) para diferentes concentraciones y
temperaturas. Para obtener un modelo para predecir la viscosidad efectiva en
función de la concentración, la temperatura, el gradiente de velocidad (8u/D) y sus
interacciones, fue necesario realizar transformaciones en la base de datos.
Para valores lógicos de velocidad de estos fluidos a través de conductos circulares
(0.5 m/s a 3 m/s) y para los diámetros comúnmente empleados en las industrias
azucarera y alimentaria (6.3, 7.6, 10.2 y 15.2 cm) se determinaron los gradientes
de velocidad en tuberías (8u/D). Con estos gradientes se calcularon los
correspondientes du/dy. Esto permitió hacer una selección de la información que
se poseía. Posteriormente con los respectivos valores de índice de consistencia
(K) e índice de flujo (n) reportados, se determinaron las viscosidades efectivas. Las
ecuaciones empleadas para hacer estas transformaciones fueron: 8u/D = [4n/(3n
+1)] du/dy
n
n-1
µe = K [(3n + 1)/4] [ 8u/D]
La información fue organizada como se muestra en la Tabla 1, en forma de
ejemplo, para ser procesada estadísticamente mediante el programa profesional
STATGRAPHICS. La validación de los modelos también se hizo con este
programa, mediante pruebas de hipótesis entre los valores medios de datos
experimentales obtenidos en el laboratorio y los resultados que brindaron los
modelos determinados.
Para la evaluación en la práctica de los modelos obtenidos se introdujeron los
mismos como ecuaciones en el software CALRED el cual permite realizar el diseño
y/o evaluación de sistemas de redes de tuberías. El mismo se aplicó en la
evaluación de sistemas de transporte hidráulico de mieles finales en el CAI
"Camilo Cienfuegos" y en la destilería de alcohol "Héctor Molina".
El procesamiento estadístico de la información permitió obtener modelos
matemáticos para pulpas de guayaba, pulpas de tomate y mieles finales de la
industria azucarera.
En la tablas de la 2 a la 4 se presentan los resultados de las pruebas de
significación de los parámetros (test de Student) y de ajuste de los modelos (test
de Fisher) realizada para un nivel de significación de 95 %.
En la Tabla 2 se recogen los resultados relacionados con pulpas de guayaba
empleándose 40 datos. Como se puede observar en todos los casos las variables
independientes estudiadas se relacionan con la viscosidad efectiva con un alto
nivel de significación destacándose los altos valores del estadígrafo al ser
comparado con el valor crítico. Como era de esperar se obtuvieron valores de
coeficiente que muestran que el aumento de la concentración provocará un
aumento de la viscosidad efectiva así como el inverso del gradientede velocidad y
que un aumento en la temperatura provocará una disminución en la viscosidad
efectiva. Se observa que el inverso del gradientede velocidad (g) resulta la variable
independiente de mayor significación y entre las interacciones el término C*1/g
también tiene un peso importante en la viscosidad efectiva.
En el análisis de varianza de la regresión se puede observar que el valor de F
experimental es superior al crítico (Fcrit=2.16), y que se obtuvo un alto coeficiente
de correlación múltiple. En el análisis de los residuos se pudo comprobar que
existe una distribución uniforme sin tendencia alguna. Este modelo fue
determinado para valores de concentración (C) entre 6 y 17.6 % de sólidos y
temperaturas entre 10 y 25 °C.
En la Tabla 3 se recogen los resultados relacionados con las mieles finales de la
industria azucarera empleándose 48 datos . Como se puede observar en todos los
casos las variables independientes estudiadas se relacionan con la viscosidad
efectiva con un alto nivel de significación, destacándose los altos valores del
estadígrafo al ser comparado con el valor crítico excepto en los casos de 1/g y
1/g*C los cuales aceptamos por estar por encima de un valor de significación de un
90 %. Como era de esperar se obtuvo un comportamiento de las variables
independientes similar al caso anterior. Se observa que en este caso la
concentración (C) resulta la variable independiente de mayor significación sobre la
viscosidad efectiva. En el modelo de las mieles no aparece la temperatura ya que
se experimentó sólo para 40°C.
En el análisis de varianza de la regresión se puede observar que el valor de F
experimental es superior al crítico (Fcrit=2.58), y que se obtuvo un alto coeficiente
de correlación múltiple. En el análisis de los residuos se pudo comprobar que
existe una distribución uniforme sin tendencia alguna. Este modelo fue
determinado para valores de concentración (C) entre 73 y 78 % de sólidos.
En la Tabla 4 se recogen los resultados relacionados con pulpas de tomate
empleándose 38 datos. Se puede observar que las variables independientes
estudiadas se relacionan con la viscosidad efectiva. En este caso la variable
concentración, incluyendo el cuadrado y el cubo de la misma, así como sus
interacciones con el inverso del gradiente de velocidad, resultaron significativas
para el cálculo de la viscosidad efectiva.
En el análisis de varianza de la regresión se puede observar que el valor de F
experimental es también superior al crítico (Fcrit=2.42), y que se obtuvo un alto
coeficiente de correlación múltiple. En el análisis de los residuos se pudo
comprobar que existe una distribución uniforme sin tendencia alguna. Este modelo
fue determinado para valores de concentración (C) entre 4.3 y 19.7 % de sólidos y
para una temperatura 25 °C.
La transportación frecuente de fluidos no-newtonianos exige del conocimiento de
las propiedades reológicas de los mismos y su comportamiento para obtener
resultados confiables en cualquier tipo de cálculo relacionado con ellos. En
sistemas de bombas y tuberías, tanto en trabajos de evaluación como de diseño,
resulta imprescindible aplicar los métodos específicos para estos casos. Los
trabajos relacionados con el diseño y evaluación de estos sistemas exigen de un
volumen considerable de cálculos complejos y de la utilización de gran cantidad de
información que se recoge en formas de gráficos y tablas lo cual explica el tiempo
que se requiere para la solución manual de estas tareas.
El programa posibilita por tanto la solución rápida y eficiente de tareas o problemas
que se presentan tanto en las industrias como en centros de investigación o
proyectos donde se hace necesario transportar por sistemas de bombas-tuberías.
Esto tiene implicaciones económicas, pues el personal técnico puede tener
respuesta a un problema en un corto tiempo el cual requiere de varios días de
trabajo. Además por ser las soluciones asociadas extensas y engorrosas, la
probabilidad de errores es elevada, aspecto que es también eliminado con la
utilización del programa .
Los trabajos de selección de bombas y evaluación de alternativas, tan frecuente en
la práctica, también pueden tener respuestas inmediata si se utiliza el programa.
Para la validación de los modelos obtenidos se realizaron pruebas de hipótesis
entre los valores predicho por el modelo y valores experimentales obtenidos en
laboratorio no encontrándose diferencia significativas entre las medias, por tanto
los modelos obtenidos pueden ser empleados para determinar la viscosidad
efectiva de los productos modelados.
Tomando en consideración la concentración de sólidos, la temperatura de las
mieles y la características de la instalación se realizaron los cálculos pertinentes
obteniéndose los resultados que se muestran en las tablas 5 y 6.
En la tabla 5 aparecen los datos fundamentales de la instalación donde se realizó
la validación. En la tabla 6 aparecen los resultados de la experimentación. En ésta
se puede observar cómo la velocidad varía en función de los diámetros de cada
sección de la misma forma que lo hace la viscosidad efectiva, pero en este caso no
es sólo por la variación del diámetro sino también por el cambio que sufre el
gradiente por la variación de la velocidad. Esto como es de esperar se refleja en el
valor del número de Reynolds siendo mayor en la descarga porque es superior la
velocidad e inferior la viscosidad efectiva en relación con la de la succión. También
se puede comprobar que el régimen de flujo es netamente laminar que es el
usualmente encontrado en fluidos no-newtonianos. El resto de los resultados se
comporta adecuadamente.
De la aplicación del programa se pudo apreciar la validez de las ecuaciones para
el cálculo de la viscosidad efectiva y las facilidades que brinda su introducción en
el software para la evaluación y diseño de redes de tuberías y bombas.
Tabla 1. Algunos datos experimentales para el procesamiento estadístico. Pulpas
de guayaba .
T °C
10
20
20
25
Concentración
(% sólidos)
6
11.4
9.9
17.6
-1
g (s )
me (Pas)
41.4
29.7
102.65
117.6
0.786
7.024
1.124
0.0443
Tabla 2. Correlación para las pulpas de guayaba. Resultados del ajuste del modelo
Variable
independiente
Constante
C
T
1/g
C*T
C*1/g
Coeficiente
Error estadístico
t
5.8365
1.57423
-1.83703
903.38
0.196657
291.219
0.435776
0.054019
0.092374
23.4497
0.0102618
2.80532
13.388
29.1422
-19.8869
38.5242
19.1641
103.81
Nivel
significación
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
de
Análisis de Varianza
Modelo
Error
Suma
de
cuadrados
140.78
0.01166
Cuadrado
medio
10.476
0.0004
F
P
26051
0.000
Coeficiente de Correlación (R) = 99.98 Fcrit = 2.16 Error estándar de estimación =
0.020
Tabla3. Correlación para mieles finales de la Industria Azucarera. Resultados del
ajuste del modelo
Variable
independiente
Constante
C
1/g
1/g*C
2
C
t crítica= 1.96
Coeficiente
Error estadístico
t
311.331
-2.42229
-169.795
2.3432
0.05792
29.5191
0.7222
99.6201
1.3279
0.0051
10.54
-10.25
-1.70
1.76
11.17
Nivel
significación
0.0000
0.0000
0.0850
0.0240
0.0000
de
Análisis de varianza
Modelo
Error
Suma
de
cuadrados
15.2434
0.03626
Cuadrado
medio
3.9600
0.00850
F
P
462.00
0.000
Coeficiente de Correlación (R) = 98.77 Fcrit = 2.58 Error estándar de estimación =
0.092
Tabla 4. Correlación para pulpas de tomate. Resultados del ajuste del modelo
Variable
independiente
Constante
1/g*C
C^2*1/g
Coeficiente
Error estadístico
t
2.02847
-3.24086
0.961383
0.530777
1.03623
0.170156
3.8217
-3.12755
5.65
Nivel
significación
0.0006
0.0038
0.0000
de
C^3*1/g
C
C^2
C^3
t crítica
-0.0301702
-0.760992
0.080657
-0.002323
0.006078
0.199801
0.020856
0.000614
-4.96399
-3.80874
3.86738
-3.78319
0.0000
0.0006
0.0005
0.0007
1.96
Análisis de varianza
Modelo
Error
Suma
de
cuadrados
27.1126
0.049533
Cuadrado
medio
4.51877
0.0015978
F
P
2828.07
0.000
Coeficiente de Correlación (R) =99.91 Fcrit = 2.42 Error estándar de estimación =
0.03
Tabla 5. Datos de la instalación a evaluar.
Diámetro
mm
Succ
...Desc
154.1
102.3
Longitud m
Altura m
Succ
...Desc
Succ
...Desc
Presión
kPa
Succ
...Desc
4 .........45
1........15
1 ..........1
3
Flujo m /s
densidad
3
kg/m
0.0186
1377
Pérdidas
friccionales
m
Succ...Des
c
0.233
11.92
Carga
dinámica
total m
Tabla 6. Resultados de la evaluación.
efectiva
Pas
Velocidad
m/s
Reynolds
Succ...Des
c
0.586
0.513
Succ...Des
c
Succ...Des
c
1 .......2.26
362 ....549
Factor
fricción
Succ...Des
c
0.176
0.133
27.2
LECCIÓN 29. EFECTO EN LA TRANSFERENCIA DE CALOR
En la industria de alimentos, la transferencia de calor en fluidos no newtonianos en
flujo laminar es una situación frecuente. En la literatura se recogen expresiones
para la velocidad de transferencia de calor, y para su uso, la identificación de
modelo reológico utilizado y el conocimiento de la condición de restricción usada:
temperatura en la pared constante o flujo de calor constante en la pared, resultan
imprescindible. De igual manera se debe precisar cómo ha sido definida la
diferencia de temperatura, antes de calcular y utilizar un valor de coeficiente de
transferencia de calor determinado con ellas. En general, cuatro propiedades son
fundamentales: densidad, conductividad térmica, constantes reológicas y
capacidad calórica del material.
El mecanismo de transferencia de calor a través de un fluido en flujo laminar, es el
de conducción. En la práctica, la convección natural se puede presentar para el
caso de bajas viscosidades y bajos flujos.
Transferencia de calor para flujo laminar en conductos.
2
El coeficiente de transferencia de calor hc (W/m K)puede evaluarse de cartas
basadas en la solución de la ecuación de transporte pertinente o a partir de
ecuaciones empíricas de varios autores.
Se conoce que para flujo laminar en tuberías:
2
2
-1
dT/dz = a / uz [ d T/dr + r dT/dr]
donde: a difusividad térmica ; uz velocidad axial; r y z coordenadas radial y axial.
La solución conlleva a números adimensionales Nu = hc D/k llamado Nusselt y Gz
= m Cp/kL llamado Graetz. Aquí k: conductividad térmica W/mK; m: flujo
másico;Cp: capacidad calórica J/kgK. El término k/rCp = a
La velocidad lineal puede expresarse en función del radio haciendo uso del
esfuerzo cortante y de un apropiado modelo reológico. La ecuación diferencial
puede solucionarse para encontrar T=f(r,z) para diferentes condiciones de
contorno. Valores de coeficientes de transferencia de calor locales hc= f( z) y
medios hm se obtendrán de estos tratamientos. En los textos de Fenómenos de
Transporte se puede encontrar diversas soluciones de la ecuación diferencial en
dependencia de las suposiciones que se realicen para la solución matemática y de
las condiciones de contorno.
1/3
Para fluidos newtonianos se encuentra la ecuación Num = hm D/k = 1.75 (Gz)
donde hm se define para ser utilizado con una DT= Tw - 0.5 (Tent + Tsal). Esta
ecuación es válida para Gz> 100.
Para fluidos que cumplan el modelo de Bingham se obtiene:
4
1/3
Num= hm D/k = 1.75 [(m Cp /kL) (3(1-c)/(c - 4c + 3))] . Aquí c= so/sw y se aplica
4
si (mCp/kL) (3(1-c)/(c - 4c + 3))> 100.
Para fluidos que cumplan la ley de potencia la literatura reporta soluciones en
forma de gráficos de Numvs Gz, aumentando el Num a medida que aumenta el Gz
.
Una solución generalizada se alcanza aplicando la solución aproximada de
Leveque a la ecuación diferencial obteniendo:
1/3
1/3
Num= hm D/k = 1.75 d Gz
donde: d = (3n' + 1) / 4n' = [(-du/dr)w para el fluido no newtoniano] / [(-du/dr)w para
el fluido newtoniano]. Sustituyendo queda: [(-du/dr)w para el fluido no newtoniano] /
8<u>/D
n'
Recordemos que n' se define a partir de sw=K' (8<u>/D) donde K' y n' varían con
8<u>/D. El valor de n' se calcula de la pendiente de la curva log sw vs log 8<u>/D
Para fluidos que cumplan la ley de potencia d = (3n + 1) / 4n.
4
Para fluidos que cumplan el modelo de Bingham d = (1-c) / (1-1.75 c + 1/3 c ). Esta
ecuación es válida si Gz > 100 y n>0.1
En la ecuación, el valor de hm se utiliza para DT= Tw - 0.5 (Tent + Tsal).
Ecuaciones empíricas.
Se han desarrollado ecuaciones empíricas por diversos autores que toman en
cuenta la variación de la viscosidad con la temperatura.
Para fluidos newtonianos:
1/3
0.14
hm D/k= 2.0 (mCp/kL) (h/hw)
En esta ecuación hm es para ser utilizado con DT= Tw - 0.5 (Tent + Tsal)
Para fluidos de Bingham, se grafica ln jH vs ln NRe y se obtiene una recta:
2/3
jH= (hm/Cpr<u>) (Cph/k)
-2/3
0.14
(hw/h)
(L/D)
1/3
4
[(3(1-c)/(c - 4c + 3))]
-1/3
=1.86 ( r <u>
D / hpl)
El valor de hm se corresponde con la media logarítmica de temperatura.
Para fluidos que cumplen la ley de potencia:
1/3
0.14
hm D/k= 2.0 (mCp/kL) [ (Kb( 3n+1))/(Kw*2(3n-1))] Ecuación de Charm y Merrit
y se corresponde con la media logarítmica de las diferencias de temperatura.
Ecuación generalizada
Si no existe convección natural: (Ecuación de Metzner,Vaughn y Houghton que
depende del Gz)
Para considerar la variación radial de la consistencia del fluido con la temperatura
bajo flujo laminar, se reporta la ecuación:
Si Gz>20 y n' >0.1 (casos más comunes)
Num= hm D/k = 1.75 d
(h/hw)
0.14
1/3
Gz
1/3
0.14
(h/hw)
1/3
= 1.75 (mCp/kL)
1/3
((3n'+1)/4n')
Si Gz <20 y/o n'<0.10
1/3
1/3
0.14
hm D/k= 1.75 (mCp/kL) D (h/hw)
, donde D= relación entre los coeficientes
de transferencia de calor no newtonianos y newtonianos.
En estas ecuaciones se supone que la temperatura en la pared sea constante.
Aquí: hm: coeficiente medio de transferencia de calor; Kb: índice de consistencia
evaluado a la temperatura media del seno del fluido; Kw: índice de consistencia del
n-1
fluido evaluado a la temperatura de la pared; h :K 8 ; hw: h evaluada a la
temperatura de la pared.
Si existe convección natural:
En el caso de fluidos menos viscosos, la convección natural puede ser apreciable
e influir en la velocidad de transferencia de calor.
Si los tubos son horizontales:
1/3
0.4 1/3
0.14
Num= hm D/k = 1.75 d [Gz + 12.6 (NPr,w NGr,w D/L ] (h/hw) Ecuación de
Metzner y Gluck
Para el cálculo de NPr,w y NGr,w se utiliza el valor de viscosidad aparente para la
temperatura y el gradiente de velocidad en la pared.
0.75
1/3
0.14
Num= hm D/k = 1.75 [Gz + 0.0083 (NPr,w NGr,w
]
(h/hw)
Ecuación de
Oliver y Jenson.
Ambas usan hm con DT= Tw - 0.5 (Tent + Tsal)
Ejemplo:
Un plástico de Bingham fluye a 355 kg/h y 37°C por una tubería de cobre de 2.56
cm de diámetro. Luego de una longitud suficiente para alcanzar el perfil de
velocidad desarrollado, el fluido entra a una sección de calentamiento de 1.83 m
de longitud en la que el tubo de cobre se rodea de una camisa de vapor que
3
condensa a 93°C. Se encontraron las siguientes propiedades: r= 1043 kg/m ; Cp=
2
3342 J/kgK; k= 1.211 W/mK; hpl 42°C = 0.089 Pas; so 42°C= 7.2 kg/ms .
Compruebe si con dicha longitud de tubo, la temperatura de salida del fluido
posibilita utilizar las propiedades encontradas.
Solución
2
2
<u> = 4m/p D r = 4* 355/(3.14 * 0.0256 * 1043 * 3600) = 0.18 m/s
4
Num= hm D/k = 1.75 [(m Cp /kL) (3(1-c)/(c - 4c + 3))]
Para el plástico de Bingham:
3
1/3
4
Q/pR =( sw/4hpl) [1-1.75 c + 1/3 c ] donde c= so/sw
3
4
Qhpl /pR sw = [3-4 c + c ] / 12
4
<u>hpl/R so = [3-4 c + c ] / 12c = 0.18 * 0.089/ ( 0.0128* 7.2) = 0.174
De aquí se puede calcular c= 0.503
4
Num = 1.75{ [ 355 * 3342 / ( 3600* 1.211* 1.83)] [ 3(1-0.503)/ 0.503 - 4*0.503 + 3]
1/3
}
Num = 10.41
2
hm= Num*k/D = 10.41 * 1.211/0.0256 = 493 W/m K
Planteando balance de energía en la sección de calentamiento:
Q= m Cp (Tsal - Tent) = hm p D L ( Tw - 0.5 (Tent + T sal))
493 * 3342 / 3600 ( Tsal -37) = 493 * 3.14* 0.0256* 1.83 (93 - 0.5(37 + Tsal))
Despejando Tsal = 48.1°C
Como la viscosidad plástica y el esfuerzo de fluencia estaban a 42°C, que es la
temperatura media entre 37 y 48.1°C, es válido el uso de éstas.
Ejemplo:
Un fluido que cumple la ley de potencia fluye a 0.073 kg / s y 37°C, por un tubo de
cobre de 0.0256 m de diámetro. Luego de una longitud suficiente para alcanzar el
perfil de velocidad desarrollado, el fluido entra a una sección de calentamiento de
1.83 m de longitud en la que el tubo de cobre se rodea de una camisa de vapor
3
que condensa a 93°C. Se encontraron las siguientes propiedades: r= 1204 kg/m ;
n
n
Cp= 3342 J/kgK; k= 1.211 W/mK; n = 0.4; K37°C=144 Pa s ; K60°C = 100 Pas ;
n
K93°C = 64.5 Pas . Determine hm y Tsal. Realice el cálculo con cada una de las
relaciones válidas estudiadas para tener un estimado de valores mínimos y
máximos. Se conoce que la caída de presión a lo largo de la sección de
-1
calentamiento es 111988 Pa y que el coeficiente de expansión be = 0.00061 K .
Solución
1/3
a) Utilizando la ecuación Num= hm D/k = 1.75 d Gz
d= (3*0.4+1) / (4*0.4) = 1.375
Gz = m Cp/ kL = (0.073*3342) / (1.211 * 1.83)= 110
Num = 1.75 ( 1.375 )
1/3
( 110)
1/3
= 9.3
1/3
2
hm= Num * k /D = 9.3* 1.211 / 0.0256 = 440 W/m K
Del balance de energía se calcula Tsal
m Cp (Tsal - Tent) = hm p D L ( Tw - 0.5 (Tent + T sal))
Tsal = [hm p D L ( Tw - 0.5 Tent)+ m Cp Tent] / [(0.5 hm p D L ) + m Cp] = 50.1°C
b) Utilizando la ecuación de Charm y Merrit
1/3
0.14
Num = hm D/k= 2.0 (mCp/kL) [ (Kb( 3n+1))/(Kw *2(3n-1))]
Requiere Kb a la temperatura media del fluido. Tomemos como temperatura de
salida la obtenida en el inciso anterior.
T media = 0.5 (37 + 54.5) =45.8°C
A partir de los tres valores de K dados de dato se puede calcular la dependencia
de K vs T según:
n
K = Ko [ exp ( E / RT)] donde R es la constante de los gases. Se encuentra que
n
Ko= 0.746 Pas
E/R = 4097 K, n=0.4
n
Para 45.8°C = 318.8 K se encuentra K = 127.4 Pas
Num =2.0 [(0.073* 3342/(1.211* 1.83)]
14.8
1/3
0.14
[ (127.4( 3*0.4+1))/(64.5 *2(3*0.4-1))]
2
hm= 14.8* 1.211/0.0256= 700 W/m K
Tsal = 56.5°C
c) Utilizando la ecuación de Metzner,Vaughn y Houghton, sin convección natural:
Num= hm D/k = 1.75 d
Num = 1.75 ( 1.375 )
1/3
1/3
Gz
1/3
( 110)
0.14
(h/hw)
1/3
0.14
(127.4/ 64.5)
2
= 10.23
hm= 10.23* 1.211/0.0256= 484 W/m K
Tsal= 51.2 °C
d) Utilizando la ecuación de Metzner y Gluck con convección natural:
1/3
0.4 1/3
0.14
Num= hm D/k = 1.75 d [Gz + 12.6 (NPr,w NGr,w D/L ] (h/hw)
hap = sw/ gw = DPD/4L / gw = 111988* 0.0256 /(4*1.83) / gw = 391.6 /gw
n
En la pared, el valor del gradiente de velocidad es: sw = Kw gw
=
1/0.4
-1
gw = (391.6/ 64.5) = 90.8 s
hap = 391.6/ 90.8 =4.31 Pas
NuPr,w= Cp hap /k = 3342* 4.31 / 1.211 =11894
DT= Tw - 0.5 (Tent + Tsal) = 93 - 0.5 (37 + 54.5)=47.3°C Se consideró la Tsal del
primer inciso como aproximación.
3
2
2
NuGr,w = be DT D r g / hap = 0.00061*47.3 * 0.0256
2
=0.357
Num= hm D/k = 1.75 d
1/3
0.4 1/3
[Gz + 12.6 (NPr,w NGr,w D/L ]
Num= hm D/k = 1.75* 1.375
0.14
64.5)
3
1/3
* 1204
2
* 9.8 / 4.39
0.14
(h/hw)
0.4 1/3
[110+ 12.6 (0.357*11894*0.0256/1.83 ) ]
(127.4/
= 11.96
2
hm = 565 W/m K
Tsal = 53.3 °C
Como se aprecia los valores se encuentran entre 50.5°C y 56.5°C para la
2
2
temperatura de salida y entre 440 W/m K y 700 W/m K para hm.
Transferencia de calor en flujo turbulento
Cuando en un cilindro fluye un líquido caliente, estando la pared del cilindro a una
temperatura menor, se aprecian 3 zonas en el interior del cilindro: una turbuenta
desarrollada en el centro, una laminar cerca de la pared del cilindro y una
transiente entre ambas. En la región central, la energía se transfiere rápidamente
debido a los eddies, con lo que el perfil de temperatura varía muy poco. En la capa
laminar los eddies son despreciables y el calor se transfiere por conducción, con lo
que la variación del perfil de temperatura es pronunciada. En la zona del transiente
se manifiestan ambos mecanismos.
El comportamiento de la temperatura para el flujo turbulento, tomando en cuenta
las fluctuaciones debidas a las eddies se representa por T = T + T', donde T'
representa la fluctuación y T la variable independiente de los cambios en el tiempo.
La ecuación diferencial que relaciona el transporte de calor en flujo turbulento es:
(l)
(t)
(l)
rCp DT/Dt = - ( Ñ.q ) - Ñ . q + m F v + mF v
(l)
(t)
(l)
donde q =-kÑT ;F v = disipación viscosa
Para poder resolver la ecuación y encontar los perfiles de temperatura, se han
desarrollado teorías y correlaciones semiempíricas. Una de ellas es la de la
longitud de mezclado de Prandtl según la cual el transporte de momentun y de
energía se realiza en flujo turbulento por un mecanismo similar y:
(t)
2
(t)
2
qy = -rCp l |dux/dy| dT/dy. Aquí l es la longitud de mezclado. Esta ecuación es
válida en conductos y se recomienda que l = k1 y donde y es la distancia de la
pared.
Para la región cercana a la pared Deissler propuso la ecuación:
2
qy = -rCp a ux y (1-exp(-a ux y/n ))dT/dy, siendo n la viscosidad cinemática = m/r
El uso de estas expresiones generales para el caso de un cilindro conlleva a la
siguiente solución:
En la región central: Los perfiles de temperatura y velocidad son similares.
Definiendo variables adimensionales
+
+
+
0.5
u = uz/u* ; T = rCp u* (T-Tw)/qw ; s = s u* r/m, siendo u* = (sw/r)
; s=R-r
+
+
+
+
+
T - T1 = 1/ k1 ln s /s1 Para s >26 y s1 = 26 posición entre la zona transiente y
turbulenta desarrollada.
(l)
(t)
Para la región cercana a la pared: qr + qr = qw
+
+
T =òds /[NPr
+
-1
2 + +
2 + +
+
+ a u s (1-exp(-a u s ))] Esta expresión se integra entre 0 y s y es
válida para s < 26.
Como se puede apreciar el perfil dependerá de la posición y del Número de
Prandtl. A mayor NPr el perfil es menos pronunciado, es decir la diferencia de
temperatura entre la región laminar y la turbulenta es menor.
Correlaciones obtenidas del análisis dimensional
Para fluidos newtonianos, si NRe > 10000, 0.7> NPr < 700, L/D >60
0.8
1/3
-0.054
Num =0.036 NRe NPr (L/D)
Cuando hay efectos de entrada por ser L/D <60, Nusselt recomienda el uso de la
ecuación válida para 10< L/D<400, evaluando las propiedades a la temperatura
representativa del seno del fluido (bulk) Num =0.023 NRe
-1
0.8
NPr
-1/3
1/3
0.14
(mb/mw)
0.14
.
Cuando NRe > 20000, al representar log (NumNReb NPrb (mb/mw) ) vs log
NReb las curvas convergen en una línea recta. A medida que el flujo aumenta,
aumenta el Número de Reynolds, la temperatura de salida disminuye
primeramente hasta NRe = 2100, luego aumenta hasta NRe = 8000 y luego
decrece nuevamente.
Aunque el flujo turbulento es deseable porque incrementa la velocidad de
transferencia de calor, el alcanzarlo en fluidos no newtonianos no es común debido
a la alta consistencia. Los estudios no son amplios y se limitan al flujo en
conductos circulares.
Para fluidos que cumplen la ley de potencia, Clapp obtuvo la siguiente correlación
empírica:
n
2-n
n-1 0.99
n-1
0.4
hmD/k = 0.0041 ( D <u> r / K' 8 )
[(K'Cp/k) (8<u>/D) ]
Otras ecuaciones particulares pueden ser encontradas en literatura especializada
en dependencia del fluido en estudio.
Ejemplo
Estudio experimental de la transferencia de calor para fluidos que cumplen la ley
de potencia. (Desarrollados por I. Filkova y colaboradores)
5
Para que exista convección natural se debe cumplir que Gr Pr > 8 * 10 . Para
fluidos que cumplan la ley de potencia el máximo valor encontrado de Gr Pr =
1867, de donde predominará la convección forzada.
Perfiles de velocidad y temperatura.
Una tubería circular puede dividirse en tres zonas: entrada, transiente y la región
de flujo totalmente desarrollada.
Entrada: Los perfiles de velocidad y temperatura se desarrollan simultáneamente.
Se requiere una longitud hidráulica para lograr el perfil desarrollado (lh) .
Para fluidos newtonianos lh = 0.064 NRe D
Para fluidos que cumplan la ley de potencia lh = 0.05 NRePL D
Transiente:El perfil de velocidad está totalmente desarrollado pero no el de
temperatura.Se define una longitud térmica lT = 0.036 NPe D donde NPe = D u Cp
r / k. Observe cómo la longitud térmica es independiente del comportamiento
reológico del fluido.
Se trabajó con 4 fluidos no newtonianos, 3 soluciones de CMC y jugo de tomate y
seleccionaron las siguientes ecuaciones para verificar los resultados
experimentales:
Región de entrada:
+
1/3
Nux=1.41[p(3n+1)/(8 x n)]
1/3
Nux=4.36[(3n+1)/(4n)]
Región transiente:
(K/Kw)
(0.1/n0.7)
(0.1/n0.7)
(K/Kw)
1/3
Válida para X=2x/NPeD < 0.05
Válida para X=2x/NPeD >0.05
1/3
Nux=1.411[(3n+1)/(4 n)] Grx
Los resultados obtenidos fueron:
La longitud hidráulica encontrada fue menor que la predicha por lh = 0.05 NRePL
D o sea la región de entrada es más corta y pesa menos en el proceso de
transferencia.
-0.36
Se encontró una ecuación para la región de entrada Nux = 1.229 X
para X = 2x/NPe D < 0.05, siendo x la distancia axial.
Para el transiente: Nux = 1.972 Gzx
0.274
1/3
[(3n+1)/(2(3n-1)) (K/Kw)]
para X > 0.05
LECCIÓN 30. EFECTO EN LA TRANSFERENCIA DE MASA
Generalidades (Recordatorio de la asignatura Fenómenos de Transporte)
La ley de Fick describe el movimiento de una especie, digamos A, a través de una
mezcla, debido al gradiente de concentración de A, de la zona de alta
concentración de A a la de baja concentración de A. (La Termodinámica
demuestra que es el potencial químico la variable pero bajo determinadas
consideraciones puede expresarse en función de la concentración, lo cual facilita
los cálculos). En la mezcla, las velocidades de las diferentes especies son distintas
por lo que se hace uso de una velocidad local que promedie la de las diferentes
especies.Así se definen:
Velocidad de la especie i respecto a ejes fijos:
u = S( ri ui) /Sri = velocidad másica promedio
u* = S(ci ui)/Sci= velocidad molar promedio.
Velocidad difusional de la especie i respecto a la de la mezcla:
ui - u = velocidad difusional respecto a u
ui - u* = velocidad difusional respecto a u*
De igual forma se define el flujo másico relativo a ejes estacionarios :
ni = ri * ui (másico)
Ni = ci * ui (molar)
El flujo másico relativo a la velocidad másica promedio
ji = ri ( ui - u) (másico)
Ji = ci ( ui - u ) (molar)
El flujo másico relativo a la velocidad molar promedio
ji* = ri ( ui - u*) (másico)
Ji* = ci ( ui - u* ) (molar)
Los más utilizados son Ni, ji, Ji*.
En dependencia del flux utilizado y del gradiente utilizado la Ley de Fick establece
que:
Flux
Ja*
ja
Gradiente
Ñ xa
Ñ wa
1ra Ley de Fick
Ja* = c DabÑ xa
ja= -r DabÑ wa
Na
Ñ xa
Na= -c DabÑ xa+
xa(Na+Nb)
2
Dab: difusividad másica (m /s); c: concentración molar total; xa: fracción molar; wa
: fracción másica.
Si deseamos expresar el número de moles de la especie a que atraviesa una
unidad de área en una unidad de tiempo en una dirección determinada, por
ejemplo z:
Naz= -c Dabdxa/dz + xa(Naz+Nbz)
Ejemplo en que el mecanismo de difusión es molecular:
Se necesita transferir una mezcla de metano y aire (xmetano= 0.8) desde un
recipiente a 101kPa y 20°C hasta otro a iguales condiciones pero que contiene una
mezcla de metano y aire (xmetano=0.1). La distancia entre los tanques es del 0.1
m y el diámetro del conducto 2 cm. Calcular la velocidad de transporte del metano
si el mecanismo por el que se transfiere es la difusión molecular. Se conoce que
-5
2
Dab = 1.68* 10 m /s
Solución:
Si la temperatura y la presión son constantes y el transporte es sólo por difusión
molecular Na =-Nb, de donde
Naz= -c Dabdxa/dz = - (P/RT) Dabdxa/dz
Para z= 0 ; xa=0.8
Para z= 0.1; xa= 0.1
Sustituyendo e integrando:
Naz= - 101000/(8.314* 293) (1.68* 10
-5 ) (0.8-0.1) / 0.1
= 4.9 * 10
-3
Para calcular la velocidad de transporte Naz= Naz* área= 4.9 * 10
2
-6
2
mol/m s
-3
* (3.14* 0.02
/4)= 1.5* 10 mol/s.
Ejemplo en el que el mecanismo de difusión involucra transporte molecular y
flujo global:
Un tanque abierto cilíndrico está lleno de metanol hasta una altura de 0.6 metros
del borde superior. El diámetro del tanque en la sección ocupada es de 1.8m. En la
parte superior, el tanque se estrecha teniendo 1.2 m de diámetro. Esa sección
sobre el nivel de metanol, de área variable, está ocupada por aire estacionario. La
circulación de aire exterior garantiza que la concentración de metanol en la boca
del tanque pueda considerarse despreciable. El tanque y el aire están a 101 kPa y
2
25°C. La difusividad del metanol en el aire a esas condiciones es 0.159 cm /s.
Calcular la velocidad de escape de metanol del tanque.
Solución:
La situación física será metanol difundiéndose a través de 0.6m de aire
estacionario, desde el nivel del líquido en el tanque hasta el borde superior de
éste.
La concentración de metanol en el aire en la superficie del líquido se determina a
partir de los datos de presión de vapor del metanol a 25°C que es 17.9 kPa.
Como el aire está estático Nbz = 0
Naz = -c Dab dxa/dz + xaNaz
Naz = (-cDab / (1-xa)) (dxa/dz)
Como el área es variable debemos encontrar la relación del diámetro con z. Se
conoce que para z=0, el diámetro es 1.8m y que para z=0.6, el diámetro es 1.2m,
de donde D = 1.8 - z
2
Si Naz = moles de a /t/área = flujo molar de a/ área = fma/0.7854D :
2)
fma dz/ (0.7854 (1.8-z) = (-cDab / (1-xa)) (dxa)
De la ley de Dalton Pa = xaP de donde xa= 17.9/101= 0.1776
Los límites de integración serán:
z=0; xa= 0.1776
z=0.6; xa=0
-1
-1
Naz [ 1.2 - 1.8 ]/ 0.7854= (P/RT)Dab [- ln (1-0.1776)]
-4
Naz= 3.6*10 mol/s
Ecuaciones de cambio para sistemas binarios y multicomponentes.
La ecuación de continuidad para el componente A de un sistema binario en
coordenadas cilíndricas es : (Coordenadas r: radial,q:angular,z:axial)
-1
-1
dca/dt + r (d (rNar)/dr+ r (dNaq/dq + dNaz/dz) = Ra, donde Ra son los moles
producidos por unidad de volumen y por unidad de tiempo.
Si r y Dab son constantes:
-1
-1
-2
2
2
dca/dt + ur dca/dr + uq r (d ca/dq)+uz dca/dz =Dab [r (d (rdca/dr)/dr + r d ca/dq
2
2
+ d ca/dz ] +Ra
El análisis físico de la situación bajo estudio llevará a la solución de la ecuación
diferencial.
Cuando el sistema es multicomponente:
La ecuación de continuidad para cada especie es: rDwi/Dt = - Ñ.ji) + ri
La ecuación de movimiento es: r Du/Dt = - [Ñ. p] + S ri gi
donde p = s + Pd; siendo p el tensor de presiones, s el tensor de esfuerzo; P la
presión estática y d un vector unitario.
La ecuación de energía es:
2
rD(U+.5 u )/Dt= -(Ñ.q) - (Ñ.[p.u]) + S (ni.gi)
Utilización de coeficientes de transferencia para el análisis del flujo laminar
en tubos.
Cuando se trabaja con líquidos muy viscosos, el régimen laminar es común, a
pesar de que los coeficientes de transferencia son menores que para el régimen
turbulento. Si los componentes de la mezcla tienen densidades diferentes, las
variaciones de densidad debidas a los gradientes de concentración, inducirán la
convección natural, incrementando la velocidad de transferencia de masa por
encima de la que se debía esperar para solamente la difusión.
Las analogías entre la transferencia de calor y la de masa permiten utilizar las
correlaciones ya estudiadas para la transferencia de calor, para expresar el
transporte de masa, si se modifican el NPr por el NSc y el Nu por el Nuab. Esta
analogía es válida cuando se consideran las propiedades físicas constantes,
pequeñas velocidades de transferencia de masa, no disipación viscosa, no
reacción química en el fluido, difusión molecular y condiciones de contorno
similares. El NSc = mDab/r
Así por ejemplo para la convección libre alrededor de un objeto sumergido:
Num = f(NGr, NPr) para la transferencia de calor
Nuabm = igual función ( NGrab, NSc) para la transferencia de masa
De forma análoga:
-1
-1/3
jH= Nu NRe NPr
-1
2/3
= h/(rCpm) (Cpm/k)
-1/3
para la transferencia de calor
2/3
jD= Nuab NRe NSc = kx/(c u) (m/rDab) para la transferencia de masa
Estas analogías permiten determinar perfiles de concentración a partir de perfiles
de temperaturas o coeficientes de transferencia de masa a partir de correlaciones
para determinar coeficientes de transferencia de calor.
Coeficientes de transferencia de masa para flujos turbulento en tubos.
Para transporte molecular:
Naz = Naz/A = kc' (ca1- <ca>) donde la fuerza motriz es la Dc y la resistencia
-1
(Akc')
0.83
0.33
Nuab=kc'D/Dab = 0.023 (NRe)
(NSc)
Los datos exclusivos para gases arrojan un exponente para el NSc de 0.44, válido
para NSc entre 0.6 y 2.5. Para líquidos NSc= 1000. Usar 0.44 o 0.33 no afecta
prácticamente.
La mayor parte del gradiente de concentración cae en la subcapa laminar al igual
que sucedía con el gradiente de temperatura y el de velocidad.
Cuando se tiene un fluido que se difunde a través de otro estacionario:
0.83
0.33
Nuab=kcD/Dabcbml/ct = 0.023 (NRe)
(NSc)
Aquí = cbml = (cb1 - <cb>)/ ln (cb1/<cb>) o sea la media logarítmica y b es el otro
componente
Ejemplo:
Una columna de pared húmeda de 5cm de diámetro contiene aire y CO2 que
fluyen a 1m/s. En un punto de la columna la concentración de CO2 en el aire es
xCO2= 0.1. En el mismo punto la concentración de CO2 en el agua en la interfase
aire-agua es xCO2 =0.005. La columna opera a 1010kPa y 25°C . Calcule el
coeficiente de transferencia de masa y el flujo de masa en el punto en
consideración.
Solución:
2
Dab a 25°C y presión atmosférica= 0.164cm /s; NSc = 0.94
Se requiere corregir el valor de Dab para la presión de trabajo. NSc no necesita
corrección.
2
Dab2=Dab1 (P1/P2)= 0.164 (101/1010) = 0.0164 cm /s
La presión parcial de CO2 en la fase gaseosa= 0.1 Ptotal = 101 kPa
La concentración de CO2 en el líquido en la interfase es 0.005. La presión parcial
de CO2 en la fase gaseosa en la interfase es la presión de vapor sobre el líquido.
De la ley de Henry se tiene :
PCO2 = H xCO2. Como la constante de Henry es 1640atm: PCO2 = 1640 * 0.005=
8.2 atm = 828.2 kPa.
Dada la baja concentración de CO2 se puede considerar las propiedades de la
mezcla como las del aire:
m aire = 0.018 mPas
r aire = 11.9 kg/m3
-3
NRe = r<u> D/m = 11.9*1*0.05/0.018 * 10 =33055 (Verificado el flujo turbulento)
El aire es muy poco soluble en agua de donde estamos ante el caso de difusión a
través de un gas que no se difunde.
Calculemos cbml/ct = Pbml/Pt
Pbml = (Pb1 - <Pb>)/ ln (Pb1/<Pb>)
Como Pb=Pt-PCO2
Pbml= [(1010-828.2) - (1010-101)] / ln [(1010-828.2)/(1010-101)]=451.8kPa
Pbml / Pt = 451.8 / 1010 = 0.447
kc= 0.023 (Dab /D) (Pt/Pbml)(NRe)
-4
0.83
0.33
(NSc)
0.83
kc= 0.023 (0.0164*10 /0.05) (1/0.447) (33055)
-3
kc = 9.32 * 10 m/s
0.33
(0.94)
-3
Naz = -kc/RT ( PCO21 - <PCO2>) = - 9.32 * 10
-3
2
/( 8.314*298) (828.2-101)=
2.73*10 mol/m s.
La transferencia se realiza desde la pared hasta el centro del tubo, dado el signo
negativo.
Transferencia de masa en la interfase.
Las operaciones industriales de transferencia de masa pueden implicar el contacto
entre dos fases. La columna de paredes mojadas (como el ejemplo anterior) tiene
áreas de transferencia pequeñas de donde se prefiere el uso de burbujas,
aspersiones, etc . En éstas se ponen en contacto dos fases para transferir masa a
través de una interfase. Los solutos que se transfieren de una fase a la otra pasan
por la interfase, debiendo quedar definidas las capas de resistencias que atraviesa
desde la concentración del soluto en el seno, digamos de la fase líquida, hasta la
concentación de soluto en el seno de la fase gaseosa.
Na = - (Pai-PaG)/ (1/AkG)= - (caL - Cai)/ (1/AkL) donde :
Na : velocidad de transferencia del soluto
2
kG:coeficiente de transferencia de masa para la fase gaseosa (mol/sPa m )
2
3
kL: coeficiente de transferencia de masa para la fase líquida (mol/sm mol/m )
Se define una resistencia total para la transferencia de masa con área común A
1/AKG = 1/AkG + m/AkL
1/AKL = 1/mAkG + 1/AkL
donde m es un factor de distribución que relaciona la presión parcial Pa* del soluto
en la fase gaseosa en equilibrio con una concentración de soluto en la fase líquida
ca* y KG y KL los coeficientes totales de transferencia de masa de la fase gaseosa
y líquida respectivamente.
Na = - (Pa*-PaG)/ (1/AKG)= - (caL - ca*)/ (1/AKL)
Transferencia de oxígeno en fermentadores
Cuando se burbujea un gas soluble en un líquido, el flux se expresa como: J = kLa
(c*g - cL), siendo c*g la concentración de saturación del gas en el líquido, cL es la
concentración de gas en el seno del líquido, Pg es la presión parcial de gas en la
fase gaseosa y kLa el coeficiente volumétrico de transferencia de gas. c*g= Pg /
kH donde kH es la contante de la ley de Henry. La determinación de kLa requiere
de suposiciones como la de que la concentración del gas en el seno del fluido es
constante. Esto se cumple si los fermentadores son de tamaño pequeño e
intermedio y los fluidos no son muy viscosos.
Para transferir un gas (por ejemplo aire) a un fluido en un tanque agitado, el gas se
tiene que dispersar en el líquido. A velocidades de agitación bajas, el patrón de
flujo depende de la corriente de gas, pero si se aumenta la velocidad de agitación
(unas 3 veces respecto a la potencia de expansión isotérmica del gas) el patrón de
flujo será controlado por el agitador, con lo que habrá que aumentar aún más la
potencia del agitador para que las burbujas de gas alcancen el fondo del tanque
(unas 5 veces respecto a la de la energía de expansión de la corriente del gas).
Por otra parte si a agitación fija se incrementa el flujode gas, el agitador no podrá
dispersar el gas (Transferencia de masa y mezclado de procesos biológicos. E.
Galindo, UNAM, México) . En el caso de fluidos viscosos, en general se puede
plantear que al aumentr la viscosidad, se forman cavidades de aire con valores
bajos de aireación, disminuyendo la potencia gaseada en relación con la potencia
cuando no hay gas.
Correlaciones para determinar kLa
Son muchas las correlaciones empíricas que se recogen en la literatura. Para
fluidos de baja viscosidad, en general siguen la expresión:
a
b
kLa a (Pg/V) us
Pg: potencia de agitación en conduciones aireadas (W)
3
V: volumen del líquido (m )
-1
us: velocidad superficial del gas (m s )
Cuando los fluidos son viscosos no newtonianos, la tendencia es a que aumente
kLa a medida que aumente la velocidad de agitación. Las correlaciones son del
tipo:
-m
kLa a h siendo m = 0.4 - 0.6
Cuando la aereación es la controlante el exponente es 0.33.
Los trabajos de Nienow con carboximetilcelulosa (CMC) presentan la siguiente
correlación:
-0.45
0.66
0.34
3
kLa a h
(Pg/V)
(Qg) donde Qg es el flujo volumétrico de gas (m /s).
A partir de esta correlación puede analizarse que en las etapas finales de la
fermentación de un fluido viscoso, para aumentar el valor de kLa es necesario
variar la potencia de agitación, ya que la reducción del coeficiente por efecto del
valor de viscosidad es grande. Esto no sucede así en los inicios de la fermentación
en que la viscosidad es aún relativamente baja.
Ejemplo:
Transferencia de oxígeno en sistemas fermentativos no newtonianos.
Son muchos los sistemas fermentativos que se caracterizan por un
comportamiento seudoplástico. Debido a esta seudoplasticidad ocurren problemas
de mezclado en caldos de fermentación en tanques agitados, los que originan
problemas con la transferencia de oxígeno y problemas para el escalado. En
muchos caldos la viscosidad aumenta apreciablemente durante el curso de la
fermentación por el incremento de la masa celular y/o la acumulación de productos
de alta masa molar. Esto sucede por ejemplo con caldos de fermentación de
polisacáridos extracelulares, hongos, levaduras de alta densidad, etc. Los altos
niveles de viscosidad que se alcanzan y que con el incremento en los rendimientos
de los procesos siguen en elevación, dificultan el escalamiento de un producto por
no lograrse los niveles adecuados de transferencia de oxígeno y mezclado en la
escala mayor.
Se estudió un sistema de fermentación para la producción de xantano, de una
naturaleza muy seudoplástica y que cumple la ley de potencia. Se modeló el
sistema de fermentación considerando el fermentador constituido por 3
compartimientos, V1, V2, V3, 2 de ellos (V1 y V2) con la posibilidad de intercambio
de flujo entre ellos:
• V1: región agitada a altos gradientes de velocidad y baja viscosidad (buen
mezclado y transferencia de oxígeno)
• V2: región de bajo gradiente de velocidad y alta densidad (pobre mezclado y
transferencia de oxígeno).
• V3: zona muerta.
La modelación arrojó que aumentando la zona agitada, instalando impelentes
múltiples, aumentando el diámetro del impelente y/o aumentando la velocidad de
agitación, se mejoraban las características.
El uso del NRe modificado vs NPo permite predecir el consumo de potencia en un
fluido no newtoniano.
h = K' (8 <u> /D)
n'-1
n
= K ((3n+1)/4n) (8 <u> /D)
a
b
n-1
c
Para estimar kLa se usa: kLa = (Pg/V) us h
3
Para concentaciones de xantano de 30 kg/ m (K= 22 Pas, n = 0.26) se encontró
-1
3
3
kLa = 0.004 - 0.008 s y P/V = 2 - 4.5 kW/ m en un reactor de 0.05 m con
3
3
impelente de turbina de 6 hojas y consumo de oxígeno de 0.5 m /m min.
Al reemplazar la turbina por un impelente Intermig axial de diámetro impelente/
diámetro tanque = 0.6, kLa es 4 veces mayor y el consumo de potencia igual.
Resumen de las analogías entre las transferencias de masa, calor y
momentum.
La analogía de Reynolds.
Fue el primer reconocimeinto al comportamiento análogo de las velocidades de
transferencia de momentum y calor. Su aplicación es limitada, pero para estudiar
los fenómenos en la capa límite ha sido de gran utilidad. Postula que los
mecanismos de transferencia de calor y momentum son iguales y por tanto:
h/Cp*r*<u> = f/8 = NSt = Número de Stanton= Nu/ (NRe* NPr ) Caracteriza datos
para gases en fujo turbulento.
Puede escribirse una analogía para la transferencia de masa: kc' = f/8 válida
también para gases en flujo turbulento.
Finalmente se ha concluido que cuando NPr = NSc = 1 los mecanismos para la
transferencia de masa, calor y momentum son idénticos.
La analogía de Colburn
2/3
0.14
NSt NPr (mw/m)
= f/8 = jH Esta ecuación es un enunciado de la analogía de
Colburn y es válida para 10000 < NRe < 300000 y 0.6< NPr<100. Nótese que si
NPr = 1 y (mw/m) =1 coincide con la analogía de Reynolds.
2/3
De igual forma se obtiene: kc'/<u> * (NSc)
300000 y 0.6< NSc<2500
Así jH = jN = f/8 y de ahí:
2/3
= f/8 = jD Válida para 2000 < NRe <
2/3
(h/Cpr ) NPr = kc' (NSc)
Otras analogías se han desarrollado y presentan un mejor grado de extensión
(Ejemplo la analogía de Martinelli).
Ejemplo:
Compare el valor del Nu del aire dado por la ecuación empírica apropiada, con el
predicho por las analogías de Reynolds y de Colburn, para el calentamiento del
aire a 38°C en un tubo de temperatura en la pared 66°C, si el NRe = 100000
Datos:
2
m
m
Cp(J/kg°C NPr(38°C
mPas(38° J/sm (°C/
mPas(66°
)
)
m)
C)
C)
0.0255
1004.58
0.71
0.02
Aire
0.018
Solución:
La ecuación empírica apropiada es Nu= 0.023 (NRe)
0.8
1/3
Nu= 0.023 (100000) (0.71)
Por la analogía de Reynolds:
0.14
(0.018/0.02)
0.8
1/3
(NPr)
0.14
(mw/m)
= 204 Valor más preciso
0.2
f=0.184/ (NRe) Para NRe = 100000, f= 0.0184
NSt = f/8 = 0.0184/8= 0.0023
Nu= NRe NPr f/8= 100000* 0.71* 0.0023 = 164.2 Mayor alejamiento
Por la analogía de Colburn:
NSt NPr
2/3
0.14
(mw/m)
1/3
= f/8
0.14
1/3
0.14
Nu= NRe NPr f/8 (m/mw) = 100000 * 0.71 * 0.0023* (0.018/0.02) = 204
Preguntas y problemas propuestos
1. El perfil de velocidad para un fluido newtoniano se expresa según: u= (DP/4mL
2
2
)(R -r ). Exprese el gradiente de velocidad en función de la posición radial.
(Recuerde que g = -du/dr).
2. Si Ud. deseara mantener un perfil de velocidad lo más uniforme posible, ¿qué
material seleccionaría, un puré de albaricoque o uno de melocotón, ambos de 17%
de sólidos y a 26 °C?(Utilice los datos del apéndice 6 del texto básico)
n
3. Una compota de manzana (cumple la ley de potencia con K= 60Pas ; n= 0.3; r =
3
1050 kg/m ) se bombea a 27°C desde un tanque abierto a través de una tubería
sanitaria de 0.0254 m hacia un segundo tanque, abierto que se encuentra a mayor
altura. El flujo másico es 1 kg/s y recorre 30m de conducto con 2 codos y una
válvula de ángulo. El tanque suministrador mantiene un nivel de líquido de 3m y la
compota abandona el sistema a una altura de 12m sobre el nivel del suelo.Calcule
la energía de bombeo. (Tomado de C. Daubert)
4. Se utiliza una bomba para mover catsup desde el fondo de un recipiente
cilíndrico. El nivel del fluido se encuentra 10m sobre el nivel de la bomba. El
diámetro de la tubería que conecta la bomba con el recipiente es de 5cm , tiene 8m
de longitud y posee un codo a 90°C. Las propiedades del catsup son: r= 1150
3
n
kg/m , constantes de la ley de potencia K= 10.5 Pa s y n= 0.45. Si el flujo
volumétrico es 35 L/min y el tanque se encuentra a 45kPa, calcule la presión a la
entrada de la bomba requerida para entregar dicho flujo.
n
5. Un fluido que cumple con la ley de potencia (K= 13.6 Pa s ; n= 0.4; r =1094
3
kg/m )se bombea a un flujo másico de 600 kg/h desde un recipiente de gran
diámetro hasta un punto de descarga a 10 m de altura sobre la superficie del
líquido en el tanque. El fluido abandona el recipiente a través de una tubería de
5.25 cm de diámetro,que está colocada a 3m por debajo de la superficie del líquido
en el tanque. Luego de 15m existe una contracción a una tubería de 3.8 cm de
diámetro la cual se extiende horizontalmente 5 m hasta la entrada de la bomba. La
salida de la bomba alimenta 12m de tubería de 3.81cm de diámetro, la que
contiene un codo a 90° colocado a 6m de la bomba. El líquido dirigido
verticalmente por el codo pasa a una tuberíade 7.3cm de diámetro. Este último
tramo tiene 30 m de longitud y finaliza en un codo a 90° que descarga el fluido
horizontalmente a la atmósfera Determine la potencia del motor de la bomba para
una eficencia global de 0.4.
6. Por un tubo liso de 0.03 m de diámetro interior fluye aire a 310K y presión
atmosférica. El tubo tiene una longitud de 5 m. La caída de presión entre los
extremos del tubo es 7500 Pa. Estime el coeficiente de transferencia de calor por:
• La ecuación empírica apropiada.
• La analogía de Reynolds
• La analogía de Colburn
BIBLIOGRAFÍA
1. Bird, R.; W. Stewart y E. Lightfoot: Transport Phenomena, Ed. Revolucionaria,
Instituto del Libro, Cuba, p. 79, 1969.
2. Bongenaar, J. y col.: A method for characterizing the rheological properties of
viscous fermentation broths. Biotechnology and Bioengineering, Vol 15, 201 206, USA, 1973.
3. Broadfoot, R.; K. Miller: Rheological studies of massecuites and molasses. Int.
Sugar J. Vol 92 (1098), 107 - 110, Ingaterra, 1990: Vol 92 (1099), 143 - 147,
GB, 1990.
4. Castell - Pérez, M.; J. Steffe: Evaluating shear rates for power law fluids in mixer
viscosity. J. Texture Stud. 21, 439 - 453, USA, 1990.
5. Castell - Pérez, M.; J. Steffe; R. Moreira: Simple determination of power law flow
curves using a paddle type mixer viscometer. J. Text. Stud, 22, 303 - 316, USA,
1991.
6. Chirinos, M. y col.: Slip flow of bitume in water emulsion in a tube viscometer,
Proceedings of the Fourth European Rheology Conference, Ed. C. Gallegos,
España, p. 182, 1994.
7. Davidson, V.; J. White; G. Hayward: On line viscosity measurement in food
systems. En: Eng. And Foods Tomo 1 Editores: W. Spiess and H. Schubert.
Elsevier App. Sc. 752- 760, GB, 1989.
8. Díaz, I.; R. Consuegra: El ultrasonido como método de medición continua de
masas cocidas de tercera. Tec. Quím. Año 3 ( 3 ), 89 – 96, Cuba, 1982.
9. DIN 53019: Medida de la viscosidad y curvas de flujo mediante un viscosímetro
de rotación con geometría standard, Parte I, mayo, 1980.
th
10. Eirich, F.: Rheology: theory and applications, Ed. Academic Press, 3 Ed. Vol 1,
USA, p.575,1968.
11. Foust, A. y col.: Principios de Operaciones Unitarias, Ed. Continental, p.188,
México, 1987.
12. Garcell, L.; A. Díaz; G. Surís: Transferencia de cantidad de movimiento, calor y
masa, Editorial Pueblo y Educación, Cuba, 1988.
13. Glasstone, S.: Tratado de Química Física, Ed. Revolucionaria, Instituto del
Libro Cuba, 1968.
14. Gondrit, P.; L. Petit: Viscosity measurement on disordered and ordered
suspensions under oscillating shear flow. Proceedings of the Fourth European
Rheology Conference. Ed. C. Gallegos, 65 - 66, España, 1994.
15. González Alomá, C.: Estudio reológico de fluidos en el proceso de
cristalización de azúcar crudo. Trabajo de diploma. Facultad Azucarera,
ISPJAE, Cuba,1987.
16. González del Valle, I.: Design and calibration of a concentric cylinder
viscometer, Tesis de maestría, Louisiana State University, USA, 1970.
17. Happel, J.; H. Brenner: Low Reynolds number hydrodynamics, Ed. Prentice
Hall, USA, 1965.
18. Hatzikiriakos,S.; J. Dealy: Start- up pressure transients in a capillary rheometer.
Polymer Eng. and Sc. Vol 34 (6), 493 -499, USA, 1994.
19. Holland, F.; F. Chapman: Liquid mixing and processing in stirred tanks. Lever
Brothers Company, USA, 1966.
20. Hyman, W.: Rheology of power law fluids, Ind. Eng. Chem. Fundamentals, Vol
15 (3), 215-218, GB, 1976.
21. Kemblowski, Z.; B. Kristiansen: Rheometry of fermentation liquids.
Biotechnology and Bioengineering, Vol 28, 1474 - 1483, USA, 1986.
22. Kemblowski, Z.; J. Sek; P. Budzyuski: The concept of rotacional rheometer with
helical screw impeller. Rheol. Acta, 27, 82 - 91, Alemania, 1988.
23. Kemblowski, Z.; P. Budzyuski; P Owczarz: On line measurements of the
rheological properties of fermentation broths. Rheol. Acta 29, 588 - 593,
Alemania, 1990.
24. Leong - Poi, L.; D. Allen: Direct measurement of the yield stress of fermentation
broths with the rotating vane technique. Biotechnology and Bioengineering, Vol
40, 403- 312, USA,1992.
25. Maddleman, S.: The flow of high polymers continuum and molecular rheology,
Ed. Interscience Publishers, USA, 1968.
26. Maudarbocus, S.: El viscosímetro de orificio: una nueva técnica para medir
viscosidad de masas cocidas y mieles. Proc. Int: Soc: Cuban Cane Tech. Vol 3,
2257 - 2263, Cuba, 1980.
27. Mendivar, J.; R. Connely; K. Hsu: Application of a mixing recorder to determine
fundamental rheological properties of food materials. En: Eng. And Food. Tomo
1. Editores: W. Spies and H. Schubert. Elsevier App. Sc. 49 - 58, GB, 1989.
28. Metzner, A.; R. Otto: Agitation of non newtonian fluids. AICHE J. 3 (1),3 - 10,
USA, 1957.
29. Migrahi, S.; Z. Berk: Flow behaviour of concentrated orange juice: mathematical
treatment, J. Texture Stud., 3, p. 69 - 79, USA, 1972.
30. Muller, H.: Introducción a la reología de los alimentos, Ed. Acribia, España,
1992.
31. Ness, J.N.: Massecuites viscosity: some observations with a pipeline
viscometer. Proc. Aust. Soc. Sugar Cane Tech. , 195 - 200, Australia, 1980.
32. Newton, I.S: Philosophie Naturalis, Book 2 Section 9, 1687. En: Muller, H.
Introducción a la reología de alimentos, Ed. Acribia, España, p. 167, 1992.
33. Ofoli, R. y col.: A generalized rheological model for inelastic fluid foods, J.
Texture Stud., 18, p. 213 - 230, USA, 1987.
34. Olsvik, E.; B. Kristiansen: On line rheological measurements and control in
fungal fermentation. Biotechnology and Bioengineering, Vol 40, 375 – 387,
USA, 1992.
35. Pace, G.: Fermentor design and fungal growth. En: Fungal Biotech J. Editores:
E. Smith; D. Berry; B. Kristiansen. Academic Press 95 – 110, GB, 1980.
36. Picque, D.; G. Corrieu: New instrument for on – line viscosity massecuite of
fermentation media. Biotechnology and Bioengineering, Vol 31, 19 – 23, USA,
1988.
37. Qiu, G.; M.Rao: Quantitative estimates of slip of food suspensions in a
concentric cylinder viscometer, En: Eng. And Foods, T-I, Spiess, W; M.
Schubert (Editors) Ed. Elsevier App. Sc. GB, 40 -47, 1989.
38. Rao, M.: Predicting the flow properties of food suspensions of plant origin, Food
Tech., 41 (3), 85-88, USA, 1987.
39. Rodríguez I.; A. García; L. Fleites: Viscosímetro capilar para suspensiones
fibrosas. Centro Azúcar, 12 (3), 95 - 100, Cuba, 1985.
40. Roels, J. y col.: The rheology of mycelial broths. Biotechnogy and
Bioengineering, Vol 16, 181- 208, USA, 1974.
41. Sapronova, L.A.; V.I. Tuzhilkin: Análisis de la viscosidad de los productos en la
fabricación de azúcar refino mediante un viscosímetro ultrasónico. Sajarnaia
Prom. Junio, 53 - 55, URSS, 1981.( en ruso).
42. Sarmiento,G. y col.: Measurement of the rheological characteristics of slowly
settling floculated suspensions. Ind. Eng. Chem. Process Des. Dev. Vol 18 (4)
746- 750, GB, 1979.
43. Schramm, G.: Introducción a la viscosimetría práctica, Editado por Haake
Mess-Technik, Alemania, 1984.
44. Skelland, A.: Non newtonian flow and heat transfer, Ed. Revolucionaria,
Instituto del Libro, Cuba, p. 4 -17, 1970.
45. Steffe, J.: Rheological methods in food process engineering, Ed. Pergamon
Press, USA, 1992.
46. Toledo, R.: Fundamentals of food process engineering, Ed. Chapman Hall, 2
Ed., 161 - 231, USA, 1994.
47. Valverde, J.; A. de Lucas; L. Zumalacárregui and G. Surís: Improved Method
for Determining Rheological Parameters of Suspensions. AICHE J. Vol.43 (8),
1997, 2141-2145.
48. Valverde, J.; L. Zumalacárregui; A. de Lucas and G. Surís: An Improved
Method for Determining Rheological Parameters of Suspensions: Statistical
Approach. Trans. I. Chem. Eng. Vol.75 Part A, 1997, 784-791.
49. Velasco,.D.: Reología y mezclado de caldos de fermentación miceliales de
interés industrial. Tesis de Maestría. Instituto de Biotecnología UNAM, México,
1994.
50. Whorlow, R.: Rheological techniques, Ed. J. Wiley and Sons, USA, 1980.
51. Zumalacárregui, L: Estudio reológico de fluidos azucarados. Equipamiento
utilizado. Tesis de Doctorado. Ciudad de la Habana. 1997.