el sistema internacional de unidades en “la tecnología del concreto”

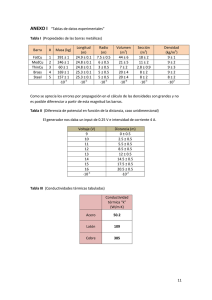
EL SISTEMA INTERNACIONAL DE UNIDADES EN
“LA TECNOLOGÍA DEL CONCRETO”
Autor: Ing. Jesús David Osorio
Las propiedades de los constituyentes del concreto se expresan en cantidades físicas, entre
las cuales figuran: la fuerza, el tiempo, la temperatura, la densidad y otras más. Muchos de
estos términos, tales como la temperatura y el tiempo, hacen parte del vocabulario
cotidiano, sin embargo expresados de esta manera pueden resultar insignificantes y no
adquieren el alcance que tienen, cuando se trata de estimar las propiedades que determinan
el comportamiento del concreto.
Las unidades que se han utilizado para designar las cantidades físicas han variado de un
lugar geográfico a otro, porque estaban asociadas a las características culturales de cada
pueblo, no obstante, durante el último siglo y como respuesta al avance que ha tenido el
desarrollo en todos los campos, se han hecho esfuerzos para mejorar el entendimiento
entre los científicos de todas las naciones y se ha adoptado el Sistema Internacional de
Unidades (abreviado con el símbolo SI), que se puede definir como el conjunto
sistemático y organizado de unidades adoptado por convención en el cual el producto o
cociente de dos o más de sus magnitudes, da como resultado la unidad derivada
correspondiente.
En Colombia sobre la tecnología del concreto se han conservado unidades tales como la
pulgada, el pie y la libra, en razón a que éstas se utilizaban como unidades regionales hasta
la década de los 80 en los Estados Unidos, y gran parte de los equipos utilizados para la
producción y el control de calidad de concreto eran procedentes de este país. Sin embargo,
en los Estados Unidos ya se inició el proceso de conversión al Sistema Internacional y las
normas que se están emitiendo, así como los equipos que se están produciendo, trabajan
con las unidades del sistema internacional (SI).
Con este orden de ideas, en Colombia es obligatorio utilizar el Sistema Internacional, los
informes que tengan implicaciones contractuales deben ser preparados en este sistema. En
los casos en que las unidades del Sistema Internacional no sean muy familiares, es
recomendable escribir entre paréntesis el valor con las unidades que sí lo sean. Ejemplo:
21 MPa (210 kg/cm2), (3000 PSI), 28 MPa (280 kg/cm2), (4000 PSI), 35 MPa (350
kg/cm2) (5000 PSI).
La nomenclatura, definiciones y símbolos de las unidades del Sistema Internacional de
Unidades se presentan en la Norma Técnica Colombiana NTC 1000.
1. Patrones del sistema internacional de unidades
Las unidades de medida son el valor de una magnitud para la cual se admite, que su valor
numérico es igual a uno (1) y permiten hacer una comparación cuantitativa entre diferentes
valores de una misma magnitud. Se acepta mundialmente que estas unidades de medida
tengan un patrón que garantice que una medición sea igual en cualquier sitio. Como en el
caso de la tecnología del concreto las magnitudes que más importan son la longitud, el
tiempo y la masa; a continuación, se presenta una breve descripción de los patrones
definidos para dichas magnitudes.
1.1. Patrón de longitud
El primer patrón internacional fue una barra de aleación Platino-Iridio conocida como
metro patrón y conservada en la oficina internacional de pesas y medidas, cerca de París,
Francia. Este metro se definió como la sustancia entre dos rayas trazadas sobre unos
botones de oro cerca a los extremos de la barra. Como el metro patrón no era muy
accesible, se hicieron copias maestras exactas de él y se mandaron a los laboratorios de
normas de las diferentes naciones. Estos patrones secundarios se usaron para comparar
otras barras todavía más accesibles, de tal forma que cada regla o calibrador derivaba su
autoridad legal del metro patrón a través de una cadena larga y complicada.
Posteriormente, se adoptó la longitud de una onda de luz como patrón de longitud, de tal
manera que el metro se define como la longitud del trayecto recorrido en el cesio por la luz
durante un intervalo de tiempo de 1/ 299 792 458 segundos.
1.2 Patrón de tiempo
La medición del tiempo presenta dos aspectos diferentes: en la vida cotidiana interesa
saber la hora del día para ordenar las actividades, mientras que en los laboratorios interesa
conocer cuánto dura un fenómeno.
Cualquier fenómeno natural que se repita puede usarse para medir el tiempo, por ello
desde tiempos antiguos se utilizó la rotación de la tierra al rededor de su eje o alrededor
del sol. Posteriormente, los relojes de cristal de cuarzo, basados en la vibración natural
periódica de una laminilla de cuarzo y en la actualidad los relojes atómicos basados en el
átomo de cesio, con los cuales es posible definir el segundo como la duración de 9 192
631 770 períodos de la radicación correspondiente a la transición entre los dos niveles del
estado fundamental del átomo de Cesio 133.
1.3 Patrón de masa
El patrón internacional adoptado es la masa de un prototipo de Platino-Iridio que se
conserva desde 1889 en la oficina internacional de pesas y medidas cerca de París,
Francia. Esta masa se definió y de ella se pueden hacerse replicas exactas que manejan los
laboratorios de normas de las diferentes naciones.
En la tabla No 1 se presentan las magnitudes fundamentales en el Sistema Internacional de
Unidades y en la tabla 2 se enumeran las unidades suplementarias y las aceptadas por el
SI.
Tabla 1. Nombres de las magnitudes utilizadas en el Sistema Internacional de Unidades.
UNIDADES SI FUNDAMENTALES
MAGNITUD
UNIDAD
SIMBOLO DEFINICION
LONGITUD
metro
m
Es la unidad SI de longitud
MASA
kilogramo
kg
Es la unidad SI de masa
TIEMPO
segundo
s
Es la unidad SI de tiempo
CORRIENTE
ampere
A
Es la unidad SI de intensidad de
ELÉCTRICA
corriente eléctrica
TEMPERATURA
kelvin
K
Es la unidad SI de temperatura
TERMODINÁMICA
termodinámica
INTENSIDAD
candela
cd
Es la unidad SI de intensidad
LUMINOSA
luminosa
CANTIDAD
DE mol
mol
Es la unidad SI de cantidad de
SUSTANCIA
sustancia
UNIDADES SI DERIVADAS QUE NO TIENEN NOMBRES ESPECIALES
MAGNITUD
NOMBRE
SIMBOLO
SUPERFICIE
metro cuadrado
m²
VOLUMEN
metro cúbico
m3
DENSIDAD
kilogramo por metro cubico
kg/m3
VELOCIDAD
metro por segundo
m/s
VELOCIDAD ANGULAR
radian por segundo
rad/s
ACELERACIÓN
metro por segundo cuadrado
m/s2
ACELARACIÓN ANGULAR
radian por segundo cuadrado
rad/s2
UNIDADES SI DERIVADAS QUE TIENEN NOMBRES ESPECIALES
MAGNITUD
UNIDAD
SIMBOLO
FRECUENCIA
hertz
Haz
FUERZA
newton
N
PRESIÓN
pascal
Pa
ENERGÍA,TRABAJO,CANTIDAD DE CALOR
joule
J
CANTIDAD
DE
ELECTRICIDAD,
CARGA watt
W
ELÉCTRICA
DIFERENCIA DE PONTENCIAL, VOLTAJE
coulomb
C
CANTIDAD ELÉCTRICA
farad
V
RESISTENCIA ELÉCTRICA
ohm
F
FLUJO LUMINOSO
lumen
W
ILUMINACIÓN
lux
lx
Tabla 2. Unidades suplementarias y aceptadas por el sistema internacional de unidades.
UNIDADES SI SUPLEMENTARIAS
MAGNITUD
UNIDAD SIMBOL DEFINICION
O
ÁNGULO PLANO radian
rad
Es la unidad SI de ángulo plano
ÁNGULO SÓLIDO estereoradi sr
Es la unidad SI de ángulo sólido
an
UNIDADES ACEPTADAS QUE NO PERTENECEN AL SI
MAGNITUD
NOMBRE SIMBOLO Valor en unidades SI
MASA
tonelada
t
1t=1000kg
TIEMPO
minuto
min
1min=60segundos
hora
h
1h=60min=3600segundos
día
d
1d=24h=86400segundos
TEMPERATURA grado
ºC
ºC=K-273,15 o K=ºC+273,15
Celsius
ÁNGULO PLANO grado
º
1º=(p/180)radianes
minuto
’
1’=(1º/60)=(p/10800)radianes
segundo
”
1”=( 1’/60)=(p/648000)radianes
VOLUMEN
litro
lól
1=1dm3=1 decímetro cúbico
2. Reglas para usar los símbolos
No se deben usar puntos después del símbolo de las unidades del Sistema Internacional.
En los casos en que por regla de puntuación gramatical se deba colocar un signo de
puntuación, éste se coloca dejando un espacio en blanco entre el símbolo y el
respectivo signo. Ejemplo: kg , MPa , ºC .
Los símbolos nunca se pluralizan, siempre se escriben en singular porque ellos
solamente representan la unidad. Ejemplo: 1 kg , 10 kg , 100 kg , etc. Sin embargo,
cuando se escribe el nombre de una unidad en plural se debe hacer de acuerdo con las
reglas de la gramática. Ejemplo: kilogramo- kilogramos, newton-newtons
No se deben abreviar los nombres de las unidades, siempre se debe escribir el nombre
completo o el símbolo correcto. Ejemplo: grs no corresponde a gramos, lo correcto es
escribir gramos o g.
No se deben combinar los nombres y símbolos al expresar el nombre de una unidad
derivada. Ejemplo: kilogramo/m³ , lo correcto es kg/m³ o kilogramo/metro cúbico.
Todos los símbolos del Sistema Internacional de Unidades se escriben en minúsculas,
excepto aquellos que provienen del nombre de científicos. Ejemplo: kilogramo - kg ,
Pascal - Pa y Newton - N .
Los símbolos deben estar separados un espacio en blanco de los valores numéricos.
Ejemplo 21 MPa , 5 m , 5 g .
Todo valor numérico debe expresarse con su unidad, incluso cuando se repite o cuando
se especifica la tolerancia. Ejemplo: 24 h ± 4 h .
El nombre completo de las unidades del Sistema Internacional de Unidades se escribe
con la letra minúscula, con la única excepción de grado Celsius, salvo al comenzar la
frase o luego de un punto.
Correcto
gramo
newton
metro
Incorrecto
Gramo
Newton
Metro
2.1 Uso de la coma
La coma es reconocida como el signo ortográfico de escritura de los números, empleados
en informes de laboratorio.
La ventaja de usar la coma para separar la parte entera del decimal es muy grande ya que
es más visible que un punto y por lo tanto no se pierde en el fotocopiado, ampliación o
reducción de informes. Así mismo, se distingue mucho más fácilmente que un punto y no
puede ser alterada, mientras que un punto puede ser transformado en coma.
2.2 Uso de los prefijos
Los prefijos se anteponen a los nombres o símbolos de las unidades para denotar los
múltiplos o submultiplos de las mismas, por ejemplo para indicar que se trata de 1000
gramos se antepone el prefijo kilo a la unidad gramo. Los prefijos que se usan en el
Sistema Internacional de Unidades se consignan en la tabla 3.
Tabla 3. Prefijos que se usan en el Sistema internacional de Unidades.
NOMBRE
exa
penta
tera
giga
maga
kilo
hecto
deca
SIMBOLO
E
P
T
G
M
K
H
Da
FACTOR
1018
1015
1012
109
106
103
102
101
NOMBRE
deci
centi
mili
micro
nano
pico
femto
atto
SIMBOLO
d
c
m
m
n
p
f
a
FACTOR
10-1
10-2
10-3
10-6
10-9
10-12
10-15
10-18
Todos los nombres de los prefijos del Sistema Internacional de Unidades se escriben
con letra minúscula. Ejemplo: kilo, mega, mili, micro.
Los símbolos de los prefijos para formar múltiplos se escriben con letra latina
mayúscula, excepto el prefijo kilo, que por convención se escribe con letra (k)
minúscula.
Los símbolos de los prefijos para formar los submúltiplos se escriben con letra latina
minúscula, excepto el símbolo del prefijo micro, para el cual se usa la letra (mu)
minúscula del alfabeto griego.
No se deben usar dos o más prefijos delante del símbolo o nombre de la unidad de
medida.
Es recomendable escoger los múltiplos y submúltiplos de las unidades de manera que
los valores numéricos estén entre 1 y 1000.
La fecha se debe escribir en el orden siguiente: año, mes, día utilizando un guión para
separarlos.
Ejemplo:
9 de mayo de 2010
10-05-09
2.3 Factores de conversión
En las tablas 4 a la 10 se presentan las unidades más comunes en la tecnología de concreto
y los factores para convertir de una unidad a otra. A continuación se indica la forma de
usar estas tablas.
 Localice la columna con el nombre de la unidad que desea convertir.
 Dentro de esta columna identifique el renglón que tiene el número uno (1). Es la celda
que está sombreada.
 Desplácese en el mismo renglón hasta encontrar la columna de la unidad a la que
desea convertir. Este es el factor de conversión.
 Multiplique por este factor y el valor resultante estará en las unidades de esa columna.
Tabla No 4. Factores de conversión de unidades de longitud.
Km
m
cm
105
100
1
10
30,48
2,54
1000
1
0,01
10-3
0,3048
0,0254
1
10-3
1 x 10-5
10-6
3,048 x 10-4
2,54 x 10-5
LONGITUD
mm
6
10
1000
10
1
304,8
25,4
pie (ft)
3281
3,281
0,03281
3,281 x 10-3
1
2,778 x10-2
pulgada (in)
3,937 x 107
39,370
0,3937
3,937 x 10-2
12
1
Ejemplo:
Para convertir pulgadas a metros, el factor de conversión es 0,0254 , de tal forma que al
multiplicar pulgadas por 0,0254 se obtiene su equivalente en metros:
5 in * 0,0254 m/in = 0,127 m
Para convertir pies a centímetros, el factor de conversión es 30,48 , de tal forma que al
multiplicar pies por 30,48 se obtiene su equivalente en centímetros
3 ft * 30,48 cm/ft = 91,44 cm
Tabla No 5. Factores de conversión de unidades de área.
AREA
km²
1
10-6
10-10
10-12
9,29 x 10-8
6,45 x 10-10
m²
10-6
1
10-4
10-6
9,29 x 10-2
6,45 x 10-4
cm²
1010
104
1
10-2
929
6,4516
mm²
1012
106
100
1
92900
645,16
ft2
1,076 x 107
10,764
1,076 x 10-3
1,076 x 10-5
1
6,944 x 10-3
in2
1,550 x 109
1550
0,1550
1,550 x 10-3
144
1
Ejemplo:
Para convertir pulgadas cuadradas (in²) a centímetros cuadrados, el factor de conversión
es 6,4516, de tal forma que al multiplicar pulgadas cuadradas por 6,4516 se obtiene su
equivalente en centímetros cuadrados:
25 in² * 6,4516 cm²/in²= 161,29 cm²
Para convertir centímetros cuadrados a pies cuadrados, el factor de conversión es 1,076
x 10-3, de tal forma que al multiplicar centímetros cuadrados por 1,076 x 10-3 se
obtiene su equivalente en pies cuadrados.
5 000 cm² * 1,076 x 10-3 ft²/cm² = 5,38 ft²
Tabla No 6. Factores de conversión de unidades de volumen.
m
3
3
dm (l)
1
10-3
10-6
2,832 x 10-2
3,788 x 10-3
1,639 x 10-5
10-3
1
10-3
28,32
3,785
1,639 x 10-2
VOLUMEN
cm (ml)
ft3
106
35.311
3
10
3,531 x 10-2
3,531 x 10-5
1
2,832 x 10-4
1
3
3,785 x 10
0,1337
16,387
5,787 x 10-4
3
Galón*
264,17
0,2642
2,642 x 104
7,481
1
4,329 x 10-3
in3
6102
61,02
6,102 x 10-2
1728
231
1
* Galón americano
Ejemplo:
Para convertir pies cúbicos a decímetros cúbicos (Litros), el factor de conversión es
28,32 , de tal forma que al multiplicar pies cúbicos por 28,32 se obtiene su equivalente
en decímetros cúbicos:
0,5 ft3 * 28,32 dm3/ft3 = 14,16 dm3 (l)
Para convertir litros a metros cúbicos, el factor de conversión es 10-3, de tal forma que
al multiplicar litros por 10-3 se obtiene su equivalente en metros cúbicos.
5 000 l * x 10-3 m3/l = 5 m3
Tabla No 7. Factores de conversión de unidades de masa.
MASA
tonelada
1
10-3
10-6
4,536 x 10-4
kg
1000
1
10-3
0,4536
g
106
1000
1
453,6
lb
2.205 x 103
2,2046
2,204 x 10-3
1
Ejemplo:
Para convertir libras a kilogramos, el factor de conversión es 0,4536, de tal forma que
al multiplicar libras por 0,4536 se obtiene su equivalente en kilogramos:
5 lb * 0,4536 kg/lb = 2,268 kg
Para convertir toneladas a libras, el factor de conversión es 2,204 x 103, de tal forma
que al multiplicar toneladas por 2,204 x 103 se obtiene su equivalente en libras.
0,5 t * x 2,204 x103 lb/t = 1 102 lb
Tabla 8. Factores de conversión de unidades de densidad
DENSIDAD
3
t/m
g/cm3
1
10-3
27,680
1,602 x 10-2
kg/m
1000
1
27680
16,019
3
lb/in3
0,03613
3,613 x 10-5
1
5,787 x 10-4
lb/ft3
62,43
6,243 x 10-2
1,728 x 103
1
Ejemplo:
Para convertir libras por pulgada cúbica a tonelada por metro cúbico (o g/cm3) , el factor
de conversión es 27,68 , de tal forma que al multiplicar libras por pulgada cúbica por
27,68 se obtiene su equivalente en tonelada por metro cúbicos:
0,55 lb/in3 * 27,68 (t/m3)/(lb/in3) = 15,224 t/m3
Para convertir libras por pie cúbico a kilogramos por metro cúbico, el factor de
conversión es 16,019, de tal forma que al multiplicar libras por pie cúbico por 16,019 se
obtiene su equivalente en kilogramos por metro cúbico.
150 lb/ft3 * x 16,019 (kg/m3)/(lb/ft3) = 2 402,85 kg/m3
Tabla No 9. Factores de conversión de unidades de fuerza.
kN
1
10-3
9,807 X 10-3
9,964
4,448 X 10-3
N
3
10
1
9,807
9964
4,448
FUERZA
kgf
101,96
0,10196
1
1016
0,45455
tonf
0,1004
1,004 X 10-4
9,842 X 10-4
1
4,464 X 10-4
lbf
224,82
0,2248
2,2048
2240
1
Ejemplo:
Para convertir libras fuerza a kilonewtons, el factor de conversión es 4,448 x 10 -3 , de
tal forma que al multiplicar libras fuerza por 4,448 x 10 -3 se obtiene su equivalente en
kilonewtons:
1500 lbf * 4,448 x 10 -3 (kN)/(lb f) = 6,72 kN
Para convertir kilogramos fuerza a newtons, el factor de conversión es 9,807 , de tal
forma que al multiplicar kilogramos fuerza por 9,807 se obtiene su equivalente en
newtons.
500 kgf * 9.807 (N)/(kgf) = 4 903,5 N
Tabla No 10. Factores de conversión de unidades de esfuerzo.
N/mm²
MPa
1
0,001
9,807 x 10-2
0,100
6,895 x 10-3
kN/m²
kPa
1000
1
98,07
100
6,895
ESFUERZO
kp
kgf /cm²
10,197
1,019 x 10-2
1
1,0197
7,031 x 10-2
bar
10
0,0100
0,9807
1
6,895 x 10-2
psi
lbf /in2
145,04
0,14504
14,223
14,504
1
Ejemplo:
Para convertir libras fuerza por pulgada cuadrada a megapascales, el factor de
conversión es 6,865 x 10 -3 , de tal forma que al multiplicar libras fuerza por pulgada
cuadrada por 6,895 x 10 -3 se obtiene su equivalente en megapascales:
3040 psi * 6,895 x 10 -3 (MPa)/(psi) = 21 MPa
Para convertir kilogramos fuerza por centímetro cuadrado a megapascales, el factor de
conversión es 9,807 x 10-2, de tal forma que al multiplicar kilogramos fuerza por
centímetro cuadrado por 9,807 x 10-2 se obtiene su equivalente en megapascales.
214 kgf/cm² * 9.807 x 10
-2
(MPa)/(kgf/cm²) = 21 MPa