universidad distrital francisco jose de caldas facultad de ciencias y

UNIVERSIDAD DISTRITAL FRANCISCO JOSE DE CALDAS
FACULTAD DE CIENCIAS Y EDUCACIÓN
PROYECTO CURRICULAR DE MATEMÁTICAS
PROYECTO:
TRANSFORMADA DE FOURIER EN GRUPOS ABELIANOS FINITOS
Presentado por:
DIEGO ALEJANDRO GUZMAN DIAZ
Director:
MILTON LESMES ACOSTA
Bogota, D.C.
29 de octubre de 2015
UNIVERSIDAD DISTRITAL FRANCISCO JOSE DE CALDAS
FACULTAD DE CIENCIAS Y EDUCACIÓN
PROYECTO CURRICULAR DE MATEMÁTICAS
PROYECTO:
TRANSFORMADA DE FOURIER EN GRUPOS ABELIANOS FINITOS
TRABAJO DE GRADO PARA ASPIRAR AL TITULO DE MATEMÁTICO.
Presentado por:
DIEGO ALEJANDRO GUZMÁN DIAZ
Director:
MILTON LESMES ACOSTA
Bogota, D.C.
29 de octubre de 2015
Tabla de Contenidos
Preliminares
0.1. Introducción . . . . . . . . . .
0.2. Planteamiento del Problema
0.3. Objetivos . . . . . . . . . . . .
0.3.1. Objetivo General . . .
0.3.2. Objetivos Especı́ficos .
II
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ii
iii
iv
iv
iv
1. Conceptos Basicos
1.1. Concepto de grupo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Grupos Abelianos Localmente Compactos . . . . . . . . . . . . . . .
1
1
4
2. Representación de grupos finitos
2.1. Equivalencia unitaria e irreducibilidad . . .
2.2. El álgebra de grupo . . . . . . . . . . . . . . .
2.3. Caracteres . . . . . . . . . . . . . . . . . . . . .
2.4. Transformada de Fourier en grupos finitos
2.5. Ejemplos de la Transformada de Fourier . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
6
. 7
. 7
. 9
. 11
. 12
Conclusiones
15
Bibliografı́a
16
i
Preliminares
0.1.
Introducción
En la construcción de esta monografı́a de antemano se dará una definición de Representaciones unitarias finito-dimensionales que son la base de esta monografı́a, esta definición se
aplicara en la creación de equivalencias unitarias e irreducibilidad de las mismas, álgebras
de grupos, caracteres y relaciones de ortogonalidad y en el análisis de Fourier.
Ahora se quieren presentar resultados sobre la Representación de grupos finitos, que puedan aplicarse para obtener propiedades o demostrar teoremas sobre los grupos mismos.
En matemática la palabra representación básicamente significa función que preserva estructuras. Luego, en teorı́a de grupos y anillos, una representación es un homomorfismo.
Mas especı́ficamente, deberı́a ser un homomorfismo desde un objeto (grupo o anillo) que
uno esta tratando de estudiar hacia otro que es mas fácil de entender.
Un problema fundamental de la teorı́a es determinar todas las representaciones de dimensión finita de un grupo dado G, sobre un cuerpo algebraicamente cerrado K. Este
problema no sólo es interesante en sı́ mismo y por sus aplicaciones en otros campos, sino
que es importante para entender la estructura interna del grupo G. Las posibles soluciones
de estos problemas se encuadran en dos casos radicalmente diferentes: cuando la caracterı́stica del cuerpo es cero o no divide al orden del grupo G, y cuando la caracterı́stica de
K divide al orden de G.
ii
iii
0.2.
Planteamiento del Problema
Las representaciones de grupos finitos no solo se limitan a homomorfismo de funciones,
también es posible ampliarla a isomorfismos de funciones, pero lo principal es ver las
representaciones a través de transformadas de Fourier con gran aplicación de los caracteres
en la creación de estas transformadas.
Debido a lo anterior se ve la necesidad de plantear la siguiente pregunta ¿ ES POSIBLE
DESARROLLAR LA TEORÍA NECESARIA DESDE EL ÁLGEBRA, ANÁLISIS Y TOPOLOGIA PARA LA REPRESENTACIÓN DE GRUPOS FINITOS Y EN PARTICULAR LA TRANSFORMADA DE FOURIER DE FUNCIONES SOBRE LOS GRUPOS
ABELIANOS FINITOS? para una mayor comprensión del tema.
iv
0.3.
Objetivos
0.3.1.
Objetivo General
Analizar, comprender y explicar los detalles matemáticos implı́citos en el desarrollo de
representación de grupos finitos y como puede aplicarse al álgebra de grupo, caracteres y
análisis de Fourier.
0.3.2.
Objetivos Especı́ficos
Definir el desarrollo de la representación de grupos finitos.
Detallar la creación de álgebras de grupo y caracteres aplicando las representaciones.
Implementar la teorı́a de representación de grupos finitos al análisis de Fourier.
Capı́tulo 1
Conceptos Basicos
En este capitulo se dan a conocer algunos conceptos matemáticos importantes para el
desarrollo y realización de este trabajo.
1.1.
Concepto de grupo
”
Definición 1.1.1 Un grupo es un conjunto de elementos {g1 , g1 , . . .} dotados de una
ley de composición (multiplicacion), que a cada par ordenado gi , gj ∈ G le asigna otro
elemento gi gj de forma tal que se satisfacen las siguientes propiedades
1. (Cierre). La ley de composición es interna, si gi , gj ∈ G , entonces gi gj ∈ G
2. (asociatividad). Para todo gi , gj , gk ∈ G se tiene que gi (gj gk ) = (gi gj )gk
3. (elemento unidad). Existe un único elemento, denotado usualmente e, con la propiedad de que ∀gi ∈ G se cumple que egi = gi e = gi
4. (inverso). para cada gi existe un único elemento gi−1 tal que gi−1 gi = gi gi−1 = e
Definición 1.1.2 La multiplicación en general no es conmutativa; es decir, en general
gi gj 6= gj gi . Decimos que G es abeliano cuando gi gj = gj gi para todo par gi , gj .
Definición 1.1.3 El numero de elementos de G se denomina orden de G, y se designa
como (G).
1
2
Si el orden es un numero finito, decimos que G es un grupo grupo finito. La forma mas
inmediata de presentar a un grupo finito consiste en mostrar su tabla de multiplicidad,
.
g1
g2
..
.
g1
g1 g1
g2 g1
..
.
g2
g1 g2
g2 g2
..
.
...
...
...
..
.
g(G)
g1 g(G)
g2 g(G)
..
.
g(G)
g(G) g1
g(G) g2
...
g(G) g(G)
en al que no puede haber repetición de elementos en una misma fila, gg1 6= gg2 , ni
columna g1 g 6= g2 g. la propiedad de asociatividad ha de verificarse separadamente. Si el
grupo es abeliano, la tabla es simétrica respecto de la diagonal principal.
Ejemplo
las simetrı́as de paralelepı́pedo orientado con la composición de rotaciones. Es uno de
los dos grupos finitos de orden 4. Es abeliano,
.
e
Ry (π)
Rz (π)
e
e
Ry (π)
Rz (π)
Ry (π)
Ry (π)
e
Rx (π)
Rz (π)
Rz (π)
Rx (π)
e
Definición 1.1.4 Para todo elemento g de un grupo finito, existe un numero natural n tal
que g n = e, al que se denomina orden de g. Al conjunto {g, g 2 , . . . , g n ≡ e} se le denomina
ciclo de g en G
Definición 1.1.5 Sea una aplicación entre dos grupos f : G → G, , tal que preserva sus
respectivas leyes de composicion, es decir:
∀g1 , g2 , g3 ∈ G
g1 g2 = g3 ⇒ f (g1 )f (g2 ) = f (g3 )
Si la aplicación es uno a uno se le denomina isomorfismo (se dice en este vaso que
G y G, son isomorfos).
Definición 1.1.6 Si la correspondencia no es uno a uno pero se preserva la ley de composición se dice que G y G, son homomorfos, Si G = G, la aplicación recibe el nombre
de automorfismo.
3
Ejemplo
Sean Z6 = {e, a, a2 , a3 , a4 , a5 } y Z2 = {e, , b}. La aplicación σ : Z6 → Z2 :
σ(e) = σ(a2 ) = σ(a4 ) = e,
σ(a) = σ(a3 ) = σ(a5 ) = b
es un homomorfismo. En cambio, ρ : Z6 → Z6 :
ρ(e) = e
ρ(a) = (a5 )
ρ(a2 ) = a4
ρ(a3 ) = a3
ρ(a4 ) = a2
ρ(a5 ) = a
es un automorfismo (a cada elemento se le asocia su inverso y el grupo es abeliano).
Definición 1.1.7 la notación de ciclos permite identificar los elementos de Sn de un
modo sencillo. Consiste en identificar ciclos cerrados de permutaciones dentro del elemento
considerado.
Definición 1.1.8 Un ciclo de dos elementos es llamado trasposicion. Cualquier n-ciclo
puede ser escrito como el producto de n-1 trasposiciones:
(12. . . n) = (1n). . . (13)(12).
Definición 1.1.9 Un subgrupo H de un grupo G que a su vez forma un grupo bajo la
misma ley de composición de G. El elemento neutro y el propio G son dos subgrupos triviales (impropios) de G. Cualquier otro subgrupo que no sea ninguno de estos de denomina
subgrupo propio. Solo hace falta verificar que la composición es cerrada en H y que todo
elemento tiene inverso. Cuando G es finito solo debe verificarse que la ley de composición
es cerrada (el inverso existe trivialmente: si hr = e entonces hr−1 = h−1 )
Definición 1.1.10 Dos elementos g1 y g2 de un grupo G son conjugados si existe un
tercer elemento g talque g2 = gg1 g −1 . Si actúa sobre un espacio vectorial, la equivalencia
bajo conjugación surge de la ambigüedad en la elección de la base de dicho espacio. La conjugación establece relación de equivalencia ∼ entre los elementos de G. Efectivamente
podemos verificar que es:
1. (reflexiva) a ∼ a, en virtud de que a = ea = ae.
2. (simétrica) a = gbg −1 ⇒ b = g , ag ,−1 , con g , = g −1 .
3. (transitiva) a = gbg −1 y b = hch−1 , ⇒ a = (gh)c(gh)−1 .
Definición 1.1.11 dada una relación de equivalencia, la clase de equivalencia de un
elemento g, que denotaremos como (g), se define por:
4
(g) = {g , ∈ G|g , ∼ g}
La subdivisión de un conjunto en clases de equivalencia es una partición en subconjuntos disjuntos. Si g , ∈ (g) y g , ∈ (h), g , = g1 gg1−1 y g , = g2 hg2−1 . Por lo tanto,
h = (g2−1 g1 )g(g2−1 g1 )−1 , es decir (h) = (g). Todo grupo G admite una descomposición
en clases de conjugación. El elemento e constituye una clase conjugada. El numero de
clases de conjugación es menor o igual (si es abeliano) que el orden del grupo.
Definición 1.1.12 Un subgrupo normal o invariante H ⊂ G verifica
gHg −1 = H ∀g ∈ G
Están compuestos de clases de conjugación completas. Ademas, sus cosets por la izquierda
y por la derecha coinciden gH = Hg
Definición 1.1.13 Un grupo G es simple si no posee ningún subgrupo invariante propio.
Se dice que G es semisimple si ninguno de sus subgrupos invariantes es abeliano.
Definición 1.1.14 Sea g ∈ G, se denomina centralizador de g al conjunto de todos
los elementos x ∈ G que conmutan con g, xg = gx. Es un subgrupo (no necesariamente
abeliano). De hecho, si xg = gx e yg = gy, xyg = gxy (ley interna) y ∃x−1 tal que
x−1 x = e, entonces, x−1 xg = x−1 gx = gx−1 x ⇒ x−1 g = gx−1 (incluye al inverso).
Definición 1.1.15 El centro Z, de un grupo Ges el subconjunto de elementos z, que
conmutan con todos los elementos de G,
Z = {z ∈ G | zg = gz
∀g ∈ G}
Es la intersección de todos los centralizadores. Es invariante y abeliano.”[2]
1.2.
Grupos Abelianos Localmente Compactos
”Un grupo abeliano localmente compacto (LCA) es un grupo abeliano, digamos G,
que es al mismo tiempo un espacio localmente compacto Hausdorff y las operaciones del
grupo son continuas. Para ser precisos : si escribimos la operación del grupo como adición,
el requisito de continuidad es que tanto asignaciones x 7→ −x de G en G y (x, y) 7→ x + y
de GxG en G son continuos. para un x ∈ G fijo, la funcion y 7→ x + y es un homomorfismo
de G sobre sı́ mismo que se lleva a 0 en x. Ası́, la naturaleza topológica de G en cualquier
x ∈ G es el mismo ya que está en 0.
5
Ejemplo
Cualquier grupo abeliano G es trivialmente un grupo LCA con la topologı́a discreta.
El grupo cı́rcular T y la recta real R con la topologı́a usual.
Sea G un grupo LCA y H un subgrupo cerrado , entonces H con la estructura
inducida es un grupo LCA . Lo mismo es cierto para el grupo cociente G/H si le
aplicamos la topologı́a cociente canónica es decir, si estamos de acuerdo en que un
conjunto U de G/H es abierto si y sólo si, su preimagen en G es abierta.
LA MEDIDA HAAR
Sea G un grupo abeliano localmente compacto. Una medida de Haar sobre G es una
medida regular positivo µ Borel que tiene las dos propiedades siguientes:
1. µ(E) < ∞ si E es compacto;
2. µ(E + x) = µ(E) para todo grupo medible E ⊂ G y todo x ∈ G.
Una prueba que existe siempre una medida de Haar y que es único por la multiplicación por
una constante positiva; por abuso de lenguaje se puede por lo tanto, hablar de la medida
de Haar. La medida de Haar de G es finita si y sólo si, G es compacto y es entonces por
lo general normalizado para tener una solo medida total. Si G = T o G = Tn la medida
de Haar es simplemente la medida normalizada de Lebesgue. Si G = R la medida de
Haar es de nuevo un múltiplo de la medida de Lebesgue. Si G es discreto, la medida de
Haar es generalmente normalizada para tener una sola medida en cada punto. Si G es la
suma directa de G1 y G2 , la medida de Haar G es la medida del producto de las medidas
de Haar G1 y G2 . La medida de Haar en la suma directa completa de una familia de
grupos compactos es el producto de las correspondientes medidas de Haar normalizadas.
En particular, la medida de Haar en el grupo D corresponde a la bien conocida medida
Lebesgue en el conjunto de Cantor, el homeomorfismo definido anteriormente también
preserva la medida.”[5]
Capı́tulo 2
Representación de grupos finitos
”A lo largo de esta monografia G denotara un grupo f inito al que le dotamos de la
topologia discreta, convirtiéndolo de este modo en grupo topológico. También G se dota
de una medida, la medida de contar o número de elementos.
Definición: Representaciones finito- dimensionales
Sea G un grupo finito. Una representación (lineal) de G (sobre k) es un par (V, π), donde
V es un espacio vectorial y π es un homorfismo de grupos.
π : G → GL(V ).
En tal caso también diremos que π es una representación (lineal) de G en V . Para simplificar la notación, y si no hay peligro de confusión, dada una representación (V, π) de G
para cada g ∈ G y cada v ∈ V notaremos gv := π(g)(v), de manera que se tiene las reglas
1v = v, g(hv) = (gh)v, g, h ∈ G, v ∈ V .
De manera análoga, podemos definir una representacion matricial de G de orden d (sobre
k) como un homomorfismo de grupos π : G → GL(d, k). Toda representación matricial de
G de orden d determina una representación (lineal) es el espacio vectorial k d
Un ejemplo de ver las representaciones sobre grupos finitos es tomar a Z12 y realizar su
representación a través de matrices como se muestra a continuación:
π : Z12 →
1
0
0 Z12
!
6
7

π : Z12
2.1.

1 0
0


→ 0 1
0 
0 0 Z12
Equivalencia unitaria e irreducibilidad
Si π1 y π2 son representaciones unitarias de G, un operador de entrelazado para π1 yπ2 es
un operador lineal T : Vπ1 → Vπ2 , donde Vπ es un espacio de Hilbert (finito-dimensional, no
nulo) tal que Tπ1 (g) = π2 (g)T para todo g ∈ G. El conjunto de estos operadores se denota
por HomG (Vπ1 , Vπ2 ). Vπ1 y Vπ2 se dicen unitariamante equivalentes si HomG (Vπ1 , Vπ2 )
contiene algún operador unitario. Escribiremos EndG (Vπ ) para HomG (Vπ , Vπ ).
Supongamos que M es un subespacio de Vπ , M se dice una subespacio invariante por
π si π(g)M ⊂ M para todo g ∈ G. Si M es un subespacio invariante no nulo de π, la
restricción de π a M
π M (g) ≡ π(g) |M
define una representación de G en M , se dice una subrepresentacion de π. Si π admite
un subespacio invariante no trivial (es decir, distinto de {0} y de Vπ ) diremos que π es
reducible, en otro caso π sera irreducible. De ahora en adelante π denotara representaciones unitarias irreducibles mientras que ρ denotara cualquier representación unitaria.
2.2.
El álgebra de grupo
Dado un grupo G, una función ϕ : G → C se puede expresar como Σg ϕ(g)δg donde δg
representa la delta de Dirac en g. El conjunto de tales funciones es un C-espacio vectorial
con la suma de funciones punto a punto. Queremos dotar a este espacio vectorial de un
producto interno heredado del producto en G. Para ello imponemos δg ∗ δh ≡ δgh de donde
se sigue la siguiente definición
ϕ1 ∗ ϕ2 = (
X
ϕ1 (g)δg ) ∗ (
g∈G
X
h∈G
ϕ2 (h)δh ) ≡
X
ϕ1 (g)ϕ2 (h)δgh =
g,h∈G
X X
(
ϕ1 (gh−1 )ϕ2 (h))δg
g∈G h∈G
Definición: Álgebra de grupo
Dado un grupo finito G, el espacio vectorial A(G) de funciones en G con valores en C se
dice algebra del grupo G cuando lo dotamos del producto de convolucion.
8
X
(ϕ1 ∗ ϕ2 (g)) ≡
ϕ1 (gh−1 )ϕ2 (h)
h∈G
y de la involucion
ϕ? (g) ≡ ϕ(g −1 )
Proposición 2.2.1 Sea ρ : G → U (Vρ ) una representacion de G, definimos la aplicación
ρ̃ : A(G) → End(Vp ) como
X
ρ̃(ϕ) ≡
ϕ(g)ρ(g)
(1.1)
g∈G
Entonces ρ̃ satisface
1. ρ̃(λ1 ϕ1 + λ2 ϕ2 ) = λ1 ρ̃(ϕ1 ) + λ2 ρ̃(ϕ2 )
2. ρ̃(ϕ1 ∗ ϕ2 ) = ρ̃(ϕ1 )oρ̃(ϕ2 )
3. ρ̃(ϕ? ) = ρ̃(ϕ)?
4. ρ̃(δ1 ) = 1Vρ
Recı́procamente, si ρ̃ satisface las propiedades (1), (2), (3) y (4) entonces existe una
representación unitaria ρ de G que verifica (1.1)
Observacion : Si dotamos a (A(G), +, ∗, ?) de la norma
X
kϕk2A(G) ≡
|ϕ(g)|2
g∈G
obtenemos una ? − algrbra de Banach con unidad δ 1 . De hecho este espacio no es mas que
es espacio de Hilbert L2 (G). En esta terminologı́a, la aplicación ρ̃ es una ?−representacion
del algebra de Banach A(G) y el teorema anterior afirma que existe una biyeccion entre
representaciones de G y ?−representaciones de A(G).
De ahora en adelante se manejara la siguiente notación:
1. Escribiremos indistintamente δg o g, con esta nueva notación la convolucion se comporta como el producto usual
(
X
g∈G
ϕ1 (g)g) ∗ (
X
h∈G
ϕ2 (h)h) =
X
ϕ1 (g)ϕ2 (h)gh =
g,h∈G
2. Nos referiremos a la función ρ̃ también por ρ.
3. Escribiremos indistintamente A(G) o L2 (G).”[1]
X X
(
ϕ1 (gh−1 )ϕ2 (h))g
h∈G h∈G
9
2.3.
Caracteres
”Un carácter en un grupo abeliano finito G es un homomorfismo continuo de G en el
grupo multiplicativo de los números complejos de módulo 1, que es decir, una función de
valor complejo-continua ξ(x) en G que satisface:
| ξ(x) |= 1 y ξ(x + y) = ξ(x)ξ(y).”[5]
Ejemplo
Si trabajamos sobre el grupo Z4 con los elementos Z4 = {0, 1, 2, 3} con la función ξ que es
el carácter se obtienen los siguientes resultados:
ξ1
0→1
1→i
2 → −1
3 → −i
ξ2
0→1
1 → −1
2→1
3 → −1
ξ3
0→1
1 → −i
2 → −1
3→i
ξ4
0→1
1→1
2→1
3→1
podemos darnos cuenta que ξ1 = e2πin , ξ2 = eπin , ξ3 = e3πin/2 y ξ4 = 1 donde los valores
de n son los mismos valores de Z4 , donde el conjunto de {ξ1 , ξ2 , ξ3 , ξ4 }, forman un grupo
abeliano finito.
”El carácter trivial es ξ(x) = 1 la identidad. Si G no es trivial hay caracteres que no
son triviales en él.
El conjunto G de todos los caracteres de G es claramente un grupo conmutativo multiplicativo (bajo la multiplicación puntual). Cambiamos la notación y escribimos la operación
b como la suma y la reemplazamos ξ(x) por < x, ξ > o algunas veces por
del grupo de G
iξx
e .
b al estipular que la convergencia en G
b es equivalente a
Introducimos una topologı́a de G
b son
la convergencia uniforme sobre subconjuntos compactos de G (los elementos de G
b está dado por conjuntos de
funciones en G). Por lo tanto, una base de vecindades 0 en G
la forma {ξ : | < x, ξ > −1| < ξ para todo x ∈ K} donde K es un subconjunto compacto
b son trasladados a vecindades de 0. No es
de G y ξ > 0. Vecindades de otros puntos en G
b es un grupo abeliano finito; lo llamamos el grupo dual
difı́cil ver que con esta topologı́a G
de G.
b El teorema de dualidad
Para cada x ∈ G, la funcion ξ 7→< x, ξ > define un carácter en G.
b tiene esta forma y que la topologı́a
de Pontryagin establece que todos los caracteres en G
10
b coincide con la topologı́a
de convergencia uniforme sobre subconjuntos compactos de G
b es el grupo dual de G, entonces G es el dual de G.
b
original en G. En otras palabras, si G
Ejemplo:
Para G = T con la topologı́a usual cada carácter tiene la forma de t 7→ e−int para cada
entero n, la topologı́a de convergencia uniforme sobre T es claramente la topologı́a discreta
b = Z. Del mismo modo, comprobamos Z
b = T; esto ilustra el teorema de dualidad de
yT
Pontryagin.
11
2.4.
Transformada de Fourier en grupos finitos
Definición: Transformada de Fourier en grupos finitos
Sea G un grupo finito y ϕ ∈ L2 (G), definimos la transf ormada de F ourier de ϕ como
ϕ(π)
b
≡ π(ϕ) =
X
ϕ(g)π(g) ∈ End(Vπ )
g∈G
ver definición en el libro Audrey Terras, Fourier Analysis on Finite Groups and Applications, pagina 261.
Teorema 2.4.1 Propiedades basicas de la transformada de Fourier en un grupo
finito.
1. P ropiedad de convolucion para la T ransf ormada de F ourier en G. Definiremos
la convolución de dos funciones ϕ1 y ϕ2 en G en el capı́tulo sobre el álgebra de grupo.
(ϕ1 ∗ ϕ2 (g)) ≡
X
ϕ1 (gh−1 )ϕ2 (h)
h∈G
entonces
ϕ\
c1 (π) · ϕ
c2 (π).
1 ∗ ϕ2 (π) = ϕ
La multiplicación de la derecha es la multiplicación de matrices.
2. Cambio de la T ransf ormada de F ourier por una representación regular multiplicada
por π. Para ϕ ∈ L2 , define [L(g)ϕ](h) = ϕ(g −1 h) = ϕg (h) si h, g ∈ G. Entonces
tenemos
d
d para todo π ∈ G
g ](π) = π(g)ϕ(π),
b
[ϕ
c? (π) = ϕ(π)
3. ϕ
b ? , donde ϕ? (g) = ϕ(g −1 )
4. ϕ(1)
b
=
P
g∈G
ϕ(g)1C ∈ End(C) ' C, donde 1 denota la representación trivial.”[5]
12
2.5.
Ejemplos de la Transformada de Fourier
Para ejemplos sobre grupos abelianos finitos de orden n es importante conocer el siguiente
teorema,
Teorema 2.5.1 Teorema Fundamental de Grupos abelianos
Cada grupo finito abeliano G es isomorfo a un producto directo de grupos cı́clicos, es
decir,
G∼
= (Z/m1 Z) ⊕ · · · ⊕ (Z/mr Z),
donde el grupo de la derecha se compone de todos los vectores (a1 , ..., ar ), donde aj ∈
Z/mj Z. Y la adición de dos vectores es componente a componente, es decir,
(a1 , ..., ar ) + (b1 , ..., br ) = (a1 + b1 , . . . , ar + br ).
Por otra parte, podemos tomar el mj tal que mj divide mj+1 , para todo j. Entonces el
cantidad de mj está determinada únicamente por G.
Ejemplo 1
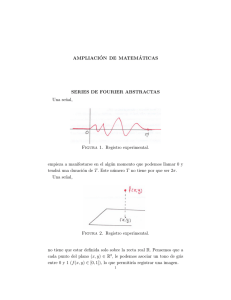
Transformada de Fourier en (Z12,+ ).
Se consideran en este grupo funciones ϕ ∈ L2 (Z12 ), que nos definen ϕ(g), g = 0,1,2,...,11.
Los caracteres para este caso son π(g) = e−2πigx/12 .
Luego la transformada de Fourier esta dada por:
X
X
ϕ(x)
b
=
ϕ(g)π(g) =
ϕ(g)e−2πigx/12
g∈Z12
g∈Z12
Gracias al anterior teorema se pueden descomponer los grupos abelianos finitos.
si la función es como la gráfica (figura 2.1),
Figura 2.1: Función en el espacio 1D
13
Ejemplo 2
Transformada de Fourier en (Z4 × Z3 , +).
consideran en este grupo funciones ϕ ∈ L2 (Z4 × Z3 ), que nos definen ϕ(g), g ∈ Z4 × Z3 .
Los caracteres para este caso son π(g) = π(g1 , g2 ) = e−2πig1 x/4 e−2πig2 y/3 .
Luego la transformada de Fourier esta dada por:
ϕ(x,
b y) =
X
g∈Z4 ×Z3
X
ϕ(g)π(g) =
ϕ(g1 , g2 )e−2πig1 x/4 e−2πig2 y/3
g∈Z4 ×Z3
si la función es como la gráfica (figura 2.2),
Figura 2.2: Función en el espacio 2D
Ejemplo 3
Ahora consideremos la Transformada de Fourier en (Z2 × Z2 × Z3 , +).
con la función ϕ definida como ϕ(g1 , g2 , g3 ) = 1, que corresponde a asociar a cada punto
del grupo el numero 1 como se muestra en la figura 2.3.
14
Figura 2.3: Función en el espacio 3D
Luego la transformada de Fourier esta dada por:
ϕ(x,
b y, z) =
X
ϕ(g)π(g)
g∈Z2 ×Z2 ×Z3
=
X
g∈Z2 ×Z2 ×Z3
ϕ(g1 , g2 , g3 )e−2πig1 x/2 e−2πig2 y/2 e−2πig1 z/3
Conclusiones
En esta monografia se ha querido mostrar una forma de representar grupos finitos, pero
fundamentalmente se enfatizo en el estudio de caracteres para grupos finitos ya que son
de gran importancia para la transformada de Fourier sobre grupo finitos y principalmente
sobre Zn .
Se enfatizo en el estudio de los caracteres para la aplicación de la Transformada de Fourier
sobre Zn también se vio su estructura basado en gráficas en diferentes dimensiones y
mostrando sus gráficas de curvas para una mayor comprensión de estas Transformadas de
Fourier.
15
Bibliografı́a
[1] Javier Parcet, Espacios en Grupos Finitos, Transformada de Fourier y Combinatoria. Universidad Autónoma de Madrid, Facultad de Ciencias, Departamento de
Matemáticas.
[2] Rafael Villaroel Florez, Introducción a la teorı́a de representaciones de grupos
finitos, 29 de Junio del 2006.
[3] Gianfranco Cariolaro. Unified Signal Theory, University of Padova (2011)
[4] Hector Merklen, Introducción a la Teorı́a de Representaciones de Álgebras, Instituto de Matemática e Estadı́stica, Universidad de Sao Paulo - BRASIL (2004).
[5] Yitzhack Katznelson, An Introduction to Harmonic Analysis, Stanford, (2002).
[6] Audrey Terras, Fourier Analysis on Finite Groups and Applications, London
Mathematical Society, (2005).
16