Tracción comprensión - Raquel Serrano Lledó

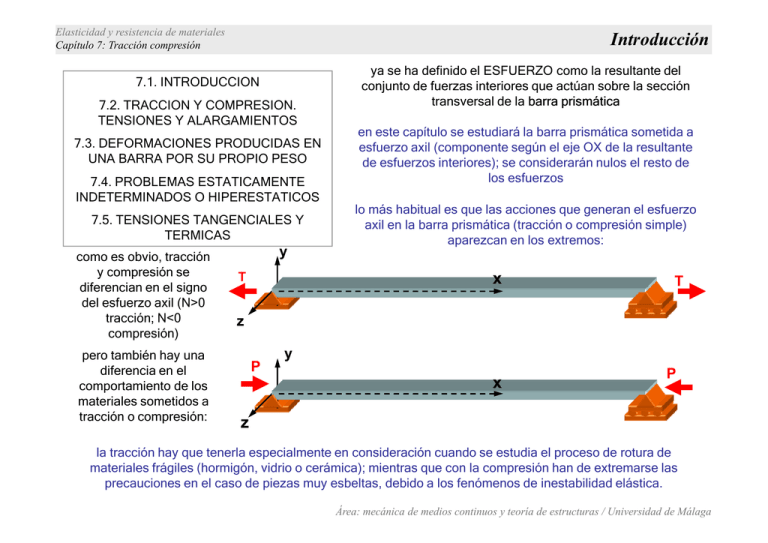
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
Introducción
7.1. INTRODUCCION
7.2. TRACCION Y COMPRESION.
TENSIONES Y ALARGAMIENTOS
7.3. DEFORMACIONES PRODUCIDAS EN
UNA BARRA POR SU PROPIO PESO
7.4. PROBLEMAS ESTATICAMENTE
INDETERMINADOS O HIPERESTATICOS
7.5. TENSIONES TANGENCIALES Y
TERMICAS
como es obvio, tracción
y compresión se
diferencian en el signo
del esfuerzo axil (N>0
tracción; N<0
compresión)
pero también hay una
diferencia en el
comportamiento de los
materiales sometidos a
tracción o compresión:
y
ya se ha definido el ESFUERZO como la resultante del
conjunto de fuerzas interiores que actúan sobre la sección
transversal de la barra prismática
en este capítulo se estudiará la barra prismática sometida a
esfuerzo axil (componente según el eje OX de la resultante
de esfuerzos interiores); se considerarán nulos el resto de
los esfuerzos
lo más habitual es que las acciones que generan el esfuerzo
axil en la barra prismática (tracción o compresión simple)
aparezcan en los extremos:
x
T
T
z
P
y
x
P
z
la tracción hay que tenerla especialmente en consideración cuando se estudia el proceso de rotura de
materiales frágiles (hormigón, vidrio o cerámica); mientras que con la compresión han de extremarse las
precauciones en el caso de piezas muy esbeltas, debido a los fenómenos de inestabilidad elástica.
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
Introducción
Una barra está sometida a tracción o compresión simple cuando, en su sección transversal, todos los
esfuerzos, a excepción del axil, son iguales a cero. Es decir han de verificarse las siguientes ecuaciones:
N(x ) =
∫σ
x
dA ( x ) ≠ 0
A(x)
Vy ( x ) = −
∫σ
xy
dA( x ) = 0
xz
dA( x ) = 0
A(x)
Vz ( x ) = −
∫σ
A(x )
M x (x) =
∫ (σ
xz
y − σ xy z) dA( x ) = 0
A(x )
M z (x) = −
∫σ
x
y dA( x ) = 0
A(x)
M y (x) =
∫σ
x
z dA( x ) = 0
A(x)
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
Tensiones y alargamientos
Ya se ha visto que en la barra prismática se trabaja con magnitudes
monodimensionales, derivadas de la integración, a lo largo de la
sección, de todas las magnitudes tridimensionales presentes en la
teoría general de la elasticidad
Recuérdese el principio de Saint-Venant: La distribución de
tensiones y deformaciones en un sólido, en una zona cercana a la de
aplicación de la carga, es la misma si se trabaja con la resultante o con
la distribución real de la carga.
En consecuencia, a lo largo de la sección transversal P=σx—A.
Hipótesis de Bernouilli (secciones planas)
Del análisis del principio de Saint-Venant se desprende
que si las tensiones son constantes a lo largo de la
sección, también lo serán las deformaciones, y si éstas
lo son, todos los puntos de la sección se van a acortar
los mismo.
mismo Luego, como consecuencia de lo anterior, se
desprende la hipótesis de Bernouilli, que establece que
las secciones planas permanecen planas y paralelas
después de la deformación.
Por tanto, partiendo de la hipótesis de Bernouilli, puede
decirse que los puntos A y B de estas figuras pasan a
ser los A’ y B’ después de la deformación, de modo que
las deformaciones, y por tanto las tensiones, serán
constantes a lo largo de la deformación.
A
B
N(x)
N(x)
lA= lB
A’
B’
N(x)
N(x)
En consecuencia, bien sea a
través del principio de SaintVenant, bien sea a partir de la
hipótesis de Bernouilli, se
llega a la conclusión de que
las tensiones en la sección
transversal son constantes.
Pueden obtenerse las
tensiones a partir de las
expresiones del esfuerzo
axil, tal y como se verá en
la diapositiva siguiente.
l’A= l’B
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
P
el esfuerzo axil
Diagrama de axil, N(x)
Integrando la tensión a lo largo de la
sección transversal …:
N = ∫ σ x dA
P
A
… y considerando que la tensión es
constante (y sale de la integral):
N = ∫ σ x dA = σ x ⋅ A ⇒ σ x =
A
N
A
Aplicando la ley de Hooke se obtendrá la
deformación.
εx =
P
Rebanada
TRACCIÓN
N
E⋅A
En tracción o en compresión, el
desplazamiento monodimensional coincide
con el alargamiento o el acortamiento,
respectivamente.
Para una coordenada x, el alargamiento de la barra de
la figura de la derecha será:
∆x
N
N⋅x
εx =
=
⇒ ∆x =
x
E⋅A
E⋅A
Por tanto, el alargamiento o acortamiento de una barra de longitud l sometida a un axil constante será:
COMPRESIÓN
∆l =
N ⋅l
E⋅A
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
tensiones producidas en una barra por su propio peso
Son las tensiones, y por tanto las deformaciones, debidas al peso propio de la
estructura distintas a las generadas por las cargas que soportan??
Las cargas distribuidas sobre una barra que
compone una estructura son cargas que actúan
por unidad de longitud, pero las cargas de peso
propio de la barra son FUERZAS DE
VOLUMEN.
Sea la barra de la figura, sometida a su peso propio y a una
carga en el extremo libre:
Ya se ha visto que para obtener las fuerzas distribuidas a
partir de las fuerzas volumétricas ha de integrarse el peso
específico sobre la sección transversal; como el peso
específico es una fuerza volumétrica constante a lo largo de
todo el volumen, la integral es igual al propio peso
específico por la dección transversal de la barra: q=γ—A
(donde q es la fuerza distribuida, γ el peso específico y A el
área de la sección transversal.)
Por tanto, las tensiones serán:
∑F
V
= 0 ⇒ N − P − q ⋅ x = 0 ⇒ N =P + q ⋅ x
y, en consecuencia, las deformaciones:
εx =
σx
E
=
P + q· x
E· A
y los alargamientos:
se calcularán esfuerzos axiles, tensiones, deformaciones,
desplazamientos y alargamientos.
εx =
x= x
du P + q·x
P + q·x
=
= ∫
dx =
dx
E· A
E
·
A
x =o
P·x + q·
x2
2
E· A
Lo cual puede representarse gráficamente así:
Para determinar el AXIL se considera una coordenada
genérica x desde el extremo cargado y se aplica equilibrio
de fuerzas en el trozo de barra limitada por la corrdenada x,
sustituyendo el resto de la barra por las tres resultantes del
equilibrio interno:
P + q· x
N = P + q· x = ∫ σ x dA = σ x · A ⇒ σ x =
A
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
tensiones producidas en una barra por su propio peso
Secciones equirresistentes
Puede verse, por tanto, que hay una variación de tensiones a lo
largo de la barra [desde P/A hasta P/A+(q—L)/A]. En
consecuencia, para que la barra no plastifique o rompa, la
tensión máxima debe ser, a lo sumo, (P+q—L)/A.
Una solución que no suponga un desaprovechamiento de
material ha de pasar por adecuar la sección al la tensión que
soporta la barra en cada sección, es decir, una disminución
progresiva de la sección desde el extremo superior hasta el
inferior, algo así:
Luego, el área mínima de la barra, necesaria para soportar la
carga más su peso propio, será:
A=
P + q·L
σt
Estudiando el equilibrio en una rebanada se obtiene la
expresión que define el área necesaria a lo largo de la barra:
Pero, si se hace así, es obvio que se está
desaprovechando material a lo largo de casi toda la
sección ya que, solamente es necesaria el área calculada
en la zona en la que la tensión es equivalente a la de la
carga soportada más el peso propio (en la parte superior
de la pieza).
q· x
A = Ao ·e
σt
Una sección formulada en esos términos es
EQUIRRESISTENTE, es decir, resiste en cada punto
lo necesario y no sobra material.
Pero, ¿es eso tan necesario?, ¿por qué no son todas las
secciones equirresistentes?
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
problemas estáticamente indeterminados o hiperestáticos
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
problemas estáticamente indeterminados o hiperestáticos
Si se analiza ahora el equilibrio puede comprobarse
que hay más incognitas que ecuaciones de equilibrio,
de modo que el axil quedará en función de las
reacciones:
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
problemas estáticamente indeterminados o hiperestáticos
Grado de hiperestaticidad: Grado de hiperestaticidad externa + grado de hiperestaticidad interna.
Hiperestaticidad externa: la que se determina analizándo sólo las reacciones en los apoyos.
Hiperestaticidad interna: la que surge de la existencia de un nº mayor de barras que las necesarias para que el
sistema sea isostático ( grado = nº de empotramientos o barras que sobran para que sea
isostático).
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
hiperestaticidad interna – externa – total...
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga
Elasticidad y resistencia de materiales
Capítulo 7: Tracción compresión
defecto de montaje
Ocurre cuando en un sistema estructural compuesto por
barras, las dimensiones de las barras en la realidad, antes
de montarlas, no corresponden con las dimensiones
teóricas (las de los planos).
En estos casos suele “forzarse” la barra para que
alcance la posición o dimensión adecuada.
Ello genera un INEVITABLE esfuerzo interno en la
barra, tanto mayor cuánto más grande sea el error
dimensional cometido.
Esf=(E·A·error)/Long.barra
EN CONSECUENCIA
Habrá que considerar que la barra se halla pre-esforzada, es decir
sumar o restar a los esfuerzos derivados de las cargas los que se han
producido por efecto de los errores dimensionales y su subsanación
en el momento de montaje
Esto mismo ocurre como consecuencia de las dilataciones o
contracciones localizadas a lo largo de una pieza, por efectos de
aplicación de calor, calor residual de otros elementos, soleamiento,
soldadura...
Área: mecánica de medios continuos y teoría de estructuras / Universidad de Málaga