ACTIVIDAD #6 – PENDIENTE EN DOS Y TRES DIMENSIONES Y

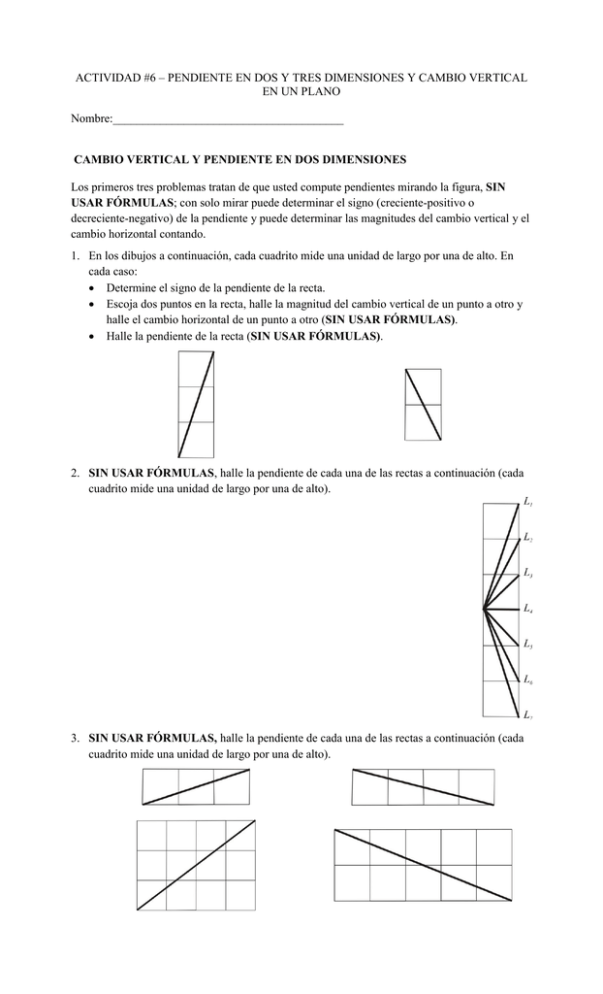
ACTIVIDAD #6 – PENDIENTE EN DOS Y TRES DIMENSIONES Y CAMBIO VERTICAL
EN UN PLANO
Nombre:_______________________________________
CAMBIO VERTICAL Y PENDIENTE EN DOS DIMENSIONES
Los primeros tres problemas tratan de que usted compute pendientes mirando la figura, SIN
USAR FÓRMULAS; con solo mirar puede determinar el signo (creciente-positivo o
decreciente-negativo) de la pendiente y puede determinar las magnitudes del cambio vertical y el
cambio horizontal contando.
1. En los dibujos a continuación, cada cuadrito mide una unidad de largo por una de alto. En
cada caso:
 Determine el signo de la pendiente de la recta.
 Escoja dos puntos en la recta, halle la magnitud del cambio vertical de un punto a otro y
halle el cambio horizontal de un punto a otro (SIN USAR FÓRMULAS).
 Halle la pendiente de la recta (SIN USAR FÓRMULAS).
2. SIN USAR FÓRMULAS, halle la pendiente de cada una de las rectas a continuación (cada
cuadrito mide una unidad de largo por una de alto).
3. SIN USAR FÓRMULAS, halle la pendiente de cada una de las rectas a continuación (cada
cuadrito mide una unidad de largo por una de alto).
4. Como la pendiente de una recta es el cambio vertical sobre el cambio horizontal, o sea,
m  V / H , entonces V  mH , o sea:
El cambio vertical es la pendiente por el cambio horizontal.
Para cada una de las rectas a continuación, use el hecho que el cambio vertical es la
pendiente por el cambio horizontal para computar el cambio vertical que corresponde a cada
cambio horizontal dado.
Recta
Cambio horizontal
H  2
H  3
H  15
Cambio vertical
V 
V 
V 
H  2
H  3
H  15
V 
V 
V 
H  2
H  3
H  15
H  7.3
V
V
V
V




PENDIENTES EN DIRECCIONES X y Y DE UN PLANO
Una recta no vertical en el espacio se dice que está en dirección x si están en un plano de la
forma y  c para alguna constante c.
5. Oscurezca tres rectas que están en dirección x en el plano de la izquierda abajo:
8
z
8
6
2
4
2
1.5
0
0
1
1
0.5
x
2
y
z
6
2
4
2
1.5
0
0
1
1
0.5
x
3
y
2
0
3
0
Una recta no vertical en el espacio se dice que está en dirección y si está en un plano de la forma
x  c para alguna constante c.
6. Oscurezca tres rectas que están en dirección y en el plano de la derecha arriba.
La pendiente de una recta en dirección x se computa como siempre, teniendo en cuenta que en
tres dimensiones vertical quiere decir hacia arriba y hacia abajo, o sea, en dirección de z:
 Decida el signo: si cuando x aumenta, z aumenta entonces el signo es positivo; si cuando
x aumenta, z disminuye entonces el signo es negativo.
 Tome dos puntos que están en la recta en dirección x.
 La magnitud de la pendiente es igual al cambio vertical dz de un punto al otro
( zfinal  zinicial ) sobre el cambio horizontal dx, ( xfinal  xinicial ), de un punto al otro.
La pendiente de una recta en dirección y se define de manera similar; cambio vertical sobre
cambio horizontal, dz / dy (donde dz  zfinal  zinicial y dy  y final  yinicial ), con el signo dependiendo
de si la z aumenta (positivo) o disminuye (negativo) cuando la y aumenta.
7. En cada uno de los planos a continuación, identifique una recta en dirección x y halle su
pendiente (use una recta con puntos cuyas coordenadas pueda identificar fácilmente):
z
7
6
5
4
3
2
1
0
0
11
2
z
8
3
5
2
1
y
0
y
1
1
1
x
x
2
2
0
3
0
8. En cada uno de los planos a continuación, identifique una recta en dirección y y halle su
pendiente (use una recta con puntos cuyas coordenadas pueda identificar fácilmente):
z
7
6
5
4
3
2
1
0
0
11
2
z
8
3
5
2
1
y
0
y
1
1
1
x
x
2
0
2
3
0
9. Sea P el plano con ecuación z  2 x  3 y  4 .
a.
b.
c.
d.
La intersección de P con el plano fundamental
La intersección de P con el plano fundamental
La intersección de P con el plano fundamental
La intersección de P con el plano fundamental
x  1 es una recta de pendiente m  ?
x  2 es una recta de pendiente m  ?
x  378 es una recta de pendiente m  ?
y  1 es una recta de pendiente m  ?
e. La intersección de P con el plano fundamental y  2 es una recta de pendiente m  ?
f. La intersección de P con el plano fundamental y  247 es una recta de pendiente m  ?
Se puede mostrar que en un plano todas las rectas en dirección x son paralelas y por ende tienen
la misma pendiente; ésta se llama mx , la pendiente en dirección x del plano. Similarmente, en
un plano todas las rectas en dirección y tienen la misma pendiente que se llama m y , la pendiente
en dirección y del plano.
10. Halle la pendiente en dirección x y la pendiente en dirección y de cada uno de los siguientes
planos:
a. z  4 x  3 y  2
b. 3x  2 y  z  0
c. z  5x  3
CAMBIO VERTICAL EN UN PLANO
En el siguiente problema recuerde que en una recta:
Cambio
vertical  =  Pendiente  × Cambio horizontal 
11. a. Use la fórmula de arriba para llenar fila a fila la tabla a continuación si comienza en el
punto dado del plano que se representa debajo de la tabla.
b. Reflexione sobre lo que hizo en la parte anterior para explicar en sus propias palabras
como se puede hallar cambio vertical en un plano.
Punto inicial
Cambio
horizontal en
dirección x
dx
(0,2,5)
Cambio
vertical en
dirección x
dz x
1
0
1
3
0
3
4
0
4
1
2
5
2
5
dx
(0,2,5)
(0,2,5)
(0,0,1)
(0,0,1)
(0,0,1)
(3, 4,12)
(3, 4,12)
(3, 4,12)
(1,2,6)
(1,2,6)
(1,2,6)
(2,3,5)
(2,3,5)
(a, b, c)
Cambio
vertical en
dirección y
Cambio
horizontal en
dirección y
dy
dz y
Cambio
vertical total
dz  dz x  dz y
0
1
1
0
5
5
0
2
2
3
4
5
4
5
dy
7
6
5
z 4
3
2
1
0
0
2
1
1
x
2
0
12. La siguiente es una tabla de valores de un plano:
y
2
4
6
5
8
11
3
6
9
1
4
7
x
1
2
3
a. Halle mx .
b. Halle m y .
c. Exprese el cambio vertical dz como función del cambio horizontal en dirección x, dx, y
el cambio horizontal en dirección y, dy.
13. El siguiente es un diagrama de contorno de un plano:
a. Halle mx .
b. Halle m y .
c. Exprese el cambio vertical dz como función del cambio horizontal en dirección x, dx, y
el cambio horizontal en dirección y, dy.