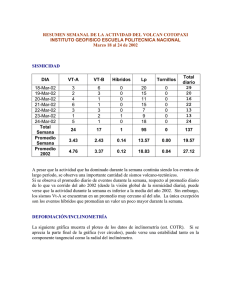
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO

UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
PROGRAMA DE POSGRADO EN CIENCIAS DE LA TIERRA
CENTRO DE GEOCIENCIAS
“APLICACIÓN DE MÉTODOS GEOFÍSICOS EN EL ESTUDIO DE LA
ESTRUCTURA CORTICAL SUPERFICIAL EN EL MUNICIPIO DE LANDA DE
MATAMOROS, QUERÉTARO”
TESIS
QUE PARA OPTAR POR EL GRADO DE:
MAESTRO EN CIENCIAS DE LA TIERRA
(SISMOLOGÍA)
PRESENTA:
ERIKA NALLELY LÓPEZ VALDIVIA
TUTOR
Dr. Juan Martín Gómez González (Centro de Geociencias, UNAM)
MIEMBROS DEL COMITÉ
Dr. Ángel Fco. Nieto Samaniego (Centro de Geociencias, UNAM)
Dr. Vsevolod Yutsis (Geociencias, IPICYT)
Dr. Héctor López Loera (Geociencias, IPICYT)
Dr. Juan Carlos Montalvo Arrieta (Facultad Ciencias de la Tierra, UANL)
MÉXICO, D. F. FEBRERO 2014
AGRADECIMIENTOS
Agradezco al Consejo Nacional de Ciencia y Tecnología por la beca otorgada para la
realización de mis estudios de maestría. Del mismo modo, este trabajo de tesis fue
realizado gracias al apoyo de los proyectos PAPIIT-IN116410: “Monitoreo de Sismicidad en
la Sierra Gorda de Querétaro” y CONACYT-60363: “Elaboración de metodologías
sismológicas en el análisis rutinario de datos de banda ancha en México”, los cuales
estuvieron a cargo del Dr. Juan Martín Gómez González.
También quiero agradecer al gobierno municipal de Landa de Matamoros (2009-2012) por
las facilidades y el apoyo prestado durante el trabajo de campo; asimismo ofrezco mi más
sincero reconocimiento a la unidad Estatal de Protección Civil del Estado de Querétaro por
el destacable apoyo y servicio proporcionados durante el desarrollo de este trabajo de
tesis.
Gracias infinitas a mi asesor de tesis, el Dr. Juan Martín Gómez González por su
incondicional apoyo y ayuda en el desarrollo de este trabajo, así como al Dr. Vsevolod
Yutsis por las grandes experiencias y enseñanzas en el trabajo de campo, al Dr. Ángel Fco.
Nieto Samaniego por su serenidad, paciencia, comprensión y consejos llenos de sabiduría,
al Dr. Héctor López Loera por su completo apoyo y asesorías y al Dr. Juan Carlos Montalvo
Arrieta por su indiscutible disposición y sugerencias en mi trabajo. Sin dejar de lado, mi
total agradecimiento a Marta Pereda por todas las facilidades brindadas durante mi
estadía en el Centro de Geociencias.
Gracias a todos mis amigos Dany, Rodri (hermano sismo-loco), Neto (ñoño), Erik (cara de
chuti), Albert, Elisius (grinch), Fitous, Chisto, Vania, Berna, Sandra, Rosy, Tali (Iván),
Chayito, Maria, a los sensei Chilo, Uru, Ángel (máster), a la buena compañía y consejos de
investigadores y compañeros de Cgeo, a mi gran y mejor AMIGA Joselin (lokilla) por
tolerarme, ser tan buena confidente y compartir miles de pato aventuras juntas, y a todos
aquellos que me faltaron por enlistar, les agradezco hacer de mis días y estancia en
Querétaro, una de las mejores experiencias de mi vida.
A mis padres por su amor infinito e incondicional, por su comprensión, paciencia,
confianza, apoyo y guía en todas las decisiones tomadas; a mis hermanos porque los
adoro, y espero este trabajo les impulse a cumplir sus sueños y metas que se propongan,
evitando decir: no puedo. A esa persona que me enamora todos los días, que entiende mi
locura, la razón de mi sonrisa y cómplice del amor que existe entre los dos: Amauri. Y
finalmente, Gracias Dios por permitirme concluir este trabajo; siempre te llevo en mi
corazón!!!
1
ÍNDICE
RESUMEN ............................................................................................................................................ 7
CAPÍTULO I
Aspectos Generales ..................................................................................................... 8
1.1
Introducción ........................................................................................................................ 8
1.2
Objetivos ............................................................................................................................. 9
1.3
Metodología ........................................................................................................................ 9
1.4
Localización ....................................................................................................................... 10
1.5
Antecedentes .................................................................................................................... 12
CAPÍTULO II
Marco Geológico ....................................................................................................... 14
2.1
Marco Tectónico................................................................................................................ 14
2.2
Estratigrafía ....................................................................................................................... 19
CAPÍTULO III
Sismicidad .............................................................................................................. 21
3.1
Sismicidad histórica ........................................................................................................... 22
3.2
Red sísmica temporal LANDA ............................................................................................ 28
3.3
Procesamiento de datos.................................................................................................... 30
3.4
Localización epicentral ...................................................................................................... 33
CAPÍTULO IV
4.1
Métodos Potenciales ............................................................................................. 38
Método Gravimétrico ........................................................................................................ 38
4.1.1
Relaciones fundamentales ........................................................................................ 38
4.1.2
Medición de la Gravedad .......................................................................................... 40
4.1.3
Reducciones gravimétricas........................................................................................ 41
4.1.4
Anomalías gravimétricas ........................................................................................... 42
4.2
Método Magnético............................................................................................................ 43
4.2.1
Relaciones Fundamentales........................................................................................ 44
4.2.2
Correcciones magnéticas .......................................................................................... 48
4.2.3
Anomalías magnéticas............................................................................................... 50
4.2.4
Aeromagnetometría .................................................................................................. 51
CAPÍTULO V
Adquisición de datos ................................................................................................. 52
5.1
Levantamiento Gravimétrico ............................................................................................ 52
5.2
Levantamiento Topográfico .............................................................................................. 58
2
5.4
Cartas Aeromagnéticas ..................................................................................................... 61
CAPÍTULO VI
6.1
Procesamiento de Datos ....................................................................................... 62
Gravimetría ....................................................................................................................... 62
6.1.1
Correcciones gravimétricas ....................................................................................... 62
6.1.2
Anomalías gravimétricas ........................................................................................... 64
6.1.3
Filtros ......................................................................................................................... 70
6.2
Aeromagnetometría .......................................................................................................... 73
6.2.1
Anomalías aeromagnéticas ....................................................................................... 73
6.2.2
Filtros ......................................................................................................................... 74
6.3
Interpretación ................................................................................................................... 80
6.3.1
Interpretación Gravimétrica ...................................................................................... 80
6.3.2
Interpretación Magnética ......................................................................................... 82
6.4
Modelado Geológico-Geofísico ......................................................................................... 83
6.4.1
Procesamiento .......................................................................................................... 84
6.4.2
Modelado Directo ..................................................................................................... 84
6.4.3
Interpretación del modelado .................................................................................... 86
CAPÍTULO VII
Análisis y discusión de resultados ..................................................................... 92
7.1
INTEGRACIÓN DE DATOS................................................................................................... 92
7.2
DISCUSIÓN ......................................................................................................................... 98
7.3
CONCLUSIONES ............................................................................................................... 101
7.4
RECOMENDACIONES ....................................................................................................... 103
REFERENCIAS BIBLIOGRÁFICAS ....................................................................................................... 104
Anexos….…………………………………………………………………………………………………………………………………… 109
3
LISTA DE FIGURAS
CAPÍTULO I
11
Figura 1.1. Ubicación de la zona de estudio en la cabecera municipal de Landa de
Matamoros y alrededores, localizada al NE del estado de Querétaro.
CAPÍTULO II
Figura 2.1. Cinturones magmáticos pre-Laramídicos y Laramídicos y el cinturón
cordillerano en el cual se ubica el área de estudio (verde) MM; Montañas Mackenzie,
MR; Montañas Rocallosas, MC; Meseta de Colorado, BLL; Bloques Laramídicos
Levantados, SN; Sierra Nevada, CP; Cordilleras Peninsulares, CPCL; Cinturón de Pliegues
y Cabalgaduras Laramídico, SMOC; Sierra Madre Occidental, SMOR; Sierra Madre
Oriental (tomado de English y Johnston, 2004).
Figura 2.2. Distribución de sectores de la Sierra Madre Oriental. (1) San Pedro del Gallo,
(2) Huayacocotla, (3) Transversal de Parras, (4) Saliente de Monterrey, (5) Valles, (6)
Cuenca de Sabinas, (7) Región Zongolica y (8) Bloque de Coahuila (tomado de Eguiluz et
al., 2000).
Figura 2.3. Paleogeografía de la porción centro-oriental de México para el AlbianoCenomaniano mostrando las principales cuencas y plataformas del Cretácico Medio y
localización del área de estudio. Los rectángulos indican áreas estudiadas por Carrasco
(1977; tomado de López D., 2003).
Figura 2.4. Mapa geológico de la zona de estudio obtenido de la carta geológica Ciudad
Valles del Servicio Geológico Mexicano (1997).
Figura 2.5. Columna estratigráfica generalizada de la Plataforma Valles-San Luis Potosí
donde se ubica el área de estudio. Modificado de Fitz (2010).
14
16
17
18
19
CAPÍTULO III
Figura 3.1. Distribución de los ocho sismos intraplaca estudiados por Suter et al. (1996)
(Tomado de León, 2010).
Figura 3.2. Distribución de la sismicidad histórica reportada por otras redes sísmicas.
23
Figura 3.3.Distribución espacial de la sismicidad registrada en el periodo de noviembre
2007 a marzo de 2009 (Tomado de León-Loya, 2010).
Figura 3.4. Distribución espacial de la sismicidad registrada en un periodo de noviembre
2007 a diciembre 2010 (Modificado de León-Loya, 2014).
Figura 3.5. Distribución de las estaciones sísmicas las cuales conforman la RSTL.
26
Figura 3.6. a) Configuración de las estaciones sísmicas (sismógrafo, Panel solar, batería y
controlador fotovoltaico). b) Vista típica de una estación sísmica.
Figura 3.7. Clasificación y visualización de un sismograma en sus tres componentes con
el programa de adquisición GeoDas.
Figura 3.8. Visualización de un evento sísmico registrado en dos estaciones con el
programa Seisan.
Figura 3.9. Procedimiento para determinar el azimut a la fuente sísmica de un registro
de onda P, usando las tres componentes del vector del movimiento del suelo, partiendo
de que los movimientos de la onda P son polarizados en el plano vertical y radial.
30
25
27
28
31
32
34
4
(Modificado de Båth, 1979).
36
Figura 3.10. Ejemplo del Diagrama de Wadati para determinar el tiempo origen de
un sismo local. El tiempo origen está dado por la intersección con el eje de tiempo
de arribo de P.
Figura 3.11. Método de Círculos para la triangulación de un hipocentro (Modificado de
Lay & Wallace, 1995).
37
CAPÍTULO IV
39
Figura 4.1 Variación teórica del campo de gravedad a nivel del mar y su gradiente
horizontal norte-sur correspondiente con la latitud. No hay gradiente este-oeste en el
campo teórico (tomado de Milsom, 2003).
Figura 4.2. Método de Nettleton para la determinación de densidad a través de un
rasgo topográfico aislado. Las reducciones gravimétricas se realizan usando densidades
entre un rango de 1.8 a 2. 8 Mg/m3 para correcciones de Bouguer y de terreno. El perfil
corresponde a un valor de 2.3 Mg/m3 que muestra la mínima correlación con la
topografía, por lo que esta densidad es tomada para representar la densidad del rasgo
(tomado de Dobrin & Savit, 1988).
Figura 4.3. (a) Valores promedio y rangos de la susceptibilidad magnética de algunos
tipos de rocas comunes, y (b) la susceptibilidad de algunos minerales importantes
(modificado de Lowrie, 2007).
Figura 4.4. Variación en intensidad, buzamiento y gradiente para un dipolo ideal
alineado a lo largo del eje de rotación de la Tierra.
Figura 4.5. Elementos geomagnéticos.
41
45
47
47
CAPÍTULO V
Figura 5.1. Distribución de los puntos de medición gravimétricos a lo largo de las
carreteras y caminos de terracería (rombos rojos) en los alrededores de la cabecera
municipal de Landa de Matamoros, Querétaro.
Figura 5.2. Gravímetro Scintrex Autograv CG-5.
53
Figura 5.3. Levantamiento topográfico realizado con una Estación Total convencional
Nikon (izquierdo) con un solo prisma (derecha) en cada punto gravimétrico.
Figura 5.4. Modelo Digital de Elevación (MDE) del área de estudio (tomado del INEGI,
2011).
59
57
60
CAPÍTULO VI
Figura.6.1. Anomalía Aire Libre en los alrededores de Landa de Matamoros, Querétaro.
65
Figura.6.2. Mapa de anomalía de Bouguer simple a)
y b)
.
Figura.6.3. Mapa de anomalía de Bouguer completa a)
y b)
.
Figura 6.4. Mapa de anomalía regional obtenida con el método de superficies de tendencia
de segundo grado.
Figura 6.5. Mapa de Anomalía residual obtenido con el método de superficies de
tendencia de segundo grado.
66
67
69
69
5
Figura.6.6. Aplicación de un filtro pasa-bajas en la Anomalía de Bouguer completa
calculada en la cabecera municipal de Landa de Matamoros.
Figura 6.7. Primera derivada vertical de la Anomalía de Bouguer completa en los
alrededores de Landa de Matamoros.
Figura 6.8. Mapa del campo magnético residual de Landa de Matamoros.
71
Figura 6.9. Mapa de reducción al polo magnético del campo magnético residual
de Landa de Matamoros.
Figura 6.10. Representación gráfica del filtro pasa baja (Geosoft Inc. 2007).
76
Figura 6.11. a) Continuación ascendente a una altura de 500m b) Continuación
ascendente a 1000m c) Continuación ascendente a 3000m d) Continuación
ascendente a 5000m del campo magnético residual.
Figura 6.12. a) Mapa de primera derivada vertical y reducción al polo magnético del CMR.
B) Mapa de primera derivada vertical y reducción al polo magnético del CMR a una altura
de 1000 msnm.
Figura.6.13. Distribución de tres perfiles gravimétricos y magnéticos en el área de estudio.
78
Figura.6.14. Modelo geológico-geofísico con datos magnéticos y gravimétricos del Perfil 1
87
Figura.6.15. Modelo geológico-geofísico con datos magnéticos y gravimétricos del Perfil 2.
88
Figura.6.16. Modelo geológico-geofísico con datos magnéticos y gravimétricos del Perfil 3.
90
Figura 6.17. Mapa de superficie en 3D del basamento metamórfico, configuración de
la cima del complejo basal grenvilliano, escala de colores muestra las profundidades
estimadas.
91
72
74
77
79
85
CAPÍTULO VII
92
Figura. 7.1. Distribución espacial de la sismicidad localizada con la técnica monoestación en el área de estudio, de noviembre de 2007 a septiembre de 2010. Los puntos
azules son los eventos localizados con una estación y los rojos con dos o más
estaciones; mientras que los triángulos negros indican las mediciones gravimétricas.
Figura 7.2. Histograma del tiempo contra el número de eventos ocurridos desde
noviembre 2007 y hasta septiembre 2010 en Landa de Matamoros, Querétaro.
Figura 7.3. Mapa aeromagnético regional clasificado en dominios magnéticos junto con
la distribución espacial de los sismos ocurridos entre noviembre de 2007 y septiembre
de 2010 en la parte central de la SMOr. Los puntos rojos indican las mediciones
gravimétricas (extremo inferior derecho), los círculos amarillos las localizaciones
epicentrales, y los triángulos negros la ubicación de las estaciones sísmicas. Nótese la
tendencia casi N-S de la sismicidad a lo largo de los dominios magnéticos.
Figura 7.4. Mapa aeromagnético con clasificación de dominios magnéticos, junto con la
distribución espacial de los sismos ocurridos en los alrededores de la cabecera
municipal de Landa de Matamoros. Los puntos rojos son los sismos localizados con una
estación y los negros con dos o más estaciones. Nótese una tendencia NE-SW y en sus
extremos dos agrupaciones de sismos.
Figura 7.5. Mapa de anomalía de Bouguer completa junto con la distribución espacial de
sismicidad (puntos) en la cabecera municipal de Landa de Matamoros. Los triángulos
negros son las mediciones gravimétricas, los puntos rojos las localizaciones con una
estación y los negros con dos o más estaciones.
93
94
96
97
6
RESUMEN
Llevamos a cabo un estudio geológico-geofísico en el municipio de Landa de Matamoros,
en el corazón de la Sierra Gorda de Querétaro. Integramos información sísmica, geológica,
gravimétrica y aeromagnética para identificar las probables estructuras sismogénicas. El
análisis de la microsismicidad local registrada entre noviembre de 2007 a septiembre de
2010, llevada a cabo con la red sísmica temporal LANDA, compuesta por sismógrafos
digitales de periodo corto, muestra el registro de más de 3000 micro-sismos (León-Loya,
2014), de los cuales relocalizamos 299 epicentros (~h < 10 km y con M L < 3). Con base en
algunas concentraciones de sismos identificamos algunas probables zonas sismogénicas,
para delimitarlas mejor realizamos la interpretación de cartas aeromagnéticas y aplicamos
el método gravimétrico. Obtuvimos los mapas de anomalías gravimétricas y magnéticas,
sus transformadas y derivadas. La información fue complementada con el uso de un
modelo digital de elevaciones. Además realizamos un mapa preliminar de la configuración
en bloques del basamento. La integración de esta información sugiere un lineamiento
estructural con una orientación NW-SE. Este coincide con un patrón de estructuras
geológicas contemporáneas con la formación de la Sierra Madre Oriental durante la
Orogenia Larámide. Construimos tres modelos geológicos-geofísicos los cuales nos
permitieron establecer la relación entre las capas sedimentarias y la estructura del
basamento subyacente. En el análisis de la información geológico-geofísica identificamos
tres tipos de fallas: fallas profundas en el basamento, fallas que van de la superficie al
basamento y las fracturas y fallas que sólo son superficiales. Con estos rasgos
estructurales definimos la presencia de dos sistemas de fallas normales regionales,
perpendiculares entre sí: NW-SE y NE-SW. La afectación de dichos sistemas por esfuerzos
tectónicos produce movimientos corticales, causantes de la microsismicidad observada.
Los monitoreos temporales reflejan un alto nivel de microsismicidad persistente y más
importante de lo que hasta ahora se creía. Por lo que esta región es probablemente una
de las zonas intraplaca más activas de México. La información generada durante esta tesis
no sólo contribuye a la investigación con nuevos conocimientos, sino también permitirá a
las autoridades de Protección Civil, y a la población en general, estar alerta sobre la
ocurrencia de sismicidad y adaptarse a nuevas condiciones que ellos desconocían o
minimizaban, así como tomar las precauciones necesarias ante la ocurrencia de nuevos
episodios sísmicos.
7
CAPÍTULO I
1.1
Aspectos Generales
Introducción
En México la sismicidad más importante ha ocurrido a lo largo de la trinchera
mesoamericana, en las diversas fronteras entre las placas tectónicas, de Cocos, Rivera y
Norteamericana, en la costa del Pacífico, en la cual son más frecuentes los sismos de
magnitudes mayores. Sin embargo, otros sismos menos “conocidos”, pero igual de
significativos, son los corticales, los cuales ocurren dentro de la placa Norteamericana y
que en su mayoría son superficiales (Kostoglodov y Pacheco, 1999).
Actualmente el número de estaciones sísmicas y su distribución en la República
Mexicana aún es deficiente para registrar toda la sismicidad que en ella ocurre, ello ha
provocado que algunos sismos moderados o pequeños, así como secuencias sísmicas,
hayan pasado desapercibidas. Ante esto, la instalación de redes sísmicas temporales en
zonas consideradas como de “menor riesgo”, ha sido una alternativa que facilita el estudio
y entendimiento sobre la sismicidad de determinada región. Sin embargo, aún es poco lo
que se ha hecho para entender el fenómeno sísmico. Por ello, nos planteamos estudiar la
sismicidad intraplaca en la parte central de la Sierra Madre Oriental (SMOr), donde se ha
reportado la ocurrencia de varios sismos. En noviembre de 2007, a partir de una serie de
sismos en el NE del estado de Querétaro se instaló una red sísmica temporal, denominada
LANDA (Gómez, 2007), en el corazón de la Sierra Gorda Queretana.
Desde 2007 la microsismicidad en la Sierra Gorda se ha mantenido relativamente
constante, su origen aún es incierto y su respectiva fuente sismogénica aún se desconoce.
Por ello, como complemento de los estudios sísmicos que se han llevado a cabo decidimos
auxiliarnos de técnicas geofísicas como la gravimetría y magnetometría. Esta nueva
información, junto con las descripciones geológicas existentes, que describen la
plataforma carbonatada Valles-San Luis Potosí (PVSLP), perteneciente al Cinturón de
Pliegues y Cabalgaduras Mexicano (CPCM), nos ha permitido avanzar en una mejor
caracterización las zonas sismogénicas.
Entre las contribuciones de este trabajo están la obtención de algunos modelos
geológico-geofísicos que facilitan el entendimiento sobre la microsismicidad intraplaca, los
cuales servirán como antecedente para la realización de futuras investigaciones que
requieran el conocimiento del modelo de velocidades. Por otro lado, también resulta
novedosa la búsqueda de las probables fuentes de sismicidad analizada por León-Loya
(2011), esta combinación representa las primeras evidencias instrumentales de sismicidad
en la región.
8
Por otro lado, dado el crecimiento demográfico en esta parte del país, esta
información puede ayudar a las autoridades de Protección Civil a entender la afectación
que puede tener el fenómeno sísmico en la población, pues ante éstos es imprescindible
tomar decisiones sobre la seguridad de la población y la infraestructura local. Hasta el
momento poco se conocía del fenómeno sísmico en la región, a partir de los estudios
realizados por Gómez et al. (2007, 2008) y León-Loya (2010 y 2014) se ha encontrado que
ésta zona es probablemente una de las zonas intraplacas más activas del país.
1.2
Objetivos
GENERAL:
Integrar datos geofísicos y geológicos que permitan caracterizar lo mejor posible
las estructuras geológicas activas probables que dan origen a la sismicidad actual en la
Sierra Gorda de Querétaro.
PARTICULARES:







Monitorear la sismicidad en la Sierra Gorda de Querétaro mediante la
actualización de una red sísmica temporal.
Relocalizar la sismicidad ocurrida entre noviembre de 2007 y septiembre de 2010.
Analizar la distribución espacial y temporal de los epicentros.
Delimitar las probables zonas sismogénicas.
Llevar a cabo monitoreos geofísicos (gravimétricos) e interpretar datos
aeromagnéticos en algunas de las áreas con mayor sismicidad.
Integrar e interpretar cualitativa y cuantitativamente los datos.
Obtener modelos geológico-geofísicos que mejor representen el área de estudio.
1.3
Metodología
Llevar a cabo el registro y análisis de datos geofísicos (sísmicos, gravimétricos y
magnetométricos) e integrar los resultados con observaciones geológicas para generar
modelos geológico-geofísicos que ayuden a describir las posibles estructuras geológicas
que dan origen a la sismicidad intraplaca actual en la Sierra Gorda de Querétaro.
La metodología que se siguió durante este trabajo fue la siguiente:
9
ETAPA I
Recopilación bibliográfica.
Localización y análisis de datos sísmicos registrados en la red sísmica temporal LANDA.
Construcción de una base de datos fundamentada en una depuración de datos mediante
criterios de selección.
Relocalización de epicentros mediante la técnica mono-estación.
Ubicación espacial de los epicentros y comparación con la geología del área de estudio.
ETAPA II
Adquisición, correcciones y procesamiento de datos gravimétricos.
Análisis de cartas aeromagnéticas.
Compilación de la información existente y análisis de perfiles gravimétricos y magnéticos.
Generación de mapas gravimétricos y magnéticos.
Elaboración de modelos geológico-geofísicos.
Integración de datos e interpretación final.
1.4
Localización
La zona de estudio se ubica en la parte NE del estado de Querétaro, dentro del municipio
de Landa de Matamoros, el cual colinda al sur con el estado de Hidalgo y al norte con el
municipio de Jalpan de Serra y el estado de San Luis Potosí (Figura 1.1). Se encuentra
primordialmente sobre la plataforma carbonatada Valles-San Luis Potosí (PVSLP), la cual
pertenece al Cinturón de Pliegues y Cabalgaduras Mexicano (CPCM) (Carrillo, 1971; Suter,
1984, 1987; Carrillo, 1990). Cubre aproximadamente 90 km2 y se encuentra dentro de las
cartas topográficas, escala 1:50 000, de Jacala (F14C49), Ahuacatlán (F14C39) y Jalpan
(F14C48), realizadas por el INEGI.
La vía principal de acceso es por la carretera Federal 120, la cual atraviesa la zona
de estudio en dirección SW-NE y pasa por las comunidades de Jalpan de Serra, Landa de
Matamoros, la Lagunita y Xilitla, entre otras. Para recorrer el área de estudio se utilizaron
otras vías de comunicación como caminos, terracerías, brechas y veredas. Hacia el norte
seguimos la carretera que comunica la cabecera municipal de Landa y el Saucillo; de oeste
a este, la terracería que va desde el Saucillo a Guayabitos; y hacia el centro de la zona de
estudio, varios caminos de terracería y brechas realizadas (Figura 1.1).
10
Uno de los ríos principales, y más cercanos, es el río Moctezuma, el cual pasa al sur
del área y tiene una dirección grosso modo NE-SW. El clima característico es semi-cálido y
sub-húmedo con lluvias en verano.
Figura 1.1. Ubicación de la zona de estudio en la cabecera municipal de Landa de
Matamoros y alrededores, localizada al NE del estado de Querétaro.
11
1.5
Antecedentes
La mayor parte de la información geológica-superficial que existe sobre la PVSLP se
ha obtenido con fines petroleros (Carrillo, 1971). Petróleos Mexicanos (Pemex) realizó
numerosos trabajos de geología de semidetalle y fotointerpretación de 1962 a 1968, así
como estudios de magnetometría terrestre, aeromagnetometría y gravimetría, además de
algunos trabajos sismológicos de tipo experimental y perforación de dos pozos de sondeo
estratigráfico en su porción central (Carrillo, 1971), sin embargo, la mayoría de la
información es clasificada. De forma suscinta citamos los trabajos más destacados sobre
los estudios realizados en la SMOr de la siguiente forma:
Carrillo Bravo (1971): Expone los resultados de trabajos exploratorios realizados por
Pemex y hace una descripción geológica y estratigráfica de la Plataforma Valles-San Luis
Potosí (PVSLP) para ubicar las zonas con alta posibilidad petrolífera.
Suter (1984): Hace un análisis sobre la deformación cordillerana a lo largo del borde este
de la PVSLP, allí se asienta que ésta es activada durante la formación del cinturón de
pliegues y cabalgaduras de la Sierra Madre Oriental (SMOr).
Suter (1987): Describe la geometría estructural de la parte frontal del cinturón de pliegues
y cabalgamientos de la SMOr, y muestra que el estilo de deformación está controlado
principalmente por la geometría y litología de los bancos carbonatados del Cretácico (El
Doctor y PVSLP).
Suter (1990): Realiza la carta geológica, hoja Tamazunchale 14Q-C (5) ubicada en la parte
centro-oriental de México, que comprende los estados de Hidalgo, Querétaro y San Luis
Potosí, a una escala 1:100 000, así como su texto explicativo.
Carrillo Martínez (1990): Cuantifica la geometría estructural del cinturón de pliegues y
cabalgaduras de la SMOr en el sector comprendido entre Peñamiller y Jalpan, Querétaro.
Suter et al. (1996): Presentan mapas de isosistas para ocho sismos someros ocurridos en
la parte central y este de la Faja Volcánica Transmexicana (FVTM). Para estos sismos,
establecen su magnitud basados en el ajuste empírico del registro instrumental, la
distribución y el máximo de su intensidad.
Eguiluz et al. (2000): Establece la extensión de la SMOr, y propone el modelo de cuña
crítica para explicar las relaciones estructurales respecto a las evaporitas, la geometría de
las estructuras, la distribución del acortamiento y estilos de deformación en la SMOr.
12
Aranda et al. (2000): Explica las variaciones en la intensidad y estilo de plegamiento
Laramídico (Cretácico Tardío-Terciario Temprano) que existen entre la Cuenca Mesozoica
del Centro de México (CMCM) y la Plataforma Valles-San Luis Potosí.
López D. (2003): Realiza estudios litológico-faciales en la porción central del margen
occidental de la PVSLP para identificar en detalle las secuencias estratigráficas de la
Formación Tamabra del Cretácico medio.
Gómez (2007): Describe los efectos provocados por una secuencia sísmica ocurrida en el
municipio de Landa de Matamoros, Querétaro, entre el 1 y 4 de noviembre de 2007.
Además de las acciones tomadas para la detección de la sismicidad local y algunas
recomendaciones para entender este fenómeno sísmico.
Gómez et al. (2008): Reportan ocho meses de observaciones sobre la sismicidad en los
municipios de Landa de Matamoros y Jalpan de Serra, Querétaro, de noviembre de 2007 a
junio de 2008.
13
CAPÍTULO II
2.1
Marco Geológico
Marco Tectónico
La zona de estudio se encuentra en la parte central del cinturón de pliegues y
cabalgaduras mexicano (CPCM), el cual es una prolongación al sur del cinturón orogénico
cordillerano de Norteamérica, que va desde Alaska y el ártico Canadiense hasta el sureste
de México con una extensión de más de 6 000 km (DeCelles, 2004), forma un segmento
importante del cinturón orogénico Circum-Pacifíco (Dickinson, 2004). Su ancho máximo es
de aproximadamente 1000 km y se localiza entre el oeste de Estados Unidos y el suroeste
de Canadá. La formación de la Cordillera se ha interpretado como la acreción múltiple de
terrenos en la margen oeste de la placa Norteamericana, la mayor parte se formó entre el
Jurásico Tardío y el Eoceno, posteriormente fue modificado por extensión durante el
Paleógeno y principios del Neógeno (DeCelles, 2004) (Figura 2.1).
La fase orogénica Hidalgoense (de Cserna, 1976;
Suter, 1984), es un evento de deformación por
acortamiento de edad Cretácico tardío - Paleoceno (80 - 55
Ma); en general tiene un estilo de piel delgada (thin
skinned), que dio lugar al cinturón de pliegues y
cabalgaduras de la Sierra Madre Oriental, en la parte
centro-oriental de México (DeCelles, 2004). Se considera
que la orogenia Hidalgoense forma parte de la Orogenia
Larámide, la cual afectó al poniente de norteamérica
(Eguiluz et al., 2000).
Figura 2.1. Cinturones magmáticos pre-Laramídicos y
Laramídicos y el cinturón cordillerano en el cual se ubica el
área de estudio (verde) MM; Montañas Mackenzie, MR;
Montañas Rocallosas, MC; Meseta de Colorado, BLL; Bloques
Laramídicos Levantados, SN; Sierra Nevada, CP; Cordilleras
Peninsulares, CPCL; Cinturón de Pliegues y Cabalgaduras
Laramídico, SMOC; Sierra Madre Occidental, SMOR; Sierra
Madre Oriental (tomado de English y Johnston, 2004).
14
Los límites temporales de la deformación y su transición hasta el establecimiento
del régimen extensional aún es tema de discusión; la mayoría de los límites sugeridos
integran relaciones de tipo estratigráfico, sedimentológico, metamorfismo y edades
isotópicas de unidades ígneas y metamórficas. Los efectos principales de la deformación
Laramide fueron deformación contractiva, levantamiento y metamorfismo, colapso
gravitacional y exhumación, que migraron de poniente a oriente progresivamente entre ca
100 Ma y 60 Ma (Cuéllar et al., 2012).
La Sierra Madre Oriental (SMOr) tiene una longitud aproximadamente de 800 km y
de 80 a 100 km de amplitud; cuyo relieve se debe a la deformación de rocas sedimentarias
mesozoicas y de su basamento, que fueron levantados, comprimidos y transportados
hacia el noreste formando pliegues y cabalgaduras durante la orogenia Laramide (Eguiluz
et al., 2000). La SMOr limita al este con la Planicie Costera del Golfo (PCG), al oeste con la
Mesa Central (MC) y al sur con la provincia morfotectónica de la Faja Volcánica
Transmexicana (FVTM).
La estratigrafía de la SMOr incluye un basamento cristalino que consta de rocas
que varían en litología y edad, desde gneises de edad Precámbrica, en Peregrina,
Tamaulipas, o el núcleo del Anticlinorio de Huayacocotla (Carrillo, 1965), esquistos de
edad preoxfordiana, hasta sedimentos del paleozoico que soportan a la columna
mesozoica. Sobre la base de esta columna sedimentaria preoxfordiana se encuentran
capas rojas (Formaciones Nazas, Cahuasas, Tenexcate y La Joya) que cubren al complejo
basal. Estos lechos rojos representan el relleno de fosas tectónicas registrando una
sedimentación continental (Eguiluz et al., 2000). Durante el Jurásico superior, se
inundaron áreas bajas, extensas y planas, sobre las cuales se depositaron evaporitas,
terrígenos y carbonatos que formaron plataformas conectadas por canales y separadas
por elementos insulares; posteriormente evolucionaron a plataformas. El control
sedimentario y estructural de los bloques paleotectónicos elevados continuó hacia el
Cretácico Inferior, donde las áreas continentales cubiertas por el mar en diferentes
tiempos desarrollaron bancos y plataformas evaporítico-carbonatadas, como la de
Coahuila (Garza, 1973), Valles-San Luis Potosí, (Carrillo, 1971), etc. La subsidencia tuvo un
fuerte control estructural (Eguiluz, 1989b, McKee et al., 1990) y se desarrolló en una etapa
tipo rift de edad Jurásico Medio, hasta el Albiano-Cenomaniano; el control de subsidencia
pudo ser por enfriamiento cortical (Eguiluz et al., 2000).
Es posible que las rocas del basamento cristalino hayan tomado el papel de
bloques paleotectónicos reactivados durante la extensión asociada a la apertura del Golfo
de México y posteriormente, durante la deformación Laramide (Anderson y Schmidt,
15
1963; Flawn et al., 1961; Tardy, 1980). Las estructuras de extensión asociadas con la
apertura del Golfo de México, produjeron horsts y grabens, los cuales controlaron la
sedimentación mesozoica (Eguiluz, 1989b; McKee et al., 1990).
Eguiluz et al. (2000) realizan un análisis estratigráfico, paleogeográfico y
morfoestructural; a lo largo del frente orogénico distinguen varios sectores que se
diferencian por el estilo y orientación de la deformación. El área de estudio se encuentra
en la parte central de la SMOr, entre los sectores de Valles y Huayacocotla (Figura 2.2).
Figura 2.2. Distribución de sectores de la Sierra Madre Oriental. (1) San Pedro del Gallo,
(2) Huayacocotla, (3) Transversal de Parras, (4) Saliente de Monterrey, (5) Valles, (6)
Cuenca de Sabinas, (7) Región Zongolica y (8) Bloque de Coahuila (tomado de Eguiluz et
al., 2000).
La integración de información estratigráfica regional permite distinguir dominios
sedimentarios que evolucionaron en cuencas y plataformas, definiéndose cuatro
elementos paleogeográficos en el CPCM, como son: plataforma El Doctor (PED), cuenca de
16
Zimapán (CZ), plataforma Valles-San Luis Potosí (PVSLP) y cuenca Tampico-Misantla (CTM)
(Figura 2.3).
Figura 2.3. Paleogeografía de la porción centro-oriental de México para el AlbianoCenomaniano mostrando las principales cuencas y plataformas del Cretácico Medio y
localización del área de estudio. Los rectángulos indican áreas estudiadas por Carrasco
(1977; tomado de López Doncel, 2003).
El área de estudio se localiza sobre la PVSLP, la cual abarca los estados de
Querétaro, San Luis Potosí e Hidalgo (Figura 2.4). Esta unidad paleogeográfica incluye
rocas sedimentarias y cuerpos ígneos efusivos y subvolcánicos del Jurásico-Cretácico. Las
rocas presentan plegamiento y cabalgamiento en amplias zonas de deformación (Suter,
1984; Fitz-Díaz, 2010). Las unidades posteriores a la deformación incluyen cuerpos ígneos
y depósitos volcánogénicos del Paleógeno y Neógeno. En la zona de estudio afloran rocas
sedimentarias marinas, del Jurásico Tardío al Cretácico Tardío, que fueron deformadas en
pliegues y cabalgaduras con una dirección NNW-SSE (Carrillo-Martínez, 1989, 1990) y
depósitos aluviales y fluviales cuaternarios que rellenan los valles (Figura 2.4).
17
Figura 2.4. Mapa geológico de la zona de estudio obtenido de la carta geológica Ciudad
Valles del Servicio Geológico Mexicano (1997).
Carrillo Bravo (1971) describió la PVSLP como una de las unidades paleogeográficas
más grande de una serie de plataformas carbonatadas aisladas que se elevaban por
encima de las cuencas de aguas profundas que las rodeaban. Dicha plataforma tuvo su
mayor extensión y desarrollo durante el Aptiano-Albiano en la porción centro-nororiental
de México, con crecimiento de bordes (isolated rimmed platform, Basañez-Loyola et al.,
1993; Wilson, 1990) y una superficie de más de 48 000 km2. Entre las cuencas y la
plataforma se desarrollaron zonas de cambios de facies correspondientes a ambientes de
plataforma interna (Formación El Abra), talud (Formación Tamabra) y cuenca (Formación
Tamaulipas).
18
2.2
Estratigrafía
La litología de la zona de estudio es representada por la columna estratigráfica
generalizada (Figura 2.5) (Fitz, 2010) y que usamos como base para la elaboración de los
modelos geológicos-geofísicos representativos del área.
En la PVSLP el basamento consta de rocas
metamórficas (gneisses de edad precámbrica) las
cuales se encuentran mayormente en el subsuelo y
afloran en algunos sitios (Anticlinorio HuizachalPeregrina). Se hallan en aparente contacto por falla con
capas rojas Triásicas (Carrillo, 1971).
El complejo basal subyace una sección de lutita
calcárea con amonites grabados, lutita carbonosa y
caliza arcillosa perteneciente a la Formación Santiago
de edad Jurásico Superior con un espesor aproximado
de 300 m.
Una secuencia evaporítica de edad Neocomiano
Aptiano denominada Formación Guaxcamá por J.
Martínez (1965, en Carrillo, 1971) se localiza en la
porción central de la PVSLP; constituida por yesos y
anhidritas bien estratificadas en capas de 5 a 50 cm de
espesor, de color gris claro a gris oscuro finamente
bandeadas por material arcilloso e intercaladas
esporádicamente por calizas y dolomitas. Su espesor
aproximado es de 310 m medidos en la localidad tipo.
Concordantemente sobre esta secuencia de
evaporitas descansa un complejo calcáreo tipo
plataforma
de
edad
Albiano-Cenomaniano,
denominado Formación El Abra, cuyo término fue
originalmente citado por Garfias (1915) y aplicado por
primera vez por Powers (1925) para designar las calizas
de los campos petroleros de la Faja de Oro. Dicha Formación ha sido estudiada por Heim
(1925 en Carrillo, 1971), Baker (1926), Díaz (1927), Adkins (1930), Nigra (1951); discutida
por J. Muir (1934) y estudiada ampliamente por Bonet (1952).
Figura 2.5. Columna estratigráfica
generalizada de la Plataforma
Valles-San Luis Potosí donde se
ubica el área de estudio.
Modificado de Fitz (2010).
19
Muir (1936) dividió la Formación El Abra en dos facies: Facies Taninul considerada
como la más antigua o subyaciendo a la Facies El Abra. Sin embargo, Carrillo (1971)
clasificó dicha Formación en tres facies principales de edades semejantes como: Facies
Pre-Arrecifal (Tamabra) caliza con estratificación gruesa a delgada y aproximadamente
1200 m de espesor; Facies Arrecifal (Taninul) caliza arrecifal de estructura masiva con un
espesor aproximado de 1100 m y Facies Post-Arrecifal (El Abra) caliza de estratificación
gruesa con 1100m de espesor.
La Formación Soyatal (Wilson y col. 1955) descansa concordantemente sobre la
Formación El Abra, es una sección de aproximadamente 300 m de espesor, de calizas
arcillosas color gris oscuro, interestratificadas con lutitas calcáreas, de edad Turoniano,
aflorantes al poniente de Zimapán y Jacala, Hgo. Definen su localidad tipo en los
alrededores de Soyatal, Qro.
En el área de estudio no se reconocen cuerpos ígneos intrusivos de edad
Paleógeno y Neógeno; por lo que, el aluvión es el último depósito de edad cuaternaria
localizado en la región, el cual descansa sobre la Formación Soyatal y consiste de
conglomerados, gravas, arenas, limos y arcillas de origen fluvial y aluvial, que se
encuentran rellenando parte de los valles.
20
CAPÍTULO III
Sismicidad
La mayor parte de la sismicidad global se encuentra concentrada en los límites de placas y
la ocurrencia de sismos dentro de ellas, se conoce como sismicidad intraplaca, la cual ha
sido responsable de una pequeña fracción de la energía liberada de esfuerzos
mundialmente (< 10 % p.e. Johnston, 1989) sin embargo, la sismicidad intraplaca no debe
considerarse tan despreciable, ya que puede generar daños relativamente importantes.
Debido a la baja atenuación que existe en la litósfera en regiones continentales estables,
el nivel de sismicidad causado por sismos intraplaca moderados alcanzan un área mayor
comparado con magnitudes similares en áreas interplaca (p.e. Nuttli 1973).
La importancia en el estudio de la sismicidad intraplaca radica en tener un mejor
conocimiento sobre la ocurrencia de los sismos y conocer las regiones con posible peligro
sísmico. La complejidad de su estudio se encuentra en su génesis. Estos sismos, por lo
general, se asocian a zonas de debilidad, usualmente identificadas como sitios donde
ocurrieron grandes deformaciones, como provincias de recientes intrusiones alcalinas, o
zonas donde la corteza fue extendida por antiguos rifts. Sin embargo, es difícil identificar
zonas especificas de debilidad y las zonas de falla intraplaca no siempre son fáciles de
correlacionar con características geológicas conocidas (Lopes et al. 2010); pues estas
regiones sísmicas, posiblemente tienen tasas de deformación tectónica más lenta que las
tasas de erosión, por ello las trazas de actividad superficial son borradas (Scholz, 2002).
La sismicidad intraplaca se ha explicado por la reactivación de zonas de debilidad
pre-existentes, por concentración de esfuerzos, o por ambos (Sykes 1978; Hinze et al.
1988; Johnston 1989). Sykes (1978) propuso que las zonas de debilidad intraplaca son los
sitios donde ocurrieron grandes deformaciones anteriores que afectaron el área, por lo
que, las intrusiones alcalinas más recientes podrían ser usadas para identificar tales zonas.
Hinze et al. (1988) estudia los distintos modelos de concentración de esfuerzos:
heterogeneidades en el basamento, contracción/expansión térmica y la deformación
isostática/flexural. Johnston (1989) atribuye la mayoría de los sismos mayores
en
regiones continentales estables debido a una corteza extendida debilitada por antiguos
rifts.
Schulte & Mooney, (2005) realizan una compilación de sismos intraplaca y muestran
que la correlación con antiguos rifts continentales no es tan significativo como se pensaba
anteriormente. Talwani & Rajendran (1991) explican que estos sismos (“midplate”) son
relacionados con la reactivación de fallas pre-existentes y concentración de esfuerzos
debido a la intersección de diferentes estructuras (Gangopadhyay & Talwani, 2005;
Yamini-Fard et al., 2006).
21
3.1
Sismicidad histórica
En México, la sismicidad intraplaca es dispersa y generalmente de una magnitud
moderada
y aunque su parte central se encuentra catalogada como zona de
bajo peligro sísmico (García y Suárez, 1996), han ocurrido eventos intraplaca históricos
con una magnitud importante, de hasta 7.0.
La concentración de esta sismicidad en el centro de México, es sobre el Cinturón
Volcánico Trans-Mexicano (TMVB) y a lo largo del margen SW del Golfo de México. Las
partes central y este de la TMVB son caracterizadas por la ocurrencia de sismicidad
intraplaca somera (Engdahl, 1988). Las ciudades más afectadas por sismos destructivos
han sido Guadalajara, Jalapa y Acambay. En esta última localidad existen reportes de
sismos ocurridos en 1734, 1854, 1873, 1912 y 1979. Los sismos más grandes incluyen el
sismo cerca de Acambay
el 19 de noviembre de 1912 (Urbina y Camacho,
1913) y el de Jalapa, 1920 ( =6.2) (Comisiones del Instituto Geológico de México, 1922),
así como dos eventos con
=5.3 desde 1976 (Tabla). La sismicidad de la región se debe a
fallas normales con dirección este-oeste que son caracterizadas por escarpes
pronunciados y el desplazamiento de rocas volcánicas cuaternarias (Suter et al., 1992,
1995a, 1995b). Los mecanismos focales de otros tres eventos (Oct 4, 1976; Feb 22, 1979
[Astiz, 1980]; March 31, 1985) muestran fallamiento normal en los planos nodales
orientados aproximadamente EW, lo cual concuerda con la extensión intra-arco que
ocurre en la TMVB (Ponce y Suarez, 1986; Suter et al., 1995a; Zuñiga et al., 2003; Dávalos
et al., 2005; Ferrari, 2011). Los mecanismos focales de la secuencia sísmica ocurrida
durante finales de 2010 y principios de 2011 en las vecindades de Peñamiller, Querétaro
también muestran en su mayoría fallas normales con pequeñas componentes laterales
consistentes con el régimen extensional al sur de la provincia “Basin and Range”
(Clemente-Chavez et al., 2013).
Suter et al. (1996) realizaron mapas isosistas para ocho sismos someros que
ocurrieron en la partes central y este del TMVB, (1887 Pinal de Amoles, 1912 Acambay,
1920 Jalapa, 1950 Ixmiquilpan, 1976 Cardonal, 1979 Maravatío, 1987 Actopan y 1989
Landa; 4.1 ≤ mb ≤ 6.9) ver Figura. Los sismos históricos más cercanos a la zona de estudio
son: Pinal de Amoles y Landa de Matamoros.
22
Figura 3.1. Distribución de los ocho sismos intraplaca estudiados por Suter et al. (1996)
(Tomado de León, 2010).
Tabla 3.1. Parámetros de la fuente y datos relacionados con la Intensidad (modificado de
Suter et al., 1996)
Localización
Fecha
Tiempo
origen
Localización
Instrumental
Lat. N
Long. W
Magnitud
(
)
Profundidad
(km)
Intensidad
Máxima
(MM)
Pinal
1887 Nov 26
05:16
21.14
99.63*
—/5.3*
?
8
Acambay
1912 Nov 19
13:55:17
19.83
99.92
6.7/6.9
5-15
11
Jalapa
1920 Ene 04
04:22:01
19.27
97.08
6.2/6.5
15
11
Ixmiquilpan 1950 Mar 11
00:42:51
20.35
98.97
—/4.9.
S
7-8
Cardonal
1976 Mar 25
23:05:06.9
20.62
99.09
—/5.3
15
8-9
Maravatío
1979 Feb 22
09:16:33
19.89
100.18
—/5.3
8±3
7-8
Actopan
1987 Ene 27
16:33:29
20.31
99.21
—/4.1
15
7-8
Landa
1989 Sept 10
13:28:40.5
21.04
99.43
—/4.6
10
7-8
El tiempo origen del sismo de 1887 está dado en hora local de San Luis Potosí, mientras que para
el resto de eventos está dado en tiempo universal. S=somero. *Localización y magnitud inferida
de la relación magnitud-intensidad derivados en Suter et al. (1996).
23
Acambay, Estado de México: Este sismo ocurrió el 19 de noviembre de 1912 con una
magnitud
, aproximadamente a 100 km al NW de la ciudad de México. Causó la
muerte de 161 personas (Urbina y Camacho, 1913, p.122) y originó la ruptura en
superficie a lo largo del sistema de fallamiento normal E-W que forman el graben
Acambay (Suter et al. 1995a), así como las fallas dentro del graben. Urbina y Camacho
(1913) realizaron con detalle el registro instrumental, observaciones geológicas y
descripción de daños y concluyen que el sismo principal ocurrió al norte de la falla
principal del graben. La longitud de la ruptura fue de 41 km y el desplazamiento vertical
fue de 50 cm. El sismo fue sentido en Santa María del Río, San Luis Potosí; Chilpancingo,
Guerrero; Ocotlán, Jalisco y Puebla, Puebla. Alcanzó intensidades de XI en varios lugares
dentro del graben Acambay (Urbina y Camacho, 1913, p.122).
Pinal de Amoles, Querétaro: El sismo principal ocurrió el 26 de Noviembre de 1887,
a las 5:16 a.m. (hora local) con una magnitud
, inferida de la relación magnitudintensidad por Suter et al. (1996). Este sismo fue sentido en Lagos de Moreno, Jalisco;
Ozuluama y Tantoyuca, Veracruz; Tepeji, Hidalgo; Morelia, Michoacán y Peotillos y Ciudad
del Maíz, San Luis Potosí (Suter et al. 1996).
Landa de Matamoros, Querétaro: El sismo principal sucedió el 10 de septiembre de
1989 con una magnitud
. La localización epicentral instrumental es
aproximadamente 15 km al SW de donde Suter et al. (1996) esperaron el epicentro
basado en la distribución de intensidad, mientras que el Servicio Sismológico Nacional lo
localiza aproximadamente a 40 km al NE. Suter et al. (1996) explican que esta discrepancia
puede deberse a una pobre distribución de estaciones sísmicas, lo cual causa una
incertidumbre de 30 a 40 km en la localización epicentral. Por otro lado, no hay una
correlación obvia de la región de alta intensidad con condiciones locales tales como
unidades geológicas superficiales de bajos valores de impedancia sísmica. (Lajoie y Helley,
1975) o una zona de alto nivel de aguas subterráneas.
El deslizamiento de rocas podría haber generado varios sismos inducidos al sur de
Landa, a lo largo del río Moctezuma. Para un sismo de esta magnitud, los deslizamientos
de roca no se esperan más allá de 5 km de la zona de ruptura (Wilson y Keefer, 1985).
Landa de Matamoros ha sido afectado por sismos anteriores, como el del 8 de mayo de
1887 (Orozco y Berra, 1887, p. 514), sin embargo, no hubo reportes en Pinal de Amoles, lo
cual sugiere que los sismos de Landa y Pinal de Amoles ocurrieron en dos zonas de
sismicidad separadas.
24
Los epicentros de Landa y Pinal de Amoles se encuentran aproximadamente a 30 km
de distancia y no hay fallas del cuaternario en superficie conocidas en la región, por lo que
es incierto si los dos eventos pudieran estar relacionados a un mismo sistema de fallas.
La sismicidad reportada por el Servicio Sismológico Nacional (SSN) desde marzo de
1998 a diciembre del 2011, son 57 eventos cuya magnitud va de 2.8 a 4.3. El NEIC reporta
55 eventos desde marzo de 1976 a julio del 2011, con magnitudes que van de 2.9 a 5.5.
(Figura 3.2). Dicha sismicidad se encuentra dentro del área delimitada por las coordenadas
20° - 22° latitud N y 98° - 100° longitud W. Esta sismicidad es relativamente baja,
comparada con la actividad interplaca del País y su distribución se observa dispersa. Una
de las principales razones porque el registro sísmico sea insuficiente puede deberse a la
pobre cobertura azimutal de las redes sísmicas, y no por la ausencia de dicha actividad,
como se pensaba anteriormente.
Figura 3.2. Distribución de la sismicidad histórica reportada por otras redes sísmicas.
25
León Loya (2010) realizó un análisis de la actividad sísmica registrada en la zona
noreste de Querétaro, conocida como Sierra Gorda; estimando la localización epicentral
de 592 eventos someros (0.1 ≤ ML ≤ 3.5) obtenidos a partir de la Red Sismológica
Temporal Landa (RSTL) por un periodo de 17 meses, desde su instalación que fue en
noviembre de 2007. La distribución espacial de sismicidad sugiere dos zonas sismogénicas
principales. Una al noreste de Querétaro, incluyendo la cabecera municipal de Landa de
Matamoros y localidades como La Lagunita, El Aguacate, Otates, Tilaco y San Antonio
Tancoyol. La segunda zona se encuentra al norte de la RSTL, al sur de la zona media de San
Luis Potosí.
Figura 3.3.Distribución espacial de la sismicidad registrada en el periodo de noviembre
2007 a marzo de 2009 (Tomado de León-Loya, 2010).
26
La importancia de realizar un estudio más detallado, basado en la actividad sísmica
registrada por la RSTL, así como el análisis a fondo de los datos sísmicos registrados de
noviembre de 2007 a septiembre de 2010, realizado por León Loya (2014), proporciona
aproximadamente ~2500 localizaciones epicentrales, cuya magnitud M L ≤ 3 y profundidad
h < 10 km; sirve de base para delimitar la información y re-localizar aproximadamente
~300 sismos locales (~h<10 km y con ML < 3) los cuales caen dentro de la zona de estudio
y se encuentran dentro de la primer zona sismogénica caracterizada por su distribución
espacial (León-Loya, 2010).
Figura 3.4. Distribución espacial de la sismicidad registrada en un periodo de noviembre
2007 a diciembre 2010 (Modificado de León-Loya, 2014).
27
3.2
Red sísmica temporal LANDA
A finales de noviembre de 2007 varias poblaciones al NE del estado de Querétaro se
alarmaron por la ocurrencia de varios sismos. Por esta razón, el Centro de Geociencias
Campus UNAM, Juriquilla inició con la instalación de una Red Sísmica Temporal Landa
(RSTL), desplegada a lo largo de la Sierra Gorda, Querétaro. La RSTL se encuentra
actualmente operando. Las estaciones sísmicas se instalaron en las poblaciones de Landa
de Matamoros (LD5), Otates (LO8), El Aguacate (LG3), Zoyapilca (LZ4), Tancoyol (LT9) y San
Antonio Tancoyol (LA4) como se observa en la Figura. y en la tabla se muestra su ubicación
geográfica.
Figura 3.5. Distribución de las estaciones sísmicas las cuales conforman la RSTL.
28
Tabla 3.2. Ubicación geográfica de las estaciones sísmicas de la RSTL (Modificado de
León-Loya, 2010)
Estación
Localidad
Latitud N
Longitud W
Elevación (msnm)
LD5
Landa de Matamoros
21.18653°
-99.32030°
1024
LO8
Otates
21.15944°
-99.21381°
1366
LG3
El Aguacate
21.27563°
-99.25241°
1147
LZ4
Zoyapilca
21.33085°
-99.26934°
1147
LT9
Tancoyol
21.39578°
-99.32650°
LA4
San Antonio Tancoyol
21.48396°
-99.30867°
1112
*LV1
Valle de Guadalupe
21.38288°
-99.19935°
1112
*Estación sísmica instalada en 2011.
Las estaciones sísmicas de la RSTL, tienen sismógrafos GeoSig triaxiales de periodo
corto modelo GBV-316 (Figura 3.6a), compuestos por geófonos de 4.5 Hz., de un
digitalizador de 16 bits y GPS para quedar referenciado espacial y temporalmente. La
energía eléctrica fue por suministro eléctrico o por el uso de panel solar, a través de una
batería de 12 v. y un controlador fotovoltaico para cada estación. La configuración de cada
estación se muestra en las Figura 3.6b.
La instalación de cada estación y los parámetros de disparo de cada sismógrafo se
eligieron con base en la operación de la red, es decir, se consideró la cantidad de
almacenamiento de la memoria del instrumento, la tasa de muestreo, los valores STA, LTA
y STA/LTA, tiempos pre y post-evento para evitar la pérdida de información, condiciones
de vibración ambiental y el grado de intensidad de los eventos; los cuales se pueden
consultar en León (2010).
29
Figura 3.6. a) Configuración de las estaciones sísmicas (sismógrafo, Panel solar, batería y
controlador fotovoltaico). b) Vista típica de una estación sísmica.
3.3
Procesamiento de datos
Los sismogramas cuantifican los movimientos del terreno mediante su representación
gráfica y sirven para entender la estructura de la Tierra y sus procesos dinámicos. Son una
mezcla complicada sobre los efectos de radiación de la fuente, el fenómeno de
propagación de ondas, así como los efectos que resultan del rango de frecuencias en el
registro del instrumento.
Kulhánek (1997), precisa que la información contenida en los sismogramas
depende del tipo de fuente (natural o inducida), de la distancia epicentral (local, regional y
telesísmica) y de la profundidad del foco (someros, intermedios y profundos). La
instrumentación sísmica a lo largo de los años, ha tenido importantes avances y
desarrollos tecnológicos, lo cual hace posible registrar y almacenar los distintos tipos de
eventos sísmicos, de acuerdo a la clasificación anterior.
30
Figura 3.7. Clasificación y visualización de un sismograma en sus tres componentes con el
programa de adquisición GeoDas.
Los sismogramas obtenidos mediante el monitoreo realizado desde noviembre de
2007 a septiembre de 2010 de la RSTL se procesaron mediante el conjunto de programas
Seisan (Havskov y Otemöller, 2008), el cual se distribuye en varios subdirectorios.
Una vez que los datos sísmicos fueron recopilados, se clasificaron de acuerdo al tipo
de fuente y se elaboró una base de datos, los eventos inducidos fueron descartados. Esto
se realiza con el programa de adquisición GeoDas (Figura 3.7) y a través de este, es posible
convertir los datos crudos a formato Seisan donde pueden ser procesados.
Se crea la base de datos del periodo de monitoreo de la RSTL en el sistema Seisan
(Havskov y Otemöller, 2008). Los archivos convertidos se clasifican por año, mes y día en
cada estación, los cuales fueron ordenados con base en el tiempo de inicio del registro,
después se compararon con el resto de las estaciones y aquellas en las cuales el tiempo de
inicio de cada registro coincidía entre sí en un intervalo de un minuto, se almacenaron en
un archivo para el mismo evento sísmico (Ej. Figura 3.8).
Posteriormente, se registraron todos los eventos sísmicos en la base de datos y con
el comando eev (programa guía), fue posible realizar la visualización de las señales, el
marcado de fases, el cálculo del azimut, localización epicentral (llama al programa
Hypocenter), solución del plano de falla, entre otros.
31
Figura 3.8. Visualización de un evento sísmico registrado en dos estaciones con el
programa Seisan.
Para realizar la localización epicentral, se utilizó el programa Hypocenter (Lienert y
Havskov, 1995), incluido en la paquetería de Seisan (Havskov y Otemöller, 2008). Este
programa permite realizar las localizaciones mediante los tiempos de arribo de las
distintas fases sísmicas, utilizando la técnica de mínimos cuadrados para su ajuste. Utiliza
procedimientos estadísticos de regresión, tales como centrado y escalamiento, para
determinar las variaciones de los tiempos de arribo con su correlación en las variaciones
en la localización hipocentral (Lienert et al., 1986). El modelo de corteza de velocidades
(Tabla 3.3) fue extraído de Nieto et al. (2005), pues la estimación de los valores de
velocidad son físicamente aceptables con la geología característica de la SMO.
La estimación de la magnitud local es a través de la técnica estándar propuesta por
Kanamori y Jennings (1978), la cual toma las amplitudes máximas de las ondas S medidas
en un sismograma. Este cálculo se encuentra incluido en los códigos de los programas de
Seisan (Havskov y Ottemöller, 2005). Los pasos realizados a detalle para el procesamiento
de las señales sísmicas, se pueden consultar en León-Loya, 2010.
32
Tabla 3.3. Modelo de velocidades de la corteza (extraído de Nieto et al., 2005).
3.4
Profundidad (km)
Velocidad (km/s)
0
5.72
5
6.44
20
6.86
30
8.21
80
8.5
Localización epicentral
Uno de las labores fundamentales de la sismología es la localización de la fuente sísmica.
Esto implica determinar el hipocentro y el tiempo origen de la fuente.
Para determinar la ubicación de la fuente sísmica se requiere de:



Identificación de fases sísmicas.
Medición del tiempo de arribo de las fases.
Velocidad de propagación de las ondas entre el hipocentro ( ) y la estación
sísmica ( ).
Una vez que se conoce la ubicación de la fuente sísmica, uno puede calcular el
tiempo de viaje de cualquier fase en particular hacia cualquier estación sísmica en un
determinado modelo de velocidades. Esto se conoce como problema Directo; donde los
tiempos de arribo son calculados sobre la base de un modelo parametrizado. El método
Inverso consiste en localizar el hipocentro, donde solo conocemos los tiempos de arribo
de las distintas fases para resolver la ubicación de la fuente y su tiempo origen (Lay &
Wallace, 1995).
33
Localización Mono-estación
Generalmente, se requieren de varias estaciones para la localizar un sismo. Sin
embargo, también es posible hacer esta tarea con una sola estación, aproximándose a la
ubicación del sismo. Este método es una estimación cruda y es posible con una sola
estación que registre el movimiento del suelo en sus tres componentes. Puesto que las
ondas P son polarizadas vertical y radialmente, el vector de movimiento de onda P se usa
para inferir el azimut hacia el epicentro.
En la figura 3.9 se puede apreciar la polarización de la onda P, si el movimiento
vertical es hacia arriba, la componente radial es dirigida lejos del epicentro. Si es hacia
abajo, la componente radial se dirige hacia el epicentro. Excepto cuando el epicentro está
en el azimut opuesto, tal que el movimiento horizontal esté rotado sobre una
componente, los dos sensores horizontales registrarán la componente radial de la onda P.
La relación de amplitudes entre las dos componentes horizontales puede ser usada, para
encontrar la proyección del vector de la onda P a lo largo del azimut hacia la fuente
sísmica (Lay & Wallace, 1995).
Figura 3.9. Procedimiento para determinar el azimut a la fuente sísmica de un
registro de onda P, usando las tres componentes del vector del movimiento del suelo,
partiendo de que los movimientos de la onda P son polarizados en el plano vertical y
radial. (Modificado de Båth, 1979).
34
La distancia a la fuente sísmica es obtenida de la diferencia entre el tiempo de arribo
de las fases P y S. Si el sismo se encuentra en un rango local, la distancia puede ser
aproximada por la siguiente relación:
donde
.Esta relación asume un sólido de Poisson. Para eventos sísmicos de la
corteza, la regla es como sigue:
Para distancias mayores, se puede hacer uso de las tablas Tiempo-Distancia (travel-time).
Si se conoce la distancia, se puede estimar el tiempo de viaje de la onda, por lo
tanto, determinar el tiempo de origen del sismo. Al comparar las diferencias de tiempo
entre conjuntos múltiples de fases con los tiempos de las curvas Tiempo-Distancia se
puede mejorar la estimación de la distancia. Si hay fases claras, se puede estimar la
profundidad de la fuente sísmica, pero no es preciso para distancias mayores a 20°,
porque el arribo de las ondas P es abrupto y sus componentes horizontales son muy
pequeñas para dar un azimut confiable.
Localización multi-estación
Cuando se tienen disponibles los tiempos de arribo de P y S de varias estaciones, la
localización puede ser bastante precisa. Si el evento es local, el tiempo origen del sismo
puede ser determinado con una técnica gráfica muy simple conocida como Diagrama de
Wadati. Consiste en graficar puntos cuyo tiempo de arribo de las ondas P se traza en las
abscisas, y las diferencias de tiempo entre las fases P y S
se marca en las
ordenadas. Debido a que la diferencia se aproxima a cero en el hipocentro, la intersección
de la línea recta ajustada con el eje de las abscisas dará el tiempo origen.
La pendiente de la recta es
Poisson como sigue:
lo cual se relaciona con la razón de
donde
35
Figura 3.10. Ejemplo del Diagrama de Wadati para determinar el tiempo origen de un
sismo local. El tiempo origen está dado por la intersección con el eje de tiempo de
arribo de P.
Una vez que el tiempo origen
ha sido estimado, la distancia epicentral
para
una estación th puede ser calculado restando este tiempo, del tiempo-trayecto de la
onda P y multiplicándolo por una velocidad promedio de P:
El epicentro debe estar en una semiesfera de radio
con centro en la estación .
Se construyen estos círculos en cada estación, y donde se intercepten en un solo punto,
serían las coordenadas del epicentro. La profundidad focal d, puede ser determinada por
la raíz cuadrada de la diferencia entre los cuadrados de la distancia de propagación
y la
distancia a lo largo de la superficie al epicentro Δ:
Por tratarse del uso de varias estaciones, siempre está implícito el error, tanto en
los datos como en la suposición de que el trayecto del rayo es rectilíneo y que la velocidad
de propagación es conocida, por lo que siempre existe dispersión en la intersección.
36
Figura 3.11. Método de Círculos para la triangulación de un hipocentro (Modificado de
Lay & Wallace, 1995).
El método para determinar el hipocentro de un sismo es llamado Método de
círculos. Se supone un semiespacio homogéneo e incluso es útil para una estructura de
velocidades heterogéneas, pero de capas planas. Por lo que, el método puede aplicarse a
una tierra esférica, pero con una ligera variación que ayuda a conceptualizar el problema
inverso.
37
CAPÍTULO IV
4.1
Métodos Potenciales
Método Gravimétrico
4.1.1 Relaciones fundamentales
Ley de Gravitación Universal
El método gravimétrico es uno de los métodos geofísicos más utilizados, el cual
considera las variaciones del campo gravitacional de la Tierra. Estas variaciones son una
consecuencia de las diferencias de densidad entre las rocas del subsuelo. El método está
basado en la ley de Gravitación Universal decretada por Newton, la cual establece la
fuerza de atracción, F, entre dos partículas con masas m1 y m2, separadas por una
distancia r, es representada por la siguiente expresión (Burguer et al., 2006):
donde, G es la constante de gravitación universal con un valor de 6.673 x 10-11 (NM2/Kg2),
ésta fue determinada por primera vez en 1798 por Lord Cavendish.
Si se asume que la Tierra es esférica, la fuerza ejercida por ésta sobre un cuerpo
esférico, de masa m en reposo, sobre su superficie es (Burguer et al., 2006):
donde, M es la masa de la Tierra y R su radio. Esto también supone que la densidad varía
únicamente con la distancia al centro de la Tierra.
En el caso de la fuerza de aceleración, ésta también es dada por la segunda Ley de
Newton, la cual establece que ésta es directamente proporcional a la masa (m) y a la
aceleración (a):
cuando la aceleración “a” es causada únicamente por la atracción gravitacional de la
Tierra, ésta es la constante de aceleración gravitacional “g”, por lo que para deducirla se
tiene que (Burguer et al., 2006):
38
por lo que, la aceleración gravitacional queda definida por:
las dimensiones de g quedan expresadas como m/s2 (SI) o cm/s2 (cgs).
En Geofísica la unidad de la aceleración gravitacional es el Gal (en honor a Galileo),
el cual es 1 cm/s2. Debido a que las variaciones en g son muy pequeñas, a menudo se
utiliza el miliGal (1 mGal = 0.001 Gal). La unidad gravimétrica
a veces es utilizada en
-6
2
lugar del mGal, por lo que, 1 gu=1x10 m/s =0.1 mGal.
Campo gravitacional Terrestre
Teóricamente, el campo de gravedad de la Tierra es casi el mismo que el de una
esfera que tiene el mismo radio promedio y masa total, pero se incrementa ligeramente
hacia los polos. El valor promedio de la gravedad sobre la superficie de la Tierra es
aproximadamente de 9.80 m/s2 o 980 000 mGal. La diferencia entre los campos ecuatorial
y el polar es cerca de 0.5 % o 5 000 mGal [=5 G]. La razón de cambio es cero en los polos,
mientras que en el ecuador y alcanza un máximo de aproximadamente 0.8 mGal por
kilometro al norte o sur a 45° de latitud (Figura 4.1) (Milsom, 2003).
Figura 4.1 Variación teórica del campo de gravedad a nivel del mar y su gradiente
horizontal norte-sur correspondiente con la latitud. No hay gradiente este-oeste en el
campo teórico (tomado de Milsom, 2003).
39
4.1.2 Medición de la Gravedad
El achatamiento de la Tierra causa un incremento en la gravedad del ecuador al
polo. Por lo que, las medidas de gravedad son de dos tipos: Absoluta y Relativa. La
primera corresponde a la determinación de la magnitud absoluta de gravedad en
cualquier lugar; la segunda consiste en medir el cambio de gravedad de un lugar respecto
a otro (ver Anexo A). En la exploración gravimétrica es necesario medir con precisión los
cambios de gravedad causados por estructuras del subsuelo. Para lograrlo se requiere un
instrumento con una sensibilidad del orden de 0.01 mGal; la importancia de su uso radica
en obtener valores de gravedad más confiables para la determinación de anomalías
gravimétricas que pueden ser de interés económico, científico o social.
Densidad de las rocas1
Para entender e interpretar correctamente las anomalías gravimétricas se necesita
información sobre la densidad de las rocas que se encuentran en el área de estudio. En
muchas ocasiones, este valor no es fácil de obtener, pues las muestras colectadas en
campo pueden estar erosionadas, por lo tanto, son menos densas que la mayor parte del
material rocoso que se supone representan, esta variación puede deberse a la pérdida de
agua de los poros de la roca. Se pueden realizar ciertas estimaciones de la densidad a
través de otros estudios como sondeos en pozos o registros radiométricos (en la
exploración de hidrocarburos), pero generalmente estos datos sólo están disponibles
durante la realización del trabajo. En la Tabla A.1 (ver Anexo A) se muestran algunos de los
valores típicos de densidad de algunas rocas y minerales.
Método de Nettleton
Nettleton (1976) propuso un método para la determinación de densidad de
manera directa de los datos de gravedad. El valor de densidad promedio correcto será el
que produzca la mínima correlación (positiva o negativa) entre la topografía y el mapa de
anomalía de Bouguer (Figura 4.2). El método puede aplicarse a un perfil o a todas las
estaciones de gravedad en el área. Este método proporciona información sobre las
densidades únicamente a profundidades relativamente someras, y puede ser fácilmente
usado sólo cuando la litología cercana a la superficie es homogénea. Ya que en muchas
1
3
3
En el SI la unidad de densidad es el kg/m , pero el Mg/m es ampliamente usado desde que los valores
numéricamente son los mismos que en el sistema cgs, en el que el agua tiene como densidad la unidad. La
3
mayoría de las rocas de la corteza tienen densidades entre 2.0 y 2.9 Mg/m . En trabajos de gravimetría se
3
usa una densidad de 2.67 Mg/m como estándar para la corteza superior, ésta es ampliamente usada en el
modelado y en las correcciones de elevación para los mapas de gravedad estandarizados.
40
áreas las características topográficas son producto de afloramientos con litología
heterogénea, y el valor de densidad determinado puede ser incorrecto (Milsom, 2003).
Figura 4.2. Método de Nettleton para la determinación de densidad a través de un rasgo
topográfico aislado. Las reducciones gravimétricas se realizan usando densidades entre
un rango de 1.8 a 2. 8 Mg/m3 para correcciones de Bouguer y de terreno. El perfil
corresponde a un valor de 2.3 Mg/m3 que muestra la mínima correlación con la
topografía, por lo que esta densidad es tomada para representar la densidad del rasgo
(tomado de Dobrin & Savit, 1988).
4.1.3 Reducciones gravimétricas
La teoría indica que si la Tierra tuviera una simetría esférica perfecta, fuese
homogénea y careciera de su movimiento de rotación, la atracción de la gravedad debería
ser la misma en cualquier parte de su superficie. Sin embargo, en la realidad no existe tal
perfección, por lo que es esencial identificar las razones por las cuales la atracción de la
gravedad varía, de manera que ésta se puede utilizar para explorar el subsuelo. Un factor
importante es la posición de observación sobre la superficie de la Tierra: El valor absoluto
de gravedad en el ecuador es 978 Gals, mientras que en los polos dicho valor es de 983.2
Gals (Burguer et al., 2006).
41
Antes de poder interpretar los resultados de un estudio gravimétrico, es necesario
corregir todas las variaciones del campo gravitacional de la Tierra que no provengan de las
diferencias de densidad de las rocas (Kearey et al., 2002). Ya que algunas de estas
variaciones son producidas por fuentes que no son de interés geológico directo (Milsom,
2003). Este proceso es conocido como reducción gravimétrica (LaFehr 1991) o reducción al
geoide, debido a que el nivel del mar es usualmente el datum utilizado.
Variación de g como una función de la latitud
Como hemos visto, la fuerza de atracción de la gravedad (g) varía con la latitud, sin
embargo, en realidad este valor representa el efecto neto de varios factores. Por ejemplo,
la rotación de la Tierra produce una fuerza centrífuga dirigida hacia el exterior de ésta, la
cual actúa en dirección opuesta a la atracción de la gravedad, por lo que el valor de g
disminuye. El efecto de la fuerza centrífuga es mayor en el ecuador y disminuye a cero
conforme nos aproximamos a los polos, por lo tanto, g es más grande en los polos que en
el ecuador por 3.4 Gals. Por otro lado, la rotación también produce que la Tierra se
deforme como si fuera un elipsoide de revolución aplanado en sus polos, donde la longitud
del radio de la Tierra es menor, mientras que en el ecuador es mayor, lo que causa que g
se incremente del ecuador a los polos por un factor de 6.6 Gals. Además, al ser el radio de
la Tierra más grande en el ecuador, existe más masa entre la superficie y el centro de la
Tierra, por lo que g decrece por 4.8 Gals del ecuador al polo. Finalmente, es así como la
rotación de la Tierra, la distancia entre el centro de la Tierra y la superficie, y la masa
contenida en este trayecto producen un incremento neto en atracción de la gravedad de
5.2 Gals cuando se va del ecuador a los polos (Burguer et al., 2006).
Las reducciones gravimétricas realizadas antes de la interpretación de los
resultados son los siguientes (para mayor información consultar anexo A):



Corrección de aire libre
Corrección de Bouguer
Corrección por terreno
4.1.4 Anomalías gravimétricas
Con el fin de hacer comparables los valores de gravedad medidos en la superficie
terrestre, con la gravedad normal, se corrigen los valores de gravedad observados. Un
valor reducido es igual al valor observado de la gravedad menos el valor previsto de la
gravedad basándose en el modelo terrestre elegido. En consecuencia, la diferencia entre
42
la gravedad observada y la gravedad calculada se denomina anomalía gravimétrica
(Dobrin, 1961; Dobrin & Savit, 1988).
Anomalía de Aire Libre
La anomalía gravimétrica de Aire Libre se obtiene determinando la diferencia entre
la gravedad observada (gobs) y la gravedad teórica (g corrección por Latitud) y la suma de
la corrección por Aire Libre (CAL), para cada estación, tomando en cuenta la gravedad
teórica sobre el elipsoide GRS80 (referencia) y la altura de la estación por encima del
elipsoide, la cual queda definida por:
Anomalía de Bouguer Simple
La anomalía de Bouguer (AB) forma la base para la interpretación de los datos
gravimétricos sobre el terreno, misma que está definida por:
Anomalía de Bouguer Completa
La anomalía gravimétrica de Bouguer se calcula determinando la diferencia entre la
gravedad observada (gobs) y la gravedad teórica (gteor) en la estación sobre el elipsoide de
referencia, la altura de la estación por encima del elipsoide, los efectos de Bouguer
y
del terreno
.
4.2 Método Magnético
Petrus Peregrinus, un italiano del siglo XIII, realizó varios experimentos importantes con
piezas esféricas de imanes. Sus hallazgos los escribió en 1269, describiendo por primera
vez los conceptos de polaridad magnética, meridianos magnéticos y la idea de que polos
iguales se repelen y opuestos se atraen (Blakely, 1996).
El método magnético se basa en el estudio del campo magnético de la Tierra, para
la investigación de anomalías magnéticas derivadas de las variaciones en las propiedades
magnéticas de las rocas subyacentes. La aplicación de los métodos magnéticos a
43
problemas geológicos avanzó en paralelo con el desarrollo de los magnetómetros. Las
aplicaciones geológicas comenzaron por lo menos desde 1630, esto hace que la
interpretación del campo magnético sea una de las técnicas de exploración geofísica más
antigua (Blakely, 1996).
Los estudios magnéticos pueden ser terrestres, marinos o aéreos. La técnica aérea
es una de las más ampliamente empleadas, debido a la velocidad de operación, lo cual la
hace muy atractiva en la búsqueda para tipos de depósitos minerales que contienen
minerales magnéticos.
La intensidad del campo magnético usualmente se mide en nanoTeslas (nT). La
unidad en el cgs, es el gamma (1 gamma = 10-5 gauss = 1 nT).
4.2.1 Relaciones Fundamentales
Las rocas no magnéticas exhiben una susceptibilidad muy baja, debido a que su
carácter magnético proviene del contenido de una proporción pequeña de minerales
magnéticos. Del mismo modo, existen ciertos tipos de rocas que contienen suficientes
minerales magnéticos que producen anomalías magnéticas significativas.
El mineral magnético más común es la magnetita, la cual tiene una temperatura
Curie de 578°C. Aunque el tamaño, la forma y la dispersión de los granos de magnetita
dentro de la roca afectan su carácter magnético, es razonable clasificar su
comportamiento magnético de rocas acorde a su contenido de magnetita en general. En
la Figura 4.3 se ilustran algunas susceptibilidades de las rocas y minerales más comunes.
En general, el contenido de magnetita determina el comportamiento magnético de
las rocas y minerales, por lo que, la susceptibilidad de las rocas es extremadamente
variable. En el caso de las rocas ígneas éstas usualmente son magnéticas, debido a un alto
contenido de magnetita. La proporción de magnetita en las rocas ígneas tiende a decrecer
con el incremento de acidez, por lo que, las rocas ígneas ácidas, generalmente son menos
magnéticas que las rocas básicas.
En el caso de las rocas metamórficas, éstas también son variables con su carácter
magnético. Si la presión parcial de oxigeno es relativamente baja o alta esto determina
que la magnetita sea reabsorbida y el fierro y oxigeno sean incorporados dentro de otras
fases minerales, o en caso contrario, resulta en la formación de magnetita como mineral
accesorio en otro tipo de reacciones metamórficas (Kearey et al., 2002).
44
Figura 4.3. (a) Valores promedio y rangos de la susceptibilidad magnética de algunos
tipos de rocas comunes, y (b) la susceptibilidad de algunos minerales importantes
(modificado de Lowrie, 2007).
Algo diferente sucede con las rocas sedimentarias, las cuales en principio no son
magnéticas, a menos que contengan una cantidad significativa de magnetita en una
fracción mineral pesada. Si las anomalías magnéticas son observadas por encima de áreas
de cobertura sedimentaria, las anomalías generalmente son causadas por rocas
subyacentes, basamento metamórfico, o por intrusiones dentro de los sedimentos
(Kearey et al., 2002).
45
Susceptibilidad
Un cuerpo colocado en un campo magnético adquiere una magnetización, la cual si
es pequeña es proporcional al campo:
M = kH,
la susceptibilidad, k, es muy pequeña para materiales naturales, y puede ser negativa
(diamagnetismo) o positiva (paramagnetismo). Los campos producidos por materiales
paramagnéticos o diamagnéticos generalmente son considerados muy pequeños como
para afectar los estudios magnéticos, pero con los magnetómetros modernos y de alta
sensibilidad existen sus excepciones. Las anomalías magnéticas más observadas se deben
a un número pequeño de sustancias ferro o ferri-magnéticas, en las cuales sus imanes
moleculares se orientan paralelos al campo magnético principal. Los materiales ferro y
ferri magnéticos pueden tener momentos magnéticos permanentes, así como inducidos,
de modo que su magnetización no es necesaria en la dirección del campo de la Tierra.
La susceptibilidad de una roca comúnmente depende del contenido de magnetita.
Las rocas ígneas ácidas y sedimentos tienen susceptibilidades pequeñas mientras que los
basaltos, gabros y serpentinitas son fuertemente magnéticas (Milsom, 2003), ver tabla A.2
en Anexo A.
Campo Magnético Terrestre (CMT)
El campo magnético de la Tierra se origina en las corrientes eléctricas que circulan
en el núcleo externo líquido, y puede ser modelado, en gran medida por una fuente
dipolar en el centro de la Tierra. Las distorsiones en el campo dipolar pueden extenderse
sobre regiones de miles de kilómetros que se deben a un número relativamente pequeño
de dipolos subsidiarios en la frontera núcleo-manto (Milsom, 2003). Las variaciones con
latitud de la magnitud y dirección de un campo dipolar ideal son alineadas a lo largo del
eje de rotación de la Tierra (ver Figura 4.4; Milsom, 2003).
En el caso de las anomalías magnéticas causadas por rocas, se trata de efectos
superpuestos sobre el campo magnético normal de la Tierra (campo Geomagnético). El
conocimiento del comportamiento del campo geomagnético es necesario para la
reducción de datos magnéticos a un datum adecuado, y para la interpretación de las
anomalías resultantes.
46
Figura 4.4. Variación en intensidad, buzamiento y gradiente para un dipolo ideal
alineado a lo largo del eje de rotación de la Tierra.
El campo geomagnético geométricamente es más complejo que el campo de
gravedad de la Tierra y exhibe una variación irregular en orientación y magnitud con la
latitud, longitud y el tiempo (Kearey et al., 2002). Para describir el vector de campo
magnético se hace uso de descriptores conocidos como elementos geomagnéticos (Figura
4.5). El vector de campo total B tiene un componente vertical Z y un componente
horizontal H en la dirección del norte magnético. El buzamiento de B es la inclinación I del
campo y el ángulo horizontal entre el norte geográfico y magnético es la declinación D. B
varía en fuerza cerca de 25 000 nT en regiones ecuatoriales hasta aproximadamente
70000 nT en los polos.
Figura 4.5. Elementos geomagnéticos.
47
Cerca del 90% del campo de la Tierra puede ser representada por el campo de un
dipolo magnético teórico en el centro de la Tierra. El momento magnético de este dipolo
geocéntrico ficticio puede ser calculado a partir del campo observado. Los efectos de cada
dipolo ficticio contribuyen a una función conocida como un armónico, y la técnica de
aproximaciones sucesivas del campo observado es conocida como análisis de armónicos
esféricos (equivalente al análisis de Fourier en coordenadas polares esféricas) (Kearey et
al., 2002).
El método ha sido usado para calcular la fórmula del IGRF (International
Geomagnetic Reference Field), el cual define el campo magnético teórico no perturbado
en cualquier punto de la superficie terrestre (Kearey et al., 2002).
4.2.2 Correcciones magnéticas
Corrección por variación diurna
El efecto por variación diurna puede ser eliminado en varias formas. Si el estudio
es hecho en el terreno, el método es similar a la corrección por deriva instrumental del
gravímetro, podría emplearse tomando una lectura con el magnetómetro en una estación
de base fija periódicamente durante todo el día. Las diferencias observadas en las lecturas
base son entonces cantidades distribuidas en las lecturas de las estaciones ocupadas
durante todo el día acorde al tiempo de observación. Se debe recordar que las lecturas
base tomadas durante un estudio gravimétrico son para corregir el efecto de deriva y
mareas, en el caso del magnetómetro son tomadas para corregir únicamente la variación
temporal en el campo medido. Dicho procedimiento es ineficiente, ya que el instrumento
tiene que regresar a la localización base, y nada práctico para estudios marinos y aéreos.
Estos problemas se resuelven utilizando un magnetómetro base, el cual es un instrumento
de lectura continua el cual registra las variaciones magnéticas en un punto fijo dentro o
cerca del área de estudio. Donde el estudio es de extensión regional los registros de un
observatorio magnético podrían ser usados. Tales observatorios registran continuamente
cambios en todos los elementos geomagnéticos. Sin embargo, la variación diurna difiere
notablemente de lugar a lugar, por lo que, el observatorio magnético utilizado no debiera
estar a más de 100 km del área de estudio.
La variación diurna durante un estudio aeromagnético puede ser evaluada
alternativamente por la disposición de numerosos puntos de cruce en el plan del estudio.
El análisis de diferencias en las lecturas de cada cruce representa el cambio del campo
sobre una serie de diferentes periodos de tiempo, permitiendo que todo el estudio sea
corregido por variación diurna por un proceso de ajuste de redes, sin la necesidad de una
48
base instrumental. Las variaciones diurnas registradas deben examinarse
cuidadosamente. Si es muy grande, las variaciones de alta frecuencia son aparentes,
resultando de una tormenta magnética, por lo que los resultados del estudio deberían
descartarse (Kearey et al., 2002).
Corrección Geomagnética
El equivalente magnético de la corrección por latitud de un estudio gravimétrico es
la corrección geomagnética, el cual elimina el efecto de un campo de referencia
geomagnética de los datos de estudio. El método más riguroso de la corrección
geomagnética es el uso del IGRF (International Geomagnetic Reference Field) el cual
expresa el campo geomagnético sin distorsiones en términos de un número grande de
armónicos, e incluye términos temporales para corregir la variación secular.
Debe considerarse, sin embargo que el IGRF es imperfecto, como los armónicos
empleados se basan en relativamente pocos y dispersos observatorios magnéticos. El IGRF
también es predictivo y extrapola de forma avanzada armónicos esféricos derivados de
datos del observatorio. Sin embargo, en áreas lejanas a observatorios puede ser un error
(Kearey et al., 2002).
Durante un estudio magnético el campo geomagnético de referencia puede
aproximarse a un gradiente uniforme definido en términos de componentes del gradiente:
latitudinal y longitudinal. Para cualquier área los valores de gradiente pueden ser
evaluados a partir de mapas magnéticos que cubren una región más grande.
Los gradientes regionales apropiados pueden obtenerse empleando una
aproximación de dipolo simple del campo de la Tierra, para ello se usan las ecuaciones
para el campo magnético de un dipolo para derivar gradientes de campo local:
Z=
μ M
μ 0 2M
H = 0 3 sin θ
3 cosθ ,
4π R
4π R
∂H Z
∂Z
=−2H , ∂θ = 2
∂θ
donde, Z y H son las componentes del campo vertical y horizontal, respectivamente, es la
colatitud en radianes, R el radio de la Tierra, M el momento magnético de la Tierra, y la
razón de cambio de Z y H con la colatitud, respectivamente (Kearey et al., 2002).
Un método alternativo de eliminar el gradiente regional, sobre un área de estudio
relativamente pequeña, es mediante el uso de análisis de tendencia.
49
Corrección por terreno y elevación
Dado que el gradiente vertical del campo geomagnético es de únicamente 0.03
nT/m en los polos y de -0.015 nT/m en el ecuador, entonces la corrección por elevación no
es usualmente aplicada. En el caso de la topografía su influencia puede ser significativa en
estudios magnéticos de terreno, pero no es completamente predecible, ya que depende
de las propiedades magnéticas de las características topógráficas, por lo que, en estudios
magnéticos es raro el uso de la corrección por terreno.
4.2.3 Anomalías magnéticas
Las anomalías magnéticas causadas por rocas son superpuestas sobre el campo
geomagnético, de la misma forma que las anomalías gravimétricas se superponen al
campo gravitacional terrestre. El método magnético es más complejo, debido a que el
campo geomagnético varía no sólo en amplitud sino también en dirección. Por su parte el
campo geomagnético normal se describe por un diagrama vectorial (Figura 4.6 (a)) los
elementos geomagnéticos están relacionados por la siguiente expresión:
Figura 4.6. Representación del vector del campo geomagnético con y
sin anomalía magnética superpuesta (tomado de Kearey et al., 2002).
Una anomalía magnética es superpuesta sobre el campo de la Tierra causado por
el cambio
en la fuerza del vector de campo total B. la anomalía produce una
componente vertical
y una componente horizontal
a un ángulo a (Figura 4.6
50
(b)). Sólo la parte de
anomalía:
en la dirección de
, denominada
, contribuyen a la
ahora, usando un diagrama vectorial similar para incluir la anomalía magnética (Figura
4.6(c))
Si la ecuación es expandida, la equivalencia de la ecuación es sustituida y los
términos
son insignificantes, por tanto la ecuación se reduce a:
Al sustituir la ecuación
en la ecuación anterior y con las descripciones
angulares de las razones de los elementos geomagnéticos queda:
donde I es la inclinación del campo geomagnético.
Las causas más comunes de las anomalías magnéticas incluyen diques, fallas, capas
plegadas o truncadas, flujos de lava, intrusiones básicas masivas, rocas de basamento
metamórfico y cuerpos minerales de magnetita. El rango de las anomalías varía en
amplitud desde unas pocas decenas de nT, por encima de basamento profundo
metamórfico, hasta varios cientos de nT debido a intrusiones básicas.
4.2.4 Aeromagnetometría
La mayoría de los estudios magnéticos a gran escala se llevan a cabo desde el aire.
El magnetómetro viaja en una cápsula conocida como “Pájaro”, para así eliminar del
instrumento el efecto magnético del avión, en ocasiones el sensor se fija en una punta o
en la cola del avión, en cualquier caso las instalaciones internas de la bobina se
compensan por el campo magnético del avión (Kearey et al., 2002).
Los estudios aeromagnéticos son más rápidos y rentables, típicamente su costo es
40% menor por cada kilometro de línea de un estudio terrestre. La mayor dificultad en los
estudios aéreos era fijar su posicionamiento. Actualmente, la disponibilidad de los GPS’s
deja de lado este problema (Kearey et al., 2002).
51
CAPÍTULO V
Adquisición de datos
En la zona de estudio aún se desconoce la profundidad sobre la estructura del
basamento, así como la ubicación espacial de las estructuras geológicas potencialmente
activas que dan origen a la sismicidad actual. Por ello, aplicamos algunos métodos
geofísicos (gravimetría y magnetometría) para obtener modelos geológico-geofísicos
derivados del modelado directo de anomalías gravimétricas y magnéticas, con el fin de
incrementar el conocimiento geológico del subsuelo y, junto con la sismicidad reportada
del lugar, identificar las posibles estructuras sismogénicas que se encuentran en una zona
donde hasta poco se consideraba exenta de sismicidad.
5.1
Levantamiento Gravimétrico
El método gravimétrico permite detectar las variaciones o anomalías causadas por
la distribución irregular de la densidad de las rocas que componen el subsuelo de la Tierra,
ello debido a que está basado en la medición de la componente vertical de la aceleración
de la gravedad terrestre (Kearey et al., 2002).
La efectividad del método depende del contraste de densidades entre las rocas,
cuanto mayor sea éste, la detección de las anomalías gravimétricas se facilita. Estas
anomalías son el resultado de los cambios existentes entre los valores observados y los
valores teóricos de gravedad en la zona de estudio, y están relacionados con las
estructuras geológicas de interés En cada estación gravimétrica, se debe registrar su
localización espacial, su elevación, hora de medición y la respectiva lectura de gravedad.
Durante un estudio gravimétrico el espaciamiento entre los puntos de medición
puede variar desde unos cuantos metros, si el caso requiere detalle, como en estudios
arqueológicos, geotécnicos o mineros; hasta varios kilómetros, como en el estudios de
reconocimientos regionales (Milsom, 2003). La densidad de puntos gravimétricos depende
de qué tan grande sea el área de estudio, de manera tal que si el campo gravitacional
varía rápidamente, la densidad de puntos debe incrementarse (Milsom, 2003), esto con el
fin de no perder detalle de tales variaciones.
En el caso del estudio que hemos llevado a cabo al NE de Querétaro, realizamos
levantamientos gravimétricos y topográficos para obtener de su interpretación modelos
que nos muestren la existencia de estructuras geológicas posiblemente activas. Se
tomaron 353 mediciones gravimétricas (Figura 5.1), simultáneamente con medidas
topográficas. El espaciamiento entre cada estación gravimétrica fue entre 250 y 300 m. La
distribución de puntos de medición fue un tanto irregular, ya que se hizo a lo largo de
52
carreteras principales, terracerías y brechas debido al tipo de relieve y ausencia de más
vías de comunicación del lugar.
Figura 5.1. Distribución de los puntos de medición gravimétricos a lo largo de las
carreteras y caminos de terracería (rombos rojos) en los alrededores de la cabecera
municipal de Landa de Matamoros, Querétaro.
Efecto de Mareas y deriva instrumental
Durante un levantamiento gravimétrico, debe corregirse el fenómeno de la deriva
instrumental, para lograrlo debe tenerse en cuenta el efecto de mareas terrestres. Pues
existen variaciones en el terreno debido a cambios en las posiciones relativas de la Tierra,
la Luna y el Sol. Las oscilaciones son más grandes durante la luna nueva y llena, donde la
Tierra, Luna y Sol están alineados. Los cambios de más de 0.05 mGal podrían ocurrir en
intervalos de tiempo inferiores a una hora, mientras que los cambios mayores pueden
53
exceder los 0.25 mGal. La suposición de linealidad hecha en la corrección por deriva podría
fallar si antes los efectos de marea no fueron eliminados.
Generalmente un instrumento geofísico no registra los mismos valores aunque la
lectura haya sido hecha repetidamente en el mismo lugar y a la misma hora. Esto puede
deberse a alguna variación del campo de gravedad en o por cambios en las propiedades
del instrumento en sí mismo, es decir, la deriva.
La corrección por deriva es el primer requisito esencial en el análisis de datos
gravimétricos, después de haber considerado el efecto de mareas. Usualmente se basa en
la repetición de lecturas hechas en una estación base, en diferentes tiempos registrados a
lo largo del día. Por ello, la lectura gravimétrica se traza en función del tiempo y se supone
que la deriva es lineal entre las lecturas consecutivas de base. La corrección por deriva en
el tiempo t es d, la cual es sustraída de los valores observados (Kearey et al., 2002).
La deriva instrumental esta a menudo relacionada con la temperatura, y es poco
probable que sea lineal entre dos lecturas consecutivas tomadas en un ambiente frío al
inicio y al final del día, cuando las temperaturas fueron mayores al mediodía. Las curvas
del estudio podrían limitarse a periodos de una o dos horas. Esta suposición de linealidad,
en el tiempo entre dos lecturas base, puede generar errores cuando existen cambios
importantes de temperatura a lo largo del día (Milsom, 2003). Sin embargo, es difícil hacer
cualquier otra suposición, excepto en algunos instrumentos modernos (p.e. CG-5), en los
que la temperatura interna es registrada y compensada automáticamente.
Para corregir manualmente por la deriva, usando la suposición lineal, las lecturas
primero son corregidas por el efecto de mareas, después se obtiene el coeficiente de
deriva, el cual resulta de la diferencia entre las lecturas inicial y final realizadas en la base
local, este resultado es entonces sustraído de cada lectura a su vez. El signo del
coeficiente de deriva es dictado por el requerimiento después de la corrección, todos los
valores relativos a la deriva deben ser cero. Después de la corrección por deriva, los
valores absolutos de gravedad de cada estación gravimétrica son obtenidos por la suma
de la gravedad absoluta de la base local con los valores corregidos por deriva.
Establecimiento de Estación base
Cuando se requieren valores de gravedad absolutos se necesita al menos una
estación base cercana a la zona de estudio, que sea de fácil acceso y en la que el valor
absoluto de gravedad sea conocido. Si la localización de la estación base presenta algún
inconveniente, se puede establecer una base local, lo cual es posible, midiendo la
diferencia en gravedad entre la estación base y la base local.
54
El principio usado en la base de referencia, de cada uno de los sitios, difiere de las
estaciones normales. La precisión del estudio general depende de la cantidad de
repeticiones de las lecturas en la base, realizadas en ambientes tranquilos y con fácil
acceso son importantes. El ruido del tráfico y otras vibraciones fuertes pueden invalidar
las lecturas gravimétricas.
Ubicación de puntos de medición gravimétrica
En nuestro caso la configuración de la adquisición de datos no fue basada en
perfiles como se realiza en la mayoría de estudios, debido a las características topográficas
de la zona de estudio. Sin embargo, posterior a la adquisición y procesamiento de los
datos se realizaron algunos perfiles para el modelado geofísico-geológico. Los sitios
elegidos para las estaciones gravimétricas se establecieron en función de su fácil acceso
por las carreteras principales y brechas, así como del relieve, las condiciones climáticas,
existencia de ruido antropogénico. Además, en nuestro estudio se trató de cubrir la mayor
parte de la zona de estudio.
Este método también es muy útil para la detección de cavidades, las cuales
incrementan varios en mGales el valor de las anomalías, sin embargo, durante las
mediciones no se encontraron evidencias de este tipo de rasgos.
Procedimiento
Morfológicamente, la zona de estudio cuenta con estructuras geológicas que
tienen una orientación característica NW-SE, debido a la deformación Laramíde de la
Sierra Madre Oriental (SMO; de Cerna, 1960, 1976; Suter, 1984; Dickinson et al., 1988;
Bird, 1988; English y Johnston, 2004), así como con estructuras menores con orientaciones
perpendiculares a éstas. Durante el levantamiento gravimétrico se realizaron 353
mediciones, con un espaciamiento entre los puntos de 250 a 300 m. Para cubrir el área de
estudio se realizaron las mediciones a lo largo de las principales vías de comunicación,
como carreteras, terracerías, y brechas. Pese a que esta estrategia ocasionó que la
distribución espacial de los recorridos fuera un tanto irregular, se buscó en lo posible
trazar los perfiles paralelos a la orientación de las principales estructuras características
geológicas, así como contar con perfiles perpendiculares a éstas para garantizar un
modelado geofísico adecuado.
La adquisición de los datos se realizó durante dos campañas de campo, la primera
realizada del 22 al 26 de enero de 2011, y la segunda del 6 al 12 de enero de 2012. Las
lecturas gravimétricas se obtuvieron a partir de la diferencia de aceleración gravitacional
55
entre la estación base de gravedad absoluta ubicada en el Centro de Geociencias (Tabla
5.1), Campus UNAM-Juriquilla, Querétaro. A partir de esta estación se estableció una
nueva base de gravedad absoluta en el área de estudio, en la plaza central de la cabecera
municipal de Landa de Matamoros (Tabla 5.1).
Tabla 5.1. Ubicación espacial de las bases Gravimétricas.
Nombre
VALOR
GRAVEDAD
ABSOLUTA
COORDENADAS
GEOGRÁFICAS
Latitud N
Localidad
Longitud W
(mGal)
CGEO, UNAM
978 098.275
20.7°
100.4°
LMBase
978 391.260
21.18°
99.32°
Centro de Geociencias,
Campus UNAM Juriquilla,
Qro
Plaza Central, Landa de
Matamoros, Qro.
Para la adquisición de datos se uso un gravímetro SCINTREX Autograv, modelo CG5 (Figura 5.2), el cual tiene una resolución estándar de 1 microGal con una desviación
estándar inferior a 5 microGals. El elemento de detección del Autograv se basa en un
sistema elástico de cuarzo fundido con anulación electrostática (SCINTREX, 2006). La
fuerza gravitacional sobre la masa de prueba es balanceada por un resorte y una fuerza de
restauración electrostática relativamente pequeña. La posición de la masa, la cual es
detectada por un transductor de desplazamiento capacitivo, se altera con el cambio en
gravedad. Un circuito de retroalimentación automática aplica voltaje DC a las placas del
capacitor produciendo una fuerza electrostática sobre la masa que lo lleva de nuevo a una
posición estable. El voltaje de retroalimentación, que es una medida del valor relativo de
gravedad en el lugar de la lectura, se convierte a una señal digital y luego se transmiten al
sistema de adquisición de datos del instrumento para el procesamiento, visualización y
almacenamiento.
56
Figura 5.2. Gravímetro Scintrex Autograv CG-5.
Este gravímetro es fácil de operar, tiene un sensor robusto, no requiere de ninguna
sujeción y es completamente pórtatil, lo cual permite agilizar las mediciones
gravimétricas. El ambiente de operación del sistema es muy estable, lo cual permite que la
deriva a largo plazo sea correctamente determinada y su corrección se reduzca a menos
de 0.02 mGal/día.
Previo a la adquisición de datos el gravímetro se configuró para que por sí solo
determinara la corrección por mareas e inclinación, ello facilitó el ajuste de los sensores
de inclinación durante la medición. El gravímetro puede tomar lecturas de gravedad por
segundo, dado que la zona es de bajo nivel de ruido, la duración de la lectura en la
estación base fue de 60 s, y en las estaciones ordinarias de 30 s. Los datos originales
fueron tomados con un error máximo de 0.002 mGal, cuando dicho error se superaba,
entonces se repetía la medición, ello con el fin de disminuir en las lecturas el efecto del
ruido antropogénico. Las medidas de gravedad relativa fueron referidas a la estación base
(LMBase, ver Tabla 5.1). Cada día, al inicio y al final, se realizó una medición en dicha base,
esto para facilitar la corrección por deriva instrumental y tener un mejor control en la
adquisición de los datos.
Según Kearey et al. (2002), para obtener una precisión aproximado de ± 0.1 mGal,
en las correcciones gravimétricas, las lecturas en el instrumento deben tener una
precisión de ± 0.01 mGal, conocerse la latitud de la estación en ± 10 m, y en el caso de la
elevación ser conocida en ± 10 mm.
57
Las diferencias en la densidad de las rocas producen cambios pequeños en el
campo de gravedad de la Tierra que pueden ser medidos usando instrumentos portables
conocidos como gravímetros (Milsom, John).
En los estudios de gravedad nacionales las variaciones relativas se determinan con
un gravímetro que puede convertirlas a valores absolutos por calibración con mediciones
absolutas hechas en las estaciones seleccionadas.
5.2
Levantamiento Topográfico
La captura de las coordenadas geográficas en cada punto de medición gravimétrica
se hizo con un GPS (Global Positioning System) pórtatil marca Garmin, usando un datum
en WGS84 (Word Geodetic System). Actualmente el GPS es el equipamiento óptimo
espacial de posicionamiento (Davis et al., 1989)
Las incertidumbres en las elevaciones de las estaciones gravimétricas son las que
cuentan con los errores más grandes en los valores durante las reducciones gravimétricas
terrestres, debido al tipo de instrumento utilizado. Las elevaciones de los puntos
gravimétricos pueden determinarse de diferentes maneras, y en ocasiones es la parte más
costosa de un estudio gravimétrico. Se pueden utilizar equipos de óptica de alta precisión,
ondas de radio, técnicas de GPS o usar de manera tradicional equipos topográficos como
el teodolito o estación total.
La mayoría de veces, la elección del equipo depende del objetivo del trabajo y del
área de estudio. En nuestro caso la estación total GPS facilitó y agiliza la realización del
levantamiento topográfico, es una herramienta útil en la obtención de los datos de
elevación con mayor precisión, sin embargo, su funcionamiento se dificulta en interiores o
debajo de una cobertura de árboles muy densa. La estación total convencional que
utilizamos incrementó el tiempo de adquisición, además el desplazamiento fue mayor al
esperado, sin embargo, se lograron buenos resultados. Para llevar un buen control en los
datos y asignarle a cada estación gravimétrica su elevación correcta, las mediciones
topográficas se hicieron en los mismos puntos gravimétricos.
El equipo que utilizamos fue una estación total marca Nikon, la cual cuenta con un
programa topográfico avanzado, su resolución es de 1 segundo y tiene un alcance, con un
solo prisma, de hasta 5 300 m (Figura 5.3).
58
Figura 5.3. Levantamiento topográfico realizado con una Estación Total convencional
Nikon (izquierdo) con un solo prisma (derecha) en cada punto gravimétrico.
5.3
Modelo Digital de Elevación (MDE)
Un modelo digital de elevación es una representación visual y matemática de los
valores de altura con respecto al nivel medio del mar, y permite caracterizar las formas de
relieve y los elementos u objetos presentes en el mismo (INEGI, 2011). Las elevaciones del
terreno se obtienen aplicando procedimiento fotogramétricos a pares de imágenes
estereoscópicas solapadas. Los DEM’s se usan con frecuencia para la creación de modelos
tridimensionales y en los programas informáticos de visualización comúnmente usados en
Ingeniería Civil, cartografía geológica, simulación de vuelo, manejo de los recursos
naturales, geodesia y fotogrametría y Ciencias de la Tierra, así como en aplicaciones
militares entre otras (INEGI, 2011). Algunas de ellas buscan generar modelos de alta
calidad que permitan el análisis específico de ciertas zonas del terreno, como son las redes
de drenaje, las cuales requieren una representación muy precisa (INEGI, 2011).
Para llevar a cabo la corrección por terreno de los datos gravimétricos se requiere
de un modelo digital de elevación (MDE) con buena resolución y cobertura de los puntos
gravimétricos tomados dentro del área de estudio (Milsom, 2003; Burguer et al., 2006).
Los MDE’s utilizados para este trabajo (Figura 5.4), fueron obtenidos de forma gratuita a
través del Instituto Nacional de Estadística, Geografía e Informática (INEGI) Estos fueron
descargados del Continuo de Elevaciones Mexicano CEM (2.0) (INEGI, 2011), los cuales
contienen las elevaciones del área de estudio, mediante puntos sobre la superficie
59
terrestre, cada valor representa su ubicación definida por coordenadas geográficas (X, Y).
A estos puntos se les integran los valores de elevación correspondiente (coordenada Z) de
cada punto, éstos se encuentran equidistantes a cada segundo de arco, las unidades de Z
están en metros.
Figura 5.4. Modelo Digital de Elevación (MDE) del área de estudio (tomado del INEGI,
2011).
60
5.4
Cartas Aeromagnéticas
Como información complementaria al levantamiento gravimétrico nos auxiliamos
del uso de cartas aeromagnéticas. En este caso consultamos la carta magnética Ciudad
Valles F14-8 (SGM, 1997), la cual contiene información sobre una superficie de 22,930
km2, y corresponde a un mapa de intensidad magnética total corregido por IGRF, obtenido
a partir de los mapas de intensidad magnética total a escala 1:50 000 de los
levantamientos aeromagnéticos realizados por el Consejo de Recursos Minerales (hoy en
día, Servicio Geológico Mexicano, SGM) entre los años 1990 y 1995.
A través del SGM se obtuvieron los datos correspondientes a una ventana que
comprende los 21° - 22° de latitud Norte, y 100° - 99° longitud Oeste, con los que se cubre
la Sierra Gorda, Querétaro. Estos datos corresponden a un mapa de campo magnético
residual obtenido a partir de los mapas de intensidad magnética total.
De acuerdo a la información reportada en las cartas del SGM, el levantamiento
aeromagnético de 1990 se efectuó en un helicóptero LAMA XC-DON. Se utilizó un
magnetómetro de protón Geometrics G-803 con sensibilidad de 0.25 nT. La altura del
vuelo se controló con un radio altímetro Sperry y se siguieron vuelos de contorno con una
altura promedio sobre el terreno de 150 m. Las líneas de trayecto siguieron un rumbo N-S
con una separación de líneas de 400m. Los vuelos aeromagnéticos del año 1995 se
realizaron en un avión Islander bimotor, se utilizó un sensor magnético de vapor de Cesio
marca Scintrex CS-2, con una resolución de 0.001 nT. Las trayectorias de vuelo se
controlaron mediante el sistema de posicionamiento global (GPS). Estas mediciones
cubren la mayor parte de la superficie con líneas de rumbo N-S, con una separación entre
ellas de 1000 m, y una altura de vuelo promedio de 450 m sobre la superficie del terreno.
61
CAPÍTULO VI
6.1
Procesamiento de Datos
Gravimetría
6.1.1 Correcciones gravimétricas
Antes de interpretar los resultados del estudio gravimétrico, es necesario corregir los
datos observados debido a todas las variaciones del campo gravitacional terrestre,
causadas por la topografía del lugar, la elevación del terreno o la diferencia en el tiempo
de adquisición, ya que no siempre el resultado se debe a las diferencias de densidad en las
rocas subyacentes.
Posterior a la adquisición de datos realizamos su procesamiento, mediante la
aplicación de una serie de correcciones. Estos datos son capturados en hojas de cálculo
(Excel) para facilitar para facilitar el cálculo de deriva instrumental y la corrección por
Latitud. Posteriormente, utilizamos el programa Oasis Montaj (Geosoft Inc., 2007) para
hacer las correcciones de Aire Libre, Bouguer y Terreno, para así obtener las anomalías
gravimétricas Aire Libre y Bouguer completa, ajenas a cualquier variación de gravedad que
no se trate del subsuelo en sí.
Con el programa Oasis Montaj (Geosoft Inc., 2007) también realizamos la
separación regional y residual de los datos gravimétricos y la aplicación de filtros. Ello
permite mejorar la anomalía gravimétrica y determinar con mayor certidumbre las
características geológicas del subsuelo.
El procesamiento de los datos comenzó con la aplicación de las correcciones por
marea y deriva. El primero se realizó automáticamente durante la adquisición de datos,
programado previamente en el gravímetro antes de iniciar el levantamiento.
La corrección por deriva instrumental se realizó a partir de un ajuste lineal. Se
registraron valores de gravedad observada al inicio y termino de cada día en la estación
base (LMBase). A partir de estas mediciones se obtuvo un coeficiente de deriva (Cd), el
cual se calcula como sigue:
62
Después de obtener el coeficiente de deriva, este valor se suma o resta del valor de
gravedad observada de cada punto medido, de manera que coincidan los valores de
gravedad al inicio y final de cada ciclo de lecturas gravimétricas. El cálculo es el siguiente:
La corrección por deriva instrumental fue realizada a través del uso de hojas de
cálculo para facilitar la operación y manejo de los datos.
La corrección por Latitud se realiza considerando a la Tierra como un elipsoide de
revolución, para ello se utilizó la International Gravity Formula (IGF), enunciada en el
capítulo 4, con el GRS80 como elipsoide. La expresión describe la relación entre la
gravedad normal a nivel del mar y la latitud de la estación gravimétrica (λ). De esta
manera, se obtiene la gravedad teórica de cada estación gravimétrica sobre el esferoide
Terrestre. Esta corrección se restó de la gravedad observada de cada punto gravimétrico.
La corrección por Aire Libre (Free Air) consiste en reducir las lecturas de la estación
gravimétrica a un solo nivel de referencia o datum. No se considera la densidad de ningún
material situado entre la altura de la estación y el nivel de referencia. En esta corrección
utilizamos la fórmula de aproximación de segundo orden de Heiskanen y Moritz (1969), ya
que ésta considera el cambio de la gravedad teórica basada en el elipsoide GRS80 con la
altura relativa al elipsoide. En nuestro caso, los puntos medidos se encuentran por encima
del nivel de referencia, por lo que adicionamos el valor de esta corrección a la gravedad
observada.
La corrección de Bouguer también depende de la elevación, tal como sucede con
la corrección de aire libre, y considera la densidad del material situado entre la estación
gravimétrica y el nivel de referencia. El efecto de esta corrección se resta cuando la
estación se localiza por encima del nivel de referencia y se suma cuando su efecto es
negativo. Se obtuvo a partir de la fórmula
(capítulo 4), donde es la elevación de la estación y la densidad del material. En nuestro
caso, se utilizó una densidad de
y
, considerando que el
material está constituido principalmente por caliza y por aluvión superficialmente. Esta
corrección fue restada del valor de gravedad observada.
63
La corrección por terreno se aplicó para compensar las lecturas gravimétricas
realizadas cerca de áreas con relieve alto. Aplicar esta corrección requiere de mayor
tiempo, después de evaluar su aprovechamiento, se pone en consideración su obtención,
ello implica un aumento en el costo de los estudios gravimétricos, además de la necesidad
de MDEs. En nuestro caso, llevamos a cabo la corrección mediante el programa Oasis
Montaj (Geosoft Inc., 2007), el cual ofrece mayor precisión y permite minimizar el tiempo
de procesamiento de los datos.
Una de las opciones del programa Oasis Montaj (Geosoft Inc., 2007) es la
determinación de la corrección topográfica como la suma de correcciones interna, media
y externa. Por lo que, el proceso inicia con la creación de dos mallas, una “Regional DEM”
y la otra “local DEM”, a partir de los modelos digitales de elevación proporcionados por el
INEGI. Con base en estas mallas generamos una malla de corrección topográfica (Regional
Terrain Correction Grid y Local Correction Distance), con los cuales se calculó la corrección
topográfica; las distancias para la corrección local y regional fueron de 100 m y 100 m - 30
km, respectivamente; consideramos una densidad del medio para la zona de estudio de
2.3 gr/cm3.
El programa Oasis Montaj (Geosoft Inc., 2007) hace uso de diferentes algoritmos
para calcular la corrección topográfica; zona cercana, intermedia y lejana (Anexo B).
6.1.2 Anomalías gravimétricas
Después de haber calculado todas las reducciones gravimétricas, se obtuvieron las
anomalías de Aire Libre, Bouguer y Bouguer completa.
La anomalía de aire libre (Free Air)
, se calcula sustrayendo la corrección
por latitud (Gravedad Teórica) de la gravedad observada y se adiciona la corrección por
elevación (Aire Libre). La anomalía (Figura 6.1) se obtuvo como sigue:
donde:
64
Figura.6.1. Anomalía Aire Libre en los alrededores de Landa de Matamoros, Querétaro.
Para el cálculo de la anomalía de Bouguer simple
, además de tener en
cuenta la elevación de cada estación gravimétrica, se consideró la densidad del material
(Figura 6.2a), y
(Figura 6.2b), de la siguiente forma:
donde:
65
a)
b)
Figura.6.2. Mapa de anomalía de Bouguer simple a)
.
y b)
Por su parte, la anomalía de Bouguer completa
compensa el excedente o
déficit de masa no contemplado por la corrección de Bouguer simple. En este caso, el
valor de la corrección por terreno se suma a la anomalía de Bouguer obtenida
anteriormente. Para ello se utilizaron dos densidades
(Figura 6.3a) y
(Figura 6.3b).
donde:
66
a)
b)
Figura.6.3. Mapa de anomalía de Bouguer completa a)
.
y b)
Cuando se realiza la corrección de Bouguer se asume que la masa existente entre
la elevación de la estación y el nivel de referencia semeja una losa infinita. Para
compensar la masa de esta losa que se extiende más allá donde la curvatura de la Tierra
debe considerarse, se aplica la corrección de la curvatura, la cual se calcula mediante la
ecuación de LaFehr (1991).
Al iniciar el procesamiento utilizamos dos densidades
y
, para caracterizar la densidad de fondo, la primera por ser característica
de la zona y la segunda por tratarse de la densidad promedio típica.
Los mapas gravimétricos representan una superposición de varios efectos, entre
ellos los rasgos estructurales profundos, conocidos como anomalías regionales. Estos
generalmente causan variaciones de gravedad de gran amplitud y son de tendencia
regional, cualquier variación en la dirección y magnitud del gradiente generalmente
presenta cambios suaves y graduales. Por su parte, los rasgos someros o anomalías
residuales, son de carácter local y simbolizan principalmente estructuras geológicas
superficiales o pequeñas, cualquier cambio en su gradiente se observa de forma más
abrupta (Rodríguez, 1974). Por lo que, el primer paso en la interpretación de las anomalías
67
gravimétricas consiste en separar estos efectos. Existen principalmente dos métodos, los
métodos gráficos y los métodos analíticos.
Los métodos gráficos consisten en determinar manualmente una curva suavizada
de las anomalías observadas, dando como resultado la anomalía regional. Tienen como
ventaja la posibilidad de utilizar la información geológica que se dispone del lugar. Sin
embargo, se requiere mucha experiencia de la persona encargada, así como un buen
conocimiento geológico, con el fin de minimizar errores durante la interpretación.
Por su parte, los métodos analíticos se basan en técnicas matemáticas para
calcular las curvas de las anomalías observadas, lo cual hace que con frecuencia sean
bastante mecánicas y puedan omitirse algunos factores geológicos que influyen en la
interpretación. Dentro de estos métodos existen tres procedimientos más comunes:



Métodos de promediación: consisten en determinar la anomalía regional como
promedio de las anomalías observadas. Dentro de estos se encuentran:
o Cálculo directo de la gravedad residual de Griffin
o Polinomios y superficies de tendencia
Métodos de segundas derivadas
Métodos de continuación ascendente y descendente del campo potencial.
Usualmente las anomalías locales del estudio gravimétrico son el principal interés y
el primer paso en su interpretación, para ello se busca la eliminación del campo regional
de las anomalías residuales.
La determinación de la anomalía regional y residual la hicimos a través de la
aplicación de métodos de superficie de tendencia (ajuste polinomial de los datos
observados), para ello utilizamos la extensión MAGMAP de Oasis Montaj (Geosoft Inc.,
2007). Para escoger el mejor grado de polinomio que se ajustara a los datos, realizamos
varios mapas regionales y residuales de 1er, 2do y 3er grado. Posteriormente los
comparamos con las características geológicas del área de estudio, de esta forma
determinamos que la mejor superficie que se ajusta a los datos gravimétricos es el
polinomio de segundo grado. La separación regional-residual fue hecha con el filtro
Regional/Residual Filter de la extensión MAGMAP. Elegimos remover del mapa de
Anomalía de Bouguer todo el efecto regional de 2do grado, y obtuvimos el mapa residual
correspondiente al grado polinómico elegido (Figura 6.5). Después sustrajimos de la
Anomalía de Bouguer el mapa residual y obtuvimos así el mapa regional (Figura 6.4).
68
Figura 6.4. Mapa de anomalía regional obtenida con el método de superficies de
tendencia de segundo grado.
Figura 6.5. Mapa de Anomalía residual obtenido con el método de superficies de
tendencia de segundo grado.
69
6.1.3 Filtros
Al realizar un estudio con métodos potenciales, se busca resaltar en los mapas algunas
anomalías que se deban a características geológicas de interés, y dejar de lado aquellas de
poca utilidad. Para ello, se aplican filtros que permitan definir y ampliar la visualización de
las anomalías de interés. Para ello utilizamos la extensión MAGMAP Filtering del programa
Oasis Montaj (Geosoft Inc., 2007), en la cual se debe estar en el dominio del número de
onda. De esta forma, aplicamos la transformada de Fourier a la Anomalía de Bouguer que
fue estimada en el dominio del espacio (ver anexo C).

Filtro Pasa baja
El campo gravimétrico puede ser procesado y analizado en forma similar a los
datos sísmicos, reemplazando la frecuencia por el número de onda. El procesamiento
puede ser más complejo pero es posible con el uso de filtros bi-dimensionales, con los que
se busca eliminar selectivamente componentes del número de onda alto o bajo de las
anomalías observadas. La aplicación de estas técnicas es similar a la continuación
ascendente o descendente. Sin embargo, no es completamente posible aislar las
anomalías locales o regionales mediante el filtrado, debido a que los espectros del
número de onda de fuentes profundas y someras se superponen.
El filtro pasa bajas permite el paso de señales con longitudes de onda larga, es
decir, bajas frecuencias e impide el paso de altas frecuencias o longitudes de onda corta,
colocando como referencia a la frecuencia de corte. La utilidad de este filtro radica en
eliminar cuerpos de altas frecuencias.
En nuestro caso, el filtro pasa baja fue aplicado a la Anomalía de Bouguer completa
(Figura 6.6) para suavizar y mejorar la visualización de las características anómalas en la
zona.
70
Figura.6.6. Aplicación de un filtro pasa-bajas en la Anomalía de Bouguer completa
calculada en la cabecera municipal de Landa de Matamoros.

Derivadas Verticales
La técnica de la derivada vertical acentúa mejor los cambios bruscos en la señal
gravimétrica, lo cual permite ubicar límites y zonas de fallas. Este filtro está dado por:
donde:
71
Después de utilizar el filtro pasa-baja en los datos, se aplicó un filtro de la primera
derivada vertical (Figura 6.7). El objetivo de su uso, fue acentuar las anomalías locales
asociadas a cuerpos pequeños y someros. Ello proporcionó una idea más clara respecto al
tipo de anomalías obtenidas. Las anomalías de carácter regional y más profundas no
muestran influencia en el mapa, ya que las derivadas decrecen con las potencias en
profundidad de las masas (Rosenbach, 1953).
Figura 6.7. Primera derivada vertical de la Anomalía de Bouguer completa en los
alrededores de Landa de Matamoros.
72
6.2
Aeromagnetometría
Los campos magnéticos y gravitacionales son campos potenciales, por lo que
tienen mucho en común y generalmente utilizan técnicas similares en su interpretación.
Por lo general, el método magnético es más complejo debido a que el campo magnético
es dipolar, mientras que el gravimétrico es monopolar. El efecto de ambos métodos nos
permiten identificar anomalías gravimétricas y magnéticas originadas por efectos
regionales y cuerpos locales. (Telford et al., 1990).
6.2.1 Anomalías aeromagnéticas
La carta aeromagnética Ciudad Valles F14-8 (SGM) corresponde a un mapa de
intensidad magnética total corregido por IGRF, escala 1:50 000. Los datos provienen de los
levantamientos aeromagnéticos realizados por el Consejo de Recursos Minerales (SGM),
los cuales fueron adquiridos a una altura de vuelo de 150 y 450 msnm durante los años
1990 y 1995 respectivamente. Posteriormente, a partir de los mapas de intensidad
magnética total se obtuvo un mapa de campo magnético residual (CMR) a través del SGM.
Dicho mapa, está definido por las coordenadas geográficas son 21° - 22° latitud N y 100° 99° longitud W, el cual incluye la parte central de la SMOr.
Campo Magnético Residual
Una vez que los datos de intensidad magnética del campo total son corregidos por
variación diurna y por la eliminación del IGRF, se obtiene el campo magnético residual. El
mapa magnético residual proporcionado por el Servicio Geológico Mexicano del área de
estudio se muestra en la figura 6.8.
73
Figura 6.8. Mapa del campo magnético residual de Landa de Matamoros.
6.2.2 Filtros
Las técnicas de suavizado, filtrado y realce de anomalías utilizadas en el
procesamiento de los datos gravimétricos son semejantes al procesado magnético, a
excepción del filtro de reducción al polo, la cual es particular de los datos magnéticos. Los
filtros utilizados también se encuentran en el dominio de la frecuencia, por lo que,
también se hace uso de la transformada de Fourier. La aplicación de estos filtros a los
datos magnéticos es a través de la extensión MAGMAP Filtering del programa Oasis
Montaj (Geosoft Inc., 2007).
74

Reducción al Polo
Una de las técnicas utilizadas en los datos aeromagnéticos, es la reducción al polo
magnético, con la cual se puede remover la influencia de latitud magnética y así, mejorar
la interpretación. El filtro de reducción al Polo, fue desarrollado por Baranov (1957) y
mejorado por Battarcharyya (1965). Esta técnica reduce el efecto bipolar de las anomalías
magnéticas, por lo que su uso es exclusivo para este tipo de datos, consiste en simular
como si la fuente geológica estuviera ubicada en el polo magnético y mejora la definición
de la geometría representativa de los cuerpos anómalos. Al aplicar esta técnica se
requiere conocer los ángulos de inclinación y declinación magnética para la localidad en
estudio, pues la respuesta magnética cambia con respecto a la latitud magnética. La
reducción al Polo está dada por la siguiente expresión:
donde:
I = Inclinación geomagnética
D = Declinación geomagnética
Inclinación para la corrección de amplitud (menor que I)
Generalmente, al realizar la adquisición de los datos, debido a la inclinación del
campo magnético terrestre se produce un desplazamiento de los datos observados con
respecto a la ubicación de los cuerpos anómalos. La aplicación del filtro de reducción al
polo ajusta dicho desplazamiento y mejora la localización de las fuentes. En la figura 6.9 se
puede observar el mapa de reducción al polo magnético resultante de aplicarlo a los datos
aeromagnéticos de este trabajo.
75
Figura 6.9. Mapa de reducción al polo magnético del campo magnético residual
de Landa de Matamoros.

Filtro pasa-bajas
Los filtros pasa-baja por definición dejan pasar las frecuencias bajas y anomalías de
longitud de onda larga atribuidas a fuentes profundas (Figura 6.10). Este filtro fue aplicado
para eliminar las altas frecuencias relacionadas con el ruido en la señal magnética o
fuentes anómalas someras.
Parámetros:
76
Figura 6.10. Representación gráfica del filtro pasa baja (Geosoft Inc. 2007).

Continuación ascendente
La medición del campo magnético sobre la superficie puede ser usada para
predecir el campo a cualquier nivel, ya sea por encima o debajo del plano de observación.
Esta es la base de los métodos de continuación ascendente y descendente, en los cuales el
campo potencial por encima o debajo del plano original de medición se calcula con el fin
de acentuar los efectos de estructuras profundas o someras respectivamente.
La aplicación de la técnica continuación ascendente nos permitió determinar la
forma de la variación magnética regional sobre el área de estudio. Esta fue realizada a
diferentes niveles sobre la superficie de medición, por lo que, fue posible destacar
estructuras relativamente profundas y distinguir la atenuación de anomalías con número
de onda más alto, es decir, estructuras someras.
Se realizó la continuación analítica ascendente de los datos aeromagnéticos
tomados a una altura de 450 msnm llevando éstos a 500, 1000, 3000 y 5000 msnm de
altura, generando cuatro diferentes mapas (Figura 6.11) que contienen ambos datos, es
decir, la altura de vuelo y la altura utilizada en el filtro de continuación ascendente.
77
Figura 6.11. a) Continuación ascendente a una altura de 500m b) Continuación
ascendente a 1000m c) Continuación ascendente a 3000m d) Continuación
ascendente a 5000m del campo magnético residual.

Derivadas verticales
En el procesamiento de datos magnéticos, es útil la aplicación de derivadas
verticales pues permiten el realce de las anomalías vinculadas a cuerpos someros. Esta
derivada vertical amplifica la longitud de onda corta y acentúa gradientes a lo largo de los
límites de fuentes magnéticas someras, por lo que también se utiliza para localizar límites
de los cuerpos magnéticos y realce en fuentes someras (Dobrin, 1961; Dobrin y Savit,
1988).
Una vez que aplicamos a los datos aeromagnéticos el filtro de reducción al polo,
utilizamos el filtro de primera derivada vertical (Figura 6.12a). También aplicamos el filtro
de continuación analítica ascendente a una altura de 1000 msnm (Figura 6.12b). En ambos
casos se busca resaltar anomalías locales y someras.
78
Figura 6.12. a) Mapa de primera derivada vertical y reducción al polo magnético del CMR.
B) Mapa de primera derivada vertical y reducción al polo magnético del CMR a una altura
de 1000 msnm.
79
6.3
Interpretación
6.3.1 Interpretación Gravimétrica
La interpretación de las anomalías del campo potencial es todo un reto. Existen
algunas ambigüedades debido a que cualquier anomalía puede ser resultado de un
número infinito de fuentes con diferentes características. Es así como surge el problema
inverso en la interpretación de los campos potenciales, el cual establece, que aunque la
anomalía de un cuerpo dado pueda calcularse de manera única, hay un número infinito de
cuerpos que podría dar lugar a cualquier anomalía especifica. Para disminuir la
incertidumbre se requiere de información adicional como las características geológicas,
pozos exploratorios y/o información geofísica complementaria, ello nos permite conocer
más sobre la naturaleza y forma que podría tener la fuente de la anomalía.
En el mapa de Anomalía de Bouguer completo (ABc) con densidad
(Figura 6.3a) se observa una tendencia regional con una orientación preferencial N30°W.
Es posible asociar esta tendencia con la dirección NNW-SSE del tren de pliegues y
cabalgaduras de la SMO (Carrillo-Martínez, 1989, 1990) formados durante el evento de
deformación contractiva Laramide (Cuéllar et al., 2012).
Los valores gravimétricos de las anomalías presentan un incremento de SW a NE
con valores que van desde -97.4 mGal a -90.2 mGal. Esta pequeña diferencia de ~7 mGal
puede ser de carácter regional en la zona de estudio y puede deberse a un levantamiento
del basamento, el cual presenta un basculamiento regional hacia el poniente, lejos del
antepaís, situado al oriente de la SMOr, según Eguiluz et al. (2000).
Los valores gravimétricos se clasifican grosso modo en dos dominios principales
separados por el lineamiento principal y regional de valores gravimétricos intermedios
entre -96 mGal y -93.6 mGal. Uno de los dominios se localiza al SW (Figura 6.3) y
representa los valores mínimos de la anomalía, los cuales pueden explicarse como áreas
de depósitos de sedimentos aluviales y fluviales cuaternarios que sirven de relleno. Cabe
mencionar que esta zona se encuentra cercana a zonas topográficamente altas.
Conforme se avanza al NE se visualiza otro dominio con valores máximos que van
desde -93 mGal a -90.2 mGal. En su parte norte-centro se encuentra un máximo relativo
en los valores, el cual podría ser causado por algún cuerpo anómalo que se encuentra más
cercano a la superficie. Cerca de este máximo relativo, se ubica al sur y este del mapa, una
serie de valores altos. Éstos están localizados de manera puntual a lo largo de una franja
anómala elongada en dirección N25°E interrumpida por pequeños cuerpos. Dichos
80
elementos podrían reflejar la dirección de una falla que inferimos se encuentra en esa
misma dirección.
En la figura 6.4 se muestra el mapa regional de la Anomalía de Bouguer completa
obtenido por el método de superficies de tendencia polinómica de grado 2. En la figura se
observa que las curvas representan los rasgos estructurales de carácter regional, las cuales
corresponden a características más profundas. También se observa la presencia del
lineamiento principal con la misma orientación NNW-SSE y un incremento gradual de los
valores gravimétricos en dirección SW al NE, dicho lineamiento coincide con las
características regionales del mapa de Anomalía de Bouguer descritas anteriormente.
El mapa residual de la figura 6.5 también fue realizado con la técnica de superficies
de tendencia polinómica grado 2. En este mapa se visualiza la presencia de dos zonas de
gradientes bajos, ubicados uno en la parte SW con una orientación al NW, y el otro de
menores dimensiones en la parte NE del mapa con una dirección hacia el NE. Se infiere
que estos cuerpos representan zonas de sedimentos aluviales y fluviales. Se trata
típicamente de depósitos cuaternarios, los cuales coinciden en ubicación con la litología
observada en el mapa geológico de la zona de estudio.
También se observan dos zonas de gradientes máximos, ubicados en la parte
norte-centro y SE del mapa (Figura 6.5), el primero se ve de mayores dimensiones con una
dirección preferencial E-W, el otro tiene una orientación NE-SW, ambos son cuerpos
pequeños y superficiales, su estudio está más allá del objetivo principal de este estudio.
Los filtros aplicados al mapa ABc, como el filtro pasa-bajas (Figura 6.6) y primera
derivada vertical (Figura 6.7), permitieron eliminar el ruido presente en la señal y resaltar
las diferentes estructuras geológicas presentes en la zona, vistas también en el mapa
residual. Este estudio se centra en la descripción de los rasgos estructurales de aspecto
regional que afectan la zona de estudio. Por lo anterior los cuerpos anómalos someros y
pequeños que encontramos sólo sirvieron de referencia para corroborar los datos y las
características estructurales expuestas en los mapas anteriores. Por ejemplo la descripción
de la anomalía de Bouguer (ABc), la regional y residual explican los dominios gravimétricos
y la presencia de dos lineamientos principales, uno con una orientación preferencial NNWSSE paralela al CPCM y el otro, al NE-SW con una dirección aparentemente perpendicular
al primero.
81
6.3.2 Interpretación Magnética
La región de estudio está constituida de rocas carbonatadas mesozoicas,
principalmente calizas y lutitas, así como de un basamento cristalino metamórfico
compuesto de gneises de edad Precámbrica. Por lo tanto, en ausencia de sedimentos
magnéticos, los datos magnéticos nos proporcionan información sobre la naturaleza y
forma del basamento cristalino.
En el mapa de campo magnético residual (Figura 6.8) se puede distinguir un
lineamiento importante con una tendencia regional y una orientación NW-SE. Ésta
coincide con las estructuras geológicas del área dispuestas aproximadamente en esa
misma dirección. Las magnitudes de las anomalías se incrementan gradualmente del SW al
NE con valores que van de -93.6 nT a -70.5 nT con una gradiente de aproximadamente 2
nT/km.
Este lineamiento separa los valores magnéticos en dos dominios principales, uno al
SW con valores bajos y otro localizado al NE del mapa con los valores más altos del CMR,
los cuales coinciden con los interpretados en los mapas gravimétricos.
La distribución de los altos y bajos magnéticos es similar a la que se visualiza en el
mapa de reducción al Polo magnético del CMR (Figura 6.9), en el cual los valores máximos
llegan a -77.4 nT y los mínimos hasta -110.6 nT. El incremento de los valores magnéticos
tiene una tendencia hacia el NE y su distribución puede deberse a la litología presente en
el área de estudio. Ello sucede con las rocas carbonatadas, las cuales carecen de
sedimentos magnéticos. Estas rocas no tienen respuesta magnética, mientras que las
rocas gnéisicas se caracterizan por presentar susceptibilidades altas.
En los mapas regionales del campo magnético residual (Figura 6.11), realizados con
la técnica de continuación analítica del campo a 500 m, 1000 m, 3000m y 5000 m se
observa la misma tendencia regional aproximada NW-SE. Los valores disminuyen hacia el
SW, coincidiendo con lo descrito anteriormente de carácter regional en el mapa de CMR y
de reducción al polo magnético.
Los valores mínimos mostrados en el mapa se extienden hacia el SW, como posible
respuesta de la profundidad del basamento en esa zona y del gran espesor de sedimentos
cuaternarios presentes en el área. Los valores relativamente altos, pueden ser producto
de la heterogeneidad del basamento tanto en profundidad como en litología.
Se le aplicó el filtro de derivadas verticales al mapa de reducción al polo magnético
para resaltar la presencia de estructuras geológicas someras y pequeñas. Ello con el fin de
82
identificar cuáles son concordantes con las anomalías identificadas en los mapas
gravimétricos. Sin embargo, no se visualizaron cuerpos anómalos correspondientes a las
observaciones en gravedad hechas anteriormente. Ello puede deberse a que dichos
cuerpos carecen de sedimentos magnéticos y no presentan una respuesta magnética
importante.
En el mapa de primera derivada vertical y reducción al polo magnético del CMR
(Figura 6.12a) se observa la presencia de ruido. Para reducirlo aplicamos un filtro de
primera derivada vertical al mapa de reducción al polo magnético con una continuación
analítica ascendente a una altura de 1000 msnm (Figura 6.12b). Como resultado se aprecia
de forma regional un lineamiento con una orientación N-S, el cual separa dos dominios
principales. Uno de ellos se encuentra al este, con los valores máximos (0.0018 nT) del
gradiente. El otro dominio se encuentra al oeste con los valores mínimos (-0.0053 nT);
ambos gradientes de localizan con una dirección N-S. En este mapa se muestra el
contraste y la distribución de las susceptibilidades magnéticas, el cual corresponde a una
posible configuración del basamento metamórfico. En el caso de los altos magnéticos,
éstos son causados por el levantamiento de dicho basamento, mientras que los bajos
pueden ser asociados a la posible profundidad de éste.
6.4
Modelado Geológico-Geofísico
La interpretación cuantitativa de los datos gravimétricos y magnéticos
generalmente se hace mediante el modelado directo. Se analizan los efectos producidos
por cambios en la distribución de las propiedades físicas (densidad y susceptibilidad
magnética) en el subsuelo. Esta distribución la modificamos hasta obtener un resultado
satisfactorio entre la curva de los datos observados y calculados de las anomalías (Dobrin,
1961; Oldenburg, 1974, Dobrin y Savit, 1988).
El modelado directo consiste en proponer y simular un cuerpo causante de una
anomalía gravimétrica o magnética. La anomalía teórica del modelo es calculada con base
en la modificación de éste, hasta que dicha anomalía estimada se parezca a la anomalía
observada. Sin embargo, no existe una interpretación única y varias soluciones pueden no
ser geológicamente realistas. La ambigüedad del modelo se restringe utilizando límites
sobre la naturaleza y forma del cuerpo anómalo, tales como contrastes en la propiedad
física, información geológica y geofísica complementaria (Kearey et al., 2002).
83
Este proceso es iterativo y el mejor ajuste entre las anomalías observadas y
calculadas es gradualmente mejorado. La anomalía de un cuerpo tridimensional puede ser
calculada por la división del cuerpo en una serie de partes horizontales y aproximar cada
parte por un polígono (Talwani y Ewing, 1960). El modelo puede iniciarse con cuerpos de
una geometría relativamente simple de modo que su interpretación se realice fácilmente
usando rutinas interactivas en una computadora (Götze y Lahmeyer, 1988). Esta técnica
propone cuerpos o polígonos de distintas formas y con cierta propiedad física, para luego
calcular el efecto gravitatorio o magnético que producen en la superficie del terreno
(Talwani y Heirtzlez, 1964).
6.4.1 Procesamiento
El procesamiento de los datos potenciales inicia con la separación de las anomalías
regionales y residuales. A cada tipo de datos se les aplican diferentes tipos de filtros, como
pasa-bajas, derivadas verticales, continuación analítica ascendente, entre otros. Ello
facilita la interpretación cualitativa de los datos; además de eliminar altas frecuencias,
relacionadas con ruido, así como, permitir el realce de los gradientes verticales de las
anomalías para poder ubicar límites de zonas de fallas, que en nuestro caso son objetivo
de estudio.
Después continuamos con el modelado directo de las anomalías gravimétricas y
magnéticas, por lo general, se usan dos técnicas de modelado, directo e inverso, en este
estudio sólo recurrimos al modelado directo.
Finalmente, realizamos la interpretación cuantitativa de los modelos geológicosgeofísicos obtenidos y se relacionan con información complementaria del área de estudio
(Pozos CEA, ver Anexo D).
6.4.2 Modelado Directo
Para el modelado directo propusimos un modelo geológico inicial y calculamos la
respuesta geofísica de los perfiles gravimétricos y magnéticos de éste. Le asignamos
valores de densidad y susceptibilidad magnética hasta obtener el mejor ajuste entre las
curvas de anomalías observadas y calculadas, que correspondan a las características
geológicas de la zona de estudio.
84
Se realizaron e interpretaron 3 perfiles gravimétricos y magnéticos tomados de los
mismos puntos de adquisición. En la figura 6.13 se puede observar la ubicación y el
trazado de los perfiles; para su realización se consideraron el mapa de Anomalía de
Bouguer completa (ABc), el mapa de campo magnético residual (CMR) y la topografía del
terreno.
Los modelos correspondientes a cada perfil se construyeron mediante la extensión
GM-SYS del programa Oasis Montaj (Geosoft Inc., 2007), el cual permite interacción con el
modelo geológico y el cálculo en tiempo real de la gravedad y respuesta magnética
(Geosoft Inc., 2007).
Figura.6.13. Distribución de tres perfiles gravimétricos y magnéticos en el área de estudio.
85
6.4.3 Interpretación del modelado
Realizamos la interpretación de los 3 perfiles gravimétricos y magnéticos con
valores de densidad y susceptibilidad magnética, y obtuvimos sus respectivos modelos
geológicos-geofísicos (Figuras 6.14, 6.15 y 6.16). Para la interpretación de los modelos se
tomaron las densidades y susceptibilidades magnéticas usando los valores mostrados en
la Tabla 6.1.
Las restricciones para la elaboración de estos modelos se basan en las
características geológicas de la zona y en la litología superficial. Éstas fueron obtenidas de
información de la carta geológica Ciudad Valles del SGM (1997) y de pozos proporcionados
por la Comisión Estatal de Aguas (CEA) (anexo D). Las utilizamos para obtener los
diferentes valores de densidad y susceptibilidad magnética en el ajuste de las anomalías
gravimétricas y magnéticas, respectivamente, tomados a partir de las tablas (Dobrin y
Savit, 1988; Telford, 1990).
Tabla 6.1. Valores de densidad y susceptibilidad magnética utilizados en el modelado
gravimétrico-magnético de los 3 perfiles interpretados.
UNIDAD
GEOLÓGICA
DENSIDAD
(G/CM 3 )
SUSCEPTIBILIDAD
MAGNÉTICA
ESPESOR
(CGS)
APROXIMADO
(M)
Aluvión
2,0
--
20 - 150
Formación Soyatal
2,35
--
~300
Formación El Abra
2,6
--
1800 - 2500
Formación Santiago
2,65
--
150 - 250
Gneiss Grenville
2,7
0,0009
--
En los tres perfiles se observa de manera general una zona de falla (lineamiento)
que se encuentra en el límite de bajos y altos gravimétricos y magnéticos. En ellos la
pendiente y aumento en los valores de las anomalías gravimétricas y magnéticas es más
fuerte hacia el bloque levantado y los menores hacia el bloque hundido. Este resultado
nos proporcionó una idea más clara sobre la configuración en bloques del complejo basal
en la Sierra Gorda.
86
Figura.6.14. Modelo geológico-geofísico con datos magnéticos y gravimétricos del Perfil 1.
NT: Nivel del Terreno.
El modelo geológico-geofísico del perfil 1 (Figura 6.14) se ubica al sureste del
mapa, su dirección preferencial es NE-SW, con una extensión de 11.3 km
aproximadamente. Este perfil es perpendicular al lineamiento NW-SE observado en los
mapas. Su función es delimitar las zonas donde hay fallas, las cuales forman parte de la
configuración de la cima del basamento cristalino.
Los valores magnéticos utilizados en los modelos fueron para el campo total
magnético de 41,844.3 nT, con una inclinación magnética de 48.983° y declinación
magnética de 5.616°. El espesor del depósito aluvial y fluvial Cuaternario varía entre 20 m
y 200 m de grosor a lo largo del perfil. La formación Soyatal tiene un espesor aproximado
que se encuentra entre los 200 m y 500 m la cual suprayace a la formación El Abra. Ésta
posee un espesor máximo (~3800 m) al oeste del perfil y disminuye conforme se va hacia
el este (~1400 m); a pesar de que esta Formación supera su espesor promedio (1800m –
2500 m) esto se puede explicar como una secuencia geológica duplicada, ya que se tratan
de rocas sedimentarias que fueron plegadas durante la orogenia Laramide.
87
La profundidad a la cima del complejo basal (Gneiss grenville) varía entre los 3400
m al suroeste y 1200 m al noreste, se le asigna una susceptibilidad magnética de 0,0009
(unidades cgs). Esta unidad subyace a la formación Santiago la cual tiene un espesor
aproximado que va de 100 m a 300 m y continúa con la misma configuración que presenta
el basamento metamórfico.
De forma general, el basamento de esta zona presenta basculamiento hacia el
oeste del perfil y la conforman una serie de fallas escalonadas con movimiento aparente
de tipo normal, cuyo plano principal buza hacia el W y aproximadamente a los 5300 m de
longitud del perfil se observa un cambio máximo en la pendiente de las anomalías
gravimétricas y magnéticas, es posible que pueda ser una de las fallas principales. Por
consiguiente, se define un sistema de fallas con una orientación NW-SE.
Figura.6.15. Modelo geológico-geofísico con datos magnéticos y gravimétricos del Perfil 2.
NT: Nivel del Terreno.
88
La Figura 6.15 corresponde al modelo geológico-geofísico del perfil 2, el cual tiene
una orientación NW-SE y un azimut de 160°. Este perfil contiene con una longitud
aproximada de 8.5 km y aunque en principio aparece paralelo a las principales estructuras
geológicas, en realidad corta a las estructuras con orientación NE-SW, mismas que se
identificaron con la geomorfología y los cauces de los ríos en la zona.
Los valores magnéticos utilizados en los modelos fueron para el campo total
magnético de 41,844.3 nT, con una inclinación magnética de 48.983° y declinación
magnética de 5.616°. En este perfil aún se observa la presencia de relleno aluvial de edad
Cuaternaria, cuyo espesor aproximado varía de 10 m a 100 m. La unidad Soyatal tiene un
espesor promedio de 300 m y presenta mayor deformación. La Formación que subyace a
esta unidad es El Abra, la cual cuenta con un espesor uniforme entre los 3000 y 3500 m.
La profundidad a la cima del basamento metamórfico se encuentra entre los 2600
m al oeste del perfil y aumenta a los 3400 m al este del perfil. Este valor se correlaciona
bien con la profundidad obtenida en el perfil 1. La buena correlación entre los perfiles y la
profundidad incrementa la certidumbre sobre los modelos propuestos. A esta unidad se le
asigna una susceptibilidad magnética de 0,0009 (unidades cgs) y subyace a la formación
Santiago, que tiene un espesor aproximado de entre 100 m y 300 m.
Se observan fallas normales en el basamento cristalino de menor dimensión a las
vistas en el perfil 1. Estas forman una serie de bloques levantados (horst) y hundidos
(graben), y de manera general se visualiza una ligera inclinación hacia el este del perfil.
Dichas estructuras nos marcan la existencia de otro sistema de fallas en una dirección NESW.
El modelo geológico-geofísico del perfil 3 se muestra en la Figura 6.16, tiene una
orientación E-W y una longitud aproximada de 4800 m. Su proyección sirve
primordialmente para una mejor caracterización acerca de la profundidad estimada del
basamento en la zona.
89
Figura.6.16. Modelo geológico-geofísico con datos magnéticos y gravimétricos del Perfil 3.
NT: Nivel del Terreno.
Los valores magnéticos utilizados en el modelado fueron para el campo total
magnético de 41,844.3 nT, con una inclinación magnética de 48.983° y declinación
magnética de 5.616°. En este perfil existe ausencia del depósito aluvial Cuaternario. La
formación El Abra tiene un espesor que varía de 1800 m a 3400 m dentro del perfil. Esta
secuencia subyace a la formación Soyatal, la cual muestra un espesor variable y una zona
de mayor deformación entre los 1500 m y 2500 m a lo largo del perfil. Es probable que
esta zona corresponda a un efecto en la pendiente máxima que se observa en el bloque
levantado y hundido del basamento.
La susceptibilidad magnética del complejo basal es de 0,0009 (unidades cgs),
mientras que la profundidad a la cima del basamento cristalino es muy variable, va desde
los 1600 m hasta los 3000 m aproximadamente. Estas profundidades conservan una
buena correspondencia con los otros perfiles interpretados. Esta unidad subyace a la
formación Santiago, que tiene un espesor aproximado de entre 100 m y 300 m.
A partir de las superficies exportadas de los tres modelos geológicos-geofísicos ya
interpretados, las cuales contienen las profundidades estimadas a la cima del basamento
90
cristalino, construimos el mapa de superficie en 3D la cima del basamento metamórfico
(Figura 6.17). De manera general, se aprecian dos dominios de profundidad separados por
el mismo lineamiento. Éste tiene una orientación NW-SE a una profundidad aproximada
de 2500 m. La profundidad tiene una tendencia descendente hacia el noreste, dejando al
suroeste del mapa los valores máximos entre 3000 m y 3400 m. En esta zona se aprecia un
alto estructural paralelo a dicho lineamiento, y un bajo estructural, a 3400 m
perpendicular a este sistema. Por lo que, nuestro análisis nos permitió distinguir bloques
en el basamento separados por los dos sistemas de fallas NW-SE y NE-SW, descritos
anteriormente.
Figura 6.17. Mapa de superficie en 3D del basamento metamórfico, configuración de
la cima del complejo basal grenvilliano. Se muestran los dos sistemas de fallas NW-SE
y NE-SW (línea blanca discontinua). Coordenadas UTM y escala de colores muestra
las profundidades estimadas.
Con base en el análisis de los tres modelos geológico-geofísicos, se puede visualizar
de manera general un fallamiento de tipo normal que afecta a las capas más superficiales,
a la capa sedimentaria y al basamento. Por lo que, dichos rasgos estructurales al estar
afectados por esfuerzos tectónicos pueden provocar alguna inestabilidad estructural que
causen movimientos corticales y probablemente sean la causa de la microsismicidad.
91
CAPÍTULO VII
7.1
Análisis y discusión de resultados
INTEGRACIÓN DE DATOS
Realizamos el análisis espacio-temporal de la sismicidad con un total de 299 epicentros
ocurridos en el área de estudio, registrados entre noviembre de 2007 y septiembre de
2010. Si bien el periodo de registro es corto para entender el comportamiento sísmico de
la zona en toda su dimensión, obtuvimos una buena idea de su distribución espacial, en
general, y de la tendencia preferencial.
Dicha distribución espacial se muestra en la figura 7.1 en ella podemos identificar
dos zonas de acumulación de eventos sísmicos, uno sobre la cabecera municipal de Landa
de Matamoros, y la otra al noreste de la zona de estudio, cuya tendencia preferencial es
NE-SW. Ello contrasta con la orientación regional descrita por León-Loya (2014).
Figura. 7.1. Distribución espacial de la sismicidad localizada con la técnica monoestación en el área de estudio, de noviembre de 2007 a septiembre de 2010. Los puntos
azules son los eventos localizados con una estación y los rojos con dos o más estaciones;
mientras que los triángulos negros indican las mediciones gravimétricas.
92
Para realizar el análisis temporal graficamos los datos y obtuvimos un histograma
del número de eventos ocurridos mensualmente durante el periodo de registro (Figura
7.2). Éstos eventos fueron localizados con al menos una estación y con un máximo de 4
estaciones. La distribución de los sismos no es constante ni sigue una tendencia definida.
La mayor concentración de eventos sísmicos ocurre a finales del 2008, la mayor parte del
2009 y en agosto y septiembre de 2010. El máximo número de eventos fue de 35 sismos
en abril de 2009, mientras que para el tiempo restante se observa una disminución en la
sismicidad. Esta variación tan drástica más allá de reflejar el comportamiento tectónico,
podría ser una consecuencia de la insuficiencia o mal funcionamiento de los equipos
sísmicos, sin embargo, eso es algo que sólo se corroborará con mayor tiempo de
observación. Por otro lado, la distribución espacial de la sismicidad ha sido muy útil en
cómo aplicar algunos métodos geofísicos como la gravimetría y aeromagnetrometría, que
son un buen complemento para caracterizar lineamientos y posibles estructuras
geológicas activas.
Figura 7.2. Histograma del tiempo contra el número de eventos ocurridos desde
noviembre 2007 y hasta septiembre 2010 en Landa de Matamoros, Querétaro.
93
Durante el reconocimiento geológico en la cabecera municipal de Landa de
Matamoros buscamos evidencias superficiales de fallas activas, ya que habíamos recibido
algunos reportes de agrietamientos y daños a construcciones. Sin embargo, no se
encontraron evidencias recientes de trazas en superficie, sino únicamente rasgos de fallas
antiguas. Estas generalmente mantienen un rumbo NW-SE, por ello es posible que dichos
daños no fueran causados por la actividad sísmica, sino por la ocurrencia de algún otro
fenómeno natural o inducido.
La distribución espacial de la sismicidad, los datos obtenidos durante el
reconocimiento geológico, y la información geofísica, sirvieron para la caracterización de
las zonas probablemente activas. De hecho, para integrar adecuadamente dicha
información analizamos la distribución espacial de la sismicidad en conjunto con los
mapas geofísicos (Figuras 7.3, 7.4 y 7.5), para así establecer una posible relación con la
génesis del fenómeno sísmico.
Figura 7.3. Mapa aeromagnético regional clasificado en dominios magnéticos junto con
la distribución espacial de los sismos ocurridos entre noviembre de 2007 y septiembre de
2010 en la parte central de la SMOr. Los puntos rojos indican las mediciones
gravimétricas (extremo inferior derecho), los círculos amarillos las localizaciones
epicentrales, y los triángulos negros la ubicación de las estaciones sísmicas. Nótese la
tendencia casi N-S de la sismicidad a lo largo de los dominios magnéticos.
94
En la figura 7.3 se muestra el mapa aeromagnético de reducción al polo ascendente
a 500 m del CMR, también se muestra la distribución espacial de la sismicidad regional
(compuesta por unos 3000 eventos) (León Loya, 2014). Para este trabajo nos
concentramos en un área limitada por las coordenadas geográficas 21° - 21°45’ latitud N y
99° - 100° longitud W. En dicho mapa se observa que la sismicidad cae en los dominios
magnéticos I, III y IV, los cuales representan los valores magnéticos máximos, intermedios
y bajos, respectivamente. En cada dominio se observa una concentración muy específica
de sismos, cuya densidad no es uniforme en todos ellos, sin embargo, sí se observa una
tendencia preferencial N-S en su distribución espacial.
De manera específica, el dominio I se ubica al norte del mapa (Figura 7.3), entre los
límites del estado de Querétaro y San Luis Potosí. Éste se caracteriza por tener valores
magnéticos altos y una sismicidad dispersa, cuyas magnitudes son las mayores en el área
(ML hasta 3.5). Sus respectivas localizaciones epicentrales tienen menor certidumbre,
debido a que se encuentran fuera del arreglo de las estaciones que conforman la red
sísmica LANDA. Por otra parte, el dominio III, parte central del mapa, se extiende desde el
noroeste hasta el sureste, está compuesto por valores magnéticos intermedios, donde
ocurre la mayor concentración de sismos. Por último, el dominio IV se localiza al sur y
contiene los valores magnéticos más bajos; en éste se infiere que los gradientes mínimos
se atribuyen a cuencas o grabenes limitados por fallas con una dirección grosso modo NWSE. Pese a que en el acercamiento sobre la imagen la sismicidad pareciera dispersa, aún se
nota una concentración de microsismos en la cabecera municipal de Landa de Matamoros,
lo cual corrobora la percepción de la población acerca de movimientos telúricos y ruidos
locales que han percibido en la vecindad.
95
Figura 7.4. Mapa aeromagnético con clasificación de dominios magnéticos, junto con la
distribución espacial de los sismos ocurridos en los alrededores de la cabecera municipal
de Landa de Matamoros. Los puntos rojos son los sismos localizados con una estación y
los negros con dos o más estaciones. Nótese una tendencia NE-SW y en sus extremos dos
agrupaciones de sismos.
En la figura 7.4 se observa un cambio en la tendencia de sismicidad hacia el N45º E,
el cual puede estar asociado con una estructura perpendicular a las estructuras regionales,
perteneciente a otro sistema de fallas.
Finalmente, la figura 7.5 muestra un acercamiento sobre la Figura 7.4, el cual
contiene el mapa de anomalía de Bouguer completo junto con la distribución espacial de
la sismicidad (puntos negros) ocurrida durante el periodo de registro. En éste el patrón de
sismicidad ya no parece tan claro, lo cual se debe a un cambio en la escala del trabajo
geofísico y a una población menor de sismos.
96
Figura 7.5. Mapa de anomalía de Bouguer completa junto con la distribución espacial de
sismicidad (puntos) en la cabecera municipal de Landa de Matamoros. Los triángulos
negros son las mediciones gravimétricas, los puntos rojos las localizaciones con una
estación y los negros con dos o más estaciones.
97
7.2
DISCUSIÓN
Nuestros resultados son la primera evidencia instrumental acerca de la microsismicidad
ocurrida entre noviembre de 2007 y septiembre de 2010, en la parte central de la Sierra
Gorda, Querétaro. La contribución de los métodos geofísicos fue facilitar el
reconocimiento de las zonas sismogénicas en la zona de estudio.
Nuestro trabajo es un complemento a la investigación realizada por León Loya
(2010, 2014), quien realizó el primer análisis regional sobre la sismicidad que ocurre en la
parte central de la SMOr. León Loya localizó más de 3000 sismos y ha explorado alguna
posible relación causa-efecto entre la sismicidad y fenómenos como el ciclo hidrológico, el
flujo de calor, el gradiente geotérmico o la presencia de fluidos que intervienen en la
ruptura de la corteza terrestre.
Durante esta investigación examinamos, a escala local, la sismicidad registrada
desde noviembre de 2007 a septiembre de 2010 en la cabecera municipal de Landa de
Matamoros y sus alrededores, en Querétaro. Localizamos 299 epicentros con magnitudes
(ML) menores a 3, cuyas profundidades son inferiores a 10 km. El monitoreo temporal y su
análisis de distribución espacio-temporal es bastante amplio en la parte central de la
SMOr y refleja que el área no está exenta de sismicidad, como se pensaba hasta hace
poco. Esta idea falsa de comportamiento “asísmico” se debe a la poca frecuencia de
sismos mayores a M4.5, además de también desconocerse la existencia de la actividad
microsísmica mostrada en este trabajo. Todo este desconocimiento ha sido causado
principalmente por la falta de una red sísmica permanente que cuente con instrumentos
de mayor sensibilidad y una buena cobertura azimutal en la región.
Recurrimos al uso de la técnica mono-estación para realizar la localización
epicentral como último recurso disponible para aprovechar la información registrada en
pocas estaciones. En nuestro caso fue de mucha utilidad al permitirnos disponer del
máximo número de eventos que de otra forma se habrían perdido. Gracias a esta
metodología logramos analizar espacial y temporalmente la microsismicidad regional. Sin
embargo, para realizar un buen análisis temporal de sismicidad se requiere de grandes
periodos de observación y registro para ser adecuado, y aunque sólo analizamos tres
años, logramos describir algunos patrones espaciales de microsismicidad.
Debido a las magnitudes tan pequeñas de la sismicidad no ha sido posible explicar
su génesis, ya que la energía de cada evento se encuentra limitado a su entorno, por esta
razón, decidimos realizar estudios adicionales que complementen la información ya
98
existente para identificar las probables zonas sismogénicas, por ello integramos la mayor
cantidad de datos posibles, como los geológicos, aeromagnéticos y gravimétricos. Este
tipo de estrategias nos parecen un buen complemento para incrementar la certidumbre
acerca de las probables zonas sismogénicas, y particularmente en el estudio de la
sismicidad intraplaca, debido a la dificultad que existe para encontrar evidencias recientes
de actividad sísmica.
Según Lopes et al., (2010) consideran la reactivación de zonas de debilidad preexistentes, la concentración de esfuerzos, o ambos, como causas principales para explicar
la génesis de la sismicidad intraplaca; sin embargo, dichas zonas de debilidad no siempre
son fáciles de identificar, ya sea por la escala en que se presentan o por las características
que las distinguen. Por ejemplo, Sykes (1978) describe las zonas de debilidad como áreas
extensas donde hubo alguna deformación mayor, mientras que Gangopadhyay & Talwani
(2005) las refieren como zonas de intersección de fallas. En la Sierra Madre Oriental las
candidatas naturales para ser las probables fuentes sismogénicas son sus estructuras
geológicas mayores, sin embargo, durante el reconocimiento geológico no encontramos
evidencias recientes de actividad sísmica, a pesar de la falta de trazas de falla en superficie
reciente no descartamos su existencia y puedan tratarse de estructuras “ciegas” que
generen dicha sismicidad.
Para delimitar mejor las probables zonas sismogénicas realizamos la interpretación
de cartas aeromagnéticas y aplicamos el método gravimétrico. A partir de esto, obtuvimos
los mapas de anomalías gravimétricas y aeromagnéticas y junto con la geomorfología local
nos ayudaron a delimitar un lineamiento regional que cruza el área de estudio, con una
tendencia preferencial NW-SE, el cual coincide con la orientación general de las
estructuras geológicas formadas durante la orogenia Laramide, asimismo con la
información geofísica fue posible corroborar el basculamiento hacia el poniente del
basamento cristalino según Eguiluz et al. (2000).
La integración de información geofísica con la geología local nos permitió la
construcción de modelos geológico-geofísicos para determinar la fuente sismogénica. A
partir de dichos modelos estimamos la estructura del subsuelo, la configuración del
basamento metamórfico y su profundidad en la parte superior. Con base en la
configuración del basamento, así como en las características geomorfológicas e
hidrológicas superficiales, como los cauces de ríos y arroyos, encontramos dos sistemas de
fallas, grosso modo, perpendiculares entre sí: NW-SE y NE-SW, con un movimiento normal
y una ligera componente lateral.
99
Uno de los sistemas de fallas se muestra en el perfil 1 (Figura 6.14), el cual
conserva la misma dirección NW-SE que tienen las estructuras geológicas regionales
formadas durante la orogenia Laramide. Este sistema corresponde a un régimen de fallas
normales escalonadas, las cuales buzan hacia el suroeste y tienen una ligera componente
lateral, que se logra deducir a través de la intercalación del perfil 1 y 2 de los modelos
geológicos-geofísicos. El otro sistema de fallas, mostrado en el perfil 2 (Figura 6.15),
exhibe una orientación preferencial NE-SW y tiene fallas de movimiento normal de menor
tamaño, las cuales forman una serie de bloques levantados (horst) y hundidos (graben) de
dimensiones reducidas. Estos sistemas podrían asociarse con el evento extensivo postlaramídico, de edad post-pliocénica (Ochoa, 1996; Ochoa et al., 1998).
Ambos sistemas de fallas (Figura 6.17) muestran la presencia de rasgos
estructurales en el área de estudio: las fallas del basamento; aquellas que van de la
superficie hasta el basamento, y las fracturas y fallas que sólo son superficiales (Figura
6.14 y 6.15). Dichos sistemas al ser afectados por esfuerzos tectónicos regionales pueden
generar alguna inestabilidad estructural capaz de producir los movimientos corticales que
causan la sismicidad en la región. De esta forma, es probable que la microsismicidad
actual refleje la reactivación de alguno o ambos sistemas de fallas.
Uno de los retos más interesantes que enfrentamos durante la elaboración de los
modelos geológicos-geofísicos fue conciliar las diferencias de escala entre los mapas
gravimétricos y aeromagnéticos, ya que la adquisición de los datos gravimétricos se
realizó con mayor detalle y en un área más limitada por la topografía del lugar, mientras
que las cartas aeromagnéticas cubren un área más regional; sin embargo, al interpretar las
anomalías gravimétricas y magnéticas ambas se lograron complementar debido a las
propiedades físicas (densidad y susceptibilidad) que caracterizan la litología del área y
facilitaron reconocer la relación que existe entre la capa sedimentaria y el complejo basal.
Por último, el fenómeno sísmico que ocurre en la parte central de la Sierra Madre
Oriental la sitúa probablemente como la región intraplaca más importante del país. Es
importante considerar que, el incremento en la densidad de población, la falta de
información sobre medidas de prevención, la carencia de normas de construcción
adecuadas al tipo de sismicidad local y la trascendencia económica de la Sierra Gorda
como patrimonio cultural y turístico para el estado, son elementos suficientes para
continuar con este tipo de investigaciones que contribuyan en el avance y progreso del
conocimiento sobre el comportamiento de la sismicidad intraplaca, la cual hoy en día,
permanece constante.
100
7.3
CONCLUSIONES
La integración de información sísmica, geofísica y geológica nos permitió proponer
algunas estructuras locales como las probables fuentes sismogénicas de la sismicidad
que actualmente ocurre en el corazón de la Sierra Gorda Queretana.
Esta investigación a escala local, es la primera evidencia instrumental sistemática
sobre la microsismicidad registrada entre noviembre de 2007 y septiembre de 2010 en
la cabecera municipal de Landa de Matamoros y sus alrededores, en Querétaro. La
microsismicidad local fue registrada con la red sísmica temporal LANDA, donde relocalizamos 299 epicentros con magnitudes menores a 3 y profundidades inferiores a
10 km. Nuestros datos muestran un alto nivel de microsismicidad con una amplia
distribución espacial en la parte central de la Sierra Madre Oriental.
Las localizaciones epicentrales con la técnica mono-estación nos facilitó identificar dos
concentraciones espaciales de microsismicidad: una en la cabecera municipal de Landa
de Matamoros y la mayor al NE de la zona de estudio.
El reconocimiento geológico y los mapas de anomalías gravimétricas y aeromagnéticas
nos ayudaron a precisar un lineamiento regional que cruza el área de estudio, con una
tendencia preferencial NW-SE, el cual coincide con la orientación de las estructuras
geológicas de la Sierra Madre Oriental. Consideramos que este lineamiento puede
tratarse de una zona de falla, el cual se encuentra en el límite de un bajo y alto
gravimétrico y magnético, observado en los perfiles 1 y 2.
Este lineamiento separa dos dominios geofísicos, uno contiene los valores altos de
anomalías gravimétricas y magnéticas, y corresponden a un levantamiento del
basamento metamórfico o al límite del escarpe de falla, mientras que los valores bajos
de anomalías se deben a depresiones o cuencas limitadas por fallas.
Se realizaron tres modelos geológico-geofísicos mediante el modelado directo y con
base en su interpretación establecimos que el basamento subyacente, se encuentra
entre 1400 m y 3400 m.s.n.m.
Los valores de las anomalías presentan un incremento general hacia el NE, el cual se
debe más a la respuesta del complejo basal que a la capa sedimentaria y confirman la
presencia de un basculamiento hacia el poniente del basamento metamórfico. La
diferencia en amplitud y longitud de onda de las anomalías magnéticas y
101
gravimétricas, la podemos explicar como un cambio de escala regional a local en el
estudio.
La información geológico-geofísica nos permitió identificar los principales rasgos
estructurales: las fallas profundas en el basamento, aquellas que van de la superficie al
basamento y las fracturas y fallas que sólo son superficiales. Con base en la
configuración en bloques del basamento, los rasgos estructurales y la geomorfología
local, determinamos la presencia de dos sistemas de fallas normales regionales,
perpendiculares entre sí: NW-SE y NE-SW.
El sistema de fallas NW-SE, corresponde a un régimen de fallas normales escalonadas,
buzan hacia el suroeste y tienen una ligera componente lateral. El otro sistema NE-SW,
consta de fallas con movimiento normal, las cuales forman una serie de bloques
levantados (horst) y hundidos (graben) de pequeñas dimensiones. Ambos sistemas de
fallas pueden asociarse al evento extensivo post-laramídico.
La distribución espacial de la microsismicidad sugiere que la actividad sísmica es
producto de la reactivación de alguna o ambas zonas de debilidad pre-existentes en la
región, representada por los sistemas de fallas normales NW-SE y NE-SW. Por lo que,
el estudio de esta microsismicidad nos muestra que la región no exhibe un
comportamiento “asísmico” como antes se creía y el alto nivel de microsismicidad
registrada durante más de 3 años la sitúa probablemente como la región intraplaca
sísmicamente más importante del país.
Este trabajo aporta información valiosa para autoridades y sociedad en general, para
tomar medidas de prevención y alternativas sobre normas de construcción adecuadas
ante la ocurrencia de cualquier actividad sísmica.
102
7.4
RECOMENDACIONES
 Se recomienda realizar más levantamientos gravimétricos a nivel regional en la
parte central de la Sierra Madre Oriental, lo cual permitirá determinar en los
mapas obtenidos las direcciones preferenciales de las anomalías gravimétricas y
demostrar su relación con las zonas de debilidad pre-existentes.
 La aplicación de métodos de inversión conjunta nos permitirá caracterizar con
mayor certidumbre las diferentes unidades geológicas, así como identificar
heterogeneidades en el subsuelo que hayan pasado desapercibidas durante el
modelado directo. Se sugiere trabajar con el modelo de inversión obtenido a
través del software de UBC (University of British Columbia, Geophysical Inversion
Facility).
 La implementación de una red sísmica permanente regional con instrumentos de
mayor sensibilidad comunicados en tiempo-real, permitirá obtener registros en
tiempo continuo, y datos de mejor calidad. Esto logrará mejorar las localizaciones
epicentrales y en un futuro poder estimar el potencial sísmico.
103
REFERENCIAS BIBLIOGRÁFICAS
Aranda, G. J., Torres, H. R., Carrasco, N. G. y Aguillón, R. A., 2000. Contrasting styles of Laramide
folding across the west-central margin of the Cretaceous Valles-San Luis Potosí carbonate
plataform, Mexico. Revista Mexicana de Ciencias Geológicas, 17 (2), 97-111.
Blakely, Richard J., 1996. Potential Theory in Gravity and Magnetic Applications. Cambrige
University Press, 464.
Cantos, F., 1974. Tratado de Geofísica Aplicada: España. Editorial Litoprint. 520.
Carrillo-Bravo, J., 1971. La plataforma Valles-San Luis Potosí. Boletín de la Asociación Mexicana de
Geólogos Petroleros, 23 (1), 106.
Clemente-Chavez, A., Figueroa-Soto, A., Zuñiga, F.R., Arroyo, M., Montiel, M., Chavez, O. 2013.
Seismicity at the northeast edge of the Mexican Volcanic Belt (MVB) and activation of an
undocumented fault: the Peñamiller earthquake sequence of 2010–2011, Querétaro,
Mexico. Nat. Hazards Earth Syst. Sci., 13, 2521–2531.
Comisión Estatal de Aguas (CEA). Comunicación Personal 2012.
Cuellar-Cárdenas, M. A., Nieto Samaniego, A. F., Levresse, G., Alaniz Álvarez, S. A., Solari, L., Ortega
Obregón, C., López Martínez, M., 2012. Límites temporales de la deformación por
acortamiento Laramide en el centro de México: Revista Mexicana de Ciencias Geológicas,
29 (1), 179-203.
Dávalos-Álvarez, Nieto-Samaniego, A.F., Alaniz-Álvarez, S. A., Gómez-González, J.M., 2005. Las
fases de deformación cenozoica en la región de Huimilpan, Querétaro, y su relación con la
sismicidad local. Revista Mexicana de Ciencias Geológicas, v. 22, núm. 2, 129-147.
DeCelles, P. G., 2004. Late Jurassic to Eocence evolution of the Cordilleran thrust belt and foreland
basin system, western U.S.A. American Journal of Science. 304, 105-168.
Dobrin, M., 1961. Introducción a la Prospección Geofísica. Barcelona: Ediciones Omega S. A. 483.
Dobrin, M. B. y C. H. Savit, 1988. Introduction to geophysical prospecting; cuarta edición: Mac
Graw Hill, Inc.
Eguiluz de Antuñano, S., Aranda, G. M., Marret, R., 2000. Tectónica de la Sierra Madre Oriental,
Mexico. Boletín de la Sociedad Geológica Mexicana. Vol. LIII. 1-26.
104
English, J. M., Johnston, S. T., 2004. The Laramide Orogeny: What Were the Driven Forces?.
International Geology Review, 46. 833-838.
ESRI, Inc., 2005. ArcGIS Desktop v. (Software).
Ferrari, L. Orozco-Esquivel, T., Manea, V. y Manea, M., 2011. The dynamic history of the TransMexican Volcanic Belt and the Mexico subduction zone. Tectonophysics.
doi:10.1016/j.tecto.2011.09.018
Fitz-Díaz, E., 2010. Progressive deformation, fluid flow and water-rock interaction in the Mexican
Fold-Thrust Belt, Central México: Minneapolis, Minnesota, Universidad de Minnesota,
Tesis doctoral.
García-Acosta, V. y G. Suárez-Reynoso. 1996. Los Sismos en la Historia de México, Fondo de
Cultura Económica - UNAM, México.
Geosoft Inc., 2006. Montaj Gravity & Terrain correction: gravity data processing extension for
Oasis montaj. Tutorial and user guide.
Geosoft Inc., 2007. Montaj MAGMAP Filtering: 2D frecuency domain processing of potential field
data extension for Oasis montaj. Tutorial.
Geosoft Inc., 2007. Oasis montaj v.6.4.2 (HJ), Standard edition (software).
Gómez-González, J. M., Barboza Gudiño, J. R., Zuñiga Dávila-Madrid, F. R., Torres Hernández, J. R.,
Guzmán Speziale, M., Mata Segura, J. L., 2005, Sismicidad en el Estado de San Luis Potosí.
Instituto de Geología, Universidad Autónoma de San Luis Potosí. Folleto Técnico 129.
Gómez-González, J.M., 2007. Reporte sobre la descripción preliminar de la actividad sísmica
ocurrida en noviembre de 2007 en el Municipio de Landa de Matamoros, Querétaro.
Gómez-González, J.M., R. Barboza Gudiño, N.A. Luque Vergara y A.G. Figueroa Soto. 2008.
Segundo reporte sobre la sismicidad en los Municipios de Landa de Matamoros y Jalpan de
Serra, Querétaro. Agosto de 2008.
Hammer S, 1939. Terrain corrections for gravimeter stations, Geophysics, 4, 184-194.
Hammer S, 1982. Critique of terrain corrections for gravity stations, Geophysics, 47, 839-840.
105
Havskov, J., Otemöller, L., 2008. SEISAN: the Eartquake analysis software. Manual, Institute of
Solid Earth Physics. University of Bergen Norway.
Instituto Nacional de Estadística, Geografía e Informática (INEGI). Querétaro Arteaga. XII Censo
General de Población y Vivienda 2000. Principales Resultados por Localidad.
Brown, J. M., Niebauer, T. M., Richter, B., Klopping, F. J., Valentine, J. G. and Buxton, W. K. 1999.
Miniaturized gravimeter may greatly improve measurements. Eos Electronic Supplement.
Kostoglodov, V., Pacheco, F. J. 1999. “Cien Años de Sismicidad en México”. Instituto de Geofísica.
UNAM.
Lafehr, T. R., 1991. An exact solution for the gravity curvature (Bullard B) correction. Geophysics,
56 (8), 1179-1184.
Lay, T. y Wallace, F. C., 1995. Modern Global Seismology. Academic Press, Inc. 217.
León Loya, R. A., 2010. Estudio de sismicidad en la Sierra Gorda de Querétaro y sus implicaciones
tectónicas. Universidad Autónoma de Nuevo León. Tesis de Licenciatura. 122.
León Loya, R. A., 2014. Estado y clasificación de la microsismicidad en la parte central de la sierra
madre oriental. Universidad Nacional Autónoma de México. Tesis de maestría. 115.
Lienert, B. R. E. and Havskov, J., 1995. A computer program for locating earthquakes both locally
and globally. Seis. Res. Lett., 66, 26–36.
López, D. R. 2003. La Formación Tamabra del Cretácico medio en la porción central del margen
occidental de la plataforma Valles-San Luis Potosí, centro - noreste de México. Revista
Mexicana de Ciencias Geológicas, 20 (1), 1-19.
Lowrie, W. 1997. Fundamentals of Geophysics. Cambridge. University Press. Cambrige, UK: 354.
Morelli, C. 1971. The International Gravity Standardization Net 1971. International Association of
Geodesy, Special Publication 4.
Morelli, C; Gantar, C; McConnell, R K ; Szabo, B ; Uotila, U. The International Gravity
Standardization Net 1971 (I.G.S.N.71).
Muir, J. M., 1936. Geology of the Tampico region: Tulsa. American Association of Petroleum
Geologists, 280
106
Nieto-Samaniego, Á. F., Alaniz-Álvarez, S. A., Camprubí-í Cano, A., 2005. La Mesa Central de
México: estratigrafía, estructura y evolución tectónica cenozoica. México. Sociedad
Geológica Mexicana Volumen Conmemorativo del Centenario Temas Selectos de la
Geología Mexicana, Tomo LVII, número III, 2005, 285-318.
Ochoa, C. H., 1996. Geología del anticlinorio de Huayacocotla, en la región de Molango, estado de
Hidalgo. Tesis de maestría. Universidad Nacional Autónoma de México, Instituto de
Geología. 91
Ochoa-Camarillo, H., Buitrón, B. E., and Silva-Pineda, A., 1998. Contribution al conocimiento de la
bioestratigrafía y tectónica del Jurásico (Anticlinorio de Huayacocotla) en la región de
Molango, Hidalgo, México. Revista Mexicana de Ciencias Geológicas, 15 (1), 57-63.
Oldenburg, D.W., 1974. The inversion and interpretation of gravity anomalies. Geophysics, 39,
526-536.
Reynolds, John M. 1997. An Introduction to Applied and Environmental Geophysics, Ed. Wiley. 796
Scintrex Ltd. (2006). CG-5 Scintrex Autograv System, Operation Manual. Document Part No.
867700. Rev. 1. Canada: 312
Moreira-Rivera, F., Flores-Aguillon, G., Reyes-Reyes, N. A., Maldonado-Lee, J.M., MartínezRodríguez, L., Carrizales-Aguilar, A., De Santiago-Céspedes, J., Arrieta-Saldaña, R., LópezAlba, L. 1997. Carta Geológico-Minera, Ciudad Valles F14-8, escala 1:250,000. Servicio
Geológico Mexicano. 2da. Edición.
Stein, S., 2007. Approaches to continental intraplate earthquakes issues. Continental Intraplate
Earthquakes: Science, Hazard, and Policy Issues.GSA Special Paper 425. 1-16, doi:
10.1130/2007.2425(1)
Suter, M., 1984. Cordilleran deformation along the eastern edge of the Valles-San Luis Potosí
carbonate platform, Sierra Madre Oriental fold-thrust belt, east-central Mexico. Geological
Society of America Bulletin, 95, 1387-1397
Suter, M., 1987. Orientation data on the state of stress in northeastern Mexico as inferred from
stress-induced borehole elongations. Journal of Geophysical Research, 92, 2614-2626.
Suter, M., 1990. Geología de la hoja Tamanzuchale, estados de Hidalgo, Querétaro y San Luis
Potosí. Carta Geológica de México, serie de 1:100,000 No. 22. Universidad Nacional
Autónoma de México.
107
Suter, M., Quintero-Legorreta O., Johnson CA. 1992. Active faults and state of stress in the central
part of the Trans-Mexican Volcanic Belt, Mexico 1. The Venta de Bravo Fault, J. Geophys.
Res., 97(B8),11983–11993, doi:10.1029/91JB00428.
Suter, M., Quintero-Legorreta, O., López-Martinez, M, Aguirre-Díaz, G., Farrar, E. 1995a. The
Acambay graben: Active intraarc extension in the trans-Mexican volcanic belt,
Mexico, Tectonics,14(6), 1245–1262, doi:10.1029/95TC01930.
Suter, M., Carrillo-Martinez, M., López-Martínez, M., Farrar, E. 1995b. The Aljibes half-graben—
Active extension at the boundary between the trans-Mexican volcanic belt and the Basin
and Range Province, Mexico Geological Society of America Bulletin, 107, 627-641,
doi:10.1130/0016-7606(1995)107<0627:TAHGAE>2.3.CO;2.
Suter, M., Carrillo-Martinez, M., Quintero-Legorreta, O., 1996. Macroseismic study of earthquakes
in the central and eastern parts of theTrans-Mexican Volcanic Belt. Bulletin of the
Seismological Society of America, 86, 1952-1963.
Suter, M., López-Martínez, M., Quintero-Legorreta, O., Carrillo-Martínez, M., 2001. Quaternary
intra-arc extension in the central Trans-Mexican volcanic belt. Geological Society of
America Bulletin, 113 (6), 693–703.
Sykes, L. R., 1978. Intraplate Seismicity, Reactivation of Preexisting Zones of Weakness, Alkaline
Magmatism, and Other Tectonism Postdating Continental Fragmentation. Reviews of
Geophysics and Space Physics, 16 (4), 621-688.
Udías V., A., Mezcua R., J. 1997. Fundamentos de Geofísica. Editorial Alianza. 480.
Urbina, F., and Camacho H., 1993. La Zona Mega sísmica Acambay-Tixmadejé, Estado de México,
conmovida el 19 de Noviembre de1912, Bol. Inst. Geol. Mex., 32, 125.
Zuñiga F. R, Pacheco J. F., Guzmán-Speziale M, Aguirre-Díaz G. J., Espíndola V. H., Nava E., 2003.
The Sanfandila earthquake sequence of 1998, Querétaro, México: activation of an
undocumented fault in the northern edge of central Trans-Mexican Volcanic Belt.
Tectonophysics, 361, 229–238.
108
ANEXO A
MÉTODOS POTENCIALES
ASPECTOS GENERALES DEL MÉTODO GRAVIMÉTRICO
Mediciones absolutas
Es difícil de estimar el valor de gravedad absoluto, para hacerlo correctamente se
requiere de un aparato complejo y un periodo prolongado de observación. En un
principio se hacía dicha medición usando péndulos grandes o técnicas de caída de
cuerpos, cuya precisión aproximada era de 0.01 gu (Kearey et al, 2002). Los instrumentos
para medir la gravedad absoluta originalmente fueron pesados, caros y lentos para leer.
Apareció una nueva generación de instrumentos que mejoró las mediciones de gravedad
absoluta en aplicaciones tanto dinámicas como estáticas (Brown et al., 1999), los cuales ya
no presentan estos inconvenientes, incluso podrían tener un uso más general en los
próximos años.
Mediciones relativas
La medición de valores de gravedad relativos, es decir, las diferencias de gravedad
entre puntos de medición, son más simples y éstas siguen el procedimiento estándar en el
estudio gravimétrico. Los valores absolutos de las estaciones de estudio pueden obtenerse
del International Gravity Standardization Network (IGSN) de 1971 (Morelli et al., 1971), se
trata de una red de estaciones en las cuales los valores absolutos de gravedad han sido
determinados con respecto a los sitios de mediciones de gravedad absoluta (Kearey et al.,
2002).
Corrección por Latitud
La corrección por latitud usualmente se hace por la sustracción de la gravedad
normal, calculada de la International Gravity Formula (IGF), a la gravedad observada o
absoluta (Milsom, 2003).
La gravedad varía con la latitud porque la forma de la Tierra no es esférica y la
velocidad de un punto sobre la superficie de la Tierra decrece de un máximo en el ecuador
a cero en los polos.
La fórmula de Clairaut relaciona la gravedad con la latitud sobre el esferoide de
referencia de acuerdo a la siguiente ecuación:
109
donde,
es el valor predicho de la gravedad a una latitud ,
es el valor de
gravedad en el ecuador y ,
son constantes dependientes de la forma y velocidad de
rotación de la Tierra. La ecuación anterior es una aproximación de una serie infinita. Los
valores de
,
y
actuales los define la IGF 1967 (
. Antes de 1967 las constantes menos precisas
fueron empleadas en el International Gravity Formula (1930). Los resultados deducidos
utilizando la formula anterior deben ser modificados antes de su incorporación dentro del
estudio gravimétrico usando la IGF 1967 por el uso de la relación:
Una alternativa, de representación más precisa de la IGF 1967 (Mittermayer 1969),
en la cual las constantes son ajustadas con el fin de minimizar los errores resultantes del
truncamiento de las series, es:
El valor
nos da el valor predicho de gravedad al nivel del mar de cualquier
punto sobre la superficie de la Tierra y es sustraído de la gravedad observada para corregir
la variación por latitud.
Corrección de Aire Libre
La corrección de aire libre (Free Air) corrige la reducción de gravedad con la altura
en aire libre resultado del aumento en distancia del centro de la Tierra, acorde con la Ley
de Newton. Esta corrección no toma en cuenta la atracción de ningún material situado por
encima del nivel del mar (Kearey et al., 2002). Para reducir al datum una observación
tomada a una altura h, es como sigue:
El valor que resulta de sustraer el valor de gravedad normal a la observada se
debe, en parte, a la altura de la estación de gravedad por encima de la superficie de
referencia. Un incremento en la altura de la estación implica un incremento en la distancia
del centro de masa de la Tierra, entonces el efecto es negativo para las estaciones por
encima del nivel del mar. La corrección de aire libre es por tanto positiva (Milsom, 2003).
Esta corrección generalmente se asocia con la elevación por encima del geoide
(nivel del mar) y no a la altura del elipsoide, en este caso Heiskanen y Moritz (1969) dan la
110
fórmula de aproximación de segundo orden para la corrección de la gravedad teórica para
la altura h en metros, relativa al elipsoide, donde:
donde los valores de parámetros para el elipsoide GRS80 son los siguientes:
Para el elipsoide GRS80 la fórmula de segundo orden es:
donde la altura del elipsoide h es en metros y
es en mGal.
Corrección de Bouguer
Las masas topográficas son distribuidas irregularmente y sus efectos son difíciles
para calcular con precisión pero su aproximación es necesaria. Esta corrección considera
la atracción gravitacional del material rocoso situado entre la estación situada a una altura
h y el datum utilizado, en este caso, el elipsoide.
Esta corrección, gBC tradicionalmente se calcula asumiendo que entre la estación
de gravedad y el datum vertical hay un slab infinito, entonces
donde
densidad del slab horizontal en
elipsoide o nivel de referencia.
(Mohr y Taylor, 2001), ρ es la
y h es la altura de la estación en metros relativa al
Para evitar el efecto de la curvatura de la Tierra, la fórmula de LaFehr (1991) es
recomendada. De acuerdo a LaFehr (1991) la selección de una capa esférica de radio 166.7
km minimiza: “las diferencias entre el efecto de la capa y la de un slab horizontal infinito
para un rango significativo de elevaciones.”
111
La elección de densidad de 2 670 kg /m3 para material de la tierra sólida por
encima o debajo del elipsoide está basado sobre la densidad promedio de la Tierra
(Chapin, 1996; Hinze, 2003). En algunos casos, el valor de la densidad dependerá de la
región y del área de estudio, utilizando otro tipo de métodos que permitan determinar la
densidad.
El enfoque más simple asume que la topografía puede ser representada por una
placa plana extendiéndose hacia el infinito en todas direcciones, con una densidad
constante y un espesor igual a la altura de la estación de gravedad por encima de la
superficie de referencia. Las montañas que sobresalen de esta superficie horizontal
imaginaria, y los valles que quedan por debajo falsean esta hipótesis, pero su efecto
gravitatorio se compensa por la corrección topográfica subsiguiente.
Las correcciones de Bouguer dependen de las densidades asumidas así como de las
alturas medidas, por lo que son diferentes de las correcciones de aire libre, la combinación
de los dos dentro de correcciones de elevación unificadas puede ser engañosa.
En la figura A.1, el efecto de la masa M registrada en el punto de observación P no
es alterada por estas correcciones. Se mantiene el efecto del cuerpo a una distancia 2h
por debajo de P, no en el punto P’ a una distancia h por debajo de él. Las correcciones no
eliminan misteriosamente el efecto de la masa m, por encima de la superficie de
referencia, ya que la corrección de Bouguer asume una densidad constante. La gravedad
de Bouguer es determinada en los puntos donde las mediciones fueron hechas (Milsom,
2003).
Figura A.1. Esquematización de las correcciones gravimétricas utilizadas para eliminar el
efecto de las desviaciones de la topografía de una superficie paralela a un datum de
referencia. La referencia de la estación de gravedad indica si el efecto se suma o se resta
(tomado de Milsom, 2003).
112
Corrección por Terreno
Las correcciones topográficas detalladas son necesarias cuando el trabajo se
encuentra en áreas de relieve alto. Aunque es posible corregir directamente la topografía
entera por encima de la superficie de referencia en un solo paso, sin hacer primero la
corrección de Bouguer, es más simple calcular la gravedad de Bouguer y luego corregir las
variaciones de la placa de Bouguer (Milsom, 2003).
Una peculiaridad de haber dos etapas es que las correcciones de segunda etapa
son siempre positivas. En la Figura A.1, la masa topográfica “A” por encima de la estación
de gravedad ejerce un tirón hacia arriba sobre el gravímetro, el efecto es negativo y la
corrección es positiva. El valle “B”, por otro lado, ocupa una región que la corrección de
Bouguer asume relleno de roca que ejerce un tirón gravitacional hacia abajo. Esta roca no
existe. La corrección por terreno debe compensar un exceso de corrección por la placa de
Bouguer y de nuevo es positiva.
Clásicamente, las correcciones por terreno son realizadas usando una malla
circular conocida como gráfico de Hammer (Figura A.2), ésta es transparente y está
dividida por líneas concéntricas y radiales (Hammer, 1939). La zona más externa se
extiende casi 22 km, más allá de este radio se considera que los efectos topográficos
generalmente son insignificantes. La malla se coloca sobre un mapa topográfico, con el
centro sobre la estación de gravedad, de esta forma se facilita estimar el promedio de
elevación topográfica en cada área (Figura A.2), la elevación de la estación de gravedad es
sustraída de estos valores, y el efecto gravitacional de cada compartimiento se determina
por referencia a tablas construidas usando la fórmula para el efecto gravitacional de un
sector de un cilindro vertical en su eje. La corrección por terreno es la suma de las
contribuciones gravitacionales de todas las áreas (Kearey et al., 2002).
Los efectos de terreno son bajos en áreas con topografía suave y raramente
exceden 1 mGal en áreas muy planas. En áreas de topografía abrupta los efectos de
terreno son considerablemente más grandes, están en un máximo en valles con laderas
escarpadas, en la base o parte superior de acantilados y en las cumbres de las montañas
(Kearey et al., 2002, Hammer, 1982). Las correcciones pueden ser extremadamente
tediosas y se requiere de una gran cantidad de tiempo para la reducción de gravedad,
además de que incrementa el costo en un estudio gravimétrico, por ello, es importante
evaluar si se requiere o no hacer esta corrección. Actualmente, este proceso puede
simplificarse con el uso de programas automatizados para la realización de esta
corrección, los cuales sólo requieren de modelos digitales de elevación (MDE), los cuales
113
en su mayoría se encuentran disponibles para distintas regiones, con ello se reduce
tiempo y costo en dicha corrección.
Figura A.2. Gráfico de Hammer (zonas E a I) sobrepuesto con un mapa topográfico. Las
dificultades en la estimación de alturas promedio en las áreas más grandes son
fácilmente apreciables (tomado de Milsom, 2003).
Los gravímetros responden únicamente a la componente vertical de la atracción
gravitacional de la Tierra sobre una masa anómala. Considerando el efecto de una masa
anómala δg, con componentes horizontal y vertical δgx y δgz, respectivamente, sobre el
campo de gravedad g y su representación sobre un diagrama (Figura A.3) (Kearey et al.,
2002).
114
Figura A.3. Relación entre el campo gravitacional y las componentes de la anomalía
gravimétrica de una masa pequeña (tomado de Kearey et al., 2002).
Al resolver las fuerzas dadas queda:
Los términos en δ2 son muy pequeños y por tanto pueden ser ignorados, por lo
que la expansión binomial de la ecuación queda como:
por lo que,
de esta manera, las perturbaciones en gravedad efectivamente corresponden a la
componente vertical de la atracción del cuerpo o masa anómala. La desviación local del
ángulo vertical
está dado por (Kearey et al., 2002):
115
donde
es usualmente insignificante.
Aplicaciones del método gravimétrico
El método gravimétrico puede tener diversas aplicaciones en conjunto con la Geología,
Tectónica, Hidrogeología, Arqueología, Geotecnia e Ingeniería, Geodesia y otras ramas de
la Geofísica (Cantos, 1974; Reynolds, 1997; Udías, 1997). Dicho método permite, por
ejemplo, delinear características mayores de la superficie terrestre, estudiar zonas de
sutura, revelar anomalías debido a intrusiones ígneas (ej. Bott et al., 1958), determinar la
geometría de acuíferos potenciales (ej. Van Overmeeren, 1975), estudiar el movimiento
temporal de agua subterránea, localización de cuencas sedimentarias, detección de
edificios enterrados, tumbas y otros artefactos, localización de cavidades (técnicas
microgravimétricas, ej. Arzi, 1975) entre otros.
Por otro lado, en aplicaciones comerciales, el método es raramente usado en
exploración de reconocimiento, debido a que éste es relativamente lento para su
ejecución, y por tanto, más caro debido a la necesidad de elevaciones determinadas
correctamente y lo largo del procedimiento de reducción.
Un desarrollo reciente importante, en estudios gravimétricos, es el diseño de
instrumentos portátiles capaces de medir gravedad absoluta con alta precisión. Aunque su
costo es alto, es posible utilizarlos para investigar movimientos de masa a gran escala en
el interior de la Tierra, así como para estudiar variaciones cíclicas pequeñas asociadas con
fenómenos neotectónicos, tales como sismos y levantamientos postglaciales (Kearey et
al., 2002). El método fue usado extensivamente por la industria del petróleo para la
localización de posibles trampas de hidrocarburos, pero con la evolución tecnológica y la
mejora de la eficiencia de los estudios sísmicos, fue desechada. Sin embargo, la
descripción del método gravimétrico permite conocer la utilidad que se le da a estudios de
pequeña, mediana y gran escala, así como de conocer la importancia de los estudios
gravitacionales (gravedad relativa y absoluta).
116
Tabla A.1 Densidades de rocas comunes y minerales1 (tomado de Milsom, 2003).
3
3
Rocas comunes
(Mg / m )
Minerales
(Mg / m )
Arena seca
1.4 – 1.65
Esfalerita
3.8 – 4.2
Serpentinita
2.5 – 2.6
Galena
7.3 – 7.7
Arena húmeda
1.95 – 2.05
Calcopirita
4.1 – 4.3
Gneiss
2.65 – 2.75
Cromita
4.5 – 4.8
Carbón
1.2 – 1.5
Pirrotita
4.4 – 4.7
Granito
2.5 – 2.7
Hematita
5.0 – 5.2
yeso
1.9 – 2.1
Pirita
4.9 – 5.2
Dolerita
2.5 – 3.1
Magnetita
5.1 – 5.3
Sal
2.1 – 2.4
Basalto
2.7 – 3.1
Caliza
2.6 - 2.7
Gabro
2.7 – 3.3
Cuarcita
2.6 – 2.7
Peridotita
3.1 – 3.4
ASPECTOS GENERALES DEL MÉTODO MAGNÉTICO
Un polo magnético aislado, si existiera, produciría un campo que obedece la ley del
cuadrado inverso, pero en la realidad, la fuente magnética fundamental es el dipolo, pero
una línea de dipolos extremo a extremo produce el mismo efecto que los polos positivo y
negativo aislados en extremos opuestos de la línea (Milsom, 2003). Dado que un dipolo
colocado en un campo magnético tiende a rotar, se dice que tiene momento magnético.
La magnetización de un cuerpo sólido es definido por su momento magnético por unidad
de volumen y es un vector que tiene dirección y magnitud (Milsom, 2003).
IGRF (International Geomagnetic Reference Field)
El IGRF fue introducido por la IAGA (International Association of Geomagnetism
and Aeronomy) en 1968 en respuesta a la necesidad de una representación armónica
esférica estándar del campo principal de la Tierra. El modelo es actualizado cada 5 años
sobre la base de observaciones de observatorios fijos. También es revisada
retrospectivamente para dar un modelo definitivo (DGRF), el modelo más reciente es de
117
generación 11, producido y publicado por el grupo de trabajo V-MOD, de la IAGA, en
diciembre de 2009.
Las variaciones del campo magnético principal de la Tierra con la latitud, longitud y
tiempo son descritas por ecuaciones determinadas experimentalmente por el IGRF
(International Geomagnetic Reference Field) definidos por 120 coeficientes numéricos de
series armónicas esféricas, de orden N=10, complementado por un modelo de variación
secular predictivo de orden N=8. Para fechas entre las épocas de los modelos, los valores
de los coeficientes son dados por interpolación lineal. La fórmula es considerablemente
más compleja que la fórmula de Gravedad equivalente a la corrección de Latitud, debido
al gran número de armónicos que se emplean (Barraclough y Malin 1971, Peddie 1983).
En estudios magnéticos, el IGRF es usado para eliminar de los datos magnéticos
aquellas variaciones magnéticas atribuibles al campo teórico (Kearey et al., 2002). Este
proporciona representaciones razonables de los campos regionales actuales en áreas bien
estudiadas, las cuales pueden utilizarse para calcular correcciones regionales. Al hacer uso
de los modelos, para evitar ambigüedades, se debe indicar que generación IGRF se está
usando.
Variaciones seculares
El campo geomagnético no puede resultar de un magnetismo permanente en el
interior de la Tierra. Se requieren momentos magnéticos dipolares mucho más grandes
que los reales y la prevalencia de temperaturas más altas que excedan el punto de
temperatura de Curie de cualquier material magnético conocido. La causa de este campo
se atribuye a la acción de dinamo, producido por la circulación de partículas cargadas en
celdas convectivas acopladas dentro del núcleo externo líquido de la Tierra (Kearey et al.,
2002).
El intercambio de dominios entre tales celdas se cree que producen cambios
periódicos en la polaridad del campo geomagnético revelado en estudios
paleomagnéticos. Los patrones de circulación dentro del núcleo no son fijos y cambian
lentamente con el tiempo. Esto se refleja en un cambio lento, progresivo y temporal en
todos los elementos geomagnéticos conocido como variación secular. Tal variación es
predecible y un ejemplo bien conocido es la rotación gradual del polo norte magnético
alrededor del polo norte geográfico (Kearey et al., 2002).
118
Variaciones diurnas
El campo magnético de la Tierra también varía debido a los cambios en la fuerza y
dirección de las corrientes que circulan en la ionosfera. En el patrón normal SQ (solarquiet), el campo es casi constante durante la noche pero decrece entre el amanecer y
cerca de las 11 a.m., luego incrementa de nuevo hasta las 4 p.m. y entonces disminuye
hasta el valor de la noche (Figura A.4), esto se conoce como variación diurna (Milsom,
2003).
Figura A.4. Variación del Campo magnético típico en un “día quieto” a latitudes medias.
Tormentas magnéticas
Los efectos aurorales a corto plazo son casos especiales de perturbaciones
irregulares conocidas como tormentas magnéticas. Estas son producidas por las manchas
y erupciones solares, a pesar de su nombre, no son meteorológicas, a menudo ocurren en
días claros y despejados. Generalmente son de inicio rápido, durante la cual el campo
magnético puede cambiar por cientos de nT, seguidos por un regreso lento e inconstante
a la normalidad. Las escalas de tiempo varían ampliamente pero los efectos pueden
persistir por horas y algunos días. Los datos aeromagnéticos se ven afectados por
irregularidades muy pequeñas, para dichos propósitos las tormentas magnéticas pueden
ser definidas, algunas veces, como desviaciones de la linealidad en la curva diurna de
aproximadamente 2 nT/hora (Milsom, 2003).
Variaciones magnéticas locales
Los puntos de Curie para materiales magnéticos geológicamente importantes
están en un rango 500-600 °C. Tales temperaturas son alcanzadas en la parte inferior de la
corteza continental pero por debajo del Moho bajo los océanos. El manto superior es
119
débilmente magnético, de modo que la base efectiva de las fuentes magnéticas locales es
la isoterma Curie por debajo de continentes y del Moho en los océanos (Milsom, 2003).
Los depósitos de magnetita masivos pueden producir campos magnéticos de
aproximadamente 200 000 nT, la cual es muchas veces la magnitud del campo normal de
la Tierra. Las anomalías de este tamaño son inusuales, pero tanto en diques, como en
flujos de basalto y algunas intrusiones grandes pueden producir campos de miles, y
ocasionalmente decenas de miles de nT. Los campos de anomalías de más de 1000 nT por
otra parte son raros, incluso en áreas de afloramiento de basamento cristalino. Las rocas
sedimentarias generalmente producen cambios de menos de 10 nT, al igual que los
cambios en la magnetización del suelo importante en la arqueología (Milsom, 2003).
Aplicaciones del método magnético
Los estudios magnéticos son una técnica rápida y rentable, representa una de las
técnicas geofísicas ampliamente usadas en términos de la longitud de líneas estudiadas
(Paterson y Reeves, 1985). El método magnético tiene un amplio rango de aplicaciones,
por ejemplo puede aplicarse en investigaciones geotécnicas y arqueológicas, o incluso
puede ser usado para delinear zonas de fallamiento y localizar características metálicas
enterradas hechas por el hombre, tales como tuberías, trabajos de minas viejas y edificios.
(Cantos, 1974; Reynolds, 1997; Udías et al., 1997) Este método generalmente se usa en la
búsqueda de depósitos minerales metalíferos, como técnica de reconocimiento de mapeo
geológico para delinear límites geológicos (Kearey et al., 2002).
La magnetometría también se usa en investigaciones regionales de la corteza a
gran escala, aunque las fuentes de anomalías magnéticas mayores tienden a restringirse a
rocas de composición básica o ultrabásica. La contribución de este método en áreas
oceánicas también ha tenido una influencia profunda sobre el desarrollo de la teoría de
las placas tectónicas (Kearey y Vine, 1996), y una visión sobre la formación de la litósfera
oceánica.
Otra aplicación son los estudios marinos, los más recientes han mostrado que la
corteza oceánica es caracterizada por un patrón de anomalías magnéticas lineales,
representadas como tiras de corteza oceánica magnetizadas alternadamente en la
dirección normal e inversa (Mason y Raff, 1961).
120
Tabla A.2. Susceptibilidades de rocas y minerales comunes (SI).
Rocas comunes
Minerales
Pizarra
0 – 0.002
Hematita
0.001 – 0.0001
Dolerita
0.01 – 0.15
Magnetita
0.1 – 20.0
Diorita
0.0005 – 0.001
Cromita
0.0075 – 1.5
Basalto
0.001 – 0.1
Pirrotita
0.001 – 1.0
Granulita
0.0001 – 0.05
Pirita
0.01 – 0.005
Riolita
0.00025 – 0.01
Sal
0.0 – 0.001
Gabro
0.001 – 0.1
Caliza
0.00001– 0.0001
121
ANEXO B
TÉCNICA UTILIZADA POR EL PROGRAMA OASIS MONTAJ (GEOSOFT INC., 2007)
PARA CALCULAR LA CORRECCIÓN TOPOGRÁFICA
Para calcular la corrección por terreno, se utilizó el programa Oasis montaj (Geosoft Inc., 2007),
éste muestrea los datos del MDE local en un grid uniforme y centrado en cada una de las
estaciones existentes (Figura A1).
Figura A1. Grid utilizado por el programa Oasis montaj para realizar la corrección topográfica
Para calcular las correcciones locales, los datos del MDE local son muestreados por un grid
centrado sobre cada una de las estaciones que serán calculadas. La corrección es calculada y se
basa en una zona cerca, intermedia y las contribuciones de una zona lejana.
122
Zona 0: Triángulo
En la zona cercana (Zona 0, de 0 a 1 celda de la estación), el algoritmo suma los efectos de cuatro
gradientes de secciones triangulares, las cuales describen una superficie entre la estación de
gravedad y la elevación de cada esquina diagonal.
La fórmula utilizada por Kane (1962) es la siguiente:
Figura A2. Atracción gravitacional de un
triángulo, utilizado para la zona 0.
Zona 1: Prisma
Para la zona intermedia (Zona 1, 1 a 8 celdas de la estación), el efecto del terreno es calculado
para cada punto utilizando un prisma rectangular empleado por Nagy (1966), con la siguiente
fórmula:
Figura A3. Atracción gravitatoria de un prisma rectangular para la zona intermedia.
123
Zona 2: Anillo seccional
En la zona lejana (Zona 2, más allá de 8 celdas), el efecto del terreno se basa en la aproximación
del segmento de un anillo seccional a un prisma cuadrado, descrito por Kane (1962).
donde,
Figura A4. Atracción gravitacional para
un anillo seccional, usado en la zona 2.
124
ANEXO C
PROCEDIMIENTO UTILIZADO PARA LA APLICACIÓN DE FILTROS POR EL
PROGRAMA OASIS MONTAJ (GEOSOFT INC., 2007).
Los mapas generados de anomalías gravimétrica y magnética se encuentran en el
dominio del espacio, para poder aplicar cualquier filtro a los datos es necesario pasar
los mapas al dominio del número de ondas, por medio de la transformada de Fourier.
Esta transformada se realizó por medio de la aplicación MAGMAP Filtering del
programa Oasis montaj (Geosoft Inc., 2007) la cual realiza los siguientes pasos:
1) Pre-procesamiento: Se prepara el grid original, expandiéndolo y
rellenando el grid a un cuadrado.
2) Transfomada de Fourier: Se transforma el grid pre-procesado del
dominio del espacio al dominio de frecuencia.
3) Aplicación del filtro: Se escoge el filtro que se quiere aplicar al grid en
el dominio de frecuencia.
4) Transformada inversa de Fourier: El grid filtrado en el dominio de
frecuencia es transformado nuevamente al dominio del espacio.
5) Post-procesamiento: Restaura los datos del grid filtrado, al mismo
tamaño y forma que el grid original.
125
ANEXO D
INFORMACIÓN LITOLÓGICA DE POZOS CERCA DEL ÁREA DE ESTUDIO
PROPORCIONADA POR LA COMISIÓN ESTATAL DE AGUAS (CEA)
En la construcción de los modelos geológico-geofísicos consideramos cortes
litológicos de tres pozos localizados en zonas cercanas al área de estudio. A
continuación se muestra su ubicación y descripción de los cortes litológicos:
RELACIÓN DE POZOS ZONA MUNICIPIOS JALPAN Y LANDA DE MATAMOROS
COORDENADAS
GEOGRÁFICAS
LAT.N
LONG. W
PROFUNDIDAD
(m)
NIVEL
ESTATICO
(m)
99°19’12.8’’
123
97
21°14’03’’
99°17’10’’
283
---
Presidencia Municipal
Landa de Matamoros
FIRCO (1992)
21°13’41’’
99°17’30’’
150
---
FIRCO (1992)
No.
NOMBRE
DEL POZO
1
La Lagunita
21°11’00’’
2
Encino Solo
3
Palo Verde
OBSERVACIONES
CORTE LITOLÓGICO POZ O LAGUNITA, LANDA DE MATAMOROS
DE
A
DESCRIPCIÓN
0.00
18.00
Boleo de Calizas
III
18.00
21.00
Caliza con Arcilla
II
21.00
75.00
Caliza muy Fracturada
II
75.00
84.00
Caliza Fracturada con Arcilla
II
84.00
105.00
Caliza Fracturada color gris claro
II
105.00
111.00
Caliza fracturada con empaque arcilloso
II
111.00
123.00
Caliza Fracturada
II
Clasifico: Ing. Ignacio Barrón Medellín
TIPO DE
MATERIAL
26 de marzo de 2003.
126
POZO ENCINO SOLO No. 1
MUNICIPIO DE LANDA DE MATAMOROS
FIDEICOMISO DE RIESGO COMPARTIDO
CORTE LITOLÓGICO
QUERÉTARO, QRO., A DICIEMBRE DE 1992
127
POZO PALO VERDE No. 1
MUNICIPIO DE LANDA DE MATAMOROS
FIDEICOMISO DE RIESGO COMPARTIDO
CORTE LITOLÓGICO
QUERÉTARO, QRO., A DICIEMBRE DE 1992
128