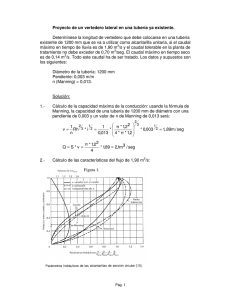
VAVA - Universidad Central del Ecuador

UNIVERSIDAD CENTRAL DEL ECUADOR
FACULTAD DE INGENIERÍA EN CIENCIAS FÍSICAS Y MATEMÁTICA
CARRERA DE INGENIERÍA CIVIL.
“DETERMINACION DEL COEFICIENTE DE RUGOSIDAD INTERNA DE LA
TUBERIA DE POLIETILENO DE ALTA DENSIDAD-RECICLADA PARA
ALCANTARILLADO DE DIAMETROS DE 100mm, 200mm, 250mm”
TRABAJO DE GRADUACIÓN PREVIO A LA OBTENCIÓN DEL TITULO DE
INGENIERO CIVIL.
AUTOR:
CHIPANTASIG CHIPANTASHI RENE RAFAEL
TUTOR:
ING. ERNESTO MARDOQUEO ORTIZ ARCINIEGA. M. Sc
QUITO - ECUADOR
2015
DEDICATORIA
A mi DIOS por el amor, la fe y esperanza en todos estos años, gracias por
toda la misericordia y perdón mostrada en mí.
A mis padres Isabel y Daniel, por haberme apoyado en todo momento, con
sus consejos, sus valores, sobre todo por su amor, a mis hermanos
especialmente a Jorge por su apoyo incondicional.
A Dolores por su sincera, noble y generosa amistad y amor atesorado en
todo este tiempo, quien me ha compartido su vida haciendo de los años
universitarios más ligeros y radiantes.
A Kerly y Landy que son el principal motor de mi vida.
A todos ellos por su apoyo y entrega incondicional, en los momentos difíciles
y supieron darme un aliento de esperanza.
ii
AGRADECIMIENTO
Al único y sabio DIOS, por darme el más grande regalo, la vida. Por su
incansable amor y perdón, quien ha sido mi compañero en el caminar diario y
me ha permitido cumplir una de mis más preciadas metas.
A mi mamita Chavelita, por su amor y paciencia, su ejemplo de esfuerzo y
constancia me han llevado a seguir incansablemente mis ideales, gracias por
sus sabios consejos, por el tiempo invertido y la esencia de su vida
entregada a sus hijos lleno de cariño y atención de forma incondicional, te
quiero mami.
A mi papa, gracias a sus consejos, cariño, esfuerzo diario y apoyo
incondicional.
A mi director de tesis Ing. Ernesto Ortiz M. Sc, por su constante y valiosa
colaboración en este trabajo, por ser un ejemplo de profesional y ante todo
por su calidad de persona. De igual forma al Ing. Efrén Ortiz por su amable
acogida y por haber depositado su confianza en mí.
A mi querida Universidad Central del Ecuador por acogerme en sus aulas,
siendo el testigo silencioso de mi crecimiento y a mis maestros mentores
quienes sembraron en mí el deseo vehemente por hacer de esta hermosa
profesión una fuente de servicio hacia la sociedad.
A mis compañeros y amigos con los cuales he compartido los esfuerzos y
logros a lo largo de mi carrera.
RENE R. CHIPANTASIG CH.
iii
AUTORIZACIÓN DE LA AUTORÍA INTELECTUAL
Yo, CHIPANTASIG CHIPANTASHI RENE RAFAEL en calidad de autor de la
tesis
realizada
sobre
“DETERMINACIÓN
DEL
COEFICIENTE
DE
RUGOSIDAD INTERNA DE LA TUBERIA DE POLIETILENO DE ALTA
DENSIDAD-RECICLADA PARA ALCANTARILLADO DE DIAMETROS DE
100mm, 200mm, 250mm”, por la presente autorizo a la UNIVERSIDAD
CENTRAL DEL ECUADOR, hacer uso de todos los contenidos que me
pertenecen o de parte de los que contienen esta obra, con fines
estrictamente académicos o de investigación.
Los derechos que como autor me corresponden, con excepción de la
presente autorización, seguirán vigentes a mi favor, de conformidad con lo
establecido en los artículos 5, 6, 8, 19 y demás pertinentes de la Ley de
Propiedad Intelectual y su Reglamento.
Quito, DM. 23 de Septiembre de 2014
CHIPANTASIG CHIPANTASHI RENE RAFAEL
FIRMA:
C.C. 1719069872
iv
CERTIFICACIÓN
En calidad de Tutor del proyecto de investigación:
“DETERMINACION DEL COEFICIENTE DE RUGOSIDAD INTERNA DE LA
TUBERIA DE POLIETILENO DE ALTA DENSIDAD-RECICLADA PARA
ALCANTARILLADO DE DIAMETROS DE 100 mm, 200 mm, 250 mm ”,
presentado y desarrollado por el señor CHIPANTASIG
CHIPANTASHI
RENE RAFAEL, previo a la obtención del Título de Ingeniero Civil, considero
que el proyecto reúne los requisitos necesarios.
En la ciudad de Quito, a los 23 días del mes de Septiembre del 2014.
Ing. Ernesto Ortiz. M. Sc
PROFESOR TUTOR
v
INFORME DEL TRABAJO DE APROBACION DEL TRABAJO
DE GRADUACION
TESIS: “DETERMINACION DEL COEFICIENTE DE RUGOSIDAD INTERNA
DE LA TUBERIA DE POLIETILENO DE ALTA DENSIDAD-RECICLADA
PARA ALCANTARILLADO DE DIAMETROS DE 100 mm, 200 mm, 250 mm”.
TUTOR: Ing. Ernesto Ortiz A.
1.- Antecedentes
Mediante Oficio FI-DCIC-2013-1044 del 29 de octubre de 2013, el Director de
la Carrera de Ingeniería Civil autoriza la correspondiente denuncia de tesis
“DETERMINACION DEL COEFICIENTE DE RUGOSIDAD INTERNA DE LA
TUBERIA DE POLIETILENO DE ALTA DENSIDAD-RECICLADA PARA
ALCANTARILLADO DE DIAMETROS DE 100 mm, 200 mm, 250mm”,
presentado por el señor : CHIPANTASIG CHIPANTASHI RENE RAFAEL,
solicitando al ingeniero ERNESTO ORTIZ A. en calidad de Tutor se sirva
analizar, dirigir y orientar; y, a su vez, emitir el presente informe tomando en
cuenta las sugerencias realizadas por los miembros de la comisión para la
elaboración del trabajo de graduación.
2.- Desarrollo de la tesis
 En el Capítulo 1 se hace referencia a los antecedentes, necesidades y
justificación para dotar al Laboratorio de Hidráulica de un equipo semiautónomo, que tiene como objetivo principal la investigación técnica,
así como la realización de prácticas estudiantiles. Una vez identificada
las necesidades existentes en el Laboratorio de Hidráulica se
seleccionó un equipo lo más autónomo posible para el desarrollo de la
vi
determinación del coeficiente de rugosidad interna de tuberías de
polietileno de alta densidad, fabricadas de materiales reciclados.
 En el Capítulo 2 se analizan las características, propiedades y
particularidades de la rugosidad de las paredes internas de tuberías
de polietileno transportando agua limpia que será nuestro elemento de
estudio. Luego se recopila toda la información necesaria sobre el tema
del flujo en tuberías a gravedad y a presión..
 En el Capítulo 3, se realiza la descripción del equipo, indicando las
generalidades sobre la construcción e instalación del mismo.
Se hace mención de los materiales que se utilizó en cada uno de los
elementos que forman parte del equipo con su respectiva justificación.
Además se detalla la construcción del equipo en sus diferentes etapas
así como su calibración.
En este mismo capítulo se describe el procedimiento de realización
de los ensayos de laboratorio para la determinación de los caudales,
pendientes longitudinales y el calado de flujo en las tuberías de 100
mm,150 mm y 250mm de diámetro.
Por otra parte se detalla la preparación del equipo, la medición y toma
de datos.
 En el Capítulo 4, se realizan los cálculos y análisis de los resultados,
experimentales, describiendo los diferentes ensayos de laboratorio
para loas diferentes relaciones de influencia entre los parámetros
hidráulicos y del geométrico.
 En el Capítulo 5, se realiza propiamente la determinación del
coeficiente
interno
de
rugosidad
con
la
metodología
y
las
justificaciones de las relaciones caudal, profundidad y coeficiente de
rugosidad.
 En el Capítulo 6, se describen las conclusiones y recomendaciones
pertinentes acerca del proceso mismo de los ensayos realizados y las
propuestas para trabajos experimentales con fines vinculados a la
producción.
vii
3.- Conclusiones sobre el trabajo de graduación.
 El equipo diseñado y construido para el Laboratorio de Hidráulica
cumplió con las expectativas propuestas inicialmente, por lo tanto este
equipo semi-autónomo, sirve para investigaciones relacionadas
a
procesos de producción con tuberías de diferentes materiales. Se
recibió y se encuentra en perfecto funcionamiento y a disposición del
Laboratorio de Hidráulica para futuros trabajos experimentales,
requiriéndose únicamente de instrumentos
de medición de última
generación que el laboratorio no dispone, pese a que se ha insistido
en su adquisición y así también para la realización de
prácticas
estudiantiles.
En virtud a lo manifestado anteriormente, todas las actividades desarrolladas
han sido satisfactorias y los resultados obtenidos en el transcurso del
desarrollo de la tesis son los esperados.
Por consiguiente emito mi aprobación a este trabajo de graduación y
recomiendo proseguir con el trámite respectivo hasta la graduación del señor
Chipantasig Chipantashi René Rafael.
.En la ciudad de Quito, a los 23 días del mes de septiembre del 2014
Ing. Ernesto Ortiz A M.Sc.
TUTOR
viii
HOJA DE CALIFICACIÓN DE LOS MIEMBROS DEL TRIBUNAL
ix
CONTENIDO
DEDICATORIA .............................................................................................. ii
AGRADECIMIENTO ..................................................................................... iii
AUTORIZACIÓN DE LA AUTORÍA INTELECTUAL .................................... iv
CERTIFICACIÓN........................................................................................... v
INFORME DEL TRABAJO DE APROBACION DEL TRABAJO DE
GRADUACION ............................................................................................. vi
HOJA DE CALIFICACIÓN DE LOS MIEMBROS DEL TRIBUNAL .............. ix
CONTENIDO ................................................................................................. x
LISTADO DE TABLAS............................................................................... xiii
LISTADO DE FIGURAS ............................................................................. xiv
LISTADO DE FOTOGRAFÍAS .................................................................... xv
RESUMEN.................................................................................................. xvi
ABSTRACT ............................................................................................... xvii
CAPITULO I .................................................................................................. 1
1. GENERALIDADES .................................................................................... 1
1.1 INTRODUCCIÓN .................................................................................. 1
1.2
ANTECEDENTES............................................................................. 2
1.3 OBJETIVOS DEL ESTUDIO ................................................................. 3
1.3.1 OBJETIVO GENERAL.................................................................... 3
1.3.2 OBJETIVOS ESPECÍFICOS .......................................................... 3
1.4 JUSTIFICACIÓN .................................................................................. 4
1.5
ALCANCE Y METODOLOGÍA .......................................................... 4
1.6 METODOLOGÍA ................................................................................... 5
CAPITULO II ................................................................................................. 6
2. MARCO TEÓRICO .................................................................................... 6
2.1. CONCEPTO DE RUGOSIDAD ............................................................ 6
2.2. RÉGIMEN UNIFORME ........................................................................ 7
2.2.1 ESTABLECIMIENTO DEL FLUJO UNIFORME .............................. 8
2.3 FLUJO UNIFORME A SUPERFICIE LIBRE. ...................................... 10
2.3.1 ECUACIONES DEL FLUJO UNIFORME ...................................... 10
x
2.3.2 ECUACIÓN DE MANNING. .......................................................... 11
2.4 FLUJO EN TUBERÍAS A GRAVEDAD Y PRESIÓN ........................... 12
2.5 RESISTENCIA AL FLUJO .................................................................. 14
2.5.1 ECUACIÓN GENERAL DE RESISTENCIA .................................. 14
2.6 CAPA LÍMITE ..................................................................................... 15
2.6.1 DESARROLLO DE LA CAPA LAMINAR ...................................... 16
2.7 DISTRIBUCIÓN DE VELOCIDADES .................................................. 18
2.8 PARÁMETROS QUE INFLUYEN AL FLUJO ...................................... 26
2.8.1 CONSERVACIÓN DE LA MASA .................................................. 26
2.8.2 CONSERVACIÓN DE LA ENERGÍA ............................................ 27
2.9 CONCEPTO DE PÉRDIDA DE CARGA ............................................. 29
2.9.1 PÉRDIDAS CONTINUAS O POR ROZAMIENTO (HRO2) ............. 30
2.9.2 PÉRDIDAS DE CARGA LOCALES, ACCIDENTALES O
SINGULARES (HLOC) .......................................................................... 31
2.10 FLUJOS EN PRESIÓN VS. FLUJOS CON SUPERFICIE LIBRE ..... 32
2.11 DETERMINACIÓN DEL CAUDAL EN TUBERÍAS A PRESIÓN Y EN
SECCIONES PARCIALMENTE LLENAS ................................................. 33
2.11.1 FÓRMULAS PARA LA DETERMINACIÓN DEL CAUDAL .......... 33
CAPITULO III .............................................................................................. 39
3.
METODOLOGÍA EXPERIMENTAL. ..................................................... 39
3.1 FLUJOS CON SUPERFICIE LIBRE ................................................... 39
3.1.1 DESCRIPCIÓN DEL MODELO DE PRUEBAS ............................ 39
3.1.2 DESCRIPCIÓN DE LOS MEDIDORES ........................................ 41
3.1.3 DESCRIPCIÓN DE LAS PRUEBAS ............................................. 44
3.2 PROCEDIMIENTO EXPERIMENTAL ................................................. 44
3.2.1 ENSAYOS .................................................................................... 46
3.3 MONTAJE PARA PRUEBAS .............................................................. 47
3.4
DESCRIPCIÓN DE LOS ENSAYOS REALIZADOS ....................... 49
3.4.1 RELACIONES GEOMÉTRICAS PARA LA SOLUCIÓN DEL
MODELO FÍSICO. ................................................................................. 52
3.5 MEDICIONES DE CAUDAL, PENDIENTE Y CALADO DEL FLUJO EN
TUBERÍAS DE DIÁMETROS DE 150MM, 200MM, 250MM ..................... 55
xi
CAPITULO IV .............................................................................................. 58
4. ANÁLISIS DE RESULTADOS EXPERIMENTALES. .............................. 58
4.1 RESULTADOS DE FLUJOS CON SUPERFICIE LIBRE ..................... 58
4.1.1. ANÁLISIS DE LA INFLUENCIA DE LA ALTURA DE FLUJO (H) . 58
4.1.2. ANÁLISIS DE LA INFLUENCIA DE LA PENDIENTE
LONGITUDINAL .................................................................................... 59
4.1.3. ANÁLISIS DE LA INFLUENCIA DEL DIÁMETRO ....................... 59
CAPITULO V ............................................................................................... 60
5. DETERMINACIÓN DEL COEFICIENTE DE RUGOSIDAD (N). .............. 60
5.1 ESTABLECIMIENTO DE CRITERIOS DE SELECCIÓN DEL VALOR
DEL COEFICIENTE DE RUGOSIDAD. .................................................... 60
5.1.1. METODOLOGÍA Y JUSTIFICACIÓN ........................................... 60
5.2. RELACIONES ENTRE CAUDAL, PROFUNDIDAD Y COEFICIENTES
DE RUGOSIDAD ENCONTRADOS ......................................................... 61
5.3 DETERMINACIÓN DEL COEFICIENTE DE RUGOSIDAD ................. 63
5.4 DESARROLLO DE LA SOLUCION DEL MODELO MATEMÁTICO DE
FLUJO GRADUALMENTE VARIADO....................................................... 64
5.4.1 MÉTODO DEL PASO FIJO .......................................................... 64
5.5 PROCEDIMIENTO PARA LA CALIBRACIÓN .................................... 66
5.5.1 OBTENCIÓN DE DATOS EXPERIMENTALES ............................ 66
5.5.2 CALCULO DEL PERFIL PARA CADA PENDIENTE Y CAUDAL. . 66
5.5.3 CÁLCULO DEL COEFICIENTE (N) EXPERIMENTAL MANNING
EN CADA TRAMO DE LA TUBERÍA. .................................................... 66
5.5.4 CALCULO DEL COEFICIENTE (N) DE MANNING TEÓRICO EN
CADA TRAMO DE LA TUBERÍA. .......................................................... 66
5.5.5 CALCULO DE LOS INDICADORES DE EFICIENCIA Y ECM ...... 66
5.5.6 GENERACIÓN DE CURVAS (N, EFICIENCIA, ECM) .................. 67
5.5.7 DETERMINACIÓN DEL COEFICIENTE (N) MANNING ............... 67
5.6 CÁLCULOS REALIZADOS ................................................................. 67
5.6.1 CALCULO DEL COEFICIENTE DE MANNING TEÓRICO EN
CADA TRAMO DE LA TUBERÍA. .......................................................... 70
5.6.2 CALCULO DE LOS INDICADORES DE EFICIENCIA Y ECM ...... 71
xii
5.7 GENERACIÓN DE CURVAS (N,EFIENCIA,ECM) Y OBTENCIÓN DEL
COEFICIENTE (N) DE MANNING ÓPTIMO ............................................. 72
5.8 DETERMINACIÓN DEL COEFICIENTE DE RUGOSIDAD (N) DE
MANNING ................................................................................................ 81
5.9 CURVAS PARA EL DISEÑO DE TUBERIAS ..................................... 82
CAPITULO VI .............................................................................................. 84
6. CONCLUSIONES RECOMENDACIONES .............................................. 84
6.1. CONCLUSIONES SOBRE EL VALOR DEL COEFICIENTE DE
RUGOSIDAD OBTENIDO PARA EL DISEÑO .......................................... 84
6.2. RECOMENDACIONES ACERCA DE LA TUBERÍA Y SU MONTAJE 84
6.3. PROPUESTAS PARA ESTUDIOS FUTUROS .................................. 85
BIBLIOGRAFÍA ........................................................................................... 86
ANEXOS ..................................................................................................... 88
LISTADO DE TABLAS
TABLA 3.1 CONDICIONES DE PRUEBA. ……………….………………………..45
TABLA 3.2 DISTANCIA Y ALTURA DE PIEZÓMETROS PARA EL DIAMETRO
DE 200MM LA PENDIENTE DEL 1%..................................................................52
TABLA N° 3.3 VARIABLES ESTABLECIDAS A
PARTIR DEL TIRANTE DE
AGUA MEDIDO EN SISTEMA HIDRÁULICO PARA D=200MM, I= 1% Y
Q= 6.9 L/S. ……………….……………………………………..…….………………55
TABLA N° 5.1 VALORES DE COEFICIENTES (N) DE MANNING
EXPERIMENTALES Y CALCULADOS PARA D=200mm, i=1%, Q=6.9l/s.. ….73
xiii
LISTADO DE FIGURAS
FIGURA. 1.1
ASPECTO DEL COLAPSO DE LA PARED INTERIOR DE LA
TUBERIA. ……………………………………………………………………………….3
FIGURA 2.1 RUGOSIDAD DE UNA TUBERIA……………………………………..7
FIGURA 2.2 FLUJO CON PENDIENTE SUBCRITICA. ………………………..….9
FIGURA 2.3 FLUJO CON PENDIENTE CRITICA. ………………………………...9
FIGURA 2.4 FLUJO CON PENDIENTE SUPERCRITICA. ………………….....…9
FIGURA 2.5 ESQUEMA DE FLUJO UNIFORME A SUPERFICIE LIBRE. …...10
FIGURA 2.6 FLUJO UNIFORME A SUPERFICIE LIBRE. ….…………………....13
FIGURA 2.7 RESISTENCIA AL FLUJO. …………………………….....…………..14
FIGURA 2.8 DESARROLLO CAPA LÍMITE LAMINAR, TURBULENTA Y
SUBCAPA LAMINAR. .……………………………………………………………….17
FIGURA 2.9 DESARROLLO CAPA LÍMITE LAMINAR EN UN CANAL CON UNA
CONDICION DE ENTRADA IDEAL…………………………………………………17
FIGURA
2.10
MOVIMIENTO
EN
UN
CONDUCTO:
A
LAMINAR,
B.
TURBULENTO. ……………………………………………………………………….18
FIGURA 2.11 DISTRIBUCION DE VELOCIDADES SOBRE UNA SUPERFICIE
DE CANAL LISO. …………………………………………………………………….19
FIGURA 2.12 FUNCION DE BLASIUS. ………...………………………………..20
xiv
FIGURA 2.13 CAPA LÍMITE LAMINAR CON LEY DE VELOCIDADES
PARABÓLICA DE SEGUNDO GRADO. …………………………………………..20
FIGURA 2.14 DISTRIBUCIÓN DE VELOCIDADES MEDIAS EN LA CAPA
LIMITE TURBULENTA, SEGÚN PARÁBOLA DE GRADO 1/M (M=7). ………..22
FIGURA 2.15 DEFINICIÓN DEL ESPESOR B DE LA SUBCAPA LAMINAR…23
FIGURA 2.16 COMPORTAMIENTO HIDRÁULICO DEL CONDUCTO. ……….24
FIGURA 2.17 PERDIDAS DE CARGA. ………….…………..………………….….31
FIGURA 2.18 COMPARACION ENTRE FLUJO A PRESION Y GRAVEDAD…33
FIGURA 3.1 CURVA DE DESCARGA DEL VERTEDERO TRIANGULAR DE
MEDIDA DE CAUDALES. ……………………………………………………………40
FIGURA 3.2 VERTEDERO TRIANGULAR. ………….…………………………….41
FIGURA 3.3 TUBO PITOT.…………………………………………………………..43
LISTADO DE FOTOGRAFÍAS
FOTOGRAFÍA N°1 ESTRUCTURA METÁLICA Y TUBERÍA DE POLIETILENO
DE ALTA DENSIDAD RECICLADA MONTADA. ………………………………….48
FOTOGRAFÍA N°2 VERTEDERO, TABLERO PIEZÓMETRO, CERCHA
METÁLICA Y TUBERÍA MONTADA. …………………………………………….…48
FOTOGRAFÍA N°3 TANQUE DONDE DESCARGA EL VERTEDERO Y
DISIPADOR DE ENERGÍA. …………………………………………………………49
xv
RESUMEN
“DETERMINACION DEL COEFICIENTE DE RUGOSIDAD INTERNA DE LA
TUBERIA DE POLIETILENO DE ALTA DENSIDAD-RECICLADA PARA
ALCANTARILLADO DE DIAMETROS DE 100 mm, 200 mm, 250mm”,
El decidir cuál es el valor óptimo del coeficiente de rugosidad (n), es el
objetivo de continuas investigaciones y supone la necesidad de un
conocimiento más profundo de los materiales con los cuales están fabricadas
las tuberías disponibles en este campo, ya que al tener en el pasado un
mercado únicamente con la alternativa de tuberías construidas en hormigón,
se ha generalizado la ejecución de diseños asumiendo el mismo
comportamiento hidráulico para todas las tuberías; esto es usando la
ecuación empírica de Manning, donde se considera un coeficiente de
rugosidad constante y que depende solamente del material de la tubería; las
tuberías de plásticos corrugados, siendo más livianas, con mayor flexibilidad,
de fácil maniobrabilidad y su aptitud de ser instalada en forma mecanizada
para la construcción de sistemas de conducción de agua a sección llena y
parcialmente llena en alcantarillados, sistemas de riego, conducción de
aguas crudas, trasvases, etc. obligando a que se evalúe el real
comportamiento y las condiciones que corresponden al flujo en tuberías con
contornos rugosos.
Debido a esta gran incertidumbre y la posibilidad de calcular este coeficiente,
se pretende a través de este trabajo realizar un modelo físico que permita su
estimación en función de los parámetros más representativos de la ecuación
de Manning.
DESCRIPTORES:
COEFICIENTE DE MANNIG / FLUJO UNIFORME / TUBERIAS CON FLUJO
PARCIALMEMTE LLENA / ALCANTARILLADOS / CAUDAL EN TUBERIAS /
FLUJO GRADUALMENTE VARIADO / PERFILES DE FLUJO EN TUBERIAS
PARCIALMENTE LLENAS.
xvi
ABSTRACT
"DETERMINATION
OF
INTERNAL
ROUGHNESS
COEFFICIENT
POLYETHYLENE PIPE-RECYCLED HIGH DENSITY FOR SEWAGE
DIAMETERS 100 MM, 200 MM, 250 MM"
Deciding what is the optimal value of the roughness coefficient (n) is the
target of ongoing research and implies the need for a deeper understanding
of the materials which are manufactured pipes available in this field
knowledge as to take into last one market only alternative pipeline built in
concrete, widespread implementation of designs assuming the same
behavior for all hydraulic pipes; this is using the empirical equation Manning,
where considered a constant coefficient that depends only roughness and
material of the pipe; plastic corrugated pipes, being lighter, more flexible,
easy maneuverability and its ability to be installed by machine for the
construction of water conveyance systems to section filled and partially filled
in sewers, irrigation systems, driving raw water, water transfers, etc. forcing
the actual behavior and the conditions that correspond to the flow in pipes
with rough edges is evaluated.
Because of this great uncertainty and the possibility of calculating this ratio, it
aims through this work make a physical model to its estimate based on the
most representative parameters of the equation of Manning.
DESCRIPTORS:
RATE MANNIG / UNIFORM FLOW
/ PIPES WITH FULL FLOW
PARCIALMEMTE / SEWER / FLOW IN PIPES / GRADUALLY VARIED
FLOW / FLOW PROFILES PARTIALLY FILLED PIPES.
xvii
CERTIFICACIÓN
Yo, Luis Alexander Ortega Ushiña con C.C. 171963339-6, con el título de
Suficiencia en el Idioma Ingles otorgado por la ESCUELA POLITECNICA
DEL EJERCITO – DEPARTAMENTO DE LENGUAS, certifico que he
traducido y revisado el resumen al idioma ingles de la tesis con el tema:
“DETERMINACION DEL COEFICIENTE DE RUGOSIDAD INTERNA DE LA
TUBERIA DE POLIETILENO DE ALTA DENSIDAD-RECICLADA PARA
ALCANTARILLADO DE DIAMETROS DE 100 mm, 200 mm, 250mm”.
Adjunto mi título que constata mi conocimiento en el idioma inglés.
Es todo cuanto puedo certificar en honor a la verdad.
Quito, 11 de Mayo de 2015
Atentamente,
Luis Alexander Ortega Ushiña
C.C. 171963339-6
xviii
xix
CAPITULO I
1. GENERALIDADES
1.1 INTRODUCCIÓN
El sistema de conducción de agua es una técnica antigua, que realizaron
múltiples civilizaciones y que se perfecciono en la época de los Griegos;
posteriormente en el Imperio Romano.
Hoy en día estas técnicas se siguen ocupando y optimizando especialmente
con el empleo de menos materiales, un claro ejemplo de ello son las grandes
construcciones de redes de alcantarillados con el uso de tuberías de
polietileno, que han facilitado el drenaje de aguas servidas haciendo que los
trabajos se realicen con mayor facilidad y menor tiempo en su instalación
mejorando rendimientos y costos totales.
Poco a poco se ha ido dejando atrás el empleo de tuberías de hormigón
debido a la serie de ventajas que tienen las tuberías de plásticos corrugados,
siendo más livianas, con mayor flexibilidad, de fácil maniobrabilidad y su
aptitud de ser instalada en forma mecanizada (Know, 1978 citado Huaiquivil
2005), para la construcción de sistemas de conducción de agua a sección
llena y parcialmente llena en alcantarillados, sistemas de riego, conducción
de aguas crudas, trasvases, etc. obligando a que se evalúe el real
comportamiento del flujo en estas nuevas tuberías que al momento ya son
utilizadas para la conducción de aguas servidas.
Con el propósito de realizar diseños correctos y confiables de las diversas
redes de alcantarillados para el drenaje de aguas (negras o pluviales)
construidos con tuberías de polietileno de alta densidad-reciclada, es
indispensable contar con el coeficiente de rugosidad de Manning (n) propio
de este material y proceso constructivo.
1
La selección optima de un coeficiente de rugosidad nos ayudará a obtener el
caudal de diseño deseado, ya que un valor alto de “n” es antieconómico y un
bajo valor aumenta el caudal, por lo cual la tubería no tendría la capacidad
hidráulica para dicho flujo (ACPA, 2002).
El decidir cuál es el valor óptimo del coeficiente de rugosidad (n), es el
objetivo de continuas investigaciones y supone la necesidad de un
conocimiento más profundo de los materiales con los cuales están fabricadas
las tuberías disponibles en este campo, ya que al tener en el pasado un
mercado únicamente con la alternativa de tuberías construidas en hormigón,
se ha generalizado la ejecución de diseños asumiendo el mismo
comportamiento hidráulico para todas las tuberías; esto es usando la
ecuación empírica de Manning, donde se considera un coeficiente de
rugosidad constante y que depende solamente del material de la tubería y de
las condiciones que corresponden al flujo en tuberías con contornos rugosos.
Debido a esta gran incertidumbre y la posibilidad de calcular este coeficiente,
se pretende a través de este trabajo realizar un modelo físico que permita su
estimación en función de los parámetros más representativos de la ecuación
de Manning.
1.2 ANTECEDENTES
La tubería de polietileno de alta densidad-reciclada corrugada, es un
conducto cilíndrico y que son consideradas físicamente lisas, para la
conducción de líquidos a superficie libre y pared exterior con perfiles que le
dan resistencia a la compresión, teniendo finalmente un elemento estructural
con doble trabajo mecánico.
Durante el proceso de fabricación de la tubería, la zona debajo del perfil sufre
un “colapso” debido al proceso de enfriamiento del tubo, provocado por la
contracción del aire caliente atrapado al interior del perfil, modificando
2
finalmente la forma del tubo interior al mostrado en la Figura 1.1, donde DN
es el diámetro nominal de la tubería, D1 es el diámetro interior y DC es el
diámetro interior del perfil.
FIG. 1.1 ASPECTO DEL COLAPSO DE LA PARED INTERIOR DE LA TUBERIA
Siendo esas ondulaciones al interior de la tubería las que han provocado que
las paredes interiores no sean lisas y que el valor del coeficiente (n) de
Manning sea determinado, ya que representa las características internas de
la superficie de la tubería, su valor depende del tipo de material, calidad del
acabado y el estado de conservación de la tubería, y que además influye en
los efectos sobre el cálculo hidráulico y finalmente el valor real del tirante de
agua al interior de la tubería.
1.3 OBJETIVOS DEL ESTUDIO
1.3.1 OBJETIVO GENERAL
 Determinar el valor del coeficiente de rugosidad (n) de Manning, para
la tubería de polietileno
de alta densidad – reciclada para
alcantarillado de diámetros diferentes incluyendo la influencia del
diámetro de la tubería, la altura del flujo y de la pendiente de la
tubería, fabricada por la empresa TUBERTOR.
1.3.2 OBJETIVOS ESPECÍFICOS
 Construcción de la instalación experimental (Banco de pruebas).
 Realización de ensayos de flujos con superficie libre.
 Evaluar mediante modelación física el comportamiento del flujo en la
tubería de pared interna corrugada.
3
 Determinar el coeficiente (n) de Manning de la tubería de alcantarillado
TUBERTOR para diámetros internos de 150mm, 200mm y 250mm.
 Establecer criterios para la selección del valor de la rugosidad para
implementación en diseños hidráulicos de tuberías
 Analizar los valores encontrados de la rugosidad para los diámetros
estudiados.
 Motivar a los fabricantes de tuberías para efectuar los estudios
necesarios que actualicen el valor del coeficiente de rugosidad de
Manning para la oferta nacional de tuberías.
1.4 JUSTIFICACIÓN
Existen tuberías de distintos materiales y capaces de trasladar el agua de
forma eficiente, pero la mayor dificultad que presentan en el momento de
hacer un diseño de drenaje o saneamiento, es la correcta selección del
coeficiente de rugosidad de Manning (n) que se emplea en el cálculo
hidráulico y que a lo largo de los últimos años se han realizado muy pocas o
ninguna investigación, en el Ecuador TUBERTOR S.A. fabrica tuberías de
PVC tipo TORTUGA según la norma NTE INEN 2059, y como parte de las
investigaciones realizadas en el Laboratorio de Hidráulica de la Facultad de
Ingeniería, Ciencias Físicas y Matemática de la Universidad Central del
Ecuador, como tema de graduación previo la obtención del título de Ingeniero
Civil se tomó la tarea e invirtió recursos propios del graduado para el análisis
y la determinación del coeficiente (n) de rugosidad interna de esta nueva
tubería fabricada por la empresa TUBERTOR, quienes facilitaron la tubería
necesaria.
1.5 ALCANCE Y METODOLOGÍA
El análisis de los resultados obtenidos en la investigación servirá para
impulsar los avances a la técnica al servicio de los ingenieros, técnicos y
operadores
responsables
del
diseño,
4
construcción,
operación
y
mantenimiento de los sistemas de alcantarillado y saneamiento. Lo cual
permitirá usar parámetros de diseño reales y aprovechar las mejores
características del flujo que se desarrollan en este moderno tipo de
conductos para la optimización del diseño.
1.6 METODOLOGÍA
Los ensayos para la obtención del coeficiente de rugosidad de Manning (n),
se realizaron en el Laboratorio de Investigaciones Hidráulicas.
Para los ensayos se utilizaron 12 metros de tuberías de polietileno de alta
densidad reciclada de 150, 200, 250 milímetro de diámetro interior.
En el Laboratorio se construyó e instaló una plataforma de metálica,
de
diseño especial para colocar diferentes tuberías. (Figura 3.4).
El flujo hacia la tubería de polietileno de alta densidad-reciclada se condujo
mediante el circuito cerrado del laboratorio y mediante una línea de impulsión
regulado por 1 válvula de compuerta, para mantener una carga hidráulica
constante en el tanque de almacenamiento temporal que descarga el flujo
mediante un vertedero triangular de 90°, que se utiliza para medir el caudal,
hacia un recipiente disipador de energía previo al ingreso del agua a la
tubería.
La instalación posee un tablero piezómetrico para la lectura de los niveles de
agua en diferentes secciones de la tubería y así también limnimetros para
medir el calado o altura de agua en cada sección de la tubería.
La modelación se realizó a partir de los datos medidos en laboratorio y
utilizando el Método ECM y eficiencias para establecer los coeficientes más
adecuados a cada modelo.
5
CAPITULO II
2. MARCO TEÓRICO
2.1. CONCEPTO DE RUGOSIDAD
En el interior de los tubos comerciales existen protuberancias
o
irregularidades de diferentes formas y tamaños cuyo valor medio se conoce
como rugosidad absoluta (e), y que puede definirse como la variación media
del radio interno de la tubería. Los experimentos de Nikuradse permitieron
determinar el valor de esta rugosidad absoluta. Consistieron en producir una
rugosidad artificial pegando en el interior de un tubo de vidrio (liso) áridos de
diferentes granulometrías tamizados, es decir, de rugosidad conocida, hasta
conseguir una pérdida de carga igual que la producida en un tubo comercial
de un material determinado con igual longitud y diámetro que el de vidrio.
Un mismo valor de rugosidad absoluta puede ser muy importante en tubos
de pequeño diámetro y ser insignificante en un tubo de gran diámetro, es
decir, la influencia de la rugosidad absoluta depende del tamaño del tubo.
Por ello, para caracterizar un tubo por su rugosidad resulta más adecuado
utilizar la rugosidad relativa (e/D), que se define como el cociente entre la
rugosidad absoluta y el diámetro de la tubería. (citado “La Mecánica de los
Fluidos”. McGraw- -Hill.)
E= e/D
El efecto de rugosidad absoluta sobre el flujo depende de su magnitud y
distribución. La medición directa de estas variables para superficies muy
pulidas requiere equipos de precisión. Pero por medidas indirectas es posible
calcular un valor para la rugosidad absoluta "e" de dimensiones lineales que
tenga en consideración el efecto combinado de la magnitud y distribución de
las irregularidades de la superficie.
Las irregularidades de la superficie generan pequeños remolinos o vórtices.
Cuando la rugosidad absoluta "e" es apreciablemente menor que el espesor
6
de la subcapa laminar , los vórtices son eliminados por la viscosidad dentro
de la subcapa laminar y su efecto desaparece, en caso contrario estos
vórtices alcanzan a sobrepasar la subcapa laminar y contribuir a la formación
de turbulencia. En el primer caso la rugosidad absoluta no ejerce ningún
efecto en la formación de turbulencia y se dice que la superficie del material
actúa como "hidráulicamente lisa", en el segundo caso los vórtices
generados por las irregularidades del material destruyen la subcapa laminar,
generan turbulencia apreciable y se dice que la superficie del material actúa
como "hidráulicamente rugosa".
En general, la rugosidad de las tuberías es única para cada material
utilizado.
FIG. 2.1 RUGOSIDAD DE UNA TUBERIA
2.2. RÉGIMEN UNIFORME
El flujo uniforme se presenta cuando todas las secciones del canal tienen
exactamente las mismas características hidráulicas.
Características del flujo uniforme.
Debe cumplir con los aspectos siguientes:
a) El tirante o calado, el área hidráulica, velocidad y el caudal en cada
sección del tubo son constantes.
b) La línea de energía, la superficie libre y el fondo de la tubería con
todas paralelas, es decir sus pendientes son todas iguales
(Sf=Sw=So=S)
c) Longitud suficiente para vencer la zona transitoria.
7
Para fines prácticos la velocidad constante puede ser sustituida por una
velocidad media constante, es decir que el flujo tiene una velocidad
constante en cada punto sobre la sección de la tubería dentro del tramo de
flujo uniforme.
El flujo uniforme no ocurre a velocidades altas, esto se debe a que cuando el
flujo uniforme alcanza una velocidad alta se hace inestable o no uniforme.
En el flujo permanente, el tirante normal o calado, la velocidad y el área
hidráulica en cada sección transversal del canal, deben permanecer
constantes en el tiempo y el espacio, además que las líneas de corriente
tienen una inclinación fija en cada punto y están por tanto fijas en el espacio
(respecto a un eje de coordenadas x,y,z).
Para el cálculo del flujo uniforme y permanente se emplean las fórmulas de
Chézy y la de Manning, para nuestro caso utilizaremos las ecuaciones de
Manning
2.2.1 ESTABLECIMIENTO DEL FLUJO UNIFORME
Cuando el flujo ocurre a gravedad, el agua encuentra resistencia a medida
que fluye aguas abajo. Esta resistencia se contrarresta generalmente por los
componentes de las fuerzas gravitacionales que actúan en el cuerpo de agua
en la dirección del movimiento, la magnitud de la resistencia, cuando otros
factores físicos se mantienen constantes, depende de la velocidad del flujo,
si el agua entra lentamente al tubo, la velocidad y por consiguiente, la
resistencia son pequeñas, y la resistencia es sobre pasada por las fuerzas de
gravedad, dando como resultado una aceleración en el tramo aguas arriba,
simultáneamente la velocidad y la resistencia se incrementan gradualmente
hasta que alcanzar un balance entre las fuerzas de gravedad y de
resistencia, dando como resultado el flujo uniforme, en el extremo aguas
abajo ocurre el caso inverso produciéndose un flujo variado.
8
En la pendiente subcrítica el agua en la zona de transición aparece
ondulante. El flujo uniforme en el tramo medio y variado en los extremos
FIG. 2.2 FLUJO CON PENDIENTE SUBCRÍTICA
En la pendiente crítica la superficie del agua el flujo es inestable, pueden
ocurrir ondulaciones en el tramo central, pero el promedio del tirante de agua
es constante y el flujo puede ser considerado uniforme.
FIG. 2.3 FLUJO CON PENDIENTE CRÍTICA
En la pendiente supercrítica después de la zona de transición el flujo se
aproxima al uniforme. La profundidad del flujo uniforme se conoce como
profundidad normal
FIG. 2.4 FLUJO CON PENDIENTE SUPERCRÍTICA
9
La profundidad del flujo uniforme se conoce como altura normal. En todas las
figuras la línea de trazos largos representa la línea de la altura normal o hn, y
la línea de trazos cortos representa la línea de altura crítica o hc.
La longitud de la zona de transición depende de la descarga y condiciones
de: entrada, forma, pendiente y rugosidad.
2.3 FLUJO UNIFORME A SUPERFICIE LIBRE.
FIG. 2.5 ESQUEMA DE FLUJO UNIFORME A SUPERFICIE LIBRE
2.3.1 ECUACIONES DEL FLUJO UNIFORME
Los parámetros hidráulicos del flujo (velocidad V, profundidad h) permanecen
constantes a lo largo del conducto. El flujo de líquidos en canales de sección
constante y gran longitud se considera uniforme.
V
0
x
,
y
0
x
,
Q
0
x
(2.1)
El flujo en un canal es el resultado de la acción de las fuerzas de gravedad
(peso) que actúan como fuerzas impulsoras, y de las fuerzas de fricción que
actúan como fuerzas retardadoras.
Cuando ambas fuerzas son iguales la aceleración del flujo es nula y por lo
tanto el flujo es uniforme.
10
Por lo tanto, las pérdidas de energía hL en la ecuación de Bernoulli se
producen solamente a consecuencia de la disminución de la cota zi en
dirección del flujo.
La pendiente del fondo del canal en el flujo uniforme en canales,
obligatoriamente la pendiente del canal debe ser positiva (S0>0)
(2.2)
En general el flujo uniforme ocurre únicamente en canales prismáticos
(constituidos con una sección transversal constante y con la misma
pendiente del canal a lo largo de su longitud) muy largos y rectos.
2.3.2 ECUACIÓN DE MANNING.
Esta ecuación es de las más utilizadas por su sencillez, donde el coeficiente
(n) de Manning, y Rh el radio hidráulico.
Originalmente fue obtenida a partir de ensayos hechos por Chézy.
V  CRh
1/ 2
S 1/ 2
(2.3)
Donde: C es el coeficiente de velocidad analizado por varios autores entre
ellos Manning según la ecuación (2.4)
C
1 1/ 6
Rh
n
(2.4)
La ecuación es netamente empírica y fue presentada por primera ocasión por
el ingeniero Irlandés Robert Manning en 1889. Es función del radio hidráulico
(R), de la pendiente de la línea de energía (S) y del coeficiente de rugosidad
n, conocido mundialmente como coeficiente n de Manning y cuyo valor
puede ser usado en ambos sistemas de unidades.
Reemplazando la ecuación 2.4 en 2.3 se obtiene:
11
V
1 2 / 3 1/ 2
Rh S
n
(2.5)
2.4 FLUJO EN TUBERÍAS A GRAVEDAD Y PRESIÓN
La identificación del tipo de flujo en una conducción es esencial debido a que
las ecuaciones de diseño solo son aplicables a ciertas condiciones de flujo o
han sido desarrolladas para casos o intervalos específicos.
Flujo libre: El movimiento ocurre por la acción de la gravedad. Se presenta
en conducciones abiertas o en las conducciones cerradas pero llenas
parcialmente.
Las características generales del flujo libre son:
 Presenta una superficie del líquido en contacto con la atmósfera,
llamada superficie libre.
 La superficie libre coincide con la línea piezométrica.
 Cuando el fluido es agua a temperatura ambiente, el régimen de flujo
es usualmente turbulento.
Cuando en un tubo circula agua ocupando parte de la sección se dice que el
tubo está trabajando como canal.
Flujo libre uniforme
Se denomina flujo uniforme en canales al movimiento que se presenta
cuando las fuerzas de fricción generadas entre el fluido y la superficie sólida
se equilibran con la componente del peso del agua en la dirección del flujo,
manteniendo la velocidad constante.
En flujo libre y uniforme, se tienen las siguientes características:
 La profundidad de la lámina de agua es constante a lo largo del canal
y las líneas correspondientes a la solera del canal, superficie libre y
alturas totales son paralelas y sus pendientes iguales.
12
 El gradiente de energía es igual al gradiente piezométrico y a la
pendiente de la solera del canal.
Sw = Sf = So
(2.6)
En el caso de la forma circular abierta a la atmósfera como es el caso de
canales de riego o conductos que sirven de alcantarillas, se acostumbra usar
la siguiente nomenclatura:
d = profundidad del agua en el tubo.
D = diámetro del conducto.
So = pendiente longitudinal del fondo del canal.
Sf = gradiente de energía.
Sw= gradiente piezométrico (pendiente longitudinal de la superficie del agua).
Como el líquido que circula por un canal no tiene variaciones en su presión
sino que siempre se conserva a la presión atmosférica, la línea del gradiente
piezométrico coincide con la superficie libre.
Por otro lado la pendiente de fondo So es exclusivamente la necesaria para
vencer la fricción en el escurrimiento; la superficie del agua y la rasante del
canal o tubería parcialmente llena son paralelas.
Sf
Sw
So
NIVEL DE REFERENCIA
FIGURA 2.6 FLUJO UNIFORME A SUPERFICIE LIBRE.
FUENTE: HIDRÁULICA DE CANALES ABIERTOS, CHOW Ven Te. Mc Graw Hill.
13
 Las pérdidas de carga por fricción para un tramo dado son iguales al
decremento en la cota de la solera: h z f = D.
 Para pendientes pequeñas de la solera, So < 10% o 6°, la altura
piezométrica es igual a la profundidad del agua medida verticalmente.
(Citado “Flujos libres”. M. C. Guevara)
Flujo a presión: El movimiento ocurre por una presión diferente a la de la
atmósfera. La conducción es cerrada y se encuentra llena.
2.5 RESISTENCIA AL FLUJO
El contacto entre el agua y las paredes del tubo está definida por las fuerzas
de cuerpo y las fuerzas de fricción que causan una resistencia (fricción) que
depende de la suavidad o aspereza del material con el cual está fabricado el
tubo, por ejemplo en las corrientes naturales la cantidad de vegetación
influye en la rugosidad al igual que cualquier otra irregularidad que genere
turbulencia.
La resistencia al flujo se puede definir también como el cociente entre la
caída de presión y el caudal.
2.5.1 ECUACIÓN GENERAL DE RESISTENCIA
Considerándose en un tramo de extensión unitaria. Siendo el movimiento
uniforme, la velocidad se mantiene a costa de la pendiente del fondo del
canal, pendiente esta que será la misma para la superficie libre del agua.
Siendo g el peso específico de la masa liquida, la fuerza que produce el
movimiento será:
14
FIG. 2.7 RESISTENCIA AL FLUJO
W   W AL
W ´ Wsen   w ALsen
F   o A   o L
 o L   w ALsen
 o   w Rh S
F Asen(2.7)
Para que el movimiento sea uniforme, debe haber equilibrio entre las fuerzas
aceleradoras y retardadoras, de modo que la fuerza F debe contrarrestar la
resistencia opuesta al flujo por la resultante debida a la fricción. Esta
resistencia al flujo puede ser considerada proporcional a los siguientes
factores:
a) peso específico del líquido
b) perímetro mojado
c) longitud del canal (=1)
d) a una cierta (V) de la velocidad media
2.6 CAPA LÍMITE
Esta teoría de capa límite encuentra su aplicación en fluidos poco viscosos
como el agua o el aire. La capa límite es la zona afectada por el esfuerzo
cortante que se genera cuando un fluido en movimiento interactúa con una
pared sólida.
En fluidos poco viscosos, los esfuerzos tangenciales son generalmente
bastante inferiores a los de inercia o peso y el estudio de su movimiento
puede considerarse semejante al de un fluido perfecto, excepto en una capa
límite próxima al contorno, donde se concentran los fenómenos de fricción.
En el interior de esta capa límite el gradiente de velocidad es bastante
grande por lo tanto el esfuerzo tangencial es considerable.
15
Para facilitar el estudio de la capa límite se comprueban experimentalmente
dos hechos fundamentales:
1. A pesar de que la perturbación que produce la fricción se propaga a
toda la zona del fluido, se puede admitir que ésta queda limitada a un
espesor finito  que determina la extensión de la capa límite en sentido
normal al contorno.
2. La forma de la curva de distribución de velocidades en secciones
sucesivas a lo largo de la capa límite se expresa por una única ley
genérica:
Régimen turbulento
u
 y
 f 
V0
 
(2.8)
Régimen laminar
(2.9)
Dónde:
u es la velocidad media temporal
Vo la velocidad media uniforme del fluido no perturbado
(y) la distancia a la pared
 el espesor de la capa límite.
2.6.1 DESARROLLO DE LA CAPA LAMINAR
En el desarrollo longitudinal de la capa límite  para fluidos que circulan entre
dos paredes próximas, se muestra un incremento progresivo, partiendo
siempre en el contorno de una velocidad nula hasta alcanzar el valor Vo.
Figura 2.8
16
La capa límite continúa su desarrollo también en movimiento turbulento, la
transición del movimiento laminar al turbulento, dentro de la capa límite, se
aprecia con un ensanchamiento más rápido.
FIGURA 2.8 DESARROLLO CAPA LÍMITE LAMINAR, TURBULENTA Y SUBCAPA
LAMINAR
FUENTE: HIDROMECÁNICA, BECERRIL ENRIQUE.
En cuanto a la distribución de velocidades, ésta tiende a ser más uniforme en
la mayor parte de la capa, sin embargo en las inmediaciones de la pared el
cambio de velocidades es bastante rápido, si la pared es lo bastante lisa, el
régimen laminar subsiste en la zona de la subcapa laminar.
FIGURA 2.9 DESARROLLO CAPA LÍMITE LAMINAR EN UN CANAL CON UNA
CONDICIÓN DE ENTRADA IDEAL
FUENTE: HIDRÁULICA DE CANALES ABIERTOS, CHOW Ven Te. Mc Graw Hill.
17
2.7 DISTRIBUCIÓN DE VELOCIDADES
Al considerar el movimiento del fluido entre dos paredes como si se tratara
de una tubería que parte de un depósito, el movimiento es perturbado desde
su sección inicial por la aparición de una capa límite, el ensanchamiento
progresivo de la capa limite en cada contorno hace que éstas se unan, a una
cierta distancia de la entrada, desapareciendo la zona en la que el
movimiento puede ser considerado como el de un fluido ideal, limitándose a
que en el eje la velocidad sea máxima e ideal y el esfuerzo cortante se anule,
entonces el fluido se desarrolla completamente en régimen laminar o
turbulento, según el valor del número de Reynolds. Como se puede apreciar
en la Figura 2.10
FIGURA 2.10 MOVIMIENTO EN UN CONDUCTO: A LAMINAR, B TURBULENTO.
FUENTE: ANÁLISIS DE FLUJO CON SECCIÓN TOTAL Y PARCIALMENTE LLENA EN
TUBERÍAS DE PVC, MALDONADO Helman.
En el caso de las tuberías, a partir de cierta sección la distribución de
velocidades es idéntica en el resto de secciones transversales, el fluido entra
en régimen y su
movimiento se debe a la existencia de una pendiente
motriz. La sección desde la cual la distribución puede considerarse como
constante, medida desde la embocadura es aproximadamente Re/30
18
diámetros en régimen laminar y de 25 y 40 diámetros en régimen
turbulento[2],
Se ha demostrado que la distribución de velocidades en régimen laminar
puede asimilarse como una parábola de segundo grado, cuyo vértice se
encuentra a la distancia  y para el régimen turbulento parábolas del grado
1/m [3]. [2]
FIGURA 2.11 DISTRIBUCIÓN DE VELOCIDADES SOBRE UNA SUPERFICIE DE CANAL
LISO
FUENTE: HIDRÁULICA DE CANALES ABIERTOS, CHOW Ven Te. Mc Graw Hill.
Adicionalmente, el valor del espesor de la capa laminar, , al asumir una
distribución de velocidades parabólica de segundo grado, en función de Re
referido a la distancia x recorrida por el fluido (Re x = Vox /) es:
  5.47
x
Rex
(2.10)
El método de la integral de momentum ec. 2.9 es muy próximo a la solución
de Blasius cuya ecuación es la siguiente (Citado Mecánica de Fluidos Diego
Alfonso Tirado Samano y Mihir Sen Universidad de Notre Dame)
19
  4.96
x
Re x
(2.11)
FIGURA 2.12 FUNCIÓN DE BLASIUS.
FUENTE: MECÁNICA DE FLUIDOS DIEGO ALFONSO SAMANO
En el análisis del movimiento uniforme, permanente, y turbulento del agua
dentro de un conducto cerrado se distinguen los tres casos de tuberías
hidráulicamente lisas, intermedias y rugosas.
FIGURA 2.13 CAPA LÍMITE LAMINAR CON LEY DE VELOCIDADES PARABÓLICA DE
SEGUNDO GRADO.
FUENTE: HIDROMECÁNICA, BECERRIL Enrique.
20
Como ley de distribución de velocidades en la capa límite turbulenta, se usa
una relación empírica propuesta por Prandtl basada en principios similares a
los utilizados en el estudio de la capa límite laminar, admitiendo que la ley de
velocidades medias se puede expresar de la forma:
1/ m
u  y
 
U r
(2.12)
Dónde:
U: es la velocidad en el eje del conducto.
R: es el radio del mismo.
Y: es la distancia a la pared.
Esta ley no representa el movimiento en las inmediaciones del contorno, aquí
existe en cambio una subcapa en régimen laminar con una variación de
velocidades parabólica de segundo grado, que por su espesor pequeño se la
puede considerar como una recta.
En la subcapa laminar no hay turbulencia, debido a la cercanía de la pared,
en esta zona la expresión que relaciona el esfuerzo cortante con la variación
de la velocidad media es:
 
du
dy
(2.13)
En la zona turbulenta en cambio se puede adoptar la expresión mediante la
hipótesis de longitud de mezcla de Prandtl [2], que relaciona:
du
 '  l
dy
2
2
(2.14)
Dónde:
: es la densidad.
L: la longitud de mezcla de Prandtl.
U: es la velocidad media temporal.
y: es la distancia a la pared.
21
FIGURA 2.14 DISTRIBUCIÓN DE VELOCIDADES MEDIAS EN LA CAPA LIMITE
TURBULENTA, SEGÚN PARÁBOLA DE GRADO 1/M (M=7).
FUENTE: HIDROMECÁNICA, BECERRIL Enrique.
Según experiencias realizadas por Nikuradse para tuberías lisas medidas
con números Re entre 4000 y 3.24x 106, la ecuación de distribución de
velocidades de Prandtl – Von Kármán es:
u
V* y
 2.5 ln
 5.5
V*

(2.15)
Y es aplicable a toda tubería lisa en régimen turbulento, es una línea recta
que puede dibujarse fácilmente ajustándose a los resultados experimentales,
mientras que la ecuación:
u V*

y

V*
(2.16)
resultante de integrar la ecuación (2.11) y hacer que u=0 para y=0, es una
exponencial. El punto de intersección de las curvas de estas dos ecuaciones
de la ley de velocidades en la subcapa laminar y en la zona turbulenta
22
respectivamente, determina el espesor de dicha subcapa, b, Figura 2.15,
resultando:
V*

 b  11.6
(2.17)
Se define como Reynolds corte de la capa límite a Re*, V* como la velocidad
de corte, u la velocidad media temporal, (y) la distancia a la pared y  la
viscosidad del fluido.
FIGURA 2.15 DEFINICIÓN DEL ESPESOR B DE LA SUBCAPA LAMINAR.
FUENTE: HIDROMECÁNICA, BECERRIL Enrique.
La velocidad del fluido en los contornos es nula, con existencia de la subcapa
laminar sobre la que actúa el principio de adherencia.
Es necesario señalar además, que para garantizar un movimiento uniforme,
la capa límite debe ser turbulenta y totalmente desarrollada, para lo cual se
requiere un Reynolds, Rex=Vox /  mayor que 3x106, referido a una distancia
(x) desde el inicio de la tubería y que es necesaria para que el calado sea
23
aproximadamente el normal [1], con ello el valor o espesor la capa límite
turbulenta totalmente desarrollada resulta ser:
  0.37 x Rex 1 / 5
(2.18)
Por otro lado si el espesor de b es mayor que las irregularidades físicas en
el interior de la tubería, entonces se dice que se trata de una tubería
hidráulicamente lisa, y el espesor de la subcapa laminar viene determinado
tan solo por consideraciones de estabilidad del movimiento laminar de lo
contrario la tubería se considera como rugosa.
FIG. 2.16 COMPORTAMIENTO HIDRÁULICO DEL CONDUCTO
FUENTE: M.E GUEVARA A.
En teoría, se pueden usar los siguientes rangos para decidir si un conducto es
hidráulicamente liso o rugoso:
Rugosidad absoluta del conducto
Espesor de la sub-capa laminar
(2.19)
24
(2.20)
(2.21)
V*= velocidad de fricción o velocidad cortante
En una tubería rugosa las protuberancias de su interior son irregulares, sin
forma y de tamaño , si éstas son lo bastante grandes en comparación con la
subcapa laminar,
provocan separación de las líneas de corriente en su
borde, se forma un remolino y aparece sobre cada una un empuje que se
puede considerar como una fuerza adicional de resistencia por forma.
Al evaluar esta fuerza resulta ser proporcional al cuadrado de la velocidad
media:
E  CS
V2
2
(2.22)
Siendo E el empuje, s la superficie que la protuberancia ofrece al movimiento
y c un coeficiente constante que dependerá de la forma de la irregularidad
así como del espesor de la subcapa límite.
Es decir que el coeficiente de fricción en las relaciones para evaluar el caudal
tiene un valor constante, entonces, el coeficiente f de Darcy – Weisbach
será constante para cada relación /D y a partir del número de Reynolds que
define un régimen con turbulencia completamente desarrollada y contorno
25
rugoso. Si la proximidad de la subcapa límite influye sobre la formación de
los remolinos, se originarán fenómenos intermedios entre b>  y b<  en las
cuales la resistencia dependerá de Re y /D.
2.8 PARÁMETROS QUE INFLUYEN AL FLUJO
Corresponden a la dinámica de fluidos que es el comportamiento de los flujos
en el tiempo y el espacio, es decir es el movimiento de los fluidos.
2.8.1 CONSERVACIÓN DE LA MASA
La conservación de la masa de un fluido a través de dos secciones (sean
éstas A1 y A2) de un conducto (tubería) o tubo de corriente establece que: la
masa que entra es igual a la masa que sale por estas secciones.
A1 .V1  A2 .V2
(2.23)
Definición de tubo de corriente: superficie formada por las líneas de corriente.
Ecuación de continuidad
Es la cantidad de flujo que fluye en un sistema por unidad de tiempo.
Q  A.v
(2.24)
Q.- la rapidez de un flujo de volumen: es el volumen del flujo de fluido que
pasa por una sección por unidad de tiempo
26
La ecuación de continuidad se puede expresar como:
(2.25)
Cuando
, que es el caso general tratándose de agua, y flujo en
régimen permanente, se tiene:
A1 .V1  A2 .V2
(2.26)
o de otra forma:
(el caudal que entra es igual al que sale)
Dónde:

Q = caudal (metro cúbico por segundo;

V = velocidad

A = área transversal del tubo de corriente o conducto
)
Que se cumple siempre y cuando entre dos secciones de la conducción no
se acumula masa, es decir, siempre que el fluido sea incompresible y por lo
tanto su densidad es constante.
2.8.2 CONSERVACIÓN DE LA ENERGÍA
La conservación de la energía indica que en un fluido en movimiento
sometido a la acción de la gravedad, la suma de las alturas geométrica,
manométrica y cinética es constante para los diversos puntos de una línea
de corriente.
Energía potencial.- debido a la elevación, la energía potencial del elemento
con respecto de algún nivel de referencia es:
PE = wz
(2.27)
En la que “w” es el peso del elemento
Energía cinética.- debido a la velocidad, en realidad, el término cinético
27
(2.28)
Varía al variar el módulo de v según el punto de la sección transversal
considerada. Para que realmente represente a la energía cinética media que
pasa por la sección, se corrige con el coeficiente de Coriolis (), quedando el
término cinético como:
(2.29)
En régimen laminar, = 2, y en régimen turbulento, = 1. Como en
Hidráulica se trabaja generalmente en régimen turbulento, este término no se
verá afectado.
Energía de flujo.- en ocasiones conocida como energía de trabajo está
representada la cantidad de trabajo necesario para mover el elemento de
fluido a través de una cierta sección en contra de la presión (P). la energía
flujo se abrevia FE y se calcula a partir de la ecuación.
FE 
P
g
(2.30)
A estos efectos es de aplicación el Principio de Bernoulli, que no es sino la
formulación, a lo largo de una línea de flujo, de la Ley de conservación de la
energía. Para un fluido ideal, sin rozamiento, se expresa
, donde



(2.31)
g aceleración de la gravedad
densidad del fluido
P presión
28
Se aprecia que los tres sumandos son, dimensionalmente, una longitud (o
altura), por lo que el Principio normalmente se expresa enunciando que, a lo
largo de una línea de corriente la suma de la altura geométrica, la altura de
velocidad y la altura de presión se mantiene constante.
Cuando el fluido es real, para circular entre dos secciones de la conducción
deberá vencer las resistencias debidas al rozamiento con las paredes
interiores de la tubería, así como las que puedan producirse al atravesar
zonas especiales como válvulas, ensanchamientos, codos, etc. Para vencer
estas resistencias deberá emplear o perder una cierta cantidad de energía.
h1  1
2
v12
p
V
p
 1  h2   2 2  2  perdidas (1,2)
2 g g
2 g g
(2.32)
O lo que es igual para α1=α2=α= 1 en condiciones preliminares
(v12  v22 ) ( p1  p2 )
(h1  h2 ) 

 perdidas (1,2)
2g
g
(2.33)
Donde pérdidas (1,2) representa el sumando de las pérdidas continuas (por
rozamiento contra las paredes) y las localizadas (al atravesar secciones
especiales)
2.9 CONCEPTO DE PÉRDIDA DE CARGA
La Ecuación de Bernoulli puede considerarse válida sólo para líquidos no
viscosos o para dos puntos muy próximos, ya que en la realidad, aunque las
transformaciones se realizan de la forma indicada, las expresiones no son
del todo exactas. En efecto, un principio elemental de la física establece que
en toda transformación energética existe una degradación, es decir, los
rozamientos convierten en calor parte de la energía transformada, por lo que
el miembro de la derecha (si la transformación se efectúa de izquierda a
29
derecha) se verá disminuido. Para que la igualdad se mantenga, la ecuación
deberá quedar:
2
v12
p
V
z1   1
 z 2  2   2 2  h(12)

2g

2g
p1
(2.34)
El término h1-2 representa las pérdidas de energía que se producen en la
transformación.
Las pérdidas de carga pueden ser de dos tipos:
2.9.1 PÉRDIDAS CONTINUAS O POR ROZAMIENTO (hro2)
Las pérdidas por rozamientos son función de la rugosidad del conducto, de la
viscosidad del fluido, del régimen de funcionamiento (flujo laminar o flujo
turbulento) y del caudal circulante, es decir de la velocidad (a más velocidad,
más pérdidas).
Si es L la distancia entre los puntos 1 y 2 (medida a lo largo de la
conducción), entonces el coeficiente (h(1-2)) / L representa la pérdida de
altura por unidad de longitud de la conducción se le llama pendiente de la
línea de energía. Denominémosla J
h ro2 JL
(2.35)
La pérdida de carga por unidad de longitud depende de la rugosidad de la
tubería, de su diámetro, del caudal que circula por ella y de su velocidad.
Cuando el flujo es turbulento (número de Reynolds superior a 4.000;
2000<Re< 4000 es el flujo de transición; Re<2000 flujo laminar), lo que
ocurre en la práctica totalidad de los casos, existen varias fórmulas, tanto
teóricas (Ecuación de Darcy-Weisbach), como experimentales (ecuación de
Hazen-Williams, ecuación de Manning, etc.), que relacionan la pendiente de
la línea de energía con la velocidad de circulación del fluido. Quizás la más
sencilla y más utilizada sea la fórmula de Manning:
30
V  k.Rh
2/3
J 1/ 2
(2.36)
Donde:

V = velocidad del agua (m/s)

k = coeficiente de rugosidad, depende del material de la tubería y del
estado de esta. Existen varias expresiones para este coeficiente
calculados en forma experimental por varios investigadores como:
Manning; Bazin; Kutter; Strickler, entre otros.

Rh = radio hidráulico de la sección = Área mojada / Perímetro mojado
(un cuarto del diámetro para conductos circulares a sección llena) (m)

J = gradiente de energía (m/m)
2.9.2 PÉRDIDAS
SINGULARES (hloc)
DE
CARGA
LOCALES,
ACCIDENTALES
O
Son producidas por perturbaciones de la corriente líquida en puntos
concretos, como derivaciones, válvulas, cambios de sección, etc.
La pérdida de carga total en una conducción será la suma de las dos:
La representación gráfica de la situación energética planteadasería la
indicada en la figura 2.17
FIG. 2.17 PERDIDAS DE CARGA
31
2.10 FLUJOS EN PRESIÓN VS. FLUJOS CON SUPERFICIE LIBRE
Si el flujo circula a tubería llena (ocupando el área transversal total) estará
sometido a condiciones de la física diferentes a las que tendría si el flujo
circula a tubería parcialmente llena (flujo libre).
Un flujo a tubería parcialmente llena estará sometido a las condiciones de la
gravedad y de la atmósfera mientras que, un flujo a tubería llena (flujo a
presión) estará sometido a condiciones de presión.
Las dos clases de flujo se comparan en la Figura 2.18. A la izquierda de ésta
se muestra el flujo en tubería a presión. Dos piezómetros se encuentran
instalados en las secciones (1) y (2) de la tubería. Los niveles de agua en
estos tubos se mantienen por acción de la presión en la tubería en
elevaciones representadas por la línea conocida como línea de gradiente
hidráulico. La presión ejercida por el agua en cada sección del tubo se indica
en el tubo piezométrico correspondiente, mediante la altura y de la columna
de agua por encima del eje central de la tubería. La energía total del flujo en
la sección con referencia a una línea base es la suma de la elevación Z del
eje central de la tubería, la altura piezométrica y la altura de velocidad V²/2g,
donde V es la velocidad media del flujo (aquí se supone que la velocidad del
canal está uniformemente distribuida a través de la sección del conducto.)
En la figura la energía está representada por la línea conocida como línea de
energía.
La pérdida de energía que resulta cuando el agua fluye desde la sección (1)
hasta la sección (2) está representada por hf. Un diagrama similar para el
flujo en canal abierto se muestra en la parte derecha de la Figura 2.18
Con propósitos de simplificación, se supone que el flujo es paralelo y que
tiene una distribución de velocidades uniforme y que la pendiente del canal
es pequeña. En este caso, la superficie de agua es la línea de gradiente
hidráulico, y la profundidad del agua corresponde a la altura piezométrica.
32
FIG. 2.18 COMPARACIÓN ENTRE FLUJO A PRESION Y GRAVEDAD
FUENTE: HIDRÁULICA DE CANALES ABIERTOS, CHOW Ven Te. Mc Graw Hill.
2.11 DETERMINACIÓN DEL CAUDAL EN TUBERÍAS A PRESIÓN Y EN
SECCIONES PARCIALMENTE LLENAS
2.11.1 FÓRMULAS PARA LA DETERMINACIÓN DEL CAUDAL
El caudal de circulación en la tubería queda perfectamente determinado al
conocer los datos de área hidráulica y velocidad.
El área es definida geométricamente y la velocidad ya sea mediante fórmulas
empíricas cuyo único beneficio es su sencillez, o la fórmula semiempírica,
donde se considera el efecto de viscosidad y la rugosidad relativa.
Las fórmulas empíricas son del tipo exponencial:
V  aD x I y
(2.37)
Donde:
a = coeficiente experimental
x e y = exponentes experimentales
33
D = diámetro de la tubería
I = gradiente de fricción
I = hf / L
hf = pérdidas por fricción
L = longitud de la tubería
Es necesario tener cuidado con las unidades, sistema MKS, puesto que la
ecuación no es homogénea y depende del sistema de unidades que se
aplique.
Según la teoría a continuación se citan las fórmulas de Chézy, Manning y
Hazen – Williams como empíricas y la fórmula semiempírica Darcy Waisbach
con su respectivo tipo de tubería y flujo de aplicación.
Chézy
V  CRh I 1/ 2
1/ 2
(2.38)
Aplicable para tubería rugosa en la zona turbulenta.
Manning
V
1 2 / 3 1/ 2
Rh I
n
(2.39)
Aplicable para tubería rugosa en la zona turbulenta.
Hazen – Williams
V  0.85CHW Rh
0.63 0.54
I
(2.40)
Su uso es común para tubos rugosos en la zona de transición o turbulenta.
34
Darcy Weisbach
Se considera a esta fórmula semiempírica, porque corrige o modifica sus
resultados teóricos con los obtenidos en la experiencia.
La ecuación se escribe:
hf  f
L V2
D 2g
(2.41)
Donde f es el coeficiente de Darcy, adimensional y dependiente del número
de Reynolds Re = V / (D) y de la rugosidad relativa  / D.
La influencia de éstos sobre el factor de fricción, f, es distinta según las
características del flujo (Re) y el tipo de tubería (/D).
Si a partir de la ecuación (2.41) se obtiene la velocidad, ecuación (2.42)
V
2 gID
f
(2.42)
y al reemplazar el diámetro D, por 4Rh, Se observa que los exponentes de la
pendiente I, y del radio hidráulico RH, son iguales a sus correspondientes en
la ecuación de Chézy. Como se muestra en la ecuación (2.43).
V
8g 1/ 2 1/ 2
I RH
f
(2.43)
Esto hace que exista una relación entre los coeficientes f de Darcy –
Weisbach y C de Chézy, expresada en la siguiente ecuación:
C
8g
f
(2.44)
35
En régimen laminar la influencia de la rugosidad desaparece y el factor de
fricción está dado por:
f 
64
Re
(2.45)
Las contribuciones más importantes las realizo Nikuradse en Gotinga,
alrededor de 1920, que obtuvo resultados de ƒ vs Re en tubos lisos que
comprendían hasta valores de Re 3x106 obteniendo la siguiente ecuación:
1
 02 log Re
f
f  0.8
(2.46)
o bien
Re f
1
 2 log
2.51
f
(2.46a)
También obtuvo la rugosidad artificial en tubos verificadas en el laboratorio,
mediante granos uniformes de arena adheridos con diferente distribución
sobre la superficie interna del tubo, de estos ensayos obtuvo la ecuación:
1
D
 2 log
 1.14
2
f
(2.47)
o bien
1
3.71D
 2 log

f
(2.47a)
En régimen turbulento, se distinguen tuberías lisas y rugosas, las
investigaciones realizadas han podido determinar ecuaciones que definen el
coeficiente de fricción para cada régimen, así como también para la zona de
transición.
La ecuación de Prandtl – Von Kármán, para régimen turbulento:
36
En tuberías lisas y régimen turbulento inicial:
1
 0.86 ln Re
f
f  0.8
(2.48)
y en tuberías rugosas y régimen con turbulencia totalmente desarrollada:
1
D
 0.86 ln  1.14
f

(2.49)
Cuando las características del flujo dependen tanto de la rugosidad como del
número de Reynolds, el factor de fricción está dado por la fórmula de
Colebrook – White para régimen de turbulencia intermedia:
  /D
1
2.51
 2 log 

f
 3.71 Re f


 (2.50)
que es igual a
  /D
1
2.51 
 0.86 ln 


f
 3.71 Re f 
(2.51)
Los estudios realizados para definir estas fórmulas han sido efectuados
principalmente sobre tuberías de sección circular, pero pueden extenderse a
otras formas de secciones transversales de flujo, como a las parcialmente
llenas, siempre que sean circulares o semicirculares.
Se dice que una tubería está trabajando a presión cuando el flujo circulante
ocupa toda el área y perímetro expresados por su diámetro, es decir:
A
D 2
4
(2.52)
P  D
(2.53)
37
Mientras que una tubería que trabaja parcialmente llena, deja parte de su
área libre. En este caso el valor del diámetro se requiere reemplazar por:
D  4 Rh
(2.54)
Siendo Rh el radio hidráulico de la sección transversal del tubo.
A D 2 / 4 D
Rh  

P
D
4
(2.55)
En este caso las fórmulas de Prandtl – Von Kármán para tubería
parcialmente llena se escriben:
Tuberías hidráulicamente lisas:
1
 0.86 ln Re f  0.8
f
(2.56)
Tuberías hidráulicamente rugosas:
1
4R
 0.86 ln H  0.95
f

(2.57)
38
CAPITULO III
3. METODOLOGÍA EXPERIMENTAL.
3.1 FLUJOS CON SUPERFICIE LIBRE
En laboratorio de Investigaciones Hidráulicas de la Facultad de Ingeniería
Ciencias Físicas y Matemática de la Universidad Central del Ecuador, se
instaló un modelo físico de pruebas a escala real que trata de simular el
comportamiento de tubería con flujo libre (alcantarillas) sometida a varias
condiciones de caudal y pendiente.
3.1.1 DESCRIPCIÓN DEL MODELO DE PRUEBAS
La instalación del sistema en el que se efectuaron las pruebas, consta de
cinco partes fundamentales:
EL TANQUE ALIMENTADOR DEL SISTEMA
De forma cuadrada, al que llega la tubería que proporciona el caudal
otorgado por las bombas del Laboratorio de Hidráulica de la Facultad de
Ingeniería Ciencias Físicas y Matemática. Anexo 3, Fotografía 3.1.
EL VERTEDERO TRIANGULAR DE PARED DELGADA.
El vertedero tiene un ángulo central  de 90, mediante el cual se controla el
caudal suministrado. Anexo 3, Fotografía 3.2.
La ecuación de descarga que se establece para la geometría del vertedero
de medida es la siguiente:
Q  Ch
5
2
(3.1)
Donde h es la carga sobre el vertedero y C el coeficiente de gasto adoptado
de acuerdo a Gourley y Crimp válido para ángulos  de 45, 60, 90 y para
profundidades w grandes
39
C
1.32 tan( / 2)
h 0.03
(3.2)
Que conduce a la siguiente formula:
Q  1.32 tan( / 2).h 2.48
(3.3)
Para el sistema experimental el vertedero tiene un ángulo central  de 90, y
realizando las operaciones respectivas se llega a la ecuación de descarga
que se expresa de la siguiente manera:
Q  1.32h 2.48
(3.4)
la que genera la siguiente gráfica:
CURVA DE DESCARGA
H
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
0.50
0.55
0.60
0.65
Q
0.000
0.001
0.004
0.012
0.024
0.042
0.067
0.098
0.136
0.182
0.237
0.300
0.372
0.454
FIGURA 3.1
CURVA DE DESCARGA DEL VERTEDERO TRIANGULAR DE MEDIDA DE
CAUDALES
40
EL TANQUE EN EL QUE DESCARGA EL VERTEDERO.
Proporciona el caudal a la tubería por medio de un orificio, la tubería a ser
ensayada se conecta directamente al tanque mediante una unión que no
permite fugas de agua. Anexo 3, Fotografías 3.3 y 3.4.
LA TUBERÍA DE POLIETILENO DE ALTA DENSIDAD – RECICLADA
Tiene una longitud total de 12.0 m aproximadamente, está instalada para
cada diámetro y condiciones experimentales indicadas en la tabla 3.1. Se
apoya cada 0.5m aproximadamente para evitar deformaciones excesivas y
mantener una pendiente uniforme. Anexo 3, Fotografías 3.5
CERCHA METÁLICA
Para el soporte de la tubería, este montaje cumple la función de simular las
diferentes combinaciones de pendientes, siendo sus dimensiones de 12 m
de largo y 60 cm de base, consta de un sistema regulador hidráulico de
pendiente. Anexo 3, Fotografías 3.6 y 3.7
ESTRUCTURA DE SALIDA
Conformada por el sistema de desagüe al cual descarga la tubería en forma
libre. Anexo 3, Fotografía 3.8.
3.1.2 DESCRIPCIÓN DE LOS MEDIDORES
VERTEDERO TRIANGULAR
Vertedor triangular. Los vertedores triangulares se recomiendan para aforar
caudales pequeños Q<30 lt/s y cargas en el rango de 0.06m < h ≤ 0.60m.
FUENTE: MANUAL DE HIDRAULICA DE CANALES GUADALUPE ESTRADA GUTIERRES
FIG. 3.2 VERTEDERO TRIANGULAR
41
PIEZOMETRO
Los piezómetros fueron construidos por mangueras transparentes de 4
milímetros de diámetro interior, con un espesor de pared de 2 milímetros
conectados al tablero piezómetro ubicado al centro de la cercha metálica e
instaladas por un extremo en la tubería con acoples roscados en una
perforación realizada en la parte baja de las tuberías ubicados cada 0.5
metros y por el otro extremo con acoples unidos a tubos fusible de 4mm de
diámetro interior (a 0,65 metros de la entrada de la tubería). Como se
muestran en el anexo 3 fotografías 3.9, 3.10 y 3.11
LIMNIMETRO
Un limnímetro es, simplemente, una escala vertical como una mira de
topografía, graduada en milímetros. Entonces, basta con leer, en la escala, el
nivel que alcanza el agua.
La medición consiste en encerar el limnímetro con respecto al fondo de la
tubería luego se debe elevar hasta el espejo de agua y anotar
cuidadosamente la altura que alcanzó el agua, medida con el limnímetro.
El limnímetro siempre debe colocarse en el mismo sitio cada vez que se
hacen las lecturas. Los limnímetros pueden ser de metal o de madera. Anexo
3 fotografía 3.12
TUBO PITOT
El tubo de Pitot, inventado por el ingeniero y físico francés Henri Pitot en el
año 1732. Henri Pitot fue el primero en medir la rapidez del agua en el río
Sena utilizando el tubo pitot, aparato de su invención.
El tubo pitot es un medidor de flujo. Son instrumentos sencillos, económicos
y disponibles en un amplio margen de tamaños.
42
Es uno de los medidores más exactos para medir la velocidad de un fluido
dentro de una tubería.
Su instalación simplemente consiste en un simple proceso de ponerlo en un
pequeño agujero taladrado en la tubería. Anexo 3 fotografía 3.13 y 3.14
El tubo Pitot tiene sección circular y generalmente doblado en L.
Consiste en un tubo de pequeño diámetro con una abertura delantera, que
se dispone contra una corriente o flujo de forma que su eje central se
encuentre en paralelo con respecto a la dirección de la corriente para que la
corriente choque de forma frontal en el orificio del tubo.
V  2 * 9.81 * h
(3.5)
FUENTE: ALEJANDRO RIVAS & GORKA SÁNCHEZ 2007-2008
FIG. 3.3 TUBO PITOT
MEDICIÓN DE PENDIENTES
Se utilizó un nivel de precisión (nivel de ingeniero). Anexo 3 fotografía 3.15
Para medir la pendiente se tomaron lecturas de cotas sobre la mira que se
localizaron sobre la cercha metálica, para el cálculo se utiliza la ecuación:
i
h1 h2
L
(3.6)
donde:
i= es la pendiente calculada
h1 y h2 = son las mediciones de cota.
L= es la distancia entre reglas
43
AFORO VOLUMETRICO
Este método permite medir caudales pequeños de agua, para ello es
necesario contar con un deposito o balde de volumen conocido en el cual se
recolectara el agua, y un cronometro con el cual se tomara el tiempo que
demora en llenarse. Este se realizara por lo menos tres veces para
promediar, con el fin de asegurar una mayor exactitud.
Para este caso en particular se utilizara este tipo de aforo ya que los
caudales son pequeños. Anexo 3 fotos 3.16 y 3.17
3.1.3 DESCRIPCIÓN DE LAS PRUEBAS
Las pruebas consisten en determinar el coeficiente de rugosidad de Manning
que permita el mejor ajuste sobre el perfil de flujo a lo largo de la tubería
dado un caudal y pendiente específicos para cada pendiente se probaron 3
caudales entre 1.9 l/s y 30 l/s
que fueron regulados por la válvula de
compuerta.
Se tomaron las lecturas de altura en cada piezómetro conectado a la tubería
para las combinaciones de caudal y pendiente.
Los caudales de agua en el interior de las tuberías y las pendientes que se
utilizaron como se detalla en la tabla 3.1.
3.2 PROCEDIMIENTO EXPERIMENTAL
El plan de pruebas consideró tubos corrugados de polietileno reciclado
producidos por la empresa TUBERTOR en los diámetros comerciales.
Diámetro nominal (mm)
Diámetro interior (mm)
170
150
220
200
275
250
Por cada uno de ellos se ensayaron para diferentes condiciones como se
detalla en la tabla 3.1.
44
CONDICIONES DE PRUEBA
TABLA 3.1
D
iE
Q
D
iE
Q
D
iE
Q
(mm)
%
(l/s)
(mm)
%
(l/s)
(mm)
%
(l/s)
0.05
0.10
0.50
1.94
6.87
7.60
2.68
0.052 12.75
0.052 13.59
3.47
19.56
23.79
1.94
6.87
7.60
2.68
0.1
12.75
19.56
23.79
1.94
6.87
7.60
2.68
0.5
3.47
12.75
2.00
13.59
23.79
250.0
1.94
2.68
0.5
19.56
200.0
1.50
13.59
3.47
150.0
1.00
0.1
6.87
1
12.75
7.60
1
13.59
3.47
19.56
23.79
1.94
6.87
7.60
2.68
1.5
12.75
1.5
13.59
3.47
19.56
23.79
1.94
6.87
7.60
2.68
3.47
2
12.75
19.56
45
2
13.59
23.79
3.2.1 ENSAYOS
Las variables hidráulicas que se logran medir en el sistema corresponden al
caudal circulante y a la profundidad de agua en la tubería.
Los valores
del caudal se obtienen mediante la curva de descarga
establecida para el vertedero triangular de pared delgada que se menciona
en la sección 3.2.1.
La carga, h, sobre el vertedero es medida a través de un piezómetro
conectado al tanque de alimentación entre la pantalla uniformizadora de flujo
y el vertedero. El sistema debe ser encerado antes de iniciar la medición.
Para la determinación de las alturas de pérdidas en la tubería, se instalan
doce piezómetros, separados una distancia de 1.0 m aproximadamente,
ubicados en la parte central e inferior de la sección transversal, una vez
instalada la tubería; las medidas que se toman en los piezómetros van desde
la parte inferior de la tubería instalada hasta lo que marca en los mismos, con
una precisión de milímetros.
Para obtener el flujo uniforme, se requiere de una longitud necesaria para el
desarrollo de la curva de remanso. Como de describe en la tabla 3.1, para
todas las condiciones de prueba se trata de una curva S2 con Yc mayor que
el Yn, iniciándose el flujo aguas arriba con una pendiente vertical al calado
crítico y tangente con cierta aproximación a la profundidad normal de flujo
hacia aguas abajo.
Por otro lado la capa límite debe ser turbulenta y totalmente desarrollada,
para lo cual se requiere que el Reynolds referido a una distancia x, Rx, sea
mayor que 3x106. Al cumplirse esto, la longitud x necesaria desde que el
calado es aproximadamente el normal, toma un valor menor que 3m .
46
En cuanto al número de Froude, éste debe ser menor que 3, para que su
efecto sobre el factor de fricción sea despreciable.
Fr 
V
g.d
(3.7)
3.3 MONTAJE PARA PRUEBAS
Para la ejecución de los ensayos, se utilizó un modelo físico a escala real
para simular el comportamiento hidráulico de la tubería de alcantarillado
Tubertor tipo tortuga de diámetros de 150mm, 200mm, 250mm, sometidas a
diferentes combinaciones de caudal y pendientes. Este modelo consta de los
siguientes partes fundamentales:
 Tubería corrugada Tubertor de 12 metros de largo, con
diámetros de 150mm, 200mm, 250mm internos.
 Circuito de cañerías cerrado y en conjunto con una motobomba
eléctrica,
regulado por 1 válvulas de compuerta, una para
mantener una carga hidráulica constante de 1.50 metros en un
tanque aguas arriba de la tubería
 Tablero piezómetro para la lectura de los niveles en los
diferentes puntos en la tubería.
 Vertedero triangular y limnimetro para el cálculo del caudal.
 Cercha metálica como soporte de la tubería.
 Disipador de energía aguas arriba para el ingreso de flujo
uniforme y aguas abajo.
El esquema completo del montaje se muestra en las fotografías siguientes:
Estructura metálica y tubería de polietileno de alta densidad reciclada
montada
47
Fotografía N°1
Vertedero, tablero piezómetro, cercha metálica y tubería montada
Fotografía N°2
Tanque donde descarga el vertedero y disipador de energía
Fotografía N°3
48
3.4
DESCRIPCIÓN DE LOS ENSAYOS REALIZADOS
Para evaluar las singularidades del sistema construido, se probó la condición
de un diámetro de 200 mm, intermedio de los que se consideran en el plan
de pruebas, y con una pendiente del 1.0 %.
Para las siguientes condiciones se detalla cómo se realizan los cálculos
respectivos, y en el anexo 1 constan los correspondientes a las demás
condiciones de prueba.
Longitud del modelo (L)
12.56 m
Diámetro nominal (Dn)
220 mm
Diámetro interior (Di)
200 mm
Radio interior (Ri)
100 cm
Pendiente física (i)
1.0 %
Tirante de agua sobre el vertedero (H)
12.0 cm
Caudal de prueba (Q)
6.90 l/s
Viscosidad cinemática del agua () a 15°C
1.0 x 106 m2/s
Alturas piezometricas (hp)
(mm)
La ubicación de los piezómetros está definida por las distancias Lx y las
alturas z referidas al nivel del suelo del laboratorio, medidas desde el inicio
de la conducción como se indica en la Figura 3.4.
49
ESQUEMA DE UBICACIÓN DE PIEZÓMETROS
Nivel Referencia
P1
P2
Pi
Pi+1
Nivel Suelo
FIGURA 3.4
50
DISTANCIA Y ALTURA DE PIEZÓMETROS PARA EL DIAMETRO DE 200MM LA
PENDIENTE DEL 1%
TABLA 3.2
PIEZ.
ΔX
(cm)
ΔX+1
(cm)
Z
(cm)
1
59.50
59.50
52.23
2
99.80
159.30
51.24
3
99.70
259.00
50.25
4
100.00
359.00
49.25
5
100.20
459.20
48.25
6
100.20
559.40
47.26
7
99.70
659.10
46.26
8
99.80
758.90
45.27
9
99.80
858.70
44.28
10
100.00
958.70
43.28
11
100.30
1059.00
42.29
12
99.70
1158.70
41.29
51
Con los valores de las alturas piezométricas (hp), leídos en los piezómetros
se obtienen los calados experimentales (h) que tienen cierta variación
respecto del calado normal calculado, hcorr, por ello para su utilización en los
cálculos es necesario realizar las siguientes correcciones:
El último valor medido es despreciado, puesto que la descarga de la tubería
es libre, semejante a un escalón, lo que hace que el calado normal tienda a
ser crítico de acuerdo a la respectiva curva de descarga.
Los valores que presentan mayor diferencia en relación del calado normal,
son reemplazados por la media ponderada, calculada con aquellos cuyo
valor tiende al normal.
3.4.1 RELACIONES GEOMÉTRICAS PARA LA SOLUCIÓN DEL MODELO
FÍSICO.
Una vez corregidos los datos, el valor usado en los cálculos de las diferentes
variables, es el promedio de los valores correspondientes a dos secciones,
una seguida de otra. Las variables que se presentan en las hojas de cálculos
del anexo N°1 se obtienen como sigue:
Área del flujo:
A
1 2
D (  sen )
8
(3.8)
dónde θ en rad:


 rad   2 cos 1 1  2
Radio hidráulico:
52
h

D
(3.9)
Rh 
1  sen 
D1 

4 
 
(3.10)
Velocidad media en la sección donde se ubica cada piezómetro:
V
Q
A
(3.11)
Energía total en cada sección:
V2
E  zh
2g
(3.12)
ESQUEMA DE VARIABLES CONSIDERADAS
FIGURA 3.5
h
Relación de llenado:
d
h

D D
(3.13)
Los resultados obtenidos para el ejemplo considerado se presentan en la
tabla 3.3
53
VARIABLES ESTABLECIDAS A PARTIR DEL TIRANTE DE AGUA MEDIDO EN SISTEMA HIDRÁULICO PARA
D=200MM, I= 1% Y Q= 6.9 L/S
TABLA N° 3.3
PIEZ.
Lxn
(cm)
L xn+i
(cm)
Z
(cm)
hp(i)
(cm)
h
(cm)
θ
Am
(rad) (cm2)
1
54.50
54.50
52.23 58.78
6.55
2
99.80
154.30
51.24 57.29
3
99.40
253.70
4
100.10
5
6
Pm
(cm)
Rh
(m)
V
(m/s)
i
(mm/mm)
2.437 89.47 24.37
0.0367
0.7678
0.0076
6.05
2.329 80.18 23.29
0.0344
0.8567
0.0065
50.25 55.85
5.60
2.230 72.01 22.30
0.0323
0.9540
0.0075
353.80
49.25 54.82
5.57
2.224 71.47 22.24
0.0321
0.9612
0.0100
99.50
453.30
48.25 53.85
5.60
2.230 72.01 22.30
0.0323
0.9540
0.0095
100.20
553.50
47.26 52.76
5.50
2.208 70.22 22.08
0.0318
0.9784
iE
0.0123
0.010
7
105.20
658.70
46.26 52.45
6.19
2.360 82.77 23.60
0.0351
0.8300
0.0112
8
99.80
758.50
45.27 51.02
5.75
2.264 74.71 22.64
0.0330
0.9195
0.0087
9
99.90
858.40
44.28 50.13
5.85
2.286 76.53 22.86
0.0335
0.8977
0.0111
10
99.90
958.30
43.28 49.27
5.99
2.316 79.08 23.16
0.0341
0.8687
0.0106
11
99.80
1058.10 42.29 48.29
6.00
2.319 79.27 23.19
0.0342
0.8667
0.0101
12
94.60
1152.70 41.29 46.84
5.55
2.219 71.11 22.19
0.0320
0.9661
54
La pendiente de la línea de energía en cada tramo, iE:
iE 
En  En1
Lxn1  Lxn
(3.14)
Los resultados de iE para cada tramo, mostrados en la tabla 3.3, difieren del
valor de la pendiente real del sistema. Como es claro, se tratan de valores
experimentales, su promedio da como resultado la pendiente de la línea de
energía igual a 1%, valor que se usa posteriormente para el cálculo del factor
de fricción.
3.5 MEDICIONES DE CAUDAL, PENDIENTE Y CALADO DEL FLUJO EN
TUBERÍAS DE DIÁMETROS DE 150MM, 200MM, 250MM
Para las condiciones de caudal y pendiente que se detallan en la tabla 3.1,
se realizan los cálculos respectivos en el anexo N° 1.
CALADO DEL FLUJO EN TUBERÍAS DE DIÁMETROS DE 150MM,
200MM, 250MM
La determinación del calado (h) del flujo para el ejemplo se lo realizo con los
diámetro de 150mm, 200mm y 250mm para una pendiente del 1% y un
caudal de 1.94l/s, 6.9 l/s y 7.60 l/s respectivamente, como se detalla en los
cálculos siguientes y considerando las demás condiciones de prueba de la
tabla 3.1.
Fórmulas utilizadas
h  hp  Z
h= calado en cm
hp= altura piezometrica observada (cm)
55
Z= nivel de referencia (cm)
Para D=150mm, i=1%
h= 56.22-52.32(cm)
h= 3.90
El caudal se calcula con la ecuación 3.4 mencionada en la sección 3.1.2
h= corresponde a la medida en el borde del vertedero que es 7.2cm =
0.072m
Q  1.32 * 0.072 2.48
Q  0.00194m 3 / s
Las pendientes se calculan con los datos obtenidos con el nivel de ingeniero,
y se calcula con la ecuación 3.6 mencionada en la sección 3.1.3
i
0.1256m
12.56m
i  0.010m / m
Para 200mm, i=1%
h= 58.78-52.23(cm)
h= 6.55
h= 12.0cm = 0.012m
Q  1.32 * 0.012 2.48
Q  0.0069m3 / s
i
0.1256m
12.56m
i  0.010m / m
56
Para 250mm, i=1%
h= 58.10-52.27(cm)
h= 5.83
h= 12.5cm = 0.0125m
Q  1.32 * 0.0125 2.48
Q  0.0076m3 / s
i
0.1256m
12.56m
i  0.010m / m
En el anexo N°1 se detallan las tablas correspondientes a los cálculos para
las demás condiciones de prueba detalladas en la tabla 3.1.
57
CAPITULO IV
4. ANÁLISIS DE RESULTADOS EXPERIMENTALES.
4.1 RESULTADOS DE FLUJOS CON SUPERFICIE LIBRE
La presentación y análisis de resultados que a continuación se realizan
corresponden a las condiciones que anteriormente se presentaron para el
diámetro de prueba 200 mm y pendiente de la tubería del 1.0%, y las demás
condiciones bajo el mismo marco de estudio, los resultados se presentan en
el anexo 1.
Los cálculos se realizan en función de los datos de calado tomados en la
investigación.
4.1.1. ANÁLISIS DE LA INFLUENCIA DE LA ALTURA DE FLUJO (h)
FIG 4.1 RELACIÓN ALTURA DE FLUJO D=200MM
Se observa que a medida que se incrementa altura de flujo o el área que el
agua ocupa en la tubería, el caudal incrementa es decir que es directamente
proporcional.
58
4.1.2. ANÁLISIS
LONGITUDINAL
DE
LA INFLUENCIA DE
LA PENDIENTE
FIG 4.2 INFLUENCIA DE LA PENDIENTE LONGITUDINAL
Se observa que el caudal se mantuvo constante es decir que a medida que
se incrementa la pendiente, el caudal permanece constante.
4.1.3. ANÁLISIS DE LA INFLUENCIA DEL DIÁMETRO
Se observa que el diámetro no tiene incidencia en el caudal que circula por
la tubería en el que para cada ensayo permanece constante.
59
CAPITULO V
5. DETERMINACIÓN DEL COEFICIENTE DE RUGOSIDAD (n).
5.1 ESTABLECIMIENTO DE CRITERIOS DE SELECCIÓN DEL VALOR
DEL COEFICIENTE DE RUGOSIDAD.
La determinación de criterios que permitieron hallar el coeficiente (n) se basó
en la generación de varios ensayos que facilitaron describir adecuadamente
la relación de los caudales utilizados con la pendiente de la tubería, en
escenarios de variabilidad con otros factores hidráulicos constantes.
5.1.1. METODOLOGÍA Y JUSTIFICACIÓN
La metodología adoptada en este caso es la clásica considerando los dos
procesos de ejecución.
El primero de calibración del coeficiente de Manning para cada una de las
pruebas con diversas condiciones de caudal y pendientes específicas. En el
segundo se utilizaran indicadores de ajuste: Eficiencia R 2, y error cuadrático
medio ECM
El proceso de calibración se tiene para cada prueba (condición de pendiente,
caudal) una serie de medida de profundidades (h), un caudal (Q) y un
espectro de coeficientes de Manning (n) para el cual se generaran valores de
eficiencia y de error cuadrático medio con los cuales se obtendrá un valor
optimo de coeficiente de Manning de la prueba.
La justificación de la metodología adoptada radica en la búsqueda un
mecanismo que nos permita establecer el comportamiento del coeficiente de
Manning (n) para diversas condiciones de flujo.
60
El coeficiente de rugosidad (n) obtenido para cada prueba con las
condiciones de caudal y pendiente es válido solo para dicha prueba, lo cual
requiere la verificación para otros posibles eventos de caudal y pendiente.
Camp en 1950 realizó experimentos que demuestran que el coeficiente de
rugosidad varía con el caudal, por lo tanto es necesario obtener un valor del
coeficiente de rugosidad que sea el más adecuado para el diseño hidráulico
en alcantarillados.
Se debió tomar en consideración que los ductos empleados en la
investigación
son
tuberías
comerciales
fabricados
por
la
empresa
TUBERTOR, con proceso de doble extrusión de PVC reciclado cuya pared
exterior es corrugada y la interior no es del todo lisa y por consiguiente no se
conoce el coeficiente de rugosidad real de este producto, lo cual amerito
investigar en el laboratorio la rugosidad “n” empleando la ecuación de
Manning como conductor de este objetivo.
5.2.
RELACIONES
ENTRE
CAUDAL,
PROFUNDIDAD
Y
COEFICIENTES DE RUGOSIDAD ENCONTRADOS
RELACIÓN CAUDAL Y COEFICIENTE DE RUGOSIDAD
FIG 5.1
61
Se comprueba que efectivamente existe una variabilidad del coeficiente de
rugosidad de Manning (n) con el caudal (Q) empleado.
Debido a que no es posible identificar un valor único del coeficiente (n) de
Manning, ya que es un parámetro que no solo depende de la rugosidad de la
tubería sino también del flujo que circula por ella, es necesario realizar un
filtrado para obtener un coeficiente de rugosidad que represente el
comportamiento hidráulico, brindando una buena eficiencia en cuanto al
ajuste del perfil de dicha prueba. El método de utilizado para el filtrado y
determinación del coeficiente (n) de Manning optimo se describe en la
sección 5.1.1.
RELACIÓN PROFUNDIDAD Y COEFICIENTE DE RUGOSIDAD
FIG. 5.3
Se observa que a medida que se incrementa altura de flujo o el área que el
agua ocupa en la tubería, la resistencia al flujo también aumenta y
consecuentemente los valores del coeficiente de rugosidad (n) de Manning.
62
Dado que el caudal y la geometría no alcanzan a describir el correspondiente
aumento de fricción, este recae en la incidencia del coeficiente (n) de
Manning.
5.3 DETERMINACIÓN DEL COEFICIENTE DE RUGOSIDAD
Calibración del coeficiente n de Manning por Prueba para las
condiciones de Caudal y pendiente.
La calibración del coeficiente (n) de Manning para cada prueba consiste en
hallar el parámetro de máximo indicador de ajuste para el perfil de dicha
prueba, es decir, el valor que reproduzca con mayor exactitud, mediante el
modelo matemático del Flujo Gradualmente Variado, el perfil del flujo medido.
Indicadores de ajuste
Por consiguiente para la determinación del coeficiente de Manning para cada
prueba se utilizaron los indicadores de ajuste siguientes.
Eficiencia:
^
P
R2  1
 (Yi  Y i ) 2
i 1
P
 (Y  Y
i 1
i
*
i
)2
donde:
Yi es el coeficiente (n) experimental i de la prueba i
Y^i= es el coeficiente (n) calculado i dela prueba i
Y*i= es el coeficiente (n) promedio de los datos experimentales de la prueba i
P= es el total de coeficientes (n) utilizados en la prueba i
63
Error cuadrático medio:
ECMi 
1 P
(Yi  Yi* ) 2

P i 1
donde:
Yi= es el coeficiente (n) experimental i de la prueba i
Y*i= es el coeficiente (n) calculada i de la prueba i
P= es el total de coeficientes (n) utilizados en la prueba i
5.4 DESARROLLO DE LA SOLUCION DEL MODELO MATEMÁTICO DE
FLUJO GRADUALMENTE VARIADO
Este describe la variación de la profundidad o calado del agua a lo largo de la
longitud del ducto, el método usado será el de paso fijo para la generación
de las series de calados dado un coeficiente n de Manning.
5.4.1 Método del paso fijo
Es una solución numérica implícita de la ecuación del FGV, que usa la
ecuación de energía, para su solución se usa una versión recursiva, en la
cual, dada una profundidad para un tramo i, se halla el calado para el tramo
i+1 con iteraciones sucesivas.
La versión recursiva de la ecuación de la energía es la siguiente:
YIK11  Ei  Ei*1
De acuerdo a la definición de energía específica, se llega la ecuación
64
Vi 2
1
Ei  Yi 
 S O Lx  sf i Lx (5.4)
2g
2
donde:
Ei= es el termino de energía en el tramo i
Yi= es la profundidad o calado de flujo
Vi= es la velocidad de flujo
So Sf= pendiente del canal y de fricción
Lx= distancia entre tramos
La ecuación 5.4 se compone de términos de profundidad o calado del agua,
altura de velocidad, altura de posición entre tramos y el término de fricción
explicado por el coeficiente (n) de Manning, respectivamente
La ecuación de energía en el siguiente tramo será:
E
*
i 1
Vi 21 1

 sf i 1 Lx (5.5)
2g 2
En la cual también tenemos términos de velocidad profundad y fricción.
Definición para el término de fricción Sf (ley de Manning),
Vi 2
sf i  n 4 / 3 (5.6)
Ri
donde:
V= velocidad media del flujo en el tramo i.
R= radio hidráulico para el tramo i respectivamente.
Entonces para un tramo dado i y una profundidad Yi, el valor de la
profundidad
Yi+1 es aquel que cumpla con Yi k11  Yi k1  Yi*1
Para nuestra investigación este paso se omitirá ya que los obtenemos los
valores de profundidad o calado de agua en la tubería del modelo físico.
65
5.5 PROCEDIMIENTO PARA LA CALIBRACIÓN
5.5.1 Obtención de datos experimentales
En este paso se registran los datos de caudal, pendiente y lectura de
profundidad o calado de agua en los piezómetros que determinaran el perfil
experimental.
5.5.2 Calculo del perfil para cada pendiente y caudal.
Se calcula el perfil experimental para la tubería bajo los parámetros de
caudal y pendiente determinados experimentalmente. Entonces para cada
prueba obtenemos un perfil.
5.5.3 Cálculo del coeficiente (n) experimental Manning en cada tramo de
la tubería.
Con las relaciones geométricas calculadas a partir de los calados obtenidos
en cada prueba realizados en la sección 3.2.2.1 se calcula el valor del
coeficiente (n) de Manning para cada tramo i de la prueba k.
5.5.4 Calculo del coeficiente (n) de Manning teórico en cada tramo de la
tubería.
Para el cálculo del coeficiente (n) de Manning teórico se procede a calcular,
para cada tramo con la pendiente física del modelo para cada condición de
caudal y pendiente.
5.5.5 Calculo de los indicadores de eficiencia y ECM
Con los valores de coeficientes (n) de Manning teóricos y experimentales
para cada prueba se procede con el cálculo de los indicadores de Eficiencia
y ECM.
66
5.5.6 Generación de Curvas (n, eficiencia, ECM)
Con la lista de coeficientes (n) de Manning calculados, eficiencias y Error
Cuadrático Medio para cada condición de caudal y pendientes
5.5.7 Determinación del coeficiente (n) Manning
Con los Coeficientes (n) de Manning óptimos para cada prueba se realiza un
promedio y se obtiene el coeficiente (n) para las tuberías de polietileno de
alta densidad reciclada fabrica por la empresa TUBERTOR
5.6 CÁLCULOS REALIZADOS
Se realiza el cálculo tipo para la tubería de diámetro 200mm, pendiente del
1%, caudal de 6.9l/s y h= 6.55 cm
De la ecuación de Manning (2.5) la cual se menciona en la sección 2.2, la
cual al reorganizarla toma la forma para el termino del coeficiente de
Manning.
n
1 2 / 3 1/ 2
(5.1)
Rh S
V
Calculo de las variables para la determinación del coeficiente de rugosidad
de Manning.
La variable velocidad es establecida de dos formas las cuales se describe a
continuación.
La primera es obtenida de la ecuación de continuidad 3.9 que se menciona
en la sección 3.2.2.
El ángulo θ se obtiene de la ecuación 3.9
67


 rad   2 cos 1 1  2
6.55 

200 
  2.437rad
El Área se obtiene de la ecuación 3.8
1
A  * 200 2 (2.437  sen2.437)
8
A  89.47cm 2
El caudal se obtiene del caculo realizado en la sección 3.2.3
Q  1.32 * 0.012 2.48
Q  0.0069m3 / s
V 
Q
A
V
0.0069m 3 / s
0.8947m 2
V  0.7678m / s
La segunda es obtenida mediante el tubo Pitot para lo cual utilizamos la
ecuación 3.5.
h  9.52cm
V  2 * 9.81* 0.0952
V  0.7634m / s
El radio hidráulico se calcula con la ecuación 3.10.
68
Rh 
1
 sen2.437 
0.201 

4
2.437 

Rh  0.0367
La pendiente de la Línea de Energía (iE) (ley de fricción de Manning) se
calcula con la ecuación 3.14.
iE 
61.79  61.03
154.30  54.50
iE  0.0076
Calculo del Coeficiente de Rugosidad de Manning para las variables
obtenidas las cuales reemplazamos en la ecuación 5.1.
Coeficiente de Rugosidad de Manning obtenida con la Velocidad media.
n
1
0.0367 2 / 3 0.00761 / 2
0.7678
n  0.0125
Coeficiente de Rugosidad de Manning obtenida con velocidad determinada
con el tubo Pitot.
n
1
0.0367 2 / 3 0.00761 / 2
0.7634
n  0.0126
En el anexo N°1 se detallan las tablas correspondientes a los cálculos del
coeficiente (n) de Manning para las demás condiciones de prueba detalladas
en la tabla 3.1.
69
5.6.1 Calculo del coeficiente de Manning teórico en cada tramo de la
tubería.
Se realiza el cálculo con las condiciones experimentales pero se utiliza la
pendiente fisca del modelo físico
Q  0.0069m3 / s
Rh  0.0367
V  0.7678m / s
i
0.1256m
12.56m
i  0.010m / m
n
1
0.0367 2 / 3 0.0101 / 2
0.7678
n  0.0144
En el anexo N°2 se detallan las tablas correspondientes a los cálculos del
coeficiente (n) de Manning teórico para las demás condiciones de prueba
detalladas en la tabla 3.1.
70
5.6.2 Calculo de los indicadores de eficiencia y ECM
VALORES
DE
COEFICIENTES
(n) DE
MANNING
EXPERIMENTALES
Y
CALCULADOS PARA D=200mm, i=1%, Q=6.9l/s
Tabla N° 5.1
n exp. n calc.
0.0125
0.0100
0.0092
0.0105
0.0104
0.0114
0.0137
0.0104
0.0122
0.0125
0.0122
0.0144
0.0124
0.0106
0.0105
0.0106
0.0103
0.0129
0.0112
0.0116
0.0121
0.0122
∑= 0.1249
PROMEDIO 0.0114
0.129
11
R2  1
 (0.1249  0.129)
2
i 1
11
 (0.1249  0.0114)
2
i 1
R 2  0.999
ECM 
1 11
(0.1249  0.129) 2

11 i 1
ECM  1.03 06
En el anexo N°2 se detallan las tablas correspondientes a los cálculos de R2
y ECM para cada prueba.
71
5.7 GENERACIÓN DE CURVAS (n,EFIENCIA,ECM) y OBTENCIÓN DEL
COEFICIENTE (n) DE MANNING ÓPTIMO
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=150mm) Y CAUDAL (Q=6.90L/s)
PARA EL DÍAMETRO
FIG. 5.6
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.0122
72
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=150mm) Y CAUDAL (Q=2.70L/s)
PARA EL DÍAMETRO
FIG. 5.7
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.011
73
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=150mm) Y CAUDAL (Q=3.5L/s)
PARA EL DÍAMETRO
FIG. 5.8
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.01069
74
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=200mm) Y CAUDAL (Q=6.9L/s)
PARA EL DÍAMETRO
FIG. 5.9
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.0107
75
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=200mm) Y CAUDAL (Q=12.8L/s)
PARA EL DÍAMETRO
FIG. 5.10
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.0112
76
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=200mm) Y CAUDAL (Q=19.6L/s)
PARA EL DÍAMETRO
FIG. 5.11
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.0111
77
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=250mm) Y CAUDAL (Q=7.60L/s)
PARA EL DÍAMETRO
FIG. 5.12
El resultado de coeficiente (n) de Manning optimo para el caudal y diámetro
descrito es de 0.01168
78
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=250mm) Y CAUDAL (Q=13.60L/s)
PARA EL DÍAMETRO
FIG. 5.13
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.0115
79
RESULTADO DEL COEFICIENTE DE MANNING (n)
(D=250mm) Y CAUDAL (Q=23.80L/s)
PARA EL DÍAMETRO
FIG. 5.14
El resultado de coeficiente (n) de Manning óptimo para el caudal y diámetro
descrito es de 0.0111
80
5.8 DETERMINACIÓN DEL COEFICIENTE DE RUGOSIDAD (n) DE
MANNING
Realizando un promedio de los valores del coeficiente (n) de Manning optimo
obtenidos para la tubería de polietileno de alta densidad reciclada en los
diámetros 150mm, 200mm y 250mm se determina el Coeficiente de
Rugosidad de Manning a continuación:
n
0.0122  0.0110  0.0107  0.0107  0.0112  0.0111  0.01168  0.0115  0.0111
9
n  0.0112
El coeficiente (n) de Manning recomendado tiene una eficiencia media
calculada de
R2 
0.9994  0.9943  0.9985  0.9998  0.9984  0.9972  0.9265  0.8727  0.6000
9
R 2  0.932
Es decir que el coeficiente (n) de Manning para posibles eventos de caudal y
pendiente, tiene una eficiencia de 93.20% o superior.
81
5.9 CURVAS PARA EL DISEÑO DE TUBERIAS
TUBERIA DE 150MM
CAUDAL vs CALADO VARIANDO LA PENDIENTE
0.030
0.001000 m/m
0.002000 m/m
0.003000 m/m
0.004000 m/m
0.005000 m/m
0.006000 m/m
0.007000 m/m
0.008000 m/m
0.009000 m/m
0.010000 m/m
0.011000 m/m
0.012000 m/m
0.013000 m/m
0.014000 m/m
0.015000 m/m
0.016000 m/m
0.017000 m/m
0.018000 m/m
0.019000 m/m
0.020000 m/m
0.025
CAUDAL
(m³/s)
0.020
0.015
0.010
0.005
0.000
0.00
0.02
0.04
0.06
0.08
CALADO
(m)
0.10
0.12
0.14
TUBERIA DE 200MM
CAUDAL vs CALADO VARIANDO LA PENDIENTE
0.060
0.002000 m/m
0.004000 m/m
0.006000 m/m
0.008000 m/m
0.010000 m/m
0.012000 m/m
0.014000 m/m
0.016000 m/m
0.018000 m/m
0.020000 m/m
0.055
0.050
0.045
CALADO
(m³/s)
0.040
0.035
0.030
0.025
0.020
0.015
0.010
0.005
0.000
0.00
0.02
0.04
0.06
0.08
0.10
0.12
CALADO
(m)
82
0.14
0.16
0.18
0.20
TUBERIA 250MM
CAUDAL vs CALADO VARIANDO LA PENDIENTE
0.12
0.002000 m/m
0.004000 m/m
0.006000 m/m
0.008000 m/m
0.010000 m/m
0.012000 m/m
0.014000 m/m
0.016000 m/m
0.018000 m/m
0.020000 m/m
0.10
CAUDAL
(m³/s)
0.08
0.06
0.04
0.02
0.00
0.00
0.05
0.10
0.15
CALADO
(m)
83
0.20
0.25
CAPITULO VI
6. CONCLUSIONES RECOMENDACIONES
6.1. CONCLUSIONES SOBRE EL VALOR DEL COEFICIENTE DE
RUGOSIDAD OBTENIDO PARA EL DISEÑO
Al determinar los mejores valores de coeficiente de Manning mediante los
métodos de eficiencia y error cuadrático. Se establece que el valor más
adecuado para el diseño en 0.0112 según los datos experimentales y los
análisis realizados.
6.2. RECOMENDACIONES ACERCA DE LA TUBERÍA Y SU MONTAJE
De las experiencias adquiridas con la tubería de polietileno de alta densidad
reciclada para
alcantarillados fabricada por TUBERTOR, se recomienda
tener presente las recomendaciones siguientes:
Soportar continuamente la tubería utilizada en toda su longitud para evitar
deformaciones y deflexiones que afecten los resultados experimentales, para
contar con una pendiente uniforme a lo largo de la tubería.
Acoplar correctamente la espiga y campana de la tubería, el anillo
elastomérico no debe ser removido por ningún motivo ya que de lo contrario
se producirán fugas, afectando los resultados experimentales.
Aplicar lubricante, jabón o grasa vegetal en el extremo del tubo y en el
interior del acople para su ensamblaje.
Insertar el extremo lubricado del tubo dentro del acople o viceversa, según
sea el caso, hasta la marca tope. Para realizar esta operación es necesario
84
utilizar una palanca o equipo mecánico, protegiendo siempre los extremos
del tubo
6.3. PROPUESTAS PARA ESTUDIOS FUTUROS
Dotar al laboratorio de Hidráulica de aparatos de medición modernos, puesto
que uno de los propósitos de toda investigación es realizar con la mayor
exactitud posible.
Seleccionar adecuadamente los aparatos de medición.
Utilizar el método más adecuado y verificar que las influencias externas no
modifique la estabilidad del modelo.
85
BIBLIOGRAFÍA
1. CHOW V., Te. (1994). Hidráulica de canales abiertos. McGraw W-Hill
Interamericana S.A., Santa Fe de Bogotá Colombia. Pág. 3-335.
2. SOTELO A., Gilberto. (2002). Hidráulica de canales. Facultad de
Ingeniería, Universidad Nacional Autónoma de México. cap.V-VI.
3. J.M. de AZEVEDO Netto, ACOSTA A. Guillermo, (1987). Manual de
Hidráulica. HARLA S.A. México. Pag. 319-324
4. HIDROMECÁNICA, BECERRIL Enrique, Editorial Dosat, S.A, Madrid
1960.
5. NIKURADSE,J.1937. Laws of flow in Rough Pipes, NACA Technical
paper No.1292.
6. http://es.scribd.com/doc/163583456/Hidraulica-de-canales-pdf
Guadalupe Estrada Gutiérrez
7. MARCOS EDUARDO GONZÁLEZ LÓPEZ Determinación del
coeficiente de rugosidad de Manning en tuberías de drenaje
(hormigón). Proyecto Previo a la Obtención del Título de Ingeniero
Civil. Universidad de Concepción Facultad de Ingeniería Agrícola,
Chillán-Chile Pág. 14-18.
8. MALDONADO Helman, Quito – Ecuador, 1999. Análisis de flujo con
sección total y parcialmente llena en tuberías de pvc
9. MARCOS CONTRERAS Flujo Uniforme (Apuntes de Clases)
Departamento de Ingeniería Civil Facultad de Ciencias Físicas y
Matemáticas Universidad de Chile.
10. DIEGO ALFONSO SAMANO Tirado Ecología y Energía Cuernavaca,
Mexico, MIHIR SEN Universidad de Notre Dame, Indiana, EE.UU. Capa
Limite. Pág. 97.
86
11. http://artemisa.unicauca.edu.co/~hidraulica/flibre.pdf
12. es.slideshare.net/clay245/teora-de-capa-limite
13. ww.unav.es/ocw/labfluidosing10708/GPL_1_Spanish_07_08.pdf
14. http://cdigital.dgb.uanl.mx/la/1020082534/1020082534_005.pdf
15. www.unav.es/ocw/labfluidosing10708/GPL_1_Spanish_07_08.pdf
87
ANEXOS
TABLAS DE
CALCULOS
FOTOGRAFÍCOS
88