Aplicaciones de Leyes de Newton

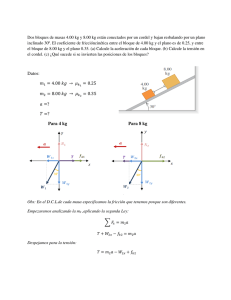
Capitulo Nº 5: [S.Z.F.Y. 5]
APLICACIONES DE LAS LEYES DE NEWTON
5-1 Pasos a seguir para resolver problemas de Dinámica
a) Comprender la situación física planteada en el enunciado, leyéndolo cuidadosamente.
b) Identificar los cuerpos cuya masa no se desprecia.
c) Representar todas las fuerzas que actúan sobre los mismos.
d) Representar (si se conoce o puede preverse) el vector aceleración (recordar que no es una
fuerza).
e) Escoger y dibujar los ejes coordenados “x” e “y” y representar el sentido positivo de cada uno. Es
conveniente seleccionar la dirección y sentido de uno de los ejes, en la dirección y sentido de la
aceleración (así cuando se aplique la segunda Ley de Newton las componentes de la aceleración
serán positivas). Si la componente de la aceleración es nula, el sentido adoptado para el eje es
arbitrario.
f) Calcular las componentes de todas las fuerzas en las direcciones de ambos ejes (para esto se
utilizan las funciones trigonométricas seno y coseno)
g) Plantear la segunda Ley de Newton para cada cuerpo, en las direcciones elegidas:
F = m . a
Fx = m . ax
Fy = m . ay
h) Comprobar que se dispone de un sistema de n ecuaciones con n incógnitas, y calcular la/s
incógnita/s resolviendo matemáticamente el sistema.
i) Verificar la validez de las soluciones halladas.
Ejemplo de resolución de un problema:
En el sistema de la Figura 5-1, el bloque A de masa mA se ubica
sobre el plano inclinado sin roce, que forma un ángulo con
respecto a la horizontal. La polea por donde cuelga el bloque B de
masa mB conectado a A, es de masa despreciable y la cuerda se
considera inextensible y también de masa despreciable. Calcular
la aceleración del sistema.
A
B

Figura 5-1
Resolución:
a) Se trata de un sistema físico que podría estar en equilibrio, en reposo o moviéndose ambos cuerpos
con velocidades constantes, o bien estar acelerados. Por acción de la atracción gravitatoria, el cuero B
puede caer, arrastrando hacia arriba al cuerpo A sobre el plano inclinado, o bien, el cuerpo A cae
sobre el plano y el cuerpo B asciende. Que ocurra cualquiera de estas situaciones dependerá, como
veremos, de las masas de los cuerpos y del ángulo del plano inclinado.
b) Identificar los cuerpos cuya masa no se desprecia: Cuerpos A y B
Capítulo N°5
1
c) Representar todas las fuerzas que actúan sobre los mismos, realizando el DCL de cada uno:
d) Representar (si se conoce o puede preverse) el vector aceleración (recordar que no es una fuerza).
De los casos que hemos considerado posibles, suponemos uno de ellos (esto es arbitrario en este
caso) que el sistema se acelera de modo que A asciende y B desciende.
aA
T2
T1
N
aB
PB 
PA
e) Escoger y dibujar los ejes coordenados “x” e “y” y representar el sentido positivo de cada uno. De
acuerdo con la aceleración que suponemos adquiere el sistema, escogemos el eje “x” en la dirección y
sentido de la aceleración para el cuerpo A y el eje “y” para el cuerpo B. De este modo, ambas
aceleraciones tienen una única componente y ésta es positiva. De este modo, la elección del sentido
positivo del eje “y” perpendicular al eje “x” en el Bloque A es indistinto, porque no hay componente
de la aceleración en esa dirección.
aA
axA ≠ 0
ayA = 0
aA
T2
y
N
axB = 0
aB ayB ≠ 0
x
T1
PB
y
PA
f) Calcular las componentes de todas las fuerzas en las direcciones de ambos ejes. En este caso, sólo es
necesario descomponerla fuerza PA:
PAX = mB . g . cos
PAy = mA . g . sen
aAx
y
N
mA . g . sen
x
T2
T1

mA . g . cos
mB . g
mA . g
ayB
y
g) Plantear la segunda Ley de Newton para cada cuerpo:
Para el Bloque A:
Fy = mA . aAy
Fx = mA . aAX
Capítulo N°5

→
→
N - mA . g . cos  = 0
T1 - mA . g . sen  = mA .aAX
2
(1)
(2)
Para el Bloque B:

Fy = mB . aBy
mB . g – T2 = mB .aBy
(3)
→
h) Comprobar que se dispone de un sistema de n ecuaciones con n incógnitas, y calcular la/s
incógnita/s resolviendo matemáticamente el sistema.
T1 = T2 = T ya que la masa de la polea se consideró despreciable.
ax = ay = a si se considera que la cuerda es de masa despreciable e inextensible.
Con estas consideraciones, la ecuación (2) queda: T = mA . g . sen  + mA .a
Y la (3) queda:
T = mB .g - mB . a
En este caso, tenemos entonces tres ecuaciones, en las que se desconocen N, T y a. Como se solicita
sólo la aceleración, la ecuación (1) no aporta información y debemos resolver el sistema de las dos
ecuaciones anteriores:
mA . g . sen  + mA .a = mB .g - mB . a
mA .a + mB . a = mB .g - mA . g . sen 
de donde obtenemos finalmente:
a=
g . (mB - mA . sen )
mA + mB
i) Verificar la validez de las soluciones halladas. Analizando la expresión anterior, vemos que:
si mB > mA . senentonces a > 0 y el sistema se acelerará según lo supuesto.
si mB < mA . senentonces a < 0 y el sistema se acelerará en el sentido opuesto al supuesto.
si mB = mA . senentonces a = 0 y el sistema no tiene aceleración, en cuyo caso puede estar en reposo
o bien moviéndose con velocidad constante en cualquiera de los dos sentidos.
También vemos que cuanto mayor es la inercia total del sistema (mA + mB), menor es la aceleración
que éste adquiere.
5-2 Fuerzas de rozamiento
Aunque la naturaleza de la interacción responsable de las fuerzas de rozamiento no es bien
conocida, parece que son debidas a interacciones entre las moléculas de ambos cuerpos en los lugares
en los que las superficies están en contacto.
Las fuerzas de rozamiento pueden ser:
 Fuerza de rozamiento estática (fre):
Se origina cuando un cuerpo en reposo sobre un plano se le aplica una fuerza para intentar
ponerlo en movimiento (aunque no llegue a deslizar). El sentido de esta fuerza de rozamiento es
tal que se opone al movimiento relativo entre las superficies de contacto.
 Fuerza de rozamiento cinética (frc):
Se origina cuando un cuerpo desliza, por ejemplo, sobre un plano.
De las mediciones experimentales se deduce que:
 La fuerza de rozamiento siempre se opone al deslizamiento de los puntos del objeto en
contacto con la superficie de apoyo respecto de la misma.
 Es paralela al plano.
Capítulo N°5
3




Depende da la naturaleza y estado de las superficies en contacto.
Es proporcional a la fuerza normal.
Es independiente de la velocidad del cuerpo, mientras ésta no sea muy elevada.
Es independiente del área (aparente) de las superficies en contacto.
FUERZA DE ROZAMIENTO CINÉTICA
La fuerza de rozamiento cinética es ejercida por el plano sobre los cuerpos y es la responsable
de que éstos disminuyan su velocidad si se dejan deslizar libremente. De aquí (primera ley de Newton)
que si queremos que un cuerpo que desliza sobre un plano no disminuya su velocidad, hemos de
empujarlo (aplicar una fuerza).
Como se puede observar tiene un valor constante y depende del valor de la normal y del coeficiente
de rozamiento.
frc = cN
Donde:
frc: es la fuerza de rozamiento cinética.
c: Coeficiente de rozamiento cinetico. Número sin unidades. Depende de la naturaleza de las
superficies y de su estado.
N: Fuerza normal o acción del plano.
FUERZA DE ROZAMIENTO ESTÁTICA
La fuerza de rozamiento estática aparece cuando aplicamos una fuerza a un cuerpo para intentar que
éste deslice. Si la fuerza aplicada está por debajo de determinado valor no se iniciará el deslizamiento,
debido a que la fuerza de rozamiento estática equilibra la fuerza aplicada. Si aumentamos el valor de
la fuerza aplicada, aumenta en la misma relación que el valor de la fuerza de rozamiento estática y el
cuerpo permanece en reposo.
Si seguimos aumentando la fuerza llegará un momento que el cuerpo comienza a deslizar. La fuerza
de rozamiento estática no puede crecer indefinidamente. Su valor máximo viene dado por la
expresión:
fre = e . N
Donde:
Fre: es la fuerza de rozamiento estática.
e: es el coeficiente de rozamiento estático. Depende de la naturaleza de las superficies en contacto y
de su estado. Tiene un valor igual o superior a c.
N: Fuerza normal o acción del plano
Una vez que la fuerza aplicada es superior al valor máximo que puede alcanzar la fuerza de
rozamiento estática, el cuerpo comienza a deslizar y aparece la fuerza de rozamiento cinética.
Ejemplos de coeficientes de rozamiento:
Materiales en contacto
Acero - acero
Aluminio - acero
Cobre - acero
e
c
0,74
0,57
0,61
0,47
0,53
0,36
Las fuerzas de fricción también pueden actuar cuando no hay movimiento relativo. Si tratamos de
deslizar por el piso un bloque, tal vez no se mueva porque el piso ejerce una fuerza de fricción igual y
opuesta sobre el bloque.
En la Figura 5-2 a, un bloque está en reposo, en equilibrio, bajo la acción de su peso y la fuerza normal
hacia arriba, la fuerza normal es igual en magnitud al peso y ejercida por el piso sobre el bloque.
En la Figura 5-2 b, aplicamos una fuerza F y gradualmente aumentamos la fuerza. Al principio, el
bloque no se mueve porque, al aumentar F, la fuerza de fricción estática fre también aumenta (su
magnitud se mantiene igual a F).
Capítulo N°5
4
En la Figura 5-2 c, muestra las fuerzas cuando F tiene un valor crítico. Si F excede dicho valor, el
bloque ya no estará en equilibrio. Para un par de superficies dado, el valor máximo de fre depende de
la fuerza normal. Los experimentos han revelado que, en muchos casos, ese valor máximo, llamado
(fre MAX, es aproximadamente proporcional a N; llamamos coeficiente de fricción estática al factor de
proporcionalidad e.
En la Figura 5-2 d, cuando se inicia el deslizamiento del bloque, la fuerza de fricción suele disminuir; es
más fácil mantener el bloque en movimiento que ponerlo en movimiento. Por lo tanto, el coeficiente
de fricción cinética suele ser menor que el de fricción estática para un par de superficies dado. Si
comenzamos con una fuerza aplicada igual a cero y aumentamos gradualmente la misma, la fuerza de
fricción varía un poco, como se muestra en la Figura 5-2 e.
a)
b)
N
c)
N
d)
F
F
fre
fre
Mayor fuerza
aplicada, el bloque a
punto de deslizarse.
Fricción estática
fre = e . N
Fuerza aplicada de
pequeña magnitud,
el bloque permanecerá en reposo.
fre < e . N
F
frc
P
P
P
No se aplica
fuerza, el bloque
está en reposo.
Sin fricción.
fre =0
N
N
P
El bloque se desliza
con rapidez
constante.
Fricción cinética
Frc =c . N
fr
e)
fre MAX.
frc
F
Bloque en reposo:
Bloque en movimiento:
La fricción estática es igual a la
fuerza aplicada
La fricción cinética es constante
Figura 5-2
5-3 Dinámica del movimiento Circular
En el movimiento circular uniforme vimos que cuando una partícula se mueve en un círculo
con rapidez constante, su aceleración siempre es hacia el centro del círculo (perpendicular a la
velocidad instantánea). La magnitud aRAD de la aceleración es constante y está dada en términos de la
rapidez v y el radio R del círculo por
aRAD = v2/R
El subíndice “rad” nos recuerda que en cada punto la aceleración siempre es radial hacia el
centro del círculo, perpendicular a la velocidad instantánea. El movimiento circular uniforme, como
todos los movimientos de una partícula, se rige por la segunda ley de Newton. Para hacer que la
Capítulo N°5
5
v
partícula acelere hacia el centro del círculo, la fuerza neta sobre la
partícula debe estar dirigida siempre hacia el centro (Figura 5-3). La
magnitud de la aceleración es constante, así que la magnitud de la
fuerza neta también debe ser constante. Si deja de actuar lafuerza
neta hacia adentro, la partícula saldrá disparada en una línea recta
tangente al círculo
La magnitud de la aceleración radial está dada por aRAD =
2
V /R, así que la magnitud de la fuerza neta sobre una partícula de
masa m, es:
Fneta = m . aRAD = m . v2/R
a
a
v
F
F
a
F
v
Figura 5-3
5-4 Ejemplos de problemas de Dinámica del movimiento Circular
a) Péndulo cónico:
Se llama péndulo cónico a un cuerpo de masa m sujeto al extremo de una cuerda de longitud L, que
describe una trayectoria circular en el plano horizontal, generando una superficie cónica (Figura 5-4).
Fy = 0
T cos  - m .g = 0
T = m .g/cos 
Fx = m . aRAD
T . sen  = m v2/R
[m .g/cos q. sen  = m v2/R
v2 = R . g . tg 
y
T . cos 

L

R
x
T . sen 
aRAD
m
m .g
Figura 5-4
b) Vuelta a una curva plana:
aRAD
Fy = 0
N - m .g = 0 → N = m .g
Fr = . N =  . m . g
Fx = m . aRAD
Fr = m . aRAD
 . m . g = m v2/R
v MAX =  . R . g
 . g . R = v2 →
R
Fr
m .g
y
c) Curva Peraltada:

Fy = 0
N cos - m .g = 0 → N = m .g/ cos 
N
x

Fx = m . aRAD
N . sen  = m . aRAD
[m .g/ cos  . cos  = m v2/R
v2MAX= g . tg  . R
m.g
R = 150 m
y
aRAD
x
Capítulo N°5
N
6
N . sen 
N . cos 
m.g
d) Movimiento circular vertical (MCUV):
A
PUNTO A:
Fy = m . aRADA
T + m . g = m . vA2/R
T
T


m.g
T
aRADC
vC
B
m.g
T
C
x
aTGC
m.g
y
vD
PUNTO D:
Fx = m . aRADD
T + m . g . sen  = m . vD2/R
m.g.sen 
aRADC
x
Capítulo N°5
D
m.g
PUNTO B:
Fy = m . aRADB
T - m . g = m . vB2/R
PUNTO C:
Fx = m . aRADC
T = m . vC2/R
Fy = m . aTGC
m . g = m . aTGC
aTGC = g
m.g.sen 
7
D

T m.g
m.g.cos 
y
aTGD
m.g.cos 
m.g
C