Trabajo Práctico No

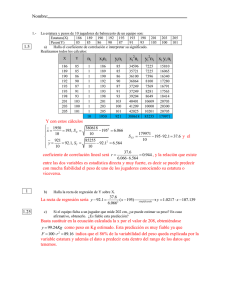
MATEMÁTICA Y ESTADÍSTICA
Trabajo Práctico No.12: Análisis de Correlación lineal simple
Contenido: Correlación lineal aplicaciones, cálculos e interpretación: Coeficiente de correlación “r” de
Pearson. Pruebas de significancia de “r”: prueba de “t”, uso de tablas. Límites de confianza de “r”.Test de
hipótesis sobre la población de “r”, Transformación de Fisher para “r” en “z”. Comparación de dos
coeficientes de correlación.
Lecturas recomendadas: Spiegel, 1991. Cap.13:289-321; Cap.14:322-356; Cap.17:411-439. Sokal &
Rohlf, 1979. Cap.4: 444-537; Cap.15:541-600. Zar, J. H., 1984. Cap. 19: 306-313. Merodio, 1986.
Cap.4: 57-65.
Idea principal
El objetivo de un estudio de dos variables cuantitativas simultáneamente, es obtener una medida
matemática de la relación entre las dos variables y dar una medida de la incertidumbre de la relación
hallada. En los casos en los que existe una relación funcional entre ambas variables se realiza análisis de
regresión. Si se trata de dos variables independientes se realiza un análisis de correlación.
La CORRELACIÓN estudia el comportamiento conjunto de dos variables aleatorias referidas a dos
características diferentes de un mismo objeto. La correlación es una técnica exploratoria que se usa para
examinar si los datos de dos variables están significativamente relacionados, en otras palabras, si los
valores de ambas variables cambian consistentemente juntos en algún sentido. Por ejemplo si el
incremento de una va acompañado por el decrecimiento de la otra. No existe ninguna expectativa que el
valor de una variable permita predecir el valor de la otra, o que no hay ninguna relación causal entre
ellas. El Coeficiente de Correlación mide la intensidad de la relación mutua entre ambas variables. Este
coeficiente considera que existe una relación lineal entre dos variables, pero ninguna de ellas se asume
que sea funcionalmente dependiente de la otra.
Los gráficos de dispersión en los que se representan pares (x,y) obtenidos de las observaciones, dan una
primera idea de la naturaleza de la relación entre dos variables. Ellos permiten analizar:
* El sentido, positivo o negativo. Se dice que la relación es positiva cuando a valores mayores de una
variable le corresponden en general valores mayores de la otra y negativa en el caso que a valores
menores de una variable le corresponden valores mayores de la otra
* La forma que podrá ser lineal, cuadrática etc. o en algunos casos no estar definida o clara.
* La intensidad, fuerte o débil, que esta dada por el grado de proximidad de los puntos a la gráfica que
supone describe el comportamiento de una función de la otra.
PARA EL DESARROLLO DEL TP SE REQUIERE EL USO DE LAS TABLAS DE VALORES CRÍTICOS DEL
COEFICIENTE DE CORRELACIÓN “R” DE PEARSON; TRANSFORMACIÓN F DE FISHER; ZR, PARA EL
COEFICIENTE DE CORRELACIÓN “R” DE PEARSON, TRANSFORMACIÓN F DE FISHER , Zr, EN EL
COEFICIENTE DE CORRELACIÓN “r” DE PEARSON .
12.1) a) Plantee un problema GEOLÓGICO que debería ser resuelto mediante la aplicación de
un análisis de correlación.
.................................................................................................................................................
.................................................................................................................................................
..........................................................................................................................................
b) Completar:
En un problema de correlación interesa explorar la relación de la variable “y” en función de
“x” y viceversa y lograr una medida de la intensidad de la relación entre ambas. El
coeficiente de correlación de Pearson es una medida de asociación lineal entre ambas
variables.
 El coeficiente de correlación varía entre ...........................................
 El signo del coeficiente de correlación indica ...........................................................
 La magnitud del coeficiente indica la .......................... de la correlación lineal. Si su
valor absoluto fuese 1, esto indicaría que..................................................................
y en el caso que fuera 0, indicaría que ......................................................................
c) Dados los siguientes valores del coeficiente de correlación: 0; -0,9; 0,7; 0,05;
¿Con qué gráfica asociaría mejor cada uno de ellos?
52
MATEMÁTICA Y ESTADÍSTICA
5.5
4.5
4.0
4.5
3.5
3.0
Y
Y
3.5
2.5
2.5
2.0
1.5
1.5
1.0
0.5
0.5
0.5
1.5
2.5
3.5
4.5
5.5
6.5
7.5
0.8
1.2
1.6
2.0
2.4
X
2.8
3.2
3.6
X
4.5
5.5
4.0
4.5
3.5
3.0
Y
Y
3.5
2.5
2.5
2.0
1.5
1.5
1.0
0.5
0.5
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
X
X
12.3) En las primeras etapas de exploración de yacimientos vetiformes de oro en la provincia
de Santa Cruz, se realizó un muestreo preliminar de la veta Carla aproximadamente cada 30
metros. En cada punto de muestreo se midió la potencia de la veta. La tabla muestra los
resultados de los análisis químicos (gr/t) y la potencia de la veta (m)
Ley (gr/t)
0.5
0.6
0.5
0.7
2
2
2
2
2
2.1
Potencia (m)
50
52
51
61
70
72
69
58
73
74
Ley (gr/t)
2.1
2.1
2.2
2.3
2.3
3.1
3.5
4.3
4.4
4.6
Potencia (m)
69
75
80
82
83
90
95
101
103
105
Ley (gr/t)
5.8
6.9
12.6
10.4
13.8
5.3
2.7
3.2
4.3
3.9
Potencia (m)
120
220
430
340
450
112
87
94
100
97
¿Existe alguna relación entre la potencia y la ley? Construya el gráfico bivariado de
dispersión. Realice una prueba de hipótesis para verificar que la relación potencia-ley se
encuentra en toda la veta.
12.4) El Complejo Volcánico Planchón- Peteroa se ubica en la Cordillera de Los Andes a los
35º 15´ L.S. y 70º 35´ L.O. incluye dos cumbres principales: al norte, el volcán Planchón
(3920 m s.n.m.) y 5 km al sur el volcán Peteroa (4107 m s.n.m.). Entre los cráteres
actualmente hay manifestaciones fumarólicas con emisiones difusas de dióxido de carbono
(flujo de CO2) asociadas a la actividad geotermal. Varios autores sostienen que el flujo de
CO2 puede incrementar notoriamente antes de una erupción. En 2010 se observo un
aumento de la actividad de las fumarolas. Con el objeto de monitorear el comportamiento del
volcán se realizó un muestreo de las emisiones de CO 2 (mol.m -2 dia-1) el área de Termas del
Azufre (flanco oriental del volcán) y se midió simultáneamente la temperatura de las
columnas de vapor (°C).
CO2
52
100
530
870
1200
1750
1803
1950
2400
2860
3000
3500
T
25
27
32
38
41
43
45
46
48
50
53
55
a) ¿Cómo es la distribución de la variable CO 2? Transforme los datos para
normalizarlos.
53
MATEMÁTICA Y ESTADÍSTICA
b) Construya el gráfico bivariado de dispersión, utilice los datos transformados. ¿Existe
alguna relación entre la concentración de CO2 y la temperatura del vapor? Realice
una prueba de hipótesis para verificar que la relación CO2 y la temperatura del vapor.
12.5) El glaciar alpino Argualas se ubica en el sudoeste de los Pirineos centrales,
anualmente presentas movimientos verticales y horizontales. Entre 1991 y 2000 se llevaron
a cabo mediciones de precisión (mm) del desplazamiento horizontal y vertical, del glaciar
utilizando 16 mojones de acero y “estación total”. En la tabla que se presenta a continuación
se indica el movimiento horizontal (MH) y vertical (MV) de los 16 mojones.
a) Construya el gráfico bivariado de dispersión (MH en el eje de las "x", MV en el eje de las "y")
¿Existe alguna relación entre los movimientos de estos puntos de control?. Realice una
prueba de hipótesis para verificar que la relación entre los movimientos se produce en todo el
glaciar.
Muestra
1
2
3
4
5
6
7
8
MH
0,13
0,26
2,49
3,6
2,25
2,05
1,37
0,72
MV
-0,23
-0,26
-0,62
-0,74
-1,44
-0,96
-0,60
-1,37
Muestra
9
10
11
12
13
14
15
16
MH
0,72
2,62
2,87
3,81
3,17
3,18
2,53
0,22
MV
-0,72
-1,72
-1,50
-1,45
-1,69
-1,70
-1,93
-0,43
b) Interesa conocer si la relación movimiento vertical-movimiento horizontal del glaciar Argulas
puede considerarse que es la misma que experimentan otros glaciares de los Pirineos cuyo
coeficiente de correlación es  = -0,73. Justifique su respuesta indicando hipótesis nula,
alternativa y nivel de significación de la prueba.
Se sugiere analizar las características de las relaciones sugeridas por el gráfico bivariado.
Realizar la transformación de Fisher del r calculado y de  y hacer el Test de hipótesis.
c) Se estudió también la relación entre los movimientos en glaciares de manto en 20 puntos de
control en la Antártida. El coeficiente de correlación calculado para esas estaciones es r =-0,69.
¿Pude considerarse que los movimientos que experimentan los glaciares alpinos y de manto
son semejantes, es decir pertenecen a la misma población? En caso afirmativo, ¿cuál es el
coeficiente de correlación de esa población? Justifique su respuesta indicando hipótesis nula,
alternativa y nivel de significación de la prueba.
Se sugiere realizar las transformaciones de Fisher para ambos r antes de hacer el Test de
hipótesis. Si acepta la hipótesis nula enunciada, calcule el coeficiente de correlación común. No
olvide expresar el resultado “z” como “r”.
12.6) Los cuerpos de agua ubicados en la zona sur del conurbano bonaerense entre Buenos
Aires y La Plata está surcada por una docena de arroyos que drenan la región en forma
perpendicular a la orilla del Río de la Plata. Estos cuerpos de agua son receptores de las
aguas residuales de la intensa actividad humana que presenta la región caracterizada por:
zonas con altas densidades poblacionales y de radicación industrial, zonas semi-rurales, con
baja densidad poblacional y algunas actividades productivas hortícolas intercaladas con
terrenos naturales.
En un trabajo de investigación se tomaron 56 muestras de agua de los arroyos. Una vez
obtenida la muestra se determinaron en el lugar la temperatura, la conductividad eléctrica, el
pH, y el oxígeno disuelto. Las botellas se transportaron en una conservadora en frío hasta
llegar al laboratorio. Allí se analizó el contenido de materia orgánica, (demanda química de
oxígeno, DQO y demanda bioquímica de oxígeno, DBO5).
La tabla que se presenta a continuación muestra los coeficientes de correlación entre las
variables.
Describa como son las relaciones entre variables (+, -) completando el triangulo superior
derecho de la tabla e indique que relaciones son significativas realizando pruebas de
hipótesis.
54
MATEMÁTICA Y ESTADÍSTICA
Temp.
Temp.
Ox. Dis.
pH
CE
DQO
DBO5
1
Ox. Dis.
0.1280
1
pH
0.0603
0.7812
1
CE
0.1303
-0.4427
-0.2701
1
DQO
DBO5
0.1049
0.0388
-0.3166
-0.3474
-0.2162
-0.2312
0.3795
0.3720
1
0.9515
1
12.7) En un trabajo de campo realizado en una quebrada en la Puna Argentina se ha medido el
espesor, en metros, de 2 secuencias rocosas (A y B). Los espesores de ambas unidades
aumentan paulatinamente desde el inicio de la quebrada hacia aguas arriba. Las medidas
efectuadas en cada estación se indican a continuación.
Estación
1
2
3
4
5
6
Espesor (m)
Unidad A
Unidad B
(x)
(y)
50
50
60
85
70
110
75
140
80
170
90
200
Espesor total (%)
Unidad A
Unidad B
(x’)
(y’)
50,0
50,0
41,4
58,6
38,9
61,1
34,9
65,1
32,0
68,0
31,0
69,0
¿Puede Ud. asegurar que existe algún tipo de vinculación entre el espesor de ambas
secuencias? Justifique su respuesta utilizando argumentos estadísticos. Para responder puede
seguir los pasos indicados a continuación:
a) Calcule la media, la desviación estándar y el coeficiente de variación de cada una de las
variables (x e y).
b) Realice un diagrama de dispersión x (en abscisas) e y (en ordenadas). ¿Cuáles son las
características de las relaciones sugeridas por el gráfico obtenido?
c) Calcule el coeficiente de correlación de Pearson (r).
d) Efectúe una prueba de significación del coeficiente de correlación (r). Utilice la tabla
disponible para tal fin.
d) Los datos obtenidos fueron convertidos a porcentajes de manera que cada par de valores
expresa la proporción relativa de cada unidad en una misma estación (columna x’e y’ de la
tabla de datos). ¿Puede Ud. afirmar que los resultados obtenidos con los datos originales y los
datos transformados son los mismos? Justifique su respuesta utilizando argumentos
estadísticos.
 Realice un diagrama de dispersión x’- y’ ¿Cuáles son las características de las
relaciones sugeridas por el gráfico obtenido?
 Calcule el coeficiente de correlación de Pearson (r) y realice una prueba de significación
para el mismo.
El problema de la suma constante: uno de las prácticas habituales en el tratamiento de datos es su
transformación de forma que para un espécimen o individuo la suma de todas las componentes
individuales sea constante (i.e. 100%).como sucede cuando se estudia la composición geoquímica
de rocas y minerales. Datos expresados como parte del todo (porcentajes o partes por millón –ppm-)
se conocen como datos composicionales. Este es un mecanismo sencillo que permite realizar
comparaciones entre muestras, sin embargo puede conducir a resultados espurios e inducir a
interpretaciones erróneas de los datos.
Esto se produce pues los porcentajes son razones numéricas complejas que contienen variables en
su denominador que representan todos los constituyentes a ser examinados. Esto trae aparejado
que los componentes de porcentajes no sean libres de variar independientemente. A medida que la
proporción de un componente aumenta, la proporción de uno o más de los otros componentes debe
decrecer. Por ejemplo si se analiza el quimismo de una roca y el contenido en sílice fuera 61,5%,
entonces el contenido de alúmina no podrá ser cualquier valor, estará restringido a ser igual ó menor
55
MATEMÁTICA Y ESTADÍSTICA
que (100 – 61,5)%. El siguiente óxido que forme parte de esta roca se verá también restringido por el
contenido de los dos elementos anteriores.
Una de los problemas que se producen al analizar datos composicionales es que se introduce un
sesgo negativo en las correlaciones, como se acaba de demostrar con los datos del ejercicio.
(Aitchison, 1986; Rollinson, 1993)
56
MATEMÁTICA Y ESTADÍSTICA
Trabajo Práctico No.13: Regresión lineal simple
Contenido: Regresión lineal simple aplicaciones, cálculos e interpretación: recta de regresión. Test de
hipótesis sobre el coeficiente de regresión: ANOVA de la regresión, test de “t”. Límites de confianza del
coeficiente de regresión.
Lecturas recomendadas: Spiegel, 1991. Cap.13:289-321; Cap.14:322-356; Cap.17:411-439. Sokal &
Rohlf, 1979.Cap.14:444-537; Cap.15:541-600. Zar, J.H., 1984, Cap. 17: 261-273. Merodio, 1986. Cap.4:
57-65. Davis, 1973. Cap.5: 192-222.
Idea principal
El análisis de REGRESIÓN enfoca el problema de explorar y modelar la relación existente entre una
variable aleatoria, respuesta, “y”, llamada variable dependiente y otra variable, controlada por el
investigador “x”, explicativa denominada variable independiente. Esto significa que la magnitud de una
de las variables (la dependiente) está determinada ó es función de la magnitud de la segunda variable (la
independiente). Cuando la relación puede expresarse a través de una recta se denomina regresión lineal,
y se agrega el adjetivo de simple pues sólo considera el caso de 2 variables. En la practica la regresión
se puede usar en situaciones donde la variable dependiente es difícil medirla o cuesta muy caro hacerlo,
pero puede ser estimada por otra variable con la que está relacionada por una función lineal.
Para el desarrollo del TP se requiere el uso de las tablas de probabilidades “t” y “F”.
13.1) a) Complete con la variable dependiente o independiente según corresponda
Variable respuesta
Variable explicativa
Presión litostática
Tamaño de los cristales en rocas plutonicas
Pendiente de sedimentos
Densidad de un magma
Selección de sedimentos epiclasticos
Granulometría de cenizas volcánicas
13.2) En las altas latitudes, los días que nieva son esperados por los alumnos de primaria y
secundaria por que existen grandes posibilidades que se suspendan las clases. Un director de
escuela en El Bolsón (Chubut) formuló la hipótesis que podría haber una relación entre la
cantidad de nieve caída durante las 24 horas previas y el número de días que se suspenden
las clases. El director analizó los siguientes datos
Nieve caída (cm)
Días de escuela cerrada




3
5
6
13
9
16
12
14
15
18
18
23
21
20
24
32
27
29
30
28
¿Cuál fue su conclusión?
Calcule la ecuación de la recta (y=a + bx), donde a representa la ordenada al origen y b
la pendiente o coeficiente de regresión. En un diagrama bivariado dibuje los datos y la
recta calculada.
¿Cuánta variabilidad de los días de escuela cerrada es explicada por la recta
calculada?
Realice una prueba de hipótesis que le permita asegurar al director de la escuela que la
tasa de nieve caída es significativamente distinta de 0.
13.3) Durante el 12 y el 15 agosto de 1991 el volcán Hudson, ubicado en el sur de Chile, hizo
erupción. Sus cenizas cubrieron parte de la Patagonia argentina y chilena provocando un gran
impacto sobre la agricultura, economía y diversos aspectos psico-sociales de las comunidades
rurales.
Evaluar el impacto de las cenizas sobre la economía del lugar es muy complejo y requiere
analizar numerosas variables, la densidad de las cenizas (g/ml) y la distancia al volcán (km)
son solo un par de ellas. La tabla presenta datos de estas dos variables tomadas en campos de
la Patagonia que fueron cubiertos por las cenizas
57
MATEMÁTICA Y ESTADÍSTICA
Densidad
Distancia
Densidad
Distancia
Densidad
Distancia
0,61
19
0,82
48
1,03
98
0,54
19
0,8
48
0,99
98
0,54
20
0,79
65
1,02
100
0,61
20
0,87
65
1,06
145
0,75
29
0,86
65
1,05
120
0,82
35
0,93
65
1,19
121
0,65
35
0,8
70
1,1
35
0,91
35
1,18
90
0,93
98
a) Se necesita determinar si la densidad de las cenizas está en función a la distancia al volcán.
Para contestar la pregunta realice un análisis de regresión:
i) Construya el gráfico bi-variado de dispersión de las variables X e Y. Incluya un punto más
cuyas coordenadas correspondan a los promedios de cada una de las variables.
ii) Calcule la ecuación de la recta (y=a + bx), donde a representa la ordenada al origen y b la
pendiente o coeficiente de regresión.
iii) Estime la densidad de las cenizas para una distancia de 110 km del volcán.
iv) Trace la recta de regresión sobre el gráfico de dispersión de ambas variables.
v) Calcule la varianza explicada y la no explicada (%) por la regresión.
vi) Efectúe un ANOVA sobre la significancia de la varianza explicada y no explicada por la
regresión.
vii) Interprete geológicamente los resultados.
b) También interesa establecer si la densidad de las cenizas aumenta a medida que nos
alejamos del volcán.
Se recomienda realizar un test de “t” sobre el coeficiente de regresión. Analice detenidamente
si se trata de un test a 1 cola (¿superior o inferior?), o a 2 colas. Justifique su elección.
Interprete geológicamente los resultados.
13.4) En un intento de interpretar las condiciones ambientales en las que se desarrolló una
cuenca sedimentaria del Paleozoico inferior se ha estudiado un largo testigo que atraviesa una
espesa sucesión estratigráfica de esta edad. Se trata de una unidad clástica constituida por
capas de arcillas intercaladas con arenas, perteneciente a un ambiente marino offshore (aguas
afuera). El geólogo ha postulado que la cuenca se ha llenado paulatinamente, y que la línea de
costa ha avanzado en dirección a la perforación, conforme a ello, el espesor de las capas de
arena ha aumentado. La unidad contiene cientos de capas por lo que se optó por medir el
espesor de las capas de arena que se encuentran a intervalos regulares de 10 cm. A
continuación se muestran las estimas de los parámetros (a y b) de una regresión como así
también sus respectivos errores y los resultados del ensayo de hipótesis efectuados a los
parámetros y la regresión realizados con un software estadístico. Interprete geológicamente
los resultados.
Regression Statistics
Multiple R
0.7627
R Square
0.5817
Adjusted R Square
0.5730
Standard Error
2.5239
Observations
50
Parametros Coefficients Standard Error t Stat P-value
Intercept
4.25
0.72
5.86 4.09E-07
Intervalo
0.02
0
8.17 1.22E-10
ANOVA
df
SS
MS
F
Significance F
Regression
1
425.18
425.18
66.75
1.22 E-10
Residual
48
305.76
6.37
Total
49
730.94
58