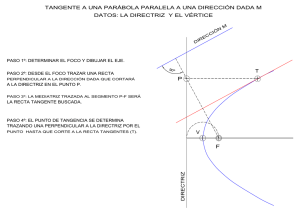
deformación de piezas prismáticas

CAPITULO 13
DEFORMACIÓN DE PIEZAS
PRISMÁTICAS
Planteamiento: Sea la pieza prismática AB que
se encuentra sometida a la acción de cargas y
ligaduras
B
y
x
Z
z
Sistema de ejes
locales en cada sección
A
Y
X
Sistema de ejes
globales
Objetivo: Determinar la nueva geometría
que adquiere la pieza
Procedimiento: Vamos a ver como se deforma una
rebanada genérica de la pieza y, luego, por integración,
Obtendremos la deformada de la pieza prismática
Los vectores de desplazamiento y de giro de una sección de la
pieza prismática tendrán tres componentes cada uno en el
sistema de referencia local
u
G
θ
⎧u x ⎫
r ⎪ ⎪
u = ⎨u y ⎬
⎪u ⎪
⎩ z⎭
⎧θ x ⎫
r ⎪ ⎪
θ = ⎨θ y ⎬
⎪θ ⎪
⎩ z⎭
Consideremos una rebanada y analicemos su cambio
de geometría para los diferentes tipos de esfuerzos:
y
x
z
ds
DEFORMACIÓN DE UNA REBANADA POR
ESFUERZO AXIL
y
x
N
G
z
N
ds duz
ds
σ
N
du z = ε ds = ds =
ds
E
AE
LA HIPÓTESIS DE NAVIER (FLEXIÓN)
Una cara de cualquier rebanada, que era plana antes de
deformarse la pieza, sigue permaneciendo plana una vez
que la pieza se ha deformado.
DEFORMACIÓN DE UNA REBANADA POR
MOMENTO FLECTOR
C
Μx h2
σCσ =
y
Ιx
2
h2
G
Canto
Mx
x
h1
Hipótesis de Navier
A
σAσ =
1
SECCION
σA =
M x AG
Ix
2CD = ε CC' ds =
ALZADO LATERAL
( compresión )
M CG
σC = x
Ix
2 AB = ε AA' ds =
Μx h1
Ιx
( tracción )
σA
E
σC
E
ds =
M x AG
ds
EI x
ds =
M x CG
ds
EI x
dθ x
Mx
AB CD
=
=
=
ds
2
AG CG 2 EI x
Mx
dθ x =
ds
EI x
CURVATURA: κ
= 1/ρ
ρ ⋅ dθ = ds = dx
dθ
dθ M
κ= =
=
ρ dx EI
1
y
ρ
ds
dx
x
DEFORMACIÓN DE UNA REBANADA POR
ESFUERZO CORTANTE
y
duy
τ
du y = γ ds = m ds
G
x
G
τm =
z
Qy
ds
γ
ds
Qy
Ωc
El área a cortante Ωc depende de la geometría de la sección y, en general, se
puede escribir como: Ωc=Ω/k. Para el caso de una sección rectangular k=6/5
(para el caso de una sección circular, por ejemplo, k=10/9)
du y = γ ds =
Qy
GΩ c
ds
DEFORMACIÓN DE UNA REBANADA POR
MOMENTO TORSOR
y
x
ωdz
Mz
G
ds
Mz
z
ds
Mz
dθ z = ω ds =
ds
GK
¿Podríamos calcular ya los desplazamientos en algún
elemento estructural simple que se encuentre cargado?
Supongamos que nos piden los desplazamientos (horizontal y
vertical) del extremo B de la ménsula de la figura sometida a la
carga inclinada que se indica:
F
45º
A
B
L
La carga anterior puede descomponerse en sus dos componentes:
F
2
2
F
A
B
2
2
2
L
2
F
F
A
2
2
F
B
A
Ley de axiles
2
2
B
A
Ley de cortantes
Ley de flectores
y
y
y
A
z
z
A
B
B
z
B
B
A
z
L-z
y
VB
A
dVB
z
B’
z
WB
⎛
wB =
L⎜ F
∫0 ⎜⎜
⎝
⎞
F 2 L
2 ⎟ dz =
2
⎟
EΩ ⎟
EΩ
⎠
2
⎞
F 2 L
⎟
2
2
vB = ⎜
dz =
⎟
0 ⎜ GΩ c ⎟
GΩ c
⎝
⎠
∫
⎛
L⎜ F
2
M (z )
dz ⋅ (L − z ) =
EI
dVB = dθ ⋅ (L − z ) =
=
VB =
F 2
F 2
EI
(L − z )
2
EI
2
L
dz ⋅ (L − z )
∫0 (L − z )
2
dz =
F 2
3
2 ⋅L
EI
3
FÓRMULAS DE NAVIER-BRESSE
B
y
x
z
Z
r
r = PB
P
A
Y
X
Giro sólido
rígido
r
r
B
Suma de giros de
las rebanadas
r
θ B = θ A + ∫ dθ
Desplazamiento inducido
por los giros de las rebanadas
A
r r
r r
B r
B
v
v
u B = u A + θ A ∧ rAB + ∫ du + ∫ dθ ∧ r
A
Desplazamiento
sólido rígido
A
Desplazamiento inducido
por los propios de las rebanadas
PIEZA PLANA CON CARGAS EN SU PLANO
Y
B
A
Z
Esfuerzos y desplazamientos en ejes locales:
Qx = Mz = My = 0
ux = θy = θz = 0
Mx = M
uy = v
Giros y desplazamientos en ejes globales:
BM
ds Criterios de signos:
θB = θ A −
A EI
∫
∫
θx = θ
Giros Momentos
⎞
N
Q
v B = v A + θ A (Z B − Z A ) + ⎜⎜
dY +
dZ ⎟⎟ −
A ⎝ EΩ
GΩ c
⎠
B⎛ N
⎞
Q
wB = w A + θ A (YB − Y A ) + ⎜⎜
dZ −
dY ⎟⎟ +
A ⎝ EΩ
GΩ c
⎠
∫
B⎛
Qy = Q
uz = w
BM
∫A EI (Z B − Z )ds
BM
∫A EI (YB − Y )ds
M
θB =θA − ∫
ds
A EI
B
B
B
A
θA
A
θA
M
ds
EI
M
ds
EI
B
A
A
B
⎞ BM
Q
⎜
(Z B − Z )ds
dZ ⎟⎟ −
v B = v A + θ A (Z B − Z A ) + ⎜
dY +
A ⎝ EΩ
A
GΩ c
EI
⎠
B⎛ N
⎞ BM
Q
(YB − Y )ds
dZ −
dY ⎟⎟ +
wB = w A + θ A (YB − Y A ) + ⎜⎜
A ⎝ EΩ
A
GΩ c
EI
⎠
∫
B⎛ N
∫
∫
?
∫
Y
B
A
Z
WA
VA
Y
WA
θA(ZB- ZA)
Y
B
θA
B
θA(YB- YA)
VA
A
Z
A
Z
B⎛ N
⎞ BM
Q
(Z B − Z )ds
dZ ⎟⎟ −
v B = v A + θ A (Z B − Z A ) + ⎜⎜
dY +
A ⎝ EΩ
GΩ c
⎠ A EI
B⎛ N
⎞ BM
Q
(YB − Y )ds
dY ⎟⎟ +
wB = w A + θ A (YB − Y A ) + ⎜⎜
dZ −
A ⎝ EΩ
GΩ c
⎠ A EI
∫
∫
∫
∫
N
ds
EΩ
Y
α
N
N
ds ⋅ senα =
dy
EΩ
EΩ
B
ds
α
A
N
N
N
dz
ds ⋅ cosα =
EΩ
EΩ
N
Alargamiento
por axil
Z
⎞
N
Q
v B = v A + θ A (Z B − Z A ) + ⎜⎜
dY +
dZ ⎟⎟ −
A ⎝ EΩ
GΩ c
⎠
B⎛ N
⎞
Q
⎜
dZ −
dY ⎟⎟ +
wB = w A + θ A (YB − Y A ) + ⎜
A ⎝ EΩ
GΩ c
⎠
∫
B⎛
∫
B
A
∫A EI (Z B − Z )ds
BM
∫A EI (YB − Y )ds
α
Q
Q
ds ⋅ cosα = −
dz
GΩ c
GΩ c
Y
BM
Q
ds
GΩ c
B
−
α
A
ds
Q
Q
Z
Q
Q
ds ⋅ senα = −
dy
GΩ c
GΩ c
B⎛ N
⎞ BM
Q
(Z B − Z )ds
v B = v A + θ A (Z B − Z A ) + ⎜⎜
dY +
dZ ⎟⎟ −
A ⎝ EΩ
GΩ c
⎠ A EI
∫
∫
⎞ BM
N
Q
⎜
(YB − Y )ds
dZ −
dY ⎟⎟ +
wB = w A + θ A (YB − Y A ) + ⎜
A
A ⎝ EΩ
GΩ c
EI
⎠
∫
B⎛
∫
B
A
M
(YB − Y )ds
EI
Y
YB
M
ds
EI
B
−
M
(Z B − Z )ds
EI
Y
A
Z
Z
ZB
PIEZA RECTA CON CARGAS EN SU PLANO
ds = dz
dy = 0
θ B = θ A − ∫A
B
y A = yB = 0
M
dz
EI
BM
Q
v B = v A + θ A (z B − z A ) + ∫A
dz − ∫A (z B − z )dz
GΩ c
EI
B
N
w B = w A + ∫A
dz
EΩ
B
Ejemplo: Determinar la flecha en B
Ley de cortantes
P
A
B
P.l
w A = wB
Ley de flectores
A
B
B P (L − z )
−P
(l − z )dz
v B = ∫A
dz − ∫A
GΩ c
EI
B
PL
P ⎡ (L − z ) ⎤
vB = −
− ⎢−
⎥
GΩ c EI ⎣
3 ⎦ z =0
Flexión
PL PL3
−
vB = −
GΩ c 3EI
3
Cortante
P
z =l
Pero, ¿qué sucede en la práctica?
v
y
h
cor tan te
B
v flexión
B
x
c
tan te
v cor
B
v flexión
B
PL
=−
GΩ c
PL3
=−
3EI
1 3
2
3E ch
GΩ c
3EI
h
⎛ ⎞
12
=
=
=
=
0
,
6
⎜ ⎟ (1 + ν )
3
2
E
ch
PL
GΩ c L
2
⎝L⎠
⋅
L
3EI
2(1 + ν ) 1,2
PL
Si hacemos, por ejemplo, L/h = 50, ν=0,2, el cociente
anterior resulta ser 0,000288.
La flecha debida al cortante es despreciable (0,03%)
frente a la de flexión.
En Resistencia de Materiales suele despreciarse la
contribución del esfuerzo cortante en el cálculo de
las flechas del elemento estructural.
Esto, de ninguna manera, quiere decir que los esfuerzos
cortantes sean nulos.
Pieza recta con cargas en su plano despreciando las
deformaciones inducidas por esfuerzo cortante y esfuerzo axil
M
θ B = θ A − ∫A dz
EI
B
BM
Q
v B = v A + θ A (z B − z A ) + ∫A
dz − ∫A (z B − z )dz
GΩ c
EI
B
w B = w A + ∫A
N
dz
EΩ
θ B = θ A − ∫A
M
dz
EI
B
B
M
v B = v A + θ A (z B − z A ) − ∫A (z B − z )dz
EI
wB = wA
B
EJEMPLO:
y
q
A
¿Flecha y giro en B?
B
z
L
qL2/2
2
M=q.(L-z) /2
Ley de momentos
flectores:
A
B
l q( L − z )
M
qL3
dz = ∫
dz =
θB = ∫
0
A EI
2EI
6EI
2
B
B q ⋅ (L − z )
M ⋅ (L − z )
q ⋅ L4
v B ↓= ∫
dz = ∫
dz =
A
A
2 EI
2 EI
8 EI
B
3
Otras aplicaciones en problemas isostáticos:
A
B
M
A
A
θA
θB
B
A
θA
B
B’
θ A ⋅ L = Flecha debida a M / L + Flecha debida a M
M 3
L
ML2
L
θA ⋅ L = −
+
3 EI
2 EI
M
M/l
M/L
M/l
M/L
l
L
θA
B
⇒ θA =
ML
en sentido horario
6 EI
M
M/l
M/L
θ B (antihorario) = θ B (antihorario producido por M / l ) + θ B (antihorario producido por M ) +
+ θ A (antihorario)
θ B (antihorari o) = −
Ml Ml Ml
+
−
2 EI EI 6 EI
⇒ θ B (antihorari o) =
Ml
3EI
APLICACIÓN A PROBLEMAS HIPERESTÁTICOS
y
B
A
M
z
L
B M
B
+
A
A
R
↑v
estado I
B
= −∫
↑ v B = v Bestado I + v Bestado II = 0
B M (L − z )
M L2
estado II
dz = −
A
EI
↑ vB
2 EI
M L2 RL3
−
+
=0
2 EI 3EI
⇒
R=
3M
2L
RL3
=
3EI
ECUACIONES DE NAIER-BRESSE PARA UNA PIEZA
RECTA CON CARGAS EN SU PLANO DESPRECIANDO
LA CONTRIBUCION A LOS MOVIMIENTOS DE LOS
ESFUERZOS CORTANTES Y AXILES
M
θ B = θ A − ∫A dz
EI
B
M
v B = v A + θ A (z B − z A ) − ∫A (z B − z )dz
EI
wB = wA
B
TEOREMAS DE MOHR
Christian Otto Mohr
(1835-1918)
PRIMER TEOREMA DE MOHR
θB = θ A + ∫
B
A
M
dz
EI
⇑ v B =⇑ v A − θ A ( z B − z A ) − ∫
B
A
M
( z B − z ) dz
EI
wB = wA
Directriz sin
deformar
“El ángulo girado por
la directriz entre dos
secciones A y B de una
pieza prismática recta
de sección constante
es igual al área del
diagrama de momentos
flectores entre ambas
secciones dividido
por el producto EI”
Ley de momentos
flectores
A
B
θA
A’
B’
Directriz deformada
M
dz
A EI
θ B −θ A = ∫
B
θB
θB-θA
EJEMPLO DE APLICACIÓN DEL PRIMER TEOREMA DE MOHR
P
¿Giro en B?
Ley de momentos flectores
P.L
A
B
0
⎛1
⎞
⎜ L ⋅ (PL )⎟
PL2
2
⎠
⎝
θB −θ A =
=
EI
2 EI
(horario)
SEGUNDO TEOREMA DE MOHR
↑ v B =↑ v A − θ A (z B − z A ) − ∫
A
BM
y
B’’’
θA.(zB-zA)
A’
B’’
B’
vA
Directriz deformada
vB
A
B
z
Directriz sin
deformar
dz
zB-z
EI
(z B − z )dz
“La distancia, en dirección
perpendicular a la directriz
sin deformar, entre un punto
B’ de la directriz deformada
a la recta tangente a la
directriz deformada en otro (A)
es igual al momento estático
del área de momentos flectores
entre las secciones A y B
respecto del eje perpendicular a
la directriz sin deformar que
pasa por el punto B, dividido
por el producto EI”
EJEMPLO DE APLICACIÓN DEL SEGUNDO TEOREMA DE MOHR
y
q
¿Flecha en B?
A
B
L
z
Ley de momentos flectores
qL2/2
.G
3/4(L)
⎞⎛ 3 ⎞
⎛1
2
⎜ L.q ⋅ L / 2 ⎟⎜ L ⎟
4
pL
3
4
⎠=
⎠⎝
↓ vB = ⎝
EI
8 EI
TERCER TEOREMA DE MOHR (TEOREMA DE LA VIGA
CONJUGADA)
PL/4
P
L
VIGA REAL
LEY DE MOMENTOS FLECTORES
PL /4
VIGA CONJUGADA
PROPIEDADES DE LA VIGA CONJUGADA:
El giro absoluto que experimenta una sección de la viga
real es igual al esfuerzo cortante, en esa misma sección
de la viga conjugada, dividido por el producto EI
La flecha en un punto de la directriz de la viga real es
igual al momento flector, en la misma sección de la viga
conjugada, dividida por el producto EI
EJEMPLO:
A
B
M
L
M
M
RA
RB
θB =
RB ML
=
EI 3 EI
ECUACIÓN DIFERENCIAL DE LA ELASTICA
z
v
M (z )
=
=−
ρ
EI
1
+
d 2v
dz 2
dv dz << 1
3
2 2
⎡
dv ⎞ ⎤
⎛
⎢1 + ⎜ ⎟ ⎥
⎢
⎝ dz ⎠ ⎥⎦
⎣
M (z )
d 2v
=−
EI
dz 2
1
¿Qué representa dv/dz?
dv
dz
z
A
Directriz sin deformar
A’
v
dv
dz
Directriz deformada
Tangente en la sección
considerada
dv
dz
representa el giro absoluto experimentado por la sección
¿Qué trascendencia tiene el hecho de despreciar dv/dz en la
deducción de la ecuación diferencial de la elástica?
M
M
A
B
M
M
A
B
z
lL
En este problema no hay reacciones en los apoyos, ni esfuerzos
cortantes en las rebanadas: es un problema de flexión pura.
En la realidad (sin despreciar nada) todas las rebanadas se deforman
por igual, experimentando el mismo giro dθ:
M
dθ =
dz ⇒
EI
dθ M
=
= cte.
dz EI
dθ 1
= = cte.
dz ρ
La elástica es un arco
de circunferencia de
radio EI/M
Veamos en que se traduce la hipótesis
Ecuación diferencial de la elástica:
Integramos una vez:
Imponemos que
dv
M
=−
z+C
dz
EI
dv dz ≈ 0 en este problema
M
d 2v
=−
EI
dz 2
dv
debe ser nula en z=L/2 por simetría:
dz
C=
M L
EI 2
dv M ⎛ L
⎞
=
⎜ − z⎟
dz EI ⎝ 2
⎠
2
Integramos por segunda vez:
M ⎛L
⎞
v=−
⎜ − z ⎟ + C′
2 EI ⎝ 2
⎠
M L2 M L2
Imponemos que v debe ser nula en z=0 (apoyo): C ′ =
=
2 EI 4 EI 8
M
v=
EI
2
⎡ L2 1 ⎛ L
⎞ ⎤
⎢ − ⎜ − z⎟ ⎥
⎠ ⎥⎦
⎢⎣ 8 2 ⎝ 2
La elástica es un arco
parabólico !!!!!
OTRO EJEMPLO DE DETERMINACION DE LA ELASTICA
q
z
v
l
L
qL /22
(
q
M (z ) = L.z − z 2
2
(
q
L.z − z 2
d v
M (z ) 2
=
−
=
dz 2
EI
EI
2
)
qL /22
)
⎞
dv
q ⎛ z3
z2
⎜⎜ − L + C ⎟⎟
=
dz 2 EI ⎝ 3
2
⎠
Por simetría de la pieza, la pendiente de la tangente a
la directriz deformada en el punto z=L/2 debe ser nula,
por lo que C=L3/12
⎞
q ⎛ z4
z 3 L3 z
⎜⎜ − L +
v=
+ C ' ⎟⎟
2 EI ⎝ 12
6 12
⎠
Cuando z=0 la flecha v es nula, por lo que C’=0, y la
ecuación de la elástica es:
q ⎛ z4
L3 z ⎞
3
⎜⎜ − L z +
⎟⎟
v=
12 EI ⎝ 2
2 ⎠
La flecha máxima se produce cuando z=L/2 y su valor es:
vmax
5qL4
=
348 EI
EL DIBUJO DE LA DEFORMADA A ESTIMA
P=20 kN
A
C
B
2m
D
1m
1m
15 kN·m
Ley de flectores
5 kN·m
A
B
A
C
B
C
D
D
OTRO EJEMPLO:
237,3 kN.m
7,68 m
3,84 m
C
28,5 kN.m
D
A
B
71,5 kN.m
294,9 kN.m
63,9 kN.m
APLICACIÓN DEL PRIMER TEOREMA DE CASTIGLIANO
Energía elástica de una pieza a flexión
Mx
dθ x =
ds
EI x
M x2
dU = M x ⋅ dθ x =
ds
EI x
M x2
U =∫
ds
EI x
P.l
P
z
Ley de flectores
A
B
l
v
z = l P (l − z )
M
P (l − z )
dz =
U =∫
ds = ∫
0
=
z
EI x − 3
EI x
EI x
2
x
2
2
2
3
l
0
P 2l 3
=
− 3 EI x