PROBLEMAS DE INTEGRALES INDEFINIDAS

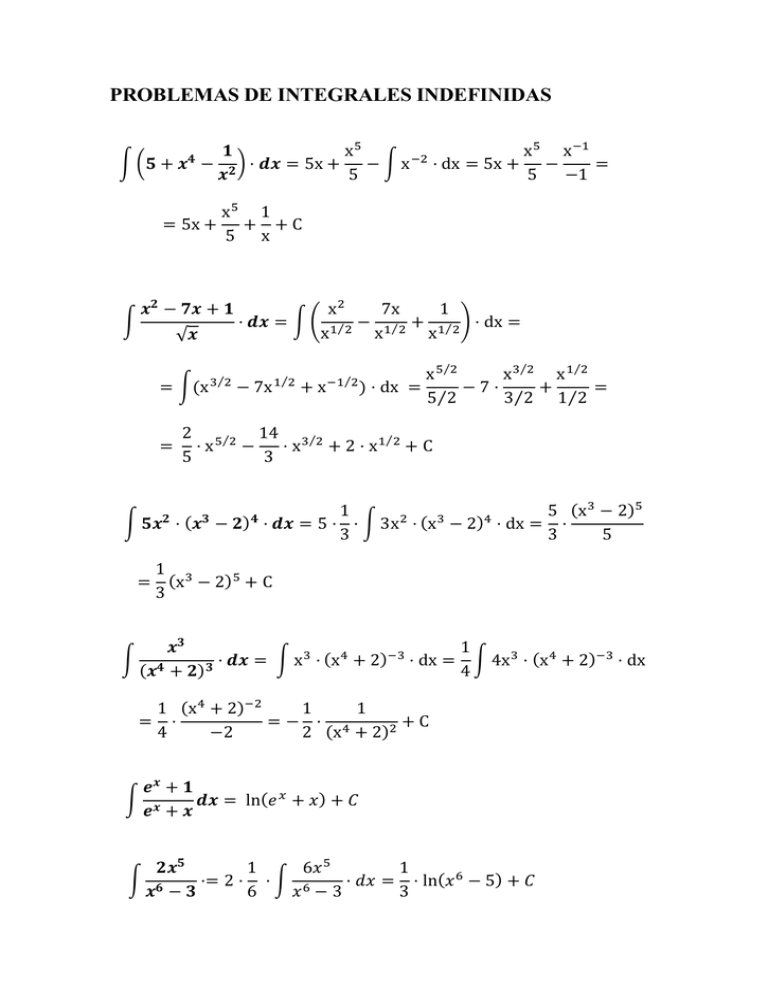
PROBLEMAS DE INTEGRALES INDEFINIDAS
Integración por partes.
Mediante la integración por partes, hallar una primitiva de la
función y = Ln (1 + x)
Calcular una primitiva de una función, es hallar su integral indefinida.
Por ello utilizaremos el método de integración por partes
 u·dv = u·v -  v·du haciendo el siguiente cambio
Aplica el método de integración por partes a la determinación de
una primitiva de la función f(x) = x · Ln x
Utilizar la integración por partes para hallar una primitiva de la
función x.sen x
Cambio de variable. (No entra en Selectividad)
Hallar las primitivas de la función cos 2x (utilizar la relación
1 + cos A = 2. cos2 A/2)
INTEGRACION FRACCIONES SIMPLES.
x3
- 1  x2 + 2x
3
2
- x - 2x
x-2
________
- 2x2
-1
+ 2x2 + 4x
____________
4x – 1
PROBLEMAS DE INTEGRALES DEFINIDAS
(PRIMITIVAS)
Calcular la primitiva de la función f(x) = 1 + tg2 x –
por el punto (,0)
0
-3
4
0
1
-1
3
0
+ tg x que pase
Para obtener la G(x) integraremos de nuevo la G'(x)
Para calcular C y D tenemos en cuenta las dos condiciones G(0) = 1 y G(1) = 0
Las constantes C, D y E se determinan a partir de las condiciones.
Para ver si el extremo (1,0) es máximo o mínimo, calculamos la f´´(x)
PROBLEMAS DE AREAS
Area comprendida entre las curvas
Corte gráfica:
e
;
.
;
Área limitada por el eje de abscisas y la curva y = x3 - 2x2. Dibújala
.
Calcular el área del recinto limitado por
abcisas. Dibuja la gráfica.
;
y el eje de
y´ = 2x - 4; y´ = 0 => 2x – 4 = 0; x = 2 posible máx. o mín.
y´´= 2 ; y´´(2) > 0
Mín. (2, -4)
4
4
0
0
Calcular el área encerrada entre las graficas de las funciones
y = x2 + 2x - 1 e y = 2x + 3, representando esquemáticamente dichas
graficas.
Para dibujar y = x2 + 2x - 1
x y
_____
-2 -1
-1 -2
0 -1
1 2
2 5
Para dibujar y = 2x + 3
x y
_____
0 3
1 5
2 7
x2 + 2x – 1 = 2x + 3  x2 – 4 = 0  x =  2
2
-2



Calcular el área limitada por la grafica f(x) = Ln x, el eje OX y la
recta tangente a dicha grafica en el punto de abscisa x = e
Para calcular la recta tangente, esta será de la forma y – yo = m ·(x – xo)
yo = Ln e = 1 pasa por (e,1)
m = y´(xo)

Para calcular los limites de integración a y b se hallan los puntos de corte entre las
dos funciones
Sabiendo que la tangente corta al eje OX en (0, 0) y en (e, 1) y que la y = Ln x lo
corta en
n x = 0  x = e0  x = 1  (1, 0)
Dibujamos la curva y su tangente
Sabiendo que  Ln x dx = x·Ln x – x por integración por partes y aplicando la regla de
e
e
0
1
;
Barrow nos queda que:
PAU Junio 1998
=
0
2π
-π
0
Considérese la región acotada que determinan las curvas y = ex
e y = e2x y la recta x = a; a) Hallar el área de dicha región para a = 1
b) Hallar un valor de a > 0 para que el área de la región sea 2.
a) Si a = 1 ==> la recta será x = 1 y este será el límite superior.
ex = e2x ==> 1 = ex ==> Ln 1 = Ln ex ==> 0 = x
1
0
a
0
Hallar el area comprendida entre las curvas
.
Corte gráfica:
e
;
;
1
-1
Hallar el área finita limitada por la curva de ecuación
y = x2 - 4x y el eje y = 0
La recta y = 0 corresponde al eje de abscisas OX
Si calculamos
:
Estos dos valores de x, son los límites de integración
4
4
0
0
Hallar el área limitada por la grafica de la función y = cos x y el eje
OX en el intervalo [0,2]
Primero se calculan los posibles puntos de corte con el eje OX
con lo que los intervalos [0, /2), (/2, 3/2), (3/2, 2) serán los limites de integración en la que se divide el área
π/2
0
Hallar el área limitada por la grafica de la función y = sen 2x y el eje
OX en el intervalo [0,2]
Primero se calculan los posibles puntos de corte con el eje OX
Los intervalos [0, /2), (/2, ), (, 3/2), (3/2, 2] serán los limites de integración
en los que se divide el área
/2
=
0
= 2 · [ ( - cos  - ( - cos 0) ] = 2 · ( 1 + 1) = 4 u2
Hallar el área limitada por la grafica de la función
eje OX en el intervalo [-1, 1]. Dibujar la grafica.
1
-1
Domínio
R . No existen asíntotas verticales.
No existen AH ni AO ya que el límite cuando x ->  de f(x) y de m son 0
Corta al eje OY Para x = 0 
Máximos y mínimos:
Posibles Puntos de inflexión:
(0, 1)
y el
Por ultimo y(-1) = ½
e y(1) = ½
Hallar el valor de a para que el area limitada por las graficas
Hallamos los cortes entre las dos funciones.
a
0
La función y = x3 - ax2 + 4x + b corta al eje de abcisas en x = 3 y tiene
un P.I en x = 2/3. Hallar a y b. Calcular el área que forma la curva
entre x = 2/3 y x = 3 . Dibujar la grafica
Si corta al eje y = 0 en x = 3 es que pasa por (3,0)
Si tiene un P.I en x = 2/3 es que y´´(2/3) = 0
y´= 3x2 - 2ax + 4;
y´´= 6x - 2a
Si pasa por (3,0);
0 = 33 – a·32 + 4·3 + b
Si hay P.I en x = 2/3
0= 6· – 2a 
0 = 27 – 9a + 12 + b;
b = - 27 + 9·2 - 12
La curva tiene de ecuación

4 – 2a = 0;
2a = 4;
b = - 21
y = x3 - 2x2 + 4x - 21
3
2/3
a=2
Representar f(x) = |x2  1|. Calcular el área entre x =  1 y x = 1.


Sabiendo que el área comprendida entre la curva y =  x y la recta
y = bx, es 1, a) Hallar b. b) Para b = 1, calcular el área que forma la
curva con la recta.
a)
2
1/b
0
b)
Se considera el recinto limitado por las curvas y = x2, x = 1, x = 2,
y = 5x. Hallar el área de dicho recinto, dibujándolo previamente
Para dibujar la parábola y = x2
Para dibujar la recta y = 5x
x y
______
-2 4
-1 1
0 0
1 1
2 4
x y
_____
0 0
1 5
2 10
2
1
Sea la función y
: a) Representarlo. b) Área de la figura
encerrada entre la curva y el eje y = 0.
Posibles máximos o mínimos:
A