Fundamentos de Derivados y Opciones
Anuncio

Fundamentos de Derivados y Opciones
Benavides
Notas de Clase
Fundamentos de Derivados y Opciones
Julián Benavides Franco
Universidad Icesi, 2013
1
Fundamentos de Derivados y Opciones
Benavides
Tabla de contenido
1.
Introducción a los Activos Derivados............................................................................. 3
1.1 Estructura de un Contrato de Futuros Peso/Dólar ........................................................ 16
1.2 Diagramas de Utilidad .................................................................................................. 20
1.3 Conceptos de Cobertura con Derivados ....................................................................... 24
1.4 Utilidad y Retorno de Inversión en opciones ............................................................... 36
2.
Proceso Lognormal ....................................................................................................... 44
3.
Valoración de Derivados utilizando la Simulación de Montecarlo .............................. 58
4.
Valoración de Derivativos, modelo discreto ................................................................ 63
5.
Modelo de Black-Scholes (tiempo continuo) ............................................................... 81
6.
Estrategias de Inversión con opciones, acciones, futuros y bonos ............................... 87
7.
Convergencia Formula de Valoración de Opciones, Discreta vs. Black-Scholes ........ 99
7.1
Ejercicio de convergencia, usando Macros.......................................................... 104
8.
Como Calcular el Portafolio Insurance....................................................................... 110
9.
Opciones Reales, una introducción............................................................................. 122
10. Ejercicios Generales ................................................................................................... 127
2
Fundamentos de Derivados y Opciones
Benavides
Fundamentos de Derivados y Opciones
1. Introducción a los Activos Derivados
Activos Derivados
Un activo o instrumento derivado es un activo cuyo valor se asocia, se desprende o es
función de otro activo, llamado activo subyacente. Por ejemplo un futuro sobre café es un
activo derivado cuyo valor depende del precio futuro del café. Es importante puntualizar
que el valor del futuro de café es diferente al precio futuro del café. El valor del futuro está
dado por el valor presente de la diferencia entre el precio forward o futuro pactado
inicialmente, X, (aunque este valor se modifica, cuando estamos hablando de un futuro
transado en bolsa) y el precio futuro del subyacente, F 0 , en el momento en que se valora el
futuro:
(
)
donde T es el tiempo al vencimiento y kf es la tasa libre de riesgo.
Los activos derivados más importantes son los forward (o contratos a plazo), los futuros y
las opciones. A continuación se describen sus características.
Forward (Contratos a Plazo) y Futuros
Es un título que da a su poseedor el derecho y la obligación de comprar o vender un activo
S, por un precio específico predeterminado, en una fecha particular. Denominaremos el
precio específico predeterminado como Precio de Ejercicio X, aunque normalmente se
conoce precio forward (futuro) . El tiempo que transcurre hasta que se debe realizar la
transacción lo denominaremos T.
Ejemplo
Suponga que usted suscribe un forward para comprar una acción de Ecopetrol por un
precio de $4500 (X) para dentro de 30 días.
Si en 30 días la acción de Ecopetrol se transa por $4600 (ST ) su utilidad será de $100 (S T –
X), obtenida al comprar un activo (cuyo valor es superior) por un precio inferior al de
mercado.
Por otro lado si en 30 días la acción de Ecopetrol se transa por $4400 la utilidad será
negativa e igual a -$100, lo cual también equivale a S T -X.
3
Fundamentos de Derivados y Opciones
Benavides
Por lo que se deduce que una función que describe el pago de un forward es S T -X. Donde el
subíndice T corresponde al momento del vencimiento.
Forward
ST
X
ST - X
Delta
4600
4500
100
100
ST
Pago
100
4000 -500
4100 -400
4200 -300
4300 -200
4400 -100
4500
0
4600 100
4700 200
4800 300
4900 400
5000 500
600
Forward
Pago
400
ST-X
200
0
4000
-200
4200
4400
4600
4800
5000
ST
-400
-600
Puesto que un futuro es en esencia lo mismo que un forward, esta función también aplica
para los futuros.
Recuerde que en cualquier transacción financiera existe una contraparte, cual es entonces el
pago que recibe la contraparte, quién se comprometió a venderle a usted la acción de
Ecopetrol en las condiciones antes descritas.
Una conclusión que puede deducirse de estas funciones de pago es que los forward y los
futuros son operaciones de suma cero, donde la utilidad de uno es la perdida del otro.
En condiciones normales al suscribir un forward, o un futuro, ninguna de las contrapartes
debe pagar una prima. Esto quiere decir que el valor esperado hoy de tal tipo de operación
es cero.
La diferencia entre forwards y futuros radica fundamentalmente en la intermediación.
Mientras que el forward es una operación sin intermediarios, la compra y venta de futuros
se realiza a través de instituciones similares a las bolsas de valores. Estas instituciones son
las que organizan el mercado de futuros, produciendo estandarización en los tipos de
activos sobre los que se pueden contratar futuros, el monto, el vencimiento, las garantías
requeridas, el ajuste de cuentas y la forma de liquidación de los mismos.
4
Fundamentos de Derivados y Opciones
Benavides
En un contrato forward, por el contrario, no existen garantías mas allá de la credibilidad de
la respectiva contraparte, sin embargo esta limitación también permite la versatilidad de los
mismos en cuanto a montos y vencimientos.
Opción
Es un título que da a su poseedor el derecho, mas no la obligación, de comprar o vender un
activo S (a veces también llamado activo subyacente) por un precio específico
predeterminado X (precio de ejercicio), en o antes de una fecha particular T (fecha de
expiración o vencimiento).
Tipos de Opciones
Call (Compra)
Derecho de compra
Put (Venta)
Derecho de venta
Cuando la opción se puede ejercer ANTES del vencimiento se conoce como una opción
tipo Americano, cuando la opción solo se puede ejercer EN la fecha de vencimiento se
conoce como tipo Europeo.
A diferencia del forward (futuro) la opción es lo que se denomina un activo contingente,
puesto que su utilidad no solo depende del precio futuro del activo subyacente, sino de una
decisión que toma el poseedor del mismo.
Otra diferencia más importante es que al comprar una opción se debe pagar una Prima, que
se entrega a la contraparte (el emisor de la opción). Cuando calculamos el valor de una
opción, en muchos casos estaremos calculando el valor de la prima.
Ejemplo
Opción CALL
Continuamos con la acción de Ecopetrol. Suponga que usted acaba de comprar una opción
Call sobre una acción de Ecopetrol. El precio de Ejercicio X es $4500 y el vencimiento es
dentro de 30 días.
Si en 30 días la acción de Ecopetrol se transa por $4600 (ST ), es óptimo ejercer la opción y
comprar la acción, su utilidad será de $100 (S T – X), obtenida al comprar un activo (cuyo
valor es superior) por un precio inferior al de mercado.
Por otro lado si en 30 días la acción de Ecopetrol se transa por $4400, no es óptimo ejercer
la opción, ya que esta le da el derecho a comprar una acción por un valor superior al que
5
Fundamentos de Derivados y Opciones
Benavides
tendría que pagar si la comprara en el mercado de acciones, por lo tanto la opción expira sin
ser ejercida y la utilidad será de cero.
Si adicionalmente se incluye el pago de la Prima se obtienen los flujos netos que produce
la compra de la opción.
¿Cuál sería entonces una función que describe los pagos recibidos por la compra de una
opción Call?
Veamos:
1. ST > X: ST – X
2. ST < X: 0
Una función que describe estos pagos es Máximo (S T -X,0).
Opcion Call
ST
4600
X
4500
C=Max(ST - X,0) 100
ST
4000
4100
4200
4300
4400
4500
4600
4700
4800
4900
5000
600
Pago
100
0
0
0
0
0
0
100
200
300
400
500
Opcion Call
Pago
400
200
0
4000
-200
Max(ST-X,0)
4200
4400
4600
4800
5000
ST
-400
-600
Como se observa la opción Call permite a su poseedor obtener utilidades en caso de un
incremento en el precio del activo subyacente y limitar las perdidas en caso de una
reducción.
Naturalmente un esquema de pagos de este tipo tiene un valor, que en este caso es la prima
que se pagó.
Opción PUT
Continuamos con la acción de Ecopetrol. Suponga que usted acaba de comprar una opción
Put sobre una acción de Ecopetrol. El precio de Ejercicio X es $4500 y el vencimiento es
dentro de 30 días.
6
Fundamentos de Derivados y Opciones
Benavides
Si en 30 días la acción de Ecopetrol se transa por $4600 (ST ), no es óptimo ejercer la
opción, ya que esta le da el derecho a vender una acción por un valor inferior al que
obtendría si la vendiera en el mercado de acciones, por lo tanto la opción expira sin ser
ejercida y la utilidad será de cero.
Por otro lado si en 30 días la acción de Ecopetrol se transa por $4400, es optimo ejercer la
opción y vender la acción, su utilidad será de $100 (X – ST ), obtenida al vender un activo
(cuyo valor es inferior) por un precio superior al de mercado.
Si adicionalmente se incluye el pago de la Prima se obtienen los flujos netos que produce
la compra de la opción.
Cual seria entonces una función que describe los pagos recibidos por la compra de una
opción Put?
Veamos:
3. ST > X:
4. ST < X:
0
X - ST
Una función que describe estos pagos es Máximo (X - ST ,0).
Opcion Put
ST
4600
X
4500
C=Max(X-ST,0)
0
ST
4000
4100
4200
4300
4400
4500
4600
4700
4800
4900
5000
600
Pago
0
500
400
300
200
100
0
0
0
0
0
0
Opcion Put
Pago
400
200
0
4000
-200
Max(X-ST,0)
4200
4400
4600
4800
5000
ST
-400
-600
Como se observa la opción Put permite a su poseedor obtener utilidades en caso de una
reducción en el precio del activo subyacente y limitar las perdidas en caso de un
incremento.
7
Fundamentos de Derivados y Opciones
Benavides
Preguntas
1. ¿Cuál seria la función de pago de los emisores de los instrumentos derivados aquí
revisados?
2. Si usted pensara que es muy probable que el precio de la acción de Ecopetrol fuera a
cambiar radicalmente en los próximos días, aunque no puede estar seguro de si a la
baja o al alza, ¿qué opción o combinación de opciones podría usted comprar o
vender para obtener una utilidad sobre esta situación?
Operaciones con opciones
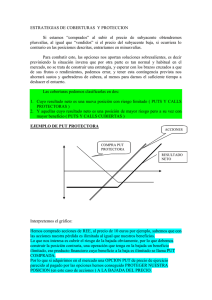
Put Protectivo
Es un concepto de cobertura que resulta al implementar una estrategia sencilla de
minimización de riesgo financiero que implica la combinación de posiciones largas (lo que
quiere decir comprar) en las acciones o portafolio a asegurar y en una Opción Put; esta
estrategia es conocida como Put Protectivo. El Put Protectivo tiene un horizonte que esta
definido por el tiempo de maduración o vencimiento de la opción Put.
Al comprar una acción S sabemos que el pago final recibido por la acción al momento de
venderla (liquidar la posición) corresponde al precio spot S t (Pago = St ), la Gráfica 1a nos
muestra este comportamiento. Para calcular el pago neto se debe restar el costo inicial de la
acción S0 . El pago neto se expresa como S t – S0 . La gráfica 1b representa estos beneficios.
Gráfica 1
a
Pagos de una acción como función
del Precio Spot St
Pago = St
b
Pagos netos (o beneficios) por la
compra de una Acción
Precio de Compra (S0 ) = 100
Pago = St – S0
Repetimos la definición de la opción Put: Una opción Put es el derecho, mas no la
obligación, de venta de un activo (en este caso una acción o portafolio de acciones) a un
precio determinado, conocido como precio de ejercicio X, en una fecha futura determinada
8
Fundamentos de Derivados y Opciones
Benavides
conocida como fecha de vencimiento o de maduración. El tiempo hasta la expiración (o
vencimiento) de la opción se denomina T. Cuando la opción puede ejercerse en cualquier
momento entre su emisión y expiración se conoce como una opción tipo americano, en caso
contrario la opción se denomina tipo europeo. Los pagos recibidos al ejercer la opción se
observan en la gráfica 2a.
Cuando el precio de ejercicio es superior al precio spot de la acción (X>S t ), el propietario
de la opción la ejerce, pues puede vender la acción S a un valor mayor al del mercado. Su
utilidad es entonces St -X. Cuando X < St el propietario no ejerce la opción, pues puede
vender la acción a un precio mayor que el pactado en la opción, su utilidad en este caso es
0. En ambos casos debe restarse la prima pagada por la compra de la opción si se quiere
obtener los pagos netos de la operación (Gráfica 2b).
Una función que describe este comportamiento es Máximo (X – St ,0).
Pagos Put
100
80
60
40
20
St
177.5
152.5
127.5
102.5
77.5
52.5
27.5
2.5
0
Gráfica 2
a
Pagos de una Opción Put en el momento
de Ejercicio
Precio de Ejercicio X =90
Pago = Max (X-St ,0)
b
Pagos netos (descontando la prima)
de una Opción Put en el momento de
ejercicio
Precio de Ejercicio X =90
Prima = 10
Pago = Max (X-St ,0) - Prima
La racionalidad que justifica la compra de una opción como la descrita anteriormente
estriba en que se elimina la posibilidad de pérdidas más allá de un nivel pre-establecido por
el precio de ejercicio X.
Un ejemplo sencillo clarifica el concepto. Supóngase que se desea comprar una acción S
cuyo precio actual es de COL$ 100. También se quiere eliminar la posibilidad de perdidas a
un 10%, pero se desea conservar la posibilidad de ganancia que implica la valorización de
la acción.
9
Fundamentos de Derivados y Opciones
Benavides
La limitación de las perdidas implica que se desea que en el momento de liquidar
posiciones se pueda vender la acción S al menos por COL$ 90. Esto se consigue
comprando una opción Put con precio de ejercicio X = COL$ 90.
Ahora debemos analizar el resultado de combinar las dos posiciones (la compra de la
acción S y de la opción Put).
El análisis del resultado puede realizarse definiendo dos rangos (1: S t < X y 2: St >X):
Función
Estrategia
Opción
Pagos
Max(X-St,0)
Pagos Netos
Max(X-St,0) - P
Acción
St
St - S0
Rango
St < X
St > X
St < X
St > X
Opción
X - St
St
0
St
X - St - P
St - S0
-P
St - S0
X
St
X - S0 - P
St - S0 - P
+ Acción
= Total
La combinación de las dos posiciones, la compra de la acción y del put, se muestra en la
gráfica 3.
Gráfica 3
a
Pagos de una Opción Put y una acción
en el momento de Ejercicio
Precio de Ejercicio X =90
Pago = Max (X-St ,0) + St
b
Pagos netos (descontando la prima)
de una Opción Put en el momento de
ejercicio
Precio de Ejercicio X =90
Prima = 10
Pago = Max (X-St ,0) – Prima + St - S0
Como se observa claramente el put protectivo (S+P), donde S es la acción y P es la prima
un Put sobre 1 acción S, permite a su poseedor beneficiarse de un incremento en el precio
de la acción y reducir las perdidas en caso de ocurrir lo contrario. La erogación inicial es S 0
+ P0 , donde S0 es el precio de compra de la acción y P 0 es la prima pagada por el Put.
10
Fundamentos de Derivados y Opciones
Benavides
El ejemplo anterior nos muestra que las posiciones en diferentes tipos de activos pueden
combinarse o sumarse para producir utilidades (perfiles de pago) que favorezcan los
intereses de su poseedor. Para los siguientes ejemplos nos concentraremos en hallar los
resultados de combinar posiciones sin descontar los pagos iniciales (prima o compra del
activo).
Call Cubierto
En este caso se combina la compra de una acción con la venta de un Call. Esta estrategia
permite obtener utilidades de la venta de un Call, minimizando el nivel de perdidas en caso
de un incremento en el precio de la acción mas allá del valor de la prima.
Ya vimos en el ejemplo anterior la función de pago que se obtiene por la compra de una
acción. La función de pago de la venta o emisión de un Call es el negativo de la obtenida
por la compra del mismo. El Call Cubierto combina estas dos funciones.
Veamos:
Suponga que se adquiere una acción por $500 y no se desea mantenerla por un largo
tiempo, se tiene la intención de venderla en cuanto su precio supere los $600. Existe alguna
manera de incrementar la ganancia? La respuesta es si: Puesto que ya se posee la acción se
puede emitir una opción Call con un precio de ejercicio de $600. El comprador de la opción
solo la ejercerá cuando el valor de la acción exceda los $600, puesto que este era el valor de
venta originalmente establecido, el emisor se siente satisfecho puesto que ha obtenido la
ganancia establecida inicial y la ha incrementado con la prima recibida C0 . El análisis del
resultado puede realizarse siguiendo la estrategia delineada para el Put Protectivo.
Que sucede en caso de una reducción en el valor de la acción?
A continuación se presenta la función de pago de la acción, donde no se ha descontado el
valor de S0 :
Accion
ST
500
- S0
= ST - S 0
Delta
0
500
100
ST
0
100
200
300
400
500
600
700
800
900
1000
1200
Pago
500
0
100
200
300
400
500
600
700
800
900
1000
Pago
Accion
1000
ST-S0
800
600
400
ST
200
0
0
200
400
600
800
1000
1200
11
Fundamentos de Derivados y Opciones
Benavides
En el caso de la venta o emisión de la opción se tiene (sin tener en cuenta la prima
recibida):
Venta Opcion Call
ST
500
X
-C=Max(ST - X,0)
600
0
+C0
0
= -C+C0
0
0
0
ST
0
100
200
300
400
500
600
700
800
900
1000
Pago
0
0
0
0
0
0
0
0
-100
-200
-300
-400
Pago
200
Venta Opcion Call
400
600
800
1000
1200
-100
-200
-Max(ST-X,0)+C0
-300
ST
-400
-500
-600
Ahora se combinan (suman) las dos funciones, lo que resulta en el Call Cubierto:
Call Cubierto
ST - S0
500
-C+C0
= ST - S0-C+C0
0
500
ST
0
100
200
300
400
500
600
700
800
900
1000
800
Pago
500
0
100
200
300
400
500
600
600
600
600
600
Call Cubierto
Pago
600
400
ST-S0-C+C0
200
0
0
200
400
600
800
1000
1200
ST
-200
-400
-600
12
Fundamentos de Derivados y Opciones
Benavides
Paridad Put-Call
Uno de los resultados más conocidos sobre las opciones europeas es la paridad Put-Call.
Este resultado establece que el valor actual de un Put y una unidad del activo subyacente S
son iguales al valor de un Call (sobre el mismo subyacente, idéntico precio de ejercicio X e
igual vencimiento T) más el valor presente de un bono libre de riesgo de descuento puro
con valor nominal de X, el precio de ejercicio, que madura en T. Esto es:
Put0 + S0 = Call0 + Pv(X)
Si el subyacente fuera una acción que paga dividendos conocidos durante la vida de las
opciones, la anterior ecuación se modifica a:
Put0 + S0 = Call0 + Pv(X) + Pv(Div)
Cuando las opciones involucradas son americanas se obtiene la siguiente desigualdad:
S0 -X ≤ Call0 - Put0 ≤ S0 - PV(X)
Ejercicio temprano
Se puede usar la paridad Put-Call para establecer particularidades respecto a la relación
entre el valor de las opciones americanas y europeas.
Analicemos el caso de las opciones Call, para esto re-expresamos la paridad de la siguiente
manera, generalizando la expresión para cualquier momento t, entre la emisión y el
vencimiento:
Callt = St - Pv(X) + Putt , adicionalmente Pv(X) = X.exp(-kf.(T-t)).
Definamos Des(X) = X-Pv(X) = X.(1-exp(-kfT))>0
Luego
Callt
=
St
–
X
Valor Intrínseco
+
Des(X)
+
Putt
Valor Temporal
Por simple inspección podemos observar que el valor del Call siempre será superior al valor
intrínseco, cuando S0 ≥X. Puesto que la única ventaja que un Call americano tiene sobre uno
Europeo es su posibilidad de ejercicio temprano, y conociendo que la utilidad en este caso
sería St – X, menor a la que se obtendría al venderlo, podemos concluir que no es óptimo
ejercer el Call antes del vencimiento y que el valor de mercado de un Call americano es
igual al de uno europeo.
Este no es el caso para el Put. Se deja al lector interesado la argumentación para este caso.
13
Fundamentos de Derivados y Opciones
Benavides
Ejercicios
Realizar el análisis anterior para las siguientes operaciones:
Long Straddle: Compra de un Call y un Put sobre una acción con el mismo precio de
ejercicio suponga que X = $500. Para que sirve? Forma (V)
Spread: Compra de un Call con un precio de ejercicio de X1 =450 y venta de un Call con un
precio de ejercicio de X2 =550.
Los spreads son combinaciones de Calls (2 o mas) o Puts (2 o mas) exclusivamente, las
cuales se compran o se venden (emiten). Forma (_/¯)
Collar: Tenencia de una acción combinada con la compra de un put (X=400) y la venta de
un call (X=600).
Paridad Put-Call:
Compare las siguientes estrategias,
a. Put Protectivo: acción mas put con precio de ejercicio X
b. Call con precio de ejercicio X mas la compra de bonos libre de riesgo (cero cupón)
y valor nominal de X.
Suponga una tasa libre de riesgo de k 0 . Que conclusión se desprende, si no hay posibilidad
de arbitraje.
Compruebe que un Put americano vale más que uno europeo.
Pruebe la relación de desigualdad Put-Call para opciones americanas.
------------------
14
Fundamentos de Derivados y Opciones
Benavides
Swaps
Un swap es un acuerdo entre dos empresas para intercambiar flujos de caja en el futuro. El
acuerdo normalmente incluye los vencimientos de dichos intercambios y la forma de
calcular su monto. Desde este punto de vista un contrato forward (a plazo) es un swap, con
un solo plazo.
Veamos un ejemplo.
Un swap de moneda es un intercambio de flujos de caja en 2 monedas diferentes,
normalmente envuelve dos bonos con similares vencimientos expresados en las 2 monedas
transadas. Se intercambian los cupones y el principal.
Suponga que General Motors ha emitido bonos denominados en yenes japoneses, debido a
que las condiciones del mercado japonés son favorables. Sin embargo el grueso de sus
ingresos esta denominado en dólares. Por otro lado Honda esta construyendo una fabrica en
USA y requiere dólares, aunque el grueso de sus ingresos esta expresado en yenes. Como
resultado de sus necesidades de efectivo y sus ingresos GM y Honda acuerdan un swap.
GM recibirá yenes que le permitirán cubrir los cupones y el principal de los bonos que
emitió en el mercado japonés y pagará dólares. Honda recibirá dólares y pagará en yenes en
su mercado local.
Pregunta Conceptual:
Establezca que el valor esperado (presente o futuro) de un swap es cero.
Para tal fin utilice los flujos que acompañan la emisión de dos bonos.
Sea el bono a expresado en yenes (valor nominal 8000, cupón 5%) y el bono b expresado
en US (valor nominal 100, cupón 7%). Suponga que la tasa actual es de 80Y/US y el
comportamiento esperado de la misma responde al efecto Fisher. Compruebe que el valor
neto de los intercambios es de cero.
---------------------
15
Fundamentos de Derivados y Opciones
Benavides
1.1 Estructura de un Contrato de Futuros Peso/Dólar
Un contrato de futuros se establece cuando el comprador de los futuros y el vendedor de los
mismos, cualquiera que sea el activo subyacente acuerdan su precio a la entrega, el número
de contratos a intercambiar y el mes de entrega.
En una bolsa establecida el vencimiento (entrega) de los contratos (la fecha en que el
intercambio se debe realizar) se realiza en un día especifico (normalmente hacia el final de
mes) de determinados meses. La cámara de compensación de la bolsa se encarga de realizar
los ajustes a las diferentes posiciones abiertas en los diferentes contratos transados.
Suponga que en Colombia existe una bolsa de futuros Peso/Dólar (TRM), que negocia
contratos C de compraventa de dólares por un monto unitario de US$ 25.000, que maduran
el 3er Miércoles de cada mes.
Garantía
La bolsa exige una garantía (Margin) en pesos igual a nxCxTRMx%n. Donde n es el
numero de contratos abiertos, C es el tamaño del contrato y TRM es la tasa de cambio spot
COL/US del día en que se pacta el futuro y %n es un valor que puede variar según la
volatilidad de la divisa y que actualmente es igual al 5%. Esta garantía tiene el propósito de
reducir el riesgo de no pago y cada contraparte debe suscribirla
Ajuste de Garantía
Si la garantía llegara a reducirse al 75% de su valor original, en virtud de las oscilaciones
de la tasa de futuros, la contraparte afectada deberá reponerla a su nivel original,
realizándose un ajuste de la garantía (Margin Call). Este nivel original es el establecido en
la fecha de apertura del contrato, no el que resulta del nuevo precio de la divisa (Esta es una
convención, no hay ninguna razón por la cual no pudiera realizarse de esta forma).
Mecánica de operación
Al cerrarse la operación, las contrapartes depositan la garantía. Al finalizar la rueda de ese
día, la bolsa calcula los ajustes que deben realizarse a cada posición. Si F 0 identifica a la
tasa a futuro pactada al cierre de la operación y F 1 a la tasa a futuro calculada por la bolsa al
final del día, la perdida o ganancia para una posición larga (compra de futuros) es igual a
n(C)(F1 -F0 ). La racionalidad de este calculo estriba en que F 1 es el precio de venta (o el
valor final del activo subyacente) y F 0 el precio de compra. Estos valores normalmente se
expresan en la moneda legal donde opera la bolsa de futuros. Naturalmente la posición
corta es el espejo de la larga con lo que la perdida o ganancia de la posición larga es la
ganancia o perdida de la corta (n(C)(F 0 -F1 )). La cámara de compensación abona o
descuenta este valor de la garantía depositada por cada contraparte. Al siguiente día la tasa
de referencia es F1 y el calculo de la utilidad es n(C)(F 2 -F1 ) para el comprador de futuros.
Toda vez que las perdidas acumuladas reduzcan la garantía por debajo de la cota mínima
aceptada (75%) la contraparte afectada deberá reponerla a su nivel original.
Al vencerse el contrato de futuros las utilidades o pérdidas acumuladas para el comprador
de futuros corresponden a:
n
Utilidad nC Fi Fi1 lo cual se simplifica en nC Fn F0 .
i 1
16
Fundamentos de Derivados y Opciones
Benavides
Si recordamos que la tasa F n corresponde al precio spot de la divisa al vencimiento del
futuro (Sn )1 , la formula para la utilidad total es:
Utilidad nC S n F0
Otra forma de contabilizar la utilidad corresponde a:
Utilidad GF GI AG
Donde GF corresponde al nivel final de la garantía (en caso de no existir ningún retiro), GI
al depósito inicial y AG a los ajustes acumulados de la garantía.
Ejemplo:
Al finalizar la rueda (o al inicio de la rueda del siguiente día) de negociación de cierto día,
2 personas, Luís y Ana, acuerdan por intermedio de sus respectivos comisionistas entrar en
un contrato de futuros Peso/Dolar. Luís acuerda comprar un (1) contrato de futuros a una
tasa de 2.850 COL/US y Ana acuerda venderlo. El contrato vence en 10 días.
Al vencimiento del contrato la tasa de futuros ha oscilado de la siguiente manera:
Ft TC COL/US
0
2,850.00
1
2,842.00
2
3
4
5
6
7
8
9
10
2,808.00
2,815.00
2,850.00
2,883.00
2,931.00
2,871.00
2,865.00
2,895.00
2,866.00
Recuerde que un contrato de futuros se liquida diariamente.
Encuentre la utilidad diaria de ambas posiciones, los cambios en los niveles de garantía, y
los ajustes requeridos a las garantías, si es que se requieren.
1
De existir diferencia entre el precio futuro al vencimiento y el spot habría lugar a arbitraje. Si F n >Sn se
compran dólares en el mercado spot y se venden en el de futuros con ganancia inmediata, si F n <Sn se realiza
la operación contraria.
17
Fundamentos de Derivados y Opciones
Benavides
Caracteristicas del Contrato
Contrato (C)
%Garantia
Garantia US
TC Spot COL/US
Garantia COL
Ajuste Garantia
Aj. Garantia COL
25,000
5.00%
1,250
2,820
3,525,000
75.00%
2,643,750
Numero de contratos (n)
1
US
Col
por contrato
de Garantia inicial
por contrato
Encuentre los valores adecuados para cada casilla y realice un ejercicio similar para la
posición opuesta.
Compra US
Luis
Ft TC COL/US
UDi =
0
2,850.00
1
2,842.00 (F1-F0)nC =
2
2,808.00 (F2-F1)nC =
3
2,815.00
:
4
2,850.00
:
5
2,883.00
:
6
2,931.00
:
7
2,871.00
:
8
2,865.00
:
9
2,895.00
:
10
2,866.00 (F10-F9)nC =
3,525,000
3,325,000
Ajuste Garantia
(AG)
-
2,475,000
3,700,000
4,575,000
5,400,000
6,600,000
5,100,000
4,950,000
5,700,000
4,975,000
1,050,000
-
Utilidad
UDi =
400,000
Total AG
1,050,000
(F10-F0)nC =
-
Garantia
850,000
175,000
875,000
825,000
1,200,000
1,500,000
150,000
750,000
725,000
Balance Final Garantia
- Ajustes de Garantia
- Garantia Inicial
= Utilidad
Directo
Util Diaria
(Fi - Fi-1)nC
200,000
-
-
Balance
Utilidad
Garantia acumulada
3,525,000
3,325,000 - 200,000
3,525,000 - 1,050,000
3,700,000 - 875,000
4,575,000
5,400,000
825,000
6,600,000 2,025,000
5,100,000
525,000
4,950,000
375,000
5,700,000 1,125,000
4,975,000
400,000
4,975,000
1,050,000
3,525,000
400,000
400,000
UDi = (F10-F0)nC = (S10-F0)nC
Luego
Comprobar esta igualdad
18
Fundamentos de Derivados y Opciones
Benavides
Plantilla Contrato de Futuros
La siguiente plantilla, una derivación de la anterior, puede modificarse a voluntad para diferentes tipos de contratos.
PERFIL DE PAGOS De UN FUTURO
Monto
Garantia pesos
Mantenimiento
Garantía en pesos
Mantenimiento
Condición Retiro
C
#COL
%M
GC
MC
US$
COL$
COL$
COL$
Fi
5,000
160
87.50%
800,000 =C*#COL
700,000 =%M*GC
1 1:Si,2:No
TC COL/US
0
1
2,400
2,420
2
3
4
5
6
7
2,455
2,415
2,385
2,450
2,465
2,500
UDi =
+ (F1-F0)nC =
+ (F2-F1)nC =
+
:
+
:
+
:
+
:
+ (F7-F6)nC =
Ui =
Ganancia:
(St-X)*Cont*n*Pos
B. F. Garantia
- Aj. T. Garantia
- Garantia Total
= Utilidad
Posición Larga:
1ro compra
2do venta
#Contratos
Posicion
Gar. Total
Mtto Total
U. diaria
Larga
Ui
=(Fi-Fi-1)nC
300,000
525,000
(600,000)
(450,000)
975,000
225,000
525,000
n
GT
M
3 +:Larga/- Corta
2,400,000 =Abs(n)GC
2,100,000 =Abs(n)MC
Garantia
Ajuste
Gi
Ai
Balance
Bi
Utilidad
acumulada
UAi
Ui
=Bi-1+Ui
=SI(Gi<M,GT-Gi,0)
2,400,000
2,700,000
(300,000)
=Gi+Ai
2,400,000
2,400,000
2,925,000
1,800,000
1,950,000
3,375,000
2,625,000
2,925,000
2,400,000
825,000
2,400,000
225,000
2,400,000 225,000
2,400,000
750,000
2,400,000
975,000
2,400,000
1,500,000
1,500,000 Aj. T. Gar.
1,500,000
(525,000)
600,000
450,000
(975,000)
(225,000)
(525,000)
300,000
(1,500,000) Ai
2,400,000
1,500,000
- 2,400,000
1,500,000
19
Fundamentos de Derivados y Opciones
Benavides
1.2 Diagramas de Utilidad
Es usual con los activos derivados trabajar con funciones de pago. Estas funciones de pago
son aplicaciones al plano cartesiano (X-Y) de los resultados de las operaciones (o
posiciones) con este tipo de activos. La función de X o variable independiente es asignada
al precio del activo subyacente (S T ), en muchos casos una acción. La variable dependiente
Y es el resultado de la estrategia de inversión.
Ejemplo:
Suponga que usted abre un contrato de compra de futuros sobre el activo S a un precio X el
cual se vence en el periodo T. Su utilidad al vencimiento Y será f(S T ) = ST -X. El
diagrama de utilidad es la expresión gráfica de esta ecuación. En los diagramas de utilidad
se pueden combinar los pagos de diferentes activos sea que estos se compren (posición
larga) o se vendan (posición corta).
A continuación se explica el procedimiento para realizar tal tarea en Excel.
Graficando Forwards
La ganancia final de una opción depende del precio final del activo subyacente.
Para un forward la ganancia al vencimiento es:
2. ST - X, cuando se compra el forward (Posición larga).
3. X - ST , cuando se vende el forward (Posición corta).
Graficaremos la posición larga.
Para graficar la ganancia del forward
como función del precio de la acción al
vencimiento ST podemos acudir a la
función de tabla de datos de Excel, para
encontrar la ganancia final del forward
para diferentes valores de ST . La tabla de
datos permite hallar el resultado de una
formula o modelo cuando una o dos
variables que la definen toman diferentes
valores.
En este caso la función o modelo es S T -X
y la variable independiente es ST . Para tal
fin deben organizarse los datos de la
siguiente forma:
20
Fundamentos de Derivados y Opciones
Benavides
Ahora debe seleccionarse la zona de la
tabla de datos (encerrada entre los bordes
oscuros)
e
invocar
el comando
[Herramientas de Datos/ Análisis Y
si/Tabla de datos], que muestra el
siguiente menú de dialogo. En este caso
la variable que cambia es S T (la columna
izquierda del área seleccionada) ubicada
en la celda B3 de la formula básica. Para
este ejemplo sencillo no existen cambios
para una segunda variable, luego el menú
debe llenarse así:
Una vez finalizado el procedimiento el
siguiente es el resultado:
Gráfica
Excel provee las herramientas
graficar este resultado:
para
21
Fundamentos de Derivados y Opciones
Benavides
Graficando Opciones
La ganancia final de una opción depende del precio final del activo subyacente.
Para una opción Call se tienen las siguientes posibilidades:
4. ST >X, en este caso es óptimo ejercer la opción y la ganancia corresponde a la
diferencia entre el precio de compra X y el valor de mercado S T . Considere que
usted vende la acción inmediatamente después de ejercer la opción, su ganancia
corresponde al precio de venta menos el precio de compra: S T -X.
5. ST <=X, en este caso la opción no se ejerce, puesto que es mas barato comprar la
acción en el mercado que ejerciendo la opción, su ganancia corresponde a 0.
Una función que representa la ganancia en todo el rango de valores de S es Max (S T -X,0).
Esta función esta definida en el Excel y por lo tanto puede usarse para graficar la ganancia
al vencimiento de la opción Call.
Para graficar la ganancia de la opción
como función del precio de la acción al
vencimiento ST acudimos nuevamente a
la función de tabla de datos de Excel, para
encontrar la ganancia final de la opción
para diferentes valores de S T . En este caso
la función o modelo es Max (S T -X,0) y la
variable es ST .
El estructura del modelo es similar al del
forward. Por tal motivo solo se presenta
el resultado final y la gráfica:
22
Fundamentos de Derivados y Opciones
Benavides
Ejercicios
1. Realice un ejercicio similar para una opción Put con X (precio de ejercicio) de
$1830.
2. ¿Cuál es el resultado de comprar una opción Put con precio de ejercicio de $1800 y
comprar una opción Call con el mismo precio de ejercicio? En este caso una
condición es que las dos opciones maduran simultáneamente (aunque esta condición
no aplica si la opciones son tipo americano).
3. Al comprar una opción se debe pagar una prima. Asuma que este valor es $40.
Incorpore este cambio en su modelo.
--------------------
23
Fundamentos de Derivados y Opciones
Benavides
1.3 Conceptos de Cobertura con Derivados
El concepto de cobertura puede entenderse fácilmente cuando un agente combina 2 posiciones
diferentes: 1) la posición, natural, que implica la exposición al riesgo; 2) la posición en el derivado
que implica una exposición opuesta al riesgo. El resultado puede implicar una eliminación total o
parcial del riesgo o, mejor aún, una exposición al riesgo limitada al lado positivo (“up side”) del
mismo.
Cobertura de una posición larga
Examinemos la exposición natural al riesgo, suponiendo, inicialmente, una posición larga. Sin
pérdida de generalidad asumamos que el agente ha emitido una factura o cuenta por cobrar (CxC)
en otra divisa que se hará efectiva en algún momento en el futuro, por ejemplo 90 días. Supóngase,
además, que el agente considera que una tasa de cambio, que llamaremos precio de equilibrio (P eq ),
no le produce ni ganancias ni perdidas en lo relativo a la exposición al riesgo cambiario. Esto
implica que el agente al considerar esta venta al exterior considera que P eq es el valor adecuado que
debe recibir por sus productos. La ganancia (o pérdida) que el agente recibiría por su exposición
cambiara por cada unidad de la divisa es: P 90 -P eq , donde P 90 es el precio de mercado de la divisa el
día 90, al cual se liquida una transacción en el mercado spot. Si el precio de equilibrio es $1,000 y
el precio de liquidación de la divisa, cuando se paga la factura y se convierte a moneda local, es
$1,100, la utilidad por divisa es $100. Por el contrario si el precio de liquidación es $900, la pérdida
es $100.
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
Peq
1100
1200
Pt
CxC
24
Fundamentos de Derivados y Opciones
Benavides
a. Cobertura tomando posición en Forwards o Futuros
Esta exposición puede compensarse hoy tomando una posición corta en forwards 2 (-F) o
vendiendo futuros de esa divisa. Si la tasa pactada de venta, o precio de ejercicio, es X, la
ganancia (o pérdida) que el agente recibiría por cada unidad de divisa es: X-P 90 . Si X es
$1,000 y el precio de liquidación de la divisa es $1,100, la pérdida por divisa es $100. Por
el contrario si el precio de liquidación es $900, la utilidad es $100.
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
X
1100
1200
Pt
-F
Las posiciones combinadas son entonces CxC – F= P 90 – P eq + X– P 90 = X– P eq , lo cual es
constante para cualquier P 90 . Si X es igual a P eq , lo ideal, el resultado de la cobertura es
cero, lo que implica una indiferencia total al riesgo.
2
Esto implica un contrato para vender la divisa en un momento específico en el futuro, en este caso en 90
días. Los contratos forward y los futuros son esencialmente el mismo contrato, solo difieren en su parte
operacional: Los forward se liquidan al vencimiento, mientras que los futuros son liquidados parcialmente en
forma diaria.
25
Fundamentos de Derivados y Opciones
Benavides
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
1100
X
Peq
CxC
-F
1200
Pt
CxC + -F
Si el precio de mercado es de $1,100, al combinar las ganancias de la cuenta por cobrar de
$100 (P 90 -P eq =$1,100-$1,000) con las pérdidas del forward -$100 (X-P 90 =$1,000-$1,100),
el resultado neto es 0. Si el precio de mercado es de $900, al combinar las pérdidas de la
cuenta por cobrar -$100 (P 90 -P eq =$900-$1,000) con las ganancias del forward $100 (XP 90 =$1,000-$900), el resultado neto también es 0. Como ya se dijo, esta posición es
perfectamente neutral al riesgo.
b. Cobertura tomando posición en Opciones
Sin embargo, el caso anterior descarta la posibilidad de obtener utilidades en caso de que la
tasa al vencimiento (P 90 ) haya evolucionado favorablemente en relación a la posición del
agente. Una alternativa que permite aprovechar esta coyuntura, en caso de presentarse, es la
compra de opciones de venta (Put). En este caso el poseedor de la opción obtiene un
derecho de venta de la divisa en el día 90, pero no la obligación3 . Esto significa que el
agente solo vende la divisa a la contraparte al precio establecido (X) si le conviene hacerlo,
lo cual sucede cuando el precio de mercado es inferior al precio de ejercicio; en este caso su
utilidad es igual a la de la venta del forward X-P 90 . Por el contrario, si el precio de mercado
es superior al precio de ejercicio, el agente simplemente no hace uso del derecho, y vende
las divisas en el mercado spot; en este caso la utilidad de la opción es cero. Por supuesto,
por este derecho de venta el agente debe pagar una prima a la contraparte. Se puede
entonces plantear la siguiente tabla para describir la utilidad de una opción de venta:
{
Esta función se describe mejor como Max(X-P t ,0), a la que se le resta la prima pagada por
la opción.
3
Esta es una opción de venta Europea, la cual solo puede ejercerse el día del vencimiento. Existen opciones
que pueden ejercerse durante la vida de la opción, estas opciones se denominan Americanas.
26
Fundamentos de Derivados y Opciones
Benavides
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
X
1100
1200
Pt
Put
La gráfica anterior supone que el precio de ejercicio es $1,000 e incluye la reducción en la
utilidad por una prima pagada de $30.
Al combinar las posiciones en la cuenta por cobrar y la opción de venta (Put), obtenemos:
{
, lo cual se simplifica a
{
Si X=P eq , como es el caso de nuestro ejemplo, el agente ha limitado sus pérdidas, cuando el
precio de la divisa cae por debajo de X, a 0 (X-P eq =$1,000 -$1,000) menos la prima;
mientras que si el precio sube por encima de X, su utilidad es P 90 -P eq , menos la prima.
27
Fundamentos de Derivados y Opciones
Benavides
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
1100
X
Peq
CxC
Put
1200
Pt
CxC + Put
La gráfica anterior supone que el precio de ejercicio es $1,000 e incluye la reducción en la
utilidad por una prima pagada de $30.
El caso merece una explicación un poco más detallada, si, por ejemplo el precio de mercado
de la divisa al vencimiento es $1,100, la utilidad por la cuenta por cobrar es $100 (P 90 -P eq =
$1,100 - $1,000); la opción vence sin ser ejercida por lo que su utilidad es 0, y la utilidad
combinada sigue siendo $100 menos la prima. En caso de un precio de la divisa de $900, se
tiene una utilidad negativa por la cuenta por cobrar de -$100 (P 90 -P eq = $900 - $1,000); la
opción se ejerce, puesto que el agente vende óptimamente a la contraparte la divisa a un
precio superior al del mercado, y se genera una utilidad de $100 (X-P t =$1,000 - $900), al
combinar ambas la utilidad es 0, con lo que el agente ha eliminado el riesgo de “down
side”, pero aprovecha la subida de precio de la divisa.
28
Fundamentos de Derivados y Opciones
Benavides
Cobertura de una posición corta
Examinemos la exposición al riesgo de una posición corta. Sin pérdida de generalidad asumamos
que el agente tiene una cuenta por pagar (CxP) en otra divisa que se hará efectiva en algún
momento en el futuro, por ejemplo los 90 días del caso anterior. Supóngase, además, que el agente
considera, al igual que antes, que una tasa de cambio, que llamaremos precio de equilibrio (P eq ), no
le produce ni ganancias ni perdidas en lo relativo a la exposición al riesgo cambiario. Esto implica
que el agente al considerar esta compra al exterior considera que P eq es el valor adecuado que debe
pagar por lo que ha adquirido. La ganancia (o pérdida) que el agente recibiría por su exposición
cambiara por cada unidad de la divisa es: P eq -P 90 , donde P 90 es el precio de mercado de la divisa el
día 90, al cual se liquida una transacción en el mercado spot. Si el precio de equilibrio es $1,000 y
el precio de liquidación de la divisa, cuando el agente adquiere la divisa y paga la factura, es
$1,100, la pérdida por divisa es $100. Por el contrario si el precio de liquidación es $900, la utilidad
es $100.
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
Peq
1100
1200
Pt
CxP
a. Cobertura tomando posición en Forwards o Futuros
Esta exposición puede compensarse hoy tomando una posición larga en forwards (+F) o
comprando futuros de esa divisa. Si la tasa pactada de venta, o precio de ejercicio, es X, la
ganancia (o pérdida) que el agente recibiría por cada unidad de divisa es: P 90 - X. Si X es
$1,000 y el precio de liquidación de la divisa es $1,100, la utilidad por divisa es $100. Por
el contrario si el precio de liquidación es $900, la pérdida es $100.
29
Fundamentos de Derivados y Opciones
Benavides
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
1100
X
1200
Pt
F
Las posiciones combinadas son entonces CxP + F= P eq – P 90 + P 90 – X= P eq – X, lo cual es
constante para cualquier P 90 . Si X es igual a P eq , lo ideal, el resultado de la cobertura es
cero, lo que implica una indiferencia total al riesgo.
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
1100
X
Peq
CxP
F
1200
Pt
CxP + F
Si el precio de mercado es de $1,100, al combinar las pérdidas de la cuenta por pagar de $100 (P eq – P 90 =$1,000 – $1,100) con las ganancias del forward $100 (P 90 – X = $1,100 –
$1,000), el resultado neto es 0. Si el precio de mercado es de $900, al combinar las
ganancias de la cuenta por cobrar $100 (P eq – P 90 =$1,000 – $900) con las pérdidas del
forward -$100 (P 90 – X = $900 – $1,000), el resultado neto también es 0. Como ya se dijo,
esta posición es perfectamente neutral al riesgo.
30
Fundamentos de Derivados y Opciones
Benavides
b. Cobertura tomando posición en Opciones
Análogamente al caso anterior, la cobertura con forwards (o futuros) descarta la posibilidad
de obtener utilidades en caso de que la tasa al vencimiento (P 90 ) haya evolucionado
favorablemente en relación a la posición del agente. Una alternativa que permite aprovechar
esta coyuntura, en caso de presentarse, es la compra de opciones de compra (Call). En este
caso el poseedor de la opción obtiene un derecho de compra de la divisa en el día 90, pero
no la obligación. Esto significa que el agente solo compra la divisa a la contraparte al precio
establecido (X) si le conviene hacerlo, lo cual sucede cuando el precio de mercado es
superior al precio de ejercicio; en este caso su utilidad es igual a la de la compra del
forward P 90 -X. Por el contrario, si el precio de mercado es inferior al precio de ejercicio, el
agente simplemente no hace uso del derecho, y compra las divisas en el mercado spot; en
este caso la utilidad de la opción es cero. Por este derecho de compra el agente debe pagar
una prima a la contraparte. Se puede entonces plantear la siguiente tabla para describir la
utilidad de una opción de compra:
{
Esta función se describe mejor como Max(P t -X,0), a la que se le resta la prima pagada por
la opción.
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
1100
X
1200
Pt
Call
La gráfica anterior supone que el precio de ejercicio es $1,000 e incluye la reducción en la
utilidad por una prima pagada de $30.
Al combinar las posiciones en la cuenta por pagar y la opción de compra (Call), obtenemos:
{
, lo cual se simplifica a
31
Fundamentos de Derivados y Opciones
Benavides
{
Si X=P eq , como es el caso de nuestro ejemplo, el agente ha limitado sus pérdidas, cuando el
precio de la divisa sube por encima de X, a 0 (X-P eq =$1,000 -$1,000) menos la prima;
mientras que si el precio cae por debajo de X, su utilidad es P eq -P 90 , menos la prima.
Gráficamente
Utilidad
250
200
150
100
50
0
-50 800
-100
-150
-200
-250
900
1000
1100
X
Peq
CxP
Call
1200
Pt
CxP + Call
La gráfica anterior supone que el precio de ejercicio es $1,000 e incluye la reducción en la
utilidad por una prima pagada de $30.
Si el precio de mercado de la divisa al vencimiento $900, la utilidad por la cuenta por pagar
es $100 (P eq -P 90 = $1,000 - $900); la opción vence sin ser ejercida por lo que su utilidad es
0, y la utilidad combinada sigue siendo $100 menos la prima. En caso de un precio de la
divisa de $1,100, se tiene una utilidad negativa por la cuenta por pagar de -$100 (P eq -P 90 =
$1,000 - $1,100); la opción se ejerce, puesto que el agente compra óptimamente a la
contraparte la divisa a un precio inferior al del mercado, y se genera una utilidad de $100
(P t -X=$1,100 - $1,000), al combinar ambas la utilidad es 0, con lo que el agente ha
eliminado el riesgo de “down side”, pero aprovecha la bajada de precio de la divisa.
Cabe preguntarse por qué es tan popular el uso de los futuros y los forwards vs. las opciones en lo
que se refiere a cobertura. La respuesta es la prima, usualmente el cambio en el valor del subyacente
debe ser relativamente muy grande para que el agente con cobertura termine en punto de equilibrio.
En nuestro ejemplo, el precio de la divisa debe subir o bajar $30 antes de que el agente, empiece a
obtener utilidades. Naturalmente un subyacente con mucha volatilidad puede subir o bajar mucho
de precio. Sin embargo, la volatilidad también incrementa el valor de la prima.
32
Fundamentos de Derivados y Opciones
Benavides
Práctica de Excel
El siguiente instructivo permite deducir el desempeño de las diferentes estrategias planteadas en
este capítulo.
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Pt
X
Peq
Prima
Utilidad
CxC
-F
CxC + -F
B
1 CxC
900
1000
1000
30
C
-100 =Pt-Peq
100 =X-Pt
0
D
E
Pt
Delta
25
800
825
850
875
900
925
950
975
1000
1025
1050
1075
1100
1125
1150
1175
1200
F
CxC
-100
-200
-175
-150
-125
-100
-75
-50
-25
0
25
50
75
100
125
150
175
200
G
-F
100
200
175
150
125
100
75
50
25
0
-25
-50
-75
-100
-125
-150
-175
-200
H
CxC + -F
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
33
Fundamentos de Derivados y Opciones
Benavides
El área sombreada de gris es una tabla de datos (Datos/Análisis Y si/Tabla de Datos) , que cambia
con Pt,
Posteriormente se pueden graficar los resultados en forma independiente o conjunta como se
muestra en la sección anterior.
Para cada estrategia descrita en el texto aplican las siguientes fórmulas:
1. Cuenta por cobrar y Forward corto
1
2
3
4
5
6
7
8
9
A
1
Pt
X
Peq
Prima
Utilidad
=B1
-F
=A7&" + "&A8
B
C
CxC
900
1000
1000
30
=B2-B4
=B3-B2
=SUMA(B7:B8)
=Pt-Peq
=X-Pt
34
Fundamentos de Derivados y Opciones
Benavides
2. Cuenta por cobrar y Opción de Venta
1
2
3
4
5
6
7
8
9
A
2
Pt
X
Peq
Prima
Utilidad
=B1
Put
=A7&" + "&A8
B
C
CxC
900
1000
1000
30
=B2-B4
=MAX(B3-B2,0)-B5
=SUMA(B7:B8)
=Pt-Peq
=Max(X-Pt,0)-Prima
3. Cuenta por pagar y Forward largo
1
2
3
4
5
6
7
8
9
A
3
Pt
X
Peq
Prima
Utilidad
=B1
F
=A7&" + "&A8
B
C
CxP
900
1000
1000
30
=B4-B2
=B2-B3
=SUMA(B7:B8)
=Peq-Pt
=Pt-X
4. Cuenta por pagar y Opción de Compra
1
2
3
4
5
6
7
8
9
A
4
Pt
X
Peq
Prima
Utilidad
=B1
Call
=A7&" + "&A8
B
C
CxP
900
1000
1000
30
=B4-B2
=MAX(B2-B3,0)-B5
=SUMA(B7:B8)
=Peq-Pt
=Max(Pt-X,0)-Prima
35
Fundamentos de Derivados y Opciones
Benavides
1.4 Utilidad y Retorno de Inversión en opciones
En capítulos anteriores se definió la función de utilidad para las opciones de compra y de
venta. Es usual descontar el valor de la prima al mostrar la utilidad neta, ignorando el hecho
de que son flujos que se dan en periodos de tiempo no coincidentes. Al llevar el pago de la
prima al momento del vencimiento t, a la tasa libre de riesgo kf, se elimina el problema.
Luego, al vencimiento la utilidad por la compra de una opción de compra o de venta sería:
Utilidad Opción de Compra =
Utilidad Opción de Venta =
(
(
)
)
(
(
)
)
C0 y P0 son el valor de las primas pagadas por la opción de compra y la opción de venta,
respectivamente, recibidas en el momento 0. La expresión exp(kft) denota el factor que
convierte los valores anteriores a valor futuro 4 .
Opción de Compra
Puesto que una opción de compra genera más utilidades potenciales cuando el precio de
ejercicio es menor, se infiere que la prima pagada por una opción tal es mayor que la prima
de una opción equivalente, que solo difiere de la primera por tener un precio de ejercicio
superior. Este hecho se observa en la gráfica a continuación para una opción de compra
(Call) con las siguientes condiciones:
Valor del subyacente en el momento de compra S 0 =100
Tiempo al vencimiento t=3/12 años
Tasa libre de riesgo kf=3.0%
Precio de ejercicio X= 90 hasta 110 en incrementos de 5 y sus correspondientes primas 5 :
X
C(0)
90
13.26
95
10.01
100
7.33
105
5.21
110
3.60
4
Esta es una tasa continua.
Las primas están calculadas con la fórmula de Black-Scholes. Se asume adicionalmente un tiempo al
vencimiento de 0.25 años y volatilidad de 35%. Esto también aplica para las primas de la opción de venta de
la siguiente sección.
5
36
Fundamentos de Derivados y Opciones
Benavides
Utilidad Call
20
15
90
95
100
10
105
110
5
0
80,00
85,00
90,00
95,00
100,00
105,00
110,00
115,00
120,00
-5
-10
-15
La gráfica ilustra la utilidad de una opción de compra (Call) al vencimiento para diferentes
precios de ejercicio y expresando las primas pagadas a valor futuro. Como se observa la
más costosa es la que tiene un precio de ejercicio más bajo, compensado por el hecho de
que es la primera que ante un cambio favorable del precio, un incremento del valor del
subyacente al vencimiento, obtiene utilidades positivas.
Si la utilidad neta es dividida por la inversión, la prima pagada expresada a valor futuro,
tenemos el retorno de la inversión, como se observa a continuación:
37
Fundamentos de Derivados y Opciones
Benavides
Retorno Call
250%
90
200%
95
100
150%
105
110
100%
50%
0%
80,00
85,00
90,00
95,00
100,00
105,00
110,00
115,00
120,00
-50%
-100%
-150%
Es interesante observar que a pesar de ser la más costosa, la opción con precio de ejercicio
de 90 es la menos agresiva de todas. La razón de este comportamiento es que el
inversionista que elige esta opción en realidad asume un menor riesgo que el inversionista
que opta por la opción con precio de ejercicio mayor.
Opción de Venta
Igual tipo de análisis puede realizarse para la opción de venta (Put). Como la utilidad
potencial crece con precios de ejercicio inferiores, las primas son mayores entre mayor sea
el precio de ejercicio. Este hecho se observa en la gráfica a continuación para una opción de
venta (Put) con condiciones similares a las anteriores:
Valor del subyacente en el momento de compra S0 =100
Tiempo al vencimiento t=3/12 años
Precio de ejercicio X= 90 hasta 110 en incrementos de 5 y sus correspondientes primas:
X
P(0)
90
2.59
95
4.30
100
6.58
105
9.42
110
12.78
38
Fundamentos de Derivados y Opciones
Benavides
Utilidad Put
20
15
90
95
10
100
105
5
110
0
80,00
85,00
90,00
95,00
100,00
105,00
110,00
115,00
120,00
-5
-10
-15
De manera análoga como sucede con la opción de compra, la opción de venta con el mayor
potencial de utilidad, en este caso la de mayor precio de ejercicio, es la más costosa. Esto se
compensa frente a variaciones favorables del subyacente al vencimiento.
Igualmente, al graficar el retorno se obtiene:
Retorno Put
350%
90
300%
95
250%
100
105
200%
110
150%
100%
50%
0%
80,00
-50%
85,00
90,00
95,00
100,00
105,00
110,00
115,00
120,00
-100%
-150%
39
Fundamentos de Derivados y Opciones
Benavides
La opción más costosa, como antes, es la menos agresiva de todas. Al elegir esta opción el
inversionista asume un riesgo menor que el inversionista que opta por la opción con precio
de ejercicio menor. Adicionalmente debe observarse que la rentabilidad de este tipo de
inversiones puede llegar, en el peor de los casos, a -100%, una perdida completa; lo que
muestra a las claras lo agresivo de este tipo de operaciones.
40
Fundamentos de Derivados y Opciones
Benavides
Práctica en Excel
Opción de Compra
El objetivo es observar numérica y gráficamente el impacto de diferentes precios al
vencimiento, St, en la utilidad neta de una posición larga en una opción de compra (Call).
Inicialmente se almacena el precio al vencimiento St en la celda C7. Los precios de
ejercicio en incrementos de 5 se almacenan en el rango C8:G8. En las celdas C9 a G9 se
formula la utilidad de la opción Max(St-X,0), con la precaución de fijar la celda C7. La
fórmula almacenada en la celda C9 es =MAX($C$7-C8,0), al copiarla hacia la derecha
hasta la celda G9, se calculan las funciones de utilidad para los diferentes precios de
ejercicio. En las celdas C11 a G11 se proyecta a valor futuro el precio de la prima y en las
celdas C12 a G12 se calcula la utilidad neta. En ambos casos se usan las fórmulas ya
descritas.
A
2
3
4
5
6
7
8
9
10
11
12
Call
Utilidad
Call
Prima(0)
Prima(t)
Utilidad Call
B
Delta X
kf
Sigma
S0
St
X
VI(t):Max(St-X,0)
C(0)
C(0)*e(kf*t)
=VI(t)-Prima(t)
C
D
E
5 Fecha
3.0% t
35.0% Vto
100
F
G
01/11/2009
0.25 años
31/01/2010
100
90
95
100
105
110
13.26
10.01
7.33
5.21
3.60
Una vez calculada la utilidad para diferentes precios de ejercicio se evalúa el efecto que
sobre ella tiene diferentes valores del activo subyacente al vencimiento (St). Esto se puede
realizar a través de una tabla de datos. Para esto se toman valores de St entre 80 y 120, en
incrementos de 2.5, los cuales se guardan en el rango B13:B29. Para calcular el resultado
de la posición se selecciona el rango B12:G29 y a través de la tabla de datos
(Datos/Análisis Y si/Tabla de datos) se define la celda C7, donde se almacena St, como la
variable independiente que cambia entre los valores ya definidos. Los resultados se grafican
como se mostró previamente.
41
Fundamentos de Derivados y Opciones
Benavides
Para el cálculo de la rentabilidad dividimos la utilidad sobre la inversión:
( ))⁄
()
( )⁄
()
( ()
.
Estos valores se almacenan en las celdas C33 a G33, en el mismo orden anterior. En el
rango B34:B50 se guardan los valores para St entre 80 y 120, análogamente al paso
anterior, y finalmente con la función tabla se calculan las rentabilidades seleccionando el
rango B33:G50, con la celda de entrada C7, que es la celda donde se almacena el valor de
St.
42
Fundamentos de Derivados y Opciones
Benavides
Opción de Venta
La única diferencia con el caso anterior es la utilidad de la opción. En este caso se debe
almacenar en las celdas C9 a G9 la función Max(X-St,0), la fórmula almacenada en la celda
C9 es =MAX(C8-$C$7,0).
En todo lo demás se procede como en el caso anterior.
A
2
3
4
5
6
7
8
9
10
11
12
Put
Utilidad
Put
Prima(0)
Prima(T)
Utilidad Put
B
Delta X
kf
Sigma
S0
St
X
VI(T):Max(X-St,0)
P(0)
P(0)*e(kf*T)
=VI(T)-Prima(T)
C
D
E
5 Fecha
3.0% T
35.0% Vto
100
F
G
01/11/2009
0.25 años
31/01/2010
100
90
95
100
105
110
2.59
4.30
6.58
9.42
12.78
43
Fundamentos de Derivados y Opciones
Benavides
2. Proceso Lognormal
El proceso lognormal presupone que el precio de un activo nunca puede ser negativo. El
precio del activo tiene una tendencia (normalmente creciente) estable a lo largo del tiempo,
sin embargo sus valores puntuales son esencialmente aleatorios.
El supuesto fundamental plantea que la distribución de probabilidad de los retornos
continuos es normal, así:
[ ̃
]
(2-1)
es el precio del activo en el periodo t, ̃
el retorno en el periodo.
Esto implica que
S
~
rt t ln t t
St
Puesto que asumimos que la distribución de rt t es normal se tiene:
[(
Distribución de ̃
⁄ )
]
√
Por lo que podemos re-expresar (1), como:
[(
⁄ )
⁄
̃
~ ~ N 0,1
] con Z
(2-2)
Si disponemos de series históricas de los precios de los activos podemos hallar los
parámetros y usando las siguientes formulas, que resultan de (2):
*
(
*
[(
)+
(
[(
)+
⁄
̃
⁄ )
⁄ )
]=(
⁄
̃
⁄ )
]=
Finalmente se obtiene:
(
⁄ )
[ (
)]
[
(
)]
;
Sabemos que t=T/n, donde T implica el horizonte sobre el cual se calculan los parámetros
y n el número de periodos en el que se divide. T es usualmente igual a un año, tomando el
valor de T = 1, por lo que t=1/n*, n* puede tomar el valor de 12 (si los datos son
mensuales), alrededor de 242 (si los datos son diarios, solo días hábiles), 365 (si los datos
son diarios, días calendario), etc.
44
Fundamentos de Derivados y Opciones
(
⁄ )
*
(
)+
Benavides
*
;
(
)+
(2-3)
Con esta expresión podemos hallar los parámetros de un proceso lognormal para un activo
particular con base en los datos históricos y simular series de precios de activos con estos
parámetros.
Veamos
1. Cálculo de la media y varianza anualizada:
En la tabla Tabla 2-1 se listan los precios de final de semana y mes del ADR6 de
Ecopetrol y se calcula su retorno de manera discreta y continua. Es usual en la práctica
de negocios el uso de retornos y tasas discretas, aun cuando la manipulación de las tasas
discretas genera las diferencias entre tasas nominales y efectivas. Este problema
desaparece cuando se usan tasas continuas. El retorno discreto se calcula como
, su contraparte continua es
(
). A menor t la diferencia
entre estos retornos se reduce.
Tabla 2-1
Precios y retornos mensuales y semanales ADR de Ecopetrol, de 03/2009 a 04/2013
Retornos discretos y continuos, no todos los periodos se muestran
Rentabilidad y Varianza
Mes-año
03/2009
04/2009
05/2009
06/2009
07/2009
08/2009
09/2009
10/2009
11/2009
12/2009
01/2010
01/2013
02/2013
03/2013
04/2013
Mes (t)
0
1
2
3
4
5
6
7
8
9
10
46
47
48
49
Precio
16.07
17.25
20.34
22.29
25.16
24.67
26.10
24.10
24.76
23.30
23.39
63.59
57.16
54.52
47.14
Retorno
Discreto
7.34%
17.91%
9.59%
12.88%
- 1.95%
5.80%
- 7.66%
2.74%
- 5.90%
0.39%
2.27%
- 10.11%
- 4.62%
- 13.54%
Retorno
Continuo
=(St+1/St)-1
:
:
:
:
:
:
:
:
:
:
:
:
:
7.09%
16.48%
9.15%
12.11%
- 1.97%
5.63%
- 7.97%
2.70%
- 6.08%
0.39%
2.24%
- 10.66%
- 4.73%
- 14.54%
=ln(St+1/St)
:
:
:
:
:
:
:
:
:
:
:
:
:
6
ADR: American Depositary Receipt. Un ADR representa 1 o más acciones de una empresa no
estadounidense, originalmente listada en otro país, que se negocian en bolsas de EE. UU.
45
Fundamentos de Derivados y Opciones
Sem-año
30/03/2009
06/04/2009
13/04/2009
20/04/2009
27/04/2009
04/05/2009
11/05/2009
18/05/2009
26/05/2009
01/06/2009
08/06/2009
16/02/2010
22/02/2010
01/03/2010
08/03/2010
15/03/2010
08/04/2013
15/04/2013
22/04/2013
Retorno
Semana (t) Precio
Discreto
0
16.07
1
16.35
1.74%
2
16.52
1.04%
3
17.09
3.45%
4
17.25
0.94%
5
19.15
11.01%
6
18.69
- 2.40%
7
19.66
5.19%
8
20.34
3.46%
9
21.66
6.49%
10
22.6
4.34%
46
24.95
2.21%
47
25.84
3.57%
48
26.78
3.64%
49
27.03
0.93%
50
26.99
- 0.15%
210
48.75 - 10.70%
211
47.25
- 3.08%
212
47.14
- 0.23%
Benavides
Retorno
Continuo
=(St+1/St)-1
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
1.73%
1.03%
3.39%
0.93%
10.45%
- 2.43%
5.06%
3.40%
6.29%
4.25%
2.19%
3.50%
3.57%
0.93%
- 0.15%
- 11.31%
- 3.13%
- 0.23%
=ln(St+1/St)
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
Ahora calculamos la media y la varianza de este título, tanto con datos mensuales como
semanales:
Mensual
n
t
Retorno
' = t
P49
¿Qué pasa?
'
Equivalencia
d'
(Anual)
12
0.083 =1/n
Discreto
2.51% =promedio(ri)
54.19 =P0.(1+')^49
2.22% =(P49/P0)^(1/49)-1
Continuo
2.20% =promedio(ri)
47.14 =P0.exp('.49)
2.20% =ln(P49/P0)/49
2.22% =exp(c ')-1
30.15% =(1+'d-mes)^n-1
30.15% =exp(c ')-1
26.36% ='c-mes .n
= tc-mes .n
Con datos mensuales, n es 12 y t es el inverso de n. Al calcular el retorno discreto
promedio mes encontramos que esta estimación no es correcta, puesto que al aplicar la
fórmula de valor futuro discreta [F=P(1+’)n ] con el valor hallado de ’=2.51% el valor
estimado de la acción para el mes 49 sería de 54.19, y no de 47.14, que es el valor correcto.
La tasa correcta se halla despejando ’ de la fórmula de valor futuro, lo cual resulta en un
valor de 2.22% (discreta).
Como se ve en el cálculo equivalente con retornos continuos, el problema es inexistente
para esta metodología. La fórmula de valor futuro continua [F=Pexp(’n)] entrega el valor
correcto usando el promedio de las tasas continuas, que es de 2.20%. Este valor coincide
cuando en la ecuación de valor futuro despejamos ’ (=ln(P0/P49)/49). Incidentalmente
podemos hallar la equivalencia entre tasas continuas y discretas, puesto que para cualquier
frecuencia de datos se cumple que 1+’d=exp(’c). Finalmente se observa que la ecuación
46
Fundamentos de Derivados y Opciones
Benavides
(3) solo se cumple para retornos continuos, =’c.n, eliminando la diferencia entre tasas
efectivas y nominales, esto significa que el promedio de los retornos continuos si estima
correctamente la media que es 2 /2, mientras que el promedio de los retornos discretos
debe ser corregido, puesto que solo estima .
El cálculo se repite para frecuencias semanales. Aquí solo cabe anotar que al convertir las
tasas semanales a anuales encontramos, como es de esperar, los mismos valores. El número
de semanas por año no es exactamente 52. Para calcular el número exacto de semanas en el
periodo multiplicamos 12 por el número de semanas en el periodo dividido por el número
de meses en el mismo: 12x212/49.
Semanal
n
t
Retorno
' = t
P212
¿Qué pasa?
'
Equivalencia
d'
(Anual)
51.92 =12.#Sem/#Mes
0.019 =1/n
Discreto
0.58% =promedio(ri)
54.68 =P0.(1+')^212
0.51% =(P212/P0)^(1/212)-1
Continuo
0.51% =promedio(ri)
47.14 =P0.exp('.212)
0.51% =ln(P212/P0)/212
0.51% =exp(c ')-1
30.15% =(1+'d-sem )^n-1
30.15% =exp(c ')-1
26.36% ='c-sem .n
= tc-sem .n
47
Fundamentos de Derivados y Opciones
Benavides
Gráfica 2-1
Evolución precio del ADR de Ecopetrol.
Nota: La línea azul solo presenta los datos mensuales
En el caso de los retornos la estimación no cambia dependiendo de la frecuencia de
muestreo, puesto que el retorno solo depende de los datos iniciales y finales. Esto no
sucede para el caso de la varianza; como se ve en la gráfica Gráfica 2-1, una menor
frecuencia de muestreo soslaya importante información respecto a la variabilidad.
A continuación se calcula la volatilidad de los retornos mensuales, usando tanto los
retornos discretos como los continuos.
Volatilidad Muestral (Datos Mensuales)
Discreto
2
2
Var. Mes
m '= m .t
0.49% =var(ri)
0.0593 mes '.n
0.0586 mes '.n
m
7.03% 2m ')1/2
6.99% 2m ')1/2
año
24.36% mes '.n1/2
24.21% mes '.n1/2
2año
Desv. Mes
Continuo
0.49% =var(ri)
48
Fundamentos de Derivados y Opciones
Benavides
Volatilidad Muestral (Datos Semanales)
Discreto
2
2
Var. Sem
m '= m t
0.09% =var(ri)
Continuo
0.09% =var(ri)
0.04619826 m '.n
0.048361 m '.n
2año
Desv. Sem
m
2.98% 2m ')1/2
3.05% 2m )1/2
año
21.49% sem '.n1/2
21.99% sem '.n1/2
Al calcular la varianza (muestral o poblacional), usando los retornos discretos o continuos,
encontramos que el valor hallado para los datos semanales es diferente, y posiblemente más
cercano a la realidad, que el hallado con datos mensuales.
Finalmente, con el cálculo de la varianza se puede mejorar el cálculo del retorno discreto,
⁄ , que reporta un valor muy cercano a la
aplicando la siguiente corrección
realidad:
Corrección Retorno Discreto (Datos Mensuales)
2
Retorno
d'
2.26% ='- /2
Corrección Retorno Discreto (Datos Semanales)
2
Retorno
d'
0.53% ='- /2
49
Fundamentos de Derivados y Opciones
Benavides
Simulación de una Trayectoria de Precios
En esta sección se usarán los cálculos previos para simular una trayectoria de precios de un
año, con frecuencia semanal (52 semanas) para el ADR de Ecopetrol. Los datos básicos
son:
Parámetros de Simulación
ADR Ecopetrol
Media ()
1.58%
Desviación ()
21.99%
1.93% semana
47.14
t
S0
Con la media y la desviación simulamos una posible realización de la trayectoria de precios
⁄
̃
del ADR de Ecopetrol implementando la ecuación (2-1):
[
]
en forma sucesiva.
Con base en los parámetros previos valores se desarrolla el siguiente modelo. Primero se
⁄
⁄
̃
̃
calcula
[
], posteriormente
[
] y así
sucesivamente hasta llegar a T.
Periodo
0
Fecha
22/04/2013
1
29/04/2013
-0.88
45.90 <--=S0.EXP(t+Z .t1/2)
2
3
4
06/05/2013
13/05/2013
20/05/2013
-0.92
0.80
0.93
44.64 <--=S1.EXP(t+Z .t1/2)
45.75
47.08
5
6
27/05/2013
03/06/2013
0.99
0.76
48.54
49.69
7
8
9
10/06/2013
17/06/2013
24/06/2013
-0.14
-0.81
-0.12
49.49
48.31
48.14
10
01/07/2013
-1.85
45.51
Z
Precio
47.14
Los valores en la columna Z son números aleatorios que responden a una distribución
normal estándar. Programas cuantitativos tales como Matlab o Mathematica tienen la
capacidad de generar una serie de este tipo. Otra posibilidad es recurrir a Excel, usando la
función de generación de números aleatorios, procedimiento que detallamos a continuación.
En primer lugar seleccionamos [Datos/Análisis de Datos] lo cual despliega la siguiente
pantalla:
50
Fundamentos de Derivados y Opciones
Benavides
Al seleccionar generación de números aleatorios debemos a continuación definir el número
de variables (columnas) y la cantidad de datos (52 semanas), además de la distribución
deseada (Normal, media = 0, desviación = 1) y la celda donde se desea ubicar el primer
dato:
La grafica resultante se muestra a continuación; los datos simulados no pretenden generar
un resultado cercano a los datos reales, puesto que apenas son una realización, entre
muchas posibles, de un proceso aleatorio, por lo que su poder predictivo es nulo:
51
Fundamentos de Derivados y Opciones
Benavides
Gráfica 2-2
Trayectoria simulada precio del ADR de Ecopetrol.
Intervalo de confianza 90%
Predicciones
Aunque el modelo lognormal no predice una trayectoria particular puede usarse para
establecer rangos de posibles realizaciones, intervalos de confianza, futuras con una
probabilidad definida (Hull, 2008). Se trabaja en este caso con el logaritmo del precio, que
según los supuestos del modelo lognormal, tiene una distribución normal. Por ejemplo, los
valores de una variable y, en un tiempo x (e.g. 6 meses) estarán entre ymax y ymin con una
certeza del z%. A continuación se plantea un modelo que permite tal tipo de cálculos.
Siguiendo con el ADR de Ecopetrol, podemos estimar el intervalo de confianza con
probabilidad del 90% en 6 meses de la siguiente manera. En primer lugar se estima el valor
( )
esperado del precio, en términos del logaritmo, en un tiempo T:
. Este
valor es 3.86, el cual equivale a un valor de US 47.51 al calcular la exponencial. La
⁄
volatilidad acumulada semestral
es 0.16. Puesto que la variable Z es normal
estándar, podemos estimar su realización en los límites superior e inferior del rango
superior estimando el inverso de la distribución normal estándar para una probabilidad del
95% (Excel: +/- INV.NORM.ESTAND(95%)). El resultado es Desv=1.64 desviaciones
52
Fundamentos de Derivados y Opciones
Benavides
estándar. En otras palabras entre -1.64 y +1.64 desviaciones estándar se encontrarán el 90%
de las realizaciones de la variable. Al multiplicar este valor por la volatilidad acumulada
(0.16), obtenemos el Delta o la magnitud en la que se afecta el valor esperado,
⁄
=0.26, hacia abajo y hacia arriba. Estos valores son, en términos del logaritmo
de la variable, los límites inferior y superior, Ln(S T min) y Ln(ST max), respectivamente, del
intervalo de confianza esperado. Los valores esperados S T min y ST max, se obtienen
nuevamente al calcular la exponencial.
Intervalo de Confianza
T
Ln(ST)
1/2 Seis meses
3.86 Ln(S0)+T
E(ST)
47.51 Exp(Ln(ST))
Desviación Semestral Acumulada
T1/2
Probabilidad
Certeza
Desv.
0.16
95.00% Cola Superior
-1
1.64 N (Pr=95%)
↑=INV.NORM.ESTAND(H9)
Valores Extremos
Delta
Ln(STmin)
0.26 Desv.T1/2
3.61 Ln(ST)-Delta
Ln(STmax)
4.12 Ln(ST)+Delta
STmin
36.79 Exp(Ln(STmin))
STmax
61.36 Exp(Ln(STmax))
En la Gráfica 2-2, se incorporaron los valores S T min y ST max para T variando entre 0 y 1
año. Este cálculo se puede realizar en Excel usando [Datos/Análisis Y si/Tabla de Datos]
definiendo como variable independiente a T, los valores se reportan a continuación:
53
Fundamentos de Derivados y Opciones
Benavides
Intervalo de Confianza
Fecha
22/04/2013
1 20/05/2013
2 17/06/2013
3 15/07/2013
4
5
6
7
8
9
10
11
12
13
12/08/2013
09/09/2013
07/10/2013
04/11/2013
02/12/2013
30/12/2013
27/01/2014
24/02/2014
24/03/2014
21/04/2014
0.08
0.15
0.23
5.00%
36.79
47.14
42.70
41.01
39.77
95.00%
61.36
47.14
52.17
54.45
56.28
0.31
0.38
0.46
0.54
0.61
0.69
0.77
0.84
0.92
1.00
38.77
37.91
37.15
36.47
35.85
35.29
34.76
34.27
33.81
33.37
57.88
59.34
60.69
61.97
63.19
64.37
65.50
66.60
67.68
68.73
T
54
Fundamentos de Derivados y Opciones
Benavides
Simulación de Trayectorias
Se presenta en este acápite un procedimiento y una macro 7 que permite simular 3
trayectorias aleatorias.
Ahora continuamos con la generación de trayectorias aleatorias y la envolvente de
probabilidad (90%) entre 0 y 26 semanas. La hoja de cálculo luce de la siguiente forma:
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
E
t
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
F
z1
G
z2
H
z3
1.55529051
2.08186975
-1.02654212
-0.230566
1.42113322
0.67235419
0.58554178
-0.49998675
-0.68564759
0.35871381
-0.33401989
1.39799795
0.61781293
-1.60237505
0.62031404
-0.9051837
1.17027639
-0.98879354
1.10131396
0.61439096
0.94688176
-0.84647127
0.58010187
-1.9901745
-1.10103429
0.18724791
0.67966084
0.65879817
0.52924293
0.45768957
-2.47382559
-0.06181153
1.5365913
-1.39455096
0.91502216
-0.53135636
0.25878535
0.8563643
-0.34796585
-0.02758043
-0.44152443
1.41465307
-0.91607035
1.01035312
-0.38502776
-0.11249767
0.47483127
0.36778374
-0.19550725
0.91154106
-0.84144631
-0.73868705
-0.71240947
-0.95084033
-0.64573896
0.45420961
-1.2405053
-0.27845545
1.0641952
0.28793011
0.54630391
0.62747063
-1.45424565
0.78230642
-1.12923999
-0.17014713
1.19007836
0.62644631
-1.19209972
0.52291739
1.39962594
-0.9863038
-0.19238769
-0.82424094
0.12698365
1.52108441
0.18678065
0.59683885
I
Tray1
100.00
104.87
111.60
108.95
108.73
113.60
116.25
118.68
117.57
115.86
117.54
116.97
122.14
124.80
119.90
122.52
120.02
124.52
121.69
126.02
128.76
132.77
130.26
132.96
126.38
123.12
124.31
J
Tray2
100.00
102.35
104.70
106.72
108.57
101.82
102.09
107.01
103.41
106.53
105.44
106.67
109.72
109.15
109.55
108.69
113.54
111.19
114.85
114.14
114.29
116.31
118.03
117.91
121.46
119.19
117.29
K
Tray3
100.00
98.48
96.34
95.05
96.68
93.83
93.52
96.74
97.95
99.89
102.09
98.49
101.10
98.42
98.39
102.14
104.39
101.44
103.38
107.95
105.50
105.41
103.48
104.31
109.28
110.34
112.68
L
Media
100.00
100.44
100.89
101.34
101.78
102.24
102.69
103.14
103.60
104.06
104.52
104.99
105.45
105.92
106.39
106.86
107.33
107.81
108.29
108.77
109.25
109.73
110.22
110.71
111.20
111.69
112.19
M
Min
100.00
95.96
94.59
93.64
92.91
92.32
91.83
91.42
91.06
90.75
90.48
90.24
90.04
89.85
89.69
89.55
89.43
89.32
89.23
89.15
89.09
89.03
88.99
88.95
88.93
88.91
88.90
N
Max
100.00
105.13
107.61
109.67
111.51
113.22
114.83
116.38
117.87
119.32
120.74
122.14
123.50
124.86
126.19
127.51
128.82
130.12
131.41
132.70
133.97
135.25
136.52
137.78
139.05
140.31
141.57
En las columnas F a H tenemos números aleatorios generados de la misma manera que en
la sección anterior. Las columnas I a K contienen las trayectorias de precios producto de las
realizaciones de los números aleatorios. En la columna L se tiene el valor medio de la
variable (Equivalente a la celda B14, nótese que el valor en la semana 26 coincide con el
valor calculado previamente). En las columnas M y N tenemos los valores mínimo y
máximo que determinan el rango del 90% de probabilidad (Equivalentes a las celdas B24 y
B25, respectivamente)
7
Una macro es un programa en VBA que automatiza o realiza cálculos diferentes a los pre -programados por
Excel.
55
Fundamentos de Derivados y Opciones
Benavides
A continuación se muestran las fórmulas para los cálculos de estos valores para la semana
1, estas fórmulas se repiten hasta la semana 26:
I
Tray1
4
5 =B8
6 =I5*EXP($B$4*$B$7+F6*$B$5*$B$7^(1/2))
J
Tray2
=I5
=J5*EXP($B$4*$B$7+G6*$B$5*$B$7^(1/2))
K
L
4
Tray3
Media
5 =J5
=K5
6 =K5*EXP($B$4*$B$7+H6*$B$5*$B$7^(1/2))
=$L$5*EXP($B$4*$E6/$B$6)
M
4
Min
5 =L5
6 =$L$5*EXP($B$4*$E6/$B$6-$B$19*$B$5*($E6/$B$6)^(1/2))
N
4
Max
5 =M5
6 =$L$5*EXP($B$4*$E6/$B$6+$B$19*$B$5*($E6/$B$6)^(1/2))
Gráficamente el resultado es el siguiente:
56
Fundamentos de Derivados y Opciones
Benavides
Gráfica 2-3
Trayectorias simulada modelo lognormal.
Intervalo de confianza 90%
Trayectorias
Precio
150,00
140,00
130,00
120,00
110,00
100,00
90,00
Semanas
80,00
0
5
Tray1
10
Tray2
15
Tray3
20
Media
25
Min
30
Max
Generación automática de una serie de Precios
El proceso anterior puede automatizarse fácilmente a través de una macro simple. La macro
transcrita a continuación permite generar tres series de números aleatorios. Para tal fin se
crean dos rangos de nombres: 1) Noal, F6:H31, donde se guardan los números aleatorios; 2)
celi, F6, la celda inicial.
A continuación se transcribe la macro:
Sub Macro1()
'
' Macro1 Macro
' Aleator
'
' Acceso directo: Ctrl+Mayús+A
'
Application.ScreenUpdating = False
Sheets("Hoja1").Select
Range("Noal").Select
57
Fundamentos de Derivados y Opciones
Benavides
' Range(Selection, Selection.End(xlDown)).Select
Selection.ClearContents
Application.Run "ATPVBAEN.XLAM!Random", ActiveSheet.Range("celi"), 3, 26 _
, 2, , 0, 1
Sheets("Gráfico1").Select
Application.ScreenUpdating = True
End Sub
--------------------Ejercicios
1. Estime cuales son los valores mínimo y máximo para un intervalo de confianza del
80% dentro de 4 meses para una variable similar a la del ejemplo previo.
2. Genere 4 trayectorias de precios, el valor medio y la envolvente para un intervalo de
confianza del 95% entre 0 y 1 año, para una variable con precio inicial de 500,
volatilidad del 25% y un retorno esperado del 14%.
3. Valoración de Derivados utilizando la Simulación de Montecarlo
Las herramientas desarrolladas en las secciones anteriores nos permiten estimar el valor de
un derivado a través de una simulación. Se valorarán en este caso opciones de compra
(Call) y venta (Put) europeas a 6 meses sobre el ADR de Ecopetrol, con un precio de
ejercicio de 50. Puesto que son derivados europeos, solo pueden ejercerse al vencimiento.
Una opción de compra (Call) se ejerce si el precio de ejercicio X es inferior al precio de
vencimiento del subyacente S T , la utilidad es en este caso de S T -X, la opción no se ejerce si
X es superior a ST , este resultado se esquematiza como el máximo entre S T -X y 0: Max(ST X, 0). Para la opción de venta (Put) la utilidad es máximo entre X-ST y 0: Max(X-ST , 0)8 .
Asumiremos que la volatilidad de los retornos es 21.99%, manteniéndose en los valores
estimados previamente, la tasa libre de riesgo es del 4% y el precio actual de la acción es
$47.14.
Parámetros de Simulación
ADR Ecopetrol
Tasa libre de riesgo (kf)
4%
Desviación ()
21.99%
Media ()
T
0.50 años
Fecha 0
22/04/2013
Fecha T
21/10/2013
S0
8
1.58% =kf-2/2
47.14
Ver Benavides (2010) y Benninga (2008).
58
Fundamentos de Derivados y Opciones
Benavides
Puesto que nuestro interés es simular los precios al vencimiento (en 0.5 años), modificamos
⁄
̃
el procedimiento previo para obtener el valor final tal que
[
]. Es
2
importante destacar que = kf- /2. La razón de este ajuste es que no tenemos mejor
información sobre el retorno esperado de la acción que la tasa libre de riesgo. Ya que el
objetivo es una muestra representativa de los posibles valores finales, repetimos el cálculo
un número suficiente de veces tal, que obtengamos la distribución de ̃ . La similitud de la
distribución de la muestra y la teórica para 3,000 realizaciones de ̃ se presenta en el
gráfico 4.
59
Fundamentos de Derivados y Opciones
Benavides
Gráfica 4
Distribución Muestra vs. Normal
Histograma de frecuencia de la muestra vs. distribución normal teórica.
3000 simulaciones
Se calculan sucesivamente S T y el valor del derivado al vencimiento. Puesto que la
expectativa más razonable respecto al rendimiento del activo es la tasa libre de riesgo,
expresamos =kf-2 /2. A continuación se presentan 2 realizaciones, de las 3000 requeridas,
de ST :
Periodo
0
̃
Precio (ST)
47.14
1
0.67
45.95
2
0.09
62.66
<--=S0 .EXP(.T+ ̃ ..T1/2 )
<--=S0 .EXP(.T+ ̃ ..T1/2 )
En la gráfica 5 se incorpora la distribución de valores finales de S T a los cálculos previos.
La línea rosada (graficada sobre el momento del vencimiento de los derivados) presenta
esta distribución. Los valores superiores al precio de ejercicio son aquellos en los cuales es
óptimo ejercer la opción de compra (Call), los valores inferiores al precio de ejercicio son
aquellos en los cuales es óptimo ejercer la opción de venta (Put). Los valores de los
derivados que corresponden a las realizaciones de los precios arriba mostrados se presentan
a continuación. Si el precio final del subyacente es 45.95, el resultado para la opción de
compra es Max(45.95-50, 0)=0 ; si el precio final es 62.66, el resultado es Max(62.6650,0)=12.66. Los cálculos correspondientes a la opción de venta se calculan en forma
análoga:
Call
Max(ST-X,0)
Put
Max(X-ST,0)
1
-
4.05
2
12.66
-
Periodo
0
60
Fundamentos de Derivados y Opciones
Benavides
Gráfica 5
Evolución ADR Ecopetrol
Las líneas verde (semana) y azul oscura (mes) representan la evolución del precio histórico del
ADR de Ecopetrol. Las líneas roja (95% superior) y violeta (5% inferior) representan la evolución
del intervalo de confianza del 90%, la línea azul clara es una posible realización del precio. La línea
horizontal punteada negra representa el precio de ejercicio X. La línea vertical negra representa el
momento del vencimiento de los derivados T. Finalmente, la curva rosada representa la distribución
de los valores de ST al momento del vencimiento.
Habiendo obtenido los valores finales, los promediamos. Encontramos así el valor esperado
del derivado, así:
Valor esperado en T de la opción de compra (Call):
Valor esperado en T de la opción de venta (Put):
∑
∑
(
(
)
)
Puesto que el retorno esperado del subyacente es k f, el valor futuro (VF) se descuenta a esta
tasa:
Valor esperado en 0 de la opción de compra (Call) o venta (Put):
(
)
A continuación se estiman los valores futuro y presente de los derivados analizados:
61
Fundamentos de Derivados y Opciones
Benavides
Valor
Futuro, VF
Valor
Presente, V0
BlackS choles
Call
2.19
2.15
2.14
Put
4.12
4.04
4.01
En la tabla anterior se presentan los valores obtenidos con la simulación con los valores
obtenidos con la fórmula de Black-Scholes, la cual se describirá en secciones posteriores.
Como se observa los resultados por ambos métodos son muy cercanos.
62
Fundamentos de Derivados y Opciones
Benavides
4. Valoración de Derivativos, modelo discreto
Los activos derivados pueden valorarse suponiendo que en el futuro inmediato solo pueden
darse 2 estados, en uno de esos estados (U) el valor del activo subyacente es superior al
valor actual, mientras que en el otro (D) el valor del activo subyacente es inferior a su valor
actual.
S1U = S0u
S0
S1D = S0d
Bajo nuestro supuesto u>1>d. Suponga además que se desea invertir en un portafolio P sin
riesgo. Para tal fin se invierte (Largo) en acciones y se vende (corto) un call. Para
descartar una solución trivial suponemos que se cumple que X, el precio de ejercicio, es tal
que S0 u>X>S0 d.
El valor (costo) actual de tal estrategia es P 0 = S0 – c0 .
El objetivo es encontrar el valor de que haga que el valor del portafolio no varíe en
ninguno de los 2 estados posibles.
En el estado U el valor del portafolio P 1U es S0 u – Max(S0 u – X, 0), por lo que tenemos
P1U = S0 u – S0 u + X
En el estado D el valor del portafolio P 1D es S0 d – Max(S0 d – X, 0), por lo que tenemos
P1D = S0 d
Puesto que nuestro propósito es que el portafolio tenga 0 riesgo, se debe cumplir que
P1U = P1D
S0 u – S0 u + X = S0 d
Resolviendo, tenemos que = (u – X/S0 )/(u – d). Puesto que este valor de genera un
portafolio sin riesgo, es correcto descontarlo a la tasa libre de riesgo r, por lo que su valor
presente es (usando su valor en el estado D) S0 d e-rt . Esto a su vez debe ser el valor de la
estrategia hoy: S0 d e-rt = S0 – c .
Al despejar tenemos que c = S0 (1- d e-rt ).
Ejercicio
Resuelva este modelo para un Put.
Generalización
La estrategia delineada en los párrafos anteriores permite valorar cualquier derivativo f. Sea
0 S0 –f0 el costo del portafolio hoy, compuesto por 0 unidades del activo subyacente y la
63
Fundamentos de Derivados y Opciones
Benavides
venta de f. Sean f1U y f1D los respectivos valores futuros en los estados U y D del derivativo
f.
El valor de es el que resuelve
0 S0 u – f1U = 0 S0 d – fD1
0 =(f1U – f1D)/[S0 (u – d)]
(Ec. 4.1)
Con este valor para 0 se garantiza un portafolio libre de riesgo. El valor presente del
portafolio debe ser igual, en ausencia de arbitraje, al valor (costo) inicial del mismo:
(0 S0 u – f1U) exp(-rt) = 0 S0 – f0
f0 =S0 + (f1U – 0 S0 u) e-rt
(Ec. 4.2 a)
En el caso del estado D esta igualdad se expresa como
f0 =0 S0 + f1D – 0 S0 d) e-rt
(Ec. 4.2 b)
Aunque será evidente en secciones posteriores, es conveniente observar que las ecuaciones
4.2 nos muestran que el valor del derivativo es igual a invertir en 0 unidades del activo
subyacente S y en un bono libre de riesgo con valor nominal de f1U – 0 S0 u ó f1D – 0 S0 d.
Definamos p = (ert – d)/(u – d) y expresemos f en función de p, f1U y f1D.
El resultado es
f0 = e-rt [pf1U +(1-p) f1D].
(Ec. 4.3)
Aunque p es una probabilidad neutral al riesgo, el inversionista promedio, averso al riesgo,
también debe aceptar el valor de f hallado por este procedimiento. La razón es que el valor
de f hallado garantiza la ausencia de arbitraje, independientemente de las preferencias del
inversionista.
Ejercicio
Compruebe que, sí p = (ert – d)/(u – d), f0 = e-rt [pf1U +(1-p) f1D].
Formulación Alternativa de la Valoración para 2 periodos
En este caso el objetivo es duplicar los pagos futuros del derivativo a través de un
portafolio que incluye 0 unidades del activo subyacente S y la inversión en bonos libres de
riesgo B.
Los supuestos del modelo son:
1. Existen 2 periodos, el periodo inicial donde se suscribe el derivado y el periodo
final donde el derivado expira. El tiempo transcurrido entre estos periodos es t.
64
Fundamentos de Derivados y Opciones
Benavides
2. El activo subyacente S, cuyo valor actual es S 0 , solo puede tomar 2 valores futuros
(lo que es equivalente a decir que el futuro solo tiene dos estados U y D): S1U o S1D.
Podemos expresar S1U = S0 u y S1D = S0 d. Los factores u y d estan asociados a la
volatilidad del activo subyacente ya conocido
3. Existe un bono cero cupón o de descuento puro sin riesgo, la tasa libre de riesgo se
denomina r. Esta tasa se compone continuamente, lo que implica que el valor futuro
de un bono con valor de B0 en el siguiente periodo es igual a B0 exp(rt),
independiente de si el estado es U o D. La tasa normalmente se expresa en términos
anuales por lo que si el tiempo transcurrido entre el periodo 0 y el 1 es 1 año, el
valor de t es igual a 1. Si el horizonte es menor, t corresponde a la fracción anual o
porcentaje transcurrido. (Si el tiempo hasta la expiración es de 5 meses, t = 5/12).
B1U = B0ert
B0
B1D = B0ert
4. Se cumple que u > ert > d.
Bajo el principio de no arbitraje, 2 activos que tengan pagos futuros idénticos deben tener el
mismo precio hoy.
Sean f1U y f1D los pagos futuros en cada estado del derivativo, los cuales para una opción
Put corresponden a:
f1U = Max[X-S0 u,0]
f1D = Max[X-S0 d,0]
Sean 0 el número de unidades del activo subyacente y B0 el monto de la inversión en el
bono libre de riesgo que componen el portafolio. Para cada estado se debe cumplir que:
f1U = 0 S0 u + B0 ert
f1D = 0 S0 d + B0 ert
Este es un sistema de 2 ecuaciones con 2 incógnitas, los valores de 0 y B0 . Despejamos las
incógnitas y encontramos que
0 = (f1U – f1D)/[S0 (u – d)]
B0 = e-rt (f1Du – f1Ud)/(u - d)
(Ec. 4.1)
(Ec. 4.4)
Observese que 0 es el mismo valor hallado previamente, cuando el valor del derivativo se
dedujo como parte de un portafolio sin riesgo.
El valor hoy del derivativo corresponde al valor de la inversión en el activo subyacente
0 S0 más el valor de la inversión en el bono libre de riesgo B0 .
65
Fundamentos de Derivados y Opciones
Benavides
Sea f0 el valor del derivativo en el momento 0, según los supuestos previos se tiene que
f0 = 0 S0 + B0
(Ec. 4.5)
Reemplazando 0 y B0 con los valores hallados en las ecuaciones 4.1 y 4.4 se tiene
f0 = (f1U – f1D)/(u – d) + e-rt (f1Du – f1Ud)/(u - d)
Lo que se convierte en (al multiplicar y dividir la primera expresión por e rt )
f0 = [(f1U – f1D)ert + (f1Uu – f1Dd)]/[(u - d)ert ]
Reagrupando términos se tiene
f0 = [(f1U (ert – d) + f1D (u – ert )]/[(u - d)ert ]
Definamos
p
= (ert – d)/(u-d)
(1-p) = (u – ert )/(u-d)
Se obtiene así
f0 = e-rt [pf1U + (1-p)f1D]
(Ec. 4.3)
Como se mencionó en la sección previa este método se conoce como valoración neutral al
riesgo.
Ejercicio
Observe las ecuaciones 4.2 y las ecuaciones 4.4 y 4.5. Compruebe que
B0 = e-rt (f1Du – f1Ud)/(u - d) = (f1U –0 S0 u)e-rt = f1D – 0 S0 d)e-rt
Las probabilidades en un mundo neutral al riesgo
Debido a que en este mundo conocemos los pagos futuros de cada activo existente con
certeza absoluta podemos hallar el valor esperado del derivativo, si conocemos la
probabilidad de ocurrencia de cada estado. Esta probabilidad puede hallarse si analizamos
el activo subyacente S.
Para cualquier activo se cumple
f i1 pfi1U 1 pf i1D
En particular para el activo subyacente tenemos:
Si1 pSi u 1 pSi d
Adicionalmente podemos plantear que en un mundo neutral al riesgo el valor futuro del
activo subyacente debe ser Si1 Si e rt , combinando las 2 últimas ecuaciones podemos
hallar el valor de p
66
Fundamentos de Derivados y Opciones
Benavides
e rt pu 1 pd
p
e rt d
ud
El valor actual del derivativo se halla de la misma forma, solo que ahora ya conocemos el
valor de p. El valor del derivativo en el periodo i es:
f i e rt pfi1U 1 pf i1D
67
Fundamentos de Derivados y Opciones
Benavides
Valoración Multi-periodo
El valor del derivativo puede calcularse de manera más precisa si el tiempo hasta la
maduración se subdivide en varios periodos. A mayor numero de periodos mas preciso es el
cálculo.
Suponga que el tiempo hasta el vencimiento del derivativo es T, el cual se expresa en años,
y se desea subdividirlo en n periodos. La duración de cada periodo t es T/n. El supuesto
anterior sobre la variación de precios se mantiene. Para cada periodo futuro el precio del
activo subyacente solo puede incrementarse en u o reducirse en d. Se cumple que u>e rt >d.
La probabilidad neutral al riesgo es nuevamente p = (e rt -d)/(u-d)
El proceso de variación del activo subyacente para tres periodos se presente en le siguiente
árbol de nodos:
0
1
2
3
S1UUU
S0u3
S1UU
S0u2
S1U
S0u
S1UUD
S0u2d
S1UD
S0ud
S0
S1D
S0d
S1UDD
S0ud2
S1DD
S0d2
S1DDD
S0d3
Bajo estas condiciones es claro que la probabilidad p no cambia entre los periodos. La
valoración del derivativo se realiza desde el vencimiento hasta el periodo 0 en un proceso
que se esquematiza, en el caso de un call europeo at-the-money, así:
68
Fundamentos de Derivados y Opciones
0
Benavides
1
2
3
f3UUU
S0u3-X
f2UU
[pf3UUU+(1-p)f3UUD]e-rt
f1U
[pf2UU+(1-p)f2UD]e-rt
f3UUD
S0u2d-X
f2UD
[pf3UUD+(1-p)f3UDD]e-rt
f0
[pf1U+(1-p)f1D]e-rt
f1D
[pf2UD+(1-p)f2DD]e-rt
f3UDD
0
f2DD
[pf3UDD+(1-p)f3DDD]e-rt
f3DDD
0
Notese que en el periodo 3 (nuestro n) los valores de f3 corresponden a los valores finales
de la opción, los cuales llamamos valores intrínsecos en secciones posteriores. Para el
periodo 2 los valores de f2 corresponden a la valoración neutral al riesgo de f3 en sus
diferentes estados. El proceso se repite hasta llegar al periodo 0.
Es posible por este método encontrar formulas para los valores de opciones call y put
europeas, para n periodos:
n n
n i
c 0 e rtn p i 1 p M axS0 u i d n i X,0
i 0 i
Ec. 4.4
n n
n i
p 0 e rtn p i 1 p M axX S0 u i d n i ,0
Ec. 4.5
i 0 i
n
n!
La expresión
, siendo n el número de periodos e i el número de subidas,
i k! n i !
corresponde a una combinatoria que expresa el número de caminos por los cuales puede
llegarse a uno de los valores (nodos) del último periodo. Por ejemplo para llegar a f3UUD es
3
posible seguir las rutas UUD, UDU o DUU, por lo que 3 , lo que puede comprobarse
2
fácilmente aplicando la fórmula.
Cuando n tiende a infinito las ecuaciones 4.4 y 4.5 tienden a los valores reportados por la
fórmula de Black-Scholes, siempre que se defina9 a u e σ
9
La fórmula también converge si
2
u er- 2 t σ
t
y d e -σ t .
t
2
y d er - 2 t σ
t
69
Fundamentos de Derivados y Opciones
Benavides
Derivados Americanos y Exóticos
La metodología planteada en la sección anterior se extiende fácilmente a derivativos de
ejercicio temprano, como las opciones americanas, y derivativos exóticos, por ejemplo
opciones americanas con precios de ejercicio variable.
Una opción americana puede ser ejercida antes del vencimiento por lo que en cada periodo
debe examinarse si es conveniente ejercerla o esperar un periodo adicional. Para este
propósito es conveniente introducir un árbol de nodos para los valores intrínsecos del
derivativo. A continuación se presenta el árbol para un call americano at-the-money.
0
1
2
3
fi3UUU
S0u3 -X
fi2UU
S0u2-X
fi1U
S0u-X
fi3UUD
S0u2d-X
fi2UD
0
f0
fi1D
0
fi3UDD
0
fi2DD
0
fi3DDD
0
La valoración del derivativo se realiza de manera similar a la planteada para la europea,
solo que en cada nodo que no corresponda al periodo final n o al periodo 0 debe efectuarse
la comparación entre el valor hallado por el método neutral al riesgo, el cual es el valor
presente de los pagos futuros del derivativo, y el valor intrínseco; el valor seleccionado
corresponde al mayor de los dos. De nuevo los valores del periodo final n son los valores
intrínsecos del derivativo al vencimiento.
La función Max (Máximo) permite evaluar en cada nodo si conviene ejercer la opción o es
mejor esperar otro periodo.
70
Fundamentos de Derivados y Opciones
Benavides
Veamos
0
1
2
3
f3UUU
S0u3-X
f2UU
Max(fi2UU,[pf3UUU+(1-p)f3UUD]e-rt)
f3UUD
S0u2d-X
f1U
i
Max(f 1U,[pf2UU+(1-p)f2UD]e-rt)
f2UD
i
Max(f 2UD,[pf3UUD+(1-p)f3UDD]e-rt)
f0
[pf1U+(1-p)f1D]e-rt
f3UDD
f1D
i
Max(f 1D,[pf2UD+(1-p)f2DD]e-rt)
0
f2DD
Max(fi2DD,[pf3UDD+(1-p)f3DDD]e-rt)
f3DDD
0
71
Fundamentos de Derivados y Opciones
Benavides
Ejemplo 1:
Calcule el valor de una opción Put Americana por el método de valoración neutral al riesgo
para un activo subyacente con precio actual de 100, un precio de ejercicio de 103, con un
tiempo para la maduración de 2 meses. La tasa libre de riesgo es de 9% anual y la
volatilidad anualizada es del 40%. Utilice dos periodos (n =2).
En este caso T = 2/12 y t =T/n.
Escriba los parámetros del modelo y encuentre los factores que determinan la evolución de
los precios del activo subyacente: t, u, d, exp(rt), p:
A
B
1
Put Americano
2
S0
3
4
X
5
T
Parametros
6
n
7
r
=sigma
8
9
t =T/n
u=exp(t1/2)
10
Factores del
11
d=1/u
Modelo
e(rt)
12
p=(ert-d)/(u-d)
13
C
D
100
103
0.166666667
2
9%
40%
0.0833
1.1224
0.8909
1.0075
0.5037
E
<--=2/12
subperiodos
<--=C5/C6
<--=EXP(C8*C9^(1/2))
<--=1/C10
<--=EXP(C7*C9)
<--=(C12-C11)/(C10-C11)
Establezca ahora la evolución de precios del activo subyacente, desde el periodo 0 hasta el
periodo 2:
A
14
15 S
16
B
C
D
E
0
1
2
SUU2: uSU1
17
SU1 uS0
18
S0, SUD2: S0, dSU1
19
SD1: dS0
20
SDD1: dSD1
u:
100.000
d:
F
uu:
125.978 <--=D17*C10
112.240 <--=C18*C10
ud:
100.000 <--=D17*C11
89.095 <--=C18*C11
dd:
79.379 <--=D19*C11
Encuentre los valores del derivativo (tipo europeo) iniciando desde el periodo final
regresando hasta el periodo 0:
72
Fundamentos de Derivados y Opciones
A
B
22 Put Europeo
23
24
PUU2: Max(SUU2-X,0)
25
C
D
E
0
1
2
PU1: e (pPUU2+(1-p)PUD2)
27
-rt
PU0: e (pPU1+(1-p)PD1)
28
-rt
PD1: e (pPUD2+(1-p)PDD2)
F
-
-rt
26
29
30
31
Benavides
7.209
PDD2: Max(SDD2-X,0)
G
<--=MAX($C$4-E16,0)
1.478 <--=(E25*$C$13+E27*(1-$C$13))/$C$12
3.000 <--=MAX($C$4-E18,0)
13.136 <--=(E27*$C$13+E29*(1-$C$13))/$C$12
23.621 <--=MAX($C$4-E20,0)
=(D26*$C$13+D28*(1-$C$13))/$C$12
Proceda ahora a hallar los valores que reportaría un ejercicio temprano del derivativo:
A
32
33
34
35
36
37
38
B
Ejercicio Anticipado
C
D
E
0
1
2
-
F
<--=MAX($C$4-D17,0)
13.905 <--=MAX($C$4-D19,0)
Compare los cursos de acción y seleccione la mejor alternativa (el máximo valor), para
finalmente encontrar el valor en el periodo cero del derivativo:
A
39
40
41
42
43
44
45
B
C
Put Americano: Comparacion valores
0
D
E
1
2
F
1.478 <--=MAX(D35,D26)
7.589 <--=(D42*$C$13+D44*(1-$C$13))/$C$12
13.905 <--=MAX(D37,D28)
La respuesta final es:
B
46
47 Respuesta
C
Put
7.589
73
Fundamentos de Derivados y Opciones
Benavides
Ejemplo 2
La siguiente hoja de Excel muestra la valoración de este mismo derivativo suponiendo 3
periodos. A diferencia del ejercicio anterior, se opta por comparar en una sola celda los
valores intrínsecos y neutral al riesgo:
1
2
3
4
5
6
7
8
9
10
11
12
13
A
B
Put Americano
Parametros
S0
100
X
103
T 0.166666667
n
3
Factores
t
u
d
ert
p
0.0556
1.0989
0.9100
1.0050
0.5030
C
D
r
Sigma
9%
40%
<--=B5/B6
<--=EXP(D4*B9^(1/2))
<--=1/B10
<--=EXP(D3*B9)
<--=(B12-B11)/(B10-B11)
A continuación se calculan los cambios en el precio del activo subyacente y el valor
intrínseco de la opción:
A
14
B
C
D
0
1
2
i
15 Si / f
16
17
uuu:
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
E
uu:
S0:
u:
109.89
-
100.00
3.00
ud:
d:
91.00
12.00
dd:
F
G
3
132.69 <--=D18*$B$10
<--=MAX($B$4-E15,0)
120.75
udu:
109.89 <--=D18*$B$11
<--=MAX($B$4-E21,0)
100.00
3.00
udd:
91.00 <--=D30*$B$10
12.00 <--=MAX($B$4-E27,0)
82.81
20.19
ddd:
75.36 <--=D30*$B$11
27.64 <--=MAX($B$4-E33,0)
74
Fundamentos de Derivados y Opciones
Benavides
Ahora hallamos el valor del put europeo:
A
37 Put Europeo
38
B
C
D
E
0
1
2
3
F
-
39
G
<--=MAX($B$4-E15,0)
40
41
-
42
43
44
45
<--=(E39*$B$13+E45*(1-$B$13))/$B$12
2.93
46
47
48
-
<--=MAX($B$4-E21,0)
=(D42*$B$13+D48*(1-$B$13))/$B$12
7.75
49
50
51
5.93 <--=(E45*$B$13+E51*(1-$B$13))/$B$12
=(C45*$B$13+C51*(1-$B$13))/$B$12
12.70
12.00 <--=MAX($B$4-E27,0)
52
53
54
19.67 <--=(E51*$B$13+E57*(1-$B$13))/$B$12
55
56
57
27.64 <--=MAX($B$4-E33,0)
Y finalmente el americano:
A
59 Put Americano
60
61
B
C
D
E
0
1
2
3
F
-
62
G
H
<--=MAX($B$4-E15,0)
63
64
-
65
<--=MAX(D19,(E62*$B$13+E68*(1-$B$13))/$B$12)
66
67
2.93
68
69
70
71
72
73
74
-
<--=MAX($B$4-E21,0)
=MAX(C22,(D65*$B$13+D71*(1-$B$13))/$B$12)
7.87
5.93 <--=MAX(D25,(E68*$B$13+E74*(1-$B$13))/$B$12)
=MAX(B25,(C68*$B$13+C74*(1-$B$13))/$B$12)
12.95
12.00 <--=MAX($B$4-E27,0)
75
76
77
20.19 <--=MAX(D31,(E74*$B$13+E80*(1-$B$13))/$B$12)
78
79
80
27.64 <--=MAX($B$4-E33,0)
75
Fundamentos de Derivados y Opciones
Benavides
Los precios hallados para el put son:
n
Europeo
Americano
2
7.21
7.59
3
7.75
7.87
Los valores hallados para el cálculo con 3 periodos son más exactos.
Modelo Risk Neutral para Divisas
Opciones Europeas
El modelo risk neutral se modifica de tal manera que
e (r rf)t d
.
p
ud
El parámetro rf es la tasa libre de riesgo del país cuya moneda es el activo
subyacente.
En el caso de una opción por dólares americanos, es la tasa libre de riesgo de ese
país.
Opciones Americanas
Se procede de igual manera que en el ejercicio anterior.
76
Fundamentos de Derivados y Opciones
Benavides
4.a Ejercicios
1. Resuelva para 2 subperiodos, con vencimiento a 2 meses
1
2
3
4
5
6
7
8
9
10
11
12
13
B
Put Americano
Parametros
S0
X
n
rf
=sigma
Factores
t =1/n
u=exp(t1/2)
d=1/u
e(rft)
=(e(rft)-d)/(u-d)
C
D
E
100
103
12 subperiodos anuales
9%
40%
0.0833
1.1224
0.8909
1.0075
0.5037
<--=1/C5
<--=EXP(C7*C9^(1/2))
<--=1/C10
<--=EXP(C6*C9)
<--=(C12-C11)/(C10-C11)
2. Resuelva el ejercicio anterior con 3 subperiodos con el mismo tiempo al vencimiento
3. Opciones Exóticas
a.
Ejercicio
Suponga un opcion PUT cuyo precio de ejercicio es variable. Los datos del activo subyacente son:
El tiempo al vencimiento es de 3 meses
S0
100
u
1.1
d
0.95
rf
6% ea
(1+rf)^t
=
1.00486755
t
1 meses 0.08333333
Precio de Ejercicio
X1
X2
X3
100
105
112
b.
Ejercicio
Suponga un opcion CALL cuyo precio de ejercicio es variable. Los datos del activo subyacente son:
El tiempo al vencimiento es de 3 meses
S0
100
u
1.1
d
0.95
rf
6% ea
(1+rf)^t
=
1.00486755
t
1 meses 0.08333333
Precio de Ejercicio
X1
X2
X3
100
105
112
Se cumple para este caso la paridad Put-Call?
77
Fundamentos de Derivados y Opciones
Benavides
Plantilla 1
William Sharpe (Premio Nobel Economía de 1990) fue el primero en sugerir el modelo
binomial. Cox, Ross y Rubinstein (1979) y Rendleman y Bartter (1979) publicaron sendos
papers, derivándolo de manera formal. La siguiente plantilla recoge los conceptos básicos
de esos primeros modelos:
Valoración Opciones
S0
X
200 rf
200 T
file: Binomial portafolio sin riesgo
10%
0,33333333
0
1
S1u
S0u
215
f1u
S0
15 Call: Max(S 0 u-X,0)
0 Put: Max(X - S 0 u,0)
200
S1d
S0d
180
f1d
0 Call: Max(S 0 d-X,0)
20 Put: Max(X - S 0 d,0)
Cálculo 0
Portafolio sin riesgo
0S0u-f1u)exp(-rfT)
Valor Derivativo
P0= 0S0-f0
Despejando
f0= 0S0-P0
=(f1u-f1d)/(S0u-S0d)
0
0,42857143 Call
-0,57142857 Put
0S0u-f1u
1
77,1428571 Call
-122,857143 Put
74,6138135 Call
-118,829407 Put
D
Monto inversión acciones
0S0
=0S0d-f1d
0
0
U
P0=
0S0u-f1u
0S0d-f1d
77,1428571 Call
-122,857143 Put
85,7142857 Call
-114,285714 Put
11,1004722 Call
4,54369234 Put
Modelo Risk-Neutral (Comprobación)
u=
S1u/S0
1,08 exp(rfT)
d=
S1d/S0
0,90
p=
1-p
(exp(rfT)-d)/(u-d)
0,77
0,23
f 0=
(f1up+(1-p)f1d)/exp(rfT)
Paridad Put-Call
S0+Put0
PV(X)+Call0
1,03
11,1004722 Call
4,54369234 Put
204,544
204,544
78
Fundamentos de Derivados y Opciones
Benavides
Plantilla 2
Modelo binomial de 2 periodos
Valoración de Opciones
Parametros
S0
X
rf
Local
u
d
exp((rf-rf1)t)
rf1
Foranea
exp(rft)
Sigma
p
1-p
T
Periodos
t
=exp(*t^(1/2)
=1/u
=(exp((rf-rf1)t)-d)/(u-d)
=T/n
Evolución de Precios
S2uu=S0u2
f2uu
S1u=S0u
f1u
S0
S2ud=S0ud
f0
f2ud
S1d=S0d
f1d
S2dd=S0d2
f2dd
Opción
f2uu
f2uu
f'1u
[pf2uu+(1-p)f2ud]/exp(rft)
f'1u
Max([pf2uu+(1-p)f2ud]/exp(rft),f1u)
Europea
f'0
[pf'1u+(1-p)f'1d]/exp(rft)
f2ud
Americana
f'0
Max([pf'1u+(1-p)f'1d]/exp(rft),f0)
f2ud
f'1d
[pf2ud+(1-p)f2dd]/exp(rft)
f'1d
Max([pf2ud+(1-p)f2dd]/exp(rft),f1d)
f2dd
f2dd
79
Fundamentos de Derivados y Opciones
Benavides
Plantilla 3
Modelo binomial de 3 periodos
Modelo Binomial, 3 periodos
Parametros
S0
X
rf
rf1
T
n
Periodos
t
1,000.00
1,030.00
5% Local
3% Foranea
0.50
3
30% Sigma
=exp(.t^(1/2))
=1/u
u
d
exp((rf-rf1)t)
exp(rft)
p
1-p
Delta
Factor
=(exp((rf-rf1)t)-d)/(u-d)
=T/n
Evolución de Precios
S0
0
S1u=S0u
S2uu=S0u2
S3uuu=S0u3
S1d=S0d
S2ud=S0ud
S3uud=S0u2d
S2dd=S0d2
S3udd=S0ud2
1
2
3
S3ddd=S0d3
X0
X1
X2
X3
f0
f1u
f1d
f2uu
f2ud
f2dd
f3uuu
f3uud
f3udd
f3ddd
f'0
f'1u
f'1d
f'2uu
f'2ud
f'2dd
f3uuu
f3uud
f3udd
f3ddd
[pf'2uu+(1-p)f'2ud]/
exp(rft)
[pf3uuu+(1-p)f3uud]/
exp(rft)
f3uuu
[pf'2ud+(1-p)f'2dd]/
exp(rft)
[pf3uud+(1-p)f3udd]/
exp(rft)
f3uud
[pf3udd+(1-p)f3ddd]/
exp(rft)
f3udd
Opción
Europea
[pf'1u+(1-p)f'1d]/
exp(rft)
f3ddd
Americana
Mx([pf'1u+(1-p)f'1d]/ Mx([pf'2uu+(1-p)f'2ud]/ Mx([pf3uuu+(1-p)f3uud]/
exp(rft),f0)
exp(rft),f1u)
exp(rft),f2uu)
f3uuu
Mx([pf'2ud+(1-p)f'2dd]/ Mx([pf3uud+(1-p)f3udd]/
exp(rft),f1d)
exp(rft),f2ud)
f3uud
Mx([pf3udd+(1-p)f3ddd]/
exp(rft),f2dd)
f3udd
f3ddd
80
Fundamentos de Derivados y Opciones
Benavides
5. Modelo de Black-Scholes (tiempo continuo)
Black, Scholes (1973) y Merton (1973) derivaron la fórmula para valorar opciones
europeas en tiempo continuo. Su argumento básico es que en cualquier momento se puede
replicar el valor de una opción como una inversión de 0 unidades del activo subyacente S 0
y una inversión con monto B0 en el activo libre de riesgo, el activo subyacente se comporta
siguiendo el modelo lognormal de precios, anteriormente discutido. Tenemos entonces que
el valor del derivado f0 es:
f0 = 0 .S0 + B0
(4)
En tiempo continuo estos valores se modifican permanentemente. El valor de 0 puede
interpretarse como la sensibilidad de la prima de la opción al valor del subyacente.
Para el caso de la opción de compra europea (Call), los valores de 0 y B0 son:
0 = N(d1 ),
B0 = - X.e
-kf.T
N(d2 )
Para el caso de la opción de venta europea (Put), los valores de 0 y B0 son:
0 = -N(-d1 ),
B0 = X.e
-kf.T
N(-d2 )
Las expresiones N(.) representan la distribución normal estándar acumulada. Los términos
d1 y d2 están definidos como:
2
1/2
d1 = [Ln(S0 /X)+(kf+ /2)T]/(T )
1/2
d2 = d1 - T
Los valores de S0 , X, kf, y T son el precio actual del subyacente, el precio de ejercicio, la
tasa libre de riesgo, la volatilidad y el tiempo al vencimiento, respectivamente.
Call Europeo: Valor esperado de la función: MAX(ST -X,0)
-kf.T
C0 =S0 N(d1 ) - Xe
N(d2 )
Put Europeo: Valor esperado de la función: MAX(X-ST ,0)
-rT
P0 = Xe N(-d2 ) - S0 N(-d1 )
81
Fundamentos de Derivados y Opciones
Benavides
Ejemplo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
A
Put Europeo
Parametros
n
Subperiodos
S0
X
T
rf
Sigma
D1
D2
N(D1)
N(D2)
C
P
B
C
D
E
F
12 subperiodos ano
2.00
100
103
0.16666667 <--=B5/B4
9%
40%
-0.00750443 <--=(LN(B6/B7)+(B9+(1/2)*B10^2)*B8)/(B10*B8^(1/2))
-0.17080375 <--=B13-B10*B8^(1/2)
0.49700617 <--=DISTR.NORM.ESTAND(B13)
0.43218904 <--=DISTR.NORM.ESTAND(B14)
5.84789548 <--=B6*B16-B7*EXP(-B9*B8)*B17
Parity
7.31442525 <--=B19+B7*EXP(-B9*B8)-B6
Calculo directo
-D1
-D2
0.00750443 <--=-B13
0.17080375 <--=-B14
N(-D1)
N(-D2)
0.50299383 <--=DISTR.NORM.ESTAND(B26)
0.56781096 <--=DISTR.NORM.ESTAND(B27)
P
Formula
7.31442525 <--=B7*EXP(-B9*B8)*B30-B6*B29
----------------------Modificaciones simples a la fórmula de Black-Scholes
Otras fórmulas también han sido desarrolladas para evaluar opciones europeas sobre
acciones que pagan dividendos:
1. Pago de Dividendos en periodos discretos y conocidos
Los dividendos se descuentan del valor actual de la Acción:
∑
toma el valor de S0 en las fórmulas anteriores, que se aplican sin cambios
adicionales, d1 también debe ajustarse en consecuencia.
2. Flujo continuo de Dividendos
Este flujo continuo se expresa a una tasa q de tal manera que:
82
Fundamentos de Derivados y Opciones
Benavides
También debe ajustarse d1 . Asimismo esto aplica a una opción sobre divisas donde
kf1 es la tasa libre de riesgo del país cuya divisa se puede adquirir o vender y la tasa
de cambio esta expresada en Moneda local sobre moneda extranjera:
3. Cuando la opción es de venta (Call) americana y paga dividendos se puede aplicar
la aproximación de Black. En este caso el valor de la opción es el máximo entre una
opción europea con vencimiento en T, que paga dividendos, como el caso anterior,
y una opción europea con vencimiento en t-m-1 , siendo este término el instante
anterior al pago del último dividendo. Lo que implica que para la segunda opción
∑
, donde tmax =tm-1 .
4. Opciones
sobre
futuros.
El
valor
de
S0
se
modifica
a
Ejercicio.
Calcule el valor de una opción de compra por 1 dólar americano a 3 meses. La
opción es at-the-money. Identifique las tasas libre de riesgo apropiadas para cada
país (Colombia y E.E. U.U.) y la volatilidad del dólar.
83
Fundamentos de Derivados y Opciones
Benavides
Ejercicio de Valoración Neutral al Riesgo y Black-Scholes
Encuentre el valor de las opciones Call y Put europea y americana para la compra de una
divisa cuyo valor en moneda local es de 1000. El tiempo al vencimiento es 4 meses (0.33
años). La volatilidad de los cambios de precio de la divisa es de 30% (anual). Las tasas
libre de riesgo en el país local y el país de origen de la divisa son 8% y 3% continuas,
respectivamente. Calcule el valor de las opciones utilizando un árbol de 3 periodos.
Calcule estos mismos valores utilizando la fórmula de Black-Scholes, para ambos métodos
compruebe la paridad Put-Call.
84
Fundamentos de Derivados y Opciones
Valoraciòn Derivativos
Put
Parametros
S0
1000
X
1000
kf
8%
k1
3%
Sigma
30%
T
0.33333333
n
3
Arbol
X
Delta
ST
Benavides
Black-Scholes
S0*
990.049834
t
u
d
exp((kf-k1)t)
exp(kft)
p
1-p
0.11111111
1.10517092
0.90483742
1.00557102
1.00892851
0.50282952
0.49717048
d1
d2
Put
18.283%
0.962%
N(-di)
0.42746665
0.49616124
59.8918367
Paridad Black-Scholes
P0+S0*
1049.94167
PV(X)+C0
1049.94167
Valor Intrinseco
0
1000
0
1
1000
2
1000
3
1000
1349.85881
0
1221.40276
0
1105.17092
0
1000
0
1105.17092
0
1000
0
904.837418
95.162582
904.837418
95.162582
818.730753
181.269247
740.818221
259.181779
Valoración
0
0
0
0
23.1076664
23.1076664
Put0
Put0Am
65.5618563
67.0491329
0
0
46.8933385
46.8933385
109.676684
112.694875
95.162582
95.162582
175.144306
181.269247
259.181779
259.181779
Paridad
S0*+P0
PV(X)+C0
1055.61169
1055.61169
85
Fundamentos de Derivados y Opciones
Valoraciòn Derivativos
Call
Parametros
S0
1000
X
1000
kf
8%
k1
3%
Sigma
30%
T
0.33333333
n
3
Arbol
X
Delta
ST
Benavides
Black-Scholes
S0*
990.049834
t
u
d
exp((kf-k1)t)
exp(kft)
p
1-p
0.11111111
1.10517092
0.90483742
1.00557102
1.00892851
0.50282952
0.49717048
d1
d2
Call
18.283%
0.962%
N(di)
0.57253335
0.50383876
76.2559211
Valor Intrinseco
0
1000
0
1
1000
2
1000
3
1000
1349.85881
349.858808
1221.40276
221.402758
1105.17092
105.170918
1000
0
1105.17092
105.170918
1000
1.1369E-13
904.837418
0
904.837418
0
818.730753
0
740.818221
0
Valoración
349.858808
349.858808
226.187693
226.187693
138.555969
138.555969
Call0
Call0Am
81.9259407
81.9259407
105.170918
105.170918
52.4150541
52.4150541
26.1226007
26.1226007
0
0
0
0
0
0
86
Fundamentos de Derivados y Opciones
Benavides
6. Estrategias de Inversión con opciones, acciones, futuros y bonos
Existen diferentes estrategias de inversión con los activos derivativos y sus subyacentes. El
resultado de estas estrategias (pago) puede ilustrarse como función del valor del subyacente
en el momento t’. Usualmente t’ corresponde a T, que identifica el vencimiento de los
títulos involucrados en la estrategia. El estudiante interesado en la inversión en activos
derivativos puede construir un modelo que le permita entender el resultado de diferentes
combinaciones al vencimiento. Si, adicionalmente, en la plantilla se involucran macros que
permitan valorar opciones americanas (aproximación binomial) y europeas (Black-Scholes)
aparte de futuros o forwards también se podrán valorar calendar spreads u otras
combinaciones que incluyan derivados que no aún no se hayan vencido y que permitan
evaluar la posibilidad de una liquidación temprana.
A continuación se delineará como se construye tal modelo.
1. Funciones de utilidad para cada los tipos de activos involucrados al vencimiento:
a. Futuro o forward: (Largo) S T -XF,T 1 , (Corto) XF,T 1-ST . XF,T 1 es el precio
pactado del futuro (ejercicio) en el vencimiento T1 y ST es el precio en el
momento de estudio.
b. Call: (Largo) Max(ST -X,0), (Corto) -Max(ST -X,0).
c. Put: (Largo) Max(X-ST ,0), (Corto) -Max(X-ST ,0).
d. Bono: X. X es el valor nominal del bono.
e. Subyacente: ST . ST es el es el precio en el momento de estudio.
2. Antes del vencimiento se pueden valorar los activos usando las siguientes fórmulas
a. Forward: ST - XF,T 1.exp(-kf.t), donde kf es la tasa libre de riesgo y t es el
tiempo que resta al vencimiento (T1 -T). En este caso ST corresponde al
precio en el momento de la valoración.
b. Opciones: Fórmula de Black-Scholes o aproximación binomial. Ver macros
más adelante
c. Bono: exp(-kf.t).X
Estructura del Modelo
1. Área de parámetros, los significados de los símbolos son los usuales. La utilidad se
evalúa en t1. Algunas posiciones no maduran aún, pudiendo madurar en t2 y t3.
Todos pueden ajustarse a voluntad.
2. También se definen los valores de S 0 , St1 , X1 a X4, que son el valor del subyacente
hoy, en t1 y diferentes valores de precios de ejercicio, respectivamente.
3. La tasa libre de riesgo y la volatilidad (Sigma) también pueden modificarse.
4. XF,t1 y XF,t2 son los precios de ejercicio de los forward, calculados llevando S 0 a los
respectivos vencimientos a la tasa libre de riesgo (e.g. XF,t1 =S0 .exp(kf.t1 )). De esta
forma no debe pagarse por el forward, dado que su valor presente es 0.
87
Fundamentos de Derivados y Opciones
Benavides
Funciones básicas
El modelo incorpora el cálculo de las primas o la inversión en activos. Se pueden elegir 16
tipos de inversiones, el subyacente, bonos, forwards y opciones europeas. La columna H
define si al calcular el resultado de la estrategia de inversión se consideran las primas
pagadas o la inversión realizada (para el caso del subyacente y el bono). Las primas de las
opciones se llevan a valor futuro (t1) para que todos los flujos correspondan al mismo
momento. Las primas se calculan con la fórmula de Black-Scholes.
Combinación de posiciones
En la siguiente tabla, celdas azules de la columna B, se definen las posiciones que se
toman. Si se agregan números enteros positivos implica que se han tomado posiciones
largas (compra) en los activos referenciados; si el número es negativo las posiciones son
cortas (venta). El valor de -1 en la celda B34, implica que se vendió una unidad del
subyacente. El valor de 0.5 en la celda B37 significa que se compró medio forward, con
vencimiento en t2, y precio de ejercicio XF,t2 . El valor de 1 en la celda B38 implica que se
compró un Call con vencimiento en t1 y precio de ejercicio X1. Las celdas en la columna D
88
Fundamentos de Derivados y Opciones
Benavides
presentan la utilidad de cada posición particular, evaluado para S t1 . El resultado global está
en la celda D50.
Resultados
En la siguiente tabla de datos se calculan los resultados hasta para cuatro de las posiciones
individuales y la utilidad total para diferentes valores de St1 . En la celda D52 se calcula el
monto total de la inversión en el momento 0. Los resultados gráficos también se presentan.
89
Fundamentos de Derivados y Opciones
Utilidad -1 unidad subyacente
Benavides
Utilidad Total Posiciones, con inversión
Utilidad 0.5 forwards
Utilidad 1 Call
Utilidad -0.5 Put
90
Fundamentos de Derivados y Opciones
Benavides
Guía para construir un modelo alternativo
1. Área de parámetros, los significados de los símbolos son los usuales. El tiempo al
vencimiento en este ejemplo es T=0.25 aunque para este ejemplo este valor no afecta los
resultados.
1
2
3
4
5
6
7
8
A
Modelo
Condicion
ST
X1
X2
X3
Vol ()
T
B
C
D
X1<X2<X3
50
30
50
70
40% rf
0.25
6%
Funciones básicas
En las siguientes celdas se ingresan las funciones de utilidad (columna B), las primas o
valores iniciales de los activos (columna C) y la utilidad o profit al descontar los costos
iniciales (columna D). Si la posición es corta, en el caso de las opciones la prima es un
ingreso recibido por vender la opción.
A
B
C
D
Costos
9
10
11
12
13
14
15
16
17
Pago
Call X1
Call X2
Call X3
Put X1
Put X2
Put X3
Accion
Bono
=MAX($B$3-B4,0)
=MAX($B$3-B5,0)
=MAX($B$3-B6,0)
=MAX(B4-$B$3,0)
=MAX(B5-$B$3,0)
=MAX(B6-$B$3,0)
=B3
=B4
Prima/Compra
10.64
0.68
0.00869
0.19681
9.94
28.96
40
29.55
Profit
=B10-C10
=B11-C11
=B12-C12
=B13-C13
=B14-C14
=B15-C15
=B16-C16
=B17-C17
Combinación de posiciones
En la siguiente tabla si se agregan números enteros positivos implica que se han tomado
posiciones largas (compra) en los activos referenciados; si el número es negativo las
posiciones son cortas (venta). El valor de -2 en la celda E22, implica que se vendieron dos
Call con precio de ejercicio X2. La combinación de posiciones de la estrategia denominada
A se ingresan en el rango E21:E28. Las estrategias B, C y D siguen la misma lógica.
91
Fundamentos de Derivados y Opciones
A
19
20 Notas
21
22
23
24
25
26
27
28
B
Benavides
C
1 Compra una unidad
-1 Venta una unidad
D
Call X1
Call X2
Call X3
Put X1
Put X2
Put X3
Accion
Bono
E
F
Posiciones
A
B
1
0
-2
0
1
0
0
1
0
-2
0
1
0
0
0
0
G
H
C
-1
2
-1
0
0
0
0
0
D
0
0
0
-1
2
-1
0
0
Resultados
En la siguiente tabla se calculan los resultados. La tabla simplemente multiplica las
posiciones por el profit (utilidad) y luego las suma. Este resultado luego se gráfica a través
de una tabla dinámica donde la variable es ST, el valor al vencimiento del activo
subyacente.
29
30
31
32
33
34
35
36
37
38
E
Resultados
=$D10*E21
=$D11*E22
=$D12*E23
=$D13*E24
=$D14*E25
=$D15*E26
=$D16*E27
=$D17*E28
=SUMA(E30:E37)
F
=$D10*F21
=$D11*F22
=$D12*F23
=$D13*F24
=$D14*F25
=$D15*F26
=$D16*F27
=$D17*F28
=SUMA(F30:F37)
G
=$D10*G21
=$D11*G22
=$D12*G23
=$D13*G24
=$D14*G25
=$D15*G26
=$D16*G27
=$D17*G28
=SUMA(G30:G37)
H
=$D10*H21
=$D11*H22
=$D12*H23
=$D13*H24
=$D14*H25
=$D15*H26
=$D16*H27
=$D17*H28
=SUMA(H30:H37)
A continuación se presenta la tabla dinámica.
92
Fundamentos de Derivados y Opciones
B
40
41
42
43 Delta
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
C
5
D
0
=D43+$C$43
=D44+$C$43
=D45+$C$43
=D46+$C$43
=D47+$C$43
=D48+$C$43
=D49+$C$43
=D50+$C$43
=D51+$C$43
=D52+$C$43
=D53+$C$43
=D54+$C$43
=D55+$C$43
=D56+$C$43
=D57+$C$43
=D58+$C$43
=D59+$C$43
=D60+$C$43
=D61+$C$43
=D62+$C$43
E
Tabla
=E20
=E38
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
Benavides
F
Dinámica
=F20
=F38
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
G
H
=G20
=G38
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=H20
=H38
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
=TABLA(,B3)
Las estrategias planteadas corresponden a lo siguiente:
J
24
25
26
27
A
B
C
D
K
Butterfly (Call)
Butterfly (Put)
-Butterfly (Call)
-Butterfly (Put)
93
Fundamentos de Derivados y Opciones
Benavides
Las cuales se grafican a continuación:
I
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
J
K
L
M
N
O
Butterfly (Call)
15
10
10
5
5
0
20
40
60
80
100
120
0
-5 0
-10
-10
-15
-15
20
15
10
10
5
5
0
20
40
60
40
60
80
100
120
80
100
120
-Butterfly (Put)
-Butterfly (Call)
15
-5 0
Q
Butterfly (Put)
15
-5 0
P
80
100
120
0
-5 0
-10
-10
-15
-15
20
40
60
Esta tabla presenta el aspecto del modelo con los resultados numéricos de la plantilla sin
incluir la tabla:
94
Fundamentos de Derivados y Opciones
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
A
Modelo
Condicion
ST
X1
X2
X3
Vol ()
T
B
Notas
D
E
F
G
H
X1<X2<X3
50
30
50
70
40% rf
6%
0.25
Pago
Call X1
Call X2
Call X3
Put X1
Put X2
Put X3
Accion
Bono
C
Benavides
20
0
0
0
0
20
50
30
C
o Profit
9.36
-0.68
-0.01
-0.2
-9.94
-8.96
10
0.45
Posiciones
A
B
C
D
1 Compra una
Callunidad
X1
1
0
-1
0
-1 Venta unaCall
unidad
X2
-2
0
2
0
Call X3
1
0
-1
0
Put X1
0
1
0
-1
Put X2
0
-2
0
2
Put X3
0
1
0
-1
Accion
0
0
0
0
Bono
0
0
0
0
Resultados
9.36
0 -9.36
0
1.36
0 -1.36
0
-0.01
0 0.009
0
0
-0.2
0 0.197
0 19.88
0 -19.9
0 -8.96
0 8.96
0
0
0
0
0
0
0
0
10.71 10.72 -10.7 -10.7
95
Fundamentos de Derivados y Opciones
Benavides
Los costos de las primas pueden ser calculados programando las siguientes macros en la
hoja de cálculo. Lo que permitiría una apreciación más correcta de la utilidad.
Macros
A continuación se presentan los códigos de 2 macros que valoran opciones americanas o
europeas. Estos macros permiten valorar opciones sobre activos que generen una tasa de
dividendos conocida de antemano u opciones sobre divisas. Los parámetros son los
siguientes:
S: Precio del subyacente en el momento de la valoración.
X: Precio de ejercicio al vencimiento.
rf: tasa libre de riesgo (local).
r1: tasa de dividendos o tasa libre de riesgo foránea.
n: periodos de la evaluación, a mayor n más precisa es la valoración.
e: 1 si la opción es europea
Function CallAmEuD(S, X, rf, r1, T, n, sigma, e)
dt = T / n
u = Exp(sigma * Sqr(dt))
d = Exp(-sigma * Sqr(dt))
r = Exp(rf * dt)
r2 = Exp((rf - r1) * dt)
Pr = (r2 - d) / (u - d)
Dim OpcPagoFin() As Double
Dim OpcPagoMed() As Double
Dim OpcPagoAme() As Double
ReDim OpcPagoFin(n + 1)
For Estado = 0 To n
OpcPagoFin(Estado) = Application.Max(S * u ^ _
Estado * d ^ (n - Estado) - X, 0)
Next Estado
For Indice = n - 1 To 0 Step -1
ReDim OpcPagoMed(Indice)
ReDim OpcPagoAme(Indice)
If e = 0 Then
For Estado = 0 To Indice
OpcPagoAme(Estado) = S * u ^ _
Estado * d ^ (Indice - Estado) - X
Next Estado
ElseIf e = 1 Then
For Estado = 0 To Indice
96
Fundamentos de Derivados y Opciones
Benavides
OpcPagoAme(Estado) = 0
Next Estado
End If
For Estado = 0 To Indice
OpcPagoMed(Estado) = Application.Max(OpcPagoAme(Estado) _
, ((1 - Pr) * OpcPagoFin(Estado) + Pr * OpcPagoFin(Estado + 1)) / r)
Next Estado
ReDim OpcPagoFin(Indice)
For Estado = 0 To Indice
OpcPagoFin(Estado) = OpcPagoMed(Estado)
Next Estado
Next Indice
CallAmEuD = OpcPagoMed(0)
End Function
----------------------------------------------------------Function PutAmEuD(S, X, rf, r1, T, n, sigma, e)
dt = T / n
u = Exp(sigma * Sqr(dt))
d = Exp(-sigma * Sqr(dt))
r = Exp(rf * dt)
r2 = Exp((rf - r1) * dt)
Pr = (r2 - d) / (u - d)
Dim OpcPagoFin() As Double
Dim OpcPagoMed() As Double
Dim OpcPagoAme() As Double
ReDim OpcPagoFin(n + 1)
For Estado = 0 To n
OpcPagoFin(Estado) = Application.Max(X - S * u ^ _
Estado * d ^ (n - Estado), 0)
Next Estado
For Indice = n - 1 To 0 Step -1
ReDim OpcPagoMed(Indice)
ReDim OpcPagoAme(Indice)
If e = 0 Then
For Estado = 0 To Indice
OpcPagoAme(Estado) = X - S * u ^ _
Estado * d ^ (Indice - Estado)
Next Estado
ElseIf e = 1 Then
For Estado = 0 To Indice
OpcPagoAme(Estado) = 0
Next Estado
End If
97
Fundamentos de Derivados y Opciones
Benavides
For Estado = 0 To Indice
OpcPagoMed(Estado) = Application.Max(OpcPagoAme(Estado) _
, ((1 - Pr) * OpcPagoFin(Estado) + Pr * OpcPagoFin(Estado + 1)) / r)
Next Estado
ReDim OpcPagoFin(Indice)
For Estado = 0 To Indice
OpcPagoFin(Estado) = OpcPagoMed(Estado)
Next Estado
Next Indice
PutAmEuD = OpcPagoMed(0)
End Function
98
Fundamentos de Derivados y Opciones
Benavides
7. Convergencia Formula de Valoración de Opciones, Discreta vs.
Black-Scholes
Cox, Ross y Rubinstein (1979) y Rendleman y Bartter (1979) independientemente,
desarrollan el modelo discreto, sugerido por Sharpe y aquí llamado “Risk Neutral”, basado
en un precio futuro de 2 estados, para la valoración de opciones. Puesto que es un modelo
recursivo, permite la incorporación de características que no pueden ser tomadas en cuenta
en la expresión explicita deducida por Black y Scholes (1973), en particular el ejercicio
temprano de la opción.
En esta sección se desarrolla la expresión general para opciones europeas que se encuentra
en el trabajo de Cox, Ross y Rubinstein. El árbol de precios del subyacente evoluciona de la
siguiente forma:
Evolución Precio S T
S0
S1
…
S2
Sn-2
Sn-1
Sn
S0und0
n-1 0
S0u d
n-2 0
S0un-1d1
S0u d
S0un-2d1
…
S0u2d0
S0u4-2d2
…
S0u1d0
…
…
1 1
S0
…
S 0u d
1
…
…
S0u0d
…
2
S0u2dn-2
…
S0u0d
S0u1dn-1
…
S0u0dn-2
S0u1dn-1
S0u0dn-1
S0u0dn
A continuación se plantea el modelo para un periodo:
[
(
)
(
)
]
Donde f denota cualquier derivado y los subíndices u y d denotan las alzas o bajas,
respectivamente.
denota el pago al vencimiento (después de n periodos), luego
de a subidas y n-a bajadas, en el caso anterior n es igual a 1. Para el caso de una opción de
compra la fórmula se convierte en:
[
(
)
(
(
)
)
(
)]
Y para 2 periodos es:
[
(
)
(
(
(
)
)
)
(
(
)
)]
99
Fundamentos de Derivados y Opciones
Benavides
Esta fórmula10 se generaliza para n periodos:
(
[∑ ( )
)
(
)]
El factor de valor presente es
, con
, donde
es la tasa libre de riesgo en
tiempo continuo, T es el tiempo a la madurez y n es el número de periodos. El número de
alzas en el precio es a . El término ( ) es la combinatoria, que se puede interpretar como el
número de caminos posibles para alcanzar un determinado nodo, si en las diferentes rutas
siempre hay a alzas.
La fórmula puede simplificarse para el caso del call (y del put), puesto que dependiendo de
la relación entre S0 y X, por debajo de cierto número de alzas, aumbral, la opción no se ejerce.
Esta relación es:
, el cual se resuelve para aumbral:
(
(
)
[ ∑ ( )
)
, con lo que la fórmula 1, se simplifica a:
( )
(
)
(
Reorganizando los términos se tiene:
(
∑ ( ) (
) (
Si se define
)]
)
)
(
, se tiene que
∑ ( ) ( ) (
)
(
∑ ( )
)
), con lo que la expresión anterior es11 :
∑ ( )
(
)
Las términos dentro de la sumatoria representan el complemento de la distribución
binomial acumulada:
(
)
∑ ( ) ( ) (
)
y
(
)
∑ ( ) ( ) (
)
La expresión final es:
(
(
))
(
(
))
Para el caso del put se tiene
10
Para un derivado genérico, sin ejercicio anticipado, la fórmula es:
[∑( )
11
(
)
]
Recuerde que
100
Fundamentos de Derivados y Opciones
(
∑ ( )
(
)
)
Benavides
∑ ( ) ( ) (
(
)
)
En el límite (cuando n→∞) estas expresiones convergen a las conocidas fórmulas de BlackScholes:
(
(
)
(
)
)
(
)
Ejemplo:
Se calcula la convergencia para una divisa S, cuyo valor actual es 1,500. Se valoran
opciones Call y Put europeas con precio de ejercicio X de 1,550, tiempo al vencimiento T
de 1 año, volatilidad de 40% y tasas libres de riesgo locales y foráneas de 4% y 1%,
respectivamente. La fórmula binomial se calcula en principio para 6 periodos.
Valoracion Call y Put
Datos
S0
X
T
kf
kf1
n
1,500
1,550
40.00%
1
4.00%
1.00%
6
años
Local
Foránea
periodos
A continuación se calculan los parámetros del modelo binomial.
Parámetros
t
u
d
0.167 =T/n
1.177 =exp(.t^(1/2))
0.849 =1/u
ekf.t
1.007
(kf-kf1).t
e
u-d
1.005
0.328
p
1-p
0.475 =(e(kf-kf1).t -d)/(u-d)
0.525
p'
1-p'
0.556 =u.p/e(kf-kf1).t
0.444
athreshold
amax
3.100 =Ln(X/(S0.d n ))/Ln(u/d)
3.000 =Entero(athreshold )
101
Fundamentos de Derivados y Opciones
Benavides
Cálculos Finales
Las fórmulas para el Call y el Put se desarrollaron en los párrafos previos; se estiman ahora
para los parámetros previos. Puesto que el propósito es ver si los valores convergen cuando
se aplica la fórmula de Black-Scholes, también se presenta este valor.
Complemento Distribución Binomial Acumulada
(1)
(2)
1- (amax,n,p')
0.45 =1-Bin(Ent(amax),n,p',1)
Acumulado
1- (amax,n,p)
0.30 =1-Bin(Ent(amax),n,p,1)
Acumulado
S 0 .e-kf 1.T.(1- (amax,n,p'))
673.56
.(1- (amax,n,p))
442.77
X.e
-kf T
(1)-(2)
230.79 =S 0 .e-kf 1.T. (amax,n,p') - X.e-kf T. (amax,n,p)
233.67
Call
Black-Scholes
(amax,n,p')
(amax,n,p)
(3)
(4)
(3)-(4)
0.55 =Bin(Ent(amax),n,p',1)
0.70 =Bin(Ent(amax),n,p,1)
X.e-kf T. (amax,n,p)
1,046.45
. (amax,n,p')
811.51
S 0 .e
-kf 1.T
234.94 =X.e-kf T.(1- (amax,n,p))-S 0 .e-kf 1.T.(1- (amax,n,p'))
237.82
Put
Black-Scholes
Paridad Put-Call
S0 e-kf1T+P0
Xe
-kfT
+ C0
1,720.02
1,720.02
Como se observa para n=6 hay una diferencia apreciable entre los 2 métodos. A
continuación se presenta la evolución del precio para valores crecientes de n:
102
Fundamentos de Derivados y Opciones
n
Benavides
1
2
4
8
16
32
64
128
Call RN
230.793
289.671
218.074
227.727
232.198
233.932
234.400
234.344
234.112
Call BS
233.673
233.673
233.673
233.673
233.673
233.673
233.673
233.673
233.673
Put RN
234.942
293.820
222.223
231.876
236.347
238.081
238.549
238.493
238.261
Put BS
237.822
237.822
237.822
237.822
237.822
237.822
237.822
237.822
237.822
256
233.851
233.673
238.000
237.822
512
1024
233.618
233.712
233.673
233.673
237.767
237.861
237.822
237.822
2048
4096
233.672
233.685
233.673
233.673
237.821
237.834
237.822
237.822
8192
16384
233.678
233.675
233.673
233.673
237.827
237.824
237.822
237.822
32768
65536
131072
233.675
233.674
233.673
233.673
233.673
233.673
237.824
237.823
237.822
237.822
237.822
237.822
Como se observa, los valores obtenidos por el método binomial se acercan a los de BlackScholes a medida que n se incrementa. Gráficamente:
103
Fundamentos de Derivados y Opciones
Benavides
El método para valoración de opciones neutral al riesgo converge a la formula de BlackScholes a medida que se incrementa el numero de subperiodos en que se divide el tiempo
hasta la maduración de la opción.
7.1 Ejercicio de convergencia, usando Macros
El siguiente ejercicio muestra como los valores convergen para las opciones tipo europeo,
tanto Call como Put. Adicionalmente se muestra como el valor de una opción Put tipo
Americano es siempre mayor que una opción Put tipo Europeo.
La simulación trabaja sobre formulas creadas a través de macros de Excel cuyo código
también se adjunta.
La valoración se realiza sobre Opciones Americanas y Europeas de las siguientes
características:
Valor del Activo Subyacente (S 0 ): 100
Precio de Ejercicio (X):
103
Tiempo para la maduración (T):
2 meses (2/12 de año)
Tasa libre de riesgo (r):
9%
Volatilidad de S (Sigma):
40%
Opciones Put
A continuación se describe la implementación del ejercicio en Excel
1
2
3
4
5
6
A
B
C
Valoracion Put
S
100
X
103
T
0.16667 <--=2/12
r
9%
Sigma
40%
Las formulas usadas para la valoración de cada tipo de opción (para 1 subperiodo) se
muestran a continuación
A
8
9
10
11
B
n
PutEu
PutBS
Putam
M
N
O
P
1
8.8037 <--=PutAmEu($B$2,$B$3,$B$5,$B$4,B8,$B$6,1)
7.3144 <--=PutBS($B$2,$B$3,$B$5,$B$4,$B$6)
8.8037 <--=PutAmEu($B$2,$B$3,$B$5,$B$4,B8,$B$6,0)
Los valores resultantes son:
8
9
10
11
A
n
PutEu
PutBS
Putam
B
1
8.8037
7.3144
8.8037
C
D
2
4
7.2094 7.3729
7.3144 7.3144
7.5886 7.6567
E
F
8
7.4127
7.3144
7.6295
16
7.3973
7.3144
7.5832
G
H
32
64
7.3638 7.3290
7.3144 7.3144
7.5396 7.5042
I
J
128
256
7.3037 7.3204
7.3144 7.3144
7.4839 7.4956
K
L
512
1024
7.3123 7.3140
7.3144 7.3144
7.4884 7.4892
104
Fundamentos de Derivados y Opciones
Benavides
Los cuales se grafican a continuación, el eje de abcisas (X), en escala logarítmica, indica el
número de subperiodos que se utilizan para las formulas:
9.0
Convergencia Valoración Put
B-S y Binomial
8.8
8.6
PutEu
PutBS
Putam
8.4
8.2
8.0
7.8
7.6
7.4
7.2
Subperiodos
7.0
1
10
100
1000
10000
Se puede observar como las formulas convergen en el caso de la valoración binomial y de
Black-Scholes para el Put Europeo.
Opciones Call
Con las mismas condiciones anteriores se muestra como se implementan las formulas para
1 subperiodo:
A
37
38
39
40
B
n
CallEu
CallBS
CallAm
M
N
O
P
1
7.33719 <--=CallAmEu($B$2,$B$3,$B$5,$B$4,B37,$B$6,1)
5.8479 <--=CallBS($B$2,$B$3,$B$5,$B$4,$B$6)
7.33719 <--=CallAmEu($B$2,$B$3,$B$5,$B$4,B37,$B$6,0)
Las cuales extendidas hasta 1024 subperiodos nos entregan los siguientes valores:
37
38
39
40
A
n
CallEu
CallBS
CallAm
B
C
D
E
F
1
2
4
8
16
7.33719 5.74291 5.90635 5.94619 5.93073
5.8479 5.8479 5.8479 5.8479 5.8479
7.33719 5.74291 5.90635 5.94619 5.93073
G
H
I
J
K
L
32
64
128
256
512
1024
5.8973 5.86245 5.83713 5.85391 5.84577 5.84744
5.8479 5.8479 5.8479 5.8479 5.8479 5.8479
5.8973 5.86245 5.83713 5.85391 5.84577 5.84744
105
Fundamentos de Derivados y Opciones
Benavides
Cuya gráfica se presenta:
8.0
Convergencia Valoración Call
B-S y Binomial
7.5
CallEu
CallBS
CallAm
7.0
6.5
6.0
5.5
Subperiodos
5.0
1
10
100
1000
10000
El estudio de la grafica nos muestra que el valor de una opción Call tipo americano y una
tipo europeo es el mismo. Ambos convergen al valor entregado por la formula de BlackScholes.
106
Fundamentos de Derivados y Opciones
Benavides
Código de Visual Basic para la implementación de las Formulas utilizadas para el
ejercicio
Valoración de una Opción Put, Tipo americano o europeo, método binomial
Function PutAmEu(S, X, rf, T, n, sigma, e)
dt = T / n
u = Exp(sigma * Sqr(dt))
d = Exp(-sigma * Sqr(dt))
r = Exp(rf * dt)
Pr = (r - d) / (u - d)
Dim OpcPagoFin() As Double
Dim OpcPagoMed() As Double
Dim OpcPagoAme() As Double
ReDim OpcPagoFin(n + 1)
For Estado = 0 To n
OpcPagoFin(Estado) = Application.Max(X - S * u ^ _
Estado * d ^ (n - Estado), 0)
Next Estado
For Indice = n - 1 To 0 Step -1
ReDim OpcPagoMed(Indice)
ReDim OpcPagoAme(Indice)
If e = 0 Then
For Estado = 0 To Indice
OpcPagoAme(Estado) = X - S * u ^ _
Estado * d ^ (Indice - Estado)
Next Estado
ElseIf e = 1 Then
For Estado = 0 To Indice
OpcPagoAme(Estado) = 0
Next Estado
End If
For Estado = 0 To Indice
OpcPagoMed(Estado) = Application.Max(OpcPagoAme(Estado) _
, ((1 - Pr) * OpcPagoFin(Estado) + Pr * OpcPagoFin(Estado + 1)) / r)
Next Estado
ReDim OpcPagoFin(Indice)
For Estado = 0 To Indice
OpcPagoFin(Estado) = OpcPagoMed(Estado)
Next Estado
Next Indice
PutAmEu = OpcPagoMed(0)
End Function
107
Fundamentos de Derivados y Opciones
Benavides
Los parámetros de la función son auto explicativos excepto el último e, el cual es 1 si se
quiere valorar una opción tipo Europeo y 0 si es tipo Americano.
Valoración de una Opción Put, Tipo europeo, formula Black-Scholes
Function PutBS(S, X, rf, T, sigma)
d1 = (Application.Ln(S / X) + (rf + sigma ^ 2 / 2) * T) / (sigma * Sqr(T))
d2 = d1 - sigma * Sqr(T)
d1n = -d1
d2n = -d2
drf = Exp(-rf * T)
PutBS = Application.NormSDist(d2n) * drf * X _
- Application.NormSDist(d1n) * S
End Function
Valoración de una Opción Call, Tipo americano o europeo, método binomial
Function CallAmEu(S, X, rf, T, n, sigma, e)
dt = T / n
u = Exp(sigma * Sqr(dt))
d = Exp(-sigma * Sqr(dt))
r = Exp(rf * dt)
Pr = (r - d) / (u - d)
Dim OpcPagoFin() As Double
Dim OpcPagoMed() As Double
Dim OpcPagoAme() As Double
ReDim OpcPagoFin(n + 1)
For Estado = 0 To n
OpcPagoFin(Estado) = Application.Max(S * u ^ _
Estado * d ^ (n - Estado) - X, 0)
Next Estado
For Indice = n - 1 To 0 Step -1
ReDim OpcPagoMed(Indice)
ReDim OpcPagoAme(Indice)
If e = 0 Then
For Estado = 0 To Indice
OpcPagoAme(Estado) = S * u ^ _
Estado * d ^ (Indice - Estado) - X
Next Estado
108
Fundamentos de Derivados y Opciones
Benavides
ElseIf e = 1 Then
For Estado = 0 To Indice
OpcPagoAme(Estado) = 0
Next Estado
End If
For Estado = 0 To Indice
OpcPagoMed(Estado) = Application.Max(OpcPagoAme(Estado) _
, ((1 - Pr) * OpcPagoFin(Estado) + Pr * OpcPagoFin(Estado + 1)) / r)
Next Estado
ReDim OpcPagoFin(Indice)
For Estado = 0 To Indice
OpcPagoFin(Estado) = OpcPagoMed(Estado)
Next Estado
Next Indice
CallAmEu = OpcPagoMed(0)
End Function
Valoración de una Opción Call, Tipo europeo, formula Black-Scholes
Function CallBS(S, X, rf, T, sigma)
d1 = (Application.Ln(S / X) + (rf + sigma ^ 2 / 2) * T) / (sigma * Sqr(T))
d2 = d1 - sigma * Sqr(T)
drf = Exp(-rf * T)
CallBS = Application.NormSDist(d1) * S - Application.NormSDist(d2) * drf * X
End Function
-------------------
109
Fundamentos de Derivados y Opciones
Benavides
8. Como Calcular el Portafolio Insurance
Una inversionista en acciones normalmente busca aprovechar las ganancias de precio de su
portafolio inicial S, llamado en adelante activo subyacente (Gráfica 1), pero también
desearía protegerse contra una caída en el precio de su portafolio. Sin ningún tipo de
protección el inversionista esta expuesto a la perdida total de su inversión si, por ejemplo,
el valor del activo subyacente ha caído a cero en el momento en que desea liquidar sus
posiciones.
Stock
250
Put
120
100
200
80
150
60
100
40
50
20
0
0
0
100
200
-20 0
300
Gráfica 1
100
200
300
Gráfica 2
Este tipo de protección puede lograrse adquiriendo un put (Gráfica 2) con precio de
ejercicio X (En este caso X=100), que se agrega a la posición inicial en S, lo que se
denomina un put protectivo. Así se garantiza que el valor del portafolio no baje de X. Si no
hay puts apropiados, debido a que el portafolio es complejo o porque el mercado de
derivativos no es activo (Caso Colombia), se puede crear un put combinando posiciones en
el portafolio original y en bonos sin riesgo (que vencen en la fecha de expiración de la
opción), con lo que se crea un portafolio que replica los pagos del Put protectivo. Puesto
que las variaciones en el precio del activo subyacente son aleatorias es necesario
rebalancear el portafolio periódicamente para ajustar las proporciones del activo subyacente
y los bonos sin riesgo. Esto no es necesario si lo que se tiene es un Put real (no sintético
como en el caso descrito) ya que los términos de ejercicio y expiración se convienen en el
momento 0 y permanecen estables. Esta técnica se conoce como “Portfolio Insurance”.
Los activos poseídos son entonces S+P. (Gráfica 3)
Put+Stock
250
200
150
100
50
0
0
100
200
300
Gráfica 3
110
Fundamentos de Derivados y Opciones
Benavides
Donde S representa la inversión en los activos del portafolio original (S 0 es el precio del
portafolio original) y P el Put (La inversión I0 debe repartirse entre estos 2 activos).
Podemos usar 2 modelos de valoración para el Portafolio “Insurance”: a) el modelo
Binomial y b) el modelo de Black-Scholes.
Se debe recordar que el modelo binomial de valoración de opciones tiene al menos 2
versiones que son en esencia el mismo método. Aquí usaremos el modelo que replica los
pagos de la opción como una combinación del activo subyacente y bonos libres riesgo.
Veamos primero como se construye este portafolio Replica o de seguimiento.
Valoración de una Opción Put
Método del Portafolio Replica o de Seguimiento (2 periodos)
Los supuestos del modelo son:
9. Existen 2 periodos, el periodo inicial donde se suscribe la opción y el periodo final
donde la opción expira.
10. El activo subyacente S, cuyo valor actual es S i, solo puede tomar 2 valores futuros
(lo que es equivalente a decir que el futuro solo tiene dos estados U y D): SU o SD.
Podemos expresar SUi = Siu y SDi = Sid. Los factores u y d multiplican al valor a S i
ya conocido. Ninguno de estos valores (SU o SD) corresponde necesariamente al
valor real que en el periodo i +1 tome el activo subyacente S. Es común observar
que el estado U corresponde a un incremento de precio (u>1) y el estado D a una
reducción (d<1)12 . Es importante notar que estos valores son suposiciones que no
coinciden necesariamente con el futuro, se utilizan solo para el calculo de las
posiciones del portafolio.
11. Existe un bono cero cupón o de descuento puro sin riesgo, la tasa libre de riesgo se
denomina rf. Esta tasa se compone continuamente, lo que implica que el valor futuro
de un bono con valor de B0 dentro de un periodo t es igual a B0 Exp(rft),
independiente de si el estado es u o d. La tasa normalmente se expresa en términos
anuales por lo que si el tiempo transcurrido entre el periodo 0 y el 1 es 1 año el
valor de t es igual a 1.
Bajo el principio de no arbitraje 2 activos que tengan pagos futuros idénticos deben tener el
mismo precio hoy. El método replica los pagos de la opción Put (en realidad el método
aplica para cualquier derivativo) en términos de activos cuyo precios, actual y futuro, en
cada estado, son conocidos.
Sean VUi y VDi los pagos futuros en cada estado de la opción Put, que corresponden (en el
caso de un Put) a:
VUi = Max[X-Siu,0]
Es usual calcular u = Exp(t1/2 ) y d = Exp(-t 1/2 ), donde es la volatilidad del activo subyacente y t el
tiempo asignado para cada subperiodo.
12
111
Fundamentos de Derivados y Opciones
Benavides
VDi = Max[X-Sid,0]
Sean y el número de unidades del activo subyacente y del bono libre de riesgo que
componen el portafolio respectivamente. Es importante notar que el valor actual de cada
bono es igual a 1. Para cada estado se debe cumplir que:
VUi = iSiu + iExp(rft)
VDi = iSid + iExp(rft)
(Ec. 1.1)
(Ec. 1.2)
Este es un sistema de 2 ecuaciones con 2 incógnitas, los valores de y . Despejamos las
incógnitas y encontramos que
i = (VUi – VD i)/(Siu – Sid)
(Ec. 2.1)
i = Exp(-rft)(VDiSiu – VUiSid)/(Siu - Sid) (Ec. 2.2)
El valor hoy de la opción Put corresponde al valor de la inversión en el activo subyacente
iSi mas el valor de la inversión en el bono libre de riesgo i (recuerde que el valor actual
del bono libre de riesgo es 1, por lo que B corresponde tanto al numero de bonos requeridos
como al valor de la inversión en bonos).
Sea P0 el valor del Put en el momento 0, según los supuestos previos se tiene que
P0 = S0 + donde el subíndice 0 indica que estos cálculos corresponden al periodo
inicial.
Recordemos que el Put protectivo corresponde a la combinación de 2 posiciones: la compra
del activo subyacente S y de un Put P. La posición del Put protectivo creada sobre 1 unidad
del activo subyacente S, tiene entonces el siguiente valor en t = 0:
S0 + P0 = (1 + )S0 +
De esta posición %S0 = (1 + 0 )S0 /[(1 + 0 )S0 + 0 ] representa el porcentaje invertido en el
activo subyacente S y %0 = 0 /[(1 + 0 )S0 + 0 ] representa el porcentaje del portafolio
invertido en bonos sin riesgo.
Si I0 representa el presupuesto de inversión disponible, el monto invertido en acciones y en
bonos es
I0S = I0 %S0
I0 = I0 %0
Debemos ahora determinar el número de unidades del activo subyacente S a comprar
#S0 = I0 %S0 /S0 = I0 (1 + 0 )/[(1 + 0 )S0 + 0 ]
El éxito del portafolio replica estriba en duplicar lo mas fidedignamente posible los pagos
del Put protectivo. Establecer los montos iniciales de la inversión en el activo subyacente y
112
Fundamentos de Derivados y Opciones
Benavides
los bonos no garantiza una proporción adecuada en todo el horizonte de vida (hasta la fecha
de expiración o fecha donde el inversionista liquida sus posiciones) de la opción puesto que
lo que se tiene es una opción sintética y no una real. Dado el comportamiento aleatorio de
los precios del activo subyacente, se requiere ajustar las posiciones con una frecuencia
determinada por el inversionista. En la vida real es costoso liquidar posiciones por lo que
un seguimiento perfecto no es posible y el inversionista debe elegir una frecuencia de ajuste
que le brinde la seguridad adecuada sin elevar demasiado los costos de transacción.
Sea la fecha de liquidación T = 1 año, asumamos que el inversionista se siente
razonablemente seguro si rebalancea su portafolio mensualmente, por lo que el numero de
ajustes es n = 12. Si lo que queremos es estructurar un Put que venza cada mes tenemos que
bajo estas condiciones t = T/n = 1/12. Si el Put vence al finalizar el horizonte de cobertura
T, entonces cambia cada periodo y es igual a t=T-iT/n, con i variando desde 0 hasta n-1.
Esto implica que u cambia cada periodo.
Es claro entonces que los cálculos anteriores deben repetirse 12 veces para ajustar de
manera adecuada las proporciones.
Al momento de realizar el primer rebalanceo el precio del activo subyacente es S 1 , por lo
que lo obtenido al cabo de un mes corresponde a
I1 = (#S0 )S1 + 0Exp(rf(T/n)).
Donde el 1er término designa al valor que toma en el periodo 1 la inversión en acciones al
multiplicar el numero de acciones que se compro en el periodo 0 por su precio actual y el
2do término al valor de los bonos habiendo transcurrido un periodo desde su compra.
Conocido el valor real del activo subyacente S 1 podemos calcular los correspondientes SU1
y SD1 , y los valores del Put VU1 y VD1 . Valores hipotéticos que permiten calcular el
portafolio de replica.
El ciclo requiere que ahora se calculen 1 y 1 . Lo que permite hallar %S1 y %1 .
Multiplicando %S por I1 hallamos el monto de la inversión en el activo subyacente y si
dividimos este valor por S1 , encontramos #S1 el numero de unidades del activo subyacente
que componen el portafolio en el periodo 1.
#S1 = %S1 I1 /S1
El ciclo se reinicia.
Veamos ahora un ejemplo práctico en Excel:
El activo subyacente S tiene un precio actual de 80, la tasa libre de riesgo es 10% (Anual),
la volatilidad del activo es de 30%. El precio de ejercicio X es de 80 se quiere asegurar el
113
Fundamentos de Derivados y Opciones
Benavides
portafolio por un año y se ajustan posiciones mensualmente. Se dispone de $1000 para
invertir. Se ignoran costos de transacción y variaciones en la tasa de interés.
Los datos en Excel lucen de la siguiente manera
A
1
B
C
D
E
Portfolio Insurance
2 Parametros
3 Periodo
4 Ii
5 Si
6 X
7 Sigma
Exp(t1/2)
8 u
9 d
=1/u
10 T
en años
11 N
Frecuencia ajuste
12 t
=T/N
13 r
14 Exp(rt)
15 Exp(-rt)
1/Exp(rt)
0
1,000.00
80.00
80.00
30%
1.0905
0.9170
1
12
0.0833
10%
1.0084
0.9917
1
77.00
<--=EXP(C7*$C$12^(1/2))
<--=1/C8
<--=C10/C11
<--=EXP(C13*$C$12)
<--=EXP(-C13*$C$12)
Se procede a calcular el Put Protectivo, iniciando con los valores de SU i y SDi y los valores
intrínsecos de la opción Put (Max(X-St ,0) para cada uno de los valores posibles (SUi y
SDi):
A
B
C
16 Put Protectivo
Siu
17 SUi
Sid
18 SDi
19
Max(X-Siu,0)
20 VUi
21 VDi
D
E
87.24 <--=C5*$C$8
73.36 <--=C5*$C$9
-
Max(X-Sid,0)
<--=MAX($C$6-C17,0)
6.64 <--=MAX($C$6-C18,0)
Ahora debemos hallar los valores de i y Bi:
A
22 Despeje
23 i
24 Bi
B
=(VUi-VDi)/(Siu-Sid)
=Exp(-rt)(VDiSiu-VUiSid)/(Siu-Sid)
C
-
D
E
F
0.4784 <--=(C20-C21)/(C17-C18)
41.38 <--=$C$15*(C21*C17-C20*C18)/(C17-C18)
Se utilizaron las ecuaciones 2 para hallar los anteriores valores. En el caso de un método
alternativo es utilizar la Ecuación 1.1 (una ves hallado ) para despejar su valor. El sentido
negativo de implica que se venden en corto –0.47 unidades del activo subyacente y que
se compran 41.38 unidades del bono libre de riesgo cuyo valor por unidad es de 1.
114
Fundamentos de Derivados y Opciones
Benavides
En consecuencia podemos hallar el valor actual del Put, multiplicando los valores hallados
previamente por los precios actuales de los activos que componen el portafolio replica,
puesto que el valor actual del bono es 1 no es necesario multiplicarlo por ningún valor:
A
25 Portafolio Réplica
Sii+Bi
26 Pi
B
C
D
E
3.12 <--=C23*C5+C24
El anterior procedimiento se puede aplicar para cualquier tipo de derivativo.
Ahora debemos extender los cálculos para hallar el monto de las inversiones a realizar en el
Put protectivo.
La cantidad disponible para inversión es $1000. Un Put suscrito sobre una unidad del activo
subyacente, en las condiciones anteriores, implica la venta de 0.47 unidades del activo y la
compra de 41.38 unidades del bono. El Put Protectivo combina en un portafolio 1 unidad
del activo subyacente con las inversiones requeridas para establecer el put sintético.
A
B
27 Put Protectivo por 1 unidad de S
(1+i)Si+Bi
28 Si+Pi
29 Inversion Si (1+i)Si
30
31
32
33
Inversion Bi Bi
Chequeo Total Inversiones
C
D
E
83.12 <--=C26+C5
41.73 <--=(1+C23)*C5
41.38 <--=C24
83.12 <--=C29+C30
Posiciones
%Si
34 %Bi
(1+i)Si/(Si+Pi)
50.21% <--=(1+C23)*C5/C28
Bi/(Si+Pi)
49.79% <--=1-C33
Habiendo calculado la inversión porcentual en el activo subyacente y el portafolio
procedemos a calcular la inversión total y el número de unidades del activo subyacente que
se requiere comprar:
A
36 Inicio de Periodo
37 Inversion Si %SiIi
38 Inversion Bi %BiIi
39 Chequeo
%SiIi+%BiIi
40 Ii
41 #Si
%SiIi/Si
B
C
D
502.083321 <--=C33*C4
497.916679 <--=C4*C34
1,000.00 <--=C37+C38
6.27604152 <--=C37/C5
Los cálculos anteriores finalizan el ejemplo para 1 periodo. Supongamos que al final del
sub-periodo (1 mes) el precio del activo subyacente ha caído hasta $77, cual es el valor del
portafolio? En un mes la inversión en bonos gana intereses (Recuerde que es una inversión
libre de riesgo) mientras que la inversión en el activo subyacente lo pierde.
115
Fundamentos de Derivados y Opciones
A
42 Fin de Periodo
43 Si+1
44 #SiSi+1
45 %BiIiExp(rt)
46 Ii+1
B
Benavides
C
D
E
77.00 <--=D5
483.26 <--=C41*C43
502.08 <--=C38*$C$14
985.34 <--=SUMA(C44:C45)
El proceso puede ahora repetirse para el siguiente periodo.
116
Fundamentos de Derivados y Opciones
Benavides
A continuación puede observarse el resultado para una simulación que cubre 9 meses:
A
1
B
C
2 Parametros
3 Periodo
4 Ii
5 Si
6 X
7 Sigma
Exp(t1/2)
8 u
9 d
=1/u
10 T
en años
11 N
Frecuencia ajuste
12 t
=T/N
13 r
14 Exp(rt)
15 Exp(-rt)
1/Exp(rt)
16 Put Protectivo
Siu
17 SUi
18 SDi
19
20 VUi
21 VDi
22 Despeje
23 i
24
25
26
27
28
D
E
F
G
H
I
J
K
L
Portfolio Insurance
Sid
Max(X-Siu,0)
Max(X-Sid,0)
=(VUi-VDi)/(Siu-Sid)
Bi
=Exp(-rt)(VDiSiu-VUiSid)/(Siu-Sid)
Portafolio Réplica
Pi
Sii+Bi
Put Protectivo por 1 unidad de S
Si+Pi
(1+i)Si+Bi
29 Inversion Si (1+i)Si
30 Inversion Bi Bi
31 Chequeo Total Inversiones
32 Posiciones
(1+i)Si/(Si+Pi)
33 %Si
Bi/(Si+Pi)
34 %Bi
35
36 Inicio de Periodo
37 Inversion Si %SiIi
38 Inversion Bi %BiIi
39 Chequeo
%SiIi+%BiIi
40 Ii
%SiIi/Si
41 #Si
42 Fin de Periodo
43 Si+1
44 #SiSi+1
45 %BiIiExp(rt)
46 Ii+1
0
1,000.00
-
7
1,223.49
8
1,199.50
80.00
80.00
30%
1.0905
0.9170
1
12
0.0833
10%
1.0084
0.9917
1
985.34
77.00
2
1,012.84
83.00
3
1,067.56
89.00
4
1,103.54
92.00
5
1,079.55
90.00
6
1,163.52
97.00
102.00
100.00
9
1,151.52
96.00
87.24
83.97
90.51
97.05
100.32
98.14
105.77
111.23
109.05
104.68
73.36
70.61
76.11
81.62
84.37
82.53
88.95
93.54
91.70
88.04
-
-
-
-
-
-
-
-
-
-
3.89
-
-
-
-
-
-
-
6.64
9.39
0.4784 -
0.7030 -
0.2699
-
-
-
-
-
-
-
41.38
58.54
24.23
-
-
-
-
-
-
-
3.12
4.41
1.82
-
-
-
-
-
-
-
83.12
81.41
84.82
89.00
92.00
90.00
97.00
102.00
100.00
96.00
41.73
22.87
60.59
89.00
92.00
90.00
97.00
102.00
100.00
96.00
41.38
83.12
58.54
81.41
24.23
84.82
89.00
92.00
90.00
97.00
102.00
100.00
96.00
50.21%
28.09%
71.44%
100.00%
100.00%
100.00%
100.00%
100.00%
100.00%
100.00%
49.79%
71.91%
28.56%
0.00%
0.00%
0.00%
0.00%
0.00%
0.00%
0.00%
502.08
276.78
723.53
497.92
708.56
289.31
1,000.00
985.34
1,012.84
6.27604152 3.594552176
8.7171895
1,067.56
1,067.56
11.9950479
1,103.54
1,103.54
11.9950479
1,079.55
1,079.55
11.9950479
1,163.52
1,163.52
11.9950479
1,223.49
1,223.49
11.9950479
1,199.50
1,199.50
11.9950479
1,151.52
1,151.52
11.9950479
77.00
83.00
89.00
92.00
90.00
97.00
102.00
100.00
96.00
103.00
483.26
298.35
775.83
1,103.54
1,079.55
1,163.52
1,223.49
1,199.50
1,151.52
1,235.49
502.08
714.49
291.73
985.34
1,012.84
1,067.56
1,103.54
1,079.55
1,163.52
1,223.49
1,199.50
1,151.52
1,235.49
117
Fundamentos de Derivados y Opciones
Benavides
Gráficamente la evolución del valor del portafolio se observa con una cota inferior:
$
PI
Si
120
1,300
110
1,200
100
1,100
90
80
1,000
70
900
60
800
50
0
1
2
3
4
5
Ii
6
7
XT
8
9
Si
10 11
12 13
mes
118
Fundamentos de Derivados y Opciones
Benavides
Modelo de Black-Scholes
Recordando que P=XExp(-rfT)N(-d2)-S0 N(-d1) (Una combinación de el activo S y bonos
sin riesgo), se tiene que
S0 +P0 = S0 (1-N(-d1))+ Xexp(-rT)N(-d2)
Lo que representa un Put protectivo sobre una unidad de S. Donde T es el tiempo para la
expiración de la opción, medido en anos (normalmente T=1, en caso contrario debe tenerse
en cuenta como esta expresada r).
La posición en el portafolio original S seria = S 0 (1-N(-d1))
La posición en el activo libre de riesgo es = Xexp(-rfT)N(-d2)
Del monto disponible para invertir se asignan a los activos representados por S (expresado
%): %S0 = S0 (1-N(-d1))/(S0 +P0 ).
En los bonos se invierte 1-%S0 .
Lo invertido en acciones (S) es I0 %S0 , lo invertido en bonos es I0 (1-%S0 ).
El numero de acciones (S) es igual #S 0 = I0 %S0 /S0 . Donde S0 es el valor de las acciones en
el tiempo 0.
El rebalanceo del portafolio ocurre a la frecuencia m definida por el inversionista (diario
N=250, semanal N=52, mensual N=12, si T=1 (1 ano)).
Una vez transcurrido un periodo, en teoría se liquidan las posiciones y se tiene un nuevo
monto a invertir (I1 ).
I1 = #S0 S1 + I0 (1-%S0 )exp(r*(T/N)).
El 1er término representa el valor de la porción del portafolio invertida en S, el 2 do termino
representa el valor de lo invertido en los bonos libres de riesgo, una vez transcurrido un
periodo.
Se recalcula el Put, teniendo en cuenta que el tiempo al vencimiento se ha reducido. T ha
cambiado a T(1-1/m) y el valor de S es S1 .
El proceso se repite hasta el vencimiento o expiración del Put.
-------------------
119
Fundamentos de Derivados y Opciones
Benavides
Plantilla
Portfolio Insurance
Inv. Binomial T'
Ii
1.000,0
Periodo (i)
970,4
0
943,9
1
921,2
2
902,9
3
890,1
4
884,5
5
888,4
894,4
900,4
906,4
912,4
918,5
6
7
8
9
10
11
T'=T-it
n*
t=T/n*
Sigma
ui = exp(T' 0.5)
1
0,92
0,83
0,75
0,67
0,58
0,50
12
0,0833
VENCIMIENTO AL FINAL DEL AÑO
30%
1,3499 1,3327 1,3150 1,2967 1,2776 1,2575 1,2363
0,42
0,33
0,25
0,17
0,08
di = 1/ui
r
exp(rT')
X
0,7408 0,7503
8,00%
1,0833 1,0761
50,00
50,00
i
Si
0
1
2
3
4
5
6
7
8
9
10
11
12
56,000 53,500 51,000 48,500 46,000 43,500 41,000 38,500 36,000 33,500 31,000 28,500 26,000
Si+1U = Si ui
75,592
71,301
67,067
62,889
58,768
54,701
50,689
46,726
42,808
38,921
35,039
31,078
Si+1D = Si di
41,486
40,143
38,782
37,403
36,006
34,592
33,163
31,722
30,275
28,834
27,427
26,136
Put Intrinseco
f i+1U = Max(X - Si+1U,0)
f i+1D = Max(X - Si+1D,0)
Portafolio Replica
i = (f i+1U - f i+1D)/[Si(u-d)]
1,2137
1,1891
1,1618
1,1303
1,0905
0,7604
0,7712
0,7827
0,7952
0,8089
0,8239
0,8410
0,8607
0,8847
0,9170
1,0689
50,00
1,0618
50,00
1,0548
50,00
1,0478
50,00
1,0408
50,00
1,0339
50,00
1,0270
50,00
1,0202
50,00
1,0134
50,00
1,0067
50,00
-
-
-
-
-
-
-
3,274
7,192
11,079
14,961
18,922
8,514
9,857
11,218
12,597
13,994
15,408
16,837
18,278
19,725
21,166
22,573
23,864
12
- 0,250 - 0,316 - 0,397 - 0,494 - 0,615 - 0,766 - 0,961 - 1,000 - 1,000 - 1,000 - 1,000 - 1,000
Bi = e-rT' (f i+1Du – f i+1Ud)/(u - d) 17,420 20,961 24,883 29,274 34,254 40,001 46,787 48,361 48,684 49,010 49,338 49,668
Pi = iSi + Bi
3,440
4,036
4,657
5,302
5,973
6,672
7,399
9,861 12,684 15,510 18,338 21,168
Porcentaje Inversión
%Si=Si(1+i)/(Si+Pi)
0,707
0,636
0,553
0,456
0,341
0,203
0,033
-
-
-
-
-
%Bi=Bi/(Si+Pi)
0,293
0,364
0,447
0,544
0,659
0,797
0,967
1,000
1,000
1,000
1,000
1,000
Ii
Inicio de Periodo
IiS=Ii %Si
IiB=Ii %Bi
1.000,0
970,4
943,9
921,2
902,9
890,1
884,5
888,4
894,4
900,4
906,4
912,4
706,9
616,9
521,9
420,0
307,8
180,4
29,4
-
-
-
-
-
293,1
353,5
422,0
501,2
595,1
709,7
855,1
888,4
894,4
900,4
906,4
912,4
Total
#Si=IiS/Si
Fin de Periodo
IfiS = #SiSi+1
1.000,0
970,4
943,9
921,2
902,9
890,1
884,5
888,4
894,4
900,4
906,4
912,4
12,6
11,5
10,2
8,7
6,7
4,1
0,7
-
-
-
-
-
675,4
588,0
496,3
398,3
291,1
170,1
27,7
-
-
-
-
-
IfiB = IiBert
295,0
355,9
424,8
504,6
599,0
714,4
860,8
894,4
900,4
906,4
912,4
918,5
Ii+1 = IfiS+IfiB
970,4
943,9
921,2
902,9
890,1
884,5
888,4
894,4
900,4
906,4
912,4
918,5
120
Fundamentos de Derivados y Opciones
Inv. Binomial t
Ii
Benavides
1,000.0
1,001.7
991.2
997.8
1,004.5
1,071.0
1,260.1
1,056.1
1,047.9
Periodo (i)
0
1
2
3
4
5
6
7
8
Tc
1
nc
Tb=Tc/nc
1,166.6
1,075.2
1,025.5
906.5
10
11
12
9
12
0.0833
nb
VENCIMIENTO EN CADA MES
1
t=Tb/nb
Sigma
u = exp(t0.5)
d=1/u
r
ert
X
0.0833
30.00%
1.0905
0.9170
8.00%
1.0067
58.50
i
Si
0
1
2
3
4
5
6
7
8
9
10
11
12
56.000 55.249 50.084 51.798 58.580 65.804 77.422 64.888 64.385 71.681 66.063 63.013 55.116
Si+1U = Si u
61.066
60.247
54.615
56.484
63.880
71.757
84.426
70.758
70.210
78.165
72.039
68.713
60.102
Si+1D = Si d
51.354
50.666
45.929
47.501
53.721
60.345
70.999
59.505
59.044
65.734
60.583
57.785
50.544
Put Intrinseco
fi+1U = Max(X - Si+1U,0)
fi+1D = Max(X - Si+1D,0)
Portafolio Replica
i = (fi+1U - fi+1D)/[Si(u-d)]
58.50
58.50
58.50
58.50
58.50
58.50
58.50
58.50
58.50
58.50
58.50
58.50
-
-
3.882
2.013
-
-
-
-
-
-
-
-
-
7.142
7.831
12.567
10.995
4.776
-
-
-
-
-
-
0.711
7.953
- 0.735 - 0.817 - 1.000 - 1.000 - 0.470
-
-
-
-
-
-
44.611
48.913
58.108
58.108
29.831
-
-
-
-
-
-
4.443
49.675
Pi = iSi + Bi
3.427
3.758
8.024
6.310
2.292
-
-
-
-
-
-
0.341
3.816
Porcentaje Inversión
%Si=Si(1+i)/(Si+Pi)
24.9%
17.1%
93.0%
15.7%
%Bi=Bi/(Si+Pi)
75.1%
82.9% 100.0% 100.0%
49.0%
0.0%
0.0%
0.0%
0.0%
0.0%
0.0%
7.0%
84.3%
Ii
Inicio de Periodo
IiS=Ii %Si
IiB=Ii %Bi
1,000.0
1,001.7
1,004.5
1,071.0
1,260.1
1,056.1
1,047.9
1,166.6
1,075.2
1,025.5
906.5
249.3
171.4
-
-
512.2
1,071.0
1,260.1
1,056.1
1,047.9
1,166.6
1,075.2
953.6
142.4
750.7
830.3
991.2
997.8
492.3
71.9
764.1
Total
#Si=IiS/Si
Fin de Periodo
IfiS = #SiSi+1
1,000.0
1,001.7
991.2
997.8
1,004.5
1,071.0
1,260.1
1,056.1
1,047.9
1,166.6
1,075.2
1,025.5
906.5
4.5
3.1
-
-
8.7
16.3
16.3
16.3
16.3
16.3
16.3
15.1
2.6
246.0
155.3
-
-
575.4
1,260.1
1,056.1
1,047.9
1,166.6
1,075.2
1,025.5
834.1
755.7
835.9
997.8
1,004.5
495.6
1,001.7
991.2
997.8
1,004.5
1,071.0
Bi = e-rt (fi+1Du – fi+1Ud)/(u - d)
IfiB = IiBert
Ii+1 = IfiS+IfiB
0.0%
991.2
0.0%
997.8
- 0.065 - 0.832
51.0% 100.0% 100.0% 100.0% 100.0% 100.0% 100.0%
-
-
1,260.1
-
-
1,056.1
-
-
1,047.9
-
-
1,166.6
-
-
1,075.2
-
-
1,025.5
72.4
906.5
121
Fundamentos de Derivados y Opciones
Benavides
9. Opciones Reales, una introducción
Muchas inversiones pueden ser aplazadas en el tiempo a la espera de condiciones
favorables para realizarlas. Algunas veces para que el inversionista disponga de esa
flexibilidad se requiere una inversión inicial menor que garantice tal flexibilidad.
El primer caso es típicamente la ampliación de capacidad de una fábrica.
Regularmente una fabrica tiene cierta capacidad de ampliación. Para obtener los beneficios
relacionados con tal ampliación se requerirá, en el futuro, realizar una inversión adicional.
Suponga que el monto de esta inversión es X. Posterior a esta inversión se obtienen unos
flujos de caja en el tiempo, cuyo valor presente denominaremos S 0 (Por el momento no nos
preocuparemos de la tasa a la cual se descuentan estos flujos).
La evaluación de proyectos estándar nos dice que si S>VP(X) el proyecto es aceptable y
debe realizarse (VPN>0). Lo que esta medida no tiene en cuenta es el valor que para el
inversionista tiene la flexibilidad de: (1) Definir en que momento realiza la ampliación y (2)
Definir si la realiza o no.
El valor adicional del proyecto esta determinado por dos parámetros adicionales hasta ahora
no contemplados: (1) El tiempo que puede dilatarse la inversión T y (2) La volatilidad de
los flujos .
La valoración por Opciones reales tiene en cuenta este valor.
Esta reflexión es particularmente pertinente en situaciones donde el proyecto inicial es poco
atractivo y gran parte del valor se obtiene a partir de una ampliación..
El segundo caso puede relacionarse con la compra de activos cuyo potencial futuro sea muy
atractivo, si cambian las condiciones del mercado.
En este caso puede ubicarse la compra de un lote urbanizable. Es posible que con los
precios actuales de la finca raíz este proyecto de urbanización no resulte viable, sin
embargo, las características cíclicas de esta actividad productiva pueden tornarlo atractivo
en cualquier momento.
En este caso X es el costo de la construcción y S el valor esperado de los activos con los
precios actuales. En este caso también incluimos la volatilidad de los precios de la finca
raíz () y el tiempo por el cual la opción es valida.
122
Fundamentos de Derivados y Opciones
Benavides
Una opción financiera es un instrumento que permite la cobertura (o apostar) o frente al
riesgo de oscilaciones en el precio de un activo.
Suponga que usted posee una acción S de una empresa cualquiera y desea cubrirse contra
una reducción en su valor. Al comprar una opción PUT usted obtiene el derecho a vender la
acción a un precio convenido en el momento de compra de la opción, este precio se
denomina Precio de Ejercicio (X). Otra condición que debe convenirse es cuanto tiempo
será valida esta posibilidad, este tiempo se denomina Tiempo a la Madurez, de
Expiración ó al Vencimiento (T). Es importante recordar que la opción, a diferencia de un
futuro, es un activo contingente: El comprador de la opción no esta obligado a ejercerla
(hacerla efectiva). Si el precio de la acción S se ha incrementado ó al menos se ha
mantenido por encima del precio de ejercicio X, no es optimo ejercer la opción.
Otra importante característica de las opciones es la que se refiere a la posibilidad de
ejercerla antes del vencimiento. Cuando las partes acuerdan que la opción puede ejercerse
en cualquier momento antes del vencimiento, la opción se conoce como tipo Americana.
Cuando la opción solo puede ejercerse al vencimiento se denomina Europea.
El valor de la opción, lo que el comprador debe pagar por obtenerla, se denomina Prima.
Debe reconocerse que cuando dos contrapartes, el vendedor y el comprador, acuerdan los
términos de una opción PUT, sus flujos son absolutamente opuestos. El comprador paga la
prima en el momento cero, la cual es recibida por el vendedor. En el momento de ejercer la
opción el comprador entrega la acción y recibe el precio de ejercicio X. El comprador, por
su parte, entrega el precio de ejercicio X y recibe la acción. Si la opción no es ejercida no
hay intercambio diferente al inicial.
Existen dos métodos y una fórmula para calcular el valor de una opción: (1) El método
binomial. (2) El método neutral al riesgo. (3) La fórmula de Black-Scholes.
Aunque conceptualmente mas elaborada, la formula de Black-Scholes es el metodo de
calculo mas expedito para la valoración de opciones.
Valoración de Opciones con la Fórmula de Black-Scholes
Black y Scholes (1973) desarrollaron una formula para la valoración de opciones con base
en el principio de no arbitraje para encontrar el valor de una opción tipo Europeo, con base
en cinco parámetros de fácil estimación:
1. S0 : El valor de la acción o activo subyacente en el momento de emitir la opción.
2. X: El precio de ejercicio de la opción.
3. T: El tiempo hasta la expiración o madurez de la opción.
4. r: La tasa de interés libre de riesgo.
5. : La volatilidad del activo subyacente.
La formula derivada por Black-Scholes para un Call es:
123
Fundamentos de Derivados y Opciones
P = S0 N(d1 ) - Xe-rT N(d2 )
Benavides
(Ec. 1)
Donde N(.) es la distribución normal acumulada y d 1 y d2 vienen dados por los siguientes
términos:
LnS o X r σ2 2 T
d1
σ2 T
d2 d1 σ T
El supuesto fundamental de la formula de Black-Scholes es que los precios del activo
subyacente están determinados por un proceso continuo tipo lognormal (E(Ln(S t+t /St )
=t, Var(Ln(St+t /St ) =2 t).
124
Fundamentos de Derivados y Opciones
Benavides
Ejercicios
1. La Empresa ABC tiene seis maquinas de hilado. Esta considerando reemplazar las
seis maquinas. Cada maquina nueva cuesta $1000 y tiene una vida útil de 5 años.
Los flujos de caja anticipados son:
Año
Flujo x maquina
0
(1,000.00)
1
220.00
2
300.00
3
400.00
4
200.00
5
150.00
Halle el Valor Presente Neto de este proyecto.
Suponga que el proyecto no es atractivo, pero el gerente de producción propone: Yo
quiero cambiar una de las maquinas hoy. Al cabo de un año si el experimento es
exitoso reemplazaría las otras cinco maquinas.
Como analizaría el proyecto en el contexto de una opción real? La tasa de descuento
para las maquinas es del 12%, la tasa libre de riesgo es de 6% y la volatilidad
asociada a la operación de las maquinas es de 40%.
2. Usted tiene los siguientes resultados de la evaluación a través de la técnica del VPN
de un proyecto industrial, el cual contempla una expansión (fase 2) en el 4 to año.
Las bases de su calculo son las siguientes:
Impuestos
k0
kF
35%
15%
45%
8.00%
El VPN de la fase 1 es de –10.16. Evaluado a la tasa k0
Los flujos de la fase 2 son los siguientes:
Fase 2
0
1
2
3
4
5
6
7
-
200.00
(144.00)
56.00
(30.00)
(46.00)
(20.00)
300.00
(216.00)
84.00
(30.00)
(69.00)
(15.00)
450.00
(324.00)
126.00
(30.00)
(103.50)
(7.50)
150.00
8.00
(158.00)
(158.00)
(13.00)
30.00
8.88
4.67
3.46
3.46
(9.75)
30.00
9.18
6.33
4.74
4.74
(4.88)
30.00
9.88
2.12
13.13
238.53
251.66
Ingresos
-Costo de bienes vendidos
=Utilidad bruta
-Depreciacion
-Gastos de Administración y Ventas
=EBIT=Utilidad Operacional
-
-
-
-
-
-
-
EBIT(1-T)
+Depreciacion
- Gastos de Capital
- Incremento en Capital de Trabajo
=Flujo de Caja Libre
+Valor Terminal
=FCL + VT
-
-
-
-
-
Halle el Valor presente del proyecto conjunto, el VPN modificado y el valor de la
opción real (defina los cinco parámetros requeridos para valorar la opción por el
125
Fundamentos de Derivados y Opciones
Benavides
método de Black-Scholes, y utilice la tabla para encontrar un valor aproximado),
invertiría usted en este proyecto?
Bibliografía
Puede consultar:
Investments Opportunities as Real Options: Getting Started on the Numbers.
Luerhman, T. HBR, Julio-Agosto 1998
Financial Modeling.
Benninga, S. MIT Press, 2nd edition, 2001
-------------------
126
Fundamentos de Derivados y Opciones
Benavides
10. Ejercicios Generales
1. Valorar un put americano a 3 meses suponiendo 3 subperiodos (halle el t apropiado)
S0 = 1000, X= 1050, Sigma=30% y una tasa libre de riesgo de 8% compuesta
continuamente.
2. Replique el ejercicio de Ecopetrol (Según la guía de clase Proceso Lognormal). Se
adjunta la serie de los precios de fin de mes de esta acción.
3. Halle las series de tiempo para otras 2 acciones que se transen (procure que sean
acciones de alta bursatilidad) en el mercado de valores colombiano. Puede
conseguir estos datos del sitio web:
http://www.supervalores.gov.co
Encuentre la media y la varianza anualizadas y simule la evolución del precio de
estas acciones siguiendo el proceso lognormal. Las notas de clase entregadas usan
conceptos del capitulo 15 de Benninga, que se incluyen en el material entregado
originalmente.
4. Con los datos de sigma y varianza de cada una de las acciones, calcule el precio de
una opción Call Europea “at the money” (S 0 =X) con un vencimiento de 4 meses y 4
subperiodos. Estime cual puede ser la tasa libre de riesgo para la economía
colombiana que pueda aplicar en este ejemplo (Sustente su respuesta)
5. Estime el ejercicio anterior para un Put americano
6. El siguiente es un modelo de un bono estructurado cuyo pago esta sujeto al valor de
un índice de bolsa (IGBVC). El bono combina el pago de una opción Call Europea
“at the money” con los pagos de un bono estándar, con valor nominal de 100:
Pago al vencimiento = Max(St-X,0)+100*(1+8%)
Suponiendo solo 2 periodos (El periodo 0 y el 1) el valor del índice puede
evolucionar de la siguiente forma:
IGBVC
0
S0:
u:
1,275.00
d:
1
1,500.00
750.00
Encuentre el valor del bono, suponiendo una tasa libre de riesgo de 11% para el
periodo. Suponga que esta tasa es discreta. Este ejercicio se puede solucionar por el
método del portafolio de replica o por el método neutral al riesgo. En el método
neutral al riesgo usted puede hallar los valores de u y d por los valores que toma el
índice, en este caso no se cumple que d=1/u.
7. Como el analista financiero de American Airlines usted debe estudiar la oferta
realizada por Boeing de vender opciones para comprar 200 aviones nuevos 777
dentro de 6 meses por un precio de $85 millones por avión. Suponga que la
volatilidad del precio de los aviones es de 45% (anual).Usando 2 subperiodos y el
hecho que el precio actual de los aviones es de $105 millones y la tasa libre de
riesgo es de 8% anual, indique cuanto debe desembolsar American por el derecho
(mas no la obligación) de comprar los aviones.
8. ¿Qué combinación de derivados, bonos y acciones produce el siguiente perfil de
utilidad?
127
Fundamentos de Derivados y Opciones
Benavides
50
40
30
20
10
0
0
20
40
60
80
100
120
128