Document

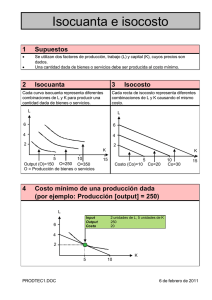
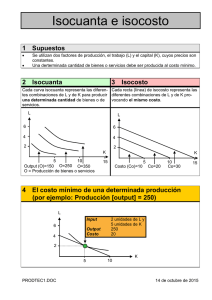
CLASE 4
Sustitución Técnica
Función de producción con dos insumos variables
• Características de las isocuantas
• Nunca se cruzan.
• Son convexas respecto al origen.
• En la parte significativa tienen pendiente negativa.
Economía de la Producción. Maestría en Manejo y Explotación
de Agrosistemas de la Caña de Azúcar
2
Línea de Isocostos
Línea de Isocosto: Refleja un nivel de gasto
determinado para dos insumos. La pendiente de la
línea de isocosto es igual a la razón negativa de los
precios de los insumos y sirve para determinar cual es
la combinación que nos garantiza la combinación de
mínimo costo entre los insumos a utilizar .
Pendiente de la linea de isocosto 
-
Precio de X1
PX1 

Precio de X 2
PX 2 
Función de producción con dos insumos variables
• La Tasa Marginal de
Sustitución
Técnica
entre insumos variables,
(TMSI) se define como la
variación en el insumo X2
cuando varia el insumo X1.
X 2
TMSI 
X1
• La pendiente de la curva
de isoproducto (de signo
negativo)
cambia
constantemente a medida
que nos movemos a lo
largo de ella, debido a
que
existe
una
sustitución
imperfecta
entre los insumos.
20/02/2014
4
Función de producción con dos insumos variables
• En una perfecta sustitución
entre insumos, la TMSI es
constante ya que la “curva”
de isoproducto será una línea
recta.
5
• Lo inverso sería una situación
de complementariedad entre
insumos, en donde una
cantidad determinada del
insumo X1 requiere otra
cantidad similar del otro
insumo X2,. Es este caso la
TMSI puede ser CERO o
infinita.
X 2
TMSI 
X 1
20/02/2014
Elasticidad de la sustitución técnica: Factor de sustitución
• Si a partir de una posición de equilibrio del productor el costo
de un factor desciende, cambiará la posición de equilibrio, se
puede restablecer el equilibrio, al reemplazar este factor,
ahora relativamente más barato, por otro, hasta que el
equilibrio se restablezca. El grado de posibilidad de sustitución
de insumo por otro se denomina elasticidad de la sustitución
técnica, y se expresa como:
eSI  X1 X 2
 X 1 X 1 TMSI X1 X 2



 X 2 X 2 TMSI X X
1 2





• El equilibrio se alcanza cuando:
P(X 1 )
TMSI  
, que es la pendiente de la linea de isocostos
P( X 2 )
Función de producción con dos insumos variables
Rendimientos a escala
7
• Constante: Cuando e SI  X1X 2  1 significa que al aumentar los
insumos en una proporción determinada, la producción
aumenta en la misma proporción.
• Creciente: cuando e SI  X1X 2  1
significa que al
aumentar los insumos en una proporción determinada, la
producción aumenta en una proporción mayor.
• Decreciente: cuando e SI  X X  1significa que al aumentar los
insumos en una proporción determinada, la producción
aumenta en una proporción menor.
1
2
Asignación óptima de dos insumos variables
Ejercicio Resuelto No. 3: A continuación se presentará un
8
ejemplo aplicado a la ganadería de leche, utilizando 2
insumos y manteniendo una producción constante de 10.5 lt.
En la tabla se presentan las combinaciones de alimentos que
producen 10.5 lts de leche con 4.0% de grasa. Determinar:
a) La tasa marginal de sustitución.
b) La gráfica de isoproducto con las líneas isocuanta e
isocosto, ¿qué tipo de sustitución tenemos?
c) La elasticidad y decidir que tipo de rendimiento a
escala se obtiene.
Asignación óptima de dos insumos variables
Datos:
9
Combinaciones
Alfalfa (kg)
Maíz (kg)
Precios Actuales ($/kg)
1
3.6
5.9
Maíz
2.7255
2
4.5
4.3
Alfalfa
0.77
3
5.5
3.2
Leche
5.00
4
6.4
2.6
5
7.3
2.1
6
8.2
1.8
7
9.1
1.5
8
10
1.3
9
10.9
1.2
10
11.8
1
11
12.7
0.9
12
13.6
0.8
Asignación óptima de dos insumos variables
Procedimiento:
a) La tasa marginal de sustitución de insumos (TMSI)
Combinaciones
X1
X2
1
3.6
5.9
2
4.5
4.3
3
5.5
3.2
4
6.4
2.6
5
7.3
2.1
6
8.2
1.8
7
9.1
1.5
8
10
1.3
9
10.9
1.2
10
11.8
1
11
12.7
0.9
12
13.6
0.8
TMSI = X2/X1
10
Asignación óptima de dos insumos variables
Procedimiento:
a) La tasa marginal de sustitución de insumos (TMSI)
11
TMSI = X2/X1
Combinaciones
X1
X2
1
3.6
5.9
2
4.5
4.3
-1.778
3
5.5
3.2
-1.100
4
6.4
2.6
-0.667
5
7.3
2.1
-0.556
6
8.2
1.8
-0.333
7
9.1
1.5
-0.333
8
10
1.3
-0.222
9
10.9
1.2
-0.111
10
11.8
1
-0.222
11
12.7
0.9
-0.111
12
13.6
0.8
-0.111
Asignación óptima de dos insumos variables
Procedimiento:
a) La tasa marginal de sustitución de insumos (TMSI)
TMSI = X2/X1
Combinaciones
X1
X2
1
3.6
5.9
2
4.5
4.3
-1.778
3
5.5
3.2
-1.100
4
6.4
2.6
-0.667
5
7.3
2.1
-0.556
6
8.2
1.8
-0.333
7
9.1
1.5
-0.333
8
10
1.3
-0.222
9
10.9
1.2
-0.111
10
11.8
1
-0.222
11
12.7
0.9
-0.111
12
13.6
0.8
XXX
-0.111
12
Asignación óptima de dos insumos variables
b) Primeramente trazaremos la línea de Isocosto
13
Curva de Isoproducto
7
6
X2
5
4
3
2
1
0
0
2
4
6
8
Economía de la Producción. Maestría en Manejo y Explotación
X1
de Agrosistemas de la Caña de Azúcar
10
12
20/02/2014
14
16
Asignación óptima de dos insumos variables
b) Primeramente trazaremos la línea de Isocosto
14
Curva de Isoproducto
7
6
X2
5
4
3
2
1
0
0
2
4
6
8
10
12
14
16
X1
La curva nos indica que tenemos una sustitución imperfecta de los recursos,
es decir se puede sustituir en diferentes proporciones
Para poder trazar la línea de Isocosto, es necesario determinar su
pendiente, la pendiente de la linea de Isocostos es:

P(X 1 )
0.77

 0.282
P(X 2 )
2.7255
Para trazar la línea de Isocostos usaremos la ecuación de la línea recta,
pues conocemos la pendiente m, y la línea de isocostos siempre va a
P(X 1 )
cruzar el punto correspondiente a TMSI  
, que es el
P(X 2 )
punto.
(X1 = 9.46, X2 = 1.42)
Ecuación de línea recta:
X 2.Iso cos to  X 2 , Equilibrio  m X 1.Iso cos to  X 1, Equilibrio
Para cada punto de la línea de isocosto, despejamos X2, Isocosto,
mientras que usaremos cada X1 = X1,isocosto
X 2.Iso costo  mX 1.Iso costo  X 1, Equilibrio   X 2, Equilibrio
X 2.Iso costo  0.282 X 1  9.5  1.4
TMSI = X2/X1
Combinaciones
X1
X2
1
3.6
5.9
2
4.5
4.3
-1.778
3
5.5
3.2
-1.100
4
6.4
2.6
-0.667
5
7.3
2.1
-0.556
6
8.2
1.8
-0.333
7
9.1
1.5
-0.333
Punto de
Equilibrio
9.5
1.4
-0.286
8
10
1.3
-0.222
9
10.9
1.2
-0.111
10
11.8
1
-0.222
11
12.7
0.9
-0.111
12
13.6
0.8
-0.111
X2, isocosto
X 2.Iso costo  2.86 X 1  9.4  1.4
Combinaciones
X1
TMSI = X2/X1
X2
X2, isocosto
1
3.6
5.9
2
6
4.5
5.5
6.4
7.3
8.2
4.3
3.2
2.6
2.1
1.8
-
1.778
1.100
0.667
0.556
0.333
3.1
2.8
2.5
2.3
2.0
1.8
7
9.1
1.5 -
0.333
1.5
Punto de
Equilibrio
9.5
1.4
10.0
10.9
11.8
12.7
13.6
1.3
1.2
1.0
0.9
0.8
0.282
0.222
0.111
0.222
0.111
0.111
1.4
1.3
1.0
0.8
0.5
0.3
3
4
5
8
9
10
11
12
-
Asignación óptima de dos insumos variables
Graficando los datos de la tabla:
18
Asignación óptima de dos insumos variables
Graficando los datos de la tabla:
19
c) Cálculo del factor de sustitución y tipo de rendimiento a escala que se
obtiene. En la gráfica de Isocosto se observan 5 puntos que se traslapan, es la
zona de equilibrio, es una zona donde los gastos se mantendrán estables. La
elasticidad o factor de sustitución se calculara para los puntos por arriba y por
abajo del equilibrio
Asignación óptima de dos insumos variables
Combinaciones
X1
TMSI = X2/X1
X2
X2, isocosto
1
3.6
5.9
2
6
4.5
5.5
6.4
7.3
8.2
4.3
3.2
2.6
2.1
1.8
-
1.778
1.100
0.667
0.556
0.333
3.1
2.8
2.5
2.3
2.0
1.8
7
9.1
1.5 -
0.333
1.5
Punto de
Equilibrio
9.5
1.4
10.0
10.9
11.8
12.7
13.6
1.3
1.2
1.0
0.9
0.8
0.282
0.222
0.111
0.222
0.111
0.111
1.4
1.3
1.0
0.8
0.5
0.3
3
4
5
8
9
10
11
12
-
Asignación óptima de dos insumos variables
•
Por arriba del equilibrio tenemos el punto 4, donde, X1 = 6.4 y X2 = 2.6,
en ese punto calcularemos el factor de sustitución:
21
eSI  X1X 2
 X1 X1 



X 2 X 2 


TMSI X1X 2
TMSI X1X 2
Combinaciones
X1
X2
TMSI = X2/X1
X2, isocosto
4
6.4
2.6
-0.667
2.263
5
7.3
2.1
-0.556
2.009
6
8.2
1.8
-0.333
1.754
Punto de
Equilibrio
9.1
1.5
-0.333
1.500
8
10
1.3
-0.222
1.246
9
10.9
1.2
-0.111
0.991
Asignación óptima de dos insumos variables
•
Por arriba del equilibrio tenemos el punto 4, donde, X1 = 6.4 y X2 = 2.6,
en ese punto calcularemos el factor de sustitución:
eSI  X1 X 2
Combinaciones
 X 1 X 1   8.2  7.3 7.3 

 



X X 2   1.8  2.1 2.1 
 2


TMSI X1 X 2
 .333  (.556)
 .556
TMSI X1 X 2
X1
TMSI = X2/X1
X2
6
7.3
8.2
7
9.1
2.1 1.8 1.5 -
Punto de
Equilibrio
9.5
1.4
5
8
9
10
10.0
10.9
11.8
1.3 1.2 1.0 -
22
X2, isocosto
0.556
0.333
2.0
1.8
0.333
1.5
0.282
0.222
0.111
0.222
1.4
1.3
1.0
0.8
Asignación óptima de dos insumos variables
•
Por abajo del equilibrio tenemos el punto 9, donde, X1 = 10.9 y X2 =
1.2, en ese punto calcularemos el factor de sustitución:
 11.8  10.9 10.9 



2.6 
 1.0  1.2
 81.75
 .222  (.111)
 .222
23
Combinaciones
X1
X2
TMSI = X2/X1
X2, isocosto
4
6.4
2.6
-0.667
2.263
6
8.2
7
9.1
1.8 1.5 -
Punto de
Equilibrio
9.5
1.4
8
9
10
10.0
10.9
11.8
1.3 1.2 1.0 -
0.333
1.8
0.333
1.5
0.282
0.222
0.111
0.222
1.4
1.3
1.0
0.8
Ejercicio
En la producción de chile se usa usan como nutrientes ácido fosfórico y
fosfonitrato, cuyas presentación son en paquete de 1.6 kg a un precio
de 0.86 USD y bulto de 50 kg de 16 USD respectivamente. Para una
producción de 40 ton/ha se conocen los datos de la curva de
isoproducto.
Fosfonitrato (kg) ácido fosfórico (kg)
93.0
12.0
85.0
13.0
75.0
14.0
70.0
17.0
71.0
18.0
75.0
20.0
85.0
21.0
93.0
22.0