InducciónelectroTema6 - IES Alfonso X el Sabio

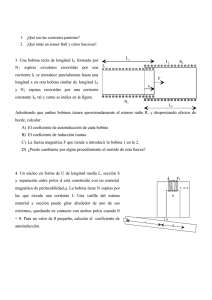
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
Desarrollo del tema.
1. Fenómenos de inducción electromagnética.
2. Fuerza electromotriz inducida . Ley de Faraday.
3. Sentido de la corriente inducida: ley de Lenz.
4. Corrientes de Foucault.
5. Corrientes autoinducidas. Coeficiente de autoinducción.
6. Energía almacenada en los fenómenos de autoinducción.
7. Inducción mutua.
1
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
1. Fenómenos de inducción electromagnética.
Por un circuito eléctrico, por donde no circula corriente, en forma de espira, se hace llagar
un campo magnético por la acción de un imán o un solenoide, colocados perpendicularmente al
circuito, en la línea que pasa por su centro, se observa que al mover el campo magnético, se
producirá una corriente inducida en el circuito, siendo observado este fenómeno gracias a un
galvanómetro colocado en él. Cuando lo aproximamos, el sentido de corriente es en sentido
contrario a las agujas del reloj,mientras que si lo alejamos, sera la circulación en sentido de las
agujas del reloj. Las experiencias efectuadas se pueden observar en la siguiente imagen:
El sentido de la corriente se opone siempre a la variación del campo magnético.
2. Fuerza electromotriz inducida . Ley de Faraday.
Si se produce una corriente eléctrica, como consecuencia del fenómeno anterior, es debido a
que existe una fuerza electromotriz inducida.
Para que se produzca una fuerza electromotriz inducida, es necesario que exista una
2
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
modificación del flujo magnético en el tiempo.
El circuito cerrado donde se origina la corriente recibe el nombre de inducido y el campo
magnético es el inductor. El inductor se puede originar por un imán permanente (magneto) un
electroimán (dinamo o alternador) . Por una bobina recorrida por una corriente alterna
(transformador) Por una bobina recorrida por una corriente continua que es interrumpida una gran
cantidad de veces por segundo ( carrete de Rühmkorff).
Un conductor AA´ , que se desplaza hacia la derecha en el
interior de un campo magnético B, dirigido hacia dentro del
plano, a la velocidad constante de v.
La fuerza producida será :
F = q . v . B , ya que v y B son dos
vectores perpendiculares entre si.
La energía necesaria para desplazar la carga será :
W = L.F = L.q.v.B
La f.e.m. generada será:
W
q
ξi =
= L .v .B
La variación de flujo magnético será :
d Φ = B .( - d S) = - B L v dt
d
, en el caso de que se produjera un
dt
número de espiras en el circuito, será :
ξi = -
L
d
dt
La fuerza electromotriz inducida es independiente de las
causas que provocan la variación del flujo y solamente de la
variación del flujo con el tiempo.
ξi = - N
3. Sentido de la corriente inducida: ley de Lenz.
Para determinar el sentido de la corriente inducida, se debe de aplicar la ley de Lenz. La ley
de Lenz indica que el sentido de las corrientes inducidas son tales que sus acciones
3
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
electromagnéticas tienden a oponerse a las causas que las producen.
Para determinar el sentido de la corriente inducida consiste en aplicar la regla de la mano
derecha: se dispone el dedo pulgar, el índice y el corazón o medio de la mano derecha de tal forma
que se construya un triedro. El pulgar indica el movimiento y el indice el campo, el corazón
indicará el sentido de la corriente.
Problema 1.- Un cuadro de 400 cm2 de sección y con 20 espiras, se encuentra situado en
la dirección normal a un campo magnético de 0.14 T y gira hasta situarse paralelamente al
campo, transcurriendo 0.25 s . ¿ Cuál es el valor de la fuerza electromotriz media inducida?
Datos .- S = 400 cm2 = 4 10-2 m2 ;;; N = 20 espiras ;;; B = 0.14 T ;;; t = 0.25 s
Determinar ξi
Resolución.- d Φ = B . d S . cos φ ; al calcular la integral Φ = -B . S . N
d
dt
=-
B. S
t
.N = -
−2
0,14 . 4 10
0,25
. 20 = - 0.448
ξi = 0.448 V
Problema 2.- Una bobina de 200 espiras y radio 0.10 m. se coloca perpendicularmente a
un campo magnético uniforme de 0.4 T . Hallar la f.e.m. inducida en la bobina si en 0.1 s:
a. Se duplica el campo magnético.
b. El campo se anula.
c. Se invierte el sentido del campo.
d. Se gira la bobina 90º en torno al eje paralelo al campo.
e. Se gira la bobina 90º en torno al eje perpendicular al campo.
Datos.- N = 200 espiras ;;; R = 0.10 m ;;; B = 0.4 T ;;; t = 0.1 s
4
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
Calcular : ξi en los diferentes casos.
S = π R2 = 3.14 . 0.12 = 0.0314 m2
Δ Φ = N (Φ2 – Φ1 )= 0.4 0.0314 . 200 = 2,513 Wb
ξi = -
2.513
= - 25,13 V.
0.1
b. El campo se anula .- Δ Φ = N (Φ2 – Φ1 )= - 0.4 0.0314 . 200 = - 2,513 Wb
ξi =
2.513
= 25,13 V.
0.1
c. Se invierte el sentido del campo
Δ Φ = N (Φ2 – Φ1 )= - 0.8 0.0314 . 200 = - 5.026 Wb
ξi =
5.026
= 50,26 V.
0.1
d. Se gira la bobina 90º en torno al eje paralelo
En este caso Δ Φ = N (Φ2 – Φ1 )= 0
ξi = = 0 V.
e. Se gira la bobina 90º en torno al eje perpendicular:
En este caso : Δ Φ = N (Φ2 – Φ1 )= - N B S cos 0 = - 2,513 Wb
ξi =
2.513
= 25,13 V.
0.1
4. Corrientes de Foucault.
Las corrientes inducidas se oponen siempre a las causas. Por esta razón, si un conductor
metálico macizo es atravesado por un campo magnético variable se originarán en su interior una
serie de corrientes en torbellino, denominándose corrientes de Foucault que reaccionan contra el
campo que las producen.
Las corrientes de Foucault son corrientes eléctricas, cerradas sobre si mismas, originadas por
inducción en los conductores macizos cuando varía el flujo magnético que los atraviesa.
Entre las experiencias donde se aprecian las corrientes de Foucault es en el fenómeno que
ocurre cuando un disco de cobre gira en el interior de un campo magnético, se detiene rápidamente
y lo hace muy lentamente si el disco está seccionado. Las corrientes de Foucault se opone al campo
5
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
magnético y por lo tanto termina por pararse.
Los inconvenientes que presentan la presencia de las corrientes de Foucault consiste en la pérdida
de energía por formación de dichas corrientes y en la aparición del calor por el efecto Joule
Como aplicaciones estriba en la utilización de los hornos de inducción en los que el material que
deseamos calentar se coloca formando un núcleo con un carrete recorrido por corrientes alternas,
consiguiéndose corrientes de Foucault muy intensas , que por efecto Joule consigue fundir al núcleo
metálico.
Para evitar las corrientes de Foucault en los núcleos de hierro de los electroimanes,
transformadores o alternadores, se procura que los núcleos no sean macizos, sino formados por
superposición de láminas de hierro aisladas entre si evitando o minimizando dichas corrientes.
Problema 3.- El conductor rectangular que aparece en la figura, de dimensiones 0.6 m y
0.3 m , posee una resistencia de 2,7 Ω y se encuentra situado en el interior del campo magnético
B = ( 5 – y ) i (S.I.) se desplaza en la dirección del eje OY y en
su sentido positivo. Sabiendo que inicialmente el lado izquierdo
del conductor rectangular coincide con el eje OZ calcular la
intensidad de corriente que circula en los casos siguientes:
a. Si se desplaza con velocidad constante de 1,5 m/s
b. Al cabo de 20 s. de comenzar su movimiento, partiendo del
reposo con la aceleración de 3 m/s2.
Datos .- a = 0.6 m ;; b = 0.3 m ;;; R = 2.7 Ω ;;; B = (5-y) i
Calcular I.
Resolución .y+0.3
y+0.3
El flujo a través de la superficie será : Φ = ∫y B . d S = ∫y (5-y) 0.6 . dy =
= 0.6 ( 5 y - y2/2)yy+0.3 = 0.873 – 0.18 y
Caso a .- y = v . t ;; Φ = 0.873 – 0.18 . 1.5 . t = 0.873 – 0.27 t
ξi = -
d
dt
= 0.27 V ;; I =
6

=
R
0.27
2.7
= 0.1 A
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
Caso b
y=
1
a t2 , ya que se mueve con m.r.u.a. Partiendo del reposo
2
Φ = 0.873 – 0.18 .
ξi = -
1
2
3. t2 = 0.873 - 0.27 t2
d
dt
= 0.54 . t (V) ; al cabo de t = 20 s, ξi = -
I =

=
R
10.8
2.7
d
dt
= 0.54 . 20 = 10.8 V
= 4 A
Problema 4.- Un disco metálico de 20 cm de radio gira con una velocidad de 1200 r.p.m.
alrededor de un eje axial con él . El disco se encuentra
en el interior de un campo magnético paralelo al eje de
rotación y un valor de 3 T . ¿ Qué diferencia de
potencial aparecerá entre el centro y el borde del disco?
Datos .- R = 20 cm = 0.2 m. ;; ω = 1200 rpm ;;;
B = 3 T. Calcular V entre el centro y el extremo.
Resolución.d Φ = B . d S ;;; dS =
ω = 2 . π. (1200/60 ) = 125.66 (rd/s)
dΦ=B.
ξi =
1
R2 . ω dt ; ξi = 2
R2 B 
2
=
1
dl . R =
2
dS =
d
; en valor absoluto ξi =
dt
1
R2 dφ =
2
1 2
R . ω dt
2
d
dt
0.22 .3 .125.66
= 7.5 V
2
Problema 5.- Sobre dos rieles rectilíneos de resistencia despreciable, dispuestos
horizontalmente a 2 m. de distancia uno del otro, se
colocan dos varillas metálicas conductoras que se
pueden mover paralelamente a sí mismas,
manteniéndose en todo momento perpendicular a
los rieles. Las dos varilla son idénticas , de 3 Ω de
resistencia y 2,5 Kg de masa cada una ,
encontrándose todo el sistema en el interior de un
campo magnético uniforme de 0.5 T de inducción .
7
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
Una varilla se aleja de la otra con una velocidad de 8 m/s . Determinar la velocidad constante
que alcanza la segunda varilla sabiendo que el coeficiente de rozamiento entre las varillas y los
rieles es de μ = 0.05
Datos .- Rieles a 2 m de distancia ;;; m = 2.5 Kg ;;; R = 3 Ω ;;; B = 0.5 T
Solución :
d Φ = B . d S = B L (8 – v) d t
d
= B . L ( 8 – v) ;;; I =
dt
La fuerza que actúa sobre la varilla será :
ξi =
2
F = I .L . B =

=
R
B. L 8−v 
R
2
B . L 8−v
= μ N = μ .m . g
R
B 2 . L2 v
B 2 . L2 8
=
- μ .m . g ; Sustituyendo valores y despejando v, resulta que
R
R
v = 0.65 (m/s)
Problema 6.- Una varilla conductora AG de 0.5 m. de longitud, se apoya sobre dos raíles
CA y DG. El conjunto se encuentra situado en un campo magnético uniforme de 0.5 T,
perpendicular al plano de la figura y dirigido hacia dentro. En estas condiciones calcular:
a. La f.e.m. inducida en la varilla cuando se desplaza hacia
la derecha con una velocidad de 4 m/s.
b. La fuerza que hay que aplicar a la varilla para que siga su
B
movimiento si la resistencia del circuito es constante e igual
a 0.2 Ω .
c. La cantidad de calor desprendido por unidad de tiempo en
el circuito.
Datos .- L = 0.5 m. ;;; B = 0.5 T ;;; ξi ?? ;;; v = 4 m/s ;;; F ?? ;;; R = 0.2 Ω ;;; Q/t ??
Resolución : a. ξi = -
d
= L . v . B = 0.5 . 4 . 0.5 = 1 V
dt
b. I= I =

=
R
1
= 5 A
0.2
F = I. L . B sen α = 5 . 0.5 . 0.5 sen 90 = 1.25 N
c La potencia P = I . ξi = 5 . 1 = 5 W
8
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
Q
t
.
= 0.24 P = 0.24 . 5 = 1.2 cal/s
Problema 7.- Un alambre conductor de sección cuadrada de longitud 0.5 m, masa 20 g y
resistencia eléctrica 0.5 Ω, desliza sin rozamiento, bajando a lo largo de dos rieles paralelos de
resistencia eléctrica despreciable, inclinados un ángulo de 35º y unidos en el extremo inferior
por otro conductor como se indica en la figura, de resistencia también nula. El conjunto se sitúa
en un campo magnético vertical y ascendente de inducción 0.8 T. Determinar en estas
circunstancias el valor de la velocidad constante con que desciende dicho alambre.
Esquema :
Fm. cosα
m g sen α
Datos .- L = 0.5 m ;;; m = 20 10-3 Kg ;;; R = 0.5 Ω ;;; α = 35º ;;; B = 0.8 T ;;; v ??
d
= L . v . B cos α
dt
Resolución.- ξi = -
I= I =

=
R
L . v . B .cos 
R
2
FM = I. L . B =
2
L . v . B . cos 
R
Del equilibrio de fuerzas ( en el esquema) :
L2 . v . B2 . cos 2 
= m . g sen α
R
Fm . cos α = m. g . sen α
Por lo tanto
v =
−3
R. m . g . sen
L2 . B2 .cos 2 
=
0.5. 20 10 . 9.8. sen35
= 0.52 m/s
2
2
2
0.5 . 0.8 . cos 35
Problema 8.-Una bobina plana MNPQ de la figura consta de 30 espiras y se encuentra
situada en el plano XOY , sometida a una inducción de 5000 Gauss perpendicular al plano y
entrante. Calcular el flujo, expresado en Wb que atraviesa cada espira de la bobina.
Cuando se invierte el sentido de inducción, en el tiempo, de 0.01 s , ¿cuál será la f.e.m.
9
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
inducida? . ¿ en qué condiciones se originará una fuerza de 1 N sobre le conductor MN de la
bobina?.
Datos .- N = 30 ;;; B = 5000 G = 0.5 T ;;; Φ ?? ;;; invierte el sentido t = 0.01 s;;; ξi ??
F = 1 N ;; condiciones.
Resolución.- d Φ = B . d S ; Φ = B X. Y . cos β = 0.5 . 0.3 . 0.15 . 1 = 0.0225 Wb
ξi = - N
d
= - 30
dt
−−
= - 30
t
F = I .L . B. N . sen β = I . 0.3 . 0.5 30 . 1 = 1 ; I =
−2. 0.0225
= 135 V
0.01
F
=
L. B. N
1
= 0.22 A
0.3. 0.5 .30
5. Corrientes autoinducidas. Coeficiente de autoinducción.
Cuando un solenoide se conecta a un circuito de corriente continua, unido a un
potenciómetro, al modificar la intensidad se produce por variación del campo magnético una serie
de corrientes inducidas. Una corriente variable provoca en un circuito corrientes inducidas.
Este fenómeno se denomina autoinducción y la fuerza
electromotriz producida es la f.e.m. de autoinducción.
La autoinducción es el fenómeno mediante el cual una
corriente de intensidad variable, que es la corriente
principal, crea en su mismo circuito otra corriente por
inducción que es la corriente autoinducida o
extracorriente
Para calcular su valor, se debe de tener en cuenta que :
dΦ= L dI
L es la constante de proporcionalidad, que recibe el
nombre de coeficiente de autoinducción.
10
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
Ξi = -
d
= -L
dt
dI
dt
L es el coeficiente de autoinducción , que se mide en Henrios . (H) . Se define como Henrio
a la autoinducción de un circuito en el que una corriente cuya intensidad varía 1 A en cada segundo
produce por autoinducción la f.e.m. de 1 voltio.
En el caso de una bobina :
N.Φ=L.I
Para calcular el coeficiente de autoinducción de un solenoide, se debe tener en cuenta :
B = μ0
ξi = - N
N.I
L
; d Φ = B . d S = μ0
d
=dt
o . S . N 2
L
N . dI . S
L
dI
;; por comparación L =
dt
o . S . N 2
L
Para determinar el sentido de la corriente, hay que tener en cuenta la ley de Lenz, es decir, se
va a oponer a la modificación del flujo magnético, apareciendo las extracorrientes como son las de
apertura y cierre de los circuitos. Se vuelven más intensas si dentro del solenoide se coloca un
núcleo de hierro.
Las extracorrientes de ruptura o de apertura son mayores que las de cierre, puesto que en
este último caso la intensidad de inducción se suma a la principal.
6. Energía almacenada en los fenómenos de autoinducción.
De la mima forma que un condensador almacena una energía, cuyo valor será :
11
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
Ep =
1
C V2
2
En el caso de una autoinducción o solenoide, EP =
1
. L . I2
2
Esta energía almacenada puede convertirse en energía eléctrica o en calor, en el caso
de que el receptor sea una resistencia.
Problema 9.-Una corriente continua de 2.5 A alimenta una bobina de 500 espiras y
produce un flujo magnético de 3.6 10-4 Wb Calcular el coeficiente de autoinducción de la bobina
sabiendo que el flujo se anula después de 0.06 segundos.
Calcular la energía que se almacena .
Datos.- I = 2.5 A ;;; N = 500 ;;; Φ = 3.6 10-4 Wb;;; t = 0.06 s
Resolución .- N . Φ = L . I ;;
E=
L =
N .
I
=
500. 3.6 10−4
= 72 mH
2.5
1
. L . I2 = 0.225 J.
2
7. Inducción mutua.
Cuando existen dos bobinas próximas (primario y secundario) , la corriente de la bobina
primera origina un flujo magnético que afecta también a la segunda bobina ΦP. Cuando se produce
una variación de corriente en el primario, se produce una variación de flujo en el secundario y da
lugar a una ξ´ inducida que se opone a la variación de flujo y crea una corriente I S en el secundario,
induciendo un flujo y una corriente en el primario. En este caso existen induciones mútuas entre los
dos circuito. La fuerza ξ´recibe el nombre de contraelectromotriz
La inducción mutua se puede considerar como :
N Φ S = M IP
12
CIDEAD . 2º BACHILLERATO. ELECTROTECNIA
Tema 6.- La Inducción Electromagnética
ξS = - N S
MPS =
Ns . s
Ip
d s
dt
=
= -M
Np.  p
Is
dIp
.
dt
= μ0
Np. Ip . Sp
NS .
Lp
1
Ip
=
Np. Ns . Sp .  o
Lp
Problema 10.- Dos bobinas, la primera de 100 espiras y la segunda de 500, se sitúan una
frente a otra . Por la primera de ellas circula una corriente de 4 A y se produce un flujo de 4 10 -4
Wb en la primera y 2 10-4 Wb en la segunda . Calcular el coeficiente de autoindución de la
primera bobina y el coeficiente de inductancia mutua en la segunda.
Datos.- NP = 100 ;;; NS = 500 ;;; IP = 4 A ;;; ΦP = 4 10-4 Wb ;;; ΦS = 2 10-4 Wb
Calcular .- L ;;; M
LP =
MPS =
Np.  p
=
Ip
100 . 4 10−4
= 10 mH
4
Ns . s
=
Ip
500. 2 10−4
= 25 mH
4
13