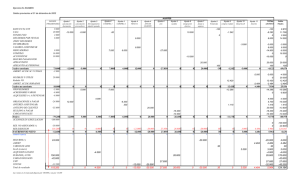
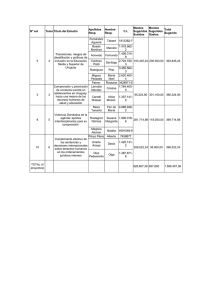
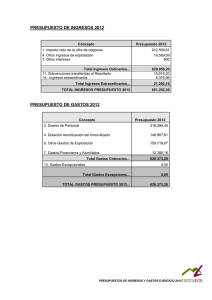
λ ω λ = µ µ κ κ κ δ µ δ δ β α ω ω ζ ω ω - prof.usb.ve.
Anuncio

MC-2415 Vibraciones Mecánicas Universidad Simón Bolívar Respuesta Libre (no amortiguada) I. Introducción Ecuación de movimiento: M&x&(t ) + Kx (t ) = 0 Solución propuesta: x (t ) = φe iλ t Problema de autovalores en la forma generalizada: [K − λ M ] φ = 0 II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal (armónica) 2 λ j =ω j N autovalores reales positivos Frecuencias propias j = 1L N Φ = [φ1 φ 2 L φ N ] Matriz modal Cambio de variable (coord. físicas a coord. modales) x (t ) = Φp (t ) N autovectores reales Modos propios IV. Medición / diagnóstico V. Bibliografía Euro Casanova, 2006 && (t ) + Kp (t ) = 0 Mp Ecuación de movimiento en coord. modales: ⎤ ⎡ µ1 ⎥ ⎢ T M = Φ MΦ = ⎢ O ⎥ masa modal ⎢⎣ µ N ⎥⎦ ⎤ ⎡κ1 ⎥ ⎢ T K = Φ KΦ = ⎢ O ⎥ rigidez modal ⎢⎣ κ N ⎥⎦ MC-2415 Vibraciones Mecánicas Universidad Simón Bolívar I. Introducción II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal Respuesta Libre: amortiguación de proporcional (i) ⎤ ⎡δ1 ⎥ amortiguación ⎢ T C = α M + β K ⇔ C = Φ CΦ = ⎢ O ⎥ modal ⎢⎣ δ N ⎥⎦ Ecuación de movimiento en coord. modales: && (t ) + C p& (t ) + Kp (t ) = 0 Mp N ecuaciones de la forma: µ j &p& j + δ j p& j +κ jp j = 0 Definiendo: ωj = κj ζj = µj IV. Medición / diagnóstico p j (t ) = e −ζ jω j t [A 1j Euro Casanova, 2006 p j (0) p& j ( 0 ) + ζ jω j p j ( 0 ) ωdj 2 µ jω j p& j ( 0 ) j = 1L N ωdj = ω j 1 − ζ j2 Cos (ω dj t ) + A2 j Sen(ω dj t ) A1 j = p j ( 0 ) A2 j = δj &p& j + 2ζ jω j p& j + ω 2j p j = 0 N ecuaciones de la forma: V. Bibliografía 52 ] j = 1L N j = 1L N Condiciones iniciales en las coordenadas modales 53 MC-2415 Vibraciones Mecánicas Universidad Simón Bolívar Respuesta Libre: amortiguación proporcional (ii) I. Introducción II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal IV. Medición / diagnóstico V. Bibliografía Condiciones iniciales en las coordenadas modales en función de las cond. iniciales en las coordenadas físicas A1 j = p j ( 0 ) = A2 j = Solución: N 1 µj p ( 0 ) = M −1ΦT Mx ( 0 ) p( 0 ) j = 1 µj φTj Mx ( 0 ) p& ( 0 ) = M −1ΦT Mx& ( 0 ) p& ( 0 ) j = 1 µj φTj Mx& ( 0 ) φTj Mx ( 0 ) p& j ( 0 ) + ζ jω j p j ( 0 ) ω dj N = x (t ) = Φp (t ) = ∑ φ j p j = ∑ φ j e j =1 N x (t ) = ∑ φ j e j =1 −ζ j ω j t 1 µj φTj M ⎛⎜ ω1dj x& ( 0 ) + ⎝ −ζ j ω j t ζj 1−ζ 2j [A Cos(ω t ) + A 1j j =1 dj ⎡1 T ⎛ 1 T 1 ⎢ µ j φ j Mx ( 0)Cos(ωdj t ) + µ j φ j M⎜⎝ ωdj x& ( 0) + ⎣ La solución es una combinación lineal de los modos x ( 0 ) ⎞⎟ ⎠ La solución decae en el tiempo 2j ζj 1−ζ 2j ] Sin(ωdj t ) ⎤ x ( 0 ) ⎞⎟ Sin(ωdj t )⎥ ⎠ ⎦ La solución es armónica Euro Casanova, 2006 54 MC-2415 Vibraciones Mecánicas Universidad Simón Bolívar Respuesta Libre: amortiguación proporcional (iii) I. Introducción Modos propios de vibración II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal Modo 1 (409Hz) Modo 4 (572Hz) IV. Medición / diagnóstico V. Bibliografía Modo 9 (1217Hz) Euro Casanova, 2006 Modo 11 (1241Hz) Modo 15 (1706Hz) 55 MC-2415 Vibraciones Mecánicas Universidad Simón Bolívar Respuesta Libre: amortiguación general I. Introducción Ecuación de movimiento: M&x&(t ) + Cx& (t ) + Kx (t ) = 0 Solución propuesta: x (t ) = φe λ t Problema de autovalores en la forma cuadrática: [Mλ II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal ⎡ ⎡− M −1C − M −1K ⎤ ⎤ ⎧λφ ⎫ ⎧0⎫ − I λ ⎢⎢ ⎥⎨ ⎬ = ⎨ ⎬ ⎥ I 0 ⎦ ⎣⎢ ⎣ ⎦⎥ ⎩ φ ⎭ ⎩0⎭ 2N autovalores complejos conjugados (parte real < 0) λ j = −a j ± b j i φ j = φRj ± φI j i Solución: N x (t ) = ∑ φ j e (− a j ±b j i )t j =1 Euro Casanova, 2006 ] + Cλ + K φ = 0 Problema de autovalores en la forma estándar: 2N autovectores complejos conjugados IV. Medición / diagnóstico V. Bibliografía 2 N = ∑ φ je −a j t j IV. Medición / diagnóstico V. Bibliografía 56 Respuesta Libre: Viga simplemente apoyada (i) Viga ( ρ, E, I, A, L) h x1 x3 x2 k1 k2 m c1 k2 m m c2 x1 ⎧ x1 ⎫ ⎪ ⎪ x ( t ) = ⎨ x2 ⎬ ⎪x ⎪ ⎩ 3⎭ k1 c2 x2 c1 x3 Frecuencias propias (sin amortiguación): ⎧ω1 ⎫ ⎧9.86659 ⎫ ⎪ EI ⎪ ⎪ ⎪ ⎨ω 2 ⎬ = ⎨39.1918 ⎬ 4 ⎪ω ⎪ ⎪83.2128 ⎪ ρ A L ⎭ ⎩ 3⎭ ⎩ φ2 M= M = ρ AL b h3 12 ⎡1 0 0 ⎤ 0 1 0⎥⎥ 4 ⎢ ⎣⎢0 0 1⎥⎦ ρ AL ⎢ ⎡ 23 − 22 9 ⎤ 192 E I ⎢ − 22 32 − 22⎥⎥ K= 7 L3 ⎢ ⎢⎣ 9 − 22 23 ⎥⎦ 2 ⎧ω1ex ⎫ ⎧ π ⎫ ⎧ 9.8696 ⎫ ⎪ ⎪ ⎪ 2⎪ EI ⎪ ⎪ EI ω 4 π = = ⎨ 2 ex ⎬ ⎨ ⎬ ⎨39.4784 ⎬ 4 4 A L ρ ⎪ω ⎪ ⎪9π 2 ⎪ ⎪83.8264 ⎪ ρ A L ⎩ 3ex ⎭ ⎩ ⎩ ⎭ ⎭ φ3 Φ = [φ1 φ 2 φ1 A = bh I= b L Modos propios: Euro Casanova, 2006 ] Sin(b j t ) MC-2415 Vibraciones Mecánicas II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal 2j La solución decae en el tiempo ! x (t = 0 ) = x 0 x& (t =0 ) = v 0 Universidad Simón Bolívar I. Introducción [A Cos(b t ) + A 1j j =1 2N constantes que dependen de las condiciones iniciales: j = 1L N ⎡ 1 φ 3 ] = ⎢⎢ 2 ⎢⎣ 1 −1 0 1 −1⎤ 2 ⎥⎥ − 1 ⎥⎦ 57 MC-2415 Vibraciones Mecánicas Universidad Simón Bolívar Respuesta Libre: Viga simplemente apoyada (ii) I. Introducción II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal M = Φ MΦ = T ⎡2 0 0⎤ 0 1 0⎥⎥ 2 ⎢ ⎢⎣0 0 2⎥⎦ E = 200 GPa Datos: ⎡ 97.35 EI ⎢ K = Φ KΦ = 3 ⎢ 0 L ⎢⎣ 0 ρ AL ⎢ −6 I = 8.3 × 10 m ρ = 7800 kg m 4 0 L = 10 m b = h = 0.1m M = 780kg ζ 1 = ζ 2 = ζ 3 = 3% 0 0.128 0 0 768 A = 0.01 m 2 3 ⎡2 0 0⎤ ⎡ 0.016 ⎢ ⎥ 7⎢ M = 390 ⎢0 1 0⎥[kg ] K = 10 ⎢ 0 ⎢⎣0 0 2⎥⎦ ⎢⎣ 0 ⎤ 0 ⎥⎥ 6924.4⎥⎦ 0 T 0 ⎤ ⎡ 0.09 ⎥ N 0 ⎥[ m ] C = ⎢⎢ 0 ⎢⎣ 0 1.15⎥⎦ 0 ⎤ 0 ⎥⎥[N s m ] 0.73⎥⎦ 0 0.34 0 ω1 = 14.42 r s ω 2 = 57.29 r s ω3 = 121.63 r s ω d 1 = 14.41 r s ω d 2 = 57.26 r s ω d 3 = 121.58 r s ω1 = 2.29 Hz ω 2 = 9.09 Hz ω3 = 19.32 Hz ω d 1 = 2.29 Hz ω d 2 = 9.11Hz ω d 3 = 19.35 Hz IV. Medición / diagnóstico N x (t ) = ∑ φ j e V. Bibliografía −ζ j ω j t A1 j = p j ( 0 ) = A2 j = [A Cos(ω t ) + A 1j j =1 1 µj dj 2j ] Sin(ωdj t ) φTj Mx ( 0 ) p& j ( 0 ) + ζ jω j p j ( 0 ) ωdj = 1 µj φTj M ⎛⎜ ω1dj x& ( 0 ) + ⎝ ζj 1−ζ 2j x ( 0 ) ⎞⎟ ⎠ Euro Casanova, 2006 58 MC-2415 Vibraciones Mecánicas Universidad Simón Bolívar Respuesta Libre: Viga simplemente apoyada (iii) I. Introducción II. Sistema de 1-GDL III. Sistemas de N-GDL Descripción Ec. de movimiento Cálculo de M y K Resp. libre No amortiguada Amort. Rayleigh Amort. general Ejemplo Resp. forzada Reducción modal IV. Medición / diagnóstico Cond. iniciales T x (0) = 0 2 0 x& ( 0 ) = 0 x2 1 A11 = A21 = 0.015 1 2 A12 = 0 A22 = 0 A13 = A23 = 0.015 1 2 1 2 3 4 5 t 1 2 3 4 5 -0.5 Cond. Iniciales (similar a modo 1) x (0) = 1 2 1 1 T 2 x& ( 0 ) = 0 x2 V. Bibliografía A11 = 0.6 A21 = 0 A12 = 0.1 A22 = 0.02 A13 = 0 Euro Casanova, 2006 0.5 A23 = 0.003 1 0.75 0.5 0.25 -0.25 -0.5 -0.75 t 59