Unidad 3. Electricidad

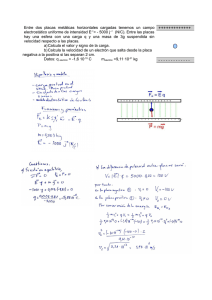
Unidad 3. Electricidad
Cuestiones de PAU.
Nota: Debido a que la mayor parte de las cuestiones de PAU de esta Unidad
mezclan los conceptos de carga, campo y potencial, se presentan todas ellas bajo un
mismo apartado.
1. (Andalucía 2010) a) Explique la relación entre campo y potencial
electrostáticos. (R: Teoría)
b) Una partícula cargada se mueve espontáneamente hacia puntos en los que el
potencial electrostático es mayor. Razone si, de este comportamiento, puede
deducirse el signo de la carga. (R: Sí, la carga debe ser negativa)
2. (Andalucía 2009) a) Enuncie la ley de Coulomb y aplique el principio de
superposición para determinar la fuerza que actúa sobre una carga en presencia de
otras dos.(R: teoría)
b) Dos cargas +q1 y –q2 están situadas en dos puntos de un plano. Explique, con
ayuda de una gráfica, en qué posición habría que colocar una tercera carga +q3
para que estuviera en equilibrio. (R: En el punto en el que se anule la fuerza
resultante. Dependerá del valor relativo de las cargas, pero estará en la línea que
une +q1 y –q2 , exceptuando el segmento ubicado entre ambas pues allí nunca se
anulará)
3. (Andalucía 2008) Una bolita de plástico de 2 g se encuentra
suspendida de un hilo de 20 cm de longitud y, al aplicar un campo
eléctrico uniforme y horizontal de 1 000 N C-1, el hilo forma un
ángulo de 15° con la vertical.
a) Dibuje en un esquema el campo eléctrico y todas las fuerzas que
actúan sobre la esfera y determine su carga eléctrica. (R: Ver
imagen, 5.25 10-6 C)
b) Explique cómo cambia la energía potencial de la esfera al aplicar
el campo eléctrico. (R: Por conservación de la energía mecánica,
ésta permanece constante y por tanto la energía potencial eléctrica
perdida es igual a la potencial gravitatoria ganada)
Datos: g = 10 m s-2.
4.(Andalucía 2007) Un electrón, con una velocidad de 6 106 m s-1, penetra en
un campo eléctrico uniforme y su velocidad se anula a una distancia de 20 cm
desde su entrada en la región del campo.
a) Razone cuáles son la dirección y el sentido del campo eléctrico. (R: El campo
eléctrico tendrá la misma dirección que la velocidad del electrón, ya que lo frena)
b) Calcule su módulo. (R: E = 511.875 N C-1)
Datos: e = 1,6 10-19 C; me = 9,1 10-31 kg.
5. (Andalucía 2007) a) Explique las analogías y las diferencias entre el campo
eléctrico creado por una carga puntual y el campo gravitatorio creado por una masa
puntual, en relación con su origen, intensidad relativa, dirección y sentido. (R:
Teoría)
b) ¿Puede anularse el campo gravitatorio y/o el campo eléctrico en un punto del
segmento que une a dos partículas cargadas? Razone la respuesta. (R: En el caso
gravitatorio sí. En el caso electrostático depende del signo de las cargas: si son
iguales sí, mientras que si son distintas nunca)
6. (Andalucía 2006) a) Una partícula con carga 2·10-6 C se encuentra en reposo
en el punto (0,0). Se aplica un campo eléctrico uniforme de 500 N C-1 en el sentido
positivo del eje OY.
a) Describa el movimiento seguido por la partícula y la transformación de energía
que tiene lugar a lo largo del mismo. (R: El movimiento resultante será un MRUA en
el sentido positivo del eje y. Irá perdiendo energía potencial electrostática y
ganando energía cinética en el mismo valor, puesto que la energía se conserva)
b) Calcule la diferencia de potencial entre los puntos (0,0) y (0,2) m y el trabajo
realizado para desplazar la partícula entre dichos puntos. (R: ΔV = 1000 V;
W = 2·10-3 J)
7. (Aragón 2010) a) Explica el concepto de campo electrostático creado por una o
varias cargas eléctricas puntuales. (R: Teoría)
b) Tres cargas eléctricas puntuales, de valores q1 = 10 nC ,
q2 = 10 nC y q3 = -20 nC, están fijas en el espacio
separadas una distancia d = 10 cm del origen de
coordenadas y distribuidas como se indica en la figura. b1.
Determina el módulo, la dirección y el sentido del campo
electrostático E en el punto A(d,0) b2. Calcula el trabajo
que tenemos que realizar para desplazar una carga q’ = 1
nC desde el punto A(d,0) hasta el origen de coordenadas
O(0,0) (R: E = 1845 N·C-1 dirección eje x sentido positivo;
W = -1.8 10-9 J)
8. (Aragón 2009) a) Enuncia y comenta la Ley de Coulomb. A partir de ella
determina el trabajo necesario para traer una carga q’, en presencia de otra carga
q, desde el infinito hasta un punto genérico. (R: Teoría)
b) Dos partículas cargadas, q1 = q2 = 2 μC están
situadas, como indica la figura, en los puntos (0,0) y
(4,0). Determina el valor del potencial electrostático en
el punto (2,2). ¿Qué trabajo tendríamos que realizar
para trasladar, desde el punto A (2,2) al punto B (2,0),
una carga q3 = 4 μC? (R: VA = 12728 V; VB=18000 V;
W = 0.021 J)
9. (Aragón 2008) a) ¿Qué potencial electrostático crea una carga puntual q’ en
cualquier punto de su entorno?. Explica el significado físico del potencial.
(R: Teoría)
b) Dos partículas puntuales de cargas q1 = 30 μC y q2 = -20 μC están situadas
respectivamente en los puntos de coordenadas (-a, 0) y (a,0) con a = 10 cm.
Determina el campo electrostático
(módulo, dir. y sentido) en el punto (0,0)
(R: E = 4.5·107 N·C-1)
c) ¿Qué trabajo tendremos que realizar para, en presencia de las cargas citadas,
trasladar una carga puntual q = 0,2 μC desde el punto (0,0) al punto (a,a)?
(R: W = 0.298 J)
10. (Aragón 2007) a) Explica el concepto de potencial eléctrico. ¿Tiene sentido
este concepto si la fuerza electrostática no fuese conservativa?
(R: Teoría; no tiene sentido)
b) Dos cargas eléctricas puntuales de valor Q1 = -9
μC y Q2 = +16 μC están fijas en el espacio ocupando
los vértices de un triángulo rectángulo (ver figura).
Calcula el potencial eléctrico en los puntos A y B.
¿Qué trabajo realizará el campo eléctrico para llevar
una carga puntual de 2 μC desde el punto B hasta el
punto A?
(R: VA = 90000 V; VB = 252000 V; W = 0.324 J)
11. (Aragón 2007) Una placa horizontal cargada
negativamente crea en sus proximidades un campo
eléctrico uniforme orientado tal y como se indica en la
figura, con intensidad E = 103 V/m. Un protón, p, penetra
en esta región, con velocidad v0 = 105 m/s perpendicular
a las líneas de E y a una distancia d = 0,2 m de la placa,
de forma que describe una trayectoria como la indicada en
la figura
a) Durante esta trayectoria, ¿se conserva la energía mecánica de p? Razona tu
contestación. Calcula la energía cinética de p cuando choca con la placa. Supón que
la única fuerza que actúa sobre p es la eléctrica. (R: Se conserva; Ec = 4.05·10-17 J)
b) Calcula la distancia L al punto de impacto. (R: L = 0.206 m)
c) Comprueba que, si el movimiento se realiza en las proximidades de la superficie
terrestre, el peso del protón es despreciable frente a la fuerza eléctrica que actúa
sobre él.
(R: Hallando la relación entre las fuerzas, la electrostática es 1010 veces mayor)
12. (Aragón 2008) a) Explica el concepto de energía potencial
eléctrica. ¿Qué energía potencial eléctrica tiene una partícula con
carga q1 situada a una distancia r de otra partícula con carga q2?
(R: Teoría)
b) La esfera de la figura, de radio R = 5 cm, está fija en el espacio
y tiene una carga uniformemente distribuida Q = 10 μC. Se libera
con velocidad inicial nula una partícula con carga q = -1 μC y masa
m = 10 g a una distancia d = 3R del centro de la esfera. Calcula la
velocidad de la partícula cuando choca con la superficie de la
esfera. (R: v = 15.49 m·s-1)
13. (Cantabria 2010) Una carga puntual de 16 nC se sitúa fija en el punto (0,3)
de un sistema de referencia (todas las distancias se dan en metros). Otra carga de
-9 nC se sitúa fija en el punto (4,0).
a) Dibujar y calcular el vector campo eléctrico creado por este sistema de cargas
en el punto (4,3). (R: E = 9 i – 9 j N·C-1)
b) Hallar el potencial eléctrico en el punto (4,3) (R: 9 V)
c) Hallar la fuerza que sufriría una partícula de carga q = 10 nC situada en el punto
(4,3). (R: F = 9·10-8 i – 9·10-8 j N)
Datos: ( k = 9’00 109 N m2C‐2, 1 nC=10‐9 C) Considera el origen de potenciales en el
infinito
14. (Cantabria 2009) Dos cargas se encuentran en el
vacío, fijas en la posición indicada en la figura. El campo
eléctrico total que crean las dos cargas en el punto A es
9
1.08 N/C y el valor de q1 es 5 nC.
a) Calcula el valor de q2 (R: q2 = 21 nC)
b) Calcula el valor y la dirección de la fuerza que la carga q1
ejerce sobre q2 (R: F = -3·10-8 i + 9·10-8 j N)
c) Calcula el valor y la dirección de la fuerza que la carga q2
ejerce sobre q1 (R: F = 3·10-8 i - 9·10-8 j) N
d) Calcula la fuerza total sobre una carga de 10 nC situada
en el punto A. (R: F = 9·10-8 i + 1.08·10-8 j N)
15. (Cantabria 2008) Una carga puntual de 2 nC se sitúa fija en el punto (2, 2)
de un sistema de referencia (todas las distancias se dan en metros). Otra carga de
-3 nC se sitúa fija en el punto (0, 3).
a) Dibujar y calcular el vector campo eléctrico creado por este sistema de cargas
en el punto (0, 0). (R: E = -1.59 i + 1.41 j N/C)
b) Hallar el potencial eléctrico en el punto (0, 0). (R: V = -2.64 V)
c) Hallar la fuerza que sufriría una partícula de carga q = 10 nC situada
en el punto (0, 0). (R: F = -1.59·10-8 i + 1.41·10-8 j N)
16. (Cantabria 2008) Las cargas libres de una esfera de cobre, aislada en el
espacio vacío, se encuentran en reposo. El radio de la esfera es 10 cm y la carga de
la esfera es 1 μC.
a) Dibujar las líneas de campo eléctrico en el exterior de la esfera. (R: Teoría)
b) Calcular el campo eléctrico en el exterior de la esfera en función de la distancia,
d, a la superficie de la misma. Indicar las unidades de d en la fórmula obtenida
(R:
·
.
/
con d expresada en metros)
17. (Cantabria 2007) En tres vértices de un cuadrado de 1 m de lado se disponen
cargas de +10 mC. Calcula:
a) El vector intensidad de campo eléctrico en el cuarto vértice.
(R: E = 121819.8 i – 121819.8 j N/C)
b) El potencial eléctrico en dicho vértice. (R: V = 243639.6 V )
c) El trabajo necesario para llevar una carga de +5 mC desde el centro del
cuadrado hasta el cuarto vértice. (R: W = -0.69 J)
18. (Cantabria 2007) a) Enuncia y comenta la expresión de la fuerza de Coulomb
entre cargas eléctricas en reposo. (R: Teoría)
En un relámpago típico, la diferencia de potencial entre la nube y la tierra es 109 V
y la cantidad de carga transferida vale 30 C. Suponemos que el campo eléctrico
entre la nube y la tierra es uniforme y perpendicular a la tierra, y que la nube se
encuentra a 500 m sobre el suelo.
b) ¿Cuánta energía se libera? (R: E = 3 1010 J)
c) Calcula el valor del campo eléctrico. (R: E = 2 1010 V/m)
19. (Castilla La Mancha 2009) En dos de los vértices
de un triángulo equilátero de 3 m de lado se sitúan dos
cargas puntuales iguales, q1=q2= +3 μC como se indica
en la figura. Determina:
a) El campo electrostático en el vértice libre S
(R: E = 3000 N C-1)
b) El potencial electrostático en el vértice libre S y en el
punto T situado en el punto medio entre las cargas.
(R: Vs = 18000 V; VT = 36000 V)
c) El trabajo realizado por las fuerzas eléctricas cuando
desplazamos una carga puntual de −2μC desde punto S
hasta el punto T. (R: WST = 0.036 J)
( k = 9’00 109 N m2C‐2, 1 μC=10‐6 C )
20. (Castilla La Mancha 2008) Dos pequeñas esferas idénticas
de masa m = 40 g y carga q están suspendidas de un punto
común mediante dos cuerdas de longitud L = 20 cm, como indica
la figura. Si por efecto de la repulsión eléctrica las cuerdas forman
un ángulo θ = 15° con la vertical, determina:
a) El valor de la tensión de las cuerdas. (R: T = 0.406 N)
b) El módulo de la fuerza eléctrica que se ejercen las esferas. (R:
F = 0.105 N)
c) El valor de la carga q. (R: Q = 3.55·10-7 N)
Datos: k = 9,00 109 N m2 C-2; g0 = 9,81 m s-2.
21. (Castilla La Mancha 2007) Explica qué son las líneas de campo eléctrico y
las superficies equipotenciales. Razona si es posible que se puedan cortar dos líneas
de campo. Dibuja esquemáticamente las líneas de campo y las superficies
equipotenciales correspondientes a una carga puntual positiva. (R: Teoría. No
pueden cortarse)
22. (Castilla La Mancha 2007) Una carga puntual de 10 nC está situada en el
punto A(0, 3) de un sistema cartesiano. Otra carga puntual de -10 nC está situada
en B(0, -3). Las coordenadas están expresadas en metros. Calcula:
a) El vector intensidad de campo eléctrico en el punto C situado en (4, 0).
(R: -4.32 j N C-1 )
b) El valor del potencial electrostático en un punto C. (R: V = 0)
c) El trabajo que realiza el campo de fuerzas eléctricas cuando una carga puntual
de 2 nC se desplaza desde el punto C hasta un punto D situado en (0, 2).
(R: W = -1.44 10-7 J)
Datos: K = 9,00 109 N m2 C-2; 1 nC = 10-9 C.
23. (Castilla La Mancha 2007) Dos esferas conductoras aisladas, de 12 y 20 cm
de radio, se encuentran en una zona del espacio vacío y con sus centros separados
10 m, están cargadas cada una con una carga de 25 10-9 C. Las cargas se ponen
en contacto mediante un hilo conductor y se alcanza una situación de equilibrio.
Calcula:
a) ¿Qué fuerza se ejercen entre sí ambas esferas cuando están aisladas?
(R: F = 5.625 10-8 N)
b) El potencial al que se encuentra cada una de las esferas antes de ponerlas en
contacto. (R: V1 = 1875 V; V2 = 1125 V)
c) La carga y el potencial de cada esfera cuando, una vez conectadas, se establece
el equilibrio. (R: V1 = V2 = 1406.25 V)
Dato: K = 9,00 109 N m2 C-2.
24. (Castilla La Mancha 2004) Si una partícula de carga positiva se mueve en la
dirección y sentido de un campo eléctrico uniforme, ¿aumentará, disminuirá o
permanecerá constante su energía potencial?, ¿y si la partícula tiene carga
negativa? Razona la respuesta. (R: Si la carga es positiva, la energía potencial
disminuirá, mientras que si la carga es negativa aumentará)
25. (Extremadura 2010) En el modelo de Bohr del átomo de hidrógeno, el
electrón de carga q = -1.6·10-19 C, describe una órbita circular en torno a un protón
de carga q’ = -q, de radio 5.3·10-15 m. La atracción del protón sobre el electrón
aporta la fuerza centrípeta necesaria para mantener al electrón en la órbita.
Calcule:
a) La fuerza de atracción eléctrica entre las partículas. (R: 8.2·10-8 N)
b) La masa del electrón si la velocidad a la que se desplaza es 2.18·106 m/s
(R: me = 9.1·10-31 kg)
26. (Extremadura 2010) Diga si la siguiente frase es CIERTA o FALSA y razone la
respuesta: “En el punto medio de separación de dos cargas eléctricas de igual valor
y signo el potencial eléctrico es nulo”
(R: Falso, sería nulo si fueran de distinto signo)
27. (Extremadura 2008) Una carga de 20 C crea un campo eléctrico. Calcule:
a) el potencial eléctrico en un punto situado a 3 m de la carga creadora.
(R: V = 6·1010 V)
b) El trabajo que hay que realizar para trasladar una carga de -2 C desde este
punto a otro punto situado a 4 m de la carga creadora. (R: W = 30000 J)
28. (Extremadura 2008) Dos cargas eléctricas están situadas en los puntos (0,0)
y (0,4) de un sistema de coordenadas en el que las distancias se miden en metros.
La primera es de 3 C y la segunda de 6 C. Calcular el potencial eléctrico en los
puntos A(0,1) y B(0,8). Datos: K0= 9·109 N·m2/C2.
(R: VA = 45000 V; VB = 16875 V)
29. (Extremadura 2006) Explique qué es un campo eléctrico y defina la
intensidad de campo eléctrico. (R: Teoría)
30. (Extremadura 2006) Diga si la siguiente frase es CIERTA o FALSA y razone la
respuesta: «El trabajo que se realiza al trasladar una masa entre dos puntos de una
misma superficie equipotencial es cero» (R: Cierta por tratarse de una fuerza
conservativa)