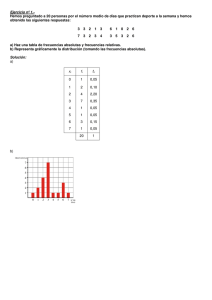
11 Hallar la varianza y la desviación típica de la siguiente serie de

11 Hallar la varianza y la desviación típica de la siguiente serie de datos:
12, 6, 7, 3, 15, 10, 18, 5.
12 Hallar la media, mediana y moda de la siguiente serie de números:
3, 5, 2, 6, 5, 9, 5, 2, 8, 6.
13. Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes:
2, 3, 6, 8, 11.
12, 6, 7, 3, 15, 10, 18, 5.
14 Se ha aplicado un test a los empleados de una fábrica, obteniéndose la siguiente tabla:
fi
[38, 44)
7
[44, 50)
8
[50, 56)
15
[56, 62)
25
[62, 68)
18
[68, 74)
9
[74, 80)
6
Dibujar el histograma y el polígono de frecuencias acumuladas.
15. Dadas las series estadísticas:
3, 5, 2, 7, 6, 4, 9.
3, 5, 2, 7, 6, 4, 9, 1.
Calcular:
La moda, la mediana y la media.
La desviación media, la varianza y la desviación típica.
Los cuartiles 1º y 3º.
Los deciles 2º y 7º.
Los percentiles 32 y 85.
7. Los pesos de los 65 empleados de una fábrica vienen dados por la siguiente tabla:
Peso
[50, 60)
[60, 70)
[70, 80)
[80,90)
[90, 100)
[100, 110)
[110, 120)
fi
8
10
16
14
10
5
2
1 Construir la tabla de frecuencias.
2 Representar el histograma y el polígono de frecuencias.
1. Los datos que se dan a continuación corresponden a los pesos en Kg. de ochenta personas:
(a)
Obténgase una distribución de datos en intervalos de amplitud 5, siendo el primer intervalo
[50; 55].
(b) Calcúlese el porcentaje de personas de peso menor que 65 Kg.
(c)
¿Cuántas personas tienen peso mayor o igual que 70 Kg. pero menor que 85?
60; 66; 77; 70; 66; 68; 57; 70; 66; 52; 75; 65; 69; 71; 58; 66; 67; 74; 61;
63; 69; 80; 59; 66; 70; 67; 78; 75; 64; 71; 81; 62; 64; 69; 68; 72; 83; 56;
65; 74; 67; 54; 65; 65; 69; 61; 67; 73; 57; 62; 67; 68; 63; 67; 71; 68; 76;
61; 62; 63; 76; 61; 67; 67; 64; 72; 64; 73; 79; 58; 67; 71; 68; 59; 69; 70;
66; 62; 63; 66;
7. Dada la siguiente distribución de frecuencias:
(a)
Li-1-Li
ni
1-3
3-7
3
29
7-8
35
8-10
26
10-13
6
13-20
1
Constrúyase una tabla en la que aparezcan las marcas de clase, las frecuencias absolutas y
relativas y las frecuencias absolutas acumuladas crecientes (o «menos de») y decrecientes (o
«más de»).
(b) Represéntese la distribución mediante un histograma y su correspondiente polígono de frecuencias.
9. Calcula la media, la varianza, la desviación típica y el coeficiente de variación de Pearson
tras Tras encuestar a 25 familias sobre el número de hijos que tenían, se obtuvieron los
siguientes datos,
Nº de hijos(Xi)
0
1
2
3
4
Nº de familias(ni)
5
6
8
4
2
25
15. Un
fabricante de
neumáticos ha
recabado,
de
los
diferentes
concesionarios,
información sobre la cantidad de miles de kilómetros recorridos por un modelo concreto de
esos neumáticos hasta que se ha producido un pinchazo o un reventón del neumático. Los
concesionarios la han proporcionado los siguientes datos:
52.452
50.432
37.748
51.831
73.808
61.065
35.807
57.277
48.698
65.854
75.850
36.949
75.548
69.010
61.477
65.585
44.411
41.886
34.754
59.888
59.449
67.632
89.116
69.483
63.692
70.003
65.996
55.989
49.677
46.502
67.467
64.398
84.588
40.709
50.238
61.390
85.720
45.313
46.724
61.752
55.643
55.912
46.681
66.519
59.168
66.313
35.884
28.625
47.012
71.360
78.635
41.715
72.635
41.463
48.996
48.172
79.426
67.662
53.324
49.011
29.480
41.128
30.252
33.412
48.240
57.884
55.257
84.656
48.662
10.504
60.951
38.420
74.239
60.727
56.155
86.070
90.565
53.751
76.580
68.629
51.179
74.582
58.708
48.035
67.124
41.830
61.030
58.267
61.979
4.3068
41.539
62.215
51.269
82.919
34.182
37.654
80.502
35.342
44.719
37.402
Se pide:
ab-
Construir una taba de frecuencias para esos datos .
Construir
las
tablas
de
frecuencias
acumuladas
ascendente
y descendente.
c-
Dibujar
el
histograma
de
frecuencias
relativas
sin
acumular
y
acumulado.
1.
d-
Calcular las principales medidas de tendencia central e interpretarlas.
e-
Obtener las medidas de dispersión más importantes e interpretarlas.
Hallar la media total
Muestra
n º de _ observaciones
_ ---
X
1
600
25,4
2
400
35,6
2. La media general de dos grupos de porristas es 78,98, si el primer grupo es de 380 con
una media de 60,35 y la del segundo grupo es de 58,6 hallar el número de integrantes
que conforman cada grupo.
3. Si la media de 300 artículos es de 98,56 y la de otros 210 es de 88,90, encuentra la media
de las dos muestras.
4. De una población de una bacteria de 1200, cuya media de crecimiento es de 256,32, se
dividen en dos para un experimento, las primeras 750 si el promedio de crecimientos de
estas es de 189,98 metros cúbicos ¿Cuál es la estatura de la otra muestra?.
5. Un grupo de 356 alpinistas, cuya velocidad de acenso es de 276,23 km/h, se divide en dos
grupos, uno con una velocidad media de ascenso de 198,56 km/h y otro con una de
234,87 km/h ¿Cuántos estudiantes hay en cada grupo?
6. se aplica un test de conocimiento a dos colegios de Cúcuta, con un coeficiente intelectual
promedio de 99,88, el colegio 1 tiene un coeficiente promedio de 88,76 y el colegio 2 de
78,56, si hay 230 alumnos en el colegio 1 cuantos hay en el colegio 2.
7. En un encuesta realizada a unos grupos de 500 consumidores por internet, el 56%
compran implementos de cocina y los restantes implementos de uso personal, si los que
consumen implementos de cocina tienen un promedio de ventas de 789000 pesos en
consumos. ¿Cuál es el menor número promedio de compras que debe realizar el otro
grupo para que el promedio de ventas de los dos sea de 989888?
8. Un grupo de 500 cantantes viaja en dos aviones, el primero lleva el 45% y el segundo los
restantes, se sabe que el peso medio de todos los cantantes es de 98,40 libras y que el de
los del segundo avión es de 5,4% menos que el de los cantantes del primer avión. ¿Cuál
es el peso medio de los atletas en cada avión?