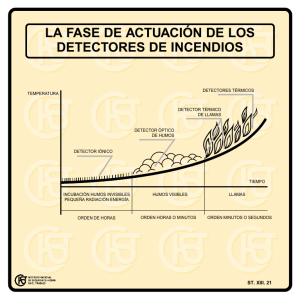
Diseño e implementación de un SPECT pre-clínico
Anuncio

UNIVERSIDAD DE VALENCIA TESIS DOCTORAL Diseño e implementación de un SPECT pre-clı́nico basado en cristales continuos Autor: Abel Orero Palomares Directores: Antonio Javier González Martı́nez Doctor en fı́sicas Javier Pavı́a Segura Doctor en fı́sicas en la Facultad de Fı́sica Departamento de Fı́sica Atómica, Molecular y Nuclear Declaración de Autorı́a Yo, Abel Orero Palomares, declaro que esta tesis con tı́tulo, “Diseño e implementación de un SPECT pre-clı́nico basado en cristales continuos” y el trabajo en ella presentado son mı́os. Confirmo que: Este trabajo fue totalmente o principalmente realizado mientras el candidato estudiaba la tesis en esta universidad. Donde ninguna parte de esta tesis ha sido previamente utilizada para una tesis o otro tı́tulo de esta universidad o cualquier otra institución, o en su defecto esto ha sido indicado claramente. Cuando he consultado los trabajos públicos de otros, se ha mencionado siempre claramente. Cuando se ha citado el trabajo de otros, la fuente siempre ha sido dada. Con la excepción de dichas fuentes, esta tesis es enteramente mi trabajo. Yo he reconocido todas las fuentes de ayuda. Cuando la tesis esta basada en el trabajo realizado conjuntamente con otros, yo he dejado claro que parte fue hecha por otros y que parte realicé yo. Firmado: Fecha: iii Agradecimientos Antes que nada me gustarı́a agradecer a todos los que, de un modo u otro, me ayudado a realizar este trabajo. En primer lugar quiero agradecer a las personas que me dieron la oportunidad de introducirme en el mundo de la Fı́sica Médica. A Magdalena Rafecas, por coger mi curriculum cuando se lo entregué y aunque no tuviera nada mostrar el interés de dárselo a José Marı́a Benlloch. A José Marı́a Benlloch por darme un voto de confianza y darme una oportunidad aunque fuera para ir a Barcelona. A Domènec Ros y a Javier Pavı́a por acogerme tan bien en Barcelona y por introducirme en el apasionante mundo de la Fı́sica Médica. Especialmente a Javier que es con el que pasé la mayor parte de mis casi 2 años en Barcelona, quien además aceptó codirigirme la tesis. A todos mis compañeros de la Unidad de Biofı́sica y Bioingenierı́a de la Universidad de Barcelona y del Departamento de Medicina Nuclear del Hospital Clinic de Barcelona, que fueron, junto con mi compañero de piso Marcos Colomer, mi familia durante mi estancia en Barcelona. Y muy especialmente a mis dos compañeros de trabajo (y amigos), Francisco Pino y Núria Roé, con quienes trabajé codo a codo, de manera espléndida, durante todo el tiempo. Una vez de vuelta a Valencia, he de agradecer a Oncovision S.A., principalmente a Noriel Pavón, por confiar en mi trabajo y aportar una parte del contrato I3P del CSIC con el que volvı́ a Valencia. También quiero agradecer a toda la gente de la empresa que me ayudó, principalmente en mis inicios con la empresa, a todos ellos, y especialmente al departamento del software y como no a Carlos Correcher, gracias por vuestra ayuda. También quiero acordarme de todos mis compañeros del Departamento de Fı́sica Médica, primero del IFIC, finalmente trasladados al I3M, por hacer que el dı́a a dı́a sea más ameno gracias a la compañı́a de todos, los que siguen y los que por un motivo o otro nos han tenido que dejar. Especialmente, me gustarı́a recordar a Ángel, que lamentablemente ya no está entre nosotros, te echamos de menos, descansa en paz. Finalmente, tengo que agradecer a Antonio J. González que me haya codirigido la tesis, gracias por tus correcciones y por tu paciencia. iv v No puedo despedirme sin agradecer a mi familia todo lo que hace y ha hecho por mi, sin ellos no estarı́a donde estoy y no creo que hubiera acabado mi tesis. A mi madre, por querer tanto a sus hijos, sin ella serı́a imposible llegar a donde he llegado. A mi hermanito mayor, José Vicente, por cuidar y preocuparse de mi siempre, desde pequeños, a su mujer, Rosario, por cuidar y querer a mi hermano y como no a mi sobrina Paula, por ser la alegrı́a de la familia. Ahh, y un abrazo a todos los primos, primas, tı́os y especialmente a mi abuelo José, que es un ejemplo a seguir en todo, y a mi abuela Antonia que falto hace muy poco, un abrazo muy fuerte, descansa en paz. Finalmente, agradecer profundamente a Loli, la que es y ha sido los últimos casi 4 años mi mayor apoyo, la que me aguanta, me soporta y me quiero todos los dı́as, los buenos y los malos. Gracias peque. Pero, por encima de todo, me gustarı́a dedicar esta tesis a mi padre, el cual, lamentablemente, falto durante estos años. Descansa en paz papa. Índice general Declaración de Autorı́a III Agradecimientos IV Lista de Figuras XV Lista de Tablas XXI Acrónimos I XXIII Introducción y objetivos 1 1. Introducción a la Medicina Nuclear 3 1.1. Medicina Nuclear . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.1.1. Cronologı́a de la Medicina Nuclear . . . . . . . . . . . . . . . 5 1.1.2. Técnicas diagnósticas . . . . . . . . . . . . . . . . . . . . . . 7 1.1.3. Tipos de estudios . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.4. Dosis de radiación . . . . . . . . . . . . . . . . . . . . . . . . 9 1.2. Tomografı́a computarizada por emisión de fotón único (SPECT) . . 10 1.2.1. Principios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 1.2.2. Aplicaciones clı́nicas . . . . . . . . . . . . . . . . . . . . . . . 11 1.2.3. SPECT para animales pequeños . . . . . . . . . . . . . . . . 12 1.2.3.1. Sistemas comerciales de SPECT para animales pequeños 13 2. Motivación y objetivos de la tesis vii 15 Contents II viii Descripción teórica 17 3. Fı́sica de detección de rayos gamma 3.1. Radiactividad . . . . . . . . . . . . . . . . . . . . . 3.2. Interacción de la radiación γ con la materia . . . . 3.2.1. Efecto fotoeléctrico . . . . . . . . . . . . . . 3.2.2. Efecto Compton . . . . . . . . . . . . . . . 3.3. Interacción de los rayos γ con un cristal centellador 3.3.1. Reflexión especular: ley de Snell . . . . . . 3.3.1.1. Reflexión interna total . . . . . . . 3.3.2. Difusión ideal . . . . . . . . . . . . . . . . . 3.3.3. Modelo hı́brido . . . . . . . . . . . . . . . . 4. La gammacámara 4.1. Cristal centellador . . . . . . . 4.2. Fotomultiplicador . . . . . . . . 4.3. Colimadores . . . . . . . . . . . 4.3.1. Tipos de colimadores . . 4.3.2. Colimador pinhole . . . 4.3.3. Colimador multipinhole . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 19 20 22 23 24 24 25 26 27 . . . . . . 29 30 31 33 35 36 39 5. Reconstrucción de imágenes tomográficas 5.1. Introducción teórica a la reconstrucción . . . . . . . . . . . . . . . . 5.2. Métodos analı́ticos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3. Métodos iterativos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3.1. Algoritmo de reconstrucción OS-EM. . . . . . . . . . . . . . . 5.3.2. Matriz de transición del sistema. . . . . . . . . . . . . . . . . 5.3.2.1. Cálculo de la matriz mediante medidas directas. . . 5.3.2.2. Cálculo de la matriz mediante simulaciones Monte Carlo. . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3.2.3. Métodos analı́ticos para el cálculo de la matriz. . . . 43 43 45 45 46 48 48 III 51 Primer prototipo SPECT: prueba de concepto 6. Elementos de un sistema SPECT de un solo detector con colimador pinhole 6.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.2. Componentes de la prueba de concepto SPECT . . . . . . . . . . . . 6.2.1. Detector de radiación: Sentinella . . . . . . . . . . . . . . . . 6.2.1.1. Cristal centellador . . . . . . . . . . . . . . . . . . . 6.2.1.2. Fotomultiplicador . . . . . . . . . . . . . . . . . . . 49 49 53 53 55 55 55 56 Contents ix 6.2.1.3. Electrónica . . . . . . . . . . . . . . . . . . . . . . . 6.2.2. Colimadores . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.2.2.1. Selección del tamaño de la apertura del colimador pinhole . . . . . . . . . . . . . . . . . . . . . . . . . 6.2.3. Soportes, contrapeso y actuador lineal para radio de giro . . 6.2.4. Motores y tarjeta de control . . . . . . . . . . . . . . . . . . . 6.3. Resultado del montaje de la prueba de concepto SPECT . . . . . . . 57 59 59 61 62 63 7. Adquisición y tratamiento de datos 7.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.2. Material y métodos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.2.1. Software disponible de la gammacámara . . . . . . . . . . . . 7.2.2. Software disponible para el control de los motores de OWIS . 7.2.3. Control conjunto de los componentes y automatización de las adquisiciones . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.2.4. Corrección del decaimiento durante la adquisición . . . . . . 7.2.4.1. Corrección del decaimiento compensando el número de cuentas detectadas. . . . . . . . . . . . . . . . . . 7.2.4.2. Corrección del decaimiento aumentando el tiempo por adquisición. . . . . . . . . . . . . . . . . . . . . 7.3. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.3.1. Interface desarrollado . . . . . . . . . . . . . . . . . . . . . . 7.3.1.1. Control de motores . . . . . . . . . . . . . . . . . . 7.3.1.2. Gammacámara. . . . . . . . . . . . . . . . . . . . . Visualización de los datos obtenidos. . . . . . . . . . . Control de la gammacámara. . . . . . . . . . . . . . . 7.3.1.3. Estudios . . . . . . . . . . . . . . . . . . . . . . . . 7.3.1.4. Sección informativa. . . . . . . . . . . . . . . . . . . Información de estado. . . . . . . . . . . . . . . . . . . Información sobre el estudio. . . . . . . . . . . . . . . 7.3.2. Datos adquiridos . . . . . . . . . . . . . . . . . . . . . . . . . 7.3.2.1. Estático . . . . . . . . . . . . . . . . . . . . . . . . . 7.3.2.2. SPECT . . . . . . . . . . . . . . . . . . . . . . . . . 7.3.2.3. Dinámico . . . . . . . . . . . . . . . . . . . . . . . . 7.3.2.4. Espectro . . . . . . . . . . . . . . . . . . . . . . . . 65 65 66 66 67 8. Calibraciones del sistema: geométrica y del 8.1. Introducción y objetivos . . . . . . . . . . . 8.2. Calibración del detector . . . . . . . . . . . 8.2.1. Material y métodos . . . . . . . . . . 8.2.1.1. Calibración en posiciones . 81 81 82 82 82 detector . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 70 70 71 73 73 73 74 74 74 74 76 76 76 77 77 77 79 79 Contents x 8.2.1.2. Calibración en energı́as . . . . . . . . . . . . . . . . 84 8.2.1.3. Corrección de uniformidad . . . . . . . . . . . . . . 86 8.2.2. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 8.2.2.1. Calibración en posiciones . . . . . . . . . . . . . . . 87 8.2.2.2. Calibración en energı́as . . . . . . . . . . . . . . . . 87 8.2.2.3. Corrección de uniformidad . . . . . . . . . . . . . . 89 8.3. Calibración geométrica del sistema SPECT . . . . . . . . . . . . . . 91 8.3.1. Introducción teórica . . . . . . . . . . . . . . . . . . . . . . . 91 8.3.1.1. Descripción de la geometrı́a de un sistema con detector único . . . . . . . . . . . . . . . . . . . . . . . 91 8.3.1.2. Proyección de una fuente puntual . . . . . . . . . . 95 8.3.2. Material y método de calibración geométrica . . . . . . . . . 96 8.3.2.1. Estimación de los parámetros . . . . . . . . . . . . . 96 8.3.2.2. Maniquı́ de calibración . . . . . . . . . . . . . . . . 97 8.3.3. Resultados de la calibración geométrica: software de calibración 99 8.3.3.1. Búsqueda del centro de masa de los puntos . . . . . 99 8.3.3.2. Minimización de la distancia entre las posiciones medidas y las estimadas . . . . . . . . . . . . . . . . . 101 8.3.3.3. Interfaz de usuario . . . . . . . . . . . . . . . . . . . 102 9. Validación de la prueba de concepto 9.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . 9.2. Material y métodos . . . . . . . . . . . . . . . . . . . . . 9.2.1. Caracterización del sistema . . . . . . . . . . . . 9.2.1.1. Uniformidad tomográfica . . . . . . . . 9.2.1.2. Sensibilidad del sistema . . . . . . . . . 9.2.1.3. Resolución espacial tomográfica . . . . 9.2.2. Estudios SPECT con animales . . . . . . . . . . 9.3. Resultados de la prueba de concepto . . . . . . . . . . . 9.3.1. Caracterización del equipo . . . . . . . . . . . . . 9.3.1.1. Uniformidad tomográfica . . . . . . . . 9.3.1.2. Sensibilidad del sistema . . . . . . . . . 9.3.1.3. Resolución espacial . . . . . . . . . . . 9.3.2. Imágenes obtenidas en los estudios con animales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.Conclusiones de la prueba de concepto 10.1. Elementos de un sistema SPECT de un solo detector con colimador pinhole . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10.2. Adquisición y tratamiento de datos . . . . . . . . . . . . . . . . . . . 10.3. Calibración del sistema: geométrica y del detector . . . . . . . . . . 10.4. Validación de la prueba de concepto SPECT . . . . . . . . . . . . . . 107 107 107 108 108 109 109 110 112 112 112 112 114 114 117 117 117 118 118 Contents IV Segundo prototipo SPECT xi 121 11.Diseño del segundo prototipo 11.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11.2. Material y métodos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11.2.1. Diseño de un nuevo colimador pinhole . . . . . . . . . . . . . 11.2.2. Diseño de un colimador multipinhole . . . . . . . . . . . . . . 11.2.2.1. Configuraciones multipinhole sin superposición en la imagen . . . . . . . . . . . . . . . . . . . . . . . . . 11.2.2.2. Configuraciones multipinhole con superposición en la imagen . . . . . . . . . . . . . . . . . . . . . . . . . 11.2.3. Diseño hardware . . . . . . . . . . . . . . . . . . . . . . . . . 11.3. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11.3.1. Colimador pinhole . . . . . . . . . . . . . . . . . . . . . . . . 11.3.2. Colimador multipinhole . . . . . . . . . . . . . . . . . . . . . 11.3.3. Implementación del sistema SPECT . . . . . . . . . . . . . . 123 123 124 124 125 12.Adquisición y calibración geométrica 12.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12.2. Material y métodos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12.2.1. Programa de adquisición de datos . . . . . . . . . . . . . . . 12.2.2. Calibración geométrica . . . . . . . . . . . . . . . . . . . . . . 12.2.2.1. Nuevos maniquı́ de calibración . . . . . . . . . . . . 12.2.2.2. Calibración geométrica de un sistema SPECT con doble cabezal detector . . . . . . . . . . . . . . . . . 12.2.2.3. Ampliación a un sistema multipinhole . . . . . . . . 12.2.2.4. Algoritmo para la reducción de mı́nimos locales. . . 12.2.2.5. Ajuste conjunto de los 4 FOV de cada una de las cámaras . . . . . . . . . . . . . . . . . . . . . . . . . 12.2.2.6. Evolución del software de calibración . . . . . . . . 12.3. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12.3.1. Nuevo software de calibración . . . . . . . . . . . . . . . . . . 12.3.2. Método de calibración con dos detectores . . . . . . . . . . . 12.3.3. Calibración con colimador multipinhole . . . . . . . . . . . . 12.3.4. Nuevo método de calibración conjunta . . . . . . . . . . . . . 137 137 138 138 139 139 13.Método de reconstrucción de imágenes 13.1. Introducción al método de reconstrucción . . . . . . . . . . . . . . . 13.2. Material y métodos de la reconstrucción . . . . . . . . . . . . . . . . 13.2.1. Cálculo de la matriz del sistema . . . . . . . . . . . . . . . . 153 153 154 154 126 128 130 131 131 132 135 139 141 145 146 147 147 147 149 149 151 Contents 13.2.1.1. Recuperación de resolución: corrección del efecto de la apertura . . . . . . . . . . . . . . . . . . . . . . . 13.2.1.2. Estimación de la sensibilidad . . . . . . . . . . . . . 13.2.1.3. Consideraciones para un colimador multipinhole . . 13.2.2. Utilización de simetrı́as en el cálculo de la matrices . . . . . . 13.2.3. Método para la corrección de la dispersión, implementación en la reconstrucción . . . . . . . . . . . . . . . . . . . . . . . 13.2.3.1. Método de doble ventana de energı́a . . . . . . . . . 13.2.3.2. Pruebas de comprobación de la corrección de la dispersión . . . . . . . . . . . . . . . . . . . . . . . . . 13.2.4. Algoritmo OS-EM estándar adaptado a nuestro sistema . . . 13.3. Resultados del método de reconstrucción . . . . . . . . . . . . . . . . 13.3.1. Aplicación de simetrı́as en el cálculo de la matriz . . . . . . . 13.3.2. Reconstrucción con colimador multipinhole . . . . . . . . . . 13.3.3. Reconstrucción con corrección de la dispersión . . . . . . . . xii 154 156 160 161 162 164 165 166 167 167 168 168 14.Imágenes obtenidas con el segundo prototipo SPECT 171 14.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 14.2. Material y métodos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 14.2.1. Caracterización del sistema . . . . . . . . . . . . . . . . . . . 171 14.2.1.1. Medidas y maniquı́ de sensibilidad . . . . . . . . . . 172 14.2.1.2. Medidas y maniquı́s de resolución . . . . . . . . . . 173 14.2.1.3. Medidas y maniquı́s de uniformidad . . . . . . . . . 175 14.2.2. Imágenes con animales pequeños . . . . . . . . . . . . . . . . 176 14.2.3. Fusión de imágenes SPECT con CT . . . . . . . . . . . . . . 177 14.3. Resultados obtenidos . . . . . . . . . . . . . . . . . . . . . . . . . . . 178 14.3.1. Caracterización del sistema. . . . . . . . . . . . . . . . . . . . 178 14.3.1.1. Resultados de sensibilidad con el maniquı́ diseñado 178 Estudio de sensibilidad en función de la ventana de energı́a utilizada. . . . . . . . . . . . . . . . . 178 Sensibilidad obtenida en función del FOV. . . . . . . . 178 14.3.1.2. Resultados de resolución con los maniquı́s diseñados 180 Imágenes de resolución. . . . . . . . . . . . . . . . . . 180 Resolución medida en función de la configuración del sistema. . . . . . . . . . . . . . . . . . . . . 182 14.3.1.3. Resultados de uniformidad con los maniquı́s diseñados183 Imágenes de uniformidad. . . . . . . . . . . . . . . . . 183 Uniformidad medida en función de la configuración del sistema. . . . . . . . . . . . . . . . . . . . . 183 14.3.2. Imágenes con animales pequeños . . . . . . . . . . . . . . . . 185 14.3.2.1. Estudios de corazón con 99m T c − M IBI . . . . . . 185 Contents xiii 14.3.2.2. Estudios óseos con 99m T c − M DP . . . . . . . . . . 186 14.3.3. Fusión de las imágenes de SPECT con imágenes de CT . . . 186 14.3.3.1. Fusión de un estudios óseo de 99m T c − M DP con CT 187 14.3.3.2. Fusión de un estudios de pulmón de 99m T c − M AA con CT . . . . . . . . . . . . . . . . . . . . . . . . . 189 15.Método de cuantificación 15.1. Introducción y objetivos de la cuantificación . . . . . . . . . . 15.2. Material y métodos . . . . . . . . . . . . . . . . . . . . . . . . 15.2.1. Relación entre cuentas de la imagen y actividad . . . . 15.2.2. Cálculo del valor Q en función del colimador y el FOV 15.3. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15.3.1. Relación entre cuentas de la imagen y actividad . . . . 15.3.2. Cálculo del valor Q en función del colimador y el FOV 16.Conclusiones y proyección futura 16.1. Conclusiones del segundo prototipo diseñado . . . . . . . . . 16.1.1. Diseño del segundo prototipo SPECT . . . . . . . . . 16.1.2. Adquisición y ampliación del método de calibración geométrica . . . . . . . . . . . . . . . . . . . . . . . . 16.1.3. Método de reconstrucción de imágenes . . . . . . . . . 16.1.4. Imágenes obtenidas con el segundo prototipo SPECT 16.1.5. Cuantificación de las imágenes reconstruidas . . . . . 16.2. Proyección futura . . . . . . . . . . . . . . . . . . . . . . . . . Bibliografı́a . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191 191 193 193 194 196 196 196 201 . . . . 201 . . . . 201 . . . . . . . . . . . . . . . . . . . . 202 202 202 203 203 205 Índice de figuras 1.1. Imagen médica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.2. Cuatro SPECT comerciales para animales pequeños. . . . . . . . . . 4 13 3.1. Comportamiento de la luz. . . . . . . . . . . . . . . . . . . . . . . . . 25 4.1. 4.2. 4.3. 4.4. 32 33 36 Esquema de un fotomultiplicador. . . . . . . . . . . . . . . . . . . . . Estructura dinódica de canales metálicos. . . . . . . . . . . . . . . . Formación de imágenes para los distintos tipos de colimadores. . . . Comparativa de sensibilidad, resolución y FOV para los 4 colimadores más utilizados. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.5. Colimador pinhole. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4.6. Colimador multipinhole con agujeros inclinados. . . . . . . . . . . . . 5.1. Representación esquemática de las dos opciones para modelizar la proyección en la matriz de transición con el colimador pinhole. (Izquierda) Proyección basado en el trazado de rayos. (Derecha) proyección vı́a vóxel. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.1. Foto del PSPMT escogido. . . . . . . . . . . . . . . . . . . . . . . . . 6.2. Placas electrónicas de la mini cámaragamma. . . . . . . . . . . . . . 6.3. Atenuación para rayos gamma de 140.5 keV en función del espesor del material de Pb y W. . . . . . . . . . . . . . . . . . . . . . . . . . 6.4. Resolución y sensibilidad de una imagen planar en función del radio de giro para los 3 colimadores de los que disponemos. . . . . . . . . 6.5. Imagen de los tres sistemas de la compañı́a OWIS utilizados en el prototipo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.6. Imágenes de la prueba de concepto SPECT desarrollado. . . . . . . . 37 37 40 50 56 58 60 61 62 63 7.1. Imagen del dialogo proporcionado por OWIS como ejemplo del control de los motores en lenguaje de programación C++. . . . . . . . . . . 67 7.2. Imagen del interfaz gráfico del software del sistema de adquisición del prototipo 1. Indicando la función de las principales partes del mismo. 73 7.3. Ampliación de la sección del interfaz gráfico referida a la gammacámara. 74 xv List of Figures xvi 7.4. Ampliación de la sección del interfaz gráfico referida a los estudios. . 7.5. Selección de steps o beds. Aparece nueva información con el número de steps y el desplazamiento y dirección entre los mismo. . . . . . . 7.6. Información del estado de la cámara y las adquisiciones. . . . . . . . 7.7. Sección donde el usuario debe rellenarse la información sobre el estudio realizado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7.8. Ejemplo de un estudio estático utilizando un maniquı́ cilı́ndrico hueco relleno de una disolución de 99m T c. . . . . . . . . . . . . . . . . . . . 7.9. 30 proyecciones de un estudio de pulmón de ratón. . . . . . . . . . . 7.10. Ejemplo de un estudio dinámico. Abdomen de una rata después de inyectar un trazador marcado con 123 I. . . . . . . . . . . . . . . . . . 75 8.1. Mascara de calibración (dimensiones en mm). . . . . . . . . . . . . . 8.2. Imagen de la máscara de calibración, sin (izquierda) y con (derecha) calibración en posiciones. . . . . . . . . . . . . . . . . . . . . . . . . 8.3. Espectro de energı́as sin calibrar (izquierda), calibrado (centro) e imagen calibrada en posiciones y energı́a seleccionando solo los eventos dentro de la ventana del 20 % centrada en el fotopico (derecha). . . . 8.4. Relación entre la energı́a emitida en keV y la medida en canales. . . 8.5. Imagen de uniformidad adquirida una vez corregida en posiciones. Junto a ella se muestran las proyecciones de la imagen sobre los ejes X e Y. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8.6. (Izquierda) Imagen de uniformidad corregida en posiciones. (Centro) Imagen de uniformidad corregida en posiciones y energı́a. (Derecha) Imagen de uniformidad corregida en posiciones, energı́a y por uniformidad. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8.7. Imagen de uniformidad obtenida una vez se aplican todas las correcciones. También se muestran las proyecciones sobre los ejes X e Y. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8.8. Imágenes con las tres rotaciones realizadas durante el cálculo. . . . . 8.9. Geometrı́a del sistema . . . . . . . . . . . . . . . . . . . . . . . . . . 8.10. Maniquı́ de calibración junto con una de sus proyecciones. . . . . . . 8.11. Imagen con los cuadrados en los que se realiza el ajuste Gaussiano. . 8.12. Maniquı́ de calibración . . . . . . . . . . . . . . . . . . . . . . . . . . 8.13. Programa de calibración en entorno visual. . . . . . . . . . . . . . . 8.14. Variación del centro de cada punto con el ángulo de proyección. Se observa la trayectoria sinusoidal que describen los puntos. . . . . . . 8.15. Ajuste por mı́nimos cuadrados de la variable m en función del radio de giro. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 76 76 77 78 78 79 87 88 88 89 90 90 94 95 98 100 101 102 104 105 9.1. Foto del maniquı́ de uniformidad utilizado para la prueba de concepto.108 9.2. Foto del maniquı́ tipo Derenzo utilizado para la prueba de concepto. 110 List of Figures 9.3. Uniformidad de la imagen reconstruida en función del número de iteraciones utilizadas. La imagen se ha obtenido con un algoritmo OSEM con 5 subsets . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.4. Resultados de la sensibilidad medida en función del FOV medidos. . 9.5. Resolución en función del FOV. . . . . . . . . . . . . . . . . . . . . . 9.6. Corte axial de una imagen reconstruida de un maniquı́ tipo Derenzo utilizado para comprobar la resolución del equipo. La imagen se ha obtenido con un algoritmo OSEM con 5 subsets y se han utilizado 5 iteraciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9.7. Secciones de un estudio de pulmón de ratón obtenidas con 99m T c − M AA: (a) axial, (b) coronal, (c) sagital de pulmón derecho y (d) sagital de pulmón izquierdo. . . . . . . . . . . . . . . . . . . . . . . . 9.8. Secciones de cabeza de ratón obtenidas con 99m T c − HDP : (a) sagital,(b, f) coronales y (c,d,e) axiales a nivel posterior, medio y anterior respectivamente. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xvii 113 113 114 115 115 116 11.1. Esquema 3D del cono de luz que suscita el colimador sobre el detector.125 11.2. Esquemático 2D de la configuración 1 de un colimador con 2 pinholes sin superposición en el detector. . . . . . . . . . . . . . . . . . . . . . 127 11.3. Esquemático 2D de un colimador con 2 “pinholes convergentes” sin superposición en el detector. . . . . . . . . . . . . . . . . . . . . . . . 127 11.4. Esquemático 2D para los dos colimadores multipinhole con superposición en el detector. Se observa que la distancia b1 es la distancia mı́nima para que los 3 agujeros vean el centro del FOV. . . . . . . . 129 11.5. Corte a la altura del detector con simulación Monte Carlo. Se muestra el detector (azul) y la zona iluminada (rojo). . . . . . . . . . . . . . 131 11.6. Fotos del colimador pinhole diseñado para este prototipo. . . . . . . 132 11.7. Imágenes del diseño Monte Carlo del sistema SPECT con uno de los colimadores multipinhole simulados. . . . . . . . . . . . . . . . . . . 132 11.8. Imágenes de una proyección de SPECT para las distintas configuraciones simuladas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133 11.9. Fotos del colimador multipinhole definitivo que se ha diseñado y desarrollado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134 11.10.Imágenes del ptototipo SPECT y el sistema SPECT una vez montado dentro del equipo Albira. . . . . . . . . . . . . . . . . . . . . . . . . 136 12.1. Software de adquisición Albira Adquirer para SPECT. . . . . . . . . 12.2. Nuevos maniquı́s de calibración adaptados para cada uno de los 4 FOVs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12.4. Ejemplo de dos proyecciones del maniquı́ de calibración a través del colimador multipinhole. . . . . . . . . . . . . . . . . . . . . . . . . . 138 140 140 143 List of Figures xviii 12.5. Imagen de las mismas proyecciones del maniquı́ de calibración, que se muestran en la figura 12.4, a través del colimador multipinhole pero utilizando la máscara de calibración. . . . . . . . . . . . . . . . . . . 144 12.6. Interfaz gráfica del programa de calibración para doble cabezal detector.148 12.7. Reconstrucción del maniquı́ de calidad de imagen adquirido con doble cabezal detector. (Arriba) Sin los parámetros ∆α0 y ∆ zp . (Abajo) Con los parámetros ∆α0 y ∆ zp . . . . . . . . . . . . . . . . . . . . . 149 12.8. Proyecciones obtenidas en el estudio de la fuente cilı́ndrica utilizando el colimador multipinhole. . . . . . . . . . . . . . . . . . . . . . . . . 150 12.9. Imagen de los cortes transaxial, coronal y sagital de la reconstrucción con colimador multipinhole. . . . . . . . . . . . . . . . . . . . . . . . 150 13.1. Esquema de la apertura de un colimador tipo pinhole. . . . . . . . . 13.2. Proyección de una fuente puntual (xi , yi , zi ) a través de una apertura pinhole ideal con diámetro D a un detector y una distancia f del colimador. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13.4. Espectro y ventanas de energı́as seleccionada para una medida real. La zona triangular rallada de la ventana principal indica la estimación de la dispersión en dicha ventana. . . . . . . . . . . . . . . . . . . . . 13.5. Imagen de los dos maniquı́es utilizados para aumentar la dispersión en el espacio objeto. . . . . . . . . . . . . . . . . . . . . . . . . . . . 13.6. Imagen del capilar reconstruido en aire . (arriba) Sin corrección de la dispersión. (abajo) Con corrección de la dispersión. . . . . . . . . . . 13.7. Imagen del capilar reconstruido en metacrilato. (arriba) Sin corrección de la dispersión. (abajo) Con corrección de la dispersión. . . . . . . . 13.8. Imagen del capilar reconstruido en teflón. (arriba) Sin corrección de la dispersión. (abajo) Con corrección de la dispersión. . . . . . . . . 156 158 162 165 166 169 169 170 14.1. Foto del maniquı́ diseñado para medir la sensibilidad del sistema. . . 172 14.2. Fotos de los maniquı́s diseñados para medir la resolución del sistema en los FOVs pequeños. . . . . . . . . . . . . . . . . . . . . . . . . . . 174 14.5. Espectro de energı́a para una medida de sensibilidad en el FOV20 tanto con el colimador pinhole como multipinhole. También se muestras las barras correspondientes a las ventanas de energı́a de ±10 % y ±15 %. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179 14.6. Sensibilidad absoluta para los dos colimadores en función de la ventana de energı́a seleccionada. Las medidas se realizaron para el FOV20.179 14.7. Sensibilidad del sistema . . . . . . . . . . . . . . . . . . . . . . . . . 180 14.8. Resolución axial obtenida mediante el colimador pinhole. . . . . . . . 180 14.9. Resolución transaxial del sistema para el colimador pinhole y el FOV20. Vistas del corte transaxial y el corte coronal. . . . . . . . . . . . . . 181 List of Figures 14.10.Resolución transaxial del sistema para el colimador pinhole y el FOV20. Comparación entre el corte transaxial reconstruido y el mismo corte del maniquı́. Se distingues todos los agujeros menos los de 0.6 mm. . 181 14.11.Comparativa de resolución en el FOV60. (Arriba) Reconstrucción con colimador multipinhole. (Abajo) Reconstrucción con colimador pinhole.182 14.12.Resolución del sistema . . . . . . . . . . . . . . . . . . . . . . . . . . 183 14.15.Uniformidad del sistema . . . . . . . . . . . . . . . . . . . . . . . . . 185 14.16.Corazón ratón . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186 14.18.Fusión de imágenes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 188 14.20.Hueso rata . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189 15.1. Relación entre las cuentas por segundo de la imagen reconstruida y la actividad de la fuente. Se compara dicha relación con distintas combinaciones de número y tamaño de vóxel ası́ como con distintos números de subsets y de iteraciones. . . . . . . . . . . . . . . . . . . 196 15.2. Relación entre las cuentas por segundo de la imagen reconstruida y la actividad de la fuente para 2 FOV y dos colimadores distintos. También se incluye la medida de una fuente puntual en diferentes posiciones del FOV. . . . . . . . . . . . . . . . . . . . . . . . . . . . 197 15.3. Relación entre las cuentas por segundo de la imagen reconstruida y la actividad de la fuente. Detalle de la zona de baja actividad, además se muestran los ajustes del FOV20ph, FOV20mph y FOV40ph. . . . 199 xix Índice de tablas 1.1. SPECT comerciales y sus principales caracterı́sticas. . . . . . . . . . 14 4.1. Caracterı́sticas principales de algunos de los cristales centelladores más utilizados. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 6.1. Caracterı́sticas principales del PSPMT H8500. 57 . . . . . . . . . . . . 8.1. Resultados obtenidos para diferentes calibraciones geométricas con la prueba de concepto. . . . . . . . . . . . . . . . . . . . . . . . . . . . 105 11.1. Relación entre los principales parámetros de un SPECT con colimador pinhole o multipinhole. . . . . . . . . . . . . . . . . . . . . . . . . . . 125 11.2. Caracterı́sticas de los 4 colimadores simulados. . . . . . . . . . . . . 130 11.3. Sensibilidad obtenidas en función del colimador. . . . . . . . . . . . 134 12.1. Resultados de la calibración del colimador multipinhole. En rojo se muestran los parámetros estimados. . . . . . . . . . . . . . . . . . . 150 12.2. Resultados obtenidos para una calibración conjunta con doble detectores. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152 13.1. Resolución obtenida para el capilar en función del maniquı́ utilizado. 170 15.1. Combinación de parámetros de reconstrucción para las pruebas de cuantificación. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194 15.2. Actividades esperadas máximas para conservar linealidad y para evitar saturación en cada FOV y colimador. . . . . . . . . . . . . . . . 198 xxi Acrónimos CT Computed Tomography FOV Field Of View MRI Magnetic Resonance Imaging PET Positron Emission Tomography PMT Photo Multiplier Tube PSPMT Position Sensitive Photo Multiplier Tube PSF Point Spread Function SPECT Single Photon Emission Computed Tomography ROI Region Of Interest PVE Partial Volume Effect xxiii For/Dedicated to/To my. . . xxv Parte I Introducción y objetivos 1 Capı́tulo 1 Introducción a la Medicina Nuclear 1.1. Medicina Nuclear La Medicina Nuclear se define como la especialidad de la medicina que emplea los isótopos radiactivos, las radiaciones nucleares, las variaciones electromagnéticas de los componentes del núcleo atómico y técnicas biofı́sicas afines, para la prevención, diagnóstico, terapia e investigación médica1 . Sus principales campos de acción son el diagnóstico por imagen y, en menor medida, el tratamiento de determinadas enfermedades mediante el uso de radiofármacos2 . La mayorı́a de las pruebas diagnósticas en Medicina Nuclear se basan en la obtención y evaluación de imágenes que son un reflejo de procesos biológicos que tienen lugar a nivel celular y subcelular. Para obtener dichas imágenes se utilizan elementos radiactivos que al desintegrarse emiten, directa o indirectamente, radiaciones electromagnéticas de energı́a comprendida en el rango de los rayos γ (ver figura 1.1). Estos elementos radiactivos radiactivas se administran a los pacientes unidos a un fármaco y las imágenes se obtienen mediante la utilización de detectores de radiación. 1 2 Definición adoptada por la Comisión Nacional de la Especialidad de Medicina Nuclear. Fármacos que han sido marcados con radionúclidos. 3 4 1.1. Medicina Nuclear Figura 1.1: Imagen médica. En las últimas décadas del siglo XX se desarrollaron nuevas técnicas de diagnóstico en el campo de la Medicina Nuclear, como la tomografı́a por emisión de fotón único (SPECT, Single Photon Emission Computed Tomography) o la tomografı́a por emisión de positrones (PET, Positron Emission Tomography). Estos avances originaron la aparición de nuevos radiofármacos y nuevas indicaciones para los ya existentes que proporcionan valiosa información funcional para el diagnóstico de diversas patologı́as. Las imágenes funcionales que se obtienen en Medicina Nuclear con los sistemas PET y SPECT se suelen combinar con las anatómicas que nos ofrece la tomografı́a computada (CT, Computed Tomography) o la resonancia magnética nuclear (RMN). Esta fusión puede realizarse mediante mediante cámaras hı́bridas (PETCT, SPECT-CT,. . . ) o mediante software, realizando el corregistro de los estudios de ambas modalidades de modo que se pueda interpretar como una sola imagen, proporcionando información más precisa y diagnósticos más exactos. Muy recientemente (RSNA 2010) se ha presentado el primer hı́brido PET-RMN que ofrece la posibilidad de adquirir con ambas modalidades [1]. 1. Introducción a la Medicina Nuclear 1.1.1. Cronologı́a de la Medicina Nuclear El primer acontecimiento relacionado con la imagen médica fue el descubrimiento de los rayos X por Wilhelm Conrad Röntgen en 1895. En ese momento nace un nuevo concepto de diagnóstico que permite obtener información de la anatomı́a y fisiologı́a del cuerpo humano mediante una técnica no-invasiva. Debido a su fácil aplicabilidad, el primer uso de los rayos X con fines médicos fue llevado a cabo en Febrero de 1896. Otro importante acontecimiento en la historia de la imagen médica, el cual fue el principio de la Medicina Nuclear, fue el descubrimiento de la radiactividad por Antoine Henri Becquerel en 1896. Inicialmente los radionúclidos fueron usados para terapia del cáncer y no para la imagen médica. Más tarde, en 1923 George de Hevesy introdujo el concepto de la utilización de los radionúclidos como radiotrazadores para hacer estudios fisiológicos. Sin embargo, la Medicina Nuclear no inicia su desarrollo como especialidad hasta finales de los años 40, momento en el que se decide utilizar la energı́a nuclear con fines médicos. 1946 constituye una fecha histórica, ya que se construye el primer reactor productor de radionúclidos. - Cronologı́a del desarrollo de la Medicina Nuclear en el mundo 1895. Descubrimiento de los Rayos X - Röentgen. 1896. Descubrimiento de la radiactividad de Uranio - Becquerel. 1898. Descubrimiento de la radiactividad natural - Marie Curie. 1913. Desarrollo del concepto de isotopı́a - Soddy. 1923. Primera utilización de un radiotrazador en la exploración biológica Hevesy. 1927. Puesta a punto de un detector de radiaciones - Geiger y Müller. 1931. Construcción del primer ciclotrón - Lawrence y Livingstone. 1934. Descubrimiento de la radiactividad artificial - Curie y Joliot. 5 6 1.1. Medicina Nuclear 1939. Primeras aplicaciones terapéuticas. 1946. Construcción del primer reactor productor de radionúclidos. 1951. Construcción del escáner con cristal de centelleo de yoduro sódico, que permite realizar las primeras gammagrafı́as - Reed y Libby. 1958. Aparición de los generadores de 99m Tc, elemento idóneo para sintetizar trazadores dadas sus posibilidades de unión a diversos fármacos. 1958. Construcción de la primera cámara de centelleo - Hal Anger. A partir de los años 60 la evolución de la Medicina Nuclear es imparable. Los acontecimientos más relevantes fueron la puesta en marcha de la técnica del SPECT en el año 1963 [2] y el desarrollo del PET entre las décadas de los 60 y 70: James Robertson construyó el primer PET 1D denominado “head-shrinker” en 1961 y hubo que esperar hasta 1970 para que se diseñara el primer PET 2D [3]. - Cronologı́a del desarrollo de la Medicina Nuclear en España 1948. Se forma el primer grupo español relacionado con los isótopos radioactivos, se realizan los primeros estudios prácticos y se publica el primer artı́culo español sobre el tema. 1949. Se adquiere el primer equipamiento para estudios diagnósticos y terapéuticos sobre el tiroides. Se monta el primer Servicio de Isótopos Radioactivos privado en Madrid. 1950. Se inaugura el primer Servicio de Isótopos Radioactivos para la Seguridad Social en Madrid. 1951. Creación de la Junta de Energı́a Nuclear (JEN). Presentación de las primeras comunicaciones de Medicina Nuclear. Publicación de los dos primeros libros en lengua castellana sobre Medicina Nuclear. 1955. Adquisición del primer gammágrafo lineal. Se crea la Comisión Asesora de Medicina y Biologı́a Animal de la Junta de Energı́a Nuclear, con el objetivo de coordinar las relaciones entre esta última y los Centros de Medicina Nuclear. 1. Introducción a la Medicina Nuclear 1958. Inauguración del Centro Nacional de Energı́a Nuclear “Juan Vigón” donde empieza la producción de isótopos radioactivos en España. 1963. Inauguración de CETIR, centro privado de referencia de la Medicina Nuclear en Barcelona. 1964. Inauguración del primer servicio de Isótopos Radioactivos independiente creado por la Seguridad Social. Se promulga la Ley de Energı́a Nuclear. 1980. Se crea el Consejo de Seguridad Nuclear. 1995. Instalación del primer PET de España, en Madrid. Desde finales de los años 60 hasta nuestros dı́as, el progreso de la Medicina Nuclear en España ha seguido un ritmo acelerado, al igual que en el resto del mundo. Se han creado numerosos centros en toda España, se ha formado un gran número de especialistas, se han desarrollado múltiples congresos, symposiums, jornadas y reuniones y se han publicado numerosos trabajos en revistas y libros [4]. 1.1.2. Técnicas diagnósticas Las pruebas diagnósticas en Medicina Nuclear proporcionan una información esencialmente funcional del órgano estudiado, a diferencia del resto de las técnicas de diagnóstico por imagen (CT, RMN, ecografı́a,. . . ) que ofrecen información estructural o anatómica. Las técnicas son no invasivas ya que para su realización únicamente precisan de la administración previa al paciente, generalmente por vı́a intravenosa, de un radiofármaco. El radiofármaco está formado por un radionúclido en forma libre o unido quı́micamente a una molécula. El radionúclido nos permite obtener la formación de la imagen y la molécula es un compuesto activo que interactuará de forma especı́fica con un tipo de célula, tejido u órgano diana. El radiofármaco se administra en cantidades muy bajas (trazas) por lo que no tiene un efecto farmacológico en el paciente y resulta indetectable con las técnicas de medida disponibles, por lo que recibe también el apelativo de radiotrazador. 7 8 1.1. Medicina Nuclear La elección del radiofármaco adecuado dependerá de la patologı́a del paciente y del órgano a estudiar. Estas técnicas nos permiten visualizar sobretodo alteraciones funcionales ya sea por un incremento o por una disminución de la cantidad de radiotrazador que se incorpore al órgano sometido a estudio. Existen radiofármacos para estudiar prácticamente todos los sistemas y órganos, desde los más antiguos que incluyen la gammagrafı́a ósea, gammagrafı́a de tiroides y el renograma hasta los más actuales que se encuentran en pleno desarrollo como los radiofármacos PET y los utilizados en el campo de la neuro-psiquiatrı́a. 1.1.3. Tipos de estudios La mayorı́a de los estudios en Medicina Nuclear son estudios in-vivo en los que es necesario administrar el radiofármaco al paciente para obtener, mediante detección externa de la radiación electromagnética, la información deseada en forma de imágenes que representan la distribución del radiofármaco. Los estudios in-vitro no precisan de la administración del radiofármaco al paciente y solamente se procesan muestras biológicas. Finalmente, existen estudios vivo/vitro, basados en la medida de muestras biológicas después de haber administrado al paciente un radiofármaco. La administración de un radionúclido dentro del cuerpo suele realizarse por vı́a intravenosa, aunque también puede administrarse por vı́a oral, combinándolo con comida, o por vı́a gaseosa inhalándolo como un gas o aerosol. La producción de radionúclidos en Medicina Nuclear se deriva o bien de procesos de fisión en reactores nucleares, los cuales producen radioisótopos con larga vida media, o bien de procesos de activación neutrónica, en un reactor nuclear, o mediante partı́culas cargadas en aceleradores (ciclotrones). En estos se producen radioisótopos con vidas medias cortas, o bien se aprovecha la ventaja de procesos de decaimiento natural en generadores dedicados, como por ejemplo, molibdeno/tecnecio o estroncio/rubidio. Los radionúclidos emisores gamma más utilizados en medicina son: - 99m Tc - 123 I con una semivida de 6.01 horas con una semivida de 13.3 horas 1. Introducción a la Medicina Nuclear - 131 I - 111 In con una semivida de 2.83 dı́as - 67 Ga con una semivida de 78 horas - 201 Tl con una semivida de 73 horas con emisión β − además de γ con una semivida de 8.02 dı́as Los radionúclidos emisores de positrones utilizados en medicina son: - 18 F con una semivida de 109.8 minutos - 13 N con una semivida de 9.96 s - 15 O con una semivida de 2.07 s - 11 C con una semivida de 20.4 s - 87 Rb 1.1.4. con una semivida de 1.27 s Dosis de radiación Un paciente sometido a un procedimiento de Medicina Nuclear recibe una dosis radiactiva. Actualmente se asume que cualquier dosis radiactiva presenta un riesgo. Las exploraciones en Medicina Nuclear son seguras ya que los radiofármacos de uso diagnóstico se administran en dosis muy pequeñas lo que hace que no tengan ninguna acción fármaco-terapéutica, ni efectos secundarios, ni reacciones adversas graves. Aun ası́, la dosis radiactiva recibida por un paciente en un estudio presenta un pequeño riesgo de inducir un cáncer. En este aspecto el riesgo es similar al de una exploración radiológica convencional, salvo que la dosis en Medicina Nuclear se suministra internamente al paciente, mientras que en radiologı́a la dosis es suministrada externamente. La dosis radiactiva de un estudio de Medicina Nuclear se expresa como una dosis efectiva en unidades de Sieverts (usualmente en el rango de los miliSievers, mSv). La dosis en un estudio se determina a partir de la actividad suministrada (unidades MegaBequerelios (MBq)), las caracterı́sticas fı́sicas del radiofármaco usado y su distribución en el cuerpo. La dosis efectiva suministrada a un paciente durante un estudio va desde los 6 µSv hasta los 37 mSv. Un estudio común de hueso con 600 MBq de 99m Tc-MDP tiene una dosis efectiva de 3 mSv [5]. Las emisiones alfa son raramente utilizadas hoy en dı́a en Medicina Nuclear, pero fueron utilizadas ampliamente antes de que se produjeran los 9 10 1.2. Tomografı́a computarizada por emisión de fotón único (SPECT) radioisótopos en los reactores nucleares y los aceleradores de partı́culas. Actualmente aún se utilizan en algún procedimiento terapéutico [6]. 1.2. Tomografı́a computarizada por emisión de fotón único (SPECT) La tomografı́a por emisión de fotón único es una técnica de imagen tomográfica en Medicina Nuclear que utiliza rayos γ. Esta técnica, muy similar a la empleada en gammagrafı́a planar (ver capı́tulo 4), se diferencia en que es capaz de generar imágenes tridimensionales (3D) del objeto. 1.2.1. Principios Del mismo modo que una imagen de rayos X es una imagen proyectada en dos dimensiones (2D) de una estructura 3D, la imagen obtenida por una gammacámara es una proyección 2D de la distribución 3D del radionucleido. Las imágenes SPECT se obtienen utilizando una gammacámara para adquirir múltiples imágenes 2D (también llamadas proyecciones) desde múltiples ángulos. Una vez se han adquirido todas las proyecciones, se utiliza un ordenador para aplicar un algoritmo de reconstrucción tomográfica a las múltiples proyecciones, produciendo una base de datos 3D. La evaluación de estos datos se realiza visualizando secciones a lo largo de cualquier eje del cuerpo, similares a los obtenidos de otras técnicas tomográficas. Para adquirir imágenes de SPECT, la gammacámara debe rotar alrededor del paciente. Las proyecciones se adquieren con diferencia angular de 3 o 6 grados. En la mayorı́a de casos se realizan imágenes planares hasta cubrir un giro de 360o para obtener una reconstrucción óptima. El tiempo por proyección puede variar de 15 a 45 segundos según la actividad utilizada y el tipo de estudio que se realice. Un sistema SPECT con multicabezal pueden acelerar la adquisición o permitir la obtención de imágenes de mayor calidad. Por ejemplo, una cámara con doble cabezal puede usarse con los cabezales enfrentados a 180o , permitiendo que 2 proyecciones 1. Introducción a la Medicina Nuclear 11 sean adquiridas simultáneamente en cada adquisición, de modo que cada cabezal requerirá únicamente un giro de hasta 180o . 1.2.2. Aplicaciones clı́nicas Debido a que el SPECT permite una localización precisa en el espacio tridimensional, se puede utilizar para obtener información acerca de la función de órganos internos, evitando la superposición de información que se produce en las imágenes planares. Gracias a esto y a la gran diversidad de los radiotrazadores existentes, las aplicaciones clı́nicas de SPECT incluyen la evaluación de funciones del cerebro, corazón, esqueleto y pulmón entre otras. A continuación se comentan brevemente algunas aplicaciones. Las aplicaciones clı́nicas más habituales del SPECT en el cerebro se basan en el uso de radiofármacos de perfusión sanguı́nea y radiofármacos ligandos de neurorreceptores. Los estudios de perfusión permiten estudiar patologı́as como la demencia, la epilepsia o los accidentes vasculares cerebrales, mientras que los radioligandos de neurorreceptores han encontrado gran aplicación clı́nica en trastornos del movimiento. En cardiologı́a, el SPECT se usa para valorar la viabilidad del tejido miocárdico y ası́ ayudar a diferenciar entre isquemia e infarto. Para obtener imágenes del esqueleto se usa como trazador el 99m T c − M DP . Éste se utiliza para la detección de un gran número de enfermedades óseas co- mo la osteomielitins, sacroileitis, espondilolisis, necrosis avascular, metástasis, artritis, etc. En el pulmón, comúnmente se lleva a cabo la medida de la ventilación y perfusión usando trazadores marcados con 99m T c para detectar tromboembolis- mos pulmonares o para evaluar la función pulmonar en pacientes con enfermedad pulmonar obstructiva crónica 12 1.2. Tomografı́a computarizada por emisión de fotón único (SPECT) 1.2.3. SPECT para animales pequeños La evolución del conocimiento de la biologı́a ha estimulado la exploración de novedosas terapias especı́ficas a nivel de seguimiento molecular asociado a enfermedades cardı́acas, desordenes neurológicos, cáncer y muchos otros procesos patológicos. A menudo, identificar el rol de una molécula en una enfermedad mediante un experimento in-vitro no necesariamente se traslada a un entendimiento de sus interacciones con otras moléculas en procesos in-vivo. Los modelos de enfermedades en pequeños animales presentan un enlace crı́tico entre descubrimientos a nivel molecular e implementación de diagnósticos o terapias clı́nicas relevantes. En particular, técnicas de imagen como SPECT permiten el estudio de procesos fisiológicos a nivel molecular gracias a imágenes obtenidas con diferentes trazadores. Esto permite medir procesos cinéticos relativamente lentos. Son también interesantes los estudios en los que se pueden seguir simultáneamente dos o más moléculas utilizando radioisótopos de diferente energı́a, en éstos la resolución energética del detector juega un papel importante. Los SPECT de uso clı́nico son de un elevado tamaño en comparación con los preclı́nicos debido a la diferencias de tamaños de las personas con respecto a las ratas o ratones que se utilizan para investigación. Esto implica que los SPECT clı́nicos tengan una baja resolución, alrededor de 7 a 10 mm. Sin embargo, si pensamos en el campo de la investigación con animales pequeños, el sujeto es mucho más reducido (aproximadamente un factor 10), por lo que se pueden utilizar detectores mas pequeños consiguiendo reducir los costes y obtener resoluciones, en algunos casos, menores al milı́metro gracias a la utilización de colimadores que permiten la amplificación del sujeto a estudio al proyectar. Esta resolución submilimétrica es la principal ventaja del SPECT con respecto a los PET de animales, ya que en éste la resolución viene limitada por el alcance del positrón (valor medio de 0.6 mm para 18 F − F DG). Por contra los sistemas SPECT de animales suelen ofrecer una peor sensibilidad que los PET de animales pequeños. 1. Introducción a la Medicina Nuclear (a) nanoSPECT (c) Inveon 13 (b) U-SPECT II (d) x-SPECT Figura 1.2: Cuatro SPECT comerciales para animales pequeños. 1.2.3.1. Sistemas comerciales de SPECT para animales pequeños En la última década se han desarrollado varios sistemas SPECT para animales pequeños. En la actualidad hay una gran variedad de equipos comerciales de SPECT especı́ficos para investigación con animales pequeños. En la figura 1.2 se observan algunos de estos equipos junto con una muestra de las imágenes que se obtienen. En la tabla 1.1 se pueden ver las caracterı́sticas que presentan algunos de los principales equipos comerciales para animales pequeños. 1.2. Tomografı́a computarizada por emisión de fotón único (SPECT) 14 Fabricante Equipo Cabezales Bioscan nanoSPECT 4 Gamma Medica x-SPECT 2 GE Healthcare Explorer SPECT 10 Molecular imaging U-SPECT 3 NeuroPhysics MollyQ 8 Siemens Inveon 1-4 Colimador 9 pinhole diámetro 0.7mm 1 pinhole diámetro 1mm 7 pinhole 75 pinhole diámetro 0.6mm 10042 canales diámetro 0.343mm multipinhole diámetro 1.0mm Detector Resolución Sensibilidad FOV 3 215x230x10mm NaI(Tl) (pixel 2mm) ≤0.5mm a 20mm ≥2000cps/MBq [20-290]mm con 33 PMT’s 112x112x6mm3 1.12mm a 20mm 137.4cps/MBq (pixel 2mm) 1.14mm a 30mm 52.1cps/MBq 112mm con 25 PMT 1.45mm a 40mm 80x80x5mm3 CzT ≤1mm ≥400cps/MBq 30mm (pixel 2.46mm) 510x380 mm2 510x380 mm2 con 6 PMT’s 150x150x10mm3 NaI (pixel 2mm) 0.45mm 22000cps/MBq [1-100a ]mm 0.8mm 31000cps/MBq [30-175]mm 1.0mm 200cps/MBq [20-160]mm Tabla 1.1: SPECT comerciales y sus principales caracterı́sticas. a Para conseguir los 100mm de FOV son necesarios varios beds Capı́tulo 2 Motivación y objetivos de la tesis El SPECT es una técnica de imagen molecular que por sus caracterı́sticas subyacentes, ha sido rápidamente adaptada para su uso en animales de laboratorio. Al igual que otras técnicas de imagen molecular, el SPECT esta basado en el principio del trazador y en su capacidad para la medida de la distribución de concentraciones muy pequeñas de compuestos. Estos trazadores suelen tener una vida media relativamente larga, lo cual facilita su disponibilidad. Además, el marcado radiactivo de ligandos con afinidad por moléculas endógenas es una práctica común en los departamentos de Medicina Nuclear de muchos hospitales, siendo estas razones fundamentales las que hacen del SPECT una técnica muy atractiva para su utilización como herramienta de investigación preclı́nica. Por otro lado, nuestro grupo de investigación se dedica fundamentalmente al desarrollo de detectores de radiación gamma, los cuales podrı́an adaptarse para su utilización como detectores en un sistema SPECT. Por estos motivos, surgió este proyecto con la intención de diseñar, calibrar y poner en funcionamiento un sistema SPECT para animales pequeños utilizando como detector la mini gammacámara que previamente se habı́a desarrollado en el grupo. 15 16 El trabajo de esta tesis consistirá en el desarrollo y puesta en marcha de dos prototipos SPECT para animales pequeños utilizando la mini gammacámara Sentinella [7]. Se realizará una primera prueba de concepto con el objetivo de comprobar la viabilidad del proyecto, dicho prototipo se diseñará y desarrollollará en el Servicio de Medicina Nuclear, Hospital Clı́nico y Provincial de Barcelona bajo la supervisión de los Doctores Javier Pavı́a y Domènec Ros y en colaboración con Núria Roé y Francisco Pino. En el segundo prototipo se pretende ampliar la prueba de concepto y desarrollar un nuevo prototipo con el que se obtenga un mayor rendimiento del SPECT también con gammacámara Sentinella. Para ello este prototipo dispondrá de 2 gammacámaras Sentinella montadas opuestas en el set-up. En este prototipo se aplicarán distintas correcciones en la reconstrucción de la imagen e incorporará un colimador intercambiable entre pinhole y multipinhole con el fin de mejorar las prestaciones del SPECT. El diseño del nuevo colimador multipinhole se optimizará mediante simulación Monte Carlo con Geant4 (versión Geant 4.9.2). Finalmente se intentará desarrollar un método de cuantificación de imagen, que permita relacionar las cuentas de la imagen reconstruida con la actividad del objeto o sujeto a estudio. Este proyecto se pretende diseñar y desarrollar en el Instituto de Fı́sica Corpuscular (IFIC) en colaboración con la empresa Oncovision bajo la tutela de José Marı́a Benlloch (Profesor de Investigación, CSIC) y Antonio J. González (Oncovision). Parte II Descripción teórica 17 Capı́tulo 3 Fı́sica de detección de rayos gamma En el capı́tulo 1 se ha introducido la Medicina Nuclear y más concretamente de los sistemas SPECT. Este capı́tulo tratará sobre la fı́sica que hay detrás de dichos sistemas. 3.1. Radiactividad Los nucleidos que se encuentran en la naturaleza pueden ser estables o inestables. A los nucleidos inestables se les denomina también nucleidos radiactivos o radionucleidos. Se conoce como proceso radiactivo a la transición espontánea desde un estado energético inicial del núcleo a un estado final. Esta transición se produce porque la energı́a total del sistema inicial es superior a la del sistema final. En la transición se produce la emisión de radiación ya sea en forma de partı́culas o de radiación electromagnética. Básicamente hay tres tipos de procesos radiactivos: 19 20 3.2. Interacción de la radiación γ con la materia Radiactividad α. La partı́cula emitida es un núcleo de 42 He formada por dos neutrones y dos protones. Solo se presenta en nucleidos pesados. Para nucleidos ligeros (A<150) es muy improbable. Radiactividad β. El núcleo emite un electrón e− (radiactividad β − ) o un positrón e+ (radiactividad β + ). En contraposición al proceso α, este tipo de radiactividad se puede presentar cualquiera que sea el número atómico Z del nucleido inicial. Emisión de rayos γ. El modelo de capas nuclear dice que en su estado de mı́nima energı́a, estado fundamental, el núcleo tendrá los nucleones situados en las capas de menor energı́a posible. Cuando el núcleo presenta una configuración en la cual los nucleones no ocupan las capas de menor energı́a se dice que está en un estado excitado. Si un núcleo se encuentra en dicho estado se producirá una transición isomérica, pasando a su estado fundamental o a un estado excitado de menor energı́a emitiendo radiación electromagnética denominada radiación γ. A este cambio de estado energético se le denomina transición isomérica. Los rayos γ emitidos tienen energı́as discretas que corresponden a la diferencias de energı́as de los estados o niveles entre los que se ha producido la transición. Un núcleo puede quedar en un estado excitado como consecuencia de cualquiera de las transiciones radiactivas anteriores o como resultado de una reacción nuclear. 3.2. Interacción de la radiación γ con la materia En la interacción de los fotones con la materia los procesos fı́sicos fundamentales son: el efecto fotoeléctrico, la dispersión de Rayleigh, el efecto Compton y la producción de pares. La probabilidad de que un rayo-γ sufra uno de estos procesos cuando atraviesa la materia está definida por la sección eficaz de cada uno de los procesos. La probabilidad de que un fotón interaccione con la materia viene dado por la sección eficaz 3. Fı́sica de detección de rayos gamma 21 atómica total que es la suma de las secciones eficaces para cada uno de los procesos fı́sicos de interacción, σtot = σpe + σray + σComp + σpar , (3.1) donde σpe es la sección eficaz de efecto fotoeléctrico atómico, σray es la sección eficaz Rayleigh, σComp es la sección eficaz Compton y σpar es la sección eficaz debido al proceso de producción de pares. Cuanto mayor es el número atómico (Z) de la materia con la que interaccionan los fotones mayor es la sección eficaz y por lo tanto más eficiente es el frenado de estos en la misma y por lo tanto existe una mayor probabilidad de que se produzcan los procesos fı́sicos anteriormente nombrados. Cuando un rayo gamma pasa a través de la materia, la probabilidad de absorción en una capa fina es proporcional al grosor de dicha capa, lo que lleva a un decrecimiento exponencial de la intensidad. N = N0 e−µd , (3.2) donde N es el número de rayos-γ transmitidos a través de la capa de grosor d, N0 el número de rayos-γ incidentes y µ es el coeficiente de atenuación lineal, el cual, se define como la fracción de fotones que interaccionan con el material por unidad de grosor. Dicho coeficiente, para un determinado material [8], está relacionado con la sección eficaz total mediante la siguiente expresión: µ= NA ρσtot , A (3.3) donde NA es el número de Avogadro, ρ es la densidad del material que atraviesan los rayos-γ y A es el número atómico del material. A partir de la ecuación (3.1) podemos obtener la expresión del coeficiente de atenuación lineal total en función de los componentes debidos a cada una de las interacciones fı́sicas de la radiación electromagnética ionizante: 22 3.2. Interacción de la radiación γ con la materia µtot = µpe + µray + µComp + µpar . (3.4) Los coeficientes de atenuación son dependientes de la energı́a. Para el rango de energı́as de los rayos γ utilizados en medicina nuclear, hasta 662 keV para el 137 Cs, la producción de pares no se produce, por lo que se puede eliminar de las ecuaciones. También debe tenerse en cuenta la dispersión de Rayleigh, que si que se produce en estos rangos energéticos, tampoco influirá en nuestro estudio ya que la sección eficaz de dicho proceso es dos ordenes de magnitud menor que los debidos al efecto Compton y el efecto fotoeléctrico, por lo que se podrá despreciar. 3.2.1. Efecto fotoeléctrico Se conoce como efecto fotoeléctrico a la interacción que se produce entre un rayo γ y un átomo obteniendo como resultado la liberación de un electrón de una capa interna con la siguiente energı́a [9]: Ee = Eγ − Ebe , donde Ebe es la energı́a de enlace del electrón. Para este proceso, la sección eficaz varı́a con la energı́a de manera discontinua dependiendo de las capas y subcapas atómicas. No hay una expresión analı́tica válida para la expresión de la probabilidad de la sección eficaz del efecto fotoeléctrico común para todos los rangos energéticos. Para energı́as de los rayos gamma en la capa K, donde se encuentran la mayorı́a de electrones que pueden sufrir efecto fotoeléctrico, la expresión para la sección eficaz es la siguiente: σpe √ 8 5 = πre2 4 2α4 Zmaterial 3 me c2 Eγ 7/2 , (3.5) donde re es el radio clásico del electrón (re ≈ 2,83 × 10−15 m), me es la masa del electrón (me = 511 keV ), α es la constante de estructura fina (α = 1/137) y c es la velocidad de la luz en el vacı́o (c = 2,998 · 108 m/s). Como se puede observar en la ecuación 3.5 la probabilidad de que se produzca absorción fotoeléctrica depende fuertemente del número atómico del absorbente (Z) y de la energı́a de fotón incidente (Eγ ). 3. Fı́sica de detección de rayos gamma 3.2.2. 23 Efecto Compton El efecto Compton o dispersión Compton es un proceso fı́sico en el cuál un fotón de energı́a Eγ interacciona con un electrón libre. Se entiende por electrón libre un electrón cuya energı́a es baja en comparación con la energı́a que lleva el rayo γ. Tras la interacción, el fotón cambia su dirección y pierde parte de su energı́a, quedándose con una energı́a Eγ ′ menor que la energı́a que poseı́a inicialmente, de esta forma el electrón escapa con una energı́a cinética, T , que será T = Eγ − Eγ ′ . La energı́a final del fotón dispersado viene dada por: Eγ ′ = Eγ , 1 + γ(1 − cosθ) (3.6) donde θ es el ángulo entre el fotón incidente y el dispersado, γ = Eγ /me c2 y me c2 es la energı́a de la masa en reposo del electrón. La energı́a máxima transferida al electrón es 2me c2 /3 para la retrodispersión, mientras que no hay pérdida de energı́a cuando el fotón dispersado sigue en la misma dirección que el fotón inicial. Esta es la dirección más probable en que se espera que el fotón se disperse como se puede deducir de la ecuación de Klein-Nishina [10] de la sección eficaz diferencial para el efecto Compton: dσ 1 re2 γ 2 (1 − cosθ)2 2 = 1 + cos θ + , dΩ 2 [1 + γ(1 − cosθ)]2 1 + γ(1 − cosθ) donde re es el radio del electrón y dσ dΩ (3.7) es la sección eficaz diferencial normalizada. Para rayos γ poco energéticos, el efecto fotoeléctrico es el proceso más relevante con independencia del número atómico del absorbente. Para energı́as del orden del M eV el efecto fotoeléctrico muestra una fuerte dependencia con Z y su probabilidad de producción es menor que la del efecto Compton. 24 3.3. Interacción de los rayos γ con un cristal centellador 3.3. Interacción de los rayos γ con un cristal centellador Una vez que el rayo γ interacciona con el cristal centellador, ya sea por efecto fotoeléctrico o por Compton, toda o parte de la energı́a se transfiere a un electrón, el cual, al desexcitarse, genera luz de centelleo que se expande isotrópicamente a través del medio. La luz generada en el interior del cristal centellador sigue las leyes fı́sicas de propagación en un medio y las de reflexión en superficies. La probabilidad de que los fotones sufran una reflexión en una interfaz óptica viene dada por el coeficiente de reflexión de la ecuación de Fresnell [11]: 1 sin2 (θi − θt ) tan2 (θi − θt ) + , R= 2 sin2 (θi + θt) tan2 (θi + θt ) (3.8) donde R es la probabilidad de reflexión y, θi y θt son respectivamente los ángulos de incidencia y de transmisión con respecto a la normal a la interfaz. Por lo tanto, la probabilidad de transmisión T será la complementaria a R, es decir, T = 1 − R. Por otra parte, dependiendo de las propiedades fı́sicas de la superficie del cristal: ı́ndice de refracción, rugosidad,. . . la luz puede sufrir reflexión especular, difusión ideal o una mezcla de ambos que denominaremos como modelo hı́brido (ver figura 3.1). 3.3.1. Reflexión especular: ley de Snell Si disponemos de dos medios en contacto, que tienen diferente ı́ndice de refracción, un rayo se refractará especularmente cuando el rayo incidente atraviese la interfaz óptica entre ambos medios. El rayo reflejado sale con el mismo ángulo que el incidente sobre la superficie entre regiones y el rayo refractado cambia de dirección dependiendo de los ı́ndices de refracción de cada región de acuerdo con la ley de la refracción de Snell: ni sin(θi ) = nt sin(θt ), (3.9) 3. Fı́sica de detección de rayos gamma 25 (a) Reflexión especular. (b) Difusión ideal. (c) Modelo hı́brido de reflexión. Podemos observar el esquema de comportamiento de la luz reflejada para un rayo de intensidad I que incide sobre una superficie difusa formando un ángulo θ con la normal. La figura muestra este comportamiento para tres ángulos diferentes. Figura 3.1: Comportamiento de la luz. donde ni y nt son los ı́ndices de refracción de la región de incidencia y la de trasmisión y, θi y θt son los ángulos de incidencia y transmisión con respecto a la normal a la superficie entre regiones respectivamente. 3.3.1.1. Reflexión interna total Dentro de la ley de Snell, un efecto a tener en cuenta es la reflexión interna total que ocurre cuando la luz incide con la superficie entre regiones con un ángulo de incidencia (θi ) mayor que el ángulo crı́tico (θC ) que se calcula con la siguiente expresión: sin θC = nt . ni (3.10) Cuando tenemos un ángulo de incidencia igual al ángulo crı́tico (θC ) el rayo refractado se desvı́a 90o respecto a la normal a la superficie entre regiones. Por lo tanto, para ángulos de incidencia mayores que el ángulo crı́tico, se dice que la luz sufre 26 3.3. Interacción de los rayos γ con un cristal centellador reflexión interna total. Como consecuencia, no hay componente refractada de la luz. Este efecto se produce siempre que se cumpla la condición ni > nt . La reflexión interna total es de interés especial cuando se usan gammacámaras con tubo fotomultiplicadores (PMT, Photo Multiplier Tubes) como en nuestro caso (ver capı́tulo 4). En ausencia de rayos refractados, algunos de los fotones ópticos que inciden en el fotocátodo podrı́an no ser detectados y por lo tanto disminuirı́an la eficiencia de detección. Esto se debe a la diferencia de los ı́ndices de refracción en las distintas interfases de la gammacámara (cristal, pegamento/grasa y fotocátodo). 3.3.2. Difusión ideal Este fenómeno se produce cuando un rayo de luz incide sobre una superficie rugosa. En esta configuración los rayos son reflejados y dispersados en todas direcciones. De la misma manera el proceso de refracción también se ve afectado y como consecuencia la luz transmitida se dispersa en el medio. En el caso ideal en el que tuviéramos un medio difusor perfecto la luz incidente sobre la superficie entre regiones seguirı́a la Ley de Lambert, en la cual la intensidad de luz de una pequeña región para un medio difusor ideal en cualquier dirección es proporcional al coseno del ángulo entre la dirección y la normal. No obstante, el número de fotones dispersados (Idisp (θr )) depende del coseno del ángulo de la luz incidente. En las distribuciones Lambertianas el ángulo de reflexión es independiente del ángulo de incidencia, como podemos observar en la siguiente ecuación: Idisp (θr ) = kd Io cos(θr ) , (3.11) donde θr es el ángulo de reflexión respecto a la normal a la superficie, kd es un parámetro dependiente de la longitud de onda de la luz que toma valores entre 0 y 1 dependiendo de la difusividad del medio e I0 = Ii · cos(θi ), donde Ii es la intensidad de la luz incidente y θi el ángulo que forma ésta con la normal a la superficie. Para un difusor ideal Lambertiano, kd = 1. En la figura 3.1(b) se muestra el esquema del comportamiento de la luz reflejada para un rayo de intensidad Ii que incide sobre una superficie difusa. 3. Fı́sica de detección de rayos gamma 3.3.3. 27 Modelo hı́brido Aunque existen varios modelos hı́bridos como por ejemplo el propuesto por Torrance y Sparrow a finales de 1960 [12], nosotros vamos a utilizar el modelo de Phong [13]. Dicho modelo describe la reflexión en un medio material de una manera muy realista, ya que es una mezcla entre la difusión ideal y la reflexión especular. En este modelo, la intensidad de la luz está formada por tres componentes: luz ambiente, luz especular y luz difusa. La luz ambiente es la luz que proviene de todas las direcciones e ilumina todas las caras del objeto por igual. La luz difusa es la luz que proviene de una dirección pero se refleja en todas direcciones. La luz especular es la luz que proviene de una dirección y se refleja sólo en una dirección. Teniendo en cuenta esta clasificación de la luz podemos calcular la intensidad de la misma con el modelo de Phong mediante la expresión: I = ka Ia + kd Iinc cosφ + ks Iinc cosm (φ − α) , (3.12) donde I es la intensidad de la luz reflejada, Ia es la intensidad de la luz ambiente, Iinc es la intensidad de la luz incidente, ka es el coeficiente de reflexión ambiente, kd es el coeficiente de reflexión difusa, ks el coeficiente de reflexión especular, α el ángulo de incidencia con respecto a la normal a la superficie para la luz que no proviene del ambiente, φ el ángulo entre la luz reflejada y la normal a la superficie y m el coeficiente superficial, el cual nos indica cuan brillante es la superficie (cuanto más brillante sea más alto será m). La selección de estos parámetros caracteriza la luz difundida y su distribución (figura 3.1(c)). La componente especular depende de la dirección de la normal a la superficie. Capı́tulo 4 La gammacámara La gammacámara o cámara gamma es un dispositivo de captura de imágenes, comúnmente utilizado en Medicina Nuclear como instrumento para el diagnóstico de enfermedades. Consta de un equipo de detección de radiación gamma. La modalidad de diagnóstico clı́nico que realizan las gammacámaras se denomina gammagrafı́a. Una gammacámara consiste en uno o más detectores (normalmente detectores de centelleo) ópticamente acoplados a un grupo de fotosensores, generalmente se utilizan los PMTs. A este conjunto ensamblado de detector y fotomultiplicador se le conoce como el cabezal de la gammacámara. Dicho cabezal se rodea de una capa de Plomo, o de Tungsteno en algunos casos, lo suficientemente gruesa para evitar la detección de radiación no deseada. Éste está unido a una estructura metálica, denominada gantry, que permite los distintos movimientos del cabezal detector (girar, acercarse y alejarse). Finalmente todo el sistema está controlado por un ordenador que gestiona los desplazamientos de las gammacámaras, ası́ como la adquisición y almacenamiento de los datos [14]. Las gammacámaras se asemejan en cierta manera a un dispositivo óptico, si bien no se conoce ningún componente que focalice y por tanto que actúe como lente para ondas electromagnéticas de longitud de onda tan alta como los rayos γ. Por este motivo es necesario utilizar colimadores para poder determinar la dirección de la que procede el rayo γ. El funcionamiento general de una cámara gamma se basa 29 30 4.1. Cristal centellador en la detección de los rayos gamma que tras ser emitidos en el cuerpo del paciente y atravesar la abertura del colimador impactan sobre el cristal centellador. En él depositan su energı́a y generan un número de fotones de centelleo que depende únicamente del material centellador y de la energı́a del rayo gamma incidente. La luz se emite isotrópicamente en el cristal y es recolectada por los PMTs. A la salida de los tubos la corriente eléctrica producida por los mismos es recogida, digitalizada y procesada por un sistema electrónico. Las señales obtenidas a la salida del sistema electrónico proporcionan la información necesaria para obtener la energı́a cedida y la posición de la interacción, que es la información necesaria para formar las imágenes. 4.1. Cristal centellador El tipo de detector que se suele utilizar en las cámaras gamma es un detector de centelleo, debido a su bajo coste respecto a los semiconductores. Estos detectores utilizan el hecho de que ciertos materiales emiten un pequeño flash de luz cuando la radiación excita sus átomos o moléculas perdiendo toda o parte de su energı́a. Las caracterı́sticas que debe cumplir un centellador ideal son: Linealidad entre la energı́a depositada y la luz emitida. Alta eficiencia de conversión de la energı́a de excitación en radiación fluorescente. Una alta eficiencia favorece la resolución espacial y la temporal. Medio transparente a la luz de su propia emisión. Tiempo de decaimiento de luz corto para que la respuesta sea rápida. Material de buena calidad óptica y fácil de producir, bajo costo y no higroscópico. Índice de refracción ≈ 1.5 para que permita un acoplamiento eficiente de la luz de centelleo al fotomultiplicador. No hay ningún material centellador que cumpla todos estos criterios a la vez por lo que habrá que sacrificar algún factor en función de los requerimientos que se tengan 4. La gammacámara para cada aplicación particular. La energı́a de la radiación incidente para los isótopos utilizados con gammacámaras no tienen suficiente energı́a para tener producción de pares, por tanto, la interacción con la materia será mediante efecto fotoeléctrico o efecto Compton. Si se minimiza la interacción Compton se evitará introducir en las imágenes información incorrecta como la que corresponde a fotones dispersados en el propio paciente. Además se evita el empeoramiento en la detección de la posición de impacto cuando la dispersión ocurre en el cristal detector y el fotón dispersado vuelve a interaccionar con el material centelleante. Por ello son más eficientes los materiales de alto número atómico (ver tabla 4.1). Densidad Número λmax1 Indice2 Luz Eficiencia3 Constante Higros3 Material (g/cm ) atómico (nm) refracción producida conversión decaimiento copicidad efectivo (fotones/keV) (ns) NaI(Tl) 3.67 50 410 1.85 38 100 230 sı́ CsI(Tl) 4.51 54 550 1.79 52 45 1000 leve CsI(Na) 4.51 54 420 1.85 39 85 630 leve CsI(puro) 4.51 54 310 1.95 17 5 16 no CsF 4.64 49 390 1.48 2 6 5 sı́ YAG(Ce) 4.55 32 550 1.82 8 15 70 no BGO 7.13 63 480 2.15 9 12 300 no LaBr3(Ce) 5.08 48 380 1.9 63 130 26 sı́ LYSO 7.3 65 428 1.82 25 75 40 no LSO 7.4 66 420 1.82 30 40 no Plásticos 1.03 375-600 1.58 10 25-30 1-3 no Tabla 4.1: Caracterı́sticas principales de algunos de los cristales centelladores más utilizados. 4.2. Fotomultiplicador En una cámara gamma los PMT son los responsables de convertir la luz que se produce en el cristal centellador en una corriente eléctrica medible. 1 Longitud de onda da la máxima emisión espectral. Índice de refracción a la longitud de onda de la máxima emisión espectral. 3 Porcentaje de luz de salida, respecto a NaI(Tl), cuando el cristal se acopla a un PMT con fotocátodo bialcalino. 2 31 32 4.2. Fotomultiplicador Figura 4.1: Esquema de un fotomultiplicador. Un PMT consta de un fotocátodo de material fotosensible acoplado a una cadena de dı́nodos que multiplica los electrones producidos en el fotocátodo generando una avalancha. Al terminar la cadena de dı́nodos, los electrones se dirigen hacia el ánodo donde se recoge su carga, la cual es proporcional a la cantidad de energı́a que depositaron los fotones en el cátodo. Todo ello se encuentra encerrado en un tubo de vacı́o y sometido a un alto voltaje escalonado a través de la estructura fotocátodo-dı́nodos-ánodo (ver figura 4.1). Si el cátodo y la cadena de dı́nodos son lineales, la corriente a la salida del PMT será directamente proporcional al número de fotones incidentes, de este modo se puede relacionar la intensidad de la corriente de salida con la energı́a depositada en el cristal. Sin embargo, no nos da información de la posición de entrada del fotón y por tanto del lugar de interacción del rayo gamma dentro del cristal. Para estimar dicha posición es necesaria la utilización de varios fotomultiplicadores, o bien, la utilización de un fotomultiplicador sensible a posición (PSPMT Position Sensitive Photo Multiplier Tubes). Si se utilizan varios fotomultiplicadores para recolectar todos los fotones emitidos por el rayo gamma al desintegrarse, la posición de incidencia será la posición de cada uno de los fotomultiplicadores en el cristal ponderada por la cantidad de luz recolectada para cada desintegración. Los PSPMT, en cambio, poseen una red de ánodos y cátodos que mantienen una separación espacial entre las nubes electrónicas originadas en los distintos fotocátodos lo que permiten relacionar la posición de salida del haz de luz con la posición del fotón incidente. La estructura más utilizada es una estructura dinódica de canales metálicos muy 4. La gammacámara finos y compactos tal y como se muestra en la figura 4.2. Con esta estructura se consigue una nube electrónica estrecha, lo que permite tener una buena resolución espacial y temporal. Esto influye también positivamente en la inmunidad del PMT a los campos magnéticos, y normalmente se refuerza con una estructura metálica que rodea al PMT (excepto en la zona del fotocátodo). Figura 4.2: Estructura dinódica de canales metálicos. En cuanto a las estructuras anódicas podemos encontrar estructuras multianódicas o de ánodos pixelados, en las que la carga queda prácticamente confinada al ánodo en que ha impactado y se lee la señal de salida de cada uno de los ánodos. 4.3. Colimadores Para obtener una imagen con una cámara gamma es necesario limitar los rayos γ que proceden de la fuente y se dirigen hacia el cristal detector. Para dicho cometido, la mayorı́a de sistemas de imagen con rayos γ utilizan colimadores. El colimador absorbe la mayor parte de los rayos gamma incidentes, dejando pasar únicamente los rayos que provienen de una dirección privilegiada, de este modo se establece una relación unı́voca entre la posición de detección y la dirección incidente [15]. 33 34 4.3. Colimadores A la hora de diseñar o seleccionar el colimador de la gammacámara hay que tener en cuenta que el sistema detector-colimador es el que nos permitirá caracterizar la gammacámara y por tanto, para un detector determinado hay que utilizar un colimador que permita ajustar el equipo a las caracterı́sticas deseadas. Algunas de las magnitudes que permiten caracterizar el sistema y que vienen definidas, o bien, ı́ntegramente por el colimador, o bien, por el sistema detector-colimador, son las siguientes: Eficiencia geométrica (G) Fracción de la radiación emitida por la fuente que es capaz de cruzar el colimador y llegar al detector. Depende principalmente del tipo de colimador seleccionado. Sensibilidad (S) Es el número de rayos gamma que atraviesan el colimador por unidad de tiempo y de actividad de la fuente. Es directamente proporcional a G; a la fracción de la radiación emitida que pertenece al fotopico que se desea medir, comúnmente conocido como branching ratio y que denotaremos por B (B=0.89 para la emisión de 140.5 keV del 99m T c [16]) y a la eficiencia cuántica del detector (Gc ) que es el porcentaje de los rayos gamma que llegan hasta el cristal que la gammacámara es capaz de detectar. Por tanto, la sensibilidad ya no depende exclusivamente del colimador como ocurre con G, sino que también depende del material y grosor elegidos para el detector. S ∝ B · G · Gc En la práctica la sensibilidad se mide dividiendo el número de cuentas detectadas por unidad de tiempo entre la actividad de la fuente emisora: S (cps/M Bq) = Cdetectadas (cps) A (M Bq) (4.1) Campo de visión Porción del espacio que puede ser visto por el detector cuando se utiliza el colimador (FOV, Field of View ). Depende del colimador y del tamaño del detector utilizado. 4. La gammacámara 35 Resolución espacial Es la mı́nima distancia a la que tienen que estar dos fuentes para que el sistema sea capaz de distinguirlas. Se tienen que distinguir las contribuciones de la resolución geométrica Rg , debida al colimador y la resolución intrı́nseca Ri , debida al cristal, fotomultiplicador y electrónica. Cada una de ellas se puede determinar como la amplitud total a mitad de altura (FWHM, Full Width at Half Maximum) de la función de dispersión obtenida con una fuente puntual (PSF, Point Spread Function). Se combinan en cuadratura para dar la resolución espacial total del sistema (Rtot ): Rtot = 4.3.1. q Rg2 + Ri2 (4.2) Tipos de colimadores El colimador ha de estar fabricado de un material altamente absorbente para los rayos gamma de las energı́as usadas en Medicina Nuclear, y solo debe dejar pasar la radiación por sus aperturas. Estas exigencias hacen que la eficiencia geométrica en general sea baja. Existen principalmente 4 tipos diferentes de colimadores según su geometrı́a: colimador paralelo, convergente, divergente y pinhole, mostrados en la figura 4.3. En la figura 4.4 se puede ver la variación de los parámetros sensibilidad, resolución y FOV con la distancia fuente-detector, para los 4 tipos de colimador descritos cuando se utiliza un detector pequeño de 40x40 mm2 [17] y [18]. El sistema esta destinado al estudio de pequeños animales (FOV entre 20 y 100 mm) y con un requerimiento de buena resolución espacial (del orden del milı́metro) para poder observar imágenes de órganos de pocos milı́metros de tamaño. Los colimadores que muestran una mejor resolución son el colimador pinhole y el convergente, sin embargo el colimador convergente, debido al pequeño tamaño del detector, solo se puede utilizar con objetos menores a 30 mm. Por tanto el colimador que mejor se adaptará a nuestro sistema es el colimador pinhole. 36 4.3. Colimadores (a) Colimador paralelo (c) Colimador divergente (b) Colimador convergente (d) Colimador pinhole Figura 4.3: Formación de imágenes para los distintos tipos de colimadores. 4.3.2. Colimador pinhole Se trata de un colimador con una única abertura de diámetro φ, denominada pinhole, situada a una distancia f del detector (distancia focal). Como se observa en la figura 4.3 con un colimador pinhole se invierte la imagen. Para minimizar los efectos de la penetración de los rayos gamma en el material atenuante alrededor de la abertura, el agujero es de tipo knife-edge con ángulo α, como se puede ver en la figura 4.5. 4. La gammacámara 37 Pinhole Paralelo Convergente Divergente Sensibilidad (mm) Sensibilidad vs distancia 800 600 400 200 0 20 30 40 50 60 70 80 90 70 80 90 70 80 90 Resolución (mm) Resolución vs distancia 20 0 20 30 40 50 60 FOV vs distancia FOV (mm) 150 100 50 0 20 30 40 50 60 Distancia fuente−colimador (mm) Figura 4.4: Comparativa de sensibilidad, resolución y FOV para los 4 colimadores más utilizados. Figura 4.5: Colimador pinhole. 38 4.3. Colimadores Campo de visión Por trigonometrı́a se puede ver que el campo de visión viene dado aproximadamente por: F OV = b LD , f donde b es la distancia entre el objeto y el colimador y LD la longitud del detector utilizado. El campo de visión y, por tanto, el tamaño de los objetos de los cuales es posible formar una imagen entera sobre el detector, dependen de las distancias b y f de manera que pueden ser más grandes o más pequeñas que el detector. En cualquier caso, como se verá a continuación, el colimador tipo pinhole es útil cuando los objetos que se quieren ver son pequeños y se utiliza un factor de amplificación grande [19]. Eficiencia geométrica La eficiencia geométrica de un colimador pinhole [20] para una fuente situada en un punto i cualquiera del FOV, a una distancia b de la abertura de diámetro φ, viene dada por la expresión: Gi = φ2e · cos3 θi , 16 · b2 (4.3) donde θi es el ángulo entre el rayo gamma procedente del punto i del FOV y la normal al colimador. Mientras que φe es el diámetro efectivo del pinhole que incluye los efectos de penetración de los rayos gamma por los bordes de la abertura definido como: v u u φe = tφ · tan (α/2) φ+2· +2· µ tan (α/2) µ 2 ! , (4.4) donde µ es el coeficiente de atenuación lineal para la energı́a y el material seleccionado. 4. La gammacámara 39 La ecuación (4.3) pone de manifiesto que la eficiencia geométrica para un colimador tipo pinhole depende cuadráticamente del tamaño de la abertura y del inverso de la distancia. Resolución espacial La resolución de un colimador pinhole se define en el plano objeto, y nos informa de la mı́nima distancia a la que pueden estar dos fuentes puntuales para considerarse distinguibles: Rg = b+f · φe . f Para obtener la resolución total hay que tener en cuenta también la resolución intrı́nseca ajustada por el factor de amplificación de la imagen, de modo que: Rtotal = 4.3.3. s Rg2 + b · Ri f 2 = s b+f · φe f 2 + b · Ri f 2 . (4.5) Colimador multipinhole El principio de funcionamiento de este colimador es el mismo que el de un colimador pinhole, pero en lugar de tener una única apertura el colimador multipinhole tiene múltiples aperturas, lo que permite obtener una imagen del FOV a través de cada una de ellas. Con estos colimadores se consiguen sensibilidades sustancialmente superiores a los colimadores pinhole. Existen dos posibles configuraciones, con y sin superposición en la imagen, según si existen, o no, zonas del detector a las que puedan llegar rayos gamma a través de más de una apertura. Campo de visión Cada uno de los agujeros tendrá su propio tamaño de FOV que viene dado por, F OVi = b LDi , f donde i = 1,...,N siendo N el número de agujeros totales del colimador. 40 4.3. Colimadores Inclinando la apertura del pinhole se desplaza el F OVi visible para dicho agujero, siendo el centro del F OVi en la dirección perpendicular a la inclinación el siguiente: Xcentro F OVi = Xpinholei + b · sin(ηi ), siendo Xcentro F OVi la posición del centro del FOV del pinholei en la dirección de inclinación de dicha apertura, Xpinholei la posición del centro de la apertura en dicha dirección y ηi el ángulo de inclinación del pinholei . Figura 4.6: Colimador multipinhole con agujeros inclinados. De este modo, se puede conseguir que el FOV para varios agujeros coincida a una distancia b determinada, dicho FOV para cada agujero se detectará en una parte diferente del cristal, ver figura 4.6. Ésto puede hacerse siempre y cuando el detector sea lo suficientemente grande, puesto que si una parte de dicho FOV, para algún agujero, cae fuera del detector esa parte del FOV se pierde. 4. La gammacámara 41 Eficiencia geométrica La eficiencia geométrica de cada uno de los pinholej del colimador multipinhole para una fuente situada en un punto i cualquiera del FOV, a una distancia bj de la abertura j de diámetro φ, viene dada por la siguiente ecuación: Gi,j = φ2e · cos3 (θi − ηj ) . 16 · b2j (4.6) Dicha ecuación es una ampliación de la ecuación (4.3) teniendo en cuenta el ángulo de inclinación del agujero. La eficiencia geométrica total para una fuente situada en un punto i será la suma de las eficiencias de todas las aperturas j del colimador Gmph = n X j=1 Gi,j ≡ F · Gph < n · Gph . (4.7) El factor F de aumento de eficiencia geométrica multipinhole respecto a la eficiencia geométrica pinhole es siempre menor que el número de pinholes y disminuye al aumentar la distancia entre agujeros y al reducir la distancia bz , siendo bz la componente perpendicular al colimador de la distancia entre las aperturas y la posición de la fuente emisora, bz es igual para todos los pinholes. Resolución espacial Para un colimador multipinhole en principio la resolución deberı́a calcularse igual que para un colimador pinhole de modo que la resolución viene dada por la ecuación (4.5). Sin embargo cuando existe superposición en el detector, es decir, que para un mismo pixel del detector el rayo gamma puede venir de más de un agujero, se tiene una incertidumbre añadida en la reconstrucción lo que conlleva una pérdida de resolución espacial. Capı́tulo 5 Reconstrucción de imágenes tomográficas 5.1. Introducción teórica a la reconstrucción El objetivo final de la técnica de SPECT es la obtención de la distribución tridimensional del trazador en el organismo u objeto a estudio. El sistema nos proporciona a través de la gammacámara proyecciones de dicha distribución a distintos ángulos. La reconstrucción de un volumen a partir de sus proyecciones es un problema que tiene solución exacta siempre que se disponga de suficientes proyecciones y que éstas sean perfectas. Sin embargo las proyecciones que se obtienen en una gammacámara distan de ser proyecciones ideales ya que están afectadas por los siguientes efectos: 1. El fenómeno de la Atenuación de fotones, algunos fotones no llegan al detector porque son absorbidos antes de alcanzar el detector. Es una pérdida de una parte de la información. 2. La detección de fotones dispersados, los cuales pueden haber cambiado de dirección. Representa la inclusión de información errónea. 3. Detección de radiación de fondo. 43 44 5.1. Introducción teórica a la reconstrucción 4. Respuesta del detector (respuesta impulsional: PSF). Depende del conjunto colimador-detector y degrada la imagen. 5. Efectos de borde de los cristales continuos. Se pierde parte de la información. 6. El ruido estadı́stico, debido a la escasa información recogida. 7. Posible perdida de información por el proceso de digitalización de los datos. Todos estos efectos conllevan que los datos obtenidos con una gammacámara sean una versión sesgada y deformada de unas proyecciones ideales, lo cual impide obtener la distribución real del trazador. La relación entre la distribución desconocida que se busca (u objeto 3D) y la cantidad fı́sica que puede ser medida (la proyección 2D) es conocida como la forward relationship. Para pasar del espacio objeto al espacio imagen se necesita una matriz de transición R, también conocida como matriz del sistema, la cual debe incluir la información geométrica y, en la medida de lo posible, los fenómenos fı́sicos que intervienen en el proceso. Si se denota la distribución desconocida como φ y la cantidad medida por la gammacámara como ψ, tenemos ψ = R · φ, cuya versión discreta se puede escribir como: y = R · x. El vector y es un muestreo de ψ. Para SPECT cada componente de y representa el número de cuentas obtenidas en un bin de la gammacámara para un ángulo determinado. El vector x es una representación finita del objeto desconocido φ. En nuestro caso, cada componente de x es el nivel de actividad en un vóxel dado. Finalmente, se tiene que el vector x que representa la distribución del trazador que buscamos será: x = R−1 · y. Sin embargo la matriz de transición, en general, no es invertible de modo que no se puede obtener la solución al problema directamente con la inversa de la matriz, por ello se deben utilizar aproximaciones para resolver el sistema. Las aproximaciones más utilizadas son los métodos analı́ticos y los iterativos, los cueles se describen brevemente a continuación. 5. Reconstrucción de imágenes tomográficas 5.2. Métodos analı́ticos Durante mucho tiempo los métodos analı́ticos fueron los más utilizados por su rapidez y sencillez a la hora de su implementación. El más conocido de los algoritmos de tipo analı́tico es el denominado Retroproyección Filtrada (RPF). En este método, la reconstrucción de la distribución del radiotrazador a partir de sus proyecciones se consigue por inversión de la transformada de Radon por medio de un algoritmo basado en el teorema de la sección central [21]. Este teorema demuestra que la Transformada de Fourier (TF) unidimensional de una proyección p(y) es una sección central de la TF bidimensional de la imagen f (x, y). Sin embargo, este método de reconstrucción no suele utilizarse demasiado si las proyecciones tienen poca estadı́stica, tal y como ocurre con los colimadores tipo pinhole debido a su baja eficiencia geométrica, ya que generan importantes artefactos en las imágenes reconstruidas cuando hay mucho ruido en las proyecciones. 5.3. Métodos iterativos Los métodos iterativos se basan en algoritmos que resuelven el problema de la reconstrucción tomográfica con un enfoque estadı́stico, lo que los hace más afines con la naturaleza del problema de la reconstrucción tomográfica, ya que la interacción de la radiación electromagnética con la materia responde a la misma esencia. A pesar de ser anteriores a la RPF, durante mucho tiempo no prosperó su difusión debido a su alta demanda computacional. La aparición de equipos más veloces y de nuevos métodos de reconstrucción basados en los anteriores, pero con modificaciones importantes atendiendo a su velocidad de cálculo, abrieron las puertas a la implementación de los métodos estadı́sticos. Tienen la ventaja, respecto de los algoritmos analı́ticos, de poder modelar y simular tanto procesos fı́sicos como fisiológicos. En particular, han demostrado ser muy exitosos cuando se incorpora la estadı́stica de Poisson, haciéndolos especialmente 45 46 5.3. Métodos iterativos interesantes para los casos de imágenes con baja cantidad de cuentas, donde la información contenida en cada vóxel está afectada de un alto porcentaje de error. Para tener un buen método de reconstrucción iterativo estadı́stico, éste debe satisfacer 5 requisitos [22]: - Parametrización finita de la imagen. - Modelo para describir el proceso fı́sico (matriz). - Modelo estadı́stico para describir los datos. - Función de coste a optimizar. - Algoritmo iterativo. Además, los métodos iterativos permiten corregir los efectos degradantes como la dispersión, la PSF o la atenuación, teniendo en cuenta dichos efectos en la matriz del sistema o en el algoritmo de reconstrucción. 5.3.1. Algoritmo de reconstrucción OS-EM. Uno de los algoritmos iterativos de reconstrucción más utilizados es el algoritmo OSEM (ordered-subset expectation-maximization), el cual es una implementación en “subconjuntos ordenados” del algoritmo ML-EM (maximum-likelihood expectation maximization) [23]. Las principales ventajas que tienen los algoritmos EM frente a otros algoritmos son las siguientes: Tienen en cuenta la naturaleza del ruido de Poisson en las proyecciones adquiridas, reduciendo ası́ los artefactos en las imágenes reconstruidas. Son robustos en aplicaciones tomográficas donde los datos adquiridos tienen un bajo número de cuentas siendo capaces de obtener reconstrucciones de buena calidad. Existen múltiples aplicaciones de algoritmos EM en SPECT. En la mayorı́a, la calidad de la imagen es buena pero la velocidad de conversión es lenta. Sin embargo, utilizar la técnica OS la cual procesa los datos en “subconjuntos ordenados” dentro de cada iteración aumenta la velocidad de conversión en un factor proporcional al 5. Reconstrucción de imágenes tomográficas 47 número de “subconjuntos ordenados”. En SPECT el proceso secuencial de dividir los datos en “subconjuntos” es muy sencillo al estar de antemano los datos separados en proyecciones, de modo que grupos ordenados de proyecciones pueden formar los sucesivos “subconjuntos ordenados”. El algoritmo EM se implementa por iteraciones (hasta la convergencia) y requiere cálculos con proyecciones y retroproyecciones. Se debe proveer al algoritmo de una estimación inicial de la actividad de la imagen para empezar la secuencia ası́ como de la matriz de pesos del sistema. Con OS-EM el algoritmo EM estándar se aplica a cada uno de los “subconjuntos ordenados” utilizando el resultado como valor inicial para el siguiente “subconjunto”. De tal modo que una iteración de OS-EM se define como un paso más a través de todos los “subconjuntos ordenados”, de modo que una iteración se puede ver como un paso más del mismo OS usando como valor inicial de reconstrucción el resultado obtenido por el último “subconjunto ordenado” de la iteración previa [24]. Cada iteración OS-EM tiene un tiempo de cálculo similar a una iteración estándar EM y se puede dividir en dos pasos: 1) Proyectamos y calculamos el valor esperado de cuentas en las proyecciones pertenecientes al “subconjunto ordenado” Si a partir de la actividad estimada utilizando la matriz del sistema: gti = J X j=1 Atj · xij . 2) Actualizamos la actividad estimada retroproyectando y comparando con las cuentas medidas en las proyecciones pertenecientes al “subconjunto ordenado” actual, como se puede ver en la ecuación (5.1). fji+1 X X gt · Aij / Atj . = fji · i g t t∈S t∈S i (5.1) i Donde gt son las cuentas medidas en el pixel t de la gammacámara, fj el número de cuentas emitidas esperadas en el vóxel j, Atj es la matriz del sistema para una 48 5.3. Métodos iterativos emisión desde el vóxel j detectado en el pixel t, siendo Si con i = 1, 2, . . . , n los conjuntos ordenados de proyecciones del algoritmo OS. Finalmente se repite la secuencia para todos los “subconjuntos ordenados” y para las iteraciones necesarias hasta alcanzar la convergencia. 5.3.2. Matriz de transición del sistema. Uno de los aspectos fundamentales para obtener una buena reconstrucción radica en la precisión con que se genere la matriz de transición del sistema. Dicha matriz es la encargada de relacionar el espacio emisor objeto 3D, en el cual se encuentra la distribución del radioisótopo, con el espacio imagen 2D, donde se detecta la radiación. La matriz se forma principalmente por consideraciones geométricas teniendo en cuenta los parámetros geométricos del sistema. También debe modelizar el colimador e incluir el tamaño y la forma de la apertura del colimador, ası́ como el número de aperturas. Por último es aconsejable que tenga en cuenta el tamaño del pixel del detector y/o el del vóxel con el que se reconstruye. Los efectos fı́sicos que pueden degradar las imágenes como son la atenuación y la dispersión también se pueden tener en cuenta en la matriz del sistema. La matriz del sistema se puede calcular por tres vı́as: mediante medidas directas, mediante simulaciones Monte Carlo o mediante cálculos analı́ticos. A continuación se describen brevemente los tres métodos. 5.3.2.1. Cálculo de la matriz mediante medidas directas. Este método consiste en calcular las probabilidades que relacionan la actividad de cada uno de los vóxeles de la imagen con los valores de cuentas que se obtienen en las proyecciones mediante medidas directas. La realización de medidas fiables y con suficiente estadı́stica para todos los vóxeles del sistema requiere mucho tiempo de medida y mucha precisión en las medidas. 5. Reconstrucción de imágenes tomográficas 5.3.2.2. Cálculo de la matriz mediante simulaciones Monte Carlo. La simulación estadı́stica o de Monte Carlo proporciona soluciones a problemas matemáticos complejos mediante el muestreo sistemático de variables aleatorias. Dicho método se emplea de forma sistemática en el diseño y caracterización de cámaras PET y SPECT. Los códigos de Monte Carlo de propósito general resultan lentos a la hora de caracterizar la matriz de sistema, dado el elevado número de eventos que se tienen que lanzar para conseguir la suficiente significación estadı́stica. El código de simulación GATE es en la actualidad el código de simulación más empleado en la caracterización y modelado de cámaras PET y SPECT. Está basado en las librerı́as de simulación de partı́culas de alta energı́a Geant4 desarrollado en el CERN de Ginebra, y está validado para un amplio número de tomógrafos. Los métodos Monte Carlo necesitan modelizar todo el sistema perfectamente. Las matrices creadas mediante métodos Monte Carlo son muy precisas pero el tiempo de cálculo necesario para crearlas puede durar semanas o incluso meses, lo que convierte el método en poco práctico. 5.3.2.3. Métodos analı́ticos para el cálculo de la matriz. Para generar la matriz del sistema mediante métodos analı́ticos se debe modelizar la operación de proyectar la distribución de actividad en el dominio objeto (3D) al dominio imagen (2D), de modo que se obtenga una imagen por cada proyección medida. En Medicina Nuclear existen dos tipos de implementaciones para describir el proceso de proyección: proyección basado en vóxeles (voxel driven projection) o basado en el trazado de rayos (ray driven projection). En el método “proyección basado en vóxeles” se parte del espacio objeto y se calcula la contribución de cada uno de los vóxeles j a las proyecciones a través del colimador. En cambio, en el método “proyección basado en el trazado de rayos ” se parte de las proyecciones e integra la actividad en el dominio objeto a lo largo del rayo proyectado asociado con cada uno de los pı́xeles de las proyecciones. En la figura 5.1 se puede ver una representación 49 50 5.3. Métodos iterativos Figura 5.1: Representación esquemática de las dos opciones para modelizar la proyección en la matriz de transición con el colimador pinhole. (Izquierda) Proyección basado en el trazado de rayos. (Derecha) proyección vı́a vóxel. 2D de cada uno de los dos métodos mencionados para modelizar la proyección con colimador pinhole. El cálculo de la matriz de sistema mediante métodos analı́ticos habitualmente solo tiene en cuenta aspectos geométricos, resultando un esquema de proyectores y retroproyectores basados en el cálculo de los parámetros de intersección con los vóxeles de la imagen. Propuestas más elaboradas de modelos analı́ticos incluyen la función de respuesta del detector o incluso la descomposición de los principales efectos que intervienen en la matriz: la geometrı́a de la cámara, la sensibilidad de los detectores y un factor que aproxima los parámetros fı́sicos (penetración en el cristal, resolución intrı́nseca, etcétera). La matriz total es la multiplicación de estas sub−matrices que son muy dispersas y pueden almacenarse en memoria. Parte III Primer prototipo SPECT: prueba de concepto 51 Capı́tulo 6 Elementos de un sistema SPECT de un solo detector con colimador pinhole 6.1. Introducción El prototipo necesario para la prueba de concepto se desarrolló y puso en funcionamiento en el departamento de Medicina Nuclear del Hospital Clinic de Barcelona, bajo la supervisión de los Doctores Javier Pavı́a y Domènec Ros. Para conseguir un sistema SPECT, deben considerarse los siguientes aspectos: (a) Componentes. El Componente principal del sistema SPECT es la gammacámara desarrollada por el Grupo de Fı́sica Médica [25] y [26] del Instituto de Fı́sica Corpuscular (IFIC, centro mixto de la universidad de Valencia y el CSIC) de Valencia. Este prototipo una vez construido fue transferido a una empresa (spin-off ) llamada “Oncovision” que actualmente lo comercializa con el nombre de “cámara Sentinella”. Sin embargo, el sistema completo precisa de otros componentes como la base, el sistema de giro, la camilla donde se 53 54 6.1. Introducción coloca el sistema a estudiar, los motores necesarios para efectuar los diferentes movimientos y el colimador. (b) Adquisición y control. La utilización de un sistema SPECT comporta la colocación del sujeto en el campo de detección y la adquisición de un conjunto de proyecciones para diferentes ángulos. Para poder llevar a cabo este proceso es necesario controlar los movimientos de la camilla y el rotor, ası́ como la captura de datos de la gammacámara. Para poder automatizar los estudios de un sistema SPECT se requiere, por tanto, desarrollar un software de adquisición con un interface de usuario que permita controlar simultáneamente la gammacámara y los motores disponibles en el sistema. (c) Calibración. Los datos adquiridos están sujetos a desviaciones de las medidas. Los sistemas no son ideales y, tanto el detector como el montaje, o geometrı́a, están sujetos a desviaciones que requieren una calibración para intentar sacar el mayor partido posible al sistema desarrollado. Se requieren dos tipos de calibraciones: calibración del detector y calibración geométrica. La calibración del detector pretende relacionar la posición y energı́a detectadas con las reales. Mientras que la calibración geométrica tiene como propósito medir y compensar las desviaciones cometidas en el montaje del equipo. (d) Reconstrucción. La técnica de SPECT tiene como objetivo obtener la distribución tridimensional del trazador en el sujeto a estudiar. Dicha distribución se consigue como solución del problema matemático inverso de la reconstrucción tomográfica. Dicho problema se caracteriza por el hecho de que la información de interés no esta disponible directamente, sino que se obtiene a partir de las medidas proporcionadas por la gammacámara, las cuales son una transformación de la distribución tridimensional deseada. (e) Objetivo. El objetivo de este primer prototipo es el de comprobar la posibilidad de utilizar la gammacámara Sentinella como detector de un sistema SPECT para animales pequeños. En este capı́tulo y en los tres siguientes se describen los elementos del sistema SPECT correspondientes a los aspectos mencionados. 6. Elementos de un sistema SPECT de un solo detector con colimador pinhole 6.2. Componentes de la prueba de concepto SPECT 6.2.1. Detector de radiación: Sentinella El primer prototipo se diseñó teniendo en cuenta la disponibilidad de una mini gammacámara operativa, Sentinella. Se trata de un detector de radiación gamma de tamaño reducido basado en un detector de centelleo. Además del cristal de centelleo y el fotomultiplicador, incorpora en la parte electrónica unas placas de reducido tamaño que actúan de tarjeta de adquisición. Se conecta a un ordenador a través de un puerto USB que permite al mismo tiempo alimentar a la gammacámara y transmitir los datos [26]. A continuación se muestra una breve descripción de los principales componentes de la gammacámara Sentinella. 6.2.1.1. Cristal centellador La gammacámara Sentinella utiliza un cristal continuo y pulido de CsI(Na) de dimensiones 50x50x4 mm3 . La superficie de entrada y las laterales están recubiertas de una capa de epoxy blanca (que actúa como reflector difuso) y otra negra, respectivamente, adheridas al cristal [27]. Como se puede ver en la tabla 4.1 mostrada en el capı́tulo 4 el material centellador que dispone la gammacámara tiene una buena salida de luz (buena resolución energética) y una elevada densidad y número atómico, esto favorece el efecto fotoeléctrico frente al efecto Compton, lo cual es deseado para nuestra aplicación. El hecho de utilizar un cristal continuo ofrece una serie de ventajas y desventajas [28] respecto a la alternativa de usar cristales pixelados. Las principales ventajas son: - Se aumenta la sensibilidad, para un mismo tamaño de cristal, ya que se evitan las áreas muertas en la zona de detección (gap entre cristales). Aunque en la actualidad, las mejoras en la fabricación de estos cristales permite reducir significativamente dicha zona, hasta reducirla a pocas decenas de micrómetros entre cristales. 55 56 6.2. Componentes de la prueba de concepto SPECT - Disminución del coste de fabricación ya que no es necesario pixelar los cristales. La principal desventaja es: - Se aumento de la compresión de las imágenes obtenidas debido principalmente a efectos de borde del cristal. 6.2.1.2. Fotomultiplicador Para las aplicaciones de la gammacámara es fundamental conseguir una buena determinación del punto en que ha impactado el rayo γ en nuestro sistema, ya que lo que intentamos es obtener la distribución espacial del emisor γ. La utilización de un cristal continuo implica la necesidad de acoplar fotomultiplicadores sensibles a posición (PSPMT). El PSPMT utilizado en nuestra aplicación es uno multianódico tipo flat panel de Hamamatsu Photonics, modelo H8500. En la figura 6.1 se muestra una foto de este PMT donde se aprecian sus reducidas dimensiones. Este pequeño tamaño junto con su reducido peso de 140 g hacen que la gammacámara pueda ser pequeña y ligera. El PSPMT viene ya protegido por una capa de metal de 0.1 mm de espesor que lo resguarda de los campos magnéticos externos. Figura 6.1: Foto del PSPMT escogido. 6. Elementos de un sistema SPECT de un solo detector con colimador pinhole La ventana del PSPMT es de cristal de borosilicato de 1.5 mm de grosor e ı́ndice de refracción 1.5. El fotocátodo está hecho de un material bialcalino. La cadena de dı́nodos consta de 12 etapas dispuestas en una estructura de canales metálicos. El ánodo está dividido en forma de matriz de 8x8 pı́xeles de tamaño 5.8x5.8 mm2 , cada uno con un espaciado de 0.28 mm entre ellos. En la tabla 6.1 se muestra un resumen de otras caracterı́sticas importantes del PSPMT escogido. respuesta espectral (nm) 300-650 λmax (nm) Vmax (V) Isalida max µA 420 -1100 100 eficiencia cuántica a 420 nm 19 % corriente negra ánodos (nA) 32 tiempo subida (ns) 0.8 tiempo tránsito (ns) 6 Tabla 6.1: Caracterı́sticas principales del PSPMT H8500. 6.2.1.3. Electrónica La electrónica de la cámara gamma portátil utiliza una red de resistencias que reduce el número de salidas del PSPMT de 64 a 4, lo que simplifica bastante la electrónica [29]. A estas 4 cargas las denotamos como QA ; QB ; QC ; QD . A partir de ellas se obtienen unos valores provisionales de la energı́a (Em ) y la posición (xm , ym ) del suceso en el cristal [30] como se muestra a continuación: xm = QA + QB − QC − QD QA + QB + QC + QD ym = QA + QD − QB − QC QA + QB + QC + QD (6.1) Em = QA + QB + QC + QD Para la formación de la imagen gammagráfica a partir de las 4 cargas arriba mencionadas, se realiza un preprocesado analógico de estas señales, una digitalización y posteriormente el envı́o de estos datos al ordenador y un postprocesado de señal antes de obtener la imagen definitiva. La sección analógica se encarga de convertir las señales de carga provenientes de la red de resistencias en señales de tensión con amplitud y forma adecuadas para 57 58 6.2. Componentes de la prueba de concepto SPECT su digitalización. Ésta integra mediante un preamplificador de carga las señales de corriente que llegan por cada uno de los cuatro canales. En la sección digital se digitalizan las amplitudes de los pulsos provenientes de la sección analógica con una precisión de hasta 12 bits (4096 canales), enviando continuamente los datos a la computadora, para su procesamiento. El fotomultiplicador se alimenta a partir de una fuente compacta de alto voltaje y polaridad negativa que se regula mediante un potenciómetro. Para obtener un compromiso entre una buena resolución en energı́as y una menor pérdida de sucesos esta diferencia de tensión debe estar entre 900 y 1000 V. La alimentación, que se obtiene a través del puerto USB del computador, es la vı́a para alimentar el resto de componentes electrónicos. Figura 6.2: Placas electrónicas de la mini cámaragamma. En el diseño de las placas se priorizó la portabilidad del sistema. Todo ello se realizó bajo consideraciones de mı́nimo ruido, altas prestaciones de estabilidad y máxima compactividad [7]. Una foto de las placas analógica, digital y de fuentes se puede ver en la figura 6.2. 6. Elementos de un sistema SPECT de un solo detector con colimador pinhole 6.2.2. Colimadores Para la prueba de concepto disponı́amos de 3 colimadores tipo pinhole que se diferenciaban entre si por el tamaño de la apertura. 6.2.2.1. Selección del tamaño de la apertura del colimador pinhole El blindaje de los colimadores es de 3 mm de espesor de Plomo (Pb) en todo el colimador, salvo en la apertura en la cual se incrusta un disco de Tungsteno (W) de 2 mm de espesor y 9 mm de diámetro en la que se ha mecanizado el agujero con un perfil en forma de diente de sierra. La distancia focal es aproximadamente de 31 mm para todos los colimadores y el ángulo α de apertura es de 53.13o . Los tres colimadores pinhole de que dispone la cámara Sentinella tienen un diámetro de 1 mm, 2.5 mm y 4 mm respectivamente. El isótopo más utilizado en SPECT es el 99m T c, se trata de un emisor gamma con el pico de la energı́a de emisión en 140.5 keV. Si nos centramos en dicha energı́a podremos calcular es espesor necesario (en Pb y W) para el correcto funcionamiento del colimador con 99m T c. El Plomo tiene una densidad de 11.34 g/cm3 y su coeficiente de atenuación másico µ de 2.721 cm2 /g para la energı́a de 140.5 keV. Por lo que el coeficiente de atenuación será: µρ = 30.8561 cm−1 . Mientras que el coeficiente de atenuación másico para el Tungsteno es µρ = 41.4337 cm−1 , siendo µ = 2.152 cm2 /g (a 140.5 keV) y la densidad 19.25 g/cm3 . La figura 6.3 presenta un gráfico que muestra, para ambos materiales, el porcentaje de fotones de 140.5 keV atenuados en función de espesor de material atravesado. Para la energı́a de 140.5 keV, con 3 mm de espesor de Pb, se atenuarán el 99.991 % mientras que con un espesor de 2 mm de W la atenuación es del 99.975 %, ligeramente menor que para el Pb como puede verse en la figura 6.3, aunque suficiente para eliminar la práctica totalidad de los fotones que se dirijan al detector por cualquier dirección distinta a la de la apertura. 59 60 6.2. Componentes de la prueba de concepto SPECT Atenuación en función del espesor del material 100 Plomo Tungsteno 99 Atenuación (%) 98 97 96 95 94 93 92 91 1 1.5 2 2.5 3 3.5 Espesor (mm) Figura 6.3: Atenuación para rayos gamma de 140.5 keV en función del espesor del material de Pb y W. Para estos colimadores la eficiencia geométrica (G) y resolución planar (Rtot ) vienen dadas por las ecuaciones 4.3 y 4.5 respectivamente (Ver sección 4.3.2), teniendo en cuenta que B = 89 % (para el fotopico de 140.5 keV del 99m T c)) y Gc = 67,3 % (para 4 mm de espesor de CsI(Na)). Para seleccionar el colimador más apropiado para esta aplicación, se realizó el cálculo de la resolución espacial y sensibilidad teórica que se obtendrı́a para distintos radios de giro, para cada uno de los tres colimadores. En la figura 6.4 se observa que para un mismo radio de giro, lo que implica un mismo FOV, la sensibilidad mejora al aumentar el diámetro del pinhole pero a costa de empeorar la resolución espacial. Cuando se diseña un SPECT es necesario encontrar un compromiso entre sensibilidad y resolución espacial. Sin embargo, dado que nuestro sistema está pensado para ser aplicado con FOV pequeños y que se pretenden realizar exploraciones que permitan distinguir objetos de pocos milı́metros de tamaño deberá primar la resolución sobre la sensibilidad. Dado que la resolución planar teórica para los colimadores de 2.5 y 4 mm no parece adecuada al tamaño de las estructuras que nos encontraremos al estudiar animales pequeños como el ratón, nos decantamos por el colimador de 1 mm de diámetro. 6. Elementos de un sistema SPECT de un solo detector con colimador pinhole Sensibilidad en función del radio de giro Sensibilidad (cpm/µCi) 1200 d=1mm d=2.5mm d=4mm 1000 800 600 400 200 0 20 25 30 35 40 45 50 45 50 Resolución en función del radio de giro Resolución (mm) 12 10 8 d=1mm d=2.5mm d=4mm 6 4 2 0 20 25 30 35 40 Radio de giro (mm) Figura 6.4: Resolución y sensibilidad de una imagen planar en función del radio de giro para los 3 colimadores de los que disponemos. 6.2.3. Soportes, contrapeso y actuador lineal para radio de giro Para poder transmitir el giro del rotor a las cámaras es necesario utilizar un soporte que anexione la cámara con el rotor (gantry), en nuestro caso se trata de un disco macizo de 70 cm de diámetro y 5 mm de espesor. La gammacámara no va unida al disco directamente, sino que con el fin de poder acercar y alejar la cámara al eje de rotación, se utilizó un actuador lineal manual, el cual permitı́a ajustar manualmente el radio de giro antes de empezar un estudio, la precisión de dicho actuador es de 0.1 mm. Finalmente, se ha incluido un contrapeso (con la misma carcasa que la cámara Sentinella), para compensar el peso de la cámara en el gantry haciendo que éste se mantenga estable incluso cuando los motores están apagados. El contrapeso requiere de otro actuador lineal para poder compensar el peso para cualquier radio de giro seleccionado. Por otro lado, el sujeto a estudio requiere de una camilla donde pueda reposar. Dicha camilla debe ser lo suficientemente grande y rı́gida para resistir el peso del animal o maniquı́ que se desee estudiar, pero a su vez lo más pequeño posible para no impedir que la gammacámara se acerque a dicho sujeto lo máximo posible. Además, 61 62 6.2. Componentes de la prueba de concepto SPECT el soporte debe estar fabricado de materiales que atenúen poco en el rango de energı́a de los rayos γ emitidos, para evitar ası́ que dicha interacción pueda repercutir negativamente en las imágenes reconstruidas. 6.2.4. Motores y tarjeta de control El detector debe poder realizar una rotación completa alrededor del sujeto durante la adquisición de un estudio de SPECT. Para poder efectuar el giro del gantry se eligió un motor de giro de la compañı́a OWIS. Se trata de un motor paso a paso bifásico modelo DTM-60, el cual denotaremos como rotor. El diámetro de la apertura es de 25 mm y el paso de 0.06o , ver figura 6.5(a). También se debe tener en cuenta que el sujeto a estudio debe poder colocarse dentro del campo de visión de la cámara, para lo cual será necesario utilizar dos motores más, uno para poder moverlo a lo largo del eje de rotación, que denotaremos por deslizador, y el otro para poder subir y bajar dicha camilla, el cual denotaremos como elevador. Estos motores también se adquirieron a la compañı́a OWIS. El deslizador es un motor paso a paso bifásico modelo VTM-80, con un desplazamiento máximo de 150 mm y un paso de 5 µm. Mientras que el elevador también es un motor paso a paso bifásico modelo HVM-100, con un desplazamiento máximo de 30 mm y un paso de 2.5 µm, ver figura 6.5(b) y figura 6.5(c), respectivamente. (a) Rotor (b) Deslizador (c) Elevador Figura 6.5: Imagen de los tres sistemas de la compañı́a OWIS utilizados en el prototipo. 6. Elementos de un sistema SPECT de un solo detector con colimador pinhole Finalmente se utiliza una tarjeta de adquisición que se conecta a un PC a través de un puerto IDE (Integrated Drive Electronics) para el control de los motores. La tarjeta permite el control simultáneo de un máximo de 3 motores mediante 3 puertos series, en dichos puertos conectaremos los tres motores mencionados con anterioridad (rotor, deslizador y elevador). La tarjeta se encarga de la alimentación de los motores y del movimiento de los mismos, ası́ como de chequear y obtener la posición de cada uno de ellos en todo momento. 6.3. Resultado del montaje de la prueba de concepto SPECT El resultado de la implementación de la prueba de concepto se puede ver en la figura 6.6. En la figura 6.6(a) se puede ver la cámara Sentinella en la parte superior del disco, mientras que en la parte inferior está el contrapeso. También se observan los desplazadores lineales utilizados para el cambio de radio de giro de la gammacámara. En la parte posterior del disco puede verse el rotor, junto al cable de conexión que va del rotor a la tarjeta de adquisición del ordenador. (a) Imagen lateral de la prueba de concepto SPECT (b) Vista angulada de la prueba de concepto SPECT Figura 6.6: Imágenes de la prueba de concepto SPECT desarrollado. 63 64 6.3. Resultado del montaje de la prueba de concepto SPECT En la figura 6.6(b) se han marcado los distintos soportes que conforman el gantry del SPECT También se muestran la camilla, ası́ como el deslizador y elevador que permiten desplazarla para poder centrarla en el FOV. Capı́tulo 7 Adquisición y tratamiento de datos 7.1. Introducción En este capı́tulo se presenta la implementación del interfaz necesario para el funcionamiento del sistema SPECT construido. Este interfaz debe permitir la realización de todos los movimientos de la camilla para posicionar el objeto en el FOV, controlar la adquisición de imágenes de la gammacámara y el giro del rotor. Para que el interfaz sirva de prototipo, más allá de su utilización en la prueba de concepto, se completa de forma que sea capaz de adquirir datos en los diferentes modos de adquisición existentes en un tomógrafo convencional para humanos. De esta forma, ha de ser posible adquirir imágenes estáticas, estudios dinámicos, secuencias de proyecciones para SPECT y estudios de SPECT de cuerpo entero. Para cada uno de estos tipos de adquisición, el sistema ha de permitir la introducción de los parámetros relativos a las condiciones de adquisición. 65 66 7.2. Material y métodos 7.2. Material y métodos Para desarrollar el software del SPECT se ha utilizado una biblioteca de enlace dinámico o DLL (dynamic-link library) creada para nuestra aplicación y que permite controlar la gammacámara mediante un software externo Además la tarjeta de control de motores de OWIS incluye las bibliotecas y los ejemplos necesarios para el manejo de sus motores. Todo lo implementado para la adquisición del sistema se ha desarrollado en entorno Windows y se ha escrito utilizando el lenguaje “Microsoft Visual Studio .NET 8 ”, el cual está basado en C++ con un tipo de programación orientada a objetos. 7.2.1. Software disponible de la gammacámara La gammacámara Sentinella dispone de un software propio para las adquisiciones de imágenes planares o 2D. Dicho software no permite la adquisición automática de una secuencia de imágenes como la necesaria en estudio de SPECT o en un estudio dinámico. Por este motivo fue necesario el desarrollo, en colaboración con el departamento de software de la empresa Oncovision, de una DLL especı́fica. Este es un término con el que se refiere a los archivos con código ejecutable que se cargan bajo demanda de un programa por parte del sistema operativo. Gracias a dicha DLL nuestro programa es capaz de manejar gran parte de las funciones de la gammacámara, como encender, adquirir, parar, guardar datos y representar los datos adquiridos mediante un diálogo. Una vez se ha puesto en marcha la cámara, es necesario indicar la ventana de energı́a ası́ como si se desea que el sistema efectúe alguna corrección intrı́nseca o extrı́nseca de uniformidad. La corrección intrı́nseca de uniformidad compensa la falta de uniformidad del detector (ver sección 8.2.1.3). Mientras que la corrección extrı́nseca de uniformidad compensa el efecto del colimador. Para nuestro sistema es necesario utilizar la corrección de uniformidad intrı́nseca pero no la extrı́nseca, puesto que la matriz del sistema ya tiene en cuenta el efecto del colimador. 7. Adquisición y tratamiento de datos El rango de energı́as que permite la gammacámara utilizada va de 20 keV a 250 keV, mientras que la tasa máxima que se puede alcanzar es de 8000 c/s. Cuando se enciende la cámara es necesario definir las correcciones que deben aplicarse ası́ como la ventana de energı́a, aunque posteriormente se pueden seleccionar todos los parámetros gracias a la DLL utilizada. 7.2.2. Software disponible para el control de los motores de OWIS Cuando se adquieren los motores junto con la tarjeta de control de OWIS, además del hardware, el fabricante proporciona un conjunto de herramientas para su manejo. Estás herramientas incluyen DLL y ejemplos para gran variedad de lenguajes de programación. Figura 7.1: Imagen del dialogo proporcionado por OWIS como ejemplo del control de los motores en lenguaje de programación C++. Como base para la parte del control de motores se ha utilizado la DLL y el software de ejemplo en C++ proporcionado por la compañı́a OWIS (ver figura 7.1). 67 68 7.2. Material y métodos 7.2.3. Control conjunto de los componentes y automatización de las adquisiciones Con las herramientas disponibles de la gammacámara y los motores se ha realizado un software de manejo del sistema completo. El software debe permitir automatizar los tipos de estudios más comunes para un sistema SPECT. Además el interfaz de usuario ha de ser intuitivo y sencillo de manejar. Las partes fundamentales del interfaz de usuario son las siguientes: 1. Control del rotor: debe permitir rotar en cualquier sentido un angulo dado, nos dará la posición del disco en cualquier momento y debe disponer de una posición de origen (o home), permitiendo ası́ mover el motor a la misma posición cada vez que se inicia un estudio lo que facilitará la reproducibilidad de los estudios. 2. Control de la camilla: (a) Elevador: se encargará de mover la camilla arriba y abajo una distancia determinada dentro del rango permitido por el posicionador, para centrar el objeto en ese eje. Al igual que el rotor debe disponer de home lo que facilitará la reproducibilidad de los estudios. (b) Deslizador: debe permitir mover la camilla adelante y atrás una distancia determinada dentro del rango permitido por el posicionador, con el fin de centrar el objeto en ese eje. Al igual que el rotor y elevador debe disponer de home lo que facilitará la reproducibilidad de los estudios. 3. Control de la cámara: se encargará de controlar las funciones de la cámara como adquirir, parar, continuar, reiniciar o aplicar alguna de las siguientes correcciones: (a) Corrección de colimador: corrige el efecto del colimador sobre la imagen, compensando el efecto del ángulo solido subtendido por cada pixel de la cámara para el colimador seleccionado. (b) Corrección de reconstrucción: aplica una función Gaussiana a cada cuenta detectada utilizando el valor de resolución espacial intrı́nseca de la cámara. Suaviza las imágenes adquiridas. 7. Adquisición y tratamiento de datos Estas dos correcciones están pensadas para imágenes 2D y no deben aplicarse cuando se quiere realizar un estudio SPECT ya que este tipo de correcciones se tienen en cuenta en la reconstrucción. 4. Visualización de los datos: permitirá visualizar los datos adquiridos en una matriz 2D que representa la gammacámara. En ella se deberán añadir cada uno de los rayos γ detectados ası́ como la posición de interacción XY dentro del cristal conforme sean detectados. Dispondrá de unos “check box” que permitirán cambiar el contraste de la imagen. La imagen es acumulativa y siempre se irán sumando los datos que llegan, hasta que se reinicie una adquisición o se borre la imagen. 5. Ventana de energı́a: se podrá seleccionar un isótopo con ventana predefinida, o bien seleccionar una ventana energética manualmente. Permitirá la opción de realizar un espectro de energı́a seleccionando el rango de energı́as a estudiar y la anchura deseada para cada una de las subventanas energéticas. 6. Adquisición de estudios: (a) Imagen estática: debe adquirir y guardar imágenes estáticas teniendo en cuenta los valores seleccionados de tiempo de adquisición, ventana de energı́a, nombre del archivo, etc. (b) Estudio dinámico: debe permitir seleccionar los parámetros necesarios para que el sistema realice automáticamente un estudio dinámico del sujeto. (c) SPECT: debe permitir realizar un estudio tı́pico de SPECT de vuelta completa o media vuelta. Antes de empezar, además de los parámetros de una adquisición estática se deben seleccionar el número de proyecciones deseadas y si se desea corregir el decaimiento. (d) SPECT cuerpo completo: deberá permitir la realización de estudios de SPECT con el FOV axial aumentado. Se debe seleccionar el número de beds o steps que se desean realizar. El software realizará varios estudios SPECT consecutivos desplazando la camilla entre ellos para poder obtener distintas zonas del sujeto en cada uno de los beds. 69 70 7.2. Material y métodos 7.2.4. Corrección del decaimiento durante la adquisición Las desintegración nuclear es un proceso probabilı́stico que se rige por la siguiente ley exponencial: t A = A0 · e− τ , siendo τ la vida media del isótopo radiactivo y t el tiempo transcurrido. Por tanto, la actividad del isotopo disminuye con el tiempo. Cuando la vida media del isótopo utilizado en el estudio es corta y los tiempos de adquisición son del orden de la misma, la actividad del isótopo se reduce con respecto al inicio del estudio y es necesario corregir dicho decaimiento durante la adquisición de las diferentes proyecciones del estudio con el fin de aumentar la homogeneidad entre las proyecciones. Se han implementado dos métodos para la corrección del decaimiento los cuales describimos a continuación. El primero es el método tradicional de corrección del decaimiento, mientras que el segundo es una nueva propuesta de resolución de este problema, de forma que deja unas proyecciones más adecuadas a los algoritmos que se basan en la estadı́stica de los datos. 7.2.4.1. Corrección del decaimiento compensando el número de cuentas detectadas. Conocida la ley de desintegración, se puede adquirir el mismo tiempo ti para cada las proyecciones y, a posteriori, corregir el número de cuentas detectadas en cada proyección para compensar el decaimiento entre proyecciones. De este modo tendremos que cada pixel i de la imagen i Cn,corregido = Cni · eλ·tn−1 , donde Cni es el número de cuentas detectados en el pixel i para la proyección n, i Cn,corregido es el número de cuentas corregidas en el pixel i para la proyección n y tn−1 es el tiempo transcurrido desde el inicio del estudio hasta el inicio de la proyección n. 7. Adquisición y tratamiento de datos Este método de corrección del decay es sencillo y funciona bien siempre y cuando el factor multiplicativo eλ·tn−1 sea cercano a uno. El inconveniente de este método es que cuando el factor eλ·tn−1 multiplica por igual la señal y el ruido, de modo que conforme va creciendo el factor disminuye la relación señal ruido (SNR) y se pierde la estadı́stica de Poisson. A medida que multiplicamos por un factor mayor la estadı́stica difiere más de la de Poisson. 7.2.4.2. Corrección del decaimiento aumentando el tiempo por adquisición. Teniendo en cuenta que el número de núcleos radioactivos de un isótopo sigue la siguiente función exponencial: N = N0 · e−λ·t , siento N0 es el número de núcleos radioactivos al inicio, t el tiempo y λ la constante de desintegración del radioisótopo. En una adquisición, entre los tiempos t1 y t2 , el número de desintegraciones del radioisótopo, D1 , seguirá la siguiente función de probabilidad: D1 = N1 − N2 = N0 · e−λ·(t1 −t0 ) − N0 · e−λ·(t2 −t1 ) , donde t0 es el tiempo inicial de la medida, el cual se puede tomar como 0. Por tanto, para una segunda medida entre los tiempos tn−1 y tn , tendremos que: h i Dn = N0 · e−λ·tn−1 · 1 − e−λ·(tn −tn−1 ) . Este método de compensación del decaimiento consiste en alargar el tiempo de cada una de las proyecciones de modo que se iguale, estadı́sticamente hablando, el número de desintegraciones en cada uno de los intervalos. Para ello tendremos que conseguir que D1 = D2 = . . . = Dn y por tanto: h i h i D1 = Dn =⇒ N0 · 1 − e−λ·t1 = N0 · e−λ·tn−1 · 1 − e−λ·(tn −tn−1 ) . 71 72 7.2. Material y métodos De donde se obtiene que: ln e−λ·t1 + e−λ·tn−1 − 1 ∆tn = −tn−1 − , λ (7.1) donde ∆tn = tn − tn−1 será el tiempo de adquisición que iguala la probabilidad de desintegraciones de la proyección n con la de la proyección 1. Con tn−1 el tiempo desde que se empezó la primera proyección y t1 el tiempo que duró la primera de las proyecciones. Si en lugar de fijar el tiempo de la primer proyección (t1 ) y calcular el tiempo del resto de proyecciones, lo que se pretende es fijar el tiempo total tendremos que: Dtotal = nproy · D1 =⇒ 1 − e−λ·ttotal = nproy · 1 − e−λ·t1 , con Dtotal igual al número total de desintegraciones durante todas las proyecciones, ttotal el tiempo total y nproy el número de proyecciones. De aquı́ podremos sacar cuanto debe valer el tiempo inicial en función del tiempo total (el resto de valores se pueden obtener a partir del tiempo de la primera proyección). ∆t1 = 1 −1 · ln 1 − · 1 − e−λ·ttotal . λ nproy (7.2) 7. Adquisición y tratamiento de datos 7.3. 7.3.1. Resultados Interface desarrollado En la figura 7.2 se muestra el interfaz gráfico del software desarrollado. Dicho programa de adquisición realizado se divide en distintas secciones: 7.3.1.1. Control de motores Es la parte del software que se encarga controlar los 3 motores disponibles (rotor, elevador y deslizador). La mayorı́a de los comandos utilizados se han exportado del software de control proporcionado por OWIS. Además del control de los motores, también se proporciona información de la posición de cada uno de ellos y de la velocidad y aceleración con la que se desplazan. Estos comandos se pueden encontrar en el cuadrante superior izquierdo del diálogo. Se encuentran divididos en 3 partes correspondientes a cada uno de los 3 motores (ver figura 7.2). Figura 7.2: Imagen del interfaz gráfico del software del sistema de adquisición del prototipo 1. Indicando la función de las principales partes del mismo. 73 74 7.3. Resultados 7.3.1.2. Gammacámara. Visualización de los datos obtenidos. Se trata de la parte del dialogo que rep- resenta una matriz XY en la cual se acumulan, desde el inicio de la última adquisición, las cuentas detectadas junto con la posición de detección. Sección derecha de la figura 7.2. Control de la gammacámara. Es la parte del software que controla las fun- ciones de la gammacámara. En esta sección del interfaz del usuario se selecciona si se quiere aplicar alguna de las dos correcciones que permite la gammacámara (corrección de colimador y corrección de reconstrucción). Además, en esta sección se selecciona el isótopo y por tanto la ventana energética que se quiere utilizar (siempre que no se realice un espectro. Finalmente también podremos adquirir imágenes 2D. En la figura 7.3) se muestra la ampliación de la sección referida a la gammacámara. Figura 7.3: Ampliación de la sección del interfaz gráfico referida a la gammacámara. 7.3.1.3. Estudios Finalmente, en la parte inferior del diálogo, ver figura 7.4, tenemos los parámetros correspondientes a las adquisiciones de un estudio, que pasamos a comentar brevemente a continuación: Grados totales. Se trata de un Combo Box en el cual se indica si se van a girar 360o o 180o . Corrección de decay. Con este Combo Box podemos seleccionar si queremos o no que se aplique la correcciones de decaimiento durante el estudio. 7. Adquisición y tratamiento de datos Fichero de imagen. En este Edit Control debemos indicar el nombre con el que se guardará el estudio. Tiempo por imagen. El tiempo de medida de cada una de las proyecciones se puede seleccionar con este Edit Control. Figura 7.4: Ampliación de la sección del interfaz gráfico referida a los estudios. Número de proyecciones. En este Edit Control se indica el número de proyecciones del estudio. Número de vueltas. Existen estudios en los cuales nos puede interesar repetir varias veces el estudio, por ejemplo, para ver como evoluciona la actividad en el sujeto con el tiempo. Este Edit Control permite indicar cuantas veces se repetirá el estudio. Al final de cada vuelta, la cámara volverá a la posición de origen con el fin de evitar una excesiva torsión de los cables. Cada uno de los estudios se guardará por separado indicando el número de estudio en el nombre de los archivos. Radio de giro. A modo informativo con este Edit Control se indica el radio de giro del estudio. Dicho dato se guardará en la cabecera del estudio. Crear serie. Este Check Box si esta activado permite que todas las proyecciones se guarden en un único archivo a modo de serie de datos. El programa permite seleccionar más de un check box de rebineado, dando como salida un archivo tipo serie por cada check box seleccionado con las opciones que hayan sido habilitadas (150x150, 100x100, 75x75 y/o 50x50). 75 76 7.3. Resultados Steps. Para realizar estudios SPECT de cuerpo completo se requiere más de un bed. Al seleccionar este Check Box se abre un desplegable con los datos de los steps como se muestra en la figura 7.5. Estos datos incluyen el número de steps y el desplazamiento de la camilla entre los distintos beds. Figura 7.5: Selección de steps o beds. Aparece nueva información con el número de steps y el desplazamiento y dirección entre los mismo. 7.3.1.4. Sección informativa. Esta sección a su vez la podemos dividir en dos secciones: información de estado e información sobre el estudio. Información de estado. Esta sección se localiza en la parte superior derecha del diálogo e informa en todo momento del estado de la cámara y de las adquisiciones en caso se que haya un estudio en marcha ver figura 7.6). Figura 7.6: Información del estado de la cámara y las adquisiciones. Información sobre el estudio. Se trata de una sección informativa rellenable, en la cual el usuario apunta todos los datos relevantes del estudio, como el sujeto, 7. Adquisición y tratamiento de datos el trazador, la actividad y una pequeña descripción si en caso de ser necesaria (ver figura 7.7). No es obligatorio rellenarlo, pero si aconsejable ya que toda esta información se guardara al final del estudio en un archivo de texto, con el mismo nombre del estudio, que estará disponible para su consulta en cualquier momento. Figura 7.7: Sección donde el usuario debe rellenarse la información sobre el estudio realizado. 7.3.2. Datos adquiridos Una vez seleccionamos todos los parámetros mencionados para el estudio podemos elegir entre cuatro tipos de estudios, los cuales hemos denotado por “SPECT”, “estático”, “dinámico” y “espectro”. 7.3.2.1. Estático Este modo es el modo más sencillo de todos. Se utiliza para adquirir una única proyección de un tiempo determinado que se guardará con el nombre indicado por el usuario. La cámara y la camilla podrán situarse en la posición que deseada para dicha adquisición (ver figura 7.8). 7.3.2.2. SPECT La adquisición SPECT es la adquisición tı́pica para la cual se diseño el programa, en este modo se realiza el estudio con los parámetros seleccionados por el usuario y 77 78 7.3. Resultados Figura 7.8: Ejemplo de un estudio estático utilizando un maniquı́ cilı́ndrico hueco relleno de una disolución de 99m T c. la cámara gira entre las distintas proyecciones un ángulo que se obtiene de dividir los grados totales del estudio entre el número de proyecciones. En la figura 7.9 se puede ver un ejemplo con algunas proyecciones de un estudio de pulmón. Figura 7.9: 30 proyecciones de un estudio de pulmón de ratón. 7. Adquisición y tratamiento de datos 7.3.2.3. Dinámico Este modo de adquisición es igual que el modo SPECT pero sin girar la cámara. De este modo todas las imágenes se obtienes desde el mismo angulo. Este modo se puede utilizar para estudios dinámicos 2D. En la figura 7.10 se muestra un ejemplo de un estudio dinámico con el abdomen de una rata. Figura 7.10: Ejemplo de un estudio dinámico. Abdomen de una rata después de inyectar un trazador marcado con 123 I. 7.3.2.4. Espectro Las funciones de la gammacámara permiten seleccionar la ventana de energı́a pero no permiten obtener el espectro de energı́a. A veces es necesario conocer el espectro de energı́a, lo cual se puede hacer mediante el modo de adquisición denotado por espectro. Cuando se utiliza dicho modo aparece un desplegable que permite seleccionar la energı́a inicial, el número de ventanas y el tamaño de dichas ventanas. En este modo de estudio tampoco se gira y lo que se realiza es un barrido energético con los parámetros del nuevo desplegable. 79 Capı́tulo 8 Calibraciones del sistema: geométrica y del detector 8.1. Introducción y objetivos Cada vez que un fotón interacciona con el cristal de la gammacámara, ésta produce una señal a la salida con la que se puede obtener la posición (x, y) de interacción en el cristal y la energı́a E del rayo gamma detectado, sin embargo los datos medidos se ven afectados por errores de medida sistemáticos y aleatorios lo que dificulta la determinación de la energı́a y la posición de cada interacción. Los errores aleatorios son inherentes a las medidas y el sistema de medida, no se pueden corregir y son los responsables de la resolución intrı́nseca energética y espacial. Por contra, los errores sistemáticos se deben intentar corregir. Para ello es necesario realizar una calibración del detector. El nuestro grupo de investigación se ha trabajado ampliamente en este tema, como se puede ver en las siguientes tesis [27] y [31]. Por otro lado, las tolerancias en la construcción de las partes mecánicas, la forma de sujeción de la cámara, la propia construcción y sistema de sujeción del colimador, ası́ como un posible desplazamiento electrónico en la determinación de las coordenadas en la cámara, hacen necesaria la inclusión de unos parámetros geométricos que 81 82 8.2. Calibración del detector calculen con precisión la posición de la cámara. De este modo se podrá relacionar con exactitud la posición de detección dentro del cristal con el origen de coordenadas del espacio objeto en cada una de las proyecciones. El objetivo de este capı́tulo es por tanto doble. En primer lugar se pretende comprobar el método de calibración del detector desarrollado previamente y validarlo con nuestro detector, en segundo lugar se pretende realizar la calibración geométrica del sistema para calcular los parámetros que caractericen la geometrı́a del sistema SPECT. 8.2. Calibración del detector La calibración intrı́nseca de la gammacámara incluye tres procesos claramente diferenciados, que son: Calibración en posiciones. Calibración en energı́as. Corrección de uniformidad. Cada uno de los procesos corrige un efecto diferente como se puede ver en el siguiente apartado. 8.2.1. 8.2.1.1. Material y métodos Calibración en posiciones Cuando un rayo gamma interacciona con nuestro cristal continuo, dicho cristal emite luz en todas las direcciones desde el lugar de la interacción. Para medir la posición del impacto en el cristal calculamos el centro de masas de la luz que llega al detector. Como el detector tiene una longitud finita se producirá un truncamiento de la luz medida que será más pronunciado conforme nos acercamos a los bordes del cristal. A este efecto se le conoce como efecto de borde del cristal continuo e implica que 8. Calibraciones del sistema: geométrica y del detector 83 la posición en la que se detectan las interacciones con respecto a la posición en que se producen se desplace hacia el centro de la imagen. Para corregir dicho efecto es necesario relacionar la posición de interacción real del rayo gamma en el cristal con la posición en la cual la gammacámara determina que se produjo la interacción. Para ello el grupo de Fı́sica Médica del IFIC diseñó una máscara de calibración de Plomo de 2 mm de espesor en la cual se han perforado unos orificios redondos de 1 mm de diámetro uniformemente distribuidos. Estos orificios (11x11) se encuentran separados entre si 4 mm, tal como se muestra en la figura 8.1. Figura 8.1: Mascara de calibración (dimensiones en mm). Para la calibración en posiciones de la imagen se coloca la máscara centrada con respecto al cristal justo encima de este. La adquisición se realiza utilizando una fuente puntual de 99m Tc con una actividad superior a 800 µCi para obtener una tasa de cuentas total de al menos 1000 c/s. La fuente debe situarse a una distancia de al menos 5 veces el campo de visión (≥ 200 mm) y centrada sobre el área útil del cristal, lo cual asegura un flujo de radiación uniforme y paralelo [32]. Para asegurar una buena estadı́stica se adquiere una imagen con 15 millones de sucesos totales, lo que nos proporciona más de 100.000 cuentas por orificio. 84 8.2. Calibración del detector La calibración en posiciones se obtiene mediante el ajuste, para toda la imagen adquirida con la máscara, de una función polinómica de grado menor o igual a 9. Para realizar los ajustes se utiliza un interprete o enlace externo de C++ denominado ROOT (http://root.cern.ch/). Se trata de un intérprete desarrollado en la Organización Europea para la Investigación Nuclear (CERN), es de libre distribución y tiene la ventaja de estar orientado al análisis numérico, recolección y presentación de datos. La función de coste a minimizar es la suma cuadrática de la diferencia entre la posición de cada uno de los puntos medidos una vez descomprimidos y la posición de su correspondiente orificio en la máscara. 8.2.1.2. Calibración en energı́as Las variaciones en la uniformidad de las alturas de los pulsos a lo largo del área sensible del PSPMT provocan que se tenga que efectuar una corrección de las energı́as medidas. Estas variaciones pueden deberse a varios factores: Efectos de borde del cristal continuo. La no uniformidad en la eficiencia de colección de luz en la interfase cristalfotomultiplicador. Variaciones espaciales en la eficiencia cuántica del fotocátodo y en el número de fotoelectrones recogidos en el primer dı́nodo. Variaciones espaciales en la ganancia de los dı́nodos. La calibración en energı́as se lleva a cabo de nuevo a partir de la imagen obtenida con la máscara de calibración (figura 8.1). La energı́a depositada en el cristal en cada interacción se obtiene a partir de la suma de las intensidades obtenidas en las cuatro esquinas de la red de resistencias (ver sección 6.2.1). Asociando dicha energı́a a la posición de la imagen reconstruida se puede rellenar un histograma en energı́as en función de la posición de detección generando de este modo un mapa de energı́as. Como para la medida se usa una fuente de 99m Tc todos los rayos gamma detectados provenientes del 99m Tc deberı́an detectarse con la misma energı́a en canales. Por 8. Calibraciones del sistema: geométrica y del detector 85 tanto, todos los picos de energı́a de cada uno de los pozos de la máscara de 11x11 utilizada se deben ajustar a un mismo valor de referencia. Utilizaremos como valor de referencia la energı́a medida para el orificio central, y ajustaremos toda la cámara también mediante una función polinómica de grado menor o igual a 9. Dicho ajuste, al igual que en la calibración en posiciones, se realiza mediante ROOT. La función de coste a minimizar por el programa es la suma cuadrática de la diferencia entre la posición del pico de energı́a de cada uno de los puntos medidos una vez corregido en energı́a y el valor que se tomó como referencia utilizando el pozo central obteniendo ası́ los factores del mapa de energı́a. Con los factores del mapa de energı́a, guardados en forma de matriz, ya tenemos todo lo necesario para reconstruir la energı́a de cada suceso. El procedimiento es el siguiente: para cada suceso que llegue se reconstruirá su posición, se calculará la energı́a medida (Em ) y se buscará en la matriz el factor de energı́a (Exnor,ynor ) que le corresponde para la posición obtenida. • Conversión de canales a energı́a Para completar la calibración en energı́a es necesario encontrar la relación existente entre la unidad de medida de la cámara, canales del ADC y la energı́a (en keV) que tiene el rayo gamma detectado. Con el fin de conseguir la relación energı́a-canales se usan varias fuentes radiactivas emisoras de rayos gamma con fotopicos conocidos y que este bien separados entre si. A continuación, se realiza una adquisición con suficiente estadı́stica para cada una de ellas. Una vez obtenido el histograma de energı́a para cada una de las imágenes adquiridas y calibradas en posición y energı́a, se selecciona como centro del fotopico, en canales, el valor máximo de cada uno de los picos de los histogramas. Los isótopos utilizados para la conversión de canales a energı́a son los siguientes: 133 Ba con 2 fotopicos en 27.5 keV y 80.9 keV, 153 Gd con el fotopico en 99.8 keV, 57 Co con el fotopico en 122.1 keV y 99m Tc con el fotopico en 140.5 keV. 86 8.2. Calibración del detector 8.2.1.3. Corrección de uniformidad La falta de uniformidad en la detección de sucesos gamma a lo largo del área sensible provoca la necesidad de realizar una corrección en la ganancia de cada una de las partes en que se subdivide el detector (corrección de uniformidad). Esta falta de uniformidad puede deberse a varios factores, los principales son: Inhomogeneidades en el cristal o en la pintura. Variaciones entre las ganancias de los dı́nodos del fotomultiplicador. Pérdidas de electrones debidas a campos externos. Preamplificadores no equilibrados. Con el fin de corregir esta falta de uniformidad entre las distintas partes del detector se realiza una adquisición de un campo de radiación uniforme sobre el área útil del cristal sin colimador ni máscara. Para ello se utiliza una fuente puntual de 99m Tc colocada a una distancia superior a 5 veces el área útil de detección del cristal y centrada en el campo de visión, asegurando de este modo un flujo uniforme y perpendicular al detector. La actividad de la fuente que se utiliza no debe superar los 100 µCi para evitar trabajar en la zona no lineal del detector (tasa de cuentas inferior a 4000 c/s). Finalmente se adquieren datos hasta obtener un número de cuentas totales superior a 25 millones. Los datos adquiridos se corrigen en posiciones y energı́a seleccionando únicamente los sucesos que entran dentro de la ventana de energı́a del ±10 %. A partir de esta imagen se obtiene la llamada matriz de uniformidad dividiendo el número de cuentas del pixel central por el número de cuentas de cada uno de los pı́xeles de la adquisición. La matriz de uniformidad resultante se utiliza para aplicar dicha corrección a las medidas sucesivas. De modo que para cada adquisición se multiplica el valor obtenido para el pixel (i,j) de la imagen por el pixel (i,j) de la matriz de uniformidad. Para validar la uniformidad de las imágenes obtenidas se utiliza la siguiente formula: U = V alorM aximo−V alorM inimo . V alorM aximo medida. Siendo U el valor de uniformidad resultante de la 8. Calibraciones del sistema: geométrica y del detector 8.2.2. 87 Resultados Para poder utilizar una cámara en el sistema SPECT debemos realizar una calibración completa de dicha cámara mediante el método explicado para validar ası́ el correcto funcionamiento del detector como gammacámara. 8.2.2.1. Calibración en posiciones Los valores de las intensidades de corriente que llegan a cada una de las 4 esquinas de la red e resistencia se guardan por separado para cada suceso, de manera que se pueden obtener las coordenadas y la energı́a correspondientes a cada una de las detecciones. Estos valores se almacenan en “modo lista”, obteniéndose al final de la medida una imagen como la que se muestra en la figura 8.2 (izquierda). A partir de esta imagen se determinan las posiciones medidas de los orificios de la máscara de calibración. Mediante el ajuste de dichos valores se obtiene la descompresión de la imagen como se observa en la figura 8.2 (derecha). 300 300 200 180 250 70 250 140 120 150 100 80 100 60 Y corregida (pixeles) Y medida (pixeles) 160 200 200 50 150 40 30 100 60 40 50 20 50 10 20 0 0 50 100 150 200 X medida (pixeles) 250 300 0 0 0 50 100 150 200 250 X corregida (pixeles) 300 0 Figura 8.2: Imagen de la máscara de calibración, sin (izquierda) y con (derecha) calibración en posiciones. 8.2.2.2. Calibración en energı́as En la figura 8.3 se muestra el espectro de energı́a obtenido para toda la imagen antes y después de la calibración en energı́a. Además también se muestra la imagen 88 8.2. Calibración del detector obtenida una vez aplicadas las calibraciones en posición y en energı́a para nuestra gammacámara, seleccionando únicamente los sucesos que entran dentro de la ventana de energı́a del ±10 % centrada en el fotopico. ×103 ×103 140 300 200 180 180 120 250 160 160 140 Numero cuentas Numero cuentas Y corregida (pixeles) 140 100 120 80 100 60 80 200 120 100 150 80 100 60 60 40 40 40 50 20 20 0 0 1000 2000 3000 4000 E medida (canales) 5000 0 0 20 1000 2000 3000 4000 E corregida (canales) 5000 0 0 50 100 150 200 250 X corregida (pixeles) 300 Figura 8.3: Espectro de energı́as sin calibrar (izquierda), calibrado (centro) e imagen calibrada en posiciones y energı́a seleccionando solo los eventos dentro de la ventana del 20 % centrada en el fotopico (derecha). • Conversión de canales a energı́a En la figura 8.4 se puede ver el resultado obtenido para nuestra gammacámara de la conversión de canales a energı́a. La lı́nea continua representa el ajuste lineal por mı́nimos cuadrados. Figura 8.4: Relación entre la energı́a emitida en keV y la medida en canales. La ecuación de la recta hallada es: EkeV = (0,0815 ± 0,0007) · Ecanales − (13,6 ± 1,1) con un coeficiente de correlación de 0.9999. 8. Calibraciones del sistema: geométrica y del detector 8.2.2.3. Corrección de uniformidad El la figura 8.5 se puede ver la imagen resultante de la adquisición sin máscara y calibrada únicamente en posiciones. Además se muestran las proyecciones a lo largo de ambos ejes. En dicha imagen se llegan a observan algunos de los pı́xeles del PSPMT. En las proyecciones se pueden apreciar picos que corresponden al centro de los pı́xeles proyectados y mı́nimos que representan las zonas de menor detección entre pı́xeles. Figura 8.5: Imagen de uniformidad adquirida una vez corregida en posiciones. Junto a ella se muestran las proyecciones de la imagen sobre los ejes X e Y. Una vez se aplica la corrección de energı́a con ventana de energı́a del ±10 % se obtiene la figura 8.6 (centro). A partir de la cual se obtiene la matriz de uniformidad, la cual se utiliza para aplicar la corrección de uniformidad a dicha medida (ver figura 8.6 (derecha)) y a las susesivas. 89 90 8.2. Calibración del detector 300 300 300 70 200 250 180 200 140 150 120 100 100 200 50 150 40 100 200 50 150 40 100 30 80 50 250 60 60 Y_corregida_XYEU (pixeles) 160 Y_corregida_XYE (pixeles) Y_corregida_XY (pixeles) 250 70 50 30 50 60 20 20 0 0 50 100 150 200 250 X_corregida_XY (pixeles) 300 0 0 50 100 150 200 250 X_corregida_XYE (pixeles) 300 0 0 50 100 150 200 250 X_corregida_XYEU (pixeles) 300 Figura 8.6: (Izquierda) Imagen de uniformidad corregida en posiciones. (Centro) Imagen de uniformidad corregida en posiciones y energı́a. (Derecha) Imagen de uniformidad corregida en posiciones, energı́a y por uniformidad. Finalmente en la figura 8.7 podemos ver como queda la imagen una vez se aplican todas las correcciones (posiciones, energı́a y uniformidad), ası́ como las proyecciones sobre los ejes X e Y. La uniformidad obtenida es inferior al 3 %. Figura 8.7: Imagen de uniformidad obtenida una vez se aplican todas las correcciones. También se muestran las proyecciones sobre los ejes X e Y. 8. Calibraciones del sistema: geométrica y del detector 8.3. Calibración geométrica del sistema SPECT Al realizar un sistema SPECT, además de las correcciones del detector mencionadas en la sección anterior, se requiere una descripción precisa de la geometrı́a del sistema para minimizar artefactos y pérdida de resolución en la reconstrucción. 8.3.1. Introducción teórica La precisión en el montaje de todos los componentes del SPECT puede ser determinante a la hora de obtener buenas imágenes reconstruidas. La mejor forma de evitar que pequeñas desviaciones en este proceso empeoren la calidad del sistema, es poder medir dichas desviaciones mediante un método de calibración geométrica. 8.3.1.1. Descripción de la geometrı́a de un sistema con detector único La geometrı́a completa de un sistema SPECT con un único detector y órbita circular se puede describir con siete parámetros [33]. De estos siete parámetros tres podremos considerarlos como intrı́nsecos al sistema detector utilizado y los otros cuatro como extrı́nsecos. Los parámetros intrı́nsecos son: la longitud focal f y los desplazamientos electrónicos eu y ev. La longitud focal es la distancia entre el punto focal (en nuestro caso el pinhole) y el detector, mientras que eu y ev describen una traslación colectiva de las imágenes proyectadas, causadas por la deriva del hardware. Los parámetros extrı́nsecos son: la distancia d, el desplazamiento mecánico m y los ángulos tilt y twist. Para describirlos convenientemente utilizaremos el concepto del rayo central, que es el rayo perpendicular al detector que pasa por el pinhole. De este modo, se tiene que, m es la distancia del rayo central al eje de rotación, d es la distancia a lo largo del rayo central entre el punto focal y el eje de rotación en ausencia de m y, por tanto, determina el radio de de giro de la órbita circular del detector. T ilt es el ángulo que forma el detector con el disco de rotación, siendo cero si el plano del detector es paralelo al plano del disco de rotación. Finalmente twist 91 92 8.3. Calibración geométrica del sistema SPECT es el ángulo formado entre la dirección vertical en la imagen (eje v de la proyección) y la proyección del eje de giro sobre el plano imagen. Los parámetros extrı́nsecos dependen de la posición del detector respecto al eje de rotación, los desplazamientos electrónicos pueden variar con el tiempo, mientras que un cambio de colimador, debido a posibles holguras en el sistema de fijación del mismo, puede modificar el valor de m. Por todo ello, es recomendable una verificación periódica de la calibración geométrica. Se asume que todos los parámetros permanecen constantes durante la adquisición. Para la calibración geométrica del sistema se utiliza el procedimiento introducido por D. Bequé et al. [34] y [35]. Dicho método se basa en la proyección tomográfica de tres fuentes puntuales conociendo la distancia entre ellas. Con los valores medidos de la posición de los centros de las tres fuentes en cada proyección y los estimados con los parámetros se calcula la función de coste F como la suma cuadrática de las diferencias entre dichos valores para todas las proyecciones y se utiliza un método de minimización para encontrar los parámetros óptimos. Los parámetros de calibración están altamente correlacionados entre ellos y por tanto la función de coste F a minimizar tiene muchos mı́nimos locales. Esto provoca que la solución óptima sea sensible a los valores iniciales del ajuste y dificulta encontrar la solución deseada. Esto reduce la precisión de los parámetros estimados. Por eso es importante un conocimiento a priori de la solución, para acercarnos al mı́nimo global de la función de coste ya que pequeños errores en uno de los parámetros estimados puede causar deterioros visibles en la imagen reconstruida [36]. Por ello, la bondad del ajuste y por tanto la validación de la calibración no debe evaluarse únicamente con la precisión en la estimación de los parámetros, sino que debe validarse con la calidad de las imágenes reconstruidas. En el caso ideal se considera el sistema formado por un detector y un colimador tipo pinhole con una apertura infinitamente pequeña. El detector rota en una órbita circular durante la adquisición. La distribución tridimensional de actividad A(x, y, z) se proyecta a través del pinhole sobre el detector. Esta distribución está definida en un sistema de coordenadas cartesianas, donde el eje z coincide con el eje de rotación. La imagen registrada en el sensor es Pθ (u, v) esta definida en el sistema de 8. Calibraciones del sistema: geométrica y del detector 93 coordenadas cartesianas uv, donde θ corresponde al ángulo de rotación del sistema (proyección actual). Los ejes del sistema de coordenadas uv están alineados con las filas y columnas de pixeles que forman el sensor. El origen del sistema de coordenadas uv es la proyección perpendicular del origen del sistema xyz en el detector, mientras que el ángulo de rotación θ se define como el ángulo entre la superficie detectora y el eje x medido en el plano xy. La orientación relativa de la distribución de actividad en el detector es diferente para cada ángulo θ. Para compensar este ángulo de rotación, la misma distribución se puede expresar en un nuevo sistema de coordenadas x′ y ′ z ′ rotando el sistema xyz alrededor del eje z, de manera que el eje x′ quede paralelo a la superficie detectora, ver figura 8.8(a). x cos θ sin θ 0 x′ y ′ = − sin θ cos θ 0 · y ′ z z 0 0 1 (8.1) Nótese que el ángulo θ expresa la orientación relativa del detector respecto al objeto A(x, y, z). Sus orientaciones absolutas no son importantes para la reconstrucción de la imagen. La orientación del sistema uv (detector) puede ser especificado de forma más precisa con los dos ángulos adicionales, llamados tilt (φ) y twist y (ψ). Para compensar el ángulo φ se rota el sistema x′ y ′ z ′ sobre el eje x′ dicho ángulo, obteniendo el sistema de coordenadas x′′ y ′′ z ′′ . Este giro tiene como resultado que los ejes x′′ y z ′′ queden paralelos a la superficie detectora. x′ y ′′ = 0 cos φ − sin φ · y ′ z′ z ′′ 0 sin φ cos φ x′′ 1 0 0 (8.2) ψ representa el ángulo entre el eje u y la dirección en la superficie detectora perpendicular al eje de rotación, esto es la orientación de los pı́xeles en la superficie detectora. 94 8.3. Calibración geométrica del sistema SPECT (a) Eje de rotación del detector respecto al eje z. (b) Giros tilt respecto al eje x’ y twist respecto al eje y” vistos desde el detector. Figura 8.8: Imágenes con las tres rotaciones realizadas durante el cálculo. Partiendo de x′′ , que es paralelo a la superficie detectora y ortogonal al eje de rotación, el ángulo ψ es por tanto el ángulo entre los ejes u y x′′ . Rotando el sistema x′′ y ′′ z ′′ sobre el ángulo ψ se obtiene finalmente un sistema de coordenadas x′′′ y ′′′ z ′′′ , en el que lo ejes x′′′ y z ′′′ son paralelos a los ejes u y v respectivamente. x′′′ cos ψ 0 − sin ψ y ′′′ = 0 z ′′′ sin ψ 1 0 x′′ · y ′′ z ′′ cos ψ 0 (8.3) En la figura 8.8(b) se muestran esquemáticamente las dos rotaciones realizadas para pasar del sistema de referencia x′ y ′ z ′ al sistema x′′′ y ′′′ z ′′′ . Una vez aplicadas las rotaciones, la geometrı́a del sistema objeto-imagen puede ser descrita por las distancias f , d y m. Como se puede en la ver figura 8.9, m forma 8. Calibraciones del sistema: geométrica y del detector Detector v 95 u f d Rayo central z''' m y''' x''' Eje de rotación Figura 8.9: El eje z es el eje de rotación del sistema imagen y el origen xyz es la intersección del rayo central con el eje x’. un ángulo ψ con el eje u y puede ser descompuesta en sus componentes en el plano uv (mu , mv ). mu = m · cos ψ mv = m · sin ψ 8.3.1.2. (8.4) Proyección de una fuente puntual Usando los parámetros y sistema de coordenadas visto en el apartado anterior, se puede calcular la proyección pinhole en el plano uv de una fuente puntual (x, y, z). La proyección viene definida por sus coordenadas (uθ , vθ ) en el sistema de coordenadas uv. Por trigonometrı́a se llega a: x′′′ −mu d+y ′′′ z ′′′ −mv d+y ′′′ = = mu −uθ f mv −vθ f Reagrupando y sustituyendo se obtiene que: (8.5) 96 8.3. Calibración geométrica del sistema SPECT uθ = f · vθ = f · m·cos ψ−x′′′ + m · cos ψ d+y ′′′ m·sin ψ−z ′′′ + m · sin ψ d+y ′′′ (8.6) Las proyecciones (uθ , vθ ) están definidas en el sistema de coordenadas uv, pero la posición proyectada del origen uv en las imágenes proyectadas es desconocida y puede verse afectada por el desplazamiento electrónico. Este desplazamiento electrónico causa una traslación colectiva de todas las posiciones detectadas (uθ , vθ ) en img la posición de las imágenes proyectadas (uimg θ , vθ ). La localización en la proyec- ción del origen uv puede, por otro lado, ser descrita por las coordenadas (eu , ev ) con respecto a algunos puntos conocidos en la proyección imagen, como por ejemplo el centro de la imagen. Usando estas coordenadas, la proyección de un punto en la imagen vendrá dada por: uimg =f· θ vθimg = f · 8.3.2. 8.3.2.1. m·cos ψ−x′′′ + m · cos ψ + eu d+y ′′′ m·sin ψ−z ′′′ + m · sin ψ + ev d+y ′′′ (8.7) Material y método de calibración geométrica Estimación de los parámetros La calibración nos plantea el problema inverso al descrito en la introducción teórica, queremos obtener los parámetros f , d, m, eu , ev , φ y ψ a partir de un conjunto de medidas obtenidas de las imágenes proyectadas de las tres fuentes puntuales, cuya posición es desconocida y lo único que conocemos es la distancia entre las mismas, que denotaremos por d12 , d13 y d23 . Para estimar la geometrı́a de una gammacámara pinhole hay que seleccionar una configuración de fuentes puntuales adecuadas. En principio, esto requiere el conocimiento de la posición de las fuentes puntuales, la distancia d y el ángulo φ. Sin embargo, asumiremos que una estimación del valor de estos parámetros será suficiente. Además, si consideramos que la ecuación (8.7) nos proporciona una muy buena estimación de la posición de los centros de los puntos en el plano uv, se puede relacionar el centro de masa estimado de una fuente puntual fı́sica, que es proyectada a través 8. Calibraciones del sistema: geométrica y del detector 97 del pinhole, con el conjunto de datos reales obtenidos en las proyecciones, es decir, con el centro de masa obtenido para cada punto y para cada una de las proyecciones medidas. Lo que se pretende con esto es encontrar los parámetros que hagan que los datos estimados se ajusten a los datos reales medidos. La bondad del ajuste se evaluará con la función de coste F por mı́nimos cuadrados. Esta función suma la diferencia al cuadrado entre la posición de los centros estimados y los medidos para cada una de las fuentes puntuales y en todas las proyecciones. La mejor estimación, corresponde a la menor distancia, eventualmente, el ajuste perfecto corresponde a F = 0. F = X X i uimg ij j − uest ij 2 + img vij − est vij 2 (8.8) donde i es el punto y j la proyección. La minimización de una función de N-variables se realiza mediante repetidos ciclos de N sucesivas minimizaciones de lı́neas unidimensionales a lo largo de direcciones conjugadas [37]. Una buena elección del maniquı́ de calibración asegura que solo los parámetros correctos puedan ser encontrados como soluciones válidas que minimicen la función de coste. Como ya hemos indicado, se debe conocer la distancia entre las tres fuentes puntuales para encontrar la solución correcta. El maniquı́ de calibración seleccionado forma un triángulo con tres fuentes puntuales colocadas en los vértices, cuyas coordenadas son xi , yi , zi con i = 1, 2, 3. Las distancias entre ellas se definen como d12 , d13 y d23 . El maniquı́ puede ser colocado en una posición arbitraria en el espacio xyz mediante 3 traslaciones y 3 rotaciones. Los parámetros f , d, φ y ψ pueden estimarse a priori utilizándolos como valores iniciales en el proceso iterativo que se emplea para su determinación. 8.3.2.2. Maniquı́ de calibración El maniquı́ de calibración se debe realizar de modo que la proyección tomográfica de dicho maniquı́ contenga suficiente información para obtener la correcta determinación de la geometrı́a del sistema [36]. Para que la estimación de los parámetros 98 8.3. Calibración geométrica del sistema SPECT geométricos sea correcta es imprescindible que las tres fuentes puntuales puedan verse y distinguirse en el espacio imagen. Para ello, los tres puntos tendrán que estar dentro del FOV y lo suficientemente separados entre si para que no se junten en ninguna proyección. El maniquı́ utilizado, ası́ como una proyección del mismo en el detector se puede ver en el esquema de la figura 8.10 Figura 8.10: Maniquı́ de calibración junto con una de sus proyecciones. En la configuración del maniquı́ de calibración es fundamental que los tres puntos se encuentren en diferentes posiciones axiales. De modo que para cualquiera de las proyecciones, cuando los puntos se proyecten a través de un colimador tipo pinhole en el eje v del sistema imagen siempre quedará uno de los tres puntos arriba, otro en el centro y el tercero abajo. En la configuración elegida para nuestro maniquı́ (figura 8.10), puede verse que para cualquier proyección, en el eje v del espacio imagen, el punto 1 siempre quedará por encima del 2 que a su vez quedará por encima del 3. 8. Calibraciones del sistema: geométrica y del detector En el eje u la posición dependerá de la proyección en la que estemos. De este modo, una vez realizada la adquisición pueden seleccionarse dos puntos de corte en el eje v que separen las imágenes en tres regiones de forma que cada uno de los puntos quede siempre en una de las tres regiones de la imagen para todas las proyecciones. Ası́, podremos encontrar los centros de masa de cada uno de los tres puntos sin superposiciones entre ellos y sin que estos se crucen, lo que podrı́a llevar a confundirnos de punto. Una vez colocado el maniquı́ de calibración, éste permanecerá quieto mientras el detector adquiere las proyecciones desde diversos ángulos hasta completar una vuelta alrededor de él. Consideraremos como posición inicial aquella en la que el detector está arriba del maniquı́ de calibración. Siguiendo con este convenio, la proyección representada en la figura 8.10 es perpendicular al plano definido por los tres puntos del maniquı́. Para evitar los problemas derivados de la calibración a diferentes radios de giro, se diseñaron varios maniquı́es con triángulos de diferentes tamaños. Ası́, en función del radio de giro que se pretenda calibrar puede usarse uno u otro maniquı́. 8.3.3. Resultados de la calibración geométrica: software de calibración Con el fin de automatizar la calibración geométrica se ha realizado un software para realizar la calibración geométrica. Dicho programa se realizó en C++. Las funciones principales del programa son dos: encontrar el centro de los 3 puntos para cada una de las proyecciones y obtener los parámetros de calibración minimizando las diferencias entre las distancias de los centros de masas medidos y estimados. 8.3.3.1. Búsqueda del centro de masa de los puntos Para cada proyección se segmenta la imagen en 3 regiones, de manera que cada una contenga uno de los puntos. El programa permite al usuario seleccionar los dos puntos de separación entre secciones y el tamaño del lado del cuadrado para el ajuste de dichos puntos. Una vez separadas en cada una de la partes, se buscará el pixel 99 100 8.3. Calibración geométrica del sistema SPECT con el valor máximo y alrededor de él se selecciona un área cuadrada que englobe a todo el punto. A partir de aquı́ una subrutina realiza un ajuste Gaussiano bidimensional que nos proporcionará las coordenadas (u,v) del centro de la distribución, las cuales consideraremos como el centro de ese punto1 . El proceso se repetirá para los 3 puntos de cada una de las proyecciones, obteniéndose ası́ las coordenadas (u,v) de todos los centros. Figura 8.11: Imagen con los cuadrados en los que se realiza el ajuste Gaussiano. En la figura 8.11 se observa una imagen de los tres puntos junto con las rayas que la separan en tres regiones y el área rectangular alrededor de los puntos. Se puede ver, que si no separásemos la imagen en 3 serı́a muy complejo distinguir la coordenada u de los tres puntos. Un factor a tener en cuenta para la correcta localización de los puntos en la imagen es lo cerca o lejos que se encuentre la cámara de los puntos, ya que el radio de giro es 1 Se ha considerado la hipótesis de que los puntos proyectados en la imagen son prácticamente redondos y se pueden ajustar mediante funciones Gaussianas. 8. Calibraciones del sistema: geométrica y del detector (a) Maniquı́ utilizado (b) Configuración Ángulo de 90o . (d) Configuración Ángulo de 270o . correcta. (c) Configuración Ángulo de 90o . correcta. (e) Configuración Ángulo de 270o . 101 incorrecta. incorrecta. Figura 8.12: Maniquı́ de calibración variable y habrá que calibrar distintos radios de giro. Si nos alejamos de los puntos, estos pueden llegar a juntarse en algunas proyecciones (ver figura 8.12(c)). Por el contrario, si nos acercamos mucho, los puntos pueden salirse del FOV en alguna de las proyecciones, tal como se muestra en la figura 8.12(e). En la figura 8.12 además de los dos ejemplos mencionados de una mala configuración del maniquı́ de calibración, se muestra uno de los maniquı́s de calibración utilizados (figura 8.12(a)) y como quedarı́a correctamente para alguno de los ángulos crı́ticos, como son los de 90o (figura 8.12(c)) y 270o (figura 8.12(e)). 8.3.3.2. Minimización de la distancia entre las posiciones medidas y las estimadas Una vez se tienen todos los centros medidos y partiendo de unos valores iniciales estimados para todos los parámetros, utilizando la ecuación 8.7 se estima la posición 102 8.3. Calibración geométrica del sistema SPECT u y v de los centros en la imagen. Posteriormente se utiliza una subrutina [37] para minimizar la función de coste de la ecuación 8.8. Las distancias d12 , d13 y d23 , entre las fuentes deben ser medidas con precisión ya que definen las ligaduras entre las posiciones de cada par de puntos fuente. Este maniquı́ es rı́gido y se puede, por tanto, mover por el espacio objeto a través de 3 rotaciones y 3 traslaciones. De este modo se irá variando la posición del maniquı́ y los valores de los parámetros de calibración hasta encontrar la configuración que ofrezca la mı́nima diferencia entre las proyecciones estimadas y medidas. Una vez se llegue a la solución, nos quedaremos con los valores de los 7 parámetros geométricos encontrados. 8.3.3.3. Interfaz de usuario Se ha desarrollado un ejecutable en entorno visual, lenguaje C++, que dota al programa de una mayor rapidez y comodidad a nivel usuario. En dicho entorno las variables se han dividido en 5 grandes grupos (ver figura 8.13) que son: Figura 8.13: Programa de calibración en entorno visual. 8. Calibraciones del sistema: geométrica y del detector Datos de entrada. En este grupo están los parámetros necesarios para cargar las imágenes de calibración adquiridas. Esos parámetros son: el nombre del archivo que contiene los datos (el cual debe contener las imágenes de todas las proyecciones realizadas en la adquisición), el tamaño del lado de la imagen en pixeles, el número de proyecciones que se han adquirido y el tamaño del pixel de la imagen en mm. Inicialización. Contiene los valores iniciales de los parámetros. Además de el valor inicial aproximado de los 7 parámetros de calibración que buscamos, en este apartado también se incluye el valor de las 3 distancias entre los puntos d12 , d13 y d23 , y el valor de los cortes que elegimos para separar la imagen en 3 partes (en pixeles). Cuando realizamos una adquisición completa de SPECT con el maniquı́ de calibración, siempre hay una proyección en la cual los puntos están más cerca entre si, con esta proyección se puede estimar el valor de los cortes y utilizar dicho valor para toda la adquisición. Parámetros de control. Este apartado contiene el valor inicial de la posición x, y, z de una de las 3 fuentes puntuales en el espacio objeto, ası́ como los tres ángulos (α, β, γ) que permiten girar al triángulo. También tenemos aquı́ la posibilidad de seleccionar el tamaño del lado del cuadrado en el que se hace el ajuste Gaussiano de los puntos (ver figura 8.11). Datos de salida. Permite seleccionar el directorio y el nombre del archivo de salida que queremos guardar. A la salida se guardaran 2 archivos tipo texto. En el primero de ellos se guardan los parámetros de calibración encontrados al final del ajuste, ası́ como la función de coste de dicho ajuste y la posición final de los 3 puntos en el espacio objeto. El segundo archivo contendrá 6 filas y tantas columnas como proyecciones se hayan tomado. Cada una de las filas corresponden a las posiciones u y v de los puntos 1, 2 y 3 respectivamente, mientras que las columnas se refieren a cada una de las proyecciones realizadas. El archivo con los centros es útil para verificar si el programa ha encontrado bien la posición de dichos centros, ya que un punto al ser proyectado a distintos ángulos describe una trayectoria sinusoidal en la imagen. En a figura 8.14 se puede ver un ejemplo que corresponde a los centros encontrados para una imagen de calibración. 103 104 8.3. Calibración geométrica del sistema SPECT Figura 8.14: Variación del centro de cada punto con el ángulo de proyección. Se observa la trayectoria sinusoidal que describen los puntos. Resultados: Una vez seleccionados todos los parámetros en el programa se puede utilizar el botón “iniciar calibración” para iniciar los cálculos y poder ver los resultados. Si el programa finaliza satisfactoriamente, sale un mensaje de “calibración finalizada” en el cuadro de texto reservado para resultados. Además se muestran los valores obtenidos para los distintos parámetros de calibración, la posición final de los 3 puntos y la función de coste del ajuste, que nos da una idea de la bondad del ajuste. Si los resultados no son satisfactorios se pueden cambiar los 7 valores iniciales de los parámetros de calibración, ası́ como los parámetros de control hasta conseguir un resultado óptimo. El valor óptimo de la función de coste depende mucho de la adquisición realizada, cuanto más actividad se tenga y mejor se separen los puntos mayor es la probabilidad de tener una función de coste baja. Normalmente las funciones de coste obtenidas están por debajo de 20, lo que implica que en promedio la distancia entre los puntos medidos y los estimados difiere en menos de 0.25 mm. Si la función de coste supera dicho valor, deberemos probar nuevos valores iniciales para los parámetros o intentar encontrar mejor la posición de los centros. La calibración geométrica debe realizarse cada vez que se varı́a el radio de giro. Ası́ mismo, si se actúa con el colimador o la gammacámara será necesario volver a 8. Calibraciones del sistema: geométrica y del detector calibrar el sistema. En la tabla 8.1 se muestra algunas de las calibraciones geométricas obtenidas con la prueba de concepto para distintos radios de giro. Donde hemos denotado por posición a la posición marcada en el desplazador lineal manual con el que se selecciona el radio de giro de la gammacámara antes de comenzar la adquisición. posición focal radio giro tilt twist m eu ev función de (mm) (mm) (mm) (rad) (rad) (mm) (mm) (mm) coste 21.0 31.96 15.73 0.026 0.0041 0.975 -2.15 0.92 9.11 23.0 31.87 17.70 0.030 0.0046 1.185 -2.61 1.06 6.50 24.0 31.77 18.64 0.027 0.0047 1.101 -2.31 0.97 4.97 31.0 32.30 25.61 0.022 0.0038 1.335 -2.55 0.65 35.16 33.0 32.26 27.73 0.027 0.0040 1.334 -2.46 0.83 28.58 35.0 32.27 29.86 0.030 0.0034 1.478 -2.66 0.95 24.73 Promedio: 32.07 0.027 0.0041 -2.46 0.90 Tabla 8.1: Resultados obtenidos para diferentes calibraciones geométricas con la prueba de concepto. Figura 8.15: Ajuste por mı́nimos cuadrados de la variable m en función del radio de giro. De los datos de la tabla 8.1 y teniendo en cuenta que los parámetros que se obtienen tiene cierto error, se puede deducir que los parámetros intrı́nsecos (f ocal, eu y ev) no varı́an con el radio. Por lo tanto, serı́a lógico obtener un valor promedio para ellos. De los parámetros extrı́nsecos, los ángulos tilt y twist son siempre muy pequeños y 105 106 8.3. Calibración geométrica del sistema SPECT apenas varı́an, por lo que también es lógico obtener el valor promedio para ellos, el valor promedio de estos 5 parámetros se muestra en la última fila de la tabla. Para el parámetro m, se puede obtener una función dependiente del radio, ya que tiene un comportamiento lineal con el radio, ver figura 8.15. Capı́tulo 9 Validación de la prueba de concepto 9.1. Introducción El objetivo final de una prueba de concepto es validar la viabilidad del proyecto. Por tanto, el objetivo final de la prueba de concepto desarrollada es obtener imágenes tomográficas a partir de las proyecciones obtenidas por la gammacámara mediante la utilización de algoritmos de reconstrucción. 9.2. Material y métodos Las imágenes reconstruidas para este primer prototipo se obtuvieron mediante un algoritmo OS-EM. El algoritmo fue adaptado para la gammacámara con colimador pinhole de un método desarrollado para gammacámaras clı́nicas con colimadores convergentes [38]. Tanto el algoritmo como la matriz de transición para este prototipo fueron realizados ı́ntegramente por el grupo de la unidad de Biofı́sica y Bioenginyeria del departamento de Ciències Fisiològicas de la Universidad de Barcelona [39]. El código se escribió en lenguaje C y se usó Linux como sistema operativo. 107 108 9.2. Material y métodos En primer lugar realizaremos una caracterización del sistema con maniquı́s, para finalmente llevar a cabo estudios con animales. En todos los estudios de SPECT las adquisiciones constan de 60 proyecciones girando 6o entre proyecciones cubriendo 360o . Cada una de las proyecciones se guarda en una matriz de 75x75 pı́xeles de tamaño 0.52x0.52 mm2 [39]. 9.2.1. Caracterización del sistema 9.2.1.1. Uniformidad tomográfica El maniquı́ utilizado para medir la uniformidad del sistema es un cilindro de metacrilato hueco de 35 mm de diámetro interior y 38 mm de exterior. La altura es de 38 mm (ver figura 9.1). Dicho maniquı́ sirve tanto para verificar la inexistencia de artefactos en la imagen reconstruida como para obtener la uniformidad del sistema. Para el estudio de uniformidad el maniquı́ se rellenó con 37 M Bq/mL de una solución de 99m T c. El radio de rotación utilizado fue de 33 mm, lo que proporciona un FOV de 42 mm. El tiempo de adquisición fue de 60 segundos por proyección. Figura 9.1: Foto del maniquı́ de uniformidad utilizado para la prueba de concepto. La uniformidad de las imágenes tomográficas reconstruidas se puede medir utilizando la siguiente ecuación: 9. Validación de la prueba de concepto 109 U nif ormidad ( %) = 100 · Vmax − Vmin , Vmax + Vmin (9.1) donde Vmax es el valor máximo y Vmin es el valor mı́nimo de la región de interés (ROI). La ROI utilizada para estas medidas es un cilindro de 10 mm de diámetro y 2.5 mm de altura. Dicho cilindro se centra con respecto al maniquı́ en las imágenes reconstruidas. 9.2.1.2. Sensibilidad del sistema La sensibilidad del sistema se obtuvo usando un maniquı́ cilı́ndrico de 4.5 mm de diámetro y 4.4 mm de altura relleno con 36,3 M Bq de una solución de 99m T c y centrado en el FOV. El tiempo total de cada estudio fue de 300 segundos para distintos FOV que van de 64.1 mm a 19.7 mm. La sensibilidad se mide a partir de la siguiente ecuación: Sensibilidad cps M Bq = Ctotales , tmedida · A (9.2) donde Ctotales es la suma de todas las cuentas obtenidas dentro de la ventana de energı́a en todas todas las proyecciones, tmedida es el tiempo total de la medida en segundos, mientras que A es la actividad medida en Megabecquerel. 9.2.1.3. Resolución espacial tomográfica La resolución tomográfica se midió utilizando una fuente lineal construida con un capilar de 0.3 mm de diámetro interior que contenı́a 37 M Bq/ml de una solución de 99m T c y colocado en el centro del FOV y paralelo al eje de rotación. Se tomaron adquisiciones de 30 segundos por proyección (tiempo total de cada estudio 30 minutos) para distintos FOV que van de 47.2 mm a 27.2 mm. La resolución en este caso se obtiene directamente con la medida de la anchura de la fuente en la imagen reconstruida. Para obtener la FWHM se promedian los 5 cortes centrales de la imagen reconstruida y se realiza el ajuste de una función gaussiana 2D. 110 9.2. Material y métodos Posteriormente se utiliza un maniquı́ tipo Derenzo [55] para verificar la resolución medida con la fuente lineal. Dicho maniquı́ contiene fuentes lineales de 7 cm de longitud y 0.3 mm de diámetro interior. Las fuentes lineales se colocan en un cilindro hueco distribuidos en 6 sectores. La distancia entre los capilares va desde 2 a 6 mm aumentando un milı́metro por cada una de las secciones y una última sección con 8 mm de diámetro de los capilares (ver figura 9.2). Los capilares se rellenan con 37 M Bq/mL de una solución de 99m T c. El FOV utilizado es de 33.9 mm con adquisiciones de 60 segundos por proyección (tiempo total del estudio 60 minutos) y la matriz de reconstrucción es de 80x80x80 vóxeles con 0.5x0.5x0.5 mm3 de tamaño cada uno. Figura 9.2: Foto del maniquı́ tipo Derenzo utilizado para la prueba de concepto. 9.2.2. Estudios SPECT con animales Para las pruebas con animales se desplazó el equipo a una instalación autorizada a trabajar con animales de investigación. Los trabajos con animales se realizaron cumpliendo la legislación española referida a la “Protección de los animales utilizados para experimentación y otros fines cientı́ficos” y en concordancia con las directivas de la Unión Europea. Siempre se anestesia a los animales antes de administrarles el trazador y se mantienen anestesiados durante todo el estudio mediante un flujo estable de anestesia gaseosa. La inyección se realiza en la cola por vı́a intravenosa una vez dormido el animal y convenientemente colocado en la camilla del equipo. 9. Validación de la prueba de concepto 111 Se han realizado dos tipos de estudios con ratones. Un estudio de perfusión pulmonar y un estudio oseo de cabeza. A continuación describiremos brevemente los dos tipos de estudios de SPECT que se han utilizado en la prueba de concepto: Pulmón con macroagregados de Albúmina. Los macroagregados de Albúmina (MAA) se utilizan en diagnostico junto con 99m T c para identificar al- teraciones anatómicas pulmonares. Los MAA se preparan con seroalbúmina humana desnaturalizada. El 90 % de las partı́culas de los MMA tiene un tamaño de 5 - 90 µm, la mayorı́a de las cuales se encuentra en el rango de 2040 µm. Normalmente se administran de 200.000 a 700.000 por via endovenosa con el paciente en decúbito supino. Las imágenes pueden adquirirse inmediatamente después de la administración, ya que la mayorı́a de las partı́culas son retenidas en el primer paso por el pulmón. Normalmente se esperan unos 5 minutos, a fin de que las partı́culas que no hallan sido atrapadas por los capilares pulmonares, lo sean por el sistema reticuloendotelial. La vida media biológica es de 2 a 9 horas y son aclaradas del pulmón por fragmentación en partı́culas más pequeñas, pasando a la circulación general. Estudios óseos con 99m T c − HDP . Para el estudio del tejido óseo propiamente dicho se utilizan bisfosfonatos (MDP, DPD y HDP) marcados con 99m T c. La primera condición para que el radiotrazador se incorpore al hueso es que el flujo sanguı́neo esté conservado. La incorporación se realiza a los cristales de hidroxiapatita, de tal forma que el grado de captación será proporcional a la presencia de aquellos cristales, que, a su vez, será proporcional a la actividad osteoblástica y, por lo tanto, al recambio metabólico óseo. Como resultado, la captación del radiotrazador será mayor allı́ donde mayor actividad osteoblástica se produzca. Una vez inyectados por vı́a endovenosa, los bisfosfonatos se distribuyen en primer lugar por el compartimiento vascular sanguı́neo, desde donde son inmediatamente extraı́dos por el hueso y simultáneamente por el riñón, de tal forma que lo que no fue captado por aquél es eliminado por la orina. Por lo tanto, transcurridas 3-4 horas, prácticamente todo el radiotrazador se habrá incorporado al hueso o habrá sido eliminado. Éste será el momento óptimo para obtener el SPECT correspondiente de la actividad metabólica ósea. 112 9.3. Resultados de la prueba de concepto En todos los estudios el tiempo de adquisición fue de 60 segundos por proyección con la matriz de reconstrucción de 100x100x100 vóxeles. El estudio de perfusión de pulmón de ratón se llevo a cabo tras inyectar 66 MBq de 99m T c − M AA. El FOV utilizado fue de 36.6 mm con un tamaño de vóxel de 0.3x0.3x0.3 mm3 para la reconstrucción. Para el estudio oseo de cabeza de ratón se realizaron 2 adquisiciones completas desplazando la camilla 10 mm entre las dos. La actividad total utilizada fue de 355 MBq de 99m T c − HDP . El FOV utilizado fue de 24.8 mm con un tamaño de vóxel de 0.23x0.23x0.23 mm3 para la reconstrucción. 9.3. 9.3.1. Resultados de la prueba de concepto Caracterización del equipo Los resultados obtenidos en las pruebas de validación del equipo se detallan a continuación. 9.3.1.1. Uniformidad tomográfica En la parte superior de la figura 9.3 se puede ver una gráfica con los resultados de uniformidad en función del número de iteraciones utilizadas donde se observa como ésta va empeorando a medida que aumenta el número de iteraciones. La parte inferior de la figura 9.3 muestra las cinco primeras iteraciones de la reconstrucción de una sección del maniquı́ uniforme. En los cortes mostrados de las distintas iteraciones se ve como la imagen reconstruida reproduce la forma del maniquı́ utilizado y carece de artefactos. 9.3.1.2. Sensibilidad del sistema En la figura 9.4 se observa como la sensibilidad disminuye cuadráticamente al incrementar el FOV observado. El valor máximo de sensibilidad medido con el prototipo es de 101.4 cps/MBq para un FOV de 19.7 mm. 9. Validación de la prueba de concepto Figura 9.3: Uniformidad de la imagen reconstruida en función del número de iteraciones utilizadas. La imagen se ha obtenido con un algoritmo OSEM con 5 subsets Figura 9.4: Resultados de la sensibilidad medida en función del FOV medidos. 113 114 9.3. Resultados de la prueba de concepto 9.3.1.3. Resolución espacial En la figura 9.5 se muestra la resolución tomográfica obtenida. Se aprecia como la resolución mejora al disminuir el FOV, ya que al acercarse al objeto aumenta el factor de amplificación mejorando ası́ la resolución (ver ecuación (4.5)). El mejor valor de resolución tomográfica medida con el prototipo es de 1.03 mm para un FOV de 27.2 mm. Resolución del equipo en función del FOV 1.6 Resolucion (mm) 1.5 1.4 1.3 1.2 1.1 1 0.9 26 30 35 40 45 50 FOV (mm) Figura 9.5: Resolución en función del FOV. Finalmente, en la figura 9.6, se muestra un corte axial de la reconstrucción de un maniquı́ tipo Derenzo en el que se puede estimar de forma visual la resolución del equipo. El FOV utilizado es de 33.9 mm. En la imagen se distinguen todos los capilares, incluidos los que están separados 2 mm entre si, aunque la imagen muestra una baja uniformidad. 9.3.2. Imágenes obtenidas en los estudios con animales En la figura 9.7 se muestran diversas secciones de la reconstrucción del estudio de perfusión pulmonar realizado con 99m T c − M AA. En la figura 9.8 se muestran las secciones axial, coronal y sagital obtenidos de la reconstrucción del estudio de cabeza de ratón con 99m T c − HDP . 9. Validación de la prueba de concepto Figura 9.6: Corte axial de una imagen reconstruida de un maniquı́ tipo Derenzo utilizado para comprobar la resolución del equipo. La imagen se ha obtenido con un algoritmo OSEM con 5 subsets y se han utilizado 5 iteraciones. Figura 9.7: Secciones de un estudio de pulmón de ratón obtenidas con 99m T c − M AA: (a) axial, (b) coronal, (c) sagital de pulmón derecho y (d) sagital de pulmón izquierdo. 115 116 9.3. Resultados de la prueba de concepto Figura 9.8: Secciones de cabeza de ratón obtenidas con 99m T c − HDP : (a) sagital,(b, f) coronales y (c,d,e) axiales a nivel posterior, medio y anterior respectivamente. Se ve claramente como el trazador muestra las diferentes estructuras oseas de la cabeza del ratón. La figura 9.8 (a) es una sección sagital que se emplea como referencia espacial del resto de vistas. En la figura 9.8 (b) se identifica el arco cigomático. En las figura 9.8 (d), (e) y (f) se observan distintas secciones de la cavidad craneal. Finalmente la figura 9.8 (c) corresponde a una de las primeras vertebras cervicales en la que se observa el canal vertebral. Capı́tulo 10 Conclusiones de la prueba de concepto 10.1. Elementos de un sistema SPECT de un solo detector con colimador pinhole - Se ha montado y puesto en marcha un sistema SPECT partiendo de una gammacámara Sentinella desarrollada previamente por nuestro grupo de fı́sica médica. - Se ha seleccionado un colimador tipo pinhole de 1 mm de diámetro con el fin de obtener una buena resolución espacial. 10.2. Adquisición y tratamiento de datos - Se ha desarrollado una aplicación de adquisición para el prototipo de SPECT que dota al usuario del control simultaneo de la gammacámara y los motores del SPECT y permite automatizar los estudios tı́picos en este tipo de equipos, como son: estáticos, dinámicos, SPECT o espectro. - Se ha propuesto un nuevo método de corrección del decay compensando la disminución de actividad entre proyecciones con un aumento del tiempo por 117 118 10.3. Calibración del sistema: geométrica y del detector proyección de modo que se iguale la probabilidad de desintegraciones de todas las proyecciones. 10.3. Calibración del sistema: geométrica y del detector - Se ha validado el método de calibración de las gammacámaras utilizado por nuestro grupo y se ha calibrado nuestra gammacámara para poder ser utilizada como detector del sistema SPECT. - Se ha desarrollado una aplicación que permite obtener los 7 parámetros que definen la geometrı́a del sistema a partir de una estudio realizado con un maniquı́ de tres puntos en el cual la distancia entre los puntos debe conocerse con exactitud. - Se han realizado calibraciones con distintos radios de giro obteniéndose en todas ellas funciones de coste bajas. También se ha verificado que la calidad de las imágenes reconstruidas mejora notablemente cuando se utilizan los 7 parámetros geométricos calibrados. 10.4. Validación de la prueba de concepto SPECT - Los resultados de sensibilidad y resolución obtenidos muestran un alto nivel de confianza en el sistema. Obteniéndose resoluciones cercanas al milı́metro con una sensibilidad de 100 cps/M Bq para un FOV de aproximadamente 20 mm. Conforme aumentamos el FOV la resolución empeora de forma lineal, mientras que la sensibilidad se reduce cuadráticamente. La uniformidad de las imágenes obtenidas es relativamente baja, lo cual se puede considerar como normal dado que no se aplica ningún tipo de corrección en la reconstrucción de imágenes llevada a cabo en la prueba de concepto. - Se han obtenido las primeras imágenes de hueso y pulmón de ratón. En ambos casos se obtienen imágenes con muy buena calidad. 10. Conclusiones de la prueba de concepto Por todo ello, podemos concluir que la prueba de concepto ha dado un resultado positivo ya que se ha demostrado que es posible realizar estudios de SPECT en animales pequeños utilizando la gammacámara de pequeño formato Sentinella con un colimador pinhole. 119 Parte IV Segundo prototipo SPECT 121 Capı́tulo 11 Diseño del segundo prototipo 11.1. Introducción Una vez verificada la viabilidad del proyecto se decidió diseñar un nuevo SPECT basado de nuevo en la mini gammacámara Sentinella. Sin embargo para este segundo prototipo se han rediseñado algunos de los componentes del sistema SPECT. En primer lugar se ha realizado una nueva carcasa y un nuevo colimador pinhole más acordes para nuestra aplicación. La nueva carcasa tiene una forma rectangular con el fin de facilitar el acoplamiento al disco de giro reduciendo ası́ algunos de los parámetros geométricos (ver capı́tulo 8.3). El nuevo colimador pinhole se ha diseñado con un nuevo sistema de sujeción que asegura la estabilidad y reproducibilidad de la posición cada vez que coloca el colimador. Uno de las mayores desventajas que se observaron en la prueba de concepto realizada con relación a otros sistemas es su baja sensibilidad. Para intentar paliar esta desventaja, el segundo prototipo consta de 2 detectores con la capacidad de adquirir imágenes simultáneamente y colocados a 180o uno respecto al otro, lo cual, aumenta la sensibilidad del sistema en un factor 2. Además se pretende diseñar un colimador multipinhole, con el objetivo de tener un sistema con dos colimadores intercambiables, donde el colimador pinhole proporcione una mayor resolución espacial y el multipinhole una mayor sensibilidad con la menor pérdida de resolución espacial posible. 123 124 11.2. Material y métodos El segundo prototipo se ha llevado a cabo en el departamento de fı́sica médica del instituto de fı́sica corpuscular (IFIC) de Valencia, bajo la supervisión de José Marı́a Benlloch (Profesor de Investigación, CSIC). El proyecto se ha coordinado conjuntamente con la empresa spin off Oncovision S. A., bajo la tutela de Antonio González, con el objetivo de una vez desarrollado el prototipo poder acoplarlo en un sistema de imagen médica completo (SPECT-PET-CT) denominado Albira. Este sistema esta destinado a la investigación con pequeños roedores en una amplia diversidad de campos como la oncologı́a, neurologı́a, farmacologı́a, etc. 11.2. Material y métodos 11.2.1. Diseño de un nuevo colimador pinhole Se ha diseñado un nuevo colimador pinhole con un nuevo sistema de sujeción y una nueva geometrı́a que aseguran una mayor reproducibilidad y estabilidad en el posicionamiento del colimador cuando éste se extrae y se vuelve a colocar. El colimador está construido de Tungsteno con un espesor de 2 mm recubierto por una carcasa de plástico negro evitando que se filtre luz y perjudique la detección de luz del cristal. La apertura pinhole se sitúa en el centro del colimador. Dicha apertura es de tipo knife-edge con un diámetro de 1 mm en el centro del colimador y 2 mm en los extremos. De este modo, el ángulo de apertura, α, es de 53.13o . Cuando se diseña un colimador pinhole lo primero que hay que tener en cuenta es el tamaño de los objetos a medir y por tanto cual será la distancia objeto-colimador (b) más pequeña que se podrá tener sin chocar con el objeto a estudiar. Una vez conocida la distancia b podremos determinar la focal (f ) del sistema. Debemos buscar la mayor f tal que el FOV sea mayor o igual que el objeto de estudio y que los rayos gamma que pasen por el agujero del colimador sigan llegando al detector. Para ello se simula mediante métodos Monte Carlo el cono de luz que pasa a través del agujero de nuestro colimador pinhole y se hace un corte a la distintas alturas. La f deseada es la menor de las distancias Para las cuales todo el detector queda completamente iluminado. De modo que a partir de este valor de f no existen “zonas muertas” en el 11. Diseño del segundo prototipo 125 Figura 11.1: Esquema 3D del cono de luz que suscita el colimador sobre el detector. detector (ver figura 11.1). Para valores de f más grandes, con el mismo valor de α, parte del cono de luz emitido cae fuera del detector y por tanto no será detectado. 11.2.2. Diseño de un colimador multipinhole Los 3 parámetros fundamentales para caracterizar un sistema SPECT son la resolución espacial, la sensibilidad y el FOV. Como vimos en la sección 4.3.2 dichos parámetros están relacionados entre ellos, de modo que mejorar uno de ellos suele repercutir negativamente en los otros 2 parámetros. En concreto, en la tabla 11.1 se puede ver qué factores hay que aumentar o disminuir para mejorar cada uno de los 3 parámetros. Mejora / si FOV Sensibilidad Resolución espacial Aumenta b; LD φe f Disminuye f b φe ; b; Ri Tabla 11.1: Relación entre los principales parámetros de un SPECT con colimador pinhole o multipinhole. 126 11.2. Material y métodos Idealmente, cuando se diseña un colimador multipinhole, se pretende que todos los agujeros tengan el mismo FOV sin superposición en el detector como se mostraba en la figura 4.6 de la sección 4.3.3. Para ello se inclinan los agujeros (salvo el central) para que a una distancia b (fijada), el campo de visión de todos los agujeros coincida. Sin embargo, esto solo se puede conseguir si el detector es mucho más grande que el FOV que se está midiendo, o bien, si se usan factores de magnificación muy pequeños, pero este segundo caso no es viable si se desean obtener buenos valores de resolución espacial. 11.2.2.1. Configuraciones multipinhole sin superposición en la imagen Una posible configuración serı́a la de utilizar varios agujeros con un ángulo de apertura pequeño como se muestra en la figura 11.2. Con esta configuración existe una zona muerta del espacio objeto que no se puede “ver” (zona rayada en azul en la figura 11.2). Esto implica una distancia b mı́nima (bmin ) a partir del cual se puede medir. Para esa distancia la sensibilidad y el FOV que se obtienen son equivalentes a la configuración con un único pinhole centrado. Esto se debe a que a pesar de haber múltiples agujeros, para un punto de emisión los rayos gamma solo pueden pasar por uno de los agujeros. Para distancias mayores a bmin la sensibilidad aumenta respecto a la configuración pinhole pero disminuye el FOV. Una segunda configuración posible de colimador es utilizar agujeros inclinados con inclinación de tipo “convergente” (ver figura 11.3). Con esta configuración se consigue aumentar el solapamiento en el espacio objeto entre los agujeros del colimador con lo que aumenta la sensibilidad para una misma distancia b. Además, también se reduce la distancia bmin a partir de la cual se puede medir. Por el contrario, este aumento de sensibilidad conlleva una disminución del FOV, por lo que para obtener un mismo FOV es necesario alejarse más, de modo que para un mismo FOV al final se obtiene la misma sensibilidad con peor resolución que con un colimador pinhole. Debido al reducido tamaño de nuestro detector, 40x40 mm2 , ninguna de las configuraciones multipinhole sin superposición en la imagen encontradas aporta una mejora teórica a la imagen final. Por lo que fueron descartados, pasando a diseñar 11. Diseño del segundo prototipo Figura 11.2: Esquemático 2D de la configuración 1 de un colimador con 2 pinholes sin superposición en el detector. Figura 11.3: Esquemático 2D de un colimador con 2 “pinholes convergentes” sin superposición en el detector. 127 128 11.2. Material y métodos un colimador multipinhole con superposición en la imagen para poder conseguir una mejora en el rendimiento del sistema. 11.2.2.2. Configuraciones multipinhole con superposición en la imagen Existen dos posibles configuraciones con superposición en la imagen: 1. Utilizar agujeros no inclinados con superposición parcial en el detector (figura 11.4(a)). 2. Utilizar un agujero central sin inclinar y el resto inclinados del tipo “divergente”, de este modo se tiene una superposición total en el detector (figura 11.4(b)). En la figura 11.4 están marcados 3 FOVs diferentes para una distancia b2 cualquiera, que corresponden a: FOV1 (en rojo): el FOV visto por los 3 agujeros. FOV2 (en morado): el FOV visto por el agujero central y al menos la mitad del resto de los agujeros. El cual coincide con el FOV del agujero central. Si dicho agujero central está en el centro del colimador se trata del mismo FOV del colimador pinhole. FOV3 (en negro): el FOV visto por al menos uno de los agujeros. Los FOVs 1 y 2 coinciden para las dos configuraciones con superposición en la imagen que hemos comentado. En principio el FOV1 deberı́a ser mayor para la configuración 1, sin embargo, al tener un detector pequeño, la parte del FOV1 que tiene de más la configuración 1, para los agujeros no centrales, “cae” fuera del detector (zona rayada de la figura 11.4 (a)) por lo que acaba perdiendo. El FOV3 es más grande para el colimador de agujeros inclinados. Por contra, para la parte central del FOV, los agujeros inclinados tienen un menor ángulo sólido y por tanto una menor sensibilidad. 11. Diseño del segundo prototipo (a) Colimador multipinhole con agujeros no inclinados. (b) Colimador multipinhole con agujeros inclinados. Figura 11.4: Esquemático 2D para los dos colimadores multipinhole con superposición en el detector. Se observa que la distancia b1 es la distancia mı́nima para que los 3 agujeros vean el centro del FOV. Antes de decidirse por una de las configuraciones multipinhole con superposición en el detector se han simulado cuatro tipos de colimadores por métodos Monte Carlo. Todos los colimadores tienen una focal de 31 mm y 5 agujeros, con un agujero central y los otros 4 en las diagonales del detector, el resto de caracterı́sticas de cada uno de ellos se pueden ver en la siguiente tabla: Para la comparación de colimadores se simulo un estudio para cada uno de los colimadores con las mismas caracterı́sticas en todos los casos. Los estudios se realizaron 129 130 11.2. Material y métodos Número de agujeros Diámetro del agujero Distancia al centro Inclinación Configuración 1 Configuración 2 Configuración 3 Configuración 4 5 5 5 5 1 mm 1 mm 1 mm 1 mm 5 mm 5 mm 4 mm 4 mm 0o 12.5o 0o 12.5o Tabla 11.2: Caracterı́sticas de los 4 colimadores simulados. utilizando dos detectores. La distancia focal utilizada en cada uno de ellos fue de 31.5 mm, con un radio de giro de 20 mm con el resto de parámetros geométricos a cero (caso ideal). Se utiliza como emisor de rayos gamma de 140 keV una fuente puntual en el centro del FOV y se simulan 25 millones de eventos emitidos isotrópicamente para una de las proyecciones de SPECT. Las simulaciones se realizaron utilizando Geant4 versión 4.9.2. Para las simulaciones se generaron los distintos colimadores, ası́ como las carcasas de las cámaras y el cristal centellador, habilitando la generación de fotones ópticos. El fotomultiplicador y la electrónica no se simularon en esta versión, puesto que no lo consideramos necesario para la comparación de colimadores. Para posicionar la desintegración detectada se utiliza el centro ponderado en energı́a, de los fotones ópticos que llegan a la cara inferior del cristal de CsI(Na) en cada una de las desintegraciones. Para simular la desviación en la posición de detección producida por PSPMT y la electrónica se convoluciona la imagen obtenida con la resolución intrı́nseca medida para nuestras gammacámaras, obteniéndose ası́ las imágenes finales. 11.2.3. Diseño hardware Este prototipo se ha diseñado con la idea de formar parte de un sistema multimodal PET-SPECT-CT orientado a la investigación pre-clı́nica y que comercializa la empresa Oncovision S.A. Por lo tanto, el software de adquisición y control de motores es común para los tres subsistemas y ha sido desarrollado por el departamento de informática de dicha empresa. Este nuevo diseño dispone de un motor de giro para desplazar los detectores alrededor del objeto a explorar, ası́ como un deslizador para el movimiento de la camilla. Además, el segundo prototipo incorpora un actuador lineal unido a cada una de 11. Diseño del segundo prototipo las dos gammacámaras permitiendo seleccionar el radio de giro de cada uno de los estudios vı́a software. En la configuración de este segundo prototipo se utilizan principalmente 4 radios de giro para el SPECT que se identifican con el FOV en milı́metros que se observa con cada unos de ellos: FOV20, FOV40, FOV60 y FOV80 respectivamente. 11.3. Resultados 11.3.1. Colimador pinhole Para calcular la mejor focal para el colimador pinhole diseñado se realizaron simulaciones Monte Carlo de dicho colimador con distintas distancias focales, obteniéndose que la menor f para la cual todo el detector queda completamente iluminado (ver figura 11.5) es de 31 mm. Figura 11.5: Corte a la altura del detector con simulación Monte Carlo. Se muestra el detector (azul) y la zona iluminada (rojo). Una vez obtenido el mejor valor de f se construyó el colimador. En la figura 11.6 se pueden ver fotos del colimador pinhole diseñado para este segundo prototipo de SPECT. 131 132 11.3. Resultados Figura 11.6: Fotos del colimador pinhole diseñado para este prototipo. 11.3.2. Colimador multipinhole Se simularon las cuatro configuraciones mencionadas para el colimador multipinhole con el fin de poder compararlas. La figura 11.7 muestra la geometrı́a del diseño Monte Carlo realizado para una de las configuraciones. En concreto se muestra la configuración 2 con agujeros inclinados. (a) Imagen simulada del diseño de las dos gammacámaras. La separación entre ellas corresponde a la configuración del FOV 20. (b) Imagen del diseño del colimador multipinhole para la configuración 2. Figura 11.7: Imágenes del diseño Monte Carlo del sistema SPECT con uno de los colimadores multipinhole simulados. Para el estudio simulado con cada uno de los cuatro colimadores se obtuvieron como resultado las imágenes mostradas en la figura 11.8. 11. Diseño del segundo prototipo (a) Adquisición simulada para la configuración (b) Adquisición simulada para la configuración 1. 2. (c) Adquisición simulada para la configuración (d) Adquisición simulada para la configuración 3. 4. Figura 11.8: Imágenes de una proyección de SPECT para las distintas configuraciones simuladas. La sensibilidad obtenida en las simulaciones teniendo en cuenta los dos detectores para cada una de la configuraciones realizadas se puede ver en la tabla 11.3. Una vez descartada la configuración 2 por su baja sensibilidad, se construyó una versión preliminar, en plomo, de las otras tres configuraciones propuestas para el colimador multipinhole y se realizaron adquisiciones reales con el fin de confirmar las datos obtenidos con las simulaciones y decantarse por una de las 3 propuestas. Las medidas reales confirmaron la sensibilidades simuladas y pusieron de manifiesto 133 134 11.3. Resultados Configuración 1 Configuración 2 Configuración 3 Configuración 4 Pinhole Interacciones 15373 ± 124 11649 ± 108 16664 ± 129 13610 ± 117 4439 ± 67 Sensibilidad (615 ± 5) cps/MBq (466 ± 4) cps/MBq (667 ± 5) cps/MBq (544 ± 5) cps/MBq (178 ± 3) cps/MBq Tabla 11.3: Sensibilidad obtenidas en función del colimador. que los FOV1 y FOV2 se reconstruyen correctamente, pero el FOV3 genera mucho ruido y algún artefacto en las imágenes reconstruidas capı́tulo 15. Por lo que el FOV útil de los colimadores multipinhole diseñados será el FOV2, que es el mismo que el FOV del colimador pinhole. Se realizaron adquisiciones de un maniquı́ tipo Derenzo para los tres colimadores y se reconstruyeron (utilizando un algoritmo de reconstrucción OS-EM, ver capı́tulo 15) sin observarse diferencias apreciables en la resolución de los 3 colimadores. Por tanto, debido a que el FOV útil y la resolución apreciada en los tres colimadores es igual, se optó por la configuración 3 para el diseño definitivo ya que proporciona una mayor sensibilidad. En la figura 11.9 se pueden ver dos fotos de dicho colimador multipinhole. (a) Foto de nuestro colimador multipinhole. (b) Ampliación de la zona de los agujeros. Figura 11.9: Fotos del colimador multipinhole definitivo que se ha diseñado y desarrollado. 11. Diseño del segundo prototipo 11.3.3. Implementación del sistema SPECT El sistema completo propuesto para este segundo prototipo SPECT incorpora dos gammacámaras con carcasa adaptada para el SPECT. Además, los colimadores disponen de un sistema de anclaje que permite el intercambio entre los colimadores pinhole y multipinhole diseñados. Cada detector se acopla a un actuador lineal que a su vez esta unido a un plato giratorio que le permite rotar de forma controlada alrededor del objeto con la ayuda de un motor. El actuador lineal dispone de un motor que nos permite modificar el radio de giro vı́a software. El sistema incluye 4 camillas intercambiables. Tres camillas para animales: una para rata, otra para ratón y otra para cabeza de ratón y una cuarta camilla construida para utilizar los diferentes maniquı́s necesarios para calibrar y caracterizar el equipo. Las camillas se acoplan a un desplazador que le permite avanzar a través de los subsistemas PET-SPECT-CT. En la figura 11.10 se muestran tres imágenes del prototipo SPECT diseñado. La figura 11.10(a) corresponde a las primeras pruebas realizadas, con un gantry provisional, un único detector, radio de giro fijo y camillas provisionales. Esta prueba se usó para validar los nuevos colimadores diseñados. Finalmente las figuras 11.10(b) y 11.10(c) muestran como queda el prototipo final montado en el disco junto al CT. 135 136 11.3. Resultados (a) Prueba diseñada para probar los colimadores multipinhole. (b) Imagen del anillo con el SPECT-CT. (c) Imagen del equipo completo PET-SPECT-CT. Figura 11.10: Imágenes del ptototipo SPECT y el sistema SPECT una vez montado dentro del equipo Albira. Capı́tulo 12 Adquisición y calibración geométrica 12.1. Introducción Para obtener un correcto funcionamiento del nuevo equipo construido, es necesario un software de adquisición con un interfaz gráfico que facilite la realización de estudios de SPECT y una calibración para obtener los parámetros geométricos necesarios en la reconstrucción de las imágenes. La interfaz necesaria puede ser similar a la desarrollada para el primer prototipo, adaptándola para la adquisición simultánea de proyecciones obtenidas en dos cámaras. Sin embargo, al tenerse que integrar en el equipo Albira, el desarrollo fue llevado a cabo por el departamento de informática de Oncovision atendiendo a las especificaciones prefijadas. Por el contrario, la determinación de los parámetros geométricos resulta más compleja que en el equipo anterior, al disponer de dos cámaras y de colimadores multipinhole. El objetivo de este capı́tulo es la ampliación del método de calibración geométrica que permita determinar los parámetros geométricos que caracterizan el sistema, incluyendo el diseño de maniquı́es y la metodologı́a empleada en la adquisición y procesado de los datos con doble detector y colimador multipinhole. 137 138 12.2. Material y métodos 12.2. Material y métodos 12.2.1. Programa de adquisición de datos Siguiendo el desarrollo que realizamos en la prueba de concepto, sus especificaciones y teniendo en cuenta las ampliaciones necesarias para el segundo prototipo, la funcionalidad y opciones que ofrece el software de adquisición desarrollado por Oncovision para este prototipo son análogas a la prueba de concepto, con algunos nuevos desarrollos, como un aspecto mejorado, una mayor sencillez para el usuario y la posibilidad de controlar dos gammacámaras a la vez. (a) Pantalla inicial. Permite controlar los motores y planificar los estudios. (b) Adquisición SPECT en proceso. Figura 12.1: Software de adquisición Albira Adquirer para SPECT. En la figura 12.1 se muestran algunas capturas pertenecientes al interfaz de usuario del software de adquisición de SPECT. La aplicación muestra los datos adquiridos 12. Adquisición y calibración geométrica durante la proyección, ası́ como la tasa de cuentas y las cuentas totales medidas. También se puede distinguir una webcam con imagen real y dos pantallas con información sobre la posición de la cama y del anillo. El software de adquisición, al estar pensado para un equipo trimodal, también permite hacer adquisiciones de PET y CT en caso de que el equipo disponga de esos módulos. 12.2.2. Calibración geométrica En el capı́tulo 8.3 vimos como realizar la calibración geométrica de un sistema SPECT con un único detector y colimador pinhole. En este capı́tulo ampliaremos el método de calibración para implementar un algoritmo más robusto y menos sensible al problema de los mı́nimos locales y, al mismo tiempo adaptarlo al nuevo prototipo con doble cabezal detector y con colimador intercambiable entre pinhole y multipinhole. 12.2.2.1. Nuevos maniquı́ de calibración Se han diseñado y fabricado unos maniquı́s de calibración adaptados para cada uno de los 4 FOVs que se utilizan en este equipo. En la figura 12.2 se pueden ver dichos maniquı́s junto con una referencia del tamaño de cada uno de ellos. Junto con los maniquı́s se diseñó un soporte valido para todos ellos, el cual se pude acoplar a una camilla creada expresamente para facilitar el sostén y su centrado dentro del sistema (ver figura 12.3(a) y figura 12.3(b)). 12.2.2.2. Calibración geométrica de un sistema SPECT con doble cabezal detector Los dos cabezales de este sistema deberán ser calibrados simultáneamente con una única adquisición completa de 360o . Deberemos adaptar el método de calibración geométrica para que se puedan calibrar los 7 parámetros geométricos de cada una de las cámaras individualmente de modo equivalente a como se hacia en el capı́tulo 8.3. Una vez calibrados los dos detectores será necesario relacionar los espacios objetos 139 140 12.2. Material y métodos Figura 12.2: Nuevos maniquı́s de calibración adaptados para cada uno de los 4 FOVs. (a) Soporte para los maniquı́s de calibración. (b) Camilla para el soporte y centrado de los maniquı́s. Figura 12.3 de las dos gammacámaras entre si, ya que al haber adquirido simultáneamente se puede afirmar que el maniquı́ de calibración debe estar en la misma posición en el espacio objeto para las dos cámaras. Para un sistema SPECT con doble cabezal detector como el nuestro, una suposición razonable es que ambas cámaras detectoras rotan alrededor de un eje de giro común durante el proceso de adquisición de datos. Para describir la geometrı́a del detector adicional necesitaremos 2 nuevos sistemas de coordenadas u2 v2 para definir el espacio de proyección del nuevo detector y x2 y2 z2 para definir el espacio objeto del segundo detector, donde z2 es paralelo al eje de rotación que como hemos dicho es común para los dos detectores. De este modo una fuente puntual arbitraria en un punto 12. Adquisición y calibración geométrica 141 p vendrá dada por (xp , yp , zp ) en el sistema de coordenadas x′′′ y ′′′ z ′′′ de la cámara 1 (ver sección 8.3.1). Para poder comparar los dos espacios objetos adecuadamente deberemos pasar a coordenadas polares, de modo que: (xp , yp , zp ) = (r ·cosα0 , r ·sinα0 , zp ) (12.1) donde r es la distancia entre el punto p y el eje de rotación. Mientras que α0 es el ángulo polar del vector distancia. De manera análoga para la cámara 2 en el sistema ′′′ ′′′ de coordenadas x′′′ 2 y2 z2 dicho punto p se podrá describir como (r ·cosα2,0 , r ·sinα2,0 , z2,p ). De este modo, se pueden relacionar los dos sistemas de coordenadas utilizando única- mente dos parámetros: una diferencia angular ∆α0 = α2,0 − α0 y una traslación en el eje de rotación ∆ zp = z2,p − zp [40]. Para obtener estos dos nuevos parámetros, una vez realizada la calibración geométrica normal para cada uno de los detectores, se asume que la posición obtenida para cada una de las tres fuentes puntuales del maniquı́ de calibración para el primer detector es (r ·cosα0 , r ·sinα0 , zp ), y para el segundo (r ·cosα2,0 , r ·sinα2,0 , z2,p ). A partir de aquı́ se pueden obtener los valores de ∆α0 y ∆ zp que mejor se ajustan al sistema de doble cabezal. Con el fin de verificar la importancia de utilizar estos dos parámetros que relacionan los ejes de coordenadas de las dos cámaras reconstruiremos una adquisición del maniquı́ de calidad de imagen, el cual se describe en el NEMA 2008 [41], utilizando y sin utilizar dichos parámetros. 12.2.2.3. Ampliación a un sistema multipinhole En sistemas multipinhole la misma distribución de actividad se proyecta en el detector a través de todas las aperturas. La geometrı́a del sistema descrita para un único pinhole deberá extenderse para que sea válida en el caso de un colimador multipinhole. Si consideramos un caso general con N aperturas que son proyectadas en un único detector. La orientación y posición del detector es obviamente idéntica para todas 142 12.2. Material y métodos las aperturas, y consecuentemente los parámetros θ, d, eu, ev, tilt, y twist son los mismos para las N aperturas. Por contra, cada apertura tendrá su propia distancia focal, fn , con n = 1, . . . , N e introducirá su propio rayo central, de modo que el desplazamiento mecánico de cada apertura (mn ), será la distancia del rayo central n al eje de rotación con n = 1, . . . , N . Puesto que mn se puede descomponer en (mun , mvn ) cada pinhole se puede describir con 3 parámetros fn , mun y mvn [42]. De este modo, si extendemos la ecuación (8.7) para todas las aperturas de un mismo colimador obtendremos: uimg θn = fn · vθimg n = fn · mun −x′′′ d+y ′′′ + mun + eu mvn −z ′′′ d+y ′′′ + mvn + ev para n = 1, . . . , N para n = 1, . . . , N (12.2) Para la calibración con colimador pinhole asumimos que la proyección de una fuente puntual a través de una apertura puede describirse únicamente con dos coordenadas, las cuales se obtienen a partir de la distribución de cuentas correspondiente a la imagen real de dicha proyección. El centro de masas de la distribución es la estimación de la posición de intersección del plano detector con la lı́nea definida por el centro de la fuente y el centro de la apertura considerada. El método de calibración utilizado hasta ahora da por hecho que para cada una de las proyecciones de las fuentes puntuales, la correspondiente fuente puntual y apertura pueden identificarse fácilmente. Para un maniquı́ de 3 puntos y un colimador pinhole como tenı́amos anteriormente, dicha identificación es relativamente fácil. Sin embargo, el mismo maniquı́ con un multipinhole de 5 aperturas requiere, o bien, un tedioso trabajo manual, o bien, un algoritmo muy sofisticado para identificar la relación entre la fuente puntual y la apertura. La figura 12.4 muestra dos ejemplos de diferentes proyecciones para un colimador de 5 aperturas donde se deberı́an distinguir 15 distribuciones diferentes correspondientes a los 3 puntos y las 5 aperturas. Se aprecia la dificultad existente para poder distinguir las 15 distribuciones y relacionarlas con su correspondiente fuente radiactiva y apertura. Debido a dicha dificultad para relacionar los puntos de la imagen con la fuente y la apertura correspondiente será necesario modificar el método de calibración para el colimador multipinhole. Aprovechando los maniquı́s diseñados para los colimadores 12. Adquisición y calibración geométrica Figura 12.4: Ejemplo de dos proyecciones del maniquı́ de calibración a través del colimador multipinhole. pinhole podemos calibrar una de las N aperturas tapando temporalmente el resto de aperturas con una máscara de calibración. Dicha máscara consiste en una lámina de plomo con una única apertura en el centro, de este modo al colocar dicha lámina delante del colimador taparemos todos los agujeros menos el central y podremos calibrar el agujero central, el cual denotaremos como 1. Una vez realizada la adquisición de calibración deberá retirarse la lámina de plomo para volver a disponer del colimador multipinhole con normalidad. Con este procedimiento obtendremos una imagen equivalente a la de la figura 12.4 pero esta vez solo se obtienen los fotones que pasan por el agujero central (ver figura 12.5). Por lo que la detección de los puntos se puede hacer de modo equivalente a como se hace con el colimador pinhole, ver sección 8.3.3.1. Al calibrar el agujero central obtenemos todos los parámetros comunes, ası́ como f1 , mu1 y mv1 . El resto de parámetros (fn , mun y mvn con n = 2, . . . , 5) se pueden, o bien estimar, o bien, calcular utilizando una única fuente puntual colocada fuera del eje de rotación [43]. El colimador está fabricado sobre una lámina plana y rı́gida de Tungsteno, como se vio en la sección 11.3.2. El mecanizado y colocación del mismo es muy preciso, de modo que la plancha de tungsteno con los agujeros queda paralela al detector. Debido a esta precisión y el conocimiento de la geometrı́a del colimador construido, 143 144 12.2. Material y métodos Figura 12.5: Imagen de las mismas proyecciones del maniquı́ de calibración, que se muestran en la figura 12.4, a través del colimador multipinhole pero utilizando la máscara de calibración. como primera aproximación hemos decidido estimar los parámetros restantes a partir de los valores obtenidos para el agujero central, por tanto, podemos aproximar las focales de todas las aperturas al valor obtenido para el agujero central: fn ∼ = f1 para n = 2, . . . , 5 (12.3) Para estimar los valores mun y mvn con n = 2, . . . , 5 podemos medir las componentes (x, y) de la distancia D de cada una de las aperturas con respecto a la apertura central del colimador, de este modo obtenemos los valores Dxn y Dyn con n = 2, . . . , 5, donde Dxn es la distancia en el eje x entre la apertura central y la apertura n y Dyn es la distancia en el eje y entre la apertura central y la apertura n. Como la lámina plana que contiene las aperturas del colimador se coloca paralela al detector, tenemos que los ejes (x, y) utilizados son paralelos a los ejes (u, v) y por tanto los valores de m de las aperturas no centrales se pueden aproximar por: mun ∼ = mu1 + Dxn para n = 2, . . . , 5 ∼ mvn = mv1 + Dyn para n = 2, . . . , 5 (12.4) 12. Adquisición y calibración geométrica Para validar este método de calibración con colimador multipinhole y las estimaciones de los parámetros fn , mun y mvn para n = 2, . . . , 5, una vez efectuada la calibración del sistema se realizó la adquisición de un estudio de SPECT utilizando una pequeña fuente cilı́ndrica consistente en una jeringa conteniendo una pequeña cantidad de 99m T c. Las adquisiciones de calibración y validación se han llevado a cabo utilizando un único detector. El detector gira una vuelta completa durante el estudio, obteniendo 60 proyecciones con 6o entre las proyecciones. El tiempo de adquisición es de 40 segundos por proyección y la ventana de energı́a utilizada es de ±10 % alrededor del pico del 12.2.2.4. 99m T c de 140 keV. Algoritmo para la reducción de mı́nimos locales. Los parámetros de calibración están altamente correlacionados entre ellos y por tanto la función de coste F a minimizar tiene muchos mı́nimos locales, tal como se indicó en el capı́tulo 8.3. Esto provoca que la solución del ajuste sea sensible a los valores iniciales utilizados lo que dificulta encontrar la solución deseada. Debido a este problema en esta versión del programa de calibración se ha decidido implementar una nueva inicialización del algoritmo, en el cual, partiendo de los parámetros iniciales aproximados del sistema, se crean 5 conjuntos diferentes de parámetros, variándolos ligeramente entre cada uno de los conjuntos mencionados. Una vez creados los 5 conjuntos de parámetros iniciales, se divide el proceso de búsqueda de parámetros ideales en tres pasos: 1. Se fijan los parámetros m, tilt, twist, eu y ev. A continuación se realiza un primer ajuste con el fin de encontrar los valores de f y d que minimizan la función de coste del sistema. 2. Se fijan los parámetros f y d encontrados en el paso 1 y se hace un barrido de los parámetros m, tilt, twist, eu y ev para obtener los valores que mejor se ajustan. 3. Se utilizan los valores obtenidos tras realizar los pasos 1 y 2 como nuevos parámetros iniciales y se realiza un ajuste fino del sistema pudiendo variar ahora todos los parámetros. 145 146 12.2. Material y métodos Este proceso de búsqueda en 3 pasos se repite para los cinco conjuntos de valores que hemos creado obteniendo ası́ 5 resultados diferentes. Finalmente tomaremos como resultado definitivo aquel cuya función de coste sea más baja. Gracias a la utilización de la búsqueda por pasos y los conjuntos de parámetros iniciales reducimos en gran medida la posibilidad de obtener como solución un mı́nimo local. 12.2.2.5. Ajuste conjunto de los 4 FOV de cada una de las cámaras Al calibrar el SPECT completo se realiza una adquisición para cada uno de los FOV que se van a utilizar, tanto con el colimador pinhole como el multipinhole. Posteriormente se hace una calibración para cada una de las adquisiciones. Sin embargo, las 4 calibraciones de un mismo colimador, aunque se hayan adquirido con distintos radios de giro y maniquı́s de calibración, se realizan sin modificar el colimador entre ellas. Por lo tanto es razonable pensar que todos los parámetros intrı́nsecos al colimador deberı́an ser iguales para los 4 FOV, mientras que los extrı́nsecos podrı́an cambiar linealmente con el desplazamiento del radio de giro realizado entre los distintos FOV (∆r). Este último parámetro es conocido y controlado desde el programa de adquisición gracias al motor utilizado para dicho fin. Ası́ pues, parece razonable hacer una calibración conjunta para todos los FOV de un mismo colimador en lugar de una calibración separada para cada uno de ellos. Para realizar la calibración conjunta de todos los FOV tenemos que separar los parámetros externos (d, m, tilt y twist) e internos (f , eu y ev) al colimador. Ası́, los parámetros internos permanecen invariantes con ∆r, mientras que los externos se dividirán en dos componentes, una componente dependiente de ∆r y otra independiente, quedando ası́: ff ov = f ; euf ov = eu; evf ov = ev. P araf ov = 20, 40, 60, 80. df ov = rf ov + db . P araf ov = 20, 40, 60, 80. mf ov = ma · ∆rf ov + mb . P araf ov = 20, 40, 60, 80. tiltf ov = tilta · ∆rf ov + tiltb . P araf ov = 20, 40, 60, 80. twistf ov = twista · ∆rf ov + twistb . P araf ov = 20, 40, 60, 80. 12. Adquisición y calibración geométrica Esta calibración conjunta aumenta considerablemente la complejidad del algoritmo de calibración ası́ como el tiempo de cálculo, pero a cambio reduce notablemente la correlación entre los parámetros obteniendo ası́ soluciones más fiables. 12.2.2.6. Evolución del software de calibración El software de calibración se ha tenido que ampliar y modificar para poder calibrar con doble cabezal y con los nuevos maniquı́s de calibración, ası́ como para poder realizar la calibración conjunta de hasta 4 FOV calibrados con distintos maniquı́s. El programa, al igual que en la prueba de concepto, se ha realizado en entorno Windows utilizando el lenguaje “Microsoft Visual Studio .NET 7 y 8 ”, basado en C/C++ y orientado a objetos. 12.3. Resultados 12.3.1. Nuevo software de calibración Al igual que en la prueba de concepto, en el interfaz del usuario, las variables están divididas en 5 grandes grupos (ver sección 8.3.3.3). Las principales diferencias del nuevo software de calibración se encuentran en la parte de datos de entrada e inicialización (ver figura 12.6) y son las siguientes: Selección de número de cámaras y dirección de giro. El nuevo software permite elegir el número de cámaras que se quieren calibrar ası́ como el sentido de giro (horario o antihorario). Si se seleccionan dos cámaras entonces aparecen automáticamente los parámetros de ambas cámaras ası́ como los dos parámetros de ajuste entre ellas ∆α0 y ∆ zp en la sección inicialización. Estos se podrán inicializar con los valores deseados. Además también aparece como seleccionable el ángulo inicial, que hace referencia a la posición de la cámara 1 en el disco en la primera proyección. 147 148 12.3. Resultados Figura 12.6: Interfaz gráfica del programa de calibración para doble cabezal detector. Selección del FOV y del maniquı́. Otra de las ampliaciones realizadas es la posibilidad de seleccionar el FOV que se quiere calibrar de los 4 disponibles en este segundo prototipo. Al seleccionar el FOV por defecto se selecciona el maniquı́ correspondiente a dicho FOV y por tanto las distancia entre puntos de ese maniquı́. El interfaz permite cambiar a otro maniquı́ siempre que se desee. Selección del número de FOVs a calibrar. El nuevo sofware permite calibrar entre 1 y 4 FOVs al mismo tiempo. Si se elige más de 1 FOV tendremos que cargar todas las adquisiciones de calibración en el orden adecuado y seleccionar los FOV que se desean calibrar de los 4 disponibles. Dicho software será valido también para calibrar el agujero central del colimador multipinhole, puesto que una vez que se usa la máscara de calibración, dicho agujero central se calibra igual que si fuera un colimador pinhole. El resto de parámetros correspondientes a los otros 4 agujeros se estiman y utilizan en la reconstrucción. 12. Adquisición y calibración geométrica 12.3.2. Método de calibración con dos detectores En la figura figura 12.7 se puede ver como varı́a la reconstrucción de una misma imagen, adquirida con doble detector, cuando se utilizan o no los parámetros ∆α0 y ∆ zp . Para obtener las imágenes hemos utilizado el software de reconstrucción desarrollado para este prototipo, el cual se describirá en el capı́tulo 13. En la imagen se aprecia claramente y de modo cualitativo la importancia de utilizar dichos parámetros para relacionar el origen de coordenadas de los dos detectores. Figura 12.7: Reconstrucción del maniquı́ de calidad de imagen adquirido con doble cabezal detector. (Arriba) Sin los parámetros ∆α0 y ∆ zp . (Abajo) Con los parámetros ∆α0 y ∆ zp . 12.3.3. Calibración con colimador multipinhole Los resultados de la calibración realizada para el colimador multipinhole enmascarando los cuatro agujeros periféricos se muestran en la siguiente tabla: La función de coste del ajuste fue de 20.6, y se han marcado en rojo los valores que se han estimado a partir del conocimiento previo del colimador. El la figura 12.8 se muestran 3 de las proyecciones adquiridas durante el estudio de la fuente cilı́ndrica tras la calibración del sistema. 149 150 12.3. Resultados número de focal radio giro pinhole (mm) (mm) 1 30.32 40.95 2 30.32 40.95 3 30.32 40.95 4 30.32 40.95 5 30.32 40.95 tilt (rad) 0.00507 0.00507 0.00507 0.00507 0.00507 twist (rad) 0.0106 0.0106 0.0106 0.0106 0.0106 mu (mm) -1.571 2.429 2.429 -5.571 -5.571 mv eu ev (mm) (mm) (mm) -0.017 1.044 0.486 3.983 1.044 0.486 -4.017 1.044 0.486 -4.017 1.044 0.486 3.983 1.044 0.486 Tabla 12.1: Resultados de la calibración del colimador multipinhole. En rojo se muestran los parámetros estimados. Figura 12.8: Proyecciones obtenidas en el estudio de la fuente cilı́ndrica utilizando el colimador multipinhole. Figura 12.9: Imagen de los cortes transaxial, coronal y sagital de la reconstrucción con colimador multipinhole. 12. Adquisición y calibración geométrica En la figura 12.9 se muestran los distintos cortes de la reconstrucción realizada utilizando el software de reconstrucción (ver capı́tulo 13). 12.3.4. Nuevo método de calibración conjunta Finalmente, para dotar de mayor autonomı́a y estabilidad al método de calibración geométrica, lo hemos adaptado introduciendo un conjunto de parámetros iniciales y la posterior calibración en tres pasos del sistema. Además se ha implementado la calibración conjunta de los 4 FOVs que se utilizan en el sistema, de tal modo que todos los parámetros intrı́nsecos al colimador serán iguales para todos los FOVs y los extrı́nsecos dependerán del desplazamiento del radio de giro entre los FOVs. Este nuevo método reduce los mı́nimos locales del método de convergencia dotando de mayor estabilidad e independencia de los parámetros iniciales al método. En la tabla 12.2 se muestran los resultados obtenidos para todos los parámetros cuando se realiza una calibración conjunta con un sistema completo de doble cabezal detector. 151 12.3. Resultados Detec- FOV rfov focal db tilta tiltb twista twistb ma mb eu ev ∆α0 ∆ zp tor (mm) (mm) (mm) (mm) (rad/mm) (rad) (rad/mm) (rad) () (mm) (mm) (mm) (rad) (mm) 1 20 0 29.19 20.43 -0.00002 -0.0049 0.00004 0.005 -0.00063 0.43 -0.42 0.71 0 0 1 40 12 29.19 20.43 -0.00002 -0.0049 0.00004 0.005 -0.00063 0.43 -0.42 0.71 0 0 1 60 27 29.19 20.43 -0.00002 -0.0049 0.00004 0.005 -0.00063 0.43 -0.42 0.71 0 0 1 80 46 29.19 20.43 -0.00002 -0.0049 0.00004 0.005 -0.00063 0.43 -0.42 0.71 0 0 2 20 0 29.76 21.24 -0.00015 -0.0011 0.0003 0.0013 -0.00024 0.038 0.003 0.16 3.120 -1.53 2 40 12 29.76 21.24 -0.00015 -0.0011 0.0003 0.0013 -0.00024 0.038 0.003 0.16 3.139 -0.89 2 60 27 29.76 21.24 -0.00015 -0.0011 0.0003 0.0013 -0.00024 0.038 0.003 0.16 3.140 -1.05 2 80 46 29.76 21.24 -0.00015 -0.0011 0.0003 0.0013 -0.00024 0.038 0.003 0.16 3.153 -1.15 152 Tabla 12.2: Resultados obtenidos para una calibración conjunta con doble detectores. Capı́tulo 13 Método de reconstrucción de imágenes 13.1. Introducción al método de reconstrucción El objetivo final de la técnica de SPECT es obtener la distribución tridimensional del trazador en el organismo, lo cual se consigue con la reconstrucción tomográfica como ya se ha comentado en el capı́tulo 5. Para este prototipo SPECT se ha adaptado un algoritmo OS-EM para la reconstrucción de imágenes. Nuestro sistema consta de dos cámaras detectoras y la posibilidad de adquirir con un colimador pinhole o un multipinhole, además necesitaremos que el software de reconstrucción pueda formar parte del equipo Albira. Por tanto, el objetivo de este capı́tulo será desarrollar un algoritmo de reconstrucción adaptado y optimizado para este nuevo equipo. La reconstrucción debe permitir la corrección de la dispersión de fotones, del efecto degradante producido por el tamaño del orificio e incluir una estimación de la sensibilidad en cada punto de la imagen para cualquier colimador o FOV utilizado. 153 154 13.2. Material y métodos de la reconstrucción 13.2. Material y métodos de la reconstrucción La matriz del sistema se calcula mediante métodos analı́ticos de proyección basado en vóxeles (voxel driven projection). Se aplican algunas correcciones en la matriz con el fin de mejorar la calidad de las imágenes reconstruidas. Además se ha adaptado dicha matriz para que se pueda aplicar con múltiples detectores y colimador multipinhole. Las matrices del sistema generalmente ocupan una gran cantidad de espacio en disco y tardan varias horas en generarse, sobretodo si son matrices multipinhole. Para intentar paliar estos inconvenientes se han aplicado simetrı́as en el cálculo de la matriz. Finalmente también describiremos el método de corrección de la dispersión que aplicaremos en la adaptación del algoritmo OS-EM. 13.2.1. Cálculo de la matriz del sistema Para generar la matriz del sistema se ha utilizado un método analı́tico para el cálculo de la matriz y dentro de los métodos analı́ticos se ha aplicado un método de proyección basado en vóxeles. En dicho método se pretende calcular la probabilidad de que un fotón emitido en un determinado vóxel de la matriz de reconstrucción sea detectado en cada uno de los pı́xeles de las proyecciones realizadas. Dicha probabilidad depende principalmente del tipo de colimador utilizado, del número de orificios que tenga y la forma de los mismos, ası́ como de eficiencia geométrica. Por ese motivo los efectos que se han considerado durante el cálculo de la matriz son los siguientes: recuperación de resolución, estimación de la sensibilidad y adaptación a colimadores multipinhole. Los cuales pasaremos a ver con más detalle a continuación. 13.2.1.1. Recuperación de resolución: corrección del efecto de la apertura Uno de los mayores efectos que causan degradación en las imágenes de SPECT con colimador pinhole es el emborronamiento de la imagen debido al tamaño no despreciable de la apertura. Corregir dicho emborronamiento es el factor principal del método de recuperación de resolución (Resolution recovery, RR). Al incluir el tamaño y la forma del orificio en la matriz del sistema se tiene en cuenta el efecto degradante 13. Método de reconstrucción de imágenes que la apertura ha producido en las proyecciones. Otro efecto que se puede incluir en la matriz para mejorar la resolución del sistema es la PSF. Ésta depende del detector utilizado y dentro del detector de la posición de detección y del ángulo de incidencia. Por tanto, para caracterizar correctamente la PSF se requiere un gran número de medidas experimentales, o bien, simulaciones muy precisas. Debido a dicha complejidad, en este prototipo no tendremos en cuenta los efectos de la PSF del sistema. La alternativa de usar el método de proyección basado en el trazado de rayos (ray driven projection) para corregir el efecto del colimador es complejo y requiere de la utilización de múltiples rayos ponderados, 7 o 21 normalmente, distribuidos uniformemente por la apertura para simular el efecto del pinhole ([44] - [45]). Sin embargo, si se utiliza la proyección basado en vóxeles la corrección de la apertura es más sencilla, ya que al ser la distancia entre el colimador y el detector un valor fijo y conocido se puede proyectar la apertura del colimador al detector para cada uno de los vóxeles utilizando la siguiente fórmula: rproy = rph · dv−d z dv−c z donde rproy es el radio de la apertura proyectado en el detector, rph es el radio de la apertura, dv−d es la distancia entre el vóxel y el detector en el eje perpendicular al z detector y dv−c es la distancia entre el vóxel y el colimador en el eje perpendicular z al detector. Además dv−d = dv−c + f siendo f la focal. Una vez se obtiene el radio z z proyectado del objeto es fácil calcular, para cada vóxel, la probabilidad de que un fotón emitido sea detectado en cada uno de los pı́xeles de la gammacámara. Debido a la mayor facilidad y precisión a la hora de implementar el efecto de la apertura, se ha optado por el método de proyección basado en vóxeles para describir el orificio. Un colimador pinhole en forma de filo de cuchillo con un ángulo de aceptación α se puede simplificar si se hace la siguiente consideración: la superficie del colimador es la misma que la de dos conos girados que se intersectan en el plano z = 0 de modo que se considera el centro del colimador en la posición (x, y) = (0, 0) y alineado con el plano z = 0 (ver figura 13.1). La intersección de la unión de estos dos conos con el colimador nos delimitará las tres elipses con las que podremos caracterizar la 155 156 13.2. Material y métodos de la reconstrucción apertura del colimador. Dichas elipses son las intersecciones en los planos z = ρ/2, z = 0 y z = −ρ/2. En el caso particular de trabajar con agujeros no inclinados las elipses se pueden simplificar por cı́rculos. Figura 13.1: Esquema de la apertura de un colimador tipo pinhole. Para una fuente puntual a una distancia h del centro del colimador un rayo gamma emitido con un ángulo θ pasa a través del centro de la apertura, mientras que un rayo gamma con ángulo de incidencia θa intersecta el plano z = 0 por fuera de la unión de los dos conos, por lo que no alcanzará nuestro detector. Para poder determinar, para cada uno de los vóxeles que rayos gamma entran por la apertura y cuales no, basta con proyectar las 3 elipses mencionadas desde cada uno de los vóxeles hasta el plano del detector. La intersección de esas 3 proyecciones en el detector proporciona la zona del detector visible para dicho vóxel y por consiguiente los rayos gamma que llegan al detector. 13.2.1.2. Estimación de la sensibilidad Para poder relacionar un vóxel de la imagen reconstruida con el resto de vóxeles no solo es necesario relacionar la actividad en dicho punto con las cuentas de las 13. Método de reconstrucción de imágenes 157 proyecciones, sino que también se necesita saber la relación existente entre las cuentas totales producidas en cada una de las proyecciones por una fuente de actividad x situada en dicho vóxel y las cuentas totales que se producirı́an en dichas proyecciones por la misma fuente situada en cualquier otro punto del espacio objeto. La mejor forma de calcular dicha relación entre los distintos puntos del espacio objeto es estimar y utilizar la sensibilidad del sistema para cada uno de dichos puntos. Una fuente puntual emite fotones isotrópicamente en todas las direcciones. En un caso ideal se puede considerar el colimador pinhole como una lámina infinitamente fina con una apertura circular de diámetro D en el centro y con un coeficiente de atenuación infinito, de modo que los rayos gamma solo pueden pasar por la apertura de diámetro D, entonces la eficiencia geométrica G para un punto cualquiera del FOV (xi , yi , zi ) es la fracción entre los fotones que llegan al detector y los emitidos desde dicho punto. Si se construye una esfera alrededor del punto (xi , yi , zi ) cuya superficie pase por elqcentro de la apertura pinhole, punto (0, 0, 0), siempre que se cumpla la condición x2i + yi2 + zi2 >> D el ángulo sólido Ω ocupado por el pinhole se puede aproximar por Ω=4·π· D2 4 · cosτ π · D2 · cos3 τ = zi 2 4 · zi2 4 · π · cosτ π· (13.1) en la cual, el numerador y el denominador de la primera ecuación representan el área de la apertura visto desde una fuente puntual (ver figura 13.2) y la superficie de una esfera respectivamente. El ángulo τ representa el ángulo entre el eje z y el rayo proyectado a través del centro de la apertura pinhole. El origen de coordenadas se sitúa en el centro de la apertura. No se ha tenido en cuenta la resolución espacial intrı́nseca del detector. Dividiendo la ecuación (13.1) por los 4 · π del ángulo sólido total de una esfera se obtiene la eficiencia geométrica del sistema para el punto (xi , yi , zi ) G (xi , yi , zi ) = d2 · cos3 τ 16 · zi2 (13.2) 158 13.2. Material y métodos de la reconstrucción Proyección u Detector f Colimador (xi, yi, zi) Figura 13.2: Proyección de una fuente puntual (xi , yi , zi ) a través de una apertura pinhole ideal con diámetro D a un detector y una distancia f del colimador. La sensibilidad como ya vimos en la sección 4.3 es directamente proporcional a la eficiencia geométrica. Por tanto, para relacionar el valor absoluto de actividad entre los vóxeles es equivalente tratar con la eficiencia geométrica o con la sensibilidad del sistema. Sin embargo, este primer modelo para el cálculo de sensibilidad, denominado “sensibilidad geométrica”, es imperfecto puesto que no tiene en cuenta efectos de penetración por los bordes de la abertura en la sensibilidad total. Anger introdujo el diámetro efectivo ( ver ecuación (4.4)) que es un poco mayor que el diámetro geométrico para intentar compensar los efectos de penetración. La introducción del diámetro efectivo mejora el modelo, pero sigue sin ser del todo realista. La sensibilidad de un colimador pinhole en forma de filo de cuchillo con un ángulo de aceptación α se puede calcular si se tiene en cuenta la consideración vista en la sección anterior. De este modo, para una fuente puntual a una distancia h del centro del colimador, los rayos gamma emitidos con un ángulo θ pasan a través del centro de la apertura, mientras que los rayos gamma con ángulo de incidencia θa 13. Método de reconstrucción de imágenes 159 intersectan el plano z = 0 en las coordenadas (x, y, z) = (ρ · cosβ, ρ · senβ, 0) siendo ρ el radio polar y β la coordenada azimutal del punto de intersección en el plano z = 0, mientras que denotaremos por ∆ L a la longitud que recorre el rayo gamma a través del medio atenuador (ver figura 13.1). Teniendo en cuenta esta definición del colimador se puede considerar que la sensibilidad total del colimador tiene dos componentes: Stot (θ) = Sgeom (θ) + Spen (θ) donde Stot (θ) es la sensibilidad total, Sgeom (θ) es la sensibilidad geométrica que viene dada por la ecuación (13.2) (renombrando zi por h) y Spen (θ) es la sensibilidad por penetración. Para calcular el término Spen (θ) se deber calcular la suma de probabilidades de todos aquellos rayos gamma que puedan alcanzar el detector sin pasar por la apertura de modo que hay que resolver las siguientes integrales: cos3 τ Spen (θ) = 4 · π h2 Z 2π dβ 0 Z ∞ d/2 dρ · ρ · e−µ∆L Para resolver las integrales es necesario introducir algunas aproximaciones [46] obteniendo finalmente el siguiente valor: Spen (θ) ≈ donde a′ = 2 + a′ · d cos3 τ 4 · h2 · a′2 (1 − γ)1/2 2 · µ · tan α2 tan2 α2 − tan2 θ · cosθ Lo que implica que la sensibilidad total se puede aproximar por: (13.3) 160 13.2. Material y métodos de la reconstrucción 1/2 tan2 τ µ·d d2 · cos3 τ cos5 τ · tan2 α2 tan2 τ · 1− + Stot (θ) ≈ + · 1− 16 · h2 16 · h2 · µ2 tan2 α2 tan2 α2 cosτ · tan α2 (13.4) Dicha fórmula se puede simplificar de modo aproximado utilizando el de y el cosx θ como se puede ver en numerosas publicaciones [46] y [47]. De modo que sensibilidad total del sistema queda finalmente como sigue: Stot (θ) = d2e · cosx τ 16 · h2 (13.5) donde x es un valor mayor que 3.0, el cual, se determina de modo numérico. En nuestro caso, para un colimador de W de 2 mm de espesor y con ángulo de aceptación de 53.13o los valores de x que mejor se ajustan a nuestro sistema en la práctica están entre 3 y 5, por lo que finalmente cogeremos un valor de x = 4. 13.2.1.3. Consideraciones para un colimador multipinhole La sensibilidad de un sistema pinhole se puede mejorar añadiendo agujeros. Cada nueva apertura añadida al colimador forma una proyección dentro del detector de modo equivalente a la apertura del pinhole, las proyecciones de diferentes aperturas pueden permitir el solapamiento como en nuestro caso. Permitiendo el solapamiento se incrementa el número de rayos gamma detectados, pero se aumenta la complejidad del sistema puesto que en las partes del detector con solapamiento el rayo gamma detectado puede venir de más de una apertura. Consecuentemente, la tarea de reconstrucción es más compleja, lo que conlleva un incremento de la varianza. Además, con más solapamiento, el sistema es más propenso a los artefactos, en particular cuando las aperturas están organizadas en estructuras regulares [48]. Si nos centramos únicamente en la matriz del sistema, el método de generación de matriz es análogo al visto anteriormente, siempre que la geometrı́a del colimador y del detector se conozcan con exactitud para todas las aperturas [49]. En ese caso la 13. Método de reconstrucción de imágenes sensibilidad Sm para cada apertura m, se puede obtener del mismo modo que vimos en el apartado anterior. En la práctica si utilizamos el método de proyección basado en vóxeles para el cálculo de probabilidades de cada uno de los vóxeles de la matriz, tendremos que realizar el método de proyección n veces, siendo n igual al número de aperturas del sistema. Las probabilidades obtenidas con la proyección a través de cada una de las aperturas se irán sumando, siendo la probabilidad total la suma de probabilidades de las n aperturas. De modo que, para cada vóxel se aumenta el número de pı́xeles del detector a los que pueden llegar los fotones emitidos desde dicho vóxel y, en consecuencia, se aumenta notablemente el tamaño de la matriz del sistema. El aumento de tamaño de la matriz es equivalente al aumento de sensibilidad del sistema. 13.2.2. Utilización de simetrı́as en el cálculo de la matrices Los mayores problemas que aparecen asociados a la utilización de las matrices de transición son el elevado tiempo de cálculo y el gran tamaño de las matrices generadas, especialmente con colimadores multipinhole. Los sistemas de 32 bits están limitados por 1 Gb de memoria máxima que puede cargar en RAM. Por lo que es conveniente limitar el tamaño de cada subset a 1 Gb de tamaño máximo. Estos problemas pueden acotar los tamaños máximos de vóxel y pı́xel que se utilizan en la reconstrucción. A continuación se describe el cálculo de los pesos de una proyección a partir de los pesos de otras de las proyecciones utilizadas. En la figura 13.3 se muestra como al girar la matriz 90o se tiene el mismo espacio objeto que en la posición inicial solo que con los indices cambiados. Por tanto, los pesos para esta proyección se pueden obtener a partir de los pesos de la proyección inicial haciendo el cambio de indices adecuados. Ası́, la utilización de simetrı́as en el cálculo de las matrices puede reducir tanto el tiempo de cálculo como el tamaño de las matrices. En el caso de coordenadas cartesianas y con una única gammacámara tenemos 2 ejes de simetrı́as lo cual reduce el tamaño de las matrices y el tiempo de cálculo en un factor 4. 161 162 13.2. Material y métodos de la reconstrucción (a) Superposición de un plano del espacio objeto (b) Superposición de un plano del espacio objeto para las proyecciones a 0o y a 18o . para las proyecciones a 0o y a 90o . Figura 13.3 Si se usan dos gammacámaras enfrentadas, donde cada una de las gammacámaras captura la mitad de los datos, se pierde una de las dos simetrı́as debido a que los parámetros geométricos de una cámara son distintos a los de la otra. Ası́ y todo mantenemos una simetrı́a lo que nos permite reducir los tamaños y tiempo de cálculo de la matriz en un factor 2. 13.2.3. Método para la corrección de la dispersión, implementación en la reconstrucción Se dice que un rayo γ es dispersado cuando ha sufrido al menos una interacción Compton antes de ser detectado. La dispersión se puede producir tanto en el objeto, como en el colimador o el detector. Si la dirección del rayo γ ha cambiado en el proceso de interacción Compton, es muy probable que se esté asignando la posición 13. Método de reconstrucción de imágenes de emisión erróneamente. La dispersión añade un fondo a la distribución de desintegraciones verdaderas, lo cual disminuye el contraste y hace que la concentración de actividad se sobrestime. El número de eventos dispersados detectados dependen del volumen y las caracterı́sticas de atenuación del objeto en estudio, ası́ como de la geometrı́a de la cámara. Multitud de métodos han sido implementados con el fin de corregir la dispersión [50], [51] y [52]. Estos métodos se pueden agrupar en 4 grandes grupos: Métodos de ajuste. Se ajusta un perfil de la dispersión utilizando las cuentas medidas fuera del objeto. Estas medidas se utilizarán para la estimación y posterior extracción del número de rayos γ dispersados dentro del objeto. Métodos de substracción por convolución. La componente dispersada dentro de la ventana de energı́a utilizada, para cada pı́xel y cada proyección, se calcula como la convolución entre la proyección del fotopico medido con una función de dispersión. Dicha función es caracterı́stica de cada uno de los sistemas utilizados y puede ser modelada como una función exponencial. Para calcular los factores de la exponencial se suele usar la medida de una función de propagación lineal (LSF) en un medio que genere dispersión. Finalmente las proyecciones corregidas de dispersión se obtienen sustrayendo la componente dispersada del total medido. Métodos de doble o triple ventana de energı́a. Se obtiene el espectro de energı́a de los datos medidos. Y se generan varias ventanas energéticas, la ventana normal de medida centrada en el fotopico y otras ventanas de baja y/o alta energı́a para medir la dispersión fuera de la ventana de medida y con ello estimar la dispersión dentro de la ventana del fotopico. Simulación. La distribución de la dispersión se modeliza principalmente mediante simulaciones Monte Carlo, pudiendo medir si el rayo γ a sufrido alguna interacción antes de llegar al detector (experimentalmente es imposible saberlo). Las simulaciones requieren como entrada la distribución del maniquı́ (o sujeto) en el espacio objeto, ası́ como su correspondiente distribución de coeficientes de atenuación. Por tanto estos métodos requieren una estimación de la distribución verdadera del sujeto como punto de partida. 163 164 13.2. Material y métodos de la reconstrucción Todos los métodos que existen de corrección de la dispersión mejoran el contraste de la imagen. Sin embargo la diferencia cuantitativamente hablando es pequeña en todos los casos, inferior al 5 % para FOVs pequeños [51]. De todos los métodos mencionados el método de la doble ventana de energı́a es el que mejor compromiso entre precisión y facilidad de implementación ofrece [52]. Por lo tanto, nos centraremos en este método seleccionando una ventana centrada en el fotopico y la otra en la zona Compton a la derecha del centroide y producida por la dispersión [53]. 13.2.3.1. Método de doble ventana de energı́a Este método considera una dispersión local para cada uno de los pı́xeles del detector y para cada una de las proyecciones. Todas las cuentas se adquieren simultáneamente usando las dos ventanas de energı́a descritas anteriormente. Con la ventana principal se adquieren las cuentas totales (Ctotal ), las cuales se componen de las cuantas provenientes de fotones primarios (Cprim ) más los fotones dispersados en cada pı́xel (Cdisp ) [53]. En la figura 13.4 se puede ver la región triangular que se obtiene en la ventana principal partiendo de las cuentas de la subventana (Ccompton ). Dicha región triangular corresponde a la estimación de las cuentas dispersadas dentro de la ventana principal (Cdisp est ). La obtención para cada desintegración detectada de los datos en modo lista, (x, y, E), permite poder generar en cada una de las proyecciones 2 imágenes, la primera con los datos obtenidos dentro de la ventana de energı́a principal y la segunda con los datos dentro de la ventana Compton. Si asumidos que la anchura de nuestra ventana principal es Wp y que la de la ventana baja es Wd , entonces Cdisp est será: Cdisp est = Ccompton Wp · Wd 2 (13.6) Las cuentas Cdisp est se obtienen para cada pı́xel de la imagen y se utilizarán en la algoritmo de reconstrucción OS-EM para corregir la dispersión. 13. Método de reconstrucción de imágenes 165 Figura 13.4: Espectro y ventanas de energı́as seleccionada para una medida real. La zona triangular rallada de la ventana principal indica la estimación de la dispersión en dicha ventana. 13.2.3.2. Pruebas de comprobación de la corrección de la dispersión Para las pruebas de dispersión se han utilizado capilares de vidrio de 3 mm de diámetro externo y 1 mm de diámetro interno y de 70 mm de longitud. Para aumentar la probabilidad de que se produzca dispersión en el objeto se fabricaron 2 maniquı́s, uno en metacrilato y el otro en teflón. Los maniquı́s son cilindros macizos de 30 mm de diámetro y 30 mm de altura y disponen de un hueco perforado para poder introducir el capilar en su interior (ver figura 13.5). El hueco es de 4 mm de diámetro y se sitúa a 4 mm del centro del maniquı́. Se realizan tres tipos de adquisiciones con el capilar para validar la corrección de la dispersión. La primera con el capilar en aire, la segunda dentro del maniquı́ de metacrilato y la tercera dentro del maniquı́ de teflón. Las adquisiciones se han realizado con un único detector girando una vuelta completa con 60 proyecciones y 45 segundos por proyección. El isótopo utilizado en las adquisiciones es el 99m T c. 166 13.2. Material y métodos de la reconstrucción (a) Maniquı́ de metacrilato (b) Maniquı́ de teflón. Figura 13.5: Imagen de los dos maniquı́es utilizados para aumentar la dispersión en el espacio objeto. 13.2.4. Algoritmo OS-EM estándar adaptado a nuestro sistema Como vimos en el capı́tulo 5, para el algoritmo OS-EM la actividad estimada retroproyectando viene dada por la ecuación (5.1). Donde tenemos que: P t∈Si Atj es la sensibilidad del escáner para el vóxel j, gt gti es la comparación entre lo medido y lo que se obtendrı́a en el caso de tener la distribución de actividad xi y finalmente: gt ·Aij gti es la retroproyección sobre el pı́xel j del cociente entre lo medido y lo que habrı́amos medido en caso de tener la distribución de actividad xi . Con estas consideraciones se aprecia que la solución a la que converge el algoritmo OS-EM es aquella imagen cuya proyección coincide con los datos medidos. Sin embargo, los datos medidos están afectados por la dispersión. Por ese motivo es conveniente modificar el algoritmo para que tenga en cuenta, en la medida de lo posible, que los datos medidos son la proyección de distribución de actividad real más la correspondiente a los fotones dispersados. De este modo podemos obtener: fji+1 X X gt · Aij / Atj . = fji · i g + st t∈S t∈S t i i (13.7) 13. Método de reconstrucción de imágenes Donde st es la estimación del dispersión en cada uno de los pı́xeles, es decir, las Cdisp est para cada pı́xeles. 13.3. Resultados del método de reconstrucción Hemos desarrollado el software necesario para la reconstrucción de las imágenes a partir de las proyecciones adquiridas. El algoritmo es una modificación de un algoritmo OS-EM estándar adaptado para nuestro sistema. Este software se puede dividir en dos partes: la matriz del sistema y el algoritmo de reconstrucción. 13.3.1. Aplicación de simetrı́as en el cálculo de la matriz Se han aplicado las simetrı́as de la matriz del sistema en coordenadas cartesianas. Existen dos ejes de simetrı́a cuando se utiliza un único detector, ya que si giramos la matriz respecto al eje Z 90o , 180o o 270o obtenemos la misma matriz de pesos reordenada. Teniendo en cuanta dichas simetrı́as, las matrices del sistema ocupan 4 veces menos espacio en disco y se generan 4 veces más rápido. La utilización de simetrı́as en la generación de las matrices también aumenta la velocidad de las reconstrucción debido a la reducción de los tamaños de la matrices que debe cargar. Las imágenes reconstruidas son idénticas a las que se obtienen cuando no se aplica ninguna simetrı́a. Cuando se utilizan simetrı́as con el algoritmo OS-EM, cada “subconjunto ordenado” debe tener el mismo número de proyecciones en cada uno de los 4 cuadrantes en que se subdivide el espacio objeto de tal modo que se debe cumplir que: n proy = kdondek ∈ N 4 · subsets siendo n proy el número de proyecciones y subsets el número e subsets. Por ejemplo, si utilizamos 60 proyecciones, el número de “subconjuntos ordenados” solo podrán ser 1, 3, 5 o 15. Cuando tenemos 2 detectores, debido a que los parámetros geométricos de ambos detectores son diferentes, se rompe una de las dos simetrı́as de modo que las matrices 167 168 13.3. Resultados del método de reconstrucción ocupan la mitad se espacio y se generan el doble de rápido que cuando no se utilizan simetrı́as. 13.3.2. Reconstrucción con colimador multipinhole Calibrando la geometrı́a del colimador y del detector para todas las aperturas y utilizando la sensibilidad Sm para cada apertura m, se puede obtener la reconstrucción multipinhole utilizando el método de proyección pinhole tantas veces como número de aperturas tenga el sistema. Como vimos en el capı́tulo 12 utilizando la reconstrucción multipinhole es posible obtener imágenes como la que se mostraba en la figura 12.9. La reconstrucción no presenta artefactos ni ningún otro tipo de anomalı́a. 13.3.3. Reconstrucción con corrección de la dispersión Para todas las adquisiciones realizadas con el capilar de 1 mm de diámetro interior se ha reconstruido con y sin corrección de dispersión. Para poder comparar los resultados con mayor precisión, se consideró 0.3 mm como tamaño de vóxel de la matriz del sistema. En la figura 13.6 mostramos las imágenes reconstruidas para la medida del capilar en aire. En ella se observa como el efecto de la corrección de la dispersión es pequeño. En las figuras 13.7 y 13.8 se pueden ver las imágenes reconstruidas con y sin corrección de dispersión para la medida del capilar en metacrilato y teflón respectivamente. En ellas se observa también, como el efecto de la corrección de la dispersión y de los maniquı́es utilizados es pequeño. Para cuantificar el efecto de la corrección de dispersión y de la utilización de los maniquı́es hemos obtenido y promediado para lo 15 mm centrales del capilar la FWHM en los ejes X e Y. Este proceso se ha repetido para los 6 estudios realizados obteniéndose los siguiente resultados: Se aprecia en los tres casos que al aplicar la corrección de dispersión se obtiene una reducción de la FWHM del capilar de aproximadamente el 3.5 %. Mientras que no se aprecian cambios significativos entre utilizar el capilar en aire o en algunos 13. Método de reconstrucción de imágenes Figura 13.6: Imagen del capilar reconstruido en aire . (arriba) Sin corrección de la dispersión. (abajo) Con corrección de la dispersión. Figura 13.7: Imagen del capilar reconstruido en metacrilato. (arriba) Sin corrección de la dispersión. (abajo) Con corrección de la dispersión. 169 170 13.3. Resultados del método de reconstrucción Figura 13.8: Imagen del capilar reconstruido en teflón. (arriba) Sin corrección de la dispersión. (abajo) Con corrección de la dispersión. Tipo de Corrección de FWHMejeX FWHMejeY material la dispersión (mm) (mm) Aire no 2.060 1.648 Aire sı́ 1.971 1.620 Metacrilato no 2.051 1.743 Metacrilato sı́ 1.976 1.697 Teflón no 1.951 1.803 Teflón sı́ 1.859 1.749 Tabla 13.1: Resolución obtenida para el capilar en función del maniquı́ utilizado. de los maniquı́es diseñados, debido principalmente a que que trabajamos en FOVs pequeños y por tanto el diámetro de los maniquı́s utilizados es pequeño y no se produce dispersión apreciable en ellos. La mayor parte de la dispersión detectada se produce en el colimador y el detector. Capı́tulo 14 Imágenes obtenidas con el segundo prototipo SPECT 14.1. Introducción En este capı́tulo se muestran las imágenes obtenidas con el segundo prototipo. En primer lugar realizaremos una caracterización del sistema para obtener ası́ los valores de sensibilidad, resolución espacial y uniformidad que somos capaces de alcanzar con el sistema propuesto. En segundo lugar se presentan las imágenes obtenidas para algunos estudios con pequeños animales. Finalmente se mostrarán varias imágenes de fusiones SPECT-CT que se obtienen cuando el sistema se monta junto con el equipo trimodal completo (PET-SPECT-CT). 14.2. Material y métodos 14.2.1. Caracterización del sistema Lo primero que se debe hacer cuando se tiene un sistema SPECT es validar y caracterizar el sistema. Los principales valores que permiten caracterizar un sistema SPECT son la sensibilidad, la resolución y la uniformidad de las imágenes obtenidas 171 172 14.2. Material y métodos con el mismo. Los resultados más relevantes se describen a continuación, algunos de los cuales fueron presentados en el World Molecular Imaging Congress 2010 [54]. 14.2.1.1. Medidas y maniquı́ de sensibilidad Para medir la sensibilidad del sistema SPECT se ha diseñado un maniquı́ estanco y cerrado de dimensiones reducidas para que se pueda utilizar en todos los FOV y cuya zona rellenable la forma un cilindro de 4 mm de altura y 4 mm de diámetro (ver figura 14.1). El tamaño reducido del maniquı́ permite medir la sensibilidad sin apenas perdidas por dispersión o atenuación. Figura 14.1: Foto del maniquı́ diseñado para medir la sensibilidad del sistema. Todas las adquisiciones de sensibilidad se han realizado con doble detector, tomando 30 proyecciones por detector describiendo un giro de 180o por detector. Las adquisiciones fueron de 30 segundos por proyección, mientras que el isótopo utilizado fue el 99m T c. 14. Imágenes obtenidas con el segundo prototipo SPECT 14.2.1.2. 173 Medidas y maniquı́s de resolución Para medir la resolución de los sistema SPECT lo más conveniente es utilizar maniquı́s tipo Derenzo [55]. Dichos maniquı́s consisten en varias regiones con capilares, dentro de cada una de las cuales los capilares tienen el mismo diámetro y la distancia entre el centro de dos capilares contiguos es siempre el doble que el diámetro del capilar. Con esta disposición de capilares se puede afirmar que si, en un perfil, la actividad entre capilares baja, al menos, hasta la mitad del máximo la resolución es igual o mejor que el diámetro de esos capilares. Se considera que la activad en el punto central entre dos capilares (I) es la mitad de la actividad máxima de cada uno de los capilares (I0 ). Sabiendo, por la disposición de capilares, que la distancia de ese punto al centro del capilar es igual al diámetro de los capilares (d). Ası́ mismo, como en ese punto tenemos la suma de las dos gaussianas vecinas, cada una de ellas debe aportar como máximo 1/4 de la actividad máxima, por lo que se puede demostrar que la resolución del equipo es menor o igual que el diámetro de los capilares de esa zona, ver en la ecuación (14.1). Si I= Por tanto: 1 d 2 d I0 . = f (x) = I0 · e− 2 ( σ ) ⇒ σ = p 4 2 · ln (4) 1 x 2 I0 F W HMm = = I0 · e− 2 ( σ ) ⇒ x = d · 2 2 s ln (2) √ = 2 · d, ln (4) donde F W HMm es la FWHM medida. Obteniendo: F W HMm p p 2 − d2 = = d2 + Re2 ⇒ Re = F W HMm r √ 2·d 2 − d2 = d. (14.1) Donde Re es la resolución espacial del sistema. Los sistema SPECT difieren entre ellos y para poder medir la resolución del sistema con precisión normalmente es necesario diseñar e implementar maniquı́s del tipo 174 14.2. Material y métodos Derenzo con los tamaños deseados. En nuestro caso hemos diseñado dos maniquı́s de dimensiones reducidas para poder utilizarlos en los FOV20 y FOV40. (a) Foto del maniquı́ diseñado para medir la resolución axial. (b) Foto del maniquı́ diseñado para medir la resolución transaxial. Los números indican el diámetro de las aperturas (mm). Figura 14.2: Fotos de los maniquı́s diseñados para medir la resolución del sistema en los FOVs pequeños. El primero es un maniquı́ abierto que permite medir la resolución axial del sistema. Se trata de un ortoedro de metacrilato de 20x20x5 mm3 . Los capilares son agujeros perforados de 3 mm de profundidad y con la disposición que se muestra en la figura 14.2(a). El segundo diseño es un maniquı́ cerrado que se acopla a la camilla de maniquı́s y que permite medir la resolución transaxial del sistema. El maniquı́ es un cilindro también de metacrilato de 20 mm de diámetro y 30 mm de altura. En su interior tiene un cilindro más pequeño con agujeros pasantes formando el maniquı́ tipo Derenzo deseado (ver figura 14.2(b)). Ademas el maniquı́ tiene dos cilindros de 1 mm de espesor a cada lado de la parte tipo Derenzo que permiten que la disolución que contiene la actividad fluya de uno a otro cilindro rellenando todos los capilares. Finalmente tiene dos tubos de 3 mm de diámetro con sus respectivos tapones, a 14. Imágenes obtenidas con el segundo prototipo SPECT 175 través de estos tubos se rellena el maniquı́ y posteriormente se cierra para asegurar la estanqueidad del mismo. (a) (b) Figura 14.3: Foto del maniquı́ utilizado para medir la resolución en los FOV60 y FOV80. Finalmente también se ha utilizado un maniquı́ diseñado previamente en el grupo con distancias mayores entre capilares para las medidas de resolución de los FOV60 y FOV80. Se trata de una maniquı́ ortoédrico cerrado de 40x40x9,5 mm3 . El maniquı́ puede abrirse y en su interior tiene otro ortoedro de 30x30x4,5 mm3 con agujeros perforados pasantes. Los agujeros esta colocados en 3 secciones, el diámetro de los agujeros de cada una de las 3 secciones es de 1 mm, 1.5 mm y 2 mm respectivamente. La distancia entre los centros de dos agujeros vecinos es siempre el doble del diámetro del agujero para cualquiera de ellos (ver figura 14.3). 14.2.1.3. Medidas y maniquı́s de uniformidad Para medir la uniformidad del sistema SPECT se han utilizado dos maniquı́s cilı́ndricos rellenables y cerrados que se acoplan a la camilla del equipo para garantizar el centrado. El primero es un cilindro pequeño, cuya parte rellenable es de 12 mm de diámetro y 8 mm de altura, el cual se utiliza para medir la uniformidad en los FOV20 y FOV40, ver figura 14.4(a). El segundo maniquı́ es un cilindro de mayor tamaño, cuya parte rellenable es de 30 mm de diámetro y 24 mm de altura que sirve para medir la uniformidad en los FOV60 y FOV80, ver figura 14.4(b). La uniformidad del sistema se define como sigue: 176 14.2. Material y métodos (a) Foto del maniquı́ utilizado para medir la uniformidad del sistema en los FOV20 y FOV40. (b) Foto del maniquı́ utilizado para medir la uniformidad del sistema en los FOV60 y FOV80. Figura 14.4: Maniquı́s utilizados para medir la uniformidad del sistema. U nif ormidad ( %) = 100 · Vmax − Vmin Vmax + Vmin (14.2) donde Vmax y Vmin son, respectivamente, el valor máximo y mı́nimo dentro de una ROI. Las ROI utilizadas son cilindros con un diámetro igual a del maniquı́ y con una altura igual a 14.2.2. 1 4 3 4 partes del diámetro de la altura del maniquı́. Imágenes con animales pequeños El sistema SPECT que aquı́ se describe ha sido utilizado para el estudio con animales pequeños en Notre Dame Integrated Imaging Facility (Indiana, USA). El doctor W. Matthew Leevy, responsable de la instalación, nos ha cedido adquisiciones de diversos estudios realizados con las diferentes configuraciones disponibles para poder estudiar y verificar el funcionamiento del sistema. A continuación describiremos brevemente los tres tipos de estudios de SPECT con animales en los que nos centraremos en este apartado: Estudios de corazón con 99m T c − M IBI. Se realiza un estudio de ratón con la configuración FOV40 y colimador pinhole cuyo objetivo es proyectar una imagen del músculo miocárdico. Para ello, se introducen 700 µCi del ra- diotrazador mediante una inyección intravenosa periférica a un ratón. Tras la inyección hay que esperar 45 minutos para dejar que se distribuya el radiofármaco. El estudio consta de 4 tomas axiales (camas), para poder ver el 14. Imágenes obtenidas con el segundo prototipo SPECT ratón completo, en las cuales se va desplazando el ratón 28 mm axialmente para tener 10 mm de solapamiento. En cada una de las camas se realizan 30 proyecciones por cámara con un tiempo total de 30 minutos por cama. Estudios óseos con 99m T c − M DP . Se realiza un estudio con una rata para la configuración FOV60 y colimador pinhole. Para dicho estudio se inyectaron 10 mCi del radiotrazador por vı́a endovenosa y se dejaron transcurrir 3-4 horas para asegurar que todo el radiotrazador se incorporase al hueso o fuese eliminado. Una vez transcurrido dicho tiempo se realizaron 4 camas, en las cuales se va desplazando la camilla 45 mm entre cama para tener 12 mm de solapamiento. En cada una de las camas se adquieren 30 proyecciones por cámara con un tiempo total de 30 minutos por cama. Pulmón con macroagregados de Albúmina (MAA). Se realiza un estudio de rata con 99m T c − M AA para la configuración FOV60 y colimador mul- tipinhole. Una vez inyectados 400 µCi del radiotrazador por vı́a endovenosa se esperan al menos 5 minutos, a fin de que las partı́culas que no hallan sido atrapadas por los capilares pulmonares lo sean por el sistema reticuloendotelial. El estudio consta de 30 proyecciones por cámara con un tiempo total de 30 minutos. 14.2.3. Fusión de imágenes SPECT con CT El prototipo SPECT diseñado se monta en un equipo modular PET-SPECT-CT. El hecho de tener en el mismo equipo un módulo CT nos permite realizar adquisiciones sucesivas de SPECT y CT para posteriormente llevar a cabo las fusiones de imágenes SPECT-CT. Estás fusiones pueden ser de gran ayuda a los investigadores, puesto que a la información fisiológica obtenida con el módulo de SPECT se añade la información morfológica que proporcionan las imágenes de CT. Antes de poder utilizar las fusiones con animales es necesario relacionar los ejes de coordenadas de ambos módulos puesto que las imágenes que se obtienen con el CT pueden estar giradas y desplazadas respecto a las imágenes del SPECT. Otro problema añadido es que el FOV del CT es fijo y coincide con el FOV que tenemos en SPECT con la configuración de FOV80. Por tanto es necesario girar, desplazar 177 178 14.3. Resultados obtenidos y “recortar” las imágenes de CT para cada configuración de SPECT. Dicho proceso de calibración de la fusión, fue llevado a cabo por el departamento de informática de la empresa Oncovision y queda fuera de los objetivos de esta memoria. A modo de resumen se puede comentar que dicho proceso se realiza utilizando los maniquı́s de calibración geométrica introducidos en la sección 12.2.2.1. Cuando se realizan las adquisiciones de SPECT para la calibración geométrica se aprovecha para realizar una adquisición de CT. A partir de las reconstrucciones de SPECT y CT de dichas adquisiciones se calibra el proceso de fusión. 14.3. Resultados obtenidos 14.3.1. Caracterización del sistema. 14.3.1.1. Resultados de sensibilidad con el maniquı́ diseñado Estudio de sensibilidad en función de la ventana de energı́a utilizada. En primer lugar, antes de medir la sensibilidad del sistema se realizó un estudio, utilizando un equipo con 1 solo detector, para ver como varı́a la sensibilidad con la ventana energética elegida. En la figura 14.5 se muestra el espectro de energı́a de una adquisición con colimador pinhole (Eph ) y otra multipinhole (Emph ), también se muestran las franjas que delimitan dos de las posibles ventajas de energı́a (±10 % y ±15 %) centradas en el fotopico de 140 keV. Sensibilidad obtenida en función del FOV. Finalmente, utilizando la ven- tana de energı́a de ±15 %, medimos la sensibilidad en función del FOV y el colimador seleccionado. Dicha medida no requiere reconstrucción de imagen ya que se obtiene a partir de las cuentas de las proyecciones. Una vez rellenado el maniquı́ de sensibilidad y medida la actividad del mismo con el activı́metro se coloca en la camilla de maniquies y se centra en el FOV. A continuación se realiza la adquisición y una vez finalizada se suman los rayos gamma obtenidos por el detector dentro de la ventana de energı́a de ±15 % para todas las proyecciones y se divide por el tiempo total de la adquisición y por la actividad de la fuente. 14. Imágenes obtenidas con el segundo prototipo SPECT 179 Espectro de energía para el FOV 20mm 4 x 10 Eph 16 E mph 14 ± 15% ± 10% Cuentas 12 10 8 6 4 2 0 40 60 80 100 120 140 160 180 200 Energía (keV) Figura 14.5: Espectro de energı́a para una medida de sensibilidad en el FOV20 tanto con el colimador pinhole como multipinhole. También se muestras las barras correspondientes a las ventanas de energı́a de ±10 % y ±15 %. Sensibilidad en función del tamaño de la ventana energética 400 Sensibilidad (cps/MBq) 350 Pinhole Multipinhole 300 250 200 150 100 50 5 10 15 20 25 30 35 Ventana energética (+− %) Figura 14.6: Sensibilidad absoluta para los dos colimadores en función de la ventana de energı́a seleccionada. Las medidas se realizaron para el FOV20. Este proceso se repite para los 4 FOVs y los dos colimadores disponibles. Los resultados obtenidos se muestran en la figura 14.7. Se obtiene que la sensibilidad máxima para el colimador multipinhole es de 715cps/M Bq mientras que para el colimador pinhole se sitúa en 205cps/M Bq 1 . 1 Los valores de sensibilidad obtenidos presentan un aumento de un factor 2 con respecto al estudio en función de la ventana energética debido a que se utilizó un sistema con dos detectores en lugar de un único detector. 180 14.3. Resultados obtenidos Sensibilidad medida en función del FOV 800 Multipinhole Pinhole 700 S (cps/MBq) 600 500 400 300 200 100 0 20 30 40 50 60 70 80 FOV (mm) Figura 14.7: Sensibilidad obtenida en cada FOV para los dos colimadores disponibles. 14.3.1.2. Resultados de resolución con los maniquı́s diseñados Imágenes de resolución. Con los maniquı́s diseñados se ha medido la resolución del sistema para los dos tipos de colimadores disponibles. Figura 14.8: Resolución axial obtenida mediante el colimador pinhole. Las imágenes reconstruidas con el maniquı́ abierto se muestran en la figura 14.8. En la imagen (2) se observa como para el FOV40 se distinguen los capilares de 1 mm pero el sistema no es capaz de distinguir los capilares de 0.8 mm. Por el contrario, para el FOV20 el sistema puede distinguir también la sección de 0.8 mm como se muestra en las imágenes (3) y (4). 14. Imágenes obtenidas con el segundo prototipo SPECT Figura 14.9: Resolución transaxial del sistema para el colimador pinhole y el FOV20. Vistas del corte transaxial y el corte coronal. Figura 14.10: Resolución transaxial del sistema para el colimador pinhole y el FOV20. Comparación entre el corte transaxial reconstruido y el mismo corte del maniquı́. Se distingues todos los agujeros menos los de 0.6 mm. La mejor resolución transaxial se obtiene con el colimador pinhole y el FOV 20, como se puede observar en las figuras 14.9 y 14.10. Partiendo de dichas imágenes se puede afirmar que la resolución transaxial del sistema es de 0.8 mm puesto que se distinguen todos los capilares salvo los que están separados 0.6 mm. Finalmente, en la figura 14.11 se muestra una comparativa de la resolución obtenida para los dos colimadores disponibles. La reconstrucción corresponde al maniquı́ de la figura 14.3 para el FOV60. Se puede apreciar como la reconstrucción multipinhole (arriba) es muy similar a 181 182 14.3. Resultados obtenidos Figura 14.11: Comparativa de resolución en el FOV60. (Arriba) Reconstrucción con colimador multipinhole. (Abajo) Reconstrucción con colimador pinhole. la pinhole (abajo), sin embargo la reconstrucción del maniquı́ tiene peor resolución y SNR cuando la adquisición se realiza con el colimador multipinhole. Las adquisiciones fueron de 45 minutos con una actividad de aproximadamente 50 MBq en ambos casos. La dos imágenes se reconstruyeron con 15 subsets y 5 iteraciones. Resolución medida en función de la configuración del sistema. La resolu- ción medida para todas las configuraciones disponibles se puede ver en la figura 14.12. Se aprecia de los resultados obtenidos como empeora la resolución al aumentar el FOV debido a que para aumentar el FOV es necesario alejarse reduciendo ası́ el factor de amplificación y por tanto perdiendo resolución. También se ve que para un mismo FOV con el colimador multipinhole tenemos peor resolución, lo cual, se debe a que al utilizar la configuración de múltiples aperturas se aumenta la complejidad del sistema disminuyendo ası́ la resolución en el método de reconstrucción. 14. Imágenes obtenidas con el segundo prototipo SPECT 183 Figura 14.12: Resolución del sistema para cada uno de los 4 FOVs y los dos colimadores disponibles. 14.3.1.3. Resultados de uniformidad con los maniquı́s diseñados Imágenes de uniformidad. Utilizando el maniquı́ mencionado para cada uno de los FOVs se obtienen las imágenes a partir de las cuales se puede calcular la uniformidad del sistema. Las adquisiciones fueron de 45 minutos, con una concentración aproximada en la disolución de 5 MBq/ml en cada uno de los casos. Las imágenes pinhole se reconstruyen utilizando el algoritmo OSEM con 5 subsets y 5 iteraciones, mientras que la reconstrucciones multipinhole se obtienen utilizando 15 subsets y 5 iteraciones. En las figuras 14.13 y 14.14 se muestran las imágenes obtenidas con ambos colimadores para el FOV40 y el FOV60, respectivamente. En todas las figuras de uniformidad mostradas se incluye, marcada en azul, la ROI utilizada para calcular la uniformidad. Uniformidad medida en función de la configuración del sistema. Los val- ores de uniformidad obtenidos para todas las configuraciones disponibles se muestran en la figura 14.15 184 14.3. Resultados obtenidos (a) Reconstrucción del maniquı́ de uniformidad con colimador multipinhole para el FOV40. (b) Reconstrucción del maniquı́ de uniformidad con colimador pinhole para el FOV40. Figura 14.13: Uniformidad para el FOV40. (a) Reconstrucción del maniquı́ de uniformidad con colimador multipinhole para el FOV60. (b) Reconstrucción del maniquı́ de uniformidad con colimador pinhole para el FOV60. Figura 14.14: Uniformidad para el FOV60. 14. Imágenes obtenidas con el segundo prototipo SPECT 185 Uniformidad medida en función del FOV 16 Multipinhole Pinhole 15 14 Uniformidad (%) 13 12 11 10 9 8 7 6 5 20 30 40 50 60 FOV (mm) 70 80 90 Figura 14.15: Uniformidad del sistema en cada uno de los 4 FOVs y para los dos colimadores disponibles. Se observa como la uniformidad obtenida con el colimador pinhole es mejor que con el multipinhole en todos los casos en torno a un 20 %. Por otro lado como solo tenemos 2 maniquı́s de uniformidad se observa una mejora de la medida de uniformidad para los FOV40 y FOV80 con respecto a los FOV20 y FOV60, en parte, porque el maniquı́ utilizado en estos casos ocupa un menor porcentaje del FOV total disponible. 14.3.2. Imágenes con animales pequeños A continuación se muestran los resultados obtenido para las pruebas realizadas con pequeños animales. 14.3.2.1. Estudios de corazón con 99m T c − M IBI La figura 14.16 muestra una imagen reconstruida del ratón una vez solapadas las 4 camas. En el plano transaxial se muestra la imagen de un corte del corazón del ratón. Esta imagen esta saturada para poder ver el corazón ya que los órganos que constituyen las vı́as de excreción del MIBI (vesı́cula biliar, intestino delgado, 186 14.3. Resultados obtenidos intestino grueso, riñones y vejiga) son los que recogen la mayor dosis por unidad de radiactividad inyectada. Figura 14.16: Secciones de un estudio de ratón con 99m T c − M IBI. En el plano transaxial se muestra un corte del corazón que es el objetivo de los estudios con 99m T c − M IBI. 14.3.2.2. Estudios óseos con 99m T c − M DP La figura 14.17 muestra dos proyecciones de la renderización 3D de una imagen reconstruida de rata una vez solapadas las 4 camas. La mayor parte de la actividad se encuentra en la vejiga del animal, pero si se satura la imagen se observa como el 99m T c − M DP se ha distribuido por el esqueleto. Al tratarse de una rata, en la parte central de la misma, no alcanzamos a ver toda la columna debido a que al aumentar el grosor del animal en esa zona la columna queda fuera del FOV60. 14.3.3. Fusión de las imágenes de SPECT con imágenes de CT En la figura 14.18 se muestra, una vez calibrada la fusión, las reconstrucciones de los módulos CT y SPECT, ası́ como la posterior fusión, para un maniquı́ de validación 14. Imágenes obtenidas con el segundo prototipo SPECT (a) Proyección sagital. (b) Proyección coronal. Figura 14.17: Renderización 3D de una reconstrucción del esqueleto de rata utilizando 99m T c − M DP . de imagen. La imagen de SPECT corresponde al FOV60 con colimador pinhole. La zona más oscura observada en las tres vistas del CT corresponde a una burbuja de aire. Ésta es también apreciable en la imagen del SPECT como un corte al tener menos resolución espacial. 14.3.3.1. Fusión de un estudios óseo de 99m T c − M DP con CT En la figura 14.19 se muestra un plano obtenido de una imagen 3D correspondiente a la fusión de las imágenes obtenidas con SPECT y con CT para un estudio óseo de ratón. El estudio SPECT se realizó con 99m T c − M DP y se medió para el FOV40 y el colimador pinhole. Al igual que en el caso del maniquı́ se observa una buena correlación y solapamiento de ambas técnicas. Esto permite ubicar con precisión los datos funcionales dentro de la estructura anatómica. 187 188 14.3. Resultados obtenidos Figura 14.18: (arriba) Reconstrucción de CT. (centro) Reconstrucción de SPECT. (abajo) Imágenes fusionadas del SPECT-CT. Figura 14.19: Imagen de la fusión SPECT-CT de un estudio óseo de ratón. La imagen de CT en escala de grises y superpuesta en color la imagen de SPECT. 14. Imágenes obtenidas con el segundo prototipo SPECT 14.3.3.2. Fusión de un estudios de pulmón de 99m T c − M AA con CT En la figura 14.20 se muestra una proyección de una imagen 3D correspondiente a la fusión de las imágenes obtenidas con SPECT y con CT para el estudio de pulmón de rata realizado. El estudio SPECT se realizó con 99m T c − M AA y se medió para el FOV80 y el colimador multipinhole. La imagen muestra claramente como la fusión de las dos técnicas puede proporcionar información complementaria. Es este caso el CT nos da la información anatómica de los tejidos de alta densidad de la zona, mientras que el estudio SPECT con MMA muestra información funcional de los pulmones. Figura 14.20: Imagen 3D de la fusión SPECT-CT de un estudio de pulmón de rata. La imagen de CT en escala de grises y superpuesta en color la imagen de SPECT. 189 Capı́tulo 15 Método de cuantificación 15.1. Introducción y objetivos de la cuantificación Una inspección visual de la imagen reconstruida a menudo es suficiente para obtener los resultados deseados, sin embargo, algunos estudios requieren el conocimiento de la actividad absoluta de ciertas regiones de interés (ROI), para lo cual es necesario cuantificar, es decir, obtener la relación entre las cuentas de la imagen y la actividad del objeto. La cuantificación de las imágenes de SPECT se ve afectada por la degradación introducida por el ruido estadı́stico, la dispersión, la atenuación, el efecto del sistema colimador/detector y el Efecto de Volumen Parcial (PVE). Por tanto, cuantos más de estos efectos se tengan en cuenta en el cálculo mejor será la cuantificación ([56] [57]). El PVE actualmente engloba 2 fenómenos distintos que hacen que la intensidad de lo valores en la imagen difiera de la que idealmente deberı́a ser. El primer efecto es el emborronamiento de las imágenes introducido por la resolución espacial finita del sistema. Este efecto incluye la pérdida de actividad en estructuras pequeñas cuando su actividad es más alta que las regiones circundantes, y la sobrestimación de actividad en estructuras con baja actividad lo que se conoce como spillover. El segundo fenómeno que contiene el PVE es el muestreo de la imagen. El espacio objeto 191 192 15.1. Introducción y objetivos de la cuantificación se muestrea en vóxeles y, dependiendo de su tamaño, obviamente el contorno de los vóxeles no se ajusta al de los objetos por lo que un vóxel puede incluir diferentes tipos de tejidos. La intensidad de señal en cada vóxel será el promedio de las intensidades de los tejidos incluidos en el vóxel [58]. Un sistema SPECT se puede caracterizar por la resolución volumétrica. Dicho volumen se aproxima por una forma cilı́ndrica de 2×F W HM de diámetro y 2×F W HM de altura. Para fuentes (o volúmenes) del tamaño de la “resolución volumétrica” o mayores, la intensidad en las imágenes refleja la suma y la concentración de actividad del volumen que representa. Para objetos más pequeños, de modo que solo se rellena parcialmente un elemento de resolución volumétrica, la suma de la intensidad de todos los pı́xeles que se atribuyen al objeto no refleja toda la concentración de actividad contenida en ellos, porque la señal se distribuye sobre un volumen mayor que el tamaño de la fuente. El efecto neto del PVE es el de reducir el contraste de la imagen, ya que se aumentan los puntos de baja actividad y se disminuyen los de alta actividad. Este efecto es especialmente severo en pequeñas estructuras [59]. El objetivo principal del trabajo es obtener en la imagen reconstruida un valor igual a la actividad del objeto en cada pı́xel, con independencia de la forma, concentración y la posición del objeto y valido para todos los FOVs y colimadores utilizados y para cualquier parámetro de la reconstrucción OS-EM, como el número de subsets o el número de iteraciones. Para obtener dicho objetivo deberemos seguir los siguientes pasos: - Encontrar un factor que relacione la actividad en cuentas por segundo (cps) de la imagen reconstruida (cuentas de la reconstrucción dividido por el tiempo de adquisición) con la actividad de la muestra radiactiva utilizada lo que denominaremos como factor Q. - Estudiar como varı́a el factor Q con el número de subsets, el tamaño del vóxel y el número de iteraciones de la reconstrucción. 15. Método de cuantificación - Estudiar el comportamiento del factor Q al variar el FOV y el tipo de colimador (pinhole o multipinhole). En caso de que sea necesario, calcular el factor Q para cada uno de los FOVs y colimadores. - Ver si al cambiar la posición de la fuente en el FOV, la relación entre la actividad reconstruida y la actividad real se mantiene constante. 15.2. Material y métodos Como vimos en el capı́tulo 13 el método de reconstrucción se basa en el algoritmo iterativo OS-EM 3D e incluye un método de corrección de la dispersión basado en técnicas de doble ventana de energı́a. Nuestro sistema SPECT está pensado para animales pequeños y por tanto el FOV máximo que tenemos es de 80x80x80 mm3 . Para FOVs pequeños el efecto de la atenuación a las energı́as que trabajamos (140 keV) no es demasiado grande. Por otro lado, la FWHM de nuestro equipo está en torno al milı́metro, lo que indica que el PVE aparecerá únicamente para objetos de tamaño menor a 2 o 3 mm. Por lo tanto, la mayorı́a de las estructuras no estarán afectados por el PVE por ser de mayor tamaño. Además, para realizar las corrección de atenuación o PVE es necesario tener un mapa de atenuación, lo que implica, o bien, la utilización de otra modalidad de imagen anatómica (CT o RMN), o bien, un conocimiento previo de la forma del objeto a estudiar. Por estos motivos, en esta versión de cuantificación de la imagen no tendremos en cuenta los efectos de la atenuación y el PVE. 15.2.1. Relación entre cuentas de la imagen y actividad En primer lugar se quiere ver la relación que existe entre las cuentas por segundo reconstruidas y la actividad, además se pretende ver como se comporta dicha relación cuando se varı́a el tamaño del vóxel reconstruido, el número de subsets o el número de iteraciones. Para realizar estas pruebas se utilizó un sistema con solo una gammacámara. Para las medidas se utilizó una fuente cilı́ndrica de 5 mm de diámetro y 6 mm de longitud. El 193 194 15.2. Material y métodos isótopo utilizado en todas las adquisiciones es el 99m Tc. La actividad inicial debe ser elevada para dejarla decaer durante 24 horas (4 semividas). La actividad inicial fue de 852 µCi, medida con el activı́metro. De tal modo que al final del estudio la actividad es de 55 µCi. Durante todo ese tiempo se realiza un estudio con 40 adquisiciones en total y 60 proyecciones por adquisición, alargando el tiempo de las adquisiciones conforme va decayendo la actividad para ası́ tener una estadı́stica similar en todas las adquisiciones. La secuencia que se siguió es la siguiente: 11 adquisiciones de 15 minutos; 8 adquisiciones de 20 minutos; 8 adquisiciones de 30 minutos; 6 adquisiciones de 45 minutos; 5 adquisiciones de 60 minutos y 2 adquisiciones de 120 minutos. Finalmente se reconstruye toda la secuencia de datos, utilizando corrección de dispersión, para 5 combinaciones de parámetros de reconstrucción diferentes. Las 5 combinaciones planteadas son las siguientes. Prueba Prueba Prueba Prueba Prueba 1 2 3 4 5 no vóxeles tamaño vóxel no 75 1.3 mm 82 1.2 mm 90 1.1 mm 100 1.0 mm 110 0.9 mm subsets no iteraciones 2 7 5 3 5 3 5 3 6 2 Tabla 15.1: Combinación de parámetros de reconstrucción para las pruebas de cuantificación. De este modo cambiamos el número de vóxeles y de subsets, pero se mantiene el tamaño de FOV reconstruido (número de vóxeles · tamaño del vóxel ). Además se conserva la relación “número de subsets · número de iteraciones” en la medida de lo posible. 15.2.2. Cálculo del valor Q en función del colimador y el FOV Las medidas para calcular el valor de Q en función del colimador y el FOV se realizaron durante varios dı́as, debido a que para cada FOV y cada colimador es necesario realizar la medida para la calibración geométrica y posteriormente el estudio de cuantificación. Las medidas se realizaron con un sistema SPECT de dos detectores. 15. Método de cuantificación Para realizar los estudios de cuantificación se utilizaron dos maniquı́s, un eppendorf y el maniquı́ de sensibilidad. El estudio del FOV20 con colimador pinhole se realizó con el maniquı́ de sensibilidad mientras que los otros 3 estudios se realizador con el eppendorf. Antes de iniciar las adquisiciones, se rellena el maniquı́ con una disolución de 99m Tc y se mide la actividad inicial del maniquı́ con el activı́metro, posteriormente el maniquı́ se coloca centrado en el FOV. En todos los estudio se deja decaer la actividad unas 20 horas aproximadamente y durante todo ese tiempo se realiza un estudio con 28 adquisiciones en total y 60 proyecciones por adquisición, alargando el tiempo de las adquisiciones conforme va decayendo la actividad para ası́ tener una estadı́stica similar en todas las adquisiciones. La secuencia que se siguió para estas medidas es la siguiente: 7 adquisiciones de 20 s por proyección; 5 adquisiciones de 30 s por proyección; 4 adquisiciones de 40 s por proyección; 4 adquisiciones de 50 s por proyección; 4 adquisiciones de 60 s por proyección; 3 adquisiciones de 75 s por proyección y 1 adquisiciones de 90 s por proyección. Posteriormente todas estas medidas deben ser procesadas y reconstruidas hasta poder obtener las actividad en cuentas por segundo de las imágenes. La actividad inicial para cada uno de los 4 estudios fue la siguiente: - FOV20 con colimador pinhole (FOV20ph) ⇒ Actividad inicial = 390 µCi - FOV20 con colimador multipinhole (FOV20mph) ⇒ Actividad inicial = 205 µCi - FOV40 con colimador pinhole (FOV40ph) ⇒ Actividad inicial = 1750 µCi - FOV40 con colimador multipinhole (FOV40mph) ⇒ Actividad inicial = 1550 µCi Además, se realizaron 4 adquisiciones en las que la posición de la fuente variaba dentro del FOV para estudiar el comportamiento del factor de cuantificación con la posición del objeto. De las 4 medidas, 3 se tomaron con el FOV40 y colimador pinhole y la última con el FOV20 y colimador multipinhole. 195 196 15.3. Resultados 15.3. Resultados 15.3.1. Relación entre cuentas de la imagen y actividad La relación encontrada entre la actividad real y las cuentas por segundo reconstruidas para las cinco combinaciones de parámetros de reconstrucción se puede ver en la figura 15.1. En ella se aprecia claramente que el factor Q es prácticamente independiente de los los parámetros de reconstrucción utilizados. 900 Voxel=75x1.3mm Subset=2 Iter=7 800 Voxel=82x1.2mm Subset=5 Iter=3 700 Voxel=90x1.1mm Subset=5 Iter=3 Voxel=100x1.0mm Subset=5 Iter=3 A (μCi) 600 Voxel=110x0.9mm Subset=6 Iter=2 500 400 300 200 100 0 0 200 400 600 800 1000 1200 1400 1600 Imagen Reconstruida (c/s) Figura 15.1: Relación entre las cuentas por segundo de la imagen reconstruida y la actividad de la fuente. Se compara dicha relación con distintas combinaciones de número y tamaño de vóxel ası́ como con distintos números de subsets y de iteraciones. 15.3.2. Cálculo del valor Q en función del colimador y el FOV En la figura 15.2 se observan los estudios de cuantificación para los 2 FOV y los 2 colimadores utilizados. En esta figura también se muestra la relación entre cuentas de imagen reconstruidas (cps) y la actividad medida para 4 medidas desplazadas 15. Método de cuantificación 197 del centro del FOV. Donde FOV40ph representa el estudio realizado para el FOV40 con colimador pinhole, FOV40mph representa el estudio realizado para el FOV40 con colimador multipinhole, FOV20ph representa el estudio realizado para el FOV20 con colimador pinhole, FOV20mph representa el estudio realizado para el FOV20 con colimador multipinhole y Despla XY representa las 4 adquisiciones realizadas variando la posición de la fuente dentro del FOV. 2000 1800 FOV40ph FOV20ph FOV20mph 1600 1400 FOV40mph Despla_XZ A (µCi) 1200 1000 800 600 400 200 0 0 1000 2000 3000 4000 5000 6000 7000 Ratereconstruida Imagen (c/s) Imagen (c/s) Figura 15.2: Relación entre las cuentas por segundo de la imagen reconstruida y la actividad de la fuente para 2 FOV y dos colimadores distintos. También se incluye la medida de una fuente puntual en diferentes posiciones del FOV. Se puede ver como para el estudio FOV40mph, a partir de (≈ 550 µ Ci), se pierde la linealidad entre la actividad y las cuentas de la imagen reconstruida, esto es debido a efectos de tiempo muerto en el detector [60]. En medidas realizadas con las gammacámaras se ha constatado que la perdida de linealidad entre la tasa de cuentas detectadas y la actividad aparece a partir de 3500 cps, siendo la tasa de cuentas máxima que alcanzan las gammacámaras Sentinella de 8000 cps. Cuando se alcanzan las 8000 cps entramos en la zona de saturación del detector, como se 198 15.3. Resultados trata de un detector del tipo paralizable, para actividades mayores la tasa de cuentas irá disminuyendo [61]. Teniendo en cuenta que cada colimador en cada uno de los FOV tiene una determinada sensibilidad (ver la sección 14.3.1.1) se puede calcular la actividad máxima que se puede utilizar sin perdida de linealidad, ası́ como la máxima actividad antes de saturar los detectores (ver tabla 15.2). Linealidad Linealidad Saturación Saturación Colimador pinhole multipinhole pinhole multipinhole FOV20 825 µCi 250 µCi 2200 µCi 650 µCi FOV40 2200 µCi 550 µCi 5750 µCi 1400 µCi FOV60 5100 µCi 1100 µCi 13500 µCi 2850 µCi FOV80 9000 µCi 2175 µCi 24100 µCi 5700 µCi Tabla 15.2: Actividades esperadas máximas para conservar linealidad y para evitar saturación en cada FOV y colimador. Por tanto, para poder cuantificar sin corrección de tiempo muerto debemos utilizar actividades menores a la actividad en que se pierde la linealidad. En el estudio realizado con el FOV40 y colimador multipinhole los detectores estaban afectados por el tiempo muerto en las primeras horas de medida, por lo que este estudio no se utilizará a la hora de calcular el factor Q. Mientras que para el resto de estudios realizados, independientemente del FOV y el colimador utilizado todos los puntos se mantienen alrededor de la misma recta, incluidas las adquisiciones realizadas desplazando la fuente, tal y como muestra la figura 15.2. Finalmente podemos obtener el factor Q de los 3 estudios válidos efectuando un ajuste por mı́nimos cuadrados para cada uno de ellos. De este modo, la pendiente de dicho ajuste será el factor Q que convierta las cuentas de la imagen reconstruidas en actividad. En la figura 15.3 se muestra el ajuste realizado para las tres rectas, donde se ha ampliado la zona de tasas reducidas para mostrar mejor dichos ajustes. Los valores obtenidos para el factor Q en cada uno de los casos son: - FOV20 con colimador pinhole ⇒ F actor Q = 0.2618 µ Ci cps - FOV20 con colimador multipinhole ⇒ F actor Q = 0.2642 - FOV40 con colimador pinhole ⇒ F actor Q = 0.2631 µ Ci cps µ Ci cps 15. Método de cuantificación Figura 15.3: Relación entre las cuentas por segundo de la imagen reconstruida y la actividad de la fuente. Detalle de la zona de baja actividad, además se muestran los ajustes del FOV20ph, FOV20mph y FOV40ph. Donde la bondad del ajuste se aprecia en los valores del coeficiente de regresión, obteniendo para los tres casos R2 >0.99 (ver figura 15.3). 199 Capı́tulo 16 Conclusiones y proyección futura 16.1. Conclusiones del segundo prototipo diseñado 16.1.1. Diseño del segundo prototipo SPECT - Se ha diseñado un segundo prototipo SPECT con dos gammacámaras Sentinella. - Se han diseñado y construido nuevos colimadores pinhole y multipinhole intercambiables, pudiendo elegir el que mejor se adapte para cada uno de los estudios. - También se han diseñado 4 camillas seleccionables: la camilla de rata, de ratón y la de cabeza de ratón para animales, ası́ como una cuarta camilla construida para utilizar los diferentes maniquı́s necesarios para calibrar y caracterizar el equipo. 201 202 16.1. Conclusiones del segundo prototipo diseñado 16.1.2. Adquisición y ampliación del método de calibración geométrica - Se ha ampliado el método de calibración geométrica de modo que sea capaz de calibrar tanto sistemas con doble cabezal detector, como sistemas con colimador multipinhole. - Se ha modificado el método de minimización para dotarlo de mayor estabilidad e independencia de los parámetros iniciales y permitir la calibración conjunta de los 4 FOV utilizados. 16.1.3. Método de reconstrucción de imágenes - Se ha adaptado un algoritmo OS-EM para la reconstrucción de las imágenes adquiridas con nuestro prototipo. - La matriz del sistema se calcula mediante métodos analı́ticos de proyección basado en vóxeles. En la matriz se modeliza la eficiencia geométrica y se corrige el efecto de la apertura. Ésta también tiene implementada el número de detectores y de aperturas del colimador utilizado, lo que permite reconstruir imágenes para las dos configuraciones de colimador disponibles. - Se han aplicado simetrı́as en el cálculo de la matriz para reducir el tamaño y el tiempo de cálculo de las mismas. - Finalmente se ha implementado un método de corrección de la dispersión basado en los métodos de doble ventana de energı́a, el cual, aporta mejoras en la calidad de las imágenes obtenidas, aunque poco significativas. 16.1.4. Imágenes obtenidas con el segundo prototipo SPECT - Se ha caracterizado el sistema, tanto con colimador pinhole como con multipinhole obteniendose los siguentes resultados: Colimador pinhole. Se han obtenido resoluciones de hasta 0.8 mm y valores de sensibilidad de hasta 205 cps/MBq con uniformidades inferiores al 10 % en todos los casos. 16. Conclusiones y proyección futura 203 Colimador multipinhole. Se han obtenido resoluciones de hasta 1.0 mm y valores de sensibilidad de hasta 715 cps/MBq con uniformidades inferiores al 13 % en todos los casos. - Finalmente, se ha validado el sistema SPECT diseñado a través de estudios de corazón, pulmón y hueso con pequeños roedores. Mostrándose además ejemplos de las fusiones SPECT-CT obtenidas con el equipo Albira, donde se observa como las imágenes anatómicas de CT puede ayudar a localizar con mayor precisión las imágenes funcionales SPECT. 16.1.5. Cuantificación de las imágenes reconstruidas - Se ha desarrollado un método de cuantificación de las imágenes reconstruidas que permite relacionar las cuentas obtenidas en la imagen con la actividad existente en ese punto del objeto. - Se ha obtenido un factor de cuantificación de Q = 0.263 µ Ci cps , el cual, es valido e independientemente del tamaño y el lugar dentro del FOV, el colimador y los parámetros de reconstrucción. Esto se ha conseguido gracias a la implementación en la matriz del sistema de las correcciones de sensibilidad, eficiencia geométrica y el número de agujeros. - Se ha determinado que los efectos de tiempo muerto en el detector empiezan a afectar a la linealidad a partir de 3500 cps. 16.2. Proyección futura - En Medicina Nuclear y especialmente cuando se utiliza la técnica SPECT el tamaño de la superficie detectora es crucial en las prestaciones finales del sistema. Por eso, se pretende diseñar un nuevo SPECT utilizando un detector con un cristal de mayor tamaño, a la vez que colimadores multipinhole con más aperturas y agujeros inclinados para aumentar la sensibilidad. Este dispositivo, permitirá asimismo, aumentar el FOV o la resolución espacial. 204 16.2. Proyección futura - Durante el proceso de calibración geométrica con colimador multipinhole se han estimado los valores de la distancia focal para los agujeros no centrales, ası́ como la distancia entre todos los agujeros. Serı́a conveniente buscar un método para medir experimentalmente dichos valores. - La mejora de la caracterización de la geometrı́a y los distintos efectos fı́sicos que atañen al sistema SPECT se traduce en un aumento de las prestaciones del sistema. Actualmente se trabaja en la generación de la matriz del sistema utilizando métodos de proyección por trazado de rayos para comparar y estudiar la posibilidad de combinar este método con el actual. Al mismo tiempo, se está trabajando en modelizar la PSF intrı́nseca del detector para incorporar dicha información en el cálculo de la matriz del sistema. - Finalmente y alternativamente a la mejora de la calidad de la imagen final, existen métodos que permitirı́an reducir los tiempos de cálculo y los tamaños de las matrices, como por ejemplo, la utilización de coordenadas polares en la generación de las matrices del sistema. Bibliografı́a [1] Pichler B.J. et al., PET/MRI hybrid imaging: devices and initial results, Eur Radiol, vol. 18, pp. 10771086 (2008). [2] Kuhl D. and Edwards R., Image separation radioisotope scanning, Radiology, vol. 80, pp.653-662 (1963). [3] Brownell G.L. et al., Quantitative dynamic studies using short-lived radioisotopes and positron detection in Proceedings of the Symposium on Dynamic Studies with Radioisotopes in Medicine, IAEA Vienna, pp. 161-172 (1971). [4] Sociedad Española de Medicina Nuclear, Historia de la M. Nuclear, Página web http : //www.semn.es/nuclear08.php. [5] Administration of Radioactive Substances Advisory Committee, Notes for Guidance on the Clinical Administration of Radiopharmaceuticals and Use of Sealed Radioactive Sources, Health Protection Agency for the Administration of Radioactive Substances Advisory Committee (2006). [6] Alpharadin L. K., A 223Ra-based alpha-particle-emitting pharmaceutical for the treatment of bone metastases in patients with cancer, Curr Opin Investig Drugs, 10, no 12, pp. 1346-58 (2009). [7] Pavón Hernández N., Diseño y desarrollo de un sistema para la obtención de imágenes de gammagrafı́a en cirugı́a radioguiada, Tesis doctoral, Universidad de Valencia, Departamento de Fı́sica Atómica, Molecular y Nuclear (2010). [8] Bailey D. et al., Positron Emission Tomography, ISBN 1852337982. 205 Bibliography BIBLIOGRAFÍA [9] Moses W. W. et al., Scintillation Non-Proportionality: Present Understanding and Future Challenges, IEEE Trans Nucl Sci, 55, no 3, pp. 1049-1053 (2008). [10] Leo W. R., Techniques for Nuclear and Particle Physics Experiments, ISBN 0387572805. [11] Bass M., Handbook of Optics, Volume 1: Fundamentals, Techniques, and Design, ISBN-10: 007047740X. [12] Torrance K. E. et al., Theory for Off-Specular Reflection From Roughened Surfaces, JOSA 57, no 9, pp. 1105-1112 (1967). [13] Phong B. T., Illumination for computer-generated images, Doctoral Dissertation, The University of Utah (1973). [14] Prince J.L. et al., Medical Imaging. Signals and Systems, ISBN 0-13-065353-5. [15] Cherry S.R., et al., Physics in Nuclear Medicine, ISBN-13 978-0-7216-8341-6. [16] Tuli J., http : //www.nndc.bnl.gov/useroutput/AR 58461 2.html, Database Manager: Jag Tuli, NNDC, Brookhaven National Laboratory. [17] Anger H.O., Scintillation camera with multichanel collimators, J Nucl Med, 5, pp. 515-531 (1964). [18] Tsui B.M., The scintillation camera, The Society of Nuclear Medicine, pp. 17-45 (1988). [19] Gimeno Olmos J., Implementació d’una màscara codificada per a una minigammacàmera d’imatge mèdica, Trabajo de investigación, universidad de Valencia, departamento de fı́sica atómica, molecular y nuclear (2005). [20] Anger H.O., Radioisotope cameras, Instrumentation in Nuclear Medicine 1, pp. 485-552 (1967). [21] Crespo Vázquez C., Procesamiento de imágenes en SPECT cerebral: Cuantificación de estudios de neurotransmisión en el sistema dopaminérgico y registro de estudios de flujo en la epilepsia farmacoresistente, Tesis de doctorado, universitat de Barcelona, Unidad de biofı́sica y Bioenginyeria, departamento de Ciències fisiològicas (2008). Bibliography [22] Fessler J. A., Penalized weighted least-squared image reconstruction for positron emission tomography, IEEE Trans Med Imag 13, no 2, pp. 290300 (1994). [23] Bruyant P. P., Analytic and Iterative Reconstruction Algorithms in SPECT, IEEE J Nucl Med 43, no 10, pp. 13431358 (2002). [24] Hudson H. M. and Larkin R. S., Accelerated image reconstruction using ordered subsets of projection data, IEEE Trans Med Imag 13, no 4, pp. 601-609 (1994). [25] Porras E. et al., Portable mini gamma camera for medical applications, Nucl Instr and Meth A 486, pp. 186190 (2002). [26] Sanchez F. et al., Design and tests of a portable mini gamma camera, Med Phys 31, no 6, pp. 1384-1396 (2004). [27] Fernandez Tomás M., Desarrollo, optimización y evaluación clı́nica de una cámara gamma portátil para diagnóstico en Medicina Nuclear, Tesis Doctoral, Universidad de Valencia, Departamento de Fı́sica Atómica, Molecular y Nuclear (2006). [28] Després P., et al., Investigation of a Continuous Crystal PSAPD-Based Gamma Camera, IEEE Trans Nucl Sci 53, no 3, 1643-1649 (2006). [29] Pavón Hernández N., Diseño, desarrollo y test de la electrónica analógica y digital para una cámara gamma portátil, Trabajo de Investigación, Universidad de Valencia, Ingenierı́a Electrónica (2002). [30] Siegel S. et al., Simple charge division readouts for imaging scintillator arrays using a multi-chanel PMT, IEEE Trans Nucl Sci 43, no 3, 1634-1641 (1996). [31] Escat Paricio B., Desarrollo, caracterización y evaluación clı́nica de una cámara gamma portátil para aplicaciones médicas, Tesis Doctoral, Universidad de Valencia, Departamento de Fı́sica Atómica, Molecular y Nuclear (2003). [32] National Electrical Manufacturers Association, Performance measurements of scintillation cameras, NEMA Standards Publication No. NU 1. Washington D.C. (1994). 207 Bibliography BIBLIOGRAFÍA [33] Rizo Ph. et al., Geometric Calibration Method for Multiple-Head Cone-Beam SPECT System, IEEE Trans Nucl Sci 41, no 6, pp. 2748-2757 (1994). [34] Beque D. et al., Characterization of Pinhole SPECT Acquisition Geometry, IEEE Trans Med Imag 22, no 5, pp. 599-612 (2003). [35] Beque D. et al., Optimization of Geometrical Calibration in Pinhole SPECT, IEEE Trans Med Imag 24, no 2, pp. 180-190 (2005). [36] Noo F. et al., Analytic method based on identification of ellipse parameters for scanner calibration in cone-beam tomography, IEEE Phys Med Biol 45, pp. 34893508 (2000). [37] Press W. H. et al., Numerical Recipes: The Art Of Scientific Computing, ISBN10: 0521880688. [38] Pareto D. et al., Iterative reconstruction with correction of the spatially variant fan-beam collimator response in neurotransmission SPET imaging, Eur J Nucl Med Mol Imag 30, no 10, pp. 1322-1329 (2003). [39] Pino F. et al., Development of a variable-radius pinhole SPECT system with a portable gamma camera, Rev Esp Med Nucl 30, no 5, pp. 286-291 (2011). [40] Wang Y. and Tsui B., Pinhole SPECT With Different Data Acquisition Geometries: Usefulness of Unified Projection Operators in Homogeneous Coordinates, IEEE Trans Med Imag, 26, no 3, pp. 298-308 (2007). [41] National Electrical Manufacturers Association, Performance measurements of Small Animall Positron Emission Tomographs, NEMA Standards Publication No. NU 2. Washington D.C. (2008). [42] Vunckx K. et al., Single and Multipinhole Collimator Design Evaluation Method for Small Animal SPECT, IEEE Trans Med Imag, 27, no 1, pp. 36-46 (2008). [43] Metzler S.D. and Jaszczak R.J., Simultaneous Multi-Head Calibration for Pinhole SPECT, IEEE Trans Nucl Sci, 53, no 1, pp. 113-120 (2006). [44] Andreyev A. , et al., Pinhole SPECT Reconstruction Using Blobs and Resolution Recovery, IEEE Trans Nucl Sci, 53, no 5, pp. 2719-2728 (2006). Bibliography [45] Vanhove C., et al., Resolution recovery in pinhole SPECT based on multi-ray projections: a phantom study, Eur J Nucl Med Mol Imag, 34, no 2, pp. 170-180 (2007). [46] Metzler S.D., et al., Analytic Determination of Pinhole Collimator Sensitivity With Penetration, IEEE Trans Med Imag, 20, no 8, pp. 730-741 (2001). [47] Smith M.F. and Jaszczak R.J., The effect of gamma ray penetration on angledependent sensitivity for pinhole collimator in nuclear medicine, Med Phys, 24, no 11, pp. 1701-1709 (1997). [48] Cao Z. , et al., Optimal number of pinholes in multi-pinhole spect for mouse brain imaging – a simulation study, Phys Med Biol, 50, no 19, pp. 4609-4624 (2005). [49] Nuyts J. , et al., Small animal imaging with multi-pinhole SPECT, Methods, 48, no 2, pp. 83-91 (2009). [50] Gilardi M.C. et al., Assessment and Comparison of Three Scatter Correction Techniques in Single Photon Emission Computed Tomography J Nucl Med, 29, no 12, pp. 1971-1979 (1988). [51] Ljungberg M. et al., Comparison of Four Scatter Correction Methods Using Monte Carlo Simulated Source Distributions J Nucl Med, 35, no 1, pp. 143-151 (1994). [52] Zaidi H., Comparative evaluation of scatter correction techniques in 3D positron emission tomography Eur J Nucl Med, 27, no 12, pp. 1813-1826 (2000). [53] Ogawa K. et al., A practical method for position-dependent compton-scatter correction in single photon emission CT IEEE Trans Med Imag, 10, no 3, pp. 408-412 (1991). [54] Orero A. et al., Performance evaluation of a novel dual head SPECT scanner for small animal imaging, World Molecular Imaging Congress, Poster Session (2010). 209 Bibliography BIBLIOGRAFÍA [55] Budinger T.F. et al., Emission computer assisted tomography with single-photon and positron annihilation photon emitters, J Comput Assist Tomogr, 1, no 1, pp. 131-145 (1977). [56] Jaszczak R. et al., Physical factors affecting quantitative measurements using camera-based single photon emission computed tomography (SPECT), IEEE Trans Nucl Sci, 28, no 1, (1981). [57] Cot A. et al., Absolute quantification in dopaminergic neurotransmission SPECT using monte carlo-based scatter correction and fully 3-dimensional reconstruction, Eur J Nucl Med, 46, no 9, pp. 14971504 (2005). [58] Du Y. et al., Partial volume effect compensation for quantitative brain SPECT imaging, IEEE Trans Med Imag, 24, no 8, pp. 969976 (2005). [59] Soret M. et al., Accuracy of partial volume effect correction in clinical molecular imaging of dopamine transporter using SPECT, Proceedings Euro Med Imag, 571, no 1-2, pp. 173176 (2007). [60] Weier H. et al., Quantum eavesdropping without interception: an attack exploiting the dead time of single-photon detectors, New J Phys, 13, no 7, pp. 073024 (2011). [61] Cranley K. et al., Correction for deadtime losses in a gamma camera/data analysis system, Eur J Nucl Med, 5, no 4, pp. 377-382 (1980).