Modelación de Sistemas de Primer Orden con Simulink y

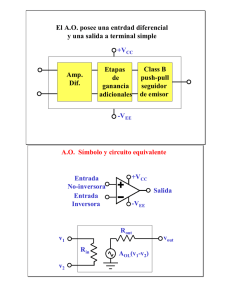
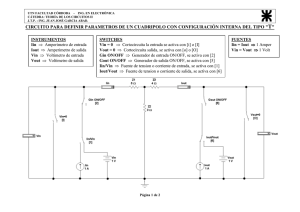
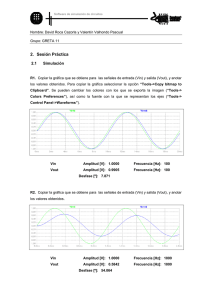
1
Encuentro de Investigación en IE, 28 — 30 de Marzo, 2007
Modelación de Sistemas de Primer Orden con Simulink y
Amplificadores Operacionales Utilizando la Técnica Didáctica
de Aprendizaje Basado en Problemas
Jorge D. Mendiola Santibáñez,
Carlos E. López Campos,
Departamento de Tecnociencias,
Universidad del Valle de México, Campus Quéretaro, CP-76230
TEL: +(442)2111900, ext. 11208, correo-e: [email protected], [email protected]
Resumen — Se ha probado la técnica denominada
Aprendizaje Basado en Problemas (ABP) para enseñar
a los estudiantes a modelar sistemas físicos
representados por ecuaciones diferenciales de primer
orden. Se incluye, la modelación con la herramienta
Simulink de Matlab, y la modelación física real
mediante circuitos de amplificadores operacionales. En
este artículo presentamos los resultados obtenidos por
los estudiantes, los cuales muestran el éxito del uso de
este método.
Abstract — It has tried the technique named Problems
Based Learning (PBL) to teach to the students modeling
physical systems represented by first order differential
equations. It is included, the modelling with the
Simulink tool of Matlab, and the real physical modelling
by operational amplifier circuits. In this article we
present the results obtained by the students, that show
the success of the use of this method.
Descriptores — ABP, AMPOP, diagramas de bloques,
Simulink, función de transferencia.
I. INTRODUCCIÓN
La técnica de Aprendizaje Basado en Problemas
(ABP), también conocida por sus siglas en inglés PBL
(Problems Based Learning), fue desarrollada y
aplicada en la década de los 60, teniendo sus orígenes
en la Universidad Case Western Reserve en los
Estados Unidos y en la Universidad McMaster en
Canadá [1, 2 , 3], lugares en los que primeramente se
utilizó con estudiantes de medicina. En la actualidad,
sin embargo, este método se ha aplicado a una gran
variedad de disciplinas, aunque debemos de añadir
que las áreas de ingeniería y ciencias no han sido de
las más favorecidas en este aspecto.
Una de las principales diferencias entre la técnica de
ABP y un método tradicional de enseñanza, es que, en
éste último, un profesor enseña por medio de la
exposición de la información, mientras que los
estudiantes juegan el papel de oyentes pasivos; por
otro lado, la técnica de ABP permite a los estudiantes
jugar un rol activo durante el cual, ellos trabajan para
investigar, desarrollar y generar su propio
conocimiento y otras capacidades.
En términos breves, la técnica de ABP consiste en
proponer un problema a los estudiantes, el cual puede
variar de grado de complejidad, dependiendo de los
objetivos de aprendizaje. Permitiendo así que ellos
comiencen a generar ideas y propuestas de solución,
las cuales deberán llevar a cabo de manera práctica
con el fin de demostrar que tan cercana a lo correcto
es su hipótesis de solución.
Durante el proceso de solución del problema, de
manera natural ellos requieren información que deben
investigar por su propia cuenta, además de que, es
durante este proceso que ellos se convierten en
generadores de su propio conocimiento.
Por supuesto, existe una enorme diferencia entre ser
un espectador pasivo cuya función se reduce a sólo
recibir, comprender y devolver conocimientos, y en
181
Encuentro de Investigación en IE, 28 — 30 de Marzo, 2007
contra parte, con una técnica como la del ABP, ser
parte activa de la solución del problema y de la
generación del propio conocimiento. Pues es en
métodos de este tipo, en los que es posible generar en
los alumnos no sólo saber, sino otro tipo de
habilidades
tales
como:
construcción
del
conocimiento, aprender a aprender, búsqueda de
información, iniciativa para generar ideas de solución,
creatividad, etc.
II. REVISIÓN DE LA METODOLOGÍA
TRADICIONAL.
Modelación de sistemas es una materia que se imparte
en las universidades donde se ofrecen licenciaturas
relacionadas
con
la
electrónica,
eléctrica,
mecatrónica, control, entre otras. El estudio de dicha
materia es fundamental para la formación del
estudiante, puesto que es una materia integradora,
donde
se involucran amplios conocimientos
matemáticos tales como álgebra, álgebra lineal,
cálculo
diferencial
e
integral,
ecuaciones
diferenciales, transformada de Laplace, etc.; por otro
lado, es una materia fundamental para abordar de
lleno la teoría de control, tanto analógico como
digital, lo cual la constituye también en una materia
de enlace entre conceptos matemáticos básicos y
conceptos avanzados de especialización profesional.
Una problemática fundamental en su impartición es la
enorme cantidad de información matemática que se
debe dominar para llegar a comprender conceptos
tales como la noción de función de transferencia; el
cual esta fuertemente relacionado con los coeficientes
de las ecuaciones diferenciales, y el uso de la
transformada directa e inversa de Laplace.
En un curso tradicional, para cubrir los temas, se suele
seguir un programa en una serie de exposiciones
orales ante los estudiantes. Sin embargo desde nuestra
experiencia, y dada la gran variedad de conceptos
involucrados, pareciera que cada tema que se estudia
fuera independiente uno del otro; y en el mejor de los
casos, la reafirmación de la teoría se lleva a cabo
mediante la solución de problemas, que son resueltos
en clase o como ejercicios de tarea.
En la Universidad del Valle de México, y en
particular en el Campus Querétaro, se ha venido
trabajando en la propuesta de metodologías para
mejorar el aprendizaje de los estudiantes que cursan la
materia de Modelación de Sistemas y todos los demás
cursos. Esta metodología, cabe mencionar, esta de
acuerdo con el modelo educativo PRAXIS que se
aplica en esta universidad.
Como se ha indicado en la Introducción, en el
presente artículo se presenta una de las técnicas
desarrolladas por nosotros, clasificada dentro de los
métodos de Aprendizaje Basado en Problemas, para
que el estudiante comprenda conceptos tales como: la
transformada de Laplace, la función de transferencia,
el álgebra de bloques y la modelación de una ecuación
diferencial mediante circuitos de amplificadores
operacionales.
En la siguiente sección se explica la estrategia y la
metodología seguidas, así como el objetivo de cada
punto planteado.
III. DESCRIPCIÓN DE LA METODOLOGÍA
PROPUESTA.
Desde el punto de vista de una importante corriente
pedagógica [4, 5], algunas de cuyas ideas estamos
incluyendo en nuestro trabajo, en el aprendizaje de
materias integradoras o de un rico contenido
conceptual, para nuestro caso de ingeniería, es muy
importante conjugar el trabajo con los diferentes
conceptos y no tratar estos como temas
independientes.
Por ejemplo, al estudiar Modelación de Sistemas, los
temas de: ecuaciones diferenciales, transformada de
Laplace y el de funciones de transferencia se deben
tratar de una manera integrada. Éste es uno de los
factores que nos permiten generar un aprendizaje
significativo [4, 5].
Otro aspecto importante a considerar es la adecuada
seriación de los temas para el uso correcto de los
antecedentes conceptuales de aprendizaje [6].
Desde esta perspectiva, planteamos el curso en el
siguiente orden:
1. Generación
de
antecedentes
para
la
proposición del problema tipo ABP que deberá
ser resuelto por los estudiantes.
182
Encuentro de Investigación en IE, 28 — 30 de Marzo, 2007
A. Primer mes de enseñanza y primer antecedente:
Transformada de Laplace aplicada a la
solución de ecuaciones diferenciales.
B. Segundo mes de enseñanza, primera semana,
segundo antecedente: Concepto de función de
transferencia.
D. Cuarto antecedente: Configuraciones básicas
con amplificadores operacionales: sumador,
seguidor, diferenciador, integrador e inversor.
En este momento se trabaja con la representación
de: un sumador, seguidor, diferenciador, integrador
e inversor y se coloca en bloques su
correspondiente función de transferencia [7].
C. Segundo mes de enseñanza,
tercer
antecedente:
Operacionales.
Se presenta como ejemplo, el caso del integrador
para condiciones iniciales iguales a cero (ver
Figura 2).
cuarta semana,
Amplificadores
Al igual que en el resto de los temas, se trabaja a
través de ejemplos.
Vout = − ∫
A los alumnos adicionalmente se les proporciona una
copia de las reducciones de bloques tomada del libro
de Ogata [7].
Una vez tratado esto, es posible explicar la definición
de función de transferencia en lazo abierto y cerrado.
Respecto al método de aprendizaje, durante las clases
se cultiva, en éste y todos los temas, el trabajo en
equipo y la resolución de ejercicios. Los ejemplos y
ejercicios son seleccionados cuidadosamente, ya que
el estudiante deberá representar en diagrama de
bloques una ecuación diferencial [7].
t
0
(a)
Vout ( s ) = −
Vin ( s )
sRC
Vin
dt
RC
(b)
−
Vin
1
sRC
Vout
(c)
(d)
Figura 2. (a) Integrador, (b) Función de transferencia considerando
condiciones iniciales cero, (c) Función de transferencia en el dominio de la
frecuencia, (d) representación en diagrama a bloques del integrador.
2. Propuesta, explicación e implementación teórica
Adicionalmente, se dan ejemplos de funciones de
transferencia en el dominio de la frecuencia; en este
caso se solicita a los alumnos recuperar la ecuación
diferencial y obtener la representación en diagramas
de bloques [7]. También se les ofrecen ejercicios y
ejemplos donde se practique la reducción de bloques
[8].
Los ejercicios y ejemplos generalmente se analizan
para el caso donde existe retroalimentación y se
llegue a la forma final representada en la siguiente
figura (Ver Figura 1.):
U
+
G(s)
H(s)
y práctica de la función de transferencia C ( s ) = 10
U (s)
11
con
amplificadores
operacionales,
quinto
antecedente.
Para mayor claridad del estudiante acerca de como
hacer la representación en bloques de una función de
transferencia, se explica, de manera expositiva
tradicional, el circuito en la Figura 3, el cual
representa a la función de transferencia
C ( s ) 10
. En
=
U ( s ) 11
este caso resulta de utilidad la representación de las
configuraciones de los operacionales mencionadas
anteriormente como en el ejemplo de la Figura 3.
R
R
G(s)
=
U 1 + G ( s) H ( s)
Figura 1. Diagrama a bloques en retroalimentación negativa.
(a)
183
Encuentro de Investigación en IE, 28 — 30 de Marzo, 2007
alrededor de una semana en la cual deberán analizar el
problema, presentar propuestas de solución,
implementarlas y finalmente entregar resultados.
Problema tipo ABP propuesto:
Función de transferencia:
Vi
-Σ
-1
-10
-1
10
S +3
Vout
Objetivo: Implementar la anterior
transferencia utilizando operacionales.
función de
Vx
IV. RESULTADOS.
1
A continuación se presenta lo reportado por los
estudiantes:
(b)
Solución: En primer lugar se analizó la función de
transferencia y obtuvimos el siguiente diagrama (ver
Figura 4.) el cual lleva dos sumadores operacionales y
un derivador.
Donde
Vx = Vin-Vout y Vout =
10Vx
De estas dos ecuaciones se
obtiene que:
(Vout /10) = Vin-Vout
Vout (11/10)= Vin
Vout /Vin= 10/11
Figura 3. (a)
Implementación de la función de transferencia
C ( s ) 10
=
con operacionales, (b) Análisis en bloques del circuito de la
U ( s) 11
Figura 3(a).
3. Propuesta del problema tipo ABP a los estudiantes:
Implementación teórica y práctica de la función de
transferencia
C ( s)
10
=
U ( s) s + 3
con
amplificadores
operacionales.
Ésta es una de las partes más importantes del proceso
de aprendizaje, pues aquí es precisamente donde los
estudiantes deberán integrar conocimientos previos
tanto prácticos como matemáticos, para a partir de
aquí, tal como lo propone la técnica de ABP, los
alumnos generen ideas de solución y durante el
desarrollo del trabajo, generen también conocimiento
conceptual significativo para sí mismos.
De esta forma, una vez explicado el circuito de la
Figura 3(a), se propone a los estudiantes el siguiente
ejercicio nuevo para ellos y más complicado que todo
lo hasta ahora aprendido, pidiendo que lo resuelvan
completamente por sí mismos, sin ninguna ayuda del
profesor. A partir de este momento ellos contarán con
Figura 4.- Circuito implementado para simular a la función de
10
transferencia
.
S +3
Como puede observarse, el circuito de la Fig. 4 está
compuesto por 5 amplificadores operacionales.
A continuación (ver Figura 5.) se explica como se
obtiene la función de transferencia en cuestión
mediante el análisis de cada operacional. Cada
operacional se denota con la letra U seguida de un
número.
184
Encuentro de Investigación en IE, 28 — 30 de Marzo, 2007
a) U1
Va = −Vin
Rf
Rin
Va = −Vin
10 KΩ
1KΩ
Va = −10Vin
b) U3
Vc = −Vout
Vc = −Vout
Rf
Rin
2KΩ
1KΩ
Vc = −2Vout
Figura 5. Obtención de la función de transferencia en la aplicación de cada
amplificador operacional.
f) Se sustituyen las ecuaciones encontradas para los
operacionales U3 y U4 en las operaciones
correspondientes a U5:
U3)
Vc = −2Vout
U4)
Vd = − SVout
U5)
Ve = −Vc − Vd
Ve = 2Vout + SVout
g) La operación anterior y la operación en U1 la
sustituimos en U6 como se muestra a continuación:
U5) Ve = 2Vout + SVout ,
Vout = − ( −10Vin ) − (2Vout + SVout )
c) U4
U1) Va = −10Vin
Vd = − RC
Ve = −( −2Vout ) − ( − SVout )
dVout
dt
Vd = −(1KΩ)(1KΩ) SVout ( S )
Vd = − SVout
U6
)
Vout = 10Vin − 2Vout − SVout
Vout = −Va − Ve
h) Por ultimo se despeja Vout como se muestra a
continuación y se obtiene la función de transferencia
solicitada:
+2Vout + SVout + Vout = 10Vin
( S + 3)Vout = 10Vin
d) U5
 Vc Vd 
Ve = − Rf 
+

 R8 R9 
Vd 
 Vc
Ve = −1KΩ
+

 1KΩ 1KΩ 
Ve = −Vc − Vd
e) U6
 Va Ve 
Vout= −Rf 
+

 R11 R12
 Va Ve 
Vout= −1KΩ
+

1KΩ 1KΩ 
Vout= −Va−Ve
Vout =
10Vin
( S + 3)
Vout
10
=
Vin
( S + 3)
En seguida se utilizó simulink para simular dicha
función de transferencia [9] tal y como se muestra
abajo (ver Figura 6.):
185
Encuentro de Investigación en IE, 28 — 30 de Marzo, 2007
matemáticamente como simulada en el software
simulink. Finalmente, y con el mismo método
didáctico, se realizó una aplicación mediante el uso de
OPAMs donde se puede observar físicamente todo el
resultado de la modelación teórica.
Figura 6. a) Señal de entrada, b) Respuesta en lazo cerrado de la
función de transferencia solicitada.
Para comprobar físicamente la función de
transferencia, se armó en protoboard el circuito de la
Figura 4, utilizando el siguiente material: 5
Amplificadores Operacionales LM 714 CN, 9
resistencias de 1KΩ, 1 resistencia de 10KΩ, 1
protoboard, Generador de ondas, 1 generador de
funciones, 1 osciloscopio, cable para proto, 1
resistencia de 2 KΩ, 1 capacitor de 1pF.
El circuito se armó, quedando de la siguiente forma
(ver Figura 7):
La metodología propuesta está de acuerdo a la
filosofía de enseñanza que se aplica en las aulas de la
Universidad del Valle de México; es decir en la
aplicación del modelo educativo PRAXIS, en el cual
se da prioridad al aprendizaje centrado en el alumno
bajo los principios de: aprender a aprender, aprender
a ser y aprender a hacer.
La propuesta de enseñanza aplicada a estudiantes de
las licenciaturas de Ing. Mecatrónica e Industrial y de
Sistemas ha dado buenos resultados, tanto en lo
motivacional como en lo académico, como se ha
podido mostrar en este trabajo.
Un punto de oportunidad detectado durante este
proceso es la observación en los alumnos de cierta
resistencia a seguir el método al inicio del curso,
prefiriéndose, sobre todo en esos momentos, mantener
una actitud pasiva sólo copiando del pizarrón, la cual
es una forma de actuar típica de la enseñanza con el
método expositivo tradicional.
REFERENCIAS
Figura 7.- Armado del circuito presentado en la Fig. 4
Finalmente los estudiantes observaron como varía la
respuesta a medida que se incrementa la frecuencia,
así como también se dieron cuenta que el capacitor
debía ser cambiado por uno de valor más pequeño, ya
que no se observaba el efecto deseado.
V. DISCUSIÓN Y CONCLUSIONES.
En este artículo se ha presentado una metodología que
se deriva del Aprendizaje Basado en Problemas
(ABP), para el estudio de la transformada de Laplace
aplicada a la solución de ecuaciones diferenciales, así
como el estudio de la función de transferencia, tanto
[1] www.samford.edu/pbl/
[2] www.udel.edu/pbl/As
[3] http://www.studygs.net/espanol/pbl.htm
[4]http://www.um.es/tonosdigital/znum6/estudios/Fde
ztoledo.htm
[5]http://biblio2.colmex.mx/bibdig/interdisciplinaried
ad/base2.htm
[6] López Campos C.E., Mendiola Santibáñez J.D.,
Loske Mehling A., “Aplicación del método de
secuenciación temática al análisis de contenidos
de los programas de estudio de la carrera de
ingeniería mecatrónica”, Primer Congreso
Interdisciplinario de la Universidad del Valle de
México, (2006).
[7] Ogata K., “Ingeniería de Control Moderna”,
Prentice Hall, (2002).
[8] Bolton W., “Mecatrónica, Sistemas de Control
Electrónico en la Ingeniería Mecánica y
Eléctrica”, Alfaomega, 2ª. Ed., (2001).
[9] Ogata K., “Problemas de Ingeniería de Control
utilizando Matlab”, Prentice Hall, (2000).