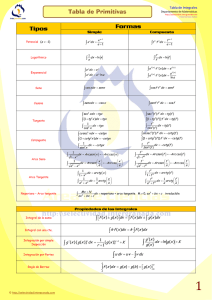
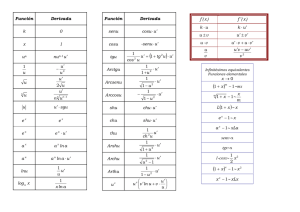
TEMA 4. FUNCIÓN REAL DE VARIABLE REAL Tabla de derivadas

TEMA 4. FUNCIÓN REAL DE VARIABLE REAL
Tabla de derivadas
f (x)  x m

f '( x )  mx m 1
f ( x )  u( x )m

f '( x )  mu( x )m 1 u '( x )
f ( x )  ax con a > 0

f '( x )  ax ln a
f ( x )  au( x ) con a > 0

f '( x )  au( x ) ln a u '( x )
f (x)  e x

f '( x )  e x
f ( x )  eu( x )

f '( x )  eu( x )u '( x )
f ( x )  loga x con a > 0

f ( x )  loga u( x ) con a > 0

f ( x )  ln x

f ( x )  ln u( x )

f ( x )  senx

1
x
u '( x )
f '( x ) 
u( x )
f '( x )  cos x
f ( x )  senu( x )

f '(x )  cos u( x ) u '(x )
f ( x )  cos x

f '( x )  senx
f ( x )  cosu( x )

f '( x )  -senu( x ) u '( x )
f ( x )  tgx

f '(x ) 
f ( x )  tgu(x )

f '( x ) 
f ( x )  cotgx

f '(x ) 
f ( x )  cotgu(x )

f ( x )  arcsenx

f '(x ) 
f ( x )  arcsenu(x )

f '( x ) 
f ( x )  arccos x

f '(x ) 
f ( x )  arccosu( x )

f '( x ) 
f ( x )  arctgx

f '( x ) 
f ( x )  arctgu( x )

f '(x ) 
f ( x )  arccotgx
f ( x )  arccotgu(x )


1
1 1
loga e 
ln a x
x
1
1 u '( x )
f '(x ) 
loga e u '( x ) 
u( x )
ln a u( x )
f '( x ) 
f '( x ) 
1
2
 1  tg2 x
cos x
u '(x )
cos2 u(x )
1


 1  tg2u( x ) u '(x )


  1  cotg2 x
sen2 x
u '( x )
f '( x ) 
  1  cotg2u( x) u '( x)
2
sen u( x )

f '( x ) 
f '(x ) 
1
1  x2
u '( x )
1  u( x )2
1
1  x2
u '( x )
1  u( x )2
1
1  x2
u '( x )
1  u( x )2
1
1  x2
u '( x )
1  u( x )2
