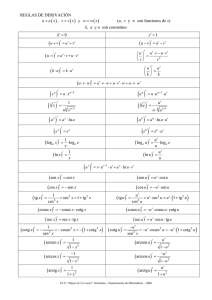
Tabla de Integrales
Anuncio

Tabla de Integrales Tabla de Primitivas Departamento de Matemáticas http://selectividad.intergranada.com © Raúl González Medina Formas Tipos Simple Potencial (a 1) x a dx 1 x dx Logarítmico Compuesta x a 1 a 1 f '·f f' ln x x f x e dx e x x a dx a ·ln a Exponencial cos xdx Seno senxdx Coseno 2 x Arco Seno 1 1x 1 2 2 2 x a x f' cos (f ) dx dx tgx 2 Arco Tangente a Neperiano – Arco tangente 2 2 cosf tg (f ) 2 2 f' dx cotgx Sen x x Arc cos a a 1 a f (x ) ln a co sec (f )·f 'dx cotg (f ) [1 cotg (f )]·f 'dx cotg (f ) dx Arcsen 1 x ·f '(x )dx 2 dx Arcsen x Arc cos x 2 f (x ) 2 2 1 a sec (f )·f 'dx tg (f ) [1 tg (f )]·f 'dx tg (f ) 2 sen ·f '(x )dx e f (x ) senf ·f 'dx co sec xdx cotgx (1 cotg x )dx cotgx Cotangente dx ln f f (x ) cos x 2 1 f a 1 a 1 cosf ·f 'dx senf 2 cos dx e senx sec xdx tgx (1 tg x )dx tgx Tangente a f' 1 f 2 f' 2 (f ) dx cotg (f ) dx Arcsen f Arc cos f f f dx Arcsen Arc cos a a a f 2 2 f' dx arctg x 1 f x 1 1 dx arctg a x2 a a 2 2 dx arctg f f f' 1 dx arctg a f 2 a Mx N dx neperiano + arco tangente M 0, ax2 bx c irreducible 2 bx c ax Propiedades de las Integrales f (x ) g (x )dx f (x )dx g (x )dx Integral de la suma k ·f (x )dx Integral con una cte. Integración por simple Inspección r g '(x )·[ g (x )] dx 1 [ g (x )]r 1 K r 1 a © http://selectividad.intergranada.com © http://selectividad.intergranada.com g'(x ) g (x ) dx ln g (x ) K u ·dv u ·v v ·du Integración por Partes Regla de Barrow k · f (x )dx f (x )dx b a g (a ) g (b ) g (x ) b 1