`fpfp −

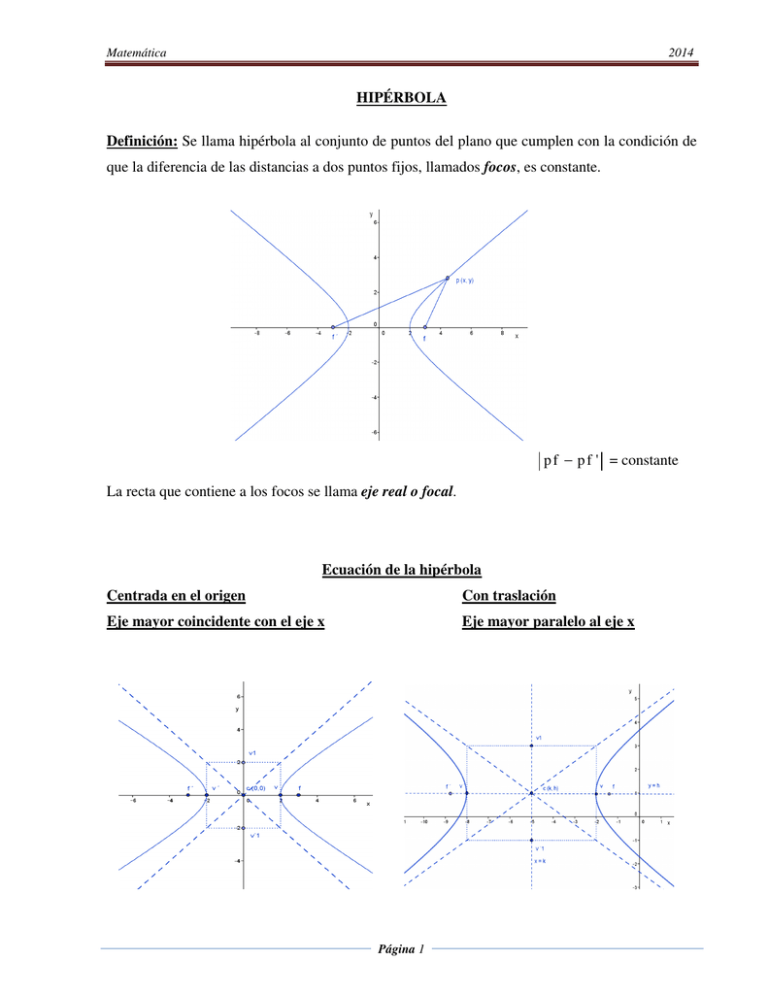
Matemática
2014
HIPÉRBOLA
Definición: Se llama hipérbola al conjunto de puntos del plano que cumplen con la condición de
que la diferencia de las distancias a dos puntos fijos, llamados focos, es constante.
p f − p f ' = constante
La recta que contiene a los focos se llama eje real o focal.
Ecuación de la hipérbola
Centrada en el origen
Con traslación
Eje mayor coincidente con el eje x
Eje mayor paralelo al eje x
Página 1
Matemática
2014
La ecuación canónica correspondiente, en cada caso, es:
x2
y2
− 2 =1
a2
b
(x − k) 2 (y − h) 2
−
=1
a2
b2
Centro c (0, 0)
Centro c (k, h)
Vértices v (a, 0) v ' (– a, 0)
Vértices v (k + a, h) v ' (k – a, h)
v1 (0, b) v1' (0, – b)
Focos
v1 (k, h + b) v1' (k, h – b)
f (c, 0) f ' (– c, 0)
Focos f (k + c, h) f ' (k – c, h)
Longitud del eje real o focal
Longitud del eje real o focal
v v' = 2 a
v v' = 2 a
Ecuación de la recta que contiene al eje
Ecuación de la recta que contiene al
real o focal
eje real o focal
y=0
Longitud del eje imaginario
v1 v'1 = 2 b
y=h
Longitud del eje imaginario
v1 v1' = 2 b
Ecuación de la recta que contiene al eje
Ecuación de la recta que contiene al
imaginario
eje imaginario
x=0
Ecuaciones de las asíntotas
y=
x=k
Ecuaciones de las asíntotas
b
b
x ; y=− x
a
a
y=
b
( x − k) + h
a
y=−
b
( x − k) + h
a
Las asíntotas de la hipérbola son las rectas que unen los vértices opuestos del rectángulo cuyo
centro está en el centro de la hipérbola y sus lados tienen longitud 2 a y 2 b.
Distancia focal f f ' = 2 c
Distancia focal f f ' = 2 c
Dominio Dom R = (– ∞, – a] ∪ [a, ∞)
Dominio
Dom R = (– ∞, k – a] ∪ [k + a, ∞)
Codominio Cod R = (– ∞, ∞)
Codominio Cod R = (– ∞, ∞)
Relación entre a, b y c
Consideremos el triángulo rectángulo o v p, llamando la hipotenusa c y los catetos a y b.
Página 2
Matemática
2014
c 2= b 2 + a 2
La relación pitagórica entre ellos es:
Excentricidad
Denotamos a la excentricidad con ε y definimos como ε = c / a y como c > a ⇒ ε > 1
Ejemplo:
Dada la expresión
9 x 2 – 36 y 2 – 324 = 0
a) ¿Cómo se denomina la gráfica?
b) Determine sus elementos.
c) Represente.
a) Como A ≠ C y de diferentes signos ⇒ se trata de una hipérbola.
b) 9 x 2 – 36 y 2 = 324 dividiendo en 324
⇒ obtenemos la ecuación canónica
x 2 y2
−
=1
36 9
Centro c (0, 0)
a 2 = 36 ⇒ a = 6
Vértices v (6, 0) v ' (– 6, 0)
b2= 9 ⇒ b=3
v1 (0, 3) v1' (0, – 3)
c 2 = a 2 + b 2 ⇒ c 2 = 36 + 9
c 2 = 45 ⇒ c =
Excentricidad
45
Focos f ( 45 , 0) f ' (– 45 , 0)
ε = c / a ⇒ ε = 45 / 5 > 1
Longitud del eje real o focal v v' = 12
Página 3
Matemática
2014
Longitud del eje imaginario v1 v1' = 6
Ecuación de la recta que contiene al eje real o focal
y=0
Ecuación de la recta que contiene al eje imaginario
x=0
Ecuaciones de las asíntotas y =
3
1
x ⇒ y= x
6
2
e
y=−
3
1
x ⇒ y=− x
6
2
c)
Ecuación de la hipérbola
Centrada en el origen
Con traslación
Eje real coincidente con el eje y
Eje real paralelo al eje y
Página 4
Matemática
2014
La ecuación canónica correspondiente, en cada caso, es:
y2
x2
−
=1
2
2
a
b
(x − k) 2 (y − h) 2
−
=1
a2
b2
Centro c (0, 0)
Centro c (k, h)
Vértices v (0, a) v' (0, – a)
Vértices v (k, h + a) v' (k, h – a)
v1 (b, 0) v1' (– b, 0)
Focos
v1 (k + b, h) v1' (k – b, h)
f (0, c) f ' (0, – c)
Longitud del eje real
Focos f (k, h + c) f ' (k, h – c)
v v' = 2 a
Longitud del eje real v v' = 2 a
Ecuación de la recta que contiene al eje
Ecuación de la recta que contiene al
real o focal
eje real o focal
x=0
Longitud del eje imaginario
v1 v'1 = 2 b
x=k
Longitud del eje imaginario
v1 v1' = 2 b
Ecuación de la recta que contiene al eje
Ecuación de la recta que contiene al
imaginario
eje imaginario y = h
y=0
Distancia focal f f ' = 2 c
Distancia focal f f ' = 2 c
Ecuaciones de las asíntotas
Ecuaciones de las asíntotas
y=
a
a
x ; y=− x
b
b
y=
a
( x − k) + h
b
y=−
a
( x − k) + h
b
Dominio Dom R = (– ∞, ∞)
Dominio Dom R = (– ∞, ∞)
Codominio
Codominio
Cod R = (– ∞, – a] ∪ [a, ∞)
Cod R = (– ∞, h – a] ∪ [h + a, ∞)
En la gráfica de una hipérbola puede ocurrir que a > b (en la generalidad de los casos que
vimos), que a < b ó que a = b.
Página 5
Matemática
2014
Hipérbolas conjugadas
Dos hipérbolas son conjugadas si el eje real de una de ellas es el conjugado de la otra.
Las ecuaciones de dos hipérbolas conjugadas con centro en (0, 0) y sus gráficas, son:
x2
y2
−
= 1 (1)
2
2
a
b
y2
x2
−
= 1 (2)
2
2
b
a
Página 6
Matemática
2014
(2)
(1)
Las ecuaciones de dos hipérbolas conjugadas con centro en (k, h) y sus gráficas, son:
(x − k) 2 (y − h) 2
−
=1
a2
b2
(1)
(y − h) 2 (x − k) 2
−
=1
b2
a2
(2)
(2)
( 1)
Ejemplos:
x2
y2
La hipérbola de ecuación
−
=1
25
9
es conjugada con la de ecuación
Página 7
y2
x2
−
=1
9
25
Matemática
2014
La hipérbola de ecuación
(x − 3) 2
(y + 2) 2
−
=1
4
16
es conjugada con la de ecuación
(y + 2) 2 (x − 3) 2
−
=1
16
4
Hipérbola equilátera rectangular
Es aquella que tiene los semiejes real e imaginario de igual longitud. Sus asíntotas son
perpendiculares.
Si el centro está en (0, 0), su ecuación sería
x2
a
2
y2
− 2 =1
a
Si el eje real es el eje x
Si el eje real es el eje y
x2–y2=a2
y2–x2=a2
Si el centro está en (k, h), su ecuación sería
(x – k) 2 – (y – h) 2 = a 2
(y – h) 2 – (x – k) 2 = a 2
(1)
Página 8
(2)
Matemática
2014
Ecuación general de la hipérbola
A partir de la ecuación canónica de la hipérbola:
(x − k) 2 (y − h) 2
−
=1
a2
b2
Desarrollando los cuadrados, acomodando términos e igualando a cero, obtenemos a la ecuación
general de la hipérbola:
Ax2+Cy2+Dx+Ey+F = 0
Condiciones de los coeficientes de la ecuación general de 2º grado para que su gráfica
represente una hipérbola (Sólo analizaremos los coeficientes A, B y C)
La ecuación general de 2º grado en las variables x e y es:
Ax2+Bxy+Cy2+Dx+Ey+F = 0
y
la ecuación general de la elipse:
A x 2 + C y 2 + D x + E y + F = 0.
Comparando los coeficientes de los términos correspondientes, deducimos que:
A ≠ 0 ∧ C ≠ 0, además A ≠ C en valor y signo.
Y el coeficiente B = 0.
Ejemplo:
Encuentre la ecuación de la hipérbola que satisface las siguientes condiciones:
f (– 2, 7), f ' (– 2, – 3) y ε = 5/3.
Conociendo las coordenadas de los focos sabemos que 2 c = 10 ∴ c = 5.
Página 9
Matemática
2014
Las coordenadas del centro serán: c (– 2, 2), punto medio entre los focos.
Además conocemos el valor de la excentricidad
ε = 5/3, como c = 5 y ε = c/a entonces
reemplazando e igualando, podemos obtener el valor de a:
5/a = 5/3 → a = 3.
Para poder escribir la ecuación canónica de la hipérbola necesitamos saber las coordenadas del
centro, los valores de a y b y además de la posición que tendrá la curva.
Sabiendo los valores de a y c, podemos obtener el valor de b, usando la relación pitagórica:
c 2= a 2 + b 2
→
b2 = c2
–
a2
→
b 2 = 25
–
9 = 16.
Los focos están en el eje mayor de la curva que contiene los vértices v y v ', y en este caso es
paralelo al eje y. El término positivo es el que contiene a la variable y
∴
(y − 2) 2 (x + 2) 2
−
=1
9
16
Ejemplo:
a) Escriba la ecuación de la hipérbola, cuya gráfica es:
b) Escriba las ecuaciones de sus asíntotas
a) Del gráfico: c (3, – 2) a = 4
b) y = 2 (x − 3) − 2
⇒
b=2
∴
(y + 2 ) 2 (x − 3) 2
−
=1
4
16
y = 2 x − 8 ; y = − 2 (x − 3) − 2
Página
10
⇒
y = − 2x + 4