recursion - UTN

Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
RECURSION
Veremos un nuevo mecanismo, una nueva técnica de diseño, para resolver
problemas: LA RECURSIÓN.
La recursión es una alternativa a la iteración o repetición, y aunque en
tiempo de ejecución y espacio de memoria ocupada la solución recursiva es menos
eficiente que la iterativa, existen numerosas situaciones en las que la recursividad
provee una solución más simple y natural a un problema.
La recursividad es una herramienta potente y útil que la aplicaremos:
- en la resolución de problemas que tengan naturaleza recursiva
- en reemplazo de la iteración cuando el lenguaje de programación elegido
NO posea ninguna estructura de control repetitiva
- cuando la solución iterativa sea de gran complejidad respecto de la
solución recursiva
¿Qué es recursión? Es una técnica que realiza una tarea T, haciendo otra
tarea T ‘ de la misma naturaleza que T, pero en algún sentido más pequeña que la
original .
De esta forma, un algoritmo recursivo expresa la solución de un problema
de tamaño N, en términos de una llamada o invocación a sí mismo. Cada invocación
se plantea sobre problemas de igual naturaleza que el original, pero de un tamaño
menor que N. Al ir reduciendo progresivamente la complejidad del problema a
resolver, llegará un momento en que la resolución será trivial y directa. Esta última
situación se denomina caso base. La forma en que se va reduciendo el tamaño del
problema original asegura que el caso base se alcance y por consiguiente, se llegue
a la solución esperada.
Un algoritmo recursivo (procedimiento o función) presenta las siguientes 3
características:
- se autoinvoca dentro de su propia definición, es decir se llama a sí
mismo dentro de su cuerpo (al menos una vez)
- presenta al menos un caso base o especial, donde se llevan a cabo
acciones distintas que aseguran la finalización del proceso y la obtención
de la solución
- en cada autoinvocación se resuelve un problema de igual naturaleza que
el original pero de menor tamaño. La reducción del tamaño del problema
asegura que se alcance el caso base.
Se deben hacer cuatro preguntas para construir una solución recursiva:
1.- Cómo representar el problema T en términos de un problema T ’ del
mismo tipo, pero más pequeño.
2.- Cómo reducir, en cada llamada recursiva, el tamaño del problema.
1
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
3.- Qué instancia del problema sirve como caso base.
4.- Qué manera de reducir el problema nos asegura que siempre será
alcanzado el caso base.
Apliquemos estas preguntas en el siguiente ejemplo: consideremos el
problema de buscar una palabra en un diccionario. Una búsqueda binaria se puede
formular como:
/*Buscar una palabra en el diccionario*/
Si diccionario tiene una sola página entonces
Ubicar la palabra en esa página
sino
Abrir diccionario en punto cercano a la mitad
Determinar a que mitad pertenece la palabra
Si la palabra pertenece a la primera mitad entonces
Buscar la palabra en la primera mitad del diccionario
sino
Buscar la palabra en la segunda mitad del diccionario
Finsi
finsi
La solución que hemos planteado está a un alto nivel de desarrollo, no nos
interesa ahora entrar en detalles de implementación. Lo que nos interesa es
examinar la estrategia de esta solución.
Hemos reducido el problema de buscar una palabra en el diccionario a
buscarla en una mitad del mismo.
Buscar en el diccionario
Buscar en la primera
mitad del diccionario
Buscar en la segunda
mitad del diccionario
- Una vez dividido el diccionario, está claro cual será la mitad en la que
debemos buscar y se buscará utilizando la misma estrategia.
- Hay un caso especial, que se maneja distinto de los demás, es el caso en
que el diccionario ha sido dividido tantas veces que tiene sólo una página. En este
punto el problema es suficientemente pequeño y se puede resolver directamente.
Este caso especial se llama caso base.
2
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Podemos ver esta forma de resolver problemas como dividir y conquistar: el
problema se resolvió primero dividiendo el diccionario en dos mitades y luego
conquistando la mitad apropiada. El problema más pequeño se resuelve aplicando la
misma estrategia.
Escribimos la solución como un procedimiento
para resaltar algunas
observaciones importantes.
Procedimiento Buscar (dic, pal)
Si diccionario tiene una sola página entonces
Ubicar la palabra en esa página
sino
Abrir diccionario en punto cercano a la mitad
Determinar a que mitad pertenece la palabra
Si la palabra pertenece a la primera mitad entonces
Buscar (primera mitad del dic, pal)
sino
Buscar (segunda mitad del dic, pal)
Finsi
Finsi
Observaciones:
1.- Una de las acciones de este procedimiento es llamarse a sí mismo. Es
decir, el procedimiento BUSCAR es llamado desde adentro del procedimiento
BUSCAR. Esto es lo que hace una solución recursiva.
2.- Cada llamada BUSCAR (diccionario, pal) pasa un diccionario de la mitad
de tamaño que el anterior. Es decir en cada llamada recursiva el tamaño del
diccionario se reduce. El problema de la búsqueda está siendo resuelto, resolviendo
otra de igual naturaleza pero más pequeño en tamaño.
3.- Hay un problema de búsqueda que resuelve en forma diferente. Cuando
el diccionario tiene una sola página, se resuelve por otro método (aquí se busca
directamente), este es el caso base. Cuando se alcanza el caso base, las llamadas
recursivas se detienen y el problema se resuelve directamente. Lo importante es
que la manera en la cual el tamaño del problema disminuye, asegura que el caso
base será alcanzado.
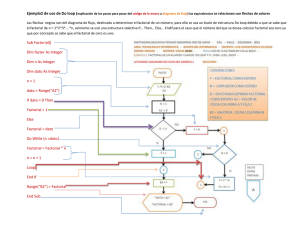
¿Cómo funciona la recursión en memoria?.
Traza de ejecución: método de la caja
Para analizar esta técnica de diseño desde el punto de vista del uso de
memoria veamos los siguientes ejemplos.
3
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Ejemplo 1: Cálculo del Factorial, se elige porque es fácil de entender y se ajusta
perfectamente al modelo dado.
Definición iterativa del factorial (con n entero positivo):
FACT (n) = n * (n-1) * (n-2) * ....* 1
FACT (0) = 1
y el factorial de un número negativo es indefinido.
Todos sabemos construir una solución iterativa para este problema
basándonos en esta definición. También podemos construir un solución recursiva
del factorial:
FACT (n) = n * FACT (n - 1)
Esta definición carece de un elemento importante, el caso base.
Como en el diccionario, un caso debe definirse diferente de todos los
demás, de lo contrario la recursión nunca se detiene.
El caso base en la recursión es el Factorial (0) el que se define simplemente
como 1.
Dado que n se asume positivo, decrementando en 1 cada vez que se llama al
factorial se sabe que siempre será alcanzado el caso base.
Definición recursiva del factorial:
1
si n = 0
Factorial (n)
n * Factorial (n -1) si n > 0
Estudiaremos los mecanismos de ejecución de esta función recursiva.
Si calculamos el Factorial (3), usando esta definición:
Factorial (3) = 3 * Factorial (2)
Factorial (2) = 2 * Factorial (1)
Factorial (1) = 1 * Factorial (0)
Factorial (0) = 1
Se alcanzó el caso base. La aplicación de la definición recursiva se detiene y
la información obtenida se puede usar para responder la pregunta original
¿factorial (3)?
Dado que:
Factorial (0) = 1 entonces, reemplazando en cada llamada
Factorial (1) = 1 * 1 = 1, entonces
Factorial (2) = 2 * 1 = 2, entonces
Factorial (3) = 3 * 2 = 6
4
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Es fácil construir una función a partir de la definición recursiva:
Function Factorial (n: entero) : entero
hacer
si (n=0) entonces Factorial :=1
sino Factorial := n * Factorial (n-1)
finsi
finhacer
finfunción
Esta función responde al modelo de solución recursiva.
1) La función Factorial se llama a sí misma
2) En cada llamada recursiva el número cuyo factorial se calcula se
disminuye en 1.
3) El Factorial (0) se maneja en forma distinta. Este caso base no produce
una llamada recursiva.
En principio la evaluación de un algoritmo recursivo no es más difícil que la
evaluación de cualquier otro algoritmo. En la práctica, sin embargo, el seguimiento
puede irse de las manos, para ello introducimos un método sistemático, llamado
método de la caja, para seguir la ejecución de funciones o procedimientos
recursivos.
Cada caja muestra la representación en memoria de la activación de una
unidad de programa y se denomina Registro de Activación de la unidad. Este
contiene toda la información necesaria para que dicha unidad pueda llevar a cabo su
ejecución: datos + información de control
* Cada llamada recursiva hecha al subprograma en el transcurso de la
ejecución va a generar una caja o registro de activación, que contendrá el
ambiente local del subprograma. Esto es, las variables y parámetros que se crean
en el llamado y se destruyen cuando se termina la ejecución.
Cada caja contendrá entonces:
-El valor de los parámetros formales.
-Las variables declaradas localmente (no existen en este ejemplo).
-Un lugar para el valor a ser retornado por cada llamada recursiva generada
a partir de la caja corriente (marcada con el rótulo).
-El valor de la función misma.
* Cuando se crea una nueva caja se dibuja una fecha desde la caja donde se
hizo la llamada hacia la nueva. Sobre la flecha se pone el nombre de la llamada
(rótulo) para indicar a donde se debe retornar.
5
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
* Comenzar la ejecución del cuerpo del subprograma con los valores
correspondientes al ámbito local de la caja corriente. Cuando termina la ejecución
de la caja corriente y se vuelve hacia atrás en las cajas, la anterior es ahora la
corriente y el nombre en la flecha indica el lugar a donde se debe retornar y
continuar la ejecución del subprograma. El valor calculado se coloca en el ítem
apropiado en la caja corriente.
Trabajando sobre este concepto vamos a seguir la Traza de Ejecución que resulta
de calcular el Factorial (3):
Llamada original: Factorial (3) comienza la ejecución
n
=3
A: Factorial (n-1) = ?
Factorial
=?
rótulo
En el punto A, se hace una llamada recursiva, y la nueva invocación de la función
Factorial comienza su ejecución.
n
=3
A: Factorial (n-1) = ?
Factorial
=?
A
A
n
=3
A: Factorial (n-1) = ?
Factorial (n-1)
=?
En el punto A, nuevamente se
hace una llamada recursiva, y la
nueva invocación de la función
Factorial comienza su ejecución.
n
=2
A: Factorial (n-1) = ?
Factorial
=?
n
=2
A: Factorial (n-1) = ?
Factorial
=?
A
n
= 13
A: Factorial (n-1) = ?
Factorial (n-1)
=?
Nuevamente, en el punto A, se hace una llamada recursiva, y la nueva invocación de
la función Factorial comienza su ejecución.
n
=3
A: Factorial (n-1) = ?
Factorial (n-1)
=?
A
n
=2
A: Factorial (n-1) = ?
Factorial
=?
A
n
= 13
A: Factorial (n-1) = ?
Factorial (n-1)
=?
A
n
= 03
A:
Factorial (n-1) = ?1
Factorial
Factorial (n-1)
=?
Se alcanza el caso base, por lo tanto la invocación de Factorial se completó y
pueden comenzar a resolverse las cajas. Se vuelve a la caja anterior y se retorna el
valor pendiente al punto del llamado (marcado con el rótulo A)
n
=3
A: Factorial (n-1) = ?
Factorial (n-1)
=?
A
n
=2
A: Factorial (n-1) = ?
Factorial
=?
6
A
n
= 13
A: Factorial (n-1) = ?1
Factorial (n-1)
= ?1
A
n
= 03
A: Factorial (n-1) = ?1
Factorial
Factorial (n-1)
=?
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
n
=3
A: Factorial (n-1) = ?
Factorial (n-1)
=?
A
n
=2
A: Factorial (n-1) = 1
Factorial
=2
n
=3
A: Factorial (n-1) = ?2
Factorial (n-1)
= 6?
A
n
=2
A: Factorial (n-1) =1
Factorial
=2
A
A
n
= 13
A: Factorial (n-1) = ?1
Factorial (n-1)
= 1?
n
= 13
A: Factorial (n-1)
(n-1)==1?
Factorial (n-1)
= 1?
A
A
n
= 03
A: Factorial (n-1) = ?1
Factorial
Factorial (n-1)
=?
n
= 03
A: Factorial (n-1) = ?1
Factorial
Factorial (n-1)
=?
Valor final retornado al programa principal: 6
Otra forma de representación gráfica del método de las caja (pila de ejecución):
Conclusión: Como se puede apreciar en los gráficos del ejemplo anterior, el espacio
de memoria necesario para ejecutar un algoritmo recursivo es mucho mayor que si
fuese un algoritmo iterativo. En un algoritmo recursivo se genera una caja o
registro de activación por cada llamada al mismo subprograma, representando en
memoria los datos necesarios para su ejecución tantas veces como sea invocado. En
un algoritmo iterativo solo existe una caja o registro de activación
correspondiente al algoritmo que contiene dicha iteración.
Ejemplo 2: Vamos a resolver de manera recursiva el problema de imprimir una
cadena de caracteres hacia atrás.
Para ello debemos responder las tres preguntas, es decir vamos a construir
la solución al problema de imprimir una cadena de longitud n hacia atrás en
términos de una cadena de longitud n -1. Esto indicaría que en cada paso recursivo
la longitud de la cadena se hace más chica. Entonces el problema de escribir una
“cadena muy pequeña” hacia atrás puede servir como caso degenerado. Una cadena
7
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
muy pequeña es la cadena vacía o nula, es decir la cadena de longitud cero.
Nuestro caso base es entonces imprimir una cadena nula y la solución a este
problema es no hacer nada (no hay nada que imprimir).
Ahora hay que determinar de qué manera se puede usar la solución de
imprimir hacia atrás un cadena de longitud n –1 para resolver el problema de
imprimir hacia atrás una cadena de longitud n. La cadena de longitud n –1 resulta
de quitar un carácter de la cadena original.
a) Veamos la siguiente solución aproximada:
Imprimir_ hacia_ atrás (S)
Si (S No es nula) entonces
Imprimir el último carácter de S
Imprimir_hacia_atrás (S menos el último carácter)
finsi
Las llamadas recursivas a Imprimir _hacia _atrás pasan sucesivamente
cadenas de longitud más chicas sacando siempre el último carácter del anterior,
entonces seguro se alcanzará el caso base (es decir la cadena nula).
Traza de ejecución usando el método de la caja:
S = ‘casa’
S=’casa’
Imprime ‘a’
S=’cas’
imprime ‘s’
S=’ca’
S=’c’
imprime ‘a’
imprime ‘c’
S=’’
no hace nada
Resultado  ‘asac’
B) Consideremos otra solución al problema, quitar el primer carácter de la cadena
en lugar del último. Analicemos la siguiente solución:
Imprimir_ hacia_ atrás (S)
Si (S No es nula) entonces
Imprimir el primer carácter de S
Imprimir_hacia_atrás (S menos el primer carácter)
finsi
¿Hace lo que se espera? No, la recursión no es mágica, se debe formular
correctamente la solución. ¿Dónde está el error?
Veamos la solución recursiva correcta:
8
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Imprimir_ hacia_ atrás (S)
Si (S No es nula) entonces
Imprimir_hacia_atrás (S menos el primer carácter)
Imprimir el primer carácter de S
finsi
Esto significa que escribimos el primer carácter recién cuando todo el resto
ya ha sido escrito.
Traza de Ejecución de Escribir_ hacia_ atrás 2: en cada caja, luego del llamado
recursivo imprime el 1º carácter
S=’casa’
imprime ‘c’
S=’asa’
imprime ‘a’
S=’sa’
S=’a’
imprime ‘s’
imprime ‘a’
S=’’
no hace nada
Resultado  ‘asac’
El resultado es el mismo que con la otra solución, imprime “asac” pero la
secuencia de cadenas que se va generando es diferente. La diferencia en la
secuencia de valores se compensa por el carácter que se imprime y en el momento
en que se imprime. En la primera solución se imprime antes de generar una nueva
caja y en la segunda al salir de la caja antes de retornar de una llamada recursiva.
El objetivo de este ejemplo es demostrar que podemos tener dos
estrategias diferentes (o más) para realizar las mismas tareas.
n
Ejemplo 3: Resolver X
Ahora veremos como podemos encontrar una solución recursiva, es decir
cómo podemos definir X a la n-ésima potencia en términos de X a una potencia más
pequeña. La respuesta está dada en las reglas de exponenciación:
XN = X * X N-1
Esto es, podemos calcular X a la N, calculando X a la N-1
y multiplicando su resultado por X.
Nuestra solución recursiva tiene un solo caso base: X0 = 1
forma:
Entonces podemos formular nuestra solución recursiva de la siguiente
X0 = 1
XN = X * X
N-1
,
si N > 0
El caso base (N=0) siempre se alcanzará.
Función potencia (x : entero 2 ; N : entero 1);
Hacer
9
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Si N=0 entonces
potencia :=1
sino
potencia := X * potencia (X, N-1)
finsi
finhacer
finfunción
Tipos de recursión.
La recursión puede ser:
 Directa: si el algoritmo recursivo presenta una o más llamadas
recursivas en su propio cuerpo.
o Simple: si presenta una sola llamada recursiva
El factorial de un nº entero positivo:
Fact(0):=1
Fact(N):= N* fact(N-1), si N>0
o Múltiple: si presenta dos o más llamados recursivos
La serie de Fibonacci:
F(0):=0
F(1):=1
F(N):= F(N-1) + F(N-2), si N>1
o Anidada: si presenta un llamado recursivo como argumento de
una llamada recursiva
La función de Ackerman:
A(m,n):= n +1, si m=0
A(m,n):=A(m-1,1), si n=0
A(m,n):=A(m-1, A(m,n-1)), si m>0 y n>0

Indirecta o cruzada: si el llamado recursivo no aparece en su cuerpo
sino que se da a través de la invocación de un algoritmo auxiliar. Es
decir, si un algoritmo A invoca a otro algoritmo B y recíprocamente,
el algoritmo B invoca al algoritmo A.
Programa Ejemplo
Procedimiento A
Hacer
….
B
….
finhacer
finProcedimiento
10
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Procedimiento B
Hacer
…
A
….
…
finhacer
finProcedimiento
……
…..
finprograma
Ventajas y desventajas del uso de recursión.
Las soluciones recursivas son elegantes y simples para problemas de
complejidad grande, presentan un diseño muy bien estructurado y modular.
Comparadas con la solución iterativa contienen menos líneas de código y son más
fáciles de analizar y leer.
Desde el punto de vista de la eficiencia, demandan más tiempo de ejecución
que las soluciones iterativas y mayor espacio de memoria debido a que cada llamado
recursivo genera una copia independiente de las variables declaradas en dicho
algoritmo, almacenadas en una zona de la memoria Ram denominadas Registro de
Activación.
Aplicación y uso.
Esta técnica de diseño se aplica fundamentalmente en lenguajes de
programación que carecen de estructuras de control repetitivas como ocurre en
aquellos pertenecientes a la programación Funcional (LISP, HASKELL) y Lógica
(APL,PROLOG). Es de amplio uso en Inteligencia Artificial como demostrador de
teoremas, y en el área matemática para los cálculos combinatorios.
Bibliografía de referencia:
- Luis Joyanes Aguilar, 2003. Fundamentos de Programación. Algoritmos y
Estructuras de Datos. Ed. Mc Graw Hill
- Luis Joyanes Aguilar, 2008. Fundamentos de Programación. Algoritmos, Estructuras
de Datos y Objetos. Ed. Mc Graw Hill
- Luis Joyanes Aguilar, 2006. Programación en Turbo/Borland Pascal 7.0. Ed. Mc
Graw Hill
- De Giusti, Madoz y otros,1998. Algoritmos, datos y programas. Conceptos básicos.
Ed. Exacta.
11
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Anexo. Ejemplos de aplicación sobre Arreglos y Listas.
1- Imprimir un vector invertido.
Procedimiento impri (V:vector; Pos: entero 2)
Hacer
Si (Pos >= 1) entonces
Imprimir: V[pos]
Impri(V, pos -1)
finsi
finhacer
finfuncion
Invocación desde el prog principal con un vector Vec de 5 elementos recorrido
desde el final: impri(Vec, 5)
2- Sumar los elementos de un vector que se encuentren en posiciones pares.
Funcion Suma (V:vector; Dim: entero 2; Pos: entero 2): entero 3
Variables
I:entero 2
Hacer
Si (Pos <= Dim) entonces
I:= pos – ENT(pos/2)
Si (I=0) entonces {está en posición par}
suma:= V[pos] + suma(V, Dim, pos + 1)
sino
suma:= suma(V, Dim, pos +1)
finsi
sino
suma:= o
{inicializa el valor de la función suma}
finsi
finhacer
finfuncion
Invocación desde el prog principal con un vector Vec de 5 elementos y a partir de
la 1º posición:
s:= suma(Vec, 5, 1)
3- Buscar el máximo elemento de un vector.
Funcion maximo (V:vector; Pos: entero 2): entero 3
Variables
m:entero 2
12
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Hacer
Si (Pos > 1) entonces
m:= máximo(V, pos – 1)
{busco el máximo del resto del vector}
si (m < V[pos]) entonces
{el elem actual es mayor que el máximo}
máximo:= V[pos]
finsi
sino
máximo:= V[1]
{el máximo es el 1º elemento}
finsi
finhacer
finfuncion
Invocación desde el prog principal:
max:= máximo(Vec,5)
4- Recuperar el contenido del i-ésimo elemento de una lista encadenada de
enteros. Suponga que i > 1 y que la lista contiene al menos i nodos.
Funcion retorna (pc:lista; i:entero 2; pos: entero 2): entero 2
Hacer
Si (pc <> nil) entonces
Si ( i=pos) entonces
retorna:= pc^.nro
Sino
retorna:= retorna( pc^.psig, i, pos + 1)
Finsi
Finsi
Finhacer
finfuncion
Invocación desde el prog principal, suponiendo una lista L ya cargada de números y
que se desea recuperar el 3º elemento de la misma:
el:=retorna (L, 3, 1)
5- Escribir una función que recibe como parámetro una lista de dígitos que van
del 1 al 9, y debe retornar el número que se obtiene a partir de sumar los
dígitos pares y restar los dígitos impares.
Ejemplo: dada la siguiente lista: 8512 (cada dígito está en un nodo), la función
retorna 2, pues 8-5+1-2=2.
Funcion opera (pc:lista): entero 3
Variables
I: entero 2
13
Apuntes teóricos
Año 2013
Prof. Lic. María Gabriela Cerra
Hacer
Si (pc <> nil) entonces
I:= pc^.nro – ENT(pc^.nro/2)
Si ( i=o) entonces
{el elem es par}
opera:= opera(pc^.psig) + pc^.nro
Sino
opera:= opera(pc^.psig) - pc^.nro
Finsi
Sino
opera:=0
Finsi
Finhacer
finfuncion
Invocación desde el prog principal, suponiendo una lista L cargada:
tot:=opera(L)
6- Eliminar de una lista encadenada de DNI un elemento en particular.
Procedimiento elim ( ref L:lista; pa: lista; pc:lista; dni: entero 8)
Hacer
Si (pc <> nil) entonces
Si ( pc^.nro= dni) entonces
{es el DNI a borrar}
Si (pa =nil) entonces
{borra el 1º elem}
L:= pc^.psig
Sino
{borra en el cuerpo}
pa^.psig:= pc^.psig
finsi
liberar(pc)
{libera la memoria de ese nodo}
Sino
elim(L, pa^.psig, pc^.psig, dni)
Finsi
Finhacer
finfuncion
Invocación desde el prog principal, suponiendo una lista Lis cargada e inicializados
pa=nil , pc=Lis y el valor del dni a buscar en doc:
Elim( Lis, nil, Lis, doc)
14