Se tiene la función objetivo f(x, y) = 3x + 4y y las restricciones: x
Anuncio

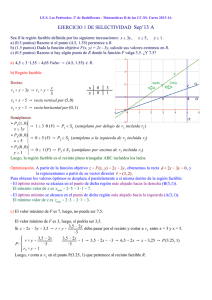
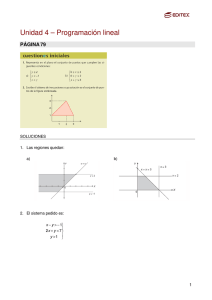
CANARIAS / SEPTIEMBRE 02. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / ÁLGEBRA / PRUEBA A / PREGUNTA 5 Se tiene la función objetivo f(x, y) = 3x + 4y y las restricciones: x ≥ 0; y ≥ 0; x ≤ y; x + y ≥ 2 Se pide: a) Representar la región de posibles soluciones. b) Hallar el punto de la región donde la función objetivo se minimiza. c) ¿Puede alcanzar la función objetivo el máximo en esa región? Solución: a) La región factible es la sombreada en la siguiente figura. b) Las rectas de nivel asociadas a la función objetivo son 3x + 4y = k; trasladándolas hacia la derecha su nivel aumenta, si se trasladan hacia la izquierda, disminuye. El punto Q es el último punto de la región factible en contacto con esas rectas de nivel. Por tanto, en ese punto se da el mínimo pedido. Las coordenadas de Q son (1, 1). c) Como las rectas pueden trasladarse indefinidamente hacia la derecha en contacto con la región factible, la función objetivo no alcanza un valor máximo en esa región. www.profes.net es un servicio gratuito de Ediciones SM