Resumen que puede usarse en el examen Tema 2. Optimización

Resumen que puede usarse en el examen
Tema 2. Optimización sobre un conjunto convexo.
Min f(x)
s.a. x ∈ X
f continuamente diferenciable sobre X ⊆ ! n , convexo, cerrado no vacío.
Propiedad 1
Sea C un convexo de ! n no vacío y f : C → ! una función convexa, entonces los
conjuntos de nivel inferior L f (α ) = {x ∈ C : f ( x ) ≤ α } son convexos para cualquier escalar
α ∈! .
Propiedad 2
Dada una colección de convexos {Ci : i ∈ I } , su intersección ∩i∈I Ci es un convexo.
Condiciones de optimalidad.
Proposición
(a) Si x* es un mínimo local de f sobre el convexo X , entonces
∇f ( x*)T ( x − x*) ≥ 0 ∀x ∈ X
(b) Si además f es convexa sobre X, la condición anterior es suficiente para asegurar que x*
minimiza f sobre X.
Proyección sobre un convexo cerrado X.
Teorema
(a) Para cada z ∈ ! n existe un único x* ∈ X que minimiza z − x sobre X. Éste vector es la
proyección de z sobre X y se denota mediante [ z ] .
+
(b) Dado z ∈ ! n , un vector x* ∈ X es la proyección de z sobre X, si y solo si:
( z − x*)T ( x − x*) ≤ 0 ∀x ∈ X .
(c) La aplicación f : ! n → ! n definida por f ( x) = [ x ] es contínua y no expansiva.
+
(d) Si X es un subespacio, un vector x* ∈ X es la proyección de z si y solo si
( z − x*)T x = 0 ∀x ∈ X
Métodos de direcciones factibles
Definición. Dado x k , una dirección factible en x k es un vector d k ≠ 0n tal que
∃δ > 0 : ∀α ∈ [0, δ ], x k + α d k ∈ X .
En estos métodos se comienza desde una solución factible x 0 y se genera una sucesión de
vectores factibles {x k } como x k +1 = x k + α k d k siendo d k una dirección de descenso factible
en x k y α k la longitud de salto adecuada.
Métodos de proyección del gradiente
El más sencillo genera una sucesión de iterados de la siguiente forma:
+
x k +1 = x k + α k ( x k − x k ) α k ∈ (0,1] , siendo x k =  x k − s k ∇f ( x k )  y s k > 0, ∀k
Para calcular la longitud de salto puede utilizarse la regla de minimización limitada o la
regla de Armijo para direcciones factibles.
Suboptimización en variedades
Min f(x)
s.a. aTj x ≤ b j j = 1,..., r
Hipótesis: Para cada x ∈ X el conjunto de vectores {a j : j ∈ A( x)} es linealmente
independiente, siendo A( x) = { j : aTj x = b j } (conjunto de índices de las restricciones activas)
Esquema general
Dado x k ∈ X se busca una dirección factible de descenso d k en el subespacio
S ( x k ) = {d : aTj d = 0 ∀j ∈ A( x k )}
(a) Si existe dicha dirección d k ∈ S ( x k ) factible de descenso, x k +1 = x k + α k d k y α k se
calcula en el intervalo {α > 0 : x k + α d k ∈ X }
(b) Si no existe ninguna, x k es estacionario sobre la variedad x k + S ( x k )
•
b1) Si x k es estacionario sobre X = {x : aTj x ≤ b j j = 1,..., r} el algoritmo para.
•
b2) Si x k no es estacionario sobre X, puede relajarse una de las restricciones j y se
obtiene una dirección factible de descenso en el subespacio
S ( x k ) = {d : aTj d = 0 ∀j ∈ A( x k ) ! { j }}
Para determinar d k ∈ S ( x k ) dirección factible de descenso se resuelven problemas
cuadráticos de la forma:
1
(P1) Min ∇f ( x k )T d + d T H k d
2
T
s.a. a j d = 0 j ∈ A( x k )
con H k matriz simétrica definida positiva.
La solución óptima de éste problema puede verse como la proyección a escala H k del
gradiente ∇f ( x k ) sobre el subespacio S ( x k ) , entonces d k = −( H k ) −1 (∇f ( x k ) + ( Ak )T µ ) ,
donde µ = − Ak ( H k ) −1 ( Ak )T )−1 Ak ( H k ) −1 ∇f ( x k ) y Ak es una matriz cuyas filas son los
vectores a j j ∈ A( x k ) .
Tenemos que: d k = 0n ⇔ ∇f ( x k ) + ( Ak )T µ = 0n ⇔ ∃µ j , j ∈ A( x k ) : ∇f ( x k ) +
∑
µ j a j = 0n
j∈A ( x k )
Entonces x k es estacionario sobre X si y solo si µ j ≥ 0, ∀j ∈ A( x k ) .
Por tanto, si d k = 0n y x k no es estacionario, existirá algún índice j tal que µ j < 0
Proposición
En las condiciones actuales ( ∇f ( x k ) + ( Ak )T µ = 0 n , µ j < 0) , sea d k la única solución
óptima del problema :
1
(P2) Min ∇f ( x k )T d + d T H k d
2
s.a aTj d = 0 j ∈ A( x k ) ! { j }
H k matriz definida positiva
Entonces d k es una dirección factible de descenso en x k .
Programación Cuadrática
1 T
x Qx + cT x
2
s.a. aTj x ≤ b j j = 1,..., r
Min
Las matrices H k y H k se toman iguales a Q.
Acerca del cálculo de la longitud de salto a lo largo de una dirección de descenso:
Si d k ≠ 0n , comprobaremos si x k + d k ∈ X , en cuyo caso x k +1 = x k + d k , si x k + d k ∉ X ,
entonces x k +1 = x k + α k d k , siendo α k = max {α > 0 : x k + α d k ∈ X } , por tanto
 bˆ

α k = min i  i : dˆi > 0 
ˆ

 di
T
k
siendo dˆ j = a j d j ∉ A( x k ), bˆ j = b j − aTj x k .
¿Por que no puede suceder que dˆ j ≤ 0 ∀j ∉ A( x k ) ?
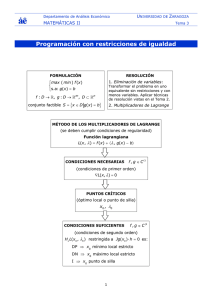
Tema 3. Teoría de los multiplicadores de Lagrange.
Condiciones necesarias para restricciones de igualdad
Consideremos el problema:
(P) Min f(x)
s.a. hi(x) = 0 i=1,...,m
f : ! n → !, hi : ! n → ! continuamente diferenciables.
Teorema de los multiplicadores de Lagrange
Sea x* un mínimo local de (P) y supongamos que los gradientes de las restricciones
{∇hi ( x*) : i = 1,..., m} son linealmente independientes.
(i)
Entonces, existe un único vector λ* = (λ1*,..., λm *)T llamado vector de los
m
multiplicadores de Lagrange, tal que ∇f ( x*) + ∑ λi * ∇hi ( x*) = 0 n
i =1
(ii)
Si, además f y h son dos veces continuamente diferenciables, se tiene que:
m
y T (∇ 2 f ( x*) + ∑ λi * ∇ 2 hi ( x*)) y ≥ 0 ∀y ∈ V ( x*) , siendo V(x*) el subespacio
i =1
de las variaciones factibles de primer orden: V ( x*) = { y : ∇hi ( x*)T y = 0 i=1,...,m}
Definición. Función lagrangiana
m
L : ! n+ m → ! , definida como L( x, λ ) = f ( x) + ∑ λi hi ( x)
i =1
Condiciones suficientes para restricciones de igualdad
Proposición.
Supongamos que f y h son dos veces continuamente diferenciables. Sean x* ∈ ! n y
λ* ∈ ! m , que satisfacen:
∇ x L( x*, λ*) = 0 n ∇ λ L( x*, λ*) = 0 m
(1)
y T ∇ 2xx L ( x*) y > 0 ∀y ≠ 0n tal que ∇h( x*)T y = 0
(2)
Entonces x* es un mínimo local estricto de f restringido a h(x) =0m . De hecho, existen
escalares γ>0 y ε>0 tales que
γ
2
f ( x) ≥ f ( x*) + x − x * ∀x : h( x) = 0m y x − x * < ε
2
La función lagrangiana aumentada
Dado cualquier escalar c, se define la función lagrangiana aumentada
m
c
2
Lc ( x, λ ) = f ( x) + ∑ λi hi ( x) + h( x)
2
i =1
Restricciones de desigualdad: condiciones de K-K-T
Consideremos el problema más general:
(ICP) Min f(x)
s.a. hi(x) = 0 i=1,...,m
g j ( x) ≤ 0 j = 1,..., r
f, hi y gj funciones continuamente diferenciables.
•
Dada una solución factible x el conjunto de restricciones de desigualdad activas se
denota A(x) = { j : g j ( x) = 0} .
•
Una solución factible es regular si el conjunto de vectores siguiente es linealmente
independiente: {∇hi ( x ), i = 1,..., m, ∇g j ( x), j ∈ A( x)}
•
Para (ICP) la función lagrangiana se define: L( x, λ , µ ) = f ( x) + ∑ λi hi ( x) + ∑ µ j g j ( x)
m
r
i =1
j =1
Condiciones necesarias de optimalidad
Sea x* un mínimo local de (ICP) que es regular.
(1) Entonces, existe un único vector (λ *, µ *) , siendo λ* = (λ1*,..., λm *)T ,
µ * = ( µ1*,..., µ r *)T llamado vector de los multiplicadores de Lagrange, tal que
∇ x L( x*, λ*, µ *) = 0n µ j ≥ 0 j = 1,..., r y µ j = 0 si j ∉ A( x*)
[ ( x*, λ*, µ *) es un punto de Karush, Kuhn y Tucker para (ICP)]
(2) Si, además f ,g y h son dos veces continuamente diferenciables, se tiene que:
y T ∇ xx L ( x*, λ*, µ *) y ≥ 0 ∀y ∈ V(x*) siendo
2
V ( x*) = { y : ∇hi ( x*)T y = 0 i=1,...,m, ∇g j ( x*)T y = 0, j ∈ A( x*)}
Condiciones suficientes de optimalidad
Sean x* ∈ ! n , λ* ∈ ! m , µ * ∈ ! r tales que:
h( x*) = 0m , g ( x*) ≤ 0r
∇ x L( x*, λ*, µ *) = 0n µ j ≥ 0 j = 1,..., r y µ j = 0 si j ∉ A( x*)
y también verifican que
y T ∇ xx L ( x*, λ*, µ *) y > 0 ∀y ∈ V(x*) y ≠ 0n siendo
2
V ( x*) = { y : ∇hi ( x*)T y = 0 i=1,...,m, ∇g j ( x*)T y = 0, j ∈ A( x*)} .
Supongamos que µ j > 0 ∀j ∈ A( x*) , entonces x* es mínimo local estricto de (ICP).
Tema 4. Métodos basados en el uso de las penalizaciones.
1. Métodos de barrera
(P)
Min f(x)
s.a. gj(x)≤0 j=1,...,r
x∈X X ⊆ ! n cerrado
f y gj continuas
Sucesión de parámetros {ε k } que verifican 0 < ε k +1 < ε k , k = 0,1, ..., con ε k → 0
Hallar x(ε k ) := arg min x∈S { f ( x) + ε k B( x)} k = 0,1, ..., siendo
S = {x ∈ X : g j ( x) < 0, j = 1,..., r} y B(x) la función barrera que está definida en S ≠ ∅ , es
continua y tiende a ∞ si alguna de las restricciones se aproxima a 0. Las más habituales:
r
r
1
B( x) = −∑ ln(− g j ( x)) y B( x) = −∑
j =1 g j ( x)
j =1
Proposición.
Cada punto límite de la sucesión {x k }
k ≥0
generada mediante un método de barrera es un
mínimo global de (P)
2. Métodos de penalización y de los multiplicadores
(P)
Min f(x)
s.a. hi(x)≤0 i=1,...,m
x∈X X ⊆ ! n
Lagrangiano aumentado: Lc ( x, λ ) = f ( x) + λ T h( x) +
c
2
h( x) , c>0
2
Proposición.
Supongamos que f y h son continuas y X un conjunto cerrado, también suponemos que
{x ∈ X : h( x) = 0m } ≠ ∅ . Para k=0, 1,..., sea x k un mínimo global del problema
Min Lck ( x, λ k )
s.a. x ∈ X
siendo {λ k } una sucesión acotada, 0<ck<ck+1 ∀k y {c k } → ∞ .
Entonces cada punto límite de la sucesión {x k } es un mínimo global de (P).
Esquema numérico del SUMT
Inicializar: Elegir ε>0, β∈[4, 10],, c0>0 y x0 ∈ ! n .Hacer k = 0
Etapa1: Empezando en xk resolver el problema
ck
2
Min Lck ( x, 0) = f ( x ) +
h( x )
2
Llamar xk+1 a la solución óptima del problema irrestringido
2
ck
Etapa 2: Si
h( x k +1 ) < ε , entonces parar.
2
En otro caso hacer c k +1 = β c k , k = k+1 y repetir la etapa 1.
Esquema numérico del método de los multiplicadores (ALAG)
Inicializar: Elegir ε>0, β∈[5, 10], c0>0, λ0 ∈ ! m . Tomar x0= 0n Hacer k = 0
Minimización de la función de penalización
Tomando como solución inicial xk, resolver el problema Min Lck ( x, λ k ) y llamar xk+1 a la
solución óptima obtenida
Si h( x k +1 ) < ε , parar y xk+1= x* es mínimo local del problema restringido.
Si h( x k +1 ) ≥ 0.25 h( x k ) , reemplazar c k por c k +1 = β c k , λ k +1 = λ k y repetir ésta etapa.
Si h( x k +1 ) < 0.25 h( x k ) , actualizar los multiplicadores λ k +1 = λ k + c k h( x k ) , y c k +1 = c k y
repetir ésta etapa.
Lck ( x, λ k ) = f ( x ) + (λ k )T h( x ) +
ck
h( x )
2
2
3. Métodos de Lagrange-Newton y programación cuadrática secuencial.
Método tipo Newton para problemas con restricciones de igualdad
Resolver el sistema lagrangiano:
∇f ( x ) + ∇h ( x ) λ = 0 n 
 ⇔ ∇L( x, λ ) = 0 n+ m
h( x ) = 0m

mediante el método de Newton : x k +1 = x k + ∆x k y λ k +1 = λ k + ∆λ k , donde ( x k , λ k ) se
obtiene resolviendo el sistema de ecuaciones:
 ∆x k 
∇ 2 L( x k , λ k )  k  = −∇L( x k , λ k ) (1)
 ∆λ 
Bajo ciertas condiciones sobre x* (mínimo local regular) se puede asegurar que, en un
entorno suyo, los puntos generados mediante (1) estan bien definidos . En éste caso
 Hk
 ∇ x L( x k , λ k ) 
Nk 
2
k
k
k
k
∇L ( x , λ ) = 

 y ∇ L( x , λ ) =  k T
k
 h( x ) 
 ( N ) 0 mxm 
siendo
H k = ∇ 2xx L( x k , λ k ) = ∇ 2 f ( x k ) + ∑ λik ∇ 2 hi ( x k ) y N k = ∇h( x k ) = (∇h1 ( x k ),..., ∇hm ( x k ) )
m
i =1
Si H k es invertible y el rango de N k es m, podemos obtener una expresión más explícita
para la iteración de Newton:
λ k +1 = (( N k )T ( H k ) −1 ( N k ))−1 (h( x k ) − ( N k )T ( H k )−1 ∇f ( x k ))
x k +1 = x k − ( H k ) −1 ∇ x L( x k , λ k +1 )
Programación Cuadrática Secuencial (SQP)
Conocido ( x k , λ k ) se determina (∆x k , λ k +1 ) resolviendo el problema cuadrático:
1
PC ( x k , λ k ) Min ∇f ( x k )T ∆x + ∆xT H k ∆x
2
k
k T
s.a. h( x ) + ( N ) ∆x = 0m
Extensión para incluir restricciones de desigualdad:
1
PC ( x k , λ k , µ k ) Min ∇f ( x k )T ∆x + ∆xT H k ∆x
2
k
s.a. hi ( x ) + ∇hi ( x k )T ∆x = 0 i = 1,..., m
g j ( x k ) + ∇g j ( x k )T ∆x ≤ 0 j = 1,..., r
m
r
i =1
j =1
siendo H k = ∇ 2xx L( x k , λ k ) = ∇ 2 f ( x k ) + ∑ λik ∇ 2 hi ( x k ) + ∑ µ kj ∇ 2 g j ( x k )