Te I σ= K.ºm.s J 1067,5 ⋅ =σ

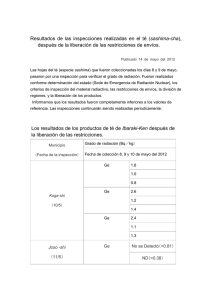
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
14
RADIACIÓN TÉRMICA.
Alrededor de 1900 se obtiene experimentalmente que la intensidad de la radiación emitida por un cuerpo
en función de la longitud de onda venía dada por una distribución como la que se muestra a continuación
para una determinada temperatura.
Con características que variaban con la temperatura como se muestra en la figura siguiente para el rango
térmico que en ella se indica.
Las primeras determinaciones realizadas por Stefan y Boltzman demostraban que la energía total emitida
estaba relacionada con la temperatura mediante:
I T = eσT 4
Conocida como Ley de Stefan-Boltzman, donde sigma es una constante universal, esto es independiente
del cuerpo considerado, conocida como constante de Stefan - Boltzman y cuyo valor en el sistema MKS
es:
σ = 5,67 ⋅ 10 − 8
J
s.m 2 .º K 4
Y donde la constante restante, conocida como emicividad, depende del cuerpo en consideración y tiene
valores comprendidos entre:
- 55 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
0 < e ≤1
Correspondiendo el valor unitario a lo que se conoce como Cuerpo Negro siendo este, aquel que es capas
de absorber la totalidad de la radiación que sobre el mismo inciden.
Otra conclusión que resulta de un análisis de las curvas mostradas anteriormente, muestra que la longitud
de onda a la que se produce la máxima emisión es inversamente proporcional a la temperatura del cuerpo,
como se lo puede apreciar claramente en la figura anterior, fenómeno conocido como Desplazamiento de
Wien, que formalmente puede expresarse como.
λ max ∝
1
T
Los primeros intentos para obtener una expresión formal del fenómeno en consideración se realizaron
suponiendo que la radiación observada estaba originada en osciladores atómicos que podrían encontrarse en
cualquier estado energético, desde cero a infinito, con una probabilidad de encontrarse en un estado
energético determinado que dependía de la temperatura según la expresión conocida como Distribución de
Probabilidades de Boltzman, que formalmente se indica a continuación:
P(ε) = Ae
−
ε
kT
Donde ( k ) es una constante universal, conocida como Constante de Boltzman, cuyo valor en el sistema
MKS, es:
k = 1,38 ⋅ 10 − 23 J / º K
Y cuya gráfica cualitativa se muestra a continuación para valores crecientes de la temperatura, en cuyo caso
se incremente la probabilidad de encontrar osciladores en estados energéticos superiores.
Teniendo en cuenta estas conclusiones y suponiendo, como ya lo mencionáramos, continuo al espectro
energético en que podían encontrarse los osciladores responsables de la emisión de radiación, no se
pudieron encontrar expresiones formales para la intensidad de la radiación emitida que dieran lugar a
resultados coincidentes con los obtenidos experimentalmente.
Con el propósito de arribar a una expresión compatible con los resultados experimentales, en 1900 Max
Planck propone para los osciladores atómicos un espectro energético discreto tal que estos solo
podrían encontrarse en niveles de energía que fueran múltiplos enteros de un valor mínimo al que
identifico como "quantum” de energía con lo que, y respetando la ley de distribución propuesta por
- 56 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
Boltzman indicada anteriormente, obtiene una expresión formal para la intensidad de la radiación en
función de la longitud de onda compatible con los resultados experimentales, que formalmente se muestra a
continuación.
I(λ ) =
8πhc
1
λ5 e hc λkT − 1
Donde ( h ) es una constante, conocida como constante de Planck, cuyo valor, determinado para lograr
coincidencia con los resultados experimentales, viene dado por:
h = 6,63 ⋅ 10 − 34 J.s
Laboratorio Virtual.
08
Radiación Térmica.
Mediante el archivo Planck.htm, incluido en la carpeta del mismo nombre, podrá acceder a
simulaciones relacionadas con el tema en consideración. La primera de ellas le permitirá observar gráficos
de la intensidad de radiación emitida en función de la longitud de onda y determinar la longitud de onda a
la que se produce la máxima emisión. Representando dicha magnitud en función de la temperatura podrá
verificar lo enunciado por la ley de desplazamientos. La segunda simulación le permitirá obtener la energía
total emitida para diferentes valores de la temperatura. Representando la mencionada cantidad en función de
la cuarta potencia de la temperatura podrá verificar la ley de Stefan - Boltzman.
15
EFECTO FOTOELÉCTRICO.
Mediante el estudio de la corriente que circula por un circuito como el indicado en la figura que
continúa donde la radiación que incide sobre la placa de la izquierda arranca electrones que son colectados
por el embudo de la derecha, muestran que dicho fenómeno tiene las propiedades que se indican a
continuación.
♦
La intensidad de la corriente está directamente relacionada con la intensidad de la radiación
incidente, al aumentar la intensidad de la radiación incidente, se incrementa la corriente que circula por
el circuito, o sea que se incrementa el número de electrones arrancados del material.
♦
Definiendo el potencial de corte ( VC ) como el potencial inverso al indicado en la figura, necesario
para frenar los electrones emitidos, con lo que la energía cinética de los mismos vendrá dada por:
T = q Vc
Experimentalmente se verifica que dicho potencial es independiente de la intensidad de la radiación
incidente, o sea que la energía de los electrones emitidos es independiente de la intensidad de la
- 57 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
radiación incidente, aspecto este realmente incompatible la teoría electromagnética de la luz, ya que al
incrementar la energía de la onda incidente debería preverse un incremento en la energía transferida a
los electrones que inicialmente se encontraban aferrados al material, con lo que el potencial de corte
debería aumentar con la intensidad de la radiación incidente.
♦
El potencial de corte y por lo tanto la energía de los electrones emitidos, depende de la frecuencia
de la radiación incidente. Aspecto este también incompatible con la teoría electromagnética de la luz,
ya que según la misma la energía de una onda electromagnética depende únicamente del cuadrado de la
amplitud del campo eléctrico y no depende para nada de la frecuencia de dicha radiación.
♦
Para cada material, existe una frecuencia mínima, conocida como frecuencia umbral, por debajo de la
cual es imposible arrancar electrones por elevada que sea la intensidad de la radiación incidente.
♦
Luego de realizar determinaciones y representando los valores obtenidos para el potencial de corte, o
sea para la energía cinética de los electrones emitidos, en función de la frecuencia de la radiación
incidente, los resultados pueden ajustarse a una recta, como la indicada cualitativamente en la primer
figura, donde su pendiente, es la constante de Planck, resultando para otros materiales, rectas con la
misma pendiente pero diferentes valores de la frecuencia umbral, como se muestra en la segunda figura.
tg α = h
Postulados de Einsten.
En 1905 y con el propósito de dar una explicación al fenómeno considerado, Einsten propone los siguientes
postulados relacionados con la naturaleza de la radiación electromagnética, cuando interactúa con la
materia:
♦
Debemos pensarla como paquetes de energía que llamó “fotones” con valores dados por:
ε = hν
Donde ( ν ) es la frecuencia de la radiación en consideración.
♦
La intensidad de la radiación vendrá dada por el número de fotones por cm2, en la unidad de tiempo,
multiplicada por la energía de los fotones involucrados, que podemos expresar como:
I=
♦
número de fotones
cm 2 . seg
hν
Al efecto fotoeléctrico debemos pensarlo como una colisión plástica entre el fotón y el electrón, en la
que el fotón cede toda su energía al electrón, con lo que la energía cinética de electrón arrancado
vendrá dada por:
T = hν − hν o
- 58 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
Donde el segundo término en el miembro de la derecha, es la energía necesaria para arrancarlo de la red
a la que el electrón se encuentra ligado, conocida como función trabajo.
Teniendo en cuenta los postulados indicados es claro entonces que al incrementar la intensidad de la
radiación incidente, se incrementará el número de electrones arrancados y no la energía de los mismos.
Análogamente, para cada material existirá una frecuencia mínima necesaria para arrancar electrones y
finalmente la energía cinética de los electrones emitidos estará relacionada en forma lineal con la frecuencia
de la radiación incidente, como se muestra en la figura siguiente.
Con el propósito de ofrecer información relacionada con órdenes de magnitud, la tabla siguiente nos muestra
los rangos de valores correspondientes al espectro de la radiación electromagnética.
Frecuencia en Hz
Longitud de Onda en metros
Laboratorio Virtual.
09
Determinación de la constante de Planck.
Mediante el archivo Fotoeléctrico.htm, podrá acceder a una simulación que le permitirá determinar,
para diferentes materiales, el potencial de corte para diferentes intensidades y frecuencias de la radiación
incidente, con lo que deberá verificar:
♦
Que el potencial de corte y por lo tanto la energía cinética de los electrones emitidos es independiente de
la intensidad de la radiación incidente y que de esta magnitud depende la intensidad de la corriente.
♦
Que para cada material existe una frecuencia mínima con la que podemos arrancar electrones,
independiente del valor que tenga la intensidad de la radiación incidente.
♦
Finalmente, deberá determinar el potencial de corte para diferentes valores de la frecuencia de la
radiación incidente y luego la constante de Planck a partir de la pendiente de la recta que mejor ajuste
al conjunto de puntos que podrá obtener luego de representar las determinaciones requeridas
inicialmente. Tarea que deberá realizar para tres materiales diferentes.
16
ELEMENTOS DE RELATIVIDAD ESPECIAL.
En 1905, Einsten publica el formalismo que hoy conocemos como Relatividad Especial, basado en los
postulados que se indican a continuación:
- 59 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa

La velocidad con que se propaga la radiación electromagnética es la misma en todos los sistemas de
referencia inerciales con traslación relativa.

Las expresiones formales de las Leyes Físicas deberán ser invariantes en forma en todos los sistemas de
referencia inerciales con traslación relativa y por lo tanto deberán satisfacer esta condición ante aquellas
transformaciones que garanticen la valides del postulado anterior.
Consecuencias inmediatas.

Al aceptar la invariancia de la velocidad con que se propaga la radiación electromagnética resulta que
dos eventos simultáneos en un sistema de referencia, ya no lo serán en un sistema que se traslada con
velocidad constante respecto del anterior, como puede observarse para la situación que se sugiere en la
figura siguiente, en cuyo caso resulta:
t ′A = t ′B
tA =

H
H
tB =
c+v
c−v
tA < tB
Se descartan las transformaciones de Galileo por no responder a lo requerido en el primer postulado ya
que dichas transformaciones no dejan invariante la velocidad con que se propaga la radiación
electromagnética, si tenemos en cuenta que a partir de las mismas resulta:
c = c′ + v t

Se puede demostrar, que las transformaciones que se indican a continuación, conocidas como
transformaciones de Lorentz, son compatibles con lo requerido por el primer postulado y por lo tanto
son las que aceptaremos como válidas en lo que continúa.
7
x = γ( x′ + v t )
y = y′ z = z ′
v 

t = γ t ′ + 2 x ′ 

c

6
γ=
5
1
v
1−  
c
4
2
3
2
1
00

0.2
0.4
0.6
x
0.8
1
1.2
Puesto que la ecuación de Newton es invariante en forma ante una transformación de Galileo pero no
ante una transformación de Lorentz, teniendo en cuenta lo requerido por el segundo postulado, es
necesario formular nuevamente la mecánica, partiendo de una ecuación que sea invariante en forma ante
una transformación de Lorentz.
- 60 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
Atendiendo lo requerido anteriormente, es posible demostrar que la ecuación fundamental de la mecánica,
invariante en forma ante una transformación de Lorentz, vendrá dada por.
Donde.
 dp
F=
dt


p=mv
Siendo (m) la masa relativista, dada por.
m
m=
v
1−  
c
2
Donde (mo) es la masa de la partícula medida en un sistema de referencia en el que se encuentra en reposo y
que en adelante reconoceremos como masa propia.
Teniendo en cuenta lo mencionado y el teorema las fuerzas vivas, es posible demostrar que la energía
cinética relativista de una partícula vendrá dada por:
T = m c 2 − mc 2
Por lo tanto, a una partícula en reposo es posible asociarle una energía relativista dada por:
ε = mc 2
Y a una partícula en movimiento, una energía relativista dada por:
ε = m c2
Con lo que es posible demostrar que la relación entre la energía y cantidad de movimiento relativista de una
partícula, vendrá dada por:
ε 2 = p 2 c 2 + m 2 c 4
17
EFECTO COMPTÓN.
Teniendo en cuenta la relación anterior, entre la energía y cantidad de movimiento relativista y puesto
que la energía de un fotón viene dada por (hν) y el mismo no existe en reposo, con lo que su masa propia
debe ser nula, de la anterior resulta al fotón deberemos asociarle una cantidad de movimiento.
p=
hν
c
- 61 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
Relación que fuera corroborada experimentalmente
por Compton en 1923, estudiando las características
de los fotones dispersados como consecuencia de su
interacción con electrones libres en un conductor, en
la que los fotones ceden parte de su energía al
electrón, como si se tratara de una colisión elástica,
tal como se sugiere en la imagen lateral.
Teniendo en cuenta la conservación de la cantidad de movimiento y energía relativista, que se indican a
continuación.
hν  hν
=
cos θ + γm  v cos φ
c
c
hν
0 =
sen θ + γm  v sen φ
c
hν  + m  c 2 = hν + γm  c 2
De las anteriores obtenemos que la frecuencia del fotón dispersado será tal que:
1 1
h
−
=
(1 − cos θ)
ν ν  mc 2
De donde obtenemos que la frecuencia del fotón dispersado vendrá dada por:
ν=
1+
hν 
mc
ν
2
(1 − cos θ)
Que como lo adelantáramos, resulta menor que la del fotón incidente, con lo que para la energía del electrón
dispersado, obtenemos:




1


Te = hν  1 −
h
ν
 1+

(1 − cos θ) 
2


mc


Resultando una transferencia máxima, cuando el fotón es retrodispersado, en cuyo caso la energía cinética
del electrón vendrá dada por:
Tmax




1

= hν  1 −
 1 + 2 hν  

m  c 2 

- 62 -
Escuela Digital de Física
Ochoa - ISBN: 987-95038-0-5
Fundamentos de la Física Moderna
Facultad de Ingeniería - Universidad Nac. de La Pampa
Y la frecuencia del fotón retrodispersado será:
ν min =
ν
hν 
1+ 2
mc 2
- 63 -