UNIDAD 10: ESTADÍSTICA UNIDIMENSIONAL

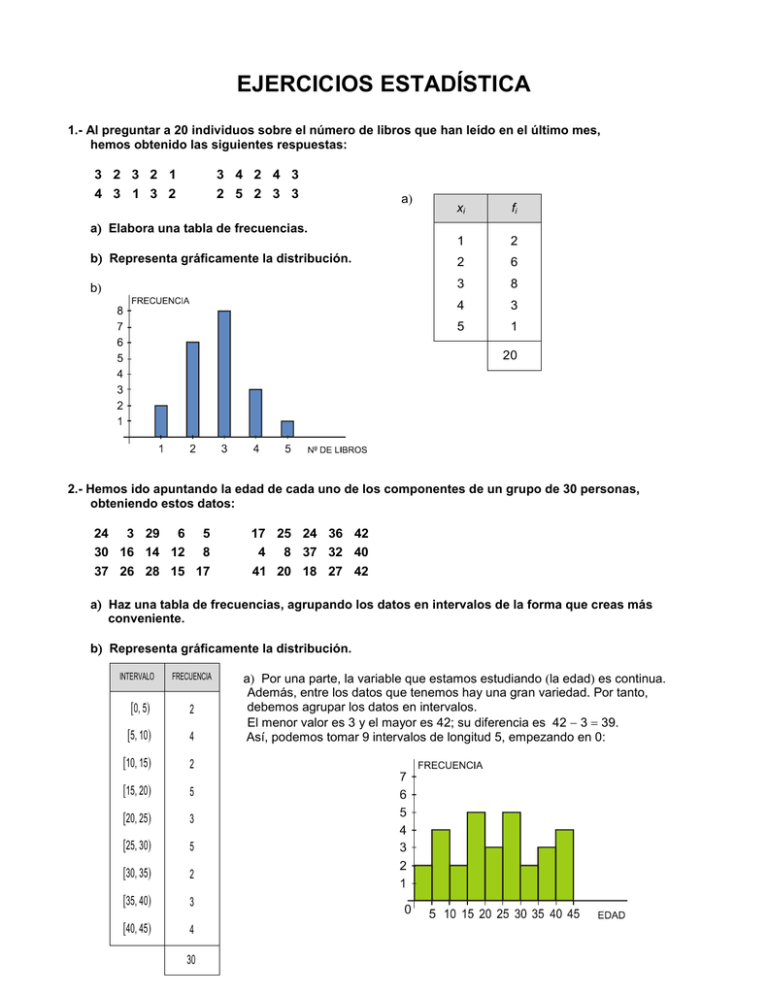
EJERCICIOS ESTADÍSTICA
1.- Al preguntar a 20 individuos sobre el número de libros que han leído en el último mes,
hemos obtenido las siguientes respuestas:
3 2 3 2 1
3 4 2 4 3
4 3 1 3 2
2 5 2 3 3
a
xi
fi
1
2
b Representa gráficamente la distribución.
2
6
b
3
8
4
3
5
1
a Elabora una tabla de frecuencias.
20
2.- Hemos ido apuntando la edad de cada uno de los componentes de un grupo de 30 personas,
obteniendo estos datos:
24 3 29 6 5
30 16 14 12 8
37 26 28 15 17
17 25 24 36 42
4 8 37 32 40
41 20 18 27 42
a Haz una tabla de frecuencias, agrupando los datos en intervalos de la forma que creas más
conveniente.
b Representa gráficamente la distribución.
INTERVALO
FRECUENCIA
0, 5
2
5, 10
4
10, 15
2
15, 20
5
20, 25
3
25, 30
5
30, 35
2
35, 40
3
40, 45
4
30
a Por una parte, la variable que estamos estudiando la edad es continua.
Además, entre los datos que tenemos hay una gran variedad. Por tanto,
debemos agrupar los datos en intervalos.
El menor valor es 3 y el mayor es 42; su diferencia es 42  3  39.
Así, podemos tomar 9 intervalos de longitud 5, empezando en 0:
3.- Se han realizado 50 lanzamientos con un dado, obteniendo los siguientes resultados:
RESULTADO
1
2
3
4
5
6
Nº DE VECES
6
10
5
7
10
12
a Calcula la media y la desviación típica.
b) ¿Qué porcentaje de resultados hay en el intervalo
 x   x   ?
a
Media:
 f x 191
x i i 
 3,82
n
50
Desviación típica:

 fi xi2
 x2 
n
885
 3,822  3,1076  1,76
50
fi xi2
xi
fi
fi xi
1
6
6
6
2
10
20
40
3
5
15
45
4
7
28
112
5
10
20
250
6
12
72
432
50
191
885
Hemos obtenido una puntuación media de 3,82, con una desviación típica de 1,76 puntos.
b) x    2,06 

x    5,58 
En el intervalo 2,06; 5,58 hay 22 resultados, que representan un 44% del total.
4.- En un grupo, A, de animales de una misma especie, el peso medio es 20,4 kg, con una desviación
típica de 3,2 kg. En otro grupo, B, de animales de una segunda especie, el peso medio es 96 kg y
la desviación típica es de 12 kg. Calcula el coeficiente de variación en los dos casos y di en cuál
de los dos grupos la variación relativa es mayor.
3,2
A


 0,157  15,7%
x A 20,4


B 12
C.V.B 

 0,125
 12,5%

xB 96

C.V.A 
La variación relativa es mayor en el grupo A.
5.- Tiramos sucesivamente una moneda y anotamos el número de lanzamientos que necesitamos
hasta obtener por primera vez cara. Realizamos el experimento 100 veces, con los siguientes
resultados:
LANZAMIENTO EN EL
QUE SALE CARA
1
2
3
4
5
6
Nº DE VECES QUE HA
OCURRIDO
48
25
16
4
5
2
Calcula Me, Q1, Q3 y p30.
Hacemos la tabla de frecuencias acumuladas:
Me  p50  2
Q1  p25  1
Q3  p75  3
p30  1
xi
fi
Fi
en %
1
48
48
48
2
25
73
73
3
16
89
89
4
4
93
93
5
5
98
98
6
2
100
100
porque para
porque para
porque para
porque para
xi  2,
xi  1,
xi  3,
xi  1,
la
la
la
la
Fi
Fi
Fi
Fi
supera el 50%.
supera el 25%.
supera el 75%.
supera el 30%.
6.- En un grupo de personas hemos preguntado por el número medio de días que practican deporte a
la semana. Las respuestas han sido las siguientes:
4 2 3 1 3
7 1 0 3 2
6 2 3 3 4
6 3 4 3 6
xi
fi
a
a Haz una tabla de frecuencias.
0
1
b Representa gráficamente la distribución.
1
2
2
3
3
7
4
3
6
3
7
1
b
20
7.- En un grupo de 30 niños, se ha medido el peso, en kilogramos, de cada uno de ellos, obteniendo
los siguientes resultados:
30 31 28 25 33
32 35 37 29 32
34 35 30 28 27
34 31 32 26 39
40 35 38 31 36
32 33 29 30 31
a Haz una tabla de frecuencias, agrupando los datos en intervalos de la forma que creas más
conveniente.
b Representa gráficamente la distribución.
a Por una parte, la variable que estamos estudiando el peso es continua. Además, entre los datos que
tenemos hay una gran variedad. Por tanto, debemos agrupar los datos en intervalos.
El menor valor es 25 y el mayor es 40; su diferencia es 40  25  15.
Así, podemos tomar 6 intervalos de longitud 3, empezando en 24,5:
b
INTERVALO
FRECUENCIA
24,5  27,5
3
27,5  30,5
7
30,5  33,5
10
33,5  36,5
6
36,5  39,5
3
39,5  42,5
1
30
8.- Las notas obtenidas en un examen de matemáticas por las alumnas y los alumnos de una clase de
4º ESO vienen reflejadas en esta tabla:
NOTA
2
3
4
5
6
7
8
9
10
Nº ALUMNOS/AS
1
2
3
5
4
6
4
3
2
a Calcula la media y la desviación típica.
b) ¿Qué porcentaje de alumnos/as hay en el intervalo  x  σ, x  σ  ?
a
Media:
 f x 190
x i i 
 6,33
n
30
Desviación típica:

 fi x
1332
 x2 
 6,332  4,33  2,08
n
30
2
i
La nota media de la clase es 6,33, con una desviación típica de 2,08.
b) x    4,25 

x    8,41
fi xi2
xi
fi
fi xi
2
1
2
4
3
2
6
18
4
3
12
48
5
5
25
125
6
4
24
144
7
6
42
294
8
4
32
256
9
3
27
243
10
2
20
200
30
190
1 332
En el intervalo 4,25; 8,41 hay 19 alumnos, que representan un 63,33% del total.
9.- En una empresa, A, el sueldo medio de los trabajadores es 950 € al mes, con una desviación
típica de 150 €. En otra empresa, B, el sueldo medio es de 1 200 € al mes, con una desviación
típica de 200 €. Calcula el coeficiente de variación en los dos casos y di cuál de las dos empresas
tiene mayor variación relativa en los sueldos.
A 150

 0,158
xA 950

 15,8%


B
200
C.V.B 

 0,167  16,7%

xB 1200

C.V.A 
La variación relativa es mayor en la empresa B.
10.- En la siguiente tabla hemos resumido los resultados obtenidos al lanzar un dado 120 veces:
Nº OBTENIDO
1
2
3
4
5
6
Nº DE VECES
18
30
21
25
17
9
Calcula Me, Q1, Q3 y p20.
Hacemos la tabla de frecuencias acumuladas:
Me  p50  3
Q1  p25  2
Q3  p75  4
p20  2
xi
fi
Fi
en %
1
18
18
15
2
30
48
40
3
21
69
57,5
4
25
94
78,3
5
17
111
92,5
6
9
120
100
porque para
porque para
porque para
porque para
xi  3,
xi  2,
xi  4,
xi  2,
la
la
la
la
Fi
Fi
Fi
Fi
supera el 50%.
supera el 25%.
supera el 75%.
supera el 20%.
11.- En un grupo de 20 personas, hemos preguntado por el número de individuos que viven en su
hogar. Las respuestas has sido las siguientes:
4 5 3 4 1
4 2 3 5 4
3 4 4 5 3
3 5 3 2 4
a Elabora una tabla de frecuencias.
b Representa gráficamente la distribución.
12.- En una clase de Educación Física de 4º ESO se ha cronometrado el tiempo, en segundos, que
tarda cada alumno/a en recorrer cierta distancia fija. Los datos obtenidos han sido los siguientes:
10, 5 9, 2 8 8, 6
9
8, 2 8,1 9, 3 9, 4 10
8
8, 4 9, 2 14 11, 6
15 12 12,5 9,2 10
10,2 9,1 8,2 8,1 8
10
9 8,6 12 8,3
a Elabora una tabla de frecuencias, agrupando los datos en intervalos de la forma que creas más
conveniente.
b Representa gráficamente la distribución.
13.- Hemos preguntado las edades a un grupo de 50 personas. Los resultados obtenidos se reflejan
en la tabla siguiente:
EDAD
0, 5
5, 10
10, 15
15, 20
20, 25
25, 30
Nº DE PERSONAS
4
8
10
9
17
2
Halla la media y la desviación típica.
14.- En un grupo, A, de personas, la estatura media es 165 cm, con una desviación típica de 10,5 cm.
En otro grupo, B, la estatura media es 140 cm y su desviación típica, 8,4 cm. Calcula el
coeficiente de variación en los dos casos y compara la dispersión de ambos grupos.
15.- Un grupo de atletas ha obtenido las siguientes puntuaciones en una prueba deportiva que se
valoraba de 0 a 5 puntos:
PUNTUACIÓN
1
2
3
4
5
Nº DE ATLETAS
4
4
12
18
12
Calcula Me, Q1 y Q3.
16.- Las notas obtenidas en un examen de matemáticas realizado en una clase de 4º ESO han sido las
siguientes:
4 5 7 5 8
3
9 6 4 5
7 5 8 4 3
10 6 6 3 3
a Ordena los datos en una tabla de frecuencias.
b Representa gráficamente la distribución.
17.- En un grupo de 30 personas hemos medido la estatura, en centímetros, de cada una de ellas,
obteniendo los siguientes resultados:
160 163 165 164 162
161 164 167 168 154
166 168 165 167 169
168 175 167 159 160
163 164 167 164 165
164 150 166 147 170
a Elabora una tabla de frecuencias, agrupando los datos en intervalos de la forma que creas más
conveniente.
b Representa gráficamente la distribución.
18.- Se ha preguntado a las alumnas y a los alumnos de una clase de 4O ESO por el tiempo que tardan
en llegar desde su casa hasta el instituto. Las respuestas se recogen en esta tabla:
TIEMPO MINUTOS
0, 5
5, 10
10, 15
15, 20
20, 25
Nº ALUMNOS/AS
10
6
9
3
2
Calcula la media y la desviación típica de esta distribución.
19.- En un examen de matemáticas realizado en 4º A de ESO, la nota media ha sido 5,2, con una
desviación típica de 2,3. En la clase de 4º B, con el mismo examen, se ha obtenido una nota media
de 7,4 y una desviación típica de 3. Calcula el coeficiente de variación en los dos casos y compara
la dispersión en ambos grupos.
20.- En la siguiente distribución, halla Me, Q1, Q3 y p90.
xi
1
2
3
4
5
6
7
fi
5
12
32
19
27
15
10
EJERCICIOS COMBINATORIA
1.- Sabiendo que los puestos de delegado y de subdelegado no pueden ser cubiertos por la misma
persona, calcula cuántas posibilidades hay para cubrir ambos cargos en una clase de 22
alumnos.
Como influye el orden, y una misma persona no puede ocupar ambos puestos 
 V22, 2  22 · 21  462
Por tanto, hay 462 posibilidades distintas.
2.- Con las letras de la palabra CUADERNO, ¿cuántas palabras, con o sin sentido, se pueden formar?
P8  8!  40 320
Se pueden formar 40 320 palabras.
3.- Un club de tenis dispone de 15 jugadores profesionales de los cuales debe seleccionar 8 para
jugar un torneo. ¿Cuántos grupos se pueden formar?
C15, 8 
V15, 8
P8

15  14  13  12  11 10  9  8
 6 435
8  7  6  5  4  3  2 1
Se pueden formar 6 435 grupos distintos.
4.- ¿De cuántas formas pueden sentarse 4 hombres y 4 mujeres en una fila de un cine si quieren estar
alternados?
Tenemos las siguientes posibilidades: H1 M1 H2 M2 H3 M3 H4 M4
M2 H3 M1 H2 M4 H1 M3 H4
En cada uno de los dos casos anteriores ocurre:
 Formas de colocar a los hombres: P4  4!  4 · 3 · 2 · 1  24 formas distintas
 Formas de colocar a las mujeres: P4  24 formas distintas
En total, existirán 2 · 24 · 24  1 152 maneras distintas de sentarse.
5.- Con las letras de la palabra ALBA, ¿cuántas palabras, con o sin sentido, se pueden hacer?
Son 12 palabras: AALB BAAL , AABL BALA , ALAB BLAA, ALBA LAAB, ABAL
LABA, ABLA
6.- Un restaurante dispone de 10 primeros platos, 8 segundos y 5 postres. ¿Cuántos menús
diferentes se pueden confeccionar?
Por cada primer plato, puedo elegir 8 segundos; como hay 10 primeros, tendremos 10 · 8  80
posibilidades para elegir el primer y segundo platos.
Elegidos los dos primeros platos, se pueden escoger 5 postres distintos; luego en total habrá
80 · 5  400 menús distintos.
7.- Los 25 municipios de una ciudad están unidos a los demás por distintas líneas de tren. ¿Cuántas
líneas habrá en total?
LBAA.
De cada municipio salen 24 líneas; como hay 25 municipios, en principio habría 24 · 25  600 líneas,
pero tenemos que considerar que las hemos contado dos veces la línea que une el municipio A con el
B es la misma que la que une B con A.
600
 300 líneas
2
Así, el número total de líneas será:
8.- Calcula el valor de la siguiente expresión:
7
7!
7  6  5! 7  6


 21;
 
2
5!2!
5!  2
2
 
 7  4  5 
     
 2  3  4
 4
4!
4  3!

 4;
 
3
1!3!
3!
 
5
5!
5  4!

5
 
4
1!4!
4!
 
Así:
7  4  5
         21  4  5  21  20  41
 2  3   4
 x  1


 x  2
b Resuelve, sin desarrollar, esta expresión:
9.- a Simplifica la expresión siguiente:
 x  1!  x  1 x  2!
 x  1
a) 

 x 1

x

2
1
!
 x  2 !
 x  2 !


 11  11
  
6 x
m  m 
 

 n  m  n
b Aplicamos la propiedad de los números combinatorios:
Así:
 11  11 
 11  11
 
        x  5 (La solución x  6 es obvia).
 6   11  6 
6 5
10.- Con las letras de la palabra JUNIO, ¿cuántas palabras, con o sin significado, podemos formar
con 4 letras, pudiendo estas repetirse?
Como influye el orden, y las letras se pueden repetir  VR5, 4  54  625
Por tanto, se pueden formar 625 palabras.
11.- ¿De cuántas formas se pueden repartir 4 bocadillos distintos entre 4 amigos, si cada uno debe
recibir solo uno?
P4  4!  24
Se pueden repartir los bocadillos de 24 formas.
12.- En una empresa se quieren contratar 5 agentes de seguridad. Si al proceso de selección se
presentan 10 personas, ¿de cuántas formas distintas se pueden ocupar las cinco plazas?
C10, 5 
V10, 5
P5

10  9  8  7  6
 252
5  4  3  2 1
Se pueden ocupar las plazas de 252 formas diferentes.
13.- Con 0, 1, 2, 3 y 4, ¿cuántos números de cinco cifras se pueden formar, sin repetir ningún dígito?
Como influye el orden, y los dígitos no se pueden repetir  P5  5!  5 · 4 · 3 · 2 · 1  120
Pero la quinta parte de estos números empezarán por 0, y por tanto serán números de cuatro cifras, no
de cinco.
1
Luego:  120  24  120  24  96
5
Hay 96 números de cinco cifras que se pueden formar con los dígitos 0, 1, 2, 3 y 4.
14.- Dos amigos juegan al futbolín y acuerdan que será vencedor el que gane dos partidas seguidas o
tres alternativas no hay empate. ¿De cuántas formas puede desarrollarse el juego?
A: gana el jugador A
B: gana el jugador B
Son 10 las formas en que puede desarrollarse el juego:
AA
ABAA
ABABA
ABABB
ABB
BAA
BABAA
BABAB
BABB
BB
15.- Queremos crear un código que conste, en primer lugar, de una vocal, y a continuación de dos
cifras distintas elegidas entre el 1 y el 9 ambos incluidos. ¿Cuántos elementos distintos
podemos conseguir con este código?
Para cada vocal, hay 9 posibilidades de elegir la primera cifra y 8 posibilidades para la segunda cifra.
Como hay 5 vocales, en total tendremos 5 · 8 · 9  360 elementos.
16.- Dadas las letras A, B, C, E, indica cuántas ordenaciones se pueden hacer sabiendo que nunca
pueden ir juntas ni dos vocales ni dos consonantes.
Las vocales se pueden organizar de 4 formas: A _ E_ _A _ E
E _ A_ _E _ A
En cada caso hay 2 posibilidades de poner las consonantes.
Por tanto, en total habrá 2 · 4  8 ordenaciones.
17.- Aplicando las propiedades de los números combinatorios, calcula el
valor de esta expresión:
 6  6  7
    
 4  5 5
y
 6  6 5  5
    
 4  5  2  3
 5  5  6
     
 2  3  3 
Luego:
 6   6   5   5    7   6 
7!
6!
7  6  5! 6  5  4  3! 7  6 6  5  4






                  
2  5!
3  2  3!
2
6
 4   5   2   3    5   3  2!5! 3!3!
 21  20  1
18.- a Simplifica la expresión siguiente:
 x  1


 x  1
 x  1!  x  1 x  x  1! x  x  1 x 2  x
 x  1
a) 





2  x  1!
2
2
 x  1 2!  x  1!
19.- ¿Cuántos números de cuatro cifras distintas podemos formar con los dígitos 2, 4, 6, 8 y 9?
20.- Con los dígitos impares, ¿cuántos números de cinco cifras distintas se pueden formar?
21.- De una lista de 12 discos, Rosa tiene que seleccionar 5 diferentes para regalar. ¿Cuántas
selecciones distintas puede hacer?
22.- Para formar la tripulación de un avión se eligen 3 comandantes y 4 azafatas entre un grupo de 11
personas, 5 de las cuales son comandantes y el resto, azafatas. ¿Cuántas tripulaciones distintas
se pueden formar?
23.- En el descanso de un partido de fútbol el marcador señalaba 0  1. ¿De cuántas formas pudo ir
variando el marcador hasta llegar al resultado final de empate a 3 goles?
24.- Si lanzamos 3 dados y una moneda, ¿cuántos resultados posibles podemos obtener?
25.- A una fiesta acuden 6 parejas. Cada persona saluda con un abrazo al resto, menos a su
compañero/a. ¿Cuántos abrazos se han dado en total en la fiesta?
26.- Simplifica:
 6! 3!   4 
    0
 4! 4!   
x!
27.- a Simplifica este cociente:
 x  2!
 2x 
 2x 
3     2     4 x
1
 
 2 
28.- Tenemos que formar un código de 6 cifras con los dígitos 0 y 1. ¿Cuántas posibilidades hay?
b Resuelve la siguiente ecuación:
29.- En una carrera organizada en un centro escolar participan los 6 finalistas de 4º ESO. ¿De cuántas
formas distintas pueden llegar a la meta?
30.- En un centro de trabajo se tienen que elegir a cuatro de sus 18 empleados para representar a la
empresa en una reunión del sector. ¿Cuántas elecciones diferentes pueden darse?
31.- ¿Cuántas ordenaciones pueden hacerse con las letras de la palabra PINCEL de modo que
comiencen y terminen por consonante?
32.- ¿Cuántos productos de tres cifras iguales o distintas podemos hacer con los números 1, 2 y 3?
33.- Pablo tiene 5 pantalones y 15 camisas distintas, ¿de cuántas formas diferentes se puede vestir?
34.- Juan tiene 20 € y decide participar en un juego que consiste en lanzar una moneda 4 veces. En
cada tirada debe apostar 20 €, que pierde si sale cruz. Si sale cara, gana 20 € más. Escribe todos
los resultados que pueden darse sabiendo que si se queda sin dinero concluye el juego.
35.- Calcula el valor de la siguiente expresión:
36.- a Simplifica esta expresión:
 x  2  !  x  1 !

x!
 x  1 !
b Resuelve la siguiente ecuación:
9! 2! 3! 4 !

5 ! 7!
6!
x
x
2   6   5x
 1
2
37.- ¿Cuántos números de cuatro cifras distintas podemos formar con los dígitos 1, 5, 8, 9 y 3?
38.- ¿De cuántas formas se pueden repartir 6 bocadillos distintos entre 6 amigos, si cada uno debe
recibir solo uno?
39.- En un centro de trabajo se tienen que elegir a cuatro de sus 10 empleados para representar a la
empresa en una reunión del sector. ¿Cuántas elecciones diferentes pueden darse?
40.- ¿Cuántas ordenaciones pueden hacerse con las letras de la palabra CLEPIN de modo que
comiencen y terminen por consonante?
41.- Tengo dos monedas de 1 €, dos de 2 € y dos de 50 cent. Tomando tres de las seis monedas,
¿cuántas sumas distintas puedo hacer?
42.- Juan tiene 20 € y decide participar en un juego que consiste en lanzar una moneda 4 veces. En
cada tirada debe apostar 20 €, que pierde si sale cruz. Si sale cara, gana 20 € más. Escribe todos
los resultados que pueden darse sabiendo que si se queda sin dinero concluye el juego.
EJERCICIOS PROBABILIDAD
1.- Metemos en una bolsa 10 bolas numeradas del 1 al 10. Extraemos una al azar y observamos el
número que tiene.
Consideramos los sucesos: A  "obtener un número menor que 5" y B  "obtener un número
mayor que 2".
a Escribe, dando todos sus casos, los sucesos A, B, A', B', A  B y A  B.
A  1, 2, 3, 4; B  3, 4, 5, 6, 7, 8, 9, 10; A'  5, 6, 7, 8, 9, 10; B '  1, 2;
A  B  1, 2, 3, 4, 5, 6, 7, 8, 9, 10  E; A  B  3, 4
b Calcula las siguientes probabilidades:
b) P  A 
P A; P B; P A'; P B'; P A  B; P A  B
4
8
6
 0,4; P B 
 0,8; P  A ' 
 0,6
10
10
10
P B ' 
2
2
 0,2; P  A  B  1; P  A  B 
 0,2
10
10
2.- Extraemos una carta de una baraja española de 40 cartas. La miramos, la devolvemos al montón y
extraemos otra. Halla la probabilidad de que:
a A  "Las dos cartas sean de oros"
b B  "La primera carta sea de oros y la segunda sea un rey"
Como son sucesos independientes:
a) P  A  P 1ª oros  P 2ª oros 
b) P B  P 1ª oros  P 2ª rey 
10 10 1 1 1

  
 0,0625
40 40 4 4 16
10 4
1 1
1

 

 0,025
40 40 4 10 40
3.- Tenemos una urna con 4 bolas blancas y 8 negras. Sacamos dos bolas a la vez. Calcula la
probabilidad de obtener:
a Dos bolas blancas.
b Dos bolas de distinto color.
Sacar dos bolas a la vez es equivalente a sacar una bola y, sin volver a introducirla en la urna, sacar
otra.
Hacemos un diagrama en árbol:
1ª bola
2ª bola
3
4
11
12
B
8N
4B
8
8N
8
B  ByB
3B
12
N
4B
N  ByN
4 3
12
1
 

 0,09
12 11 132 11
11
4
11
B  NyB
7N
7
a) P B y B 
11
N
b) P B y N  P N y B 
4 8 8 4 1 8 2 4
8 16
        2

 0,48
12 11 12 11 3 11 3 11
33 33
4.- Tomamos una ficha del dominó al azar. Halla las probabilidades siguientes:
a Que la ficha sea el cinco doble 5  5.
b Que la suma de puntos sea 7.
c Obtener un doble.
Las fichas del dominó son 28.
a
P 5  5 
1
 0,036
28
b La suma de puntos es 7 en las siguientes fichas:
6  1;
c
5  2;
P doble 
43
Por tanto:
P suma 7 
3
 0,107
28
7
 0,25
28
5.- En una bolsa tenemos 10 bolas numeradas del 1 al 10. Sacamos una al azar y anotamos el número
obtenido.
Consideramos los sucesos: A  "impar menor que 8" y B  "múltiplo de 3".
a Escribe, dando todos sus casos, los sucesos A, B, A', B', A  B y A  B.
A  1, 3, 5, 7; B  3, 6, 9; A'  2, 4, 6, 8, 9, 10; B '  1, 2, 4, 5, 7, 8, 10;
A  B  1, 3, 5, 6, 7, 9; A  B  3
b Calcula las siguientes probabilidades:
P A; P B; P A'; P B'; P AB; P AB
b) P  A 
4
3
6
 0,4; P B 
 0,3; P  A ' 
 0,6
10
10
10
P B ' 
7
6
1
 0,7; P  A  B 
 0,6; P  A  B 
 0,1
10
10
10
6.- Tenemos una urna con 6 bolas rojas y 8 verdes. Sacamos una bola al azar, observamos el color y
la volvemos a introducir en la urna. Sacamos una segunda bola y observamos su color. Calcula la
probabilidad de obtener:
a Dos bolas rojas.
b Dos bolas de distinto color.
Hacemos un diagrama en árbol:
1ª bola
6
6
14
R  RyR
14
6 6 3 3 9

  
 0,18
14 14 7 7 49
b) P R y V   P  V y R 
V  RyV
14
6
14
a) P R y R 
R
8
8
2ª bola
14
6 8
8 6 3 4 4 3 12
24

 
    
2 
 0,49
14 14 14 14 7 7 7 7 49
49
R  VyR
V
7.- Introducimos en una bolsa 10 bolas numeradas del 1 al 10. Sacamos
tres
bolas, una detrás de otra sin devolverlas a la bolsa. Calcula la
probabilidad de obtener tres números impares.
8
14
V
Hacemos un diagrama en árbol:
1ª bola
2ª bola
3ª bola
Par
Impar
Par
Par
Par
Impar
5 Pares
5 Impares
1
Par
Par
2
Impar
5P
Impar
4I
5P
4
P 3 impares 
Impar
9
Impar
3I
Par
3
8
Impar  3 impares
1 4 3 1
  
 0,083
2 9 8 12
8.- En el lanzamiento de un dado de cuatro caras, hemos obtenido las siguientes probabilidades:
Nº OBTENIDO
PROBABILIDAD
1
2
3
4
0,15 0,32 0,28
a ¿Cuál es la probabilidad de obtener un 4?
b ¿Cuál es la probabilidad de no obtener un 4?
c ¿Cuál es la probabilidad de obtener un número impar?
a Tenemos en cuenta que la suma de las probabilidades de todos los casos es igual a 1; es decir:
P 1 + P 2 + P 3 + P 4  1
Sustituyendo cada probabilidad por su valor, tenemos que:
0,15  0,32  0,28  P 4  1  P 4  1  0,15  0,32  0,28 = 0,25
b) P no 4  1  P 4 = 0,75
c) P impar  P 1  P 3  0,15  0,28  0,43
9.- En el siguiente diagrama, E representa el espacio muestral, A representa un suceso, y B, otro
suceso:
a Escribe, dando todos sus casos, los sucesos A, B, A', B', A
 B y A  B.
b Calcula las siguientes probabilidades:
P A; P B; P A'; P B'; P A  B; P A  B
A  2, 3, 4; B  4, 5, 6, 9; A'  1, 5, 6, 7, 8, 9; B '  1, 2,
3, 7, 8;
A  B  2, 3, 4, 5, 6, 9; A  B  4
b) P  A 
3 1
4
6 2
 ; P B   ; P  A '   
9 3
9
9 3
5
6 2
1
P B '  ; P  A  B   ; P  A  B 
9
9 3
9
10.- En una bolsa tenemos 5 bolas negras y 9 blancas. Extraemos una bola al azar, miramos su color,
la devolvemos a la bolsa y volvemos a sacar otra bola. Halla la probabilidad de que:
a La dos bolas sean negras.
b La primera bola sea blanca y la segunda negra.
Hacemos un diagrama en árbol:
1ª bola
2ª bola
9
9
14
14
b) P B y N 
9 5
45


 0,23
14 14 196
B
N  ByN
14
9
14
5 5
25


 0,13
14 14 196
B
5
5
a) P N y N 
14
B
N
5
14
11.- Si sacamos dos cartas de una baraja española de 40 cartas, calcula la probabilidad de obtener:
a Dos ases.
b Dos cartas del mismo palo.
a) P  dos ases  P as en la 1ª y as en la 2ª  
 P as en la 1ª   P as en la 2ª habiendo sacado as en la 1ª  
4 3
1 1




40 39 10 13

1
 0,0077
130
b) P mismo palo  P dos oros  P dos copas  P dos espadas  P dos bastos 
10 9 10 9 10 9 10 9
10 9
1 3







 4

 4 

40 39 40 39 40 39 40 39
40 39
4 13
3

 0,23
13

12.- Lanzamos dos dados y anotamos la mayor de las puntuaciones obtenidas. Calcula la probabilidad
de que esta sea:
a 4
b 2
c 6
Hacemos una tabla en la que se reflejen los posibles resultados:
er
2º dado
1 dado
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
2
3
4
5
6
3
3
3
3
4
5
6
4
4
4
4
4
5
6
5
5
5
5
5
5
6
6
6
6
6
6
6
6
a) P  4 
7
 0,194
36
b) P 2 
3
1

 0,083
36 12
c) P 6 
11
 0,306
36
13.- En el lanzamiento de un dado correcto, consideramos los sucesos: A  "obtener impar" y B 
"obtener múltiplo de 3".
a Describe, dando todos sus casos, los sucesos A, B, A', B', A  B y A  B.
b Calcula las siguientes probabilidades:
P A; P B; P A'; P B'; P A  B; P A  B
14.- Un juego consiste en tirar un dado y lanzar una moneda simultáneamente. Ganaremos si
conseguimos sacar un número impar en el dado y una cara en la moneda.
a ¿Qué probabilidad tenemos de ganar?
b ¿Y de perder?
15.- En una urna tenemos 12 bolas rojas, 10 blancas y 8 negras. Sacamos dos bolas a la vez. Calcula
la probabilidad de que:
a Las dos bolas sean blancas.
b La primera sea roja y la segunda, blanca.
16.- En un club deportivo hay apuntados 30 chicos y 30 chicas. La mitad de los chicos y la tercera
parte de las chicas juegan al tenis.
a Completa la siguiente tabla:
JUEGAN TENIS
CHICOS
CHICAS
NO JUEGAN TENIS
15
10
30
30
60
b Ayudándote de la tabla anterior, calcula las siguientes probabilidades, referidas al elegir una
persona al azar de ese club:
P chico ; P no juega tenis; P chico que no juega tenis
17.- Tomamos las 10 cartas de oros de una baraja española y elegimos al azar una de entre ellas.
Consideramos los sucesos: A  "obtener figura" y B  "obtener una carta con un número menor
que 4".
a Escribe, dando todos sus casos, los sucesos A, B, A' , B', A  B y A  B.
b Calcula las siguientes probabilidades:
P A; P B; P A'; P B'; P A  B; P A  B
18.- Lanzamos un dado tres veces seguidas. Calcula la probabilidad de obtener:
a A  "Tres cincos"
b B  "El mismo número las tres veces"
19.- De una baraja española de 40 cartas extraemos tres cartas sin reemplazamiento es decir, sin
devolverlas al mazo en cada caso. Calcula la probabilidad de que las tres cartas sean de oros.
20.- Lanzamos dos dados y sumamos los resultados obtenidos. Calcula la probabilidad de que la
suma sea:
a 7
b Menor que 5.
c Mayor que 10.
21.- En el siguiente diagrama, E representa el espacio
muestral, A representa un suceso, y B, otro suceso:
a Escribe, dando todos sus casos,
los sucesos A, B, A', B', A  B y A  B.
b Calcula las siguientes probabilidades:
P A; P B; P A'; P B'; P A  B; P A  B
22.- En una bolsa tenemos 5 bolas negras y 9 blancas. Extraemos una bola al azar, miramos su color,
la devolvemos a la bolsa y volvemos a sacar otra bola. Halla la probabilidad de que:
a
b
La dos bolas sean negras.
La primera bola sea blanca y la segunda negra.
23.- Si sacamos dos cartas de una baraja española
de 40 cartas , calcula la probabilidad de obtener:
a) Dos ases.
b) Dos cartas del mismo palo.
24.- Tomamos una ficha del dominó al azar. Halla las probabilidades siguientes:
a) Que la ficha sea el cinco doble 5-5
b) Que la suma de puntos sea 7.
c) Obtener un doble.