muestra - Curso de Dibujo por Internet

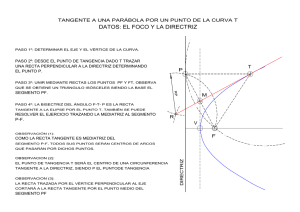
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
Presentamos unos casos de muestra del material que hemos
elaborado sobre problemas resueltos y explicados de Dibujo
Técnico para Bachillerato.
ENUNCIADO DE HIPÉRBOLA. De una hipérbola se conoce el foco F`, una asíntota
As y una tangente “t”. Hallar el otro foco, la otra asíntota, los ejes real e
imaginario y el punto de tangencia T.
Ayuda. Supuesto el problema resuelto tenemos que en una hipérbola, con sus
elementos fundamentales posicionados, se cumple el hecho de que los pies de las
perpendiculares a las tangentes (incluidas las asíntotas que son tangentes en el
punto del infinito) trazadas desde cualquira de sus focos están en la llamada
circunferencia principal, que tiene por centro al punto “o” y por radio el semieje
real oA = oA`.
Por tanto en el caso que nos ocupa, en el que se parte de una asíntota As, una
tangente, t, y un foco F`, la perpendicular desde F` a la asíntota, As, determina el
punto P; y la perpendicular a la tangente ,t, desde el foco F` establece el punto M,
estando ambos puntos situados en la circunferencia principal. El centro de dicha
circunferencia está en la mediatriz de MP y en la asíntota As, por lo que es el
punto de intersección de ambas rectas. Conocido el centro, o, dibujamos la
circunferencia de radio oM = oP, cuyo diámetro trazado por F` es el eje real AA`.
Hallamos la otra asíntota, Bs, dibujando por “o” una recta que forme un ángulo
igual al que forma el eje AA` con la asíntota, As, aportada. El simétrico de F`
respecto al centro, o, es el otro foco F.
Las perpendiculares al eje real trazadas por A y A` determinan, en su corte con las
asíntotas, los puntos X, siendo la paralela media al lado mayor del rectángulo
obtenido el eje imaginario BB`.
Para obtener el punto de tangencia “T” hallamos el simétrico F`` del foco F`
respecto a la tangente “t”, siendo el corte de dicha tangente con la prolongación
del segmento FF`` el punto de tangencia, T, buscado.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE HIPÉRBOLA. Conocemos los puntos C y D de corte de una
tangente,t, a una hipérbola con la circunferencia principal; y el corte E de otra
tangente desconocida, s, con dicha circunferencia. Se pide hallar los elementos
fundamentales de la cónica si se conoce también la medida del eje imaginario
BB`, representada por el segmento m de la figura.
Ayuda. El conocer los puntos C y D hace que esté definida la tangente, t, del
enunciado, al unirlos mediante una recta. El conocer el punto E de corte de otra
tangente, s, desconocida, con la circunferencia principal hace que los tres puntos
aportados determinen dicha circunferencia principal. Por tanto sacamos la
medida del eje real AA` coincidente con el diámetro de esta circunferencia.
que distará del centro de la circunferencia principal la mitad, “r” de la diagonal
obtenida en figura aparte, por lo que dicho punto queda determinado. La otra
tangente, no dibujada en la figura, se sacaría una vez posicionado el segundo foco
F y hallando el simétrico de F` respecto al centro o, aplicaríamos el fundamento
de la construcción anterior, y no tendríamos más que dibujar la perpendicular al
segmento EF por el punto E.
ENUNCIADO DE HOMOLOGÍA. Hallar el transformado por homología del
hexágono regular ABCDEF aportado, en una homología de centro en el punto O;
y eje y recta límite coincidentes respectivamente con los lados ED y AB del
polígono.
Ayuda. La figura tiene dos puntos A Y B en la recta límite por lo que su
transformada por homología será abierta dado que, por definición, todos los
puntos de la recta límite se convierten en puntos del infinito al aplicarles esta
trnasformación.
Las medidas del eje real AA` y del imaginario BB` (aportado según el segmento m)
nos permiten conocer la distancia focal. Esta se obtiene dibujando un rectángulo
de lados iguales a dichos segmentos, siendo la diagonal del mismo la distancia
entre los focos. La perpendicular a la tangente “t” trazada por uno de sus puntos
de corte con la circunferencia principal, por ejemplo el “C” contiene a un foco,
El lado FA tiene por homólogo a la semirecta indefinida que resulta paralela al
segmento AO y que para por el punto doble, 1, de corte del eje con la
prolongación de AF. Igual circunstancia se produce con el homólogo del lado BC.
Téngase en cuenta que los homólogos de los vértices A y B están en el infinito al
pertenecer a la recta límite RL.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE AFINIDAD. De una elipse se conoce su eje mayor AA` y una tangente t. Se pide obtener el punto de tangencia de dicha tangente con la elipse.
lado mayor es seis veces el radio desconocido de las circunferencias, y el lado
menor es valor de dicho radio.
Ayuda. La afinidad, de dirección perpendicular al eje mayor, existente entre una
elipse y la circunferencia de diámetro coincidente con dicho eje nos permite dibujar la circunferencia afín de diámetro AA`. La recta de puntos dobles en esta transformación es el eje AA`. Como la tangencia entre figuras afines se conserva, sacamos la transformada, t`, de la tangente t. Para ello prolongamos dicha recta
hasta cortar a la prolongación del eje AA` en el punto doble 1, desde el que trazamos la tangente t` a la circunferencia, siendo el afín de su punto de tangencia T`
el punto de tangencia, T, buscado.
Para dibujar el rectángulo descrito tomamos un punto cualquiera de la bisectriz
“Ai” y dibujamos una perpendicular al lado “AB” obteniendo un segmento “x”.
Construimos el rectángulo con el lado mayor “6.x” y expandimos el punto m desde A homotéticamente hasta que se posicione según “M” en la bisectriz “Bi”. La
medida del segmento “MT” es el radio de las circunferencias buscadas.
ENUNCIADO DE HOMOTECIA. Inscribir cuatro circunferencias iguales en el triángulo ABC aportado de modo que sean tangentes entre si, siendo las dos de los
extremos tangentes los lados respectivos AC y BC del triángulo.
Ayuda. Partimos del triángulo dato “ABC”. Los centros de las dos circunferencias
extremas están en las bisectrices de los ángulos A y B, es decir, en las rectas “Ai” y
“Bi”.
Analizando el caso resuelto vemos que se forma un rectángulo en el interior del
triángulo “AiB” de modo que la relación de los lados del mismo es 6:1, ya que el
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE SISTEMA DIÉDRICO. Se aportan las proyecciones de un triángulo
a-a`,b-b`,c-c` así como la frontal, F`o, de alejamiento cero de un paralelogramo
de vértices 1, 2, 3 y 4. También se aporta como dato la horizontal, Ho, de cota
cero del mismo. Un tercer lado del paralelogramo es horizontal de cota “h”, y el
cuarto lado del cuadrilátero es frontal de alejamiento “a”. Se pide obtener la
intersección de ambas formas planas.
Para sacar la intersección se podrían determinar las trazas del plano del triángulo,
y luego buscar los puntos de corte de las parejas de trazas homónimas, pero esto
es farragoso y lento en su trazado. Nosotros lo que haremos será hallar la
intersección del plano del cuadrilátero con dos lados del triángulo. Así tendremos
dos puntos “I y J” que, unidos, determinarán la intersección entre estas formas.
Según esto vamos a obtener la intersección del lado AB con el plano del
cuadrilátero, para lo cual tomamos el plano auxiliar proyectante que contiene a
dicho segmento, con su traza horizontal coincidente con la proyección horizontal,
ab, del mismo. Buscamos las intersecciones de este plano proyectante, de traza
vertical no dibujada, con los lados 1-4 y 3-4, siendo los puntos x-x` e y-y` los de
dicha intersección. La recta x`-y` corta al lado a`b` en el punto i´, que tiene su
proyección horizontal, i, en la correspondiente proyección de ab.
La construcción anterior se basa en el hecho de que la intersección de una recta
con un plano proyectante se saca buscando el corte de la traza horizontal del
plano con la correspondiente proyección de la recta, refiriendo a continuación
dicho punto de sobre la proyección vertical de la recta. Téngase en cuenta que los
puntos de un plano proyectante horizontal tienen su proyección horizontal sobre
la correspondiente traza del plano, al ser planos perpendiculares al horizontal.
Ayuda. El conocer la frontal y la horizontal de alejamiento y cota cero significa
que se tienen las trazas de un plano F`o y Ho. La horizontal de dicho plano de cota
“h” es la recta en la que se sitúa un lado del paralelogramo; y la frontal de
alejemiento “a” contiene al lado que falta para la determinación completa de su
perímetro, que es el cuadrilátero con vértices en las intersecciones, 1, 2, 3 y 4 de
estas rectas. Obsérvese cómo el lado 1-2 de la proyección horizontal es paralelo a
la traza Ho; y cómo la proyección vertical 1`-4` es paralela a la traza F`o. De esta
forma tenemos los vértices del cuadrilátero.
Por igual razonamiento se determina el punto y-y de intersección del plano del
cuadrilátero con el lado BC del triángulo. Es importante recalcar que el resultado
final de la intersección de las formas es independiente de los lados del triángulo
que se tomen para la sacar la intersección. También hacemos notar el hecho de
que alguno de los puntos de intersección pueda quedar fuera del perímetro del
polígono, como en nuestro caso ocurre con el punto i-i`. Al unir los puntos I y J se
toma sólo la parte de la recta, por ellos definida, que resulta común al interior de
ambos contornos de las formas dadas.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE SISTEMA DIÉDRICO. Establecer las partes vistas y ocultas del
conjunto de las formas aportadas en la figura cuya intersección se ha obtenido
en el problema anterior. Se trata del conjunto formado por un triángulo de
vértices ABC y un paralelogramo de vértices, 1,2 3 y 4.
AYUDA. El segmento de proyecciones j-n, j`n` es la intersección de ambas formas.
Para determinar las partes vistas y ocultas del conjunto nos basamos en que :
1º Estas son independientes en cada proyección, es decir, que el hecho que un
lado sea visto u oculto en una proyección no implica nada respecto a lo que
ocurra para ese segmento en la otra proyección. 2º Los contornos exteriores son
vistos en ambas proyecciones. 3º En la proyección horizontal es visto siempre lo
que tiene más cota, mientras que en proyección vertical es visto lo de más
alejamiento. 4º También se debe tener en cuenta que cuando un segmento corta
al plano de un polígono, como hace el lado BC con el del paralelogramo, sabemos
que dicho segmento será visto en un sentido, a partir de la intersección, y oculto
en el contrario, siendo el punto de la citada intersección aquel donde se produce
la transición de parte vista a oculta. Así por ejemplo vemos que el segmento j`c`
es visto mientras que j`b` resulta oculto. Obsévese además cómo en nuestro caso
en la proyección horizontal del segmento bjc, hemos tomado el punto w de corte
de bc con 1-2; al referir a la proyección vertical, sobre ambos segmentos, vemos
que el punto w`, situado en 1`-2` tiene más cota que el que tendríamos sobre el
lado b`-c`, por lo que en proyección horizontal el tramo jw es oculto, siendo todo
el segmento 1-2, con el que se cruza, visto. Luego si jw es oculto se cumple, según
lo antes explicado, que jb es visto en dicha proyección, por lo que el tramo yz del
lado 3-4, que con él se cruza, es oculto. Idéntico razonamiento hacemos con los
lados 1-4 y a-b, los cuales se cortan en el punto x (en la proyección horizontal). Lo
referimos a la proyección vertical sobre los lados 1`-4` y a`-b`. Observamos que
tiene más cota por pertenecer a a`-b`, lo que hace que, en la citada proyección
horizontal, a-b sea visto y x-n oculto, siendo n-1 visto.
5º Para la proyección vertical observamos el punto k`=m` de corte de 1`-2` con el
lado a´-c`. Refiriendo desde dicho punto, a las correspondientes proyecciones
horizontales de estos segmentos, vemos que el punto k tiene más alejamiento
por pertenecer al lado AC, lo que hace que este segmento en proyección vertical
sea visto y el otro oculto en el tramo k`1`. En lo que respecta al punto b`, sabemos
que es oculto, al ser el de menos alejamiento del triángulo, lo que hace que los
tramos que parten de él en proyección vertical también lo sean. Analizando ahora
el segmento b`-c` se aprecia que será oculto, como se ha dicho, hasta la
intersección j`, siendo visto el segmento j`-c`.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE SISTEMA AXONOMÉTRICO. El segmento A-a de medida H
aportado como único dato del ejercicio es un cateto de un triángulo rectángulo
isósceles, siendo el otro cateto,ab del triángulo, paralelo al plano del cuadro. Se
pide representar el triángulo.
trazada desde “o”. Se determina así el punto (o) al igual que los ejes abatidos (x) y
(z), que estar´an en verdadera magnitud. La perpendicular a C` trazada desde M
determina en (z) el punto (M), siendo (o)(M)= Hr la verdadera magnitud del
segmento de perspectiva oM y por tanto la del segmento H.
Como el triángulo a dibujar es rectángulo isósceles y el otro cateto es paralelo al
plano del cuadro, se cumple que dicho lado está en verdadera magnitud, siendo
por ello por lo que llevamos la medida (o)(M), obtenida en el abatimiento, en una
paralela a la traza C del xoy con el plano del cuadro para sacar el tercer vértice, b,
del triángulo buscado. La figura inferior muestra el triángulo Aab en el espacio
junto al sistema de ejes axonométricos, xyz, correspondientes a los de la figura de
realización del caso, procedentes de proyectar ortogonalmente, sobre el plano
del cuadro, los ejes reales (X)(Y)(Z) de un triedro trirectángulo de vértice (O).
Ayuda. Sabemos que la medida del segmento Aa=H del dibujo en la perspectiva
no coincide con su valor real, al ser paralelo al eje z, y estar este eje reducido en
cuanto a sus medidas lineales dado que es oblícuo al plano del cuadro.
Para saber la medida real de dicho segmento lo transportamos sobre el eje z
obteniendo el segmento oM. La medida real de dicho segmento se determina
abatiendo el plano xoz sobre un plano del cuadro cualquiera, C-C`-C`` que tiene
sus trazas respectivamente perpendiculares a los ejes proyectados ( x, y, z).
La semicircunferencia de diámetro C` contiene al origen “o” abatido, estando
dicho punto en el corte de la semicircunferencia citada con la perpendicular a C`
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE PERSPECTIVA CABALLERA. Sabiendo que un plano que secciona
a un cono según una parábola ha de ser es paralelo a una generatriz, hallar las
trazas del plano que secciona al cono dado según dicha cónica, conociendo el
vértice, A, de la misma y la perspectiva caballera del cono. Se debe saber
igualmente que la generatriz a la que es paralelo el plano de sección parabólica
es la diametralmente opuesta a la que contiene al vértice de la misma, siendo el
plano que la secciona de este modo perpendicular al de simetría que contiene a
estas dos generatrices. Obténgase, además de la perspectiva caballera de la
parábola sección, su proyección sobre el plano xoy.
Ayuda. Según las orientaciones teóricas expresadas en el enunciado, dibujamos la
genetartiz V1 que contiene al vértice aportado, A, de la parábola, así cómo su
diametralmente opuesta V2, a la que ha de ser paralelo el plano sección. Para
determinarlo nos basamos en que un plano paralelo a una recta contiene a una
paralela a la misma, por lo que trazamos por el punto A la paralela a la generatriz
V1, obteniendo la recta Am, siendo el punto m su traza con el plano xoy. La traza
P con el xoy del plano sección pasa por m, siendo paralela al eje x, ya que dicha
traza es perpendicular al plano definido por V-1-2, que resulta paralelo al yoz en
este caso.
Por otra parte vemos que la generatriz V1 es paralela al plano yoz, al igual que la
generatriz V2 y la recta Am, siendo este último segmento frontal respecto a yoz,
lo que implica que la traza P`` del plano sección sea paralela a la recta Am.
La traza P corta a la base del cono en los puntos 5 y 6, que pertenecen a la
parábola buscada. Para obtener más puntos de la cónica sección proyectamos
sobre yoz una serie de generatrices, como la V1, V3 y V4, y hallamos sus
intersecciones con la traza P``, se determinan una serie de puntos que, mediante
paralelas al eje x, determinan las perspectivas de los de la sección. Este sistema
de hallar intersecciones de generatrices con un plano se debe a que éste es
proyectante respecto el plano coordenado yoz. La proyección de la parábola
sobre el yoz es un segmento de la traza P``.
La proyección de la parábola sobre el plano coordenado xoy es otra parábola que
se determina hallando las proyecciones de los puntos A, B, C.. sobre dicho plano.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE PERSPECTIVA CÓNICA. El cuadrilátero ABCD es la perspectiva
del contorno de la planta rectangular de un edificio con cubierta a dos aguas,
que vierten a los lados AD y BC. La cumbrera del tejado sube una altura “H”
sobre el plano horizontal ABCD. Dibujar las 24 tejas de la cubierta descrita si la
distancia del punto de vista al plano del cuadro es P(V).
Ayuda. Al ser ABCD un rectángulo con parejas de lados paralelos, prolongamos
los opuestos para determinar los puntos de fuga F y F`. La recta F-F` es la línea del
horizonte. Garantizaremos que el cuadrilátero ABCD aportado es un rectangulo
posicionando el punto de vista abatido (V) en una semicircunferencia de diámetro
F-F`. Dicho punto se encuentra en el corte de la semicircunferencia citada con la
paralela, R, a la línea del horizonte trazada a una distancia P(V). Con el punto (V) y
los de puntos de fuga podemos hallar los puntos métricos asociados a las
direcciones que describen F y F`. Para ello trazamos sendos arcos de centros en F
y F` y radios respectivos F(V) y F`(V). Se obtienen así M y M`, siendo M el métrico
asociado a las rectas que fugan a F, y M` el asociado a las que fugan a F`. Por otra
parte las 24 tejas del total hace que a cada agua le correspondan 12=4x3, lo que
hace que el lado mayor del rectángulo AD se divida en 4 partes iguales, mientras
que la mitad de AB la dividamos en 3 partes iguales. Para dividir los segmentos
citados en partes iguales hallamos las verdaderas medidas de los mismos, para lo
cual proyectamos sobre la “LT” los puntos B y D desde los métricos M y M`
respectivamente. Se obtienen así los puntos b y d, siendo Ab la medida real del
segmento representado en cónica por AB; la medida Ad es la longitud real del
lado AD de la perspectiva. Dividimos en partes iguales por Thales los segmentos
Ab y Ad y proyectamos sobre los lados AB y AD desde M y M`, obteniendo la
división en cónica. Para dibujar la cumbrera del tejado prolongamos la recta F`m
hasta su corte con la L.T. y desde dicho corte levantamos la medida real H,
obteniendo Z que, unido con F`, determina la cumbrera dibujada por el punto
medio del rectángulo inicial. Las rectas AE y DJ son paralelas y representan dos
líneas de máxima pendiente de la cubierta, cuyo punto de fuga es F``, al cual irán
a concurrir las líneas de contorno de las tejas rectangulares representadas.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADOS DE REPRESENTACIÓN DE PIEZAS MEDIANTE SUS PROYECCIONES.
Se aporta la planta de una pieza y su alzado representado fuera de norma según
una dirección B. Se pide hallar el alzado normalizado según la dirección
perpendicular.
Ayuda. Analizamos la pieza viendo, en las proyecciones aportadas, las
correspondencias entre los puntos y elementos notables de la misma. De esta
manera podemos localizar, mediante la información de su altura, la proyección
pedida cada punto. Para realizar esto resulta saludable el realizar previamente
una interpretación espacial de la pieza, pudiéndose materializar dicho análisis
mediante un croquis (dibujo a mano alzada) sin responder a las medidas reales.
En el alzado solución puede apreciarse la existencia de dos pequeños segmentos
horizontales ligados por una línea oculta, igualmente horizontal. Esos segmentos
son importantes a la hora de su dibujo, dado que representan el alzado de la
parte de circunferencia que liga o relaciona las dos líneas verticales que limitan la
endidura realizada mediante planos verticales en el cilindro.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
Se aportan las proyecciones diédricas de una serie de piezas, se pide su representación en perspectiva.
Dibujar las vistas necesarias para definir la pieza aportada en perspectiva.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE CORTES Y SECCIONES DE PIEZAS. Dibujar la perspectiva de la
pieza cuyas vistas se aportan, hallar la vista lateral izquierda cortada según A-B,
así como el alzado al que le hemos aplicado el corte por planos paralelos según
las indicaciones de extremos C-D.
PERSPECTIVA A ESCALA:
DATOS:
ALZADO CORTADO SEGÚN C-D Y VISTA LATERAL IZQUIERDA SEGÚN A-B.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
Realizar un croquis con las vistas y cortes necesarios para la definición de la
pieza y acotar sin indicar los valores numéricos de las medidas de cada cota.
NUEVA COLECCIÓN DE PROBLEMAS RESUELTOS Y EXPLICADOS
ENUNCIADO DE ESCALAS GRÁFICAS. Partimos de un dibujo del que se desconoce la escala a la que está realizado. Suponemos que un lado del rectángulo como
el oD en la realidad mide 3,4 metros. Se desea utilizar la escala gráfica para determinar la medida del lado menor del rectángulo representado.
Ayuda. Para hacer una escala gráfica trazamos por el vértice “o” una recta inclinada cualquiera y llevamos en ella, a partir del punto “o”, 34 milímetros correspondientes a los 3,4 metros de la indicación de medida real, obteniendo el punto
X. Unimos X con el extremo D mediante una recta de trazos, y por las divisiones
de los segmentos de 10 milímetros dibujamos paralelas, obteniendo los puntos A,
B y C. Cada segmento de los obtenidos en la recta oD representa un metro a escala en el plano.
Para tener divisiones de decímetros en la contraescala prolongamos hacia la izquierda una medida oE igual a oA, y la dividimos en 10 partes iguales. Para lo cual
dibujamos hacia arriba desde el punto “o” una recta oY cualquiera y llevamos a
partir del extremo “o” diez medidas iguales de cualquier valor, obteniendo “z”.
Unimos “z” con E y trazamos paralelas a la recta zE por los puntos de la división,
para sacar en la prolongación horizontal del lado las divisiones correspondientes a
los decímetros a esta escala.
Para hacer la escala copiamos en la figura inferior las medidas obtenidas con los
puntos o, A B, C y E y prolongamos tanto como queramos para llegar hasta la medida de 9 metros (más si se necesita).
A modo de ejemplo de medición usando, la contraescala con decimales, vemos
que el segmento RS mide una longitud de 5,4 metros a la escala del dibujo.
Para sacar la medida real del lado menor del rectángulo representado colocamos
la escala aportada sobre dicho lado y tenemos que la longitud pedida es de 2,8
metros.