TEMA 1: INTERACCIÓN GRAVITATORIA PARTE 1 • Generalización

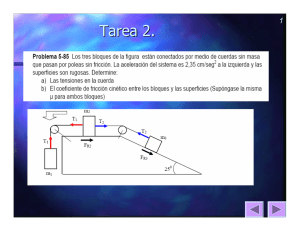
TEMA 1: INTERACCIÓN GRAVITATORIA
PARTE 1
•
•
•
•
Generalización del concepto de trabajo a una fuerza variable.
Teorema del trabajo y la energía cinética.
Fuerzas conservativas.
Energía potencial asociada a una fuerza conservativa. Trabajo y diferencia de
energía potencial. Relación entre fuerza conservativa y variación de energía
potencial. Energía potencial en un punto
• Conservación de la energía. Conservación de la energía mecánica
PARTE 2
• Descripción de una interacción: Acción a distancia y concepto de campo.
• Líneas de fuerza.
• Ley de gravitación universal. Análisis de las características de la interacción
gravitatoria entre dos masas.
• Interacción de un conjunto de masas: Principio de superposición.
• Noción de campo gravitatorio: Intensidad del campo gravitatorio de una masa
puntual.
• Campo gravitatorio terrestre. Variación de "g" con la altura
• Campo gravitatorio de un conjunto de masas.
• Energía potencial gravitatoria de una masa puntual en presencia de otra.
• Noción de potencial gravitatorio.
• Superficie equipotencial.
• Relación entre campo y potencial gravitatorio.
PARTE 3
• Leyes de Kepler
• Movimiento de masas puntuales en las proximidades de la superficie terrestre
• Satélites. Velocidad orbital y velocidad de escape.
AMPLIACIÓN
• Circulación de un vector a lo largo de un camino c
• Flujo a través de una superficie
• Flujo de la intensidad de campo a través de una superficie cerrada. Teorema de
Gauss
GENERALIZACIÓN DEL CONCEPTO DE TRABAJO A UNA FUERZA
VARIABLE
Supongamos que queremos llevar un cuerpo desde un punto A hasta otro B a lo largo de
un determinado camino:
(recuerda que el móvil no tiene porqué moverse
según la resultante de la fuerza que actúa sobre él
porque puede tener algún tipo de restricción)
r
Por definición, el trabajo realizado por la fuerza F para desplazarlo una longitud
infinitesimal es el producto escalar de la fuerza por el vector desplazamiento:
r r
dW = F • d r
dW = trabajo elemental
r
F = vector fuerza
r
r
r
d r = vector desplazamiento = dx i + dy j
El trabajo total para llevar al cuerpo desde el punto A al B por el camino c lo obtenemos
mediante la integral definida entre esos puntos:
Br
r
WA→B,c = ∫ F • d r
A ,c
En general, el trabajo realizado por una fuerza para llevar un cuerpo desde un punto A
hasta otro punto B depende del camino que se siga.
(Más adelante trataremos las fuerzas conservativas, que son aquellas que realizan el
mismo trabajo para llevar un cuerpo desde un punto hasta otro sin importar el camino
seguido.)
Lo expresamos como:
WA →B,c1 ≠ WA →B,c 2
∫
B
r r
Br
r
F • dr ≠ ∫ F • dr
A ,c1
A ,c 2
Caso particular: Cuando la fuerza es constante en módulo y dirección.
Si observas las figuras siguientes verás que para desplazamientos grandes el módulo
del vector desplazamiento no coincide con el espacio recorrido sobre la trayectoria, pero
para un desplazamiento infinitesimal sí que son iguales:
r
∆ r ≠ ∆s
r
d r = ds
pero
r r
Así que podemos poner dW = F • d r = F ⋅ dr ⋅ cos α = F ⋅ ds ⋅ cos α
si F y α son constantes podemos sacarlas de la integral:
WA→B
F. cons tan te
= ∫ F ⋅ cos α ⋅ ds = F ⋅ cos α ∫ ds = F ⋅ cos α ⋅ [s ]s BA = F ⋅ cos α ⋅ (s B − s A ) = F ⋅ s ⋅ cos α
B
sB
A
sA
WA →B
s
= F ⋅ s ⋅ cos α
F. cons tan te
Ejemplo: Un niño tira de un camión de juguete aplicando una fuerza de 20N mediante
una cuerda que forma un ángulo de 60º con la horizontal. Calcular el trabajo que realiza
cuando lo arrastra 10m.
r
r
r
Aplicando la definición general de trabajo y teniendo en cuenta que F = F cos α ⋅ i + Fsenα ⋅ j
y que en este caso como únicamente se desplaza a lo largo del eje X ( no varía de coordenada
r
r
r
r
Y con lo que siempre dy=0) y el vector desplazamiento nos quedaría d r = dx i + dy j = dx i
r
r
r
Br
x =10
r
WA→B,c = ∫ F • d r = ∫ (F cos α ⋅ i + Fsenα ⋅ j ) • dx ⋅ i
A ,c
x =0
r r
r r
recordando que i • i = 1 y que i • j = 0
Como integramos respecto a x, los límites de integración son desde xA=0 hasta xB=10
WA→B,c = ∫
x =10
x =0
F cos α ⋅ dx = [F cos α ⋅ x ]x =0 = 20 ⋅ cos 60 ⋅ (10 − 0) = 100Julios
x =10
Como en este caso la fuerza es constante también podríamos haber aplicado la
definición particular de trabajo: WA→B = F ⋅ s ⋅ cos α = 20 ⋅ 10 ⋅ cos 60 = 100 J
Observa que únicamente realiza trabajo la componente de la fuerza que lleva la
dirección del desplazamiento (F.cosα)
Ejemplo: Calcular el trabajo que hacemos para levantar verticalmente, con velocidad
constante, un cuerpo de 2 Kg hasta una altura de 3 metros.
Calcular el trabajo realizado por el peso y el trabajo realizado por la fuerza resultante.
Fíjate bien que cuando en el enunciado dice “levantar con velocidad constante” eso es
un dato muy importante, porque, de acuerdo con las leyes de Newton, quiere decir que
la suma de las fuerzas sobre el cuerpo es nula. Por tanto, si el cuerpo está sometido a la
fuerza peso=mg, la fuerza que deberemos hacer para subirlo con velocidad constante
debe tener el mismo módulo F=mg, la misma dirección y sentido contrario.
Aplicando la definición general de trabajo:
Tendremos en cuenta que el movimiento es sobre el eje Y y que por tanto no varía la
r
r
r
r
coordenada X (dx=0). El vector desplazamiento nos quedaría d r = dx i + dy j = dy j
r
r
B r
y =3
y =3
r
y =3
WA→B = ∫ FFuerzaF • d r = ∫ mg j • dy j = ∫ mg dy = [mg y]y =0 = 20(3 − 0) = 60Julios
FuerzaF
y =0
A ,c
y =0
Observa que como ahora hemos integrado respecto a dy, los límites de integración han
sido desde y=0 hasta y=3.
El trabajo que hace la fuerza peso, siguiendo el mismo procedimiento sería:
r
r
B r
y =3
y =3
r
y =3
WA→B = ∫ FPeso • d r = ∫ mg (− j) • dy j = ∫ − mg dy = [− mg y ]y = 0 = −20(3 − 0) = −60Julios
Peso
y =0
A ,c
y=0
El signo menos del trabajo se interpreta como que la fuerza pero realmente no hará
nunca ese trabajo sino que haría el contrario. Como sabemos por experiencia, el peso no
sube de forma espontánea a los cuerpos sino todo lo contrario.
El trabajo total puede obtenerse de dos formas:
• Como suma de todos los trabajos realizados por cada una de las fuerzas.
WA →B = ∑ W = 60 + (−60) = 0
TOTAL
r
• Como el trabajo que hace la fuerza resultante. Como FRe sul tan te = 0
B r
r
WA →B = ∫ FRe sul tan te • d r = 0
TOTAL
A ,c
Aplicando la definición particular de trabajo:
En este caso podemos resolver el ejercicio aplicando la definición particular de trabajo
para fuerzas constantes, ya que (para puntos próximos a la superficie terrestre) podemos
considerar que el peso no varía y tampoco la fuerza que hemos de hacer para subirlo con
velocidad contante, ya que es igual al peso y de sentido opuesto)
WA→B = F ⋅ s ⋅ cos α
Para aplicar esa expresión a la fuerza F tendremos en cuenta que: el módulo de la fuerza
es igual al peso, es decir, FFuerzaF=mg, que el espacio que recorre es s=3m y que el ángulo
que forma la fuerza que hacemos y el desplazamiento es de 0º
WA→B = FFuerzaF ⋅ s ⋅ cos α = mg ⋅ s ⋅ cos α = 20 ⋅ 3 ⋅ cos 0 = 60 J
FuerzaF
Para aplicar la expresión a la fuerza peso tendremos en cuenta que, al igual que antes, el
módulo del peso es FPeso=mg, el espacio recorrido es s=3m, pero ahora (puesto que se
mueve hacia arriba) el ángulo que forma el desplazamiento y la fuerza peso es de 180º
WA→B = FPeso ⋅ s ⋅ cos α = mg ⋅ s ⋅ cos α = 20 ⋅ 3 ⋅ cos 180 = −60 J
Peso
Observaciones:
Muchos alumnos confunden los vectores con su módulo. Especialmente cuando se trata
de movimientos en una dimensión y se suprimen los vectores unitarios de los ejes
“sustituyéndolos” solamente por su signo. Es decir que (como ocurre en este caso donde
el movimiento es solo en el eje Y) podremos escribir los vectores como:
r
r
r
FFuerzaF = mg j o simplemente +mg (con el + indicamos que lleva dirección y sentido de j )
r
r
r
FPeso = − mg j o simplemente –mg (con el – indicamos que lleva dirección y sentido de − j )
Los módulos de los vectores “nunca tienen signo” ya que el módulo solamente
indica el valor. Entiende de una vez que el signo hace referencia al sentido del
vector y no del módulo.
Ahora bién, las magnitudes escalares sí que pueden tener signo como le ocurre al
trabajo.
De acuerdo a lo anterior, sería un disparate escribir
WA→B = − mg ⋅ s ⋅ cos α = −20 ⋅ 3 ⋅ cos 180
Peso
porque al poner –mg estaríamos sustituyendo el módulo de la fuerza por su expresión
r
vectorial (aunque no le pongamos la j ). Por otro lado, el signo menos ya nos aparecerá
como consecuencia de que cos180=–1, pero si lo hiciéramos mal tendríamos dos signos
menos y el trabajo final sería positivo, que sería como decir que la fuerza peso es capaz
de hacer un trabajo y de subir un cuerpo hasta una altura mayor.
Ejemplo: Un cuerpo de 20 Kg se encuentra en la base de un plano inclinado 30º sobre
la horizontal, sin rozamiento. Un hombre tira de él y lo sube hasta una altura de 1,5 m.
a) con qué fuerza debe tirar el hombre para subirlo con velocidad constante
b) que trabajo realiza
c) si otro hombre lo sube verticalmente hasta la misma altura con la ayuda de una polea
d) ¿qué fuerza y que trabajo realizaría en este otro caso?
a) Si el hombre sube el cuerpo con velocidad constante quiere decir, de acuerdo con la
2º ley de Newton, que la suma de las fuerzas es cero, por tanto:
de la figura se deduce que para que la suma de las fuerzas sea cero, el hombre debe
ejercer una fuerza igual a la componente del peso que tiene la dirección del plano:
F = mg ⋅ senα = 20 ⋅ 10 ⋅ sen 30 = 100 New
b) El espacio recorrido sobre el plano para que ascienda 1,5m se calcula como:
1,5
sen 30 =
⇒ s = 3 metros
s
El trabajo, aplicando la expresión particular porque la fuerza es constante: (Mucho cuidado
de no confundirte con el ángulo. Aquí α es el ángulo que forma la fuerza F con el
desplazamiento, que es 0º):
W = F ⋅ s ⋅ cos α = 100 ⋅ 3 ⋅ cos 0 = 300Julios
c) El hombre que sube el cuerpo con velocidad constante con la ayuda de una polea:
Aplicando la segunda ley a todo el sistema
F − mg = ma como v=cte → a=0
F = mg = 20 ⋅ 10 = 200 New
Como vemos, al tratarse de una polea es ideal y que la fuerza
que aplicamos no tiene masa, entonces se transmite
íntegramente: F=mg
d) Como F es una fuerza constante, aplicando la expresión particular del trabajo que
realiza el hombre para subir la masa 1,5 m tendremos:
W = F ⋅ s ⋅ cos α = 200 ⋅ 1,5 ⋅ cos 0 = 300Julios
Observa que el trabajo que realiza el hombre para subir el cuerpo con velocidad
constante por el plano y por la vertical es exactamente el mismo, y eso es así porque no
hay rozamiento, sin embargo la fuerza que debe ejercer si lo sube por el plano es más
pequeña.
En el caso de que hubiese rozamiento el trabajo realizado por el plano sería mayor que
por la vertical, pero aún así la fuerza que debe ejercer sigue siendo menor, de ahí la
utilidad de los planos.
Ejemplo: Un niño tiene una pistola de juguete que funciona con un resorte, como la que
se indica en la figura. La constante de recuperación del muelle es de 500 N/m ¿Qué
trabajo realiza el niño cada vez que comprime el resorte 20 cm para cargarla?
La fuerza que debe hacer el niño para comprimir el muelle, con velocidad constante, es
exactamente igual a la fuerza recuperadora del muelle pero en sentido contrario:
FRe cuperadora = −k ⋅ x
( Muelle )
FDeformadora = k ⋅ x
( Niño )
r
r
o bien FRe cuperadora = − k ⋅ x i
( Muelle )
r
r
o bien FDeformadora = k ⋅ x i
( Niño )
El signo menos de la fuerza recuperadora se
interpreta como que esa fuerza se opone a la
deformación. (Si, como en la figura,
deformamos el resorte hacia la parte positiva
la fuerza recuperadora apunta hacia la parte
negativa y viceversa.)
En este caso la fuerza que hace el niño no es constante puesto que depende de x, por
tanto tendremos que utilizar obligatoriamente la definición general de trabajo. La fuerza
r
r
que hace el niño en forma de vector es FNiño = kx i y el vector desplazamiento, como
r
r
r
r
solo se desplaza a lo largo del eje X, nos quedaría d r = dx i + dy j = dx i
r
r
Br
x B =0 , 2
x B =0 , 2
r
1
WA→ N , Niño = ∫ FNiño • d r = ∫
kx i • dx i = ∫
kx ⋅ dx = kx 2
A
x A =0
x A =0
2
0,2
0
=
1
500(0,2 2 − 0 2 ) = 10Julios
2
Este trabajo que ha realizado el niño al cargar la pistola: W = 12 kx 2 queda almacenado en
el resorte (En forma de energía potencial como veremos más adelante). Al apretar el gatillo
r
r
y dejar libre el muelle actúa la fuerza recuperadora FRe cuperadora = − k ⋅ x i y de esta forma se
( Muelle )
nos devuelve el trabajo que realizamos al cargarla. Comprueba que el trabajo hecho por la
fuerza recuperadora para llevar el muelle desde B hasta A es también 10Julios.
POTENCIA
Dos máquinas pueden realizar el mismo trabajo, una en poco tiempo y la otra tardando
más. Para identificar a la mejor se define la potencia como el trabajo realizado en la
unidad de tiempo, así:
dW
P=
dt
teniendo en cuenta la definición de trabajo podemos encontrar otra expresión análoga:
r r
dW F • d r r r
P=
=
= F• v
dt
dt
Ejemplo
Un motor eléctrico se utiliza para elevar un peso de 250Kg desde el suelo hasta una
altura de 25m. Se emplea en la operación un tiempo de 5 minutos. Si el motor consume
500 watios ¿Cuánto vale la energía perdida?.
El trabajo que realmente hace el motor es:
Wmotor = P ⋅ t = 500 ⋅ (5 ⋅ 60) = 150000Julios
El trabajo útil es el que realmente hace falta para subir los
250Kg a la altura de 25m:
Wutil = F ⋅ s = mg ⋅ s = 250 ⋅ 10 ⋅ 25 = 62500Julios
El trabajo perdido, que se transformará en calor es:
Wperdido = Wmotor − Wutil = 87500Julios
El rendimiento del motor sería:
Re n dim iento =
Wutil
62500
100 =
100 = 41,7%
Wmotor
150000
TEOREMA DEL TRABAJO Y LA ENERCIA CINÉTICA
Si tenemos en cuenta la definición de trabajo, la segunda ley de Newton y que
r
r
v = d r dt , podemos poner que:
r
r
r r
dv r
dv r
dW = F • d r = m • d r = m • v ⋅ dt
dt
dt
r r
teniendo en cuenta que dv y v son vectores en la misma dirección y sentido y que por
tanto el coseno del ángulo que forman es 1:
r r
dW = m ⋅ dv • v = m ⋅ v ⋅ dv
WA→B,Todas las fuerzas
B
1
1
1

= ∫ mv ⋅ dv =  mv 2  = mv 2B − mv 2A
A
2
2
A 2
B
WA →B,Todas las fuerzas = Ec B − Ec A = ∆Ec
Lo que nos dice que “el trabajo realizado por la fuerza F (resultante de “todas las
fuerzas”, incluida la de rozamiento si existe) para llevar el cuerpo desde un punto A
hasta otro B es igual a la variación de energía cinética entre esos puntos”. Se conoce
como teorema de las fuerzas vivas.
Ejemplo: Si dejamos caer un cuerpo de 2Kg desde una altura de 5m ¿Qué energía
cinética tendrá al llegar al suelo?
Posiblemente la reacción de algún alumno sea calcular el valor de la velocidad al llegar
al suelo y luego aplicar la fórmula de la energía cinética. Eso estaría bien, pero vamos a
resolverlo aplicando el teorema de las fuerzas vivas.
Como el peso puede considerarse constante podemos aplicar la definición particular de
trabajo. El trabajo realizado, en este caso, por la fuerza peso que tiene la misma
dirección y sentido del desplazamiento, es:
W = F ⋅ s ⋅ cos α = mg ⋅ s ⋅ cos 0 = 20 ⋅ 5 ⋅ 1 = 100 julios
Aplicando el teorema del trabajo y la energía cinética y teniendo en cuenta que la
energía cinética en el punto A (arriba) es nula porque parte del reposo, sería:
WA →B,Todas las fuerzas = Ec B − Ec A
⇒
Ec B = 100 julios
Ejemplo: Un ciclista va a 5 m/s por una calle horizontal. Cuando se le cruza una suegra
frena para no pillarla y se detiene en 5m. ¿Cuánto vale el coeficiente de rozamiento?
Si el ciclista se termina parando, quiere decir que toda su energía cinética inicial se
disipará en rozamiento. De acuerdo con el teorema del trabajo y la energía cinética:
WA →B,Todas las fuerzas = ∆Ec
Sobre el ciclista hay tres fuerzas: peso, normal y FRoz. Como el peso y la reacción del
plano se anulan, finalmente nos queda que la fuerza resultante es igual a la fuerza de
rozamiento FRoz = µN = mg µ . Como la FRoz es una fuerza constante podemos aplicar la
definición particular de trabajo:
1
1
FRoz ⋅ s ⋅ cos180 = mv f2 − mv i2
2
2
1
mg µ ⋅ s ⋅ (−1) = − mv i2
2
µ=
⇒
v i2
52
=
= 0,25
2gs 2 ⋅ 10 ⋅ 5
Ejemplo: Un proyectil de 15gr se mueve con una velocidad de 1500m/s cuando choca
con un saco de arena y se para después de recorrer 10cm ¿Qué trabajo ha realizado la
arena sobre el proyectil?. Suponiendo constante la fuerza que realiza este trabajo,
¿cuánto vale?
El ejercicio es exacto al anterior. Aplicando el teorema del trabajo y la energía cinética
concluiremos que el trabajo realizado por la fuerza que hace la arena (fuerza de
rozamiento de la bala con la arena) debe ser igual a la energía cinética que tenía la bala:
WA→B,Todas las fuerzas = ∆Ec
WF. arena =
⇒
1
1
1
mv f2 − mv i2 = − 0,015 ⋅ 1500 2 = −16875Julios
2
2
2
La fuerza (de rozamiento) que disipa este trabajo es:
WF. arena = Farena ⋅ s ⋅ cos 180
⇒
Farena =
− 16875
= 168750 New
0,10 ⋅ (−1)
FUERZAS CONSERVATIVAS
En los ejemplos anteriores hemos visto como un cuerpo que tiene energía cinética es
capaz de realizar un trabajo. Supongamos ahora que lanzamos una piedra hacia arriba
con una determinada velocidad inicial. Ya sabemos que, si despreciamos el rozamiento,
la piedra al volver a la posición inicial tendrá la misma velocidad (aunque de sentido
opuesto). Quiere decir que tiene la misma energía cinética inicial y final, y que por tanto
el cuerpo “conserva su capacidad de hacer trabajo”. Las fuerzas gravitatorias, por tanto,
son conservativas.
Siguiendo con el mismo ejemplo, si ahora consideramos que hay rozamiento, la velocidad
de la piedra al llegar será menor que la inicial, lo que quiere decir que su energía cinética
es menor y por tanto que el rozamiento es una fuerza disipativa o no conservativa.
En general el trabajo realizado por una fuerza F al llevar un cuerpo del punto A al B
depende del camino seguido. “Decimos que una fuerza es conservativa cuando el trabajo
que realiza para llevar un cuerpo desde un punto A hasta otro B es independiente del
camino seguido y solamente depende de la posición de los puntos inicial y final”. Por tanto
si el trabajo lo hace una fuerza conservativa podemos poner que:
WA →B,c1 = WA → B,c 2
como al cambiar los límites de integración la integral cambia de signo, podemos escribir:
WA →B,c1 + WB→A ,c 2 = 0
también se escribe:
o bien, como el camino no importa
WA →B + WB→ A = 0
r r
F
∫ • dr = 0
Quiere decir que “el trabajo realizado por una fuerza conservativa a lo largo de una
trayectoria cerrada es nulo”. Fíjate como en la segunda expresión no hemos indicado el
camino seguido, puesto que al tratarse de una fuerza conservativa el trabajo es
independiente de la trayectoria seguida.
Resumiendo, podemos definir a las fuerzas conservativas diciendo:
•
•
Aquellas que al llevar un cuerpo de un punto A hasta otro B, realizan un trabajo
que no depende el camino seguido: WA →B,c1 = WA→ B,c 2 , sino que solamente de la
posición de los puntos inicial y final.
Aquellas que al recorrer una trayectoria cerrada hacen un trabajo nulo:
r r
∫ F • d r = 0 (Quiere decir que el trabajo es nulo cuando parten de un punto y,
siguiendo una trayectoria cualquiera, vuelven al mismo punto.)
Son fuerzas conservativas, obviamente las que cumplen con esas definiciones, pero a
título indicativo diremos que son fuerzas conservativas todas aquellas que no dependen
del tiempo o de la velocidad, es decir, son conservativas las fuerzas que sean constantes
(a excepción de la de rozamiento) y también aquellas que dependen de una coordenada y
actúan a lo largo de ella, como por ejemplo la fuerza elástica de un resorte.
Un tipo de fuerzas conservativas muy importantes son las fuerzas centrales, como es el
caso de las gravitatorias y eléctricas. (Fuerzas centrales son aquellas cuya dirección pasa
por un punto llamado centro de fuerzas y su módulo depende de la distancia al centro de
fuerzas)
Ejemplo: Calcular el trabajo que la fuerza peso realiza para llevar un cuerpo de 2Kg
desde el punto A hasta el B siguiendo los dos caminos de la figura
Lo primero de todo será dibujar la fuerza peso, que “siempre” vayamos por donde
vayamos es la misma: tiene un módulo de P=mg=20New y la dirección vertical hacia
r
r
abajo (en forma vectorial sería P = −20 j ). El trabajo por cada camino (teniendo en
cuenta que la fuerza peso puede considerarse constante y podremos aplicar la definición
particular de trabajo) es:
WA→B por el camino 1 será igual al WA→P + WP→B
• WA→P = F.s.cosα = 20.4.cos90 =0
• WP→B = F.s.cosα = 20.3.cos180 = –60 J
• WA→B = WA→P + WP→B = 0 +(– 60) = –60 J
Observa que en el tramo de A→P el trabajo es nulo porque la fuerza peso es
perpendicular al desplazamiento, mientras que en el tramo P→B el trabajo resulta
negativo porque la fuerza y el desplazamiento forman 180º. (El signo menos indica
que la fuerza Peso nunca realizará ese trabajo, sino el contrario)
WA→B por el camino 2
• WA→P = F.s.cosα = 20 ⋅ 5 ⋅ cos 126,87 = – 60J
Donde hemos tenido en cuenta que el espacio, de acuerdo
con el teorema de Pitágoras, es s = 4 2 + 3 2 = 5
El ángulo que forma la fuerza y el desplazamiento es
126,87º. Es igual a β+90, donde β = arctg3 / 4 = 36,87 º
A la misma conclusión llegaríamos si la trayectoria fuese
cualquier otra, porque siempre podríamos descomponerla en un trozo infinitesimal
r
r
horizontal (a través del cual el trabajo sería nulo porque P ⊥ d r ) y otro vertical (donde el
r
r
trabajo elemental sería P • dy j ).
ENERGÍA POTENCIAL
Imaginemos una maceta en lo alto de un balcón. Como consecuencia de su posición “en
un campo de fuerzas conservativo como el gravitatorio”, tiene una cierta energía
acumulada que puede convertir en trabajo en cualquier momento. Lo mismo podríamos
decir para el caso de un resorte que se encuentra desplazado respecto de su posición de
equilibrio, dado que las fuerzas elásticas también son conservativas.
Puesto que el trabajo realizado por una fuerza conservativa para llevar un cuerpo desde un
punto A hasta otro B es independiente del camino seguido y solamente depende de la
posición de los puntos, a esos puntos podemos asignarle una energía llamada potencial que
es función de la posición. Por definición, “el trabajo que hace una fuerza conservativa para
llevar un cuerpo desde un punto A hasta otro B es igual a menos la variación de energía
potencial entre esos puntos”:
WA→B,F.Conservativa = − ∆Ep = Ep A − Ep B
El signo menos indica que la fuerza conservativa del campo hace trabajo espontáneo o
real (trabajo positivo) cuando desplaza el cuerpo desde los puntos de mayor energía
potencial a los puntos con menor energía potencial. Dicho de otra forma, cualquier cuerpo
sometido a la acción de una fuerza conservativa se mueve espontáneamente desde los
puntos de mayor energía potencial a los puntos con menor energía potencial. (Observa
que WA →B,F.Conserv.Campo = + cuando EpA > EpB)
Propiedades de la energía potencial:
1. Es una energía que posee un cuerpo debida a la posición que ocupa en un campo de
fuerzas conservativas, o dicho de otra forma, es una energía que depende de la
separación entre las partículas que interaccionan.
2. De lo anterior se deduce que la Ep es una magnitud asociada a la interacción entre
dos cuerpos. Quiere decir que una masa no tiene Ep a menos que esté cerca de otra masa
como la tierra, es decir, que un cuerpo, por el simple hecho de moverse tiene asociada
una energía cinética, pero no tiene porqué tener energía potencial
3. La expresión de la energía potencial depende del tipo de fuerza conservativa. Como
demostraremos más adelante:
WA→B,F.Conservativa
= Ep A − Ep B = mg h A − mg h B
Campo Gravitatorio
puntos próximos a la Tierra
WA→B,F.Conservativa
= Ep A − Ep B = −G
Campo Gravitatorio
entre dos puntos cualquiera
WA→B,F.Conservativa = Ep A − Ep B = K
Campo Eléctrico
M⋅m
M⋅m
− −G
rA
rB
q ⋅ q´
q ⋅ q´
−K
rA
rB
1
1
WA→B,F.Conservativa = Ep A − Ep B = Kx 2A − Kx 2B
2
2
Fuerza elástica resorte
4. No tiene ningún sentido hablar de energía potencial en un punto o energía potencial
absoluta. De acuerdo con su definición como “el trabajo realizado por la fuerza
conservativa para llevar un cuerpo de un punto A hasta otro B …” vemos claramente
que solamente puede hablarse de variación de energía potencial entre dos puntos.
5. No obstante, puede definirse energía potencial absoluta asignando valor cero a la
energía potencial de un punto cualquiera. La elección del punto cuya Ep=0 es
absolutamente arbitraria. Normalmente en el campo gravitatorio y el eléctrico se suele
asignar valor cero a la Ep en el infinito (por la razón que ya veremos). En el caso de un
resorte se le asigna Ep=0 a la energía que tiene en la posición de equilibrio.
Br
r
WA→B,F.Conservativa = −∆Ep = Ep A − Ep B = ∫ FF.Conserv • d r
A
Si hacemos Ep B = 0
Si a la energía potencial del cuerpo en el punto B (o el A) le asignamos, por acuerdo, el
valor cero, entonces podríamos hablar de energía potencial absoluta en el punto A (o el
B) aunque en realidad sigue siendo una diferencia de energía potencial entre el punto y
el otro al que hemos asignado cero.
En los problemas de mecánica es corriente asignarle cero a la energía potencial en la
superficie de la tierra (aunque sea más riguroso asignar Ep ∞ = 0 ). Así, la energía
potencial de un gato en lo alto de un balcón sería: Ep = mgh como demostraremos más
adelante.
6. En un campo de fuerzas conservativas el trabajo que hacemos nosotros para llevar, contra
las fuerzas del campo y sin aceleración, un cuerpo desde un punto A hasta otro B no se
pierde, sino que queda acumulado en forma de energía potencial. Así podemos decir que “el
trabajo que hacemos nosotros para llevar un cuerpo desde un punto A hasta otro B, contra
las fuerzas del campo y sin aceleración, es igual a la variación de energía potencial entre
esos puntos”
WA→B,nosotros = Ep B − Ep A = ∆Ep = − WA →B,F.Conserv.Campo
Es lógico que el trabajo que hacemos (en contra de la fuerza conservativa para llevar el
cuerpo sin aceleración desde un punto a otro) sea igual al que hace la fuerza conservativa,
pero con distinto signo, ya que para que el cuerpo se mueva sin aceleración la fuerza que
debemos hacer debe ser exactamente igual a la conservativa pero en sentido contrario.
Así pues, el trabajo realizado por nosotros para deformar el muelle una distancia x queda
almacenado en forma de energía potencial elástica. Si soltamos el muelle él volverá a la
posición de equilibrio y realizará el mismo trabajo que hicimos para deformarlo. En otras
palabras nos devuelve el trabajo que hicimos nosotros para deformarlo. (exactamente
igual podríamos decir de la maceta en el balcón.)
Hay que recalcar que los trabajos, aunque sean iguales en valor, son realizados por
fuerzas distintas, así como que la fuerza que hacemos nosotros no es conservativa:
•
•
para subir, sin aceleración, la maceta al balcón o comprimir el resorte, nosotros
hemos de realizar una fuerza contraria al peso, o contraria a la fuerza
recuperadora en el caso del muelle.
cuando soltamos la maceta, el trabajo lo realiza ahora la fuerza conservativa: la
fuerza gravitatoria (el peso), o la fuerza recuperadora en el caso del muelle.
Quiere decir que ahora el trabajo que hicimos y estaba acumulado en Ep nos lo
devuelve el sistema.
Imagina que para llevar un cuerpo desde un punto A hasta otro B nosotros hacemos
un trabajo de 10 Julios (por ejemplo para subir un cuerpo hasta una determinada
altura), entonces, si en el punto A tenía una energía potencial x, en el punto B tendrá
una energía potencia x+10 :
Recuerda que aunque la fuerza que hacemos nosotros para llevar el cuerpo “sin
aceleración” sea igual en módulo a la fuerza conservativa peso, no por eso la fuerza que
hacemos es conservativa. (Un Seat Panda puede ir por una carretera a la misma
velocidad que un Mercedes y no por eso el Panda es un Mercedes.)
Ejemplo: Demuestra que el trabajo realizado por nosotros, contra las fuerzas del campo
y sin aceleración, queda almacenado en forma de energía potencial y es igual al trabajo
que nos devuelve la fuerza conservativa. a) Para las fuerzas elásticas de un resorte b)
Para el peso en las inmediaciones de la superficie terrestre.
Ya hemos dicho que el trabajo para llevar un cuerpo de un punto A hasta otro punto B
que hace la fuerza conservativa y el que hacemos nosotros (para llevarlo sin aceleración)
son iguales aunque de signo contrario. Eso es evidente ya que la fuerza que debemos
hacer nosotros es exactamente igual a la conservativa pero en sentido contrario.
Por otro lado, el trabajo que hace cualquier fuerza (sea la que sea) para llevar un cuerpo de
un punto A hasta otro B es igual y de signo contrario al que hace para regresarlo desde B
hasta A por el mismo camino (o por cualquier otro camino si la fuerza es conservativa). (Es
una propiedad de las integrales definidas: si cambiamos los límites de integración el
resultado es el mismo cambiado de signo.)
De acuerdo con esto y con lo anterior tendremos que WA→B,nosotros = WB→A ,F.Conserv.Campo
a) Caso del resorte:
Supongamos un resorte como el de la figura, que sigue la ley de Hooke. Para deformarlo
hemos de aplicar una fuerza exactamente igual a la fuerza recuperadora del muelle y de
r
r
sentido contrario, es decir que Fnosotros = kx ⋅ i mientras que al soltarlo quien trabaja es la
r
r
fuerza recuperadora elástica que vale Fresorte = −kx ⋅ i . Por otro lado como el
r
r
desplazamiento es según el eje X, el vector desplazamiento será: d r = dx ⋅ i
(
)
r
r B
r
r B
1
1
WA→B,nos = ∫ Fnos • d r = ∫ kx ⋅ i • dx ⋅ i = ∫ kx ⋅ dx = kx 2 BA = k x 2B − x 2A
2
2
A
A
A
Ar
r
r A
r A
1
1
WB→A ,resort = ∫ Fresort • d r = ∫ − kx ⋅ i • dx ⋅ i = ∫ − kx ⋅ dx = − kx 2 AB = k x 2B − x 2A
2
2
B
B
B
B
(
)
Como vemos el trabajo realizado por el niño para cargar la pistola queda guardado en
forma de EP y es igual al trabajo que la fuerza elástica del resorte hace para llevarlo de
nuevo del punto B al A.
Podría preguntarse ¿porqué si hemos recorrido un ciclo completo el trabajo en el ciclo
no es nulo? La respuesta es muy simple, porque los trabajos no están hechos por la
misma fuerza, ya que en el primer caso la hacemos nosotros y en el segundo el resorte.
b) Caso del campo gravitatorio, en puntos próximos a la superficie terrestre:
Por ahora nos limitaremos a demostrar para puntos próximos a la superficie terrestre
(donde el valor de g podemos considerarlo constante) el trabajo realizado por nosotros
para llevar una masa de un punto A hasta otro B queda acumulado en forma de Ep y es
igual al trabajo que el campo gravitatorio hace para llevarlo de nuevo del punto B al A.
Para subir, sin aceleración, el cuerpo desde al punto A al B tenemos que hacer una
r
r
fuerza exactamente igual al peso y de sentido contrario, es decir que Fnos = mg ⋅ j ,
mientras que para ir desde el punto B al A es la fuerza del campo gravitatorio (el peso)
r
r
la que lo lleva y por tato la que realiza el trabajo Fcampo = − mg ⋅ j . Por otro lado, en este
r
r
caso como nos movemos sobre el eje Y, el vector desplazamiento es: d r = dy ⋅ j
r
r B
r
r B
= ∫ Fnos • d r = ∫ mg ⋅ j • dy ⋅ j = ∫ mg ⋅ dy = mgy BA = mgh B − mgh A = mgh
B
WA→B,nos
A
A
A
r
r A
r
r A
= ∫ Fcampo • d r = ∫ − mg ⋅ j • dy ⋅ j = ∫ − mg ⋅ dy = − mgy
A
WB→ A ,campo
B
B
A
B
= mgh B − mgh A = mgh
B
Fíjate que en este ejemplo hemos llevado el cuerpo desde el punto A hasta el B
siguiendo la vertical, pero sería igual si hubiésemos seguido otro camino cualquiera:
En efecto, el resultado sería exactamente el mismo. En este caso al movernos en dos
r
r
r
dimensiones el vector desplazamiento sería d r = dx ⋅ i + dy ⋅ j . Al realizar el producto
r
escalar de la fuerza, tanto de la que hacemos nosotros que tiene dirección j como de la
r
que hace el campo, que tiene dirección − j por el vector desplazamiento nos quedaría
r r
lo mismo, ya que como sabemos i • j = 0 porque son vectores perpendiculares y el
coseno de 90º es nulo.
Ejemplo: Un cuerpo de 20 Kg se encuentra en la base de un plano inclinado 30º sobre
la horizontal, sin rozamiento. Un hombre tira de él y lo sube hasta una altura de 1,5 m.
a) con qué fuerza debe tirar el hombre para subirlo con velocidad constante
b) que trabajo realiza
Ya resolvimos este mismo ejemplo mas arriba por métodos dinámicos, ahora lo
resolveremos teniendo en cuenta que el trabajo que hace el hombre para llevar el cuerpo
desde el punto A hasta el B es igual a la diferencia de energía potencial. Además si
consideramos el nivel cero de energía potencial en el punto mas bajo, el A, entonces:
WA →B,nosotros = ∆Ep = Ep B − Ep A = mgh B = 20 ⋅ 10 ⋅ 1,5 = 300Julios
Ejemplo: Calcular la variación de energía potencial que experimenta un cuerpo de
70Kg, cuando lo trasladamos desde el punto A(1,2) hasta otro B(5,10).
Br
r
r
r
r B
∆Ep = WA →B, nosotros = ∫ Fnosotros • d r = ∫ mg ⋅ j • (dx i + dy j) = mg ⋅ y
A
y =10
y=2
= 70 ⋅ 10 ⋅ (10 − 2) = 5600J
A
Evidentemente, podríamos haber resuelto como ∆Ep = mgh B − mgh A
Si tomamos nivel cero de Ep en y=0 tendremos ∆Ep = mgh B − mgh A = mg10 − mg 2 = 5600J
Si tomamos nivel cero de Ep en y=2 (que es el punto más bajo) ∆Ep = mgh B − mgh A = mg8 = 5600J
Como puedes ver el resultado es independiente del nivel cero de Ep porque la energía
potencial es un escalar y se trata de restar la Ep que hay en dos puntos.
FORMA GENERAL DEL PRINCIPIO DE CONSERVACIÓN DE LA ENERGIA
De acuerdo con el teorema del trabajo y la energía cinética, el trabajo realizado por la
fuerza resultante de todas las fuerzas (sean conservativas o no) para llevar el cuerpo
desde un punto A hasta otro B es igual a la variación de energía cinética entre esos
puntos: WA→B,Todas las fuerzas = ∆Ec o bien podríamos escribirlo como:
WA→B,campo + WA→B
F.Conservativas
= ∆Ec
F. NoConservat
Por otro lado, como por definición, “el trabajo que hacen las fuerzas conservativas para
llevar un cuerpo desde un punto A hasta otro B es igual a menos la variación de energía
potencial entre esos puntos”, podemos poner que
WA→B,campo = − ∆Ep
F.Conservativas
Así que restando nos queda que
∆Ec + ∆Ep = WA→B
F. NoConservat
o bien que:
Ec A + Ep A + WA→B
= Ec B + Ep B
F. NoConservat
Eso quiere decir que la energía mecánica al final puede ser mayor o menor que la
inicial. Todo depende del signo del trabajo de las fuerzas no conservativas, es decir del
sentido de las fuerzas no conservativas:
• En el caso más frecuente de que se trate de las fuerzas de rozamiento la energía
al final siempre será menor que la inicial, puesto que la fuerza de rozamiento
tiene sentido contrario al desplazamiento y en consecuencia el trabajo que
realiza siempre es negativo (al llevar sentido contrario al desplazamiento el
r r
r
r
producto escalar FRoz • d r resulta negativo − i • i = −1 ).
Ec A + Ep A + WRoz = Ec B + Ep B
• En el caso de que sobre el cuerpo actúe una fuerza no conservativa en la
dirección del desplazamiento la energía mecánica al final es mayor que la
inicial. Es el caso de cuando un coche sube acelerando por una cuesta. El trabajo
realizado por el motor del coche es responsable que el arriba tenga más energía
que al principio.
Ec A + Ep A + WMotor = Ec B + Ep B
Si observas bien la expresión ∆Ec + ∆Ep = WA→B
verás que arriba de la
F. NoConservat
cuesta el coche tiene mayor energía tanto si sube con velocidad constante como
si aumenta de velocidad mientras sube. Lógico, ya que en ambos casos el motor
debe realizar trabajo. Si sube, con velocidad constante, (para que ΣF=0 el motor
debe ejercer la fuerza necesaria para compensar a la componente del peso en
dirección de la cuesta) tendremos que el trabajo del motor se invirtió en
aumentar la energía potencial del coche ∆Ep = WA→B
. Si sube,
F. NoConservat
aumentando de velocidad, tendremos que el trabajo del motor se invirtió en
aumentar la energía potencial del coche y en aumentar su energía cinética:
∆Ec + ∆Ep = WA→B
F. NoConservat
Principio de conservación de la energía mecánica
Es una particularización del principio general de conservación de la energía, que dice,
que si sobre un cuerpo “solamente actúan fuerzas conservativas” entonces se conserva
la energía mecánica. Resulta evidente, ya que si todas las fuerzas son conservativas
WA→B
=0
F. NoConservat
∆Ec + ∆Ep = 0
o lo que es igual:
Ec A + Ep A = Ec B + Ep B = E = const
Nos dice que “Si todas las fuerzas que actúan sobre la partícula son conservativas, la
suma de la energía cinética y potencial es igual para cualquier punto”. A la suma de Ec
y Ep se le llama energía mecánica.
Este teorema que viene a decir que la Ec y Ep pueden variar de unos puntos a otros, pero
que su suma (la energía mecánica) permanece constante, dicho de otra forma, como
∆Ec + ∆Ep = 0 si aumenta la energía cinética (∆Ec↑) eso implica que disminuya la
potencial (∆Ep↓), como ocurre cuando un cuerpo cae en caída libre o desliza por un plano
inclinado “sin rozamiento”.
Ejemplo: Una niña se tira por un tobogán desde una altura de 2 metros.
a) ¿Con qué velocidad llegaría abajo si despreciamos el rozamiento?
b) ¿Con qué velocidad llegaría abajo suponiendo que el coeficiente de rozamiento es 0,5.?
a) Teniendo en cuenta que no hay rozamiento y el resto de las fuerzas son conservativas,
podemos aplicar el teorema de conservación de la energía mecánica. La energía
potencial que la niña tiene arriba se transformará en cinética cuando llegue abajo. Es
decir, de acuerdo con la conservación de la energía mecánica ∆Ec + ∆Ep = 0 la
disminución de energía potencial (∆Ep↓) debe ser exactamente igual al aumento de su
energía cinética (∆Ec↑)
Ec A + Ep A = Ec B + Ep B
⇒
mgh A +
1
1
mv 2A = mgh B + mv 2B
2
2
v A = 2 g h A = 2 ⋅ 10 ⋅ 2 = 4,47m / s
Como vemos, al no haber rozamientos el resultado es el mismo que si la niña cayera en
caída libre desde esa altura. Lógico porque al tratarse de fuerzas conservativas el trabajo
que realizan al llevar el cuerpo de un punto a otro es independiente del camino seguido.
b) Cuando hay rozamiento (que una fuerza no conservativa) ya no se conserva la energía
mecánica, pero sí que se conserva la energía total. Como la fuerza de rozamiento es
constante, su trabajo podemos obtenerlo como con la expresión particular:
WA→B
= FRoz ⋅ s ⋅ cos α = (mg cos 30 ⋅ µ) ⋅ s ⋅ cos 180
F. NoConservat
F.Rozamiento
Ec A + Ep A + WA →B
= Ec B + Ep B
F. NoConservat
mgh A + (mg cos 30 ⋅ µ) ⋅ s ⋅ cos 180 =
1
mv 2B
2
v B = 2,31m / s
Como vemos, de acuerdo con la conservación de la energía total ∆Ec + ∆Ep = WA → B
F. NoConservat
la disminución de energía potencial (∆Ep↓) se emplea en parte en aumentar la energía
cinética (∆Ec↑) y otra parte se pierde en rozamiento transformándose en calor.
Ejemplo:
¿Con qué velocidad hemos de lanzar una piedra para que llegue hasta una altura h?
Vamos a resolver este sencillo ejercicio, con todo cuidado, para reparar en la forma de
aplicar el principio de conservación de la energía. Presta atención porque es bastante
sutil.
1º Lo habitual es suponer “que ya le hemos comunicado a la piedra la velocidad
necesaria, vo”.
En este caso la piedra tendría una Ec y comenzaría a subir: El aumento de energía
potencial (∆Ep↑) se consigue a costa de disminuir energía cinética (∆Ec↓)
Si despreciamos el rozamiento contra el aire se conservaría la energía mecánica porque
la única fuerza sobre la piedra es el peso, que es conservativa:
∆Ec + ∆Ep = 0
→
Ec Suelo + Ep Suelo = Ec h + Ep h
1
m v o2 = m g h
2
de donde v o = 2 g h
2. Supongamos ahora que estamos en el instante inmediatamente anterior: “Cuando la
piedra aun estaba parada sobre el suelo”. Si no hacemos nada por ella, parada seguiría.
Para que la piedra comience a subir debemos comunicarle una energía mediante una
fuerza que hacemos nosotros y que NO es conservativa. Por tanto, entre el momento en
que la piedra está parada y el que está a una altura h, no se conserva la energía
mecánica, aunque sí se conserva la energía total:
∆Ec + ∆Ep = WA→B
→
Ec Suelo + Ep Suelo + WA→ B
F. NoConservat
= Ec h + Ep h
F. NoConservat
Si el trabajo realizado por la fuerza no conservativa
WA→B
se lo comunicamos en forma de
F. NoConservat
energía cinética, tendremos que:
1
2
m v que
le propina = Ep h
2
la FNCons
de donde v que le propina = 2 g h
la FNCons
Ejemplo: Cuando sobre un muelle helicoidal, situado verticalmente sobre una mesa,
colocamos una masa de 1Kg, éste se comprime 2cm. Calcular la deformación que
experimentaría el muelle si le dejamos caer la misma masa desde una altura de 1m.
Con el primer dato y aplicando la ley de Hooke calcularemos la constante de
recuperación del muelle. (teniendo en cuenta que le fuerza que deforma al muelle es el
peso de la masa):
mg 1 ⋅ 10
F = kx
⇒
k=
=
= 500 N / m
x
0,02
Balance de energías:
Punto A: toda la energía es potencial gravitatoria (Ec=0 porque está parado y la Epelástica=0
porque el muelle está relajado).
Tramo AB: a medida que desciende ∆Epgravitat↓, ∆Ec↑ y ∆Epelástica=0 porque el muelle sigue igual.
Punto B: casi toda la energía inicial se ha transformado en Ec pero aun le queda un poco
de Epgravitat (mghA = EcB+mghy).
Tramo BC: al chocar con el muelle comienza a comprimirlo acumulándose toda la energía
que tiene en potencial elástica: ∆Epgravitat↓, ∆Ec↓ y ∆Epelástica↑.
Punto C: toda su energía es potencial elástica (Ec=0 porque está parado y la Epgravitat=0
porque ha llegado al nivel cero de Ep gravitatoria.)
Aplicaremos el principio de conservación entre el
punto A y C, porque de esta forma toda la energía
potencial gravitatoria se transforma en energía
potencial elástica:
∆Ec + ∆Epgravitat + ∆Epelástica =0
Ec A + Ep gravit ,A + Ep elast ,A = Ec C + Ep gravit ,C + Ep elast ,C
mgh A =
1 2
ky
2
1 2
ky
2
⇒
mg(1 + y) =
y = 0,2m
Ejemplo: Un bloque de 3Kg, que parte del reposo,
desliza 7,6m hacia abajo por un plano inclinado 20º
sobre la horizontal y continua recorriendo 2,75m
por un plano horizontal, hasta que choca con un
resorte y finalmente se detiene después de
comprimirlo 15cm, como se muestra en la figura.
Calcular la constante elástica del muelle sabiendo
que el coeficiente de rozamiento es 0,2.
Si tenemos en cuenta que la energía potencial que el bloque tiene arriba, punto (A),
menos la que pierde en rozamientos debe ser igual a la energía potencial elástica del
resorte al final (D)
Aplicando la conservación de la energía entre la posición inicial y final tenemos que:
Ec A + Ep gravit ,A + Ep elast ,A + WA→B
= Ec D + Ep gravit , D + Ep elast ,D
F. NoConservat
1
Kx 2
2
1
3 ⋅ 10 ⋅ 2,6 − [3 ⋅ 10 cos 20 ⋅ 0,2 ⋅ 7,6 + 3 ⋅ 10 ⋅ 0,2 ⋅ (2,75 + 0,15)] = K ⋅ 0,15 2
2
K = 1576 N / m
mgh A + (µ mg cos 20 ⋅s ⋅ cos 180 + µ mg ⋅s´⋅ cos 180) =
E2B.S2011
a) Energía potencial asociada a una fuerza conservativa.
b) Una partícula se desplaza bajo la acción de una fuerza conservativa. ¿Aumenta o
disminuye su energía potencial? ¿Y su energía cinética? Razone las respuestas.
a) Teoría
b) Cualquier partícula bajo la acción de una fuerza conservativa se mueve
espontáneamente hacia donde la energía potencial es menor, ya que por definición
WA→B,F.Conservativa = − ∆Ep = Ep A − Ep B . (Eso precisamente es lo que indica el signo menos)
De acuerdo con el principio de conservación de la energía mecánica, ∆Ec + ∆Ep = 0 , la
disminución de energía potencial exige que aumente la energía cinética.
Es lo que ocurre cuando cae una piedra: La piedra se mueve bajo la acción de la fuerza
conservativa peso hacia donde disminuya su energía potencial (EpB<EpA) y al hacerlo aumenta
su energía cinética (EcB>EcA)
E6B.S2011
a) Conservación de la energía mecánica.
b) Se lanza hacia arriba por un plano inclinado un bloque con una velocidad v0.
Razone cómo varían su energía cinética, su energía potencial y su energía mecánica
cuando el cuerpo sube y, después, baja hasta la posición de partida. Considere los casos:
i) que no haya rozamiento; ii) que lo haya.
a) Teoría
b) Si no hay rozamiento se conservará la energía mecánica, ∆Ec + ∆Ep = 0 . Si el
bloque sube por el plano aumentará su energía potencial gravitatoria y la conservación
de la energía mecánica exige que disminuya en la misma cantidad la energía cinética.
(Ello explica que a medida que asciende el bloque vaya disminuyendo de velocidad
hasta pararse, en cuyo momento toda la energía cinética inicial se habrá transformado en
potencial)
Cuando hay rozamiento ya no se conserva la energía mecánica, aunque sí la energía
total, ∆Ec + ∆Ep = WA→B
. Ahora la disminución de Ec se invierte en parte en
F. NoConservat
trabajo contra la fuerza de rozamiento (WF.No.Conserv es negativo) y el resto en aumentar
la energía potencial. Naturalmente, como ahora solamente una parte de la energía
cinética se emplea en aumentar la energía potencial el bloque subiría hasta una altura
menor que cuando no había rozamiento y la totalidad de la Ec se convertía en Ep.
E5B.S2011
Un bloque de 200 kg asciende con velocidad constante por un plano inclinado 30º
respecto a la horizontal bajo la acción de una fuerza paralela a dicho plano. El
coeficiente de rozamiento entre el bloque y el plano es 0,1.
a) Dibuje en un esquema las fuerzas que actúan sobre el bloque y explique las
transformaciones energéticas que tienen lugar durante su deslizamiento.
b) Calcule el valor de la fuerza que produce el desplazamiento del bloque y el aumento
de su energía potencial en un desplazamiento de 20 m.
g = 10 m s−2
a) Si el bloque asciende con velocidad constante quiere decir, de acuerdo con la 1ª ley
de Newton, que la fuerza resultante sobre el bloque es nula.
Sobre el bloque hay 4 fuerzas: el peso, la reacción del plano, la fuerza de rozamiento y la
fuerza F paralela al plano (que es la que debe compensar a la fuerza de rozamiento y a la
componente del peso en dirección del plano para que el bloque se mueva con velocidad
constante).
Respecto de un SR con el eje X paralelo al plano, las fuerzas en forma de vector serían:
r
r
r
r
r
P = − mg sem30 i − mg cos 30 j = −1000 i − 1732 j
r
r
r
N=
mg cos 30 j =
+ 1732 j
r
r
r
FRoz = −mg cos 30 ⋅ µ i
= − 173,2 i
r r
r
F=F
=F
––––––––––––––––––––––––––––––––––––––––
r
r r
ΣF = F − 1173,2 i
r
Como v =constante
r
r r
→ ΣF = F − 1173,2 i = 0
r
r
→ F = 1173,2 i
Transformaciones energéticas: Puesto que hay rozamiento no se conserva la energía
mecánica, aunque sí la energía total, ∆Ec + ∆Ep = WA→B
. Como la velocidad es
F. NoConservat
constante ∆Ec=0, el aumento de energía potencial se debe íntegramente al trabajo
realizado por la fuerzas no conservativas, es decir al trabajo realizado por la fuerza F y
al la FRoz. Puesto que el trabajo que hace la FRoz es negativo, la fuerza F debe realizar el
trabajo necesario para aumentar la Ep y para compensar el que se pierde en rozamiento.
r
r
b) La fuerza F paralela al plano, para que suba con velocidad constante, es F = 1173,2 i
El aumento de energía potencial para un desplazamiento de 20m, o lo que es igual para
un ascenso de h=20.sem30=10 m, podemos calcularlo de tres formas:
* Aplicando directamente la ecuación de la energía potencial gravitatoria. Tomando
nivel cero de energía potencial en el punto más bajo del plano:
∆Ep = Ep B − Ep A = mgh B − mgh A = 200 ⋅ 10 ⋅ 10 = 20000J
* Aplicando la conservación de la energía: ∆Ec + ∆Ep = WA→B
En este caso las
F. NoConservat
fuerzas no conservativas son la fuerza de rozamiento y la que hacemos paralela al plano:
∆Ec + ∆Ep = WA →B,F.Rozamiento + WA →B,F
∆Ec + ∆Ep = FRoz ⋅ s ⋅ cos180 + F ⋅ s ⋅ cos 0
∆Ec + ∆Ep = 173,2 ⋅ 20 ⋅ (−1) + 1732 ⋅ 20 ⋅ 1 = 20000 J
Observa, una vez más, que al utilizar la expresión particular del trabajo para fuerzas
constantes, al sustituir el valor de las fuerzas escribimos su módulo, por eso al sustituir
la fuerza de rozamiento no se puso el signo menos que tiene en su forma vectorial.
* Aplicando la definición de energía potencial: “el trabajo que una fuerza conservativa
para llevar un cuerpo desde un punto A hasta otro B es igual a menos la variación de
energía potencial entre esos puntos”: WA→B,F.Conservativa = −∆Ep
r
r
r
Teniendo en cuenta que en este caso la fuerza conservativa es el peso: P = −1000 i − 1732 j
y que solamente la componente Px realiza trabajo (porque la componente Py es perpendicular al
desplazamiento), tenemos que:
WA→B,F.Conservativa = −∆Ep
Px ⋅ s ⋅ cos 180 = −∆Ep
1000 ⋅ 20 ⋅ (−1) = − ∆Ep
(La componente x del peso forma 180º con el desplazam.)
→ ∆Ep = 20000 J
Por supuesto, también podríamos utilizar para el peso su módulo total, es decir, P=mg,
pero en tal caso tendríamos que tener en cuenta que el ángulo que forma el peso con el
desplazamiento es de 240º (observa la figura).
P ⋅ s ⋅ cos 240 = −∆Ep
(El peso forma 240º con el desplazamiento)
2000 ⋅ 20 ⋅ (−0,5) = −∆Ep → ∆Ep = 20000 J
Al mismo resultado llegaríamos si calculamos el trabajo que hace el peso aplicando la
definición general de trabajo:
WA →B,F.Conservativa = −∆Ep
r
r
r x =20
B
WA→B,Peso = ∫ (−1000 i − 1732 j) • dx i = ∫ − 1000dx = −20000 = − ∆Ep
x =0
A
E4A.S2011
Un bloque de 2 kg se encuentra situado en la parte superior de un plano inclinado
rugoso de 5 m de altura. Al liberar el bloque, se desliza por el plano inclinado llegando
al suelo con una velocidad de 6 m s−1.
a) Analice las transformaciones energéticas que tienen lugar durante el deslizamiento y
represente gráficamente las fuerzas que actúan sobre el bloque.
b) Determine los trabajos realizados por la fuerza gravitatoria y por la fuerza de
rozamiento.
g = 10 m s−2
a) Transformaciones energéticas: Puesto que hay rozamiento no se conserva la energía
mecánica, aunque sí la energía total, ∆Ec + ∆Ep = WA →B
. Al descender disminuye la
F. NoConservat
energía potencial gravitatoria y esa disminución se emplea en aumentar su energía cinética y en
trabajo en rozamiento (ten en cuenta que siempre el trabajo que hace la fuerza de rozamiento es
negativo y por tanto en la expresión anterior sería como ∆Ec ↑ + ∆Ep ↓ + WA →B,F.Roz = 0 )
b) Teniendo en cuenta que ∆Ec + ∆Ep = WA→B
y si tomamos nivel cero de energía
F. NoConservat
potencial en el punto B, por ser el más bajo, podemos poner que:
Ec A + Ep A + WA→B
= Ec B + Ep B
F. NoConservat
mgh A + WA →B
F. NoConservat
WA→B
=
1
mv 2B
2
→
2 ⋅ 10 ⋅ 5 + WA→B
F. NoConservat
=
1
2 ⋅ 62
2
= −64 J, lógico ya que en este caso la fuerza no conservativa es la de rozamiento y
F. NoConservat
su trabajo siempre es negativo porque dicha fuerza siempre tiene sentido contrario al
desplazamiento, y en consecuencia forman ángulo de 180º.
Seguramente ahora verás con mayor claridad las transformaciones energéticas que
tienen lugar, ya que de la ecuación se deduce claramente que la energía inicial (100 J,
toda potencial) se ha transformado en cinética (36 J) y en trabajo en rozamiento (−64 J)
El trabajo realizado por la fuerza peso es de +100 Julios, ya que la fuerza peso es la única
fuerza conservativa y por definición de variación de energía potencial tenemos que
WA →B,F.Conservativa = WA →B,F.Peso = −∆Ep = −(−100) = +100 J
(ten en cuenta que ∆Ep =EpB – EpA = 0 – 100 = − 100 J)
También podríamos calcular el trabajo realizado por la fuerza peso aplicando la
definición de trabajo particularizada para fuerzas constantes, y teniendo en cuenta que
solamente realiza trabajo la componente del peso que tiene la dirección del
desplazamiento, es decir la componente Px = mgsenα.
WA→B,Peso = Px ⋅ s ⋅ cos 0 = mg senα ⋅
5
⋅ cos 0 = +100 J
senα
Sin embargo calcular el trabajo perdido en rozamiento utilizando la definición de
trabajo WA→B,F.Roz = FRoz ⋅ s ⋅ cos 180 es bastante más laborioso que como lo hemos
resuelto aplicando la conservación de la energía, porque nos obliga a calcular el valor de
la FRoz utilizando métodos dinámicos.
La fuerza de rozamiento tendríamos que obtenerla aplicando la segunda ley de Newton
y las ecuaciones del movimiento rectilíneo y uniforme:
mg senα − FRoz = m a
v = at
1
s = a t2
2
5
s=
senα
FRoz = 12,8 senα
Ahora ya podemos sustituir y tendremos:
WA→B,F.Roz = FRoz ⋅ s ⋅ cos 180 = 12,8 senα ⋅
5
⋅ cos 180 = −64 J
senα