Ondas

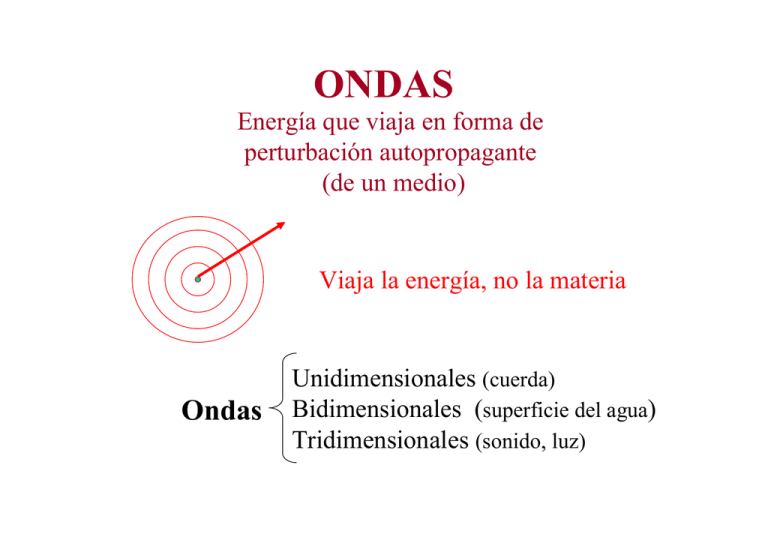
ONDAS
Energía que viaja en forma de
perturbación autopropagante
(de un medio)
Viaja la energía, no la materia
Ondas
Unidimensionales (cuerda)
Bidimensionales (superficie del agua)
Tridimensionales (sonido, luz)
CLASIFICACIÓN DE LAS ONDAS
• Longitudinales (sonido, resorte)
c
y
v
x
• Transversales (cuerda, superficie del agua)
y
v
c
x
CLASIFICACIÓN DE LAS ONDAS
• Ondas mecánicas (sonido, resorte, cuerda)
requieren de un medio que se deforma,
y esta es la perturbación que se propaga
• Ondas Electromagnéticas (luz, ondas de radio)
No requieren de ningún medio,
y se propagan hasta en el vacío
E
c
H
Frente de Ondas
PLANA
ESFÉRICA
CILÍNDRICA
Ondas Unidimensionales
y
c
t=0
x
y
t>0
ct
x
y = φ(x,0)
y = φ(x,t)
y = φ(x - ct)
Si la onda viaja a la derecha:
y = φ(x - ct)
Si la onda viaja a la izquierda: y = φ(x + ct)
Ecuación de Ondas Unidimensionales
y = φ(x - ct) = φ(u) ..... con u = x - ct
∂φ
∂x
dφ(u)
=
du
dφ’(u)
∂2φ
=
2
du
∂x
∂φ
∂t
=
dφ(u)
du
dφ’(u)
∂2φ
= -c
2
du
∂t
=
dφ(u)
du
∂u
∂x
=
d2φ(u)
φ’’(u)
=
2
du
∂u
∂t
= -c φ’(u)
∂u
∂x
= φ’(u)
d2φ(u)
∂u
2 φ’’(u)
c
= c2
=
du2
∂t
∂2φ
1
= 2
2
c
∂x
∂2φ
∂t2
Ecuación General de Ondas
∂2φ
∂2φ
∂2φ
1
+
+
= c2
2
2
2
∂x
∂y
∂z
1
2
∇ φ= 2
c
∂2 φ
∂t2
φ(x, y, z, t)
∂2φ
∂t2
Solución de la Ecuación Diferencial
∂2φ
1
= 2
2
c
∂x
∂2φ
∂t2
φ(x-ct) = A sen [k(x – ct) + δ] = A sen (kx - ωt + δ)
A ... Amplitud del movimiento
ω ... Frecuencia Angular [rd/s]
δ ... Constante de Fase [rd]
k ...Número de onda [1/m]
φ(x0,t)
A
T
A
ck=ω
T = 2π / ω [s]
t
f = 1/T [Hz]
ω = 2πf [rd/s]
Foto tomada en t = t0
φ(x,t0)
A
λ
A
x
Si T = 2π / ω [s] ... análogamente λ = 2π / k [m]
como c = ω / k
ω
λ
=
c=
= λf [m/s]
k
T
Ondas en Cuerdas
yT
T
θ(x +Δx)
θ(x)
x
x +Δx
Ley de Newton:
para: tg θ ~ sen θ ~ θ < 6°
m
μ=
l
x
[kg/m]
F=ma
T sen θ(x +Δx) – T sen θ(x) = m ay
∂2y
T tg θ(x +Δx) – T tg θ(x) ~ μ Δx
2
∂t
∂y
∂y
–
∂x (x +Δx)
∂x (x)
μ ∂2y
~
Δx
Τ ∂t2
y=φ
∂2φ
1
= 2
2
c
∂x
∂2φ
∂t2
∂y
... tg θ(x) =
∂x
c=
Τ
μ
Ondas Longitudinales
F l0
σ
Y=
=
ε
A Δl
Δu (1)
F = A Y Δl = A Y
Δx
l0
Ley de Newton: F = m a
2u
∂
F(x +Δx) – F(x) = Δm
∂t2
x
u(x)
x +Δx
u(x +Δx)
F(x)
x
F(x +Δx)
Δm
Δm = ρ A Δl
... y por (1)
A Y Δu(x+Δx) - A Y Δu(x)
∂2u
= ρ A Δx
c=
Δx
∂t2
∂u
∂u
–
∂x (x +Δx)
∂x (x)
∂2u
1
ρ ∂2y
= 2
~
2
c
Δx
∂x
Y ∂t2
Y
ρ
∂2u
∂t2
Ondas Longitudinales
∂2u
1
= 2
2
c
∂x
Sólidos:
F l0
σ
Y=
=
ε
A Δl
Fluidos:
B=
B = -V dP
dV
-ΔP
ΔV/V
∂2u
∂t2
c=
Y
c=
B
ρ
ρ
... es el módulo de compresibilidad del fluido
Para el sonido: c ∼ 340 m/s, a temperatura ambiente
Sonido como Onda Longitudinal
pA
pA
(p+Δp)A
vt
ct
B = -ΔP
V
ΔV
= -ΔP
ρ=m/V=nM/V
ct
vt
= -ΔP
c
v
Velocidad del Sonido
en función de la Temperatura
Proceso Adiabático: pV γ = constante
... derivando:
... de donde:
B = - V. dp / dV = γ p
γ p
γ
= ρ =
= M
nM / V
c=
B
a.T
a= γ R
M
(1)
(2)
pV = n R T
... y como:
c2
dp / dV . V γ + γ p V γ - 1 = 0
pV
n
γ
= M RT
c12
T1
=
2
c2
T2
ct
Transporte de Energía
Δm = ρ ΔS Δl = ρ ΔS c Δt
En un M.A.S.:
E = U(t) + K(t) =
1
m ω2 A2
2
ΔE = 1 Δm ω2 A2 = 1 ρ ΔS c Δt ω2 A2
2
2
ΔE
Intensidad de una onda: I = ΔS Δt =
I =
1
ρ ω2 A2 c
2
ΔP
ΔS
[w/m2]
NIVEL DE INTENSIDAD
β = 10 log I
I0
[dB]
Para el sonido: I0 = 10-12 [w/m2] = 0 dB
β
120 dB
0 dB
Umbral de Dolor
Umbral de Sensibilidad
20
25.000
f [Hz]
Nivel de Intensidad
en Ondas Volumétricas
I = ΔP =
ΔS
ΔP
4 π r2
I1 =
I2 =
r2
r1
ΔP
4 π r12
I1
I2
ΔP
4 π r22
I2 = I1 (
r12
r22
β2 = β1 - 20 log (r2 / r1)
)
=
r22
r12
Interferencia de Ondas
F1
F2
φ1(t) = A sen (kx - ωt)
r1
r2
φ2(t) = A sen (kx - ωt)
φ(t) = A [sen (k r1 - ωt) + sen (k r2 - ωt) ]
pero: senα + senβ = 2sen[(α+β)/2].cos[(α−β)/2]
φ(t) = 2A cos (k Δr /2) sen (k rp - ωt)
rp = (r1 + r2 )/2
Interferencia
Constructiva: (k Δr /2) = n π
Destructiva: (k Δr /2) = n π + π/2
Δr = n λ + λ/2
Δr = n λ
φ(t) = [2A cos (k Δr /2)] sen (k rp - ωt)
φ(t) = A(Δr) sen (k rp - ωt)
A(Δr) = 2A cos (k Δr /2)
... y como: I = 1 ρ ω2 A2 c
2
I(Δr) = 4 I0 cos2(k Δr /2)
I0
A(Δr)
Δr
Principio de Huygens
1678
“Cada punto de un frente de onda puede ser
considerado como una fuente secundaria de ondas
que se expanden en todas las direcciones con
rapidez igual a la rapidez de propagación de una
onda”