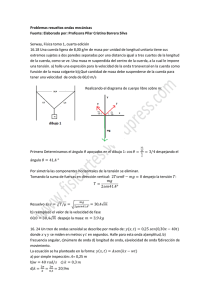
1 F v = = densidad de inercial factor rigidez o d elasticida de factor

DEPARTAMENTO DE CIENCIAS BÁSICAS
LABORATORIO FISICA
ASIGNATURA: FISICA II
LABORATORIO 3: ONDAS TRANSVERSALES EN UNA CUERDA
I. OBJETIVOS GENERALES
a) Determinar la velocidad de las ondas en una cuerda conocidas la tensión y la densidad
Lineal de masa de la cuerda
b) Determinar la relación entre la longitud de onda y la frecuencia
c) Obtener la relación entre la longitud de onda y la tensión aplicada, graficando λ contra F
II. INTRODUCCIÓN
Una onda es una perturbación del equilibrio de un sistema que se propaga de una región de
espacio a otra. Si la onda necesita de algún medio material para propagarse, la onda se
denomina “onda mecánica”. Las ondas mecánicas pueden ser transversales, longitudinales
o una combinación de ambas, es decir longi-transversales.
Al viajar la onda por el medio, las partículas que forman el medio sufren desplazamientos de
varios tipos dependiendo de la naturaleza de la onda, si los desplazamientos del medio son
perpendiculares a la dirección de propagación de la onda, decimos que se trata de una onda
transversal.
Consideremos como sistema a un hilo o cuerda tensa en estado de equilibrio (en reposo), e
imprimimos a un extremo, una pequeña perturbación (pulso) hacia arriba, la perturbación
viaja a lo largo de la cuerda y secciones sucesivas de ésta repiten el movimiento que
hicimos al extremo pero en instantes posteriores sucesivos. La rapidez de la onda en la
cuerda está determinada por las propiedades elásticas e inelásticas del medio. Debe
tomarse en cuenta que la rapidez de la onda no es la rapidez con que se mueven las
partículas cuando son movidas por la onda.
La ecuación general para determinar la rapidez de propagación de las ondas en un medio
depende de dos factores y está dada por:
v=
factor de elasticidad o rigidez
=
factor inercial de densidad
1
F
µ
En el caso de ondas transversales propagadas a lo largo de una cuerda flexible, el factor de
elasticidad o rigidez se debe a la fuerza de tensión aplicada a la cuerda y el factor inercial
corresponde a la densidad lineal de la cuerda. Si se miden F y µ es posible calcular la
rapidez. La rapidez de la onda también se puede determinar produciendo ondas
estacionarias y usando la relación:
v = λf
Donde:
f: Frecuencia
λ: Longitud de onda
III. TAREA PREVIA
Defina los siguientes términos:
Densidad lineal de masa
Longitud de onda
Onda estacionaria
Onda viajera
Ondas transversales
Velocidad de propagación de las ondas transversales en una cuerda
Resolver problemas de ondas transversales de los libros sugeridos en la teoría.
IV. MATERIALES Y EQUIPO
Vibrador electromagnético
Dinamómetro
Barra, soporte y base
Nueces
Pinza Universal
Cuerda
Polea
Apoyo móvil
2
V. PROCEDIMIENTO
1. En está práctica se utilizará un vibrador electromagnético de 60Hz de frecuencia que
comunicará pulsos senoidales a una cuerda flexible horizontal y cuya fuerza de tensión
se medirá directamente con un dinamómetro conectado verticalmente al extremo de la
cuerda después de pasar ésta por una polea tal como se muestra en la figura No. 1.
Dinamómetro
•
Vibrador
Polea
Apoyo
móvil
Figura No. 1
2.
Mida la longitud y la masa de la cuerda. Determinar su densidad lineal y anote los
datos en la hoja de resultados.
Longitud de la cuerda: _______ m
Masa de la cuerda: __________ kg
µ = ____________ kg/m
Frecuencia de la red eléctrica :________ Hz
3.
Con el equipo dispuesto tal como se ilustra en la figura N0 1 ajuste la altura del
dinamómetro de tal forma que indique una tensión de 1.0 N en la cuerda.
4.
Ponga a funcionar el vibrador eléctrico y luego mueva el apoyo
posición que permita observar ondas estacionarias de tres vientres.
5.
Mida la longitud de onda a partir del nodo que coincide con el apoyo, pero antes
discuta con sus compañeros de trabajo la mejor forma de hacerlo.
6.
Repita los pasos anteriores para fuerzas de tensión de 1.5, 2.0 y 2.5 y 3.0 N. y
coloque sus resultados en la tabla 1
3
buscando una
F (N)
1.0
L(m)
λ (m )
1.5
2.0
2.5
3.0
Tabla No.1
VI. ANALISIS DE RESULTADOS
1. Con las medidas de longitud y masa de la cuerda, calcule la densidad lineal (µ) con sus
respectivas unidades.
2. Complete la tabla No 2, deje constancia de los cálculos realizados.
Tabla No.2
F (N)
L(m)
F
λ (m)
µ
1.0
λ f (m/s)
F
µ
λ
1.5
2.0
2.5
3.0
fvibrador = _____ Hz
3. Compare los valores de la velocidad de propagación de las ondas con los datos Obtenidos
por el producto λ f ¿es así como se esperaba?. Explique.
4. ¿Qué se puede concluir de los valores obtenidos de frecuencia f ( s-1 ).¿es así como
esperaba?. Explique.
5. Elabore en papel milimetrado y en papel logarítmico el gráfico de λ vrs.F ¿Es el gráfico
tal como se esperaba ? ¿Debe pasar por el origen? Explique y compare ambos gráficos
4
6. A partir del gráfico obtenga la ecuación que relaciona λ y F. Obtenga la ecuación aplicando
regresión lineal.
7. En base a v = λf y v =
F
obtenga una expresión para obtener µ a partir de los datos de la
µ
tabla 2. y Compare con los valores de µ obtenido experimentalmente en el numeral 1 y concluya
al respecto.
CUESTIONARIO
1. Explique cómo a partir de una onda viajera se obtienen las ondas estacionarias en una
cuerda.
2. Distinga claramente entre la velocidad de propagación de una onda transversal y la
velocidad de las partículas de un pequeño segmento de la cuerda en un instante dado.
3. Para la pregunta anterior escriba una ecuación para cada una de estas dos velocidades.
4. Si la tensión F y la densidad lineal µ son constantes o fijas, ¿cómo afectará la reducción de
la longitud de la cuerda a las frecuencias de resonancia?
5. En base a los objetivos de la practica
conclusiones
y a los resultados obtenidos, elabore sus
5
LABORATORIO 3: ONDAS TRANSVERSALES EN UNA CUERDA
ASIGNATURA: FISICA II
GRUPO DE LABORATORIO:____ _______
FECHA DE REALIZACIÓN DE LA PRÁCTICA: ____________
MESA No. _______
FECHA DE ENTREGA DEL REPORTE : ____________________
NOMBRE DEL DOCENTE: ______________________________________
ALUMNOS:
No.
1
NOMBRES
CARNET
FIRMA
G. T
2
3
4
Longitud de la cuerda: _________________ m
Masa de la cuerda: __________ kg
F (N)
1.0
µ = ____________ kg/m
Frecuencia de la red eléctrica :________ Hz
L(m)
λ (m )
1.5
2.0
2.5
3.0
Tabla No.1
6
DEPARTAMENTO DE CIENCIAS BÁSICAS
LABORATORIOS DE FÍSICA Y QUÍMICA
TABLA DE COTEJO
NOTA
Nombre de la Práctica: ONDAS TRANSVERSALES EN UNA CUERDA
Docente: __________________________________________ Fecha _________________ G. L.
_______
Miembros del Grupo
APELLIDOS
No
NOMBRES
CARNÉ
FIRMA
G.T.
1
2
3
4
No.
1
2
3
4
5
6
7
Aspectos a evaluar
%asig.
Presentación y orden
5
Tablas 1 y 2 con sus cálculos
10
Comparación de velocidades de propagacion
5
10
Gráfico λ vrs F
10
Ecuación empírica que relaciona λ y F
Expresión para calcular µ
10
Análisis mecánico para obtener la velocidad
10
de la onda en una cuerda
v =
8
9
10
11
F
µ
Velocidad de una partícula y la velocidad
de la onda.
Ecuación empírica v-F de una onda
transversal
¿Cómo se afecta las frecuencias de
resonancias con F y µ fijos y por la reducción
de la cuerda?
Conclusiones
TOTAL DE PUNTOS
7
5
10
10
15
100
%obten. Observaciones