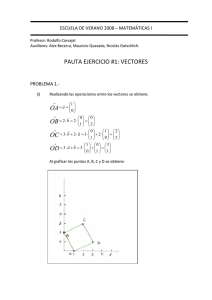
Unidad 4 Espacios vectoriales reales

Unidad 4
Espacios vectoriales reales
4.1
Subespacios
Si V es un espacio vectorial y W un subconjunto no vacı́o de V. Entonces W es un subespacio
de V si se cumplen las siguientes condiciones
• Si u y v son vectores cualquiera en W, entonces u + v esta en W.
• Si c es cualquier numero real y u es cualquier vector en W, entonces cu esta en W.
Para determinar si u + v esta en W se siguen los siguientes pasos:
1. Elegir dos vectores cualesquiera de W y realizar la suma de ellos
2. Comparar el vector obtenido de la suma y verificar si pertenece a W, esto es, es de
la misma forma de los vectores que pertenecen a W.
Ejemplos:
1. Considerar el subconjunto W de R4 de todos los vectores de la forma (a, b, c, d), donde
c = d = 0.
Se escribe el vector genérico de W considerando las condiciones dadas (a = b = 0). O
sea, (a, b, 0, 0)
Se eligen los vectores u y v utilizando nombres diferentes para los reales, por ejemplo:
u = (a1 , b1 , 0, 0 y v = (a2 , b2 , 0, 0)
La suma es (a1 , b1 , 0, 0) + (a2 , b2 , 0, 0) = (a1 + a2 , b1 + b2 , 0, 0), para verificar si esta suma
esta en W, hacemos a = a1 + a2 y b = b1 + b2 y verificamos si estos valores coinciden
con las caracterı́sticas de los vectores en W, (a, b, 0, 0). Para este caso vemos que sı́, ya
que no hay ninguna relación entre a y b
1
4.1. SUBESPACIOS
2. Considerar el subconjunto W de R4 de todos los vectores de la forma (a, b, c, d), donde
a−b=2
Se escribe el vector genérico de W considerando las condiciones dadas (a − b = 2). O
sea, (a, b, c, d)
Se elijen los vectores u y v utilizando nombres diferentes para los reales, por ejemplo:
(a1 , b1 , c1 , c2 ) y v = (a2 , b2 , c2 , d2 ), donde a1 − b1 = 2 y a2 − b2 = 2
La suma es (a1 + a2 , b1 + b2 , c1 + c2 , d1 + d2 ), si hacemos a = a1 + a2 y b = b1 + b2 .
Para que el vector suma esté en W se debe cumplir que a − b = 2. Considerando las
condiciones a1 − b1 = 2 y a2 − b2 = 2, se obtiene que
(a1 + a2 ) − (b1 + b2 ) = (a1 − b1 ) + (a2 − b2 ) = 2 + 2 = 4
por lo cual u + v no esta en W.
Para determinar si cu esta en W se procede de manera similar.
Ejercicios sección 6.2: 5, 6, 7, 10, 17
4.1.1
Combinación lineal
Sean v1 , v2 , · · · vk vectores en un espacio vectorial V, Un vector v es una combinación
lineal de v1 , v2 , · · · vk si
v = c1 v 1 + c2 v 2 + · · · ck v k
(4.1)
para ciertos números reales c1 , c2 , · · · ck
El desarrollo de la ecuación 4.1 lleva a un Sistema de Ecuaciones Lineales, de manera que,
si este sistema el consistente, el vector v es una combinación lineal de v1 , v2 , · · · vk ,
y si es inconsistente no lo es.
4.1.2
Conjunto generador de un espacio vectorial
Un conjunto de vectores S = v1 , v2 , · · · vk de un espacio vectorial V generan a V, si
cada vector en V es una combinación lineal de v1 , v2 , · · · vk . Se dice que S genera a V,
y se escribe gen S = V .
Para determinar si un conjunto de vectores v1 , v2 , · · · vk generan el espacio vectorial V
se realizan los pasos:
Paso 1. Seleccionar un vector arbitrario v en V.
Paso 2. Determinar si v es una combinación lineal de los vectores dados (Determinar la
consistencia del sistema de ecuaciones resultante). Si lo es, los vectores dados generan a
V ; si no, los vectores dados no generan a V.
Gilberto Aguilar Miranda
2
UNIDAD 4. ESPACIOS VECTORIALES REALES
Ver ejemplos 1, 2 y 3 (pag. 292) y ejemplo 6 (pag. 293)
Hacer los siguientes ejercicios de la sección 6.3: 2, 4, 6
4.1.3
Independencia lineal
Un conjunto de vectores v1 , v2 , · · · vk en un espacio vectorial V son linealmente independientes si la ecuación
c1 v 1 + c2 v 2 + · · · + ck v k = 0
(4.2)
tiene solución única y esta es nula (c1 = c2 · · · ck = 0). En caso contrario, son linealmente dependientes.
El procedimiento para determinar si los vectores v1 , v2 , · · · vk son linealmente independientes o linealmente dependientes es:
Paso 1. Plantear la ecuación 4.2, la cual conduce a un sistema de ecuaciones lineales
homogéneo.
Paso 2. Si el sistema homogéneo tiene solución única (la trivial), entonces los vectores
son linealmente dependientes; si tiene un numero infinito de soluciones, entonces los
vectores son linealmente dependientes.
Ver ejemplos 7, 8 y 9 (pag. 295) y ejemplo 11 (pag. 296).
Hacer los siguientes ejercicios de la sección 6.3: 10, 12 y 16.
4.2
Bases de un espacio vectorial
Para describir completamente un espacio vectorial V, se utiliza un conjunto de vectores de V
que lo genere. El conjunto mı́nimo de vectores de V que describe totalmente a V se llama
base del espacio vectorial.
Definición: Los vectores v1 , v2 , · · · vk en un espacio vectorial V forman una base para
V, si son linealmente independientes y generan al espacio V.
Si se tiene un conjunto de vectores S = v1 , v2 , · · · vk de vectores en un espacio vectorial
V, y gen S = W . Un subconjunto de S es una base para W.
Gilberto Aguilar Miranda
3
4.3. RANGO DE UNA MATRIZ
Para obtener una base para W que contenga vectores de S = {v1 , v2 , · · · vk }, se sigue
el siguiente procedimiento
Paso 1. Formar la ecuación 4.2
c1 v 1 + c2 v 2 + · · · + ck v k = 0
paso 2. Construir la matriz extendida asociada con el sistema de ecuaciones lineales
homogéneo resultante y llevarla a la forma escalonada reducida por filas.
paso 3. Los vectores de S correspondientes a las columnas que contienen a los 1s
principales constituyen una base para gen S = W .
Ver ejemplo 2 (pag. 303), ejemplos 3 y 4 (pag. 304) e interpretar teoremas 6.5 (pag. 305)
y 6.6 (pag. 306). Ver ejemplo 5 (pag. 309). Hacer los siguientes ejercicios de la sección 6.4:
2, 3, 4, 7,9, 11, 12
Si se tiene la forma de todos los vectores de un subespacio vectorial W, para obtener una
base para W, se expresa un vector arbitrario de W como una combinación lineal de vectores
(ver ejemplo de clase), los vectores de la combinación lineal constituyen una base para W.
Hacer los siguientes ejercicios de la sección 6.4: 19, 20, 21, 30.
4.2.1
Dimensión
La dimensión de un espacio vectorial no nulo es la cantidad de vectores de una de sus bases.
4.3
Rango de una matriz
Para una matriz A de m × n, las filas de A
v1 = (a11 , a12 , · · · , a1n )
v2 = (a21 , a22 , · · · , a2n )
..
.
vm = (am1 , am2 , · · · , amn )
considerados como vectores de Rn generan un subespacio de Rn , denominado espacio
fila de A. Análogamente, las columnas de A






a12
a1n
a11
 a21 
 a22 
 a2n 






w1 =  ..  , w2 =  ..  , · · · wm =  .. 
 . 
 . 
 . 
am1
am2
amn
Gilberto Aguilar Miranda
4
UNIDAD 4. ESPACIOS VECTORIALES REALES
consideradas como vectores de Rm , generan un subespacio de Rm , denominada el espacio
columna de A.
Para determinar una base (y la dimensión) del espacio fila de una matriz A, se utiliza la
propiedad anterior. Esto es, se lleva la matriz a la forma escalonada reducida por filas, una
base para el espacio fila de A está formado por las filas no nulas (ver ejemplo de clase).
La dimensión del espacio fila y la dimensión del espacio columna son iguales.
Si las matrices A y B son equivalentes por filas, entonces los espacios fila de A y B son iguales
La dimensión del espacio fila (columna) de una matriz se conoce como rango de la matriz.
El procedimiento anterior se utiliza para determinar una base para un subespacio de Rn .
Si S = {v1 , v2 , · · · vk } es un conjunto de vectores de Rn , y gen S = W , una base para
W se obtiene con el siguiente procedimiento:
Paso 1. Formar una matriz A con los vectores de S como filas.
Paso 2. Determinar la forma escalonada por filas de A.
Paso 3. Las filas no nulas de esta matriz forman una base para W
La base que se obtiene no necesariamente tiene vectores de S, ver el ejemplo de clase.
Ver los ejemplos 1 (pag. 329), 2 (pag. 330) y 3 (pag. 331)
4.4
Vectores de coordenadas
Lo que hace del concepto de base algo realmente útil es que, recurriendo a ellas, cualquier
vector queda identificado mediante los coeficientes de la única combinación lineal que lo expresa en función de los vectores de la base. A estos coeficientes se les llama coordenadas. En
un espacio vectorial de dimensión finita, si se dispone de una base, conocer un vector viene
a ser lo mismo que conocer sus coordenadas.
Ejemplo.
Dada la base S = {(2, 3), (5, 2)} para R2 y el vector v = (4, 1), el vector de coordenadas de
v respecto a la base S se obtiene de la siguiente manera:
Se obtienen los coeficientes de la única combinación lineal del vector v
c1 (2, 3) + c2 (5, 2) = (4, 1)
(2c1 , 3c1 ) + (5c2 + 2c2 ) = (4, 1)
(2c1 + 5c2 , 3c1 + 2c2 ) = (4, 1)
Gilberto Aguilar Miranda
5
4.4. VECTORES DE COORDENADAS
aplicando la definición de vectores en R2
2c1 + 5c2 = 4
3c1 + 2c2 = 1
la solución de este sistema de ecuaciones lineales es
c1 = −
3
11
c2 =
8
11
Entonces el vector de coordenadas es
−3/11
[v]S =
8/11
Para el vector w = (2, 4) se obtiene
c1 (2, 3) + c2 (5, 2) = (2, 4)
(2c1 + 5c2 , 3c1 + 2c2 ) = (2, 4)
aplicando la definición de vectores en R2
2c1 + 5c2 = 2
3c1 + 2c2 = 4
la solución de este sistema de ecuaciones lineales es
c1 = −
13
11
c2 =
8
11
Entonces el vector de coordenadas es
13/11
[w]S =
8/11
Para los vectores v y w y el escalar k se cumple
[v + w]S = [v]S + [w]S
[kv]S = k[v]S
ambas propiedades se pueden combinar para obtener
[k1 v1 + k2 v2 + · · · + kn vn ]S = k1 [v1 ]S + k2 [v2 ]S + · · · + kn [vn ]S
Gilberto Aguilar Miranda
6
(4.3)
UNIDAD 4. ESPACIOS VECTORIALES REALES
4.4.1
Cambio de base
Sea V un espacio vectorial de dimensión n. Hemos visto que cualquier vector v queda determinado de manera única conociendo un sistema de coordenadas respecto de una base de
V . Ahora bien, si elegimos otra base de V , v tendrá otras coordenadas, distintas a las
anteriores. Como, a veces, hay que realizar cambios de base en los espacios vectoriales, nos
preguntamos:
¿Qué relación guardan las coordenadas del vector respecto de ambas bases?
Para determinar la relación, se utilizará un espacio vectorial de dimensión 2.
Si se tienen las bases S = {u1 , u2 } y T = {v1 , v2 } para R2 y el vector w. Si las
coordenadas del vector w respecto a la base S son (a1 , a2 ), el vector w ∈ R2 se puede
expresar como
w = a1 u1 + a2 u2
Los vectores de la base S se pueden escribir como combinaciones lineales de los vectores de
la base T, esto es:
u1 = b1 v1 + b2 v2
u2 = c1 v1 + c2 v2
o sea, las coordenadas de u1 respecto a la base T son (b1 , b2 ), y las coordenadas de u2 respecto
a la base T son (c1 , c2 ).
Si se sustituyen las expresiones para u1 y u2 como combinaciones lineales de v1 y v2 en
la ecuación w = a1 u1 + a2 u2 , se tiene
w = a1 u1 + a2 u2 = a1 (b1 v1 + b2 v2 ) + a2 (c1 v1 + c2 v2 )
= (a1 b1 + a2 c1 )v1 + (a1 b2 + a2 c2 )v2
donde se identifica que (a1 b1 + a2 c1 ) y (a1 b2 + a2 c2 ) son las coordenadas de w respecto a la
base T, y se puede escribir
a1 b 1 + a2 c 1
[w]T =
a1 b 2 + a2 c 2
a1 b 1
a2 c 1
b1
c
=
+
= a1
+ a2 1
a1 b 2
a2 c 2
b2
c2
b1 c 1
a1
=
b2 c 2
a2
las columnas de las matriz se identifican como los vectores de coordenadas de u1 , u2 respecto
a la base T, y el vector columna como el vector de coordenadas de w respecto a la base S,
por lo que
[w]T = [u1 ]T [u2 ]T [w]S
Gilberto Aguilar Miranda
7
4.4. VECTORES DE COORDENADAS
Para un un espacio vectorial V de dimensión n y las bases S = {u1 , u2 , · · · , un } y
T = {v1 , v2 , · · · , vn }, se generaliza a
(4.4)
[w]T = [u1 ]T [u2 ]T · · · [un ]T [w]S
A la matriz [u1 ]T [u2 ]T · · · [un ]T se le conoce como la matriz de transición o matriz
de cambio de base de la base S a la base T y se denota como PT ←S o algunas veces simplemente como P.
La relación entre las coordenadas de un vector respecto a dos bases se obtiene por medio de
una ecuación matricial
[w]T = PT ←S [w]S
Ejemplo. Encontrar la matriz de transición de la base S = {(2, 3), (1,
2)} a la base
−2
T = {(4, 1), (3, −1)}, luego usar esta matriz para determinar [w]T si [w]S =
5
Como se indica en la ecuación 4.4, la columnas de la matriz de transición corresponden
a los vectores de coordenadas de los vectores de la base origen (en este caso S ) respecto a la
base destino (T ). Se obtienen las coordenadas de los vectores de la base S
(2, 3) = b1 (4, 1) + b2 (3, −1)
(1, 2) = c1 (4, 1) + c2 (3, −1)
En forma matricial se escriben
2
4
3
4 3
b1
= b1
+ b2
=
3
1
−1
1 −1 b2
1
4
3
4 3
c1
= c1
+ c2
=
2
1
−1
1 −1 c2
Se tienen dos sistemas de ecuaciones lineales con la misma matriz de coeficientes, que
sabemos, tienen solución única y que se pueden resolver por Gauss-Jordan
4 3 2 1
1 0 11/7
1
'
1 −1 3 2
0 1 −10/7 −1
Las coordenadas para el vector (2,3) son ((11/7, −10/7), y para el vector (1,2) son (1,-1). La
matriz de transición es
11/7
1
−10/7 −1
El vector de coordenadas [w]T se calcula con
11/7
1
−2
13/7
=
−10/7 −1
5
−15/7
Hacer los siguientes ejercicios de la sección 6.7: 2, 3, 7, 8, 13, 21, 23.
Gilberto Aguilar Miranda
8
UNIDAD 4. ESPACIOS VECTORIALES REALES
4.5
Espacios con producto interno
Sea V un espacio vectorial real. Un producto interno en V es una función que asigna a
cada par ordenado de vectores u y v de V un número real, denotado por (u, v) que satisface
las propiedades:
1. (u, u) ≥ 0 y (u, u) = 0 si y solo si u = 0
2. (u, v) = (v, u)
3. (u + v, w) = (u, w) + (v, w)
4. (cu, v) = c(u, v))
p
La longitud de un vector se define como kuk = (u, u).
La distancia entre dos vectores se define como d(u, v) = ku − vk.
Dos vectores son ortogonales si su producto interno es cero, (u, v) = 0. Un conjunto de
vectores es ortogonal si cada par de vectores es ortogonal. Un conjunto ortogonal de vectores
es ortonormal si todos los vectores tienen longitud de uno.
El producto interno mas importante de Rn es el producto punto definido cuando se vio
el producto de matrices.
Si u = (u1 , u2 , · · · , un ) y v = (v1 , v2 , · · · , vn ) el producto interno estándar o canónico es
(u, v) = u · v = u1 v1 + u2 v2 + · · · + un vn
4.5.1
(4.5)
Proceso de Gram-Schmidt
Sea S = {u1 , u2 , u3 , · · · , un } una base para un espacio vectorial V, el proceso de
Gram-Schmidt permite obtener una base ortonormal T = {v1 , v2 , v3 , · · · , vn } para V a
partir de la base S.
El procedimiento para determinar la ecuación general que permite obtener una base ortogonal es el siguiente.
Se toman los vectores u1 y u2 , y se elige v1 = u1 . Estos dos vectores son una base para un
subespacio de V, ahora se busca un vector v2 en ese subespacio tal que sea ortogonal a v1 .
Entonces los vectores v1 y v2 son una base ortogonal para el subespacio.
Como v2 pertenece al subespacio, se puede expresar como una combinación de los vectores
u1 y u2
v2 = c1 v1 + c2 u2
Gilberto Aguilar Miranda
9
4.5. ESPACIOS CON PRODUCTO INTERNO
y como se requiere que sea ortogonal a v1
v1 · v2 = 0
si se sustituye la ecuación de v2 en el producto punto y se simplifica
v1 · (c1 v1 + c2 u2 ) = c1 (v1 · v1 ) + c2 (v1 · u2 ) = 0;
Se tiene una sola ecuación y dos valores a determinar, c1 y c2 , por lo que se puede elegir
arbitrariamente una de ellas, por conveniencia se elige c2 = 1, entonces se tiene que
c1 = −
Y el vector v2 es
u2 · v1
v1 · v 1
v2 = u2 −
u2 · v1
v 1 · v1
u2
Ahora se agrega el tercer vector, u3 , para tener la base {v1 , v2 , u3 } para otro subespacio
de V, y a partir de ella se obtiene una base ortogonal {v1 , v2 , v3 }. Para obtener el vector v3 se
sigue el mismo procedimiento que se utilizó anteriormente, donde v3 pertenece al subespacio
y es ortogonal a v1 y a v2 , por lo que:
v3 = c1 v1 + c2 v2 + c3 u3
v1 · v3 = 0
v2 · v3 = 0
al sustituir la combinación de v3 en las ecuaciones del producto punto se obtiene:
v1 · (c1 v1 + c2 v2 + c3 u3 ) = c1 (v1 · v1 ) + c2 (v1 · v2 ) + c3 (v1 · u3 )
= c1 (v1 · v1 ) + c3 (v1 · u3 ) = 0
v2 · (c1 v1 + c2 v2 + c3 u3 ) = c1 (v2 · v1 ) + c2 (v2 · v2 ) + c3 (v2 · u3 )
= c1 (v2 · v2 ) + c3 (v1 · u3 ) = 0
Si se elige arbitrariamente c3 = 1
v1 · u3
v1 · v 1
v2 · u3
c2 = −
v2 · v 2
c1 = −
Por lo que
v3 = u3 −
Gilberto Aguilar Miranda
v1 · u3
v1 · v1
10
v1 −
v2 · u3
v2 · v2
v2
UNIDAD 4. ESPACIOS VECTORIALES REALES
De manera similar, se determina el resto de los vectores de la base ortogonal. La ecuación
para la obtención de los vectores de la base ortogonal, se pueden escribir de la siguiente
manera:
vi = ui −
i−1 X
ui · vj
j=1
v j · vj
vj
Ver ejemplos 3 (pag. 354), 4 ( pag. 357) y 5 (pag. 357).
Hacer los siguientes ejercicios de la sección 6.7: 2, 3, 8, 19.
Gilberto Aguilar Miranda
11
(4.6)